电机系统建模与分析大作业
(完整word版)电力电子电路建模与分析大作业

西安理工大学研究生课程论文/研究报告课程名称:电力电子系统建模与分析任课教师:完成日期: 2016 年 7 月 5 日专业:电力电子与电力传动学号:姓名:同组成员:成绩:题目要求某用户需要一直流电源,要求:直流输出24V/200W,输出电压波动及纹波均<1%。
用户有220V交流电网(±10%波动变化)可供使用:(1) 设计电源主电路及其参数;(2) 建立电路数学模型,获得开关变换器传函模型;(3) 设计控制器参数,给出控制补偿器前和补偿后开环传递函数波特图,分析系统的动态和稳态性能;(4)根据设计的控制补偿器参数进行电路仿真,实现电源要求;(5) 讨论建模中忽略或近似因素对数学模型的影响,得出适应性结论(量化性结论:如具体开关频率、具体允许扰动幅值及频率等)。
主要工作本次设计主要负责电源主电路及其参数的的设计,以及建立电路数学模型并获得开关变换器传函模型这两部分内容,具体如下:(1) 本次设计电源主电路及其参数,采用从后向前的逆向设计思想。
首先根据系统输出要求,设计了后级DC/DC型Buck电路的参数。
接着设计了前级不控整流电路以及工频变压器的参数.考虑到主电路启动运行时的安全性,在主电路中加入了软启动电路;(2) 本次DC/DC变换器的建模并没有采用传统的状态空间平均方法,而是采用更为简单、直观的平均开关建模方法,建立了Buck变换器小信号交流模型.最后,推到出了开关变换器的传递函数模型,并给出了Buck电路闭环控制框图。
1 设计主电路及其参数1.1主电路设计根据题目要求,系统为单相交流220V/50Hz 输入,直流24V/200W 输出。
对于小功率单相交流输入的场合,由于二极管不控整流电路简单,可靠性高,产生的高次谐波较少,广泛应用于不间断电源(UPS )、开关电源等场合。
所以初步确定本系统主电路拓扑为:前级AC-DC 电路为电源经变压器降压后的二极管不控整流,后级DC —DC 电路为Buck 斩波电路,其中Buck 电路工作在电感电流连续模式(CCM),前后级之间通过直流母线和直流电容连接在一起。
matlab机电系统仿真大作业
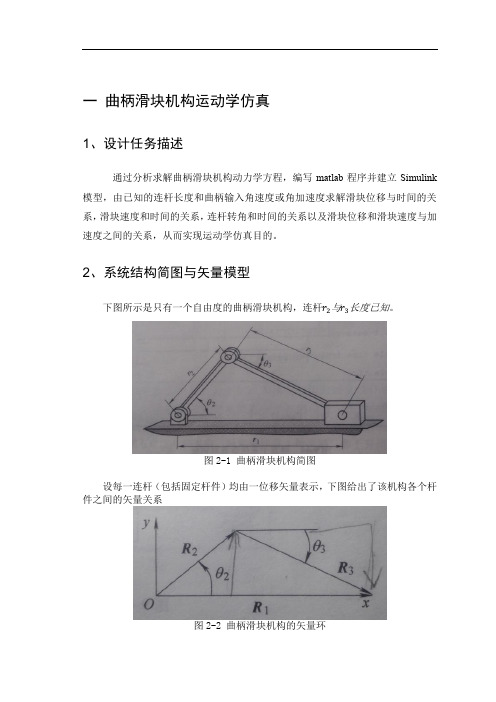
一曲柄滑块机构运动学仿真1、设计任务描述通过分析求解曲柄滑块机构动力学方程,编写matlab程序并建立Simulink 模型,由已知的连杆长度和曲柄输入角速度或角加速度求解滑块位移与时间的关系,滑块速度和时间的关系,连杆转角和时间的关系以及滑块位移和滑块速度与加速度之间的关系,从而实现运动学仿真目的。
2、系统结构简图与矢量模型下图所示是只有一个自由度的曲柄滑块机构,连杆r2与r3长度已知。
图2-1 曲柄滑块机构简图设每一连杆(包括固定杆件)均由一位移矢量表示,下图给出了该机构各个杆件之间的矢量关系图2-2 曲柄滑块机构的矢量环3.匀角速度输入时系统仿真3.1 系统动力学方程系统为匀角速度输入的时候,其输入为ω2=θ2,输出为ω3=θ3,θ3;v 1=r 1,r 1。
(1) 曲柄滑块机构闭环位移矢量方程为:R 2+R 3=R 1(2) 曲柄滑块机构的位置方程{r 2cos θ2+r 3cos θ3=r 1r 2sin θ2+r 3sin θ3=0(3) 曲柄滑块机构的运动学方程通过对位置方程进行求导,可得{−r 2ω2sin θ2−r 3ω3sin θ3=r 1r 2ω2cos θ2+r 3ω3cos θ3=0由于系统的输出是ω3与v 1,为了便于建立A*x=B 形式的矩阵,使x=[ω3v 1],将运动学方程两边进行整理,得到{v 1+r 3ω3sin θ3=−r 2ω2sin θ2−r 3ω3cos θ3=r 2ω2cos θ2将上述方程的v1与w3提取出来,即可建立运动学方程的矩阵形式(r 3sin θ31−r 3cos θ30)(ω3v 1)=(−r 2ω2sin θ2r 2ω2cos θ2) 3.2 M 函数编写与Simulink 仿真模型建立3.2.1 滑块速度与时间的变化情况以及滑块位移与时间的变化情况仿真的基本思路:已知输入w2与θ2,由运动学方程求出w3和v1,再通过积分,即可求出θ3与r1。
非线性大作业—直流电动机调速系统的建模与控制系统的设计

3、PBH秩判据
线性定常系统(1)为完全能控的充分必要条件是,对矩阵A的所有特征值 均成立, ( )或等价地表示为 , 也即(SI-A)和B是左互质的。
4、PBH特征向量判据
线性定常系统(1)为完全能控的充分必要条件是A不能有与B的所有列相正交的非零左特征向量。也即对A的任一特征值,使同时满足 , 的特征向量 。
所谓最优控制,就是根据建立的系统的数学模型,选择一个容许的控制规律,在一定的条件下,使得控制系统在完成所要求的控制任务时,使某一指定的性能指标达到最优值、极小值或极大值。本文利用线性二次型最优调节器(LQR)方法对移动高架吊车进行最优控制。控制目的是使移动高架吊车能在不平衡点达到平衡,并且能够经受一定的外加干扰[8]。
能控性的直观讨论:
从状态空间的角度进行讨论:输入和输出构成系统外部变量,状态为系统内部变量。能控性主要看其状态是否可由输入影响。每一个状态变量的运动都可由输入来影响和控制,由任意的始点到达原点,为能控,反之为不完全能控。具体来说就是指外加控制作用u(t) 对受控系统的状态变量x(t)和输出变量y(t)的支配能力,它回答了u(t)能否使x(t)和y(t)作任意转移的问题。
3.1.2能控性判据
我们利用线性系统的能控性判据来判断其能控性。
设线性定常系统状态方程为:
(1)
1、格拉姆矩阵判据
线性定常系统(1)为完全能控的充分必要条件是,存在时刻,使如下定义的格拉姆(Gram)矩阵 为非奇异。
其中,该判据的证明用到了范数理论中的矩阵范数,在此不再赘述。
2、秩判据
线性定常系统(1)为完全控的充分必要条件是 ,
2 直流电动机调速系统数学模型的建立
《机电系统建模与仿真》实验指导书(研究生)

《机电系统建模与仿真》实验指导书王红茹编写适用专业:机械工程________________________江苏科技大学机械工程学院2015年11月实验一:多闭环直流伺服系统仿真分析实验学时:2 实验类型:综合实验要求:必修 一、实验目的1. 掌握运用MATLAB/Simulink 进行多闭环伺服控制系统仿真分析的方法。
二、实验内容及原理主要针对工程领域常用的自动控制系统--双闭环控制系统进行建模与仿真实验,并对其原理进行详细介绍。
采用PI 控制器的转速负反馈单闭环调速系统能在系统稳定的前提下实现转速无静差,但不能满足调速系统对动态性能要求较高时的场合,且对扰动的抑制能力也较差。
双闭环调速系统是在单闭环调速的基础上,将转速和电流分开控制,分别设计转速、电流两个控制器,且转速控制器的输出作为电流控制器(内环)的给定输入,从而形成转速、电流双闭环控制。
这种双闭环调速系统是直流调速的一种典型形式。
以双闭环V-M 调速系统为例,介绍运用MATLAB/Simulink 进行双闭环控制系统动态分析的方法。
双闭环V-M 调速系统的结构如图1.1所示。
图中,直流电机参数:kW P nom 10=,V U nom 220=,A I nom 5.53=,min /1500r n nom =,电枢电阻Ω=31.0a R ,系统主电路总电阻Ω=4.0R ,电枢回路电磁时间常数s T a 0128.0=,机电时间常数s T m 042.0=;三相桥平均失控时间s T s 00167.0=,触发器放大系数30=s K ; 电流反馈系数A V K i /072.0=,电流环滤波时间常数s T oi 002.0=;转速反馈系数r V K t min/0067.0⋅=,转速环滤波时间常数s T on 01.0=。
①电流环、转速环选型原则。
电流环的重要作用是保持电枢电流在动态过程中不超过允许值,且突加控制作用时超调量越小越好。
电流环的控制对象是双惯性型的,两个惯性时间常数之比为1049.3002.000167.00128.0<=+=+oi s a T T T 。
机电一体化(机电一体化系统建模与分析)

(一)动态系统的经典数学模型及其分析
物理的动力学系统,动态过程;能量、信号的转换作用。 系统数学模型的建立方法:
1)分析法(解析法),得到解析模型(机理模型); 2)系统辨识。 系统的非线性、时变性的处理
用解析法建立系统微分方程、传递函数的一般步骤(经典模型)
➢分析系统工作原理和系统中变量的关系,确定系统的输入量与输 出量 ➢选择合适的中间变量,根据基本的物理定律,列写出系统中每一 个元件的输入与输出的微分方程式 ➢消去其余的中间变量,求得系统输出与输入的微分方程式 ➢对非线性项加以线性化 ➢或做拉普拉斯变换,变代数方程消元或用方框图等效、梅逊公式 等方法形成传递函数。
电气网络
(a)R-C电路1
(b)R-C电路2 R、C换位
(c)R-L-C电路
(d)R-C滤波网络
以(d)为例说明
I1sUr sR1Uc1s,I2sUc1sR2Ucs Uc1sI1sC1SI2s ,UcsC12SI2s
负载效应
机械网络 (机械振动基础)
单自由度系统
c
md2 dyt2 (t)cdyd(tt)ky(t)F(t)
状态变量的个数一般等于系统所包含的独立储能元件 的数目。一个n阶系统有n个独立的状态变量,为状态的最 大线性无关组,或称最小变量组。选择不唯一,一般取系统 中易于测量观测的量作状态变量。
前述的M-C-K系统的状态空间表达式即为: R-L-C系统的状态空间表达式即为:
状态空间表达式为现代控制理论的基本模型!同时也是动力学系 统研究的一种重要模型。 现代控制理论与经典控制理论特性的比较:
三自由度系统及其固有模态振型
连续体振动系统 均匀简支梁:
简支梁的前三阶主振型可形如下图所示:
电机控制大作业

目录一、仿真实验目的和要求 (3)二、仿真实验内容 (3)三、仿真步骤与结果分析 (4)1. 各个模块功能介绍 (4)(1)速度给定模块 (4)(2)转矩给定模块 (5)(3)速度控制模块 (7)(4)电流控制模块 (8)(5)PWM波生成模块 (11)(6)滤波模块 (13)(7)测量模块 (15)(8)直流电机模块 (16)2. 仿真结果分析 (19)(1)恒转速、恒转矩输入 (19)(2)恒转速、阶跃转矩输入 (20)(3)阶跃转速、恒转矩输入 (21)(4)阶跃转速、阶跃转矩 (22)(5)增大给定转速 (22)(6)减小给定转速 (23)(7)增大给定转矩 (23)(8)减小给定转矩 (24)3. 转速PI调节器参数对电机运行性能的影响 (25)(1)增大比例系数Kp (25)(2)减小比例系数Kp (25)(3)增大积分系数Ki (26)(4)减小积分系数Ki (27)4. 电流调节器改用PI调节器仿真 (27)5. 加入位置闭环控制 (31)6. 速度无超调 (34)四、实验心得、体会 (35)电机控制大作业:直流电机双闭环控制调速系统一、仿真实验目的和要求1.加深对直流电机双闭环PWM调速模型的理解2.学会利用MATLAB中的SIMULINK工具进行建模仿真3.掌握PI调节器的使用,分析其参数对电机运行性能的影响。
二、仿真实验内容图1 直流电机双闭环控制调速系统原理图实验电路图如上图所示,实验要求(*为必做实验):1.描述每个模块的功能(*)2.仿真结果分析:包括速度改变、转矩改变下的电机运行性能,并解释响应现象(*)3.转速PI调节器参数对电机运行性能的影响(*)4.电流调节器改用PI调节器(*)5.加入位置闭环6.速度无超调三、仿真步骤与结果分析1.各个模块功能介绍(1)速度给定模块图2 速度给定模块原理图速度给定模块通过一个单刀双掷开关控制,分为两种方式:一种为恒速度给定,一种为阶跃速度给定。
电机数学模型与仿真分析开卷试题

华中科技大学研究生课程考试答题本考生姓名考生学号系、年级类别考试科目考试日期年月日《电机数学模型与仿真分析》开卷试题试题:一台绕线型感应电动机,定转子均为三相对称绕组,不考虑开槽和谐波磁势的影响,不计磁路饱和,参考正向自行规定。
1.选择适当坐标系,使其各电感系数均为常数,写出相应定转子变换矩阵,并画出相应坐标系下的物理模型,写出在此坐标系下的电压、磁链基本方程式以及变换前后的电感系数表达式。
2.若采用x ad基值系统,利用此标幺值基本方程,画出相应的运算电路,并讨论其在瞬态和稳态分析中的应用。
3.利用适合的坐标系模型方程,求解感应电动机正常稳态运行时的电流、电磁转矩表达式、导出相应的等效电路,并与电机学的结果进行分析对比。
4.假设该电机在理想空载下(定子加额外对称电压、转差率为0、三相电流为0),电机端发生三相对称突然短路,选择适当坐标系下的模型,利用解析法导出并分析定子电流的变化规律(假设在此变化过程中转速不变)。
第一问解答一、在相坐标系统中的方程式 1. 正方向确定和简化假设本题规定线圈轴线的正向即使该磁场轴线的正方向,电流正方向为产生正向磁链的电流方向,回路两端的电压正方向符合电动机惯例。
则有:ψk =L k i k ,u k =p ψk +i k r k为了简化分析,本题做出如下假设:(1)电机铁磁部分的磁路为线性,即不计磁路饱和; (2)不考虑开槽和谐波磁势的影响; (3)定转子均为三相对称绕组。
2. 电压方程式和磁链方程式图1 感应电机设电机的定子三相绕组轴线为A 、B 、C ,则在空间上固定,以A 轴为参考坐标轴:转子绕组轴线a 、b 、c 随转旋转,转子a 轴和定子A 轴间的电角度θ为空间角位移变量。
(1)定子A 、B 、C 三相绕组的电压方程式可表示为:⎪⎩⎪⎨⎧+=+=+=C s C CB s B B A s A A ir p u i r p u i r p u ψψψ 转子a 、b 、c 三相绕组的电压方程式可表示为:⎪⎩⎪⎨⎧+=+=+=c r c cb r b b ar a a ir p u i r p u i r p u ψψψ (2)磁链方程为:⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡c b a C B A cc cbcacCcBcAbc bb ba bC bB bA ac ab aa aC aB aA Cc Cb Ca CC CB CA Bc Bb Ba BC BB BA Ac Ab Aa AC AB AAc b a C B A i i i i i i L M M M M M M L M M M M M M L M M M M M M L M M M M M M L M M M M M M L ψψψψψψ二、感应电机的自感系数与互感系数1. 定、转子绕组自感系数首先分析定子A相绕组的自感系数L AA。
机电系统分析大作业

一种主动智能矫形器的设计专业:机械工稈1309班学号:1049721302830老师:刘有源姓名:夏文文武汉理工大学2014年6月一种主动智能矫形器的设计摘要:本文旨在设计出一种智能矫形器。
首先,搭建整体的智能矫形器框架原理图,通过逐步分析各个模块来实现整体的设计。
接着,将对矫形器的设计思路与方法进行具体的说明,以此进行具体的机构设计,以及这样设计与现今流行的矫形器相比较有什么优点。
最后,论述了信息的控制机理和对控制系统的设计。
关键词:智能;设计思路;控制机理;控制系统1引言智能假肢是20世纪后10年发展起来的具有高性能的新一代假肢。
与普通假肢相比,其主要功能特点是能根据外界条件变化和工作要求,自动调整假肢系统的参数,使其工作可靠,运动自如,具有更好的仿生性。
本文主要研究下肢膝上假肢,膝关节是膝上假肢系统的核心部件,是保证截肢者能站立和行走的关键所在。
由于膝关节是人体最主要的承重关节,它负重多且运动量大,是下肢活动的枢纽。
随着对假肢性能要求的不断提高,下肢假肢不仅要满足能够站立和行走者两个基本功能,还要求步态自然,与健侧(健全下肢一侧)对称性好,能适应步行状态的变化。
例如步行速度变化,路况(坡道,楼梯)的变化等;此外还要在使用者可能被障碍物绊倒的紧急情况下的保证安全等。
这些功能是普通假肢无法实现的。
2智能矫形器整体框架的构建本文依据信息理论和智能控制理论,提出了人体和假肢结合的新型下肢假肢控制方案。
如图1所示,该方案由两个重要部分组成,一是控制机理的研究,主要实现生物信息到物理控制信息的转换,为假肢的控制提供依据。
二是假肢中的控制系统的研究,主要实现假肢的运动控制,将机器人设计(关节与灵巧机构)与控制技术(协调控制、姿态步态规划和伺服控制)移植到下肢假肢的研制上。
生物信恵反馈图1智能矫形器总体设计框架3矫形器的设计3.1矫形器的材料用于制作矫形器的材料包括金属、皮革、橡胶、纤维等五大类,每一类又可分为若干品种。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
不变
Ψf
Rq
Lq
B
J
增10%
减10%
增10%
减10%
增10%
减10%
增10%
减10%
增10%
减10%
iq上限
15.2
15.1
15.1
15.1
15.1
15.3
15.1
15.2
15.2
15.2
15.2
13.9
13.9
13.9
13.9
13.9
13.8
13.9
13.9
ω上限
(ωs=80)
87
88
86
87
88
87
87
87
88
88
87
ω下限
(ωs=80)
73
72
74
73
73
73
73
73
73
72
73
ω上限
(ωs=120)
123
123
122
123
123
123
123
122
124
123
123
ω下限
(ωs=120)
112
110
113
112
112
112
112
112
111
111
112
求解结果与原数据下计算结果相比,变化均小于2%,说明控制对参数不敏感,是robust的。
图3
下面详述其中“用四阶龙格库塔方法计算下一时刻的iq和ω的算法。
定义变量矩阵 ,根据(12)式和(13)式可得
其中 , 。
将所求区间[0,t]按步长h等分成n份,若已知ti时刻的xi,经图3所示方法判断Uq,可通过下面的方法计算ti+1时刻的xi+1。
五、
在Matlab环境下编写m文件实现上面的算法。
图9
3
将微分方程重写如下
从图5可以看到,当Ucd=200V,Ψf=1Wb,Rq=0.5Ω,Lq=0.05H,J=0.002kg/m3,B=0.1N/m时,iq的波动范围是13.9~15.2A,ω的波动范围是73~87rad/s(ωs=80rad/s),112~123(ωs=120rad/s)。
下面分别将Ψf,Rq,Lq,B,J增加或减少10%,计算并观察iq和ω的波动范围,结果如表1所示。
四
使用功率管实现滞环控制,当电流超过Ih或转速超过设定转速(ωs)+2rad/s时,断开功率管,电流通过续流二极管形成回路;当电流小于Il或转速低于设定转速-2rad/s时开通功率管,续流二极管截止。引入0,1变量flag1和flag2。
为了便于用四阶龙格-库塔方法求解上面的微分方程,将变量离散化,且全部采用国际单位制(SI)。算法思想如图3所示。
七
1
四阶龙格库塔法的精度是o(h5),取步长为0.005,此时计算结果(图6)与上面步长为0.00005已大不相同。
图6
2
定义flag=flag1*flag2,作出flag随时间的变化曲线如图7所示。
图7
图8
图8为图7的局部放大图,放大了功率管开关频率最快的时间段,此时fmax≈2kHz。功率管可以选用IRGI 4065(300V/28A),如图9所示,单只价格为¥2。
xlabel('t(s)');
ylabel('iq(A)/w(rad/s)');
axis([0 T -10 140]);
holdoff;
六
图4
仿真结果如图4所示,从图中可以看到,当设定速度为80rad/s时,转速在73~87rad/s间波动,当转速上升时,电枢电流容易达到上限值Ih,此时flag2关断功率管,电流在13.9~15.2A间波动(下面分析中的电流波动也是这种情况)。
二、作业要求
一台永磁直流电动机及其控制系统如图1所示。直流电源Udc=200V;电机永磁励磁f=1Wb,电枢绕组电阻Rq=0.5ohm、电感Lq=0.05H;转子转动惯量J=0.002kgm2;系统阻尼转矩系数B=0.1Nm/(rad/s),不带负载;用滞环控制的方法进行限流保护,电流上限Ih=15A、下限Il=14A;功率管均为理想开关器件;电机在t=0时刻开始运行,并给定阶跃(方波)转速命令,即,在0~0.2s是80rad/s,在0.2~0.4s是120rad/s,在0.4~0.6s是80rad/s如此反复,用滞环控制的方法进行转速调节(滞环宽度±2rad/s)。用四阶龙格-库塔求解电机的电流与转速响应。
x=[iq;w];
xx=x;
cnt=1;
%用龙格库塔方法计算程序自己编!!!
while(t<T)
% Do
% It
% Yourself
end
%绘图
figure;
plot(tt,xx(1,:),'-r');
holdon;
plot(tt,xx(2,:),'-b');
gridon;
title('iq和w随时间变化曲线');
本科上机大作业报告
课程名称:
电机系统建模与分析
姓名:
许*
学号:
3100******
学院:
电气工程学院
专业:
电气工程及其自动化
指导教师:
沈**
提交日期:
2013年4月5日
一、作业目的
1.熟悉永磁直流电动机及其调速系统的建模与仿真;
2.熟悉滞环控制的原理与实现方法;
3.熟悉Rungle-Kutta方法在仿真中的应用。
图1
三、模型的
参照一般化电机模型,本例永磁直流电动机可等效为图2的模型。Uq是加在电枢绕组两端的电压,永磁体看做开路的fd绕组。
图2
电气状态方程:
将(2)式和(3)式代入(1)式可得
其中,p是海氏算子。因为Lq是常数,故(4)式可写作
机械状态方程:
将(7)~(10)式代入(6)式,可得
将(5)式和(11)式整理得到
八、改进
1
将程序中Ih和Il分别设置为14.8和14.2,转速控制设置为ωs±1。计算结果如图10所示。
图10
电流波动在14.1~14.9之间,转速波动分别在75~86和115~122之间。经过调整,电流大小满足了设计要求,但是转速波动很大。此时功率管的开关频率为fmax=3.3kHz。
若转速控制设置为ωs±0,即不用滞环控制,则转速波动较小,如图11所示,此时fmax=3.3kHz。
代码如下:
T=1;%求解时间
h=0.00005;%步长
%变量定义
Ucd=200;
pf=1;
Rq=0.5;
Lq=0.05;
J=0.002;
Ih=15;
Il=14;
B=0.1;
w1=80;
w2=120;
A=[-Rq/Lq, -pf/Lq; pf/J, -B/J];
%设置初始值
t=0;
tt=t;
iq=0; w=0;
从图中还可以看到,存在电流为负的时刻,这是不符合实际的,因为二极管的单向导通性不允许电流反向。若计算得到的iq小于0,且功率管处于关断状态,可令iq=0,此时Uq为电机作发电机运行时的电势。即
图5
仿真结果如图5所示,改进的模型不再有iq<0的情况,原来iq<0时转速下降很快,图5显示实际情况转速下降的要慢一些。
