一次函数第3课时PPT课件
合集下载
人教版八年级数学课件《一次函数(第3课时)》

你能求出这条直线的解析式吗?
分析:直线y=-3x+2与y轴的交点为(0,2),于是得知该直线过
点(0,2),(2,-6),再用待定系数法求解即可.
答案:y=-4x+2 .
课堂检测
拓广探索题
已知一次函数y=kx+b(k≠0)的自变量的取值范围是- 3≤x≤ 6, 相应函数值的范围是- 5≤y≤ - 2 ,求这个函数的解析式.
分析:(1)当- 3≤x≤ 6时,- 5≤y≤ - 2,实质是给出
了两组自变量及对应的函数值; (2)由于不知道函数的增减性,此题需分两种情况讨论.
答案: y 1 x 4或y 1 x 3 .
3
3
课堂小结
用待定系数法 求一次函数的
解析式
1. 设所求的一次函数解析式
为y=kx+b;
2. 根据已知条件列出关于k,b
选取
画出
函数解析
满足条件的两定点
式y=kx+b 解出 (x1, y1)与(x2, y2 ) 选取
从形到数
一次函数的
图象直线l
数学的基本思想方法: 数形结合
探究新知 考点 1 已知两点利用待定系数法求一次函数的解析式 一次函数图象经过点(9,0)和点(24,20),写出函数解析式.
解:设这个一次函数的解析式为y=kx+b(k≠0).
解:设一次函数的解析式为y=kx+b(k≠0).
∵一次函数y=kx+b的图象过点(0,2),
∴b=2.
∵一次函数的图象与x轴的交点是( 2 ,0),则
1 2 2 2, 解得k=1或-1.
k
2
k
故此一次函数的解析式为y=x+2或y=-x+2.
分析:直线y=-3x+2与y轴的交点为(0,2),于是得知该直线过
点(0,2),(2,-6),再用待定系数法求解即可.
答案:y=-4x+2 .
课堂检测
拓广探索题
已知一次函数y=kx+b(k≠0)的自变量的取值范围是- 3≤x≤ 6, 相应函数值的范围是- 5≤y≤ - 2 ,求这个函数的解析式.
分析:(1)当- 3≤x≤ 6时,- 5≤y≤ - 2,实质是给出
了两组自变量及对应的函数值; (2)由于不知道函数的增减性,此题需分两种情况讨论.
答案: y 1 x 4或y 1 x 3 .
3
3
课堂小结
用待定系数法 求一次函数的
解析式
1. 设所求的一次函数解析式
为y=kx+b;
2. 根据已知条件列出关于k,b
选取
画出
函数解析
满足条件的两定点
式y=kx+b 解出 (x1, y1)与(x2, y2 ) 选取
从形到数
一次函数的
图象直线l
数学的基本思想方法: 数形结合
探究新知 考点 1 已知两点利用待定系数法求一次函数的解析式 一次函数图象经过点(9,0)和点(24,20),写出函数解析式.
解:设这个一次函数的解析式为y=kx+b(k≠0).
解:设一次函数的解析式为y=kx+b(k≠0).
∵一次函数y=kx+b的图象过点(0,2),
∴b=2.
∵一次函数的图象与x轴的交点是( 2 ,0),则
1 2 2 2, 解得k=1或-1.
k
2
k
故此一次函数的解析式为y=x+2或y=-x+2.
《一次函数》ppt完美课件3

x y=-x+1
的正、负对函数图象有 什么影响?
当k>0时,y随x的增
大而增大;当k<0时,y
随x的增大而减小.
y=-2x+1
《一次函数》完美实用课件3(PPT优 秀课件 )
《一次函数》完美实用课件3(PPT优 秀课件 )
五、回顾与反思
在本节课中,我们经历了怎样的过程?有怎 样的收获?
1.一次函数的图象与性质,常数k,b的意义 和作用.
《一次函数》完美实用课件3(PPT优 秀课件 )
3.备选题.
(1)将直线y=3x向下平移2个单位,得到直
线
.
(2)下列一次函数中,y随x的增大而减小的
是( )
A.y3x2 B.y 1 x 1 3
C.y3 3x D.y 31 x
《一次函数》完美实用课件3(PPT优 秀课件 )
《一次函数》完美实用课件3(PPT优 秀课件 )
第十九章 一次函数
19.2 一次 函数 19.2.2 一次函数(第二课时)
学习目标
1、正确理解一次函数的图象与k,b之间的关系。 2.体会研究函数的一般步骤与方法。
一、复习与反思
1.正比例函数的图象与性质.
一般地,正比例函数y=kx(k是常数,k≠0)的图象 是一条经过原点的直线,我们称它为直线y=kx.
《一次函数》完美实用课件3(PPT优 秀课件 )
三、巩固与应用
画出函数y=2x-1与y=-0.5x+1的图象.
x
01
y=2x-1 y
y=2x-1 -1 1
y=-0.5x+1 1 0.5
1
-1 O
-1
1
x
y=-0.5x+1
一次函数3修订版PPT课件

23:31
10
小 结
经过本节课的学习, 1、经过本节课的学习,你 你有哪些收获? 有哪些收获?
1。用待定系数法求函数解析式的一 2、本节课主要运用什么方 般步骤。
法来解决一些简单的实际 2。认识分段函数。 问题?
3。数形结合解决问题的一般思路。
23:31
11
布置作业
1.必做题: 教科书第35页习题第5,6题
2.选做题: 教科书第35页第10题.
23:31 12
谢 谢 大 家 谢谢大家
23:31
13
K=-2, b=3
23:31 3
整理归纳
从数到形
从形到数 数学的基本思想方法:数形结合
23:31
4
挑战自我
下图表示的函数是正比例函数吗? 是一次函数吗?你是怎样认为的?
y/千米 小明从家里出发去菜地浇水, 又去玉米地锄草,然后回家,其 中x表示时间,y表示小明离他家 的距离。
2
1.1
23:31
0
我们称此类函数为 分段函数.
23:31
100 0 5 10 15 x/分6
演练场:
基础知识巩固:
1.若一次函数y=3x-b的图象经过点P(1,-1), 则该函数图象必经过点( B )
A (-1,1) C (-2,2) B (2,2) D (2,一2)
2、若直线y=kx+b平行直线y=-3x+2,且与y轴交于 点(0,-5),则k= -3 ,b= -5 。
23:31
∴ 3k+b=5 解得 k=2 b=-1 -4k+b=-9 ∴这个一次函数的解析式为y=2x-1 象这样先设出函数解析式,再根据条件 确定解析式中未知的系数,从而具体写出 这个式子的方法,叫做待定系数法.
北师大版八年级上册数学《函数》一次函数3精品PPT教学课件
本节课你的收获?
1、函数的定义:
一般的,在某个变化过程中,有两个变量x和y,如果 给定一个x值,相应的就确定一个y值,那么我们称y是 x的函数(function),其中x是自变量, y是因变量。
2、函数的表示法:可以用三种方法
①图象法、
②列表法、
2020/11/23
③解析式法(关系式法) 16
感谢你的阅览
初一我们学习了《变量之间的关系》,在上述的问题 中有几个变量?用什么方法表示了它们的变化关系?
2020/11/23
5
做一做 问题二、瓶子或罐头盒等圆柱 形的物体,常常如图摆放。想一 想:
1、随着层数的增加,物 体的总数和如何变化的?
2、请填写下表:
层数n
1
2
物体总数y 1
3
2020/11/23
, 3、其中对于给定的每一个层数n
一般的,在某个变化过程中,有两个变量x和y,
如果给定一个x值,相应的就确定一个y值,那么
我们称y是x的函数(function),其中x是自变量,
y是因变量。
2020/11/23
8
问题一、下图反映了旋转时间t(分)与摩天轮上的一点的 高度h (米)之间的关系。
t/分 0 1 2 3 4 5
h/米 3 11 37 45 37 11
11
练一练
下面各题中分别有几个变量?你能将其中某个变量看成 是另一个变量的函数吗?
(1)每一个同学购一本代数书,书的单价为2元, 则x个同学共付y元。 y = 2x
(2)计划购买50元的乒乓球,则所购的总数y (个)
与单价x (元)的关系。
y
=
50
x
(3)一个铜球在0 ℃的体积为1000cm3,加热后温度每增 加1℃,体积增加0.051cm3,t℃时球的体积为Vcm3 。
第3课时一次函数的图像(课件)

图象与y轴的交点坐标是 (0,5) ,可以看作是由直线
y=-6x向 上 平移 5 个单位长度得到的;一次函数
y=-6x-5的图象与y轴的交点坐标是(0,-5) ,可以看作
是由直线y=-6x向
平移
下
5个单位长度得到的.
联系上面结果,你能总结出什么吗?
(1)一次函数的图象是一条直线;
(2)直线y=kx+b(k≠0)与直线y=kx(k≠0)互相平行;
为什么?
3.正比例函数图象的画法:因为两点确定一条直线,
所以可用两点法画正比例函数y=kx(k≠0)的图象.一
般地,过原点和点(1,k)(k是常数,k≠0)的直线,
即正比例函数y=kx(k≠0)的图象.
新知探究 跟踪训练
1. 正比例函数 y = (k−2)x 的图象如图所示,则 k 的取值
y
k−2<0
一次函数y=kx+b(k≠0)的图象可以由直线y=kx(k≠0)
沿 y 轴向上(b>0)或向下(b<0)平移 个单位长度
得到.
3.一次函数图象的画法
(1)两点法:因为两点确定一条直线,所以一般选取
直线y=kx+b(k,b是常数,k≠0)与两坐标轴的交点,
y
即(0,b)与(- ,0)画直线.
-3
-6
5
y=-6x-5
1
-2
-5
-8
-11
y=-6x+5
-1 O 1
仔细视察图中三个函数的
图象,看看你能发现什么?
y=-6x-5 y=-6x
-5
x
思考 根据图象的视察结果正确填写下列各空格.
(1)这三个函数的图象形状都是
y=-6x向 上 平移 5 个单位长度得到的;一次函数
y=-6x-5的图象与y轴的交点坐标是(0,-5) ,可以看作
是由直线y=-6x向
平移
下
5个单位长度得到的.
联系上面结果,你能总结出什么吗?
(1)一次函数的图象是一条直线;
(2)直线y=kx+b(k≠0)与直线y=kx(k≠0)互相平行;
为什么?
3.正比例函数图象的画法:因为两点确定一条直线,
所以可用两点法画正比例函数y=kx(k≠0)的图象.一
般地,过原点和点(1,k)(k是常数,k≠0)的直线,
即正比例函数y=kx(k≠0)的图象.
新知探究 跟踪训练
1. 正比例函数 y = (k−2)x 的图象如图所示,则 k 的取值
y
k−2<0
一次函数y=kx+b(k≠0)的图象可以由直线y=kx(k≠0)
沿 y 轴向上(b>0)或向下(b<0)平移 个单位长度
得到.
3.一次函数图象的画法
(1)两点法:因为两点确定一条直线,所以一般选取
直线y=kx+b(k,b是常数,k≠0)与两坐标轴的交点,
y
即(0,b)与(- ,0)画直线.
-3
-6
5
y=-6x-5
1
-2
-5
-8
-11
y=-6x+5
-1 O 1
仔细视察图中三个函数的
图象,看看你能发现什么?
y=-6x-5 y=-6x
-5
x
思考 根据图象的视察结果正确填写下列各空格.
(1)这三个函数的图象形状都是
一次函数(3)精选教学PPT课件

开心胸,便会云蒸霞蔚,快乐将永远伴随着你!
• 学习重点: 用待ห้องสมุดไป่ตู้系数法求一次函数解析式,初步了解分段函数.
问题1 前面,我们学习了一次函数及其图象和性 质,你能写出两个具体的一次函数解析式吗?如何画出 它们的图象?
y=3x-1 y=-2x+3
两点法——两点确定一条直线
思考: 反过来已知一个一次函数的图象经过两个具体的点, 你能求出它的解析式吗?
例1 已知一次函数的图象过点(3,5)与(-4, -9),求这个一次函数的解析式.
变式 已知 y是 x的一次函数,当 x=-1时 y=3,当 x =2 时 y=-3,求 y关于 x 的一次函数解析式.
归纳
函数解析式 y =kx+b
选取 解出
满足条件的两 定点(x1,y1) 与(x2,y2)
画出 选取
(2)写出付款金额 y(单位:元)与购买种子数量 x(单位:kg)之间的函数解析式,并画出函数图象.
思考1 一次购买1.5 kg 种子,需付款多少元? 思考2 一次购买3 kg 种子,需付款多少元?
课堂小结
(1)本节课,我们研究了什么,得到了哪些成果? (2)用待定系数法求一次函数解析式的解题步骤是
八年级 下册
19.2.2 一次函数(3)
课件说明
• 本课是在学习一次函数图象及其性质的基础上,学 习用待定系数法确定一次函数解析式的方法,并初 步学习分段函数.
课件说明
• 学习目标: 1.学会用待定系数法求一次函数解析式; 2.了解分段函数的表示及其图象;能初步应用一次 函数模型解决现实生活中的问题,体会一次函数 的应用价值.
我开始虚伪,听着谎言却装做一无所知;我学会窥探,四处打听如蛇之祟行,而十分看轻自己; 我的故事越编越好,好莱坞金牌编剧也没这般丰富多采,只为让他多留一分钟。
• 学习重点: 用待ห้องสมุดไป่ตู้系数法求一次函数解析式,初步了解分段函数.
问题1 前面,我们学习了一次函数及其图象和性 质,你能写出两个具体的一次函数解析式吗?如何画出 它们的图象?
y=3x-1 y=-2x+3
两点法——两点确定一条直线
思考: 反过来已知一个一次函数的图象经过两个具体的点, 你能求出它的解析式吗?
例1 已知一次函数的图象过点(3,5)与(-4, -9),求这个一次函数的解析式.
变式 已知 y是 x的一次函数,当 x=-1时 y=3,当 x =2 时 y=-3,求 y关于 x 的一次函数解析式.
归纳
函数解析式 y =kx+b
选取 解出
满足条件的两 定点(x1,y1) 与(x2,y2)
画出 选取
(2)写出付款金额 y(单位:元)与购买种子数量 x(单位:kg)之间的函数解析式,并画出函数图象.
思考1 一次购买1.5 kg 种子,需付款多少元? 思考2 一次购买3 kg 种子,需付款多少元?
课堂小结
(1)本节课,我们研究了什么,得到了哪些成果? (2)用待定系数法求一次函数解析式的解题步骤是
八年级 下册
19.2.2 一次函数(3)
课件说明
• 本课是在学习一次函数图象及其性质的基础上,学 习用待定系数法确定一次函数解析式的方法,并初 步学习分段函数.
课件说明
• 学习目标: 1.学会用待定系数法求一次函数解析式; 2.了解分段函数的表示及其图象;能初步应用一次 函数模型解决现实生活中的问题,体会一次函数 的应用价值.
我开始虚伪,听着谎言却装做一无所知;我学会窥探,四处打听如蛇之祟行,而十分看轻自己; 我的故事越编越好,好莱坞金牌编剧也没这般丰富多采,只为让他多留一分钟。
八年级数学上册教学课件《一次函数的应用(第3课时)》
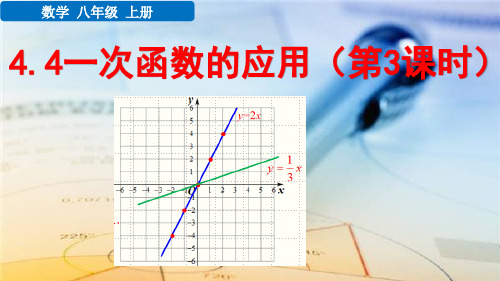
这里不能 出现k1,b 两个字母,
如果出现
就代错值.
O 1 23 4 5 6
x/ 吨
探究新知
(5)l1对应的函数表达式是 l2对应的函数表达式是
y/元
l1
6000
5000
4000
3000
2000
1000
O 1 23 4 5 6
4.4 一次函数的应用
y=1000x
,
y=500x+2000 .
l2
x/ 吨
探究新知
4.4 一次函数的应用
(6)l1与l2对应的两个一次函数y=k1x +b1与y=k2x+b2中,k1,k2
的实际意义各是什么?可疑船只A与快艇B的速度各是多少? 解: k1表示快艇B的速度,k2表示可疑船只A的速度.可疑船只A
的速度是0.2海里/分,快艇B的速度是0.5海里/分.
s /海里
s /海里
8
l2 A
6
l1 B
4
2
O 2 4 6 8 10 12 1415 t /分
探究新知
4.4 一次函数的应用
(4)如果一直追下去,那么B能否追上 A?
解:如图延伸l1 、l2 相交于点P. 因此,如果一直追下去,那么B一定能追上A.
s /海里
8 6 4
l2 A P l1 B
2
O 2 4 6 8 10 12 14 t /分
2000
1000
O 1 23 4 5 6
x/ 吨
探究新知
4.4 一次函数的应用
(2)当销售量为6吨时,销售收入= 6000 元,销售成本=5000元;
(3)当销售量为 4吨时,销售收入等于销售成本;
一次函数第三课时课件

∴
∴
∴这个函数的解析式为y=-2x+3
0+b 3
b3
2、某车油箱现有汽油50升,行驶时,油箱中的余油量y(升) 是行驶路程x(km)的一次函数,其图象如图所示;求y与x的 函数关系式,并写出自变量x的取值范围。
解:设函数解析式为y = kx+b, 因为:图象过点(60,30)和点(0,50), 所以:
∴这个函数的解析式为y = 2x-1
待定系数法
先设出函数解析式,再根据条件确定解析 式中未知的系数,从而具体写出这个式子 的方法,叫做待定系数法.
用待定系数法求一次函数解析式的步骤
①设出一次函数解析式y=kx+b; ②根据条件确定解析式中未知的系数k、b; ③将 k、b 代入 y=kx+b,得到所求函数解析式.
(1)一次函数y=kx+b的图象有怎样的特征? 复 一次函数y=kx+b的图象是一条直线,我们 习 称它为直线y=kx+b,它可以看作由直线y=kx平移
|b|个单位长度得到。 (2)一次函数解析式y=kx+b中的k、b的正负对函 数图象有什么影响? 当k>0时,直线y=kx+b从左到右上升,即y随x的 增大而 增大; 当k<0时,直线y=kx+b从左到右下降, 即y随x的增 大而减小 。 当b>0时,图形与y轴的交点在y轴的正半轴 当b=0时,图形与y轴的交点在原点 当b<0时,图形与y轴的交点在y轴的负半轴。
60k b
ห้องสมุดไป่ตู้解得
30 0 b 50
1 k 3
① ②
y/升 50
30
b 50
y与x的函数关系式为 0 1 y x 50 0 x 150 3
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解:(1)把点(1,2)和点(-1,6)代入
y=ax+b得:
2=a+ b 解得 6=-a+b
a=-2 b=4
∴一次函数的解析式:y=-2x+4
y 2x 4
(2)如图,直线y=-2x+4与y轴的交点A(0,4)与x轴的交点B(2,0) ∴OA=4,OB=2
∴S △AOB =
OA × OB=4
四、综合应用
3.一个函数的图象是经过原点的直线,并且这 条直线过第四象限及点(-2,-3a)与点(a,6) ,求这个函数的解析式.
4.小明将父母给的零用钱按每月相等的数额存
放在储蓄盒内,准备捐给希望工程,盒内钱数y(元
)与存钱月数x(月)之间的关系如图所示,根据下
图回答下列问题:
y
(1)求出y关于x的函
120
• 学习重点: 用待定系数法求一次函数解析式,初步了解分段函数.
问题1 前面,我们学习了一次函数及其图象和性 质,你能写出两个具体的一次函数解析式吗?如何画出 它们的图象?
y=3x-1 y=-2x+3
两点法——两点确定一条直线
思考: 反过来已知一个一次函数的图象经过两个具体的点, 你能求出它的解析式吗?
学习总结
经常不断地学习,你就什么都知道。你知道得越多,你就越有力量 Study Constantly, And You Will Know Everything. The More
You Know, The More Powerful You Will Be
结束语
当你尽了自己的最大努力时, 失败也是伟大的,所以不要放 弃,坚持就是正确的。
选取 解出
满足条件的两 定点(x1,y1) 与(x2,y2)
画出 选取
一次函数的 图象直线l
(待定系数法)
二、探求新知
例5 “黄金1号”玉米种子的价格为5元/kg. 如果一次购买2kg以上的种子,超过2kg部分的种子 价格打8折.
(1)填写下表.
购买量/kg 0.5 1 1.5 2 2.5 3 3.5 4 …
例1 已知一次函数的图象过点(3,5)与(-4, -9),求这个一次函数的解析式.
变式 已知 y是 x的一次函数,当 x=-1时 y=3,当 x =2 时 y=-3,求 y关于 x 的一次函数解析式.
二、提出问题,形成思路
求下图中直线的函数解析式.
y
解:设y=kx.
∵经过点(1,2),
2
1
∴ k=2.
(1)若直线y=ax+b过点(1,2)和(2,-1) ,求解析式
(2)y与x-1成正比例,当x=2,y=3 时,求解析式。(试说明思路)
(3)直线y=kx+b与y=3x平行,且过(1,2
),求解析式。(试说明思路)
一次函数y=ax+b经过点(1,2)、点(-1,6),求: (1)这个一次函数的解析式; (2)直线与两坐标轴围成的面积;
1.写出两个一次函数,使它们的图象都经过点 (-2,3).
2.生物学家研究表明,某种蛇的长度y(cm)是其 尾长x(cm)的一次函数,当蛇的尾长为6 cm时,蛇长 为45.5 cm;当尾长为14 cm时,蛇长为105.5 cm.当蛇 的尾长为10 cm时,这条蛇的长度是多少?
y=7.5x+0.5
75.5 cm
-2 -1 O 1 2 x
∴y=2x.
求下图中直线的函数解析式.
解:设y=kx+b.
y
ቤተ መጻሕፍቲ ባይዱ
∵经过点(3,0), (2,0),
3 2
∴ 2k+b=0,
1
b=3.
O 1 2 3x
k=-,
b=3.
∴y=-x+2.
反思小结:
确定正比例函数的解析式需要一个条件,确定 一次函数的解析式需要两个条件.
归纳
函数解析式 y =kx+b
八年级 下册
19.2.2 一次函数(3)
课件说明
• 本课是在学习一次函数图象及其性质的基础上,学 习用待定系数法确定一次函数解析式的方法,并初 步学习分段函数.
课件说明
• 学习目标: 1.学会用待定系数法求一次函数解析式; 2.了解分段函数的表示及其图象;能初步应用一次 函数模型解决现实生活中的问题,体会一次函数 的应用价值.
数解析式.
80
(2)根据关系式计算
,小明经过几个月才能存够
40
200元? y=20x+40
O 12 3 4 x
8个月
课堂小结
(1)本节课,我们研究了什么,得到了哪些成果? (2)用待定系数法求一次函数解析式的解题步骤是
什么? (3)我们是如何建立一次函数模型解决实际问题的? (4)书写分段函数的解析式时要注意什么?
When You Do Your Best, Failure Is Great, So Don'T Give Up, Stick To The End
演讲人:XXXXXX 时 间:XX年XX月XX日
/元
(2)写出购买量关于付款金额的函数解析式,并 画出函数图象.
解:设购买量为x千克,付款金额为y元.
当0≤x≤2时, y=5x;
当x>2时, ∴y=10+0.8 × 5(x-2)=4x+2.
思考1 一次购买1.5 kg 种子,需 付款多少元?
思考2 一次购买3 kg 种子,需付 款多少元?
(2)用待定系数法求函数解析式
付款金额 2.5 5 7.5 10 12.5 15 17.5 20 …
/元
购买例量/k5g 0“.5 黄1金1号1.5”玉2 米种2.5子的3 价格3.5为54元/kg…. 如果一次购买2kg以上的种子,超过2kg部分的种子 价付格款打金额8折2..5 5 7.5 10 12.5 15 17.5 20 …
