最新一年级数学(数阵图)
一年级奥数春季班-简单的数阵图
2
中 ，使 每 条 线 上 三 个 数 相 加 的和
dōuděngyú
都 等 于 12。
【例 5】(★★★★)
bǎ
zhèwǔgèshùfēnbiétiánrùxiàmiandekòng
把 3，4，5，6，7 这 五 个 数 分 别 填 入 下 面 的 空
gé lǐ shǐhéngxíng shùhángdesāngèshùxiāngjiādōu
格 里， 使 横 行 、 竖 行 的 三 个 数 相 加 都
dé
得 15。
【例 6】(★★★★★)
bǎ
zhè gèshùfēnbiétiánrùyòutúzhōng
把 1，2，3，4，5，6，7 这 7 个 数 分 别 填 入 右 图 中 ，
shǐdéměitiáozhíxiànshàngde gèshùdehéxiāngděng
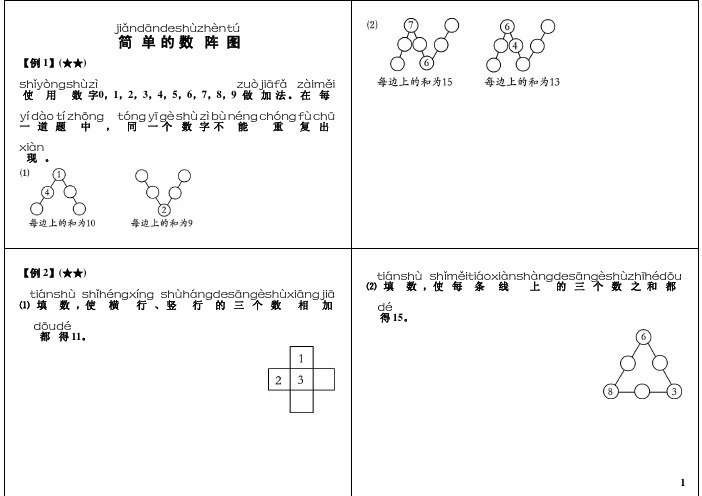
jiǎndāndeshùzhèntú 简 单的数 阵 图
【例 1】(★★)
shǐyòngshùzì
zuòjiāfǎ zàiměi
使 用 数 字0，1，2，3，4，5，6，7，8，9 做 加 法 。 在 每
yí dào tí zhōng tóng yī gè shù zì bù néng chóng fù chū
⑵ 填 数 ，使 每 条 线 上 的 三 个 数 之 和 都
dé
得 15。
1
【例 3】(★★★)
zàiměigèfānggézhōngtiánrùshìdàngdeshù shǐměiyī
在 每 个 方 格 中 填 入 适 当 的 数 ，使 每 一
héngxíng shùhángdehéyǐ jíliǎngxiéhángdesāngèshù横 行 、 竖 行 的源自和 以及 两 斜 行 的 三 个 数
一年级数学(数阵图)(推荐文档)
《数阵图》
第一类题：比较简单，已知两个数，求剩下的一个数，不需要试，直接就可以写出答案K填数，使横行、竖行的三个数相加都得11.
1L
22□
□
第二类题：需要找到突破口，即，找到已经有2个数字的某一行，某一列，或者是斜行
3.在每个方格中填入适当的数，使每一横行、竖行的和以及两斜行的三个数之和都是
18.
4、要使表格中每行、每列和两条对角线上的三个数的和都为彳8.下面每个方框里应填什么数？
7
E £6
8
‘册亏/的拱老血幻儿疋取匕第三类题：开放型，没有特定答案
5.在下面的O 中填上适当的数，使每条线上的三个数相加都等于15.
6.在下面的O 里填上适当的数，使每条线上的三个数之和都是12.
5, 6六个数，分别填入O 内，使每条线上3个数的和相等.
2＞把乙3, 4, 5, E 这五个数分别填入圆圈中，使每条线上三
个数相加的和 都等于1 2.
3.把1,乙3, 4* 5, 6 7这七个数分别填入O 里*使每条直线上的三个数
相加的和都为12-
头芬吨L /隔趨错隣F ：勺儿囂碧
荷
具务号/ JK 翔老师的儿童教肓
把 1, 2, 3, 4,。
最新一年级数学巧填数阵图
一年级数学巧填数阵图
1、一年级数学巧填数阵图11.
2、一年级数学巧填数阵图15.
3、在每个方格中填入适当的数，使每一横行、竖行的和以及两斜行的三个数
之和都是18.
4、要使表格中每行、每列和两条对角线上的三个数的和都为18，下面每个方框里应填什么数？
5、在下面的○中填上适当的数，使每条线上的三个数相加都等于15.
6、在下面的○里填上适当的数，使每条线上的三个数之和都是12.
提高篇
1、把1，2，3，4，5，6六个数，分别填入○内，使每条线上3个数的和相等.
2、把2，3，4，5，6这五个数分别填入圆圈中，使每条线上三个数相加的和
都等于1 2.
3、把1，2，3，4，5，6，7这七个数分别填入○里，使每条直线上的三个数
相加的和都为12.。
一年级-第六讲-简单数阵
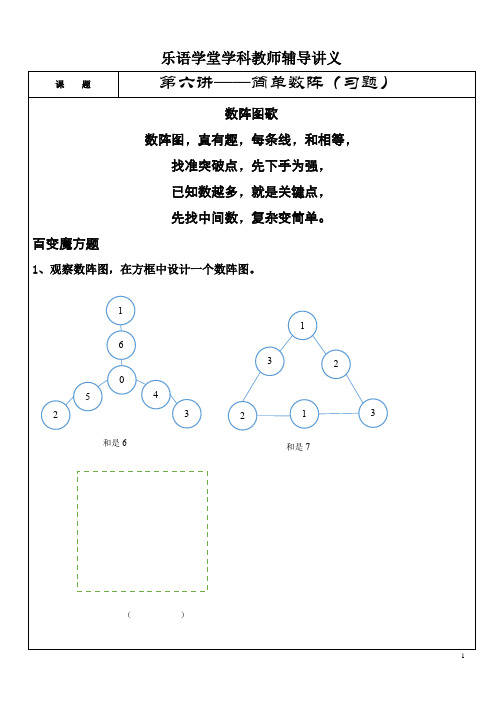
乐语学堂学科教师辅导讲义
数阵图歌
数阵图，真有趣，每条线，和相等，
找准突破点，先下手为强，
已知数越多，就是关键点，
先找中间数，复杂变简单。
百变魔方题
1、观察数阵图，在方框中设计一个数阵图。
1
6
5 2
4
3
1
3
2
2
3
1
和是6和是7
（）
2、在下面的数阵图中按要求填上合适的数。
3、把2、3、
4、5四个数填入下面四个空格里，使横行、竖行三个数相加的数都是8.
4、把2、4、6、8四个数填入右面四个圈里，使横行、竖行三个数相加的数都是11。
1
1
31
31
每条线上的数字和是8
5
2
4
2
1
3
1
5
2
4
每条线上的数字和是9
每条线上的数字和是10
5、把1、2、3、4、5填入下面数阵图的圈里。
6、在下面图中填数，使每条线上的三个数相加都得15.
7、在圈里贴星，使每条线上都有一个蓝色的、红色的和黄色的星星。
5
7 6
9
每条线上的数字和是8
每条线上的数字和是9
每条线上的数字和是10
1。
数阵图练习题
数阵图练习题数阵图（Number Grid）是一种用数字组成的图形，在数学教学中常用来培养学生的逻辑思维和解题能力。
下面是一些数阵图练习题，帮助你巩固自己的数学知识和解题技巧。
1. 数阵图中的数列在数阵图中，每个数字都和相邻的数字有一定的关系。
观察下面的数阵图，并找出横向和纵向的数列规律。
```1 2 3 4 56 7 8 9 1011 12 13 14 1516 17 18 19 2021 22 23 24 25```横向数列：1, 2, 3, 4, 5纵向数列：1, 6, 11, 16, 21根据观察，我们可以得出结论：横向数列的公差为1，纵向数列的公差为5。
2. 数阵图中的数学运算在数阵图中，数字之间的运算规律也是一种常见的题型。
观察下面的数阵图，并计算出横向和纵向数学运算的结果。
```1 4 9 16 252 6 12 20 303 8 15 24 354 10 18 28 405 12 21 32 45```横向数学运算：1^2, 2^2, 3^2, 4^2, 5^2 （平方）纵向数学运算：1^2, 2^2, 3^2, 4^2, 5^2 （平方）根据观察，我们可以得出结论：横向数学运算是计算每个数字的平方，纵向数学运算也是计算每个数字的平方。
3. 数阵图中的缺失数字在数阵图中，有时候会有一些数字缺失。
观察下面的数阵图，并找出其中的缺失数字。
```3 6 9 12 1518 ? 24 27 3033 36 39 42 4548 51 ? 57 6063 66 69 ? 75```根据观察，我们可以得出结论：缺失数字分别为21、54、72。
4. 数阵图中的数学规律在数阵图中，数字之间可能会存在一些数学规律。
观察下面的数阵图，并找出其中的数学规律。
```1 123 58 13 21 34 5589 144 233 377 610987 1597? 4181 6765 10946```根据观察，我们可以得出结论：这是一个斐波那契数列的数阵图。
数阵图(二)(含详细解析)
1. 了解数阵图的种类2. 学会一些解决数阵图的解题方法3. 能够解决和数论相关的数阵图问题.一、数阵图定义及分类：1. 定义：把一些数字按照一定的要求，排成各种各样的图形，这类问题叫数阵图.2. 数阵是一种由幻方演变而来的数字图.数阵图的种类繁多，这里只向大家介绍三种数阵图：即封闭型数阵图、辐射型数阵图和复合型数阵图.3.二、解题方法：解决数阵类问题可以采取从局部到整体再到局部的方法入手： 第一步：区分数阵图中的普通点(或方格)和关键点(或方格)；第二步：在数阵图的少数关键点(一般是交叉点)上设置未知数，计算这些关键点与相关点的数量关系，得到关键点上所填数的范围；第三步：运用已经得到的信息进行尝试．这个步骤并不是对所有数阵题都适用，很多数阵题更需要对数学方法的综合运用．复合型数阵图【例 1】 由数字1、2、3组成的不同的两位数共有9个，老师将这9个数写在一个九宫格上，让同学选数，每个同学可以从中选5个数来求和．小刚选的5个数的和是120，小明选的5个数的和是111．如果两人选的数中只有一个是相同的，那么这个数是_____________．313233212223131211【考点】复合型数阵图 【难度】3星 【题型】填空 【关键词】迎春杯，中年级，决赛，3题【分析】 这9个数的和：111213212223313233++++++++10203031233198=++⨯+++⨯=（）（）例题精讲知识点拨教学目标5-1-3-2.数阵图由小刚和小明选的数中只有一个是相同的，可知他们正好把这9个数全部都取到了，且有一个数取了两遍．所以他们取的数的总和比这9个数的和多出来的部分就是所求的数．那么，这个数是12011119833+-=．【答案】33【例 2】 如图1，圆圈内分别填有1，2，……，7这7个数。
如果6个三角形的顶点处圆圈内的数字的和是64，那么，中间圆圈内填入的数是 。
【考点】复合型数阵图 【难度】3星 【题型】填空 【关键词】希望杯，五年级，复赛，第5题，5分【解析】 2 【答案】2【例 3】 如下图（1）所示，在每个小圆圈内填上一个数，使得每一条直线上的三个数的和都等于大圆圈上三个数的和.（1）17894【考点】复合型数阵图 【难度】3星 【题型】填空 【解析】 为叙述方便，先在每个圆圈内标上字母，如图（2），（2）a cb49817则有a+4+9=a+b+c （1）b+8+9=a+b+c （2）c+17+9=a+b+c （3）（1）+（2）+（3）：（a+b+c ）+56=3（a+b+c ），a+b+c=28，则 a=28－（4+9）=15，b=28－（8+9）=11，c=28-（17+9）=2解：见图.1789411215【答案】17 89411215【例 4】请你将数字1、2、3、4、5、6、7填在下面图（1）所示的圆圈内，使得每个圆圈上的三个数之和与每条直线上的三个数之和相等.应怎样填？【考点】复合型数阵图【难度】3星【题型】填空【解析】为了叙述方便，将各圆圈内先填上字母，如图（2）所示.设A+B+C=A+F+G=A+D+E=B+D+F=C+E+G=k （A+B+C）+（A+F+G）+（A+D+E）+（B+D+F）+（C+E+G）=5k，3A+2B+2C+2D+2E+2F+2G=5k，2（A+B+C+D+E+F+G）+A=5k，2（1+2+3+4+5+6+7）+A=5k，56+A=5k.，因为56+A为5的倍数，得A=4，进而推出k=12，因为在1、2、3、5、6、7中，1+5+6=7+3+2=12，不妨设B=1，F=5，D=6，则C=12-（4+1）=7，G=12-（4+5）=3，E=12-（4+6）=2.，解：得到一个基本解为：（见图）7654321【答案】7654321【例 5】在左下图的每个圆圈中填上一个数，各数互不相等，每个圆圈有3个相邻(即有线段相连的圆圈)的圆圈。
数阵
数阵图(一)在神奇的数学王国中，有一类非常有趣的数学问题，它变化多端，引人入胜，奇妙无穷。
它就是数阵，一座真正的数字迷宫，它对喜欢探究数字规律的人有着极大的吸引力，以至有些人留连其中，用毕生的精力来研究它的变化，就连大数学家欧拉对它都有着浓厚的兴趣。
那么，到底什么是数阵呢？我们先观察下面两个图：左上图中有3个大圆，每个圆周上都有四个数字，有意思的是，每个圆周上的四个数字之和都等于13。
右上图就更有意思了，1～9九个数字被排成三行三列，每行的三个数字之和与每列的三个数字之和，以及每条对角线上的三个数字之和都等于15，不信你就算算。
上面两个图就是数阵图。
准确地说，数阵图是将一些数按照一定要求排列而成的某种图形，有时简称数阵。
要排出这样巧妙的数阵图，可不是一件容易的事情。
我们还是先从几个简单的例子开始。
例1把1～5这五个数分别填在左下图中的方格中，使得横行三数之和与竖列三数之和都等于9。
同学们可能会觉得这道题太容易了，七拼八凑就写出了右上图的答案，可是却搞不清其中的道理。
下面我们就一起来分析其中的道理，只有弄懂其中的道理，才可能解出复杂巧妙的数阵问题。
分析与解：中间方格中的数很特殊，横行的三个数有它，竖列的三个数也有它，我们把它叫做“重叠数”。
也就是说，横行的三个数之和加上竖列的三个数之和，只有重叠数被加了两次，即重叠了一次，其余各数均被加了一次。
因为横行的三个数之和与竖列的三个数之和都等于9，所以(1+2+3+4+5)+重叠数=9+9，重叠数=(9+9)-(1+2+3+4+5)=3。
重叠数求出来了，其余各数就好填了(见右上图)。
例2把1～5这五个数填入下页左上图中的○里(已填入5)，使两条直线上的三个数之和相等。
分析与解：与例1不同之处是已知“重叠数”为5，而不知道两条直线上的三个数之和都等于什么数。
所以，必须先求出这个“和”。
根据例1的分析知，两条直线上的三个数相加，只有重叠数被加了两遍，其余各数均被加了一遍，所以两条直线上的三个数之和都等于[(1+2+3+4+5)+5]÷2=10。
(完整)一年级数学巧填数阵图
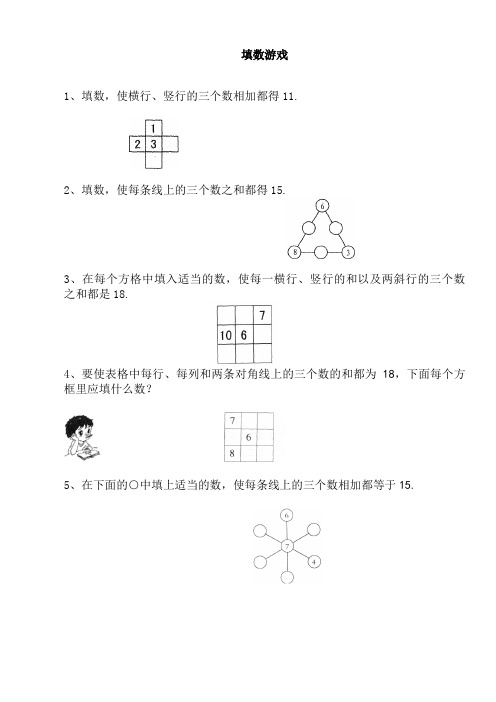
填数游戏
1、填数，使横行、竖行的三个数相加都得11.
2、填数，使每条线上的三个数之和都得15.
3、在每个方格中填入适当的数，使每一横行、竖行的和以及两斜行的三个数之和都是18.
4、要使表格中每行、每列和两条对角线上的三个数的和都为18，下面每个方框里应填什么数？
5、在下面的○中填上适当的数，使每条线上的三个数相加都等于15.
6、在下面的○里填上适当的数，使每条线上的三个数之和都是12.
提高篇
1、把1，2，3，4，5，6六个数，分别填入○内，使每条线上3个数的和相等.
2、把2，3，4，5，6这五个数分别填入圆圈中，使每条线上三个数相加的和都等于1 2.
3、把1，2，3，4，5，6，7这七个数分别填入○里，使每条直线上的三个数相加的和都为12.。
人教版数学思维之数阵图(一)
数阵图(一)
1. 将1~6分别填在图中,使每条边上的三个○内的数的和相等.
2. 把1~8.
3. 把1~9.
4. 把1~10填入图中,使五条边上三个○内的数的和相等.
5. 将1~8个数分别填入图中,使每个圆圈上五个数和分别为20,21,22.
6. 把1~7填入下图中.
7. 把1~16填入下图中,使每条边上4个数的和相等,两个八边形上8个数的和也相等.
8. 把4~9填入下图中,使每条线上三个数的和相等,都是18.
9. 把1~8这8个数填入下图,使每边上的加、减、乘、除成立.
10. 把0~9填入10个小三角形中,使每4个小三角形组成的大三角形的和相等.
11. 把1~11填入图中,使每条线上三个数的和相等.
12. 把1~8,填入图中,使每条线及正方形四个顶点上的数的和相等.
13. 把1~9,填入下图中,使每条线段三个数和及四个顶点的和也相等.
14. 把17,23,25,31,46,53,58,66,72,88,94,100十二个数填入下图,使任意三个相邻的数相加的和除以7的余数相等.。
小学数学数阵图
解题过程
边和X3 = a+b+c+d+e+f+g+2c 14X3 = 1+2+3+4+5+6+7+2c 42 = 28+2c 14 = 2c c= 7
2020/12/9
例1 （★★）
将1~7这七 个数字， 分别填入 2 图中各个 ○内，使 每条线段 上的三个 ○内数的 和都等于 14。
1
6
7
5
4
3
先填入边和，直线上微调，满足圆圈。
【超常大挑战】(★★★★★)
a ,b ,c ,d ,e, f, g ,h ,I ,处分别填入1至9， 如果每个圆环所填的数的和都相等， 那么这个相等的和最大是多少？最少是多少？
a+e+i+c+g+2(b+d+f+h)=和×5 45+b+d+f+h=和×5 b+d+f+h最大时为6,7,8,9 此时和为15 b+d+f+h最小时为1,2,3,4 和为11 当和为15时无解，和为14有解 最大为14，最小为11
行 业 PPT模 板 ： /hangye/ PPT素 材 下 载 ： /sucai/ PPT图 表 下 载 ： /tubiao/ PPT教 程 ： /powerpoint/ Excel教 程 ： /excel/ PPT课 件 下 载 ： /kejian/ 试 卷 下 载 ： /shiti/
圈和X2=数字和+a+b 圈和X2=36+a+b 圈和等于21 a+b=6 则a 和b有两种可能1,5和2,4
一年级数学 简单数阵
例3、玩一玩使每条线上三个数相加等于图中间的数。
请至少填三种答案。
1、请把2~8七个数字填入圆中，使四边形顶点上的四个数相加和相等。（填两种）
2、请把数字1~7用三种不同的方式填入下图，要求每条线上的和相等。
A：请把1 , 2 , 3 , 4 , 5填入下面数阵图的圆圈里。
和是8 和是9 和是10
B：请在圆圈里涂色，使每条线上都有一个蓝色的、红色的和黄色的圆片。
1、请在下面的数阵图中按要求填上合适的数。
和是8 和是9 和是10
2、 请在下列图中填数，使每条线上的三个数相加都得15.
3、请把2 ,4 ,6 ,8四个数填入四个圆圈里，使横行竖行三个数相加的得数是9.
简单数阵
10+0= 3+13= 2+14= 1+18= 16+2= 11+2= 3+10= 17+2= 10+4= 13+1= 8+12= 17+3= 0+17= 2+16= 12+8=
在下列表的空格里填上合适的数，使每横行、
竖行的三个数相加等于10.
例1、认识简单“数阵图”。
（1） （2）
每行每列三个数的和都是（ ） 每行每列三个数的和都是（ ）
一年级奥数数阵图
第十二讲 xx数阵图数学乐园晶晶和莹莹来到了雪精灵国，天空中到处飘着洁白剔透的雪花，就像下面图中的样子.一个雪精灵告诉她们：“你们只要能够把1～7这七个数填在雪花的七个花瓣上，使每三个位于同一直线上的花瓣上的数之和都相等，你们就能见到雪精灵国的女王了.”你能帮她们填一填吗?.小朋友们，你喜欢这样的填数字游戏吗？要想准确的填出图中的每一个数，可不是一件容易的事，这就要我们小朋友们认真去观察图，观察数字的排列规律，这样才能找到填图的方法.下面我们就一起来学习吧！基础篇使用数字0，1，2，3，4，5，6，7，8，9做加法.在每一道题中，同一个数字不能重复出现.拓展练习(1)填数，使横行、竖行的三个数相加都得11. (2)填数，使每条线上的三个数之和都得15.在每个方格中填入适当的数，使每一横行、竖行的和以及两斜行的三个数之和都是18.要使表格中每行、每列和两条对角线上的三个数的和都为18，下面每个方框里应填什么数？拓展练习在下列两图的空格中填上数，使横行和竖行或每条对角线上的三个数相加都等于15.把1，2，3，4，5，6六个数，分别填入○内，使每条线上3个数的和相等.提高篇把3，4，5，6，7这五个数分别填入下面的空格里，使横行、竖行的三个数相加都得15.拓展练习把2，3，4，5，6这五个数分别填入圆圈中，使每条线上三个数相加的和都等于1 2.把1，2，3，4，5，7分别填入○里，使每一个大椭圆上的四个数之和等于13.把1，2，3，4，5，6，7这七个数分别填入○里，使每条直线上的三个数相加的和都为12.拓展练习把1～9这九个数字填入下列圆圈内，使每条横线、竖线、斜线连接起来的三个圆圈内的数之和都等于15.把2，3，4，5，6，7，8这七个数分别填入圆圈中，使两个正方形中四个数之和相等19.拓展：如果使两个正方形中四个数之和相等21，又应该怎样填？我会做一做把1，2，3，4，5，6，7这7个数分别填入右图中，使得每条直线上的3个数的和相等.练习十二1. 在下面的○里填上适当的数，使每条线上的三个数之和都是12.2.把3～8这6个数，填在下图中使得每行、每列和两条对角线上的三个数的和都为18.3. 把1，2，3，4，5这五个数分别填入下面的○里，使横行、竖行的三个数相加都得10.4. 把3，4，5，7，9，11，13这七个数分别填入○里，使每条直线上的三个数相加的和都为20.5. 将1，2，3，4，5，6这6个数分别填入下图中，使两个大圆xx4个数的和都等于14.6.把数字1，2，3，5，6，7，9填在下面的○里，使每边上的和为15.小朋友，你在少年宫里走过“勇敢者的道路”吗？道路崎岖，充满艰难险阻.但是，它能培养小朋友的勇敢精神和不怕困难的毅力.这里有两幅图，也叫“勇敢者的道路”.图中的道路狭窄、曲折，不易通过，需要小朋友细心和有耐心.现在请小朋友用一枝铅笔，按照图中箭头的方向画出通行路线，而且线条不能碰到两边的“围墙”.小朋友，这可真不容易哦！。