高等数学讲义课件 第3节 泰勒公式
合集下载
第三节泰勒公式39页PPT

Q
(n n
1
)
(
)
f (n1) ( )
(n 1) !
(在x0与x之间 )
Pn(n1)(x)0,Rn(n1)(x) f(n1)(x)
Rn(x)f(n(n 1)1()!)(xx0)n1
Qn(n1)(x)(n1)!
(在x0与x之间 )
证毕!
上页 下页 返回 结束
p8(x)比 p2(x)在更大的范围内更接近余弦函数.
上页 下页 返回 结束
(1) 若f(x)在x0连续 , 则有 xl im x0 f(x)f(x0) 由极限和无穷小量间的关系
f(x)f(x0)
f(x)f(x0)
用常数代替函 数误差太大
(2) 若f(x)在x0可导 , 由微分有
f(x 0 x ) f(x 0 ) f(x 0 ) x
余项 公式
Rn(x)f(n (n 1)1())!(xx0)n1
① 称为 f ( x)的 n 阶泰勒公式
②
(
.
在
x
0与x
之间)
公式 ② 称为n 阶泰勒公式的拉格朗日余项 .
证明: Pn(x) R n(x)f(x)P n(x)
上页 下页 返回 结束
余其项中f ( :x R ) n (x Pf n)(( xx ) 0 f() n ( n 1f )1( )( x )!0 () x x f x( (0x n )n 0 )n) ( !1 x0f)②(2((x !x0 )(x 在x0)xn x0与0)R2 xn之(x间①) )
f(x)coxs
p1(x)
y1
y=1
令:p8(0)f(0),求出a0 1
p8 (0)f(0) a1 0
泰勒公式课件98855

(nR n(1n)) (2n()nRn(xn0)()x00)
Rn(n1)( )
(n 1) !
(在 x0与 x n之)间 ,
即
(R xnR(xnx)(0x))nf(1(nn 1R1 )(()n(nn!)1(1)x() !)x0)n1.
例1 求函f(数 x)1按 (x1)的幂展开 x
拉格日型n余 阶项 泰的 勒.公式 解 f(n)(x)(x1n)n1n!, f(n1)(x)(1)nxn 1 (n 21).!
f(nn)(!x0)(xx0)nRn(x),
其中 Rn(x)f((nn 11)()!)(xx0)n1(在 x0与 x之)间 .
带有拉格朗日型余项的n 阶泰勒公式
证 令 R n (x ) f(x ) p n (x )则,有
Rn(x0)Rn (x0) R n (n )(x 0)0 , 且 R n (n+ 1)(x)f(n+ 1)(x).( pn (n1)(x)0)
3) 已知项数 n 和误差限 , 确定公式中 x 的
适用范围.
例2 计算无理数 e 的近似值 , 使误差不超过 106.
解 在 e x 的麦克劳林公式 中令 x = 1 , 得
e 1 11 1e (0 1 ).
2! n ! (n 1 )! 由于 0ee3,欲使
Rn(1)
(n
3 1)
!106,
Rn(x)f((nn 11)()!)(xx0)n1 (在 x0与 x之)间 .
当 x 0 的 在某 f(n 1 ) 邻 (x ) M ( 域 常 )时 ,内 数 有 Rn(x)(nM 1)!xx0n1.
显 R n ( x ) 然 o ( x ( x 0 ) n )( x x 0 ).
2 泰勒公式的特例 (1) 当 n = 0 时, 泰勒公式变为拉格朗日中值定理
Rn(n1)( )
(n 1) !
(在 x0与 x n之)间 ,
即
(R xnR(xnx)(0x))nf(1(nn 1R1 )(()n(nn!)1(1)x() !)x0)n1.
例1 求函f(数 x)1按 (x1)的幂展开 x
拉格日型n余 阶项 泰的 勒.公式 解 f(n)(x)(x1n)n1n!, f(n1)(x)(1)nxn 1 (n 21).!
f(nn)(!x0)(xx0)nRn(x),
其中 Rn(x)f((nn 11)()!)(xx0)n1(在 x0与 x之)间 .
带有拉格朗日型余项的n 阶泰勒公式
证 令 R n (x ) f(x ) p n (x )则,有
Rn(x0)Rn (x0) R n (n )(x 0)0 , 且 R n (n+ 1)(x)f(n+ 1)(x).( pn (n1)(x)0)
3) 已知项数 n 和误差限 , 确定公式中 x 的
适用范围.
例2 计算无理数 e 的近似值 , 使误差不超过 106.
解 在 e x 的麦克劳林公式 中令 x = 1 , 得
e 1 11 1e (0 1 ).
2! n ! (n 1 )! 由于 0ee3,欲使
Rn(1)
(n
3 1)
!106,
Rn(x)f((nn 11)()!)(xx0)n1 (在 x0与 x之)间 .
当 x 0 的 在某 f(n 1 ) 邻 (x ) M ( 域 常 )时 ,内 数 有 Rn(x)(nM 1)!xx0n1.
显 R n ( x ) 然 o ( x ( x 0 ) n )( x x 0 ).
2 泰勒公式的特例 (1) 当 n = 0 时, 泰勒公式变为拉格朗日中值定理
高等数学 第三章 微分中值定理与导数的应用 第三节 泰勒公式

§3. 泰勒(Taylor)公式 一,问题的提出
1.设 f ( x ) 在 x0 处连续,则有
f ( x ) ≈ f ( x0 )
[ f ( x ) = f ( x0 ) + α ]
仅仅是无穷小
2.设 f ( x ) 在 x0 处可导,则有
f ( x ) ≈ f ( x 0 ) + f ′( x 0 )( x x 0 )
五,小结
1.Taylor 公式在近似计算中的应用;
y= x
y = sin x
五,小结
1.Taylor 公式在近似计算中的应用;
y= x
y = sin x
o
x y= x 3!
3
五,小结
1.Taylor 公式在近似计算中的应用;
y= x
y = sin x
o
x3 x5 y= x + 3! 5!
x3 y= x 3!
x
x2 x3 思 ∵ e x = 1 + x + + + o( x 3 ) 2! 3! 考 x3 题 sin x = x + o( x 3 ) 3!
解 e x sin x x (1 + x ) = 答 ∴ lim 3 x →0 x
x2 x3 x3 3 3 1 + x + + + o( x ) x + o( x ) x (1 + x ) 2! 3! 3! lim x →0 x3 x3 x3 + o( x 3 ) 1 = lim 2! 3! 3 = . x →0 x 3
y = 1+ x
o o
不足: 1,精确度不高; 2,误差不能估计. 问题: 寻找函数 P ( x ) ,使得 f ( x ) ≈ P ( x )
1.设 f ( x ) 在 x0 处连续,则有
f ( x ) ≈ f ( x0 )
[ f ( x ) = f ( x0 ) + α ]
仅仅是无穷小
2.设 f ( x ) 在 x0 处可导,则有
f ( x ) ≈ f ( x 0 ) + f ′( x 0 )( x x 0 )
五,小结
1.Taylor 公式在近似计算中的应用;
y= x
y = sin x
五,小结
1.Taylor 公式在近似计算中的应用;
y= x
y = sin x
o
x y= x 3!
3
五,小结
1.Taylor 公式在近似计算中的应用;
y= x
y = sin x
o
x3 x5 y= x + 3! 5!
x3 y= x 3!
x
x2 x3 思 ∵ e x = 1 + x + + + o( x 3 ) 2! 3! 考 x3 题 sin x = x + o( x 3 ) 3!
解 e x sin x x (1 + x ) = 答 ∴ lim 3 x →0 x
x2 x3 x3 3 3 1 + x + + + o( x ) x + o( x ) x (1 + x ) 2! 3! 3! lim x →0 x3 x3 x3 + o( x 3 ) 1 = lim 2! 3! 3 = . x →0 x 3
y = 1+ x
o o
不足: 1,精确度不高; 2,误差不能估计. 问题: 寻找函数 P ( x ) ,使得 f ( x ) ≈ P ( x )
高等数学课件3-3泰勒公式

n
n 1
Rn( 2 ) n( n 1)( 2 x0 )
( 2在x0与1之间)
如此下去,经过( n 1) 次后,得
Rn ( x ) ( x x0 )
n1
R
n 1!
( 在 x0与 n之间 ,也在 x 0 与 x 之间)
$3-3Taylor公式 9
( n1 ) n
$3-3Taylor公式 2
例如, 当 x 很小时, e 1 x , ln( 1 x ) x
x
ye
ye
x
x
y x
y ln(1 x )
y 1 x
o o
$3-3Taylor公式 3
不足: 1、精确度不高; 2、误差不能估计. 问题:
寻找函数 P ( x ) ,使得 f ( x ) P ( x ) ,
两函数 Rn ( x ) 及 ( x x 0 )
n1
在以 x 0 及 x 为
端点的区间上满足柯西中值定理的条件,得
Rn ( x ) ( x x0 )
n1
Rn ( x ) Rn ( x0 ) ( x x0 )
n1
0 ( 1 在 x 0 与 x 之间 )
R n ( 1 ) ( n 1 )( 1 x 0 )
f
(4)
(0) 0,
… ,
f
(n)
( 0 ) 依次取 0, ,, 1 . 1 0 -
若令n=2m,则
sin x x x
3
x
5
x
7
m 1 … ( 1)
x
2 m 1
3!
5!
7!
n 1
Rn( 2 ) n( n 1)( 2 x0 )
( 2在x0与1之间)
如此下去,经过( n 1) 次后,得
Rn ( x ) ( x x0 )
n1
R
n 1!
( 在 x0与 n之间 ,也在 x 0 与 x 之间)
$3-3Taylor公式 9
( n1 ) n
$3-3Taylor公式 2
例如, 当 x 很小时, e 1 x , ln( 1 x ) x
x
ye
ye
x
x
y x
y ln(1 x )
y 1 x
o o
$3-3Taylor公式 3
不足: 1、精确度不高; 2、误差不能估计. 问题:
寻找函数 P ( x ) ,使得 f ( x ) P ( x ) ,
两函数 Rn ( x ) 及 ( x x 0 )
n1
在以 x 0 及 x 为
端点的区间上满足柯西中值定理的条件,得
Rn ( x ) ( x x0 )
n1
Rn ( x ) Rn ( x0 ) ( x x0 )
n1
0 ( 1 在 x 0 与 x 之间 )
R n ( 1 ) ( n 1 )( 1 x 0 )
f
(4)
(0) 0,
… ,
f
(n)
( 0 ) 依次取 0, ,, 1 . 1 0 -
若令n=2m,则
sin x x x
3
x
5
x
7
m 1 … ( 1)
x
2 m 1
3!
5!
7!
高等数学方明亮32泰勒公式.ppt
上页
下页
返回
在泰勒公式中若取 x0 0 , x (0 1) , 则有
f (0) f (0)x f (0) x2 f (n) (0) xn
2!
n!
称为麦克劳林( Maclaurin )公式 .
由此得近似公式
若在f (fx公)(式x)成f(立xf0(的)0)区f间(fx上0()0()xfx(nx1)0f()2x()!0)fxM22(x!,0则) (x有误fx(0nn差))!(20估)计xn式
Rn (x)
f (n1) ( )
(n 1) !
(
x
x0
)n1
当在 x0 的某邻域内 f (n1) (x) M 时
Rn (x)
M (n 1)!
x
x0
n1
Rn (x) o((x x0 )n ) (x x0 )
2024年9月27日星期五
4
目录
上页
下页
返回
泰勒中值定理 :
阶的导数 , 则当
时, 有
2024年9月27日星期五
27
目录
上页
下页
返回
f (x0),
1 2!
f
( x0 ) ,
,
1 n!
f
(n) (x0 )
故
pn
(x)
f
( x0
)
f
(x0 1f
n!
)(x x0 ) (n) (x0 )(x
1
2! f x0 )n
(
x0
)(x
x0
)2
2024年9月27日星期五
2
目录
上页
下页
返回
2. 余项估计
令 Rn (x) f (x) pn (x)(称为余项) , 则有
D3_3泰勒公式(PPT)-文档资料

称为麦克劳林( Maclaurin )公式 . 例1. 求 y ln cos x 在 x 处的带有拉格朗日余项 的2阶 4 泰勒公式. 解: 要求到3阶导数
目录
上页
下页
返回
结束
1 2 f ln ln 2, 2 4 2
2
f x tan x f 1 4
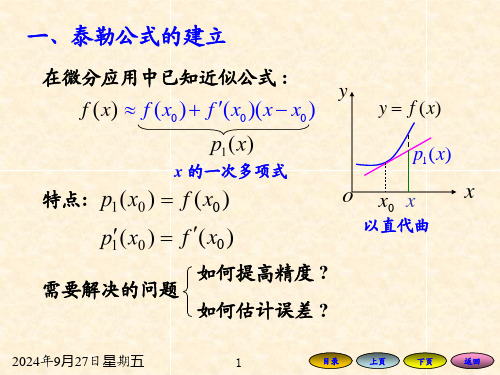
f ( x) f ( x0 ) f ( x0 )( x x0 )
x 的一次多项式
y
y f ( x)
p1 ( x)
特点:
f ( x0 ) f ( x0 )
O
x0 x
x
目录
上页
下页
返回
结束
为了提高精确度,我们考虑用n次多项式来近似 f ( x)
pn ( x) a0 a1 ( x x0 ) a2 ( x x0 ) 2 an ( x x0 ) n f x a0 f ( x0 ), 要求满足
3 5
f
(k )
f 0 1,
f 0 0, f 0 1,
π (0) sin k 2 4 f 0 0,
2 m 1 x x x sin x x (1) m1 R2m ( x) (2m 1) ! 3! 5!
f x sec x f 2, f x 2sec2 x tan x 4 2 1 ln cos x ln 2 x x 4 2 4 3 1 2 sec tan x 3 4
f ( x0 ) ( x x0 ) 2 f ( x0 ) f ( x0 )( x x0 ) 2! f (3) ( ) ( x x0 )3 3!
高等数学(第二版)上册课件:泰勒公式

分析
近 1.若在 x0点相交
似 程
Pn (x) f (x0)
度 越
2.若有相同的切线
来
越 好
Pn' (x) f ' (x0)
3.若弯曲方向相同
Pn'' (x) f '' (x0 )
y
y f (x)
0 x0
x
(1) 求 n 次近似多项式
Pn (x0) f (x0)
p'n (x0 )
f
' n
所以
f (x) 8 10(x 1) 9(x 1)2 6(x 1)3 (x 1)4
【例3.3.4】 求 f (x) ex2 的带有佩亚诺余项麦克劳林展开式
解
因为 ex 1 x x2 xn o(xn1)
2!
n!
用 x2代替公式中的 x,即得
ex2 1 x2 x4 x2n o(x2n2 )
2!
n!
【例3.3.1】 求 f (x) ex 的n阶麦克劳林展开式
解 由于 f ' (x) f ''(x) f (n) (x) ex,
所以 f '(0) f ''(0) f (n) (0) 1 ,
取拉格朗日余项,得麦克劳林展开式为
ex 1 x x2 xn e x xn1
则误差 R(x)= f (x) P(x)
设函数 f (x)在含有 x0 的开区间 (a, b) 内具有直到 (n+1) 阶导数,P(x) 为
多项式函数
pn(x)
a 1
(x
x0
)
a2
(x
x0
)2
an(x x0)n
考研高数总复习泰勒公式(讲义)PPT课件

即,泰勒公式是一阶微分近似式和拉氏公式的 推广
2.取 x0 0,
在0 与x 之间,令 x (0 1)
则余项
Rn ( x)
f (n1) (x) x n1
(n 1)!
Foil 10
麦克劳林(Maclaurin)公式
f ( x) f (0) f (0)x f (0) x 2 f (n) (0) x n
误差 Rn ( x) f ( x) P:
1.若在 x 0 点相交
近
似 程
Pn ( x0 ) f ( x0 )
度 越
2.若有相同的切线
来 越
Pn( x0 ) f ( x0 )
好 3.若弯曲方向相同
Pn( x0 ) f ( x0 )
y
o
皮亚诺形式的余项
f (x)
n k0
f
(k)( x0 )( x k!
x0 )k
o[( x
x0 )n ]
Foil 9
注意:
1. 当n 0 时,泰勒公式变成拉氏中值公式
f ( x) f ( x0 ) f ( )( x x0 )
(在x
与
0
x之
间)
当 n=1 时,略去余项,得到一阶微分近似式
f (x) f (x0 ) f '(x)(x x0 )
注 意 到 f ( x ) (n1) e x
代入公式,得
e x 1 x x 2 x n e x x n1 (0 1).
2!
n! (n 1)!
Foil 13
由公式可知
ex 1 x x2 xn
2!
n!
估计误差 (设 x 0)
Rn ( x)
ex x n1 (n 1)!
2.取 x0 0,
在0 与x 之间,令 x (0 1)
则余项
Rn ( x)
f (n1) (x) x n1
(n 1)!
Foil 10
麦克劳林(Maclaurin)公式
f ( x) f (0) f (0)x f (0) x 2 f (n) (0) x n
误差 Rn ( x) f ( x) P:
1.若在 x 0 点相交
近
似 程
Pn ( x0 ) f ( x0 )
度 越
2.若有相同的切线
来 越
Pn( x0 ) f ( x0 )
好 3.若弯曲方向相同
Pn( x0 ) f ( x0 )
y
o
皮亚诺形式的余项
f (x)
n k0
f
(k)( x0 )( x k!
x0 )k
o[( x
x0 )n ]
Foil 9
注意:
1. 当n 0 时,泰勒公式变成拉氏中值公式
f ( x) f ( x0 ) f ( )( x x0 )
(在x
与
0
x之
间)
当 n=1 时,略去余项,得到一阶微分近似式
f (x) f (x0 ) f '(x)(x x0 )
注 意 到 f ( x ) (n1) e x
代入公式,得
e x 1 x x 2 x n e x x n1 (0 1).
2!
n! (n 1)!
Foil 13
由公式可知
ex 1 x x2 xn
2!
n!
估计误差 (设 x 0)
Rn ( x)
ex x n1 (n 1)!
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
公式 ① 称为 的 n 阶泰勒公式 .
公式 ② 称为n 阶泰勒公式的拉格朗日余项 .
注意到 Rn (x) o[(x x0 )n ]
③
在不需要余项的精确表达式时 , 泰勒公式可写为
f (x)
f (x0 )
f (x0 )(x x0 )
f
( 2
x0 !
)
(
x
x0
)
2
f
(n) (x0 ) (x n!
在 x0 与x
之间)
误差
( 在 x0 与x 之间) d f
在泰勒公式中若取 x0 0 , x (0 1) ,则有
f (0) f (0)x f (0) x2 f (n)(0) xn
2!
n!
称为麦克劳林( Maclaurin )公式 .
由此得近似公式
f ( x) f (0) f (0)x f 若在f (公x) 式 成f (立x0的) 区f间(x上0 )(fx(nx10)
x0 )n
o[(x
x0 )n ]
④
公式 ③ 称为n 阶泰勒公式的佩亚诺(Peano) 余项 .
* 可以证明:
④ 式成立
f (பைடு நூலகம்)
f (x0 )
f (x0 )(x x0 )
f
( x0 2!
)
(x
x0
)2
特例:
f
(n) (x0 n!
)
(x
x0
)n
f (n1) ( )
(n 1) !
(
x
x0 )n1
第三节 泰勒 ( Taylor )公式
泰勒中值定理 :
阶的导数 , 则当
时, 有
f (x)
f (x0 )
f (x0 )(x x0 )
f
( x0 2!
)
(
x
x0
)2
f
(n) (x0 n!
)
(
x
x0
)
n
Rn
(
x)
①
其中 Rn (x)
f (n1) ( )
(n 1) !
(
x
x0
)n1
( 在 x0 与x 之间) ②
()2x(!0))fx22(Mx!0,则) (x有误fx(0nn差))!(2估0) 计xn式
f
(
n) (x0 ) (x n ! Rn( x)
x0
)(nnM f1()(nn!1x)1()n!)1((x在x0x)0n与1
x
之间)
( 在 x0
与x
之间)
(1) 当 n = 0 时, 泰勒公式变给为出拉格朗日中值定理
f (x) f (x0 ) f ( )(x x0 )
( 在 x0 与x 之间)
(2) 当 n = 1 时, 泰勒公式变为
可见
f
(x)
f
(x0 )
f
(x0 )(x x0 )
f
( )
2 (!
(x x0 )2
