1.3 空间几何体的表面积与体积导学案

合集下载

空间几何体的表面积与体积导学案高三数学一轮复习

第八章第二节空间几何体的表面积与体积一、学习目标【课标解读】了解球、棱柱、棱锥、台的表面积和体积的计算公式. 【衍生考点】1.空间几何体的表面积与侧面积2.空间几何体的体积3.与球有关的切、接问题二、相关知识回顾 1.多面体的表(侧)面积因为多面体的各个面都是平面,所以多面体的侧面积就是 ,表面积是侧面积与底面面积之和.【微点拨】当台体的上底面与下底面全等时,台体变为柱体;当台体上底面缩为一个点时,台体变为锥体.柱体、锥体、台体的体积公式间有如下联系:【微拓展】球的截面的性质 (1)球的截面是圆面;(2)球心和截面(不过球心)圆心的连线垂直于截面;(3)球心到截面的距离d 与球的半径R 及截面圆的半径r 的关系为【微思考】如何求不规则几何体的体积?【常用结论】1.与体积有关的几个结论(1)一个组合体的体积等于它的各部分体积的和或差. (2)底面面积及高都相等的两个同类几何体的体积相等. 2.长方体的外接球V 柱体=Sh V 台体=13(S'+ S 'S +S )hV 锥体=13Sh.r=√R 2-d 2.(1)球心:体对角线的交点. (2)半径:r=a 2+b 2+c 22(a ,b ,c 分别为长方体的长、宽、高).3.正四面体的外接球与内切球(正四面体可以看作是正方体的一部分)(1)外接球:球心是正四面体的中心;半径r= 64a (a 为正四面体的棱长). (2)内切球:球心是正四面体的中心;半径r= 612a (a 为正四面体的棱长).三、考点精讲精练考点一空间几何体的表面积与侧面积【典例突破】例1.(1)(2021四川成都三诊)某几何体的三视图如图所示,已知网格纸上的小正方形边长为1,则该几何体的表面积为( )A.(20+8 2)πB.(20+4 2)πC.(24+8 2)πD.(24+4 2)π(2)(2021河南安阳高三三模)为了给热爱朗读的师生提供一个安静独立的环境,某学校修建了若干“朗读亭”.如图所示,该朗读亭的外形是一个正六棱柱和正六棱锥的组合体,正六棱柱两条相对侧棱所在的轴截面为正方形,若正六棱锥与正六棱柱的侧面积之比为 7∶8,则正六棱锥与正六棱柱的高的比值为( ) A. 32 B.23C. 34D.12对点训练1(1)(2020全国Ⅱ,理10)已知△ABC 是面积为的等边三角形,且其顶点都在球O 的球面上.若球O的表面积为16π,则O 到平面ABC 的距离为(2)(2021陕西西安检测)下图网格纸中小正方形的边长为1,粗线画出的是一个几何体的三视图,则该几何体的表面积为( ) A.4 10π+4 29π+6πB.4 15π+4 29π+6πC.2 15π+2 29π+6πD.2 10π+2 29π+6π 考点二空间几何体的体积(多考向探究) 考向1.简单几何体的体积【典例突破】例2.(1)(2021北京,8)某一时间段内,从天空降落到地面上的雨水,未经蒸发、渗漏、流失而在水平面上积聚的深度,称为这个时段的降雨量(单位:mm).24 h 降雨量的等级划分如下:在综合实践活动中,某小组自制了一个底面直径为200 mm,高为300 mm 的圆锥形雨量器.若一次降雨过程中,该雨量器收集的24 h 的雨水高度是150 mm(如图所示),则这24 h 降雨量的等级是( )9 34A.小雨B.中雨C.大雨D.暴雨(2)(2021浙江杭州二模)某四棱锥的三视图(图中每个小方格的边长为1)如图所示,则该四棱锥的体积为( )A.4B.83C.43D.1考向2.不规则几何体的体积【典例突破】例3.(1)(2021河南开封模拟)《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有刍甍,下广三丈,袤四丈;上袤二丈,无广;高一丈,问:积几何?”其意思为:“今有底面为矩形的屋脊状的楔体,下底面宽3丈,长4丈;上棱长2丈,高一丈.问它的体积是多少?”已知1丈为10尺,现将该楔体的三视图给出如下图所示,其中网格纸上小正方形的边长为1丈,则该楔体的体积为( ) A.5 000立方尺 B.5 500立方尺 C.6 000立方尺 D.6 500立方尺(2)一个由半球和四棱锥组成的几何体,其三视图如下图所示.则该几何体的体积为( )A.13+2π3B.13+ 2π3C.13+2π6D.1+2π6对点训练2(1)(2021山东莱州高三检测)如图所示,半径为R 的半圆内(其中∠BAC=30°)的阴影部分以直径AB 所在直线为轴,旋转一周得到一个几何体,则该几何体的体积为 .(2)(2021福建龙岩高三模拟)某广场设置了一些多面体形或球形的石凳供市民休息.如图①的多面体石凳是由图②的正方体石块截去八个相同的四面体得到,且该石凳的体积是m m 3,则正方体石块的棱长为 .考点三与球有关的切、接问题(多考向探究) 考向1.几何体的外接球问题【典例突破】例4.(1)(2021广西玉林模拟)攒尖是古代中国建筑中屋顶的一种结构形式,宋代称为撮尖,清代称攒尖,依其平面有圆形攒尖、三角攒尖、四角攒尖、八角攒尖,也有单檐和重檐之分.多见于亭阁式建筑、园林建筑.某四角攒尖,它的主要部分轮廓可以近似看作一个正四棱锥,其三视图如图所示,则这个四棱锥外接球的表面积为( )(2)(2021甘肃兰州月考)已知四棱锥P-ABCD 的底面ABCD 是矩形,AD=1,AB=2,侧棱P A ⊥底面ABCD ,且直线PB 与CD 所成角的余弦值为 ,则四棱锥P-ABCD 的外接球的表面积为 .对点训练3(1)(2021四川成都二诊)已知圆柱的两个底面的圆周在体积为的球O 的球面上,则该圆柱的侧面积的最大值为( )160 0003 2 5532π3(2)(2021河北邯郸三模)在上、下底面均为正方形的四棱台ABCD-A1B1C1D1中,已知AA1=BB1=CC1=DD1=,AB=2,A1B1=1,则该四棱台的表面积为;该四棱台外接球的体积为.考向2.几何体的内切球问题【典例突破】例5.(1)(2021四川成都石室中学高三)《九章算术》中将四个面都为直角三角形的三棱锥称之为鳖臑,若三棱锥P-ABC 为鳖臑,P A⊥平面ABC, P A=BC=4,AB=3,AB⊥BC,若三棱锥P-ABC有一个内切球O,则球O的体积为()A.9π2B.9π4C.9π16D.9π(2)(2021山东潍坊三模改编)圆锥的内切球(与圆锥的底面及侧面都相切的球)的表面积与该圆锥的表面积之比的最大值为.对点训练4(1)(2021广西桂林、崇左二模)有一底面半径与高的比值为12的圆柱,则该圆柱的表面积与其内切球的表面积之比为()∶3∶2∶1∶3(2)(2021云南昆明一中高三月考)在封闭的正四棱锥内有一个体积为V的球.若正四棱锥的底面边长为43,侧棱长为215,则V的最大值是()A.36πB.32π3C.9π2D.4π32。

空间几何体的表面积和体积导学案

高三数学导学案【学习目标】（1）了解柱体、锥体、台体的表面积计算方法（不要求记忆公式），掌握其推导过程；（2）能利用所学公式进行简单立体几何图形的表面积和体积的计算；（3）进一步掌握数学转化思想、类比思想，提高分析问题和解决问题的能力；培养空间想象能力、逻辑推理能力和计算能力；（4）运用运动变化的观点认识图形的和谐、对称、规范；【重难点】（1）在高考命题中几何体的表面积和体积以中低档题目出现的可能性较大，有时在解答题中占据其中一问，属容易题；（2）从考查形式上看，主要以选择题和填空题的形式出现；（3）从能力要求上看，重点考查空间想象能力和从立体问题向平面问题转化的能力。

【学习过程】一、知识梳理（复习教材必修2P 25~P 33页有关内容，填空梳理有关知识） 1表中S 表示面积，c ′、c 分别表示上、下底面周长，h 表斜高，h ′表示斜高，l 表示侧棱长。

2旋转体的面积和体积公式表中l 、h 分别表示母线、高，r 表示圆柱、圆锥与球冠的底半径，r 1、r 2分别表示圆台上、下底面半径，R 表示半径 3.球球的定义：_________________________________________________________________________. 球的截面性质：_____________________________________________________________________. 球的大圆：_________________________________________________________________________. 球的小圆：_________________________________________________________________________. 球面距离：__________________________________________________________________________. 地球的经度：________________________________________________________________________. 地球的纬度：________________________________________________________________________. 【热点典例】热点一：几何体的表面积课堂活动设计例1、已知几何体的三视图如图所示,它的表面积是( ).4.2.3.6A B C D ++例2、一个正方体的体积是8，则这个正方体的内切球的表面积是( ) A ．8π B ．6π C ．4πD ．π例3、已知三棱锥的三视图如图所示，则它的外接球表面积为( ) A ．16π B ．π C ．4πD ．2π（2）(2010·新课标全国卷)设长方体的长、宽、高分别为2a、a、a，其顶点都在一个球面上，则该球的表面积为 ( )A．3πa2B．6πa2 C．12πa2 D．24πa2【反思】本题做错的是第题问题探究：【错因】【总结】1．在求多面体的侧面面积时，应对每一侧面分别求解后再相加，对于组合体的表面积应注意重合部分的处理．2．以三视图为载体考查几何体的表面积，关键是能够对给出的三视图进行恰当的分析，从三视图中发现几何体中各元素间的位置关系及数量关系．3．圆柱、圆锥、圆台的侧面是曲面，计算侧面积时需要将这个曲面展为平面图形计算，而表面积是侧面积与底面圆的面积之和．4．求球的表面积关键是求出球的半径．热点二：几何体的体积例4、（1）(2009山东卷理)一空间几何体的三视图如图所示,则该几何体的体积为( ).A.2π+4π+C. 2π+D. 4π俯视图（2） 7.用大小相同的且体积为1的小立方块搭一个几何体，使它的主视图和俯视图如右图所示，则它的体积的最小值与最大值分别为( ) A ．9与13 B ．7与10 C ．10与16 D ．10与15（3）下面的三个图中，上面的是一个长方体截去一个角所得多面体的直观图，它的正视图和侧视图在下面画出（单位：cm ）。

《空间几何体的表面积与体积》导学案[1].

空间几何体的表面积与体积导学案上课时间2012年8月日第节学生姓名班级【学习目标】1. 通过对柱、锥、台体及球的研究,会理解柱、锥、台体、球的表面积、侧面积和体积的求法2. 记住柱、锥、台体及球的表面积、侧面积和体积计算公式,会用柱、锥、台体及球的有关公式进行简单计算和解决实际问题导学过程】、独学具体内容安排:阅读教材P23-P27（一空间几何体的表面积1. 棱柱、棱锥、棱台的表面积、侧面积棱柱、棱锥、棱台是由多个平面图形围成的多面体, 它们的表面积就是, 也就是; 它们的侧面积就是.2. 圆柱、圆锥、圆台的表面积、侧面积圆柱的侧面展开图是,长是圆柱底面圆的,宽是圆柱的设圆柱的底面半径为r ,母线长为l , 则S 圆柱侧S 圆柱表圆锥的侧面展开图为, 其半径是圆锥的,弧长等于,设r 为圆锥底面半径, l 为母线长,则侧面展开图扇形中心角为,S 圆锥侧, S 圆锥表圆台的侧面展开图是, 其内弧长等于, 外弧长等于,设圆台的上底面半径为r , 下底面半径为R , 母线长为l , 则侧面展开图扇环中心角为,S 圆台侧圆台表2 nr2 nr2n r '2 nr3. 球的表面积如果球的半径为R ,那么它的表面积S= O '（二空间几何体的体积1. 柱体的体积公式=2. 锥体的体积公式锥体=3. 台体的体积公式台体=4. 球的体积公式球= 二、对学群学具体内容安排:例 1. 一个三棱柱的底面是正三角形, 边长为4, 侧棱与底面垂直,侧棱长10, 求其侧面积、表面积和体积.例2.已知球的直径是6,求它的表面积和体积.例3.如图,一个空间几何体的正视图、侧视图和俯视图都是全等的等腰直角三角形，直角边长为1,求这个几何体的表面积和体积侧视图正视图三、课堂训练：1.已知球的表面积是64，求它的体积2. 如图，一个空间几何体的主视图和左视图都是边长为1的正三角形，俯视图是一个圆，那么这个几何体的侧面积是.3. 如图是一个几何体的三视图.根据图示,可计算出该几何体的侧面积为.卒1*;第3题图第4题图4.如图是某几何体的展开图.（1这个几何体的名称是；（2画出这个几何体的三视图；（3求这个几何体的体积.（取3.143. 一空间几何体的三视图如图所示，则该几何体的体积为（.2.A. 2 n +B. 4 n +C. 2 n +四、课后作业1.正四棱锥S-ABCD各侧面均为正三角形，侧棱长为5,求它的侧面积、表面积和体积.2.如图是一个几何体的三视图，若它的体积是a =3.体积为8的一个正方体，其全面积与球0的表面积相等，则球0的体积等于.俯视图侧视图正视图2222题图4. 下图是一个几何体的三视图，根据图中数据,可得该几何体的表面积是（A.9 nB.10 nC.11 n D . 12 n5. 某几何体的三视图如下，根据图中标出的尺寸（单位:cm，则这个几何体的体积A 34000cm 3B 38000cm 332000cm D .34000cm6. 一个棱锥的三视图如图，则该棱锥的表面积为(A. 48+12 B. 48+24 C. 36+12 D.7. 某高速公路收费站入口处的安全标识墩如图所示.墩的上半部分是正四棱锥P EFGH -,下半部分是长方体ABCD EFGH -.图5、图6分别是该标识墩的正视图和俯视图.(1请画出该安全标识墩的侧视图；(2求该安全标识墩的体积.正视图侧视图俯视图俯视图侧视图666。

苏教版数学高一《空间几何体的表面积和体积》精品导学案

§1．3 空间几何体的表面积和体积 1．3．1 空间几何体的表面积【课时目标】 1．进一步认识柱体、锥体、台体及简单组合体的结构特征，了解它们的有关概念．2．了解柱体、锥体、台体的表面积的计算公式．3．会利用柱体、锥体、台体的表面积公式解决一些简单的实际问题．1．常见的几个特殊多面体的定义(1)__________________的棱柱叫做直棱柱． (2)正棱柱是指底面为____________的直棱柱．(3)如果一个棱锥的底面是____________，并且顶点在底面的正投影是底面中心，我们称这样的棱锥为正棱锥．正棱锥的侧棱长都相等．(4)正棱锥被______________的平面所截，______________之间的部分叫做正棱台． 2．直棱柱、正棱锥、正棱台的侧面展开图及侧面积(1)直棱柱的侧面展开图是____________(矩形的长等于直棱柱的底面周长c ，宽等于直棱柱的高h)，则S 直棱柱侧＝______；(2)正棱锥的侧面展开图是由各个侧面均为全等等腰三角形组成的图形(正棱锥底面周长为c ，斜高为h ′)，则S 正棱锥侧＝__________；(3)正棱台的侧面展开图是由各个侧面均为全等等腰梯形组成的图形，(正棱台的上、下底面周长分别为c ′，c ，斜高为h ′)，则有：S 正棱台侧＝____________．．3．圆柱、圆锥、圆台的侧面展开图及侧面积圆柱、圆锥、圆台的侧面展开图分别是____________、________和________．S 圆柱侧＝2πrl ，S 圆锥侧＝12cl ＝πrlS 圆台侧＝12(c ＋c ′)l ＝π(r ＋r ′)l一、填空题1．用长为4、宽为2的矩形做侧面围成一个高为2的圆柱，此圆柱的轴截面面积为________．2．一个圆柱的侧面展开图是一个正方形，则这个圆柱的全面积与侧面积的比为__________．3．中心角为135°，面积为B 的扇形围成一个圆锥，若圆锥的全面积为A ，则A ∶B ＝__________．4．三视图如图所示的几何体的表面积是__________．5．一个长方体的长、宽、高分别为9,8,3，若在上面钻一个圆柱形孔后其表面积没有变化，则孔的半径为________．6．正六棱锥的高为4 cm ，底面最长的对角线为4 3 cm ，则它的侧面积为________ cm 2．7．底面是菱形的直棱柱，且侧棱长为5，它的体对角线的长分别是9和15，则这个棱柱的侧面积是________．8．一个正四棱柱的体对角线的长是9 cm，全面积等于144 cm2，则这个棱柱的侧面积为________ cm2．9．如图(1)所示，已知正方体面对角线长为a，沿阴影面将它切割成两块，拼成如图(2)所示的几何体，那么此几何体的表面积为________．二、解答题10．已知正四棱台(上、下底是正方形，上底面的中心在下底面的投影是下底面中心)上底面边长为6，高和下底面边长都是12，求它的侧面积．11．圆台的上、下底面半径分别为10 cm和20 cm．它的侧面展开图扇环的圆心角为180°，那么圆台的表面积是多少？(结果中保留π)12．有一塔形几何体由3个正方体构成，构成方式如图所示，上层正方体下底面的四个顶点是下层正方体上底面各边的中点．已知最底层正方体的棱长为2，求该塔形的表面积(含最底层正方体的底面面积)．能力提升13．如图所示，为了制作一个圆柱形灯笼，先要制作4个全等的矩形骨架，总计耗用9．6米铁丝，再用S平方米塑料片制成圆柱的侧面和下底面(不安装上底面)．(1)当圆柱底面半径r取何值时，S取得最大值？并求出该最大值(结果精确到0．01平方米)；(2)若要制作一个如图放置的、底面半径为0．3米的灯笼，请作出用于制作灯笼的三视图(作图时，不需考虑骨架等因素)．1．在解决棱锥、棱台的侧面积、表面积及体积问题时往往将已知条件归结到一个直角三角形中求解，为此在解此类问题时，要注意直角三角形的应用．2．有关旋转体的表面积的计算要充分利用其轴截面，就是说将已知条件尽量归结到轴截面中求解．而对于圆台有时需要将它还原成圆锥，再借助相似的相关知识求解．§1．3 空间几何体的表面积和体积 1．3．1 空间几何体的表面积答案知识梳理1．(1)侧棱和底面垂直 (2)正多边形 (3)正多边形 (4)平行于底面截面和底面2．(1)一个矩形 ch (2)12ch ′ (3)12(c ＋c ′)h ′3．矩形扇形扇环作业设计 1．8π解析易知2πr ＝4，则2r ＝4π，所以轴截面面积＝4π×2＝8π．2．1＋2π2π解析设底面半径为r ，侧面积＝4π2r 2，全面积为＝2πr 2＋4π2r 2，其比为：1＋2π2π．3．11∶8解析设圆锥的底面半径为r ，母线长为l ，则2πr ＝34πl ，则l ＝83r ，所以A ＝83πr 2＋πr 2＝113πr 2，B ＝83πr 2，得A ∶B ＝11∶8． 4．7＋ 2解析图中的几何体可看成是一个底面为直角梯形的直棱柱．直角梯形的上底为1，下底为2，高为1，棱柱的高为1．可求得直角梯形的四条边的长度为1,1,2，2，表面积S 表面＝2S 底＋S 侧面＝12(1＋2)×1×2＋(1＋1＋2＋2)×1＝7＋2． 5．3解析由题意知，圆柱侧面积等于圆柱上、下底面和，即2πr ×3＝2πr 2，所以r ＝3． 6．30 3解析由题意知，底面边长为2 3 cm ，侧棱长为l ＝16＋12＝27 cm ，斜高h ′＝28－3＝5 (cm )，∴S 侧＝6·12·23·5＝30 3 (cm 2)．7．160解析设底面边长是a ，底面的两条对角线分别为l 1，l 2，而l 21＝152－52，l 22＝92－52，而l 21＋l 22＝4a 2，即152－52＋92－52＝4a 2，a ＝8，S 侧面积＝ch ＝4×8×5＝160．8．112解析设底面边长、侧棱长分别为a 、l ，⎩⎪⎨⎪⎧a 2＋a 2＋l 2＝92a 2＋4al ＝144，∴⎩⎪⎨⎪⎧a ＝4l ＝7， ∴S 侧＝4·4·7＝112 (cm 2)． 9．(2＋2)a 2解析由已知可得正方体的边长为22a ，新几何体的表面积为S 表＝2×22a ×a ＋4×⎝⎛⎭⎫22a 2 ＝(2＋2)a 2． 10．解如图，E 、E 1分别是BC 、B 1C 1的中点，O 、O 1分别是下、上底面正方形的中心，则O 1O 为正四棱台的高，则O 1O ＝12．连结OE 、O 1E 1，则OE ＝12AB＝12×12＝6，O 1E 1＝12A 1B 1＝3．过E 1作E 1H ⊥OE ，垂足为H ，则E 1H ＝O 1O ＝12，OH ＝O 1E 1＝3， HE ＝OE －O 1E 1＝6－3＝3．在Rt △E 1HE 中，E 1E 2＝E 1H 2＋HE 2＝122＋32 ＝32×42＋32＝32×17，所以E 1E ＝317．所以S 侧＝4×12×(B 1C 1＋BC)×E 1E＝2×(12＋6)×317＝10817． 11．解如图所示，设圆台的上底面周长为c ，因为扇环的圆心角是180°，故c ＝π·SA ＝2π×10，所以SA ＝20，同理可得SB ＝40，所以AB ＝SB －SA ＝20， ∴S 表面积＝S 侧＋S 上＋S 下＝π(r 1＋r 2)·AB ＋πr 21＋πr 22＝π(10＋20)×20＋π×102＋π×202 ＝1 100π(cm 2)．故圆台的表面积为1 100π cm 2．12．解易知由下向上三个正方体的棱长依次为2，2，1．考虑该几何体在水平面的投影，可知其水平面的面积之和为下底面积最大正方体的底面面积的二倍．∴S 表＝2S 下＋S 侧＝2×22＋4×[22＋(2)2＋12]＝36． ∴该几何体的表面积为36．13．解由题意可知矩形的高即圆柱的母线长为9.6－8×2r 8＝1．2－2r ，∴塑料片面积S ＝πr 2＋2πr(1．2－2r)＝πr 2＋2．4πr －4πr 2＝－3πr 2＋2．4πr ＝－3π(r 2－0．8r)＝－3π(r －0．4)2＋0．48π．∴当r ＝0．4时，S 有最大值0．48π，约为1．51平方米． (2)若灯笼底面半径为0．3米，则高为1．2－2×0．3＝0．6(米)．制作灯笼的三视图如图．1．3．2 空间几何体的体积【课时目标】 1．了解柱、锥、台、球的体积公式．2．会利用柱体、锥体、台体的体积公式解决一些简单的实际问题．1．柱体、锥体、台体的体积柱体：V ＝______，V 圆柱＝________．锥体：V ＝________，V 圆锥＝________．台体：V ＝____________，V 圆台＝13πh(r ′2＋r ′r ＋r 2)．其中S 、S ′为底面面积，h 为高，r 、r ′为底面半径． 2．球的表面积和体积S 球＝________，V 球＝__________ 其中R 是球的半径．一、填空题1．把球的表面积扩大到原来的2倍，那么体积扩大到原来的________倍． 2．正方体的内切球和外接球的体积之比为__________．3．长方体的一个顶点上的三条棱长分别为3,4,5，且它的8个顶点都在同一个球面上，则这个球的表面积为________．4．一个圆锥与一个球的体积相等，圆锥的底面半径是球半径的3倍，圆锥的高与球半径之比为________．5．设某几何体的三视图如下(尺寸的长度单位为m )．则该几何体的体积为________m 3．6．棱长为a 的正方体中，连结相邻面的中心，以这些线段为棱的八面体的体积为________．7．已知一个球与一个正三棱柱的三个侧面和两个底面相切，若这个球的体积是32π3，则这个三棱柱的体积是________．8．若某几何体的三视图(单位：cm )如图所示，则此几何体的体积是______cm 3．9．圆柱形容器内盛有高度为8 cm的水，若放入三个相同的球(球的半径与圆柱的底面半径相同)后，水恰好淹没最上面的球(如图所示)，则球的半径是______cm．二、解答题10．如图所示，在三棱柱ABC－A1B1C1中，E、F分别为AB、AC的中点，平面EB1C1F 将三棱柱分成两部分，求这两部分的体积之比．11．已知正三棱锥V—ABC的主视图，俯视图如图所示，其中V A＝4，AC＝23，求该三棱锥的表面积与体积．能力提升12．有一个倒圆锥形容器，它的轴截面是一个正三角形，在容器内放一个半径为r的铁球，并注入水，使水面与球正好相切，然后将球取出，求这时容器中水的深度．13．有三个球，第一个球内切于正方体，第二个球与这个正方体各条棱相切，第三个球过这个正方体的各个顶点，求这三个球的表面积之比．1．利用球的半径、球心到截面圆的距离、截面圆的半径可构成直角三角形，进行相关计算．2．解决球与其他几何体的切接问题，通常作截面，将球与几何体的各量体现在平面图形中，再进行相关计算．3．柱体、锥体、台体的体积之间的内在关系为V 柱体＝Sh ――→S ′＝S V 台体＝13h(S ＋SS ′＋S ′)――→S ′＝0V 锥体＝13Sh ．4．“割补”是求体积的一种常用策略，运用时，要注意弄清割补前后几何体体积之间的数量关系．1．3．2 空间几何体的体积答案知识梳理1．Sh πr 2h 13Sh 13πr 2h 13(S ′＋S ′S ＋S)h2．4πR 2 43πR 3作业设计 1．2 2解析由面积扩大的倍数可知半径扩大为原来的2倍，则体积扩大到原来的22倍． 2．1∶3 3解析关键要清楚正方体内切球的直径等于棱长a ，外接球的直径等于3a ．两球体积之比为a 3：(3a)3＝1∶33． 3．50π解析外接球的直径2R ＝长方体的体对角线＝a 2＋b 2＋c 2(a 、b 、c 分别是长、宽、高)． 4．4∶9解析设球半径为r ，圆锥的高为h ，则13π(3r)2h ＝43πr 3，可得h ∶r ＝4∶9． 5．4解析由三视图可知原几何体是一个三棱锥，且三棱锥的高为2，底面三角形的一边长为4，且该边上的高为3，故所求三棱锥的体积为V ＝13×12×3×4×2＝4 m 3．6．a 36解析连结正方体各面中心构成的八面体由两个棱长为22a 的正四棱锥组成，正四棱锥的高为a 2，则八面体的体积为V ＝2×13×(22a)2·a 2＝a 36．7．48 3解析由43πR 3＝32π3，得R ＝2．∴正三棱柱的高h ＝4．设其底面边长为a ，则13·32a ＝2，∴a ＝43．∴V ＝34(43)2·4＝483．8．144解析此几何体为正四棱台与正四棱柱的组合体，而V 正四棱台＝13(82＋42＋82×42)×3＝112，V 正四棱柱＝4×4×2＝32，故V ＝112＋32＝144．9．4解析设球的半径为r cm ，则πr 2×8＋43πr 3×3＝πr 2×6r ．解得r ＝4．10．解截面EB 1C 1F 将三棱柱分成两部分，一部分是三棱台AEF －A 1B 1C 1，另一部分是一个不规则几何体，故可以利用棱柱的体积减去棱台的体积求得．设棱柱的底面积为S ，高为h ，则△AEF 的面积为14S ，由于V 1＝V AEF －A 1B 1C 1＝13·h·(S4＋S ＋S 2)＝712hS ，剩余的不规则几何体的体积为V 2＝V －V 1＝hS －712hS ＝512hS ，所以两部分的体积之比为V 1∶V 2＝7∶5． 11．解由主视图与俯视图可得正三棱锥的直观图如图所示，且V A ＝VB ＝VC ＝4，AB ＝BC ＝AC ＝23，取BC 的中点D ，连结VD ，则VD ＝VB 2－BD 2＝42－(3)2＝13，∴S △VBC ＝12×VD ×BC ＝12×13×23＝39， S △ABC ＝12×(23)2×32＝33， ∴三棱锥V —ABC 的表面积为3S △VBC ＋S △ABC ＝339＋33＝3(39＋3)．点V 在底面ABC 上的射影为H ，则A ，H ，D 三点共线，VH 即为三棱锥V —ABC 的高，VH ＝VD 2－HD 2＝ VD 2－⎝⎛⎭⎫13AD 2 ＝(13)2－12＝23，∴V V —ABC ＝13S △ABC ·VH ＝13×33×23＝6，所以正三棱锥的体积是6．12．解由题意知，圆锥的轴截面为正三角形，如图所示为圆锥的轴截面．根据切线性质知，当球在容器内时，水深为3r ，水面的半径为3r ，则容器内水的体积为V ＝V 圆锥－V 球＝13π·(3r)2·3r －43πr 3＝53πr 3，而将球取出后，设容器内水的深度为h ，则水面圆的半径为33h ，从而容器内水的体积是V ′＝13π·(33h)2·h ＝19πh 3，由V ＝V ′，得h ＝315r ．即容器中水的深度为315r ．13．解设正方体的棱长为a ．如图所示．①正方体的内切球球心是正方体的中心，切点是正方体六个面的中心，经过四个切点及球心作截面，所以有2r 1＝a ，r 1＝a 2，所以S 1＝4πr 21＝πa 2．②球与正方体的各棱的切点在每条棱的中点，过球心作正方体的对角面得截面，2r2＝2a，r2＝22a，所以S2＝4πr22＝2πa2．③正方体的各个顶点在球面上，过球心作正方体的对角面得截面，所以有2r3＝3a，r3＝32a，所以S3＝4πr23＝3πa2．综上可得S1∶S2∶S3＝1∶2∶3．。

高中数学立体几何初步 1_3 空间几何体的表面积与体积 1_3_1 空间几何体的表面积导学案(无答案)

1.3.1 空间几何体的表面积
学习目标: 1.了解棱柱、棱锥、棱台的侧面积
2.会求一些简单几何体的表面积.
重点与难点: 掌握特殊几何体-------棱柱 , 棱锥 , 棱台的侧面积公式. 活动一、引入新课
1.平面展开图
2.直棱柱及侧面积公式
3. (1)正棱柱及侧面积公式
(2).正棱锥及侧面积公式
(3).正棱台及侧面积公式
4.三个公式之间的联系
5..圆柱的侧面积公式
6 圆锥的侧面积公式
7 圆台的侧面积公式
8.圆柱、圆台、圆锥侧面积公式之间的关系
活动二、例题剖析
例1.已知正六棱柱的高为h , 底面边长为a , 求全面积.
A B
C D
F E
F1
E1D
1
׳
C1
B1
A1
例3.直角三角形△ABC的两条直角边长分别为AC=4 , BC=3 ,以BC所在直线为轴, 将此三角形旋转一周, 求所得旋转体的表面积.
变1：以AB所在直线为轴
例4.一个直角梯形上、下底和高的比为2:
求它旋转而成的圆台的上底面积、下底
面积和侧面积的比.
C
A
B C
A
B
活动三、课堂练习
1求底面边长为2m,高为1m的正三棱锥的全面积.
2.如果用半径为4的半圆形铁皮卷成一个圆锥筒，那么这个圆锥筒的高是多少？
活动四、课堂小结
巩固几个公式。

立体几何表面积与体积的计算导学案

1.1.3空间几何体的表面积与体积第1课时班级姓名组别代码评价【使用说明与学法指导】1．先精读一遍教材P23-25页 ,用红色笔进行勾画；再针对导学案二次阅读并解决预习探究案中的问题；训练案在自习或自主时间完成。

2．预习时可对合作探究部分认真审题，做不完或者不会的正课时再做，对于选做部分BC 层可以不做。

3．找出自己的疑惑和需要讨论的问题并记录下来，准备课上讨论质疑。

【学习目标】1.了解柱、锥、台的表面积计算公式,了解圆柱（锥、台）侧面积公式的推导过程。

2.会用以上公式解决相应的面积问题。

3.通过圆柱（锥、台）侧面积公式的推导过程，体验到侧面展开，化曲面为平面的解题方法。

4.通过和谐、对称、规范的图形，享受数学的美，引发学兴趣。

【学习重点】掌握柱、锥、台表面积的计算公式。

【学习难点】利用相应公式求柱、锥、台体的表面积。

【预习案】认真阅读课本第23--25页，用红色笔标记重点内容并完成下列问题：问题1：棱柱、棱锥、棱台都是由多个平面图形围成的几何体，它们的侧面展开图是什么？如何计算它们的表面积？（以正三棱柱、棱锥、棱台为例说明）问题2：圆柱、圆锥、圆台都是旋转体，它们的侧面展开图是什么？如何计算它们的表面积？问题3：组合体的表面积如何计算？【探究案】探究一：例1：已知棱长为a，各面都是等边三角形的四面体S—ABC，求它的表面积？探究二：例2：如图，一个圆台形花盆盆口直径20 cm，盆底直径为15cm，底部渗水圆孔直径为1.5 cm，盆壁长15cm．那么花盆的表面积约是多少平方厘米（取3.14，结果精确到1毫升）？【课堂小结】我的疑问：（至少提出一个有价值的问题）cm20cm今天我学会了什么？【训练案】（时间：15分钟）1、正方体的全面积为24 cm 2，则它的棱长是（）A ．2cmB ．6cmC ．4cmD ．8cm2、用长为4，宽为2的矩形做面围成一个圆柱，则此圆柱的侧面积为（）A ．2πB ．π8C ．4πD ．83、有一个几何体的三视图及其尺寸如下（单位cm ），则该几何体表面积为：（）A 224cm πB 215cm πC 224cm πD 都不正确 4、课本p27页练习21.1.3空间几何体的表面积与体积第2课时班级姓名组别代码评价【使用说明与学法指导】1.先精读一遍教材P25-26页 ,用红色笔进行勾画；再针对导学案二次阅读并解决预习探究案中的问题；训练案在自习或自主时间完成。

高中数学必修21.3 空间几何体的表面积与体积教案

1.3空间几何体的表面积与体积教学任务分析:根据柱，锥，台的结构特征，并结合它们的展开图，推导它们的表面积的计算公式，从度量的角度认识空间几何体；用极限思想推导球的体积公式和表面公式，使学生初步了解利用极限思想解决问题的基本步骤，体会极限思想的基本内涵。

与此同时，培养学生积极探索的科学精神，培养学生的思维能力，空间想象能力。

教学重点：柱体，锥体，台体的表面积和体积的计算公式。

教学难点：球的体积和表面积的推导教学设计：1．从学生熟悉的正方体和长方体的展开图入手，分析展开图与其表面积的关系。

其目的是㈠复习表面积的概念，即表面积是各个面的面积的和㈡介绍求几何体表面积的方法，把它们展开成平面图形，利用平面图形求面积的方法，求立体图形的表面积。

2．通过类比正方体和长方体的表面积，讨论棱柱，棱锥，棱台的表面积问题。

实际上，求棱柱，棱锥，棱台的表面积问题可转化成求平行四边形，三角形和梯形问题。

3．利用计算机或实物展示圆柱的侧面可以展开成一个矩形。

圆锥的侧面可以展开成一个扇形。

随后的有关圆台表面积的探究，也可以按照这样的思路进行教学。

说明圆台表面积公式时,可推导侧面积公式。

圆台侧面积的推导：设圆台侧面的母线长为，上，下底周长分别是，半径分别是则S 圆台侧=()x c x l c '-+2121=()[]x c c cl '-+21()()()l r r l c c c c l c c c cl S c c l c x lx x c c '+='+=⎥⎦⎤⎢⎣⎡'-''-+='-'=∴+='π2121圆台侧在分别学习了圆柱，圆锥，圆台的表面积公式后，可以引导学生用运动，变化的观点分析它们之间的关系。

圆柱可看成上，下两底面全等的圆台，圆锥可看成上底面半径为零的圆台。

因此，圆柱，圆锥可看成圆台的特例。

（可用计算机演示）4．柱体，锥体和台体的体积从正方体，长方体的体积公式引入到一般棱柱的体积也是V=Sh若有时间，可推导棱锥的体积公式棱锥的体积公式的推导如图,设三棱柱ABC-ABC 的底面积(即ΔABC 的面积)为S ，高（即点A ¹到平面ABC 的距离）为h ，则它的体积为Sh ，沿平面A ¹BC 和平面A ¹B ¹C ，将这个三棱柱分割为3个三棱锥，其中三棱锥1，2的底面积相等（S ΔA ¹AB=S ΔA ¹B ¹B ），高也相等点C 到平面AB ，BA 的距离）三棱锥也有相等的底面积，和相等的高（点A ¹到平面BCC ¹B ¹ 的高）因此，这三个三棱锥的体积相等，每个三棱锥体积是sh ，得sh台体推导出台体的体积公式V=S ¹+Sh让学生思考，柱体，锥体台体的体积公式之间的联系。

空间几何体的表面积及体积学案

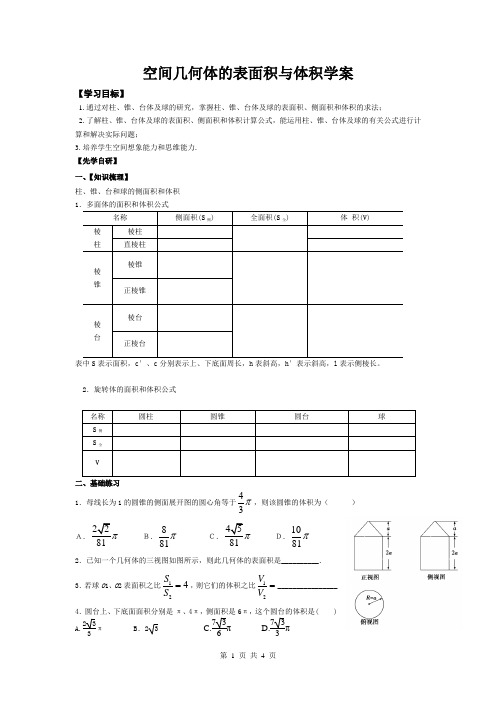
空间几何体的表面积与体积学案【学习目标】1.通过对柱、锥、台体及球的研究，掌握柱、锥、台体及球的表面积、侧面积和体积的求法；2.了解柱、锥、台体及球的表面积、侧面积和体积计算公式，能运用柱、锥、台体及球的有关公式进行计算和解决实际问题；3.培养学生空间想象能力和思维能力. 【先学自研】一、【知识梳理】柱、锥、台和球的侧面积和体积 1．多面体的面积和体积公式表中S 表示面积，c ′、c 分别表示上、下底面周长，h 表斜高，h ′表示斜高，l 表示侧棱长。

2．旋转体的面积和体积公式二、基础练习1．母线长为1的圆锥的侧面展开图的圆心角等于43π，则该圆锥的体积为（）Ａ．81Ｂ．881π Ｃ．81Ｄ．1081π 2．已知一个几何体的三视图如图所示，则此几何体的表面积是__________． 3．若球O 1、O 2表面积之比124S S =，则它们的体积之比12VV =________________ 4．圆台上、下底面面积分别是π、4π，侧面积是6π，这个圆台的体积是( )A.233π B ．2 3 C.736π D.733π5．一个长方体共一顶点的三个面的面积分别是6,3,2，这个长方体对角线的长是（）A ．23B ．32C ．6D ．66．已知棱台两底面面积分别为80和245，截得这个棱台的棱锥的高是35，求棱台的体积7．已知直三棱柱底面各边的比为17∶10∶9，侧棱长为16 cm ，全面积为1440 cm 2，求底面各边之长.8．设正四棱锥的底面边长为a ，侧棱长为2a ，求对角面的面积和侧面积.【点拨讲解】例1 、已知棱长为a ，各面均为等边三角形的四面体S ABC -，求它的表面积及体积变式1：一个正三棱锥的侧面都是直角三角形，底面边长为a ，求它的表面积及体积变式2：从一个正方体中，如图那样截去4个三棱锥后，得到一个正三棱锥A —BCD ，求它的体积是正方体体积的几分之几？例2、(1)已知球的一个截面的面积为9π，且此截面到球心的距离为4，则球的表面积为__________.(2)一个球内有相距9 cm 的两个平行截面，它们的面积分别为49π cm 2和400π cm 2，求球的表面积．(3)已知球面上过,,A B C 三点的截面和球心的距离是球半径的一半，且2AB BC CA ===，则球的表面积为例3、（1）长方体的一个顶点上的三条棱长为3、4、5，若它的八个顶点都在同一个球面上，求出此球的表面积和体积.（2）记与正方体各个面相切的球为1O ，与各条棱相切的球为2O ，过正方体各顶点的球为3O 则这3个球的体积之比为（3）半球内有一个内接正方体，，求球的表面积和体积。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

§1.3 空间几何体的表面积与体积导学案（3课时）
【使用说明及学法指导】
1.先精读一遍教材P23—P23，用红色笔进行勾画，找出柱、锥、台体的表面积、体积的计算公式并识记；再针对导学案二次阅读并回答；
2.找出自己的疑惑和需要讨论的问题准备课上讨论质疑.
【学习目标】
1.通过学习掌握柱、锥、台、球表面积、体积的计算公式并会灵活运用，会求简单组合体的表面积和体积.
2.通过对柱、锥、台表面积和体积的公式的探究学习,体会观察、类比、归纳的推理方法.
3.通过从量的角度认识几何体的过程，培养学生的空间想象能力和思维能力.
【重点难点】
1. 重点：求圆柱、圆锥、圆台的侧面积，求柱体、锥体、台体、球的表面积与体积；
2. 难点：柱体、锥体、台体的侧面展开图及这三类几何体之间关系的理解.
【预习自学】
1. 多面体的表面积是几何体表面的面积，表示几何体表面的大小；体积是几何体所占空间的大小.
2. 探究1：棱柱、棱锥、棱台的表面积问题：我们学习过正方体和长方体的表面积，以及它们的展开图（右图），你觉得它们展开图与其表面积有什么关系吗？
结论：正方体、长方体是围成的多面体，其表面积就是，也就是展开图的面积.
新知1：棱柱、棱锥、棱台都是多面体，它们的表面积就是其 . 试试1：想想下面多面体的侧面展开图都是什么样子，它们的表面积如何计算？
探究2：圆柱、圆锥、圆台的表面积问题：根据圆柱、圆锥的几何特征，它们的侧面展开图是什么图形？它们的表面积等于什么？你能推导它们表面积的计算公式吗？
新知2：（1）设圆柱的底面半径为，母线长为，则它的表面积等于，即
（2）设圆锥的底面半径为，母线长为，则它的表面积等于，即S= . 试试2：圆台的侧面展开图叫扇环，扇环是怎么得到的呢？（能否看作是个大扇形减去个小扇形呢？）你能试着求出扇环的面积吗？从而圆台的表面积呢？
（3）设圆台的上、下底面半径分别为，，母线长为，则它的表面积等于，即S= .
反思：想想圆柱、圆锥、圆台的结构，你觉得它们的侧面积之间有什么关系吗？
※ 典型例题
例1 已知棱长为，各面均为等边三角形的四面体，求它的表面积.
例2 如图,一个圆台形花盆盆口直径为20,盆底直径为15,底部渗水圆孔直径
为,盆壁长15.为了美化花盆的外观,需要涂油漆.已知每平方米用100毫升油漆,涂100个这样的花盆需要多少油漆(取3.14,结果精确到1毫升)?
探究3：主体、锥体与台体的体积
初中我们学习了正方体、长方体、圆柱的体积公式（为底面面积，为高），是否柱体的体积
都是这样求呢？锥体、台体的体积呢？
新知：经过证明(有兴趣的同学可以查阅祖暅原理)
柱体体积公式为：（为底面积，为高）；锥体体积公式为：（为底面积，为高）；
台体体积公式为：（，分别为上、下底面面积，为高）.
补充：柱体的高是指的距离；锥体的高是的距离；台体的高是指的距离. 反思：思考下列问题
⑴比较柱体和锥体的体积公式，你发现什么结论？
⑵比较柱体、锥体、台体的体积公式，你能发现三者之间的关系吗？
※ 典型例题
例 3 有一堆规格相同的铁制(铁的密度是)六角螺帽共重5.8，已知底面是正六边形，边长为12，内孔直径为10，高为10，问这堆螺帽大约有多少个(取3.14)？
正四棱锥
正四棱台正六棱柱
探究4：球的体积和表面积
球没有底面,也不能像柱体、锥体、台体那样展成平面图形，它的体积和表面积的求法涉及极限思想(一种很重要的数学方法).经过推导证明：
球的体积公式：V=
；球的表面积公式：S= ，其中，为球的半径.
显然，球的体积和表面积的大小只与半径有关.
※典型例题
例4 如图，圆柱的底面直径与高都等于球的直径(即圆柱内有一内切球)，求证：
（1）球的体积等于圆柱体积的；
（2）球的表面积等于圆柱的侧面积.
【课后练习与能力提升】（课上与课后完成）
1. 某四棱锥的三视图如图所示，该四棱锥的表面积是( )
A．32 B．16＋16 2 C．48 D．16＋32 2
第1 题第2题第3题
2. 若一个正三棱柱的三视图如图所示，则这个正三棱柱的表面积为（）
A. B. C. D.
3. 如图所示，圆锥的底面半径为1，高为，则圆锥的表面积为（）
A.π
B.2π
C.3π
D.4π
4. 已知某个几何体的三视图如图所示，根据图中标出的尺寸（单位：cm）,可得这个几何体的体积是（）
A. cm3
B.cm3
C.2 000 cm3
D.4 000 cm3
第4题第5题第6题
5.一个几何体的三视图如图所示，则该几何体的体积为_______________．
6. 一个空间几何体的正视图、侧视图、俯视图为全等的等腰直角三角形，如果直角三角形的直角边长为1，那么这个几何体的体积为（）
A.1
B.
C.
D.
7. 右图是一个几何体的三视图，则它的表面积为( )
A．4π B.
15π
4
C．5π D.
17π
4
8. 已知某几何体的俯视图是如图所示的矩形，正视图（或称主视图）是一个底边长为8、高为4的等腰三角形，侧视图（或称左视图）是一个底边长为6、高为4的等腰三角形.
（1）求该几何体的体积V；
（2）求该几何体的侧面积S.
9. 如图，在边长为4的立方体中，求三棱锥的体积.
10. 如图，一个正方体的顶点都在球面上，它的棱长是a cm，求球的体积．。