《圆锥曲线抛物线》导学案(复习版).docx
圆锥曲线定义复习导学案

圆锥曲线定义复习导学案学习目标:知识目标:理解并掌握圆锥曲线的定义能力目标:能用定义处理轨迹,最值范围问题情感目标:激发学生的学习兴趣,培养学生不断发现,探究的精神,培养教学审美意识。
学习过程问题1:若点P6=,则动点P的轨迹为()A、椭圆B、双曲线C、线段D、圆变式探究:能否对上式略作改动,使P点轨迹有所改变?问题2=表示的曲线为抛物线,请类比探究方程()230x y m=-+>又表示何种曲线。
三、反馈练习1、动点P22x y=--,则动点P轨迹为()A、椭圆B、双曲线C、抛物线D、两条直线2、(全国高考题)已知:动圆M与圆()221:42C x y++=外切,与圆()222:42C x y-+=内切,则动圆圆心M的轨迹方程为。
3、(08苏、锡、常、缜四市联考)设双曲线221916x y-=的右焦点F,P是双曲线上任意一点,点A 的坐标为(9,2),则35PA PF+的最小值为。
A、9B、365C、425D、545合作探究:问题1:请同学们观察反馈练习中第3题PF前的系数35与离心率e的关系。
你能否找到规律,并能将这一规律推广到所有的圆锥曲线中(可自己举例探究)问题2:在问题1的基础上,将PF前系数变为1,则又可用什么方法处理?是否可将这一题型推广到所有圆锥曲线中。
四、课后练习1、探究方程()10m=>表示什么曲线2、一动圆与已知圆()22131O x y=++=外切,与圆()222:381O x y-+=内切试求动圆圆心轨迹方程。
五、课堂小结1、第一定义:形式:两个定点,定值(之差、之和),注意2a与2c间关系第二定义:形式定点,定直线、距离之比,注意定点与定直线的位置关系及比值范围2、利用定义解决最值问题形如1|PA PFe+及轨迹问题。
高三数学 第十二章 圆锥曲线—抛物线1 复习教案

第七节 抛物线一、复习目标:1、掌握抛物线的定义和标准方程,会运用定义和会求抛物线的标准方程,能通过方程研究抛物线的几何性质;2、围绕焦半径、焦点弦,运用数形结合和代数方法研究抛物线的性质 二、重难点:重点:掌握抛物线的定义和标准方程,会运用定义和会求抛物线的标准方程,能通过方程研究抛物线的几何性质。
难点: 与焦点有关的计算与论证三、教学方法:探析归纳,讲练结合 四、教学过程(一)、谈最新考纲要求及新课标高考命题考查情况,促使积极参与。
学生阅读复资P124页教师讲解,增强目标意识及参与意识。
(二)、知识梳理,方法定位(学生完成复资P124页填空题,教师准对问题讲评)1.抛物线的标准方程、类型及其几何性质 (0>p ):2.抛物线的焦半径、焦点弦 ①)0(22≠=p px y的焦半径=PF 2P x +;)0(22≠=p py x的焦半径=PF 2P y +;② 过焦点的所有弦中最短的弦,也被称做通径.其长度为2p. ③ AB 为抛物线pxy 22=的焦点弦,则=B A x x42p ,=B A y y 2p -,||AB =p x x B A ++3.pxy 22=的参数方程为⎩⎨⎧==pty pt x 222(t 为参数),pyx22=的参数方程为⎩⎨⎧==222pty ptx (t 为参数).4.重难点问题探析:围绕焦半径、焦点弦,运用数形结合和代数方法研究抛物线的性质 (1).要有用定义的意识问题1:抛物线y=42x 上的一点M 到焦点的距离为1,则点M 的纵坐标是( )A. 1617B. 1615C.87D. 0点拨:抛物线的标准方程为y x 412=,准线方程为161-=y ,由定义知,点M 到准线的距离为1,所以点M的纵坐标是1615(2).求标准方程要注意焦点位置和开口方向问题2:顶点在原点、焦点在坐标轴上且经过点(3,2)的抛物线的条数有点拨:抛物线的类型一共有4种,经过第一象限的抛物线有2种,故满足条件的抛物线有2条(3).研究几何性质,要具备数形结合思想,“两条腿走路” 问题3:证明:以抛物线焦点弦为直径的圆与抛物线的准线相切 点拨:设AB 为抛物线的焦点弦,F 为抛物线的焦点,点''、B A 分别是点B A 、在准线上的射影,弦AB 的中点为M ,则''BB AA BF AF AB +=+=,点M到准线的距离为ABBB AA 21)''(21=+,∴以抛物线焦点弦为直径的圆总与抛物线的准线相切 (三)、基础巩固导练1.过抛物线x y 42=的焦点作一条直线与抛物线相交于A 、B 两点,它们的横坐标之和等于)(422R a a a ∈++,则这样的直线( )A.有且仅有一条B.有且仅有两条C.1条或2条D.不存在[解析]C44)1(52||22≥++=++=++=a a a p x x AB B A ,而通径的长为4.2. (08·浙江8)在平面直角坐标系xOy 中,若抛物线24x y =上的点P 到该抛物线焦点的距离为5,则点P 的纵坐标为 ( ) A. 3 B. 4 C. 5 D. 6[解析] B 利用抛物线的定义,点P 到准线1-=y 的距离为5,故点P 的纵坐标为4.3. (07福建5)两个正数a 、b 的等差中项是92,一个等比中项是且,b a >则抛物线2()y b a x =-的焦点坐标为(D )A .1(0,)4-B .1(0,)4C .1(,0)2-D .1(,0)4-4.(09江苏8) 如果1P ,2P ,…,8P 是抛物线24y x =上的点,它们的横坐标依次为1x ,2x ,…,8x ,F 是抛物线的焦点,若)(,,,21*∈N n x x x n 成等差数列且45921=+++x x x ,则||5F P =( ).A .5B .6C . 7D .9 [解析]B 根据抛物线的定义,可知12ii i pPF x x =+=+(1i =,2,……,n ),)(,,,21*∈N n x x x n 成等差数列且45921=+++x x x ,55=x ,||5F P =65、(08山东9)抛物线,42F x y 的焦点为=准线为l ,l 与x 轴相交于点E ,过F 且倾斜角等于60°的直线与抛物线在x 轴上方的部分相交于点A ,AB ⊥l ,垂足为B ,则四边形ABEF 的面积等于( ) A .33 B .34 C .36 D .38[解析] C. 过A 作x 轴的垂线交x 轴于点H ,设),(n m A ,则1,1-=-=+==m OF OH FH m AB AF ,32,3)1(21==∴-=+∴n m m m四边形ABEF 的面积==⨯++32)]13(2[2136 6、设O 是坐标原点,F 是抛物线24y x =的焦点,A 是抛物线上的一点,FA 与x 轴正向的夹角为60,则OA为 .解:过A 作AD x ⊥轴于D ,令FD m =,则m FA 2=即m m 22=+,解得2m.(四)、小结:1.求抛物线方程要注意顶点位置和开口方向,以便准确设出方程,然后用待定系数法.2.利用好抛物线定义,进行求线段和的最小值问题的转化.3.涉及抛物线的弦的中点和弦长等问题要注意利用韦达定理,能避免求交点坐标的复杂运算.4、解决焦点弦问题时,抛物线的定义有广泛的应用,应注意焦点弦的几何性质.(五)、作业布置:课本P76页中A组3、6、9 B组中1、4课外练习:复资P125页变式训练中1、2、3、4 随堂训练中3、4、5五、教学反思:。
【优质】高三数学《圆锥曲线》复习教案-范文word版 (9页)

本文部分内容来自网络整理,本司不为其真实性负责,如有异议或侵权请及时联系,本司将立即删除!== 本文为word格式,下载后可方便编辑和修改! ==高三数学《圆锥曲线》复习教案【小编寄语】数学网小编给大家整理了高三数学《圆锥曲线》复习教案,希望能给大家带来帮助!90题突破高中数学圆锥曲线1.如图,已知直线L:的右焦点F,且交椭圆C于A、B两点,点A、B在直线上的射影依次为点D、E。
(1)若抛物线的焦点为椭圆C的上顶点,求椭圆C的方程;(2)(理)连接AE、BD,试探索当m变化时,直线AE、BD是否相交于一定点N?若交于定点N,请求出N点的坐标,并给予证明;否则说明理由。
(文)若为x轴上一点,求证:2.如图所示,已知圆定点A(1,0),M为圆上一动点,点P在AM上,点N在CM上,且满足,点N的轨迹为曲线E。
(1)求曲线E的方程;(2)若过定点F(0,2)的直线交曲线E于不同的两点G、H(点G在点F、H之间),且满足的取值范围。
3.设椭圆C:的左焦点为F,上顶点为A,过点A作垂直于AF的直线交椭圆C于另外一点P,交x轴正半轴于点Q,且⑴求椭圆C的离心率;⑵若过A、Q、F三点的圆恰好与直线l:相切,求椭圆C的方程.4.设椭圆的离心率为e=(1)椭圆的左、右焦点分别为F1、F2、A是椭圆上的一点,且点A到此两焦点的距离之和为4,求椭圆的方程.(2)求b为何值时,过圆x2+y2=t2上一点M(2, )处的切线交椭圆于Q1、Q2两点,而且OQ1⊥OQ2.5.已知曲线上任意一点P到两个定点F1(- ,0)和F2( ,0)的距离之和为4.(1)求曲线的方程;(2)设过(0,-2)的直线与曲线交于C、D两点,且为坐标原点),求直线的方程.6.已知椭圆的左焦点为F,左、右顶点分别为A、C,上顶点为B.过F、B、C作⊙P,其中圆心P的坐标为(m,n).(Ⅰ)当m+n>0时,求椭圆离心率的范围;(Ⅱ)直线AB与⊙P能否相切?证明你的结论.7.有如下结论:“圆上一点处的切线方程为”,类比也有结论:“椭圆处的切线方程为”,过椭圆C:的右准线l上任意一点M引椭圆C的两条切线,切点为 A、B.(1)求证:直线AB恒过一定点;(2)当点M在的纵坐标为1时,求△ABM的面积8.已知点P(4,4),圆C:与椭圆E:有一个公共点A(3,1),F1、F2分别是椭圆的左、右焦点,直线PF1与圆C相切.(Ⅰ)求m的值与椭圆E的方程;(Ⅱ)设Q为椭圆E上的一个动点,求的取值范围.9.椭圆的对称中心在坐标原点,一个顶点为,右焦点与点的距离为。
高考数学专题复习系列 圆锥曲线与方程导学案

圆锥曲线与方程1.掌握椭圆的定义、标准方程、简单的几何性质、了解椭圆的参数方程.2.掌握双曲线的定义、标准方程、简单的几何性质.3.掌握抛物线的定义、标准方程、简单的几何性质.4.了解圆锥曲线的初步应用.圆锥曲线是高中数学的一个重要内容,它的基本特点是数形兼备,兼容并包,可与代数、三角、几何知识相沟通,历来是高考的重点内容。
纵观近几年高考试题中对圆锥曲线的考查,基本上是两个客观题,一个主观题,分值21分~24分,占15%左右,并且主要体现出以下几个特点:1.圆锥曲线的基本问题,主要考查以下内容:①圆锥曲线的两种定义、标准方程及a、b、c、e、p五个参数的求解.②圆锥曲线的几何性质的应用.2、求动点轨迹方程或轨迹图形在高考中出现的频率较高,此类问题的解决需掌握四种基本方法:直译法、定义法、相关点法、参数法.3.有关直线与圆锥曲线位置关系问题,是高考的重热点问题,这类问题常涉及圆锥曲线的性质和直线的基本知识以及线段中点、弦长等,分析这类问题时,往往要利用数形结合思想和“设而不求”的方法、对称的方法及韦达定理,多以解答题的形式出现.4.求与圆锥曲线有关的参数或参数范围问题,是高考命题的一大热点,这类问题综合性较大,运算技巧要求较高;尤其是与平面向量、平面几何、函数、不等式的综合,特别近年出现的解析几何与平面向量结合的问题,是常考常新的试题,将是今后高考命题的一个趋势.第1课时 椭圆1.椭圆的两种定义(1) 平面内与两定点F 1,F 2的距离的和等于常数(大于21F F )的点的轨迹叫椭圆,这两个定点叫做椭圆的 , 之间的距离叫做焦距.注:①当2a =|F 1F 2|时,P 点的轨迹是 . ②当2a <|F 1F 2|时,P 点的轨迹不存在.(2) 椭圆的第二定义:到 的距离与到 的距离之比是常数e ,且∈e 的点的轨迹叫椭圆.定点F 是椭圆的 ,定直线l是 ,常数e 是 .2.椭圆的标准方程(1) 焦点在x 轴上,中心在原点的椭圆标准方程是:12222=+by ax ,其中( > >0,且=2a )(2) 焦点在y 轴上,中心在原点的椭圆标准方程是12222=+b x a y ,其中a ,b 满足: .(3)焦点在哪个轴上如何判断? 3.椭圆的几何性质(对12222=+by ax ,a > b >0进行讨论)(1) 范围: ≤ x ≤ , ≤ y ≤(2) 对称性:对称轴方程为 ;对称中心为 .(3) 顶点坐标: ,焦点坐标: ,长半轴长: ,短半轴长: ;准线方程: .(4) 离心率:=e ( 与 的比),∈e ,e 越接近1,椭圆越 ;e 越接近0,椭圆越接近于 .(5) 焦半径公式:设21,F F 分别为椭圆的左、右焦点,),(00y x P 是椭圆上一点,则=1PF ,22PF =4.焦点三角形应注意以下关系(老师补充画出图形): (1) 定义:r 1+r 2=2a(2) 余弦定理:21r +22r -2r 1r 2cos θ=(2c )2(3) 面积:21F PF S ∆=21r 1r 2 sin θ=21·2c | y 0 |(其中P(00,y x )为椭圆上一点,|PF 1|=r 1,|PF 2|=r 2,∠F 1PF 2=θ)变式训练2:已知P (x 0,y 0)是椭圆12222=+by a x (a >b >0)上的任意一点,F 1、F 2是焦点,求证:以PF 2为直径的圆必和以椭圆长轴为直径的圆相内切.证明 设以PF 2为直径的圆心为A ,半径为r .∵F 1、F 2为焦点,所以由椭圆定义知|PF 1|+|PF 2|=2a ,|PF 2|=2r ∴|PF 1|+2r =2a ,即|PF 1|=2(a -r )连结OA ,由三角形中位线定理,知 |OA |=.)(221||211r a r a PF -=-⨯= 故以PF 2为直径的圆必和以长轴为直径的圆相内切.评注 运用椭圆的定义结合三角形中位线定理,使题目得证。
2019-2020学年高中数学 第二章《圆锥曲线》复习导学案新人教版选修1-1.doc

2019-2020学年高中数学 第二章《圆锥曲线》复习导学案新人教版选修1-1【知识归纳】一、椭圆、双曲线、抛物线性质注意:1.涉及圆锥曲线的焦点三角形(圆锥曲线上一点与两个焦点构成的三角形)问题首选圆锥曲线的第一定义解题2.与双曲线22221x y a b -=共渐近线的双曲线标准方程为2222x y a bλ-=(0λ≠),(其中0λ>是焦点在x 轴上的双曲线;0λ<是焦点在y 轴上的双曲线)3.椭圆方程的一般形式:221(0,0,)+=>>≠mx ny m n m n 4.双曲线方程的一般形式:221(0)+=<mx ny mn二.点00(,)P x y 与圆锥曲线的位置关系 1. 点00(,)P x y 与椭圆22221x y +=的位置关系:2. 点00(,)P x y 与抛物线的位置关系:三.直线与圆锥曲线的位置关系 1.2.直线与双曲线的位置关系注:与渐近线平行的直线与双曲线只有一个交点; 3.直线与抛物线的位置关系注:与抛物线对称轴平行或重合的直线与抛物线只有一个交点.4、其它:(1)弦长问题: 若斜率为k 的直线被圆锥曲线所截得的弦为AB ,设1122(,),(,)A x y B x y ,则弦长21=-=AB x 或12y =-=(2)焦点弦(即过焦点的弦)1)计算焦点弦长的方法:①利用弦长公式21-AB x ;②利用焦半径公式; 2)抛物线22(0)y px p =>的焦点弦(过焦点的弦)为AB ,1122(,),(,)A x y B x y ,则有①12=++AB x x p ;②212y y p =-,2124p x x =;③112AF BF p+=四.求轨迹的常用方法(一般步骤:①建系;②设点;③列式;④化简;⑤证明)1.直接法:直接通过建立,x y 之间的关系,构成(,)0F x y =,是求轨迹的最基本的方法; 2.坐标转移法:若动点(,)P x y 依赖于另一动点00(,)Q x y 的变化而变化,并且00(,)Q x y 又在某已知曲线上,则可先用,x y 的代数式表示00,x y ,再将00,x y 代入已知曲线得到要求的轨迹方程;3.定义法:如果能够确定动点的轨迹满足某已知曲线定义,则可由曲线的定义直接写出方程;4.参数法:当动点(,)P x y 坐标之间的关系不易直接找到,也没有相关动点可用时,可考虑将,x y 均用一个中间变量(如斜率k 等)表示,得参数方程,再消去参数得关于,x y 的方程. 【基础自测】1、与⊙O :22x y +=1及⊙C :22(4)x y -+=4都外切的动圆M 的圆心的轨迹是( )A 、椭圆B 、抛物线C 、双曲线D 、双曲线的一支2、若9k <,则椭圆22+1259x y =与椭圆22+1259x y k k=--的( ) A 、长轴长相等 B 、短轴长相等 C 、离心率e 相等 D 、焦距相等 3、顶点是原点,对称轴是坐标轴,且焦点在直线3412x y -=上的抛物线的方程是 . 4、双曲线13622=-y x 的渐近线与圆)0()3(222>=+-r r y x 相切,则r = . 【典例复习】例1、椭圆的中心在原点,左焦点F 1 (0),右顶点A 2(2,0),设点A(1,12).(1)求该椭圆的标准方程;(2)若P 是椭圆上的动点,求线段PA 的中点M 的轨迹方程。
高中数学《抛物线的简单几何性质》(导学案)
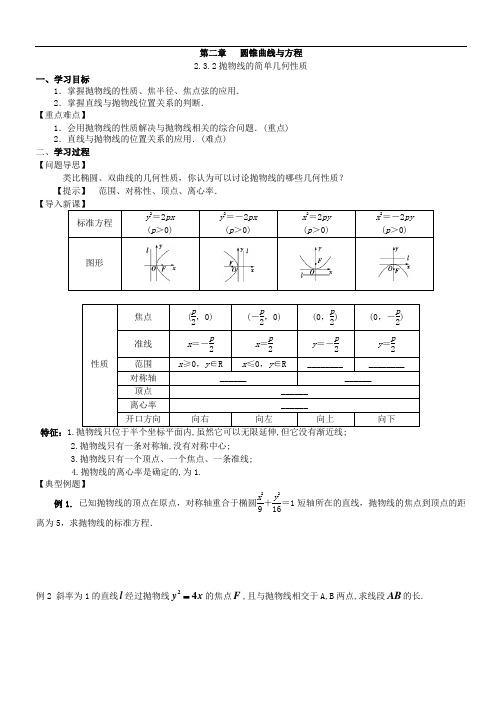
第二章 圆锥曲线与方程 2.3.2抛物线的简单几何性质一、学习目标1.掌握抛物线的性质、焦半径、焦点弦的应用. 2.掌握直线与抛物线位置关系的判断. 【重点难点】1.会用抛物线的性质解决与抛物线相关的综合问题.(重点)2.直线与抛物线的位置关系的应用.(难点) 二、学习过程 【问题导思】类比椭圆、双曲线的几何性质,你认为可以讨论抛物线的哪些几何性质? 【提示】 范围、对称性、顶点、离心率. 【导入新课】标准方程y 2=2px (p >0) y 2=-2px (p >0) x 2=2py(p >0)x 2=-2py(p >0)图形性质焦点 (p2,0) (-p2,0) (0,p2)(0,-p2)准线x =-p 2x =p 2y =-p 2y =p 2范围 x ≥0,y ∈R x ≤0,y ∈R________________对称轴 ____________顶点 ______ 离心率 ______ 开口方向向右 向左向上向下特征:1.2.抛物线只有一条对称轴,没有对称中心;3.抛物线只有一个顶点、一个焦点、一条准线;4.抛物线的离心率是确定的,为1. 【典型例题】例1. 已知抛物线的顶点在原点,对称轴重合于椭圆x 29+y 216=1短轴所在的直线,抛物线的焦点到顶点的距离为5,求抛物线的标准方程.例2 斜率为1的直线l 经过抛物线24y x 的焦点F ,且与抛物线相交于A,B 两点,求线段AB 的长.例3 求过点P(0,1)且与抛物线y2=2x只有一个公共点的直线方程.【变式拓展】1.已知抛物线的顶点在原点,对称轴为y轴,顶点到准线的距离为4,求该抛物线的方程并指出焦点坐标与准线方程.2.直线l:y=kx+1,抛物线C:y2=4x,当k为何值时,l与C有:(1)一个公共点;(2)两个公共点;(3)没有公共点.3.求顶点在原点,焦点在x轴上且截直线2x-y+1=0所得弦长为15的抛物线方程.三、总结反思(1)本节课我们学习了抛物线的几个简单几何性质:范围、对称性、顶点坐标、离心率等概念及其几何意义. (2)了解了研究抛物线的焦半径,焦点弦和通径这对我们解决抛物线中的相关问题有很大的帮助.(3)在对曲线的问题的处理过程中,我们更多的是从方程的角度来挖掘题目中的条件,认识并熟练掌握数与形的联系.在本节课中,我们运用了数形结合,待定系数法来求解抛物线方程,在解题过程中,准确体现了函数与方程以及分类讨论的数学思想.求抛物线弦长问题的方法:(1)一般弦长公式|AB|=|x1-x2|·1+k2=|y1-y2|·1+1k2.(2)焦点弦长设AB是抛物线y2=2px(p>0)的一条过焦点F的弦,A(x1,y1),B(x2,y2),则弦长:|AB|=|AF|+|BF|=x1+x2+p.即求抛物线的焦点弦长,通常是利用焦半径,把点点距转化为点线距(点到准线的距离)解决,这体现了抛物线的特殊性以及求抛物线焦点弦的便捷特点.四、随堂检测1.抛物线x2=-8y的通径为线段AB,O为抛物线的顶点,则AB长是( )A.2B.4C.8D.12.(2015·兰州高二检测)过抛物线y2=4x的焦点作直线交抛物线于A(x1,y1),B(x2,y2)两点,如果x1+x2=6,那么|AB|= ( )A.6B.8C.9D.103.(2015·阜新高二检测)已知直线l过抛物线C的焦点,且与C的对称轴垂直,l与C交于A,B两点,|AB|=12,点P为C的准线上一点,则△ABP的面积为( )A.18B.24C.36D.484.已知过抛物线y2=6x焦点的弦长为12,则该弦所在直线的倾斜角是( )A.错误!未找到引用源。
《圆锥曲线(4):点、直线与抛物线的位置关系》导学案(复习版)

《圆锥曲线(4):点、直线与抛物线的位置关系》导学案(复习版)一.知识全解(一)点与抛物线的位置关系:1.知识:设点()00,P x y 是抛物线所在平面内的一点,则:(1)P 在抛物线内⇔(2)P 在抛物线上⇔(3)P 在抛物线内⇔2.全解:1)2)(二)直线与抛物线的位置关系1.知识:1)分类概念:(1)相离:直线与抛物线有 个交点叫相离。
(2)相切:直线与抛物线有 个交点,且不与抛物线的 平行叫相切。
(3)相交:直线与抛物线有 个交点,或与抛物线的 平行叫相交。
2)分类判定:设直线:(0)l y kx b k =+≠,抛物线2:2C y px =,联立消去y 得:2222()0k x kb p x b +-+=则:(1)当0k =时,直线与抛物线 (“相离”“ 相切”“ 相交”),且与抛物线对称轴 (“平行”或“相交”)。
(2)当0k ≠时,当0∆>时,直线与抛物线 (“相离”“ 相切”“ 相交”),有 个交点; 当=0∆时,直线与抛物线 (“相离”“ 相切”“ 相交”),有 个交点;当0∆<时,直线与抛物线 (“相离”“ 相切”“ 相交”),有 个交点。
(3)当斜率不存在时,直线与抛物线 (“相离”“ 相切”“ 相交”),有 个交点。
2.全解:1)画图说明直线与抛物线相离有哪几种位置关系?2)画图说明直线与抛物线相切有哪几种位置关系?3)画图说明直线与抛物线相交有哪几种位置关系?4)判断:(1)直线与抛物线若相切,则直线与抛物线只有一个交点;(2)直线与抛物线只有一个交点,则直线与抛物线相切;(3)直线与抛物线相交,则直线与抛物线有两个交点;(4)直线与抛物线有两个交点,则直线与抛物线相交。
(三)抛物线的弦:1.知识(1)概念:连接抛物线上任意两点的 叫抛物线的弦。
(2)性质:设AB 是抛物线的弦,直线AB 的斜率为k ,()11,A x y ,()22,B x y ,弦中点()00,M x y 。
圆锥曲线导学案.docx

.2.1.1 椭圆及其标准方程(第 1 课时)高二·一部数学组文2017 年4月3日【学习目标】1、能从具体情境中抽象出椭圆的模型;2、理解椭圆的定义,会求椭圆的标准方程.【学习重点】1、理解椭圆的定义和标准方程;2、认识椭圆标准方程的特征.【学法指导】1、带着预习案中问题导学中的问题自主设计预习提纲,通读教材容,对概念、关键词进行梳理,作好必要的标注和笔记。
2、认真完成基础知识梳理,在“我的疑惑”处填上自己不懂的知识点,在“我的收获”处填写自己对本课自主学习的知识及方法收获。
3、熟记基础知识梳理中的重点知识。
【自主学习】一、问题导学在椭圆的标准方程中,a2和 b2能相等吗?二、知识梳理1.椭圆的定义:我们把与两个定点F1, F2的等于常数()的点的轨迹叫做椭圆.这两个定点叫做椭圆的,两间的距离叫做椭圆的.用数学符号可以把定义表示为.2.椭圆的标准方程:( 1)当在x轴上时,标准方程为().当在 y 轴上时,标准方程为().( 2)参数a,b, c之间的关系是:① 等量关系;② 不等关系三、预习自测1.已知A3,0 , B 3,0 ,动点 M 分别满足下列关系,问:M的轨迹是否存在,若存在,是什么曲线?(1)MA MB 10;(2)MA MB 6;(3)MA MB 4.2.已知椭圆的方程如下,写出a, b, c 的值及焦点坐标:.( 1) x2y 21; ( 2)x 2y 21; (3) x 2 2 y 2 2 .25 916 253.写出适合下列条件的椭圆的标准方程:( 1) a4, b 1,焦点在 x 轴上;( 2) a 4, c 15 ,焦点在 y 轴上;( 3) a 10, c 6【合作探究】判断下列方程是否表示椭圆,若是,写出a, b, c 及焦点坐标x 2 y 2 x 2y 2 x 2y 2 x 2 y 2 2 3y 21.( 1)41;(2)1;(3) 1;(4)41;( 5) 2x443343【拓展延伸】已知 F 11,0 , F 2 1,0 是椭圆的两个焦点,并且经过点A 1,3,求它的标准方程.2【当堂检测】 1.若 F 1, F 2 分别是椭圆 3x 2 5y 230 的左、右焦点, M 是椭圆上的任一点, 且 MF2 ,1则 MF 2.2 .已知椭圆 kx 2y 2 1的焦点在 x 轴上,则 k 的取值围是.3 .写出适合下列条件的椭圆的标准方程: ( 1)焦点在 x 轴上,焦距等于4 ,并且经过点 P 0, 3 ;( 2) a c 9, a c 1..: 2.1.1 椭圆及其标准方程(第 2 课时)高二·一部数学组文2017 年 4 月 3 日【学习目标】1、理解椭圆定义,掌握椭圆的标准方程;2、会求与椭圆有关的轨迹问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《圆锥曲线(3):抛物线的基本知识》导学案(复习版)一. 知识全解(一)概念1・知识:1) __________________________________________ 定义:平面内与一个定点F 和一条定直线/( ___________________________________________ )的距离—的点的轨迹叫做抛物 线,点F 叫做抛物线的—,定直线/叫做抛物线的 _________ c (简称:一动两定距离相等)2) 定义式:设动点为M,定点为F,定直线为且动点到定点距离为|MF|,动点到定直线 的距离为d ,则由抛物线的定义可知抛物线上的点满足 _______________2 •全解:1) 平面内与一个定点F 和一条定直线/的距离相等的点的轨迹是抛物线,对吗?为什么? 2) 平面平面内与一个定点F 和一条定直线/(/不过F )的距离不等的点的轨迹一定不是抛 物线,对吗?为什么?3) 判断下列轨迹是不是抛物线,若是指出焦点和准线。
(二)标准方程1・知识:1)标准方程:(1) _____________________________________________________ 焦点在兀轴正半轴: (2) ________________________________________________ 焦点在y 轴正半轴: (3) ________________________________________________ 焦点在牙轴负半轴: (4) ________________________________________________ 焦点在y 轴负半轴: 2) 标准方程下的图形:(1) ________________________________________________ 焦点在兀轴正半轴: (2) ________________________________________________ 焦点在y 轴正半轴: (3) ________________________________________________ 焦点在牙轴负半轴: (4) ________________________________________________ 焦点在y 轴负半轴: 3) 焦点坐标:(1)标准方程为y 2=2px (p > 0) u>焦点坐标是 ___________ (2) _____________________________________________ 标准方程为x 2=-2py (p>0) <^>焦点坐标是 ___________________________________________(3) _____________________________________________ 标准方程为于=2卞(/7>0)0焦点坐标是 _____________________________________________ 。
(4) _____________________________________________ 标准方程为兀2 = -2py (p > 0) O 焦点坐标是 _________________________________________ o4)准线方程:(1) (2) (3过定点且与定直线 动点M 到点F (4, 动点M 到点F (4, 动点M 到点F (4, (不过定点)相切的动圆的圆心的轨迹。
0)的距离与它到直线l:x = -6的距离相等, 0)的距离比它到直线l:x = -6的距离大2, 0)的距离比它到直线l:x = -6的距离小2, 则点M 的轨迹。
则点M 的轨迹。
则点M 的轨迹。
(1)标准方程为y2=2px(p > 0) O准线方程是_____________ o(2)标准方程为x2 =-2py(p>Q)^准线方程是______________(3) _____________________________________________ 标准方程为y2=2px(p>0)^>准线方程是 ______________________________________________ o(4) _____________________________________________ 标准方程为x2=-2py(p>0)^准线方程是 ______________________________________________ o2 •全解:1)在利用轨迹法求抛物线标准方程时,是如何建立直角坐标系的?2)标准方程特征:(1)整体上是—元—次—项等式;(2)局部上等号左边的项是—元—次式,且系数为_;等号右边—元—次式,且系数为—。
3)__________________________________________________________________ 参数意义:标准方程中参数P的几何意义是 ___________________________________________ 。
4)知道抛物线的标准方程,如何确定其焦点的位置?(先定轴后定向)3)知道抛物线的标准方程,如何求准线方程?(先定变量后定方向)4)下列方程是抛物线方程,若是请将英化成标准形式,并指出焦点、准线以及画出草图。
(1)4x2-3y=0 ;(2)2>,2+A/3X = 0 o(3)2y2 = x;(4)x2 +4y = 0 o5)根据下列条件,直接写出抛物线的标准方程(1)焦点坐标为(2, 0)o3(2)准线x = — o2(3)焦点到准线的距离是2A/2 o(三)简单性质1・知识:1)对称性:抛物线是轴对称图形,标准情况下,其对称轴:(1)_______________________________________ 标准方程为y2=±2px(p>0)^对称轴是o(2) _______________________________________ 标准方程为x2= ±2py(p>0)^对称轴是o2)范围:(1)______________________________________________ 标准方程为y2 =2px(p > 0) o范围是。
(2) _________________________________________ 标准方程为x2=-2py(p>0) <^>范围是 ______________________________________________(3) _________________________________________ 标准方程为y2 = 2px(p>0) o范围是o(4)_________________________________________ 标准方程为x2 =-2py(p>0) o范围是。
3)___________________ 顶点:抛物线和_________________________ 的交点叫其顶点,标准情况下顶点为 ________ 。
4离心率(1)定义:________________________________________________________(2)収值:_____2 .全解:1)抛物线有儿条对称轴,其对称轴和坐标轴是什么关系?2)抛物线是无界曲线吗?为什么?3)抛物线的顶点是原点,对吗?4)抛物线的离心率与椭圆的离心率有何区别?5)抛物线焦点、顶点、准线与其对称轴之间的位置关系是什么?6)指出下列抛物线的顶点、焦点、准线、对称轴、范围。
.3(1)宀一y;4・(2)(3)八討(4)x2 =-4y o二.技能全解1.利用定义法求抛物线的标准方程例1:点M到点F(4, 0)的距离比它到直线Z:x + 6 = 0的距离小2.求点M的轨迹。
变式:点M到点F(3, 0)的距离比它到直线l:x = -l的距离大2.求点M的轨迹。
2.利用待定系数法求抛物线的标准方程例2:求过点A(-3,2V6)的抛物线的标准方程。
变式:求过点(73,-6 )的抛物线的标准方程。
3.根据抛物线的标准方程求其简单的几何性质。
例3:求抛物线y2=12y/3x的对称轴、范围、顶点、焦点、准线、通径,并画出草图。
变式:求抛物线x2=-8y的对称轴、范围、顶点、焦点、准线、通径,并画出草图。
三.题型全解1・求抛物线的标准方程例1:动圆P与定圆C:(x-l)2 + y2 = 1外切且与y轴相切,求圆心P的轨迹。
变式:点A(-2, 0)关于P的对称点为B,当P在抛物线y = 2x2±移动时,求B点的轨迹。
例2:求对称轴是坐标轴,焦点在直线3兀-4y-12 = 0上的抛物线标准方程。
变式:求对称轴是坐标轴,焦点在直线3x-5y-36 = 0上的抛物线标准方程。
例3:已知抛物线的顶点在原点,焦点在坐标轴上,J1其上一点A (—3, m)到焦点F 的 距离是5,求抛物线的方程。
变式:如图24,直线厶和厶相交于点M,厶丄厶,点NJ 、, 以A 、B为端点的曲线段C 上的任一点到人距离与到点N 的距离相等,若厶AMN 为锐角三角形,|AN|=3, |BN|=6,建立适当的坐标系,求曲线段C 的方程。
2 •求抛物线的简单性质例4:求抛物线x 2 = ay(a 0)的对称轴、范围、顶点、焦点、准线、通径。
变式:求抛物线y 2=px(p^0)的对称轴、范围、顶点、焦点、准线、通径。
四. 针对演练1. 抛物线y = 2x 2的焦点坐标是( ) A. B. C ・ D.(2 , (8 > < 8< 4丿2. 动点P 到直线x + 4 = 0的距离与它到点M(2,0)的距离之差为2,则点P 的轨迹是 ( )A.直线B.椭圆C.双曲线D.抛物线3. 圆心在y 2 = 2x 上,且与x 轴及抛物线准线均相切的圆的方程是( )Utl UU1U 4. 设O 为坐标原点,F 为抛物线y 2 = 4x 的焦点,A 为抛物线上一点,若OA AF = -4, 则点A 的坐标为( )A. (2,±2V2); B ・(1,±2); C. (1,2); D. (2,20)。
5. 抛物线尸=8兀上一点P 到顶点的距离等于它们到准线的距离,这点坐标是A. (2, 4)B. (2, ±4)C. (1, 2V2 )D. (1, ±2迈)2 26. 若抛物线y 2=2px 的焦点与椭圆^- + ^- = 1的右焦点重合,则卩的值为() A. -2 B. 2 C. -4 D.47. 过抛物线b=4x 的焦点作直线交抛物线于A(x } , yj, 〃(吃,儿)两点,如果(1 y .A. x ——+(y - 2)~ = 1 C. (x-l)2+(y-2)2 =4 1 y 9B. x ——+ (y± 1)~ = 1\ 2丿 D. (x-l)2+(y±2)2 =4A. 10 B・ 8 C. 6 D. 48.过点(2, -3)的抛物线的标准方稈是___________________________________________ o9.抛物线y2=2x±的两点A、B到焦点的距离之和是5,则线段中点的横坐标是10. __________________________________________________________ 焦点在直线x-2y-4 = 0上的抛物线的标准方程_________________________________________11.已知抛物线),=-6兀,以此抛物线的焦点为圆心,且与抛物线的准线相切的圆的方程是 ___________________________ O12.抛物线y2 =2px(p>0)有一内接直角三角形,直角顶点在原点,一直角边的方程是y=2x,斜边长为5JJ,求此抛物线方程。
