平面弯曲问题
合集下载
第1节 平面弯曲的概念和实例
第七章 直梁弯曲时的内力和应力
第七章 直梁弯曲时的内力和应力
第七章 直梁弯曲时的内力和应力
二、静定梁的基本形式 梁的支座形式：工程中常见的梁的支座有以下三 种形式。 1）固定铰支座：如图a所示，固定铰支座限制梁在 支承处任何方向的线位移，其支座反力可用两个正 交分量表示，即沿梁轴线方向的 FAx 和垂直于梁轴 线方向的FAy。
第七章 直梁弯曲时的内力和应力
第一节
平面弯曲的概念和实例
一、平面弯曲 弯曲变形：当杆件受到垂直于轴线的外力作用或 受到作用面平行于轴线的外力偶作用时，杆件的 轴线会由直线变为曲线，这种变形称弯曲变形。 梁：以弯曲变形为主的杆件称作梁。 直梁：工程中常见的轴线是直线的梁。 平面弯曲：若梁的外力及支 座反力都作用在纵向对称面 内，则梁弯曲时轴线将变成 此平面内的一条平面曲线， 该弯曲变形称为平面弯曲。
或
第七章 直梁弯曲时的内力和应力 2）活动铰支座：如图b所示，活动铰支座只能限制 梁在支承处垂直于支承面的线位移，支座反力可用 一个分量FRA表示。 3）固定端支座：如图c所示，固定端支座限制梁在 支承处的任何方向线位移和角位移，其支座反力有 两个正交力FAx、FAy和一个力偶分量MA。
或
MA
第七章 直梁弯曲时的内力和应力 静定梁的形式：根据梁的支座情况，工程中常见 的静定梁可以简化成以下三种形式。 1）简支梁：梁的支座一端是 固定铰支座，另一端是活 动铰支座。 2）外伸梁：梁的支座与简支 梁相同，只是梁的一端或 两端伸出在支座之外。 3）悬臂梁：梁的一端自由， 另一端是固定支座。
第七章 直梁弯曲时的Biblioteka 力和应力三、梁上载荷的简化
1）集中力：集中力作用在梁上的很小一段范围内， 可近似简化为作用于一点，如图所示的力F。单位 为牛顿（N）或千牛顿（kN）。 2）集中力偶：作用在微小梁段上的力偶，可近似 简化为作用于一点，如图所示的力偶M。单位为牛 顿· 米（N· m）或千牛顿· 米（KN· m）。 3）分布载荷：沿梁轴线方 向、在一定长度上连续分布 的力系，如图所示的均布载 荷q。其大小用载荷集度表 示，单位为牛顿/米（N/m） 或千牛/米（kN/m）。
弹性力学：平板弯曲问题的有限元分析(1)
其中为薄板的弯曲刚度9899薄板的弹性曲面微分方程薄板横截面上的内力称为薄板横截面上的内力称为薄板内力薄板内力是指薄板横截面的单是指薄板横截面的单位宽度上由应力合成的位宽度上由应力合成的主矢量主矢量和和主矩主矩
平板弯曲问题的有限元分析(1) Kirchhoff弹性薄板理论
参考文献： “弹性力学(下册)”第13章。徐芝纶
x
2w
2 (z2
2
2
)dz 4
E 3 12(1 2 )
x
2w
(c)
同样，在y为常量的截面上，每单位宽度内的 y , yx , yz
也分别合成如下的弯矩，扭矩，和横向剪力：
M y
2 2
z
y dz
E
12(1
3
2
)
(
2w y2
2w x2
)
(d)
M yx
2
2
z yxdz
E 3 12(1 2 )
(9-6)
( z )z q
(f)
2
将(9-6)式代入薄板上板面的边界条件：
得：
E
12(1
3
2
)
4
w
q
(9-7)
或 D4w q， (9-8)
其中
D
E
12(1
3
2
)
(9-9)
薄板的弹性曲面微分方程
为薄板的弯曲刚度
§9-３ 薄板横截面上的内力
► 薄板横截面上的内力，称为薄板内力，是指薄板横截面的单 位宽度上，由应力合成的主矢量和主矩。
对z积分，得到： z
2(1 2 )
2
( 4
z
z2 )4w 3
F3 (x,
平板弯曲问题的有限元分析(1) Kirchhoff弹性薄板理论
参考文献： “弹性力学(下册)”第13章。徐芝纶
x
2w
2 (z2
2
2
)dz 4
E 3 12(1 2 )
x
2w
(c)
同样，在y为常量的截面上，每单位宽度内的 y , yx , yz
也分别合成如下的弯矩，扭矩，和横向剪力：
M y
2 2
z
y dz
E
12(1
3
2
)
(
2w y2
2w x2
)
(d)
M yx
2
2
z yxdz
E 3 12(1 2 )
(9-6)
( z )z q
(f)
2
将(9-6)式代入薄板上板面的边界条件：
得：
E
12(1
3
2
)
4
w
q
(9-7)
或 D4w q， (9-8)
其中
D
E
12(1
3
2
)
(9-9)
薄板的弹性曲面微分方程
为薄板的弯曲刚度
§9-３ 薄板横截面上的内力
► 薄板横截面上的内力，称为薄板内力，是指薄板横截面的单 位宽度上，由应力合成的主矢量和主矩。
对z积分，得到： z
2(1 2 )
2
( 4
z
z2 )4w 3
F3 (x,
弯曲-理论力学,经典
②精确适用于纯弯曲梁；
③对于横力弯曲的细长梁(跨度与截面高度比l/h>5)，
上述公式的误差不大，但公式中的M应为所研究截面
上的弯矩，即为截面位置的函数。
M ( x) y 1 M ( x) , Iz ( x) EI z
26 材料力学多媒体_孙艳 例题
b III、三种典型截面对中性轴的惯性矩 1.矩形截面 h
2qa 2qa FS图
2qa2
M图
6qa2
15 材料力学多媒体_孙艳 例题
Ⅱ、平面曲杆 面内受力时的内力——轴力、剪力、弯矩 弯矩的符号约定——使杆的曲率增加（即外侧受拉） 为正 作平面曲杆内力图的约定与刚架相同。 F m B m
A
材料力学多媒体_孙艳
R
O
16 例题
例 一端固定的四分之一圆环，半径为R，在自由端 B受轴线平面内的集中荷载F作用如图，试作出其内 力图。 F h F m FS( B m FN( z M R ( A O O 解：取分离体如图写出其任意横截面m-m上的内力 方程： FN F sin 0 π/2
E
E
A
ydA E I yz 0
E
Sz 0
中性轴z通过截面形心
(2) M y
A
zydA
(3) M z y dA
A
E
A
y dA
2
E
Iz M
M EI z
24
1
材料力学多媒体_孙艳
例题
4.纯弯曲梁横截面上的应力(弯曲正应力)：
My ①距中性层y处的应力： Iz ②梁的上下边缘处，弯曲正应力取得最大值，分别 为：
第四章 平面弯曲解析
14
4.2.2 剪力方程和弯矩方程 剪力图和弯矩图
(1)剪力方程和弯矩方程
剪力和弯矩沿着梁轴线分布的数学表达 式:
Q=Q(x) M=M(x)
(2)剪力方程和弯矩图
以x为横坐标，剪力Q为纵坐标→Q-x图。 以x为横坐标，弯矩M为纵坐标→M-x图。
15
[例4-1] 试作出如图所示简支梁的剪力图和弯矩图。
第4章 平面弯曲
平面弯曲计算 简单超静定梁的求解 压杆的稳定性简介
1
第
4.1 平面弯曲的概念和实例
4
4.2 平面弯曲的内力分析
章
4.3 平面弯曲的正应力计算
4.4 平面弯曲的变形计算
平
面 4.5 简单超静定梁的求解
弯 曲 4.6 压杆稳定性简介
目录
2
4.1 平面弯曲的概念和实例
(1)实例：
桥式起重机
A
y 2 dA
2 h
y2
bdy
b13
2
y
3
2
h
2
bh3 12
bh3
WZ
IZ ym ax
12
h
2
bh2
6
28
(2)圆形截面
D
Iz
y2dA
A
3 sin 2 dd
2
2
3d sin 2 d
D 4
0
0
64
(3)圆环形截面
Wz
Iz ymax
D4 64 D3
D 2 32
内径为d 外径为
2) 纵线(a-a,b-b)弯曲成曲线， 且梁的一侧伸长，另一侧缩 短。
纯弯曲梁的变形特点 图4-10 纯弯曲梁的变形特点
平面弯曲
z z A A A z
•
有
EIz
1 M = M及 = ρ ρ EIz
式中，1/ρ表示中性层的曲率。反映梁产生弯曲变 形的程度；EIz表示梁抵抗弯曲变形的能力，称为 抗弯刚度。由式(4-44)可知，在指定截面上M为一 定值时，梁的抗弯刚度越大，曲率越小，梁的弯 曲变形也越小。 将 σ = E ⋅ ε = E y 代入得
ρ
My σ = Iz
式(4-45)是计算梁在纯弯曲时横截面上任意一点的 正应力公式。 式中，M——横截面上的弯矩； y——所求点到中性轴的距离； Iz——整个截面对中性轴的惯性矩。 正应力σ的正负号可根据变形判断，以中性轴为界 ，变形后凸边的纤维受拉，应力为正(拉 应力) ，凹边的纤维受压，应力为负(压应力)。
(2) 求梁的最大正应力值，及最大正应力值发生的 位置。该梁为等截面梁，在全梁范围内惯性矩为 一常数，任意截面的上下边缘至截面中性轴的距 离均相等。所以最大正应力发生在最大弯矩截面 的上下边缘处。 则最大正应力为
M max
ql 2 2 × 52 = = kN ⋅ m = 6.25kN ⋅ m 8 8 M max ymax M max h 6.25 × 106 × 200 = = = = 6.25N/mm 2 = 6.25MPa 8 IZ 2I Z 2 × 10
距中性轴y处的纵向纤维 a1a2的原长为，变形后 的长度，所以纤维的 伸长量为，相应的纵 向线应变为： ydφ y ε= = ρ dφ ρ 上式表明：各纤维的纵 向线应变与它到中性 层的距离成正比
距中性层最远的上、下 边缘处的线应变最大 ，而中性层上线应变 为零。
2. 物理方面 假设梁在纯弯曲时纵向 纤维之间无挤压作用 ，梁内各点处于单向 受力状态，材料在线 弹性范围内。则
•
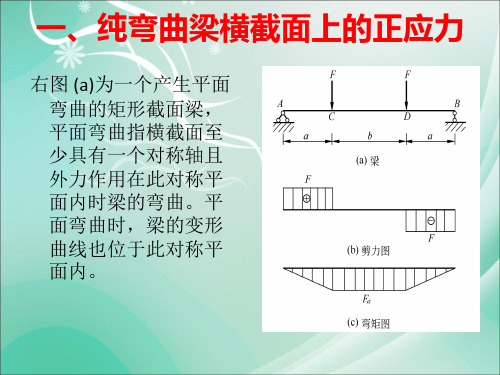
有
EIz
1 M = M及 = ρ ρ EIz
式中，1/ρ表示中性层的曲率。反映梁产生弯曲变 形的程度；EIz表示梁抵抗弯曲变形的能力，称为 抗弯刚度。由式(4-44)可知，在指定截面上M为一 定值时，梁的抗弯刚度越大，曲率越小，梁的弯 曲变形也越小。 将 σ = E ⋅ ε = E y 代入得
ρ
My σ = Iz
式(4-45)是计算梁在纯弯曲时横截面上任意一点的 正应力公式。 式中，M——横截面上的弯矩； y——所求点到中性轴的距离； Iz——整个截面对中性轴的惯性矩。 正应力σ的正负号可根据变形判断，以中性轴为界 ，变形后凸边的纤维受拉，应力为正(拉 应力) ，凹边的纤维受压，应力为负(压应力)。
(2) 求梁的最大正应力值，及最大正应力值发生的 位置。该梁为等截面梁，在全梁范围内惯性矩为 一常数，任意截面的上下边缘至截面中性轴的距 离均相等。所以最大正应力发生在最大弯矩截面 的上下边缘处。 则最大正应力为
M max
ql 2 2 × 52 = = kN ⋅ m = 6.25kN ⋅ m 8 8 M max ymax M max h 6.25 × 106 × 200 = = = = 6.25N/mm 2 = 6.25MPa 8 IZ 2I Z 2 × 10
距中性轴y处的纵向纤维 a1a2的原长为，变形后 的长度，所以纤维的 伸长量为，相应的纵 向线应变为： ydφ y ε= = ρ dφ ρ 上式表明：各纤维的纵 向线应变与它到中性 层的距离成正比
距中性层最远的上、下 边缘处的线应变最大 ，而中性层上线应变 为零。
2. 物理方面 假设梁在纯弯曲时纵向 纤维之间无挤压作用 ，梁内各点处于单向 受力状态，材料在线 弹性范围内。则
工程力学习题库-弯曲变形
第8章 弯曲变形本章要点【概念】平面弯曲，剪力、弯矩符号规定，纯弯曲，中性轴，曲率，挠度，转角。
剪力、弯矩与荷载集度的关系；弯曲正应力的适用条件；提高梁的弯曲强度的措施；运用叠加法求弯曲变形的前提条件；截面上正应力分布规律、切应力分布规律。
【公式】 1. 弯曲正应力 变形几何关系：yερ=物理关系：Ey σρ=静力关系：0N AF dA σ==⎰，0y AM z dA σ==⎰，2zz AAEI EM y dA y dA σρρ===⎰⎰中性层曲率：1MEIρ=弯曲正应力应力：，My Iσ=，max max z M W σ=弯曲变形的正应力强度条件：[]maxmax zM W σσ=≤ 2. 弯曲切应力矩形截面梁弯曲切应力：bI S F y z z S ⋅⋅=*)(τ，A F bh F S S 2323max ==τ工字形梁弯曲切应力：dI S F y z z S ⋅⋅=*)(τ，A F dh F S S ==max τ圆形截面梁弯曲切应力：bI S F y z z S ⋅⋅=*)(τ，A F S 34max =τ弯曲切应力强度条件：[]ττ≤max3. 梁的弯曲变形梁的挠曲线近似微分方程：()''EIw M x =-梁的转角方程：1()dwM x dx C dx EIθ==-+⎰ 梁的挠度方程：12()Z M x w dx dx C x C EI ⎛⎫=-++ ⎪⎝⎭⎰⎰ 练习题一. 单选题1、 建立平面弯曲正应力公式zI My /=σ,需要考虑的关系有（）。
查看答案A 、平衡关系,物理关系，变形几何关系B 、变形几何关系，物理关系，静力关系；C 、变形几何关系，平衡关系，静力关系D 、平衡关系, 物理关系，静力关系；2、 利用积分法求梁的变形，不需要用到下面那类条件（）来确定积分常数。
查看答案A 、平衡条件B 、边界条件C 、连续性条件D 、光滑性条件3、 在图1悬臂梁的AC 段上，各个截面上的（）。
《平面弯曲变形》课件
平面弯曲变形的应用实 例
桥梁和建筑结构的平面弯曲变形分析
桥梁结构：桥梁 的平面弯曲变形 分析，包括梁、 拱、索等结构
建筑结构：建筑结构 的平面弯曲变形分析， 包括框架、剪力墙、 筒体等结构
变形原因：荷载、 温度、湿度、地 震等外部因素引 起的变形
变形影响：对结构 安全性、稳定性、 耐久性的影响
变形控制：通过设 计、施工、维护等 手段控制变形，保 证结构安全
剪切应力的分布规律：剪切应力在剪切面上分布不均匀，靠近剪切面中心处应力较小， 远离剪切面中心处应力较大
剪切应力的影响因素：剪切力、剪切面形状、材料性质等
剪切应力的应用：在工程设计中，需要考虑剪切应力对结构的影响，以避免结构破坏 或失效。
平面弯曲变形的能量平 衡
弹性势能与动能之间的关系
弹性势能：物体在弹性形变过 程中储存的能量
感谢观看
汇报人：
平面弯曲变形可以分为弹性变形和塑性变形两种类型。
弹性变形是指物体在外力作用下，其形状和尺寸发生变化，但外力消失后，物体可以 恢复到原来的形状和尺寸。
塑性变形是指物体在外力作用下，其形状和尺寸发生变化，但外力消失后，物体不能 恢复到原来的形状和尺寸。
平面弯曲变形的分类
弯曲变形：物体在外力作用下发生弯曲变形 扭转变形：物体在外力作用下发生扭转变形 弯曲-扭转变形：物体在外力作用下同时发生弯曲和扭转变形 弯曲-弯曲变形：物体在外力作用下同时发生弯曲和弯曲变形
平面弯曲变形的稳定性 分析
稳定性分析的基本概念
稳定性分析的目的：确定结构在受力作用下的稳定性 稳定性分析的方法：有限元分析、能量法等 稳定性分析的指标：临界载荷、临界应力等 稳定性分析的应用：结构设计、优化等
稳定性分析的方法和步骤
第十一章 弯曲问题的进一步研究与组合变形
max
M z ,max Wz M y ,max Wy
19.3 103 5.18 103 6 402 10 48.3 106
155 106 Pa 155MPa
故此梁满足正应力强度条件
讨论：若F力的作用线与y轴重合，即＝0，则梁的最大正应力为 M max 20 103 6 max 49.8 10 Pa 49.8MPa 远小于155MPa 6 Wz 402 10
对称轴
FA
问题：当梁不具有纵向对称平面，或梁虽具有纵向对称平面，但 外力的作用面与该纵向对称平面间有一夹角，则该梁发生什么变 形呢？
F
F F
z
C
F
C
z
C
z
y
y
y
斜弯曲
斜弯曲
平面弯曲与扭转
工程中的许多受力构件往往同时发生两种或两种以上的基本变形， e 称为组合变形。 F
Me
F
（轴向压缩 和弯曲） 偏心压缩
a
z
C
wz
wy b
y
z
z
C
a
F
w
y
F
y
F
讨论： （1）若梁的截面是正方形，由于Iy=Iz，所以b =，故梁不会 发生斜弯曲，而发生平面弯曲。正多边形也是如此。 （2）若梁的截面是圆形，由于Iy=Iz，所以b =，故梁不会发 生斜弯曲，而发生平面弯曲。
例11-2 外力F通过截面形心，且与y方向的 夹角＝15°，材料许用应力[170MPa, 试校核此梁的强度。 解： 梁跨中截面上的弯矩最 2m 大，故为危险截面，该截面 上的弯矩值为 M Fl 1 20 4 20kN.m
例11-1 悬臂梁的横截面分别采用如图所示三种截面，在自由 端受集中力F作用，F力均通过这些截面的形心C。试指出这三 种截面梁各产生何种变形形式。
M z ,max Wz M y ,max Wy
19.3 103 5.18 103 6 402 10 48.3 106
155 106 Pa 155MPa
故此梁满足正应力强度条件
讨论：若F力的作用线与y轴重合，即＝0，则梁的最大正应力为 M max 20 103 6 max 49.8 10 Pa 49.8MPa 远小于155MPa 6 Wz 402 10
对称轴
FA
问题：当梁不具有纵向对称平面，或梁虽具有纵向对称平面，但 外力的作用面与该纵向对称平面间有一夹角，则该梁发生什么变 形呢？
F
F F
z
C
F
C
z
C
z
y
y
y
斜弯曲
斜弯曲
平面弯曲与扭转
工程中的许多受力构件往往同时发生两种或两种以上的基本变形， e 称为组合变形。 F
Me
F
（轴向压缩 和弯曲） 偏心压缩
a
z
C
wz
wy b
y
z
z
C
a
F
w
y
F
y
F
讨论： （1）若梁的截面是正方形，由于Iy=Iz，所以b =，故梁不会 发生斜弯曲，而发生平面弯曲。正多边形也是如此。 （2）若梁的截面是圆形，由于Iy=Iz，所以b =，故梁不会发 生斜弯曲，而发生平面弯曲。
例11-2 外力F通过截面形心，且与y方向的 夹角＝15°，材料许用应力[170MPa, 试校核此梁的强度。 解： 梁跨中截面上的弯矩最 2m 大，故为危险截面，该截面 上的弯矩值为 M Fl 1 20 4 20kN.m
例11-1 悬臂梁的横截面分别采用如图所示三种截面，在自由 端受集中力F作用，F力均通过这些截面的形心C。试指出这三 种截面梁各产生何种变形形式。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
将三个结点的位移和面积坐标代入上式，可
得：a1=wi ， a2=wj， a3=wm。代入上式对Li ，Lj求导，注意Lm=1-Li-Lj，可得
L w i w iw ma4Lja5(L mL i)a6Lja7(L 2 j2LjL m ) a8(4L iL mL 2 i L 2 m )a9(L 2 j2L iLj)
Li Lj Lm及其一阶导数在三个结点为零， 对于确定待定参数 无用；考虑到用结点位移表示待定参数时计算方便，不考虑二
次和三次的前三项。因此，只能在剩下的6个三次项中选择三 个或利用某种线性组合。考虑对称性，假设位移模式为：
w=α1L1+α2L2+α3L3+α4L12L2+21L1L2L3+α5L22L1+21L1L2L3 +α6L22L3+21L1L2L3+α7L32L2+21L1L2L3 +α8L32L1+21L1L2L3 +α9L12L3+21L1L2L3
第十章 平板弯曲问题
主要内容：
薄板弯曲理论基本假设和基本方程 基于薄板理论的非协调板单元 基于薄板理论的协调板单元
1、薄板弯曲理论基本假设和基本方程
基本假设 ——Kirchhoff假设
（1）直法线假设：薄板中面法线变形后仍保持为法线 。由此，板中面内剪应变为零。
（2）忽略板中面的法线应力分量，且不计其引起的应 变。
薄板弯曲问题中的弹性矩阵[D]
[D]12(1E3t 2)1
1
0
1
10D0
1
0
0
1
0 0 2 0 0 2
D0
Et3
12(1
2)
➢内力矩表示薄板应力的公式
{}1t23z{M}
平衡方程
2M x2x2 2x M yx y 2M y2yq(x,y)0
由广义应力应变关系及几何关系代入平衡方程得 由W的微分方程：
对于三角形单元，面积坐标的一、二、三次齐次分
别有以下项：
一次项Li,： Lj,Lm
二次 L 2 i,L 2 j项 ,L 2 m ,L iL ： j,L jL m ,L m L i
Li Lj Lm 1
Li
Ai A
三 L 3 i, 次 L 3 j,L 3 m ,L 2 iL j, 项 L 2 jL m ,L 2 m L i,L ： iL 2 j,L jL 2 m ,L m L 2 i,L iL jL m
每个角结点有6个参数 w i, w x i, w y i, 2 x w 2 i, 2 y w 2 i, x 2 w y i,i 1 ,2 ,3
每个边中结点有1个参数
w n k
,k
4,5,6
共21个条件恰好可以确定21个待定系数
每个边界w是5次变化，两端节点分别有6个结点参数：
j,m)
Nji 12LiLj 12(LiL2j L2iLj)
利用：w,Li Lwi cj w x bj w y bjx cjy
w,Lj
w Lj
ci
w x bi
w y bix
ciy
bi yi ym, ci xmxi
(i, j,m)
将w,Lii和w,Lji变换成θxi、 θyi，从而得到相应于θxi、 θyi的形函数Nxi、 Nyi
L w j w jw ma4(L mL j)a5L ia6L ia7(L 2 jL 2 m4L jL m ) a8(2L iL mL 2 i)a9(2L iL jL 2 i)
将结点的面积坐标代入上述两式，可得6个关 于a4~a9的方程，求解后可得a4~a9：
a4
1 2
( w , Ljj w , Ljm
{}z{}
应力
x
{}y[Dp]{}z[Dp]{}
xy
[D0 ]
E
1
2
1
1
0
0
1
0 0 2
内力：板单位宽度
上弯矩Mx 、 My和 Mxy ，为应力分量 在板截面上的合力
矩：
Mx
t
[M]My Mxy
2 t
z{}dz
2
弹性矩阵
t
2 t
2
z2[Dp
]{}dz
t3 12[Dp
]{}
[D][]
{ai}
单元结点位移列阵
a1
{a}e
a
2
w
i xi
yi
w
i
(
w y
)
i
w ( x ) i
a
3
a 4
2、位移模式
矩形薄板单元有4个结点，12个结点位移分 量，1个挠度独立变量，根据选取位移函数的原 则，取：
w (x ,y ) a 1 a 2 x a 3 y a 4 x 2 a 5 x y a 6 y 2 a 7 x 3 a 8 x 2 y a 9 x2 y a 1y 0 3 a 1x 1 3 y a 1x 2 3y
),
a5
1 2
( w , Lii w , Lim
),
a6
1 2
( w , Lii w , Lij w , Lji w , Ljj
),
a7
w j
wm
1 2
( w , Ljj
w , Ljm
)
a8
wi
wm
1 2
( w , Lii w , Lim
)
w,Lij 表示w对Li的 偏导数在j点的值。
在常应变下，校正函数对项恒为零，对原来位移函数W0
的完备性没有干扰。且边界上的法向导数 w n 可以唯一
的确定。故单元是协调元。
3、多结点参数的协调元
多结点参数：结点参数中除w和 w n 外，还包含 w的二阶导数，甚至更高阶项。
Eg：图示的三角形板单元， 位移采用完全5次多项式，其 中包含21个待定系数，可以用 21个结点的条件决定。
wi
,
w s
i
,
2w s2
i
可唯一的确定边界上5次变化的w，
在边界上位移w是协调的
在每个边界 w
n
是4次变化，两端节点分别有4个结点
参数
w n
i
,
2w ns
i
还有边中结点
w n
共5个结点参数
w
可唯一确定边界上4次变化的 n
，在边界上 w
n
是协调的
故这种单元完全满足协调性要求
{P }eqa 1b ba1b a1ba1ba
3 3 3 3 33 3 3
非协调板单元可以通过分片试验，当单元划分不断缩 小时，计算结果可以收敛于精确解答，但是收敛并非 一定是单调的，即不一定是精确解的上界或下界。
2.2 薄板三角形单元
a 1 a 2 x a 3 y a 4 x 2 a 5 x a 6 y y 2 a 7 x 3 a 8 x 2 y a 9 x 2 a 1 y y 3 0
3、基于薄板理论的协调板单元
非协调板单元的收敛性是以分片试验为条件的即使收 敛也非单调，不能对解的上下界作出估计。
经典薄板理论范围内使板单元满足协调性 要求的方法：
1）增加结点参数 结点参数中包含w的二次导数 项
2）保持结点3个参数前提下采取其他措施，如附加 校正函数法、在分割法等。
1、3结点的协调元
1-3项刚体位移 4-5项常应变
单元间法线导数 可能不连续
非协调元
将结点坐标和结点位移代入上式，可解出 a1~a12，再代入该式并整理得位移函数
w[N]{a}e
式中形函数
[N ][N 1N 2N 3N 4] [N]i [Ni NxiNy]i
Ni
81(1i)(1i)(2i
i2
2
Nxi 81bi(1i)(1i)(12) Nyi 81ai(1i)(1i)(12)
问题：
1、为什么结点位移参数
要取
yi
w ？x i
2、在矩形单元中四结点12自由度薄板单元位移四次
项为什么选x3y和xy3,而没有选其它四次项？选用x4
和y4将导致什么结果？
3、四结点12自由度薄板单元挠度和转角协调，法向 转角不协调，所以称其为非协调元，如何来证明？
4、对于非协调的矩形单元除广义坐标法外还有什么 方法可更容易的确定插值函数？
（3）薄板中面内的各点没有平行于中面的位移，即中 面不 变形。
利用上述假设将平板弯曲问题转化为二维问题， 且全部应力和应变可以用板中面挠度w表示。
w w (x,y) uw z vw z
x
y
基本方程
(1)位移：由假设（1）、（3），有
(2)应变
w w (x,y) uw z vw z
x
y
由假设（1）、（2），薄板弯曲问题只需要考虑三
D 0( 4 xw 42x 2 4 w y2 4 yw 4)q(x,y)
边界条件
（1）位移边界条件
S1
w |s1 w
（2）混合边界条件
w n s1
S2
w |s2 w
Mn |s2 Mn
其中
(Qn
Mns S
（3）力边界条件
S 3 Mn |s3 Mn
) Vn
s3
Mn|s2D02nw2 2sw2
1、位移模式
三角形单元能较好地适应斜 边界，实际中广泛应用。单 元的结点位移仍然为结点处 的挠度wi和绕x，y轴的转角
θxi、θyi，独立变量为wi。
三角形单元位移模式应包含9个参数。若考虑完全 三次多项式，则有10个参数。若以此为基础构造位 移函数，则必须去掉一项。无法保证对称。经过许 多研究，问题最后在面积坐标下得以解决。
a9
wi
wj