平行四边形证明题练习
平行四边形(含答案)

平行四边形参考答案典型例题例1.证明:∵DM⊥AC, BN⊥AC,DM=BN,AM=CN ∴△ADM≌△CBN ∴AD=CB,∠DAM=∠BCN ∴AD∥CB ∴平行四边形ABCD是平行四边形例2.解:∵BC∥AD,BC=AD, ∴ED=BF∴四边形BFDE是平行四边形,所以EB与DF平行且相等①成立,因为ED=BF,四边形BFDE仍是平行四边形,所以EB与DF仍平行且相等②成立,只要ED=BF,就成立③成立。
∵∠ABC=∠ADC, ∠BAD=∠BCD, ∠ABE=∠CDF∴∠EBF=∠EDF, ∠BED=∠BFD∴四边形BFDE是平行四边形,所以EB与DF平行且相等例3.解:PF∥AB,PE∥AC,则四边形AEPF是平行四边形,其周长为2(PE+PF)点P是BC的三等分点,则13PF CPAB CB==,23PE BPAC BC==, 又AB=AC,所以2(PE+PF)=2*12()33+AB=2AB例4.解:①连结AC,BD②将AD和BC四等分,连结对应分点③连结AC,取BC和AD的中点分别为E、F,连结AE、CF例5.解:CF=BE ∵DE∥BC EF∥AC ∴四边形EDCF是平行四边形∴CF=ED ∵BD平分∠ABC, ∠CBD=∠BDE ∴∠DBE=∠BDE ∴BE=ED ∴CF=BE例6.解:连结BD,则GF∥BD,HE∥BD, GF=HE=12BD,所以四边形EFGH是平行四边形例7.(1)证明:旋转90°时,EF⊥AC,又AB⊥AC 则AB∥EF,又AF∥BE,所以四边形ABEF是平行四边形(2)∵AO=CO,∠AOF=∠COE, ∠OAF=∠OCE∴△AOF≌△COE ∴AF=CE(3)可能。
此时EF⊥BD,旋转的角度为∠AOF=90°-∠AOB, AC=2,AO=1=AB,所以∠AOB=45°,所以旋转的角度为45°双基练习1.19,112.1203.1444.185. 50°6.C7.D8.D9.解:∵∠AEB=∠DAE, ∠DAE=∠BAE∴AB=BE=BC-CE=3∴周长为2(AD+AB)=18巩固练习1.AO=CO或BO=DO2.C3.D4.C5.156.187.15,108.解:∵AO=CO,EO为公共边,∠AOE=∠COE∴△AOE≌△COE,∴AE=CE∴周长为CD+DE+CE=CD+AD=89.10.DF和AE相互平分。
平行四边形证明练习题

平行四边形证明练习题一.解答题1.如图所示,已知在平行四边形ABCD 中,中,BE=DF BE=DF BE=DF.求证:∠DAE=∠BCF..求证:∠DAE=∠BCF.2.在▱ABCD 中,中,E E ,F 分别是BC BC、、AD 上的点,且BE=DF BE=DF.求证:.求证:.求证:AE=CF AE=CF AE=CF..3.如图,四边形ABCD 是平行四边形,是平行四边形,E E 、F 分别是BC BC..AD 上的点,∠1=∠2求证:△ABE≌△CDF.4.如图,已知:平行四边形ABCD 中,中,E E 是CD 边的中点,连接BE 并延长与AD 的延长线相交于F 点.求证:点.求证:BC=DF BC=DF BC=DF..5.如图,在▱ABCD 中,中,AC AC 交BD 于点O ,点E 、点F 分别是OA OA、、OC 的中点,请判断线段BE BE、、DF 的关系,并证明你的结论.6.已知:如图,▱ABCD 中,中,E E 、F 是对角线AC 上的点,且AE=CF AE=CF.求证:△ABE≌△CDF..求证:△ABE≌△CDF.8.如图,在等腰梯形ABCD 中,AD∥BC,中,AD∥BC,AB=CD=AE AB=CD=AE AB=CD=AE.四边形.四边形AECD 是平行四边形吗?为什么?9.如图,.如图,E E 、F 是平行四边形ABCD 的对角线AC 上的两点,上的两点,AE=CF AE=CF AE=CF.求证:.求证:.求证:DE=BF DE=BF DE=BF..1010.如图,四边形.如图,四边形ABCD 中,中,AD=BC AD=BC AD=BC,AE⊥BD,CF⊥BD,垂足为,AE⊥BD,CF⊥BD,垂足为E 、F ,AE=CF AE=CF,求证:四边形,求证:四边形ABCD 是平行四边形.1111.如图,在△ABC .如图,在△ABC 中,中,AD AD 是中线,点E 是AD 的中点,过A 点作BC 的平行线交CE 的延长线于点F ,连接BF BF.. 求证:四边形AFBD 是平行四边形.1212.如图,在等腰梯形.如图,在等腰梯形ABCD 中,AD∥BC,中,AD∥BC,AB=DC AB=DC AB=DC,DE∥AB,,DE∥AB,,DE∥AB,AD+DC=BC AD+DC=BC AD+DC=BC..求证:(1)DE=DC DE=DC;;(2)△DEC 是等边三角形.1313.已知:如图,.已知:如图,.已知:如图,E E 、F 是平行四边形ABCD 的对角线AC 上的两点,上的两点,AE=CF AE=CF AE=CF..求证:(1)△ADF≌△CBE;1414.如图,平行四边形.如图,平行四边形ABCD 中,点E 、F 、G 、H 分别在AB AB、、BC BC、、CD CD、、AD 边上且AE=CG AE=CG,,AH=CF AH=CF..求证:四边形EFGH 是平行四边形.1515.如图,在平行四边形.如图,在平行四边形ABCD 中,中,E E 、F 是对角线AC 上的点,且AE=CF AE=CF..(1)猜想探究:)猜想探究:BE BE 与DF 之间的关系: _________(2)请证明你的猜想.1616.如图,.如图,.如图,E E 、F 是平行四边形ABCD 对角线AC 上的两点,且BE∥DF.求证:∠1=∠2.1717.如图,已知.如图,已知E ,F 分别是▱ABCD 的边AB AB,,CD 的中点.求证:的中点.求证:ED=BF ED=BF ED=BF..1818.如图,.如图,.如图,BD BD 是▱ABCD 的对角线,∠ABD 的平分线BE 交AD 于点E ,∠CDB 的平分线DF 交BC 于点F .求证:四边形DEBF 为平行四边形.1919.如图,在.如图,在▱ABCD 中,对角线AC 与BD 交于点O ,已知点E 、F 分别为AO AO、、OC 的中点,证明:四边形BFDE 是平2020.如图所示,.如图所示,.如图所示,A A ,E ,F ,C 在一条直线上,在一条直线上,AE=CF AE=CF AE=CF,过,过E ,F 分别作DE⊥AC,BF⊥AC,若AB=CD AB=CD,可以得到,可以得到BD 平分EF EF,为什么?说明理由.,为什么?说明理由.2121.如图,△ABC .如图,△ABC 的中线BD BD、、CE 交于点O ,F 、G 分别是OB OB、、OC 的中点.求证:求证:EF=DG EF=DG 且EF∥DG.2222.已知如图所示,.已知如图所示,▱ABCD 的对角线AC AC、、BD 交于O ,GH 过点O ,分别交AD AD、、BC 于G 、H ,E 、F 在AC 上且AE=CF AE=CF,,求证:四边形EHFG 是平行四边形.平行四边形证明练习题参考答案与试题解析一.解答题(共22小题)1.如图所示,已知在平行四边形ABCD 中,中,BE=DF BE=DF BE=DF.求证:∠DAE=∠BCF..求证:∠DAE=∠BCF.考点: 平行四边形的性质;平行线的性质;全等三角形的判定与性质.分析: 根据平行四边形性质求出AD∥BC,且AD=BC AD=BC,推出∠ADE=∠CBF,求出,推出∠ADE=∠CBF,求出DE=BF DE=BF,证△ADE≌△CBF,推出,证△ADE≌△CBF,推出∠DAE=∠BCF 即可.解答: 证明:∵四边形ABCD 为平行四边形,∴AD∥BC,且AD=BC AD=BC,,∴∠ADE=∠CBF又∵BE=DF,∴BF=DE,∵在△ADE 和△CBF 中,∴△ADE≌△CBF,∴∠DAE=∠BCF.点评: 本题考查了平行四边形性质,平行线性质,全等三角形的性质和判定的应用,关键是求出证出△ADE 和△CBF全等的三个条件,主要考查学生的推理能力.2.在▱ABCD 中,中,E E ,F 分别是BC BC、、AD 上的点,且BE=DF BE=DF.求证:.求证:.求证:AE=CF AE=CF AE=CF..考点: 平行四边形的性质;全等三角形的判定与性质.分析: 根据平行四边形的性质得出AB=CD AB=CD,∠B=∠D,根据,∠B=∠D,根据SAS 证出△ABE≌△CDF 即可推出答案.解答: 证明:∵四边形ABCD 是平行四边形,∴AB=CD,∠B=∠D,∵BE=DF,∴△ABE≌△CDF,∴AE=CF.点评: 本题主要考查对平行四边形的性质,全等三角形的性质和判定等知识点的理解和掌握,能根据性质证出△ABE≌△CDF 是证此题的关键.求证:△ABE≌△CDF.考点: 平行四边形的性质;全等三角形的判定.分析: 利用平行四边形的性质和题目提供的相等的角可以为证明三角形全等提供足够的条件.解答: 证明:∵四边形ABCD 是平行四边形,∴∠B=∠D,∴∠B=∠D,AB=CD AB=CD AB=CD,,∴在:△ABE 与△CDF 中,∴△ABE≌△CDF(∴△ABE≌△CDF(ASA ASA ASA))点评: 本题考查了平行四边形的性质及全等三角形的判定,根据平行四边形找到证明全等三角形足够的条件是解决本题的关键.4.如图,已知:平行四边形ABCD 中,中,E E 是CD 边的中点,连接BE 并延长与AD 的延长线相交于F 点.求证:点.求证:BC=DF BC=DF BC=DF..考点: 平行四边形的性质;全等三角形的判定与性质.分析: 由四边形ABCD 是平行四边形,可得AD∥BC,根据平行线的性质即可求得∠EBC=∠F,∠C=∠EDF,又由E是CD 边的中点,根据AAS 即可求得△EBC≌△EFD,则问题得证.解答: 证明:∵四边形ABCD 是平行四边形,∴AD∥BC,∴∠EBC=∠F,∠C=∠EDF,又∵EC=ED,∴△EBC≌△EFD(∴△EBC≌△EFD(AAS AAS AAS)), ∴BC=DF.点评: 此题考查了平行四边形的性质以及全等三角形的判定与性质.此题难度不大,解题的关键是要注意数形结合思想的应用.5.(2013•莒南县二模)如图,在▱ABCD 中,中,AC AC 交BD 于点O ,点E 、点F 分别是OA OA、、OC 的中点,请判断线段BE BE、、DF 的关系,并证明你的结论.边形的判定定理“对角线互相平分的四边形是平行四边形”判定BFDE 是平行四边形,从而得出BE=DF BE=DF,,BE∥DF.解答: 解:由题意得:解:由题意得:BE=DF BE=DF BE=DF,BE∥DF.理由如下:,BE∥DF.理由如下:连接DE DE、、BF BF..∵ABCD 是平行四边形,∴OA=OC,∴OA=OC,OB=OD OB=OD OB=OD,,∵E,∵E,F F 分别是OA OA,,OC 的中点,∴OE=OF,∴BFDE 是平行四边形,∴BE=DF,BE∥DF.点评: 本题考查了平行四边形的基本性质和判定定理的运用.性质:①平行四边形两组对边分别平行;②平行四边形的两组对边分别相等;③平行四边形的两组对角分别相等;④平行四边形的对角线互相平分.判定:①两组对边分别平行的四边形是平行四边形;②两组对边分别相等的四边形是平行四边形;③两组对角分别相等的四边形是平行四边形;④对角线互相平分的四边形是平行四边形;⑤一组对边平行且相等的四边形是平行四边形.6.已知:如图,▱ABCD 中,中,E E 、F 是对角线AC 上的点,且AE=CF AE=CF..求证:△ABE≌△CDF.考点: 平行四边形的性质;平行线的性质;全等三角形的判定.分析: 根据平行四边形的性质得出AB∥DC,AB∥DC,AB=CD AB=CD AB=CD,根据平行线的性质推出∠BAC=∠DCF,根据,根据平行线的性质推出∠BAC=∠DCF,根据SAS 证出即可. 解答: 证明:∵四边形ABCD 是平行四边形,∴AB∥DC,∴AB∥DC,AB=CD AB=CD AB=CD,,∴∠BAC=∠DCF,∵AE=CF,∴△ABE≌△CDF.点评: 本题主要考查对平行四边形的性质,全等三角形的判定,平行线的性质等知识点的理解和掌握,能推出证△ABE≌△CDF 的三个条件是解此题的关键.7.如图,已知在▱ABCD 中,过AC 中点的直线交CD CD,,AB 于点E ,F .求证:.求证:DE=BF DE=BF DE=BF..考点: 平行四边形的性质;平行线的性质;全等三角形的判定与性质.解答: 证明:∵四边形ABCD ABCD 是平行四边形,是平行四边形,∴DC=AB,DC∥AB,∴∠ECA=∠BAC,∠CEO=∠AFO,∵OA=OC,∴△AOF≌△COE,∴CE=AF,∵DC=AB,∴DE=BF.点评: 本题主要考查对平行四边形的性质,平行线的性质,全等三角形的性质和判定等知识点的理解和掌握,解此题的关键是根据平行四边形的性质证出△AOF 和△COE 全等.8.如图,在等腰梯形ABCD 中,AD∥BC,中,AD∥BC,AB=CD=AE AB=CD=AE AB=CD=AE.四边形.四边形AECD 是平行四边形吗?为什么?考点: 等腰梯形的性质;平行线的判定与性质;等腰三角形的性质;平行四边形的判定.分析: 根据等腰三角形性质求出∠B=∠C,根据等腰三角形性质推出∠AEC=∠B=∠C,推出AE∥CD,根据平行四边形的判定推出即可.解答: 解:是平行四边形,理由:∵四边形ABCD 是等腰梯形,AD∥BC,∴AB=DC,∠B=∠C,∵AB=AE,∴∠AEB=∠B,∴∠AEB=∠C,∴AE∥DC,又∵AD∥BC,∴四边形AECD 是平行四边形.点评: 本题考查了等腰三角形的性质,等腰梯形的性质,平行线的性质和判定,平行四边形的判定等知识点的应用,关键是根据题意推出AE∥CD,培养了学生分析问题和解决问题的能力,题目较好,综合性比较强.9.如图,.如图,E E 、F 是平行四边形ABCD 的对角线AC 上的两点,上的两点,AE=CF AE=CF AE=CF.求证:.求证:.求证:DE=BF DE=BF DE=BF..考点: 平行四边形的性质;全等三角形的判定与性质;平行四边形的判定.分析: 连接BE BE,,DF DF,,BD BD,,BD 交AC 于O ,根据平行四边形性质求出OA=OC OA=OC,,OD=OB OD=OB,推出,推出OE=OF OE=OF,根据平行四边形的,根据平行四边形的判定推出四边形BEDF 是平行四边形即可.解答: 证明:连接BE BE,,DF DF,,BD BD,,BD 交AC 于O ,∵四边形ABCD 是平行四边形,∴OA=OC,∴OA=OC,OD=OB OD=OB OD=OB,,∴四边形BEDF 是平行四边形,∴DE=BF.点评: 本题考查了平行四边形的性质和判定等应用,关键是能熟练地运用平行四边形的性质和判定进行推理,此题的证明方法二是证△AED≌△CFB,推出DE=BF DE=BF..1010.如图,四边形.如图,四边形ABCD 中,中,AD=BC AD=BC AD=BC,AE⊥BD,CF⊥BD,垂足为,AE⊥BD,CF⊥BD,垂足为E 、F ,AE=CF AE=CF,求证:四边形,求证:四边形ABCD 是平行四边形.考点: 平行四边形的判定;平行线的性质;全等三角形的判定与性质.分析: 求出∠AED=∠CFB=90°,根据HL 证Rt△AED≌Rt△CFB,推出∠ADE=∠CBD,得到AD∥BC,根据平行四边形的判定判断即可.解答: 证明:∵AE⊥BD,CF⊥BD,∴∠AED=∠CFB=90°,在Rt△AED 和Rt△CFB 中,∴Rt△AED≌Rt△CFB(∴Rt△AED≌Rt△CFB(HL HL HL)), ∴∠ADE=∠CBD,∴AD∥BC,∵AD=BC,∴四边形ABCD 是平行四边形.点评: 本题考查了平行四边形的判定,平行线的性质,全等三角形的性质和判定等知识点的应用,关键是推出AD∥BC,主要考查学生运用性质进行推理的能力.1111.如图,在△ABC .如图,在△ABC 中,中,AD AD 是中线,点E 是AD 的中点,过A 点作BC 的平行线交CE 的延长线于点F ,连接BF BF.. 求证:四边形AFBD 是平行四边形.考点: 平行四边形的判定;全等三角形的判定与性质.专题: 证明题.分析: 求出AE=DE AE=DE,∠AFE=∠DCE,证△AEF≌△CED,推出,∠AFE=∠DCE,证△AEF≌△CED,推出AF=DC AF=DC,得出,得出AF∥BD,AF∥BD,AF=BD AF=BD AF=BD,根据平行四边形的判定推,根据平行四边形的判定推出即可.解答: 证明:∵E 为AD 中点,∴∠AFE=∠DCE,在△AEF 和△CED 中∵,∴△AEF≌△CED(∴△AEF≌△CED(AAS AAS AAS)), ∴AF=DC,∵AD 是△ABC 的中线,∴BD=DC,∴AF=BD,即AF∥BD,AF∥BD,AF=BD AF=BD AF=BD,,故四边形AFBD 是平行四边形.点评: 本题考查了平行四边形的性质和判定,全等三角形的性质和判定,关键是推出AF=DC=BD AF=DC=BD..1212.如图,在等腰梯形.如图,在等腰梯形ABCD 中,AD∥BC,中,AD∥BC,AB=DC AB=DC AB=DC,DE∥AB,,DE∥AB,,DE∥AB,AD+DC=BC AD+DC=BC AD+DC=BC..求证:(1)DE=DC DE=DC;;(2)△DEC 是等边三角形.考点: 等腰梯形的性质;等边三角形的判定;平行四边形的判定与性质.分析: (1)证出平行四边形ABED ABED,,推出DE=AB DE=AB,,即可推出答案;(2)根据BE=AD BE=AD,,AD+DC=BC AD+DC=BC,,BE+EC=BC BE+EC=BC,,推出DC=EC 即可证出答案.解答: 证明:(1)∵AD∥BC,DE∥AB,∴四边形ABED 是平行四边形,∴DE=AB,∵AB=DC,∴DE=DC.(2)证明:∵BE=AD,)证明:∵BE=AD,AD+DC=BC AD+DC=BC AD+DC=BC,,BE+EC=BC BE+EC=BC,,∴DC=EC,由(由(11)知:)知:DE=DC DE=DC DE=DC,,∴DE=DC=EC,∴△DEC 是等边三角形.点评: 本题主要考查对等腰梯形的性质,平行四边形的性质和判定,等边三角形的判定等知识点的理解和掌握,证出平行四边形ABED 和DC=EC 是解此题的关键.1313.已知:如图,.已知:如图,.已知:如图,E E 、F 是平行四边形ABCD 的对角线AC 上的两点,上的两点,AE=CF AE=CF AE=CF..求证:(1)△ADF≌△CBE;(2)连接DE DE、、BF BF,试判断四边形,试判断四边形DEBF 的形状,并说明理由.分析: (1)根据平行四边形的性质对边平行且相等得到AD 与BC 平行且相等,由AD 与BC 平行得到内错角∠DAF与∠BCA 相等,再由已知的AE=CF AE=CF,根据“SAS”得到△ADF ,根据“SAS”得到△ADF 与△CBE 全等;(2)由()由(11)证出的全等,根据全等三角形的性质得到DF 与EB 相等且∠DFA 与∠BEC 相等,由内错角相等两直线平行得到DF 与BE 平行,根据一组对边平行且相等的四边形为平行四边形即可得到四边形DEBF 的形状.解答: 证明:(1)∵ABCD 是平行四边形,∴AD=BC,AD∥BC(∴AD=BC,AD∥BC(11分)∴∠DAF=∠BCA(∴∠DAF=∠BCA(22分),∵AE=CF, ∴AE+EF=CF+EF,即AF=CE AF=CE((3分)∴△ADF≌△CBE(∴△ADF≌△CBE(44分)(2)四边形DEBF 是平行四边形(是平行四边形(55分)∵△ADF≌△CBE,∴∠DFA=∠BEC,∴∠DFA=∠BEC,DF=BE DF=BE DF=BE,,∴DF∥BE,∴四边形DEBF 是平行四边形(是平行四边形(66分)点评: 本题综合考查了全等三角形的判断与性质,以及平行四边形的判断与性质.其中第2问是一道先试验猜想,再探索证明的新型题,其目的是考查学生提出问题,解决问题的能力,这类几何试题将成为今后中考的热点试题.1414.如图,平行四边形.如图,平行四边形ABCD 中,点E 、F 、G 、H 分别在AB AB、、BC BC、、CD CD、、AD 边上且AE=CG AE=CG,,AH=CF AH=CF..求证:四边形EFGH 是平行四边形.考点: 平行四边形的判定与性质;全等三角形的判定与性质.分析: 易证得△AEH≌△CGF,从而证得对应边BE=DG BE=DG、、DH=BF DH=BF.故有△BEF≌△DGH,根据两组对边分别相等的四边.故有△BEF≌△DGH,根据两组对边分别相等的四边形是平行四边形而得证.解答: 证明:在平行四边形ABCD 中,∠A=∠C(平行四边形的对边相等);又∵AE=CG,又∵AE=CG,AH=CF AH=CF AH=CF(已知)(已知), ∴△AEH≌△CGF(∴△AEH≌△CGF(SAS SAS SAS)), ∴EH=GF(全等三角形的对应边相等);在平行四边形ABCD 中,中,AB=CD AB=CD AB=CD,,AD=BC AD=BC(平行四边形的对边相等)(平行四边形的对边相等), ∴AB﹣∴AB﹣AE=CD AE=CD AE=CD﹣﹣CG CG,,AD AD﹣﹣AH=BC AH=BC﹣﹣CF CF,,即BE=DG BE=DG,,DH=BF DH=BF..又∵在平行四边形ABCD 中,∠B=∠D,∴△BEF≌△DGH;∴GH=EF(全等三角形的对应边相等);∴四边形EFGH 是平行四边形(两组对边分别相等的四边形是平行四边形).点评: 本题考查了平行四边形的判定和性质、全等三角形的判定和性质.平行四边形的判定方法共有五种,应用时要认真领会它们之间的联系与区别,同时要根据条件合理、灵活地选择方法.1515.如图,在平行四边形.如图,在平行四边形ABCD 中,中,E E 、F 是对角线AC 上的点,且AE=CF AE=CF..(1)猜想探究:)猜想探究:BE BE 与DF 之间的关系: 平行且相等(2)请证明你的猜想.考点: 平行四边形的判定与性质.分析: (1)BE 平行且等于DF DF;;(2)连接BD 交AC 于O ,根据平行四边形的性质得出OA=OC OA=OC,,OD=OB OD=OB,推出,推出OE=OF OE=OF,得出平行四边形,得出平行四边形BEDF即可.解答: (1)解:)解:BE BE 和DF 的关系是:的关系是:BE=DF BE=DF BE=DF,BE∥DF,,BE∥DF,故答案为:平行且相等.(2)证明:连接BD 交AC 于O ,∵ABCD 是平行四边形,∴OA=OC,∴OA=OC,OB=OD OB=OD OB=OD,,∵AE=CF,∴OE=OF,∴BFDE 是平行四边形,∴BE=DF,BE∥DF.点评: 本题考查了平行四边形的性质和判定的应用,主要检查学生能否熟练地运用平行四边形的性质和判定进行推理,题型较好,通过此题培养了学生分析问题和解决问题的能力,同时培养了学生的观察能力和猜想能力.1616.如图,.如图,.如图,E E 、F 是平行四边形ABCD 对角线AC 上的两点,且BE∥DF.求证:∠1=∠2.考点: 平行四边形的判定与性质;全等三角形的判定与性质.分析: 由三角形全等(△ABE≌△CDF)得到BE=DF BE=DF,所以四边形,所以四边形BFDE 是平行四边形,根据对角相等即可得证. 解答: 证明:∵四边形ABCD 是平行四边形(已知),∴AB=CD,AB∥CD(平行四边形的对边平行且相等),∴∠BAE=∠DCF(两直线平行,内错角相等);∵BE∥DF(已知),∴∠BEF=∠DFE(两直线平行,内错角相等),∴∠AEB=∠CFD(等量代换),∴△ABE≌△CDF(∴△ABE≌△CDF(AAS AAS AAS)); ∴BE=DF(全等三角形的对应边相等),∵BE∥DF,∴四边形BEDF 是平行四边形(对边平行且相等的四边形是平行四边形),∴∠1=∠2(平行四边形的对角相等).点评: 本题主要考查平行四边形的性质和三角形全等的判定,需要熟练掌握并灵活运用.平行四边形的判定定理:对边平行且相等的四边形是平行四边形.1717.如图,已知.如图,已知E ,F 分别是▱ABCD 的边AB AB,,CD 的中点.求证:的中点.求证:ED=BF ED=BF ED=BF..考点: 平行四边形的判定与性质.分析: 根据平行四边形的性质得到AB∥CD,AB=CD AB=CD,,根据线段的中点的定义得到EB=AB AB,,DF=CD CD,,即BE=DF BE=DF,,BE∥DF,得到平行四边形EBFD EBFD,根据平行四边形的性质即可得到答案.,根据平行四边形的性质即可得到答案.解答: 证明:∵四边形ABCD 是平行四边形,∴AB∥CD,∴AB∥CD,AB=CD AB=CD AB=CD,,∵E,∵E,F F 分别是▱ABCD 的边AB AB,,CD 的中点,∴EB=AB AB,,DF=CD CD,,∴BE=DF,∵BE∥DF,∴四边形EBFD 是平行四边形,∴ED=BF.点评: 本题主要考查对平行四边形的性质和判定的理解和掌握,能灵活运用平行四边形的性质和判定进行证明是解此题的关键.1818.如图,.如图,.如图,BD BD 是▱ABCD 的对角线,∠ABD 的平分线BE 交AD 于点E ,∠CDB 的平分线DF 交BC 于点F .求证:四边形DEBF 为平行四边形.考点: 平行四边形的判定与性质;角平分线的定义.分析: 根据平行四边形性质和角平分线定义求出∠FDB=∠EBD,推出DF∥BE,根据平行四边形的判定判断即可. 解答: 解:∵四边形ABCD 是平行四边形,∴AD∥BC,AB∥CD,∴∠CDB=∠ABD,∵DF 平分∠CDB,平分∠CDB,BE BE 平分∠ABD,∴∠FDB=∠CDB,∠EBD=∠ABD,∴∠FDB=∠EBD,∴DF∥BE,∵AD∥BC,即ED∥BF,∴四边形DEBF 是平行四边形.点评: 本题考查了角平分线定义,平行四边形的性质和判定等的应用,关键是推出DF∥BE,主要检查学生能否运用定理进行推理,题型较好,难度适中.1919.如图,在.如图,在▱ABCD 中,对角线AC 与BD 交于点O ,已知点E 、F 分别为AO AO、、OC 的中点,证明:四边形BFDE 是平行四边形.考点: 平行四边形的判定与性质;全等三角形的判定与性质.分析: 利用“平行四边形的对角线互相平分”的性质推知OA=OC OA=OC,,OB=OD OB=OD;然后由已知条件“点;然后由已知条件“点E 、F 分别为AO AO、、OC 的中点”可以证得OE=OF OE=OF;最后根据平行四边形的判定定理“对角线相互平分的四边形为平行四边形”;最后根据平行四边形的判定定理“对角线相互平分的四边形为平行四边形”即可证得结论.解答: 证明:∵四边形ABCD 是平行四边形,∴OA=OC,∴OA=OC,OB=OD OB=OD OB=OD(平行四边形的对角线互相平分)(平行四边形的对角线互相平分). 又∵点E 、F 分别为AO AO、、OC 的中点,∴OE=OF.∴四边形BFDE 是平行四边形(对角线相互平分的四边形为平行四边形).点评: 本题考查了平行四边形的判定与性质.平行四边形的判定方法共有五种,应用时要认真领会它们之间的联系与区别,同时要根据条件合理、灵活地选择方法.2020.如图所示,.如图所示,.如图所示,A A ,E ,F ,C 在一条直线上,在一条直线上,AE=CF AE=CF AE=CF,过,过E ,F 分别作DE⊥AC,BF⊥AC,若AB=CD AB=CD,可以得到,可以得到BD 平分EF EF,为什么?说明理由.,为什么?说明理由.考点: 全等三角形的判定与性质;垂线;直角三角形全等的判定;平行四边形的判定与性质.分析: 求出∠AFB=∠CED=90°,DE∥BF,推出AF=CE AF=CE,连接,连接BE BE、、DF DF,根据,根据HL 证Rt△ABF≌Rt△CDE,推出DE=BF DE=BF,,得出平行四边形DEBF DEBF,根据平行四边形的性质推出即可.,根据平行四边形的性质推出即可.解答: 解:解:BD BD 平分EF EF,理由是:,理由是:证法一、连接BE BE、、DF DF..∵DE⊥AC,BF⊥AC,∴∠AFB=∠CED=90°,DE∥BF,∵AE=CF,∴AE+EF=CF+EF,即AF=CE AF=CE,,在Rt△ABF 和Rt△CDE 中,∴Rt△ABF≌Rt△CDE,∴DE=BF,∵DE∥BF,∴四边形DEBF 是平行四边形,∴BD 平分EF EF;;证法二、∵DE⊥AC,BF⊥AC,∴∠AFB=∠CED=90°,DE∥BF,∵AE=CF,∴AE+EF=CF+EF,即AF=CE AF=CE,,在Rt△ABF 和Rt△CDE 中,∴Rt△ABF≌Rt△CDE,∴DE=BF,∵在△BFG 和△DEG 中,∴△BFG≌△DEG(∴△BFG≌△DEG(AAS AAS AAS)), ∴EG=FG,即BD 平分EF EF..点评: 本题考查了平行四边形的性质和判定,垂线,全等三角形的性质和判定等知识点的运用,关键是得出平行四边形DEBF DEBF,题目比较好,难度适中.,题目比较好,难度适中.2121.如图,△ABC .如图,△ABC 的中线BD BD、、CE 交于点O ,F 、G 分别是OB OB、、OC 的中点.求证:求证:EF=DG EF=DG 且EF∥DG.考点: 三角形中位线定理;三角形的角平分线、中线和高;平行四边形的判定与性质.分析: 根据三角形的中位线推出DE∥BC,DE∥BC,DE=DE=BC BC,,GF∥BC,GF∥BC,GF=GF=BC BC,,推出GF=DE GF=DE,,GF∥DE,GF∥DE,得出平行四边形得出平行四边形DEFG DEFG,,根据平行四边形的性推出即可.解答: 证明:∵BD、证明:∵BD、CE CE 是△ABC 的中线,∴DE∥BC,∴DE∥BC,DE=DE=BC BC,,同理:GF∥BC,同理:GF∥BC,GF=GF=BC BC,,∴GF=DE,GF∥DE,∴四边形DEFG 是平行四边形,∴EF=DG,EF∥DG.点评: 本题考查了平行四边形的性质和判定,三角形的中位线,三角形的中线等知识点,主要检查学生能否熟练的运用性质进行推理,题目比较典型,难度适中,通过做此题培养了学生分析问题和解决问题的能力.考点: 平行四边形的判定与性质.分析: 根据平行四边形性质得出OA=OC OA=OC,,AD∥BC,推出OE=OF OE=OF,,∠GAO=∠HCO,∠AGO=∠CHO,根据AAS 证△AGO≌△CHO,推出OG=OH OG=OH,根据平行四边形的判定推出即可.,根据平行四边形的判定推出即可.解答: 证明:∵四边形ABCD 是平行四边形,∴OA=OC,AD∥BC,∵AE=CF,∴OE=OF,∵AD∥BC,∴∠GAO=∠HCO,∠AGO=∠CHO,在△AGO 和△CHO 中,∴△AGO≌△CHO(∴△AGO≌△CHO(AAS AAS AAS)), ∴OG=OH,∵OE=OF,∴四边形EHFG 是平行四边形.点评: 本题考查了全等三角形的性质和判定,平行线的性质,平行四边形的性质和判定等知识点,注意:平行四边形的对角线互相平分,对角线互相平分的四边形是平行四边形.。
平行四边形证明题

1如图,已知D是△ABC的边AB上一点,CE∥AB,DE交AC于点O,且OA=OC.求证:四边形ADCE是平行四边形.2、如图,F、C是线段AD上的两点,AB∥DE,BC∥EF,AF=DC,连接AE、BD,求证:四边形ABDE 是平行四边形.3、如图,点A、F、C、D在同一直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠A=∠D,AF=DC.求证:四边形BCEF是平行四边形.4、如图,E、F是平行四边形ABCD的对角线AC上的两点,AE=CF.求证:四边形DEBF是平行四边形.5如图,已知□ABCD的对角线AC , BD相交于点O ,直线EF经过点O ,且分别交AB ,CD于点E ,F。
求证:四边形BFDE是平行四边形..6、如图,平行四边形ABCD中,AE⊥BC,CF⊥AD,垂足分别是E、F.求证:△ABE≌△CDF.7、已知ABCD是平行四边形,用尺规分别作出△BAC与△DAC共公边AC上的高BE、DF.求证:BE=DF.8、如图,在▱ABCD中,点E是DC的中点,连接AE,并延长交BC的延长线于点F.(1)求证:△ADE和△CEF的面积相等(2)若AB=2AD,试说明AF恰好是∠BAD的平分线9、如图,在平行四边形ABCD中,点E、F是对角线AC上两点,且AE=CF.试说明:∠EBF=∠FDE.10如图,在正方形ABCD中,AB=4,P是线段AD上的动点,PE⊥AC于点E,PF⊥BD于点F,则PE+PF的值为()11、已知:如图,四边形ABCD是平行四边形,DE∥AC,交BC的延长线于点E,EF⊥AB于点F,求证:AD=CF.12、如图,在正方形ABCD中,点E在对角线AC上,点F在边BC上,连接BE、DF,DF交对角线AC于点G,且DE=DG.(1)求证:AE=CG;(2)试判断BE和DF的位置关系,并说明理由.13、如图,点B、C、E是同一直线上的三点,四边形ABCD与四边形CEFG都是正方形,连接BG、DE.求证:BG=DE;14、已知:P是正方形ABCD对角线BD上一点,PE⊥DC,PF⊥BC,E、F分别为垂足.求证:AP=EF.15、如图,AC是菱形ABCD的对角线,点E,F分别在AB,AD上,AE=AF.求证:CE=CF.15、如图,四边形ABCD是矩形,直线L垂直分线段AC,垂足为O,直线L分别于线段AD,CB的延长线交于点E,F,证明四边形AFCE是菱形.16、如图,E、F是四边形ABCD的对角线AC上两点,AE=CF,DF∥BE,DF=BE.(1)求证:四边形ABCD是平行四边形;(2)若AC平分∠BAD,求证:▱ABCD为菱形.17、如图所示,在菱形ABCD中,∠BAD=120°,AB=4.求:(1)对角线AC,BD的长;(2)菱形ABCD的面积.18、如图,四边形ABCD是矩形,点E是边AD的中点.求证:EB=EC.19、如图,矩形ABCD的对角线AC、BD交于点O,∠AOB=60°,AB=3,求BD的长.20、在矩形ABCD中,已知AB=2,BC=4,对角线AC的垂直平分线分别交AD、AC于点E、O,连接CE,求CE的长.21、已知:矩形ABCD中,对角线AC与BD交于点O,∠BOC=120°,AC=4cm,求矩形ABCD的周长.。
完整版)平行四边形典型证明题(已分类)

完整版)平行四边形典型证明题(已分类)1.在平行四边形ABCD中,平分线AE交DC于点E,已知∠DAE=25°,求平行四边形ABCD各角的度数。
2.如图,将长方形ABCD沿EF折叠后,交点G在ED和BC上,点D、C分别落在D′、C′的位置上,已知∠EFG=55°,求∠AEG的度数。
3.如图,在平行四边形ABCD中,点E、F分别在BD上,且BE=DF,证明四边形AECF是平行四边形。
4.如图,在平行四边形ABCD中,点E、F分别在对角线BD上,且∠DAE=∠BCF。
1)证明AE=CF。
2)证明AE∥CF。
5.如图,在平行四边形ABCD中,点E在BC上平分∠BAD,点F在AD上平分∠BCD,证明四边形AECF是平行四边形。
6.如图,点D、E、F分别是△XXX各边中点。
1)证明四边形ADEF是平行四边形。
2)已知AB=AC=10,BC=12,求四边形ADEF的周长和面积。
7.如图,在△ABC中,点D、E分别为AB、AC边的中点,将△ADE绕点E顺时针旋转180°得到△CFE。
证明四边形DBCF是平行四边形。
8.如图,矩形纸片ABCD中,AD=8cm,AB=6cm,先沿对角线BD对折,点C落在点C′的位置,BC′交AD于点G。
1)证明AG=C′G。
2)求△BDG的面积。
9.如图,矩形ABCD中,AC与BD相交于点O,已知AO=3,∠OBC=30°,求矩形的周长和面积。
10.如图,在矩形ABCD中,AE平分∠BAD,已知∠1=15°。
1)求∠2的度数。
2)证明BO=BE。
11.如图,矩形ABCD中,AE平分∠BAD,CE∥BD,DE∥AC。
1)判断四边形OCED的形状,并证明。
2)已知AB=6,BC=8,求四边形OCED的面积。
12.在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠ACD 的平分线于点F。
(完整版)平行四边形证明典型题
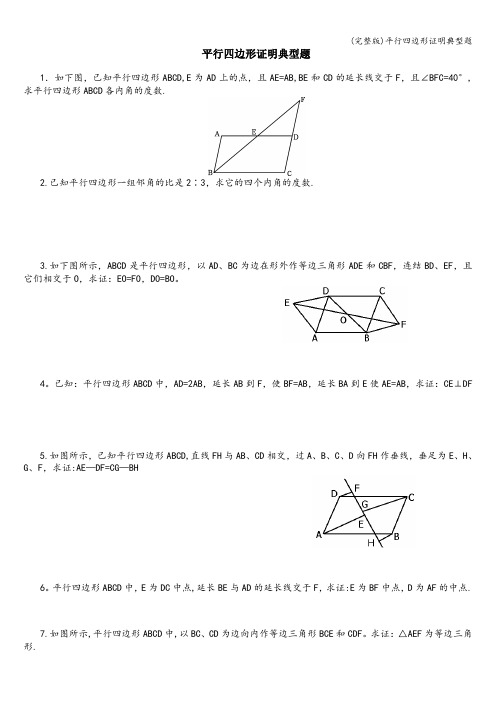
平行四边形证明典型题1.如下图,已知平行四边形ABCD,E为AD上的点,且AE=AB,BE和CD的延长线交于F,且∠BFC=40°,求平行四边形ABCD各内角的度数.2.已知平行四边形一组邻角的比是2∶3,求它的四个内角的度数.3.如下图所示,ABCD是平行四边形,以AD、BC为边在形外作等边三角形ADE和CBF,连结BD、EF,且它们相交于O,求证:EO=FO,DO=BO。
4。
已知:平行四边形ABCD中,AD=2AB,延长AB到F,使BF=AB,延长BA到E使AE=AB,求证:CE⊥DF5.如图所示,已知平行四边形ABCD,直线FH与AB、CD相交,过A、B、C、D向FH作垂线,垂足为E、H、G、F,求证:AE—DF=CG—BH6。
平行四边形ABCD中,E为DC中点,延长BE与AD的延长线交于F,求证:E为BF中点,D为AF的中点.7.如图所示,平行四边形ABCD中,以BC、CD为边向内作等边三角形BCE和CDF。
求证:△AEF为等边三角形.8。
如图所示,在△ABC中,BD平分∠B,DE∥BC交AB于E,EF∥AC交BC于F,求证:BE=FC9。
如图所示,平行四边形ABCD中,E是AB的中点,F是CD中点,分别延长BA和DC到G、H,使AG=CH,连结GF、EH,求证:GF∥EH10.如图所示,平行四边形ABCD中,E、F分别在AD、BC上,且AE=CF,AF与BE相交于G,CE与DF相交于H.求证:EF与GH互相平分11.在四边形ABCD中,AB∥DC,对角线AC、BD交于O,EF过O交AB于E,交DC于F,且OE=OF,求证:四边形ABCD是平行四边形.12。
如图所示,已知△ABC,分别以AB、BC、AC为边向BC同侧作等边三角形ABE、BCD、ACF。
求证:DEAF 为平行四边形.13。
已知:如下图,在四边形ABCD中,AB=DC,AE⊥BD,CF⊥BD,垂足分别是E、F,AE=CF,求证:四边形ABCD 是平行四边形.14.点O是平行四边形ABCD的对角线的交点,△AOB的面积为7cm2,求平行四边形ABCD的面积.15.有两个村庄A和B位于一条河的两岸,假定河岸是两条平行的直线,现在要在河上架一座与河岸垂直的桥PQ,问桥应架在何处,才能使从A到B总的路程最短。
平行四边形的判定练习题(含答案)

平行四边形的判定练习题(含答案)(1)因为AD∥BC,AB=CD,所以ABCD是平行四边形.()(2)因为AB∥CD,AD=BC,所以ABCD是平行四边形.()(3)因为AD∥BC,AD=BC,所以ABCD是平行四边形.()(4)因为AB∥CD,AD∥BC,所以ABCD是平行四边形.()(5)因为AB=CD,AD=BC,所以ABCD是平行四边形.()(6)因为AD=CD,AB=AC,所以ABCD是平行四边形.()5.已知AD∥BC,要使四边形ABCD为平行四边形,需要增加条件________.6.如图所示,∠1=∠2,∠3=∠4,问四边形ABCD是不是平行四边形.7.如图所示,在四边形ABCD中,AB=CD,BC=AD,E,F 为对角线AC上的点,且AE=CF,求证:BE=DF.8.如图所示,D为△ABC的边AB上一点,DF交AC于点E,且AE=CE,FC∥AB.求证:CD=AF.9.如图所示,已知四边形ABCD是平行四边形,在AB 的延长线上截取BE=•AB,BF=BD,连接CE,DF,相交于点M.求证:CD=CM.10.如图所示,在四边形ABCD中,DC∥AB,以AD,AC为边作□ACED,延长DC•交EB于F,求证:EF=FB.知能点2 三角形的中位□线11.如图所示,已知E为□ABCD中DC边的延长线上的一点,且CE=DC,连接AE,分别交BC,BD于点F,G,连接AC交BD于点O,连接OF,求证:AB=2OF.12.如图所示,在ABCD中,EF∥AB且交BC于点E,交AD于点F,连接AE,BF•交于点M,连接CF,DE交AD.于点N,求证:MN∥AD且MN=1213.如图所示,DE是△ABC的中位线,BC=8,则DE=_______.14.如图所示,在□ABCD中,对角线AC,BD交于点O,OE∥BC交CD•于E,•若OE=3cm,则AD的长为(). A.3cm B.6cm C.9cm D.12cm 15.如图所示,在四边形ABCD中,E,F,G,H分别是AB,BC,CD,AD的中点,•则四边形EFGH是平行四边形吗?为什么?16.如图所示,在△ABC中,AC=6cm,BC=8cm,AB=10cm,D,E,F分别是AB,BC,CA的中点,求△DEF的面积.规律方法应用17.如图所示,A,B两点被池塘隔开,在A,B外选一点C,连接AC和BC,•并分别找出AC和BC的中点M,N,如果测得MN=20m,那么A,B两点间的距离是多少?18.如图所示,在□ABCD中,AB=2AD,∠A=60°,E,F 分别为AB,CD的中点,EF=1cm,那么对角线BD的长度是多少?你是怎样得到的?19.如图所示,在△ABC中,E为AB的中点,CD平分∠ACB,AD⊥CD于点D.•(BC-AC).试说明:(1)DE∥BC.(2)DE=12开放探索创新20.如图所示,在△ABC中,∠BAC=90°,AD⊥BC于D,BE平分∠ABC交AD•于E,EF∥BC交AC于F,那么AE与CF相等吗?请验证你的结论.中考真题实战21.(长沙)如下左图所示,在四边形ABCD中,AB∥CD,要使四边形ABCD•为平行四边形,则应添加的条件是________.(添加一个即可)22.(呼和浩特)如上右图所示,已知E,F,G,H是四边形ABCD各边的中点,•则S四边形EFGH :S四边形ABCD的值是_________.23.(南京)已知如图19-1-55所示,在Y ABCD中,E,F分别是AB,CD的中点.求证:(1) △AFD≌△CEB.(2)四边形AECF是平行四边形.答案:1.C 2.C 3.D4.(1)× (2)× (3)∨ (4)∨ (5)∨ (6)×5.AD=BC或AB∥CD6.解:∵∠1=∠2,∴AD∥BC.又∵∠3=∠4,∴AB∥CD.∴四边形ABCD是平行四边形.7.证明:∵AB=CD,BC=AD,∴四边形ABCD是平行四边形.∴AB∥CD,∴∠BAE=∠DCF.又∵AE=CE,∴△ABE≌△CDF(SAS),∴BE=EF.8.证明:∵FC∥AB,∴∠DAC=∠ACF,∠ADF=∠DFC.又∵AE=CE,∴△ADE≌△CFE(AAS),∴DE=EF.∵AE=CE,∴四边形ADCF为平行四边形.∴CD=AF.9.证明:∵四边形ABCD是平行四边形.∴AB//DC.又∵BE=AB,∴BE//DC,∴四边形BDCE是平行四边形.∵DC∥BF,∴∠CDF=∠F.同理,∠BDM=∠DMC.∵BD=BF,∴∠BDF=∠F.∴∠CDF=∠CMD,∴CD=CM.10.证明:过点B作BG∥AD,交DC的延长线于G,连接EG.∵DC∥AB,∴ABGD是平行四边形,∴BG// AD.在□ACED中,AD//CE,∴CE//BG.∴四边形BCEG为平行四边形,∴EF=FB.11.证明:∵四边形ABCD是平行四边形,∴AB//CD,AD=BC.∵CE=CD,∴AB//CE,∴四边形ABEC为平行四边形.∴BF=FC,∴OF//1AB,即AB=2OF.212.证明:∵四边形ABCD是平行四边形,∴AB∥CD,AD∥BC.又∵EF∥AB,∴EF∥CD.∴四边形ABEF,ECDF均为平行四边形.又∵M,N分别为Y ABEF和Y ECDF对角线的交点.∴M为AE的中点,N为DE的中点,即MN为△AED的中位线.∴MN∥AD且MN=12AD.13.4 14.B15.解:EFGH是平行四边形,连接AC,在△ABC中,∵EF是中位线,∴EF//12AC.同理,GH//12AC.∴EF//GH,∴四边形EFGH为平行四边形.16.解:∵EF,DE,DF是△ABC的中位线,∴EF=12AB,DE=12AC,DF=12BC.又∵AB=10cm,BC=8cm,AC=6cm,∴EF=5cm,DE=3cm,DF=4cm,而32+42=25=52,即DE2+DF2=EF2.∴△EDF为直角三角形.∴S△EDF =12DE·DF=12×3×4=6(cm2).17.解:∵M,N分别是AC,BC的中点.∴MN是△ABC的中位线,∴MN=12AB.∴AB=2MN=2×20=40(m).故A,B两点间的距离是40m.18.解:连接DE.∵四边形ABCD是平行四边形,∴AB//CD.∵DF=12CD,AE=12AB,∴DF//AE.∴四边形ADFE是平行四边形.∴EF=AD=1cm.∵AB=2AD,∴AB=2cm.∵AB=2AD,∴AB=2AE,∴AD=AE.∴∠1=∠4.∵∠A=60°,∠1+∠4+∠A=180°,∴∠1=∠A=∠4=60°.∴△ADE是等边三角形,∴DE=AE.∵AE=BE,∴DE=BE,∴∠2=∠3.∵∠1=∠2+∠3,∠1=60°,∴∠2=∠3=30°.∴∠ADB=∠3+∠4=90°.=cm).19.解:延长AD交BC于F.(1)∵AD⊥CD,∴∠ADC=∠FDC=90°.∵CD平分∠ACB,∴∠ACD=∠FCD.在△ACD与△FCD中,∠ADC=∠FDC,DC=DC,∠ACD=∠FCD.∴△ACD≌△FCD,∴AC=FC,AD=DF.又∵E为AB的中点,∴DE∥BF,即DE∥BC.(2)由(1)知AC=FC,DE=12BF.∴DE=12(BC-FC)=12(BC-AC).20.解:AE=CF.理由:过E作EG∥CF交BC于G,∴∠3=∠C.∵∠BAC=90°,AD⊥BC,∴∠ABC+∠C=90°,∠ABD+∠BAD=90°.∴∠C=∠BAD,∴∠3=∠BAD.又∵∠1=∠2,BE=BE,∴△ABE≌△GBE(AAS),∴AE=GE.∵EF∥BC,EG∥CF,∴四边形EGCF是平行四边形,∴GE=CF,∴AE=CF.21.答案不唯一,如AB=CD或AD∥BC.22.1223.解:(1)在□ABCD中,AD=CB,AB=CD,∠D=∠B.∵E,F分别为AB,CD的中点,∴DF=12CD,BE=12AB,∴DF=BE,∴△AFD≌△CEB.(2)在□ABCD中,AB=CD,AB∥CD.由(1)得BE=DF,∴AE=CE,∴四边形AECF是平行四边形.。
平行四边形典型证明题
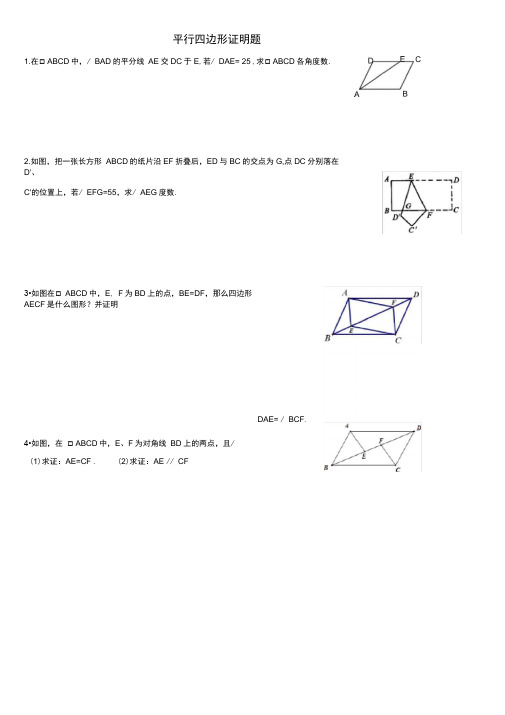
平行四边形证明题1.在口ABCD中,/ BAD的平分线AE交DC于E,若/ DAE= 25°,求口ABCD各角度数.2.如图,把一张长方形ABCD的纸片沿EF折叠后,ED与BC的交点为G,点DC分别落在D'、C'的位置上,若/ EFG=55,求/ AEG度数.3•如图在口ABCD中,E, F为BD上的点,BE=DF,那么四边形AECF是什么图形?并证明4•如图,在口ABCD中,E、F为对角线BD上的两点,且/(1)求证:AE=CF . (2)求证:AE // CF CDAE= / BCF.5•如图,口ABCD中,AE平分/ BAD交BC于点E, CF平分/ BCD交AD于点F,求证:四边形AECF是平行四边形D6.如图,点D、E、F分别是△ ABC各边中点.(1)求证:四边形ADEF是平行四边形.(2)若AB=AC=10 , BC=12,求四边形ADEF的周长和面积7•如图,在△ ABC中,点D,E分别是AB,AC边的中点,若把△ ADE绕着点E顺时针旋转180°得到△ CFE .8.如图,一张矩形纸片ABCD,其中AD = 8cm, AB = 6cm,先沿对角线点G.(1)求证:AG= C'G. (2) 求厶BDG的面积求证:四边形DBCF是平行四边形。
BD对折,点C落在点9•如图,矩形ABCD中,AC与BD相交于点O.若AO=3 , / OBC=30°,求矩形的周长和面积。
10.如图,在矩形ABCD中,AE平分/ BAD,/ 1 = 15° . ( 1)求/ 2的度数.(2)求证:BO= BE .11.如图,0为矩形ABCD寸角线的交点,DE AC CE// BD(1)试判断四边形(2)若AB= 6, BC= 8,求四边形OCE啲面积.12.在厶ABC中,点0是AC边上的一个动点,过点0作直线MN/ BC,设MN交/BCA的平分线于点E,交/ ACD的平分线于点F,求证:(1) E(=F0(2)当点0运动到何处时,四边形AECf是矩形?13.如图,BD是菱形ABCD勺对角线,点E,F分别在边CD,DA上,且CE=AF求证:/DBF=/ DBE.AAl ____ \一Nffc14.如图,在菱形 ABCD 中, E 为AD 中点,EF 丄AC 交CB 的延长线于 F.求证:AB 与EF 互相平分.17.已知:如图所示,△ ABC 中,E 、F 、D 分别是AB AC BC 上的点,且 DE// AC, DF// AB,要使四边形 AEDF 是菱形, 15.如图,在平行四边形 求证:四边形AFCE 是菱形.16.在口 ABCD 中,对角线 四边形AECF 是什么形状?并证明在不改变图形的前提下,你需添加的一个条件是___ —试证明:这个多边形是菱形4 / 7ABCD 中,0是对角线AC 与BD 相交于点0, BC18.如图,在正方形 ABCD 中,点G 是BC 上任意一点,连接 AG 过B, D 两点分别作 BEL AG D 巳AG 垂足分别为 E, F 两点,求证:△ ADF ^A BAE19.如图,已知点 E 为正方形 ABCD 勺边BC 上一点,连结 AE 过点D 作DGLAE 垂足为 G 延长DG 交AB 于点F .求证:①BF =CE ②DF LAE20.如图,在正方形 ABCD 中 , M 为AB 的中点, 21.在 Rt △ ABC 中,/ ACB=90DECF 为正方形,CD 平分/ ACB ,过点D 分别作DE 丄BC,DF 丄AC ,垂足分别为 E,F.求证: 四边形图6MN LMD22. 在厶ABC中,/ BAC=45 ° , AD丄BC于点D,将厶ABD沿AB所在的直线折叠,使点D落在点E处,将△ ADC沿23. 如图,△ ABC中,AB=AC,AD是厶ABC的角平分线,点0为AB的中点,连接DO并延长到点E,使OE=OD连接AE,BE.(1)求证:四边形AEBD是矩形.(2)当厶ABC满足什么条件时,矩形AEBD是正方形,并证明•24. 已知菱形ABCD的两条对角线分别为6和8,M、N分别是边BC、CD的中点,P是对角线BD上一点,贝U PM+PN的最小值为多少?AC所在的直线折叠,使点D落在点F处,分别延长EB,FC使其交于点M,判断四边形25.如图,在直角梯形ABCD中,/ ABC=90 , AD// BC, AD=4, AB=5 BC=6点P是AB上的一个动点,当PC+PD的值最小时,最小值为.6题图丿。
八下数学第十八章平行四边形证明题专项·练习
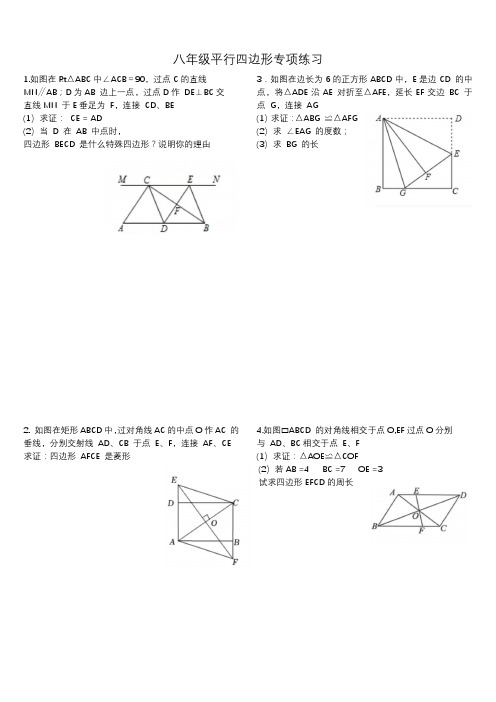
八年级平行四边形专项练习1.如图在Rt△ABC中∠ACB=90,过点C的直线MN∥AB;D为AB 边上一点,过点D作DE⊥BC交直线MN 于E垂足为F,连接CD、BE(1)求证:CE = AD(2)当D 在AB 中点时,四边形BECD 是什么特殊四边形?说明你的理由2. 如图在矩形ABCD中,过对角线AC的中点O作AC 的垂线,分别交射线AD、CB 于点E、F,连接AF、CE 求证:四边形AFCE 是菱形3.如图在边长为6的正方形ABCD中,E是边CD 的中点,将△ADE沿AE 对折至△AFE,延长EF交边BC 于点G,连接AG(1)求证:△ABG ≌△AFG(2)求∠EAG 的度数;(3)求BG 的长4.如图▭ABCD 的对角线相交于点O,EF过点O分别与AD、BC相交于点E、F(1)求证:△AOE≌△COF(2)若AB =4 BC =7 OE =3试求四边形EFCD的周长5如图BD 是△ABC 的角平分线,过点D作DE∥BC交AB于点E,DF∥AB 交BC 于点F(1)求证:四边形BEDF是菱形;(2)若∠ABC =60°∠ACB =45°CD =6√2求菱形BEDF的面积6.如图在△ABC中中线BE、CD 交于点O,F、G 分别是OB、OC 的中点求证:(1) DE ∥FG(2) DG 和EF 互相平分.7. 如图在△ABC 中AB=AC ,D为BC上一点以AB、BD 为邻边作平行四边形ABDE连接AD、EC(1)求证:△ADC ≌△ECD ;(2)若BD =CD 求证:四边形ADCE 是矩形8.如图在Rt△ABC 中∠ACB =90°,过点C 的直线MN ∥AB , D为AB 边上一点,过点D作DE⊥BC ,交直线MN于E,垂足为F,连接CD、BE(1)求证:CE = AD(2)当D在AB中点时,四边BECD是什么特殊四边形?说明你的理由9.如图四边形ABCD是正方形,点E在BC延长线上,DF ⊥AE 于点F 点G在AE 上且∠ABG =∠E求证:AG = DF10. 如图是直角三角尺△ABC 和等腰直角三角尺△ BCD放置在同一平面内,斜边BC重合在一起∠A =∠BDC =90°∠ABC =30°BD = CD DE⊥AB 交AB 于点E 作DF⊥AC 交AC 的延长线于点F (1)求证:四边形AEDF 是正方形(2)当AC =4时,求正方形AEDF 的边长11.如图点0是口ABCD 对角线的交点,过点0作直线分别交AB、CD 的延长线于点E、F求证:BE = DF12. 如图,四边形ABCD是平行四边形,∠BAD的角平分线AE交CD 于点F,交BC的延长线于点E(1)求证:BE = CD(2)若BF 恰好平分∠ABE ,连接AC、DE求证:四边形ACED 是平行四边形13.如图1在正方形ABCD 中,E、F分别是边AD、DC 上的点且AF⊥BE(1)求证:AF = BE(2)如图2在正方形ABCD 中,M、N、P、Q 分别是边AB、BC、CD、DA 上的点且MP⊥NQ 判断MP 与NQ 是否相等?并说明理由14.如图在平行四边形ABCD中,0为对角线交点,DP 平分∠ADC,CP 平分∠BCD,AB =6 AD =10则OP的长是多少?15. 如图矩形ABCD中延长AB至E,延长CD至F . BE = DF连接EF与BC、AD 分别相交于P、Q两点(1)求证:CP = AQ(2)若BP =1 PQ =2 ∠AEF =45°求矩形ABCD 的面积16.如图在Rt△ABC中∠BAC =90° AD⊥BC于D BG 平分∠ABC EF∥BC交AC 于F求证:AE = CF17.如图将矩形纸片ABCD沿对角线AC 折叠,使点B 落到点B '的位置,AB '与CD 交于点E(1)试找出一个与△AED 全等的三角形,并加以证明;(2)若AB =8 DE =3 , P为线段AC上的任意一点PG⊥AE 于G PH⊥EC于H 试求PG + PH的值并说明理由18.如图在△ABC 中AB = BC ,BD 平分∠ABC 四边形ABED 是平行四边形,DE 交BC 于点 F 连接CE求证:四边形BECD 是矩形19.如图1将边长为4cm的正方形纸片ABCD沿EF折叠(点E、F 分别在边AB、CD上,使点B 落在AD 边上的点M 处,点C落在点N处,MN与CD交于点P,连接EP (1)如图②若M 为AD 边的中点①△AEM 的周长=cm②求证:EP = AE + DP(2)随着落点M 在AD 边上取遍所有的位置(点M 不与A、D 重合),△PDM的周长是否发生变化?若发生变化,直接写出△ PDM 的周长,若发生变化,请说明理由。
