简谐运动的能量
简谐运动的回复力和能量

简谐运动的回复力和能量简谐运动是一种在物理学中经常出现的现象,它是指一种物体在作往复振动时,其位移随时间变化呈现出正弦曲线的运动。
简单来说,就是物体在一定的位置上来回振动,比如一个摆锤在悬挂在绳子上摆动,或者是一个弹簧在振动。
这种运动具有回复力和能量的特点,下面将分别进行讨论。
回复力的定义和特点在简谐运动中,回复力指的是弹性势能的作用力,它是当物体离开平衡位置时,受到的恢复力,使物体朝向平衡位置方向移动。
回复力的大小和方向与物体离开平衡位置的距离成正比,反向指向平衡位置。
具体来说,回复力的公式为F = -kx,其中k是弹性系数,x是物体离开平衡位置的距离。
回复力对于简谐运动来说是一个非常重要的特性,因为它是使物体朝向平衡位置恢复的力量,同时也是振动维持的关键因素。
在简谐运动中,振动的频率、周期和振幅都取决于回复力的大小和弹性系数的变化。
当振幅变大时,回复力也会变大,当弹性系数增大或减小时,回复力的大小也会发生相应的变化。
能量的定义和特点能量是指物体的运动状态所具有的“有用”的物理量。
在简谐运动中,能量由动能和势能组成,它们之间通过运动的转化实现互相转换。
简谐运动的总能量等于动能和势能的和,它是一个守恒量,也就是说在运动过程中能量的总和始终保持不变。
具体来说,当物体在平衡位置附近振动时,它具有最小的动能和弹性势能;当物体脱离平衡位置时,弹性势能会转化为动能,同时物体有更大的动能;当物体到达到最远的位置时,它的动能最大,而弹性势能为零。
这意味着,简谐运动所产生的能量是从一种形式到另一种形式的转化。
简谐运动是一种常见的物理现象,它具有回复力和能量的特点。
回复力是指物体朝向平衡位置方向恢复的力量;能量由动能和势能组成,是物体运动状态的“有用”物理量。
回复力和能量是简谐运动的关键特性,它们直接决定了运动的频率、周期和振幅变化,因此在研究简谐运动时非常重要。
高二物理简谐运动能量

全家人都知道这个说法,在姐姐的心灵深处,樟木箱子早已深深地扎下了根。 光阴似箭,姐姐真的到了谈婚论嫁的时候了。正在紧锣密鼓地准备婚礼时,友人也给弟弟介绍了一个女朋友。当女朋友第一次上门时,看着樟木箱子,不经意地对弟弟说,这只樟木箱子做工可真好。妈妈 唯恐为了一只樟木箱子惹起儿子女朋友的不快,妈妈变卦了,她忘了已经多次许愿给自己的女儿了。 姐姐出嫁那天,虽是她一生大喜的日子,也没有阻挡她向自己的丈夫哭诉。架不住日积月累,丈夫终于在一天酒后,借酒壮胆来到了久违的岳母家,把身旁的小舅子打了个口鼻出 血…… 弟弟的几个朋友听说后愤愤不平。他们打得姐夫满脸血水趴在地上,姐夫被人抬到医院,大夫说须做眼球摘除手术,可怜的姐夫成了独眼瞎。这时的姐姐逢人就说,是我让丈夫去讨要樟木箱子,我要跟独眼瞎的丈夫过一辈子。弟弟只是个打手,是母亲指使他打了自己的丈夫。 她还说不要任何医疗赔偿,就是要把打人的弟弟送进监狱。 这个由一只樟木箱子引起的家庭伤害案,其实也是关于诚信的话题。亲人之间,甚至是母女之间,也要讲诚信。这个很是个别的案例,给人的思考真是一言难尽。 88、“少”的哲学 早在1583年,作为药理学家和 学者的帕拉斯尔萨斯就说过一句极其中肯而精彩的话:“只有剂量能决定一种东西没有毒。”直到今天,这句话仍然不失其意义。姑且不论中国民间“是药三分毒”的说法,就是人们一般不可须臾离开的裹腹之物———食物,也并非是“韩信点兵,多多益善”。食物如果过多,也可能造 成副作用和中毒,正所谓过犹不及。 最近,美英一个专家小组经过考察和比较研究指出,中国对肝癌的化疗用药不仅品种多而且剂量大,比美英一般用药量多一半。结果是,肝癌病人的死亡率不仅比国外高,而且即使能达到有效治疗,患者的存活期也不过一两年或二三年,相比之 下,国外的肝癌病人的治愈率不仅高于中国的肝癌病人,而且一般存活年限也比中国肝癌病人多一倍,至少是五六年。 为什么会有这样迥然相异的结果呢其中的原理很简单。肝癌本来就极大地损害了肝脏的功能,如果这时再对病人大剂量用药和用多种药,肝脏的负担更重。所以许 多肝癌病人并非死于癌症,而是死于药物中毒。尽管医生的用药是用心良苦,但结果却是事与愿违。 少,但是有效,不仅是用药的一种方法,而且是生活早就阐明的一个简单道理。简单而实用比繁琐哲学好得多。 89、爱下棋的国王 有一个爱下象棋的国王,他常和大臣、 象棋高手对弈。几年来,每次下棋国王都是赢家,大家都恭维他为天下独一无二的象棋高手。 一日,国王微服私访。他来到京城一家酒店,一个十来岁的小姑娘正和一个青年人下象棋。那小姑娘把青年人杀得一败涂地。国王坐下来和小姑娘对弈,不多一会就损兵折将,成了小姑娘 的手下败将。国王不服输,又和小姑娘下了一盘,结果是同样惨败。国王这才心服口服。 小姑娘笑着说:“我的父亲才是高手呢。他曾被选入宫中和国王对弈只是他输给了国王。”国王说:“为什么会输给国王呢”小姑娘哈哈大笑道:“父亲说,国王高兴就能国泰民安,他是故意 输给国王的。” 国王回到宫中,闭门反思,他想:太平盛世,其实不是我个人的功劳,还有各种各样的人要作出让步,或以不同的方式相助我啊是的,各行各业的兴旺与成功,上上下下的默契和互动作用是何等的重要呢。 90、暗示的力量 多年前的一个傍晚,一个叫亨利 的青年移民,站在河边发呆。这天是他30岁生日,可他不知道自己是否还有活下去的必要。因为亨利从小在福利院里长大,身材矮小,长相也不漂亮,讲话又带着浓厚的法国乡下口音,所以他一直很瞧不起自己,连最普通的工作都不敢去应聘,没有工作,也没有家。 就在亨利徘徊 于生死之间的时候,他的好朋友约翰兴冲冲地跑过来对他说:“亨利,告诉你一个好消息” 我刚刚从收音机里听到一则消息,拿破仑曾经丢失了一个孙子。播音员描述的相貌特征,与你丝毫不差” “真的吗,我竟然是拿破仑的孙子”亨利一下子精神大振。联想到爷爷曾经以矮 小的身材指挥着千军万马,用带着泥土芳香的法语发出威严的命令,他顿感自己矮小的身材同样充满力量,讲话时的法国口音也带着几分高贵和威严。第二天一大早,亨利便满怀自信地来到一家大公司应聘。 20年后,已成为这家大公司总裁的亨利,查自己并非拿破仑的孙子,但这早已 不重要了。 91、从“两可之说”到“两面思维” 春秋战国时期有一个名家学派。该学派的创始人叫邓析。我国古代文献称邓析“操两可之说,设无穷之辞”。下面的故事就是邓析“操两可之说”的典型事例: 郑国夏季常洪水泛滥。有一富人不幸被洪水淹死,尸体被某人捞起。 死者家属得知后,想出钱赎回尸体。但得尸者要价太高。死者家属无奈,便请邓析出主意。邓析对死者家属说:“你安心等着吧。那尸体如果你不去买,别人是不会去买的。”死者家属觉得有道理:对啊,我是那尸体的唯一买主,我若不买,得尸者便一无所得,那我就耐着性子再等一等, 看他如何!过了一阵,得尸者见死者家属不再来赎尸,而尸体眼看就要腐烂了,情急之下也去请邓析出主意。邓析说:“你安心等着吧。死者家属只能到你这儿来买尸体,不可能到别处去买。”得尸者觉得没错:是啊,我是那尸体的唯一卖主,只此一家别无分号,我再耐心等一等,死者 家属迟早会来的。故事的结局虽不得而知,但可以预见,如果死者家属和得尸者都遵从邓析的意见一直等下去,结果只能是两败俱伤。 邓析在死者家属和得尸者之间左右逢源,“操两可之说”的做法既不可取,更不值得效仿。但邓析的观察问题、分析问题的方式与方法,却有值得 我们思考之处。在这个故事中,我们看到的是邓析的“两面思维”,即从正反两个方面来思考同一事物。这是一种辩的思维方式。如果死者家属和得尸者也懂得“两面思维”,每一方都既看到自己有利的一面,也看到自己不利的一面,在知己知彼的情况下坐下来认真谈判,双方都做出一 点让步,结果就会是“双赢”,而不是“双输”了。 92、责任 那天晚上,在单位加班,8点多钟时,我出去吃饭,在路上,一个八、九岁的小姑娘拦住了我。 “叔叔,你能帮我一个忙吗?”“什么事?”“那边下水道的井盖开了,你能帮我把它放好吗?”听了她的话,我 才注意到,在自行车道上,一块井盖错了位,虚虚地搭在井口。我走上前去用脚踩了踩,不在意的话,人踏上去会跌落井下的。在我掂量井盖重量的时候,小姑娘用一种期待和信赖的目光看着我。 这忙,我能不帮吗? 在小姑娘和一个过路女同志的帮助下,折腾了半天,好不容 易才将它恢复原状,踩了踩,终于没事了。“谢谢叔叔!”小姑娘高兴地骑着车走了。 站在路边,我又想起小姑娘的话,她说的是“你能帮我一个忙吗”——她说的是帮她的忙,而这块井盖的错位,该是谁的事呢?如果没有这个小姑娘,也许,明天的报纸和电视上又会有“窨井伤 人”的新闻,或者是“井盖开了,该谁来管”之类的报道。从小女孩的话中,从她期盼的目光中,我分明看到了一种责任,一种发自内心的善良——小姑娘一定认为,她是第一个发现的人,就有义务将井盖恢复原状。 93、有与无 越有学问的人,也许“知道”的事情越少。比方 当对面坐着智力游戏明星。越是“知道”很多的人,也许越没有学问。比方说坐在电脑面前的网恋大师。 一个学者,一开口上下五千年地引经据典,五分钟后还说不出一句属于他自己的话,我劝你就是出于礼貌,你也要尽早抽身退席,因为这种讲演,其实,也是一种盗版。一个官 员,一开口就是“既要……又要……”,而且成串成串地说出来,方方面面都有了,其实这种报告等于什么也没有说,只表明他说过了,有了错,出了事,与他没有关系。 在文坛上,会一时红得发紫的新星,有时也会在你惊讶他突然冒出来之余,马上惊奇地发现他又突然消失得无 影无踪。这种彗星,见得多了,就能发现规律性的特性:无背景有胆量,所以在名家众多高手如云的文坛,也能振臂一呼叫人惊诧一回。 无才华却有勇气,骂倒鲁迅,横扫当今一切名流,自开门户,有主义有流派有世界最新写作方式,让人知道又有颗彗星扫过文坛。 越是年纪 小的时候,越容易得到大评语,比方说“是个天才”,比方说“能当大官当总统当联合国秘书长”;有评价容易,因为兑现的日子还遥遥无期;越到老了越不容易得到这样的评价,因为人老了,资格有了,能力有了,可惜兑现的时间没有了。 94、珍贵东西慢慢长 从读小学起, 我就一直很努力地学习,可成绩总是平平。有一段时间,我曾对自己失去了信心。 父亲带我去公园,指着园内的两排树问我:“你知道那些是什么树吗?”我一看,一排是白杨,一排是银杏,与高大的白杨相比,银杏显得十分矮小。父亲说:“我特意问过公园管理员,这两排树是 同时栽下的。栽下时,都一样高。它们享受同样的阳光,同样的水土,同样的条件,到后来,白杨为什么长得高大,而银杏却生得矮小呢?”父亲见我回答不上来,接着说:“孩子,要知道,珍贵的东西总是慢慢成长。” 95、保护孩子的天性 1979年6月,中国曾派一个访问团, 去美国考察初级教育。回国后,写了一份3万字的报告,在见闻录部分,有四段文字: ▲学生无论品德优劣、能力高低,无不趾高气扬、踌躇满志,大有“我因我之为我而不同凡响”的意味。 ▲小学二年级的学生,大字不识一斗,加减乘除还在掰手指头,就整天奢谈发明创造。 在他们手里,让地球调个头,好像都易如反掌似的。 ▲重音、体、美,而轻数、理、化。无论是公立还是私立学校,音、体、美活动无不如火如荼,而数、理、化则乏人问津。 ▲课堂几乎处于失控状态。学生或挤眉弄眼,或谈天说地,或跷着二郎腿,更有甚者,如逛街一般, 在教室里摇来晃去。 最后,在结论部分,是这么写的:美国的初级教育已经病入膏肓,可以这么预言,再用20年的时间,中国的科技和文化必将赶上和超过这个所谓的超级大国。 在同一年,作为互访,美国也派了一个考察团来中国。他们在看了、、西安的几所学校后,也写了 一份报告,在见闻录部分,也有四段文字: ▲中国的小学生在上课时喜欢把手端在胸前,
简谐运动的能量
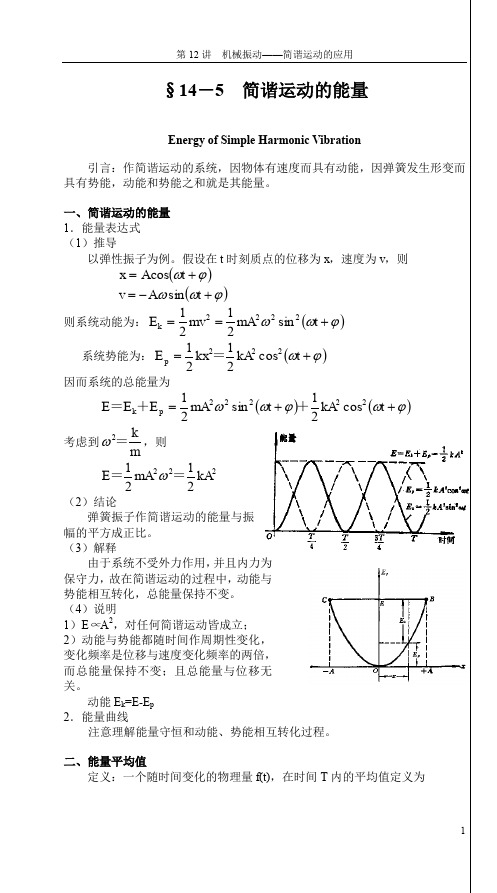
例1.用机械能守恒定律求弹簧振子的运动方程。
解:弹簧振子在振动过程中,机械能守恒,即
两边对时间求导,得
即
令 ,则
其解为
代入守恒方程可得
A=A’
例2.劲度系数为k、原长为l、质量为m的匀质弹簧,一端固定,另一端系一质量为M的物体,在光滑的水平面上作直线运动,求其运动方程。
2.共振角频率与共振振幅:
1)共振角频率:系统发生共振时强迫力的角频率称为共振角频率,用ωr表示。用求极值的方法
计算可得
2)共振振幅
3)共振时受迫振动位移与强迫力之间的相位差
3.说明:
1)ωr略小于ω0,当阻尼因子β趋于零而发生共振现象时,共振角频率等于系统的固有角频率,ωr=ω0;
2)当β→0,ωr=ω0时,共振振幅趋于无穷大,这种情况称为尖锐共振;此时受迫振动位移与强迫力之间的相位差为
考虑到 ,则
(2)结论
弹簧振子作简谐运动的能量与振幅的平方成正比。
(3)解释
由于系统不受外力作用,并且内力为保守力,故在简谐运动的过程中,动能与势能相互转化,总能量保持不变。
(4)说明
1)E∝A2,对任何简谐运动皆成立;
2)动能与势能都随时间作周期性变化,变化频率是位移与速度变化频率的两倍,而总能量保持不变;且总能量与位移无关。
动能Ek=E-Ep
2.能量曲线
注意理解能量守恒和动能、势能相互转化过程。
二、能量平均值
定义:一个随时间变化的物理量f(t),在时间T内的平均值定义为
因而弹簧振子在一个周期内的平均动能为
因而弹簧振子在一个周期内的平均势能为
结论:简谐运动的动能与势能在一个周期内的平均值相等,它们都等于总能量的一半。
简谐运动的能量

根据机械能守恒定律,有
将上式对时间求导,整理后可得
或写成
式中
可见,当弹簧质量远小于物体的质量时,且系统作微小运动时,弹簧振子的运动可以认为是简谐运动,振动周期为
因而,周期比不计弹簧质量时要大。不过当m=M时,与严格计算结果相比较,误差也是不大于1%。
Composition of Simple Harmonic Vibration
§
Energy of Simple Harmonic Vibration
引言:作简谐运动的系统,因物体有速度而具有动能,因弹簧发生形变而具有势能,动能和势能之和就是其能量。
一、简谐运动的能量
1.能量表达式
(1)推导
以弹性振子为例。假设在t时刻质点的位移为x,速度为v,则
则系统动能为:
系统势能为:
因而系统的总能量为
1.应用1——记忆振幅公式
由能量守恒关系可得:kA2/2=mv02/2+kx02/2
解之即得:
2.应用2——推导简谐运动相关方程
在忽略阻力的条件下,作简谐运动的系统只有动能和势能(弹性势能和重力势能),且二者之和保持不变,因而有
将具体问题中的动能与势能表达式代入上式,经过简化后,即可得到简谐运动的微分方程及振动周期和频率。这种方法在工程实际中有着广泛的应用。
2.两个分振动的频率相差较大,但有简单的整数比关系:
此时合振动的轨迹为封闭的图形,称为李萨如(Lissajou's Figures)图形。该图形的的具体形状取决于两个互相垂直方向简谐运动的频率之比合初相位,并且该图形坐标轴的切点之比与频率之比相等。用此方法可以测量一未知振动的频率与相互垂直方向的两个简谐运动的相位差。
振子恰好从准周期运动变为非周期运动。与弱阻尼和过阻尼比较,在临界阻尼情况下振子回到平衡位置而静止下来所需时间最短。
简谐运动能量

§9-4 简谐运动的能量
§9-4 简谐运动的能量
能量是伴随运动而存在的, 能量是伴随运动而存在的 , 简谐运动同样具有动 能和势能。 能和势能。
以水平弹簧振子为例) 一、简谐振动的能量(以水平弹簧振子为例 简谐振动的能量 以水平弹簧振子为例
x = A cos( ω t + ϕ )
v = −ωA sin( ω t + ϕ )
3、 机械能 、
情况同动能。 情况同动能。
1 2 1 2 2 E = Ek + E p = kA = mω A 2 2
理学院 物理系
E不随时间变化,简谐振动系统机械能守恒。 不随时间变化,简谐振动系统机械能守恒。 不随时间变化
大学物理
§9-4 简谐运动的能量
二、简谐振动系统的能量特点
x, v
o
能量 动画) 简 谐 运 动 能 量 图(动画 动画
Ek max
1 2 = kA , Ek min = 0 2
t +T
1 Ek = T
1 2 ∫ Ek dt = 4 kA t
2、 势能 、
x = A cos( ω t + ϕ )
1 2 1 2 = kA cos 2 (ω t + ϕ ) E p = kx 2 2
E p max , E p min , E p
简谐运动能量守 恒,振幅不变
Ep
C
1 E = kA 2
2
简谐运动势能曲线
E
Ek
Ep
−A
O
B
xபைடு நூலகம்
+A
x
理学院 物理系
大学物理
§9-4 简谐运动的能量
能量守恒 简谐运动方程 1 2 1 2 E = mv + kx = 常量 2 2 d 1 2 1 2 ( mv + kx ) = 0 dt 2 2 dv dx mv + kx =0 dt dt d2x k + x = 0 2 dt m
简谐运动的回复力和能量 课件

5.理想化模型 (1)力的角度:简谐运动所受回复力不考虑摩擦阻力. (2)能量角度:简谐运动没有考虑因克服阻力做功带来 的能量损耗.
一、简谐运动的判断
例1:弹簧下端挂一质量为M的钢球,如右图所示,试证 明此系统在竖直方向上做的机械振动为简谐运动.
证明:设弹簧的劲度系数为k,在弹性限度内把钢球向下 拉一段距离至A点.如图甲所示. 在钢球振动中到达平衡位置O点下方某一点B,此时振 子的位移为x. 在平衡位置时,弹簧伸长x0. 由平衡方程Mg-kx0=0. 在B点F回=Mg-k(x+x0)=-kx. 由于B是振动中的任一位置,可见钢球受 合外力与它的位移的关系符合简谐运动 的受力特点.即该振动为简谐运动.
(4)式中“k”虽是系数,但有单位,其单位由F和x的单 位决定,为N/m. (5)简谐运动中,回复力F=-kx,因x=Asin(ωt+φ).故 F=-kAsin(ωt+φ),可见回复力随时间按正弦规律变 化,简谐运动是一个变加速运动. (6)判断一个振动是否为简谐运动可根据此振动的回复 力是否满足F=-kx来判断.如果一个振动系统,它的回 复力满足F=-kx,则此振动一定为简谐运动.
二、简谐运动的回复力
例2:如右图所示,物体A置于物体B上,一轻弹簧一端固定,另一 端与B相连,在弹性限度范围内,A和B在光滑水平面上往复运 动(不计空气阻力),并保持相对静止.则下列说法正确的是( ) A.A和B均做简谐运动 B.作用在A上的静摩擦力大小与弹簧的形变量成正比 C.B对A的静摩擦力对A做功,而A对B的静摩擦力对B不做功 D.B对A的静摩擦力始终对A做正功,而A对B的静摩擦力对B 做负功
置 的 距 离k为mg .
由简谐运动的特点知最高点离平
衡 位 置 的mg距.k离 也 为
4_1_3简谐运动的能量和实例
3. 机械能
1 2 E = E k + E p = kA 2
1 2 E p = kA cos 2 (ω t + ) 2
1 2 2 E k = kA sin (ω t + ) 2
简谐运动系统机械能守恒, 简谐运动系统机械能守恒, 机械能守恒 能量没有输入(因是自由振动 因是自由振动), 能量没有输入 因是自由振动 , 因无阻尼), 也无损耗 (因无阻尼 , 因无阻尼 各时刻机械能=起始能量E 时输入的能量)。 各时刻机械能=起始能量 0 (t =0时输入的能量 。 时输入的能量
fn
重力的切向分量为 f t = mg sin θ 对悬点的恢复力矩 M = l ( mg sin θ ) 由转动的牛顿第二定律, 由转动的牛顿第二定律,得 l ( mg sin θ ) = Jα sin 很小时, 在角位移θ很小时, θ ≈ θ lmg α= θ --- 简谐运动 J
2
方法2 方法
J T = 2π mgl c
简谐运动中线量-角量的对比 简谐运动中线量-角量的对比 线量
线量 位移 加速度 恢复力 牛顿第 二定律 x(t)=Acos(ω t+)
a ( t ) = ω x ( t )
2
角量
θ ( t ) = θ m cos(ωt + )
α ( t ) = ω θ ( t )
2
ω=
k m
L ~ m
磁 1 2 E B = Li 能 2
ω=
1 LC
ω
三、稳定平衡位置附近的微小振动 物体一离开该平衡位置就受到恢复力而返回。 物体一离开该平衡位置就受到恢复力而返回。 在该位置,势能必为最小值。 在该位置,势能必为最小值。 dE p 保守力: 保守力:F = 势能: 势能: E p = E p ( x ) dx 一 将势能在x=0的平衡位置展开 将势能在 的平衡位置展开 定 是 d 2E p dE p 1 2 x +L 简 x+ E p ( x ) = E p ( 0) + dx 2! dx 2 x=0 x =0 谐 势能 dE p 运 平衡 d 2E p >0 动 dx = 0 最小 2 dx 稳定 x=0
第五节 简谐运动的能量
第五节 简谐运动的能量 阻尼振动 第六节 受迫振动 共振一、简谐运动的能量:1、振子在振动过程中动能和势能相互转化,机械能守恒。
如图所示的单摆,在振动过程中能量转化情况2、注意:能量的大小和振幅有关,和振动系统回复力与位移的比例系数有关。
振幅越大,比例系数越大,振动能量越大。
二、阻尼振动与无阻尼振动:1、阻尼振动:振幅逐渐减小的振动叫做阻尼振动。
注意:1)振幅减小,能量也减小; 2)阻尼振动的周期不变。
2、无阻尼振动:振幅不变的振动叫做无阻尼振动。
注意:1)可能是振动系统摩擦和阻力不计,振动能量无损失;2)可能是振动虽有能量损失,但不断补充能量,使振动等幅。
三、受迫振动: 1、概念:1)自由振动:不受其它外力,只在系统内部的弹力或重力作用下的振动叫做自由振动;2)驱动力:作用于质点的周期性的外力叫做驱动力;3)受迫振动:物体在周期性驱动力作用下的振动叫做受迫振动。
2、特点:1)物体做受迫振动时的振动频率等于驱动力的频率,而与物体的固有频率无关;2)物体做受迫振动的振幅与驱动力的频率和物体的固有频率有关,二者相差越小,物体做受迫振动的振幅越大。
四、共振: 1、共振曲线:2、条件:当驱动力的频率跟物体的固有频率相等(固驱f f )时,受迫振动的振幅最大,这种现象叫做共振。
3、共振的应用和防止: 利用:让驱动力频率接近或等于固有频率防止:让驱动力频率远大于或远小于固有频率五、振动的分类:1、按振动特点分:简谐运动、非简谐运动;2、按形成原因分:自由振动(内力)、受迫振动(外力);3、按振动振幅分:等幅振动(无阻尼)、减幅振动(阻尼)。
说明:简谐运动必为无阻尼振动(等幅);实际的简谐运动必为受迫振动;实际的自由振动必为阻尼振动;理想的简谐运动是指无阻尼自由振动,实际上不存在。
例题:A 、B 两个弹簧振子,固有周期分别为f 、4f ,它们均在频率为3f 的驱动力作用下做受迫振动,则下列说法中正确的是:A 、振子A 的振幅较大,振动频率为4f ;B 、振子B 的振幅较大,振动频率为3f ;C 、振子A 的振幅较大,振动频率为3f;D 、振子B 的振幅较大,振动频率为4f 。
3 简谐运动的回复力和能量
3简谐运动的回复力和能量一、简谐运动的回复力1.简谐运动如果质点所受的力与它偏离平衡位置位移的大小成正比,并且总是指向平衡位置,质点的运动就是简谐运动.2.回复力(1)定义:使振动物体回到平衡位置的力.(2)方向:总是指向平衡位置.(3)表达式:F=-kx.二、简谐运动的能量1.能量转化弹簧振子运动的过程就是动能和势能互相转化的过程.(1)在最大位移处,势能最大,动能为零.(2)在平衡位置处,动能最大,势能最小.2.能量特点在简谐运动中,振动系统的机械能守恒,而在实际运动中都有一定的能量损耗,因此简谐运动是一种理想化的模型.一、简谐运动的回复力1.回复力(1)回复力的方向总是指向平衡位置,回复力为零的位置就是平衡位置.(2)回复力的性质回复力是根据力的效果命名的,可能由合力、某个力或某个力的分力提供.它一定等于振动物体在振动方向上所受的合力,分析物体受力时不能再加上回复力.例如:如图2甲所示,水平方向的弹簧振子,弹力充当回复力;如图乙所示,竖直方向的弹簧振子,弹力和重力的合力充当回复力;如图丙所示,m随M一起振动,m的回复力由静摩擦力提供.图22.回复力公式:F=-kx(1)k是比例系数,其值由振动系统决定,与振幅无关.只有水平弹簧振子,回复力仅由弹力提供,k为劲度系数.(2)“-”号表示回复力的方向与偏离平衡位置的位移的方向相反.3.简谐运动的加速度由F=-kx及牛顿第二定律F=ma可知:a=-km x,加速度a与位移x的大小成正比,方向与位移方向相反.4.物体做简谐运动的判断方法(1)简谐运动的回复力满足F=-kx;(2)简谐运动的振动图象是正弦曲线.例1(多选)如图3所示,弹簧振子在光滑水平杆上的A、B之间做往复运动,下列说法正确的是()图3A.弹簧振子运动过程中受重力、支持力和弹簧弹力的作用B.弹簧振子运动过程中受重力、支持力、弹簧弹力和回复力的作用C.振子由A向O运动过程中,回复力逐渐增大D.振子由O向B运动过程中,回复力的方向指向平衡位置二、简谐运动的能量1.简谐运动中,振动系统的动能和势能相互转化,平衡位置处动能最大,势能最小;最大位移处动能为零,势能最大,但总的机械能不变.2.对于同一个振动系统,振幅越大,振动的能量越大.3.简谐运动是一种无能量损失的振动,所以其振幅保持不变,又称为等幅振动.例2如图4所示,一水平弹簧振子在A、B间做简谐运动,平衡位置为O,已知振子的质量为M.图4(1)简谐运动的能量取决于______,振子振动时动能和______相互转化,总机械能______.(2)振子在振动过程中,下列说法中正确的是________.A.振子在平衡位置,动能最大,弹性势能最小B.振子在最大位移处,弹性势能最大,动能最小C.振子在向平衡位置运动时,由于振子振幅减小,故总机械能减小D.在任意时刻,动能与弹性势能之和保持不变三、简谐运动中各物理量的变化1.如图5所示为水平的弹簧振子示意图,振子运动过程中各物理量的变化情况如表所示.图5振子的运动A→O O→A′A′→O O→A位移方向向右向左向左向右大小减小增大减小增大回复力方向向左向右向右向左大小减小增大减小增大加速度方向向左向右向右向左大小减小增大减小增大速度方向向左向左向右向右大小增大减小增大减小振子的动能增大减小增大减小弹簧的势能减小增大减小增大系统总能量不变不变不变不变2.说明:(1)简谐运动中各个物理量对应关系不同.位置不同,则位移不同,加速度、回复力不同,但是速度、动能、势能可能相同,也可能不同.(2)简谐运动中的最大位移处,F、a、E p最大,E k=0;在平衡位置处,F=0,a=0,E p=0,E k最大.(3)位移增大时,回复力、加速度和势能增大,速度和动能减小;位移减小时,回复力、加速度和势能减小,速度和动能增大.例3(2018·金华市十校高二上学期期末联考)如图6甲所示,弹簧振子以O点为平衡位置,在A、B两点之间做简谐运动.取向右为正方向,振子的位移x与时间t的关系图象如图乙所示,下列说法正确的是()图6A.t=0.8 s时,振子的速度方向向右B.t=0.2 s时,振子在O点右侧6 cm处C.t=0.4 s和t=1.2 s时,振子的加速度相同D.从t=0.4 s到t=0.8 s的时间内,振子的动能逐渐增大例4如图7所示,平台沿竖直方向做简谐运动,一物体置于振动平台上始终随平台振动,两者保持相对静止.以下说法正确的是()图7A.振动平台位于最高点时,物体对平台的压力最大B.振动平台位于最低点时,物体对平台的压力最大C.物体速度最大时,对平台的压力最大D.物体加速度最大时,对平台的压力最大1.(简谐运动的回复力)(多选)关于简谐运动的回复力,以下说法正确的是()A.简谐运动的回复力不可能是恒力B.做简谐运动的物体的加速度方向与位移方向总是相反C.简谐运动中回复力的公式为F=-kx,其中k是弹簧的劲度系数,x是弹簧的长度D.做简谐运动的物体每次经过平衡位置合力一定为零2.(简谐运动中各物理量的变化)(2018·诸暨牌头中学高二上学期期中)如图8所示,虚线和实线分别为甲、乙两个弹簧振子做简谐运动的图象,则下列说法正确的是()图8A.任意时刻,甲振子的位移都比乙振子的位移大B.t=0时,甲、乙两振子的振动方向相反C.前2 s内,甲、乙两振子的加速度均为正值D.第2 s末,甲的加速度达到其最大值,乙的速度达到其最大值3.(简谐运动的能量)(2018·沈阳市郊联体高二上学期期末)把一个小球套在光滑细杆上,球与轻弹簧相连组成弹簧振子,小球沿杆在水平方向做简谐运动,它围绕平衡位置O在A、B间振动,如图9所示,下列结论正确的是()图9A.小球在O位置时,动能最小,加速度最小B.小球在A、B位置时,动能最大,加速度最大C.小球从A经O到B的过程中,回复力先做正功,后做负功D.小球从B到O的过程中,振动的能量不断减小4.(简谐运动的表达式及各物理量的变化)如图10所示为一弹簧振子的振动图象,试完成以下问题:图10(1)写出该振子简谐运动的表达式;(2)在第2 s末到第3 s末这段时间内,弹簧振子的加速度、速度、动能和弹性势能各是怎样变化的?(3)该振子前100 s的总位移是多少?路程是多少?一、选择题考点一简谐运动的回复力和加速度1.对于弹簧振子的回复力和位移的关系,下列图中正确的是()2.如图1甲所示,一弹簧振子在A、B间做简谐运动,O为平衡位置,图乙是弹簧振子做简谐运动时的位移—时间图象,则关于弹簧振子的加速度随时间的变化规律,下列四个图象中正确的是()图考点二简谐运动的能量3.如图4所示为某个弹簧振子做简谐运动的振动图象,由图象可知()图4A.在0.1 s时,由于位移为零,所以振动能量为零B.在0.2 s时,振子具有最大势能C.在0.35 s时,振子具有的能量尚未达到最大值D.在0.4 s时,振子的动能最大4.(2018·南昌高二检测)如图7所示,一水平弹簧振子在光滑水平面上的B、C两点间做简谐运动,O为平衡位置.已知振子由完全相同的P、Q两部分组成,彼此拴在一起.当振子运动到B点的瞬间,将P拿走,则以后Q的运动和拿走P之前相比有()图7A.Q的振幅不变,通过O点的速率减小B.Q的振幅不变,通过O点的速率增大C.Q的振幅增大,通过O点的速率增大D.Q的振幅减小,通过O点的速率减小考点三简谐运动中各物理量的变化5.(多选)如图8所示是某一质点做简谐运动的振动图象,下列说法正确的是()图8A.在第1 s内,质点速度逐渐增大B.在第1 s内,质点加速度逐渐增大C.在第4 s内,质点的动能逐渐增大D.在第4 s内,质点的势能逐渐增大6.(多选)如图9为某一质点的振动图象,由图可知,在t1和t2两时刻|x1|>|x2|,质点速度v1、v2与加速度a1、a2的关系正确的是()图9A.|v1|<|v2|,方向相同B.|v1|<|v2|,方向相反C.|a1|>|a2|,方向相同D.|a1|>|a2|,方向相反3简谐运动的回复力和能量[学科素养与目标要求]物理观念:1.知道回复力的概念.2.知道振幅越大,振动的能量越大.科学思维:1.会根据简谐运动的回复力特点,判断及分析常见的简谐运动.2.理解简谐运动的动力学特征. 科学探究:通过探究,理解简谐运动中位移、回复力、加速度、速度、动能、势能的变化情况.一、简谐运动的回复力1.简谐运动如果质点所受的力与它偏离平衡位置位移的大小成正比,并且总是指向平衡位置,质点的运动就是简谐运动.2.回复力(1)定义:使振动物体回到平衡位置的力.(2)方向:总是指向平衡位置.(3)表达式:F=-kx.二、简谐运动的能量1.能量转化弹簧振子运动的过程就是动能和势能互相转化的过程.(1)在最大位移处,势能最大,动能为零.(2)在平衡位置处,动能最大,势能最小.2.能量特点在简谐运动中,振动系统的机械能守恒,而在实际运动中都有一定的能量损耗,因此简谐运动是一种理想化的模型.一、简谐运动的回复力如图所示为一个水平方向的弹簧振子模型(水平杆光滑),O点为振子的平衡位置,A、O间和B、O间距离都是x.(1)振子在O点时受到几个力的作用?分别是什么力?(2)振子在A、B点时受到哪些力的作用?(3)除重力、支持力、弹簧弹力外,振子在O、A、B点还受到回复力的作用吗?回复力有什么特点?答案(1)两个力.重力、支持力.(2)A点:重力、支持力、弹簧向右的弹力;B点:重力、支持力、弹簧向左的弹力.(3)不受.回复力是指将振动的物体拉回到平衡位置的力,是按照力的作用效果来命名的,不是一种新型的力,所以分析物体的受力时,不分析回复力.回复力可以由某一个力提供(如弹力),也可能是几个力的合力,还可能是某一个力的分力,归纳起来,回复力一定等于物体沿振动方向所受的合力.1.回复力(1)回复力的方向总是指向平衡位置,回复力为零的位置就是平衡位置.(2)回复力的性质回复力是根据力的效果命名的,可能由合力、某个力或某个力的分力提供.它一定等于振动物体在振动方向上所受的合力,分析物体受力时不能再加上回复力.例如:如图2甲所示,水平方向的弹簧振子,弹力充当回复力;如图乙所示,竖直方向的弹簧振子,弹力和重力的合力充当回复力;如图丙所示,m随M一起振动,m的回复力由静摩擦力提供.图22.回复力公式:F=-kx(1)k是比例系数,其值由振动系统决定,与振幅无关.只有水平弹簧振子,回复力仅由弹力提供,k为劲度系数.(2)“-”号表示回复力的方向与偏离平衡位置的位移的方向相反.3.简谐运动的加速度由F=-kx及牛顿第二定律F=ma可知:a=-km x,加速度a与位移x的大小成正比,方向与位移方向相反.4.物体做简谐运动的判断方法(1)简谐运动的回复力满足F=-kx;(2)简谐运动的振动图象是正弦曲线.例1(多选)如图3所示,弹簧振子在光滑水平杆上的A、B之间做往复运动,下列说法正确的是()图3A.弹簧振子运动过程中受重力、支持力和弹簧弹力的作用B.弹簧振子运动过程中受重力、支持力、弹簧弹力和回复力的作用C.振子由A向O运动过程中,回复力逐渐增大D.振子由O向B运动过程中,回复力的方向指向平衡位置答案AD解析弹簧振子运动过程中受重力、支持力和弹簧弹力,回复力是根据效果命名的力,它是由物体受到的具体的力所提供的,在此情景中弹簧的弹力充当回复力,故A正确,B错误;回复力与位移的大小成正比,由A向O运动过程中位移的大小在减小,故此过程回复力逐渐减小,C错误;回复力总是指向平衡位置,故D正确.二、简谐运动的能量如图所示为水平弹簧振子,振子在A、B之间往复运动.(1)从A到B的运动过程中,振子的动能如何变化?弹簧弹性势能如何变化?振动系统的总机械能是否变化?(2)如果把振子振动的振幅增大,振子回到平衡位置的动能是否增大?振动系统的机械能是否增大?(3)实际的振动系统有空气阻力和摩擦阻力,能量是否损失?理想化的弹簧振动系统,忽略空气阻力和摩擦阻力,能量是否损失?答案(1)振子的动能先增大后减小弹簧的弹性势能先减小后增大总机械能保持不变(2)振子回到平衡位置的动能增大系统的机械能增大(3)实际的振动系统,能量逐渐减小理想化的弹簧振动系统,能量不变.1.简谐运动中,振动系统的动能和势能相互转化,平衡位置处动能最大,势能最小;最大位移处动能为零,势能最大,但总的机械能不变.2.对于同一个振动系统,振幅越大,振动的能量越大.3.简谐运动是一种无能量损失的振动,所以其振幅保持不变,又称为等幅振动.例2如图4所示,一水平弹簧振子在A、B间做简谐运动,平衡位置为O,已知振子的质量为M.图4(1)简谐运动的能量取决于______,振子振动时动能和______相互转化,总机械能______.(2)振子在振动过程中,下列说法中正确的是________.A.振子在平衡位置,动能最大,弹性势能最小B.振子在最大位移处,弹性势能最大,动能最小C.振子在向平衡位置运动时,由于振子振幅减小,故总机械能减小D.在任意时刻,动能与弹性势能之和保持不变答案(1)振幅弹性势能守恒(2)ABD解析(1)简谐运动的能量取决于振幅,振子振动时动能和弹性势能相互转化,总机械能守恒.(2)振子在平衡位置两侧往复运动,在平衡位置处速度达到最大,动能最大,弹性势能最小,所以A正确;在最大位移处速度为零,动能为零,此时弹簧的形变量最大,弹性势能最大,所以B正确;振幅的大小与振子的位置无关,在任意时刻只有弹簧的弹力做功,所以机械能守恒,所以C错误,D正确.三、简谐运动中各物理量的变化1.如图5所示为水平的弹簧振子示意图,振子运动过程中各物理量的变化情况如表所示.图5振子的运动 A →O O →A ′ A ′→O O →A 位移 方向 向右 向左 向左 向右 大小 减小 增大 减小 增大 回复力 方向 向左 向右 向右 向左 大小 减小 增大 减小 增大 加速度 方向 向左 向右 向右 向左 大小 减小 增大 减小 增大 速度方向 向左 向左 向右 向右 大小增大 减小 增大 减小 振子的动能 增大 减小 增大 减小 弹簧的势能 减小 增大 减小 增大 系统总能量不变不变不变不变2.说明:(1)简谐运动中各个物理量对应关系不同.位置不同,则位移不同,加速度、回复力不同,但是速度、动能、势能可能相同,也可能不同.(2)简谐运动中的最大位移处,F 、a 、E p 最大,E k =0;在平衡位置处,F =0,a =0,E p =0,E k 最大. (3)位移增大时,回复力、加速度和势能增大,速度和动能减小;位移减小时,回复力、加速度和势能减小,速度和动能增大.例3 (2018·金华市十校高二上学期期末联考)如图6甲所示,弹簧振子以O 点为平衡位置,在A 、B 两点之间做简谐运动.取向右为正方向,振子的位移x 与时间t 的关系图象如图乙所示,下列说法正确的是( )图6A.t =0.8 s 时,振子的速度方向向右B.t =0.2 s 时, 振子在O 点右侧6 cm 处C.t =0.4 s 和t =1.2 s 时,振子的加速度相同D.从t =0.4 s 到t =0.8 s 的时间内,振子的动能逐渐增大 答案 D解析 由题图乙知,t =0.8 s 时,图象切线的斜率为负,说明振子的速度为负,即振子的速度方向向左,故A 错误.在0~0.4 s 内,振子做减速运动,不是匀速运动,所以t =0.2 s 时,振子不在O 点右侧6 cm 处,故B 错误.t =0.4 s 和t =1.2 s 时,振子的位移大小相等、方向相反,由a =-kxm ,知加速度大小相等、方向相反,故C 错误.t =0.4 s 到t =0.8 s 的时间内,振子的位移减小,正向平衡位置靠近,速度逐渐增大,动能逐渐增大,故D 正确.例4 如图7所示,平台沿竖直方向做简谐运动,一物体置于振动平台上始终随平台振动,两者保持相对静止.以下说法正确的是( )图7A.振动平台位于最高点时,物体对平台的压力最大B.振动平台位于最低点时,物体对平台的压力最大C.物体速度最大时,对平台的压力最大D.物体加速度最大时,对平台的压力最大答案 B[学科素养] 通过对例3、例4的分析,一方面让学生进一步了解了简谐运动中的各物理量之间的关系,另一方面也提高了学生获取和处理信息的能力,体现了“物理观念”与“科学思维”的学科素养.1.(简谐运动的回复力)(多选)关于简谐运动的回复力,以下说法正确的是( )A.简谐运动的回复力不可能是恒力B.做简谐运动的物体的加速度方向与位移方向总是相反C.简谐运动中回复力的公式为F =-kx ,其中k 是弹簧的劲度系数,x 是弹簧的长度D.做简谐运动的物体每次经过平衡位置合力一定为零答案 AB解析 根据简谐运动的定义可知,物体做简谐运动时,受到的回复力为F =-kx ,k 是比例系数,x 是物体相对平衡位置的位移,回复力不可能是恒力,故A 正确,C 错误;回复力方向总是指向平衡位置,与位移方向相反,根据牛顿第二定律,加速度的方向与回复力的方向相同,所以做简谐运动的物体的加速度方向与位移方向总是相反,故B 正确;做简谐运动的物体每次经过平衡位置回复力为零,但是合力不一定为零,故D 错误.2.(简谐运动中各物理量的变化)(2018·诸暨牌头中学高二上学期期中)如图8所示,虚线和实线分别为甲、乙两个弹簧振子做简谐运动的图象,则下列说法正确的是( )图8A.任意时刻,甲振子的位移都比乙振子的位移大B.t =0时,甲、乙两振子的振动方向相反C.前2 s 内,甲、乙两振子的加速度均为正值D.第2 s 末,甲的加速度达到其最大值,乙的速度达到其最大值答案 B解析 简谐运动的图象反映了振子的位移与时间的关系,甲振子的位移有时比乙振子的位移大,有时相同,有时比乙振子的位移小,故A 错误;根据切线斜率的正负表示速度的方向可知,t =0时,甲、乙两振子的振动方向相反,故B 正确;由a =-kx m分析可知,前2 s 内乙振子的加速度为正值,甲振子的加速度为负值,故C 错误;第2 s 末甲的位移等于零,加速度为零,通过平衡位置,速度达到其最大值,乙的位移达到最大值,加速度达到其最大值,速度为零,故D 错误.3.(简谐运动的能量)(2018·沈阳市郊联体高二上学期期末)把一个小球套在光滑细杆上,球与轻弹簧相连组成弹簧振子,小球沿杆在水平方向做简谐运动,它围绕平衡位置O 在A 、B 间振动,如图9所示,下列结论正确的是( )图9A.小球在O 位置时,动能最小,加速度最小B.小球在A 、B 位置时,动能最大,加速度最大C.小球从A 经O 到B 的过程中,回复力先做正功,后做负功D.小球从B 到O 的过程中,振动的能量不断减小答案 C解析 振子经过平衡位置时,速度最大,位移为零,所以在O 位置时动能最大,回复力为零,加速度为零,故A 错误;在A 、B 位置时,速度为零,位移最大,回复力最大,加速度最大,故B 错误;由于回复力指向平衡位置,所以振子从A 经O 到B 的过程中,回复力先做正功,后做负功,故C 正确;振子的动能和弹簧的弹性势能相互转化,且总量保持不变,即振动的能量保持不变,故D 错误.4.(简谐运动的表达式及各物理量的变化)如图10所示为一弹簧振子的振动图象,试完成以下问题:图10(1)写出该振子简谐运动的表达式;(2)在第2 s 末到第3 s 末这段时间内,弹簧振子的加速度、速度、动能和弹性势能各是怎样变化的?(3)该振子前100 s 的总位移是多少?路程是多少?答案 (1)x =5sin π2t (cm) (2)见解析 (3)0 5 m 解析 (1)简谐运动图象的一般表达式是x =A sin(ωt +φ0),由振动图象可得振幅A =5 cm ,初相φ0=0,周期T =4 s ,则角速度ω=2πT =π2rad/s 故该振子简谐运动的表达式为x =5sin π2t (cm) (2)由题图可知,在t =2 s 时,振子恰好通过平衡位置,此时加速度为零,随着时间的延续,位移为负值且不断增大,即离开平衡位置的距离变大,回复力变大,加速度指向平衡位置且变大,速度不断变小,动能不断减小,弹性势能逐渐增大.当t =3 s 时,加速度达到最大,速度等于零,动能等于零,弹性势能达到最大值.(3)振子经一周期位移为零,路程为4×5 cm =20 cm ,前100 s 刚好经过了25个周期,所以前100 s 振子位移x =0,振子路程s =25×20 cm =500 cm =5 m.一、选择题考点一 简谐运动的回复力和加速度1.对于弹簧振子的回复力和位移的关系,下列图中正确的是( )答案 C解析 由简谐运动的回复力公式F =-kx 可知,C 正确.2.如图1甲所示,一弹簧振子在A 、B 间做简谐运动,O 为平衡位置,图乙是弹簧振子做简谐运动时的位移—时间图象,则关于弹簧振子的加速度随时间的变化规律,下列四个图象中正确的是( )图答案 C解析 加速度与位移的关系为a =-kx m ,而x =A sin ωt ,所以a =-kA msin ωt ,则可知C 选项正确. 考点二 简谐运动的能量3.如图4所示为某个弹簧振子做简谐运动的振动图象,由图象可知( )图4A.在0.1 s 时,由于位移为零,所以振动能量为零B.在0.2 s 时,振子具有最大势能C.在0.35 s 时,振子具有的能量尚未达到最大值D.在0.4 s 时,振子的动能最大答案 B 解析 弹簧振子做简谐运动,振动能量不变,选项A 错;在0.2 s 时位移最大,振子具有最大势能,选项B 对;弹簧振子的振动能量不变,在0.35 s 时振子具有的能量与其他时刻相同,选项C 错;在0.4 s 时振子的位移最大,动能为零,选项D 错.4.(2018·南昌高二检测)如图7所示,一水平弹簧振子在光滑水平面上的B 、C 两点间做简谐运动,O 为平衡位置.已知振子由完全相同的P 、Q 两部分组成,彼此拴在一起.当振子运动到B 点的瞬间,将P 拿走,则以后Q 的运动和拿走P 之前相比有( )图7A.Q的振幅不变,通过O点的速率减小B.Q的振幅不变,通过O点的速率增大C.Q的振幅增大,通过O点的速率增大D.Q的振幅减小,通过O点的速率减小答案 B 解析振幅为偏离平衡位置的最大距离,即速度为零时的位移大小,振子到B点时速度为零,OB间距等于振幅,此时拿走P,振子速度仍然为零,故Q的振幅不变;简谐运动中势能和动能之和守恒,到达B点时,动能为零,弹性势能最大,此时拿走P,系统机械能不变,回到O点时动能不变,根据E k=12m v2,振子质量减小,速率一定增大,B正确.考点三简谐运动中各物理量的变化5.(多选)如图8所示是某一质点做简谐运动的振动图象,下列说法正确的是()图8A.在第1 s内,质点速度逐渐增大B.在第1 s内,质点加速度逐渐增大C.在第4 s内,质点的动能逐渐增大D.在第4 s内,质点的势能逐渐增大答案BC解析在第1 s内,质点由平衡位置向正向最大位移处运动,速度减小,位移增大,回复力和加速度都增大,故A错误,B正确;在第4 s内,质点由负向最大位移处向平衡位置运动,速度增大,位移减小,动能增大,势能减小,故C正确,D错误.6.(多选)如图9为某一质点的振动图象,由图可知,在t1和t2两时刻|x1|>|x2|,质点速度v1、v2与加速度a1、a2的关系正确的是()图9A.|v1|<|v2|,方向相同B.|v1|<|v2|,方向相反C.|a1|>|a2|,方向相同D.|a1|>|a2|,方向相反答案AD解析在t1时刻,质点向平衡位置运动,在t2时刻,质点远离平衡位置运动,故速度v1与v2方向相同,由于|x1|>|x2|,所以|v1|<|v2|,A对,B错;在t1和t2时刻,质点离开平衡位置的位移方向相反,因而回复力方向相反,加速度方向相反,但|x1|>|x2|,t1时刻回复力大于t2时刻回复力,故|a1|>|a2|,C错,D对.。
简谐运动的总能量公式
简谐运动的总能量四川宣汉第二中学金菊英(636150)一.总能量公式:221KA E =简谐运动是一种理想化的振动.对简谐运动来说,一旦供给振动系统以一定的能量,使它开始振动。
在振动过程中动能和势能不断地发生相互转换。
但动能和势能总和不变,即机械能守恒,也即是总能量不变。
在不同的简谐运动中这个总能量写出的具体形式可能不一样,比如单摆往往会写成初始的势能形式。
但它们可以统一于一个公式之中:221KA E =。
其中,E 是总能量,K 是KX F -=中的比例系数,A 为简谐运动的振幅,正因为总能量不变,所以A 也是一个不变量。
弹簧振子和单摆是两种典型的简谐运动,下面我们分别对其加以证明。
二.论证弹簧振子符合此公式:用外力把弹簧振子从平衡位置移到振幅处。
弹力的大小随形变而发生变化(L K F ∆=弹F ,其中L ∆表示形变量),但它呈一种线性变化,所以可以求出这个过程中外力的平均值:20KA F +=。
再根据变力做功的公式就可以求出外力所做的功:22120KA A KAFA W =+==。
通过外力做功使弹簧振子在振幅处具有221KA 的机械能,(振幅处表现为势能)。
在弹簧振子运动过程中动能和势能不断转换,但总能量始终是221KA E =。
三.论证单摆符合此公式情景:如图一,一个摆长为l ,质量为m 的单摆在A ,B 之间做简谐运动。
其最大摆角为α。
1. 单摆的K 。
单摆是用重力的一个分力充当回复力的,其回复力大小可以写为θsin mg F =,(θ为摆球的瞬时摆角)θ<α,由于θ很小, sin θ=l x ||,(x 为离开平衡位置O 的位移,) 加上符号,x l mgl xmg F -=-=,所以对单摆来说K=l mg2. 单摆的能量单摆在整个简谐运动过程中的总能量等于在振幅处的重利势能。
图一 B 点:E=E P =)cos 1(α-mgl ①利用数学知识,在三角形COB 中:αcos 2222COCB CB CO OB -+=,其中OB 为振幅,CO ,BO 均为摆长,于是可得αcos 22222l l l A -+=)c o s 1(222α-=l A 222c o s l A=-α ②由①②可得:E=222l Amgl =221A lmg 3. 由1已经知道对单摆来说K=l mg,综合1、2,可得: E=221A l mg=221KA 对于221KA E =还可以用高等数学的方式给予证明,不管是什么形式的简谐运动,其总能量都可以写为221KA E =四.常见例题关于简谐运动能量的题都不难,大多以选择题出现。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解: 简谐运动的总能量为
E E pE k
1kA 2 2
当 x=1 kA2 1 E 2 2 4
Ek
E
E
p
3 4
E
动能和势能各占总能量的一半时:
1 2
kx
2 0
1 2
1 kA2 2
x0
1 A0.707A 2
大学物理
振动学基础
第5讲 简谐运动的能量
简谐运动的能量
简谐运动的能量
简谐运动物体的能量及其变化有什么特点?
简谐运动的能量
简谐运动的能量
弹簧振子的动能为
Ek
1 mv 2
2
1 m
2
A2
s2in
2t
弹簧的弹性势能
Ep
1 kx 2
2
1 kA 2
2
cos 2 t
系统的总机械能为
E Ek Ep
1 kA2 1 m2A2
(3)动能和势能的变化其频率为两倍ω;;
(4)动能和势能变化位相相反.
简谐运动的能量
(5)振动强度:
E 1m2A2 1 kA22
2
(6)简谐运动的判据之二:
Ep
1 2
kx
2
x2
Ep
E
Ek
A
Ep
O x A
x
简谐运动的能量
简谐运动的能量
例题 当简谐运动的位移为振幅的一半时, 其动能和势能 各占总能量的多少?物体在什么位置时其动能和势能各占总 能量的一半?
22
——系统机械能守恒
(1)动能和势能的平均值:
简谐运动的能量
Ep
1 T
T
0 Epdt
1 T
T 1 kA2cos2 tdt 1kA2
02
4
Ek
1 T
T
0 Ekdt
1 T
T 1 kA2sin 2 tdt 1 kA2
02
4
即
Ep
Ek
1 kA 2 4
1E 2
(2)机械能守恒——简谐运动动力学特征之二;
