高考专题突破一
2022年高考数学总复习专题突破一利用导数证明不等式

第1课时 利用导数证明不等式题型一 将不等式转化为函数的最值问题[例1] [2017·全国卷Ⅲ]已知函数f (x )=ln x +ax 2+(2a +1)x . (1)讨论f (x )的单调性;(2)当a <0时,证明f (x )≤-34a-2.[听课记录]类题通法将不等式转化为函数最值来证明不等式,其主要思想是依据函数在固定区间的单调性,直接求得函数的最值,然后由f (x )≤f (x )max 或f (x )≥f (x )min 直接证得不等式.巩固训练1:已知函数f (x )=ax -e x (e 为自然对数的底数).(1)当a =1e时,求函数f (x )的单调区间及极值;(2)当2≤a ≤e +2时,求证:f (x )≤2x .题型二 构造函数法证明不等式[例2] 设a 为实数,函数f (x )=e x -2x +2a ,x ∈R . (1)求f (x )的单调区间与极值;(2)求证:当a >ln 2-1且x >0时,e x >x 2-2ax +1. [听课记录]类题通法待证不等式的两边含有同一个变量时,一般地,可以直接构造“左减右”的函数,利用导数研究其单调性,借助所构造函数的单调性即可得证.巩固训练2:已知函数f (x )=e x -ax (e 为自然对数的底数,a 为常数)的图象在点(0,1)处的切线斜率为-1.(1)求a 的值及函数f (x )的极值; (2)证明:当x >0时,x 2<e x .题型三 将不等式转化为两个函数的最值进行比较[例3] 已知函数f (x )=eln x -ax (a ∈R ). (1)讨论f (x )的单调性;(2)当a =e 时,证明:xf (x )-e x +2e x ≤0. [听课记录]类题通法在证明的不等式中,若对不等式的变形无法转化为一个函数的最值问题,可以借助两个函数的最值进行证明.巩固训练3:已知函数f (x )=e x 2-x ln x .求证:当x >0时,f (x )<x e x +1e.题型四 双变量不等式的证明[例4] [2020·天津卷]已知函数f (x )=x 3+k ln x (k ∈R ),f ′(x )为f (x )的导函数. (1)当k =6时:(ⅰ)求曲线y =f (x )在点(1,f (1))处的切线方程;(ⅱ)求函数g (x )=f (x )-f ′(x )+9x的单调区间和极值.(2)当k ≥-3时,求证:对任意的x 1,x 2∈[1,+∞),且x 1>x 2,有f ′(x 1)+f ′(x 2)2>f (x 1)-f (x 2)x 1-x 2.[听课记录]类题通法破解含双参不等式的证明的关键一是转化,即由已知条件入手,寻找双参所满足的关系式,并把含双参的不等式转化为含单参的不等式;二是巧构造函数,再借用导数,判断函数的单调性,从而求其最值;三是回归双参的不等式的证明,把所求的最值应用到双参不等式,即可证得结果.巩固训练4:[2018·全国卷Ⅰ]已知函数f (x )=1x-x +a ln x .(1)讨论f (x )的单调性;(2)若f (x )存在两个极值点x 1,x 2,证明:f (x 1)-f (x 2)x 1-x 2<a -2.[预测] 核心素养——逻辑推理、数学运算已知函数f (x )=2x +(1-2a )ln x +ax.(1)讨论f (x )的单调性;(2)如果方程f (x )=m 有两个不相等的解x 1,x 2,且x 1<x 2,证明:f ′⎝⎛⎭⎫x 1+x 22>0.状 元 笔 记两个经典不等式的应用(1)对数形式:x ≥1+ln x(x>0),当且仅当x =1时,等号成立.(2)指数形式:e x ≥x +1(x ∈R ),当且仅当x =0时,等号成立.进一步可得到一组不等式链:e x >x +1>x >1+ln x (x >0,且x ≠1).[典例1] (1)已知函数f (x )=1ln (x +1)-x,则y =f (x )的图象大致为( )(2)已知函数f (x )=e x ,x ∈R .证明:曲线y =f (x )与曲线y =12x 2+x +1有唯一公共点.【解析】 (1)因为f (x )的定义域为⎩⎪⎨⎪⎧x +1>0,ln (x +1)-x ≠0,即{x |x >-1,且x ≠0}, 所以排除选项D ;当x >0时,由经典不等式x >1+ln x (x >0),以x +1代替x ,得x >ln(x +1)(x >-1,且x ≠0),即x >0或-1<x <0时均有f (x )<0,排除A 、C ;易知B 正确.(2)证明:令g (x )=f (x )-⎝⎛⎭⎫12x 2+x +1=e x -12x 2-x -1,x ∈R ,则g ′(x )=e x -x -1,由经典不等式e x ≥x +1恒成立可知,g ′(x )≥0恒成立, 所以g (x )在R 上为单调递增函数,且g (0)=0.所以函数g (x )有唯一零点,即两曲线有唯一公共点. [典例2] 已知函数f (x )=x -1-a ln x . (1)若f (x )≥0,求a 的值;(2)证明:对于任意正整数n ,⎝⎛⎭⎫1+12⎝⎛⎭⎫1+122·…·⎝⎛⎭⎫1+12n <e. 【解析】 (1)f (x )的定义域为(0,+∞),①若a ≤0,因为f ⎝⎛⎭⎫12=-12+a ln 2<0,所以不满足题意; ②若a >0,由f ′(x )=1-a x =x -ax知,当x ∈(0,a )时,f ′(x )<0;当x ∈(a ,+∞)时,f ′(x )>0; 所以f (x )在(0,a )上单调递减,在(a ,+∞)上单调递增, 故x =a 是f (x )在(0,+∞)的唯一最小值点. 因为f (1)=0,所以当且仅当a =1时,f (x )≥0, 故a =1.(2)证明:由(1)知当x ∈(1,+∞)时,x -1-ln x >0.令x =1+12n ,得ln ⎝⎛⎭⎫1+12n <12n . 从而ln ⎝⎛⎭⎫1+12+ln ⎝⎛⎭⎫1+122+…+ln ⎝⎛⎭⎫1+12n <12+122+…+12n =1-12n <1. 故⎝⎛⎭⎫1+12⎝⎛⎭⎫1+122·…·⎝⎛⎭⎫1+12n <e. [典例3] 设函数f (x )=ln x -x +1. (1)讨论f (x )的单调性;(2)求证:当x ∈(1,+∞)时,1<x -1ln x<x .【解析】 (1)由题设知,f (x )的定义域为(0,+∞),f ′(x )=1x-1,令f ′(x )=0,解得x =1.当0<x <1时,f ′(x )>0,f (x )在(0,1)上单调递增; 当x >1时,f ′(x )<0,f (x )在(1,+∞)上单调递减.(2)证明:由(1)知f (x )在x =1处取得最大值,最大值为f (1)=0. 所以当x >0且x ≠1时,ln x <x -1.故当x ∈(1,+∞)时,ln x <x -1,x -1ln x>1.①因此ln 1x <1x -1,即ln x >x -1x ,x -1ln x<x .②故当x ∈(1,+∞)时恒有1<x -1ln x<x .第1课时 利用导数证明不等式 课堂题型讲解题型一例1 解析:(1)f (x )的定义域为(0,+∞),f ′(x )=1x +2ax +2a +1=(x +1)(2ax +1)x .若a ≥0,则当x ∈(0,+∞)时,f ′(x )>0, 故f (x )在(0,+∞)上单调递增.若a <0,则当x ∈⎝⎛⎭⎫0,-12a 时,f ′(x )>0; 当x ∈⎝⎛⎭⎫-12a ,+∞ 时,f ′(x )<0. 故f (x )在⎝⎛⎭⎫0,-12a 上单调递增,在⎝⎛⎭⎫-12a ,+∞ 上单调递减. (2)证明:由(1)知,当a <0时,f (x )在x =-12a处取得最大值,最大值为f ⎝⎛⎭⎫-12a =ln ⎝⎛⎭⎫-12a -1-14a.所以f (x )≤-34a -2等价于ln ⎝⎛⎭⎫-12a -1-14a ≤-34a -2,即ln ⎝⎛⎭⎫-12a +12a +1≤0. 设g (x )=ln x -x +1,则g ′(x )=1x-1.当x ∈(0,1)时,g ′(x )>0;当x ∈(1,+∞)时,g ′(x )<0, 所以g (x )在(0,1)上单调递增,在(1,+∞)上单调递减. 故当x =1时,g (x )取得最大值,最大值为g (1)=0. 所以当x >0时,g (x )≤0.从而当a <0时,ln ⎝⎛⎭⎫-12a +12a +1≤0, 即f (x )≤-34a-2.巩固训练1 解析:(1)当a =1e 时,f (x )=1e x -e x ,令f ′(x )=1e-e x =0,得x =-1.当x <-1时,f ′(x )>0;当x >-1时, f ′(x )<0.∴函数f (x )的单调递增区间为(-∞,-1),单调递减区间为(-1,+∞). 当x =-1时,函数f (x )有极大值-2e;没有极小值.(2)证明:令F (x )=2x -f (x )=e x -(a -2)x , ①当a =2时,F (x )=e x >0, ∴f (x )≤2x .②当2<a ≤2+e 时,F ′(x )=e x -(a -2)=e x -e ln (a -2). 当x <ln (a -2)时,F ′(x )<0; 当x >ln (a -2)时,F ′(x )>0;∴F (x )在(-∞,ln (a -2))上单调递减,在(ln (a -2),+∞)上单调递增. ∴F (x )≥F (ln (a -2))=e ln (a-2)-(a-2)ln (a-2)=(a-2)[1-ln (a-2)],∵2<a≤2+e,∴a-2>0.1-ln (a-2)≥1-ln [(2+e)-2]=0,∴F(x)≥0,即f(x)≤2x.综上,当2≤a≤e+2时,f(x)≤2x.题型二例2解析:(1)由f(x)=e x-2x+2a,x∈R,得f′(x)=e x-2,x∈R,令f′(x)=0,得x=ln 2.于是当x变化时,f′(x),f(x)的变化情况如下表:故f(f(x)在x=ln 2处取得极小值,极小值为f(ln 2)=e ln 2-2ln 2+2a=2(1-ln 2+a),无极大值.(2)证明:设g(x)=e x-x2+2ax-1,x∈R,于是g′(x)=e x-2x+2a,x∈R.由(1)知当a>ln 2-1时,g′(x)最小值为g′(ln 2)=2(1-ln 2+a)>0.于是对任意x∈R,都有g′(x)>0,所以g(x)在R上单调递增.于是当a>ln 2-1时,对任意x∈(0,+∞),都有g(x)>g(0).又g(0)=0,从而对任意x∈(0,+∞),g(x)>0.即e x-x2+2ax-1>0,故e x>x2-2ax+1.巩固训练2解析:(1)由f(x)=e x-ax,得f′(x)=e x-a.因为f′(0)=1-a=-1,所以a=2,所以f(x)=e x-2x,f′(x)=e x-2.令f′(x)=0,得x=ln 2,当x<ln 2时,f′(x)<0,f(x)在(-∞,ln 2)上单调递减;当x>ln 2时,f′(x)>0,f(x)在(ln 2,+∞)上单调递增.所以当x=ln 2时,f(x)取得极小值,且极小值为f(ln 2)=e ln 2-2ln 2=2-2ln 2,f(x)无极大值.(2)证明:令g(x)=e x-x2,则g′(x)=e x-2x.由(1)得g′(x)=f(x)≥f(ln 2)>0,故g(x)在R上单调递增.所以当x>0时,g(x)>g(0)=1>0,即x2<e x.题型三例3解析:(1)f′(x)=ex-a(x>0),①若a≤0,则f′(x)>0,f(x)在(0,+∞)上单调递增;②若a >0,则当0<x <ea 时,f ′(x )>0;当x >ea时,f ′(x )<0.故f (x )在⎝⎛⎭⎫0,e a 上单调递增,在⎝⎛⎭⎫ea ,+∞ 上单调递减. (2)证明:因为x >0, 所以只需证f (x )≤e xx-2e ,当a =e 时,由(1)知,f (x )在(0,1)上单调递增,在(1,+∞)上单调递减. 所以f (x )max =f (1)=-e , 记g (x )=e xx-2e(x >0),则g ′(x )=(x -1)e xx 2,所以当0<x <1时,g ′(x )<0,g (x )单调递减,当x >1时,g ′(x )>0,g (x )单调递增,所以g (x )min =g (1)=-e , 综上,当x >0时,f (x )≤g (x ),即f (x )≤e xx -2e ,即xf (x )-e x +2e x ≤0.巩固训练3 证明:要证f (x )<x e x +1e ,∵x >0只需证e x -ln x <e x +1e x ,即e x -e x <ln x +1e x.令h (x )=ln x +1e x (x >0),则h ′(x )=e x -1e x2 ,易知h (x )在⎝⎛⎭⎫0,1e 上单调递减,在⎝⎛⎭⎫1e ,+∞ 上单调递增,则h (x )min =h ⎝⎛⎭⎫1e =0,所以ln x +1e x≥0.再令φ(x )=e x -e x ,则φ′(x )=e -e x ,易知φ(x )在(0,1)上单调递增,在(1,+∞)上单调递减, 则φ(x )max =φ(1)=0,所以e x -e x ≤0.因为h (x )与φ(x )不同时为0,所以e x -e x <ln x +1e x ,故原不等式成立.题型四例4 解析:(1)(ⅰ)当k =6时,f (x )=x 3+6ln x ,故f ′(x )=3x 2+6x .可得f (1)=1,f ′(1)=9,所以曲线y =f (x )在点(1,f (1))处的切线方程为y -1=9(x -1),即y =9x -8.(ⅱ)依题意,g (x )=x 3-3x 2+6ln x +3x,x ∈(0,+∞).g ′(x )=3x 2-6x +6x -3x 2 ,整理可得g ′(x )=3(x -1)3(x +1)x 2.令g ′(x )=0,解得x =1.当x 变化时,g ′(x ),g (x )的变化情况如表:所以,函数g (x )的单调递减区间为(0,1),单调递增区间为(1,+∞).g (x )的极小值为g (1)=1,无极大值.(2)证明:由f (x )=x 3+k ln x ,得f ′(x )=3x 2+kx.对任意的x 1,x 2∈[1,+∞),且x 1>x 2,令x 1x 2 =t (t >1),则(x 1-x 2)[f ′(x 1)+f ′(x 2)]-2[f (x 1)-f (x 2)]=(x 1-x 2)⎝⎛⎭⎫3x 21 +k x 1+3x 22 +k x 2 -2(x 31 -x 32 +k ln x 1x 2 ) =x 31 -x 32 -3x 21 x 2+3x 1x 22 +k (x 1x 2 -x 2x 1 )-2k ln x 1x 2 =x 32 (t 3-3t 2+3t -1)+k ⎝⎛⎭⎫t -1t -2ln t .① 令h (x )=x -1x -2ln x ,x ∈[1,+∞).当x >1时,h ′(x )=1+1x 2 -2x =⎝⎛⎭⎫1-1x 2 >0,由此可得h (x )在[1,+∞)单调递增,所以当t >1时,h (t )>h (1),即t -1t -2ln t >0.因为x 2≥1,t 3-3t 2+3t -1=(t -1)3>0,k ≥-3,所以x 32 (t 3-3t 2+3t -1)+k ⎝⎛⎭⎫t -1t -2ln t ≥(t 3-3t 2+3t -1)-3⎝⎛⎭⎫t -1t -2ln t =t 3-3t 2+6ln t +3t-1.② 由(1)(ⅱ)可知,当t >1时,g (t )>g (1),即t 3-3t 2+6ln t +3t >1,故t 3-3t 2+6ln t +3t -1>0.③由①②③可得(x 1-x 2)[f ′(x 1)+f ′(x 2)]-2[f (x 1)-f (x 2)]>0.所以,当k ≥-3时,对任意的x 1,x 2∈[1,+∞),且x 1>x 2,有f ′(x 1)+f ′(x 2)2 >f (x 1)-f (x 2)x 1-x 2.巩固训练4 解析:(1)f (x )的定义域为(0,+∞), f ′(x )=-1x 2 -1+ax =-x 2-ax +1x 2.①若a ≤2,则f ′(x )≤0,当且仅当a =2,x =1时,f ′(x )=0,所以f (x )在(0,+∞)上单调递减.②若a >2,令f ′(x )=0,得x =a -a 2-42 或x =a +a 2-42.当x ∈⎝ ⎛⎭⎪⎫0,a -a 2-42 ∪(a +a 2-42 ,+∞)时,f ′(x )<0;当x ∈⎝ ⎛⎭⎪⎫a -a 2-42,a +a 2-42 时, f ′(x )>0.所以f (x )在⎝ ⎛⎭⎪⎫0,a -a 2-42 ,⎝ ⎛⎭⎪⎫a +a 2-42,+∞ 上单调递减,在⎝ ⎛⎭⎪⎫a -a 2-42,a +a 2-42 上单调递增.(2)证明:由(1)知,f (x )存在两个极值点时,当且仅当a >2. 由于f (x )的两个极值点x 1,x 2满足x 2-ax +1=0, 所以x 1x 2=1,不妨设x 1<x 2,则x 2>1. 由于f (x 1)-f (x 2)x 1-x 2 =-1x 1x 2 -1+a ·ln x 1-ln x 2x 1-x 2 =-2+a ln x 1-ln x 2x 1-x 2=-2+a-2ln x 21x 2-x 2, 所以f (x 1)-f (x 2)x 1-x 2<a -2等价于1x 2 -x 2+2ln x 2<0.设函数g (x )=1x -x +2ln x ,由(1)知,g (x )在(0,+∞)上单调递减.又g (1)=0,从而当x ∈(1,+∞)时,g (x )<0. 所以1x 2 -x 2+2ln x 2<0,即f (x 1)-f (x 2)x 1-x 2<a -2.高考命题预测预测 解析:(1)f ′(x )=2+1-2a x -a x 2 =2x 2+(1-2a )x -a x 2=(x -a )(2x +1)x 2(x >0).①当a ≤0时,x ∈(0,+∞),f ′(x )>0,f (x )单调递增; ②当a >0时,x ∈(0,a ),f ′(x )<0,f (x )单调递减; x ∈(a ,+∞),f ′(x )>0,f (x )单调递增.综上,当a ≤0时,f (x )在(0,+∞)上单调递增;当a >0时,f (x )在(0,a )上单调递减,在(a ,+∞)上单调递增.(2)证明:由(1)知,当a ≤0时,f (x )在(0,+∞)上单调递增,f (x )=m 至多一个解,不符合题意;当a >0时,f (x )在(0,a )上单调递减,在(a ,+∞)上单调递增,则f ′(a )=0.不妨设0<x 1<a <x 2,要证f ′⎝⎛⎭⎫x 1+x 22 >0,即证x 1+x 22 >a ,即证x 1+x 2>2a ,即证x 2>2a -x 1,又f (x )在(a ,+∞)上单调递增,即证f (x 2)>f (2a -x 1),因为f (x 2)=f (x 1),所以即证f (x 1)>f (2a-x 1),即证f (a +x )<f (a -x ).令g (x )=f (a +x )-f (a -x )=⎣⎡⎦⎤2(a +x )+(1-2a )ln (a +x )+a a +x-⎣⎡⎦⎤2(a -x )+(1-2a )·ln (a -x )+a a -x=4x +(1-2a )ln (a +x )-(1-2a )ln (a -x )+a a +x -aa -x ,g ′(x )=4+1-2a a +x +1-2a a -x -a (a +x )2 -a(a -x )2=4+2a (1-2a )a 2-x 2 -2a (a 2+x 2)(a +x )2(a -x )2 =4x 2(x 2-a 2-a )(a +x )2(a -x )2 .当x ∈(0,a )时,g ′(x )<0,g (x )单调递减,又g (0)=f (a +0)-f (a -0)=0,所以x ∈(0,a )时,g (x )<g (0)=0,即f (a +x )<f (a -x ), 即f (x )>f (2a -x ).又x 1∈(0,a ),所以f (x 1)>f (2a -x 1), 所以f ′⎝⎛⎭⎫x 1+x 22 >0.。
高考数学专题知识突破:考点1 集合的概念与运算
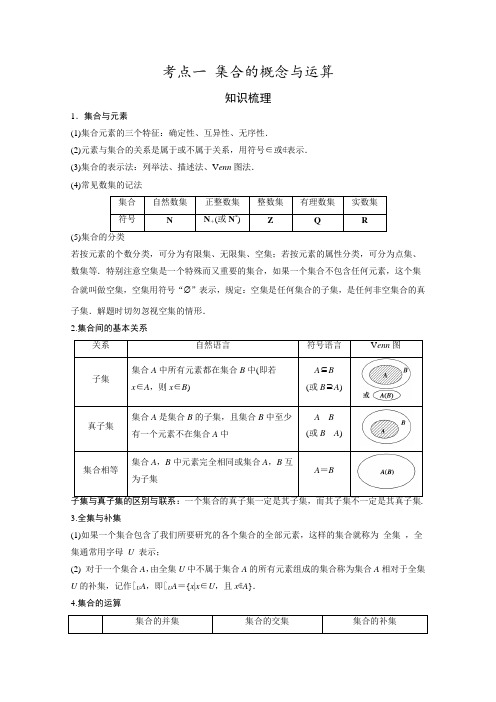
考点一集合的概念与运算知识梳理1.集合与元素(1)集合元素的三个特征:确定性、互异性、无序性.(2)元素与集合的关系是属于或不属于关系,用符号∈或∉表示.(3)集合的表示法:列举法、描述法、V enn图法.(4)常见数集的记法集合自然数集正整数集整数集有理数集实数集符号N N+(或N*)Z Q R(5)集合的分类若按元素的个数分类,可分为有限集、无限集、空集;若按元素的属性分类,可分为点集、数集等.特别注意空集是一个特殊而又重要的集合,如果一个集合不包含任何元素,这个集合就叫做空集,空集用符号“∅”表示,规定:空集是任何集合的子集,是任何非空集合的真子集.解题时切勿忽视空集的情形.2.集合间的基本关系关系自然语言符号语言V enn图子集集合A中所有元素都在集合B中(即若x∈A,则x∈B)A⊆B(或B⊇A)真子集集合A是集合B的子集,且集合B中至少有一个元素不在集合A中A B(或B A)集合相等集合A,B中元素完全相同或集合A,B互为子集A=B3.全集与补集(1)如果一个集合包含了我们所要研究的各个集合的全部元素,这样的集合就称为全集,全集通常用字母U表示;(2) 对于一个集合A,由全集U中不属于集合A的所有元素组成的集合称为集合A相对于全集U的补集,记作∁U A,即∁U A={x|x∈U,且x∉A}.4.集合的运算集合的并集集合的交集集合的补集图形符号A∪B={x|x∈A,或x∈B}A∩B={x|x∈A,且x∈B}∁U A={x|x∈U,且x∉A} 5.集合关系与运算的常用结论(1)子集个数公式:若有限集A中有n个元素,则A的子集个数为2n个,非空子集个数为2n -1个,真子集有2n-1个.(2) A∩B=A⇔A⊆B,A∪B=B⇔A⊆B.(3)(∁U A)∩(∁U B)=∁U(A∪B),(∁U A)∪(∁U B)=∁U(A∩B) .典例剖析题型一集合的基本概念例1已知集合A={0,1,2},则集合B={x-y|x∈A,y∈A}中元素的个数是答案 5解析列表根据集合中元素的互异性知,B中元素有0,-1,-2,1,2,共5个.变式训练已知集合A={0,1,2},B={(x,y)|x∈A,y∈A,x-y∈A},则集合B中有________个元素.答案 6解析因为x-y∈A,∴x≥y.当x=0时,y=0;当x=1时,y=0或y=1;当x=2时,y=0,1,2.故集合B={(0,0),(1,0),(1,1),(2,0),(2,1),(2,2)},即集合B中有6个元素.解题要点研究集合问题,通常从代表元素入手,考查其所代表的是数还是点,如果代表元素是数x,则是数集,如果代表元素是数对(x,y),则是点集.在列举集合的元素时可借助表格,或根据元素特征分类列举,列举时应做到不重不漏.例2 设a ,b ∈R ,集合{1,a +b ,a }=⎩⎨⎧⎭⎬⎫0,b a ,b ,则b -a =________.答案 2解析 因为{1,a +b ,a }=⎩⎨⎧⎭⎬⎫0,b a ,b ,且由a 在分母的位置可知a ≠0,所以a +b =0,则ba =-1,所以a =-1,b =1.所以b -a =2.变式训练 已知集合A ={m +2,2m 2+m },若3∈A ,则m 的值为________. 答案 -32解析 因为3∈A ,所以m +2=3或2m 2+m =3. 当m +2=3,即m =1时,2m 2+m =3,此时集合A 中有重复元素3,所以m =1不符合题意,舍去; 当2m 2+m =3时,解得m =-32或m =1(舍去),此时当m =-32时,m +2=12≠3符合题意,所以m =-32.解题要点 对于含字母参数的集合,应准确进行分类讨论,列出方程或方程组求出字母参数的值.需要特别注意的是,求出字母参数值后,还要检验是否违反了集合中元素的互异性. 题型二 集合间的基本关系例3 集合A ={-1,0,1},A 的子集中,含有元素0的子集共有 个 答案 4解析 根据题意,在集合A 的子集中,含有元素0的子集有{0}、{0,1}、{0,-1}、{-1,0,1},共四个.变式训练 设M 为非空的数集,M ⊆{1,2,3},且M 中至少含有一个奇数元素,则这样的集合M 共有 个 答案 6解析 集合{1,2,3}的所有子集共有23=8(个),其中一个奇数元素也没有的集合有两个:∅和{2},故满足要求的集合M 共有8-2=6(个).解题要点 解题关键是弄清符合题意的集合其元素应满足的条件.在元素较少时可以采取穷举法列出所有满足条件的集合. 例4 设,若,则a 的取值范围是 .答案解析 根据题意作图:由图可知,,则只要即可,即a 的取值范围是.变式训练 已知集合()2{|540},,,A x x x B a A B =-+≤=-∞⊆,则a 的取值范围是 . 答案 (4,)+∞解析 []2{|540}1,4A x x x =-+≤=,∵,根据题意作图:由图可知,只要即可,即a 的取值范围(4,)+∞.解题要点 对于这类用不等式表示的数集之间的包含关系时,常常借助数轴进行求解.在解题时应注意端点是否可以取到. 题型三 集合的基本运算例5 已知集合A ={1,2,3},B ={2,4,5},则集合A ∪B 中元素的个数为________. 答案 5解析 A ∪B ={1,2,3,4,5},共有5个元素.变式训练 已知集合A ={x |x 2-x -2≤0},集合B 为整数集,则A ∩B 等于________. 答案 {-1,0,1,2}解析 A ={x |x 2-x -2≤0}={x |-1≤x ≤2},B 为整数集,A ∩B ={-1,0,1,2}.解题要点 求解集合交、并首先应对各个集合进行化简,准确弄懂集合中的元素,求并集时相同的元素只算一个.例6 已知全集U =R ,A ={x |x ≤0},B ={x |x ≥1},则集合∁U (A ∪B ) =________. 答案 {x |0<x <1}解析 ∵A ={x |x ≤0},B ={x |x ≥1}, ∴A ∪B ={x |x ≤0或x ≥1}, 在数轴上表示如图.∴∁U (A ∪B )={x |0<x <1}.变式训练 已知集合A ={x |x 2-2x >0},B ={x |-<x <},则A ∪B =________.答案 R解析 ∵x (x -2)>0,∴x <0或x >2. ∴集合A 与B 可用数轴表示为:由图象可以看出A ∪B =R .解题要点 集合的基本运算是历年高考的热点,常与不等式的解集、函数的定义域、值域相结合命题,解题时先求出各个集合,然后借助数轴求交并是基本方法.当堂练习1. 已知集合{1,2,3,4}U =,集合={1,2}A ,={2,3}B ,则()UA B =________.2.若集合M ={-1,0,1},N ={0,1,2},则M ∩N 等于________. 3.已知{菱形},{正方形},{平行四边形},则之间的关系为_______4.已知集合A ={(x ,y )|-1≤x ≤1,0≤y <2,x 、y ∈Z },用列举法可以表示集合A 为________. 5.设集合M ={0,1,2},N ={x |x 2-3x +2≤0},则M ∩N = .课后作业1.已知集合A ={x |2<x <4},B ={x |(x -1)(x -3)<0},则A ∩B 等于________. 2.设集合M ={x |x 2+2x =0,x ∈R },N ={x |x 2-2x =0,x ∈R },则M ∪N =________. 3.已知集合M ={x |-3<x ≤5},N ={x |x <-5或x >4},则M ∪N 等于________. 4.若集合A ={x ∈R |ax 2+ax +1=0}中只有一个元素,则a =________. 5.已知全集{0,1,2,3,4}U =,集合{1,2,3}A =,{2,4}B =,则UA B ()= ________.6.已知集合{1,2,3,4}A =,2{|,}B x x n n A ==∈,则AB =________.7.满足条件{0,2}∪M ={0,1,2}的所有集合M 的个数为________. 8.已知集合A ={1,3,m },B ={1,m },A ∪B =A ,则m =________. 9.设全集U ={1,2,3,4,5,6},A ={1,2},B ={2,3,4},则A ∩(∁U B )等于________.10.已知A ={3,5,6,8}且集合B 满足A ∩B ={5,8},A ∪B ={2,3,4,5,6,7,8},则这样的集合B 有________个.11.若集合A ={x |-5<x <2},B ={x |-3<x <3},则A ∩B 等于 .12.已知集合A ={x |x =3n +2,n ∈N },B ={6,8,10,12,14},则集合A ∩B 中元素的个数为 13. 已知A ={x |2a <x ≤a +8},B ={x |x <-1或x >5},若A ∪B =R , 则a 的取值范围是________.当堂练习答案1. 答案 {4}解析 因为A ∪B ={1,2,3},全集U ={1,2,3,4},所以U (A ∪B )={4}.2.答案 {0,1}解析 由集合M ={-1,0,1},N ={0,1,2},得到M ∩N ={0,1}. 3.答案4.答案 {(-1,0),(-1,1),(0,0),(0,1),(1,0),(1,1)}解析 集合A 表示不等式组⎩⎪⎨⎪⎧-1≤x ≤1,x ∈Z ,0≤y <2,y ∈Z 确定的平面区域上的格点集合,所以用列举法表示集合A 为{(-1,0),(-1,1),(0,0),(0,1),(1,0),(1,1)}. 5.答案 {1,2}解析 由x 2-3x +2=(x -1)(x -2)≤0,解得1≤x ≤2,故N ={x |1≤x ≤2},∴M ∩N ={1,2}.课后作业答案1.答案 (2,3)解析 ∵A ={x |2<x <4},B ={x |(x -1)(x -3)<0}={x |1<x <3}, ∴A ∩B ={x |2<x <3}=(2,3). 2.答案 {-2,0,2}解析 先确定两个集合的元素,再进行并集运算.集合M ={0,-2},N ={0,2}, 故M ∪N ={-2,0,2}. 3.答案 {x |x <-5或x >-3}解析 在数轴上表示集合M 和N ,如图所示,则数轴上方所有“线”下面的部分就是M ∪N ={x |x <-5或x >-3}. 4.答案 4解析 a =0时,ax 2+ax +1=0无解,此时,A =∅,不合题意;a ≠0时,由题意得方程ax 2+ax +1=0有两个相等实根,则⎩⎪⎨⎪⎧Δ=a 2-4a =0a ≠0,解得a =4.5.答案 {0,2,4}解析 ∵UA ={0,4},U AB ()={0, 2,4}.6.答案 {1,4}解析 ∵x =n 2,n ∈A ,∴x =1,4,9,16. ∴B ={1,4,9,16}.∴A ∩B ={1,4}. 7.答案 4解析 由题可知集合M 中必有1,满足条件的M 可以为{1},{0,1},{2,1},{0,1,2}共4个. 8.答案 0或3解析 ∵A ∪B =A ,∴B ⊆A ,∵A ={1,3,m },B ={1,m },∴m ∈A ,故m =m 或m =3,解得m =0或m =3或m =1,又根据集合元素的互异性m ≠1,所以m =0或m =3. 9.答案 {1}解析 ∵∁U B ={1,5,6},∴A ∩(∁U B )={1,2}∩{1,5,6}={1}. 10.答案 4解析 ∵A ∩B ={5,8},∴5,8∈B ,又∵A ∪B ={2,3,4,5,6,7,8}而A ={3,5,6,8}, ∴2,4,7∈B ,∴3,6可以属于B ,也可不属于B . ∴这样的B 有22=4(个). 11.答案 {x |-3<x <2}解析 由题意,得A ∩B ={x |-5<x <2}∩{x |-3<x <3}={x |-3<x <2}. 12.答案 2解析 A ={…,5,8,11,14,17…},B ={6,8,10,12,14},集合A ∩B 中有两个元素. 13. 答案 -3≤a <-12解析 ∵B ={x |x <-1或x >5},A ∪B =R , ∴⎩⎪⎨⎪⎧2a <-1,a +8≥5, 解得-3≤a <-12.。
2022年高考政治二轮复习专题突破练一人类社会发展的进程与趋势含解析

专题突破练一人类社会发展的进程与趋势一、选择题(共15小题,每小题3分,共45分)1.经历几百万年漫长的历史阶段后,原始社会最终走向解体。
下列对原始社会解体原因的分析正确的是( )①共同劳动取代个体劳动②私有制的产生导致贫富分化③生产资料转归氏族公有④贫富分化导致氏族成员地位不平等A.①③B.②④C.①④D.②③2.在奴隶社会存在着奴隶主阶级和奴隶阶级两大对立阶级,奴隶主阶级为了维护自身利益,建立了军队、法庭、监狱等机关,形成了奴隶制国家。
这说明奴隶制国家( )①是协调阶级矛盾的机构②是对奴隶阶级进行统治的工具③是阶级压迫的暴力机关④脱离了当时生产力发展水平A.①③B.①④C.②③D.②④3.商鞅变法规定“为田开阡陌封疆”,废除井田制,国家承认土地私有,确立了土地私有制,这是历史的进步。
对此认识正确的是( )A.封建制生产关系与较低的生产力水平相适应B.封建制生产关系的出现是生产力发展的结果C.封建制生产关系的出现是历史的必然D.封建制生产关系是在奴隶社会后期出现的4.“印子钱,一还三;利滚利,年年翻;一年借,十年还;几辈子,还不完”和“爷娘妻子走相送,尘埃不见咸阳桥。
牵衣顿足拦道哭,哭声直上干云霄”分别体现的地主阶级剥削农民的方式是( )①榨取地租②向农民放高利贷③强迫农民缴纳苛捐杂税④从事各种徭役A.①④B.②③C.②④D.①③5.在资本主义社会,矿上的工人,一个人一天生产五斤矿砂,矿主至少赚十五块钱,而矿工的工钱,每天却只有两角。
这揭露了( )①资本家为工人提供了就业机会②资本家在生产过程中占有工人创造的剩余价值③资本家与工人之间存在着剥削关系④生产社会化与资本主义私人占有之间的矛盾A.①②B.①③C.②③D.②④6.20世纪30年代,英国某经济学家曾把上街购物的家庭主妇称作爱国者。
他认为,现在我们所需要的,不是勒紧裤腰带过日子,而是需要一种发展扩张、积极活跃的精神,要多干一些实事,多买一些东西,多制造一些商品。
高考排列组合专题突破

一排列组合不同问题解法1.相邻问题并组法题目中规定相邻的几个元素并为一个组(当作一个元素)参与排列.【例1】A、B、C、D、E五人并排站成一排,如果A、B必须相邻且B在A的右边,那么不同的排法种数有[ ]A.60种 B.48种 C.36种D.24种2.相离问题插空法元素相离(即不相邻)问题,可先把无位置要求的几个元素全排列,再把规定相离的几个元素插入上述几个元素间的空位和两端.【例2】七个人并排站成一行,如果甲乙两个必须不相邻,那么不同排法的种数是[ ]A.1440 B.3600C.4820 D.48003.定序问题缩倍法在排列问题中限制某几个元素必须保持一定顺序,可用缩小倍数的方法.【例3】A、B、C、D、E五个人并排站成一排,如果 B必须站A的右边(A、B可不相邻),那么不同的排法种数有[ ]A.24种B.60种C.90种D.120种4.标号排位问题分步法把元素排到指定号码的位置上,可先把某个元素按规定排入,第二步再排另一个元素,如此继续下去,依次即可完成.【例4】将数字1,2,3,4填入标号为1,2,3,4的四个方格里,每格填一个数,则每个方格的标号与所填数字均不相同的填法有[ ]A.6种B.9种C.11种D.23种5.有序分配问题逐分法有序分配问题是指把元素按要求分成若干组,可用逐步下量分组法.【例5】有甲、乙、丙三项任务,甲需2人承担,乙丙各需1人承担,从10人中选出4人承担这三项任务,不同的选法总数有[ ]A.1260种B.2025种C.2520种D.5040种四名优等生保送到三所学校去,每所学校至少得一名,则不同的保送方案的总数是_________.6.多元问题分类法元素多,取出的情况也有多种,可按结果要求,分成不相容的几类情况分别计算,最后总计.【例6】由数字 0,1,2,3,4,5组成且没有重复数字的六位数,其中个位数字小于十位数字的共有[ ] A.210个B.300个C.464个D.600个【例7】从1,2,3,…100这100个数中,任取两个数,使它们的乘积能被7整除,这两个数的取法(不计顺序)共有多少种?【例8】从1,2,…100这100个数中,任取两个数,使其和能被4整除的取法(不计顺序)有多少?7.交叉问题集合法某些排列组合问题几部分之间有交集,可用集合中求元素个数公式n(A∪B)=n(A)+n(B)-n(A∩B) 【例 9】从6名运动员中选出4个参加4×100m接力赛,如果甲不跑第一棒,乙不跑第四棒,共有多少种不同参赛方法?8.定位问题优先法某个(或几个)元素要排在指定位置,可先排这个(几个)元素,再排其他元素.【例10】1名老师和4名获奖同学排成一排照像留念,若老师不在两端,则有不同的排法有________种.9.多排问题单排法把元素排成几排的问题,可归结为一排考虑,再分段处理.【例11】6个不同的元素排成前后两排,每排3个元素,那么不同的排法种数是[ ]10.“至少”问题间接法关于“至少”类型组合问题,用间接法较方便.【例13】从4台甲型和5台乙型电视机中任取出3台,其中至少要甲型和乙型电视机各一台,则不同取法共有[ ]A.140种B.80种C.70种D.35种11.选排问题先取后排法从几类元素中取出符合题意的几个元素,再安排到一定位置上,可用先取后排法.【例14】四个不同的球放入编号为1,2,3,4的四个盒中,则恰有一个空盒的放法共有________种12.部分合条件问题排除法在选取总数中,只有一部分合条件,可从总数中减去不合条件数,即为所求.【例16】以一个正方体顶点为顶点的四面体共有[ ]13 平均分组问题:例一 6本不同的书,按下列要求各有多少种不同的选法:(1)分给甲、乙、丙三人,每人2本;(2)分为三份,每份2本;(3)分为三份,一份1本,一份2本,一份3本;(4)分给甲、乙、丙三人,一人1本,一人2本,一人3本;(5)分给甲、乙、丙三人,每人至少1本。
《导与练》高考生物二轮复习课件:第一部分 专题突破 专题一 细胞的分子组成 【KS5U 高考】

4.(2018·全国Ⅲ卷,30)回答下列与蛋白质相关的问题:
专题一 细胞的分子组成
[最新考纲] 1.蛋白质、核酸的结构和功能(Ⅱ) 2.糖类、脂质的种类和作用(Ⅱ) 3.水和无机盐的作用(Ⅰ)
知识串联回顾 核心考点突破
知识串联回顾
思维串联·纵横联系
答案:①C、O、N、H ②离子 ③溶剂 ④能源物质 ⑤储能物质 ⑥生 物膜 ⑦固醇 ⑧结构 ⑨功能 ⑩遗传信息
解析:DNA的基本单位为脱氧核苷酸,RNA的基本单位为核糖核苷酸,所有细 胞生物的遗传物质均为DNA,病毒只有一种核酸,即DNA或RNA,且病毒没 有细胞结构;同一个体中,处于分裂状态的细胞和不分裂的细胞DNA含量不同, 由于基因的选择性表达,因此不同细胞中的RNA含量也有差异;细胞衰老时, 细胞体积缩小,但是细胞核体积增大,因此核质比增大;tRNA分子内也存在碱 基对,其基本组成单位之一(腺嘌呤核糖核苷酸)可用于合成ATP。
解析:控制不同蛋白质合成的基因不同,基因中碱基数量可能相同,但碱基的 排列顺序不同;同一人体的不同细胞所含DNA相同,由于基因的选择性表达, 导致细胞中RNA不同;蛋白质由DNA控制合成,故蛋白质功能多样性的根本 原因是控制其合成的DNA具有多样性;转录时,基因两条链中一条链作为模板。
6.核酸和蛋白质是细胞内重要的生物大分子。下列叙述错误的是( D ) A.RNA聚合酶的识别位点位于DNA上 B.血红蛋白参与血液中氧气的运输 C.抗体的合成需要DNA和RNA的参与 D.DNA和蛋白质是核糖体的组成成分
2023年高考政治二轮复习第一部分专题突破专题一货币价格与居民消费第一课时客观题轻松满分

过关微专题一 货币价格与居民消费
高考二轮总复习 • 政治
返回导航
3.(2020·全国卷Ⅱ)一双限量版运动鞋,官网标价千余元,线上倒
手几次价格就能翻到几万;有人甚至声称自己靠炒鞋月入十几万……一
段时间以来,炒鞋不断升温,引发媒体关注,并纷纷提示风险。炒鞋行
为存在风险的原因在商品交换 ②鞋的价格远远高
B.①④
C.②③
D.②④
过关微专题一 货币价格与居民消费
高考二轮总复习 • 政治
返回导航
【解析】 建立健全生态产品价值实现机制,以保障自然生态系统 休养生息为基础,增值自然资本,厚植生态产品价值,这说明生态产品 有使用价值,其利用要合理有效,①正确;生态产品有商品属性,其价 值能否实现受多种因素制约,“其价值必然会实现”说法过于绝对化, ②排除;“充分发挥市场在资源配置中的决定性作用,推动生态产品价 值有效转化”意味着生态产品有价值,价值实现要通过市场途径,③正 确;生态产品的价值来源于人类劳动,④错误。
于鞋的价值,背离了价值规律 ③借助网络交易平台炒鞋,货币难以充
当流通媒介 ④资本追逐不断推高价格,鞋的价值越来越难以实现
A.①②
B.①③
C.②④
D.③④
过关微专题一 货币价格与居民消费
高考二轮总复习 • 政治
返回导航
【解析】 商品交换以价值量为基础实行等价交换,商品的价格围 绕价值上下波动,鞋的价格远远高于价值,显然背离了价值规律,②正 确;炒鞋行为的背后是资本在追逐利益,因此,资本追逐不断推高价 格,几次倒手身价翻了好几番,会最终导致鞋很难卖出去,其价值越来 越难以实现。鞋卖不出去,摔坏的就是鞋的持有者,因此会存在一定的 风险,④正确;炒鞋过程中的鞋依然是商品,是使用价值和价值的统一 体,交易过程仍然是商品交换,①说法错误;借助网络交易平台炒鞋, 货币仍然执行的是流通手段的职能,依然充当商品交换的媒介,③说法 错误。
高考语文20分钟专题突破(1):字音

语文20分钟专题突破(1):字音 1.下列各组词语中加点的字,注音全都正确的一组是 ( ) A.编纂(zuǎn) 囤货(dùn) 浸渍(zé) 色厉内荏(rěn) B.隽永(juàn) 饿殍(piǎo) 偌大(ruò) 繁文缛节(rǔ) C.载体(zài) 璞玉(pú) 骠勇(piào) 凿壁偷光(záo) D.档(dàng)期粗犷(kuàng) 皴裂(cūn)? 良莠不齐(yǒu) 2.下列词语中加点的字的读音相同的一组是 A.酝酿熨贴 韵味面有愠色? 意味蕴藉 B.侮辱怃然?舞弊? 忤逆不孝妩媚多姿 C.嗜好吞噬 对峙恃才傲物? 舐犊情深 D.毕竟庇佑?媲美? 刚愎自用?奴颜婢膝 3.下列加点的字的注音全都正确的一项是 A.慰藉jí? 栈道zhàn 庖厨páo忐忑tán tè B.吮血shǔn 酒馔zhuàn 口讷nà? 挟持xié C.戏谑xuè 青冢zhǒng? 商贾gǔ? 伉俪kàng D.省亲xǐng 猿猱náo 赧然nǎn 菜畦jì 4.下列各组加点的字的读音完全不同的一组是 A.倏忽 枢纽 毁家纾难? 自出机杼? B.蹊跷? 溪水? 栖身之所? 休戚与共 C.调函 粜米 千里迢迢? 武装挑衅? D.湛蓝? 客栈? 战战兢兢? 破绽百出 5.下列注音有两处错误的一项 A.果脯pú? 省xǐng察炽zhí热? 傣dǎi族 B.纰Pī漏? 单chán于? 埋mái怨? 叨tāo扰 C.辟bì邪 衙桓huán? 牲畜chù 惊蛰zhí D.摸mó样? 应yīng允? 折shé耗? 解jiè押 6.下列词语中加点的字注音完全正确的一项是( ) A.遒劲(jìn)长篇累(lěi)牍发酵(jiào)垂涎(xián)三尺 B.粗糙(zào)牵强(qiǎng)附会内讧(hòng)自惭形秽(huì) C.执拗(niù)言简意赅(gāi)角(jué)色花团锦簇(cù) D.慰藉(jié)教学相长(zhǎng)惬(xiá)意戛(jiá)然而止 7.下列加点的字,读音全都正确的一组是 A. 挑衅xìn 惩罚chéng 暴殄天物zhěn? 开门揖盗yī B. 角色jué 戛然jiá 徇私枉法xún 刚毅木讷nè C. 强劲jìng 饮马yìn 穷兵黩武dú 擢发难数zhuó D. 戏谑nuè? 参与yù 力能扛鼎gāng? 怏怏不乐yàng 8. 下列各组词语中加点字的读音都不相同的一组是() A. 酝酿 酗酒 醍醐灌顶 酣畅淋漓 B. 翡翠 心扉 文采斐然 蜚短流长 C. 绚丽 嶙峋 以身殉职 徇私舞弊 D. 脓 馈赠 振聋发聩 功亏一篑 9.下列加点的字读音完全相同的一项是 A.诧异? 岔路 姹紫嫣红?差之毫厘,谬以千里 B.笃学亵渎?穷兵黩武?初生牛犊不怕虎 C.犀利? 潮汐?熙来攘往?桃李不言,下自成蹊 D.嗜好俟机?肆无忌惮?偷鸡不成蚀把米 10.下列词语中加点字读音完全相同的一组是 ? A.沏茶? 栖息? 休戚相关? 期期艾艾 ? B.余暇? 裴葭? 闻名遐尔? 白璧微瑕 ? C.饯行? 践诺? 图穷匕见? 从谏如流 ? D.殷红? 荫翳? 万马齐喑? 绿草如茵 11.下列各组加点字的读音,完全不相同的一组是A.信笺 贱恙 饯行 浅尝辄止 以践前誓B.嫌弃 赚钱 缣帛 谦谦君子 以丰补歉C.苋菜 舰艇 端砚 昙花一现 图穷匕见D.讣告 扑灭 朴实 前仆后继 赴汤蹈火12.下列加点的字的读音,全都不相同的一组是A.牛犊 渎职 文牍 买椟还珠 穷兵黩武 B.战栗 砧板 玷污 拈轻怕重掂斤播两C.创造 抢劫 悲怆 沧海桑田 满目疮痍 D.发霉 后悔 草莓 诲人不倦 风雨如晦13.下列加点的字的读音,全部都相同的一组是A.驰骋? 伶俜? 聘请? 娉婷B.通牒? 喋血? 谍报? 城堞C.掾吏? 椽条? 鸟喙? 姻缘D.辍学?啜泣? 点缀? 掇拾14.下列字的读音与所给读音全都相同的一组A.累lěi?累次?拖累日积月累成果累累B.作zuò 作孽?作祟作威作福自作自受C.着zháo? 着慌?着魔歪打正着衣食无着D.靡mǐ? 颓靡 奢靡靡靡之音风靡一时15.下列加点的字的读音,全都不相同的一组是A.跋扈?踯躅?蹙额踟蹰不前一蹴而就? B.整饬?饷银?气馁?文过饰非以飨读者C.翌日?蓊郁?翱翔?翻云覆雨?振翮高飞D.磨砺?麾下奢靡? 麻木不仁?摩肩接踵16.下列词语中加点字的读音,完全相同的一组是A.划桨? 划算? 划价? 划一不二? B.着装? 着眼? 着落? 着手成春C.抹杀? 抹黑? 抹粉? 转弯抹角?D.妥帖? 请帖? 字帖? 服服帖帖.下列加点字的读音与所给注音全都相同的一组A.帖tiē?妥帖请帖字帖?服帖B.畜xù 畜产?畜牧畜养 牲畜C.创chuàng 草创?创伤? 首创 创造D.乘chéng乘便 乘客? 乘兴 乘势.下列词语中加点的字,读音全都正确的一组是A.谛(dì)听 横(hén)祸 丢三落(là)四 B.沮(jǔ)丧? 窥(kuī)视 宁(nìn)缺毋滥C.褒(bǎo)贬 透辟(pì)? 卓(zhuó)尔不群 D.当(dàn)真 牵掣(chè) 屡见不鲜(xiǎn)19.选出加点字读音完全不相同的一组 A.电荷? 恐吓? 短褐? 奉和一首 B.虽然? 脑髓? 深邃? 半身不遂 C.矩形? 沮丧? 踽踽独行? 前倨后恭 D.浣沙? 幻灯? 涣然? 美轮美奂20.下列加点字的读音与所给读音完全相同的一组A.劲jìng劲敌遒劲疾风劲草刚劲挺拔B.泊bó?停泊?漂泊淡泊名利水泊梁山C.应yīng?应届 应允应声而落应有尽有D.鲜xiǎn鲜见?鲜有?寡廉鲜耻屡见不鲜C【解析】A劲jìng;B糙cāo; D惬 qiè 7.[解析]选C(暴殄天物tiǎn,徇私枉法xùn ,戏谑xuè) 8.[解析]A(A. yùn xù tí hānB. Fěi fēi fěi fēiC.xuàn xún xùn xùn 9.[解析]选C(C项全读“xī”;A项依次读“chà、chà、chà、chā”;B项依次读“dǔ、dú、dú、dú”;D项依次读“shì、sì、sì、shí”。
2023年高考数学二轮复习第二篇经典专题突破专题一三角函数和解三角形第1讲三角函数的图象和性质

返回导航
专题一 三角函数和解三角形
高考二轮总复习 • 数学
所以 ω=-16+23k,k∈Z, 所以 ω=52,f(x)=sin 52x+π4+2, 所以 fπ2=sin 54π+π4+2=1. 故选 A.
返回导航
专题一 三角函数和解三角形
高考二轮总复习 • 数学
返回导航
2.(2022·全国甲卷)设函数 f(x)=sin ωx+π3在区间(0,π)恰有三个极
返回导航
【解析】 f′(x)=-sin x+sin x+(x+1)cos x=(x+1)cos x,所以 f(x) 在区间0,π2和32π,2π上 f′(x)>0,即 f(x)单调递增;在区间π2,32π上 f′(x)<0, 即 f(x)单调递减,又 f(0)=f(2π)=2,fπ2=π2+2,f32π=-32π+1+1=- 32π,所以 f(x)在区间[0,2π]上的最小值为-32π,最大值为π2+2.故选 D.
值点、两个零点,则 ω 的取值范围是
( C)
A.53,163
B.53,169
C.163,83
D.163,169
专题一 三角函数和解三角形
高考二轮总复习 • 数学
返回导航
【解析】 依题意可得 ω>0,因为 x∈(0,π),所以 ωx+π3∈π3,ωπ+π3,
要使函数在区间(0,π)恰有三个极值点、两个零点,
又 y=sin x,x∈π3,3π的图象如下所示:
则52π<ωπ+π3≤3π,解得163<ω≤83,即 ω∈163,83.故选 C.
专题一 三角函数和解三角形
高考二轮总复习 • 数学
返回导航
3.(2022·全国甲卷)将函数 f(x)=sin ωx+π3(ω>0)的图象向左平移π2个 单位长度后得到曲线 C,若 C 关于 y 轴对称,则 ω 的最小值是 ( C )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高考专题突破一 高考中的不等式问题【考点自测】1.若a ,b ,c ∈R ,且a >b ,则下列不等式一定成立的是( ) A.a +c ≥b -c B.(a -b )c 2≥0 C.ac >bc D.c 2a -b>0 答案 B解析 A 项,当c <0时,不等式a +c ≥b -c 不一定成立;C 项,当c =0时,ac =bc ;D 项,c =0时,c 2a -b =0;B 项,由a >b 可得a -b >0, 因为c 2≥0,所以(a -b )c 2≥0. 故选B.2.若当x >-3时,不等式a ≤x +2x +3恒成立,则a 的取值范围是________.答案 (-∞,22-3]解析 设f (x )=x +2x +3=(x +3)+2x +3-3,因为x >-3,所以x +3>0, 故f (x )≥2(x +3)×2x +3-3=22-3,当且仅当x =2-3时等号成立, 所以a 的取值范围是(-∞,22-3]. 3.若实数x ,y 满足⎩⎪⎨⎪⎧x +y ≥0,x ≤1,x -2y ≥0,则|x |+|y |的取值范围是________.答案 [0,2]解析 |x |+|y |表示可行域内一点到x ,y 轴的距离之和,作出不等式组表示的可行域,由可行域可知在点(0,0)处取得最小值0,在点(1,-1)处取得最大值2,所以|x |+|y |∈[0,2]. 4.若关于x 的方程x 2+4x +|a -2|+|a +1|=0有实根,则实数a 的取值范围为________.答案 ⎣⎡⎦⎤-32,52 解析 由方程x 2+4x +|a -2|+|a +1|=0有实根,可得Δ=42-4×1×(|a -2|+|a +1|)≥0,整理得|a -2|+|a +1|≤4.∵|a -2|+|a +1|代表数轴上的点a 到2和-1两点的距离和,故由|a -2|+|a +1|≤4得a 的取值范围为⎣⎡⎦⎤-32,52.题型一 含参数不等式的解法例1 解关于x 的不等式x 2+ax +1>0(a ∈R ). 解 对于方程x 2+ax +1=0,Δ=a 2-4.(1)当Δ>0,即a >2或a <-2时,方程x 2+ax +1=0有两个不等实根x 1=-a -a 2-42,x 2=-a +a 2-42,且x 1<x 2,所以原不等式的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x <-a -a 2-42或x >-a +a 2-42; (2)当Δ=0,即a =±2时,①若a =2,则原不等式的解集为{x |x ≠-1}; ②若a =-2,则原不等式的解集为{x |x ≠1};(3)当Δ<0,即-2<a <2时,方程x 2+ax +1=0没有实根,结合二次函数y =x 2+ax +1的图象,知此时原不等式的解集为R .思维升华 解含参数的一元二次不等式的步骤(1)若二次项含有参数应讨论是否等于0,小于0,和大于0,然后将不等式转化为二次项系数为正的形式.(2)判断方程的根的个数,讨论判别式Δ与0的关系.(3)当方程有两个根时,要讨论两根的大小关系,从而确定解集形式.跟踪训练1 (1)若不等式ax 2+8ax +21<0的解集是{x |-7<x <-1},那么a 的值是________. 答案 3解析 由题意可知-7和-1为方程ax 2+8ax +21=0的两个根. ∴-7×(-1)=21a,故a =3.(2)若关于x 的不等式|x -1|+|x +m |>3的解集为R ,则实数m 的取值范围是__________. 答案 (-∞,-4)∪(2,+∞)解析 依题意得,|x -1|+|x +m |≥|(x -1)-(x +m )|=|m +1|,即函数y =|x -1|+|x +m |的最小值是|m +1|,于是有|m +1|>3,m +1<-3或m +1>3,由此解得m <-4或m >2.因此实数m 的取值范围是(-∞,-4)∪(2,+∞). 题型二 线性规划问题例2 若实数x ,y 满足不等式组⎩⎪⎨⎪⎧x -y +2≥0,2x -y -5≤0,x +y -4≥0, 则z =|x +2y -4|的最大值为________.答案 21解析 方法一 作出不等式组表示的平面区域.如图中阴影部分(含边界)所示.z =|x +2y -4|=|x +2y -4|5·5,则几何含义为阴影区域内的点到直线x +2y -4=0的距离的5倍.由⎩⎪⎨⎪⎧x -y +2=0,2x -y -5=0,得点B 的坐标为(7,9),显然,点B 到直线x +2y -4=0的距离最大,此时z max =21.方法二 由图可知,阴影区域内的点都在直线x +2y -4=0的上方,显然此时有x +2y -4>0,于是目标函数等价于z =x +2y -4,即转化为一般的线性规划问题.显然,当直线经过点B 时,目标函数取得最大值,z max =21.思维升华 对线性规划问题的实际应用,关键是建立数学模型,要找准目标函数及两个变量,准确列出线性约束条件,然后寻求最优解,最后回到实际问题.跟踪训练2 (1)(2017·浙江“超级全能生”联考)若实数x ,y 满足不等式组⎩⎪⎨⎪⎧x -2y +2≥0,x +2y +2≥0,2x -y -1≤0,则2|x +1|+y 的最大值为( ) A.143 B.193 C.4 D.1答案 B解析 可行域为如图所示阴影部分,即△ABC 及其内部,其中A (-2,0),B ⎝⎛⎭⎫43,53,C (0,-1),因此当x ≥-1时,z =2x +2+y 过点B 时取最大值193;当x <-1时,z =-2x -2+y 过点A 时取最大值2. 综上,2|x +1|+y 的最大值是193. 故选B.(2)(2017·杭州调研)一个化肥厂生产甲、乙两种混合肥料,生产1车皮甲种肥料的主要原料是磷酸盐4吨,硝酸盐18吨;生产1车皮乙种肥料需要的主要原料是磷酸盐1吨,硝酸盐15吨.现库存磷酸盐10吨,硝酸盐66吨,在此基础上生产这两种混合肥料.如果生产1车皮甲种肥料产生的利润为10 000元,生产1车皮乙种肥料产生的利润为5 000元,那么适当安排生产,可产生的最大利润是________元. 答案 30 000解析 设生产甲种肥料x 车皮,生产乙种肥料y 车皮,则z =10 000x +5 000y ,约束条件为⎩⎪⎨⎪⎧4x+y≤10,18x+15y≤66,x≥0,y≥0,画出可行域如图阴影部分(含边界)所示,由图可知,在D(2,2)处z有最大值,且z max=10 000×2+5 000×2=30 000(元).题型三基本不等式的应用例3 (1)在面积为定值9的扇形中,当扇形的周长取得最小值时,扇形的半径是() A.3 B.2C.4D.5答案 A解析设扇形的半径为r,其弧长为l,由题意可得S=12lr=9,故lr=18.扇形的周长C=2r+l≥22rl=22×18=12,当且仅当2r=l,即r=3,l=6时取等号.(2)已知a>0,b>0,c>1,且a+b=1,则⎝⎛⎭⎫a2+1ab-2·c+2c-1的最小值为______.答案4+2 2解析∵a2+1ab=a2+(a+b)2ab=2a2+2ab+b2ab=2ab+ba+2≥2 2ab·ba+2=22+2,当且仅当⎩⎪⎨⎪⎧2a b =b a ,a +b =1,即⎩⎪⎨⎪⎧a =2-1,b =2-2时等号成立, ∴⎝ ⎛⎭⎪⎫a 2+1ab -2·c +2c -1≥22c +2c -1=22(c -1)+2c -1+2 2≥222(c -1)·2c -1+22=4+22,当且仅当22(c -1)=2c -1,即c =1+22时,等号成立.综上,所求最小值为4+2 2.思维升华 (1)应用型问题解题时需认真阅读,从中提炼出有用信息,建立数学模型.(2)应用基本不等式求最值要注意检验等号成立的条件,不要忽视问题的实际意义. 跟踪训练3 (1)设x ,y 均为正实数,且32+x +32+y =1,则xy 的最小值为( )A.4B.4 3C.9D.16答案 D解析 由32+x +32+y=1可得xy =8+x +y .∵x ,y 均为正实数,∴xy =8+x +y ≥8+2xy (当且仅当x =y 时等号成立),即xy -2xy -8≥0, 解得xy ≥4,即xy ≥16,故xy 的最小值为16.(2)某栋楼的建筑成本由土地使用权费和材料工程费构成,已知土地使用权费为2 000元/m 2;材料工程费在建造第一层时为400元/m 2,以后每增加一层费用增加40元/m 2.要使平均每平方米建筑面积的成本费最低,则应把楼盘的楼房设计成________层. 答案 10解析 设应把楼房设计成x 层,每层有面积y m 2,则平均每平方米建筑面积的成本费为 k =2 000y +y ×400+y ×440+…+y ×[400+40(x -1)]xy=2 000x +20x +380≥2 2 000x ·20x +380=780,当且仅当2 000x=20x ,即x =10时取等号,故应把楼房设计成10层. 题型四 绝对值不等式例4 已知函数f (x )=|2x -a |+|2x +3|,g (x )=|x -1|-2. (1)解不等式|g (x )|<5;(2)若y ∈{y |y =f (x )-2}是y ∈{y |y =|g (x )|}的充分条件,求实数a 的取值范围. 解 (1)由|g (x )|=||x -1|-2|<5得, -3<|x -1|<7,∴|x -1|<7,解得-6<x <8. ∴原不等式的解集为{x |-6<x <8}.(2)∵y ∈{y |y =f (x )-2}是y ∈{y |y =|g (x )|}的充分条件, ∴{y |y =f (x )-2}⊆{y |y =|g (x )|},又f (x )-2=|2x -a |+|2x +3|-2≥|a +3|-2, g (x )=||x -1|-2|≥0,∴|a +3|≥2,解得a ≥-1或a ≤-5.思维升华 (1)解绝对值不等式可以利用绝对值的几何意义,零点分段法、平方法、构造函数法等.(2)利用绝对值三角不等式可以证明不等式或求取值.跟踪训练4 (1)已知函数f (x )=|x -5|+|x +3|+|x -3|+|x +5|-c ,若存在正实数m ,使f (m )=0,则不等式f (x )<f (m )的解集是________. 答案 (-m ,m )解析 由|-x -5|+|-x +3|+|-x -3|+|-x +5|=|x -5|+|x +3|+|x -3|+|x +5|可知,函数f (x )为偶函数,当-3≤x ≤3时,f (x )取最小值16-c .结合题意可得c ≥16.由f (m )=0得f (x )<0,即|x -5|+|x +3|+|x -3|+|x +5|-c <0,结合图象(图略)可知,解集为(-m ,m ).(2)不等式|x -2|+|x +1|≥a 对于任意x ∈R 恒成立,则实数a 的取值范围为__________. 答案 (-∞,3]解析 当x ∈(-∞,-1]时,|x -2|+|x +1|=2-x -x -1=1-2x ≥3;当x ∈(-1,2)时,|x -2|+|x +1|=2-x +x +1=3; 当x ∈[2,+∞)时,|x -2|+|x +1|=x -2+x +1=2x -1≥3, 综上可得|x -2|+|x +1|≥3,∴a ≤3.1.解关于x 的不等式x 2-(2+m )x +2m <0. 解 原不等式可化为(x -2)(x -m )<0.①当m >2时,不等式(x -2)(x -m )<0的解集为 {x |2<x <m };②当m <2时,不等式(x -2)(x -m )<0的解集为 {x |m <x <2};③当m =2时,不等式(x -2)(x -m )<0的解集为∅. 综上所述:当m >2时,不等式的解集为{x |2<x <m }; 当m <2时,不等式的解集为{x |m <x <2}; 当m =2时,不等式的解集为∅.2.已知函数f (x )=x 2-6x +9+x 2+8x +16. (1)求f (x )≥f (4)的解集;(2)设函数g (x )=k (x -3),k ∈R ,若f (x )>g (x )对任意的x ∈R 都成立,求k 的取值范围. 解 (1)f (x )=x 2-6x +9+x 2+8x +16=(x -3)2+(x +4)2=|x -3|+|x +4|,∵f (x )≥f (4),即|x -3|+|x +4|≥9,∴⎩⎪⎨⎪⎧ x ≤-4,3-x -x -4≥9或⎩⎪⎨⎪⎧-4<x <3,3-x +x +4≥9或⎩⎪⎨⎪⎧x≥3,x-3+x+4≥9,解得x≤-5或x≥4,∴f(x)≥f(4)的解集为{x|x≤-5或x≥4}.(2)f(x)>g(x),即f(x)=|x-3|+|x+4|的图象恒在g(x)=k(x-3)图象的上方,又∵f(x)=|x-3|+|x+4|=⎩⎪⎨⎪⎧-2x-1,x≤-4,7,-4<x<3,2x+1,x≥3,g(x)=k(x-3)的图象恒过定点P(3,0),作函数y1=f(x),y2=g(x)的图象如图,其中k PB=2,A(-4,7),∴k P A=-1,由图可知,要使得f(x)的图象恒在g(x)图象的上方,则需-1<k≤2,∴实数k的取值范围为(-1,2].3.(2017·浙江省绍兴第一中学期末)设函数f(x)=⎪⎪⎪⎪x-52+|x-a|,x∈R.(1)求证:当a=-12时,不等式ln f(x)>1成立;(2)已知关于x的不等式f(x)≤a在R上有解,求实数a的取值范围.(1)证明由f(x)=⎪⎪⎪⎪x-52+⎪⎪⎪⎪x+12=⎩⎪⎨⎪⎧-2x+2,x<-12,3,-12≤x≤52,2x-2,x>52,得函数f(x)的最小值为3,从而f(x)≥3>e,所以ln f(x)>1成立.(2)解 由绝对值不等式的性质得 f (x )=⎪⎪⎪⎪x -52+|x -a |≥⎪⎪⎪⎪⎝⎛⎭⎫x -52-(x -a ) =⎪⎪⎪⎪a -52, 所以f (x )的最小值为⎪⎪⎪⎪52-a ,从而⎪⎪⎪⎪52-a ≤a , 解得a ≥54,因此a 的取值范围为⎣⎡⎭⎫54,+∞.4.已知x ,y ∈(0,+∞),x 2+y 2=x +y .(1)求1x +1y的最小值; (2)是否存在x ,y 满足(x +1)(y +1)=5?并说明理由.解 (1)由题意可知1x +1y =x +y xy =x 2+y 2xy ≥2xy xy=2, 当且仅当x =y =1时,等号成立.所以1x +1y的最小值为2. (2)不存在.理由:因为x 2+y 2≥2xy ,所以(x +y )2≤2(x 2+y 2)=2(x +y ),又x ,y ∈(0,+∞),所以0<x +y ≤2,从而有(x +1)(y +1)≤⎣⎢⎡⎦⎥⎤(x +1)+(y +1)22≤4, 因此不存在x ,y 满足(x +1)(y +1)=5.5.(2016·浙江)已知a ≥3,函数F (x )=min{2|x -1|,x 2-2ax +4a -2},其中min{p ,q }=⎩⎪⎨⎪⎧p ,p ≤q ,q ,p >q . (1)求使得等式F (x )=x 2-2ax +4a -2成立的x 的取值范围;(2)①求F (x )的最小值m (a );②求F (x )在区间[0,6]上的最大值M (a ).解 (1)由于a ≥3,故当x ≤1时,(x 2-2ax +4a -2)-2|x -1|=x 2+2(a -1)(2-x )>0, 当x >1时,(x 2-2ax +4a -2)-2|x -1|=(x -2)(x -2a ).所以使得等式F (x )=x 2-2ax +4a -2成立的x 的取值范围是[2,2a ].(2)①设函数f (x )=2|x -1|,g (x )=x 2-2ax +4a -2,则f (x )min =f (1)=0,g (x )min =g (a )=-a 2+4a -2,所以由F (x )的定义知m (a )=min {}f (1),g (a ),即m (a )=⎩⎪⎨⎪⎧0,3≤a ≤2+2,-a 2+4a -2,a >2+ 2. ②当0≤x <2时,F (x )=f (x ),此时M (a )=f (0)=2. 当2≤x ≤6时,F (x )=g (x ),此时M (a )=max{g (2), g (6)}=max{2,34-8a },当a ≥4时,34-8a ≤2;当3≤a <4时,34-8a >2, 所以M (a )=⎩⎪⎨⎪⎧ 34-8a ,3≤a <4,2,a ≥4.6.已知函数f (x )=|x +m |+|2x -1|(m ∈R ).(1)当m =-1时,求不等式f (x )≤2的解集;(2)设关于x 的不等式f (x )≤|2x +1|的解集为A ,且⎣⎡⎦⎤34,2⊆A ,求实数m 的取值范围.解 (1)当m =-1时,f (x )=|x -1|+|2x -1|, 由f (x )≤2得|x -1|+|2x -1|≤2,上述不等式可化为⎩⎪⎨⎪⎧ x ≤12,1-x +1-2x ≤2 或⎩⎪⎨⎪⎧ 12<x <1,1-x +2x -1≤2或⎩⎪⎨⎪⎧x ≥1,x -1+2x -1≤2, 解得⎩⎪⎨⎪⎧ x ≤12,x ≥0或⎩⎪⎨⎪⎧ 12<x <1,x ≤2或⎩⎪⎨⎪⎧ x ≥1,x ≤43, ∴0≤x ≤12或12<x <1或1≤x ≤43, ∴原不等式的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪0≤x ≤43. (2)∵f (x )≤|2x +1|的解集包含⎣⎡⎦⎤34,2,∴当x ∈⎣⎡⎦⎤34,2时,不等式f (x )≤|2x +1|恒成立,即|x +m |+|2x -1|≤|2x +1|在⎣⎡⎦⎤34,2上恒成立,∴|x +m |+2x -1≤2x +1,即|x +m |≤2,∴-2≤x +m ≤2,∴-x -2≤m ≤-x +2在⎣⎡⎦⎤34,2上恒成立,∴(-x -2)max ≤m ≤(-x +2)min ,∴-114≤m ≤0, 即实数m 的取值范围是⎣⎡⎦⎤-114,0.。
