决策树的例题
管理学决策树习题及答案
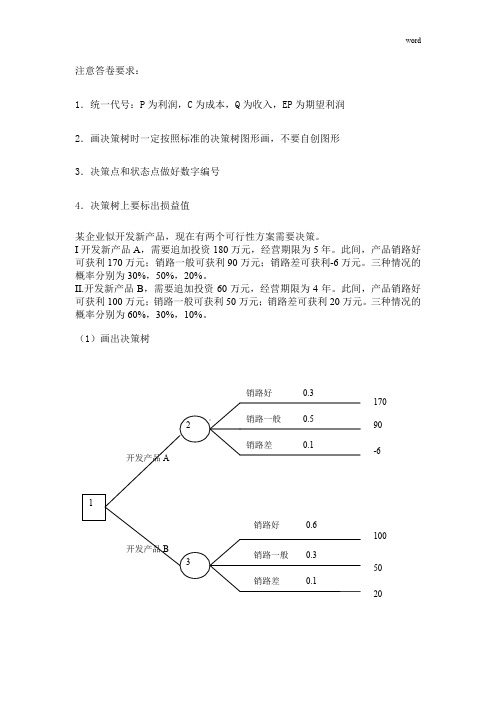
注意答卷要求:1.统一代号:P 为利润,C 为成本,Q 为收入,EP 为期望利润 2.画决策树时一定按照标准的决策树图形画,不要自创图形 3.决策点和状态点做好数字编号 4.决策树上要标出损益值某企业似开发新产品,现在有两个可行性方案需要决策。
I 开发新产品A ,需要追加投资180万元,经营期限为5年。
此间,产品销路好可获利170万元;销路一般可获利90万元;销路差可获利-6万元。
三种情况的概率分别为30%,50%,20%。
II.开发新产品B ,需要追加投资60万元,经营期限为4年。
此间,产品销路好可获利100万元;销路一般可获利50万元;销路差可获利20万元。
三种情况的概率分别为60%,30%,10%。
(1)画出决策树销路好 0.317090 -61005020(2)计算各点的期望值,并做出最优决策求出各方案的期望值:方案A=170×0.3×5+90×0.5×5+(-6)×0.2×5=770(万元)方案B=100×0.6×4+50×0.3×4+20×0.1×4=308(万元)求出各方案的净收益值:方案A=770-180=590(万元)方案B=308-60=248(万元)因为590大于248大于0所以方案A最优。
某企业为提高其产品在市场上的竞争力,现拟定三种改革方案:(1)公司组织技术人员逐渐改进技术,使用期是10年;(2)购买先进技术,这样前期投入相对较大,使用期是10年;(3)前四年先组织技术人员逐渐改进,四年后再决定是否需要购买先进技术,四年后买入技术相对第一年便宜一些,收益与前四年一样。
预计该种产品前四年畅销的概率为0.7,滞销的概率为0.3。
如果前四年畅销,后六年畅销的概率为0.9;若前四年滞销,后六年滞销的概率为0.1。
相关的收益数据如表所示。
(1)画出决策树(2)计算各点的期望值,并做出最优决策投资收益表单位:万元解(1)画出决策树,R为总决策,R1为二级决策。
人工智能决策树例题经典案例

人工智能决策树例题经典案例一、经典案例:天气预测决策树在天气预测中有广泛应用,下面是一个关于是否适宜进行户外运动的示例:1. 数据收集:- 温度:高(>30℃)/中(20℃-30℃)/低(<20℃)- 降水:是/否- 风力:高/中/低- 天气状况:晴朗/多云/阴天/雨/暴雨- 应该户外运动:是/否2. 构建决策树:- 根据温度将数据分为三个分支:高温、中温、低温- 在每个分支中,继续根据降水、风力和天气状况进行划分,最终得到是否适宜户外运动的决策3. 决策树示例:温度/ / \高温中温低温/ | | \ |降水无降水风力适宜/ \ | | / \是否高中低| |不适宜适宜- 如果温度是高温且有降水,则不适宜户外运动- 如果温度是高温且无降水,则根据风力判断,如果风力是高,则不适宜户外运动,如果风力是中或低,则适宜户外运动 - 如果温度是中温,则不论降水和风力如何,都适宜户外运动- 如果温度是低温,则需要考虑风力,如果风力是高,则适宜户外运动,如果风力是中或低,则不适宜户外运动4. 参考内容:决策树的构建和应用:决策树通过对输入特征进行划分,构建了一棵树形结构,用于解决分类或回归问题。
构建决策树主要包括数据预处理、特征选择、划分策略和停止条件等步骤。
特征选择可以使用信息增益、基尼指数等算法,划分策略可以使用二叉划分或多叉划分,停止条件可以是叶子节点纯度达到一定阈值或达到预定的树深度。
决策树的应用包括数据分类、特征选择和预测等任务。
天气预测案例中的决策树:将天气预测问题转化为分类问题,通过构建决策树,可以得到识别是否适宜户外运动的规则。
决策树的决策路径可以用流程图或树状图表示,帮助理解和解释决策过程。
决策树的节点表示特征值,分支表示判断条件,叶子节点表示分类结果。
决策树的生成算法可以基于启发式规则或数学模型,如ID3、C4.5、CART等。
决策树的优缺点:决策树具有可解释性强、易于理解和实现、能处理非线性关系等优点。
决策树例题(共10张PPT)

【例题8】
【解】第一步:将题意表格化
自然状态
概率
天气好
0.3
天气坏
0.7
行动方案
开工
不开工
40000
-1000
-10000
-1000
【例题8】
❖ 第二步:画决策树图形,根据第一步所列的表格, 再绘制决策树,如下图;
【例题8】
• 假设有一项工程,施工管理人员需要决定 下月是否开工。如果开工后天气好,则可 投标不中时,则对A损失50万元,对B损失100万元。
现采用决策树方法进行决策 3,天气坏的概率是0.
为国家创收4万元,若开工后天气坏,将给 若考虑的是损失时,则取最小期望值。
B、从出发点向右引出若干条直线,这些直线叫做方案枝; 3,天气坏的概率是0.
国家造成损失1万元,不开工则损失1000元。 某承包商拥有的资源有限,只能在A和B两个工程中选A或B进行投标,或者对这两项工程都不参加投标。
该承包商过去也承包过与A、B类似的工程,根据统计资料,每种方案的利润和出现的概率如下表所示。 一般按反向的时间程序逐步计算,将各方案的几种可能结果的数值和它们各自的概率相乘,并汇总所得之和,其和就是该方案的期望值。
概率
0.3 0.5 0.2 0.2 0.6 0.2 0.3 0.5 0.2 0.3 0.6 0.1
【例题9】
【解】第一步:将题意表格化
概率分叉点
3,天气坏的概率是0.
(自 然 状 态 点 )
投标不中时,则对A损失50万元,对B损失100万元。
损益值
但根据过去该承包商投标经验资料,他对A或B投标又有两种策略:一种是投高标,中标的机会是0.
决策树例题分析和解答课件

非确定性决策方法
是指决策者对环境情况几乎一无所知,决 策者只好根据自己的主观倾向进行决策
1、乐观决策(极大极大决策 、大中取大)
决策者持乐观态度,有具有较强的实力,担心失 去获利的机会。愿冒大的风险,意图大的回报 。 决策者凭借冒险精神,在不知道未来各种可能 状态发生概率的前提下,将各个方案在各种状 态下可能取得的最大收益值作为该方案的收益 值,然后,再从各方案收益值中找出最大收益 值的方案。
350
220
250
需求量较低 -150 -350
50
90
需求量很低 -350
-700 -100
-50
21
损益值 方案 甲 乙 丙 丁
状态 需求量 需求量 需求量较 需求量 max
较高 一般
低
很低
600 400 800 350 350 220 400 250
-150 -350 50 90
-350 600 -700 800 -100 350 -50 400
600×0.7+(--350 ×0.3)=315
28
决策准则小结
不同决策者甚至同一决策者在不同决 策环境下对同一个问题的决策可能截 然不同,并没有所谓的“正确答案”。 决策准则的选取主要取决于决策者对 于决策的性格和态度,以及制定决策 时的环境
所有的准则都不能保证所选择的方案 在实际情况发生时会成为最佳方案
2
决策方案评价
作物类别
玉米 棉花 花生 合计 资源供给量 资源余缺量
占用耕 忙季耗用 灌水用量 地面积 工日数 (立方米) (公顷)
20
1200
45000
5.333
560
12000
8
决策树习题练习(答案)

决策树习题练习(答案)决策树习题练习答案1.某投资者预投资兴建一工厂,建设方案有两种:①大规模投资300万元;②小规模投资160万元。
两个方案的生产期均为10年,其每年的损益值及销售状态的规律见表15。
试用决策树法选择最优方案。
表1 各年损益值及销售状态销售状态概率损益值(万元/年)大规模投资小规模投资销路好 0.7100 60 销路差 0.3 -2020【解】(1)绘制决策树,见图1;100×10 -20×10 60×1020×10 销路好0.7 销路差(0.3)销路好0.7 销路差(0.3)大规模小规模 340 340 3202 31 图1 习题1决策树图(2)计算各状态点的期望收益值节点②:节点③:将各状态点的期望收益值标在圆圈上方。
(3)决策比较节点②与节点③的期望收益值可知,大规模投资方案优于小规模投资方案,故应选择大规模投资方案,用符号“//”在决策树上“剪去”被淘汰的方案。
2.某项目有两个备选方案A和B,两个方案的寿命期均为10年,生产的产品也完全相同,但投资额及年净收益均不相同。
A方案的投资额为500万元,其年净收益在产品销售好时为150万元,,销售差时为50万元;B方案的投资额为300万元,其年净收益在产品销路好时为100万元,销路差时为10万元,根据市场预测,在项目寿命期内,产品销路好时的可能性为70%,销路差的可能性为30%,试根据以上资料对方案进行比选。
已知标准折现率ic=10%。
【解】(1)首先画出决策树150 5010010 销路好0.7 销路差0.3 销路好0.7 销路差0.3 -500 -3002 31 图2 决策树结构图此题中有一个决策点,两个备用方案,每个方案又面临着两种状态,因此可以画出其决策树如图18。
(2)然后计算各个机会点的期望值机会点②的期望值=150(P/A,10%,10)×0.7+(-50)(P/A,10%,10)×0.3=533(万元) 机会点③的期望值=100(P/A,10%,10)×0.7+10(P/A,10%,10)×0.3=448.5(万元) 最后计算各个备选方案净现值的期望值。
决策树练习题-多级决策树

销路好0.7 销路好
100
10
前三年的期望收入 3 =0.7×40×3+0.3×10×3=93 × × × ×
销路差0.3 销路差
8
不 扩 建
-30 E(11)=40×0.9+10×0.1×7=259 ( ) × × ×
销路好0.9 销路好
销路差0.1 销路差
40
11
销路差0.1 销路差
10
E(3)= 93 ( ) 93+0.7×469+0.3×70-140 × × -140=302.3
• 第二步:对于节点2即改建车间
• 后七年的期望收入=0.7×E(6)+0.3×E(7) • E(6)=0.9×40×7+0.1×10×7=259 (万元) • E 7 =1.0 10 7=70 E(7)=1.0×10×7=70 (万元) • 前三年的期望收入=0.7×40×3+0.3×10×3=93 • E(2)= 93 +0.7×259+0.3×70-140=155.3 (万元)
不同状态下各方案的每年损益值/万元
状态及概率 损益值 方案 新建车间 A1 改建车间 A2 改建后扩建 A3 销路好 0.7 销路一般 0.3
100 40 100
-30 10 -30
• • • •
解题步骤: 解题步骤: (1)画出多级决策树 ) (2)计算各节点的期望收益 ) (3)通过比较各期望收益,选择方案。 )通过比较各期望收益,选择方案。
4
-30
E(5)=1.0×(-30)×7= -210 ( ) × )
1
新建
销路差0.3 销路差 销路差1.0 销路差
-30
决策树实例计算

决策树实例计算计算题⼀ 1.为⽣产甲产品,⼩⾏星公司设计了两个基本⽅案:⼀是建⼤⼯⼚,⼆是建⼩⼯⼚。
如果销路好,3年以后考虑扩建。
建⼤⼯⼚需投资300万元,建⼩⼯⼚需投资160万元,3年后扩建另需投资140万元。
扩建后可使⽤7年,其年度损益值与⼤⼯⼚相同。
每种⾃然状态的预测概率及年度损益值如下表:前 3 年后 7 年根据上述资料试⽤决策树法做出决策。
四、计算题(15分)答:建⼤⼚收益=581-300=281建⼩⼚收益=447-160=287所以应选择建⼩⼚⽅案。
⼆⼭姆公司的⽣产设备已经落后,需要马上更新。
公司有⼈认为,⽬前产品销路增长,应在更新设备的同时扩⼤再⽣产的规模。
但也有⼈认为,市场形势尚难判断,不如先更新设备,3年后再根据形势变化考虑扩⼤再⽣产的规模问题。
这样,该公司就⾯临着两个决策⽅案。
决策分析的有关资料如下:A、现在更新设备,需投资35万元, 3年后扩⼤⽣产规模,另需投资40万元。
B、现在更新设备的同时扩⼤再⽣产的规模,需投资60万元。
C、现在只更新设备,在销售情况良好时,每年可获利6万元;在销售情况不好时,每年可获利4、5万元。
D、如果现在更新与扩产同时进⾏,若销售情况好,前3年每年可获利12万元;后7年每年可获利15万元;若销售情况不好,每年只获利3万元。
E、每种⾃然状态的预测概率如下表前 3 年后 7 年根据上述资料试⽤决策树法做出决策。
答案:结点7收益值=0、85×7 × 15+0、15 ×7 ×3=92、4(万元)结点8收益值=0、85×7 ×6+0、15 ×7 ×4、5=40、4(万元)结点9收益值=0、1×7 × 15+0、9 ×7 ×3=29、4(万元)结点10收益值=0、1×7 × 6+0、9 ×7 ×4、5=32、6(万元)结点1收益值=0、7×[52、4+(3 × 6)]+0、3 ×[32、6+(3 × 4、5)]=63、1(万元)结点2收益值=0、7×[92、4+(3 × 12)]+0、3 ×[29、4+(3 × 3)]=101、4(万元)答:⽤决策树法进⾏决策应选择更新扩产⽅案,可获得收益41、4万元。
决策树算法例题经典

决策树算法例题经典
案例1:购物产品推荐。
假设当前我们需要进行购物产品推荐工作,用户可以选择若干项属性,例如品牌、价格、颜色、是否有折扣等等,在已知一些样本的基础上,构
建一棵决策树,帮助用户快速得到最佳购买推荐。
如果用户选择的品牌为A,则直接推荐产品P3;如果选择品牌为B,
则继续考虑价格,如果价格低于100,则推荐产品P1,否则推荐产品P2。
如果用户选择的品牌为C,则直接推荐产品P4。
当然,这只是一个简单的例子,实际应用场景中可能会有更多的属性
和样本。
因此,在构建决策树时需要考虑选取最优特征,避免过度拟合等
问题。
案例2:疾病预测。
假设有一组医学数据,其中包括患者的年龄、性别、身高、体重、血
压等指标以及是否患有糖尿病的标签信息。
我们希望构建一个决策树来帮
助医生快速判断患者是否可能患有糖尿病。
如果患者年龄大于45岁,则进一步考虑体重,如果体重高于120kg,则判断为高风险群体;否则判断为低风险群体。
如果患者年龄不超过45岁,则直接判断为低风险群体。
当然,这只是一个简单的例子,实际应用场景中可能会有更多的指标
和样本。
因此,在构建决策树时需要考虑选取最优特征,避免过度拟合等
问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• 最大概率法、收益期望值法、决策树法★
决策树法 • 将损益期望值法中的各个方案的情况用一个概率树
来表示,就形成了决策树。它是模拟树木生长的过 程,从出发点开始不断分枝来表示 所分析问题的各 种发展可能性,并以各分枝的损益期望值中的最大 者作为选择的依据。 • 决策树的画法、 决策树的例子 • 例题8、例题9、例题10
【例题8】
【解】第一步:将题意表格化
自然状态
概率
天气好
0.3
天气坏
0.7
行动方案
开工
不开工
40000
-1000
-10000
-1决策树图形,根据第一步所列的 表格,再绘制决策树,如下图;
开工
5000 B
开气好0.3 天气坏0.7
40000 -10000
A
不开工
-1000
决策树的画法
• A、先画一个方框作为出发点,又称决策节点; • B、从出发点向右引出若干条直线,这些直线叫
做方案枝; • C、在每个方案枝的末端画一个圆圈,这个圆圈
称为概率分叉点,或自然状态点; • D、从自然状态点引出代表各自然状态的分枝,
称为概率分枝; • E、如果问题只需要一级决策,则概率分枝末端
画三角形,表示终点 。
1
决策 结点
概率分叉点
(自然状态点) 概率枝
方案分枝 2
概率枝
方案分枝
概率枝
3
概率枝
概率分叉点
(自然状态点)
图4-1 决策树
损益值 损益值 损益值 损益值
【例题8】
• 假设有一项工程,施工管理人员需要决定 下月是否开工。如果开工后天气好,则可 为国家创收4万元,若开工后天气坏,将给 国家造成损失1万元,不开工则损失1000元。 根据过去的统计资料,下月天气好的概率 是0.3,天气坏的概率是0.7。请做出决策。 现采用决策树方法进行决策
概率
0.3 0.5 0.2 0.2 0.6 0.2 0.3 0.5 0.2 0.3 0.6 0.1
【例题9】
开气好0.3
-1000
C
天气坏0.7
-1000
【例题8】
• 第三步:计算期望值 • 一般按反向的时间程序逐步计算,将各方案的
几种可能结果的数值和它们各自的概率相乘, 并汇总所得之和,其和就是该方案的期望值。 • 第四步:确定决策方案:在比较方案考虑的是 收益值时,则取最大期望值;若考虑的是损失 时,则取最小期望值。 • 根据计算出的期望值分析,本题采取开工方案 较好。
【例题9】
• 某承包商拥有的资源有限,只能在A和B两个 工程中选A或B进行投标,或者对这两项工程 都不参加投标。
• 但根据过去该承包商投标经验资料,他对A或 B投标又有两种策略:一种是投高标,中标的机 会是0.3;另一种是投低标,中标的机会是0.5。 这样共有A高、A低、不投、B高和B低五种方 案。
• 该承包商过去也承包过与A、B类似的工程, 根据统计资料,每种方案的利润和出现的概率 如下表所示。投标不中时,则对A损失50万元, 对B损失100万元。根据上述情况,试画出决 策树
【例题9】
方案 A高 A低 B高 B低
效果
优 一般 赔 优 一般 赔 优 一般 赔 优 一般 赔
可能的利润(万元)
5000 1000 -3000 4000 500 -4000 7000 2000 -3000 6000 1000 -1000
