物理竞赛热学
高中物理竞赛十年预赛真题热学纯手打word版含答案

十年真题-热学(预赛)1.(34届预赛2)系统1和系统2质量相等,比热容分别为C 1和C 2,两系统接触后达到够达到共同的温度T ,整个过程中与外界(两系统之外)无热交换.两系统初始温度T 1和T 2的关系为A .T 1=C 2C 1(T -T 2)-TB .T 1=C 1C 2(T -T 2)-T C .T 1=C 1C 2(T -T 2)+T D .T 1=C 2C 1(T -T 2)+T 2.(31届预赛1)一线膨胀系数为α的正立方体物块,当膨胀量较小时,其体膨胀系数等于A .αB .α1/3C .α3D .3α3.(29届预赛1)下列说法中正确的是A .水在0℃时密度最大B .一个绝热容器中盛有气体,假设把气体中分子速率很大的如大于v A 的分子全部取走,则气体的温度会下降,此后气体中不再存在速率大于v A 的分子C .杜瓦瓶的器壁是由两层玻璃制成的,两层玻璃之间抽成真空,抽成真空的主要作用是既可降低热传导,又可降低热辐射D .图示为一绝热容器,中间有一隔板,隔板左边盛有温度为T 的理想气体,右边为真空.现抽掉隔板,则气体的最终温度仍为T4.(28届预赛2)下面列出的一些说法中正确的是A .在温度为20ºC 和压强为1个大气压时,一定量的水蒸发为同温度的水蒸气,在此过程中,它所吸收的热量等于其内能的增量.B .有人用水银和酒精制成两种温度计,他都把水的冰点定为0度,水的沸点定为100度,并都把0刻度与100刻度之间均匀等分成同数量的刻度,若用这两种温度计去测量同一环境的温度(大于0度小于100度)时,两者测得的温度数值必定相同.C .一定量的理想气体分别经过不同的过程后,压强都减小了,体积都增大了,则从每个过程中气体与外界交换的总热量看,在有的过程中气体可能是吸收了热量,在有的过程中气体可能是放出了热量,在有的过程中气体与外界交换的热量为零.D .地球表面一平方米所受的大气的压力,其大小等于这一平方米表面单位时间内受上方作热运动的空气分子对它碰撞的冲量,加上这一平方米以上的大气的重量.5.(27届预赛2)烧杯内盛有0℃的水,一块0℃的冰浮在水面上,水面正好在杯口处.最后冰全部融化成0℃的水.在这过程中A .无水溢出杯口,但最后水面下降了B .有水溢出杯口,但最后水面仍在杯口处C .无水溢出杯口,水面始终在杯口处D .有水溢出杯口,但最后水面低于杯口6.(27届预赛3)如图所示,a和b是绝热气缸中的两个活塞,它们把气缸分成甲和乙两部分,两部分中都封有等量的理想气体.a是导热的,其热容量可不计,与气缸壁固连.b 是绝热的,可在气缸内无摩擦滑动,但不漏气,其右方为大气.图中k为加热用的电炉丝.开始时,系统处于平衡状态,两部分中气体的温度和压强皆相同.现接通电源,缓慢加热一段时间后停止加热,系统又达到新的平衡,则A.甲、乙中气体的温度有可能不变B.甲、乙中气体的压强都增加了C.甲、乙中气体的内能的增加量相等D.电炉丝放出的总热量等于甲、乙中气体增加内能的总和7.(27届预赛4)一杯水放在炉上加热烧开后,水面上方有“白色气”;夏天一块冰放在桌面上,冰的上方也有“白色气”.A.前者主要是由杯中水变来的“水的气态物质”B.前者主要是由杯中水变来的“水的液态物质”C.后者主要是由冰变来的“水的气态物质”D.后者主要是由冰变来的“水的液态物质”8.(26届预赛3)一根内径均匀、两端开中的细长玻璃管,竖直插在水中,管的一部分在水面上.现用手指封住管的上端,把一定量的空气密封在玻璃管中,以V0表示其体积;然后把玻璃管沿竖直方向提出水面,设此时封在玻璃管中的气体体积为V1;最后把玻璃管在竖直平面内转过900,让玻璃管处于水平位置,设此时封在玻璃管中的气体体积为V2.则有A.V1>V0≥V2B.V1>V0>V2C.V1=V2>V0D.V1>V0,V2>V09.(25届预赛4)如图所示,放置在升降机地板上的盛有水的容器中,插有两根相对容器的位置是固定的玻璃管a和b,管的上端都是封闭的,下端都是开口的.管内被水各封有一定质量的气体.平衡时,a管内的水面比管外低,b管内的水面比管外高.现令升降机从静止开始加速下降,已知在此过程中管内气体仍被封闭在管内,且经历的过程可视为绝热过程,则在此过程中A.a中气体内能将增加,b中气体内能将减少B.a中气体内能将减少,b中气体内能将增加C.a、b中气体内能都将增加D.a、b中气体内能都将减少10.(25届预赛5)图示为由粗细均匀的细玻璃管弯曲成的“双U形管”,a、b、c、d 为其四段竖直的部分,其中a、d上端是开口的,处在大气中.管中的水银把一段气体柱密封在b、c内,达到平衡时,管内水银面的位置如图所示.现缓慢地降低气柱中气体的温度,若c中的水银面上升了一小段高度Δh,则A.b中的水银面也上升ΔhB.b中的水银面也上升,但上升的高度小于ΔhC .气柱中气体压强的减少量等于高为Δh 的水银柱所产生的压强D .气柱中气体压强的减少量等于高为2Δh 的水银柱所产生的压强11.(31届预赛9)图中所示的气缸壁是绝热的.缸内隔板A 是导热的,它固定在缸壁上.活塞B 是绝热的,它与缸壁的接触是光滑的,但不漏气.B 的上方为大气.A 与B 之间以及A 与缸底之间都盛有n mol 的同种理想气体.系统在开始时处于平衡状态,现通过电炉丝E 对气体缓慢加热.在加热过程中,A 、B 之间的气体经历_________过程,A 以下气体经历________过程;气体温度每上升1K ,A 、B 之间的气体吸收的热量与A 以下气体净吸收的热量之差等于_____________.已知普适气体常量为R .答案:等压、等容、nR解析:在加热过程中,AB 之间的气体的压强始终等于大气压强与B 活塞的重力产生的压强之和,故进行的是等压变化,由于隔板A 是固定在气缸内的,所以,A 以下的气体进行的是等容变化,当气体温度升高1K 时,AB 之间的气体吸收的热量为Q 1=P ΔV +ΔU ,A以下的气体吸收的热量为Q 2=ΔU ,又根据克拉伯龙方程p ΔV =nR ΔT ,所以Q 1-Q 2=p ΔV=nR .12.(28届预赛6)在大气中,将一容积为0.50m 3的一端封闭一端开口的圆筒筒底朝上筒口朝下竖直插人水池中,然后放手,平衡时,筒内空气的体积为0.40m 3.设大气的压强与10.0m 高的水柱产生的压强相同,则筒内外水面的高度差为 .答案:2.5m13.(34届预赛13)横截面积为S 和2S 的两圆柱形容器按图示方式连接成一气缸,每隔圆筒中各置有一活塞,两活塞间的距离为l ,用硬杆相连,形成“工”字形活塞,它把整个气缸分隔成三个气室,其中Ⅰ、Ⅲ室密闭摩尔数分别为ν和2ν的同种理想气体,两个气室内都有电加热器;Ⅱ室的缸壁上开有一个小孔,与大气相通;1mol 该种气体内能为CT(C 是气体摩尔热容量,T 是气体的绝对温度).当三个气室中气体的温度均为T 1时,“工”字形活塞在气缸中恰好在图所示的位置处于平衡状态,这时Ⅰ室内空气柱长亦为l ,Ⅱ室内空气的摩尔数为32ν.已知大气压不变,气缸壁和活塞都是绝热的,不计活塞与气缸之间的摩擦.现通过电热器对Ⅰ、Ⅲ两室中的气体缓慢加热,直至Ⅰ室内气体的温度升为其初始状态温度的2倍,活塞左移距离d .已知理想气体常量为R ,求:(1)Ⅲ室内气体初态气柱的长度;(2)Ⅲ室内气体末态的温度;(3)此过程中ⅠⅢ室密闭气体吸收的总热量.解析:(1)设大气压强为p 0.初态:Ⅰ室内气体压强为p 1;Ⅲ室内气体压强为p 1′,气柱的长度为l ′.末态:Ⅰ室内气体压强为p 2;Ⅲ室内气体压强为p 2′.由初态到末态:活塞左移距离为d .对初态应用气体状态方程,对Ⅰ室气体有:p 1lS =νRT 1 ①对Ⅱ室内气体有:p 0(l 2×S +l 2×2S )=32ν0RT 1②对Ⅲ室内气体有:p1′l′(2S)=(2ν)RT1③由力学平衡条件有:p1′(2S)=p1S+p0(2S-S) ④由题给条件和①②③④式得:l′=ν2ν1+ν0l=2νν+ν0l⑤(2)对末态应用气体状态方程,对Ⅰ室内气体有:p2(l-d)S=νRT2=νR·2T1⑥对Ⅲ室内气体有:p2′(l′+d)(2S)=(2ν)RT2′⑦由力学平衡条件有:p2′(2S)=p2S+p0(2S-S) ⑧联立②⑤⑥⑦⑧和题给条件得:T2′=2νl+(ν+ν0)d(l-d)(ν+ν0)⎝⎛⎭⎫1+ν02νl-dl T1⑨(3)大气对密闭气体系统做的功为W=p0(2S-S)(-d)=-p0Sd=-dlν0RT1⑩已利用②式.系统密闭气体内能增加量为:ΔU=νC(T2-T1)+(2ν)C(T2′-T1)=νC(2T2′-T1) ⑪由⑨⑩式得:ΔU=2νl+(ν+ν0)d(l-d)(ν+ν0)⎝⎛⎭⎫2ν+l-dlν0CT1-νCT1⑫系统吸收的热量为:Q=ΔU-W=2νl+(ν+ν0)d(l-d)(ν+ν0)⎝⎛⎭⎫2ν+l-dlν0CT1-νCT1+dlν0RT1⑬参考评分:第(1)问9分,①②③④式各2分,⑤式1分.第(2)问4分,⑥⑦⑧⑨式各1分.第(3)问7分,⑩⑪式各2分,⑫式1分,⑬式2分.14.(33届预赛16)充有水的连通软管常常用来检验建筑物的水平度.但软管中气泡会使得该软管两边管口水面不在同一水平面上.为了说明这一现象的物理原理,考虑如图所示的连通水管(由三段内径相同的U形管密接而成),其中封有一段空气(可视为理想气体),与空气接触的四段水管均在竖直方向;且两个有水的U形管两边水面分别等高.此时被封闭的空气柱的长度为L a .已知大气压强P 0、水的密度ρ、重力加速度大小为g ,L 0≡P 0/(ρg).现由左管口添加体积为ΔV =xS 的水,S 为水管的横截面积,在稳定后:(1)求两个有水的U 形管两边水面的高度的变化和左管添水后封闭的空气柱的长度;(2)当x <<L 0、L a<<L 0时,求两个有水的U 形管两边水面的高度的变化(用x 表出)以及空气柱的长度.已知1+z ≈1+12z ,当z <<1. 解析:解法(一)(1)设在左管添加水之前左右两个U 形管两边水面的高度分贝为h 1和h 2,添加水之后左右两个U 形管两边水面的高度分别为h 1L 和h 1R 、h 2L 和h 2R .如图所示,设被封闭的空气的压强为p ,空气柱的长度为L b .水在常温常压下可视为不可被压缩的流体,故:2h 1+x =h 1L +h 1R ①2h 2=h 2L +h 2R ②由力学平衡条件有:p 0+ρgh 1L =p +ρgh 1R ③p 0+ρgh 2R =p +ρgh 2L④由于连通管中间高度不变,有:h 1+h 2+L a =h 1R +h 2L +L b ⑤由玻意耳定律得:p 0L a =pL b ⑥联立①②③④⑤⑥式得p 满足的方程:L 0p 0p 2+⎝⎛⎭⎫L a -L 0-x 2p -p 0L a =0 解得:p =p 02L 0⎣⎡⎦⎤L 0-L a +x 2+⎝⎛⎭⎫L a -L 0-x 22+4L a L 0 ⑦ 将⑦式带入⑥式得:L b =12⎣⎡⎦⎤L a -L 0-x 2+⎝⎛⎭⎫L a -L 0-x 22+4L a L 0 ⑧ 由①②③④⑦式得:Δh 1L ≡h 1L -h 1=x -Δh 1R=x -L 02+14[L 0-L a +x 2+⎝⎛⎭⎫L a -L 0-x 22+4L a L 0] ⑨ =5x -2L a -2L 08+14⎝⎛⎭⎫L a -L 0-x 22+4L a L 0 Δh 1R ≡h 1R -h 1=L 0+x 2-p 2ρg=L 0+x 2-14⎣⎡⎦⎤L 0-L a +x 2+⎝⎛⎭⎫L a -L 0-x 22+4L a L 0 ⑩=3x +2L a +2L 08-14⎝⎛⎭⎫L a -L 0-x 22+4L a L 0 Δh 2L ≡h 2L -h 2=L 02-p 2ρg =L 02-14⎣⎡⎦⎤L 0-L a +x 2+⎝⎛⎭⎫L a -L 0-x 22+4L a L 0 ⑪ =2L a +2L 0-x 8-14⎝⎛⎭⎫L a -L 0-x 22+4L a L 0 Δh 2R ≡h 2R -h 2=-Δh 2L=x -2L a -2L 08+14⎝⎛⎭⎫L a -L 0-x 22+4L a L 0 ⑫ (2)在x <<L 0和L a <<L 0的情形下,由⑧式得:L b ≈L a ⑬⑦式成为:p ≈p 0(1+x 2L 0) ⑭ 由⑨⑩⑪⑫⑬⑭式得:Δh 1L ≈34x ⑮ Δh 1R ≈-Δh 2L =Δh 2R ≈14x ⑯ 参考评分:第(1)问14分,①②③④⑤⑥⑦⑧式各1分,⑨⑩式各2分,⑪⑫式各1分;第(2)问6分,⑬⑭式各1分,⑮⑯式各2分.解法(二)(1)设U 形管1左侧末态水面比初态上升x 2+y ,右侧末态水面比初态上升x 2-y ,U 形管2左侧末态水面比初态下降y ,右侧末态水面比初态上升y .由玻意耳定律得: L a L 0=L b (L 0+2y ) ①由几何关系有:L a -x 2+2y =L b ②将②式带入①式得:L a L 0=(L a -x 2+2y ) (L 0+2y ) ③解得: y =x 8-L 04-L a 4+14⎝⎛⎭⎫L 0+L a -x 22+2xL 0 ④ 此即U 形管2左侧末态比初态水面下降值,也是右侧末态比初态水面上升值(负根y=x 8-L 04-L a 4-14⎝⎛⎭⎫L 0+L a -x 22+2xL 0不符合题意,已舍去).U 形管1左侧末态比初态水面上升:x 2+y =5x -2L a -2L 08+14⎝⎛⎭⎫L a +L 0-x 22+2xL 0 ⑤ 右侧末态比初态水面上升:x 2-y =3x +2L a +2L 08-14⎝⎛⎭⎫L a +L 0-x 2 2+2xL 0 ⑥ 将④式带入②式得:L b =L a -x 2+2y =2L a -2L 0-x 4+12⎝⎛⎭⎫L a +L 0-x 22+2xL 0 ⑦ (2)在x <<L 0和L a <<L 0的情形下,④⑤⑥⑦式中的根号部分⎝⎛⎭⎫L a +L 0-x 22+2xL 0=L a 2+L 02+x 24+2L 0L a -xL 0-xL a +2xL 0 =L 01+L a 2L 02+x 24L 02+2L a L 0-xL a 2L 02+x L 0≈L 0⎣⎡⎦⎤1+12(L a 2L 02+x 24L 02+2L a L 0-xL a L 02+x L 0 =L 0+12⎣⎡⎦⎤L a 2L 0+x 24L 0+2L a -xL a L 0+x ⑧ ≈L 0+12(2L a +x ) =L a +L 0+x 2⑧式在推导过程中用到了1+z ≈1+12z ,当z <<1. 将⑧式带入④⑤⑥⑦式中分别得到:y ≈x 8-L 04-L a 4+14⎝⎛⎭⎫L 0+L a +x 2=x 4⑨ x 2+y ≈x 2+x 4=3x 4⑩ x 2-y ≈x 2-x 4=x 4⑪ L b ≈L a 2-L 02-x 4+12⎝⎛⎭⎫L 0+L a +x 2=L a ⑫参考评分:第(1)问14分,①式4分,②③式各1分,④式3分,⑤式2分,⑥式1分.第(2)问6分,⑨⑩式各2分,⑪⑫式各1分.15.(32届预赛15)如图,导热性能良好的气缸A 和B 高度均为h (已除开活塞的厚度),横截面积不同,竖直浸没在温度为T 0的恒温槽内,它们的底部由一细管连通(细管容积可忽略).两气缸内各有一个活塞,质量分别为m A =2m 和m B =m ,活塞与气缸之间无摩擦,两活塞的下方为理想气体,上方为真空.当两活塞下方气体处于平衡状态时,两活塞底面相对于气缸底的高度均为h /2.现保持恒温槽温度不变,在两活塞上面同时各缓慢加上同样大小的压力,让压力从零缓慢增加,直至其大小等于2m g (g 为重力加速度)为止,并一直保持两活塞上的压力不变;系统再次达到平衡后,缓慢升高恒温槽的温度,对气体加热,直至气缸B 中活塞底面恰好回到高度为h /2处.求:(1)两个活塞的横截面积之比S A ∶S B .(2)气缸内气体的最后的温度.(3)在加热气体的过程中,气体对活塞所做的总功.解析:(1)平衡时气缸A 、B 内气体的压强相等,故:m A g S A =m B g S B① 由①式和题给条件得: S A ∶S B =2∶1 ②(2)两活塞上各放一质量为2m 的质点前,气体的压强p 1和体积V 1分别为:p 1=2mg S A =mg S B③ V 1=32S B h ④ 两活塞上各放一质量为2m 的质点后,B 中活塞所受到的气体压力小于它和质点所受重力之和,B 中活塞将一直下降至气缸底部为之,B 中气体全部进入气缸A .假设此时气缸A 中活塞并未上升到气缸顶部,气体的压强p 2=4mg S A =2mg S B⑤ 设平衡时气体体积为V 2,由于初态末态都是平衡态,由理想气体状态方程有:p 1V 1T 0=p 2V 2T 0⑥ 由③④⑤⑥式得: V 2=34S 0h =38S A h ⑦ 这时气体的体积小于气缸A 的体积,与活塞未上升到气缸顶部的假设一致.缓慢加热时,气体先等压膨胀,B 中活塞不动,A 中活塞上升;A 中活塞上升至顶部后,气体等容升压;压强升至3mg S B时,B 中活塞开始上升,气体等压膨胀.设当温度升至T 时,该活塞恰好位于h 2处.此时气体的体积变为V 3=52S B h ⑧ 气体压强 p 3=3mg S B⑨ 设此时气缸内气体的温度为T ,由状态方程有:p 2V 2T 0=p 3V 3T⑩ 由⑤⑦⑧⑨⑩式得: T =5T 0 ⑪(3)升高恒温槽的温度后,加热过程中,A 活塞上升量为h -38h =58h ⑫ 气体对活塞所做的总功为W =4mg ·58h +3mg ·h 2=4mgh ⑬ 参考评分:第(1)问3分,①式2分,②式1分;第(2)问13分,③④⑤⑥式各2分,⑦⑧⑨⑩⑪式各1分;第(3)问4分,⑫⑬式各2分.16.(31届预赛14)1mol 的理想气体经历一循环过程1-2-3-1,如p -T 图示所示,过程1-2是等压过程,过程3-1是通过p -T 图原点的直线上的一段,描述过程2-3的方程为c 1p 2+c 2p =T ,式中c 1和c 2都是待定的常量,p 和T 分别是气体的压强和绝对温度.已知,气体在状态1的压强、绝对温度分别为P 1和T 1,气体在状态2的绝对温度以及在状态3的压强和绝对温度分别为T 2以及p 3和T 3.气体常量R 也是已知的.(1)求常量c 1和c 2的值;(2)将过程1-2 -3 -1在p -v 图示上表示出来;(3)求该气体在一次循环过程中对外做的总功.解析:(1)设气体在状态i (i =1、2、3)下的压强、体积和温度分别为p i 、V i 和T i ,由题设条件有:c 1p 22+c 2p 2=T 2 ①c 1p 32+c 2p 3=T 3 ②由此解得:c 1=T 2p 3-T 3p 2p 22p 3-p 32p 2=T 2p 3-T 3p 1p 12p 3-p 32p 1③ c 2=T 2p 32-T 3p 22p 2p 32-p 22p 3=T 2p 32-T 3p 12p 1p 32-p 12p 3④ (2)利用气体状态方程pV =RT 以及V 1=R T 1p 1、V 2=R T 2p 2、V 3=R T 3p 3⑤ 可将过程2—3的方程写为p V 2-V 3p 2-p 3=V +V 2p 3-V 3p 2p 2-p 3⑥ 可见,在p -V 图上过程2-3是以(p 2,V 2)和(p 3,V 3)为状态端点的直线,过程3-1是通过原点直线上的一段,因而描述其过程的方程为:p T =c 3 ⑦ 式中c 3是一常量,利用气体状态方程pV =RT ,可将过程3-1的方程改写为:V =R c 3=V 3=V 1 ⑧ 这是以(p 3,V 1)和(p 1,V 1)为状态端点的等容降压过程.综上所述,过程1-2-3-1在p -V 图上是一直角三角形,如图所示.(3)气体在一次循环过程中对外做的总功为:W =-12(p 3-p 1)(V 2-V 1) ⑨ 利用气体状态方程pV =RT 和⑤式,上式即:W =-12R (T 2-T 1)⎝⎛⎭⎫p 3p 1-1 ⑩ 参考评分:第(1)问8分,①②③④式各2分;第(2)问10分,⑤⑥式各2分,过程1-2-3-1在p -V 上的图示正确得6分;第(3)问2分,⑩式2分.17.(30届预赛14)如图所示,1摩尔理想气体,由压强与体积关系的p-V 图中的状态A 出发,经过一缓慢的直线过程到达状态B ,已知状态B 的压强与状态A 的压强之比为12,若要使整个过程的最终结果是气体从外界吸收了热量,则状态B 与状态A 的体积之比应满足什么条件?已知此理想气体每摩尔的内能为32RT ,R 为普适气体常量,T 为热力学温度.解析:令ΔU 表示系统内能的增量,Q 和W 分别表示系统吸收的热量和外界对系统所做的功,由热力学第一定律有:ΔU =Q +W ①令T 1和T 2分别表示状态A 和状态B 的温度,有:ΔU =32R (T 2-T 1) ②令p 1、p 2和V 1、V 2分别表示状态A 、B 的压强和体积,由②式和状态方程可得: ΔU=32(p 2V 2-p 1V 1) ③由状态图可知,做功等于图线下所围面积,即:W =-12(p 1+p 2)(V 2-V 1) ④要系统吸热,即Q >0,由以上格式可得:32(p 2V 2-p 1V 1)+12(p 1+p 2)(V 2-V 1)>0⑤按题意,p 2p 1=12,带入上式,可得:V 2V 1>32 ⑥参考评分:①②③式各3分,④式4分,⑤式3分,⑥式2分.18.(29届预赛14)由双原子分子构成的气体,当温度升高时,一部分双原子分子会分解成两个单原子分子,温度越高,被分解的双原子分子的比例越大,于是整个气体可视为由单原子分子构成的气体与由双原子分子构成的气体的混合气体.这种混合气体的每一种成分气体都可视作理想气体.在体积V =0.045m 3的坚固的容器中,盛有一定质量的碘蒸气,现于不同温度下测得容器中蒸气的压强如下:试求温度分别为1073K 和1473K 时该碘蒸气中单原子分子碘蒸气的质量与碘的总质量之比值.已知碘蒸气的总质量与一个摩尔的双原子碘分子的质量相同,普适气体常量R =8.31J·mol -1·K -1解析:以m 表示碘蒸气的总之,m 1表示蒸气的温度为T 时单原子分子的碘蒸气的质量,μ1、μ2分别表示单原子分子碘蒸气和双原子分子碘蒸气的摩尔质量,p 1、p 2分别表示容器中单原子分子碘蒸气和双原子分子碘蒸气的分压强,则由理想气体的状态方程有:p 1V =m 1μ1RT ① p 2V=m -m 1μ2RT②其中,R 为理想气体常量. 根据道尔顿分压定律,容器中碘蒸气的总压强p 满足:p =p 1+p 2 ③设α=m 1m 为单原子分子碘蒸气的质量与碘蒸气的总质量的比值,注意到μ1=12μ2 ④ 由以上各式解得:α=μ2V mR ·p T-1 ⑤ 带入有关数据可得,当温度为1073K 时,α=0.06 ⑥ 当温度为1473K 时,α=0051 ⑦ 参考评分:①②③⑤式各4分,⑥⑦式各2分.19.(26届预赛15)图中M 1和M 2是绝热气缸中的两个活塞,用轻质刚性细杆连结,活塞与气缸壁的接触是光滑的、不漏气的,M 1是导热的,M 2是绝热的,且M 2的横截面积是M 1的2倍.M 1把一定质量的气体封闭在气缸为L 1部分,M 1和M 2把一定质量的气体封闭在气缸的L 2部分,M 2的右侧为大气,大气的压强p 0是恒定的.K 是加热L 2中气体用的电热丝.初始时,两个活塞和气体都处在平衡状态,分别以V 10和V 20表示L 1和L 2中气体的体积.现通过K 对气体缓慢加热一段时间后停止加热,让气体重新达到平衡太,这时,活塞未被气缸壁挡住.加热后与加热前比,L 1和L 2中气体的压强是增大了、减小还是未变?要求进行定量论证.解析:解法(一)用n 1和n 2分别表示L 1和L 2中气体的摩尔数,p 1、p 2和V 1、V 2分别表示L 1和L 2中气体处在平衡状态时的压强和体积,T 表示气体的温度(因为M 1是导热的,两部分气体的温度相等),由理想气体状态方程有:p 1V 1=n 1RT ①p 2V 2=n 2RT ②式中R 为普适气体常量.若以两个活塞和轻杆构成的系统为研究对象,处在平衡状态时有:p 1S 1-p 2S 1+p 2S 2-p 0S 2=0 ③已知S 2=2S 1 ④有③④式得:p 1+p 2=2p 0 ⑤由①②⑤三式得:p 1=2n 1n 2p 0V 2V 1+n 1n 2V 2 ⑥若⑥式中的V 1、V 2是加热后L 1和L 2中气体的体积,则p 1就是加热后L 1中气体的压强.加热前L 1中气体的压强则为p 10=2n 1n 2p 0V 20V 10+n 1n 2V 2 ⑦ 设加热后L 1中气体体积的增加量为ΔV 1,L 2中气体体积的增加量为ΔV 2,因连接两活塞的杆是刚性的,活塞M 2的横截面积是M 1的2倍,故有:ΔV 1=ΔV 2=ΔV ⑧加热后L 1和L 2中气体的体积都是增大的,即ΔV >0.(若ΔV <0,即加热后活塞是向左移动的,则大气将对封闭在气缸中的气体做功,电热丝又对气体加热,根据热力学第一定律,气体的内能增加,温度将上升,而体积是减小的,故L 1和L 2中气体的压强p 1和p 2都将增大,这违反力学平衡条件⑤式)于是有V 1=V 10+ΔV ⑨V 2=V 20+ΔV ⑩由⑥⑦⑨⑩四式得:p 1-p 10=2n 1n 2p 0(V 10-V 20)ΔV ⎣⎡⎦⎤V 10+ΔV +n 1n 2(V 20+ΔV )⎝⎛⎭⎫V 10+n 1n 2V 20 ⑪由⑪式可知:若加热前V 10=V 20,则p 1=p 10,即加热后p 1不变,由⑤式知p 2亦不变;若加热前V 10<V 20,则p 1<p 10,即加热后p 1必减小,由⑤式知p 2必增大;若加热前V 10>V 20,则p 1>p 10,即加热后p 1必增大,由⑤式知p 2必减小.参考评分:得到⑤式3分,得到⑧式3分,得到⑪式8分,最后结论6分. 解法(二)设加热前L 1和L 2中气体的压强和体积分别为p 10、p 20和V 10、V 20,以p 1、p 2和V 1、V 2分别表示加热后L 1和L 2中气体的压强和体积,由于M 1是导热的,加热前L 1和L 2中气体的温度是相等的,设为T 0,加热后L 1和L 2中气体的温度也相等,设为T .因为加热前、后两个活塞和轻杆构成的系统都处在力学平衡状态,注意到S 2=2S 1,力学平衡条件分别为:p 10+p 20=2p 0 ①p 1+p 2=2p 0 ②由①②两式得:p 1-p 10=-(p 2-p 20) ③根据理想气体状态方程,对L 1中的气体有:p 1V 1p 10V 10=T T 0④ 对L 2中气体有:p 2V 2p 20V 20=T T 0⑤ 由④⑤两式得:p 1V 1p 10V 10=p 2V 2p 20V 20⑥ ⑥式可改写成:⎝⎛⎭⎫1+p 1-p 10p 10⎝⎛⎭⎫1+V 1-V 10V 10=⎝⎛⎭⎫1+p 2-p 20p 20⎝⎛⎭⎫1+V 2-V 20V 20 ⑦ 因连接两活塞的杆是刚性的,活塞M 2的横截面积是M 1的2倍,故有:V 1-V 10=V 2-V 20 ⑧把③⑧式带入⑦式得:⎝⎛⎭⎫1+p 1-p 10p 10⎝⎛⎭⎫1+V 1-V 10V 10=⎝⎛⎭⎫1-p 1-p 10p 20⎝⎛⎭⎫1+V 1-V 10V 20 ⑨ 若V 10=V 20,则由⑨式得p 1=p 10,若加热前L 1中气体的体积等于L 2中气体的体积,则加热后L 1中气体的压强不变,由②式可知加热后L 2中气体的压强亦不变;若V 10<V 20,则由⑨式得p 1<p 10,若加热前L 1中气体的体积小于L 2中气体的体积,则加热后L 1中气体的压强必减小,由②式可知加热后L 2中气体的压强必增大;若V 10>V 20,则由⑨式得p 1>p 10,若加热前L 1中气体的体积大于L 2中气体的体积,则加热后L 1中气体的压强必增大,由②式可知加热后L 2中气体的压强必减小;参考评分:得到①式和②式或得到③式得3分,得到⑧式得3分,得到⑨式得8分,最后结论得6分.。
高中物理竞赛热学篇

13、课程:液体表面现象
1、表面张力
2、球形液面内外压强差
3、任意弯曲液面内外压强差
4、液体、固体交界面现象
5、毛细现象
6、知识精炼(一)
7、知识精炼(二)
8、知识精炼(三)
14、课程:真题回顾
1、知识精炼(一)
2、知识精炼(二)
3、知识精炼(三)
4、奥托循环
5、狄塞尔循环
6、知识精炼
7、吸放热转换
8、振动自由度解锁
9、课程:热力学第二定律
1、热力学第二定律
2、克劳修斯表述
3、两种表述等价性
4、可逆与不可逆
5、卡诺定理
6、热力学温标
10、课程:熵
1、熵
2、克劳修斯等式
3、态函数熵
4、小结
5、知识精炼(一)
6、知识精炼(二)
7、温熵图
8、一些不可逆过程中熵计算
1、自由度
2、能量按自由度均分定理
3、知识精炼
4、理想气体内能及比热
7、课程:热力学第一定律
1、热力学过程
2、功与热量
3、热力学第一定律
4、等容、等压、等温过程
5、绝热过程
6、多方过程
7、知识精炼(一)
8、混合气体绝热过程
9、知识精炼(二)
8、课程:循环过程
1、循环过程及其效率
2、卡诺循环
3、卡诺循环效率
1、气体分子速率分布
2、最可几与平均速率
3、高斯微积分
4、平方速率平均值
5、气体速度分布函数
6、知识精炼(一)
7、知识精炼(二)
8、知识精炼(三)
5、课程:玻尔兹曼分布律
1、玻尔兹曼分布
初中物理竞赛专题——热学
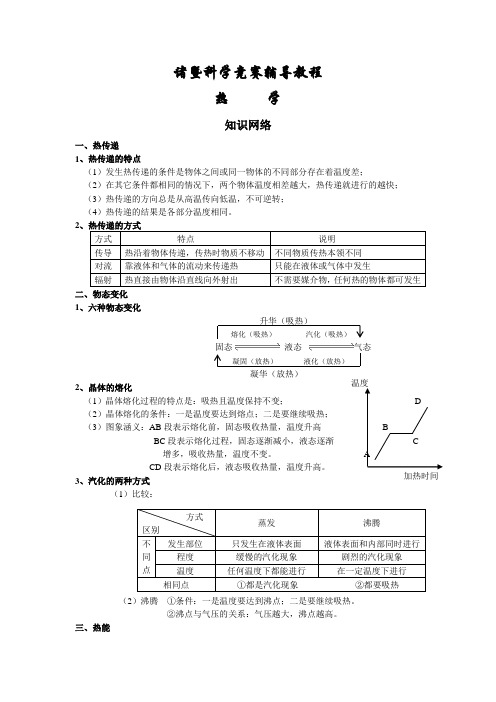
诸暨科学竞赛辅导教程热 学知识网络一、热传递1、热传递的特点(1)发生热传递的条件是物体之间或同一物体的不同部分存在着温度差;(2)在其它条件都相同的情况下,两个物体温度相差越大,热传递就进行的越快;(3)热传递的方向总是从高温传向低温,不可逆转;(4)热传递的结果是各部分温度相同。
2二、物态变化1、六种物态变化凝华(放热) 2、晶体的熔化 (1)晶体熔化过程的特点是:吸热且温度保持不变; (2)晶体熔化的条件:一是温度要达到熔点;二是要继续吸热; (3)图象涵义:AB 段表示熔化前,固态吸收热量,温度升高 BC 段表示熔化过程,固态逐渐减小,液态逐渐 增多,吸收热量,温度不变。
CD 段表示熔化后,液态吸收热量,温度升高。
3、汽化的两种方式(1)比较:(2)沸腾 ①条件:一是温度要达到沸点;二是要继续吸热。
②沸点与气压的关系:气压越大,沸点越高。
三、热能加热时间1、分子运动论的内容物质是由分子构成的;分子永不停息地做无规则的运动;分子之间有相互作用的引力和斥力。
2、热能、热量和温度(1)物体中大量分子做无规则运动所具有的能,叫做热能;(2)热量是物体在热传递过程中,吸收或放出热的多少,是物体改变热能的多少;(3)温度表示物体的冷热程度;(4)物体温度升高,热能增加;温度降低,热能减小。
3、改变热能的两种方法做功 外界对物体做功,物体的热能增加(机械能 热 能)方法 物体对外界做功,物体的热能减小(热 能 机械能)热传递 物体吸收热量,热能增加(别的物体 物体)物体放出热量,热能减小(物体 别的物体)4、物质的比热(1)比热是物质的一种特性。
比热的定义式:C= Q 吸/(m △t ),物质的比热与物体的质量、体积、温度变化的大小等无关。
水的比热是4.2×103焦/(千克·℃),水的比热比一般物质的比热要大。
(2)热平衡方程:①物体温度改变时,吸热和放热的计算公式:Q 吸 = c m ( t -t 0 ) Q 放 = c m ( t 0-t )②在热传递过程中,如果没有热量损失,高温物体放出的热量等于低温物体吸收的热量Q 吸 = Q 放四、热能的利用——热机热机是把热能转化为机械能的机器。
高级中学物理竞赛热学

高中物理竞赛——热学一.分子动理论1、物质是由大量分子组成的(注意分子体积和分子所占据空间的区别)对于分子(单原子分子)间距的计算,气体和液体可直接用3分子占据的空间,对固体,则与分子的空间排列(晶体的点阵)有关。
【例题1】如图6-1所示,食盐(N a Cl )的晶体是由钠离子(图中的白色圆点表示)和氯离子(图中的黑色圆点表示)组成的,离子键两两垂直且键长相等。
已知食盐的摩尔质量为58.5×10-3kg/mol ,密度为2.2×103kg/m 3,阿伏加德罗常数为6.0×1023mol-1,求食盐晶体中两个距离最近的钠离子中心之间的距离。
【解说】题意所求即图中任意一个小立方块的变长(设为a )的2倍,所以求a 成为本题的焦点。
由于一摩尔的氯化钠含有N A 个氯化钠分子,事实上也含有2N A 个钠离子(或氯离子),所以每个钠离子占据空间为 v =Am olN 2V而由图不难看出,一个离子占据的空间就是小立方体的体积a 3 , 即 a 3 =Am ol N 2V =Am ol N 2/M ,最后,邻近钠离子之间的距离l =2a【答案】3.97×10-10m 。
〖思考〗本题还有没有其它思路?〖答案〗每个离子都被八个小立方体均分,故一个小立方体含有81×8个离子 =21分子,所以…(此法普遍适用于空间点阵比较复杂的晶体结构。
) 2、物质内的分子永不停息地作无规则运动固体分子在平衡位置附近做微小振动(振幅数量级为0.1A 0),少数可以脱离平衡位置运动。
液体分子的运动则可以用“长时间的定居(振动)和短时间的迁移”来概括,这是由于液体分子间距较固体大的结果。
气体分子基本“居无定所”,不停地迁移(常温下,速率数量级为102m/s )。
无论是振动还是迁移,都具备两个特点:a 、偶然无序(杂乱无章)和统计有序(分子数比率和速率对应一定的规律——如麦克斯韦速率分布函数,如图6-2所示);b 、剧烈程度和温度相关。
大学物理竞赛-热学试题

等T膨胀:
dEk=0; 内压强引起的势能变化:
dEP
PidV
a
Va2
dV
d( a V
)
dE
dEk
dEP
d ( V
)
E V2 d ( a ) a( a a )
V1
V
V1 V2
(3)
Q吸
A
E
RT
ln
V2 V1
b b
例 真实气体在气缸内以温度T1等温膨胀,推动活 塞做功,活塞移动距离为L。若仅考虑分子占有体 积去计算功,比不考虑时为——;若仅考虑分子 间存在作用力去计算功,比不考虑时——;
(a)大; (b)小; (c)都一样;
答案:(a); (b)
解:(P
a V2
)(V
b)
RT
a:反映分子间引力;b:反映气体分子本身体积;
气体对外做功:A V2 PdV
V2 ( RT1
a V1 )dV
V1 V b V 2
RT1
ln
V2 V1
b b
a( 1 V2
1) V1
(1)仅考虑分子体积: a=0, ln V2 b ln V2
V1 b
V1
, 作功增加;
(2)仅考虑分子间引力: b=0, a( 1 1 ) 0
V2 V1
,作功减小;
一、理想气体状态方程 • PV=RT • P n k T
真实气体: 范德瓦尔斯方程
(P
a V2
)(V
b)
RT
• P RT
M
*
二、气体动理论
1. 微观量与宏观量的关系
•
P
2 3
n
t
t
若把某一初态定为参考态,则:S
物理竞赛讲座《热学》

2
1熔解和凝固 物质从固态变为液态叫熔解,从液态变为固态叫凝固。 晶体在物质熔解时,固态和液态可以共存的温度叫熔点。同种晶 体在某一压强下的熔点也是其凝固点。
物态变化
晶体在熔解(或凝固)过程中温度保持在熔点(或凝固点)不变。 非晶体无一定的熔点。非晶体在熔解(或凝固)过程中,温度不 停地上升或下降。 晶体的熔点与压强有关。熔解时体积膨胀的晶体,随所受压强增 大,溶点升高;熔解时体积缩小的晶体(如冰、锑),随所受压 强增大,溶点降低。 晶体中渗杂质后,溶点一般降低。
沸腾是在液体表面和内部同时发生的汽化 过程,沸腾发生时,它的饱和汽压必须等于外 界压强,沸腾时液体的温度不变,这个温度称 为该液体的沸点;外部压强增大,液体的沸点 升高;外部压强降低,沸点降低;不同的液体 在相同的压强下沸点不同。 从宏观角度,沸腾不同于蒸发,但从分子 运动论观点,两者并无本质差别。沸腾时,在 气、液分界面上汽化仍以蒸发的方式在进行, 只是在液体内部同时出现大量小气泡上浮起至 液面破裂,大大增加了汽化的速度。
有同学采用这样的解法
(76 20) 60 76 96 300 T2
T2 380K
P PV 1V1 2 2 T1 T2
水银溢出经历了哪几个阶段?
第1阶段为等压膨胀过程,水银上升了16cm
V1 V2 T1 T2
T2 380K
第2阶段,继续加热,水银将外溢,气体 压强将减小,体积V将增大,PV乘积的变 化规律就只能借助于数学工具进行讨论, PV/T=C,当PV最大时,T就是题中要求的 最高温度。
由此得到 b1 b H 时,
注入细管内水银柱的长度有最大值xmax
xmax b H
重点高中物理竞赛热学

重点高中物理竞赛热学高中物理竞赛——热学一.分子动理论1、物质是由大量分子组成的(注意分子体积和分子所占据空间的区别)对于分子(单原子分子)间距的计算,气体和液体可直接用3分子占据的空间,对固体,则与分子的空间排列(晶体的点阵)有关。
【例题1】如图6-1所示,食盐(N a Cl )的晶体是由钠离子(图中的白色圆点表示)和氯离子(图中的黑色圆点表示)组成的,离子键两两垂直且键长相等。
已知食盐的摩尔质量为58.5×10-3 kg/mol ,密度为 2.2×103kg/m 3,阿伏加德罗常数为6.0×1023mol -1,求食盐晶体中两个距离最近的钠离子中心之间的距离。
【解说】题意所求即图中任意一个小立方块的变长(设为a )的2倍,所以求a 成为本题的焦点。
由于一摩尔的氯化钠含有N A 个氯化钠分子,事实上也含有2N A 个钠离子(或氯离子),所以每个钠离子占据空间为v=Am olN 2V而由图不难看出,一个离子占据的空间就是小立方体的体积a 3,即a 3=Am ol N 2V =Am ol N 2/M ρ,最后,邻近钠离子之间的距离l=2a【答案】3.97×10-10m 。
〖思考〗本题还有没有其它思路?〖答案〗每个离子都被八个小立方体均分,故一个小立方体含有8 1×8个离子=21分子,所以…(此法普遍适用于空间点阵比较复杂的晶体结构。
) 2、物质内的分子永不停息地作无规则运动固体分子在平衡位置附近做微小振动(振幅数量级为0.1A 0),少数可以脱离平衡位置运动。
液体分子的运动则可以用“长时间的定居(振动)和短时间的迁移”来概括,这是由于液体分子间距较固体大的结果。
气体分子基本“居无定所”,不停地迁移(常温下,速率数量级为102m/s )。
无论是振动还是迁移,都具备两个特点:a 、偶然无序(杂乱无章)和统计有序(分子数比率和速率对应一定的规律——如麦克斯韦速率分布函数,如图6-2气体分子的三种速率。
物理竞赛热学专题精编大全(带答案详解)

物理竞赛热学专题精编大全(带答案详解)一、多选题1.如图所示为一种简易温度计构造示意图,左右两根内径粗细均匀的竖直玻玻璃管下端通过软管相连接,在管中灌入某种液体后环境的温度。
重复上述操作,便可在左管上方标注出不同的温度刻,将左管上端通过橡皮塞插入小烧瓶中。
调节右管的高度,使左右两管的液面相平,在左管液面位置标上相应的温度刻度。
多次改变烧瓶所在度,为了增大这个温度计在相同温度变化时液面变化的髙度,下列措施中可行的是()A.增大液体的密度B.增大烧瓶的体积C.减小左管的内径D.减小右管的内径【答案】BC2.如图所示为两端封闭的U形玻璃管,竖直放置,管内左、右两段封闭空气柱A、B 被一段水银柱隔开,设原来温度分别为T A和T B,当温度分别升高△T A和△T B时,关于水银柱高度差的变化情况,下列说法中正确的是()A.当T A=T B,且△T A=△T B时,h一定不变B.当T A=T B,且△T A=△T B时,h一定增大C.当T A<T B,且△T A<△T B时,h一定增大D.当T A>T B,且△T A=△T B时,h一定增大【答案】BD【解析】【详解】AB.由于左边的水银比右边的高ℎ,所以右边的气体的压强比左边气体的压强大,即P B> P A,设在变化的前后AB两部分气体的体积都不发生变化,即AB做的都是等容变化,则根据PT =ΔPΔT可知,气体的压强的变化为ΔP=PΔTT,当T A=T B,且ΔT A=ΔT B时,由于P B>P A,根据ΔP=PΔTT可知ΔP B>ΔP A,ℎ一定增大,故选项A错误,B正确;C.当T A<T B,且ΔT A<ΔT B时,由于P B>P A,根据ΔP=PΔTT可知不能判断ΔP B和ΔP A变化的大小,所以不能判断ℎ的变化情况,故选项C错误;D.当T A>T,且ΔT A=ΔT B时,由于P B>P A,根据ΔP=PΔTT可知ΔP B>ΔP A,ℎ一定增大,故选项D正确;3.下列叙述正确的是()A.温度升高,物体内每个分子的热运动速率都增大B.气体压强越大,气体分子的平均动能就越大C.在绝热过程中外界对气体做功,气体的内能必然增加D.自然界中进行的涉及热现象的宏观过程都具有方向性【答案】CDA.温度升高,气体分子的平均动能增大,但是个别分子运动速率可能减小,故A错误;B.温度是气体分子的平均动能变化的标志。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
N 4 (
m
3
)
2
e
mv 2 2kT
v
2
v
N
2kT
4
(
v
( v )2
)2 e vp
v
vp
vp
v p : v 1.41 :1.59
设 v vp
v v v p
v
பைடு நூலகம்
1.59 1.41
v
p
1.13v p
N
4
(vp
( v p )2
)2 e vp
0.13v p
N vp
f
(v
p
)
4
(m
2kT
)3 2
( 2kT m
)
e
m 2 kT
2 kT m
4
(
m
)1 2
e 2kT
(vP )N2 (vP )H2
( f (vP ))N2 ( f (vP ))H2
8. 设气体分子服从麦克斯韦速率分布律,v 代表平均速率,v p代
表最可几速率,v 为一固定的速率间隔,则速率在 v v
z 2d 2nv 2d 2 p 8kT p kT M T
3.一大气压下,27 C 时空气分子的平均动能是_1_._0_4__1_0__2_0 J____。
空气主要由氮气、氧气构成,可看作双原子分子。室温下振 动自由度未激活,分子的自由度为5,所以一个分子的平均 动能为:
5 kT 5 1.381023 300 1.041020 J 22
v 2 3kT v 8kT
m
m
三者均与压强无关,故仍有
v 2 485m/s
vp
2 v 2 396m/s 3
v 8 v 2 447m/s
3
vp
2kT m
6.某气体在温度T1时的分子最可几速率与在温度T2时的分子 方均根速率相等,则T1 / T2 =_______。这种气体在压强为p
时的密度为 ,此时它的分子方均根速率v2 __________ 。
vp
4 e1 0.13 10.8%
是恒定值,不随温度而变。
9. 真实气体在气缸内以温度 T1 等温膨胀,推动活塞作功,活 塞移动距离为L。若仅考虑分子占有体积去计算功,比不考 虑时为a( );若仅考虑分子之间存在作用力去计算功,比不考 虑时为b( )。
(a)大;(b)小;(c)一样。
可用范德瓦尔斯气体代表真实气体来粗略讨论分子体积及分子 间引力的影响。1mol范氏气体在Tl温度下等温膨胀,作功为:
所以分之间引力的影响是使作功减少。
V2 V1
10.在地面上竖立一根弯管,管的两端各连接一个盛水容器,弯 管和容器都是绝热的,设初始时两容器中的温度相同(都等于 T),管内充满温度为T的饱和水蒸汽。在考虑重力作用的情况 下,上述状态能否保持不变?为什么?如果发生变化,则最终状 态与上述状态的差别何在?
范围内的分子的百分率随着温度的增加将___减__少______ ,
速率在 vp到 v 之间的分子的百分率随着温度的增加将 ____不__变_______。
f (v)
T1 T2 T1
矩形面积减小
O v1 v v2 v
v
v1 v v2 v
根据麦克斯韦速率分布律,在任意速率区间 v ~ v v 内的
2
P
2r 2
n n0e kT n0e 2kT
R
N
TH
因
R
R 2r 2
N
0 n2rHdr 2Hn0
e 2kT rdr
4.有一个边长为10cm的立方体容器,内盛处于标准状态下的 He气,则单位时间内原子碰撞一个器壁面的次数的数量级为
(a)1020s1 (b)1026s1
(c )1032 s 1
单位时间内碰一个器壁面的分子数为:
1 nvA 1 pA 8RT 7.491025 / s
6
6 kT M
5.氧气在温度为27℃、压强为1个大气压时,分子的方均根 速率为485米/秒,那么在温度为27℃、压强为0.5个大气压 时,分子的方均根速率为________米/秒,分子的最可几速 率为________米/秒,分子的平均速率为______米/秒。
v 2 3kT v 8kT
m
m
vp
2kT m
2kT1 3kT2
m
m
T1 / T2 3 / 2
v 2 3kT 3nkT 3 p
m
nm
7.已知氮气分子的麦克斯韦速率分布曲线如图,试在该图上 定性画出相同温度下氢气分子的速率分布曲线。
f(v)
N2
H2
v
vp
2kT m
又 mN2 mH2
每个分子的质量同为,圆筒绕轴以恒角速度 旋转,桶内气
体的状态达到平衡后其温度为T,试求桶内气体分子的数密度
n的分布规律。(注:不考虑重力的影响。)
解:每个分子受的惯性离心力为 2r ,
其相应的势能变化规律为
d P 2rdr
选转轴上为势能的零点,则
0
P
d
P
r 2rdr
0
所以 所以
P
1 2r2
(
p
a Vm2
)(Vm
b)
RT
历届考题:
1.一定量的理想气体盛于容器中,则该气体分子热运动的平均 自由程仅决定于
(A)压强p
(B)体积V
(C)温度T
(D)分子的平均碰撞频率
v
z
1
2d
2n
1
2d 2N
/V
V
2d 2N
N不变
2. 在下面四种情况中,何种将一定能使理想气体分子平均碰撞 频率增大?
(a)增大压强,提高温度 (c)降低压强,提高温度 (b)增大压强,降低温度 (d)降低压强,保持温度不变
物理竞赛辅导
热学
基本公式:
气体动理论
参见张三惠《大学物理学》第二册《热学》第83页 特别注意:
1.平均碰撞频率 z 2d 2vn
2.平均自由程
1
2d
2n
kT
2d 2 p
3.玻耳兹曼分布率:平衡态下某状态区间(粒子能量
为E)的粒子数密度 n n0eE / kT
4. 范德瓦耳斯方程:
1mol气体 5. 输运过程
解:在重力作用下,上述状态不能保持不 变。 因为在重力作用下,气体平衡条件要求压 强随高度而减小,而上端容器中水与蒸汽 平衡要求上端容器中蒸汽压为pT(温度为T 时的饱和蒸汽压),同样,下端容器中水 汽平衡要求下容器中蒸汽压亦为pT,这三 个条件不能同时成立。最终状态下水将完 全出现在下端容器中。
11. 如图所示,一半径为R高为H的圆筒内盛有N个气体分子,
A
V2 pdV
V1
( V2 RT1 V1 V b
a V2
)dV
RT1
ln
V2 V1
b b
a( 1 V2
1) V1
只考虑分子体积影响时,可取a=0,由于 lnV2 b lnV2 ,
所以分子体积的影响是使作功增加。
V1 b V1
只考虑分子之间引力的影响,可取b=0,由于 a( 1 1 ) 0 ,
