基于Matlab小波工具箱的数字图像处理及小波分析
Matlab中的小波变换与小波包分析方法详解

Matlab中的小波变换与小波包分析方法详解引言近年来,小波变换在信号处理领域中得到了广泛的应用。
小波变换是一种能够捕捉信号时频特性的有效工具,可以用来分析、压缩和去噪各种类型的信号。
本文将详细介绍Matlab中的小波变换和小波包分析方法,以帮助读者更好地理解和应用这一强大的信号处理技术。
一、小波变换(Wavelet Transform)小波变换是一种将信号分解成不同尺度的基函数的技术。
与传统的傅里叶变换相比,小波变换具有更好的时频局部化特性。
Matlab中提供了丰富的小波分析工具箱,可以方便地进行小波变换的计算。
1.1 小波基函数小波基函数是小波变换的基础。
不同类型的小波基函数适用于不同类型的信号。
在Matlab中,我们可以使用多种小波基函数,如Daubechies小波、Haar小波和Morlet小波等。
1.2 小波分解小波分解是指将信号分解成多个尺度的小波系数。
通过小波分解,我们可以获取信号在不同尺度上的时频特性。
Matlab中提供了方便的小波分解函数,例如'dwt'和'wavedec'。
1.3 小波重构小波重构是指根据小波系数重新构建原始信号。
通过小波重构,我们可以恢复原始信号的时域特性。
在Matlab中,可以使用'idwt'和'waverec'函数进行小波重构。
二、小波包分析(Wavelet Packet Analysis)小波包分析是对小波变换的进一步扩展,它允许对信号进行更精细的分解和重构。
小波包分析提供了一种更灵活的信号分析方法,能够获得更详细的时频特性。
2.1 小波包分解小波包分解是指将信号分解成具有不同频带的小波包系数。
与小波分解相比,小波包分解提供了更高的分辨率和更详细的频谱信息。
在Matlab中,可以使用'wavedec'函数进行小波包分解。
2.2 小波包重构小波包重构是根据小波包系数重新构建原始信号。
Matlab中的小波分析与多尺度处理方法

Matlab中的小波分析与多尺度处理方法一、引言Matlab是一款非常强大的数学软件,它提供了丰富的工具和函数库,方便用户进行各种数学分析和数据处理。
在Matlab中,小波分析和多尺度处理方法被广泛应用于信号处理、图像处理、模式识别等领域。
本文将介绍Matlab中的小波分析与多尺度处理方法的基本原理和应用。
二、小波分析的原理小波分析是一种基于函数变换的信号分析方法。
其基本原理是将信号分解成一系列不同尺度和频率的小波基函数,然后利用小波基函数对信号进行分析和重构。
Matlab提供了丰富的小波函数和工具箱,方便用户进行小波分析。
在Matlab中,小波函数使用wavedec进行信号分解,使用waverec进行信号重构。
用户只需指定小波基函数和分解的尺度,就可以对信号进行小波分析。
小波分析可以用于信号压缩、噪声滤波、特征提取等多个方面的应用。
三、多尺度处理方法的应用多尺度处理是一种基于信号的不同尺度特征进行分析和处理的方法。
在Matlab 中,多尺度处理方法有多种应用,下面将介绍几个常见的应用。
1. 周期信号分析周期信号是指具有明显周期性的信号。
在Matlab中,可以利用多尺度处理方法对周期信号进行分析和处理。
用户可以选择不同的尺度和频率范围对周期信号进行分解,提取出不同尺度下的周期特征。
这种方法可以用于周期信号的频谱分析、频率特征提取等。
2. 图像处理图像处理是多尺度处理方法的典型应用之一。
在Matlab中,可以利用小波变换对图像进行多尺度分解和重构。
通过选择不同的小波基函数和尺度,可以提取图像的纹理、边缘等特征。
这种方法在图像去噪、图像压缩等领域有广泛的应用。
3. 信号压缩信号压缩是多尺度处理方法的重要应用之一。
在Matlab中,可以利用小波变换对信号进行分解,然后根据信号的特征选择保留重要信息的分量进行压缩。
这种方法可以有效地减小信号的数据量,提高信号传输效率。
四、小波分析与多尺度处理方法的案例研究为了更好地理解Matlab中小波分析与多尺度处理方法的应用,下面将以一个案例研究为例进行说明。
Matlab中的小波变换与小波分析技术

Matlab中的小波变换与小波分析技术引言:小波变换(Wavelet Transform)是一种强大的信号分析技术,能够在时间与频率上同时提供信息。
与传统的傅里叶变换相比,小波变换可以应对非平稳信号,并在信号分析中提供更多的细节和局部特征。
在Matlab中,小波变换及其相关分析技术被广泛应用于各个领域,如图像处理、信号处理、数据压缩等。
本文将介绍Matlab中的小波变换与小波分析技术,并探讨其在实践中的应用。
一、小波变换的基本原理小波变换通过将信号与不同尺度和位移的小波基函数相乘,来获得信号在不同频率和时域上的表示。
与傅里叶变换可以提供整个频谱信息不同,小波变换能够提供信号的时间局部特征。
小波基函数具有紧凑支持,可以在时间和频率上实现局部化。
Matlab中提供了丰富的小波变换函数,如cwt、dwt、wt、swt等。
其中,cwt 函数实现了连续小波变换,dwt函数实现了离散小波变换,wt函数实现了小波变换的可视化分析,swt函数实现了离散小波变换的平移不变性。
二、小波变换的应用1. 图像处理小波变换在图像处理中具有广泛的应用。
通过对图像进行小波分解,可以将图像信号分解成不同频带的小波系数。
这些小波系数包含了图像的细节和轮廓信息,可以用于图像去噪、边缘检测、纹理分析等。
在Matlab中,可以使用wavedec2函数对图像进行二维小波分解,然后使用wrcoef函数对分解得到的小波系数进行重构,实现图像的去噪和增强等操作。
2. 信号处理小波变换在信号处理中也有广泛的应用。
通过对信号进行小波分解,可以将信号分解成不同频带的小波系数。
这些小波系数可以用于信号去噪、特征提取、模式识别等。
在Matlab中,可以使用dwt函数对信号进行离散小波分解,然后使用idwt函数对分解得到的小波系数进行重构,实现信号的去噪和分析等操作。
3. 数据压缩小波变换在数据压缩领域被广泛应用。
通过对信号或图像进行小波分解,可以将信号或图像的能量在频域上进行稀疏表示,然后通过舍弃部分系数进行数据压缩。
MATLAB环境下小波变换处理图像设计

tl ’ ie 第二次压缩 图像 ’ t( ) ;
程 序 2 基 于 二 维 小 波 分 析 的 图 像 边 缘提 取程 序 :
c e ral l a l ;
作 者 简 介 :张 俊 , , 南 开 封 人 , 科 , 理 工 程 师 。 主 要研 究 方 向 : 算 机 应 用 。 女 河 本 助 计
边缘提取 。一个 图像作小波分解后 , 可得 到… 系列不 同分辨率
的子 图像 , 同 分 辨 率 的 子 图像 对应 的频 率 是 不 相 同 的 。高 分 不 辨 率 ( 高 频 ) 图像 上 大 部 分 点 部 接 近 于 0 越 是 高 频 这 种 现 即 子 , 象 越 明 显 。对 一 个 图像 来 说 , 现 图 像 最 主要 的部 分 是低 频 部 表 分 , 以 一 个 最 简 单 的压 缩 方 法 是 利用 小 波 分 解 , 掉 图像 的 所 去
C= { R
lo 。 <。 d ( JI ‘ )J
h = ro f( ,Ssm8 1; lw ce2 C ,y ’) h ,’ , v = rof( c ,y ’) lw ce2V,Ssm8 1; ,’ , d -vce2 ,Ssm8 1; l rof( c ,y ’)  ̄ d , , c=a,l l 1; l [l ; , ] h vd sb l (2 )maec) u po 2 2; g (1; t i
c 2 . c 2; a =025 a
高频部分而只保 留低频部分 。 程序 1基于二维小波分析 的图像压缩处理程序 :
cc; l
sb lt 2 )maec2; lr pga(5 ) upo( 4; g(a) ooma(r 2 6) 2 i c y ;
a ss ua e; xi q r
Matlab基于小波变换的图形图像处理

Matlab基于小波变换的图形图像处理刘鹏远;骆升平【摘要】小波分析是当前数学中一个迅速发展的新领域,在Madab中,图像的增强、除噪、压缩是其应用领域中的一个方面.文中首先介绍了小波分析的历史与现状,然后详细地说明了当前小波分析在图像方面的各个应用领域和研究的意义,以及其研究工具Madab组成和特点,从理论上讲解了小波变换的由来、定义和特点,在分析中所涉及到的连续小波变换、离散小波变换、二维小波变换.通过小波分析的理论研究,应用Madab来实现了一般图像的压缩、除噪和增强,然后利用小波分析的工具箱打开图形接口方式,来实现相关小波分析的应用.由于小波分析在图像中有许多的优点,因此小波分析在各个应用领域也越来越广.%The issue of wavelet analysis is fast -developing in maths. The history and current situations of the wavelet analysis are introduced in the article, as well as its application and significance. Then the origin, definition and characteristics of the wavelet transform are stated. For continuous wavelet transform, discrete wavelet transform and two-dimensional wavelet transform, the wavelet analysis theory and Matlab are taken to achieve image compression, denoising and enhancement. The wavelet analysis toolbox is adopted to open graphics interface to realize the relevant application. Owning many advantages in the field of image compressing, wavelet analysis is being used in more and more areas.【期刊名称】《江西理工大学学报》【年(卷),期】2011(032)001【总页数】3页(P66-68)【关键词】小波分析;小波变换;图形接口方式;Matlab【作者】刘鹏远;骆升平【作者单位】中山职业技术学院计算机工程系,广东,中山,528404;北京赛四达科技有限公司,北京,100029【正文语种】中文【中图分类】TP391.41Abstract:The issue of wavelet analysis is fast-developing in maths.The history and current situations of the wavelet analysis are introduced in the article,as well as its application and significance.Then the origin,definition and characteristics of the wavelet transform are stated.For continuous wavelet transform,discrete wavelet transform and two-dimensional wavelet transform,the wavelet analysis theory and Matlab are taken to achieve image compression,denoising and enhancement.The wavelet analysis toolbox is adopted to open graphics interface to realize the relevant application.Owning many advantages in the field of image compressing,wavelet analysis is being used in more and more areas.Key word:wavelet analysis;wavelet transform;graphical interface;Matlab Matlab是由Math works公司开发的一种主要用于数值计算及可视化图形处理的工程语言.它将数值分析、矩阵计算、图形图像处理、信号处理和仿真等诸多强大的功能集成在较易使用的交互式计算机环境之中,为科学研究、工程应用提供了一种功能强、效率高的编程工具[1-3].Matlab名字由Matrix(矩阵)和Laboratory(实验室)两词的前三个字母组合而成.20世纪70年代后期时任美国新墨西哥大学计算机科学系主任的Clever Moler博士和他的同事构思并为学生设计了一组调用LINPACK和EISPACK库程序的“通俗易用”的接口,此即为用FORTRAN编写的萌芽状态的Matlab.以后几年,Matlab作为免费软件在大学里使用,深受大学生们的喜爱[1-3].Matlab产品族由大量不同功能的产品系列组成:(1)Matlab.它集计算、可视化及编程于一身.在Matlab中,无论是问题的提出还是结果的表达都采用人们习惯的数学描述方法,而不需要用传统的编程语言进行前后处理.这一特点使Matlab成为了数学分析、算法开发及应用程序开发的良好环境.Matlab是Math works产品家族中所有产品的基础.(2)Matlab Toolbox.为了支持不同的专业领域的用户,Matlab还提供了大量的面向专业领域的工具箱.以往开发复杂的编程算法需要花费很长的时间才能完成,而且调试需要花费更多的时间.而使用Matlab语言和Matlab工具箱,用户可以专注于算法研究,编程只需要几行就可以完成,而且可以很快地画出图形,从而迅速地进行多种算法的比较,从中找出最好的方案.Matlab工具箱中的大多数函数都是通过M文件编写的,用户可以察看其中的源码,通过适当的修改,便可以形成自己的特殊算法.(3)Matlab compiler.利用Matlab compiler可以从M文件自动产生优化C代码.通过将Matlab代码转换为C或C++,编译器可以有效地加快Matlab应用程序的开发速度和应用程序的运行速度.(4)Simulink.它是用来建模、分析和仿真各种动态系统的交互环境,包括连续系统、离散系统和混杂系统.Simulink提供了采用鼠标拖放的方法建立系统框图模型,不需要书写一行代码.Simulink还支持Stateflow,用来仿真事件驱动过程.(5)Stateflow.它提供了图形工具,帮助用户设计和分析事件驱动系统.Stateflow基于有限状态机理论,能够建立和仿真复杂的反应和事件驱动系统.这样,Simulink的用户可以在他们的模型之中描述事件驱动行为.通过Simulink和Stateflow可以在统一的环境下设计、建立和仿真整个嵌入式系统的行为. (6)Real-time Workshop.它直接将 Simulink,Stateflow,DSP Blockset和Communication Blockset建立的模型自动生成代码(若模型包含Stateflow图时还需要有 Stateflow Coder).通过 Real-Time Workshop,能够为嵌入式控制系统和DSP应用速度生成C代码.它支持连续时间、离散时间和混杂系统,带触发使能的子系统,带事件驱动行为的系统.(7)Simulink模块库.作为Simulink建模系统的补充,Math Works公司开发了专用功能块程序包.如DSP Blockset和Communication Blockset等.通过使用这些程序包,用户可以迅速地对系统进行建模与仿真.更重要的是用户还可以对系统模型进行代码生成,并将生成的代码下载到不同的目标机上.二维离散小波变换函数.二维离散小波变换是将二维图像在不同的尺度上进行分解,分解的结果为:近似分量cA、水平细节分量cH、垂直细节分量cV和对角细节分量cD.反之,可以利用二维小波分解的结果在不同尺度上重构图像.(1)Dwt2函数和Idwt2函数.Dwt2函数为一层二维离散小波分解.(2)Wavedec2函数和Waverec2函数.Wavedec2函数为多层二维离散小波分解.(3)Dwtmode函数.Dwtmode函数设置离散小波变换信号(图像)的扩展模式,扩展模式表示处理分析边界变形问题的不同方法.(4)Appcoef2函数和Detcoef2函数.Appceof2函数用来提取二维信号小波分解的近似系数.(5)Wrcoef2函数和Upcoef2函数.Wrcoef2函数从多层二维小波分解细节系数重构某一层信号.(6)Upwlev2函数.Upwlev2函数实现二维小波分解的单层重构.(7)Wenergy2函数.函数计算二维小波分解的能量.(8)Wcodemat函数.Wcodemat函数为扩展的伪彩色矩阵比例.(9)Wfilters函数.Wfilters函数设计小波滤波器.(10)Swt2函数和Iswt2函数.Swt2函数计算离散二维平稳小波变换.(11)Wpdec2函数和Wprec2函数.这两个函数是二维小波包变换分析函数.Wpdec2函数实现小波包分解,Wprec2函数实现小波包重构.二维离散小波分析——图形接口方式:(1)启动二维离散小波分析图形工具.小波工具箱主菜单中选择Wavelet2-D,出现二维离散小波分析图形工具.(2)装载信号.单击[File]→[Load signal]菜单命令,选择MATLAB的文件. (3)分析图像.在图中的右上角选择基本小波为bior3.7和尺度数Level为2.选择好以上参数后,就可以单击[Analyze]按钮.进行相关的操作[4].图像增强问题描述.图像经二维小波分解后,图像的轮廓主要体现在低频部分,而细节部分则体现在高频部分,因此,通过对低频分解系数进行增强处理,对高频分解系数进行衰减处理,即可以达到图像增强的作用[5].小波增强实例.load woman;subplot(121);image(X);colormap(map);title('原始图像');%画出原图像[c,s]=wavedec2(X,2,'sym4');%进行两层小波分解len=length(c);%处理分解系数,突出轮廓,弱化细节for I=1:lenif(c(I)>350)c(I)=2*c(I);elsec(I)=0.5*c(I);endendnx=waverec2(c,s,'sym4');%分解系数重构subplot(122);image(nx);title('增强图像')%画出增强图像代码运行如图1所示.小波除噪与压缩函数.(1)Ddencmp函数.函数用于求除噪或压缩的缺省值.(2)Thselect函数.函数用于除噪阀值选择.(3)Wdencmp函数.Wdencmp函数用小波进行降噪或压缩.(4)Wpdencmp函数.Wpdencmp函数利用小波包进行图像的除噪或压缩. (5)Wpthcoef函数.Wpthcoef函数计算小波小波包系数阀值话.(6)Wthcoef2函数.Wthcoef2函数计算二维小波系数阀值化(一维为wthceof函数).(7)Wthresh函数.Wthresh函数设置软硬阀值.Matlab实现小波变换压缩.将小波分析引入图像压缩的范畴也是一个重要的手段,并且有着它自己的特点.小波变换压缩的特点在于压缩比高、压缩速度快,压缩后能保持信号与图像的特征基本不变,且在传输过程中可以抗干扰等等.一个图像作小波分解后,可得到一系列不同分辨率的子图像,不同分辨率的子图像对应的频率是不相同的.高分辨率(高频)子图像上大部分点的数值都接近于0,分辨率越高越明显.而对于一个图像来说,表现图像的最主要的部分是低频部分,所以最简单的压缩方法是利用小波分解去掉图像的高频部分而只保留低频部分[6]. 小波图像分析总结.由于近年来小波技术越来越多在用于图像处理技术中,而图像的增强、去噪、压缩等更是其中的重点,Matlab就是其有效的工具.不管是对图像的增强、去噪、压缩来说,其原理基本上都是一样,都是利用小波分析的方法(即小波变换),首先是要对图像进行层分解提取分解的低频和高频系数,然后对其各频率(竖直、水平、斜向)进行重构或弱化细节部分,突出近似部分.由于在编程环境下有许多地方需要值得改进,而利用其工具箱具有独特的优点,能实现许多功能,能够更好的满足用户的需要[7-8].小波图像分析展望:近年来,Matlab在各个领域应用中越来越广泛,而小波分析又是基于Matlab的,其强大的工具箱也是实现各种图像变换的基础,由于Matlab本身的优点是效率高、使用方便、扩充的能力强、绘图又很方便.因此,在今后几年内,基于Matlab的各种图像分析技术将会越来越成熟,其应用领域也会越来越广泛.【相关文献】[1]张志涌.精通Matlab6.5版[M].北京:航空航天大学出版社,2003.[2]张兆礼.现代图像处理技术及Matlab实现[M].北京:人民邮电出版社,2001.[3]王家文,曹宇.Matlab6.5图形图像处理[M].北京:国防工业出版社,2004.[4]秦前清,杨宗凯.实用小波分析技术[M].西安:西安电子科技大学出版社,1994.[5]程正兴.小波分析算法与应用[M].西安:西安交通大学出版社,1998.[6]邱庚香,陈德海.基于小波变换的信号去噪应用[J].江西理工大学学报,2003,24(4):13.[7]James H McClellan,Sidncy C Burrus,Alan V puter-Based Exercises for Signal Processing Using Matlab 5-1st ed[M].USA:Prentice Hall,1997.[8]Patrick Marchand.Graphics and GUIs with Matlab-Third Edition[M].USA:CRC Press,2003.。
小波分析MATLAB工具箱简介

小波分析MATLAB工具箱简介MATLAB的小波分析一、小波分析用于降噪的基本过程1、分解过程:选定一种小波,对信号进行N层分解;2、作用阈值过程:对分解得到的各层系数选择一个阈值,并对细节系数进行软阈值处理;3、重建过程:降处理后的系数通过小波重建恢复原始信号;二、基本降噪模型函数一维离散小波分解命令Dwt [cA cD] = dwt(X,’wname’)使用小波’wname’对型号X 进行单层分解,求得的近似系数存放于数组cA中,细节系数存放在数组cD 中;[cA cD] = dwt(X,’wname’,’mode’,MODE) 利用MODE方式进行扩展[cA cD] = dwt(X,Lo_D,Hi_D) 利用指定滤波器进行小波分解Wanedec [C, L] = wavedec(X,N,’wname’) 使用wname的小波进行N层分解,C为层数,L为各层系数Idwt X= idwt(cA,cD,’wname’) 利用小波wname把近似系数CA和CD重建为上一层近似系数XX= idwt(cA,cD,’wname’,L) 重建至L层Waverec X= waverec(C,L,‘wname‘)重建为原始信号Wrcoef X = wrcoef(‘type’,C,L,’wname’,N) 通过分解系数重构指定的数,type为a 或者dX= wrcoef(‘type’,C,L,’wname’) 把分解系数重建至最高层Upcoef Y= upcoef(O,X,’wname’,N)用适当的滤波器作用在X上N次,求得重建系数Y,O为a表示低通滤波器,d表示高通滤波器Detcofe D= detcoef(C,L,N)从分解系数中提取第N层近似系数D= detcoef(C,L,N)提取至最后一层Appcoef A= appcoef(C,L,’wname’,N) 用小波从分解系数中提取第N层系数Wnoisest stdc = woisest(c,l,s)根据传入的小波分解系数[c,l]对s中标识的小波层数求得其标准差,作为对噪声强度的估计;Ddencmp [THR,SORH,KEEPAPP,CRIT] = ddencmp(IN1,IN2,X) 根据传入的参数IN1 和IN2所指定的方式,对输入信号X求得其降噪或压缩的各级阈值。
matlab小波工具箱小波分析步骤
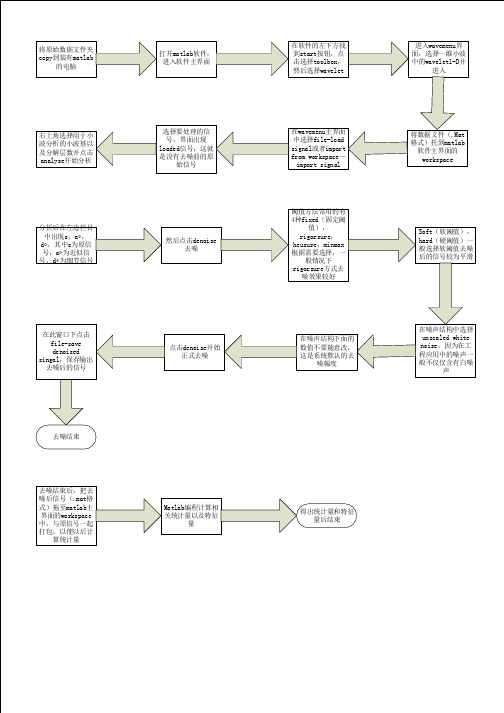
选择要处理的信 号,界面出现 loaded信号,这就 是没有去噪前的原 始信号
在wavemenu主界面 中选择file-load signal或者import from workspace— import signal
将数据文件(.Mat 格式)托到matlab 软件主界面的 workspace
分析后在左边栏目 中出现s,a*, d*,其中s为原信 号,a*为近似信 号,d*为细节信号
点击denoise开始 正式去噪
在噪声结构下面的 数值不要随意改, 这是系统默认的去 噪幅度
在噪声结构中选择 unscaled white noise,因为在工 程应用中的噪声一 般不仅仅含有白噪 声
去噪结束
去噪结束后,把去 噪后信号(.mat格 式)拖至matlab主 界面的workspace 中,与原信号一起 打包,以便以后计 算统计量
Matlab编程计算相 关统计量以及特征 量
得出统计量和特征 量后结束
将原始数据文件夹 copy到装有matlab 的电脑
打开matlab软件, 进入软件主界面
在软件的左下方找 到start按钮,点 击选择toolbox, 然后选择wavelet
Hale Waihona Puke 进入wavemenu界 面,选择一维小波 中的wavelet1-D并 进入
右上角选择用于小 波分析的小波基以 及分解层数并点击 analyse开始分析
然后点击denoise 去噪
阈值方法常用的有 4种fixed(固定阈 值), rigorsure, heusure,minmax 根据需要选择,一 般情况下 rigorsure方式去 噪效果较好
Soft(软阈值), hard(硬阈值)一 般选择软阈值去噪 后的信号较为平滑
小波分析MATLAB实例

小波分析MATLAB实例小波分析是一种信号处理方法,可以用于信号的时频分析和多尺度分析。
在MATLAB中,可以使用Wavelet Toolbox实现小波分析。
这个工具箱提供了丰富的函数和工具,可以方便地进行小波分析的计算和可视化。
小波分析的核心是小波变换,它将信号分解成一组不同尺度和频率的小波基函数。
在MATLAB中,可以使用`cwt`函数进行连续小波变换。
以下是一个小波分析的MATLAB实例,用于分析一个心电图信号的时频特性。
首先,导入心电图信号数据。
假设心电图数据保存在一个名为`ecg_signal.mat`的文件中,包含一个名为`ecg`的变量。
可以使用`load`函数加载这个数据。
```MATLABload('ecg_signal.mat');```接下来,设置小波变换的参数。
选择一个小波基函数和一组尺度。
这里选择Morlet小波作为小波基函数,选择一组从1到64的尺度。
可以使用`wavelet`函数创建一个小波对象,并使用`scal2frq`函数将尺度转换为频率。
```MATLABwavelet_name = 'morl'; % 选择Morlet小波作为小波基函数scales = 1:64; % 选择1到64的尺度wavelet_obj = wavelet(wavelet_name);scales_freq = scal2frq(scales, wavelet_name, 1);```然后,使用`cwt`函数进行小波变换,得到信号在不同尺度和频率下的小波系数。
将小波系数的幅度平方得到信号的能量谱密度。
```MATLAB[wt, f] = cwt(ecg, scales, wavelet_name);energy = abs(wt).^2;``````MATLABimagesc(1:length(ecg), scales_freq, energy);colormap('jet');xlabel('时间(样本)');ylabel('频率(Hz)');```运行整个脚本之后,就可以得到心电图信号的时频图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
k k ,2/)]2(t ψ1+⊃j j V V图2.2 Mallat重构示意图三、常用小波函数介绍在小波分析理论在数学和工程领域中一个很重要的问题就是小波基的选择,选择一个最优的小波基,可以使图像处理更加优化。
在小波分析理论中有很多种的小波函数,下面介绍一些常用的小波基函数:3.1 Haar小波Haar小波是Haar于1990年提出的一种正交小波,它是小波理论分析发展过程中最早用到的的小波。
Haar小波是由一组互相正交归一的函数集,即Haar函数衍生产生的,是具有紧支撑的正交小波函数,其定义如下[5]:1012()1121tt tψ≤≤⎧⎪=-≤≤⎨⎪⎩其他(3.1)Haar小波是一个最简单的时域不连续的小波,它类似一个阶梯函数,由于它的紧支撑性和正交性,使得Haar小波的应用很普遍。
图3-1所示为Haar波的函数图像。
图3-1 Haar小波函数图像由于Haar小波在时域上是不连续的,所以作为基本小波性能不是特别好。
但也有自己的优点:①计算简单;②在2ja=的多分辨率系统中Haar小波构成一组最简单的正交归一的小波族。
因为()tψ不但与(2),()j t j Zψ∈正交,而且与自己的整数位移正交。
③()tψ的傅里叶变换是:24()sin()2j e jaψΩΩ=-ΩΩ(3.2)3.2Mexican hat(墨西哥草帽)小波Mexican Hat 小波又被称Marr 小波。
Marr 小波函数就是高斯函数的二阶导数,其表达式为:222()(1)t t t e ψ-=- (3.3)222()2e ωψωπω= (3.4)因为它的形状像墨西哥帽的截面,所以也称为墨西哥帽函数。
墨西哥帽函数在时间域与频率域都有很好的局部化,并且满足0)(=⎰∞∞-dx x ψ (3.5)由于它的尺度函数不存在,所以不具有正交性。
其波形如图3-2所示。
Marr 小波的时域、频域都有很好的局部特性,但由于它的正交性尺度函数不存在,所以不具有正交性,主要用于信号处理和边缘检测。
图3-2 Mexicat 小波函数图像3.3Morlet 小波Morlet 小波是高斯下的单频率复正弦函数:22()jwt t t e e ψ-=⋅ (3.5)式中,j 表示虚数,ω常数。
其波形如图3-3所示。
虽然Morlet 小波有解析表达式,但其不具有正交性的同时也不存在紧支集。
Morlet 小波的特点是能够提取信号中的幅值和相应信息,广泛应用于地球物理信号处理中。
图3-3 Morlet 小波函数图像3.4Daubechies(dbN)小波Daubechies 小波是法国学者Daubechies 所创造,Daubechies 小波的研究是基于对尺度取为2的整数幂条件下的小波变换。
Daubechies 小波无明确的解析方程(除N =1外),不具有对称性,可以由尺度函数求出。
但{}k h 的传递函数的模的平方有显式表达式。
假设∑-=+-=101)(N k k k N k y C y P ,其中,k N k C +-1为二项式的系数,则有)2(sin )2(cos )(2220ωωωP m N = (3.6)其中 ∑-=-=120021)(N k ik k e h m ωω Daubechies 小波是紧支集正交小波,它的出现使离散小波分析成为可能。
Daubechies 系列的小波简写为dbN ,其中N 表示阶数,图3-4所示为db2小波的形状。
(a)db2小波函数 (b )db2的尺度函数图3-4 db2的小波函数和尺度函数3.5 Meyer小波Meyer小波的小波函数ψ(x)是在频域中进行定义的,Meyer小波是具有紧支撑的正交小波。
122122324(2)sin((||1)),[,]2233348()(2)cos((||1)),[,]2233280,||[,]33jje v x xx e v x xxωωππππππππψππππ-∧-⎧-∈⎪⎪⎪=-∈⎨⎪⎪∉⎪⎩(3.7)其中()v为构造Meyer小波的辅助函数,其函数图像如图3-5所示。
(a) Meyer小波函数(b)Meyer尺度函数图3-5 Meyer小波函数和尺度函数四、小波分析在图像处理中的应用4.1 基于小波分析的图像压缩二维小波分析用于图像压缩是小波分析应用的一个重要方面。
它的特点是压缩比高,压缩速度快,压缩后能保持图像的特征基本不变,且在传递过程中可以抗干扰。
小波分析用于图像压缩具有明显的优点[6]。
基于小波分析的图像压缩方法很多,比较成功的有小波包、小波变换零树压缩、小波变换矢量量化压缩等。
下面是一幅图像信号(即二维信号),利用二维小波分析对图像进行压缩。
一幅图像作小波分解后,可得到一系列不同分辨率的子图像,不同分辨率的子图像对应的频率是不相同的。
高分辨率(即高频)子图像上大部分点的数值都接近于0,越是高频,这种现象越明显。
对一幅图像来说,表现一个图像最主要的部分是低频部分,所以最简单的压缩方法是利用小波分解,去掉图像的高频部分而只保留低频部分。
利用MATLAB中的小波分析工具箱中某个小波函数对图像进行压缩处理,本实验利用二维小波函数“sym4“对图像进行压缩。
图4-1 小波工具箱如图4-1所示,可以看出,第一次压缩提取的是原始图像中小波分解第一层的低频信息,此时压缩效果较好,压缩比较小;第二次压缩是提取第一层分解低频部分的低频部分(即小波分解第二层的低频部分),其压缩比较大,压缩效果在视觉上表现良好,基本上看不出与第一次有太大变化。
但是第三次压缩和第四次压缩就有明显差异,看起来已经比较模糊了。
这种最简单的压缩方法,只保留原始图像中低频信息,不经过其他处理即可获得较好的压缩效果。
我们还可以继续对图像进行压缩,以提取其低频信息。
从理论上说,可以获得任意压缩比的压缩图像]3[。
(a)原始图像(b)分解后低频和高频信息(c)第一次压缩图像 (d)第二次压缩图像(e)第三次压缩图像 (f)第四次压缩图像图4-2 利用二维小波“sym4“压缩的图像 4.2基于小波分析的图像去噪处理噪声可以理解为妨碍人的视觉器官或系统传感器对所接收图像源进行理解或分析的各种因素。
一般噪声是不可预测的随机信号,它只能用概率统计的方法去认识。
噪声对图像处理十分重要,它影响图像处理的输入、采集、处理的各个环节以及输出结果的全过程。
若输入伴有较大噪声,必然影响处理全过程及输出结果。
因此一个良好的图像处理系统,不论是模拟处理还是计算机处理无不把减少最前一级的噪声作为主攻目标。
去噪已成为图像处理中极其重要的步骤。
对二维图像信号的去噪方法同样适用于一维信号,尤其是对于几何图像更适合。
二维模型可以表述为:,,,,0,1,...,1i j i j i j i j m σ⋅=-s()=f()+e() (4.1)其中,(,)e i j 是噪声。
二维信号用二维小波分析的去噪步骤有3步:(1)二维信号的小波分解。
选择一个小波和小波分解的层次N ,然后计算信号s 到第N 层的分解。
(2)对高频系数进行阈值量化。
对于从1到N的每一层,选择一个阈值,并对这一层的高频系数进行软阈值量化处理。
(3)二维小波的重构。
根据小波分解的第N层的低频系数和经过修改的从第一层到第N层的各层高频系数计算二维信号的小波重构。
下面给出一幅含有噪声的图像,利用小波分析“db2“函数对信号进行去噪处理。
如图4-2所示。
(a)原始图像(b)第一次去噪后的图像(c)第二次去噪后的图像图4-3 利用小波函数”db2”对图像进行去噪从图中可以观察到第一次去噪已经滤去了大部分的高频噪声,但对比去噪图像与原始图像相比可以看出,第一次去噪后的图像中还是含有不少的高频噪声;第二次去噪是在第一次去噪的基础上,再次滤去其中的高频噪声。
五、总结通过对多分辨率分析和Mallat算法的学习以及常用小波的认识,了解到了小波分析在分析数学领域的地位以及其在数字图像处理和信号处理等方面重要性。
可以利用MATLAB中的小波函数对图像进行压缩、去噪、增强以及锐化等处理。
更为简单地就是利用MATLAB中小波处理工具箱,对图像进行增强、去噪等处理。
小波的应用围非常广泛,而每个领域都有自己特定的处理方式。
小波分析的应用是与小波分析的理论研究紧密地结合在一起的。
现在,它在科技信息领域取已经得了令人瞩目的成就。
对性质随时间稳定不变的信号,处理的理想工具仍然是傅立叶分析,但在实际应用中,绝大多数信号是非稳定的,小波分析正是适用于非稳定信号的处理工具。
图像处理的针对性很强,因此选择合适的小波处理图像是比较好的处理方法。
参考文献。
