湖南大学信息论与纠错编码
信息论课程讲义-第五章 纠错编码原理
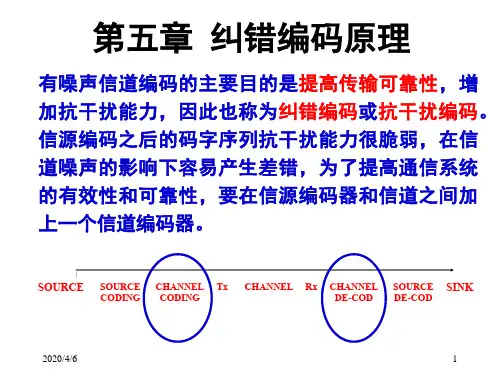
p(yj/x1),p(yj/x2),……,p(yj/xn)
中的最大者，则我们就将yj译成x*，这种译码方法称 为“最大似然译码准则”。
最大似然译码准则利用了信道转移概率，而不用后
验概率，将更方便。
p( x*
/
yj)
p(x* ) p( y j / p( y j )
x )
2020/4/6
15
这时的最小平均错误译码概率为：
因为：p(xi,yj)=p(xi)p(yj/xi); 而p(yj)可以由p(xi,yj)的(i=1,2, …,n)求和得到。
因此，在这种情况下，平均错误译码概率只与 译码准则有关了。通过选择译码准则可以使平 均译码概率达到最小值。
2020/4/6
10
m
m
Pe p( y j )P{e / y j} p( y j ){1 P[F( y j ) xi / y j ]}
2. 虽然Pe与译码准则有关，但无论什么准则 该不等式都成立。
3. 当信源和信道确定后，信道疑义度给定了 译码错误概率的下限。
2020/4/6
22
H(X/Y)
logn log(n-1)
2020/4/6
H(Pe)+Pelog(n-1)
Pe
(n-1)/n 1
23
5.2 信道编码基本概念
5.2.1 信道编码定理
0 p=3/4
1-p=1/4 0
p=3/4
1
2020/4/6
1-p=1/4
1
5
⑵译码准则
设一个有噪声离散信道，输入符号集X，输出符号集Y， 信道转移概率为P(Y/X);
X
p(yj/xi)
Y
X:{x1,x2,…..,xn}。 Y:{y1,y2,……ym} P(Y/X):{p(yj/xi); i=1,2,…n; j=1,2,…m
信息论与编码原理课程实验
《信息论与编码》课程实验湖南大学计算机与通信学院2010年5月1日目录课程实验大纲 (3)实验一信道容量的迭代算法程序设计 (4)实验二唯一可译码判决准则 (9)实验三 Huffman 编码方案程序设计 (15)实验四 LZW编码方案程序设计 (20)实验五Shanoon编码方案程序设计 (23)实验六循环码的软件编、译码实验 (27)实验七BCH码最大似然译码器设计 (31)课程实验大纲实验一 信道容量的迭代算法程序设计一、实验目的（1）进一步熟悉信道容量的迭代算法；（2）学习如何将复杂的公式转化为程序；（3）掌握C 语言数值计算程序的设计和调试技术。
二、实验要求（1）已知：信源符号个数r 、信宿符号个数s 、信道转移概率矩阵P 。
（2）输入：任意的一个信道转移概率矩阵。
信源符号个数、信宿符号个数和每个具体的转移概率在运行时从键盘输入。
（3）输出：最佳信源分布P*，信道容量C 。
三、信道容量迭代算法1：procedure CHANNEL CAPACITY(r,s,(jip ))2：initialize:信源分布ip =1/r ，相对误差门限σ，C=—∞4：5：6：C2211log [exp(log )]rsji ij r j p φ==∑∑7：until C Cσ∆≤8：output P*=()i rp ,C9：end procedure-------------------------------------------------------------------------------------------------------四、参考代码/*********************************************************************Author: Hop Lee *Date : 2003.06.25 *Copyright: GPLPurpose: Caculate the capacity of a given channel*********************************************************************/#include<stdio.h> #include<math.h> #include<stdlib.h> #include<unistd.h> #include<values.h>#define DELTA 1e -6 /* delta,the threshold */int main( void) {register int i,j; register int k;21211exp(log )exp(log )sji ij j r sjiij r j p pφφ===∑∑∑ip 1i jiri jii p p p p=∑ijφfloat *p_i=NULL;float **p_ji=NULL;float **phi_ij=ij=NULL;float C,C_pre,validate;float * sum=NULL;float p_j;/*Read the number of input symbol:r,* and the mumber of output symbol:s*/fscanf(stdin,"%d",&r);fscanf(stdin,"%d",&s);/*Allocation memory for p_i,p_ji and phi_ij */p_i=(float *)calloc(r,sizeof(float));p_ji=(float **)calloc(r,sizeof(float));for(i=0;i<r;i++)p_ji[i]=(float *)calloc(s,sizeof(float));phi_ij=(float **)calloc(r,sizeof(float*));for(i=0;i<r;i++)phi_ij[i]=(float *)calloc(s,sizeof(float))/*Read the channel transition probability matrix p_ji */ for(i=0;i<r;i++)for(j=0;j<s;j++)fscanf(stdin,"%f",&p_ji[i][j]);/*Validate the input data */for(i=0;i<r;i++){validate=0.0;for(j=0;j<s;j++){validate +=p_ji[i][j];}if(fabs(validate -1.0)>DELTA){fprintf(stdout,"invalid input data.\n");exit(-1);}fprintf(stdout,”Starting..\n”);/*initialize the p_i and phi_ij*/for(i=0;i<r;i++){p_i[i]=1.0/(float)r;}/* initialize C and iteration counter :k,and temprory variable*/ C=-MAXFLOAT;/*MAXFLOAT was defined in<values.h>k=0;sum=(float *)calloc(r,sizeof(float));/*Start iterate*/do{k++;/* Calculate phi_ij(k) first */for(j=0;j<s;j++){p_j=0.0;for(i=0;i<r;i++)p_j+=p_i[i]*p_ji[i][j];if(fabs(p_j)>=DELTA)for(i=0;i<r;i++)phi_ij[i][j]=p_i[i]* phi_ji[i][j]/p_j;elsefor(i=0;i<r;i++)phi_ij[i][j]=0.0;}/*calculate p_i(k+1) then*/p_j=0.0;for(i=0;i<r;i++){sum[i]=0.0;for(j=0;j<s;j++){/* prevent divided by zero*/if(fabs(phi_ij[i][j])>=DELTA)sum[i]+=p_ji[i][j]*log2( phi_ij[i][j])/ log2(2.0);}sum[i]=pow(2.0,sum[i]); p_j+=sum[i];}for(i=0;i<r;i++){p_i[i]=sum[i]/p_j;}/*and C(k+1)*/C_pre=C;C= log2(p_j)/ log2(2.0);}while(fabs(C-C_pre)/C>DELTA);free(sum);sum=NULL;/*Output the result*/fprint(stdout,”The iteration number is %d.\n\n”,k);fprint(stdout,”The capacity of the channel is %.6f bit/symbol.\n\n”,C); fprint(stdout,”The best input probability distribution is :\n”);for(i=0;i<r;i++)fprint(stdout,”%.6f”,p_i[i]);fprint(stdout,”\n”);/* Free the memory we allocation before with stack sequence*/for(i=s-1;i>=0;i--){free(phi_ij[i]);phi_ij[i]=NULL;}free(phi_ij);phi_ij=NULL;for(i=r-1;i>=0;i--){free(p_ji[i]);p_ji[i]=NULL;}free(p_ji);p_ji=NULL;free((p_i);p_i=NULL;exit(0);}实验二唯一可译码判决准则一、实验目的（1）进一步熟悉唯一可译码判决准则；（2）掌握C语言字符串处理程序的设计和调试技术。
信息论第9章 纠错编码资料
7
在通信中信源编码、信道编码与数据转换编码常常是同时使用的。
任何一位错误。
接收到序 列
译出序列
显然表中的译码方法不能同时 检测出二位错误。因为如果发生 二位错误，则译码器会错误的
000
0
001
0
把它作为一位错误而“纠正”了 所以r=2的重复码可以发现 二位错误或者纠正一位错误，
0
0
但二者不能兼得。
011
1
100
0
101
1
110
1
30
例2。如果用r=3的重复编码。该编码器实现 “0” “0000” ， “1” “1111”
12
13
其中分组码又可分循环码和非循环码： 循环码——该码书的特点是，若将其全部码字分成 若干组，则每组中任一码字中码元循环移位后仍是这 组的码字。 非循环码——任一码字中码元的循环移位后不一定 再是该码书中的码字 。 按照纠正错误类型可分为纠正随机错误码、纠正突发 错误码、纠正随机与突发错误码以及纠正同步错误码 等。
26
汉明重量
27
检错与纠错：
信道编码提供了对于信息传输发生差错的 控制能力。这种控制能力由编码器的纠错 能力与检错能力来表征。检错是指当信息 在信道上传输发生错误时，译码器能发现 传输有误，并及时的告诉接受者；而纠错 则是译码器能自动纠正这个错误的能力。 下面以重复码为例说明编码的纠错和检错 能力。
湖南大学信息论与编码试题二参考答案
课程名称：信息论与编码 使用班级：信息安全07级1-3班一、选择题（每题2分，共10分）1、A2、A3、A4、D5、A二、填空题（每空2分，共30分）1、可能 存在2、率失真 限失真信源编码定理3、条件4、齐次5、≥6、统计1、 7、突发 8、信息率失真函数 9、>, ≤10、差错 11、反馈重发、混合纠错三、(15分) 略四（20分）解：（1）()0.811H X =比特/符号………………………………………..（2分） 因为()()121210()()()()(0.250.75)01p y p y p x p x ⎛⎫== ⎪⎝⎭………..（2分） 所以()0.811H Y =比特/符号…………………………………………….（2分）（2）2221112(/)()(/)log (/)()(1,0)()(0,1)0..........................................i j i j i i j H Y X p x p y x p y x p x H p x H ===-=+=∑∑（2分） ()()(/)()0.811/H XY H X H Y X H X =+==比特符号……………… （2分） (/)()()0H X Y H XY H Y =-=………………………………………… （2分）（3）、(;)()(/)0.8100.81/IXY HX HX Y =-=-=比特符号…… （2分） （4）、因为信道容量()max(()(/))max ()1/i i p x p x C H Y H Y X H Y =-==（）比特符号 （4分） 所以改变信源的概率分布后，收到Y 后能获得的最大信息量为1比特/符号，此时信源的概率分布为等概率分布，即12()()0.5p x p x == 。
（2分）五（20分）解：（1）（3分）（2分） 信源熵：221()()log ()0.811/i i i H X p x p x ==-≈∑比特信源符号 平均码长：2111()111/44i i i K p x k ===⨯+⨯=∑码符号信源符号 （3分） 编码效率：()0.811H X Kη== （2分） 注：答案不唯一，其他答案适当给分（2）（3分） 41()1933127(1233)/21616161032i ii p k K L α===⨯⨯+⨯+⨯+⨯=∑码元信源符号（3分） 编码效率2()()()0.8110.96127/32log H X H X H X R K m Kη===≈≈…………………（2分） （3）由（1），（2）知道，对扩展信源（或信源序列）进行编码时，编码效率更高，并且对于变长编码，L 不需要很大就可以达到相当高的编码效率。
信息论与纠错编码题库 (1)
第三章 离散信源无失真编码3.2离散无记忆信源，熵为H[x]，对信源的L 长序列进行等长编码，码字是长为n 的D 进制符号串，问：（1）满足什么条件，可实现无失真编码。
（2）L 增大，编码效率 也会增大吗？ 解：（1）当log ()n D LH X ≥时，可实现无失真编码；（2）等长编码时，从总的趋势来说，增加L 可提高编码效率，且当L →∞时，1η→。
但不一定L 的每次增加都一定会使编码效率提高。
3.3变长编码定理指明，对信源进行变长编码，总可以找到一种惟一可译码，使码长n 满足D X H log )(≤n <D X H log )(+L 1,试问在n >D X H log )(+L1时，能否也找到惟一可译码？ 解：在n >D X H log )(+L1时，不能找到惟一可译码。
证明：假设在n >D X H log )(+L1时，能否也找到惟一可译码，则由变长编码定理当n 满足D X H log )(≤n <D X H log )(+L 1，总可以找到一种惟一可译码知：在n ≥DX H log )( ① 时，总可以找到一种惟一可译码。
由①式有：Ln ≥L X H )(logD ② 对于离散无记忆信源，有H(x)=LX H )( 代入式②得：n L≥ D x H log )(即在nL≥Dx H log )(时，总可以找到一种惟一可译码；而由定理给定熵H （X ）及有D 个元素的码符号集，构成惟一可译码，其平均码长满足D X H log )(≤n L <DX H log )(+1 两者矛盾，故假设不存在。
所以，在n >D X H log )(+L1时，不能找到惟一可译码。
3.7对一信源提供6种不同的编码方案：码1~码6，如表3-10所示信源消息 消息概率 码1 码2 码3 码4 码5 码6 u1 1/4 0 001 1 1 00 000 u2 1/4 10 010 10 01 01 001 U3 1/8 00 011 100 001 100 011 u4 1/8 11 100 1000 0001 101 100 u5 1/8 01 101 10000 00001 110 101 u6 1/16 001 110 100000 000001 1110 1110 u71/161111111000000000000111111111（1） 这些码中哪些是惟一可译码？ （2） 这些码中哪些是即时码？（3） 对所有唯一可译码求出其平均码长。
湘大信息论与编码试卷及答案
一、填空题（每空1分，共30分）（1）在现代通信系统中，信源编码主要用于解决信息传输中的有效性，信道编码主要用于解决信息传输中的可靠性，加密编码主要用于解决信息传输中的安全性。
（2）不可能事件的自信息量是____∞___,必然事件的自信息是0 。
（3）离散平稳无记忆信源X的N次扩展信源的熵等于离散信源X的熵的N倍。
（4）在信息处理中，随着处理级数的增加，输入和输出消息之间的平均互信息量会减少。
（5）若一离散无记忆信源的信源熵H（X）等于 2.5，对信源进行等长的无失真二进制编码，则编码长度至少为3 。
（6）假设每个消息的发出都是等概率的，四进制脉冲所含信息量是二进制脉冲的 2 倍。
（7）对于香农编码、费诺编码和霍夫曼编码，编码方法惟一的是香农编码。
霍夫曼编码方法构造的是最佳码。
（8）已知某线性分组码的最小汉明距离为3，那么这组码最多能检测出_2___个码元错误，最多能纠正___1__个码元错误。
（9）设有一个离散无记忆平稳信道，其信道容量为C，只要待传送的信息传输率R_小于_C（大于、小于或者等于），则存在一种编码，当输入序列长度n足够大，使译码错误概率任意小。
（10）平均错误概率不仅与信道本身的统计特性有关，还与_译码规则和编码方法有关（11）互信息I(X。
Y)与信息熵H(Y)的关系为：I(X。
Y)_小于__（大于、小于或者等于）H(Y)。
（12）克劳夫特不等式是唯一可译码__存在___的充要条件。
{00，01，10，11}是否是唯一可译码？___是____。
（13）差错控制的基本方式大致可以分为前向纠错、反馈重发和混合纠错。
（14）如果所有码字都配置在二进制码树的叶节点，则该码字为唯一可译码。
（15）设信道输入端的熵为H(X)，输出端的熵为H(Y)，该信道为无噪有损信道，则该信道的容量为 Max H（Y）。
（16）某离散无记忆信源X，其符号个数为n，则当信源符号呈等概_____分布情况下，信源熵取最大值___log（n）。
信息论与编码第八章纠错编码
•
内容提要
一、纠错码的基本概念 二、纠错编码的代数基础 三、线性分组码 四、循环码 五、卷积码
•
内容提要
➢ 一、纠错码的基本概念 二、纠错编码的代数基础 三、线性分组码 四、循环码 五、卷积码
•
1.信道纠错编码
•一、纠错码的基本概念
•
•一、纠错码的基本概念
011
0111010
100
1001110
101
1010011
110
1101001
111
1110100
•三、线性分组码
•
3. 线性分组码编码
生成矩阵和校验矩阵关系
•三、线性分组码
• 例题
•已知生成矩阵为
•求其校验矩阵H，如果将H作为生成矩阵，则所生成的码字是什么？
•由于 •G=[Ik Pk*(n-k)]
•
•三、线性分组码
1.分组码相关定义 •校验位和信息位
对于2k个n长码字全体构成的分组码 ，其码字中的k位称为信息位，n-k位 称为校验位或监督位。
消息序列 000
码字 0000000
例如，当k=3，n=7时，可能的消息序 列数m=2k=8个，可能的长为n=7的预 选序列有27=128个。具体如表：
•二、纠错编码的代数基础
•
1. 群
•二、纠错编码的代数基础
•
1. 群
•二、纠错编码的代数基础
•
1. 群
•二、纠错编码的代数基础
•
1. 群
•模p乘
令p为一个素数(例如p=2,3,5,7,11,…)
•二、纠错编码的代数基础
易验证模p乘法满足交换律和结合律，其单位元是1。G中任何元素i关 于模p乘法都有逆元。
信息论与编码纠错第7章
uˆ
信宿
模型突出了以控制差错为目的的纠错码编、译码器，因此也称为 差错控制系统。
2．差错控制系统的分类 按其纠错能力的不同可分为两种：检错码和纠错码。
⑴ 检错码：能发现错误但不能纠正错误的码； ⑵ 纠错码：不仅能发现错误而且还能纠正错误的码。
按差错控制系统类型，可分为前向纠错、重传反馈和混合纠错等三种方式。
一．信道纠错编码
近年来，随着计算机、卫星通信及高速数据网的飞速发展，数据的交 换、处理和存储技术得到了广泛的应用，人们对数据传输和存储系统的可 靠性提出了越来越高的要求。因此，如何控制差错、提高数据传输和存储 的可靠性，成为现代数字通信系统设计工作者面临的重要课题。
香农第二定理指出，当信息传输速率低于信道容量时，通过某种编译 码方法，就能使错误概率为任意小。目前已有了许多有效的编译码方法， 并形成了一门新的技术——纠错编码技术。
1．码的最小距离 码C中不同码字之间距离的最小值称码C的最小距离。
dmin min d (ci，cj) ci , cj C, i j
【例】（2，1）重复码
00
0
00
01 10
好好
好
11 好好好好
00
好好好好好好好好好 好 好 好 好 好 “ 00” 好 好 “ 11” 好 好 好 好 好
1
11
01 好 好 好
10
11
（2，1）重复码可以检出一个错误，但错误不能纠正。
（3，1）重复码
0
000
001 好 好
010
000 好 好 好 好 好 好
构成一个（n，n - 1）线性分组码：R = (n-1)/n
n2
n2
n1
由最后一个方程： cn1 ui cn1 ui 0 ci 0
信息论中的编码理论与纠错码
信息论中的编码理论与纠错码信息论是一门研究信息传输和处理的学科，它的核心是信息的编码与解码。
编码理论和纠错码是信息论中的重要内容，它们在保证信息传输可靠性和效率方面起着至关重要的作用。
一、编码理论的基本概念编码理论是指将信息转化为特定的编码形式，以便在传输和存储过程中能够更加高效地进行处理和传递。
编码理论的基本概念包括源编码和信道编码。
源编码是将信息源中的符号转化为编码序列的过程。
常见的源编码方法有霍夫曼编码、香农-费诺编码等。
这些编码方法通过对出现频率较高的符号进行较短的编码，从而提高信息的传输效率。
信道编码是为了提高信息传输在信道中的可靠性而进行的编码。
信道编码通过在发送端添加冗余信息，使得接收端能够在一定程度上纠正错误。
常见的信道编码方法有奇偶校验码、循环冗余校验码等。
二、纠错码的原理与应用纠错码是一种能够在传输过程中检测和纠正错误的编码方式。
它通过在发送端添加冗余信息，并在接收端利用这些冗余信息对接收到的信息进行纠错。
纠错码的原理是利用冗余信息进行错误检测和纠正。
常见的纠错码包括海明码、RS码等。
海明码通过在原始信息中添加冗余位，使得接收端能够检测到错误的位置，并进行纠正。
RS码则通过在原始信息中添加多余的校验位，使得接收端能够纠正一定数量的错误。
纠错码在通信领域中有着广泛的应用。
在无线通信中，由于信道的干扰和噪声，信息传输容易出现错误。
纠错码的应用可以提高信道传输的可靠性，保证信息的正确接收。
在存储介质中，纠错码也被广泛应用于磁盘、闪存等存储设备，以保证数据的完整性和可靠性。
三、编码理论与纠错码的发展编码理论和纠错码的发展经历了多个阶段。
早期的编码方法主要是基于统计学的方法，如霍夫曼编码。
随着信息论的发展，信息熵的概念被引入到编码理论中，使得编码方法更加高效和优化。
纠错码的发展也经历了多个阶段。
早期的纠错码主要是基于奇偶校验码的原理，但其纠错能力有限。
后来，海明码的提出使得纠错码的纠错能力得到了大幅提升。
信息论与编码纠错第5章
信道
y
信道译码器 xˆ
信源输出序列 u ，经信道编码器编成码字 x f (u) 并输入信
道，由于干扰，信道输出 y ，信道译码器对估值得 xˆ F ( y) 。
信息论与编码
1-p
【例】给定二元对称信道，信道固有错误概率为p（p < 0.5） 0
0 p
编码规则：为提高可靠性，每个信道符号重复三次发送。 1
原原原原原 1
0
0
0
信息论与编码
信源输出序列为：
u{1, 0, 1, 1}
信道输入序列为： x { 1 1 1 ,0 0 0 ,1 1 1 ,1 1 1 }
原原原原 1
0
1
1
原 原 原 111 原 原 原 111
000 111 111
p
p2
p3
001 001 000
原原原原原 1
0
0
0
由于p的存在，使得传输出错，故信道输出为：y { 1 1 1 ,0 0 1 ,0 0 1 ,0 0 0 }
离散无记忆二进制对称信道，固有误码率为p (p<0.5)，信源输出序列为三 位二进制数字。 编码规则：为提高传输效率，仅向信道发送一位，预先将信源输出序列进行择
多编码：信源输出的三位符号中有两位或3位是1，信源序列编码为1， 若三位符号中有两位或3位是0，就将此信源序列编码为0。
译码规则：将接收的一位符号重复三次译出，即若接收到1就译码为111，即若 接收到0就译码为000。
0.5p(e/000)0.5p(e/111)3 4
误比特率
p1
1 3
3 4
1 4
（2）再设p≠0，计算由于信道噪声引起的错误概率p2。
信息论与纠错编码编码习题答案
第1章 信息论基础1.7 ⎥⎥⎦⎤⎢⎢⎣⎡=⎥⎦⎤⎢⎣⎡36136236336436536636536436336236112111098765432)(X q X 1.8 p (s 0 ) = 0.8p (s 0 ) + 0.5p (s 2 )p (s 1 ) = 0.2p (s 0 ) + 0.5p (s 2 ) p (s 2 ) = 0.5p (s 1 ) + 0.3p (s 3 ) p (s 3 ) = 0.5p (s 1 ) + 0.7p (s 3 ) p (s 0 ) + p (s 1 ) + p (s 2 ) + p (s 3 ) = 1 p (s 0 ) =3715， p (s 1 ) = p (s 2 ) = 376，p (s 3 ) = 37101.9 P e = q (0)p + q (1)p = 0.06(1-0.06)﹡1000﹡10 = 9400 < 9500 不能1.10 ⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡------------=22222222)1(0)1()1(00)1(0)1()1(000000)1()1(0)1(00000)1()1(0)1(p p p pp p p p p p p p p p p p p p p p p p p p P 第2章 信息的度量2.4 logk2.5 I (X ; Y Z )= I (X ; Y )+ I (X ; Z ∣Y ) 2.7 010434()()()111111p s p s p s === H = 0.25(Bit/符号)2.8 H = 0.82(Bit/符号) 2.10 （1）1()log225.6()52!i I x Bit =-= （2）1352!()log ()log 413!39!i i I x q x =-=（3）)/(4.713log 234log 52log 521log )(符号－Bit U H ==⨯===（4）)/(7.313log 131log )(符号Bit X H ==- 2.11（1）H (X ) = log6 = 2.58 (Bit/符号) （2）H (X ) =2.36 (Bit/符号)（3）I (A+B=7) = - log1/6 = log6 = 2.585 (Bit) 2.12 （1）I (x i ) = -log1/100 = log100（2）H(X)=log100.2.13 039.0log )(-=Y X I2.14 R t =1000/4 (码字/秒) × H (U ) =250×9＝2250（Bit/秒） 2.15 ―log p = log 55/44。
信息论_纠错编码
信息论的旅程3、信源的输出中含有多 少信息？可压缩程度？ 4、传输信息的最高 速率（信道容量）第九章 纠错编码6、有噪信道编码 5、无失真信源编码 9、纠错编码2009-12-227、限失真信源编码研究目的：提高通信传输的可靠性！通过分析纠错编码 研究目的 的性质和构建纠错码来检查并纠正信道传输中的错误。
2本章的研究内容 背景香农第二定理 => 在任何信道中，信道容量是 进行可靠传输的最大信息传输率！ 如何实现（如何编码）？主要内容基本概念概述 概述 纠错工作方式 纠错工作方式目标：通过信道编码，检测并纠正传输中 出现的错误。
纠错编码的主要研究内容1. 2.纠错码分类 线性分组码 纠错码分类汉明码 循环码3 4纠错编码的基本理论 具体的纠错编码 线性分组码、汉明码、循环码1.1、纠错编码基本概念 –概述 香农第二定理证明，当 R < C 时 PE → 0 的码存 在。
证明过程采用的是随机编码的方法：随机编码所得的码集很大，通过搜索得到好码的 方法在实际上很难实现； 即使找到了好码，这种码的码字也没有规律，不 便于译码。
1.1、纠错编码基本概念 –概述（续） 近世代数（抽象代数）是信道编码理论用到的 最重要的数学工具，它包括群论、环论、域论、 格论、线性代数等许多分支。
纠错编码是提高传输可靠性的最主要的措施之 一。
纠错编码的基本思路：发送端：根据一定的规律在待发送的信息码元中 人为的加入一些冗余码元（监督码元）。
接收端：按照既定的规则检验信息码元与监督码 元之间的关系。
如果传输过程出错，则信息码元与 监督码元之间的关系将受到破坏，从而发现错误。
6真正实用的信道编码方法还需要通过各种数 学工具来构造，使码具有好的结构性以便于 译码。
51纠错编码 – 概述 香农第二定理提出，在满足 R<C 的条件下， 高效率、高可靠性的码字是存在的。
但，如 何进行信道编码？随机编码构造困难，且不具有规律性 利用数据工具设计编码算法，结构性好！1.2、基本概念 – 纠错工作方式信道中的干扰：随机噪声random error，码元翻转脉冲干扰burst error, 一串错误纠错编码 – 提高传输的可靠性！ 基本思路发送端：根据一定的规律在待发送的信息码元中 人为的加入一些冗余码元（监督码元） 接收端：……7纠错工作方式：反馈重传 (ARQ) 前向纠错 (FEC) 混合纠错 (HEC)81.2、基本概念 – 纠错工作方式（续）1.1.2、基本概念 – 纠错工作方式（续）2.反馈重传(ARQ - Automatic Repeat reQuest)m检错 编码前向纠错(FEC - Forward Error Correction)m纠错 编码C信道Y检错 译码ˆ mC信道Y纠错 译码ˆ m反馈发送端经编码后发出能够发现错误的码，接收 端收到后检验，如果发现传输中有错误，则通过反 馈系统把这一判断结果反馈回发端，然后发送端把 前面发出的信息重新传送一次，直到接收端认为正 确地收到信息为止。
信息论与纠错编码题库
第八章线性分组码8.1 什么是检错码？什么是纠错码？两者有什么不同？答：能发现错误但不能纠正错误的码称为检错码；不仅能发现错误而且还能纠正错误的码称为纠错码。
8.2 试述分组码的概念，并说明分组码的码率r的意义。
答：分组码是把信息序列以每k个码元分组，即每k个码元组成一个信息组。
n表示码长,k 表示信息位的数目，码率r=k/n，它说明在一个码字中信息为所占的比重。
8.3 什么是码的生成矩阵和校验矩阵？一个（n，k）线性分组码的生产矩阵和校验矩阵各是几行几列的矩阵？答：线性分组码的2个码字将组成n维向量空间的一个k维子空间，而线性空间可由其基底张成，因此线性分组码的个码字完全可由k个独立的向量组成的基底张成。
设k个向量为（7.3-2）将它们写成矩阵形式：（7.3-3）（n,k）码中的任何码字，均可由这组基底的线性组合生成。
即C=MG=(mk-1,mk-2,m0)G式中 M=(mk-1,mk-2,m0)是k个信息元组成的信息组。
这就是说，每给定一个信息组，通过式（7.3-3）便可求得其相应的码字。
故称这个由k 个线性无关矢量组成的基底所构成的k×n阶矩阵G为码的生成矩阵（Generator Matrix）。
校验矩阵H 的每一行代表求某一个校验位的线性方程的系数(n-k)线性分组码有r=n-k 个校验元，故须有r 个独立的线性方程，因此H 矩阵必由线性无关的r 行组成，是一个(n-k)×n 阶矩阵，一般形式为一个（n,k ）线性分组码生成矩阵有k 行n 列校验矩阵有(n-k)行n 列。
8.4 什么样的码成为系统码？系统码的生成矩阵和校验矩阵在形式上有何特点？答：若信息组为不变的形式，称在码字的任意k 位中出现的码为系统码；一个系统码的生成矩阵G ，其左边k 行k 列是一个k 阶单位方阵，系统码的校验矩阵H ，其右边r 行r 列组成一个r 阶单位方阵。
8.5 什么是对偶码？试举例说明之。
信息论与编码纠错第6章
Dk —序列中第k个符号的平均失真
上式表明离散无记忆N次扩展信道的输入符号序列和输出符号序列之间 的平均失真，等于单个符号xki与ykj之间失真统计值的总和。 若矢量信源是原离散无记忆信源的N次扩展，且矢量信道也是无记忆的 N次扩展，则每个 D k 对一维信源信道所取的均值相等，即
D1 Dk DN D
第6章 率失真编码
《信息论与编码》
第四章： 率失真编码
主讲：刘立
内容提要
数据压缩是信息传输和处理的重要研究内容，率失真理论研
究的就是在允许一定失真的前提下，对信源的压缩编码。率失真 信源编码定理（香农第三定理）指出：率失真函数R ( D ) 就是在 给定失真测度条件下，对信源熵可压缩的最低程度。 本章只限于研究率失真理论最基本的内容，失真测度，率失
，经过信道转移概率矩阵为
的信道传输，失真测度为平方误差失真测度，
求平均失真。 【解】由平均失真计算公式得：
D
p( x
i 1 j 1 I J
I
J
i
y j )d i j
p( x ) p( y
i i 1 j 1
I
J
j
xi )d i j
3 p( y
i 1 j 1
1
j
【解】根据 d
d d
( 2)
(N )
1 ( X ,Y ) N
1 2 1 2
d (x
k 1
N
k
, yk )
，得
失真测度矩阵为：
0 0.5 0.5 1 0.5 0 1 0.5 0.5 1 0 0.5 1 0.5 0.5 0
(00， )＝ 00 (01 00)＝ ，
信息论与编码纠错第1章
信息论与编码
2. 信道分类：
（1）根据输入和输出信号的特点可分为： 离散信道：输入和输出都是时间上离散、取值离散的随机序列。离 散信道有时也称为数字信道。 连续信道：输入和输出都是时间上离散、取值连续的随机序列，又 称为模拟信道。 半连续信道：输入、输出序列一个是离散的，而另一个是连续的。 波形信道：输入和输出都是时间和取值均连续的随机信号。
（1）信源编码器：对信源输出的消息进行适当的变换和处理， 以达到减少或消除信源冗余度来提高信息的传输速率。
（2）信道编码器：对信源编码器的输出进行变换和处理，通过 增加冗余度来提高信息传输的可靠性。
信息论与编码
信源
信源编码器
信道编码器
等等等等 等等等等
等等等等等等等
信 道
干 扰
源
信宿
信源译码器
信道译码器
p(s3 )
a1:2/3 a1:1/2
a1:1/4
p
(s2
)
1 3
p ( s1 )
3 4
p(s2 )
1 2
p(s3 )
s3
p (s3 )
1 4
p(s2 )
p ( s1 ) p ( s 2 ) p ( s 3 ) 1
p (s1)
3 13
解方程组，可得平稳时各状态的概率分布：
p (s2)
二．离散无记忆信源
离散无记忆信源（Discrete Memoryless Source，简记为DMS） 输出的是单个符号的消息，不同时刻发出的符号之间彼此统计独立， 而且符号集中的符号数目是有限的或可数的。
离散无记忆信源的数学模型为离散型的概率空间，即
X p(X)xp1(x1)
x2 p(x2)
信息论与编码纠错第3章
信息论与编码
7．唯一可译码
定义：如果码的任意N次扩展码都是非奇异码，则称该码为惟一可译码。
信源消息 u1 各消息概率 p(u1) 码1 00 码2 00 码3 0 码4 1
u2
u3 u4
p(u2)
p(u3) p(u4)
11
10 11
01
10 11
1
00 11
10
100 1000
例中的码1不是唯一可译码。
11 1000
3．变长码
若码字集合C中的所有码字cm (m = 1,2, …,M)，其码长不都相同，称 码C为变长码，例中列出的码3、码4 就是变长码。
信息论与编码
4．奇异码
对奇异码来说，从信源消息到码字的映射不是一一对应的。例中的码 1，信源消息u2和u4都用码字11对其编码，因此这种码就是奇异码，奇异码 不具备惟一可译性。
输效率，这是信源编码应考虑的问题，这章讨论在不允
许失真情况下的信源编码。等长编码定理给出了等长编 码条件下，其码长的下限值，变长编码定理（香农第一 定理）给出了信源无失真变长编码时其码长的上、下限 值。本章还介绍了三种通用信源编码方法：香农编码法、
费诺编码法和霍夫曼编码法。
信息论与编码
§3.1 概 述
消息
信源
um=um1um2...umL
信源编码器
码字cm=cm1cm2...cmn
信源符号集{a1,a2,...ak}
信道符号（码符号）集{b1,b2,...bD}
信息论与编码
【例】中文电报编码：
信 源
10000个常 用汉字
信源编码器I
四位二进制数 0000－9999
信源编码器II
二进制信道