课时冲关练(二) 1.2
二年级上数学课时练+试卷1.2 认识线段、解决问题三

1.2 认识线段、解决问题1.在线段的下面画√。
2.量一量。
AB= BC= AC= BD= AD= CD= 3.画一画。
(1)画一条8厘米长的线段。
(2)画一条比3厘米长2厘米的线段。
4.图中各有几条线段。
5. 在括号里填上合适的单位。
(1)一支铅笔长20()。
(2)旗杆高10()。
(3)一根手指大约宽1()。
(4)一块橡皮长3()。
6.圈出合适答案。
答案:1.2. 2cm 2cm 4cm 6cm 8cm 4cm3. 略4. 6 65. (1)cm (2)m (3)cm (4)cm6. 长窄短1、《巩乃斯的马》:a、有的疯狂地向前奔跑,像一队尖兵,要去踏住那闪电;有的来回奔跑,俨然像临危不惧、收拾残局的大将;小马跟着母马,认真而紧张地跑,不再顽皮、撒欢,一下子变得老练了许多。
B、我久久地站在那里,发愣,发痴,发呆。
我见到了,见过了,这世间罕见的奇景,这无可替代的伟大的马群,这古战场的再现,这交响乐伴奏下的复活的雕塑群和油画长卷!2、《天马》:a、中国旅游的图形标志是“天马”。
它的象征意义是:历史悠久的文化古国——中国,正在腾空飞速前进。
B、课文开头先点明了“天马”是我国旅游局1983年确定的中国旅游图形标记;再介绍这个图形标记的来历;接着介绍这件文物珍品的历史价值和艺术成就;然后介绍“天马”的外形特征;最后介绍“天马”名称的由来及把“天马”作为中国旅游图形标志的意义所在。
C、天马体态轻盈,神形兼备,无论从正面、侧面的哪个角度去看,都是极为生动健美的。
天马昂首扬尾,四蹄腾空,自由奔放,动作协调,既使人感受到力量,又激发人们的想象。
3、《古诗二首》:a、《房兵曹胡马》是唐朝诗人杜甫的作品,描写了一匹雄健的战马的品格,表达了诗人对朋友的期望,更表达了作者积极进取、建功立业的抱负和博大的胸襟。
B、诗的前四句写了马的雄健,是实写;后四句转写马的品格,由咏物转为言志,是虚写。
C、诗里刻画骏马的骨骼劲挺的诗句是“锋棱瘦骨成”;刻画骏马双耳的诗句是“竹批双耳峻”;描写骏马奔驰的句子是“风入四蹄轻”。
最新高考数学(文)总复习:课时冲关(Word版,页,含答案)

第一章 集合与常用逻辑用语第1节 集 合 学生用书 课时冲关一[基础训练组]1.(2018·全国Ⅱ卷)已知集合A ={1,3,5,7},B ={2,3,4,5},则A ∩B =( ) A .{3} B .{5}C .{3,5}D .{1,2,3,4,5,7}解析:C [A ={1,3,5,7},B ={2,3,4,5},∴A ∩B ={3,5},故选C.]2.(2019·石嘴山市一模)集合P ={x |0≤x <3},M ={x ||x |≤3},则P ∩M =( ) A .{1,2} B .{0,1,2} C .{x |0≤x <3}D .{x |0≤x ≤3}解析:C [集合P ={x |0≤x <3},M ={x ||x |≤3}={x |-3≤x ≤3},则P ∩M ={x |0≤x <3}.] 3.(2019·张家口市模拟)如图,I 为全集,M 、P 、S 是I 的三个子集,则阴影部分所表示的集合是( )A .(M ∩P )∩SB .(M ∩P )∪SC .(M ∩P )∩∁I SD .(M ∩P )∪∁I S解析:C [图中的阴影部分是M ∩P 的子集,不属于集合S ,属于集合S 的补集的子集,即是∁I S 的子集,则阴影部分所表示的集合是(M ∩P )∩∁I S .故选C.]4.(2019·漳州市模拟)满足{2018}⊆A 的集合A 的个数为( )A .1B .2C .3D .4解析:C [满足{2018}⊆A 的集合A 可得:A ={2018},{2018,2019},{2018,2020}.因此满足的集合A 的个数为3.]5.已知集合P ={x |x 2≤1},M ={a }.若P ∪M =P ,则a 的取值范围是( ) A .(-∞,-1] B .[1,+∞)C .[-1,1]D .(-∞,-1]∪[1,+∞)解析:C [因为P ∪M =P ,所以M ⊆P ,即a ∈P ,得a 2≤1,解得-1≤a ≤1,所以a 的取值范围是[-1,1].]6.已知集合A ={y |y =x 2-1},B ={x |y =lg(x -2x 2)},则∁R (A ∩B )=( )A.⎣⎢⎡⎭⎪⎫0,12 B .(-∞,0)∪⎣⎢⎡⎭⎪⎫12,+∞C.⎝ ⎛⎭⎪⎫0,12 D .(-∞,0]∪⎣⎢⎡⎭⎪⎫12,+∞ 解析:D [A ={y |y =x 2-1}=[0,+∞),B ={x |y =lg(x -2x 2)}=⎝ ⎛⎭⎪⎫0,12,所以A ∩B =⎝ ⎛⎭⎪⎫0,12,所以∁R (A ∩B )=(-∞,0]∪⎣⎢⎡⎭⎪⎫12,+∞.] 7.(2019·合肥市模拟)已知A =[1,+∞),B =⎩⎨⎧⎭⎬⎫x ∈R |12a ≤x ≤2a -1,若A ∩B ≠∅,则实数a 的取值范围是( )A .[1,+∞)B.⎣⎢⎡⎦⎥⎤12,1 C.⎣⎢⎡⎭⎪⎫23,+∞ D .(1,+∞)解析:A [因为A ∩B ≠∅,所以⎩⎪⎨⎪⎧2a -1≥1,2a -1≥12a ,解得a ≥1,故选A.]8.(2019·石家庄市模拟)函数y =x -2与y =ln(1-x )的定义域分别为M ,N ,则M ∪N =( ) A .(1,2]B .[1,2]C .(-∞,1]∪[2,+∞)D .(-∞,1)∪[2,+∞)解析:D [使x -2有意义的实数x 应满足x -2≥0,∴x ≥2,∴M =[2,+∞),y =ln(1-x )中x 应满足1-x >0,∴x <1,∴N =(-∞,1),所以M ∪N =(-∞,1)∪[2,+∞),故选D.]9.已知集合A ={(x ,y )|x ,y ∈R ,x 2+y 2=1},B ={(x ,y )|x ,y ∈R ,y =4x 2-1},则A ∩B 的元素个数是________.解析:集合A 是以原点为圆心,半径等于1的圆周上的点的集合,集合B 是抛物线y =4x 2-1上的点的集合,观察图像可知,抛物线与圆有3个交点,因此A ∩B 中含有3个元素.答案:310.已知集合A ={x |4≤2x≤16},B =[a ,b ],若A ⊆B ,则实数a -b 的取值范围是________. 解析:集合A ={x |4≤2x ≤16}={x |22≤2x ≤24}={x |2≤x ≤4}=[2,4],因为A ⊆B ,所以a ≤2,b ≥4,所以a -b ≤2-4=-2,即实数a -b 的取值范围是(-∞,-2].答案:(-∞,-2]11.对于集合M 、N ,定义M -N ={x |x ∈M ,且x ∉N },M ⊕N =(M -N )∪(N -M ).设A ={y |y =3x,x ∈R },B ={y |y =-(x -1)2+2,x ∈R },则A ⊕B =________.解析:由题意得A ={y |y =3x,x ∈R }={y |y >0},B ={y |y =-(x -1)2+2,x ∈R }={y |y ≤2},故A-B ={y |y >2},B -A ={y |y ≤0},所以A ⊕B ={y |y ≤0,或y >2}.答案:(-∞,0]∪(2,+∞)12.(2019·淮南市一模)若A ={x |ax 2-ax +1≤0,x ∈R }=∅,则a 的取值范围是________. 解析:∵A ={x |ax 2-ax +1≤0,x ∈R }=∅,∴a =0或⎩⎪⎨⎪⎧a >0Δ=-a2-4a <0,解得0≤a <4.∴a 的取值范围是[0,4).答案:[0,4).[能力提升组]13.集合U =R ,A ={x |x 2-x -2<0},B ={x |y =ln(1-x )},则图中阴影部分所表示的集合是( )A .{x |x ≥1}B .{x |1≤x <2}C .{x |0<x ≤1}D .{x |x ≤1}解析:B [易知A =(-1,2),B =(-∞,1),∴∁U B =[1,+∞),A ∩(∁U B )=[1,2).因此阴影部分表示的集合为A ∩(∁U B )={x |1≤x <2}.]14.设P ,Q 为两个非空实数集合,定义集合P *Q ={z |z =a ÷b ,a ∈P ,b ∈Q },若P ={-1,0,1},Q ={-2,2},则集合P *Q 中元素的个数是( )A .2B .3C .4D .5解析:B [当a =0时,无论b 取何值,z =a ÷b =0; 当a =-1,b =-2时,z =(-1)÷(-2)=12;当a =-1,b =2时,z =(-1)÷2=-12;当a =1,b =-2时,z =1÷(-2)=-12;当a =1,b =2时,z =1÷2=12.故P *Q =⎩⎨⎧⎭⎬⎫0,12,-12,该集合中共有3个元素.]15.若集合A ={x |(a -1)x 2+3x -2=0,x ∈R }有且仅有两个子集,则实数a 的值为________. 解析:由题意知,方程(a -1)x 2+3x -2=0,x ∈R ,有一个根,∴当a =1时满足题意,当a ≠1时,Δ=0,即9+8(a -1)=0,解得a =-18.答案:1或-1816.(2019·西城区一模)某班共有学生40名,在乒乓球、篮球、排球三项运动中每人至少会其中的一项,有些人会其中的两项,没有人三项均会.若该班18人不会打乒乓球,24人不会打篮球,16人不会打排球,则该班会其中两项运动的学生人数是________.解析:设同时会打乒乓球和篮球的学生有x 人, 同时会打乒乓球和排球的学生有y 人, 同时会打排球和篮球的学生有z 人,∵该班18人不会打乒乓球,24人不会打篮球,16人不会打排球, ∴该班会打乒乓球或篮球的学生有24人, 会打乒乓球或排球的学生有16人, 会打篮球或打排球有22人, ∴x +y +z =24+16+22-40=22. ∴该班会其中两项运动的学生人数是22. 答案:22第2节 命题、充分条件与必要条件学生用书 课时冲关二[基础训练组]1.命题“若a 2+b 2=0,a ,b ∈R ,则a =b =0”的逆否命题是( ) A .若a ≠b ≠0,a ,b ∈R ,则a 2+b 2=0 B .若a =b ≠0,a ,b ∈R ,则a 2+b 2≠0 C .若a ≠0且b ≠0,a ,b ∈R ,则a 2+b 2≠0 D .若a ≠0或b ≠0,a ,b ∈R ,则a 2+b 2≠0解析:D [写逆否命题只要交换命题的条件与结论,并分别否定条件与结论即可.]2.(2019·晋城市一模)设a ∈R ,则“a >3”是“函数y =log a (x -1)在定义域上为增函数”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件解析:A [因为函数y =log a (x -1)在定义域(1,+∞)上为增函数,所以a >1, 因此“a >3”是“函数y =log a (x -1)在定义域上为增函数”的充分不必要条件.]3.(2019·天津市模拟)“m =1”是“圆C 1:x 2+y 2+3x +4y +m =0与圆C 2“x 2+y 2=4的相交弦长为23”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件解析:A [由题意知圆C 1与圆C 2的公共弦所在的直线是3x +4y +m +4=0,故(0,0)到3x +4y +m +4=0的距离d =|m +4|5=4-3=1,即|m +4|=5,解得m =1或m =-9.故m =1是m =1或m =-9的充分不必要条件,故选A.]4.(2019·大庆市模拟)已知条件p :|x -4|≤6,条件q :x ≤1+m ,若p 是q 的充分不必要条件,则m 的取值范围是( )A .(-∞,-1]B .(-∞,9]C .[1,9]D .[9,+∞)解析:D [由|x -4|≤6,解得-2≤x ≤10,即p :-2≤x ≤10;又q :x ≤1+m ,若p 是q 的充分不必要条件,则1+m ≥10,解得m ≥9.故选D.]5.(2019·洛阳市一模)若x >m 是x 2-3x +2<0的必要不充分条件,则实数m 的取值范围是( ) A .[1,+∞)B .(-∞,2]C .(-∞,1]D .[2,+∞)解析:C [由x 2-3x +2<0得1<x <2,若x >m 是x 2-3x +2<0的必要不充分条件, 则m ≤1,即实数m 的取值范围是(-∞,1].]6.(2019·南昌市模拟)a 2+b 2=1是a sin θ+b cos θ≤1恒成立的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件D .既不充分也不必要条件解析:A [因为a sin θ+b cos θ=a 2+b 2sin (θ+φ)≤a 2+b 2,所以由a 2+b 2=1可推得a sinθ+b cos θ≤1恒成立.反之,取a =2,b =0,θ=30°,满足a sin θ+b cos θ≤1,但不满足a 2+b 2=1,即由a sin θ+b cos θ≤1推不出a 2+b 2=1,故a 2+b 2=1是a sin θ+b cos θ≤1恒成立的充分不必要条件.故选A.]7.(2019·新余市模拟)“m >1”是“函数f (x )=3x +m-33在区间[1,+∞)无零点”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件 解析:A [因为函数f (x )=3x +m-33在区间[1,+∞)上单调递增且无零点,所以f (1)=31+m-33>0,即m +1>32,解得m >12,故“m >1”是“函数f (x )=3x +m -33在区间[1,+∞)无零点的充分不必要条件,故选A.]8.(2019·焦作市质检)设等比数列{a n }的公比为q ,前n 项和为S n .给出命题s :若|q |=2,则S 6=7S 2,则在命题s 的逆命题、否命题、逆否命题中,错误命题的个数是( )A .3B .2C .1D .0解析:B [若|q |=2,则q 2=2,S 6=a 1-q61-q=a 1-q2+q 2+q 41-q=7·a 1-q 21-q=7S 2,所以原命题为真,从而逆否命题为真;而当S 6=7S 2时,显然q ≠1,这时a 1-q 61-q=7·a 1-q 21-q,解得q =-1或|q |=2,因此,逆命题为假,否命题为假,故错误命题的个数为2.]9.(2019·西宁市模拟)《左传·僖公十四年》有记载:“皮之不存,毛将焉附?”这句话的意思是说皮都没有了,毛往哪里依附呢?比喻事物失去了借以生存的基础,就不能存在.皮之不存,毛将焉附?则“有毛”是“有皮”的_______条件(将正确的序号填入空格处).①充分条件 ②必要条件 ③充要条件 ④既不充分也不必要条件解析:由题意知“无皮”⇒“无毛”,所以“有毛”⇒“有皮”即“有毛”是“有皮”的充分条件. 答案:①10.在△ABC 中,角A ,B ,C 所对应的边分别为a ,b ,c ,则“a ≤b ”是“sin A ≤sin B ”的__________条件.解析:由正弦定理,得a sin A =bsin B ,故a ≤b ⇔sin A ≤sinB.答案:充要11.(2019·曲靖市一模)若“x >a ”是“x 2-5x +6≥0”成立的充分不必要条件,则实数a 的取值范围是_________.解析:由x 2-5x +6≥0得x ≥3或x ≤2,若“x >a ”是“x 2-5x +6≥0”成立的充分不必要条件,则a ≥3,即实数a 的取值范围是[3,+∞). 答案:[3,+∞)12.(2019·日照模拟)已知条件p :2x 2-3x +1≤0,条件q :x 2-(2a +1)x +a (a +1)≤0.若非p 是非q 的必要不充分条件,则实数a 的取值范围是________.解析:由2x 2-3x +1≤0,得12≤x ≤1,∴命题p 为⎩⎨⎧⎭⎬⎫x |12≤x ≤1.由x 2-(2a +1)x +a (a +1)≤0,得a ≤x ≤a +1, ∴命题q 为{x |a ≤x ≤a +1}.非p 对应的集合A =⎩⎨⎧⎭⎬⎫x |x >1或x <12, 非q 对应的集合B ={x |x >a +1或x <a }. ∵非p 是非q 的必要不充分条件, ∴a +1≥1且a ≤12,∴0≤a ≤12,即实数a 的取值范围是⎣⎢⎡⎦⎥⎤0,12.答案:⎣⎢⎡⎦⎥⎤0,12 [能力提升组]13.(2019·合肥市模拟)祖暅原理:“幂势既同,则积不容异”.它是中国古代一个涉及几何体体积的问题,意思是两个同高的几何体,如果在等高处的截面积恒相等,那么体积相等.设A ,B 为两个同高的几何体,p :A ,B 的体积不相等,q :A ,B 在等高处的截面积不恒相等,根据祖暅原理可知,p 是q 的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件解析:A [设命题a :“若p ,则q ”,可知命题a 是祖暅原理的逆否命题,则a 是真命题.故p 是q 的充分条件.设命题b :“若q ,则p ”,若A 比B 在某些等高处的截面积小一些,在另一些等高处的截面积大一些,且大的总量与小的总量相抵,则它们的体积还是一样的.所以命题b 是假命题,即p 不是q 的必要条件.综上所述,p 是q 的充分不必要条件.故选A.]14.(2019·保定市模拟)已知条件p :4x -1≤-1,条件q :x 2+x <a 2-a ,且非q 的一个充分不必要条件是非p ,则a 的取值范围是( )A.⎣⎢⎡⎦⎥⎤-2,-12 B.⎣⎢⎡⎦⎥⎤12,2 C .[-1,2] D.⎝ ⎛⎦⎥⎤2,12∪[2,+∞) 解析:C [由4x -1≤-1,移项得4x -1+1≤0,通分得x +3x -1≤0,解得-3≤x <1; 由x 2+x <a 2-a ,得x 2+x -a 2+a <0.由非q 的一个充分不必要条件是非p ,可知非p 是非q 的充分不必要条件,即p 是q 的必要不充分条件,即条件q 对应的x 取值集合是条件p 对应的x 取值集合的真子集.设f (x )=x 2+x -a 2+a ,如图,则⎩⎪⎨⎪⎧f -=-a 2+a +6≥0,f=-a 2+a +2≥0,∴⎩⎪⎨⎪⎧-2<a <3-1≤a ≤2∴-1≤a ≤2,故选C.]15.给出下列命题:①“数列{a n }为等比数列”是“数列{a n a n +1}为等比数列”的充分不必要条件; ②“a =2”是“函数f (x )=|x -a |在区间[2,+∞)上为增函数”的充要条件; ③“m =3”是“直线(m +3)x +my -2=0与直线mx -6y +5=0互相垂直”的充要条件;④设a ,b ,c 分别是△ABC 三个内角A ,B ,C 所对的边,若a =1,b =3,则“A =30°”是“B =60°”的必要不充分条件.其中真命题的序号是________.解析:对于①,当数列{a n }为等比数列时,易知数列{a n a n +1}是等比数列,但当数列{a n a n +1}为等比数列时,数列{a n }未必是等比数列,如数列1,3,2,6,4,12,8显然不是等比数列,而相应的数列3,6,12,24,48,96是等比数列,因此①正确;对于②,当a ≤2时,函数f (x )=|x -a |在区间[2,+∞)上是增函数,因此②不正确;对于③,当m =3时,相应的两条直线互相垂直,反之,这两条直线垂直时,不一定有m =3,也可能m =0.因此③不正确;对于④,由题意得b a =sin Bsin A=3,若B =60°,则sin A=12,注意到b >a ,故A =30°,反之,当A =30°时,有sin B =32,由于b >a ,所以B =60°或B =120°,因此④正确.综上所述,真命题的序号是①④.答案:①④16.设命题p :2x -1x -1<0,命题q ∶x 2-(2a +1)x +a (a +1)≤0,若p 是q 的充分不必要条件,则实数a 的取值范围是________.解析:2x -1x -1<0⇒(2x -1)(x -1)<0⇒12<x <1,x 2-(2a +1)x +a (a +1)≤0⇒a ≤x ≤a +1.由题意,得⎝ ⎛⎭⎪⎫12,1⊆[a ,a +1].故⎩⎪⎨⎪⎧a ≤12,a +1≥1,解得0≤a ≤12.答案:⎣⎢⎡⎦⎥⎤0,12第3节 量词与逻辑联结词 学生用书 课时冲关三[基础训练组]1.(2019·安阳市模拟)已知命题p :存在x 0∈(-∞,0),2x 0<3x 0,则非p 为( ) A .存在x 0∈[0,+∞),2x 0<3x 0 B .存在x 0∈(-∞,0),2x 0≥3x 0 C .任意x 0∈[0,+∞),2x<3xD .任意x ∈(-∞,0),2x≥3x解析:D [由特称命题的否定为全称命题,可得 命题p :存在x 0∈(-∞,0),2x 0<3x 0,则非p 为:任意x ∈(-∞,0),2x≥3x,故选D.]2.(2019·济南市一模)若命题“p 或q ”与命题“非p ”都是真命题,则( ) A .命题p 与命题q 都是真命题 B .命题p 与命题q 都是假命题 C .命题p 是真命题,命题q 是假命题 D .命题p 是假命题,命题q 是真命题解析:D [命题“p 或q ”与命题“非p ”都是真命题, 则p 是假命题,q 是真命题,故选D.]3.(2019·濮阳市一模)已知m ,n 是两条不同的直线,α,β是两个不重合的平面.命题p :若α∩β=m ,m ⊥n ,则n ⊥α;命题q :若m ∥α,m ⊂β,α∩β=n ,则m ∥n .那么下列命题中的真命题是( )A .p 且qB .p 或非qC .非p 且qD .非p 且非q解析:C [直线垂直于平面内的一条直线,不能确定该直线与平面垂直,命题p 是假命题;命题q 满足直线与平面平行的性质定理,命题q 是真命题;所以非p 是真命题,可得非p 且q 是真命题.故选C.]4.已知命题p :若a =0.30.3,b =1.20.3,c =log 1.20.3,则a <c <b ;命题q :“x 2-x -6>0”是“x >4”的必要不充分条件,则下列命题正确的是( )A .p 且qB .p 且(非q )C .(非p )且qD .(非p )且(非q )解析:C [因为0<a =0.30.3<0.30=1,b =1.20.3>1.20=1,c =log 1.20.3<log 1.21=0,所以c <a <b ,故命题p 为假命题,非p 为真命题;由x 2-x -6>0可得x <-2或x >3,故“x 2-x -6>0”是“x >4”的必要不充分条件,q 为真命题,故(非p )且q 为真命题,选C.]5.(2019·沈阳市模拟)命题p :“任意x ∈N +,⎝ ⎛⎭⎪⎫12x ≤12”的否定为( )A .任意x ∈N +,⎝ ⎛⎭⎪⎫12x >12B .任意x ∉N +,⎝ ⎛⎭⎪⎫12x >12C .存在x 0∉N +,⎝ ⎛⎭⎪⎫12x 0>12D .存在x 0∈N +,⎝ ⎛⎭⎪⎫12x 0>12 解析:D [命题p 的否定是把“任意”改成“存在”,再把“⎝ ⎛⎭⎪⎫12x ≤12”改为“⎝ ⎛⎭⎪⎫12x 0>12”即可,故选D.]6.短道速滑队组织6名队员(含赛前系列赛积分最靠前的甲乙丙三名队员在内)进行冬奥会选拔赛,记“甲得第一名”为p ,“乙得第二名”为q ,“丙得第三名”为r ,若p 或q 是真命题,p 且q 是假命题,(非q )且r 是真命题,则选拔赛的结果为( )A .甲得第一名、乙得第二名、丙得第三名B .甲得第二名、乙得第一名、丙得第三名C .甲得第一名、乙得第三名、丙得第二名D .甲得第一名、乙没得第二名、丙得第三名解析:D [(非q )且r 是真命题意味着非q 为真,q 为假(乙没得第二名)且r 为真(丙得第三名);p 或q 是真命题,由于q 为假,只能p 为真(甲得第一名),这与p 且q 是假命题相吻合;由于还有其他三名队员参赛,只能肯定其他队员得第二名,乙没得第二名,故选D.]7.(2019·玉溪市模拟)有四个关于三角函数的命题:p 1:存在x ∈R ,sin x +cos x =2; p 2:存在x ∈R ,sin 2x =sin x ;p 3:任意x ∈⎣⎢⎡⎦⎥⎤-π2,π2,1+cos 2x2=cos x ; p 4:任意x ∈(0,π),sin x >cos x .其中真命题是( ) A .p 1,p 4 B .p 2,p 3 C .p 3,p 4D .p 2,p 4解析:B [因为sin x +cos x =2sin ⎝⎛⎭⎪⎫x +π4,所以sin x +cos x 的最大值为2,可得不存在x ∈R ,使sin x +cos x =2成立,得命题p 1是假命题; 因为存在x =k π(k ∈),使sin 2x =sin x 成立,故命题p 2是真命题; 因为1+cos 2x 2=cos 2x ,所以1+cos 2x 2=|cos x |,结合x ∈⎣⎢⎡⎦⎥⎤-π2,π2得cos x ≥0由此可得1+cos 2x2=cos x ,得命题p 3是真命题;因为当x =π4时,sin x =cos x =22,不满足sin x >cos x ,所以任意x ∈(0,π),使sin x >cos x 不成立,故命题p 4是假命题.故选B.] 8.(2019·瓦房店市一模)下列说法错误的是( )A .命题“若x 2-4x +3=0,则x =3”的逆否命题是“若x ≠3,则x 2-4x +3≠0” B .“x >1”是“|x |>0”的充分不必要条件C .命题p :“存在x ∈R ,使得x 2+x +1<0”,则非p :“任意x ∈R ,x 2+x +1≥0” D .若p 且q 为假命题,则p 、q 均为假命题解析:D [命题“若x 2-4x +3=0,则x =3”的逆否命题是“若x ≠3,则x 2-4x +3≠0”,故A 正确;由x >1,可得|x |>1>0,反之,由|x |>0,不一定有x >1,如x =-1, ∴“x >1”是“|x |>0”的充分不必要条件,故B 正确;命题p :“存在x ∈R ,使得x 2+x +1<0”,则非p :“任意x ∈R ,x 2+x +1≥0”,故C 正确; 若p 且q 为假命题,则p 、q 中至少有一个为假命题,故D 错误.] 9.(2019·银川市模拟)命题“存在x 0∈R,2x 0>3”的否定是________.解析:因为特称命题的否定是全称命题,所以,命题“存在x 0∈R,2x 0>3”的否定是:“任意x ∈R,2x≤3”.答案:任意x ∈R,2x≤310.若命题“任意x ∈R ,kx 2-kx -1<0”是真命题,则k 的取值范围是________.解析:命题“任意x ∈R ,kx 2-kx -1<0”是真命题,当k =0时,则有-1<0;当k ≠0时,则有k <0且Δ=(-k )2-4×k ×(-1)=k 2+4k <0,解得-4<k <0,综上所述,实数k 的取值范围是(-4,0].答案:(-4,0]11.(2019·西宁市一模)命题“存在x ∈R ,x 2-(m -1)x +1<0”为假命题,则实数m 的取值范围为________.解析:命题“存在x ∈R ,x 2-(m -1)x +1<0”为假命题, 可得任意x ∈R ,x 2-(m -1)x +1≥0恒成立, 即有Δ=(m -1)2-4≤0,解得-1≤m ≤3, 则实数m 的取值范围为[-1,3]. 答案:[-1,3]12.若命题p :关于x 的不等式ax +b >0的解集是⎩⎨⎧⎭⎬⎫x |x >-b a ,命题q :关于x 的不等式(x -a )(x -b )<0的解集是{x |a <x <b },则在命题“p 且q ”、“p 或q ”、“非p ”、“ 非q ”中,是真命题的有________.解析:依题意可知命题p 和q 都是假命题,所以“p 且q ”为假、“p 或q ”为假、“非p ”为真、“非q ”为真.答案:非p ,非q[能力提升组]13.已知命题p 1:存在x 0∈R ,使得x 20+x 0+1<0成立;p 2:对任意x ∈[1,2],x 2-1≥0.以下命题为真命题的是( )A .(非p 1)且(非p 2)B .p 1或(非p 2)C .(非p 1)且p 2D .p 1且p 2解析:C [∵方程x 20+x 0+1=0的判别式Δ=12-4=-3<0,∴x 20+x 0+1<0无解,故命题p 1为假命题,非p 1为真命题;由x 2-1≥0,得x ≥1或x ≤-1.∴对任意x ∈[1,2],x 2-1≥0,故命题p 2为真命题, 非p 2为假命题.∵非p 1为真命题,p 2为真命题, ∴(非p 1)且p 2为真命题,选C.]14.已知命题p :任意x ∈R,2x+12x >2,命题q :存在x 0∈⎣⎢⎡⎦⎥⎤0,π2,使sin x 0+cos x 0=12,则下列命题中为真命题的是( )A .非p 且非qB .非p 且qC .p 且非qD .p 且q解析:A [命题p :任意x ∈R,2x+12x >2,当x =0时,命题不成立.所以命题p 是假命题,则非p是真命题;命题q :任意x ∈⎣⎢⎡⎦⎥⎤0,π2,使sin x +cos x =2sin ⎝ ⎛⎭⎪⎫x +π4∈[1,2],所以存在x 0∈⎣⎢⎡⎦⎥⎤0,π2,使sin x 0+cos x 0=12,不正确,则非q 是真命题.所以非p 且非q .故选A.]15.若“任意x ∈⎣⎢⎡⎦⎥⎤-π4,π4,m ≤tan x +1”为真命题,则实数m 的最大值为________. 解析:由“任意x ∈⎣⎢⎡⎦⎥⎤-π4,π4,m ≤tan x +1”为真命题,可得-1≤tan x ≤1,∴0≤tan x +1≤2,∴实数m 的最大值为0.答案:016.(2019·洛阳市一模)已知p :任意x ∈⎣⎢⎡⎦⎥⎤14,12,2x <m (x 2+1),q :函数f (x )=4x +2x +1+m -1存在零点,若“p 且q ”为真命题,则实数m 的取值范围是________.解析:已知p :任意x ∈⎣⎢⎡⎦⎥⎤14,12,2x <m (x 2+1),故m >2x x 2+1.令g (x )=2x x 2+1,则g (x )在⎣⎢⎡⎦⎥⎤14,12递增,所以g (x )≤g ⎝ ⎛⎭⎪⎫12=45,故p 为真时:m >45;q :函数f (x )=4x +2x +1+m -1=(2x +1)2+m -2,令f (x )=0,得2x=2-m -1. 若f (x )存在零点,则2x=2-m -1>0, 解得m <1, 故q 为真时,m <1.若“p 且q ”为真命题,则实数m 的取值范围是⎝ ⎛⎭⎪⎫45,1. 答案:⎝ ⎛⎭⎪⎫45,1第二章 函数、导数及其应用 第1节 函数的概念及其表示 学生用书 课时冲关四[基础训练组]1.若函数y =f (x )的定义域为M ={x |-2≤x ≤2},值域为N ={y |0≤y ≤2},则函数y =f (x )的图像可能是( )解析:B [可以根据函数的概念进行排除,使用筛选法得到答案.] 2.(2016·全国Ⅱ卷)下列函数中,其定义域和值域分别与函数y =10lg x的定义域和值域相同的是( )A .y =xB .y =lg xC .y =2xD .y =1x解析:D [函数y =10lg x的定义域和值域均为(0,+∞);函数y =x 的定义域和值域均为R ,不满足要求;函数y =lg x 的定义域为(0,+∞),值域为R ,不满足要求;函数y =2x的定义域为R ,值域为(0,+∞),不满足要求;函数y =1x的定义域和值域均为(0,+∞),满足要求.故选D.]3.已知f ⎝ ⎛⎭⎪⎫1+x x =x 2+1x 2+1x ,则f (x )=( )A .(x +1)2(x ≠1) B .(x -1)2(x ≠1) C .x 2-x +1(x ≠1)D .x 2+x +1(x ≠1) 解析:C [f ⎝ ⎛⎭⎪⎫1+x x =x 2+1x 2+1x =x +2x 2-x +1x +1,令x +1x=t ,得f (t )=t 2-t +1(t ≠1),即f (x )=x 2-x +1(x ≠1).故选C.]4.(2015·全国Ⅰ卷)已知函数f (x )=⎩⎪⎨⎪⎧2x -1-2,x ≤1-log 2x +,x >1,且f (a )=-3,则f (6-a )=( )A .-74B .-54C .-34D .-14解析:A [当a ≤1时,2a -1-2=-3,无解;当a >1时,-log 2(a +1)=-3,得a =7, 所以f (6-a )=f (-1)=2-2-2=-74,故选A.]5.(2019·孝义市模拟)已知函数f (x )=⎩⎪⎨⎪⎧x 2,x ≤1x +4x-3,x >1,( )A .[1,+∞)B .[0,+∞)C .(1,+∞)D .[0,1)∪(1,+∞)解析:B [由f (x )=⎩⎪⎨⎪⎧x 2,x ≤1x +4x-3,x >1,知当x ≤1时,x 2≥0; 当x >1时,x +4x-3≥2x ·4x -3=4-3=1,当且仅当x =4x,即x =2时取“=”. 取并集得f (x )的值域是[0,+∞).]6.图中的图像所表示的函数的解析式f (x )=________.解析:由图像知每段为线段.设f (x )=ax +b ,把(0,0),⎝ ⎛⎭⎪⎫1,32和⎝ ⎛⎭⎪⎫1,32,(2,0)分别代入求解,得⎩⎪⎨⎪⎧a =32,b =0,⎩⎪⎨⎪⎧a =-32,b =3.答案:f (x )=⎩⎪⎨⎪⎧32x ,0≤x ≤13-32x ,1<x ≤27.若函数y =f (x )的值域是[1,3],则函数F (x )=1-2f (x +3)的值域是________. 解析:∵1≤f (x )≤3,∴-6≤-2f (x +3)≤-2, ∴-5≤1-2f (x +3)≤-1,即F (x )的值域为[-5,-1]. 答案: [-5,-1]8.(2019·东莞市模拟)已知函数f (x )=ax -b (a >0),f (f (x ))=4x -3,则f (2)=__________. 解析:∵f (x )=ax -b ,∴f (f (x ))=f (ax -b )=a (ax -b )-b =a 2x -ab -b =4x -3.∴⎩⎪⎨⎪⎧a 2=4ab +b =3,且a >0,∴a =2,b =1.∴f (x )=2x -1,∴f (2)=2×2-1=3. 答案:39.二次函数f (x )满足f (x +1)-f (x )=2x ,且f (0)=1. (1)求f (x )的解析式; (2)解不等式f (x )>2x +5.解:(1)设二次函数f (x )=ax 2+bx +c (a ≠0). ∵f (0)=1,∴c =1.把f (x )的表达式代入f (x +1)-f (x )=2x ,有a (x +1)2+b (x +1)+1-(ax 2+bx +1)=2x .∴2ax +a +b =2x . ∴a =1,b =-1. ∴f (x )=x 2-x +1.(2)由x 2-x +1>2x +5,即x 2-3x -4>0, 解得x >4或x <-1.故原不等式解集为{x |x >4,或x <-1}. 10.已知函数f (x )=x ·|x |-2x . (1)求函数f (x )=0时x 的值;(2)画出y =f (x )的图像,并结合图像写出f (x )=m 有三个不同实根时,实数m 的取值范围.解:(1)由f (x )=0可解得x =0,x =±2,所以函数f (x )=0时,x 的值为-2,0,2. (2)f (x )=x |x |-2x ,即f (x )=⎩⎪⎨⎪⎧x 2-2x ,x ≥0,-x 2-2x ,x <0.图像如图,由图像可得实数m ∈(-1,1).[能力提升组]11.(2019·遂宁市模拟)设函数f (x )=x -1,则f ⎝ ⎛⎭⎪⎫x 2+f ⎝ ⎛⎭⎪⎫4x 的定义域为( ) A.⎣⎢⎡⎦⎥⎤12,4 B .[2,4]C .[1,+∞)D.⎣⎢⎡⎦⎥⎤14,2 解析:B [∵函数f (x )=x -1的定义域为[1,+∞),∴⎩⎪⎨⎪⎧x 2≥14x ≥1,解得2≤x ≤4.∴f ⎝ ⎛⎭⎪⎫x 2+f ⎝ ⎛⎭⎪⎫4x 的定义域为:[2,4].]12.已知f (x )=⎩⎪⎨⎪⎧1x +2,-1≤x ≤0,x 2-2x ,0<x ≤1,若f (2m -1)<12,则m 的取值范围是( )A .m >12B .m <12C .0≤m <12D.12<m ≤1 解析:D [由题得⎩⎪⎨⎪⎧ -1≤2m -1≤0,12m +1<12,或⎩⎪⎨⎪⎧0<2m -1≤1,m -2-m -12,解得12<m ≤1,故选D.]13.若函数f (x )=x 2+2ax -a 的定义域为R ,则a 的取值范围为________. 解析:由题意知x 2+2ax -a ≥0恒成立.∴x 2+2ax -a ≥0恒成立, ∴Δ=4a 2+4a ≤0,∴-1≤a ≤0. 答案:[-1,0]14.行驶中的汽车在刹车时由于惯性作用,要继续往前滑行一段距离才能停下,这段距离叫做刹车距离.在某种路面上,某种型号汽车的刹车距离y (米)与汽车的车速x (千米/时)满足下列关系:y =x 2200+mx +n (m ,n 是常数).如图是根据多次实验数据绘制的刹车距离y (米)与汽车的车速x (千米/时)的关系图.(1)求出y 关于x 的函数表达式;(2)如果要求刹车距离不超过25.2米,求行驶的最大速度. 解:(1)由题意及函数图像,得⎩⎪⎨⎪⎧402200+40m +n =8.4,602200+60m +n =18.6,解得m =1100,n =0,所以y =x 2200+x100(x ≥0).(2)令x 2200+x100≤25.2,得-72≤x ≤70.∵x ≥0,∴0≤x ≤70.故行驶的最大速度是70千米/时.第2节 函数的单调性与最值 学生用书 课时冲关五[基础训练组]2.已知函数f (x )=2ax 2+4(a -3)x +5在区间(-∞,3)上是减函数,则a 的取值范围是( )A.⎝ ⎛⎭⎪⎫0,34B.⎣⎢⎡⎭⎪⎫0,34C.⎝ ⎛⎦⎥⎤0,34 D.⎣⎢⎡⎦⎥⎤0,34 解析:D [当a =0时,f (x )=-12x +5,在(-∞,3)上是减函数;当a ≠0时,由⎩⎪⎨⎪⎧a >0-a -4a ≥3,得0<a ≤34.综上,a 的取值范围是0≤a ≤34.]3.(2019·聊城市模拟)函数y =ln (x 2-4x +3)的单调减区间为( ) A .(2,+∞) B .(3,+∞) C .(-∞,2)D .(-∞,1)解析:D [令t =x 2-4x +3>0,求得x <1,或x >3, 故函数的定义域为{x |x <1,或x >3},且y =ln t .由二次函数的性质得,t 在区间(-∞,1)上为减函数,在区间(3,+∞)为增函数,又y =ln t 在t ∈(0,+∞)上为增函数,根据复合函数单调性的判断方法,知函数y =ln (x 2-4x+3)的单调减区间为(-∞,1).]4.已知f (x )=⎩⎪⎨⎪⎧a -x +4a ,x <1,log a x ,x ≥1是(-∞,+∞)上的减函数,那么a 的取值范围是( ) A .(0,1)B.⎝ ⎛⎭⎪⎫0,13C.⎣⎢⎡⎭⎪⎫17,13 D.⎣⎢⎡⎭⎪⎫17,1 解析:C [由题意知⎩⎪⎨⎪⎧3a -1<0,0<a <1,a -+4a ≥log a 1,即⎩⎪⎨⎪⎧a <13,0<a <1,a ≥17,所以17≤a <13.故选C.]5.已知函数f (x )=x 2-2ax +a 在区间(-∞,1)上有最小值,则函数g (x )=f xx在区间(1,+∞)上一定( )A .有最小值B .有最大值C .是减函数D .是增函数解析:D [由题意知a <1,∴g (x )=f x x =x +ax-2a ,当a <0时,显然g (x )在区间(1,+∞)上单调递增,当a >0时,g (x )在[a ,+∞)上是增函数,故在(1,+∞)上为增函数,∴g (x )在(1,+∞)上一定是增函数.]6.(2019·日照市模拟)已知奇函数f (x )为R 上的减函数,若f (3a 2)+f (2a -1)≥0,则实数a 的取值范围是________.解析:∵奇函数f (x )为R 上的减函数, ∴不等式f (3a 2)+f (2a -1)≥0, 等价为f (3a 2)≥-f (2a -1)=f (1-2a ),即3a 2≤1-2a ,即3a 2+2a -1≤0,得(a +1)(3a -1)≤0,得-1≤a ≤13,即实数a 的取值范围是⎣⎢⎡⎦⎥⎤-1,13. 答案:⎣⎢⎡⎦⎥⎤-1,137.设函数f (x )=ax +1x +2a在区间(-2,+∞)上是增函数,那么a 的取值范围是________. 解析:f (x )=ax +2a 2-2a 2+1x +2a =a -2a 2-1x +2a,定义域为(-∞,-2a )∪(-2a ,+∞), ∵函数f (x )在区间(-2,+∞)上是增函数,∴⎩⎪⎨⎪⎧2a 2-1>0-2a ≤-2即⎩⎪⎨⎪⎧2a 2-1>0a ≥1,解得a ≥1.答案:[1,+∞)8.(2019·沈阳市一模)已知函数f (x )=|log 3x |,实数m ,n 满足0<m <n ,且f (m )=f (n ),若f (x )在[m 2,n ]的最大值为2,则nm=________.解析:∵f (x )=|log 3x |,正实数m ,n 满足m <n ,且f (m )=f (n ),∴-log 3m =log 3n ,∴mn =1. ∵f (x )在区间[m 2,n ]上的最大值为2,函数f (x )在[m 2,1)上是减函数,在(1,n ]上是增函数, ∴-log 3m 2=2,或log 3n =2.若-log 3m 2=2是最大值,得m =13,则n =3,此时log 3n =1,满足题意条件.此时n m =3÷13=9.同理:若log 3n =2是最大值,得n =9,则m =19,此时-log 3m 2=4,不满足题意条件. 综合可得 m =13,n =3,nm =9.答案:9 9.已知f (x )=xx -a(x ≠a ),(1)若a =-2,试证f (x )在(-∞,-2)内单调递增;(2) 且f (x )在(1,+∞)内单调递减,求a 的取值范围. 解:(1)证明:任取x 1<x 2<-2, 则f (x 1)-f (x 2)=x 1x 1+2-x 2x 2+2=x 1-x 2x 1+x 2+.∵(x 1+2)(x 2+2)>0,x 1-x 2<0, ∴f (x 1)<f (x 2).∴f (x )在(-∞,-2)内单调递增. (2)任设1<x 1<x 2,则f (x 1)-f (x 2)=x 1x 1-a -x 2x 2-a=a x 2-x 1x 1-a x 2-a.∵a >0,x 2-x 1>0,∴要使f (x 1)-f (x 2)>0,只需(x 1-a )(x 2-a )>0恒成立,∴a ≤1. 综上所述知a 的取值范围是(0,1].10.(2019·西安市模拟)已知定义在R 上的函数f (x )满足: ①f (x +y )=f (x )+f (y )+1,②当x >0时,f (x )>-1. (1)求f (0)的值,并证明f (x )在R 上是单调增函数. (2)若f (1)=1,解关于x 的不等式f (x 2+2x )+f (1-x )>4. 解:(1)令x =y =0得f (0)=-1. 在R 上任取x 1>x 2,则x 1-x 2>0,f (x 1-x 2)>-1.又f (x 1)=f ((x 1-x 2)+x 2)=f (x 1-x 2)+f (x 2)+1>f (x 2), 所以,函数f (x )在R 上是单调增函数. (2)由f (1)=1,得f (2)=3,f (3)=5.由f (x 2+2x )+f (1-x )>4得f (x 2+x +1)>f (3),又函数f (x )在R 上是增函数,故x 2+x +1>3,解得x <-2或x >1, 故原不等式的解集为{x |x <-2,或x >1}.[能力提升组]11.(2019·天津市一模)已知函数f (x )是定义在R 上的偶函数,且在区间[0,+∞)上对于任意两个不相等的实数x 1,x 2恒有f x 1-f x 2x 1-x 2<0成立,若实数a 满足f (log 6a )≥f (-1),则a 的取值范围是( )A.⎣⎢⎡⎦⎥⎤16,6 B.⎣⎢⎡⎭⎪⎫16,+∞ C .(0,6]D .(-∞,6]解析:A [根据题意,函数f (x )在区间[0,+∞)上有f x 1-f x 2x 1-x 2<0成立,则函数f (x )在区间[0,+∞)上是减函数,又函数f (x )为偶函数,则f (log 6a )≥f (-1)等价于f (|log 6a |)≥f (1), 即|log 6a |≤1,解得-1≤log 6a ≤1,所以16≤a ≤6.]12.设函数y =f (x )在(-∞,+∞)内有定义.对于给定的正数k ,定义函数f k (x )=⎩⎪⎨⎪⎧f x ,f x k ,k ,fx k ,取函数f (x )=2-|x |.当k =12时,函数f k (x )的单调递增区间为( )A .(-∞,0)B .(0,+∞)C .(-∞,-1)D .(1,+∞)解析:C [由f (x )>12,得-1<x <1.由f (x )≤12,得x ≤-1或x ≥1.所以f 12(x )=⎩⎪⎨⎪⎧2-x,x ≥1,12,-1<x <1,2x,x ≤-1.故f 12(x )的单调递增区间为(-∞,-1).]13.对于任意实数a ,b ,定义min{a ,b }=⎩⎪⎨⎪⎧a ,a ≤b ,b ,a >b .设函数f (x )=-x +3,g (x )=log 2x ,则函数h (x )=min{f (x ),g (x )}的最大值是________.解析:依题意,h (x )=⎩⎪⎨⎪⎧log 2x ,0<x ≤2,-x +3,x >2.当0<x ≤2时,h (x )=log 2x 是增函数,当x >2时,h (x )=3-x 是减函数,∴h (x )在x =2时,取得最大值h (2)=1.答案:114.已知f (x )是定义在[-1,1]上的奇函数,且f (1)=1,若a ,b ∈[-1,1],a +b ≠0时,有f a +f ba +b>0成立.(1)判断f (x )在[-1,1]上的单调性,并证明它;(2)解不等式:f ⎝ ⎛⎭⎪⎫x +12<f ⎝ ⎛⎭⎪⎫1x -1;(3)若f (x )≤m 2-2am +1对所有的a ∈[-1,1]恒成立,求实数m 的取值范围. 解:(1)任取x 1,x 2∈[-1,1],且x 1<x 2, 则-x 2∈[-1,1],∵f (x )为奇函数, ∴f (x 1)-f (x 2)=f (x 1)+f (-x 2) =f x 1+f -x 2x 1+-x 2·(x 1-x 2),由已知得f x 1+f -x 2x 1+-x 2>0,x 1-x 2<0,∴f (x 1)-f (x 2)<0,即f (x 1)<f (x 2). ∴f (x )在[-1,1]上单调递增. (2)∵f (x )在[-1,1]上单调递增,∴⎩⎪⎨⎪⎧x +12<1x -1,-1≤x +12≤1,-1≤1x -1≤1.∴-32≤x <-1.所以,不等式的解集为⎩⎨⎧⎭⎬⎫x |-32≤x <-1.(3)∵f (1)=1,f (x )在[-1,1]上单调递增. ∴在[-1,1]上,f (x )≤1. 问题转化为m 2-2am +1≥1,即m 2-2am ≥0,对a ∈[-1,1]恒成立. 设g (a )=-2m ·a +m 2≥0.①若m =0,则g (a )=0≥0,对a ∈[-1,1]恒成立.②若m ≠0,则g (a )为a 的一次函数,若g (a )≥0,对a ∈[-1,1]恒成立,必须有g (-1)≥0且g (1)≥0, ∴m ≤-2或m ≥2.∴m 的取值范围是m =0或m ≥2或m ≤-2.第3节 函数的奇偶性与周期性学生用书 课时冲关六[基础训练组]1.(2019·呼和浩特市一模)下列函数中,既是偶函数又在(-∞,0)上单调递减的函数是( ) A .y =-x 3B .y =2|x |C .y =x -2D .y =log 3(-x )解析:B [选项A ,函数是奇函数,不满足条件;选项B ,函数是偶函数,当x <0时,y =2|x |=2-x=⎝ ⎛⎭⎪⎫12x 是减函数,满足条件;选项C ,函数是偶函数,当x <0时,y =x -2=1x 2是增函数,不满足条件;选项D ,函数的定义域为(-∞,0),不关于原点对称,为非奇非偶函数,不满足条件.故选B.]2.(2019·赣州市一模)已知偶函数f (x )在[0,+∞)单调递减,f (2)=0,若f (x -1)>0,则x 的取值范围是( )A .(3,+∞)B .(-∞,-3)C .(-∞,-1)∪(3,+∞)D .(-1,3)解析:D [由偶函数f (x )在[0,+∞)单调递减,f (2)=0,得f (x )=f (|x |),因为f (x -1)>0,则f (|x -1|)>f (2),即|x -1|<2,解得-1<x <3,即x 的取值范围是(-1,3).故选D.]3.(2019·保定市一模)已知函数f (x )=⎩⎪⎨⎪⎧1,x >0-1,x <0,设g (x )=f xx 2,则g (x )是( ) A .奇函数,在(-∞,0)上递增,在(0,+∞)上递增 B .奇函数,在(-∞,0)上递减,在(0,+∞)上递减 C .偶函数,在(-∞,0)上递增,在(0,+∞)上递增 D .偶函数,在(-∞,0)上递减,在(0,+∞)上递减解析:B [根据题意,g (x )=f xx 2=⎩⎪⎨⎪⎧1x 2,x >0,-1x 2,x <0,其定义域关于原点对称.设x >0,则-x <0,g (-x )=-1-x2=-1x2=-g (x );设x <0,则-x >0,g (-x )=1-x2=1x2=-g (x ),故g (x )为奇函数.又g (x )=1x2=x -2在区间(0,+∞)上递减,则g (x )在(-∞,0)上也递减.故选B.]4.已知f (x )=lg ⎝ ⎛⎭⎪⎫21-x +a 是奇函数,则使f (x )<0的x 的取值范围是( )A .(-1,0)B .(0,1)C .(-∞,0)D .(-∞,0)∪(1,+∞)解析:A [∵f (x )=lg ⎝ ⎛⎭⎪⎫21-x +a 是奇函数,∴f (-x )+f (x )=lg ⎝⎛⎭⎪⎫21+x +a +lg ⎝ ⎛⎭⎪⎫21-x +a =0,解得a =-1,即f (x )=lg 1+x 1-x ,由f (x )=lg1+x 1-x <0,得0<1+x1-x<1,解得-1<x <0,故选A.] 5.(2019·安庆市模拟)定义在R 上的奇函数f (x )满足:f (x +1)=f (x -1),且当-1<x <0时,f (x )=2x-1,则f (log 220)等于( )A.14 B .-14C .-15D.15解析:D [∵f (x +1)=f (x -1),∴函数f (x )是周期为2的周期函数, 又∵log 232>log 220>log 216,∴4<log 220<5, ∴f (log 220)=f (log 220-4)=f ⎝ ⎛⎭⎪⎫log 254 =-f ⎝⎛⎭⎪⎫-log 254.又∵x ∈(-1,0)时,f (x )=2x-1,∴f ⎝ ⎛⎭⎪⎫-log 254=-15,f (log 220)=15.故选D.]6.已知f (x ),g (x )分别是定义在R 上的奇函数和偶函数,且f (x )-g (x )=⎝ ⎛⎭⎪⎫12x,则f (1),g (0),g (-1)之间的大小关系是________.解析:在f (x )-g (x )=⎝ ⎛⎭⎪⎫12x 中,用-x 替换x ,得f (-x )-g (-x )=2x,由于f (x ),g (x )分别是定义在R 上的奇函数和偶函数,所以f (-x )=-f (x ),g (-x )=g (x ),因此得-f (x )-g (x )=2x.于是解得f (x )=2-x-2x 2,g (x )=-2-x +2x2,于是f (1)=-34,g (0)=-1,g (-1)=-54,故f (1)>g (0)>g (-1).答案:f (1)>g (0)>g (-1)7.(2019·惠州市模拟)已知函数f (x )=2x -2-x,则不等式f (2x +1)+f (1)≥0的解集是________. 解析:根据题意,有f (-x )=2-x-2x =-(2x -2-x)=-f (x ),则函数f (x )为奇函数, 又函数f (x )在R 上为增函数,f (2x +1)+f (1)≥0等价于f (2x +1)≥-f (1),即f (2x +1)≥f (-1),所以2x +1≥-1,解得x ≥-1,即不等式的解集为[-1,+∞). 答案:[-1,+∞)8.(2019·泰安市模拟)定义在R 上的函数f (x )满足f (x +y )=f (x )+f (y ),f (x +2)=-f (x )且f (x )在[-1,0]上是增函数,给出下列几个命题:①f (x )是周期函数;②f (x )的图像关于x =1对称;③f (x )在[1,2]上是减函数;④f (2)=f (0),其中正确命题的序号是________(请把正确命题的序号全部写出).解析:f (x +y )=f (x )+f (y )对任意x ,y ∈R 恒成立.令x =y =0, 所以f (0)=0.令x +y =0,所以y =-x ,所以f (0)=f (x )+f (-x ). 所以f (-x )=-f (x ),所以f (x )为奇函数.因为f (x )在x ∈[-1,0]上为增函数,又f (x )为奇函数,所以f (x )在[0,1]上为增函数.由f (x +2)=-f (x )⇒f (x +4)=-f (x +2)⇒f (x +4)=f (x ),所以周期T =4,即f (x )为周期函数.f (x +2)=-f (x )⇒f (-x +2)=-f (-x ).又因为f (x )为奇函数,所以f (2-x )=f (x ),所以函数关于x =1对称. 由f (x )在[0,1]上为增函数,又关于x =1对称,所以f (x )在[1,2]上为减函数. 由f (x +2)=-f (x ),令x =0得f (2)=-f (0)=f (0). 答案: ①②③④9.已知函数f (x )=⎩⎪⎨⎪⎧-x 2+2x ,x >0,0,x =0,x 2+mx ,x <0是奇函数.(1)求实数m 的值;(2)若函数f (x )在区间[-1,a -2]上单调递增,求实数a 的取值范围. 解:(1)设x <0,则-x >0,所以f (-x )=-(-x )2+2(-x )=-x 2-2x . 又f (x )为奇函数,所以f (-x )=-f (x ), 于是x <0时,f (x )=x 2+2x =x 2+mx , 所以m =2.(2)由(1)知f (x )在[-1,1]上是增函数, 要使f (x )在[-1,a -2]上单调递增.结合f (x )的图像知⎩⎪⎨⎪⎧a -2>-1,a -2≤1,所以1<a ≤3,故实数a 的取值范围是(1,3].10.已知函数f (x )是定义在R 上的奇函数,且它的图像关于直线x =1对称. (1)求证:f (x )是周期为4的周期函数;(2)若f (x )=x (0<x ≤1),求x ∈[-5,-4]时,函数f (x )的解析式. 解:(1)证明:由函数f (x )的图像关于直线x =1对称, 有f (x +1)=f (1-x ),即有f (-x )=f (x +2). 又函数f (x )是定义在R 上的奇函数, 故有f (-x )=-f (x ).故f (x +2)=-f (x ). 即f (x )是周期为4的周期函数.(2)由函数f (x )是定义在R 上的奇函数,有f (0)=0.x ∈[-1,0)时,-x ∈(0,1],f (x )=-f (-x )=-x .故x ∈[-1,0]时,f (x )=-x .x ∈[-5,-4]时,x +4∈[-1,0], f (x )=f (x +4)=--x -4.从而,x ∈[-5,-4]时,函数f (x )=--x -4.[能力提升组]11.函数f (x )满足f (x )·f (x +2)=13,若f (1)=2,则f (99)等于( ) A .13 B .2 C.213D.132 解析:D [∵f (x )·f (x +2)=13,∴f (x +2)=13f x,则f (x +4)=13fx +=1313f x=f (x ),故函数f (x )的周期为4, ∴f (99)=f (3)=13f=132.] 12.(2019·佛山市一模)已知f (x )=2x+a2x 为奇函数,g (x )=bx -log 2(4x+1)为偶函数,则f (ab )=( )A.174B.52 C .-154D .-32解析:D [根据题意,f (x )=2x+a2x 为奇函数,则有f (-x )+f (x )=0,即(2-x+a2-x )+⎝⎛⎭⎪⎫2x+a 2x =0,解得a =-1.。
人教版二年级上册数学课时练第二单元《连加、连减和加减混合》02附答案

课时练第2单元100以内的加法和减法〔二〕连加、连减和加减混合一、单项选择题1.三个加数都是24,和是〔〕。
A.62B.48C.72D.242.一根电线长50米,先用去13米,又用去17米,还剩多少米?错误的算式是〔〕。
A.50-13+17B.50-13-17C.50-〔13+17〕3.60元可以换1个50元和〔〕个5元。
A.2B.20C.104.停车场有卡车35辆,有轿车38辆。
开走了17辆,现在有〔〕辆车。
A.66B.46C.56二、判断题5.妈妈给小明买了一个生日蛋糕,花了48元,妈妈给售货员2张20元的,1张5元和3张1元的,钱正好够。
〔〕6.75-18+12=75-30=45〔〕三、填空题7.22+11+55=________8.11+12+13=________×39.在横线上填上》>〞》<〞或》=〞30-15+9________6×3+667-29-12________67-〔29-12〕4×〔54÷6〕________18+8×25+35÷5________〔25+7〕÷44×9÷6________72÷9×27×9-18________8×8-19四、计算题10.直接写出得数38+45=54+27=83-47=65-28=700+600=50+570=390+80=810-70=81÷9=58÷7=88-18+5=60-0+25=11.直接写出得数15+20=54-50=20+75=80+10=17+53=17+13=29-10=22+37=90-54=46+25-17=五、解答题12.小方有38个苹果,小红有26个苹果,被小丽拿走了48个苹果。
现在还有多少个苹果?六、综合题13.按运算顺序计算。
〔1〕24+8-6〔2〕28÷7×6〔3〕3×6÷9七、应用题14.看图答复19元36元6元9元27元〔1〕买1辆和2辆需要多少元?〔2〕的价钱是的多少倍?〔3〕买3辆需要多少元?答案解析局部一、单项选择题1.C2.A3.A4.C二、判断题5.正确6.错误三、填空题7.888.129.=;<;>;>;<;=四、计算题10.38+45=83;54+27=81;83-47=36;65-28=37;700+600=1300;50+570=620;390+80=470;810-70=740;81÷9=9;58÷7=8……2;88-18+5=75;60-0+25=85.11.解:15+20=35;54-50=4;20+75=95;80+10=90;17+53=70;17+13=30;29-10=19;22+37=59;90-54=36;46+25-17=54。
人教版小学二年级下册数学课时同步练习试题及答案(全册)
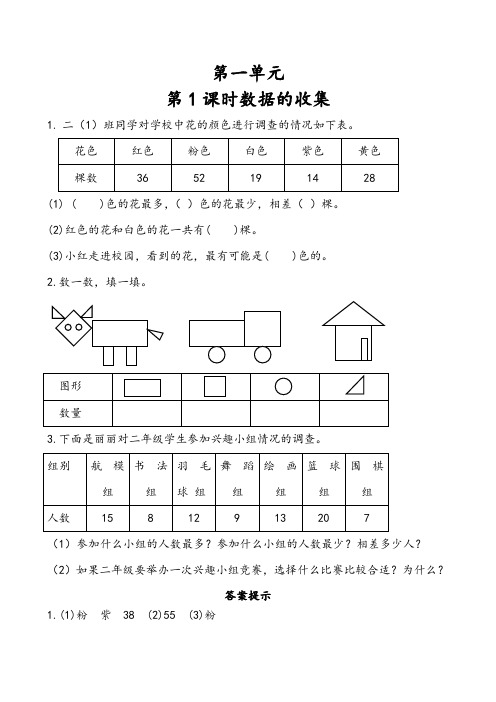
第一单元第1课时数据的收集1. 二(1)班同学对学校中花的颜色进行调查的情况如下表。
(1) ( )色的花最多,( )色的花最少,相差( )棵。
(2)红色的花和白色的花一共有( )棵。
(3)小红走进校园,看到的花,最有可能是( )色的。
2.数一数,填一填。
3.下面是丽丽对二年级学生参加兴趣小组情况的调查。
(1)参加什么小组的人数最多?参加什么小组的人数最少?相差多少人? (2)如果二年级要举办一次兴趣小组竞赛,选择什么比赛比较合适?为什么?答案提示1.(1)粉 紫 38 (2)55 (3)粉2.5 3 4 43.(1)篮球组围棋组 13人(2)篮球因为参加这个小组的人数最多。
第2课时用多种方法对数据进行记录整理2.用画“正”字的方法先数一数,再填一填。
(1)(2) ( )的个数最多,()的个数最少。
2.下面是几位小朋友对森林动物园中几种小动物的数量统计情况。
小刺猬:正正正正正正正正正正小象:√√√√√√√√小猴子:○○○○○○鳄鱼:□□□□□(1)根据上面的统计情况把下面的表格补充完整。
(2)()最多,()最少,相差()只。
(3)小猴子和小刺猬一共有()只。
(4)这些小动物一共有()只。
3.下面是某路口1分钟内通过的车辆的统计情况。
小轿车:客车:货车:面包车:(1)哪种车辆通过的最多?哪种车辆通过的最少?(2)如果一个2辆车,通过的车最多的有多少辆?答案提示1.正正正正正正 (1)7 4 12 (2)2.(1)50 8 6 5(2)小刺猬鳄鱼 45 (3)56 (4)693.(1)小轿车通过的最多;货车通过的最少。
(2)16第3课时练习一3.光明小学四个课外活动小组的学生人数情况如下:数学小组:男生12人、女生11人。
美术小组:男生10人、女生11人。
航模小组:男生18人、女生7人。
音乐小组:男生15人、女生15人。
根据上面的数据完成下面的统计表,并回答问题。
(1) ( )小组的男生人数最多。
2019届高三语文一轮复习第二部分专题二课时冲关十八小说阅读训练(二)环境描写练习案

课时冲关十八小说阅读训练(二)环境描写[对点练]阅读下面的文字,完成文后题目。
洗礼[法]莫泊桑男人们打扮得漂漂亮亮,在农庄门前等候。
五月的太阳把它明亮的光辉倾泻在开着花的苹果树上。
苹果树周围,不断有雪片似的小花瓣撒下来,落入深深的草丛,草丛中蒲公英盛开如火,虞美人好像点点血滴。
一只乳房饱满的大肚子母猪睡在厩肥堆边;一大群小猪在它周围转来转去,它们的尾巴像绳子似的卷曲着。
突然间,在那些庄院的大树后面,响起了教堂的钟声,当当当,这微弱而又遥远的召唤在欢乐的天空里播送着。
燕子像箭一样地掠过蓝色天空。
牛圈的气味掺杂着苹果树甜蜜蜜的气息不时飘过。
那些男人中间的一个转身对着房子喊道:“快点,快点,梅利娜,打钟啦!”他大约三十岁光景,是个魁梧的庄稼汉。
他的父亲,一个老头儿,像橡树的躯干那样虬劲盘结,说道:“女人家总不肯早点准备好。
”老头儿的另外两个儿子笑了,其中一个对刚才高声叫喊的大哥说:“去催催吧,波利特。
不然到了中午也出不来。
”那年轻人走进房子去了。
这当儿,保姆在门口出现了,裹在白襁褓里的两个月的婴儿睡在她的肚子上。
随后,那母亲也挽着丈夫的胳膊出来了。
她长得高大壮实,才十八岁,气色红润,面带笑容。
亲属都跟在后面出发了。
保姆抱着怀里的小生命,小心地避开路上的水洼。
老人们规规矩矩地走着。
年轻人却想跳舞了,他们望着路边那些来看热闹的姑娘们。
婴儿的父亲和母亲一本正经地跟在孩子后面,这孩子日后要在人世上代替他们,要继续他们的姓氏,当蒂这个姓氏在全区是有名的。
现在可以望见有尖顶钟楼的教堂了,那钟声在召唤新生的婴儿第一次到天主的家里来。
一条狗跟着他们。
有人扔给它几颗糖杏仁,它就围着人欢蹦乱跳。
教堂的门敞开着。
神父正在祭坛前面等候。
他是个高个子、红头发的年轻人,瘦而结实,也姓当蒂,是孩子的叔叔,孩子父亲的另外一个兄弟。
他按照仪式给他的侄子施了洗礼。
洗礼完毕,这一家人在门口等着神父脱掉祭披又上路了。
现在大家走得很快,因为心里惦记着那顿饭。
2015年高考数学一轮复习课时训练大题冲关集训(二)

大题冲关集训(二)1.已知函数f(x)=2sin(x-),x∈R.(1)求f()的值;(2)设α,β∈[0,],f(3α+)=,f(3β+2π)=,求cos(α+β)的值.解:(1)f()=2sin(×-)=2sin =.(2)由f(3α+)=,得2sin[×(3α+)-]=2sin α=,∴sin α=.由f(3β+2π)=,得2sin[×(3β+2π)-]=2sin(β+)=2cos β=,∴cos β=,∵α,β∈[0,],∴cos α===,sin β===,故cos(α+β)=cos αcos β-sin αsin β=×-×=.2.(2013珠海二模)已知函数f(x)=Asin(ωx+ϕ){A>0,ω>0,|ϕ|<}(x∈R)的部分图象如图所示.(1)求f(x)的解析式;(2)若g(x)=f(x-)+f(x)且tan α=3,求g(α).解:(1)由题中图象知A=1,=-(-)=,∴T=π,∴ω==2,又2×(-)+ϕ=0得ϕ=,∴f(x)=sin(2x+).(2)∵f(x)=sin(2x+),∴g(x)=sin+sin(2x+)=sin(2x-)+sin(2x+)=(sin 2xcos-cos 2xsin)+sin 2xcos+cos 2xsin=2sin 2x.∵tan α=3,∴g(α)=2sin 2α====.3.(2013肇庆一模)已知函数f(x)=Asin(4x+ϕ)(A>0,0<ϕ<π)在x=时取得最大值2.(1)求f(x)的最小正周期;(2)求f(x)的解析式;(3)若α∈[-,0],f(α+)=,求sin(2α-)的值.解:(1)f(x)的最小正周期为T==.(2)由f(x)的最大值是2知,A=2,又f(x)max=f()=2sin(4×+ϕ)=2,即sin(+ϕ)=1,∵0<ϕ<π,∴<+ϕ<,∴+ϕ=,∴=,∴f(x)=2sin(4x+).(3)由(2)得f(α+)=2sin[4(α+)+]=,即sin(α+)=,∴cos α=,∵α∈[-,0],∴sin α=-=-=-,∴sin 2α=2sin αcos α=2×(-)×=-,cos 2α=2cos2α-1=2×()2-1=-,∴sin(2α-)=sin 2αcos -cos 2αsin=-×+×=-.4.(2013年高考山东卷)设△ABC的内角A,B,C所对的边分别为a,b,c,且a+c=6,b=2,cos B=.(1)求a,c的值;(2)求sin(A-B)的值.解:(1)由余弦定理得cos B=,即=cos B,得=.∴ac=9.联立得a=3,c=3.(2)由a=3,b=2,c=3,∴cos A==,∴sin A==,又cos B=得sin B=,∴sin(A-B)=sin Acos B-cos Asin B=×-×=.5.(2013重庆育才中学月考)在△ABC中,a、b、c分别为角A、B、C 的对边,若m=(sin2,1),n=(-2,cos 2A+1),且m⊥n.(1)求角A的大小;(2)当a=2,且△ABC的面积S=时,求边c的值和△ABC的面积. 解:(1)由于m⊥n,所以m·n=-2sin2+cos 2A+1=1-2cos2+2cos2A-1=2cos2A-cos A-1=(2cos A+1)(cos A-1)=0.所以cos A=-或cos A=1(舍去),又A∈(0,π),故角A为.(2)由S=及余弦定理得=absin C,整理得tan C=.又C∈(0,π),所以C=.由(1)知A=,故B=C=.又由正弦定理=得c=2,所以△ABC的面积S=acsin B=.6.(2013浙江金丽衢十二校联考)在△ABC中,角A、B、C的对边分别为a、b、c,C=,b=5,△ABC的面积为10.(1)求a、c的值;(2)求sin(A+)的值.解:(1)∵Sabsin C=10,∴a×5×sin =20,得a=8.c2=a2+b2-2abcos C,c===7.(2)∵=,∴sin A===,cos A===,sin(A+)=sin Acos+cos Asin=×+×=.7.(2013惠州市二调)设函数f(x)=msin x+cos x(x∈R)的图象经过点(,1)(1)求f(x)的解析式,并求函数的最小正周期;(2)若f(α+)=且α∈(0,),求f(2α-)的值.解:(1)∵函数f(x)=msin x+cos x(x∈R)的图象经过点(,1),∴msin +cos =1,∴m=1,∴f(x)=sin x+cos x=sin(x+),∴函数的最小正周期T=2π.(2)f(α+)=sin(α++)=sin(α+)=cos α=,∴cos α=.又因为α∈(0,),∴sin α==,∴f(2α-)=sin(2α-+)=sin 2α=2sin αcos α=.。
新人教部编版小学二年级上册数学全册课时练习题
全册课时练习题目录第一单元《长度单位》课时练 (1)1.1统一单位 (1)1.2厘米和用厘米量 (2)1.3米和用米量 (3)1.4认识线段 (5)第二单元《100以内的加法和减法》课时练 (7)2.1两位数加两位数 (7)2.2两位数减两位数—不退位减 (9)2.4用数学 (13)2.5连加、连减 (15)2.6加减混合 (17)2.7加减法的估算 (19)第三单元《角的初步认识》 (21)3.1角的初步认识 (21)3.2直角的初步认识 (23)第四单元《表内乘法(一)》课时练 (25)4.1乘法的初步认识 (25)4.25的乘法口诀 (27)4.32、3、4的乘法口诀 (29)4.4乘加、乘减 (31)4.5用数学 (33)4.66的乘法口诀 (35)第五单元《观察物体》课时练 (37)5.1观察物体 (37)5.3镜面对称 (41)第六单元《表内乘法(二)》课时练 (43)6.17的乘法口诀 (43)6.2倍数的认识 (45)6.38的乘法口诀 (47)6.49的乘法口诀 (49)第七单元《认识时间》课时练 (51)7.1认识时间 (51)第八单元《数学广角一搭配(一)》课时练 (53)8.1数学广角一搭配 (53)第一单元《长度单位》课时练1.1统一单位一、我会看,我会估。
绳子大约有(那么长。
绳子大约有(那么长。
二、我会用作标准。
大约()个长。
大约()个长。
大约()个长。
大约()个长。
三、比高矮。
小马大约有()个高。
山羊大约有()个高。
公鸡大约有()个高。
3条绳子绕在3个大小相同的瓶子上。
()最长,()最短。
数学小博士A B C学校班级姓名学号………….…………………………….密………………………………………封………………..…………………..线…………………………………….…………………….…………………….. 1.2厘米和用厘米量一、看一看,填一填。
1.()厘米01234567892.()厘米01234567893.()厘米1110945678二、量一量,填一填。
中考地理一练通第一部分教材知识冲关八下第七章南方地区课时二“东方明珠”—香港和澳门祖国的神圣领土—台
气候类型 亚热带季风气候
2.港澳与祖国内地的密切联系 (1)发展条件 A.不利条件:香港和澳门地狭人稠,自然资源匮乏。 B.有利条件:两地充分发挥地理位置的优势,依托祖国内地强有力的支持。 (2)经济特点:经济十分繁荣,被誉为“⑦东方明珠”。 香港是重要的国际金融中心、贸易中心、信息服务中心及⑧航运中心。澳门⑨博彩 旅游业发达,是其经济发展的支柱产业。 (3)香港与祖国内地的经济联系十分密切,与内地的经济合作优势互补,互惠互利。 香港与珠江三角洲地区的合作以“⑩前店后厂”为基本模式,香港是“店”,珠江三角 洲地区是“厂”。 内地:丰富的自然资源,众多廉价的劳动力,土地租金低。 香港:充足的资金,先进的技术和管理经验,先进的设备。
第七章 南方地区
课时二 “东方明珠”——香港和澳门、祖国的神圣领土—— 台湾省
考点1 “东方明珠”——香港和澳门
1.特别行政区的概况
项目 香港特别行政区
澳门特别行政区
地理位置 珠江口东岸,与广东省①深圳市相邻 珠江口西岸,与广东省②珠海市相邻
组成
由③香港岛、九龙、“新界”组成 由④澳门半岛、氹仔岛和路环岛组成
符合题意。
人口
约710万(2010年)
约55万(2010年)
面积
1 104平方千米(2010年)
29.7平方千米(2010年)
回归时间 1997年7月1日
1999年12月20日
区花
紫荆花
⑤莲花
政治制度 “⑥一国两制”,祖国内地实行社会主义制度,港、澳实行资本主义制度
土地利用 “上天”——建设高层建筑,“下海”——填海造地
包括台湾岛,以及附近的澎湖列岛、钓鱼岛、赤尾屿等许多小 岛,面积共约36 000平方千米
1.2第二课时知能演练轻松闯关
1.(2019·芜湖质检)在△中,A=60°,=1,=2,则S△的值为()D.2解析:选△=··A=.2.三角形的两边长为3 、5 ,其夹角的余弦是方程5x2-7x-6=0的根,则此三角形的面积是()A.6 22C.8 2D.10 2解析:选A.∵5x2-7x-6=0的两根为-、2,设已知两边夹角为C,则C=-( C=2>1不可能,舍去).∴C=C)=.∴S△=×3×5×=6(2).3.如图,△中,⊥,D在边上,已知=2,=1,∠=45°,则=()A.2 B.5C.4 D.1解析:选B.设=x,==,则=,由余弦定理可知x2=5+4+(1+x)2-2×××,解得x=5.4.(2019·烟台高二检测)如果等腰三角形的周长是底边长的5倍,则它的顶角的余弦值为()A.-C.-解析:选B.设等腰三角形的底边长为a,顶角为θ,则腰长为2a,由余弦定理得,θ==.5.(2019·天津质检)在△中,c=,b=1,B=30°,则△的面积为()或或或解析:选B.根据正弦定理,==30°=.∵c>b,∴C>B=30°,∴C=60°或120°.当C=60°时,A=180°-(B+C)=180°-(30°+60°)=90°,∴△的面积S==;当C=120°时,A=180°-(30°+120°)=30°,∴△的面积S==×1×30°=.6.三角形的一边长为14,这条边所对的角为60°,另两边之比为8∶5,则这个三角形的面积为.解析:设另两边分别为8x,5x,则60°=,解得x=2.故两边长分别是16,10.所以三角形的面积S=×16×10× 60°=40 .答案:407.(2019·高考课标全国卷)在△中,B=120°,=7,=5,则△的面积为.解析:由余弦定理知2=2+2-2·120°,即49=25+2+5,解得=3.故S△=·120°=×5×3×=.答案:8.(2019·湛江调研)在△中,已知B=45°,D是边上一点,=5,=7,=3,则=.解析:在△中,C===.又0°<C<180°,∴C=.在△中,B)=C),∴=B) =××7=.答案:9.在△中,∠A=60°,b=1,S△=,求边a,c.解:由面积公式得×1×c· 60°=,∴c=4.又由余弦定理得a2=1+42-2×1×4× 60°=1+16-2×1×4×=13,∴a=.10.(2019·高考江西卷)在△中,角A,B,C的对边分别为a,b,c.已知3(B-C)-1=6C.(1)求A;(2)若a=3,△的面积为2,求b,c.解:(1)由3(B-C)-1=6 C,得3( C-C)=-1,即(B+C)=-,从而A=-(B+C)=.(2)由于0<A<π,=,所以=.又S△=2,即=2,解得=6.由余弦定理a2=b2+c2-2,得b2+c2=13,解方程组错误!得错误!或错误!1.若△的周长等于20,面积是10,B=60°,则边的长是()A.5 B.6C.7 D.8解析:选C.设△中A、B、C的对边分别为a、b、c,已知B=60°,则由题意,得错误!即错误!解得b=7,∴边的长为7.2.在△中,D为边上一点,=,∠=120°,=2.若△的面积为3-,则∠=.解析:由∠=120°知∠=60°又因为=2,所以S△=· 60°=3-.所以=2(-1),又因为=,所以=-1.过A点作⊥于E点,则S△=·=3-,所以=,又在直角三角形中,=1,所以=,在直角三角形中,=,所以△是等腰直角三角形,所以∠=45°,在直角三角形中,=2-3,所以∠===2+,所以∠=75°,所以∠=180°-75°-45°=60°.答案:60°3.(2019·高考浙江卷)在△中,内角A,B,C的对边分别为a,b,c,且A=B.(1)求角B的大小;(2)若b=3,C=2 A,求a,c的值.解:(1)由A=B及正弦定理A)=B),得B=B,所以B=,所以B=.(2)由C=2 A及A)=C),得c=2a.由b=3及余弦定理b2=a2+c2-2 B,得9=a2+c2-.所以a=,c=2.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课时冲关练(二)
向量运算与复数运算、算法、合情推理 A 组(30 分钟 80 分) 一、选择题(每小题 5 分,共 60 分) 1.(2014·广东高考)已知复数 z 满足(3+4i)z=25,则 z= ( A.-3+4i B.-3-4i C.3+4i ) D.3-4i
【解析】选 D.方法一:因为|3+4i|=5,|3+4i|2=25, 所以 z= 3+4i =3-4i. 方法二:因为(3+4i)z=25, 所以 z= =3-4i. ) D.-2
2.设向量 a=(4,x),b=(2,-1),且 a⊥b,则 x 的值是 ( A.8 B.-8 C.2
【解析】选 A.因为 a⊥b,所以 a·b=4×2-x=0,解得 x=8. 3.执行如图所示的程序框图,输出的 S 值为 ( )
【解析】a+λb=(1,2)+λ(1,0)=(1+λ,2), 因为(a+λb)∥c, 所以 4(1+λ)-3×2=0,解得λ= .
Go the distance
答案:
B 组(30 分钟 80 分) 一、选择题(每小题 5 分,共 60 分) 1.(2014·梅州模拟)如果复数 (b∈R)的实部和虚部互为相反数,那么 b 等于 ( A. B. C.D.2 )
同方向的单位向量为 ( )
A. C.
B. D. =(3,-4),
【解析】选 A.由点 A(1,3),B(4,-1)得向量 = 则与向量 =5, 同方向的单位向量为 = =
. )
6.若复数(1+ai)2(i 为虚数单位)是纯虚数,则实数 a= ( A.±1 B.-1 C.0 D.1
【解析】选 A.(1+ai)2=1+2ai+a2i2=1-a2+2ai,要使复数是纯虚数,则有 1-a2=0 且 2a≠0,解得 a=±1. 7.(2014·梅州模拟)阅读如图所示的程序框图,则输出的 S= ( )
【解析】选 A.由题意 知 (a-b)·a=a2-a·b=2-a·b=0, 所以 a·b=2.设 a 与 b 的夹角为θ,
Go the distance
则 cosθ=
ab = a b
,θ= .
12.如图,在边长为 2 的正六边形 ABCDEF 中,动圆 Q 的半径为 1,圆心在线段 CD(含 端点)上运动,P 是圆 Q 上及内部的动点,设向量 m+n 的取值范围是 ( ) =m +n (m,n 为实数),则
D.4
Go the distance
【解析】选 C.由框图知,x 与 y 的函数关系为 , y= 由 y=x 得,
若 x≤2,则 x2=x x=0 或 x=1,若 2<x≤5, 则 2x-3=x x=3,若 x>5,显然 ≠x, 故满足题意的 x 值有 0,1,3,故选 C. 4.设 z 是复数,则下列命题中的假命题是 A.若 z2≥0,则 z 是实数 B.若 z2<0,则 z 是纯虚数 C.若 z 是纯虚数,则 z2≥0 D.若 z 是纯虚数,则 z2<0 【解题提示】设出复数的代数形式,复数问题转化代数式求解,进行验证,从而得 出正确的答案. 【解析】选 C.设 z=a+bi,a,b∈R z2=a2-b2+2abi. 对选项 A:若 z2≥0,则 b=0 z 为实数, 所以 z 为实数正确.
【解析】选 C. 根据复数除法法则 ( 分子分母同时乘以分母的共轭复数 ) 得 = + = + i, 因 为 该 复数的 实 部与 虚 部互为 相 反数 , 所 以
=0 b=- ,故选 C. ,且 a⊥(a+b),则 a 与 b 的夹角为 ( C. D. )
2.已知向量 a,b,满足|a|=3,|b|=2 A. B.
)=(1+t)
此时 m+n=1+t+1-t=2,取得最小值. ②当动圆 Q 的圆心为点 D 时,取点 P 为 AD 的延长线与☉Q 的交点, = = ( + )= + ,
此时 m+n= + =5 取得最大值,
Go the distance
因此 m+n 的取值范围是[2,5],故选 C. 二、填空题(每小题 5 分,共 20 分) 13.(2013·山东高考改编)复数 z= 【解析】z= 所以|z|= 答案:5 14. (2014·湖北高考)设 a 是一个各位数字都不是 0 且没有重复数字的三位数. 将组成 a 的 3 个数字按从小到大排成的三位数记为 I(a),按从大到小排成的三位 数记为 D(a)(例如 a=815,则 I(a)=158,D(a)=851).阅读如图所示的程序框图,运 行相应的程序,任意输入一个 a,输出的结果 b= . =-4-3i, =5. (i 为虚数单位),则|z|= .
A.-10
B.-3
C.4
D.5
【解析】选 A.第一次运行,满足条件循环 S=2-1=1,k=2. 第二次运行,满足条件循环 S=2×1-2=0,k=3.
Go the distance
第三次运行,满足条件循环 S=2×0-3=-3,k=4. 第四次运行,满足条件循环 S=2×(-3)-4=-10,k=5. 此时不满足条件,输出 S=-10. 【加固训练】某程序框图如图所示,该程序运行后输出的 k 的值是 ( )
【解题提示】设出复数的代数形式,利用运算法则进行计算. 【解析】选 D.设 z=a+bi(a,b∈R), 则 =a-bi,z+ =2a=2, 故 a=1,(z- )i=-2b=2, 故 b=-1,所以 z=1-i.
Go the distance
5.(2013·辽宁高考)已知点 A(1,3),B(4,-1),则与向量
[来源:学科网]
A.14 C.30 【解析】选 C.第一次循环,S=1,i=2, 第二次循环,S=1+4=5,i=3,
B.20 D.55
Go the distance
第三次循环,S=5+9=14,i=4, 第四次循环,S=14+16=30,i=5>4, 结束循环,输出 S=30. 8.观察下图 1 2 3 4 3 4 5 6 7 4 5 6 7 8 9 10 … 则第几行的各数之和等于 20152 ( A.2 015 B.2 013 ) C.1 007 D.1 008
Go the distance
5.(2014·黄冈模拟)在△ABC 中,( A. B. -3 =0. )⊥ , C.
-3
)⊥
,则角 A 的最大值为 ( D.
)
【解析】选 A.由( 可得( -3 )·
化简可得| cosA=
|cosB=3|
|cos(π-C).
= + ≥ ,0<A<π.
所以 0<A≤ . 6.(2013· 江西高考)阅读如下程序框图,如果输出 i=5,那么在空白矩形框中应填 入的语句为 ( )
【解析】选 D.由题设图三行各数和为 25=52, 第四行各数和为 49=72,…, 所以第 n 行各数和为(2n-1)2. 令 2n-1=2015,解得 n=1008.
[来源:]
9.(2013·安徽高考)设 i 是虚数单位, 是复数 z 的共轭复数,若 z· i+2=2z,则 z= ( A.1+i C.-1+i ) B.1-i D.-1-i
【 解 析 】 选 D.a ⊥ (a+b) a · (a+b)=a2+a · b=|a|2+|a||b|cos<a,b>=0, 故 cos<a,b>==- ,故所求夹角为 .
3.(2014·揭阳模拟)如图所示的程序框图,能使输入的 x 值与输出的 y 值相等的 x 值个数为 ( )
A.1
B.2
C.3
A.s=2 i-2 C.s=2 i
B.s=2 i-1 D.s=2 i+4
【解析】选 C.由题意知矩形框中的语句必须满足两个条件,i=5 时 s≥10,且 i=3 时 s<10,经验证只有选项 C 适合. 7.(2014·天津高考)已知菱形 ABCD 的边长为 2,∠BAD=120°,点 E,F 分别在边 BC,DC 上,BE=λBC,DF=μDC.若 A. B. · C. =1, · =- ,则λ+μ= ( D. )
A.4
B.5
C.6
D.7
【解析】选 A.对于 k=0,S=1,k=1,对于 k=1,S=3,k=2,对于 k=2,S=3+23=11,k=3, 而对于 k=3,S=11+211>100, k=4,故不符合条件,输出的 k=4. 4.(2014· 江西高考) 是 z 的共轭复数,若 z+ =2,(z- )i=2(i 为虚数单位),则 z= ( A.1+i C.-1+i B.-1-i D.1-i )
A.(1,2]
B.[5,6]
C.[2,5]
D.[3,5]
【解析】选 C.如图所示,
①设点 O 为正六边形的中心,则
=
+
.
当动圆 Q 的圆心为点 C 时,与边 BC 交于点 P,点 P 为边 BC 的中点,连接 OP, 则 因为 所以 = + 与 = , 共线,所以存在实数 t,使得 +t = + +t( =t , +(1-t) ,
Go the distance
【解析】选 A.设 z=a+bi(a,b∈R), 则 =a-bi,由 z· i+2=2z, 得(a2+b2)i+2=2(a+bi) 2-2a+(a2+b2-2b)i=0, 由复数相等的定义可得 a=1,b=1,所以 z=1+i. 10.(2014· 韶关模拟)执行如图所示的程序框图,若输出的结果是 16,则判断框内 的条件为 ( )
