专题(九)一辅助圆定点定长
中考数学专题复习—道是无圆却有圆(构造辅助圆)

中考复习之——道是无圆却有圆(构造辅助圆)许多几何问题虽然与圆无关,但是若能根据问题的条件、图形特点添补圆或找出潜在的圆,就能充分运用圆的丰富性质为解题服务,使问题获得简解或巧解,下列情形不妨作出辅助圆。
一、定点定长隐藏圆:1.有公共端点的等线段;2.与“等腰三角形”相关问题的讨论;3.解与“旋转”相关的问题。
二、定弦定角隐藏圆:1.与“直角、垂直”相关问题的探讨;2.其他特殊角(30°,45°,60°,120°等)问题的探讨。
三、判定四点共圆的方法:①平面内到某一定点等距离的几个点在同一个圆上。
②同斜边的直角三角形各个顶点共圆。
③同底同侧张角相等的三角形各个顶点共圆。
④一组对角互补的四边形的各个顶点共圆。
⑤一个外角等于内对角的四边形各个顶点共圆。
⑥对角线AC 、BD 相交于点P ,若PA ·PC=PB ·PD ,则四边形各个顶点共圆。
★常用方法归类:一、找定点,寻定长→现“圆形”1.如图,正方形ABCD 的边长为2,将长为2的线段QF 的两端放在正方形相邻两边上同时滑动,点Q 从点A 出发,沿A →B →C →D →A 方向滑动到点A 为止;同时点F 从点B 出发,沿B →C →D →A →B 方向滑动到点B 为止,在这个过程中,线段QF 的中点M 所经过的路线围成的图形面积为 。
2.在矩形ABCD 中,已知AB=2cm ,BC=3cm ,现有一根长为2cm 的小棒EF 紧贴着矩形的边,按逆时针方向滑动一周,则小棒EF 的中点P 在运动过程中所围成的图形面积为 。
3.如图,在矩形ABCD 中,AB=2,AD=3,点E、F 分别为AD 、DC 边上的点,且EF=2,G 为EF 中点,P 为BC边上的一个动点,则PA+PG 的最小值为 。
4.(自贡)如图,在矩形ABCD 中,AB=4,AD=6,E 是AB 边的中点,F 是线段BC 边上的动点,将ΔEBF 沿EF 所在直线折叠得到ΔEB ’F ,连接B ’D ,则B ’D 的最小值为 。
九年级数学寒假作业【专题09】圆的有关性质(学)

试题分析:过点O作OD⊥AB于点D,连接OA,由垂径定理可知AD= AB,设OA=r,则OD=r-2,在Rt△AOD中,利用勾股定理即可求r的值.
知识点
与圆有关的角
概念
(1)圆心角:顶点在圆心的角叫圆心角.
(2)圆周角:顶点在圆上,两边都和圆相交的角叫做圆周角.
公理、定理和公式
圆心角的性质:圆心角的度数等于它所对的弧的度数.
圆周角的性质:
①圆周角等于它所对的弧所对的圆心角的一半.
②同弧或等弧所对的圆周角相等;在同圆或等圆中,相等的圆周角所对的弧相等.
③90°的圆周角所对的弦为直径;半圆或直径所对的圆周角为直角.
④圆内接四边形的对角互补;外角等于它的内对角.
∴∠ABD=∠ACD=45°
温馨提醒
在解题时应充分分清与圆有关的角。
典型例题和解析
例题:如图,在⊙O中,直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,则BC=( )cm,∠ABD=( )
试题分析:利用直径所对的圆周角是直角和同弧所对的圆周角相等求解。
解:∵AB是直径∴∠ACB=90°
∴BC= (cm)
∵CD是∠ACB的平分线,∴∠ACD= ∠ACB=45°
1.
知识点
与圆的有关概念
概念
1.平面内到定点的距离等于定长的点组成的图形叫做圆.定点叫做圆心,定长叫做半径.
2.连接圆上任意两点间的线段叫做弦.经过圆心的弦叫做直径
公理、定理和公式
垂径定理及推论:两条弧.
(2)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
(3)弦的垂直平分线过圆心,且平分弦对的两条弧.
(4)平分一条弦所对的两条弧的直线过圆心,且垂直平分此弦.
精心构造辅助圆,解决问题少困难

精心构造辅助圆 解决问题少困难圆是几何中具有美学价值的一种图形,不仅曲线光滑圆润,美丽迷人,是美好象征的化身,而且几何性质众多,在解决诸多数学问题中,显示出非常重要的作用,有圆的参与,将会使一个比较困难的问题简单起来,所以,在解决一些与圆有关的问题中,要深入挖掘圆的信息,精心构造辅助圆,利用圆的几何性质和圆的方程,发挥出圆的价值,让这些问题迎刃而解,实现“精心构造辅助圆,解决问题少困难”的理想目标.一、利用方程,构造圆在平面上涉及动点轨迹的问题中,直接求解问题比较困难时,可以先考虑建立直角坐标系,特别是有垂直条件与对称条件时,就更要考虑解析法,求出动点的轨迹方程,如果满足圆方程的结构特点,就可以构造圆,让圆的几何性质闪耀光彩,使问题得到解决.例1. (2016届北京西城期末理科)如图,正方形ABCD 的边长为6,点E ,F 分别在边AD ,BC 上,且2DE AE =,2CF BF =.如果对于常数λ,在正方形ABCD 的四条边上,有且只有6个不同的点P 使得=PE PF λ⋅成立,那么λ的取值范围是( )(A )(0,7)(B )(4,7)(C )(0,4)(D )(5,16)- 图1解:以D 为坐标原点,DC 所在直线建立直角坐标系,设点(,)P x y ,则点(0,4),(6,4)E F ,所以(0,4),=(6-x,4-y)PE x y PF =--,由=PE PF λ⋅得动点P 的轨迹方程是:22(3)(4)9x y λ-+-=+,所以动点P 的轨迹是一个以(3,4)为圆心, 9λ+为半径的圆,所以“在正方形ABCD 的四条边上,有且只有6个不同的点P 使得=PE PF λ⋅成立”等价于“圆与正方形四条边有且仅有6个不同交点”,当且仅当3913λ<+<,解得:04λ<<,所以选C.评析:通过解析法揭穿了动点P 的几何意义,为实现问题的转化起到了桥梁作用,通过几何背景的分析,抽象代数特征,促使问题圆满解决,其间,由代数方程,构造了一个圆,将原问题转化为直线与圆的位置关系讨论,从而建立起了不等式,实现了向量问题坐标化,几何问题代数化的转化目标.从而减少了解题的困难程度. 例2.直线:(2)l y k x =+与曲线2:465C y x x =----有且仅有两个不同公共点.求实数k 的取值范围.解:由曲线2:465C y x x =----的方程可以构造出半圆:22(3)(+4)4x y -+=且4y ≤-. E FD P C A BE FD P C A B x y 图2如图所示:要使直线l 与曲线C 有且仅有2个公共点,则需AB AC k k k <≤其中AB 为半圆的切线,(1,4)C -,半圆的圆心到直线:(2)l y k x =+的距离是2342202372,211k kd k k ++-±==⇒=+由图可知:20237=21AB k --,43AC k =- 所以实数k 的取值范围是202374(,]213--- 评析:解决本题的关键是由曲线C 的方程构造半圆,然后由图形抽象代数条件,完全回避了探究较复杂的一元二次方程在区间[1,5]上有两个不等实根的条件.所以在解决解析几何的问题时,一定要分析曲线方程的结构特点,抓住构造几何图形的机会,将会让图形闪耀光辉.相关问题:1.(2019届北京昌平区高三上期末理科)设点12,F F 分别为椭圆22:195x y C +=的左、右焦点,点P 是椭圆上任意一点,若使得12PF PF m ⋅=成立的点恰好是4个,则实数m 的值可以是( ) BA .B .C .5D .8 2.(2019届北京西城区高三上期末理科) 设双曲线22: 13y C x -=的左焦点为F ,右顶点为A . 若在双曲线C 上,有且只有2个不同的点P 使得=PF PA λ⋅成立,则实数λ的取值范围是____. (-2,0)二、利用定义,构造圆圆的定义是:在平面内到定点的距离等于定长的点的集合叫做圆.即动点满足一定点和一定长的轨迹可以生成圆,在解决问题的过程中,如能构造出这样的几何条件,就可以构造辅助圆,将原问题转化为圆的问题求解,可能使复杂问题简单化.例3. 设直线:,圆,若在圆C 上存在两点,在直线 上存在一点M ,使得,则的取值范围是( )A. [18,6]-B. [652,652]-+C. [16,4]-D. [652,652]---+解:考虑极端情形:当,MP MQ 是圆C 的切线时,如果此时的M 点轨迹与直线有公共点,那 么对于,MP MQ 不都是圆C 的切线时,都能在直线上存在符合条件的M 点.所以“在圆C 上存 在两点,在直线上存在一点M ,使得”等价于“当,MP MQ 是圆C 的切线时,M 点的轨迹与直线有公共点”.而当,MP MQ 是圆C 的切线时,易证:四边形MPCQ 是正方形,所 以MC 的长是定值2,且C 为定点,因此,动点M 的轨迹是以C 为圆心,2为半径的圆, C 123l 340x y a 22 (2)2C x y :,P Q l 90PMQ a l l ,P Q l 90PMQ l AD C B即M 点的轨迹方程是22(2)4x y -+=,直线2164a ≤⇒-≤≤,所以选C.评析:根据极端性原理,抓住几何条件构造点M 的圆轨迹是解决本题的关键,而构造圆的关键在于构造定值(即半径)与配套的定点(即圆心),所以在解决解析几何问题时,要时刻关注定值的出现于定点的出现,特别是在解决有关椭圆、双曲线问题中,要紧扣椭圆、双曲线定义,关注定值的相关信息与定点的相关信息.例4.过点(1,2)P --作圆22:(3)(4)1C x y -+-=的两切线,PA PB ,其中,,A B 为切点,求直线AB 的方程.解:由圆的切线性质可知:=PA PB ,所以由圆的定义可知:,A B 在以PA 为直径,P 为圆心的圆上,=PA PB =于是可得圆P 的方程:22(1)(2)52x y +++=,将圆C 的方程与圆P 的方程相减可得公共弦AB 所在的直线方程为:812710x y +-=评析:本题的解决中利用了等长线段构造辅助圆,从而出现了两圆公共弦的大好时机.具有一个公共定点的等长线段的另一个端点在一个圆上,这就是圆定义的灵活运用,在解决问题中要注意这些信息.相关问题:已知椭圆C: 22143x y +=的左右焦点分别是12,F F ,点P 是椭圆C 上的动点,N 是线段1F P 的延长线上一点,点M 是2NPF ∠的平分线上一点,且20PM F M ⋅=,直线:34150l x y --=与x 轴、y 轴交点分别为,A B ,求ABM ∆面积的最大值. 1258三、利用垂直,构造圆圆有一个重要性质是:直径上的圆周角是直角.反过来说,直角三角形的直角顶点在以斜边为直径,斜边中点为圆心的圆上,这显然是一个真命题.这也是构造辅助圆的依据,所以当垂直条件出现时,要注意辅助圆的构造,可能使原问题转化为圆的问题,从而获得解题思路. 例5. 已知圆和两点,,若圆上存在点,使得,则的最大值为( )A .7B .6C .5D .4解:由于,所以可以构造一个圆:点P 在以AB 为直径的圆上,记此圆为圆O ,点P 又在圆C 上,所以“圆上存在点,使得”等价于“圆O 与圆C 有公共点”, 所以1146m CO m m -≤≤+⇒≤≤,所以的最大值为6.选B.评析:从垂直条件出发,构造了一个辅助圆,实现了将原问题转化为两圆位置关系的转化目标,使问题轻松获解,其间表现出辅助圆的重要作用. l ()()22:341C x y -+-=(),0A m -()(),00B m m >C P 90APB ∠=m 90APB ∠=C P 90APB ∠=m例6.过点(0,4)P 的直线l 交椭圆22:14x C y +=于不同两点,A B (A 在PB 之间),O 为坐标原点.当90PAO ∠=,求直线l 的斜率.解:按照通常用到的方法,将直角用斜率之积为-1或用向量的数量积为0写出坐标关系,再用直线与曲线联立,出韦达定理,代入求值.但是在直角中不涉及,A B 两点坐标,只涉及A 点的坐标,所以直曲联立与韦达定理不好使.基于此,需要变换思路,由直角构造圆,点A 在PO 为直径的圆上,于是得到下列解法:设00(,)A x y ,则2200(2)4x y +-=,220044x y +=,消去0x 得:002,23y y ==-(舎),0x =l的斜率是24k -=24k -== 评析:由此题的解答可见:由垂直条件构造辅助圆是构造方程的主要依据,这种方法仅是直曲联立用韦达定理方法的补充,不能迷信它.比如将本题的条件90PAO ∠=改为90AOB ∠=,就没有必要构造辅助圆了,直接用斜率之积为-1或用向量的数量积为0,写出坐标关系,直曲联立出韦达定理,代入求值比较简单.相关问题:设点P 是双曲线22:1169x y C -=上一点,12,F F 是双曲线C 的左右焦点,且120PF PF ⋅=,求点P 到x 轴的距离. 95四、利用换元,构造圆由于圆的方程是特殊的二元二次方程,特殊性表现在两个方面:一是没有两元的交叉项,二是两元的二次项系数相等。
2023年中考数学专项复习课件:辅助圆在解题中的应用

模型分析
(2)当∠C=90°时,点C在⊙O上运动(如图②,不与点A,B重合).其中 AB为⊙O的直径;(3)当∠C>90°时,点C在如图③所示的 上运动( 不与点A,B重合).其中 ∠AOB+∠ACBA=B 180°
1 2
模型应用
12. 如图,在矩形 ABCD中,AB=4,BC=6,E是矩形内部的一个动点 ,且AE⊥BE,则线段CE的最小值为2__1_0__2___.
r-d
0
d-r
连接OD并延长交
连接OD交⊙O于
此时点E的位置
点E与点D重合
⊙O于点E
点E
模型应用 1. 如图,在平面直角坐标系中,⊙M的半径为2,圆心M的坐标为(3,4) ,P是⊙M上的任意一点,PA⊥PB,且PA,PB分别与x轴交于点A,B. 若点A,B关于原点O对称,则AB的最小值为_6_______.
对的劣弧BD上运动,连接OA,OP,则AP≤OA+OP,
∴当O,A,P三点共线时,AP取得最大值,最大值即为OA+OP的值.
过点O作OQ⊥AB于点Q,
∵∠DPB=120°,∴∠BAD=60°,
∵AD=BD=6,∴∠OAQ=30°,AQ= 1 AB=3,
2
∴OA=2 3 ,∴OA+OP=4 3,
∴AP的最大值为4 3 .
15 4
过点C作CP的垂线,与PB的延长线交于点Q,则CQ的最大值为______.
第8题图
第9题图
10. 如图,在四边形ABCD中,BD=4,∠BAD=∠BCD=90°,则四边
形ABCD面积的最大值为___8_____.
11. 如图,等腰直角△ABC的斜边AB下方有一动点D,∠ADB=90°,
CE
第1题图
九年级数学上册第24章: 辅助圆(隐圆)专题练习(无答案)
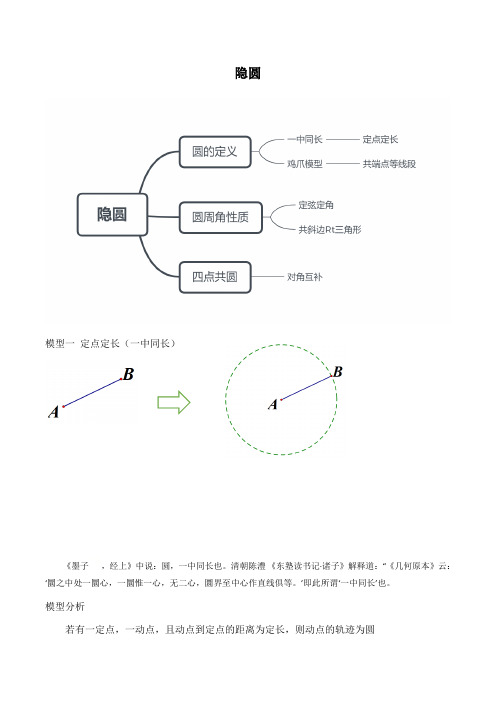
隐圆模型一定点定长(一中同长)《墨子,经上》中说:圆,一中同长也。
清朝陈澧《东塾读书记·诸子》解释道:“《几何原本》云:‘圜之中处一圜心,一圜惟一心,无二心,圜界至中心作直线俱等。
’即此所谓‘一中同长’也。
模型分析若有一定点,一动点,且动点到定点的距离为定长,则动点的轨迹为圆模型实例如图,在矩形ABCD中,AB=4,AD=8,点E是AB中点,点F是BC 上一点,把△BEF沿着EF翻折,点B落在点B'处,求B'D的最小值.练习:如图,OA⊥OB,P、Q分别是射线OA、OB上两个动点,C是线段PQ的中点,且PQ=4,则在线段PQ滑动的过程中,点C运动形成的路径长为_________2、如图,在Rt△ABC中,∠C=90°,AC=6,∠A=60°,点F在边AC上,并且CF=2,点E为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是_________3图2图BC OABC OAABC O图13、如图,在矩形ABCD 中,AB=4,BC=8,P 、Q 分别是直线BC 、AB 上的两个动点,AE=2,△AEQ 沿EQ 翻折形成△FEQ ,连接PF ,PD ,则PF+PD 的最小值是_________.模型二 共端点,等线段模型(鸡爪模型)12BCA D模型分析(1)若有共端点的三条等线段,可考虑构造辅助圆; (2)构造辅助圆是方便利用圆的性质快速解决角度问题。
模型典例如图 1,四边形 ABCD 中,AB=AC=AD ,若∠CAD=76°,则∠CBD=__________度。
练习1、如图,△ABC 和△ACD 都是等腰三角形,AB=AC ,AC=AD ,连接BD 。
求证:∠1+∠2=90°。
2、如图,在△ABC 内有一点 D,使得 DA=DB=DC,若∠DAB=20°,则∠ACB=__________模型三定弦定角模型分析若有一固定线段AB及线段AB所对的角(∠C)固定,则点C可以看作是以AB为弧的圆上运动.模型典例如图在△ABC中,BC=2,∠A=45°,求△ABC的面积最大值.练习1、如图,Rt△ABC中,∠ACB=90°,AC=4,BC=3,P为一动点,且PA⊥PC,连接BP,则BP的最大值为_____2、如图,△ABC中,AB=AC=2,BC=2√3,D点是△ABC所在平面上的一个动点,且∠BDC=60°,则△DBC面积的最大值是E BCADF模型四 共斜边的直角三角形模型分析:(1)共斜边的两个直角三角形,同侧或异侧,都会得到四点共圆;(2)四点共圆后可以根据圆周角定理得到角度相等,完成角度等量关系的转化,是证明角相等重要的途径之一。
巧构辅助圆,妙解几何问题

巧构辅助圆,妙解几何问题发布时间:2021-01-25T10:27:21.677Z 来源:《基础教育课程》2020年10月作者:裴爱文[导读] 初中数学教学中圆是至关重要的教学内容。
而在几何问题中涉及利用隐形圆巧妙求解的问题甚多,在教学中倘若能适时引导学生恰当地运用辅助圆便能有效促进学生解题能力的提升。
为此,本文尝试从运用圆的定义、直角三角形构造90°圆周角、三角形外接圆等几个例题进行介绍,以帮助师生更好的运用辅助圆巧妙求解相关几何问题。
西工大附中分校裴爱文摘要:初中数学教学中圆是至关重要的教学内容。
而在几何问题中涉及利用隐形圆巧妙求解的问题甚多,在教学中倘若能适时引导学生恰当地运用辅助圆便能有效促进学生解题能力的提升。
为此,本文尝试从运用圆的定义、直角三角形构造90°圆周角、三角形外接圆等几个例题进行介绍,以帮助师生更好的运用辅助圆巧妙求解相关几何问题。
关键词:构造;辅助圆;几何问题作为中考每年的必考内容之一,圆的这部分知识非常重要,近几十年来各省的数学试题中的题目我们都能发现压轴题会涉及到这方面内容的考查。
这类试题乍一看,不能马上反应出要用圆的相关来知识求解。
但若对题目经过解读与深度思考、剖析之后,我们发现根据题设的相关条件常常是能构造出辅助圆,进而使问题快速求解。
那么如何有效、恰当地构造出一个妥帖的辅助圆是此类问题突破的关键,为此我将结合具体案例来谈谈如何巧构辅助圆求解几何问题。
一、立足基础,利用圆的定义构造辅助圆初中学生所熟知的圆的定义是指平面内到一个定点的距离等于定长的所有点组成的图形。
基于圆的定义这个基本原理,是学生必须掌握的最基本的辅助圆添加方式。
下面给出利用圆的定义构造辅助圆的例题进行阐述说明。
二、能力导向,利用90°的圆周角所对的弦是直径构造辅助圆在初中几何试题中如果题目出现了内角为90度角的三角形,我们就可以利用用90度的圆周角所对的弦为直径这一原理来构造辅助圆,然后将问题转化成圆中的问题,利用辅助圆的相关知识来解决几何问题中遇到的难以解决的问题,有效培养学生的数学思维能力。
九年级数学上学期期末专题09 巧用隐圆,妙解压轴

专题09巧用隐圆妙解压轴实例讲解:(包含以上多种模型)已知在正方形ABCD中,∠MAN =45°,连接BD与AM,AN 分别交于E、F两点。
从图中找出3组四点共圆及一组5点共圆。
详解: 由题意可得:∠BDF=∠FHE=45°⇒点A,M,F,D四点共圆。
⇒∠AMF=90°∠HFM=45°同理,可得点A,B,E,N四点共圆。
∠ANE=90°,∠NEH=45°∠NEH=∠HFM⇒点M,E,F,N四点共圆。
∠FME=∠ECF=∠FME=90°⇒点N,F,C,E,M五点共圆。
图如右:一.隐圆之定点定长FEMB CDAOHNMEB CDFOHNME CDFAOHNMEB CD1.如图,正方形ABCD ,边长为4,点P 和点Q 在正方形的边上运动,且PQ =4,若点P 从点B 出发沿B →C →D →A 的路线向点A 运动,到点A 停止运动;点Q 从点A 出发,沿A →B →C →D 的路线向点D 运动,到达点D 停止运动.它们同时出发,且运动速度相同,则在运动过程中PQ 的中点O 所经过的路径长为 .2.已知:如图,在正方形ABCD 中,E 、F 分别是AD 、CD 的中点. (1)线段AF 与BE 有何关系.说明理由;(2)延长AF 、BC 交于点H ,则B 、D 、G 、H 这四个点是否在同一个圆上.说明理由.二.隐圆之定弦定角3.在△ABC 中,AB =4,∠C =45°,则√2AC +BC 的最大值为 .4.如图,在矩形ABCD 中,AD =5,AB =3√3,点E 在AB 上,AE EB=12,在矩形内找一点P ,使得∠BPE =60°,则线段PD 的最小值为( )A .2√7−2B .2√13−4C .4D .2√35.问题提出(1)如图①,已知△ABC为边长为2的等边三角形,则△ABC的面积为;问题探究(2)如图②,在△ABC中,已知∠BAC=120°,BC=6√3,求△ABC的最大面积;问题解决(3)如图③,某校学生礼堂的平面示意为矩形ABCD,其宽AB=20米,长BC=24米,为了能够监控到礼堂内部情况,现需要在礼堂最尾端墙面CD上安装一台摄像头M进行观测,并且要求能观测到礼堂前端墙面AB区域,同时为了观测效果达到最佳,还需要从点M出发的观测角∠AMB=45°,请你通过所学知识进行分析,在墙面CD区域上是否存在点M满足要求?若存在,求出MC的长度;若不存在,请说明理由.三.隐圆之直角动点6.如图,在矩形ABCD中,AB=8,BC=5,P是矩形内部一动点,且满足∠P AB=∠PBC,则线段CP的最小值是.7.如图,等边△ABC的边长为6,D为BC边上的中点,P为直线BC上方的一个动点,且满足∠P AD=∠PDB,则线段CP长的最大值为.8.如图,在矩形ABCD中,AB=8,BC=6,点P在矩形的内部,连接P A,PB,PC,若∠PBC=∠P AB,则PC的最小值是()A.6B.√73−3C.2√13−4D.4√13−4四.隐圆之对角互补。
九年级数学上册第24章:-辅助圆(隐圆)专题练习(无答案)

隐圆模型一定点定长(一中同长)*《墨子,经上》中说:圆,一中同长也。
清朝陈澧《东塾读书记·诸子》解释道:“《几何原本》云:‘圜之中处一圜心,一圜惟一心,无二心,圜界至中心作直线俱等。
’即此所谓‘一中同长’也。
(模型分析若有一定点,一动点,且动点到定点的距离为定长,则动点的轨迹为圆模型实例}如图,在矩形ABCD中,AB=4,AD=8,点E是AB中点,点F是BC 上一点,把△BEF沿着EF翻折,点B落在点B'处,求B'D的最小值.练习:%如图,OA⊥OB,P、Q分别是射线OA、OB上两个动点,C是线段PQ的中点,且PQ=4,则在线段PQ滑动的过程中,点C运动形成的路径长为_________$2、如图,在Rt△ABC中,∠C=90°,AC=6,∠A=60°,点F在边AC上,并且CF=2,点E为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是_________,)3、如图,在矩形ABCD中,AB=4,BC=8,P、Q分别是直线BC、AB上的两个动点,AE=2,△AEQ 沿EQ翻折形成△FEQ,连接PF,PD,则PF+PD的最小值是_________..)3图2图BC OABC OAABC O图1…模型二 共端点,等线段模型(鸡爪模型)|]模型分析(1)若有共端点的三条等线段,可考虑构造辅助圆; (2)构造辅助圆是方便利用圆的性质快速解决角度问题。
模型典例<如图 1,四边形 ABCD 中,AB=AC=AD ,若∠CAD=76°,则∠CBD=__________度。
12BCA D:练习1、如图,△ABC 和△ACD 都是等腰三角形,AB=AC ,AC=AD ,连接BD 。
》求证:∠1+∠2=90°。
/2、如图,在△ABC 内有一点 D ,使得 DA=DB=DC ,若∠DAB=20°,则∠ACB=__________[#模型三定弦定角·;模型分析》若有一固定线段AB及线段AB所对的角(∠C)固定,则点C可以看作是以AB为弧的圆上运动.模型典例如图在△ABC中,BC=2,∠A=45°,求△ABC的面积最大值.&;练习1、如图,Rt△ABC中,∠ACB=90°,AC=4,BC=3,P为一动点,且PA⊥PC,连接BP,则BP的最大值为_____)¥2、如图,△ABC中,AB=AC=2,BC=2√3,D点是△ABC所在平面上的一个动点,且∠BDC=60°,则△DBC面积的最大值是;#模型四共斜边的直角三角形》模型分析:{(1)共斜边的两个直角三角形,同侧或异侧,都会得到四点共圆;E BCAD FEBCADGF(2)四点共圆后可以根据圆周角定理得到角度相等,完成角度等量关系的转化,是证明角相等重要的途径之一。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
假期作业专题(九)一辅助圆定点定长 姓名__________学号__________
知识点
1、定点定长作圆:点A 为定点,点B 为动点,且AB 长度固定,
则点B 的轨迹是以点A 为圆心,AB 长为半径的圆。
2、点圆最值问题:如图,当圆上的点在A 点的位置时离P 的距离最近,
当圆上的点在B 的位置时离P 的距离最远。
例题赏析:如图,在矩形ABCD 中,4=AB ,6=AD ,E 是AB 边的中点,F 是线面BC 边上的动点,将EBF ∆沿EF 所在的直线折叠得到F EB '∆,连接D B ',求D B '的最小值。
分析:因为点E 为一个定点,221'===AB EB EB 是一个定值, 所以可以看成点'B 在以点E 为圆心,'EB 为半径的圆上运动,
再根据点圆最值求出D B '的最小值。
解:如图,点E 为圆心,'EB 为半径作圆,
当点E ,'B ,D 三点共线时D B '的值最小。
︒=∠90A ,22
1==AB AE ,6=AD 1026222=+=∴DE ,
2102''-=-=∴EB DE D B
练习1:如图,已知平行四边形ABCD ,点E 为AD 边上的一点,点F 为边AB 上的动点,将AEF ∆沿EF 折叠得到EF A '∆,请在图中画出点'A 在平行四边形内(含边上的点)的运动轨迹。
练习2:如图,在边长为2的菱形ABCD 中,︒=∠60A ,
M 是AD 边的中点,N 是AB 边上的一动点,将AMN ∆沿MN 所在的直线翻折得到MN A 1∆,连接C A 1,求C A 1的长度的最小值.
练习3:如图,在ABC Rt ∆中,︒=∠90C ,︒=∠30B ,AC=6,点F 在边AC 上,并且CF=2,点E 为边BC 上的动点,将CEF ∆沿直线EF 翻折,点C 落在点P 处,求点P 到边AB 距离的最小值。
练习4:如图,等边ABC ∆中,AB=6,点D 在BC 上,BD=4,点E 为边AC 上一动点(不与点C 重合),CDE ∆关于DE 的轴对称图形为FED ∆,连结AF ,BF ,求ABF ∆的最小值。
练习5:如图,3=AB ,点C 为平面内的一个动点且2=AC ,
(1)请在图中画出点C 运动的轨迹;
(2)连结BC ,当B ∠最大时,求BC 的长。
