数字灰度图像的基本运算处理 正文讲解
数字灰度图像的基本运算处理 正文讲解

1前言介绍一种用可视化数值计算软件MATLAB实现的数字图像处理系统平台,系统使用MATLAB中提供的GUI设计系统可视化的用户界面,下拉式的菜单方便用户选择对图像的处理。
用户可以随意选择要处理的图片。
但是该系统只支持灰度图片,可实现内容主要包括灰度图像的代数运算、几何运算。
基于数字图像处理的一些基本原理,利用MATLAB 设计程序进行对灰度图像的处理。
有部分处理运算有很多种方法,我选择了最简单、最明了的方法。
数字图像处理又称为计算机图像处理,它是指将图像信号转换成数字信号并利用计算机对其进行处理的过程。
理论上讲,图像是一种二维的连续函数,然而在计算机上对图像进行数字处理的时候,首先必须对其在空间和亮度上进行数字化,这就是图像的采样和量化的过程。
二维图像进行均匀采样,就可以得到一幅离散化成M×N样本的数字图像,该数字图像是一个整数阵列,因而用矩阵来描述该数字图像是最直观最简便的了。
随着计算机的发展,图像处理技术在许多领域得到了广泛应用,用于图像处理的软件也很多,如PHOTOSHOP、PAINTSHOP、GIMP、SaperaProcessing、MATLAB等,其中大部分软件都是基于广告策划和图像修饰处理而设计的应用软件,进行图像处理时并不是很方便。
而MATLAB(矩阵实验室) 它在矩阵运算上有自己独特的特点,在矩阵运算处理具有很大的优势,因此用MATLAB处理数字图像非常的方便。
不仅如此,MATLAB提供了丰富的图形命令和图形函数,而且其面向对象的图形系统具有强大的用户界面(GUI)生成能力。
这样,用户就可以充分利用系统提供的 GUI 特性,编写自己需要的图形界面,从而可以高效地进行图像处理。
MATLAB支持五种图像类型,即索引图像、灰度图像、二值图像、RGB图像和多帧图像阵列;支持BMP、GIF、HDF、JPEG、PCX、PNG、TIFF、XWD、CUR、ICO等图像文件格式的读,写和显示。
数字图像的灰度处理简述

数字图像的灰度处理数字图像处理的目的和意义:图象处理着重强调的是在图象之间进行的各种变换,对图象进行各种加工以改善图象的视觉效果。
在图象的灰度处理中,增强操作、直方图及图象间的变换是实现点操作的增强方式,又被称作灰度变换。
本文主要介绍了一些数字图像灰度处理的方法,其中图象取反是实现图象灰度值翻转的最直接的方法;灰度切分可实现强化某一灰度值的目的。
对直方图进行均衡化修正,可使图象的灰度间距增大或灰度均匀分布、增大反差,使图象的细节变得清晰。
数字图像处理是20世纪60年代初期所形成的一门涉及多领域的交叉学科。
所谓数字图像处理,又称为计算机图像处理,就是指用数字计算机及其它有关的数字硬件技术,对图像施加某种应算和处理,从而达到某种预期的目的。
在大多数情况下,计算机采用离散的技术来处理来自连续世界的图像。
实际上图像是连续的,计算机只能处理离散的数字图像,所以要要对连续图像经过采样和量化以获得离散的数字图像。
数字图像处理中图像增强的目的是改善图像的视觉效果,针对给定图像的应用场合,有目的地强调图像的整体或局部特性,扩大图像中不同物体特征之间的差别,满足某些特殊分析的需要。
其方法是通过一定手段对原图像附加一些信息或变换数据,有选择地突出图像中感兴趣的特征或者抑制图像中某些不需要的特征,使图像与视觉响应特性相匹配。
而通过改变图像的灰度以期达到一种很好的视觉效果是图像增强的一种手段。
灰度变换的目的是为了改善画质,使图像显示效果更加清晰。
图像的点应算是一种既简单又重要的技术,它能让用户改变图像数据占据的灰度范围。
一幅输入图像经过点应算后将产生一幅新的输出图像,由输入像素点的灰度值决定相应的输出像素点的灰度值。
图像的点应算可以有效的改变图像的直方图分布,以提高图像的分辨率和图像的均衡。
点应算可以按照预定的方式改变一幅图像的灰度直方图。
除了灰度级的改变是根据某种特定的灰度变换函数进行之外,点应算可以看作是“从像素到像素”的复制操作。
灰度图像处理

•
•
• 对于数字图像,可以对上述公式做离散近似。若原图像f(x,y)在像素点(x,y)处的灰度为rk,则直方 图均化后的图像g(x,y)在点(x,y)处的灰度sk为
图像去噪
去噪的方法很多,常用的有:平滑滤波和中值滤波 1、平滑滤波 在假定加性噪声是随机独立分布的条件下,利用领域的平均或加权平 均可以有效抑制噪声干扰。图像平滑实际是低通滤波,让信号的低频部分 通过,阻截属于高频部分的噪声信号,显然,在减少随机噪声点影响的同时, 由于图像边缘部分也处在高频部分,平滑过程会导致边缘模糊化 平滑模板的思想是:通过待处理点和周围8个相邻点的平均来去除突然 变换的点,从而滤掉一定的噪声,其代价是图像有一定程度的模糊
图像锐化
1、一阶微分算子算法 图像处理种常用的微分方法就是求梯度。对于一个连续函数f(x,y),它在点(x,y)处的梯度是一个矢量,定义为
点(x,y)梯度的幅度即为梯度矢量的模:
(1)
对于数字图像f(x,y),由于数字图像的离散性,采用差分运算来近似替代微分运算,在其像素点(i,j)处,x方向和y方向上 的一阶差分定义为
增强后图像在(i,j)处的灰度值为
Sobel算子在计算x方向和y方向上的梯度时,不像普通梯度算子那样只用两 个像素灰度差值来表示,而是采用两列或两行像素灰度加权和的差值来表 示,这使得Sobel算子具有如下优点: (1)引入了加权平均,将距离远近产生的影响考虑进去,对图像中的随机噪声 具有一定的平滑作用 (2)由于Sobel算子采用间隔两行或者两列的差分,所以图像中边缘两侧的像 素得到增强。Sobel算子得到的锐化图像的边缘显得粗而亮
图像锐化
3、拉普拉斯算子算法 拉普拉斯算子是一种十分常用的图像边缘增 强处理算子。拉普拉斯算子是线性二次微分算子, 具有各向同性和位移不变性,从而满足不同走向 的图像边缘的锐化要求。 对于连续图像f(x,y),它的拉普拉斯算子为 当图像模糊是由于扩散现象引起时,拉斯运算 结果的k倍,即 。f为模糊图像,g为锐化 以后的图像,k是与扩散效应有关的系数。
灰度变换的基本原理

灰度变换的基本原理灰度变换是数字图像处理中一种常见的操作技术,它通过改变图像中每个像素的亮度值,从而实现图像的增强或调整。
灰度变换的基本原理是将原始图像的灰度级映射到一个新的灰度级,使得图像的视觉效果更加理想。
在进行灰度变换之前,我们需要了解一些基本概念。
首先,灰度级是指图像中每个像素的亮度值,通常用0到255的整数表示,其中0代表黑色,255代表白色。
其次,灰度变换函数是将原始图像的灰度级映射到新的灰度级的函数,它决定了图像的最终效果。
常用的灰度变换函数包括线性变换、对数变换、幂律变换等。
线性变换是最简单的一种灰度变换方法,它通过一条直线的斜率和截距来调整图像的亮度。
对数变换和幂律变换则是非线性变换方法,它们通过对原始图像的灰度级取对数或幂次来改变图像的亮度分布。
灰度变换的具体步骤如下:首先,读入原始图像,并将其转换为灰度图像。
然后,选择合适的灰度变换函数,并根据函数的定义计算每个像素的新灰度级。
最后,将新的灰度级赋值给每个像素,并生成处理后的图像。
灰度变换在图像处理中有着广泛的应用。
首先,它可以用于图像增强,即通过调整图像的亮度和对比度,使图像更加清晰和鲜明。
其次,灰度变换可以用于图像的调整和校正,例如校正图像的曝光不足或过度曝光的问题。
此外,灰度变换还可以用于图像的压缩和编码,从而减少图像的存储空间和传输带宽。
灰度变换虽然简单,但在实际应用中需要根据具体情况选择合适的变换函数和参数。
例如,在图像增强中,可以根据图像的亮度分布选择线性变换、对数变换或幂律变换。
对于高动态范围图像,可以采用自适应灰度变换方法,根据图像的局部特征进行变换。
需要注意的是,灰度变换可能会引入一些副作用,例如图像的噪声会被放大,导致图像质量的下降。
因此,在进行灰度变换时,需要考虑图像的特点和应用需求,避免不必要的变换和误操作。
灰度变换是数字图像处理中一种重要的操作技术,它通过改变图像的灰度级来实现图像的增强和调整。
灰度变换的基本原理是将原始图像的灰度级映射到一个新的灰度级,从而改变图像的亮度分布和视觉效果。
数字图像处理-图像基本运算
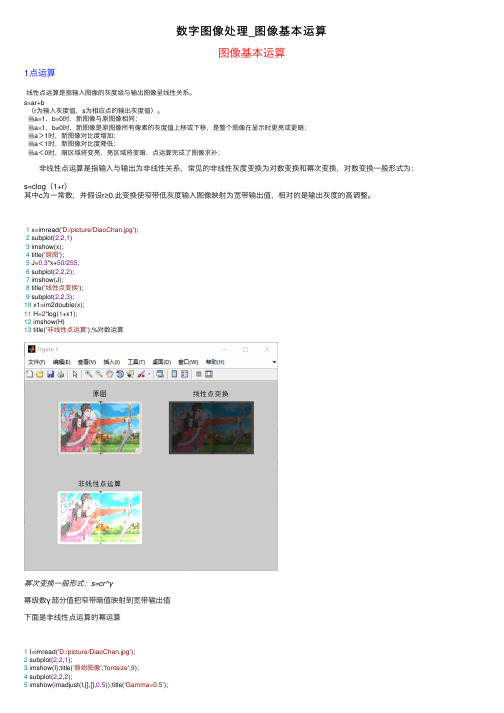
数字图像处理_图像基本运算图像基本运算1点运算线性点运算是指输⼊图像的灰度级与输出图像呈线性关系。
s=ar+b(r为输⼊灰度值,s为相应点的输出灰度值)。
当a=1,b=0时,新图像与原图像相同;当a=1,b≠0时,新图像是原图像所有像素的灰度值上移或下移,是整个图像在显⽰时更亮或更暗;当a>1时,新图像对⽐度增加;当a<1时,新图像对⽐度降低;当a<0时,暗区域将变亮,亮区域将变暗,点运算完成了图像求补; ⾮线性点运算是指输⼊与输出为⾮线性关系,常见的⾮线性灰度变换为对数变换和幂次变换,对数变换⼀般形式为:s=clog(1+r)其中c为⼀常数,并假设r≥0.此变换使窄带低灰度输⼊图像映射为宽带输出值,相对的是输出灰度的⾼调整。
1 x=imread('D:/picture/DiaoChan.jpg');2 subplot(2,2,1)3 imshow(x);4 title('原图');5 J=0.3*x+50/255;6 subplot(2,2,2);7 imshow(J);8 title('线性点变换');9 subplot(2,2,3);10 x1=im2double(x);11 H=2*log(1+x1);12 imshow(H)13 title('⾮线性点运算');%对数运算幂次变换⼀般形式:s=cr^γ幂级数γ部分值把窄带暗值映射到宽带输出值下⾯是⾮线性点运算的幂运算1 I=imread('D:/picture/DiaoChan.jpg');2 subplot(2,2,1);3 imshow(I);title('原始图像','fontsize',9);4 subplot(2,2,2);5 imshow(imadjust(I,[],[],0.5));title('Gamma=0.5');7 imshow(imadjust(I,[],[],1));title('Gamma=1');8 subplot(2,2,4);9 imshow(imadjust(I,[],[],1.5));title('Gamma=1.5');2代数运算和逻辑运算加法运算去噪处理1 clear all2 i=imread('lenagray.jpg');3 imshow(i)4 j=imnoise(i,'gaussian',0,0.05);5 [m,n]=size(i);6 k=zeros(m,n);7for l=1:1008 j=imnoise(i,'gaussian',0,0.05);9 j1=im2double(j);10 k=k+j1;11 End12 k=k/100;13 subplot(1,3,1),imshow(i),title('原始图像')14 subplot(1,3,2),imshow(j),title('加噪图像')15 subplot(1,3,3),imshow(k),title(‘求平均后的减法运算提取噪声1 I=imread(‘lena.jpg’);2 J=imnoise (I,‘lena.jpg’,0,0.02);3 K=imsubtract(J,I);4 K1=255-K;5 figure;imshow(I);7 figure;imshow(K1);乘法运算改变图像灰度级1 I=imread('D:/picture/SunShangXiang.jpg')2 I=im2double(I);3 J=immultiply(I,1.2);4 K=immultiply(I,2);5 subplot(1,3,1),imshow(I);subplot(1,3,2),imshow(J);6 subplot(1,3,3);imshow(K);逻辑运算1 A=zeros(128);2 A(40:67,60:100)=1;3 figure(1)4 imshow(A);5 B=zeros(128);6 B(50:80,40:70)=1;7 figure(2)8 imshow(2);9 C=and(A,B);%与10 figure(3);11 imshow(3);12 D=or(A,B);%或13 figure(4);14 imshow(4);15 E=not(A);%⾮16 figure(5);17 imshow(E);3⼏何运算平移运算实现图像的平移1 I=imread('lenagray.jpg');2 subplot(1,2,1);3 imshow(I);4 [M,N]=size(I);g=zeros(M,N);5 a=20;b=20;6for i=1:M7for j=1:N8if((i-a>0)&(i-a<M)&(j-b>0)&(j-b<N)) 9 g(i,j)=I(i-a,j-b);10else11 g(i,j)=0;12 end13 end14 end15 subplot(1,2,2);imshow(uint8(g));⽔平镜像变换1 I=imread('lena.jpg');2 subplot(121);imshow(I);3 [M,N]=size(I);g=zeros(M,N);4for i=1:M5for j=1:N6 g(i,j)=I(i,N-j+1);7 end8 end9 subplot(122);imshow(uint8(g));垂直镜像变换1 I=imread('lena.jpg');2 subplot(121);imshow(I);3 [M,N]=size(I);g=zeros(M,N);4for i=1:M5for j=1:N6 g(i,j)=I(M-i+1,j);7 end8 end9 subplot(122);imshow(uint8(g));图像的旋转1 x=imread('D:/picture/DiaoChan.jpg');2 imshow(x);3 j=imrotate(x,45,'bilinear');4 k=imrotate(x,45,'bilinear','crop');5 subplot(1,3,1),imshow(x);6 title(‘原图')7 subplot(1,3,2),imshow(j);8 title(‘旋转图(显⽰全部)')9 subplot(1,3,3),imshow(k);10 title(‘旋转图(截取局部)')⼏种插值法⽐较1 i=imread('lena.jpg');2 j1=imresize(i,10,'nearest');3 j2=imresize(i,10,'bilinear');4 j3=imresize(i,10,'bicubic');5 subplot(1,4,1),imshow(i);title(‘原始图像')6 subplot(1,4,2),imshow(j1);title(‘最近邻法')7 subplot(1,4,3),imshow(j2);title(‘双线性插值法')8 subplot(1,4,4),imshow(j3);title(‘三次内插法')放缩变换1 x=imread('D:/picture/ZiXia.jpg')2 subplot(2,3,1)3 imshow(x);4 title('原图');5 Large=imresize(x,1.5);6 subplot(2,3,2)7 imshow(Large);8 title('扩⼤为1.5');9 Small=imresize(x,0.1);10 subplot(2,3,3)11 imshow(Small);12 title('缩⼩为0.3');13 subplot(2,3,4)14 df=imresize(x,[600700],'nearest');15 imshow(df)16 title('600*700');17 df1=imresize(x,[300400],'nearest');18 subplot(2,3,5)19 imshow(df1)20 title('300*400');后记:(1)MATLAB基础知识回顾1:crtl+R是对选中的区域注释,ctrl+T是取消注释2:有的代码中点运算如O=a.*I+b/255 ,其中b除以255原因是:灰度数据有两种表式⽅法:⼀种是⽤unit8类型,取值0~255;另⼀种是double类型,取值0~1。
灰度化原理

灰度化原理灰度化是数字图像处理中的一种常见操作,它将彩色图像转换为灰度图像,使得图像中的每个像素都只有一个灰度值。
灰度化原理是基于人眼对颜色和亮度的感知特性,通过灰度化可以简化图像处理的复杂度,提高图像处理的效率,同时也有利于图像的分析和识别。
在数字图像中,每个像素的颜色由红、绿、蓝三个颜色通道组成,每个通道的取值范围是0-255。
灰度化的原理就是根据这三个颜色通道的取值,按照一定的权重将它们合成为一个灰度值。
常见的灰度化算法有加权平均法、最大值法、最小值法等,其中加权平均法是最常用的一种。
加权平均法的灰度化原理是将红、绿、蓝三个颜色通道的取值分别乘以一定的权重,然后将它们相加得到一个灰度值。
通常情况下,绿色对人眼的亮度感知最强,红色次之,蓝色最弱,因此在加权平均法中,绿色的权重最大,红色次之,蓝色最小。
这样得到的灰度值就能比较好地反映出人眼对图像的亮度感知。
灰度化的原理不仅仅局限于彩色图像,对于灰度图像,同样可以进行灰度化操作。
在这种情况下,灰度化的原理就是直接将像素的灰度值作为其灰度值,不需要再进行颜色通道的合成。
这样可以省去颜色通道的权重计算,简化灰度化的过程。
灰度化的原理虽然简单,但在数字图像处理中起着至关重要的作用。
通过灰度化,可以将彩色图像转换为灰度图像,从而简化图像处理的复杂度;同时,灰度图像的灰度值只有一个通道,便于图像的分析和识别;另外,灰度化还可以减小图像的存储空间,提高图像处理的效率。
总的来说,灰度化原理是基于人眼对颜色和亮度的感知特性,通过一定的权重将彩色图像的颜色通道合成为一个灰度值,从而简化图像处理的复杂度,便于图像的分析和识别。
灰度化在数字图像处理中有着广泛的应用,是图像处理中的基础操作之一。
数字逻辑 灰度变换

数字逻辑灰度变换数字逻辑中的灰度变换数字逻辑是计算机科学中的一个重要分支,它涉及到数字电路、逻辑门、布尔代数等知识。
在数字逻辑中,灰度变换是一种常见的图像处理方法,用于调整图像的亮度和对比度,使图像更加清晰和易于观察。
灰度变换是将图像中的像素值进行线性或非线性变换,从而改变图像的亮度和对比度。
在数字图像处理中,通常将灰度值定义为0到255之间的整数,其中0表示黑色,255表示白色。
灰度变换可以用以下公式表示:g(x,y) = T[f(x,y)]其中,f(x,y)表示原始图像中像素点的灰度值,g(x,y)表示变换后的灰度值,T是变换函数。
灰度变换的常见类型包括线性变换、对数变换、伽马变换等。
线性变换是最基本、最常见的灰度变换,它将原始图像中的灰度值映射到一个新的灰度级范围中,常用的线性变换有拉伸变换、压缩变换、反转变换等。
对数变换是一种非线性变换,它能够将图像中亮度较低的区域放大,以便更好地观察图像中的细节。
对数变换的公式为:g(x,y) = c × log[1 + f(x,y)]其中,c是常数,f(x,y)表示原始图像中像素点的灰度值。
伽马变换也是一种非线性变换,它能够增强图像中的对比度和细节,并且可以根据需求进行调整。
伽马变换的公式为:g(x,y) = A × f(x,y)^γ其中,A和γ是常数,f(x,y)表示原始图像中像素点的灰度值。
除了上述常见的灰度变换类型之外,还有一些特殊的灰度变换,如直方图均衡化、直方图匹配等。
直方图均衡化是一种可以提高图像对比度和亮度的方法,它能够使图像中的灰度级分布更加均匀。
直方图匹配是一种将图像的灰度级映射到一个指定的灰度范围的方法,以便更好地观察和分析图像。
总的来说,灰度变换是数字图像处理中的一项基本技术,它能够改善图像的质量,并且可以根据需求进行调整。
在实际应用中,我们需要根据具体的需求选择合适的灰度变换方法,并且需要进行参数调整和优化,以确保处理效果最佳。
数字图像处理实验指导书资料

实验一 灰度图像的对比度线性展宽一、实验目的让学生通过使用对图像采用线性对比度展宽的方法进行处理,获得对图像画质的改善。
二、实验原理与方法对比度线性展宽处理,其实质是对图像灰度值的一个线性映射——通过这种方式来实现突出图像中重要信息的目的。
通常情况下,处理前后的图像灰度级是相同的,即处理前后的图像灰度级都为[0,255]。
那么,从原理上讲,我们就只能通过抑制非重要信息的对比度来腾出空间给重要信息进行对比度展宽。
设原图像的灰度为),(j i f ,处理后的图像的灰度为),(j i g ,对比度线性展宽的原理示意图如图1.1所示。
假设原图像中我们关心的景物的灰度分布在[a f ,b f ]区间内,处理后的图像中,我们关心的景物的灰度分布在[a g ,b g ]区间内。
在这里)(a b g g g -=∆)(a b f f f -=∆<,也就是说我们所关心的景物的灰度级得到了展宽。
根据图中所示的映射关系中分段直线的斜率我们可以得出线性对比度展宽的计算公式:b g a g a b )j图1.1 对比度线性展宽映射关系),(j i f α, a f j i f <≤),(0=),(j i g a a g f j i f +-)),((β,b a f j i f f <≤).,( (1-1)b b g f j i f +-)),((γ,255),(<≤j i f f b(m i ,3,2,1 =;n j ,3,2,1 =) 其中,a a f g =α,a b a b f f g g --=β,bbf g --=255255γ,图像的大小为m ×n 。
三、实验内容与步骤1.熟悉MATLAB 语言的使用,主要包括图像处理相关的语句、表达式,以及变量的使用。
2.按照所给出的参考伪代码编写程序,实现对一幅灰度图像的对比度线性展宽。
3.调整α,β,γ的值,观察对处理结果的影响。
四、思考问题1.在映射关系中,分段直线的斜率的大小对图像处理结果有哪些影响? 2.在进行对比度展宽的时候,如果确定和选取所关心的景物?五、参考伪代码程序[image, map]=imread(‘实验图像.BMP’);%读入一幅灰度图像,放在二维数组变量image 中。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1前言介绍一种用可视化数值计算软件MATLAB实现的数字图像处理系统平台,系统使用MATLAB中提供的GUI设计系统可视化的用户界面,下拉式的菜单方便用户选择对图像的处理。
用户可以随意选择要处理的图片。
但是该系统只支持灰度图片,可实现内容主要包括灰度图像的代数运算、几何运算。
基于数字图像处理的一些基本原理,利用MATLAB 设计程序进行对灰度图像的处理。
有部分处理运算有很多种方法,我选择了最简单、最明了的方法。
数字图像处理又称为计算机图像处理,它是指将图像信号转换成数字信号并利用计算机对其进行处理的过程。
理论上讲,图像是一种二维的连续函数,然而在计算机上对图像进行数字处理的时候,首先必须对其在空间和亮度上进行数字化,这就是图像的采样和量化的过程。
二维图像进行均匀采样,就可以得到一幅离散化成M×N样本的数字图像,该数字图像是一个整数阵列,因而用矩阵来描述该数字图像是最直观最简便的了。
随着计算机的发展,图像处理技术在许多领域得到了广泛应用,用于图像处理的软件也很多,如PHOTOSHOP、PAINTSHOP、GIMP、SaperaProcessing、MATLAB等,其中大部分软件都是基于广告策划和图像修饰处理而设计的应用软件,进行图像处理时并不是很方便。
而MATLAB(矩阵实验室) 它在矩阵运算上有自己独特的特点,在矩阵运算处理具有很大的优势,因此用MATLAB处理数字图像非常的方便。
不仅如此,MATLAB提供了丰富的图形命令和图形函数,而且其面向对象的图形系统具有强大的用户界面(GUI)生成能力。
这样,用户就可以充分利用系统提供的 GUI 特性,编写自己需要的图形界面,从而可以高效地进行图像处理。
MATLAB支持五种图像类型,即索引图像、灰度图像、二值图像、RGB图像和多帧图像阵列;支持BMP、GIF、HDF、JPEG、PCX、PNG、TIFF、XWD、CUR、ICO等图像文件格式的读,写和显示。
MATLAB对图像的处理功能主要集中在它的图像处理工具箱(Image Processing Toolbox)中。
图像处理工具箱是由一系列支持图像处理操作的函数组成,可以对图像进行诸如几何操作、线性滤波和滤波器设计、图像变换、图像分析与图像增强、二值图像操作以及形态学处理等图像处理操作。
2方案设计2.1系统基本方案本系统利用MATLAB语言设计程序进行灰度图像处理,主要功能包括灰度图像的代数运算、几何运算,基本上包含了图像的所有变换和运算。
菜单式选择图像处理运算清晰方便,可视化的界面形象生动、使用方便、交互性强、具有无限的扩展能力。
2.2系统流程图2.3 MATLAB的语言特点(1)语言简洁紧凑,使用方便灵活,库函数极其丰富。
运算符丰富。
(2) MATLAB既具有结构化的控制语句(如for循环,while循环,break语句和if 语句),又有面向对象编程的特性。
(3)程序限制不严格,程序设计自由度大。
(4)MATLAB的图形功能强大。
(5)MATLAB的缺点是,它和其他高级程序相比,程序的执行速度较慢。
(6)由于MATLAB的程序不用编译等预处理,也不生成可执行文件,程序为解释执行,所以速度较慢。
2.4 设计最终方案决定虽然可用高级编程语音(比如c#、delphi等),但实现工具选用matlab较为方便。
、3系统的设计原理3.1各模块功能及图像处理原理3.1.1代数运算代数运算是指两幅输入图象之间进行点对点的加、减、乘、除运算得到输出图象的过程。
如果记输入图象为A(x,y)和B(x,y),输出图象为C(x,y),则有如下四种简单形式: C(x,y) = A(x,y)+B(x,y) C(x,y) = A(x,y)-B(x,y) C(x,y) = A(x,y)×B(x,y) C(x,y) = A(x,y)/ B(x,y)对于图像的代数运算应注意以下问题:(1)代数运算的结果很容易超出数据类型允许的范围,有些运算(如除法)会产生分数结果,这个结果是不能用整数类型描述的,所以在图像代数运算中会采用以下的截取规则:①超出数据类型允许的范围的值用数据类型的最大值代替;②分数的结果采用四舍五入的方法整取。
(2)在使用Matlab中代数运算函数时,不用进行数据类型的转换,这些函数可以接受uint8和uint16数据类型,并返回相同格式的图象结果。
(3)可以使用+、-、*、/等基本算术运算符来进行图像的算数操作运算,但是不同于Matlab中提供的运算函数,必须在运算前将图像转换为适合进行算数运算的双精度数据类型。
(4)任何一个代数运算,都必须保证输入图像的大小相等,且数据类型一致。
在该功能模块中主要设计了图像的求补、叠加、减法、线性组合、乘法、除法运算。
3.1.2几何运算在该功能模块中主要包含了改变图像大小、图像水平镜像、垂直镜像、图像转置、图象旋转、图像裁剪。
1.放缩操作:MATLAB 影像工具箱中的immersize 函数可以通过一种特定的插补方法来改变图像的大小。
该函数的语法如下面所述:B=immersize (A,m ,method )。
如果用户没有指定插补方法,则该函数将采用缺省的近邻插补方法。
另外,我们还可以根据指定的放大系数来改变图像的大小。
例如,下面的代码可以将X 中的像素数目增加一倍。
Y=immersize (X ,2)。
其中2为放大的系数。
如果希望缩小系数,只需将放大系数设置在0到1之间即可。
2.旋转操作:在MATLAB 处理工具箱中的imrotate 函数可以通过一种特定的插补方法来改变图像显示的角度。
该函数的语法如下所示:B=imrotate (A,angle ,method )该函数以图像中心点为基准,以角度 angle 逆时针方向旋转。
指定 angle 为负值,可实现图像顺时针旋转。
该函数是旋转图像 A ,使用指定的差值方法, method 是可以有下列值之一的一个文本字符串,默认值是包含在大括号({}).如果用户没有指定插补方法,则该函数将采用缺省的近邻插补方法。
另外,用户还需指定旋转的角度。
图像的几何变换可以看成是像素在图像内的移动过程,该移动过程可以改变图像中物体对象(像素)之间的空间关系。
完整的几何运算需要由两个算法来实现:空间变换算法和灰度插值算法。
空间变换主要用来保持图像中曲线的连续性和物理的连通性,一般都采用数学函数形式来描述输入、输出图像相应像素间的空间关系。
空间变换一般定义为(,)(',')[(,),(,)]g x y f x y f a x y b x y ==,其中,f 便是输入图像,g 表示输出图像,坐标(',')x y 指的空间变换后的坐标,要注意这时的坐标已经不是原来的坐标(,)x y 了,(,)a x y 和(,)b x y 分别图像的x 和y 坐标的空间变换函数。
灰度级插值主要是对空间变换后的像素赋予灰度值,使之恢复原位置处的灰度值,在几何运算中,灰度级插值是必不可少的组成部分。
因为图像一般用整数位置处的像素来定义。
而在几何变换中,(,)g x y 的灰度值一般由处在非整数坐标上的(,)f x y 的值来确定,即g 中的一个像素一般对英语f 中的几个像素之间的位置,反过来看也是一样,即f 中的一个像素往往被映射到g 中的几个像素之间的位置。
3.2 MATLAB 程序编写及具体操作3.2.1界面设计该系统的界面设计程序MainInterface.m 主要运用了Matlab GUI 中的figure(图形窗口)、uimenu(图形窗口主菜单)两个对象。
在GUI 中所有的对象创建都有着相同的格式: handle=function(‘propertyname ’, propertyvalue,…)uimenu 对象的一些常用属性如表1所示:表1 uimenu 对象的属性列表在本系统菜单设计过程中主要使用了figure、uimenu的Backgroundcolor、Callback、Label、Position 、Separator、Visible属性。
在被处理图片打开之前除“文件”、“帮助”菜单的visible属性为“on”,即可见外其它均为“off”。
3.2.2代数运算函数3.2.3图像代数运算(1)图像加法函数imadd语法格式Y=imadd (X)说明:imadd函数用于产生两张图像的叠加效果,其中X,Y是类型相同的数组。
imadd 函数还可以通过指定常数参数增强一张图像的亮度。
在本系统中就采用了此方法,指定常数参数增强灰度图像的亮度。
(2)图像减法函数imsubtract语法格式:Y= imsubtract (X))说明:说明:imadd函数用于产生两张图像的叠加效果,其中X,Y是类型相同的数组。
subtrac函数还可以通过指定常数参数降低一张图像的亮度。
在本系统中就采用了此方法,指定常数参数降低灰度图像的亮度。
(3)图像乘法运算immultiply和图像除法运算mdivide图像的乘法、除法、减法运算类似于叠加运算。
乘法函数immultiply用于对两张图像进行掩膜操作,即屏蔽掉图像的某些部分。
使用乘法函数时需指定缩放参数,如果大于1则增强图像亮度,反之则减弱图像亮度。
除法函数imdivide通常用于校正成像设备的非线性误差,也可以用于检测两张图像之间的差别,它给出的是相应像素值的变化比率,而不是每个像素值的绝对差异。
减法函数imsubtract通常用于检测图像变化以及运动物体的图像处理。
3.2.4图像几何运算(1)改变图像大小函数imresize语法格式:Y=imresize(X,M,Method)说明:其中X表示需要进行操作的图像,M是放大的倍数,一般来说M是大于0的实数,如果M大于1表示放大图像,小于1则表示缩小图像。
Method参数用来选择使用何种插值方法,其值及其含义如下:’nearest’最近邻插值法、’bilinear’双线性插值法、’bicubic’双三次插值法,默认为’nearest’。
imresize还可以指定图像输出大小,即传递一个向量参数给imresize函数,其中参数的两个分量分别指定输出图像的行数和列数。
如要将原图像X输出为200Χ480的图像,命令为:Y=imresize(X,[200 480])。
在本系统中采用了后一种方法,并使用了随机产生函数,使得图像改变大小随机性。
(2)图像水平镜像fliplr、垂直镜像flipud、转置ctranspose语法格式:Y=fliplr(X) Y=flipud(X) Y=ctranspose (X)说明:水平镜像函数fliplr是将图像沿垂直轴翻转矩阵,即将矩阵左右方向翻转。
垂直镜像函数flipud是将图像沿水平轴翻转矩阵,即将矩阵水平方向翻转。
