第8届全国大学生数学竞赛(非数学类)预赛参考解答
2024年全国中学生数学奥林匹克竞赛(预赛)加试参考答案与评分标准(A卷)

2024年全国中学生数学奥林匹克竞赛(预赛)暨2024年全国高中数学联合竞赛加试(A 卷)参考答案及评分标准说明:1.评阅试卷时,请严格按照本评分标准的评分档次给分.2.如果考生的解答方法和本解答不同,只要思路合理、步骤正确,在评卷时可参考本评分标准适当划分档次评分,10分为一个档次,不得增加其他中间档次.一.(本题满分40分)给定正整数r .求最大的实数C ,使得存在一个公比为r 的实数等比数列1{}n n a ,满足n a C 对所有正整数n 成立.(x 表示实数x 到与它最近整数的距离.)解:情形1:r 为奇数.对任意实数x ,显然有12x ,故满足要求的C 不超过12. 又取{}n a 的首项112a ,注意到对任意正整数n ,均有1n r 为奇数,因此1122n n r a .这意味着12C 满足要求.从而满足要求的C 的最大值为12. …………10分 情形2:r 为偶数.设*2()r m m N .对任意实数 ,我们证明1a 与2a 中必有一数不超过21m m ,从而21m C m . 事实上,设1a k ,其中k 是与1a 最近的整数(之一),且102. 注意到,对任意实数x 及任意整数k ,均有x k x ,以及x x .若021m m ,则121m a k m . 若1212m m ,则22221m m m m ,即21m m r m m ,此时 2121m a a r kr r r m . …………30分 另一方面,取121m a m ,则对任意正整数n ,有1(2)21n n m a m m ,由二项式展开可知11(211)(1)2121n n n m m a m K m m ,其中K 为整数,故21n m a m .这意味着21m C m 满足要求. 从而满足要求的C 的最大值为212(1)m r m r .综上,当r 为奇数时,所求C 的最大值为12;当r 为偶数时,所求C 的最大值为2(1)r r . …………40分二.(本题满分40分)如图,在凸四边形ABCD 中,AC 平分BAD ,点,E F 分别在边,BC CD 上,满足||EF BD .分别延长,FA EA 至点,P Q ,使得过点,,A B P 的圆1 及过点,,A D Q 的圆2 均与直线AC 相切.证明:,,,B P Q D 四点共圆.(答题时请将图画在答卷纸上)证明:由圆1 与AC 相切知180BPA BAC CAD CAF PAC ,故,BP CA 的延长线相交,记交点为L .由||EF BD 知CE CF CB CD.在线段AC 上取点K ,使得CK CE CF CA CB CD ,则||,||KE AB KF AD . …………10分由ABL PAL KAF ,180180BAL BAC CAD AKF ,可知ABL KAF ∽,所以KF AB AL KA. …………20分 同理,记,DQ CA 的延长线交于点L ,则KE AD AL KA. 又由||,||KE AB KF AD 知KE CK KF AB CA AD,即KE AD KF AB . 所以AL AL ,即L 与L 重合.由切割线定理知2LP LB LA LQ LD ,所以,,,B P Q D 四点共圆.…………40分三.(本题满分50分)给定正整数n .在一个3n ×的方格表上,由一些方格构成的集合S 称为“连通的”,如果对S 中任意两个不同的小方格,A B ,存在整数2l ≥及S 中l 个方格12,,,lA C C CB ==,满足iC 与1i C +有公共边(1,2,,1i l −).求具有下述性质的最大整数K :若将该方格表的每个小方格任意染为黑色或白色,总存在一个连通的集合S ,使得S 中的黑格个数与白格个数之差的绝对值不小于K .解:所求最大的K n =.对一个由小方格构成的集合S ,记b S 是S 中的黑格个数,w S 是S 中的白格个数. 用[,]i j 表示第i 行第j 列处的方格,这里13i ≤≤,1j n ≤≤.对于两个方格[,]A i j =,[,]B i j ′′=, 定义它们之间的距离为(,)||||d A B i i j j ′′=−+−.首先,如果将方格表按国际象棋棋盘一样黑白间隔染色,我们证明对任意连通的集合S ,均有||b w S S n −≤,这表明K n ≤.设[1,1]是黑格,并记{0,1}ε∈,满足(mod 2)n ε≡.先证b w S S n −≤.可不妨设S 包含所有黑格,这是因为若S 不包含所有黑格, 取不属于S 的黑格A 满足(,)d A S 最小,这里(,)min (,)B Sd A S d A B ∈=.易知(,)1d A S =或2.若(,)1d A S =,取{}S S A ′=,则S 仍是连通的,且b w S S ′′−更大. 若(,)2d A S =,则存在与A 相邻的白格C ,而C 与S 中某个方格B 相邻,取{,}S S A B ′= ,则S 仍是连通的,且bw S S ′′−不变. 因而可逐步扩充S ,使得S 包含所有黑格,保持S 的连通性,且b w S S −不减.考虑白格集合{[,]|}k W i j i j k =+=,3,5,,1k n ε++,每个k W 中至少有一个方格属于S ,否则不存在从黑格[1,1]A S =∈到黑格[3,1]B n ε=−+的S 中路径.故1()2w S n ε≥+,而1(3)2b S n ε=+,故b w S S n −≤. …………10分 类似可证w b S S n −≤.同上,可不妨设S 包含所有白格, 从而1(3)2w S n ε=−. 再考虑黑格集合{[,]|}k B i j i j k =+=, 4,6,,2k n ε+−,每个k B 中至少有一个黑格属于S ,否则不存在从白格[1,2]A =到白格[3,]B n ε=−的S 中路径. 从而1()2b S n ε≥−,故w b S S n −≤. …………20分 下面证明K n =具有题述性质,即对任意的染色方案,总存在连通的集合S , 使得b w S S n −≥.设表格中共有X 个黑格和Y 个白格,在第二行中有x 个黑格和y 个白格. 于是3X Y n +=, x y n +=.故()()()()2X y Y x X Y x y n −+−=+−+=.由平均值原理可知max{,}X y Y x n −−≥.不妨设X y n −≥.取S 为第二行中的y 个白格以及所有X 个黑格.由于S 包含第二行中所有方格,因而S 是连通的. 而b S X =,w S y =,b w S S X y n −=−≥.综上所述,max K n =. …………50分四.(本题满分50分)设,A B 为正整数,S 是一些正整数构成的一个集合,具有下述性质:(1) 对任意非负整数k ,有k A S ;(2) 若正整数n S ,则n 的每个正约数均属于S ;(3) 若,m n S ,且,m n 互素,则mn S ;(4) 若n S ,则An B S .证明:与B 互素的所有正整数均属于S .证明:先证明下述引理.引理:若n S ,则n B S .引理的证明:对n S ,设1n 是n 的与A 互素的最大约数,并设12n n n ,则2n 的素因子均整除A ,从而12(,)1n n .由条件(1)及(2)知,对任意素数|p A 及任意正整数k ,有k p S .因此,将11k A n 作标准分解,并利用(3)知11k A n S .又2|n n ,而n S ,故由(2)知2n S .因112(,)1k A n n ,故由(3)知112k A n n S ,即1k A n S .再由(4)知k A n B S (对任意正整数k ). ① …………10分设n B C D ,这里正整数C 的所有素因子均整除A ,正整数D 与A 互素,从而(,)1C D .由(1)及(2)知C S (见上面1k A n S 的证明). 另一方面,因(,)1D A ,故由欧拉定理知()1D D A .因此()()(1)()0(mod )D D A n B A n n B D ,但由①知()D A n B S ,故由(2)知D S .结合C S 及(,)1C D 知CD S ,即n B S .引理证毕. …………40分回到原问题.由(1),取0k 知1S ,故反复用引理知对任意正整数y ,有1By S .对任意*,(,)1n n B N ,存在正整数,x y 使得1nx By ,因此nx S ,因|n nx ,故n S .证毕. …………50分。
全国大学生数学竞赛(非数学类)大纲及历年预赛试卷

余弦函数,以及它们的和与积 7. 欧拉(Euler)方程. 8. 微分方程的简单应用 五、向量代数和空间解析几何 1. 向量的概念、向量的线性运算、向量的数量积和向量积、向量的混合积. 2. 两向量垂直、平行的条件、两向量的夹角. 3. 向量的坐标表达式及其运算、单位向量、方向数与方向余弦. 4. 曲面方程和空间曲线方程的概念、平面方程、直线方程. 5. 平面与平面、平面与直线、直线与直线的夹角以及平行、垂直的条件、点到平面和
f ( y) x2[1 f ( y)]3
1 x2 (1 f ( y))
f ( y) [1 f ( y)]2 x2[1 f ( y)]3
解法 2 方程 xe f (y) ey ln 29 取对数,得 f ( y) ln x y ln ln 29
(1)
方程(1)的两边对 x 求导,得 f ( y) y 1 y x
4.设函数 y y(x) 由方程 xe f ( y) ey ln 29 确定,其中 f 具有二阶导数,且 f 1 ,
则
d2 y dx 2
________________.
解法 1 方程 xe f ( y) ey ln 29 的两边对 x 求导,得
e f ( y) xf ( y) ye f ( y) e y y ln 29
即
[ 1 f ( y) y]xe f ( y) ye y ln 29 x
因 e y ln 29 xe f ( y) 0 ,故 1 f ( y) y y,即 y
1
,因此
x
x(1 f ( y))
d2 y dx 2
y
1 x2 (1 f
( y))
f ( y) y x[1 f ( y)]2
点到直线的距离. 6. 球面、母线平行于坐标轴的柱面、旋转轴为坐标轴的旋转曲面的方程、常用的二次
第八届全国大学生数学竞赛决赛(数学类3、4)参考答案一面

其中: x0 ∈ E , x2 ∈ E , · · · , xn ∈ E ; x1 ∈ / E, x3 ∈ / E, · · · , xn−1 ∈ / E. 构造如下: ∀n ⩾ 1, 先取 x0 = 0, x2 , x4 , · · · , xn−2 ∈ E, xn = 1
数学家
|χE (xi ) − χE (xi−1 )| → ∞, 即
因此, 当且仅当 a > 27 或 a < −37 时方程有虚根 ∫∫ ax dy dz + (x + a)2 dx dy √ (a > 0 为常数), 3. 计算曲面积分 I = x2 + y 2 + z 2 S √ 其中 S : z = − a2 − x2 − y 2 , 取上侧. I = π 答案:− a3 2 x2 + y 2 ⩽ a2 解: 令曲面 S1 : , 取下侧, 则 S1 ∩ S 为闭下半球的内侧. z = 0 令其内部区域为 Ω, 令 D 为 xOy 平面上的圆域 x2 + y 2 ⩽ a2 , 则利用高斯公式, 得 {∫ ∫ } ∫∫ [ ] 1 2 I= − axdy dz + (z + a) dxdy a S ∪S1 S1 [ ∫∫∫ ] ∫∫ 1 − (3a + 2z )dv + = a2 dxdy a Ω D [ ] ∫∫∫ 1 4 4 = −2πa − 2 z dv + πa a Ω ∫ ∫ a ∫ 0 2 2π = −πa3 − dθ rdr √ z dz a 0 0 − a2 −r 2 π = − a3 2
ˆ(x) ∈ S . 于是, 在 R 上有界, 从而 f ∫
A
数学家
−∞
ˆ(x)e2πixy dy 收敛, 而 f
第八届全国大学生数学竞赛决赛(数学类3、4)参考答案一面

dt
−∞ ∫ +∞ −A
f (x − t)e2πity dy sin(2πAt) dt πt (3) (15 分)
= ∫ =
−∞ −∞ +∞
f (x − t)
f (x − t) − f (x) sin(2πAt)dt + f (x) πt
∫ 由 f ∈ S 易得积分
+∞
−∞
f (x − t) − f (x) dt 收敛, 从而由黎曼引理可得 πt ∫
(1)
而利用分部积分立即得到 ˆ(x), (f (n) )∧ (x) = (2πix)n f 结合 (1)—(2) 并利用 f ∈ S , 可得对任何 m, k ⩾ 0. xm dk ˆ 1 f (x) = k dx (2πi)m ∫
+∞
∀n ⩾ 0
(2)
∫
R
) dm ( (−2πiy )k f (y ) e−2πixy dy m dy
数学家
Leabharlann
第八届中国大学生数学竞赛决赛三、 四级试卷
(数学类,2017 年 3 月 18 日) 考试形式: 闭卷 考试时间: 180 分钟 满分: 150 分
一、填空题 (本题满分 20 分, 共 4 小题, 每小题 5 分) α1 α2 α3 α4 1. 设 x4 + 3x2 + 2x + 1 = 0 的 4 个根为 α1 , α2 , α3 , α4 . 则行列式 α2 α3 α4 α1 α3 α4 α1 α2 α4 α1 α2 α3 答案:0 2. 设 a 为实数,关于 x 的方程 3x4 − 8x3 − 30x2 + 72x + a = 0 有虚根的充分必要条件是 a 满足 答案:a > 27 or a < −37 解: 记: f (x) = 3x4 − 8x3 − 30x2 + 72x + a 故 f ′ (x) = 12x3 − 24x2 − 60x + 72 = 12(x3 − 2x2 − 5x + 6) = 12(x − 1)(x − 3)(x + 2) f 在 −2 和 −3 取得极小值 152 + a 和 −27 + a, f 在 1 取得极大值 37 + a. =
第八届全国大学生数学竞赛决赛试题参考答案(非数学类,

(3)
∫∫∫( ) ∫ ∫ ∫ I = 1
1− (x2 + y2 + z2)
x2 + y2 + z2 dv = 1
2π dθ
π sin ϕ
1
(1 −
ρ 2 )ρ 3dρ
=
π
.
2Ω
20
0
0
6
3
五、设 n 阶方阵 A, B 满足 AB = A+B ,证明:若存在正整数 k ,使 Ak = O ( O 为零矩阵),则 行列式 B + 2017 A = B .
1 k
−
ln
n
.
(1)证明:极限
lim
n→∞
an
存在;
∞
∑ (2)记
lim
n→∞
an
=
C
,讨论级数
n =1
(an
−C)
的敛散性.
解 (1)利用不等式:当 x > 0 时, x < ln(1+ x) < x ,有 1+ x
1
an
−
an−1
=
1 n
−
ln
n n −1
=
1 n
−
ln
⎛⎜⎝1 +
1⎞ n −1⎟⎠
第八届全国大学生数学竞赛决赛试题参考答案
(非数学类, 2017 年)
一、填空题
1.过单叶双曲面
x2 4
+
y2 2
− 2z2
= 1 与球面
x2
+
y2
+
z2
=
4
的交线且与直线
⎧x = 0 ⎨⎩3y + z
全国大学生数学竞赛试题解答及评分标准非数学类

全国大学生数学竞赛试题解答及评分标准非数学类Standardization of sany group #QS8QHH-HHGX8Q8-GNHHJ8-HHMHGN#全国大学生竞赛历年试题名师精讲(非数学类)(2009——2013)第五届全国大学生数学竞赛预赛试卷(非数学类)一、 解答下列各题(每小题6分共24分,要求写出重要步骤)1.求极限(lim 1sin nn →∞+.解因为()sin sin 2sin n ππ==……(2分);原式lim 1exp lim ln 1sin nn n n →∞→∞⎡⎤⎛⎫⎛⎫=+=+⎢⎥ ⎢⎥⎝⎝⎣⎦………………………………………………………………………………………(2分);14exp lim exp n n n e →∞⎛⎫⎛⎫=== ⎝⎝……(2分) 2.证明广义积分0sin xdx x +∞⎰不是绝对收敛的解 记()1sin n n nx a dx xππ+=⎰,只要证明0n n a ∞=∑发散即可。
……………………(2分)因为()()()()10112sin sin 111n n n a x dx xdx n n n ππππππ+≥==+++⎰⎰。
…………(2分)而()021n n π∞=+∑发散,故由比较判别法0n n a ∞=∑发散。
……………………………………(2分)3.设函数()y y x =由323322x x y y +-=确定,求()y x 的极值。
解 方程两边对x 求导,得22236360x xy x y y y ''++-= ………………(1分)故()2222x x y y y x+'=-,令0y '=,得()200x x y x +=⇒=或2x y =-………(2分)将2x y =-代入所给方程得2,1x y =-=,将0x =代入所给方程得0,1x y ==-,…………………………………(2分)又()()()()()2222222222422x xy y y x x x y yy x y yx''++--+-''=-()()()0,1,02,1,0200220010,1020x y y x y y y y ''====-==+---''''==-<=>-, 故()01y =-为极大值,()21y -=为极小值。
全国大学生数学竞赛试题解答及评分标准 非数学类

全国大学生竞赛历年试题名师精讲(非数学类)(2009——2013)第五届全国大学生数学竞赛预赛试卷(非数学类)一、 解答下列各题(每小题6分共24分,要求写出重要步骤)1.求极限(lim 1sin nn →∞+.解因为()sin sin 2sinn ππ==……(2分);原式lim 1exp lim ln 1sin nn n n →∞→∞⎡⎤⎛⎫⎛⎫=+=+⎢⎥ ⎢⎥⎝⎝⎣⎦=2.证明广义积分0sin xdx x ⎰不是绝对收敛的解 记()1sin n n nx a dx xππ+=⎰,只要证明0n n a ∞=∑发散即可。
……………………(2分)因为()()()()10112sin sin 111n n n a x dx xdx n n n ππππππ+≥==+++⎰⎰。
…………(2分) 而()021n n π∞=+∑发散,故由比较判别法0n n a ∞=∑发散。
……………………………………(2分)3.设函数()y y x =由323322x x y y +-=确定,求()y x 的极值。
解 方程两边对x 求导,得22236360x xy x y y y ''++-= ………………(1分)故()2222x x y y y x +'=-,令0y '=,得()200x x y x +=⇒=或2x y =-………(2分)将2x y =-代入所给方程得2,1x y =-=,将0x =代入所给方程得0,1x y ==-,…………………………………(2分)又()()()()()2222222222422x xy y y x x x y yy x y y x ''++--+-''=-()()()0,1,02,1,0200220010,1020x y y x y y y y ''====-==+---''''==-<=>-,故()01y=-为极大值,()21y-=为极小值。
第8届全国大学生数学竞赛(非数学类)预赛试卷及答案
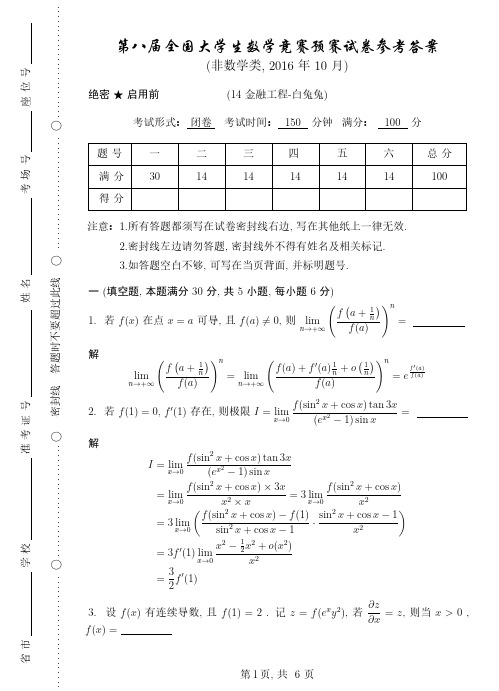
从而
x0
=
2
,
y0
=
1
,
得
z0
=
x20 2
+ y02
=
3
,
从而所求切平面为
2(x − 2) + 2(y − 1) − (z − 3) = 0
即 二 (本题满分 14 分)
2x + 2y − z = 3
设 f (x) 在 [0, 1] 可导, f (0) = 0, 且当 x ∈ (0, 1) , 0 < f ′(x) < 1 .
座位号
考场号
姓名
第八届全国大学生数学竞赛预赛试卷参考答案
(非数学类, 2016 年 10 月)
绝密 ⋆ 启用前
(14 金融工程-白兔兔)
考试形式: 闭卷 考试时间: 150 分钟 满分: 100 分
题号 一
二
三
四
五
六
总分
满 分 30
14
14
14
14
14
100
得分
注意:1.所有答题都须写在试卷密封线右边, 写在其他纸上一律无效. 2.密封线左边请勿答题, 密封线外不得有姓名及相关标记. 3.如答题空白不够, 可写在当页背面, 并标明题号.
(∫ a
)2 ∫ a
试证当 a ∈ (0, 1) ,
f (x) dx > f 3(x) dx .
0
0
(∫ x
)2 ∫ x
证明 设 F (x) =
f (t) dt − f 3(t) dt , 则 F (0) = 0 且要证明 F ′(x) > 0
0
0
∫x
设 g(x) = 2 f (t) dt − f 2(x) , 则 F ′(x) = f (x)g(x)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
0
0
设 g(x) 2 x f (t)dt f 2(x) , 0
则 F '(x) f (x)g(x) ,
...............................3' ... .........................5'
由于 f (0) 0, f '(x) 0 ,故 f (x) 0 ,从而
解。该曲面在点 (x0, y0, z0 ) 的切平面的法向量为 (x0, 2 y0, 1) 。又该切平面于已知平面平行, 从而两平面法向量平行,故 x0 2 y0 1 。
2 2 1
从而
x0
2,
y0
1,得
z0
x02 2
y02
3 ,从而所求切平面为
2(x 2) 2( y 1) (z 3) 0 ,
3lim x0
f (sin2 x cos x) x2
所以
I=3lim x0
f
(sin2 x cos x) f sin2 x cos x 1
(1)
sin2
x
cos x 1 x2
3f '(1) lim sin2 x cos x 1 3 f '(1) lim(sin2 x 1 cos x )
M
1 2
u
2
v2
w2 2
dudvdw
A
,
其中 A 1 1 1 1 V . 24 4 4 2
ቤተ መጻሕፍቲ ባይዱ
.............................4'
记 I
u2
v2
w2
dudvdw
2
d
d
1
r2
r 2 sindr
4
.
000
5
由于 u 2 ,v2 , w2 在 上积分都是 I / 3 , 故
x2 y2 z 2 , 求质量 M (x2 y2 z 2 )dxdydz .
解. 由于 : x 1 2 y 1 2 2 z 1 2 1 , 是一个椭球, 2 2 2
..........................2'
其体积为 V 2 2 . 作变换 u x 1 , v y 1 , w 2 z 1 , 将 变为单位球
=
lim
n
n
n k 1
[ xk
xk 1
f
(x)
f
(
xk
)]dx
=
lim
n
n
x0
x2
x x0
2
x2
3 f '(1)(1 1)= 3 f '(1) 22
3. 设 f (x) 有连续导数,且 f (1) 2 .记 z f (ex y2 ) ,若 z z ,求 f (x) 在 x 0 的表达 x
式.
解: 由题设得 z f '(e x y 2 )ex y 2 f (ex y 2 ) . 令 u ex y 2 ,得到当 u 0 有 x
第 8 届全国大学生数学竞赛(非数学类)预赛参考解答 (2016 年 10 月)
一 填空题(满分 30 分,每小题 5 分)
1.
若
f (x) 在点 x a 可导,且
f (a) 0 ,则 lim n
f
(a 1 n
f (a)
)
n
=
。
解:
lim n
f
(a 1 n
f (a)
)
n
=
只要证明 g(x) 0 , x 0 。 而 g(0) 0 ,我们只要证明 g '(x) 0,0 x a 。
而 g '(x)=2f (x)[1 f '(x)] 0 ,得证。
................6'
三(满分 14 分)某物体所在的空间区域为 : x2 y 2 2z 2 x y 2z , 密度函数为
即 2x 2y z 3。
二(满分 14 分)设 f (x) 在[0,1] 上可导, f (0) 0 ,且当 x (0,1) ,0<f '(x) 1。试证当
a (0,1) ,
a
2
f (x)dx
a f 3(x)dx 。
0
0
证: 设 F(x)
x
2
f (t)dt
x f 3(t)dt ,则 F(0) 0 且要证明 F '(x) 0.
f '(u)u f (u) , 即 f '(u) 1 , 从而 ln f (u)' (ln u)' .
f (u) u
所以有 ln f (u) ln u c1 , f (u) cu . 再而由初始条件得 f (u) 2u .
故当 x 0 有 f (x) 2x .
4. 设 f (x) ex sin 2x ,求 f (4) (0) 。
lim
n
f
(a)
f (a) 1 n
f (a)
(
1 n
)
n
f (a)
e f (a)
。
2.
若
f (1)=0 ,
f
'(1) 存在,求极限 I
lim x0
f (sin2 x cos x) tan 3x (ex2 1)sin x
.
解:
I= lim x0
f
(sin 2
x cos x2 x
x) 3x
f
k n
1 2
。
证明
将区间[0,1] n 等分,设分点 xk
k n
,则 xk
1 n
,且
lim
n
n
1 f (x)dx 1
0
n
n k 1
f
1 n
=
lim
n
n
n k 1
xk f (x)dx n f
xk 1
k 1
xk
xk
......................3'
3
2
2
2
: u2 v2 w2 1, 而 (u,v, w) 2 , 故 dudvdw 2dxdydz 且 (x, y, z)
M 1
u
1
2
v
1
2
w
1
2
dudvdw
.
2 2 2 2 2
因一次项积分都是 0 , 故
.............................4'
M 1 1 1 1 I A 3 2 2
23 3 6
6
.............................4'
四(满分 14 分)设函数 f (x) 在闭区间[0,1] 上具有连续导数, f (0) 0, f (1) 1 。证明:
lim
n
n
1 f (x)dx 1
0
n
n k 1
解。由 Taylor 展式得
f
(
x)
1
x
1 2!
x2
1 3!
x3
+o( x3
)
2x
1 3!
(2x)3
o(
x
4
)
所以
f
(x) 展式的
4 次项
1(2x)3 x+ 2 x4
3!
3!
x4
,从而
f
(4) (0) 4!
1,故
f
(4) (0)
24 。
5. 求曲面 z x2 y2 平行于平面 2x 2 y z 0 的切平面方程。 2
