北师大版数学八年级上册第三章单元测试题(含答案可打印)
北师大版数学八年级(上册)第三章测试题(附参答案)
北师八上数学测试卷第三章1.如果将电影票上“6排3号”简记为(6,3),那么“10排10号”可记为;(7,1)表示的含义是.2.在平面直角坐标系中,点(-4,4)在第象限.3.若点A(7,-3)关于y轴的对称点是B,则线段AB的长是.4.已知点P在第二象限,若该点到x轴的距离为3,到y轴的距离为1,则点P的坐标是.5.如图1所示,小强告诉小华图中A,B两点的坐标分别为(-3,5),(3,5),小华一下就说出C 在同一坐标系的坐标是.图16.若我军战舰要攻打敌军战舰,需要知道( )A.我军战舰的位置B.敌军战舰相对于我军战舰的方向C.敌军战舰相对于我军战舰的距离D.B、C选项都需要7.若点A关于x轴的对称点的坐标是A’(-5,4),则点A的坐标是( )A.(-5,-4)B.(5,4)C.(5,-4)D.(-5,4)8.在如图2所示的直角坐标系中,点M,N的坐标分别为( )图2A.M(-1,2),N(2,1)B.M(2,-1),N(2,1)C.M(-1,2),N(1,2)D.M(2,-1),N(1,2)9.点P(-1-b2,3+a2)一定在( )A.第一象限B.第二象限C.第三象限D.第四象限10.图3是某古塔周围的建筑群的平面示意图,这座古塔的位置用A(5,4)表示.某人从点B 出发到古塔,他所走的路线中,错误的是( )图3A.(2,2)➝(2,4)➝(4,5)B.(2,2)➝(2,4)➝(5,4)C.(2,2)➝(4,2)➝(4,4)➝(5,4)D.(2,2)➝(2,3)➝(5,3)➝(5,4)11.如图4所示,已知棋子“车”的坐标为(-2,3),棋子“马”的坐标为(1,3),则棋子“炮”的坐标为( )图4A.(3,2)B.(3,1)C.(2,2)D.(-2,2)12.若点(a-1,3)在y轴上,则a的值为( )A.1B.-1C.0D.313.过两点A(-2,-2),B(-2,5)作直线,则直线( )A.平行于y轴B.平行于x轴C.与y轴相交D.无法确定14.线段MN在平面直角坐标系中的位置如图5所示,线段M1N1与MN关于y轴对称,则点M 的对应点M1的坐标为( )图5A.(4,2)B.(-4,2)C.(-4,-2)D.(4,-2)15.如图6所示:(1)写出A,B,C三点的坐标;(2)若△ABC各顶点的纵坐标不变,横坐标都乘-1,请你在同一坐标系中描出对应的点A’,B’,C’,并依次连接这三个点,所得的△A’B’C’与原△ABC有怎样的位置关系?图616.如图7,是用一个“树干”和一把“扇子”在方格纸上摆出的图案.如果用(0,0)表示M的位置,用(2,1)表示N的位置,那么(1)图①中A,B,C,D,E的位置分别为;(2)图②中A,B,C,D,E,F,G的位置分别为;(3)在图①和图②中分别找出(4,11)和(8,10)的位置.图717.如图8所示,已知点A(-1,-2),B(4,-2)和C(4,3),求正方形ABCD的顶点D的坐标.图818.如图9所示,在平面直角坐标系中,有A(0,1),B(-1,0),C(1,0)三点.若点D与A,B,C三点构成平行四边形,请写出所有符合条件的点D的坐标,并画出图形.图919.△ABC在如图10所示的平面直角坐标系中.(1)画出△ABC关于y轴对称的△A1B1C1;(2)画出△ABC关于x轴对称的△A2B2C2.图1020.在如图11所示的海域中,有各种目标,根据要求填空.(1)对于我军潜艇来说,在南偏东60°的方向上有哪些目标: ;(2)敌舰B(距我军潜艇的图上距离为1.8 cm)在我军潜艇的方向上,距我军潜艇的实际距离是千米;(3)敌舰C现距我军潜艇的图上距离为1 cm,沿我军潜艇北偏东30°的方向以60千米/时的速度逃跑,可绕过正前方暗礁(暗礁距我军潜艇的图上距离为3 cm),我军潜艇须沿方向,至少以的速度追击,才能将敌舰追上,且没有触礁的危险.图1121.如图12,有8×8的正方形网格,按要求操作,并计算.(1)在8×8的正方形网格中建立平面直角坐标系,使点A的坐标为(2,4),点B的坐标为(4,2);(2)将点A向下平移5个单位,再关于y轴对称得到点C,求点C坐标;(3)画出三角形ABC,并求其面积.图12参考答案1.(10,10) 7排1号2.二3.144.(-1,3)5.(-1,7)6.D7.A8.A9.B10.A11.A12.A13.A14.D15.解:(1)A(3,4),B(1,2),C(5,1);(2)△A’B’C’与△ABC关于y轴对称.16.(1)A(10,8),B(7,10),C(5,9),D(3,8),E(9,1)(2)A(7,0),B(0,3),C(2,6),D(4,7),E(10,7),F(12,6),G(14,3)(3)略17.解:点A(-1,-2),B(4,-2)和C(4,3)在平面直角坐标系内的位置如图8所示.连接AB,有AB∥x轴,且AB=5;连接BC,有BC∥y轴,且BC=5,过点C作CM⊥y轴,过点A作AN⊥x轴,AN 与CM交于点D,则D(-1,3).18.解:符合条件的点D的坐标分别是D1(2,1),D2(-2,1),D3(0,-1),图略.19.解:(1)(2)如图:20.(1)敌舰A和小岛(2)正东180(3)北偏东30°90千米/时21.解:(1)如图所示:(2)点A向下平移5个单位得到点(2,-1),关于x轴对称的点C(-2,-1);(3)S=5×6-6×3÷2-4×5÷2-2×2÷2=9.。
北师大版八年级数学上册 第三章 位置与坐标单元综合检测(含答案)
第三章位置与坐标综合测试一、选择题1、如图所示，小颖从家到达莲花中学要穿过一个居民小区，若小区的道路均是正南或正东方向，小颖走下面哪条线路不能到达学校( )A．(0，4)→(0，0)→(4，0) B、(0，4)→(4，4)→(4，0)C．(0，4)→(1，4)→(1，1)→(4，1)→(4，0) D．(0，4)→(3，4)→(4，2)→(4，0)2、如图所示，有一种“怪兽吃豆豆”的游戏，怪兽从点O(0，0)出发，先向西走1cm，再向北走2cm，正好能吃到位于点A的豆豆，如果点A用（－1，2）表示，那么(1，－2)所表示的位置是( ) A．点A B．点B C．点C D．点D3、如果点P（a，b）在x轴上，那么点Q(ab，－1)在( )A、y轴的正半轴上B、y轴的负半轴上C、x轴的正半轴上D．x轴的负半轴上4、在平面直角坐标系中，一个多边形各个顶点的纵坐标保持不变，横坐标分别乘－1，则所得的多边形与原多边形相比( )A、多边形形状不变，整体向左平移了1个单位；B、多边形形状不变，整体向下平移了1个单位C、所得多边形与原多边形关于y轴成轴对称；D．所得多边形与原多边形关于x轴成轴对称5、如图所示，已知点A(－1，0)和点B(1，2)，在坐标轴上确定点P，使得三角形ABP为直角三角形，则满足这样条件的点P共有( )A、2个B、4个C、6个D．7个6．若点M(x，y)的坐标满足关系式xy＝0，则点M在( )．A、原点B、x轴上C、y轴上D、x轴上或y轴上7．若点N到x轴的距离是1，到y轴的距离是2，则点N的坐标是( )．A、(1，2)B、(2，1)C、(1，2)，(1，－2)，(－1，2)，(－1，－2)D、(2，1)，(2，－1），(－2，1)，(－2，－1）8．已知点A(a，－b)在第二象限，则点B(3－a，2－b)在( )．A、第一象限B、第二象限C、第三象限D、第四象限9．已知三角形的三个顶点坐标分别是(－2，1)，(2，3)，(－3，－1)，把△ABC运动到一个确定位置，在下列各点坐标中，( )是平移得到的．A、(0，3)，(0，1），(－1，－1)B、(－3，2)，(3，2)，(－4，0)C、(1，－2)，(3，2)，(－1，－3)D、(－1，3)，(3，5)，(－2，1)二、填空题10．若点P(m－3，m＋1)在第二象限，则m的取值范围是______．11．已知点P在第二象限，且到x轴的距离是2，到y轴的距离是3，则点P的坐标为______．12．△ABC的三个顶点A(1，2)，B(－1，－2)，C(－2，3)，将其平移到点A′(－1，－2)处，使A与A′重合．则B、C两点坐标分别为____________．13．平面直角坐标系中的一个图案的纵坐标不变，横坐标分别乘－1，那么所得的图案与原图案会关于______对称．14．在如下图所示的方格纸中，每个小正方形的边长为1，如果以MN所在直线为y轴，以小正方形的边长为单位长度建立平面直角坐标系，使A点与B点关于原点对称，则此时C点的坐标为______、15．观察如图所示的图形，若图中“鱼”上点P的坐标为(4，3、2)，则点P的对应点P1的坐标应为____、16、在平面直角坐标系中，已知A、B的坐标分别为(2，0)、(0，1)，若将线段AB平移至CD，且点A的对应点C的坐标为(3，b)，点B的对应点D的坐标为（a，3），则a+b=____、三、解答题17、某地区两条交通主干线l1与l2互相垂直，并交于点O，l1为南北方向，l2为东西方向．现以l2为x轴，l1为y轴，取100 km为1个单位长度建立平面直角坐标系，根据地震监测部门预报，该地区最近将有一次地震，震中位置在P（1，－2）处，影响区域的半径为300 km．(1)根据题意画出平面直角坐标系，并标出震中位置．(2)在平面直角坐标系内画出地震影响的范围，并判断下列城市是否受到地震影响、城市：O(0,0),A(－3,0),B(0,1),C(－1、5,－4),D（0，－4），E（2，－4）．18．在如图所示的方格图中，我们称每个小正方形的顶点为“格点”，以格点为顶点的三角形叫做“格点三角形”，根据图形回答下列问题．(1)图中格点三角形A'B'C'是由格点三角形ABC通过怎样的变换得到的？(2)如果以直线a，b为坐标轴建立平面直角坐标系后，点A的坐标为（－3，4），请写出格点三角形DEF各顶点的坐标，并求出三角形DEF的面积．19、在直角坐标系中，我们把横、纵坐标都为整数的点叫做整点．整点P从原点O出发，速度为1 cm/s，且整点P做向上或向右运动，运动时间(s)与整点个数（个）的关系如下表：根据上表中的规律，回答下列问题：(1)当整点P从点O出发4s时，可以得到整点P的个数为____；(2)当整点P从点O出发8s时，在如图所示的直角坐标系中描出可以得到的所有整点；(3)当整点P从点O出发____s时，可以达到整点(16，4)的位置、20．如果点P(1－x，1－y)在第二象限，那么点Q(1－x，y－1)关于原点的对称点M在第几象限？21、如图，小虫A从点(0，10)处开始，以每秒3个单位长度的速度向下爬行，小虫B同时从点(8,0)处开始，以每秒2个单位长度的速度向左爬行，2秒钟后，它们分别到达点A'、B'．(1)写出点A'、B'的坐标；(2)求出四边形AA'B'B的面积．参考答案1、D解析因为小区道路均是正南或正东方向，所以由(3，4)不能直接到达（4,2）、2、D解析以点为原点，东西方向为横轴，南北方向为纵轴建立平面直角坐标系，则A（－1,2），B（1,2），C（2,1），D（1，－2）、3、B解析：∵点P(a，b)在x轴上，∴b=0，∴ab=0．∴点Q(ab，－1)在y轴的负半轴上．故选B、4、C5、C6．D7．D8．A9．D．10．－1＜m＜3．11．(－3，2)．12．B＇(－3，－6)，(－4，－1)．13．y轴．14．(2，－1)．15、（4，2、2）解析：对比图中“鱼头”的坐标，图中“鱼头”O的坐标为(0，0)，图中“鱼头”O1的坐标为（0，－1），可以看作“鱼头”O1是由“鱼头”O向下平移1个单位长度得到的，由平移的规律可得点P1的坐标为(4，2、2)．16、3解析：∵两点A(2，0)，B(0，1)，把线段AB平移后点A的对应点C的坐标为(3，b)，点B的对应点D的坐标为(a，3)，∴线段是向右平移1个单位，再向上平移了2个单位，∴a=0+1=1，b=0+2=2．∴a+b=1+2=3．17、分析：地震影响区域是以震中为圆心，半径为300km的圆内部分（包括圆周），圆外部分为不受影响的地区、解：(1)图略．(2)图略，O，D，E会受到地震影响，而A，B，C不会受到地震影响．18、解：(1)图中格点三角形A'B'C'是由格点三角形ABC向右平移7个单位长度得到的．(2)如果以直线a，b为坐标轴建立平面直角坐标系后，点A的坐标为（－3，4），则格点三角形DEF各顶点的坐标分别为D(0,－2),E(－4,－4),F(3,3)．如图所示，S三角形DEF=S三角形DGF+s三角形GEF=1151515 22⨯⨯+⨯⨯=．19、解：（1）根据表中所示的规律，点的个数比时间数多1，由此可计算出整点P从O点出发4s时整点P的个数为5、(2)由表中所示规律可知，横、纵坐标的和等于时间，则得到的整点为(0,8),(1,7),(2,6),(3,5),(4,4),(5,3),(6,2),(7,1)，(8，0)．所描各点如图所示：(3)由表中规律可知，横、纵坐标的和等于运动时间，因此可得16+4=20(s)、20、解：因为点P（1－x，1－y）在第二象限，所以1－x<0，1－y>0，即y－1<0,所以点Q（1－x ，y －1）在第三象限．又知点M 与点Q 关于原点对称，所以点M 在第一象限．21、解：(1)OA '=OA －AA '=10－3×2=4, ∴点A '的坐标为（0,4）、 ∵OB '=OB －BB '=8－2×2=4, ∴点B '的坐标为(4，0)．(2)四边形AA 'B 'B 的面积=△AOB 的面积－△A 'OB '的面积 =1110844=408=3222⨯⨯-⨯⨯-、 www 、czsx 、com 、cn。
北师大版数学八年级上册第三章单元测试题(含答案_可打印)
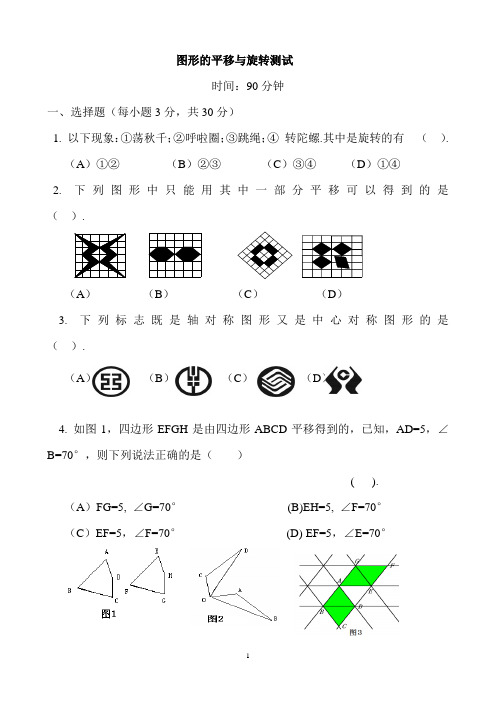
图形的平移与旋转测试时间：90分钟一、选择题（每小题3分，共30分）1. 以下现象：①荡秋千；②呼啦圈；③跳绳；④转陀螺.其中是旋转的有（）.（A）①②（B）②③（C）③④（D）①④2. 下列图形中只能用其中一部分平移可以得到的是（）.（A）（B）（C）（D）3. 下列标志既是轴对称图形又是中心对称图形的是（）.（A）（B）（C）（D）4. 如图1，四边形EFGH是由四边形ABCD平移得到的，已知，AD=5，∠B=70°，则下列说法正确的是（）( ).（A）FG=5, ∠G=70°(B)EH=5, ∠F=70°（C）EF=5，∠F=70°(D) EF=5，∠E=70°5. 如图3，△OAB绕点O逆时针旋转90°到△OCD的位置，已知∠AOB=45°，则∠AOD的度数为.（A）55°（B）45°（C）40°（D）35°6. 同学们曾玩过万花筒，它是由三块等宽等长的玻璃片围成的.如图是看到的万花筒的一个图案，如图3中所有小三角形均是全等的等边三角形，其中的菱形AEFG可以看成是把菱形ABCD以A为中心（）.（A）顺时针旋转60°得到（B）逆时针旋转60°得到（C）顺时针旋转120°得到（D）逆时针旋转120°得到7. 如图，甲图案变成乙图案，既能用平移，又能用旋转的是（）.8. 下列图形中，绕某个点旋转180°能与自身重合的图形有（）（1）正方形；（2）等边三角形；（3长方形；（4）角；（5）平行四边形；(6)圆. （A）2个（B）3个（C）4个（D）5个9. 如图4，Rt△ABC沿直角边BC所在直线向右平移到Rt△DEF,则下列结论中，错误的是（）（A）BE=EC （B）BC=EF（C）AC=DF （D）△ABC≌△DEF10. 下列这些复杂的图案都是在一个图案的基础上，在“几何画板”软件中拖动一点后形成的，它们中每一个图案都可以由一个“基本图案”通过连续旋转得来，旋转的角度正确的是（）.（A）︒90 30（B）︒60（D）︒45（C）︒二、填空题（每小题3分，共30分）11. 在旋转的过程中，要确定一个图形的旋转后的位置，除了知道原来图形的位置和旋转方向外，还需要知道 和 .12. 如图5所示，右边的图形是左边的图形向右平移 格得到的.13. 如图6，在Rt OAB ∆中，90OAB ∠=︒，6OA AB ==，将OAB ∆绕点O 沿逆时 针方向旋转90︒得到11OA B ∆，则线段1OA 的长是 ；1AOB ∠的度数是 .14. 下列图形中，不能由图形M 经过一次平移或旋转得到的是 .15. 小明把自己的左手手印和右手手印按在同一张白纸上，左手手印 ____（填“能”或“不能”）通过旋转与右手手印完全重合在一起. 16. 如图7，已知面积为1的正方形ABCD 的对角线相交于点O ，过点O 任作一条直线分别交AD BC ，于E F ，，则阴影部分的面积是 ．17. 如图8所示，在平面内将Rt △ABC 绕直角顶点C 逆时针旋转90°得到Rt △EFC.图7B若AB=5,BC=1,则线段BE 的长为 ．18. 如图9，P 是正方形ABCD 内一点，将△ABP 绕点B 顺时针方向旋转一定的角度后能与△CB /P 重合.若PB=3，则P /P = ．19. 如图10所示，△ABC 与△111C B A 关于直线m 对称，将△111C B A 向右平移得到△222C B A , 由此得出下列判断：（1）AB//22B A ;(2)∠A=∠2A ;(3)AB=22B A ,其中正确有 ．（填序号）20. 聪聪和亮亮玩一种游戏，他们要将图 11（1)和图11（2）中的三角形通过水平或竖直平移的方法得到图11（3），平移的过程中，每次水平或竖直平移一格，先拼完的为胜， 聪聪选择了图11（1），亮亮选择了图11（2），那么______先获胜. 三、简答题（共60分）21.（8分）如图12，将四边形ABCD 绕O 点旋转后得到一个四边形，请在图中依次标上点A ，B ，C ，D 的对应点E ，F ，G ，H ：22. （10分）如图13，四边形ABCD 是平行四边形，（1）图中哪些线段可以通过平移而得到；（2）图中哪些三角形可以通过旋转而得到.23.(10分）如图14，△ABC是等腰直角三角形，BC是斜边，P为△ABC内一点，将△ABP绕点A逆时针旋转后与△ACP/重合，如果AP=3，那么线段P P/的长是多少？24.（12分）把正方形ABCD绕着点A，按顺时针方向旋转得到正方形AEFG，边FG与BC交于点H（如图15）.试问线段HG与线段HB相等吗？请先观察猜想，再说明你的理由.25.（10分）同学们用直尺和三角板画平行线，这种画平行线的方法利用了怎样的移动？由此我们得出了什么结论？26.（10分）请你以“爱护地球，保护地球----植树造林”为题，以等腰三角形为“基本图形”利用平移设计一组有意义的图案，完成后与同学进行交流．参考答案一、选择题1.D2.B3.A4.B5.B6.C7.B8.C9.A 10.C 二、填空题11. 旋转中心，旋转角 12. 4 13. 6，135° 14. ③ 15. 能 16. 4117. 7 18. 2319. （1）（2）（3） 20. 亮亮 三、简答题 21. 略22. （1）AB 和DC ，AD 和BC ，AO 和OC ，BO 和OD ．（2）△AOB 和△COD ，△COB 和△AOD ，△CDA 和△ABC ，△ABD 和△CBD.23. 解：根据旋转的性质可知将△ABP 绕点A 逆时针旋转后与△ACP / 重合△ABP ≌△ACP /,所以AP=A P /,∠BAC=∠PA P /=90°.所以在Rt △AP P /中，P P /=233322=+.24. 解：相等.连接AH ，根据旋转性质，因为AG=AB ，AH=AH ，∠AGH=∠ABH=90°,所以△AGH ≌△ABH,所以HG=HB. 25. 平移，平行公理：同位角相等两直线平行.26. 略。
北师大版初中数学八上第三章综合测试试题试卷含答案
第三章综合测试第Ⅰ卷 （选择题 共30分）一、选择题（每题3分，共30分）1.下列关于确定一个点的位置的说法中，能具体确定点的位置的是（ ） A .东北方向B .东经3510'︒，北纬12︒C .距点A 100米D .偏南，8000米2.在平面直角坐标系中，点(2020，所在的象限是（ ） A .第一象限B .第二象限C .第三象限D .第四象限3.如图，ABC △与DFE △关于y 轴对称，若点A 的坐标为()4,6−，则点D 的坐标为（ ）A .()4,6−B .()4,6C .()2,1−D .()6,24.若()A a b ,，(),B a d 表示两个不同的点，且0a ≠，则这两个点在（ ） A .平行于x 轴的直线上B .第一、三象限两坐标轴夹角平分线上C .平行于y 轴的直线上D .第二、四象限两坐标轴夹角平分线上5.甲、乙两名同学用围棋子做游戏，如图所示，现轮到黑棋下子，黑棋下一子后白棋下一子，使黑棋的5个棋子组成轴对称图形，白棋的5个棋子也组成轴对称图形，则下列下子方法不正确的是[说明：棋子的位置用数对表示，如点A 在()6,3]（ ）A .黑()3,7，白()5,3B .黑()4,7，白()6,2C .黑()2,7，白()5,3D .黑()3,7，白()2,66.如图，在平面直角坐标系中，四边形MNPO 的顶点P 的坐标是()3,4，边OM 在x 轴上，且OM OP =，则顶点M 的坐标是（ ）A .()3,0B .()4,0C .()5,0D .()6,07.若定义()(),,f a b b a =，()(),,g m n m n =−−，例如()()2,33,2f =，()()1,41,4g −−=，则()()56g f −，等于（ ） A .()6,5−B .()5,6−−C .()6,5−D .()5,6−8.有甲、乙、丙三个人，他们所处的位置不同，甲说：“以我为坐标原点，乙的位置是()2,3.”丙说：“以我为坐标原点，乙的位置是()3,2−−.”则以乙为坐标原点，甲、丙的坐标分别是（已知三人所建立的直角坐标系中x 轴、y 轴的方向相同，且单位长度一致）（ ） A .()3,2−−，()2,3− B .()3,2−，()2,3 C .()2,3−−，()3,2D .()2,3−−，()2,3−−9.已知点()1,0A ，()0,2B ，点P 在x 轴上，且PAB △的面积为5，则点P 的坐标为（ ） A .()4,0−B .()6,0C .()4,0−或()6,0D .无法确定10.如图所示，在平面直角坐标系中，半径均为1个单位长度的半圆1O ，2O ，3O ，…组成一条平滑的曲线，点P 从原点O 出发，沿这条曲线向右运动，速度为每秒2π个单位长度，则第2020秒时，点P 的坐标是（ ）A .()2020,0B .()2020,1−C .()2020,1D .()2019,0第Ⅱ卷 （非选择题 共70分）二、填空题（每题3分，共18分）11.若()1,3表示教室里第1列第3排的位置，则()3,1表示教室里第________列第________排的位置. 12.已知()21,32A x x −+是第一、三象限两坐标轴夹角平分线上的点，则点A 的坐标是________. 13.在同一平面直角坐标系中，一同学误将点A 的横、纵坐标的次序颠倒，写成(),A a b ；另一同学误将点B 的坐标写成关于y 轴对称的点的坐标，写成(),B b a −−，则A ，B 两点原来的位置关系是________ .14.如图是城市中某区域的示意图，小聪同学从点O 出发，先向西走100米，再向南走200米到达学校.如果学校的位置用()100,200−−表示，那么()300,200表示的地点是________.15.已知等边三角形ABC 的两个顶点的坐标分别为()4,0A −，()20B ,，则点C 的坐标为________，ABC △的面积为________.16.如图是某同学在课下设计的一款软件，蓝精灵从点O 第一跳落到点()11,0A ，第二跳落到点()21,2A ，第三跳落到点()34,2A ，第四跳落到点()44,6A ，第五跳落到点5A ________，到达点2n A 后，要向________方向跳________个单位长度落到点21n A +.三、解答题（共52分）17.（6分）如图，在ABC △中，13AB AC ==，24BC =，请你建立适当的平面直角坐标系，并直接写出A ，B ，C 三点的坐标.18.（6分）如图是一个1010⨯的正方形网格，其中正方形的顶点称为格点，网格中ABC △的顶点A ，B ，C 均在格点上，点A 的坐标为()3,4. （1）直接写出B ，C 两点的坐标；（2）将A ，B ，C 三点的纵坐标保持不变，横坐标分别乘-1，得到点1A ，1B ，1C ，在图中描出点1A ，1B ，1C ，并画出111A B C △；（3）描述图中的111A B C △与ABC △的位置关系.19.（6分）如图，雷达探测器测得六个目标A ，B ，C ，D ，E ，F 出现.按照规定的目标表示方法，目标C ，F 的位置分别表示为()6,120C ︒，()5,210F ︒. （1）按照此方法表示目标A ，B ，D ，E 的位置.A ：________；B ：________；D ：________；E ：________.（2）若目标C 的实际位置是北偏西30︒距观测站1800米，目标F 的实际位置是南偏西60︒距观测站1500米，写出目标A ，B ，D ，E 的实际位置.（3）若另有目标G 在东南方向距观测站750米处，目标H 在南偏东20︒距观测站900米处，写出目标G ，H 的位置表示.20.（6分）如图，已知在平面直角坐标系中有()2,1A −，()3,1B ，()2,3C 三点.请回答下列问题： （1）在坐标系内描出点A ，B ，C 的位置. （2）求出以A ，B ，C 三点为顶点的三角形的面积.（3）在y 轴上是否存在点P ，使以A ，B ，P 三点为顶点的三角形的面积为10？若存在，请直接写出点P 的坐标；若不存在，请说明理由.21.（6分）已知点()24,1P m m +−.根据下列条件，求出点P 的坐标. （1）点P 在y 轴上； （2）点P 在x 轴上；（3）点P 的纵坐标比横坐标大3；（4）点P 在过点()2,3A −且与x 轴平行的直线上.22.（6分）如图，四边形OABC 是一张放在平面直角坐标系中的长方形纸片，O 为原点，点A 在x 轴的正半轴上，点C 在y 轴的正半轴上，10OA =，8OC =，在OC 边上取一点D ，若将纸片沿AD 翻折，使点O 落在BC 边上的点E 处，求D ，E 两点的坐标.23.（8分）如图，在平面直角坐标系内有两点()11,A x y ，()22,B x y ，过点A ，B 分别向x 轴，y 轴作垂线，在Rt ABC △中，21AC x x =−，21BC y y =−，所以AB ==利用这一公式解决下列问题：某地震多发地区有互相垂直的两条交通主干线，以这两条主干线为坐标轴建立平面直角坐标系，1个单位长度为1 km ，地震监测部门测得该地区发生过一次地震，震中位置为()100,200P −，影响范围的半径为300 km ，如图所示，主干线沿线附近有3个城市：()300,200A −，()0,100B −，()200,0C ，则在地震中受影响的是哪些城市？为什么？24.（8分）如图，在平面直角坐标系中，直线l 过点()3,0M 且平行于y 轴.（1）如果ABC △三个顶点的坐标分别是()2,0A −，()1,0B −，()1,2C −，ABC △关于y 轴的对称图形是111A B C △，111A B C △关于直线l 的对称图形是222A B C △，写出222A B C △的三个顶点的坐标；（2）如果点P 的坐标是(),0a −，其中0a ＞，点P 关于y 轴的对称点是1P ，点1P 关于直线l 的对称点是2P ，求2PP 的长.第三章综合测试 参考答案第I 卷一、 1.【答案】B 2.【答案】D【解析】第四象限内点的坐标特点是(),+−，由此可知点2020(,所在的象限是第四象限.故选D. 3.【答案】B【解析】因为ABC △与DFE △关于y 轴对称，点6()4,A −，所以点6(4)D ,. 4.【答案】C 5.【答案】C【解析】本题可以逐项判断.在各个位置处补上棋子，观察图形得到选项A ，B ，D 都可以构成轴对称图形.故选C. 6.【答案】C【解析】如图，过点P 作PE OM ⊥于点E .因为顶点P 的坐标是(3,4)，所以3OE =，4PE =，所以5OP ==.所以5OM OP ==. 所以点M 的坐标为(5,0).故选C. 7.【答案】A【解析】根据(,)(,)f a b b a =，()(,),g m n m n =−−，可得()5,6,5()6f −=−，所以(())(5,66,)()56,5g f g −=−=−.故选A. 8.【答案】C 9.【答案】C【解析】因为0(1)A ,，()0,2B ，点P 在x 轴上，所以PAB △的AP 边上的高为2. 又因为PAB △的面积为5，所以5AP =. 而点P 可能在点()1,0A 的左边或右边， 所以0()4,P −或(6,0). 故选C. 10.【答案】A第II 卷二、11.【答案】3 1【解析】类比(1,3)表示教室里第1列第3排的位置，则(3,1)表示教室里第3列第1排的位置. 12.【答案】(7,7)−− 13.【答案】关于x 轴对称 14.【答案】超市【解析】因为()100200−−,表示从点O 出发，先向西走100米，再向南走200米，所以)300(200,表示从点O 出发，先向东走300米，再向北走200米，所以)300(200,表示的地点是超市.15.【答案】(−或(1,−− 【解析】当点C 在第二象限时，过点C 作CH AB ⊥于点H .因为0()4,A −，()2,0B ，所以6AB =.因为ABC △是等边三角形，所以3AH BH ==.由勾股定理得CH =(C −；同理，当点C 在第三象限时，(C −.所以ABC △的面积为162⨯⨯=. 16.【答案】(9,6) 正东 ()21n +【解析】因为蓝精灵从点O 第一跳落到点1()1,0A ，第二跳落到点2()1,2A ，第三跳落到点3()4,2A ，第四跳落到点4()4,6A ，所以蓝精灵先向正东跳动，再向正北跳动，每次跳动的距离为前一次的距离加1，即可求出.第五跳落到点5()9,6A .到达点2n A 后，要向正东方向跳()21n +个单位长度落到点21n A +. 三、17.【答案】解：答案不唯一，如以BC 所在直线为x 轴，过点B 作BC 的垂线为y 轴建立平面直角坐标系，如图所示：由图可知，点()12,5A ，()0,0B ，()24,0C . 18.【答案】解：（1）由图可知，()1,2B ，()5,1C . （2）如图：（3）由图可知，111A B C △与ABC △关于y 轴对称.19.【答案】解：（1）(5,30)︒ (2,90)︒ (4,240)︒ (3,300)︒（2）18006300÷= （米），目标A 的实际位置为北偏东60︒距观测站1500米； 目标B 的实际位置为正北方向距观测站600米； 目标D 的实际位置为南偏西30︒距观测站1200米； 目标E 的实际位置为南偏东30︒距观测站900米.（3）目标G 的位置表示为2.5,3(15)︒，目标H 的位置表示为(3,290)︒. 20.【答案】解：（1）描点如图.（2）如图，依题意，得AB x ∥轴，且()325AB =−−=， 所以15252ABC S =⨯⨯=△. （3）存在.因为5AB =，10ABP S =△， 所以点P 到AB 的距离为4. 又因为点P 在y 轴上，所以点P 的坐标为(0,5)或(0,)3−.21.【答案】解：（1）由题意，得240m +=，解得2m =−， 则13m −=−，所以点P 的坐标为(0,)3−. （2）由题意，得10m −=，解得1m =， 则246m +=，所以点P 的坐标为(6,0). （3）由题意，得()1243m m −=++， 解得8m =−，则2412m +=−，19m −=−，所以点P 的坐标为(12,9)−−. （4）由题意，得13m −=−， 解得2m =−，则240m +=，所以点P 的坐标为(0,)3−.22.【答案】解：由题意，可知折痕AD 所在的直线是四边形OAED 的对称轴. 在Rt ABE △中，10AE OA ==，8AB =，所以6BE ===.所以4CE =.所以8(4)E ,.在Rt DCE △中，222DC CE DE +=， 又因为DE OD =，所以()22284OD OD −+=，解得5OD =，所以()0,5D .23.【答案】解：在地震中受影响的是A 城市.理由：因为300(),200A −，()0,100B −，()200,0C ，100(),200P −，所以()100300200km PA =−+=，PB ==，PC ==.因为300km PA ＜，300km PB ＞，300km PC ＞，所以在地震中受影响的是A 城市. 24.【答案】解：（1）△A 2B 2C 2的三个顶点的坐标分别是2()4,0A ，2()5,0B ，2()5,2C . （2）①如图（a ），当03a ＜≤时，因为点P 与点1P 关于y 轴对称，()0P a −,，所以1()0P a ,.因为点1P 与点2P 关于直线3x =对称， 设20(),P x ，可得32x a+=， 即6x a =−，所以2()6,0P a −，则()2666PP a a a a =−−−=−+=.②如图（b ），当3a ＞时，因为点P 与点1P 关于y 轴对称，()0P a −,，所以1()0P a ,.初中数学 八年级上册 5 / 5因为点1P 与点2P 关于直线3x =对称，设20(),P m ，可得32m a +=，即6m a =−，所以2()6,0P a −，则()2666PP a a a a =−−−=−+=. 综上所述，2PP 的长为6.。
2022-2023学年北师大版八年级数学上册《第3章位置与坐标》单元达标测试题(附答案)
2022-2023学年北师大版八年级数学上册《第3章位置与坐标》单元达标测试题（附答案）一．选择题（共8小题，满分40分）1．在平面直角坐标系中，下列点在第三象限内的是（）A．（1，1）B．（﹣2，﹣3）C．（1，﹣2）D．（﹣3，5）2．在平面直角坐标系xOy中，以O，A，B，C为顶点的正方形的边长为3．若点A在x轴上，点C在y轴的正半轴上，则点B的坐标为（）A．（3，3）B．（3，﹣3）C．（3，3）或（﹣3，3）D．（﹣3，﹣3）或（3，﹣3）3．点P（x，y）在第四象限，且点P到x轴和y轴的距离分别为3和5，则点P的坐标为（）A．（3，﹣5）B．（﹣5，3）C．（5，﹣3）D．（﹣3，5）4．在平面直角坐标系中，有A（﹣2，a+2），B（a﹣3，4）两点，若AB∥x轴，则A，B两点间的距离为（）A．2B．1C．4D．35．已知，点M（a，2），B（3，b）关于x轴对称，则a+b＝（）A．﹣5B．﹣1C．1D．56．在平面直角坐标系中，点A（1，2）向右平移2个单位长度所得对应点为A'，则点A'的坐标是（）A．（1，4）B．（3，2）C．（﹣1，2）D．（1，0）7．将△ABC的三个顶点坐标的横坐标都乘以﹣1，并保持纵坐标不变，则所得图形与原图形的关系是（）A．关于x轴对称B．关于y轴对称C．关于原点对称D．将原图形沿x轴的负方向平移了1个单位8．如图，已知棋子“车”的坐标为（﹣2，﹣1），棋子“炮”的坐标为（3，﹣2），则棋子“马”的坐标为（）A．（1，1）B．（﹣1，1）C．（1，﹣1）D．（﹣1，﹣1）二．填空题（共8小题，满分40分）9．已知点A（﹣2，b）与点B（a，3）关于原点对称，则a﹣b＝．10．如图，在平面直角坐标系中，△OAB为等腰三角形，OA＝AB＝5，点B到x轴的距离为4，若将△OAB绕点O逆时针旋转90°，得到△OA′B′，则点B′的坐标为．11．在平面直角坐标系中，已知点A（﹣2，4），M是y轴上一动点，当AM的值最小时，点M的坐标是．12．已知线段AB∥x轴，且AB＝5，若点A的坐标为（﹣2.4），则点B的坐标为．13．在平面直角坐标系中，点M坐标为（﹣2，3），若MN∥x轴，且线段MN＝2，则点N 坐标为．14．已知平面直角坐标系第四象限内的点P（3﹣m，2m+6）到两坐标的距离相等，则点P 的坐标为．15．在平面坐标系中，点P（﹣2，1），B（3，1），则PB＝．16．一个质点在第一象限及x轴、y轴上运动，在第一秒钟，它从原点运动到（0，1），然后接着按图中箭头所示方向运动[即（0，0）→（0，1）→（1，1）→（1，0）→…，]，且每秒移动一个单位，那么第80秒时质点所在位置的坐标是．三．解答题（共6小题，满分40分）17．在平面直角坐标系中，（1）已知点P（a﹣1，3a+6）在y轴上，求点P的坐标；（2）已知两点A（﹣3，m），B（n，4），若AB∥x轴，点B在第一象限，求m的值，并确定n的取值范围；（3）在（1）（2）的条件下，如果线段AB的长度是5，求以P、A、B为顶点的三角形的面积S．18．如图，一只甲虫在5×5的方格（每小格边长为1）上沿着网格线运动．它从A处出发去看望B、C、D处的其它甲虫，规定：向上向右走为正，向下向左走为负．如果从A到B记为：A→B（+1，+4），从B到A记为：B→A（﹣1，﹣4），其中第一个数表示左右方向，第二个数表示上下方向，那么图中（1）A→C（，），B→C（，），C→D（，）；（2）若这只甲虫的行走路线为A→B→C→D，请计算该甲虫走过的最少路程；（3）若这只甲虫从A处去甲虫P处的行走路线依次为（+2，+2），（+2，﹣1），（﹣2，+3），（﹣1，﹣2），请在图中标出P的位置．19．已知点A（a﹣2，﹣2），B（﹣2，2b+1），根据以下要求确定a、b的值．（1）直线AB∥x轴；（2）A、B两点在第一、三象限的角平分线上．20．如图，在平面直角坐标系，A（a，0），B（b，0），C（﹣1，2），且|2a+b+1|+（a+2b﹣4）2＝0．（1）求a，b的值；（2）①在x轴的正半轴上存在一点M，使S△COM＝△ABC的面积，求出点M的坐标；②在坐标轴的其他位置是否存在点M，使△COM的面积＝△ABC的面积仍然成立？若存在，请直接写出符合条件的点M的坐标为．21．茅麓中学位于金坛的点O处，该校学生要到尧塘点C处购买花木．他们先向东走了6km 到达A处，又向北走了12km到达B处，又折向东走了10km到达C处，若以O为原点，过O的正东方向为x轴正方向，正北方向为y轴正方向，以1为单位长度建立直角坐标系．（1）在直角坐标系里，标出旅游路线；（2）可得点C的坐标是；CB与x轴是什么关系？．（3）求OC两地的距离；（4）若O、C两点的位置不变，在x轴上求点P，使得△OCP的面积是△OCA的面积的，试写出点P的坐标．22．如图，方格纸中每个小方格都是边长为1个单位的正方形，学校位置坐标为A（2，1），图书馆位置坐标为B（﹣1，﹣2），解答下列问题：（1）在图中建立平面直角坐标系，并标出坐标原点O；（2）若体育馆位置坐标为C（1，3），请在坐标系中标出体育馆的位置C；（3）点C绕原点顺时针旋转90°得到点D，直接写出点D的坐标；（4）顺次连接学校、图书馆、体育馆，得到△ABC，求△ABC的面积．参考答案一．选择题（共8小题，满分40分）1．解：A．（1，1）在第一象限，故本选项不符合题意；B．（﹣2，﹣3）在第三象限，故本选项符合题意；C．（1，﹣2）在第四象限，故本选项不符合题意；D．（﹣3，5）在第二象限，故本选项不符合题意．故选：B．2．解：如图，由图象知，符合条件的点B的坐标为（3，3）或（﹣3，3）．故选：C．3．解：点P（x，y）点在第四象限，且点P到x轴、y轴的距离分别为3、5，则点P的坐标为（5，﹣3），故选：C．4．解：∵AB∥x轴，∴A点和B点的纵坐标相等，即a+2＝4，解得a＝2，∴A（﹣2，4），B（﹣1，4），∴A、B两点间的距离为﹣1﹣（﹣2）＝1；故选：B．5．解：∵点M（a，2），B（3，b）关于x轴对称，∴a＝3，b＝﹣2．a+b＝3﹣2＝1，故选：C．6．解：点A（1，2）向右平移2个单位长度所得对应点为A'（3，2），故选：B．7．解：将△ABC的三个顶点坐标的横坐标都乘以﹣1，并保持纵坐标不变，则所得图形与原图形的关系是关于y轴对称，故选：B．8．解：如图所示：棋子“马”的坐标为：（1，﹣1）．故选：C．二．填空题（共8小题，满分40分）9．解：∵点A（﹣2，b）与点B（a，3）关于原点对称，∴a＝2，b＝﹣3，∴a﹣b＝2+3＝5，故答案为：5．10．解：过点B作BN⊥x轴，过点B′作B′M⊥y轴，∴∠B′MO＝∠BNO＝90°，∵OA＝AB＝5，点B到x轴的距离为4，∴AN＝3，∴ON＝8，∵将△OAB绕点O逆时针旋转90°，得到△OA′B′，∴∠BOB′＝90°，OB＝OB′，∴∠BOA′+∠B′OA′＝∠BOA+∠BOA′，∴∠BOA＝∠B′OA′，∴△NOB≌△MOB′（AAS），∴OM＝ON＝8，B′M＝BN＝4，∴B′（﹣4，8），故答案为：（﹣4，8）．11．解：如图，当AM⊥y轴时，AM取最小值．∵A（﹣2，4），∴M（0，4）．故答案是：（0，4）．12．解：∵AB⊥x轴，点A的坐标是（﹣2，4），∴点B的纵坐标是4，若点B在点A的左侧时，点B的横坐标为﹣2﹣5＝﹣7，若点B在点A的右侧时，点B的横坐标为﹣2+5＝3，所以，点B的坐标是（﹣7，4）或（3，4）．故答案为：（﹣7，4）或（3，4）．13．解：∵MN∥x轴，∴M，N点的纵坐标相等，∴点N的纵坐标为3，∵线段MN＝2，∴当点N在点M左侧时，点N的坐标为（﹣4，3）；当点N在点M右侧时，点N的坐标为（0，3）；故答案为：（﹣4，3）或（0，3）．14．解：∵点P在第四象限，点P（3﹣m，2m+6）到两坐标的距离相等，∴3﹣m＝﹣（2m+6），解得m＝﹣9．∴点P的坐标为（12，﹣12）．故答案是：（12，﹣12）．15．解：∵P（﹣2，1），B（3，1），∴PB＝3﹣（﹣2）＝5，故答案为：5．16．解：3秒时到了（1，0）；8秒时到了（0，2）；15秒时到了（3，0）；24秒到了（0，4）；35秒到了（5，0）；48秒到了（0，6）；63秒到了（7，0）；80秒到了（0，8）．∴第80秒时质点所在位置的坐标是（0，8）．三．解答题（共6小题，满分40分）17．解：（1）∵点P（a﹣1，3a+6）在y轴上，∴a﹣1＝0，解得a＝1，所以，3a+6＝3×1+6＝9，故P（0，9）；（2）∵AB∥x轴，∴m＝4，∵点B在第一象限，∴n＞0，∴m＝4，n＞0；（3）∵AB＝5，A、B的纵坐标都为4，∴点P到AB的距离为9﹣4＝5，∴以P、A、B为顶点的三角形的面积S＝×5×5＝12.5．18．解：（1）A→C（+3，+4），B→C（+2，0），C→D（+1，﹣2）；（2）1+4+2+1+2＝10；（3）点P如图所示．19．解：（1）∵直线AB∥x轴，∴2b+1＝﹣2，a﹣2≠﹣2，解得a≠0，b＝﹣；（2）∵A、B两点在第一、三象限的角平分线上，∴a﹣2＝﹣2，2b+1＝﹣2，解得a＝0，b＝﹣．20．解（1）∵|2a+b+1|+（a+2b﹣4）2＝0，又∵|2a+b+1|和（a+2b﹣4）2都是非负数，所以得，解方程组得，，∴a＝﹣2，b＝3．（2）①由（1）得A，B点的坐标为A（﹣2，0），B（3，0），|AB|＝5．∵C（﹣1，2），∴△ABC的AB边上的高是2，∴．要使△COM的面积是△ABC面积的，而C点不变，即三角形的高不变，M点在x轴的正半轴上，只需使．此时．∴M点的坐标为②由①中的对称点得，当M在y轴上时，△COM的高为1，∵△COM的面积＝△ABC的面积，∴|OM|×1＝∴OM＝±5（负值舍去），∴M2（0，5），M3（0，﹣5）．故答案为：（﹣，0），（0，5），（0，﹣5）．21．解：（1）如图所示：；（2）C的坐标是（16，12），CB∥x轴．故答案是：（16，12），平行；（3）OC＝＝20（km）；（4）△OCP的面积是△OCA的面积的，A的坐标是（6，0），则P的坐标是（3，0）或（﹣3，0）．22．解：（1）平面直角坐标系如图所示；（2）如图，点C即为所求；（3）如图，点D即为所求，D（3，﹣1）；（4）S△ABC＝3×5﹣×2×5﹣×3×3﹣×1×2＝4.5．。
北师大版数学八年级(上册)第三单元测试题
北师大版数学八年级上册第三单元测试题一．选择题（共10小题）1．点M（﹣4，﹣1）关于y轴对称的点的坐标为（）A．（﹣4，1）B．（4，1） C．（4，﹣1）D．（﹣4，﹣1）2．在平面直角坐标系中，点A的坐标为（1，2），将点A向右平移3个单位长度后得到A′，则点A′的坐标是（）A．（﹣2，2）B．（1，5） C．（1，﹣1）D．（4，2）3．下列各点中位于第四象限的点是（）A．（3，4） B．（﹣3，4）C．（3，﹣4）D．（﹣3，﹣4）4．若点A（a，3）在y轴上，则点B（a﹣3，a+2）所在的象限是（）A．第一象限B．第二象限C．第三象限D．第四象限5．已知点P1（﹣4，3）和P2（﹣4，﹣3），则P1和P2（）A．关于原点对称B．关于y轴对称C．关于x轴对称D．不存在对称关系6．已知点A（a，1）与点A′（5，b）关于坐标原点对称，则实数a、b的值是（）A．a=5，b=1 B．a=﹣5，b=1 C．a=5，b=﹣1 D．a=﹣5，b=﹣17．无论m为何值，点A（m，5﹣2m）不可能在（）A．第一象限B．第二象限C．第三象限D．第四象限8．如图，若在象棋盘上建立直角坐标系xOy，使“帥”位于点（﹣1，﹣2），“馬”位于点（2，﹣2），则“炮”位于点（）A．（﹣2，﹣1）B．（0，0） C．（1，﹣2）D．（﹣1，1）9．点C在x轴上方，y轴左侧，距离x轴2个单位长度，距离y轴3个单位长度，则点C的坐标为（）A．（2，3） B．（﹣2，﹣3）C．（﹣3，2）D．（3，﹣2）10．在平面直角坐标系中，已知A（2，﹣2），点P是y轴上一点，则使AOP为等腰三角形的点P有（）A．1个 B．2个 C．3个 D．4个二．填空题（共10小题）11．若将点A（1，3）向左平移2个单位，再向下平移4个单位得到点B，则点B的坐标为．12．已知点A的坐标为（﹣2，3），则点A关于原点对称的点B的坐标为．13．直角坐标系中点A坐标为（5，3），B坐标为（1，0），将点A绕点B逆时针旋转90°得到点C，则点C的坐标为．14．点P（m，m+3）在平面直角坐标系的y轴上，则点P的坐标是．15．已知点P1（a，﹣3）和点P2（3，b）关于y轴对称，则a+b的值为．16．点P（2，﹣3）先向左平移4个单位长度，再向上平移1个单位长度，得到点P′的坐标是．17．已知点P（2﹣a，2a﹣7）（其中a为整数）位于第三象限，则点P坐标为．18．如图，正方形ABCD的顶点B、C都在直角坐标系的x轴上，若点A的坐标是（﹣1，4），则点C的坐标是．19．若点P（m，﹣2）与点Q（3，n）关于原点对称，则（m+n）2015=．20．如图，在直角坐标系中，已知点A（﹣3，0），B（0，4），对△OAB连续作旋转变换，依次得到三角形①、②、③、④、…则三角形⑩的直角顶点与坐标原点的距离为．三．解答题（共10小题）21．求图中四边形ABCD的面积．22．如图是一个平面直角坐标系，按要求完成下列各小题．（1）写出图中的多边形ABCDEF顶点在坐标轴上的点的坐标；（2）说明点B与点C的纵坐标有什么特点？线段BC与x轴有怎样的位置关系？（3）写出点E关于y轴的对称点E′的坐标，并指出点E′与点C有怎样的位置关系．23．已知点P（a﹣2，2a+8），分别根据下列条件求出点P的坐标．（1）点P在x轴上；（2）点P在y轴上；（3）点Q的坐标为（1，5），直线PQ∥y轴；（4）点P到x轴、y轴的距离相等．24．已知点A（3，0）、B（0，2）、C（﹣2，0）、D（0，﹣1）在同一坐标系中描出A、B、C、D各点，并求出四边形ABCD的面积．25．已知点P（2x，3x﹣1）是平面直角坐标系上的点．（1）若点P在第一象限的角平分线上，求x的值；（2）若点P在第三象限，且到两坐标轴的距离和为11，求x的值．26．已知点P（2m+4，m﹣1）．试分别根据下列条件，求出点P的坐标．（1）点P的纵坐标比横坐标大3；（2）点P在过A（2，﹣3）点，且与x轴平行的直线上．27．已知点M （﹣3a +2，a +6）．（1）若点M 在x 轴上，求点M 的坐标；（2）点N （﹣4，﹣5），且直线MN ∥y 轴，求线段MN 的长度．28．在平面坐标系中△ABO 位置如图，已知OA=AB=5，OB=6，（1）求A 、B 两点的坐标．（2）点Q 为y 轴上任意一点，直接写出满足：S △ABO =S △AOQ 的Q 点坐标．29．已知点P的坐标为（2m﹣1，m+7）．（1）若点P在x轴上，试求m的值；（2）若点P在二、四象限的角平分线上，求m的值；（3）若点Q坐标为（1，2），且PQ∥y轴，求点P的坐标；（4）若点Q坐标为（1，n+3），且PQ关于x轴对称，请求出n的值．30．已知A（o，a），B（b，o），C（3，c）且|a﹣2|+（b﹣3）2+=0（1）求a，b，c的值（2）若第二象限内有一点P（m，），请用含m的式子表示四边形ABOP的面积（3）在（2）的条件下，是否存在点P，使四边形ABOP的面积为△ABC面积的2倍？若存在，求出点P的坐标，若不存在，说明理由．北师大版数学八年级上册第三单元测试题参考答案与试题解析一．选择题（共10小题）1．（2017•桂林一模）点M（﹣4，﹣1）关于y轴对称的点的坐标为（）A．（﹣4，1）B．（4，1） C．（4，﹣1）D．（﹣4，﹣1）【分析】根据平面直角坐标系中两个关于坐标轴成轴对称的点的坐标特点：关于y轴对称的点，纵坐标相同，横坐标互为相反数．【解答】解：∵平面直角坐标系中关于y轴对称的点的坐标特点：横坐标相反数，纵坐标不变，可得：点M关于y轴的对称点的坐标是（4，﹣1）．故选：C．【点评】本题考查了关于x轴、y轴对称的点的坐标，解决本题的关键是掌握好对称点的坐标规律：（1）关于x轴对称的点，横坐标相同，纵坐标互为相反数；（2）关于y轴对称的点，纵坐标相同，横坐标互为相反数；（3）关于原点对称的点，横坐标与纵坐标都互为相反数．2．（2017•历下区一模）在平面直角坐标系中，点A的坐标为（1，2），将点A 向右平移3个单位长度后得到A′，则点A′的坐标是（）A．（﹣2，2）B．（1，5） C．（1，﹣1）D．（4，2）【分析】将点A的横坐标加3，纵坐标不变即可求解．【解答】解：点A（1，2）向右平移3个单位长度得到的点A′的坐标是（1+3，2），即（4，2）．故选D．【点评】此题主要考查了坐标与图形的变化，关键是掌握横坐标，右移加，左移减；纵坐标，上移加，下移减．3．（2017春•滨海县月考）下列各点中位于第四象限的点是（）A．（3，4） B．（﹣3，4）C．（3，﹣4）D．（﹣3，﹣4）【分析】应先判断点在第四象限内点的坐标的符号特点，进而找相应坐标．【解答】解：第四象限的点的坐标的符号特点为（+，﹣），观察各选项只有C 符合条件，故选C．【点评】本题主要考查了平面直角坐标系中各象限的点的坐标的符号特点，四个象限的符号特点分别是：第一象限（+，+）；第二象限（﹣，+）；第三象限（﹣，﹣）；第四象限（+，﹣）．4．（2017春•西湖区校级月考）若点A（a，3）在y轴上，则点B（a﹣3，a+2）所在的象限是（）A．第一象限B．第二象限C．第三象限D．第四象限【分析】根据y轴上点的横坐标为0求出a，再求出点B的坐标，然后根据各象限内点的坐标特征解答．【解答】解：∵点A（a，3）在y轴上，∴a=0，∴点B（﹣3，2），∴点B在第二象限．故选B．【点评】本题考查了各象限内点的坐标的符号特征，记住各象限内点的坐标的符号是解决的关键，四个象限的符号特点分别是：第一象限（+，+）；第二象限（﹣，+）；第三象限（﹣，﹣）；第四象限（+，﹣）．5．（2017春•新野县月考）已知点P1（﹣4，3）和P2（﹣4，﹣3），则P1和P2（）A．关于原点对称B．关于y轴对称C．关于x轴对称D．不存在对称关系【分析】根据，横坐标相同，纵坐标互为相反数，即可求出P1和P2关于x轴对称的点．【解答】解：∵P1（﹣4，3）和P2（﹣4，﹣3），∴横坐标相同，纵坐标互为相反数，∴P1和P2关于x轴对称的点，故选C．【点评】本题考查平面直角坐标系关于坐标轴成轴对称的两点的坐标之间的关系，注意掌握关于x轴对称的点，横坐标相同，纵坐标互为相反数．6．（2016•武汉）已知点A（a，1）与点A′（5，b）关于坐标原点对称，则实数a、b的值是（）A．a=5，b=1 B．a=﹣5，b=1 C．a=5，b=﹣1 D．a=﹣5，b=﹣1【分析】根据关于原点对称的点的横坐标与纵坐标都互为相反数解答．【解答】解：∵点A（a，1）与点A′（5，b）关于坐标原点对称，∴a=﹣5，b=﹣1．故选D．【点评】本题考查了关于原点对称的点的坐标，两点关于原点对称，则两点的横、纵坐标都是互为相反数．7．（2016•江都区二模）无论m为何值，点A（m，5﹣2m）不可能在（）A．第一象限B．第二象限C．第三象限D．第四象限【分析】根据四个象限的符号特点分别是：第一象限（+，+）；第二象限（﹣，+）；第三象限（﹣，﹣）；第四象限（+，﹣）．【解答】解：当m＜0时，5﹣2m＞0，点A（m，5﹣2m）在第二象限，当0＜m时，点A（m，5﹣2m）在第一象限，当m时，点A（m，5﹣2m）在第四象限．故选：C．【点评】本题考查了各象限内点的坐标的符号特征以及解不等式，记住各象限内点的坐标的符号是解决的关键，四个象限的符号特点分别是：第一象限（+，+）；第二象限（﹣，+）；第三象限（﹣，﹣）；第四象限（+，﹣）．8．（2016•大兴区一模）如图，若在象棋盘上建立直角坐标系xOy，使“帥”位于点（﹣1，﹣2），“馬”位于点（2，﹣2），则“炮”位于点（）A．（﹣2，﹣1）B．（0，0） C．（1，﹣2）D．（﹣1，1）【分析】根据“帅”的位置向右平移1个单位，上移两个单位，可得答案．【解答】解：“帅”的位置向右平移1个单位，上移两个单位（0，0），故选：B．【点评】本题考查了坐标确定位置，利用点的坐标平移是解题关键．9．（2016春•苏仙区期末）点C在x轴上方，y轴左侧，距离x轴2个单位长度，距离y轴3个单位长度，则点C的坐标为（）A．（2，3） B．（﹣2，﹣3）C．（﹣3，2）D．（3，﹣2）【分析】根据平面直角坐标系中各个象限内点的坐标的符号即可解答．【解答】解：∵点C在x轴上方，y轴左侧，∴点C的纵坐标大于0，横坐标小于0，点C在第二象限；∵点距离x轴2个单位长度，距离y轴3个单位长度，所以点的横坐标是﹣3，纵坐标是2，故点C的坐标为（﹣3，2）．故选C．【点评】本题主要考查了平面直角坐标系中各个象限的点的坐标的符号特点，四个象限的符号特点分别是：第一象限（+，+）；第二象限（﹣，+）；第三象限（﹣，﹣）；第四象限（+，﹣）．10．（2016秋•红安县期中）在平面直角坐标系中，已知A（2，﹣2），点P是y 轴上一点，则使AOP为等腰三角形的点P有（）A．1个 B．2个 C．3个 D．4个【分析】由于点P的位置不确定，所以应当讨论，当OA=OP时，可得到2点，当OA=AP时，可得到一点．【解答】解：分三种情况：当OA=OP时，可得到2点；当OA=AP时，可得到一点；当OP=AP时，可得到一点；共有4点，故选D．【点评】本题考查了坐标与图形的性质及等腰三角形的判定；分情况进行分析是正确解答本题的关键．二．填空题（共10小题）11．（2017•娄底模拟）若将点A（1，3）向左平移2个单位，再向下平移4个单位得到点B，则点B的坐标为（﹣1，﹣1）．【分析】让点A的横坐标减2，纵坐标减4即可得到平移后点的坐标．【解答】解：点B的横坐标为1﹣2=﹣1，纵坐标为3﹣4=﹣1，所以点B的坐标是（﹣1，﹣1），故答案为（﹣1，﹣1）．【点评】本题考查点的平移规律；用到的知识点为：点的平移，左右平移只改变点的横坐标，左减右加；上下平移只改变点的纵坐标，上加下减．12．（2017•罗平县一模）已知点A的坐标为（﹣2，3），则点A关于原点对称的点B的坐标为（2，﹣3）．【分析】利用平面内两点关于x轴对称时：横坐标不变，纵坐标互为相反数，进行求解．【解答】解：点A的坐标为（﹣2，3），则点A关于原点对称的点B的坐标为（2，﹣3），故答案为：（2，﹣3）．【点评】本题考查了关于原点对称的点的坐标，解决本题的关键是掌握好对称点的坐标规律：关于x轴对称的点，横坐标相同，纵坐标互为相反数；关于y轴对称的点，纵坐标相同，横坐标互为相反数；关于原点对称的点，横坐标与纵坐标都互为相反数．13．（2017•常州模拟）直角坐标系中点A坐标为（5，3），B坐标为（1，0），将点A绕点B逆时针旋转90°得到点C，则点C的坐标为（﹣2，4）．【分析】根据题意画出图形，易证△ADB≌△BEC，求出CE、OE的长即可求出C 的坐标．【解答】解：如图所示，点A绕点B逆时针旋转90°到点C，∵A坐标为（5，3），B坐标为（1，0），∴AD=3，BD=4，∴AB=5，根据旋转的性质，AB=BC，∵∠ABC=90°，∴∠EBC+∠ABD=90°，∵∠DAB+∠ABD=90°，∴∠EBC=∠DAB．在△EBC和△BAD中，∴△EBC≌△BAD，∴CE=BD=4，BE=AD=3，∵OB=1，∴OE=2，∴C（﹣2，4）．故答案为：（﹣2，4）．【点评】本题主要考查了旋转变换和三角形全等的判定与性质，证明△EBC≌△BAD是解决问题的关键．14．（2017春•滨海县月考）点P（m，m+3）在平面直角坐标系的y轴上，则点P的坐标是（0，3）．【分析】根据y轴上点的横坐标为0求出m=0，再求解即可．【解答】解：∵点P（m，m+3）在平面直角坐标系的y轴上，∴m=0，∴m+3=0+3=3，所以，点P的坐标为（0，3）．故答案为：（0，3）．【点评】本题考查了点的坐标，熟记y轴上点的横坐标为0是解题的关键．15．（2017春•西湖区校级月考）已知点P1（a，﹣3）和点P2（3，b）关于y轴对称，则a+b的值为﹣6．【分析】根据“关于y轴对称的点，纵坐标相同，横坐标互为相反数”求出a、b 的值，然后相加计算即可得解．【解答】解：∵点P1（a，﹣3）和点P2（3，b）关于y轴对称，∴a=﹣3，b=﹣3，∴a+b=﹣3+（﹣3）=﹣6．故答案为：﹣6．【点评】本题考查了关于x轴、y轴对称的点的坐标，解决本题的关键是掌握好对称点的坐标规律：（1）关于x轴对称的点，横坐标相同，纵坐标互为相反数；（2）关于y轴对称的点，纵坐标相同，横坐标互为相反数．16．（2016•梧州）点P（2，﹣3）先向左平移4个单位长度，再向上平移1个单位长度，得到点P′的坐标是（﹣2，﹣2）．【分析】根据点的平移特点直接写出结论【解答】解：点（2，﹣3），向左平移4个单位，横坐标：2﹣4=﹣2，向上平移1个单位，纵坐标：﹣3+1=﹣2，∴点P'（﹣2，﹣2），故答案为：（﹣2，﹣2）【点评】此题是坐标与图形变化﹣﹣﹣平移，熟记平移的特征是解本题的关键，特征：上加，下减，右加，左减，其实图形平移也有这个特点，抓住图形的几个特殊点，也能达到目的．17．（2016•鞍山二模）已知点P（2﹣a，2a﹣7）（其中a为整数）位于第三象限，则点P坐标为（﹣1，﹣1）．【分析】根据第三象限点的坐标性质得出a的取值范围，进而得出a的值，即可得出答案．【解答】解：∵点P（2﹣a，2a﹣7）（其中a为整数）位于第三象限，∴，解得：2＜a＜3.5，故a=3，则点P坐标为：（﹣1，﹣1）．故答案为：（﹣1，﹣1）．【点评】此题主要考查了点的坐标，正确得出a的取值范围是解题关键．18．（2016•乐亭县一模）如图，正方形ABCD的顶点B、C都在直角坐标系的x 轴上，若点A的坐标是（﹣1，4），则点C的坐标是（3，0）．【分析】根据点A的坐标求出正方形的边长与OB的长度，再求出OC的长，然后写出点C的坐标即可．【解答】解：∵点A的坐标是（﹣1，4），∴BC=AB=4，OB=1，∴OC=BC﹣OB=4﹣1=3，∴点C的坐标为（3，0）．故答案为：（3，0）．【点评】本题考查了坐标与图形性质，主要利用了正方形的性质，根据点A的坐标求出正方形的边长是解题的关键．19．（2016•洛阳模拟）若点P（m，﹣2）与点Q（3，n）关于原点对称，则（m+n）2015=﹣1．【分析】根据关于原点对称的两点的横、纵坐标都是互为相反数，可得m、n的值，根据负数奇数次幂是负数，可得答案．【解答】解：由点P（m，﹣2）与点Q（3，n）关于原点对称，得m=﹣3，n=2．（m+n）2015=（﹣3+2）2015=﹣1，故答案为：﹣1．【点评】本题考查了关于原点对称的点的坐标，关于原点对称的则两点的横、纵坐标都是互为相反数，注意负数奇数次幂是负数．20．（2016•南昌校级自主招生）如图，在直角坐标系中，已知点A（﹣3，0），B （0，4），对△OAB连续作旋转变换，依次得到三角形①、②、③、④、…则三角形⑩的直角顶点与坐标原点的距离为36．【分析】先利用勾股定理得到AB=5，利用图形和旋转的性质可得到△OAB每三次旋转一个循环，并且每一个循环向前移动了12个单位，由于10=3×3+1，则可判断三角形⑩和三角形①的状态一样，且三角形⑩与三角形⑨的直角顶点相同，所以三角形⑩的直角顶点与坐标原点的距离为3×12=36．【解答】解：∵A（﹣3，0），B（0，4），∴OA=3，OB=4，∴AB==5，∵对△OAB连续作如图所示的旋转变换，∴△OAB每三次旋转后回到原来的状态，并且每三次向前移动了3+4+5=12个单位，∵10=3×3+1，∴三角形⑩和三角形①的状态一样，则三角形⑩与三角形⑨的直角顶点相同，∴三角形⑩的直角顶点的横坐标为3×12=36，纵坐标为0，∴三角形⑩的直角顶点与坐标原点的距离为36．故答案为36．【点评】本题考查了坐标与图形变化﹣旋转：图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标．常见的是旋转特殊角度如：30°，45°，60°，90°，180°．解决本题的关键是确定△OAB连续作旋转变换后三角形的状态的变换规律．三．解答题（共10小题）21．（2017春•滨海县月考）求图中四边形ABCD的面积．【分析】由图可得：四边形ABCD的面积=矩形EFGH的面积﹣△AEB的面积﹣△AHD的面积﹣△BFC的面积﹣△CGD的面积，即可解答．【解答】解：如图，S四边形ABCD=S矩形EFGH﹣S△AEB﹣S△AHD﹣S△BFC﹣S△CDG==25．【点评】本题考查了坐标与图形性质，解决本题的关键是结合图形四边形ABCD 的面积=矩形EFGH的面积﹣△AEB的面积﹣△AHD的面积﹣△BFC的面积﹣△CGD的面积．22．（2017春•邢台县月考）如图是一个平面直角坐标系，按要求完成下列各小题．（1）写出图中的多边形ABCDEF顶点在坐标轴上的点的坐标；（2）说明点B与点C的纵坐标有什么特点？线段BC与x轴有怎样的位置关系？（3）写出点E关于y轴的对称点E′的坐标，并指出点E′与点C有怎样的位置关系．【分析】（1）根据平面直角坐标系写出各点的坐标即可；（2）根据点的坐标并结合图形解答即可；（3）根据图形写出点E′的坐标，再根据关于原点对称的点的坐标特征解答．【解答】解：（1）点A的坐标为（﹣2，0），点B的坐标为（0，﹣3），点D的坐标为（4，0），点F的坐标为（0，3）；（2）点B与点C的纵坐标相等，线段BC平行于x轴；（3）点E关于y轴的对称点的坐标为（﹣3，3），它与点C关于原点对称．【点评】本题考查了关于x轴、y轴对称的点的坐标，熟练掌握平面直角坐标系与点的关系是解题的关键．23．（2016春•沂水县期中）已知点P（a﹣2，2a+8），分别根据下列条件求出点P的坐标．（1）点P在x轴上；（2）点P在y轴上；（3）点Q的坐标为（1，5），直线PQ∥y轴；（4）点P到x轴、y轴的距离相等．【分析】（1）利用x轴上点的坐标性质纵坐标为0，进而得出a的值，即可得出答案；（2）利用y轴上点的坐标性质横坐标为0，进而得出a的值，即可得出答案；（3）利用平行于y轴直线的性质，横坐标相等，进而得出a的值，进而得出答案；（4）利用点P到x轴、y轴的距离相等，得出横纵坐标相等或相反数进而得出答案．【解答】解：（1）∵点P（a﹣2，2a+8），在x轴上，∴2a+8=0，解得：a=﹣4，故a﹣2=﹣4﹣2=﹣6，则P（﹣6，0）；（2））∵点P（a﹣2，2a+8），在y轴上，∴a﹣2=0，解得：a=2，故2a+8=2×2+8=12，则P（0，12）；（3）∵点Q的坐标为（1，5），直线PQ∥y轴；，∴a﹣2=1，解得：a=3，故2a+8=14，则P（1，14）；（4）∵点P到x轴、y轴的距离相等，∴a﹣2=2a+8或a﹣2+2a+8=0，解得：a1=﹣10，a2=﹣2，故当a=﹣10则：a﹣2=﹣12，2a+8=﹣12，则P（﹣12，﹣12）；故当a=﹣2则：a﹣2=﹣4，2a+8=4，则P（﹣4，4）．综上所述：P（﹣12，﹣12），（﹣4，4）．【点评】此题主要考查了点的坐标性质，用到的知识点为：点到坐标轴的距离相等，那么点的横纵坐标相等或互为相反数以及在坐标轴上的点的性质．24．（2016秋•东至县期中）已知点A（3，0）、B（0，2）、C（﹣2，0）、D（0，﹣1）在同一坐标系中描出A、B、C、D各点，并求出四边形ABCD的面积．【分析】已知A，B，C，D的坐标，再直角坐标系中画出四边形，再求四边形ABCD 的面积．【解答】解：如图所示：S ABCD=S△AOB+S△BOC+S△COD+S△AOD=（3×2+2×2+2×1+1×3）=．所以，四边形ABCD的面积为．【点评】本题考查了坐标与图形的性质，属于基础题，做题时重点要掌握把不规则四边形的面积看做成几个三角形面积的和．25．（2016秋•景德镇期中）已知点P（2x，3x﹣1）是平面直角坐标系上的点．（1）若点P在第一象限的角平分线上，求x的值；（2）若点P在第三象限，且到两坐标轴的距离和为11，求x的值．【分析】（1）根据角平分线上的点到角的两边的距离相等可得第一象限角平分线上的点的横坐标与纵坐标相等，然后列出方程求解即可；（2）根据第三象限的点的横坐标与纵坐标都是负数，然后列出方程求解即可．【解答】解：（1）由题意得，2x=3x﹣1，解得x=1；（2）由题意得，﹣2x+[﹣（3x﹣1）]=11，则﹣5x=10，解得x=﹣2．【点评】本题考查了坐标与图形性质，主要利用了角平分线上的点到角的两边的距离相等的性质，各象限内点的坐标特征．26．（2016春•宜阳县期中）已知点P（2m+4，m﹣1）．试分别根据下列条件，求出点P的坐标．（1）点P的纵坐标比横坐标大3；（2）点P在过A（2，﹣3）点，且与x轴平行的直线上．【分析】（1）根据横纵坐标的大小关系得出m﹣1﹣（2m+4）=3，即可得出m的值，进而得出P点坐标；（2）根据平行于x轴点的坐标性质得出m﹣1=﹣3，进而得出m的值，进而得出P点坐标．【解答】解：（1）∵点P（2m+4，m﹣1），点P的纵坐标比横坐标大3，∴m﹣1﹣（2m+4）=3，解得：m=﹣8，∴2m+4=﹣12，m﹣1=﹣9，∴点P的坐标为：（﹣12，﹣9）；（2）∵点P在过A（2，﹣3）点，且与x轴平行的直线上，∴m﹣1=﹣3，解得：m=﹣2，∴2m+4=0，∴P点坐标为：（0，﹣3）．【点评】此题主要考查了坐标与图形的性质，根据已知得出关于m的等式是解题关键．27．（2016秋•吉安期中）已知点M（﹣3a+2，a+6）．（1）若点M在x轴上，求点M的坐标；（2）点N（﹣4，﹣5），且直线MN∥y轴，求线段MN的长度．【分析】（1）根据点M在x轴上即可得出a+6=0，由此即可得出a值，将其代入点M的坐标中即可得出结论；（2）根据点M、N的坐标结合直线MN∥y轴，即可得出﹣3a+2=﹣4，由此即可得出a值，将其代入点M的坐标中求出点M的坐标，再利用两点间的距离公式求出线段MN的长度即可．【解答】解：（1）∵点M（﹣3a+2，a+6）在x轴上，∴a+6=0，即a=﹣6，∴点M的坐标为（20，0）．（2）∵点M（﹣3a+2，a+6），点N（﹣4，﹣5），直线MN∥y轴，∴﹣3a +2=﹣4，即a=2，∴点M 的坐标为（﹣4，8），∴线段MN 的长度为8﹣（﹣5）=13．【点评】本题考查了坐标与图形性质、解一元一次方程以及两点间的距离，解题的关键是：（1）根据点M 在x 轴上找出关于a 的一元一次方程；（2）根据直线MN ∥y 轴找出关于a 的一元一次方程．28．（2016春•滦县期中）在平面坐标系中△ABO 位置如图，已知OA=AB=5，OB=6，（1）求A 、B 两点的坐标．（2）点Q 为y 轴上任意一点，直接写出满足：S △ABO =S △AOQ 的Q 点坐标．【分析】（1）过A 作x 轴的垂线，垂足为C ，根据等腰三角形三线合一的性质得出OC=CB=OB=3，利用勾股定理求出AC==4，得出A 点的坐标，由OB=6，得出B 点的坐标；（2）根据三角形面积公式求出S △ABO =OB•AC=12，S △AOQ =OQ•OC=OQ ，由S △ABO =S △AOQ 得出OQ=12，求出OQ=8，进而得到Q 点坐标．【解答】解：（1）如图，过A 作x 轴的垂线，垂足为C ，∵OA=AB=5，OB=6，∴OC=CB=OB=3，∴AC===4，∴A 点的坐标为（3，4）．∵OB=6，∴B 点的坐标为（6，0）；（2）∵S=OB•AC=×6×4=12，△ABOS△AOQ=OQ•OC=OQ•3=OQ，∴OQ=12，∴OQ=8，∴Q点坐标为（0，8）或（0，﹣8）．【点评】本题考查了坐标与图形性质，等腰三角形的性质，勾股定理，三角形的面积，利用数形结合与分类讨论是解题的关键．29．（2016春•丹江口市期中）已知点P的坐标为（2m﹣1，m+7）．（1）若点P在x轴上，试求m的值；（2）若点P在二、四象限的角平分线上，求m的值；（3）若点Q坐标为（1，2），且PQ∥y轴，求点P的坐标；（4）若点Q坐标为（1，n+3），且PQ关于x轴对称，请求出n的值．【分析】（1）根据x轴上点的纵坐标为0，可列方程解得m；（2）根据二、四象限的角平分线上点的横纵坐标互为相反数可解得m；（3）平行于y轴直线上的点的纵坐标相等，可得m，代入解得点P的坐标；（4）关于x轴对称的两个点横坐标相等，纵坐标互为相反数，可解得m，解得n．【解答】解：（1）∵点P在x轴上，∵m+7=0，m=﹣7；（2）∵点P在二、四象限的角平分线上，∵2m﹣1+m+7=0，∴m=﹣2；（3）∵Q坐标为（1，2），且PQ||y轴，∴2m﹣1=1，∴m=1；∴p点坐标为：（1，8）；（4）∵Q坐标为（1，n+3），且PQ关于x轴对称，∴2m﹣1=1，∴m=1，∴m+7=8，∴n+3=﹣8，∴n=﹣11．【点评】本题主要考查了点的坐标，熟记坐标的特点是解答此题的关键．30．（2016春•宜春校级期中）已知A（o，a），B（b，o），C（3，c）且|a﹣2|+（b﹣3）2+=0（1）求a，b，c的值（2）若第二象限内有一点P（m，），请用含m的式子表示四边形ABOP的面积（3）在（2）的条件下，是否存在点P，使四边形ABOP的面积为△ABC面积的2倍？若存在，求出点P的坐标，若不存在，说明理由．【分析】（1）由绝对值、偶次方、算术平方根的性质即可得出结果；（2）S ABOP=S△AOB+S△AOP，即可得出结果；（3）由三角形的面积求出m的值，即可得出结果．【解答】解：（1）根据题意得：a﹣2=0，b﹣3=0 c﹣4=0得a=2，b=3，c=4（2）S ABOP=S△AOB+S△AOP=×2×3+×2×（﹣m）=3﹣m；（3）存在；理由如下：，∴3﹣m=12，∴m=﹣9，∴．【点评】本题考查了坐标与图形性质、三角形面积的计算；熟练掌握坐标与图形性质是解决问题的关键．。
北师大版八年级数学上册 第三章 位置与坐标 单元测试卷(有答案)
北师大版八年级数学上册第三章位置与坐标单元测试卷题号一二三总分得分一、选择题（本大题共10小题，共30分）1.根据下列表述，能确定位置的是()A. 天益广场南区B. 凤凰山北偏东42°C. 红旗影院5排9座D. 学校操场的西面2.若点M(m−3,m+1)在平面直角坐标系的x轴上，则点M的坐标是()A. (0,4)B. (−2,0)C. (−4,0)D. (4,0)3.在直角坐标系中，点P(3,−1)所在的象限是()．A. 第一象限B. 第二象限C. 第三象限D. 第四象限4.如图，是一局象棋残局，已知表示棋子“馬”和“車”的点的坐标分别为(4,3)，(−2,1)，则表示棋子“炮”的点的坐标为()A. (−3,3)B. (3,2)C. (1,3)D. (0,3)5.若点B(a,0)在以点A(−1,0)为圆心，2为半径的圆外，则a的取值范围为()A. −3<a<1B. a<−3C. a>1D. a<−3或a>16.已知点O(0,0)，点A(−3,2)，点B在y轴的正半轴上，若三角形AOB的面积为12，则点B的坐标为()A. (0,8)B. (0,4)C. (8,0)D. (0,−8)7.在平面直角坐标系中，点A(2,3)与点B关于y轴对称，则点B的坐标为()A. (−2,3)B. (−2,−3)C. (2,−3)D. (−3,−2)8.如图，正方形ABCD的边长为4，点A的坐标为(−1,1)，AB平行于x轴，则点C的坐标为()．A. (3,1)B. (−1,1)C. (3,5)D. (−1,5)9.如图，有A，B，C三点，如果A点用(1,1)来表示，B点用(2,3)表示，则C点的坐标的位置可以表示为()．A. (6,2)B. (5,3)C. (5,2)D. (2,5)10.如图，一个粒子在第一象限和x，y轴的正半轴上运动，在第一秒内，它从原点运动到(0,1)，接着它按图所示在x轴、y轴的平行方向来回运动，(即(0,0)→(0,1)→(1,1)→(1,0)→(2,0)→⋯)且每秒运动一个单位长度，那么2019秒时，这个粒子所处位置为()A. (5,44)B. (6,44)C. (44,5)D. (44,6)二、填空题（本大题共5小题，共15分）11.如图，如果所在的位置坐标为(−1,−2)，所在的位置坐标为(2,−2)，则所在位置坐标为．12.在平面直角坐标系中，点M(−1,m2+2)一定在第______象限．13.某镇三个厂址的地理位置如下：汽车配件厂在兽药厂的正南1000m，酒厂在汽车配件厂的正西800m处，以正东、正北方向为x轴、y轴正方向建立直角坐标系，若酒厂的坐标是(−800,−1000)，则选取的坐标原点是___________．14.已知点A(m−5,1)，点B(4,m+1)，且直线AB//y轴，则m=______．15.点P(2,3)到x轴的距离是_____________；点Q(5,−12)到原点的距离是_____________．三、解答题（本大题共6小题，共55分）16.在平面直角坐标系中，已知点P(2m+4,m−1)，试分别根据下列条件，求出点P的坐标．(1)点P在y轴上；(2)点P的纵坐标比横坐标大3．17.已知：如图(1)写出图中A，B，C，D各点的坐标(小正方形的边长为1个单位)；(2)已知点E(2,−2)，F(0,−2)，M(−1,2)，在直角坐标系中描出点E，F，M．18.如图(小方格的边长为1)，这是某市部分简图．(1)请你根据下列条件建立平面直角坐标系(在图中直接画出)：①火车站为原点；②宾馆的坐标为(2,2)．(2)市场、超市的坐标分别为______ 、______ ；(3)请将体育场、宾馆和火车站看作三点，用线段连起来，得△ABC，然后将此三角形向下平移4个单位长度，再画出平移后的△A′B′C′(在图中直接画出)；(4)根据坐标情况，求△ABC的面积．19.如图，甲、乙两船同时从小岛A出发，甲船沿北偏西20°的方向以40海里/时的速度航行；乙船沿南偏西80°的方向以30海里/时的速度航行．半小时后，两船分别到达B，C两处．(1)以1cm表示10海里，在图中画出B，C的位置．(2)求A处看B，C两处的张角∠BAC的度数．20.如图，A(−1,0)，C(1,4)，点B在x轴上，且AB=4．(1)求点B的坐标，并画出△ABC；(2)求△ABC的面积；(3)在y轴上是否存在点P，使以A、B、P三点为顶点的三角形的面积为12？若存在，请直接出点P的坐标；若不存在，请说明理由．答案和解析1.【答案】C【解析】【分析】本题考查了位置的确定，确定一个位置需要两个条件，二者缺一不可．根据坐标确定位置的定义对各选项分析判断后利用排除法求解．【解答】解：A、天益广场南区，不能确定位置，故本选项错误；B、凤凰山北偏东42°，没有明确具体位置，故本选项错误；C、红旗影院5排9座，能确定位置，故本选项正确；D、学校操场的西面，不能确定位置，故本选项错误；故选C．2.【答案】C【解析】【分析】本题考查了点的坐标，熟记x轴上的点的纵坐标等于0是解题的关键．根据x轴上的点的纵坐标等于0列式求出m的值，即可得解．【解答】解：∵点M(m−3,m+1)在平面直角坐标系的x轴上，∴m+1=0，解得m=−1，∴m−3=−1−3=−4，即点M的坐标为(−4,0)．故选C．3.【答案】D【解析】【分析】本题主要考查坐标确定位置，熟练掌握各象限内点的坐标的特点是解决本题的关键，第一、二、三、四象限内的点的坐标符号分别是(+,+)、(−,+)、(−,−)、(+,−)，根据点的横纵坐标的符号可得所在象限．【解答】解：∵点P(3,−1)的横坐标是正数，纵坐标是负数，∴点P(3,−1)在第四象限，故选D．4.【答案】C【解析】【分析】此题主要考查了坐标确定位置，正确得出原点的位置是解题关键．直接利用已知点的坐标确定原点的位置，进而得出棋子“将”的点的坐标．【解答】解：如图所示：由题意可得，“帅”的位置为原点位置，则棋子“炮”的点的坐标为：(1,3).故选C．5.【答案】D【解析】解：以A(−1,0)为圆心，以2为半径的圆交x轴两点的坐标为(−3,0)，(1,0)，∵点B(a,0)在以A(1,0)为圆心，以2为半径的圆外，∴a<−3或a>1．故选：D．熟记“设点到圆心的距离为d，则当d=R时，点在圆上；当d>R时，点在圆外；当d<R 时，点在圆内”即可解答本题考查了对点与圆的位置关系的判断的知识点，解答本题的关键是理解点B在以A(1,0)为圆心，以2为半径的圆内的含义，本题比较简单．【解析】【分析】本题考查了三角形的面积公式，坐标与图形性质，正确的识别图形是解题的关键．由于点B在y轴正半轴上，则B点的横坐标为0，只需求出B点的纵坐标即可．由△AOB的面积及OA的长，易求得B点纵坐标的绝对值，由此可得出B点的坐标．【解答】解：设点B的坐标为(0,b)．∵点O(0,0)，A(−3,2)，∴△AOB以OB为底，OB上的高为3，×3×b=12，由题意得：S△OAB=12∴b=8，即点B的坐标为(0,8)．故选A．7.【答案】A【解析】【分析】本题考查了关于x轴、y轴对称的点的坐标，解决本题的关键是掌握好对称点的坐标规律：(1)关于x轴对称的点，横坐标相同，纵坐标互为相反数；(2)关于y轴对称的点，纵坐标相同，横坐标互为相反数；(3)关于原点对称的点，横坐标与纵坐标都互为相反数．根据“关于y轴对称的点，纵坐标相同，横坐标互为相反数”解答．【解答】解：点A(2,3)关于y轴对称点的坐标为B(−2,3)．8.【答案】C【解析】【分析】本题考查了正方形的性质，坐标与图形的性质，根据图形明确正方形的边长与点的坐标的关系是解题的关键．根据正方形的边长加上点A的横坐标得到点C的横坐标，正方形的边长加上点A的纵坐标得到点C的纵坐标，从而得解．【解答】解：如图，∵正方形ABCD的边长为4，点A的坐标为(−1,1)，∴点C的横坐标为−1+4=3，点C的纵坐标为1+4=5，∴点C的坐标为(3,5)．故选C．9.【答案】C【解析】【分析】根据已知两点的坐标确定符合条件的平面直角坐标系，然后确定其它点的坐标．由已知条件正确确定坐标轴的位置是解决本题的关键．解决此类问题需要先确定原点的位置，再求未知点的位置，或者直接利用坐标系中的移动法则“右加左减，上加下减”来确定坐标．【解答】解：由A位置点的坐标为(1,1)，B点的坐标为(2,3)可以确定平面直角坐标系中x轴与y 轴的位置．根据所建坐标系从而可以确定C点的坐标(5,2)．故选C．【解析】【分析】本题考查的是点的坐标的确定及图形规律有关知识．应先判断出走到坐标轴上的点所用的时间以及相对应的坐标，此时点在坐标轴上，进而得到规律．【解答】解：观察可以发现，点到(2,0)用4=22秒，到(0,3)用9=32秒，到(4,0)用16=42秒，则可知当点离开x轴时的横坐标为时间的平方，当点离开y轴时的纵坐标为时间的平方，此时时间为偶数时点在x轴上，时间为奇数时，点在y轴上．∵2019=452−6=2025−6，∴第2025秒时，动点在(0,45)在此处向下一秒是(0,44)，再向右5秒得的第2019秒的位置，此时点坐标为(5,44)故选A．11.【答案】(−3,1)【解析】【分析】此题主要考查了点的坐标，根据已知得出原点的位置是解决问题的关键，根据士与相的位置，得出原点的位置即可得出炮的位置，即可得出答案．【解答】解：∵所在的位置坐标为(−1,−2)，所在的位置坐标为(2,−2)，得出原点的位置，如图：∴所在位置坐标为：(−3,1)．故答案为(−3,1)．12.【答案】二【解析】解：∵点M(−1,m2+2)的横坐标−1<0，纵坐标m2+2>0，∴符合点在第二象限的条件，故点M(−1,m2+2)一定在第二象限．故答案为：二．根据点在第二象限的坐标特点解答即可．本题主要考查平面直角坐标系中各象限内点的坐标的符号，关键是根据点在第二象限的坐标特点解答．13.【答案】兽药厂【解析】【分析】此题考查利用点的坐标解决实际问题的能力和阅读理解能力．解决此类问题的关键是利用已知条件确定原点的位置．根据题意，找到汽车配件厂和兽药厂的坐标，由此即可确定选取的坐标原点．【解答】解：∵酒厂在汽车配件厂的正西800m处，酒厂的坐标是(−800,−1000)，∴汽车配件厂的坐标是(0,−1000)，又∵汽车配件厂在兽药厂的正南1000m，∴兽药厂的坐标是(0,0)，∴选取的坐标原点是兽药厂．故答案为兽药厂．14.【答案】9【解析】解：∵点A(m−5,1)，点B(4,m+1)，且直线AB//y轴，∴m−5=4，解得m=9．故答案是：9．根据平行于y轴的直线上的点的横坐标相同进行解答．本题考查了坐标与图形性质．15.【答案】3；13【解析】【分析】本题考查了点的坐标，勾股定理，熟记点到x轴的距离等于纵坐标的绝对值，到y轴的距离等于横坐标的绝对值.根据点到x轴的距离等于纵坐标的绝对值，到y轴的距离等于横坐标的绝对值解答；利用勾股定理列式求出到原点的距离．【解答】解：点P(2,3)到x轴的距离是3，点Q(5,−12)到原点的距离是√52+122=13，故答案为3；13．16.【答案】解：(1)令2m+4=0，解得m=−2，所以P点的坐标为(0,−3)；(2)令m−1−(2m+4)=3，解得m=−8，所以P点的坐标为(−12,−9)．【解析】【试题解析】本题考查了点的坐标，用到的知识点为：y轴上的点的横坐标为0；平行于x轴的直线上的点的纵坐标相等．(1)让横坐标为0求得m的值，代入点P的坐标即可求解；(2)让纵坐标−横坐标=3得m的值，代入点P的坐标即可求解；17.【答案】解：(1)由图可得，A(2,4)，B(−3,3)，C(2,0)，D(−4,−1)；(2)由题意知，在直角坐标系中描出点E，F，M如下图：．【解析】本题考查了坐标与图形性质，平面直角坐标系的建立，根据已知点的坐标找出坐标原点的位置并建立平面直角坐标系，然后准确找出对应点的位置是解题的关键．(1)可直接从图中得到坐标；(2)直接在图中描出点E、F、M．18.【答案】解：(1)如图所示：(2)(4,3)；(2,−3)(3)△A′B′C′如上图所示；(4)△ABC面积=3×6−12×2×2−12×4×3−12×1×6=18−2−6−3=7．【解析】【分析】本题考查了坐标确定位置：平面坐标系中的点与有序实数对一一对应；记住平面内特殊位置的点的坐标特征．会利用面积的和差计算不规则几何图形的面积．(1)利用火车站和宾馆的坐标画出直角坐标系；(2)利用坐标系中各象限点的坐标特征写出市场、超市的坐标；(3)把体育场、宾馆和火车站的横坐标不变，纵坐标减去4描出各点即可得到△A′B′C′；(4)用矩形的面积分别减去三个三角形的面积求解．【解答】解：(1)见答案；(2)市场的坐标为(4,3)，超市的坐标为(2,−3)；故答案为(4,3)；(2,−3)；(3)见答案；(4)见答案．19.【答案】解：(1)由题意可知：(2)∠BAC=90°−80°+90°−20°=80°．【解析】本题主要考查了方向角和作图与测量的知识点，解题关键点是熟练掌握方向角的作法．(1)利用方向角的作法进行作图，即可解答；(2)利用角的运算法则进行计算，即可解答．20.【答案】解：∵正方形ABCD的顶点A(0,0)，B(4,0)，∴正方形可能在第一象限或第四象限，当正方形在第一象限时，点C(4,4)，点D(0,4)，当正方形在第四象限时，点C(4,−4)，点D(0,−4)，∴顶点C、D的坐标分别是(4,4)，(0,4)或(4,−4)，(0,−4)．【解析】本题考查了正方形的性质以及坐标与图形性质：利用点的坐标确定线段的长度和直线与坐标的位置关系．根据正方形的性质得到点C的横坐标与B点的横坐标相同，纵坐标与点D的纵坐标相同，点D的横坐标与A点的横坐标相同，纵坐标与点C的纵坐标相同；根据题意可知，需要分两种情况考虑．21.【答案】解：(1)点B在点A的右边时，−1+4=3，点B在点A的左边时，−1−4=−5，所以，B的坐标为(3,0)或(−5,0)，△ABC如图所示：×4×4=8；(2)△ABC的面积=12×4ℎ=12，(3)设点P到x轴的距离为h，则12解得ℎ=6，点P在y轴正半轴时，P(0,6)，点P在y轴负半轴时，P(0,−6)，综上所述，点P的坐标为(0,6)或(0,−6)．【解析】(1)分点B在点A的左边和右边两种情况解答；(2)利用三角形的面积公式列式计算即可得解；(3)利用三角形的面积公式列式求出点P到x轴的距离，然后分两种情况写出点P的坐标即可．本题考查了坐标与图形性质，主要利用了三角形的面积，难点在于要分情况讨论．。
北师大版八年级数学上册第三章单元测试卷含答案
第三章单元测试卷(时间：100分钟满分：120分)一、选择题(本大题共10小题，每小题3分，共30分)1. 气象台为预测台风，首先要确定台风中心的位置，下列说法能确定台风中心位置的是(C)A．距台湾200海里B．位于台湾与海口之间C．位于东经120.8度，北纬32.8度D．位于西太平洋2. 在如图所示的直角坐标系中，点M，N的坐标分别为(A)A．M(－1，2)，N(2，1) B．M(2，－1)，N(2，1)C．M(－1，2)，N(1，2) D．M(2，－1)，N(1，2),第2题图),第5题图),第6题图),第7题图)3. 点P(m＋3，m－1)在x轴上，则点P的坐标为(C)A．(0，－2) B．(2，0) C．(4，0) D．(0，－4)4. 已知A(－1，－4)，B(－1，3)，则(C)A．A，B关于x轴对称B．A，B关于y轴对称C．直线AB平行于y轴D．直线AB垂直于y轴5. 在一次科学探测活动中，探测人员发现一目标在如图所示的阴影区域内，则目标的坐标可能是(B)A．(－3，300) B．(7，－500) C．(9，600) D．(－2，－800)6. 如图，小明从点O出发，先向西走40米，再向南走30米到达点M，如果点M的位置用(－40，－30)表示，那么(10，20)表示的位置是(B)A．点A B．点B C．点C D．点D7. 线段MN在直角坐标系中的位置如图所示，线段M1N1与MN关于y轴对称，则点M的对应点M1的坐标为(D)A．(4，2) B．(－4，2) C．(－4，－2) D．(4，－2)8. 若点P(a，b)在第三象限，则M(－b，－a)应在(A)A．第一象限B．第二象限C．第三象限D．第四象限9. 在直角坐标系中，将点A(2，－3)的横坐标乘以－1，纵坐标不变，得到A′点，连接OA，OA′，AA′，则△OAA′的面积是(B)A．12 B．6 C．4 D．310. 到x轴的距离为2，且到y轴的距离为3，这样的点共有(A)A．4个B．3个C．2个D．1个二、填空题(本大题共6小题，每小题4分，共24分)11. 点A(－3，－4)在第三象限，到y轴的距离为3.12. 若点P(x，y)满足xy<0，则点P在第二或四象限内．13. 如图，“”所在的位置坐标为(－1，－2)，“”所在的位置坐标为(4，－2)，则“”所在的位置坐标为(2，1)．14. 已知点A(m－1，3)与点(2，n＋1)关于x轴对称，则m＝3，n＝－4.15. 在平面直角坐标系中，将点(－b，－a)称为点(a，b)的“关联点”(例如点(－2，－1)是点(1，2)的“关联点”)．如果一个点和它的“关联点”在同一象限内，那么这点在第二、四象限．16. 如图，一个机器人从O点出发，向正东方向走3 m到达A1点，再向正北方向走6 m到达A2点，再向正西方向走9 m到达A3点，再向正南方向走12 m到达A4点，再向正东方向走15 m到达A5点，按如此规律走下去，相对于点O，机器人走到A6时是(9，12)位置．三、解答题(一)(本大题共3小题，每小题6分，共18分)17. 如图，确定点A，B，C，D，E，F，G的坐标．请说明点B和点F有什么关系？解：A(－4，4)，B(－3，0)，C(－2，－2)，D(1，－4)，E(1，－1)，F(3，0)，G(2，3)．因为点B和点F横坐标互为相反数且纵坐标相等，所以点B和点F关于y轴对称18. 如图是某校的平面示意图，若校门的位置用(3，0)来表示，则图书室、教学楼、会议室的位置如何表示？解：图书室(1，1)，教学楼(5，2)，会议室(5，4)19. 在如图所示的正方形网格中，每个小正方形的边长为1，格点三角形(顶点是网格线的交点的三角形)ABC的顶点A，C的坐标分别为(－4，5)，(－1，3)．请在如图所示的网格平面图内作出平面直角坐标系，(1)请作出△ABC关于y轴对称的△A′B′C′；(2)写出点B′的坐标．解：(1)图略(2)B′(2，1)四、解答题(二)(本大题共3小题，每小题7分，共21分)20. 在平面直角坐标系中，有点A(－2，a＋3)，B(b，b－3)．(1)当点A与点B关于y轴对称时，求a的值；(2)当点B到x轴的距离是它到y轴的距离2倍时，求点B所在的象限位置．解：(1)由题意得b＝2，a＋3＝b－3，得a＝－4(2)由题意得|b－3|＝2|b|，解得b＝－3或b＝1，当b＝－3时，点B(－3，－6)在第三象限；当b＝1时，点B(1，－2)在第四象限21. 如图是某台阶的一部分，如果点A的坐标为(0，0)，B点的坐标为(1，1)．(1)请建立适当的平面直角坐标系，并写出点C，D，E，F的坐标；(2)如果该台阶有10级，你能得到该台阶的高度吗？解：(1)以A点为原点，水平方向为x轴，建立平面直角坐标系，所以C，D，E，F各点的坐标分别为C(2，2)，D(3，3)，E(4，4)，F(5，5)(2)每级台阶高为1，所以10级台阶的高度是1022. 如图，已知四边形ABCD.(1)写出点A，B，C，D的坐标；(2)试求四边形ABCD的面积．(网格中每个小正方形的边长均为1)解：(1)A(－2，1)，B(－3，－2)，C(3，－2)，D(1，2)(2)S四边形ABCD＝3×3＋2×12×1×3＋12×2×4＝16五、解答题(三)(本大题共3小题，每小题9分，共27分)23. 【阅读材料，获取新知】在航空、航海等领域我们经常用距离和角度来确定点的位置．规定如下：在平面内取一个定点O，叫极点，引一条射线Ox，叫做极轴，再选定一个单位长度和角度的正方向(通常取逆时针方向)．对于平面内任何一点M，用ρ表示线段OM(有时也用r表示)，θ表示从Ox到OM的角度，ρ叫做点M的极径，θ叫做点M的极角，有序数对(ρ，θ)就叫点M的极坐标，这样建立的坐标系叫做极坐标系．通常情况下，M的极径坐标单位为1(长度单位)，极角坐标单位为rad(或°)．例如：如图①，点M到点O的距离为5个单位长度，OM与Ox的夹角70°(Ox的逆时针方向)，则点M的极坐标为(5，70°)；同理，点N到点O的距离为3个单位长度，ON与Ox的夹角50°(Ox的顺时针方向)，则点N的极坐标为(3，－50°)．【利用新知，解答问题】请根据以上信息，回答下列问题：如图②，已知过点O的所有射线等分圆周且相邻两射线的夹角为15°.(1)点A的极坐标是(4，75°)；点D的极坐标是(3，－30°)；(2)请在图②中标出点B(5，45°)，点E(2，－90°)；(3)怎样从点B运动到点C？小明设计的一条路线为：点B→(4，45°)→(3，45°)→(3，30°)→点C.请你设计与小明不同的一条路线，也可以从点B运动到点C.解：(1)A(4，75°)，D(3，－30°)(2)如图所示：(3)点B→(5，30°)→(5，15°)→(4，15°)→点C24. 先阅读下列一段文字，再解答问题．已知在平面内有两点P1(x1，y1)，P2(x2，y2)，其两点间的距离公式为P1P2＝（x2－x1）2＋（y2－y1）2，同时，当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时，两点间距离公式可简化为|x2－x1|或|y2－y1|.(1)已知点A(2，4)，B(－3，－8)，试求A，B两点间的距离；(2)已知点A，B在平行于y轴的直线上，点A的纵坐标为5，点B的纵坐标为－1，试求A，B两点间的距离；(3)已知点A(0，6)B(－3，2)，C(3，2)，判断线段AB，BC，AC中哪两条是相等的？并说明理由．解：(1)依据两点间的距离公式，可得AB＝（－3－2）2＋（－8－4）2＝13(2)当点A，B 在平行于y轴的直线上时，AB＝|－1－5|＝6(3)AB与AC相等．理由：因为AB＝（－3－0）2＋（2－6）2＝5，AC＝（3－0）2＋（2－6）2＝5，BC＝|3－(－3)|＝6，所以AB＝AC25. 已知A(0，1)，B(2，0)，C(4，3)．(1)在坐标系中描出各点，画出△ABC；(2)求△ABC的面积；(3)设点P在坐标轴上，且△ABP与△ABC的面积相等，求点P的坐标．解：(1)如图所示：(2)S △ABC ＝3×4－12×2×3－12×2×4－12×2×1＝4(3)当点P 在x 轴上时，△ABP 的面积＝12AO ·BP ＝4，即12×1×BP ＝4，解得BP ＝8，所点P的坐标为(10，0)或(－6，0)；当点P 在y 轴上时，△ABP 的面积＝12BO ·AP ＝4，即12×2×AP ＝4，解得AP ＝4，所以点P 的坐标为(0，5)或(0，－3)，所以点P 的坐标为(0，5)或(0，－3)或(10，0)或(－6，0)。
北师大版八年级数学上册第三章《位置与坐标》 测试题(含答案)
北师大版八年级数学上册第三章《位置与坐标》测试题（含答案）一、选择题1、共享单车提供了便捷、环保的出行方式．小白同学在北京植物园打开某共享单车APP，如图，“”为小白同学的位置，“★”为检索到的共享单车停放点．为了到达距离最近的共享单车停放点，下列四个区域中，小白同学应该前往的是(A)A．F6 B．E6 C．D5 D．F72、已知点A在第二象限，到x轴的距离是5，到y轴的距离是6，点A的坐标为(B)A．(－5，6) B．(－6，5) C．(5，－6) D．(6，－5)3、若点N在第一、三象限的角平分线上，且点N到y轴的距离为2，则点N的坐标是(C)A．(2，2) B．(－2，－2) C．(2，2)或(－2，－2) D．(－2，2)或(2，－2)．4、如图，建立适当的平面直角坐标系后，正方形网格上的点M，N的坐标分别为(0，2)，(1，1)，则点P的坐标为(B)A．(－1，2) B．(2，－1) C．(－2，1) D．(1，－2)5、在平面直角坐标系中，点A的坐标为(－3，4)，那么下列说法正确的是(C)A．点A与点B(3，－4)关于x轴对称 B．点A与点C(－4，－3)关于x轴对称C．点A与点D(3，4)关于y轴对称 D．点A与点E(4，3)关于y轴对称6、如图，在平面直角坐标系中，△ABC关于直线m(直线m上各点的横坐标都为1)对称，点C的坐标为(4，1)，则点B的坐标为(A)A．(－2，1) B．(－3，1) C．(－2，－1) D．(－2，－1)7、过点A(－3，2)和点B(－3，5)作直线，则直线AB(A)A．平行于y轴 B．平行于x轴 C．与y轴相交 D．与y轴垂直8、在平面直角坐标系中，坐标是整数的点称作格点，第一象限的格点P(x，y)满足2x ＋3y＝7，则满足条件的点有(A)A．1个 B．2个 C．3个 D．4个9、如图所示，一方队正沿箭头所指的方向前进，A的位置为三列四行，表示为(3，4)，那么C的位置应表示为(D)A．(4，5) B．(5，4) C．(4，2) D．(4，3)10、如图，在平面直角坐标系中，点A的坐标为(3，－2)，直线MN∥x轴且交y轴于点C(0，1)，则点A关于直线MN的对称点的坐标为(C)A．(－2，3) B．(－3，－2) C．(3，4) D．(3，2)二、填空题11、如图，点A 的坐标是(3，3)，横坐标和纵坐标都是负数的是点C ，坐标是(－2，2)的是点D ．12、若点P(a ＋13，2a ＋23)在第二、四象限的角平分线上，则a ＝－13．13、如图是某校的平面示意图的一部分，若用(0，0)表示图书馆的位置，(0，－3)表示校门的位置，则教学楼的位置可表示为(5，0)．14、若点M(x ，y)在第二象限，且|x|－2＝0，y 2－4＝0，则点M 15、在平面直角坐标系中，△ABC 的位置如图所示，已知点A 的坐标是(－4，3)． (1)点B 的坐标为(3，0)，点C 的坐标为(－2，5)； (2)△ABC 的面积是10；(3)作点C 关于y 轴的对称点C ′，那么A ，C ′两点之间的距离是16、在平面直角坐标系中，若干个边长为1个单位长度的等边三角形，按如图中的规律摆放．点P 从原点O 出发，以每秒1个单位长度的速度沿着等边三角形的边“OA 1→A 1A 2→A 2A 3→A 3A 4→A 4A 5…”的路线运动，设第n 秒运动到点P n (n 为正整数)，则点P 2 019的坐标是(2 0192，2)．三、解答题17、如图，在一次海战演习中，红军和蓝军双方军舰在战前各自待命，从总指挥部看： (1)南偏西60°方向上有哪些目标？(2)红方战舰2和战舰3在总指挥部的什么方向上？(3)若蓝A 距总指挥部的实际距离200 km ，则红1距总指挥部的实际距离是多少？解：(1)蓝C ，蓝B. (2)北偏西45°. (3)600 km.18、如图，在平面直角坐标系内，已知点A(8，0)，点B 的横坐标是2，△AOB 的面积为12.(1)求点B 的坐标；(2)如果P 是平面直角坐标系内的点，那么点P 的纵坐标为多少时，S △AOP ＝2S △AOB? 解：(1)设点B 的纵坐标为y. 因为A(8，0)， 所以OA ＝8.则S △AOB ＝12OA ·|y|＝12，解得y ＝±3.所以点B 的坐标为(2，3)或(2，－3)． (2)设点P 的纵坐标为h. 因为S △AOP ＝2S △AOB ＝2×12＝24， 所以12OA ·|h|＝24，即12×8|h|＝24，解得h ＝±6.所以点P 的纵坐标为6或－6. 19、在平面直角坐标系中：(1)已知点P(a －1，3a ＋6)在y 轴上，求点P 的坐标；(2)已知两点A(－3，m)，B(n ，4)，若AB ∥x 轴，点B 在第一象限，求m 的值，并确定n 的取值范围；(3)在(1)(2)的条件下，如果线段AB 的长度是5，求以P ，A ，B 为顶点的三角形的面积S.解：(1)因为点P(a －1，3a ＋6)在y 轴上， 所以a －1＝0，解得a ＝1. 所以3a ＋6＝3×1＋6＝9， 故P(0，9)． (2)因为AB ∥x 轴， 所以m ＝4.因为点B 在第一象限， 所以n ＞0. 所以m ＝4，n ＞0.(3)因为AB ＝5，A ，B 的纵坐标都为4， 所以点P 到AB 的距离为9－4＝5. 所以S △PAB ＝12×5×5＝12.5.20、(1)在数轴上，点A 表示数3，点B 表示数－2，我们称A 的坐标为3，B 的坐标为－2.那么A ，B 的距离AB ＝5；一般地，在数轴上，点A 的坐标为x 1，点B 的坐标为x 2，则A ，B 的距离AB ＝|x 1－x 2|；(2)如图1，在平面直角坐标系中点P 1(x 1，y 1)，点P 2(x 2，y 2)，求P 1，P 2的距离P 1P 2； (3)如图2，在△ABC 中，AO 是BC 边上的中线，利用(2)的结论说明：AB 2＋AC 2＝2(AO 2＋OC 2)．解：(2)因为在平面直角坐标系中，点P1(x1，y1)，点P2(x2，y2)，所以P1P2＝（x1－x2）2＋（y1－y2）2.(3)设A(a，d)，C(c，0)，因为O是BC的中点，所以B(－c，0)．所以AB2＋AC2＝(a＋c)2＋d2＋(a－c)2＋d2＝2(a2＋c2＋d2)，AO2＋OC2＝a2＋d2＋c2.所以AB2＋AC2＝2(AO2＋OC2)．21、在某河流的北岸有A，B两个村子，A村距河北岸的距离为1千米，B村距河北岸的距离为4千米，且两村相距5千米，B在A的右边，现以河北岸为x轴，A村在y轴正半轴上(单位：千米)．(1)请建立平面直角坐标系，并描出A，B两村的位置，写出其坐标；(2)近几年，由于乱砍滥伐，生态环境受到破坏，A，B两村面临缺水的危险．两村商议，共同在河北岸修一个水泵站，分别向两村各铺一条水管，要使所用水管最短，水泵站应修在什么位置？在图中标出水泵站的位置，并求出所用水管的长度．解：(1)如图，点A(0，1)，点B(4，4)．(2)找A关于x轴的对称点A′，连接A′B交x轴于点P，则P点即为水泵站的位置，PA ＋PB ＝PA ′＋PB ＝A ′B 且最短(如图)． 因为A(0，1)，B(4，4)，所以A ′(0，－1)． 所以A ′B ＝42＋（4＋1）2＝41. 故所用水管的最短长度为41千米．22、如图，在平面直角坐标系中，AB ∥CD ，AB ＝CD ，CD 在x 轴上，B 点在y 轴上，若OB ＝OC ，点A 的坐标为(－3－1，3)．求：(1)点B ，C ，D 的坐标； (2)S △ACD .解：(1)因为点A 的坐标为(－3－1，3)．所以点A 到y 轴的距离是|－3－1|＝3＋1，到x 轴的距离是3， 所以AB ＝CD ＝3＋1，OB ＝OC ＝ 3. 所以OD ＝1.所以点B 的坐标为(0，3)，点C 的坐标为(3，0)，点D 的坐标为(－1，0)． (2)S △ACD ＝12CD ·OB ＝12×(3＋1)×3＝3＋32.23、如图，在长方形OABC 中，O 为平面直角坐标系的原点，A ，C 两点的坐标分别为(3，0)，(0，5)，点B 在第一象限内．(1)写出点B 的坐标；(2)若过点C 的直线CD 交AB 于点D ，且把AB 分为4∶1两部分，写出点D 的坐标； (3)在(2)的条件下，计算四边形OADC 的面积．解：(1)因为A ，C 两点的坐标分别为(3，0)，(0，5)． 所以点B 的横坐标为3，纵坐标为5. 所以点B 的坐标为(3，5)．(2)若AD ∶BD ＝4∶1，则AD ＝5×41＋4＝4，此时点D 的坐标为(3，4)．若AD ∶BD ＝1∶4，则AD ＝5×11＋4＝1，此时点D 的坐标为(3，1)．综上所述，点D 的坐标为(3，4)或(3，1)． (3)当AD ＝4时，S 四边形OADC ＝12×(4＋5)×3＝272，当AD ＝1时，S 四边形OADC ＝12×(1＋5)×3＝9.综上所述，四边形OADC 的面积为272或9.24、如图，在平面直角坐标系中，已知A(0，a)，B(b ，0)，C(b ，c)三点，其中a ，b ，c 满足关系式|a －2|＋(b －3)2＝0，(c －5)2≤0.(1)求a ，b ，c 的值；(2)如果在第二象限内有一点P(m ，53)，请用含m 的式子表示四边形APOB 的面积；(3)在(2)的条件下，是否存在点P ，使四边形AOBC 的面积是四边形APOB 的面积的2倍？若存在，求出点P 的坐标，若不存在，请说明理由．解：(1)由已知|a －2|＋(b －3)2＝0，(c －5)2≤0可得： a －2＝0，b －3＝0，c －5＝0， 解得a ＝2，b ＝3，c ＝5. (2)因为a ＝2，b ＝3，c ＝5， 所以A(0，2)，B(3，0)，C(3，5)． 所以OA ＝2，OB ＝3.所以S 四边形ABOP ＝S △ABO ＋S △APO ＝12×2×3＋12×(－m)×2＝3－m.(3)存在．因为S 四边形AOBC ＝S △AOB ＋S △ABC ＝3＋12×3×5＝10.5，所以2(3－m)＝10.5，解得m ＝－94.所以存在点P(－94，53)，使四边形AOBC 的面积是四边形APOB 的面积的2倍．25、如图，在平面直角坐标系xOy 中，A ，B 两点分别在x 轴、y 轴的正半轴上，且OB ＝OA ＝3.(1)求点A ，B 的坐标；(2)若点C(－2，2)，求△BOC 的面积；(3)点P 是第一，三象限角平分线上一点，若S △ABP ＝332，求点P 的坐标．解：(1)因为OB ＝OA ＝3，所以A ，B 两点分别在x 轴，y 轴的正半轴上．所以A(3，0)，B(0，3)．(2)S △BOC ＝12OB ·|x C |＝12×3×2＝3. (3)因为点P 在第一，三象限的角平分线上，所以设P(a ，a)．因为S △AOB ＝12OA ·OB ＝92＜332. 所以点P 在第一象限AB 的上方或在第三象限．当P 1在第一象限AB 的上方时，S △ABP 1＝S △P 1AO ＋S △P 1BO －S △AOB ＝12OA ·yP 1＋12OB ·xP 1－12OA ·OB ， 所以12×3a ＋12×3a －12×3×3＝332，解得a ＝7. 所以P 1(7，7)．当P 2在第三象限时，S △ABP 2＝S △P 2AO ＋S △P 2BO ＋S △AOB ＝12OA ·yP 2＋12OB ·xP 2＋12OA ·OB. 所以12×3×(－a)＋12×3×(－a)＋12×3×3＝332，解得a ＝－4. 所以P 2(－4，－4)．综上所述，点P 的坐标为(7，7)或(－4，－4)．。
八年级上册数学单元测试卷-第三章 位置与坐标-北师大版(含答案)
八年级上册数学单元测试卷-第三章位置与坐标-北师大版(含答案)一、单选题(共15题，共计45分)1、点P（-3，2）到x轴的距离为（）A.-3B.-2C.3D.22、一条东西向道路与一条南北向道路的交汇处有一座雕像，甲车位于雕像东方5 km处，乙车位于雕像北方7 km处.若甲、乙两车以相同的速度向雕像方向同时驶去，当甲车到雕像西方1 km处时，乙车在（）A.雕像北方1 km处B.雕像北方3 km处C.雕像南方1 km处 D.雕像南方3 km处3、在平面直角坐标系中，若点P（x-2，1-x）在第四象限，则x的取值范围是（）A. 1< x<2B.x<1C.x>2D.x<24、如图，在平面直角坐标系中，点A在第一象限，⊙A与x轴交于B（2，0）、C（8，0）两点，与y轴相切于点D，则点A的坐标是（）A.（5，4）B.（4，5）C.（5，3）D.（3，5）5、点P在第三象限，且它到x轴、y轴的距离分别为3和4，则点P的坐标为（）A.(4，－3 )B.(3，4)C.(－3，4)D.(－4，－3)6、已知点P位于x轴上方，到x轴的距离为2，到y轴的距离为5，则点P坐标为( )A.(2，5)B.(5，2)C.(2，5)或(-2，5)D.(5，2)或(-5，2)7、已知M（1，﹣2），N（﹣3，﹣2），则直线MN与x轴，y轴的位置关系分别为（）A.相交，相交B.平行，平行C.垂直相交，平行D.平行，垂直相交8、在平面直角坐标系中，点P（2，﹣3）所在的象限是（）A.第一象限B.第二象限C.第三象限D.第四象限9、象棋在中国有着三千多年的历史，由于用具简单，趣味性强，成为流行极为广泛的益智游戏.如图，是一局象棋残局，已知表示棋子“車”的点的坐标为，棋子“炮”的点的坐标为，则表示棋子“馬”的点的坐标为（）A. B. C. D.10、如图，在平面直角坐标系中，矩形的顶点在坐标原点，边在轴上，在轴上，如果矩形与矩形关于点位似，且矩形的面积等于矩形面积的，那么点的坐标是( )A. B. C. 或 D. 或11、在平面直角坐标系中，点P（－2，－3）所在的象限是（）A.第一象限B.第二象限C.第三象限D.第四象限12、点P在第二象限，P到x轴的距离是4，到y轴的距离是3，那么点P的坐标为（）A.(-4，3)B.(-3，-4)C.(-3，4)D.(3，-4)13、一个长方形在直角坐标系中三个顶点的坐标为（-1，-1），（-1，2），（3，-1），则第四个顶点的坐标为（）A.（2，2）B.（3，2）C.（3，3）D.（2，3）14、如图所示是一个围棋棋盘局部，把这个围棋棋盘放置在一个平面直角坐标系中，白棋的坐标是，白棋的坐标是，则黑棋的坐标是A. B. C. D.15、若点A(-2，n)在x轴上，则点B(n-1，n+1)在（）.A.第一象限B.第二象限C.第三象限D.第四象限二、填空题(共10题，共计30分)16、如图，在平面直角坐标系中，A（4，4），点D在y轴上，若△ABC的面积等于△BCD 的面积，则点D的坐标可能是________（只写一个即可）．17、在平面直角坐标系中，AB＝2，且AB∥x轴，若点A的坐标为（1，2），则点B的坐标为________．18、如图，把正方形铁片OABC置于平面直角坐标系中，顶点A的坐标为（3，0），点P （1，2）在正方形铁片上，将正方形铁片绕其右下角的顶点按顺时针方向依次旋转90°，第一次旋转至图①位置，第二次旋转至图②位置…，则正方形铁片连续旋转2017次后，点P的坐标为________．19、若点M(a＋3，a－2)在y轴上，则点M的坐标是________．20、在平面直角坐标系中，点A的坐标为（﹣1，3），线段AB∥x轴，且AB=4，则点B的坐标为________ .21、若点A关于y轴对称的点是(2，3)，则点A的坐标为________.22、如图，在平面直角坐标系中，点B在x轴上，是等边三角形，，则点A的坐标为________.23、若x2＋bx＋c＝(x＋5)(x－3)，其中b，c为常数，则点P(b，c)关于y轴对称的点的坐标是________．24、点P（1，﹣2）关于x轴对称的点的坐标为P′________．25、已知点P（3，-1）关于原点的对称点Q的坐标是（a+b，b-1），则a b的值是________三、解答题(共5题，共计25分)26、如图,直线AB交x轴于点B,交y轴于点A（0,4）,直线DM⊥x轴正半轴于点M,交线段AB于点C,DM=6,连接DA,∠DAC=90°,AD:AB=1:2．（1）求点D的坐标；（2）求经过O、D、B三点的抛物线的函数关系式．27、在平面直角坐标系中，点A（a，3﹣2a）在第一象限．（1）若点A到x轴的距离与到y轴的距离相等，求a的值；（2）若点A到x轴的距离小于到y轴的距离，求a的取值范围．28、如图所示，将图中的点（﹣5，2），（﹣3，4），（﹣1，2），（﹣4，2），（﹣2，2），（﹣2，3），（﹣4，3）做如下变化：（1）横坐标不变，纵坐标分别减4，再将所得的点用线段依次连接起来，所得的图形与原来的图形相比有什么变化？（2）纵坐标不变，横坐标分别加6，再将所得的点用线段依次连接起来，所得的图形与原来的图形相比有什么变化？（3）求出以点（﹣5，2），（﹣3，4），（﹣1，2）为顶点的三角形的面积？29、如图所示，方格纸中的每个小方格都是边长为个单位长度的正方形，在建立平面直角坐标系后，的顶点均在格点上．①以原点为对称中心，画出与关于原点对称的．②将绕点沿逆时针方向旋转得到，画出，并求出的长．30、如图所示，在平面直角坐标系中，求三角形ABO的面积．参考答案一、单选题(共15题，共计45分)2、A3、C4、A5、D6、D7、D8、D9、D10、D11、C12、C13、B14、A15、B二、填空题(共10题，共计30分)16、17、18、20、21、22、23、24、25、三、解答题(共5题，共计25分)29、。
第3章 位置与坐标 北师大版八年级上册数学单元测试题(含答案)
北师大版八年级上册数学第三章测试题（附答案）一、单选题（共12题；共24分）1.如图，用坐标（1，﹣2）表示学校的位置，用（3，2）表示书店的位置，则表示邮局位置的点的坐标是（ ）A. （﹣1，﹣3）B. （3，1）C. （1，3）D. （﹣3，﹣1）2.如图是在方格纸上画出的小旗图案，若用(2，1)表示A点，(2，5)表示B点，那么C点的位置可表示为（）A. (3，5)B. (4，3)C. (3，4)D. (5，3)3.平面直角坐标系xOy中，如果有点P（﹣2，1）与点Q（2，﹣1），那么：①点P与点Q关于x轴对称；②点P与点Q关于y轴对称；③点P与点Q关于原点对称；④点P与点Q都在y=-的图象上，前面的四种描述正确的是( )A. ①②B. ②③C. ①④D. ③④4.已知点A的坐标为（0，0），点B的坐标为（4，0），点C在y轴上，△ABC的面积是10，则点C的坐标可能是（）A. （0，10）B. （5，0）C. （0，﹣5）D. （0，4）5.在平面直角坐标系中，点（-1，m2+1）一定在（）A. 第一象限B. 第二象限C. 第三象限D. 第四象限6.已知点P（x,|x|），则点P一定（）A. 在第一象限B. 在第一或第二象限C. 在x轴上方D. 不在x轴下方7.小莹和小博士下棋，小莹执圆子，小博士执方子．如图，棋盘中心方子的位置用（﹣1，0）表示，右下角方子的位置用（0，﹣1）表示．小莹将第4枚圆子放入棋盘后，所有棋子构成一个轴对称图形．他放的位置是（）A. （﹣2，1）B. （﹣1，1）C. （1，﹣2）D. （﹣1，﹣2）8.若点P关于x轴对称点为P1（2a+b，3），关于y轴对称点为P2（9，b+2），则点P坐标为（）A. （9，3）B. （﹣9，3）C. （9，﹣3）D. （﹣9，﹣3）9.已知点M到x轴的距离为1，到y轴的距离为2，则M点的坐标可能是（）A. （1，2）B. （-1，-2）C. （1，-2）D. （-2，1）10.如图，半径为1个单位长度的圆从点P（﹣2，0）沿x轴向右滚动一周，圆上的一点由P点到达P′点，则点P′的横坐标是（ ）A. 4B. 2πC. π﹣2D. 2π﹣211.定义：平面内的直线l1与l2相交于点O ，对于该平面内任意一点M ，点M到直线l1、l2的距离分别为a、b ，则称有序非实数对（a ，b）是点M的“距离坐标”，根据上述定义，距离坐标为（2，1）的点的个数有（ ）.A. 2个B. 3个C. 4个D. 5个12.在平面直角坐标系中，对于点P（x,y）,我们把点Q（-y+1,x+1）叫做点P的伴随点.已知点A1的伴随点为A2,A2的伴随点为A3……这样依次得到点A1,A2,A3……A n,若点A1（2,2），则点A2019的坐标为（）A. （-2，0）B. （-1，3）C. （1，-1）D. （2，2）二、填空题（共6题；共12分）13.把点P（﹣2，3）绕坐标原点旋转180°后对应点的坐标为________.14.同学们玩过五子棋吗？它的比赛规则是只要同色五子先成一条直线就算胜．如图是两人玩的一盘棋，若白①的位置是(1，－5)，黑②的位置是(2，－4)，现在轮到黑棋走，你认为黑棋放在_______位置就可获胜．15.已知点P(2，3)，点A与点P关于y轴对称，则点A的坐标是________ 。
北师大版数学八年级上册第三章测试题附答案
北师大版数学八年级上册第三章测试题（时间：90分钟分值：100分）姓名：班级：等级：一、选择题(每小题4分，共28分)1．下面的叙述能确定物体位置的是()①图书大厦在火车站的西北方向；②上午8点，小红在人民商场一层的东北角等我；③小明家在自强小区14号楼3单元501室；④体育馆在距人民广场650米的地方．A．①② B．②③C．①②③ D．②③④2．在平面直角坐标系中，点(－3，2)在()A．第一象限 B．第二象限C．第三象限 D．第四象限3．（2018•湘潭）如图，点A的坐标（﹣1，2），则点A关于y轴的对称点的坐标为（）A．（1，2）B．（﹣1，﹣2）C．（1，﹣2）D．（2，﹣1）4．坐标平面上有一点A，且点A到x轴的距离为3，点A到y轴的距离恰为点A到x 轴距离的2倍．若点A在第二象限，则点A的坐标为()A．(－3，6) B．(－3，2)C．(－6，3) D．(－2，3)5．如图1，△ABC与△DEF关于y轴对称，已知A(－4，6)，B(－6，2)，F(2，1)，则点D的坐标为()图1A．(－4，6) B．(4，6) C．(－2，1) D．(6，2)6．已知点P(x，y)在第四象限，且|x|＝3，|y|＝5，则点P的坐标是()A．(－3，5) B．(5，－3) C．(3，－5) D．(－5，3)图27．如图2，在平面直角坐标系中，半径均为1个单位长度的半圆O1，O2，O3，…组成一条平滑的曲线，点P从原点O出发，沿这条曲线向右运动，速度为每秒π2个单位长度，则第2018秒时，点P的坐标是()A．(2016，0) B．(2017，0)C．(2018，0) D．(2017，1)二、填空题(每小题4分，共32分)8．若电影院中的5排2号座位记为(5，2)，则3排5号座位记为________．9．若点P(a，－b)在第二象限内，则点(－a，－b)在第________象限．10．已知第三象限内的点P(x，y)的坐标满足|x|＝5和y2＝9，则点P的坐标是________．11．若点M(a＋3，a－2)在y轴上，则点M的坐标是________．12．若点M在第一、三象限的角平分线上，且点M到x轴的距离为2，则点M的坐标是________．13．若点A(1－x，5)，B(3，y)关于y轴对称，则x＋y＝________．14．在平面直角坐标系中，若点M(－1，3)与点N(x，3)之间的距离是5，则x的值是________．15．在平面直角坐标系中，孔明做走棋的游戏，其走法是：棋子从原点出发，第1步向右走1个单位长度，第2步向右走2个单位长度，第3步向上走1个单位长度，第4步向右走1个单位长度……依此类推，第n步的走法是：当n能被3整除时，则向上走1个单位长度；当n被3除，余数为1时，则向右走1个单位长度；当n被3除，余数为2时，则向右走2个单位长度，当走完第100步时，棋子所处位置的坐标是________．三、解答题(共40分)16．(6分)在平面直角坐标系中，已知点A(－3，－1)，B(－1，0)，C(－2，3)，请在图中画出△ABC，并画出与△ABC关于y轴对称的图形．17.(8分)如图3，平行四边形ABCD中，AB＝4，BC＝2.若把它放在平面直角坐标系中，使AB在x轴上，点C在y轴上，如果点A的坐标为(－3，0)，求点B，C，D的坐标．图318．(8分)图4是某市部分地区的示意图，请你建立适当的直角坐标系，并写出图中各地点相应的坐标(图中小正方形的边长均为1)．图419．(8分)在平面直角坐标系xOy中，已知A(－1，5)，B(4，2)，C(－1，0)三点．(1)点A的对称点A′的坐标为(1，－5)，点B关于x轴的对称点B′的坐标为________，点C关于y轴的对称点C′的坐标为________；(2)求(1)中的△A′B′C′的面积．20．(10分)在如图5所示的平面直角坐标系中，已知A，B两村庄的坐标分别为(2，2)，(7，4)，一辆汽车从原点O出发，在x轴上行驶．(1)汽车行驶到什么位置时，离A村最近？在图中标出此点，并写出此点的坐标；(2)汽车行驶到什么位置时，离B村最近？在图中标出此点，并写出此点的坐标；(3)汽车行驶到什么位置时，与A，B两村的距离之和最小？在图中标出此点的位置．图5参考答案1．， B 2．B 3．， A 4．， C 5．B 6．， C 7．， C8．(3，5)9．一10． (－5，－3)11．(0，－5)12．(2，2)或(－2，－2)13． 914．－6或415．(100，33)16．略17．解：因为AB＝4，点A的坐标为(－3，0)，设点B的坐标为(b，0)，则b－(－3)＝b＋3＝4，所以b＝1，所以点B的坐标为(1，0)．设点C的坐标为(0，c)，由OB＝1，BC＝2，得OC＝BC2－OB2＝22－12＝3，所以点C的坐标为(0，3)．因为CD∥AB，所以点D的坐标为(－4，3)．所以点B，C，D的坐标分别为(1，0)，(0，3)和(－4，3)．18．解：答案不唯一，如建立如图所示的直角坐标系，则各地点相应的坐标为：教育局(－2，3)，苏果超市(－1，1)，怡景湾酒店(－4，－2)，同仁医院(2，－3)．19．解：(1)(4，－2) (1，0)(2)如图，因为A ′(1，－5)，B ′(4，－2)，C ′(1，0)， 过点B ′作x 轴的平行线交A ′C ′于点D ，则B ′D ⊥A ′C ′， 所以A ′C ′＝|－5－0|＝5，B ′D ＝|4－1|＝3， 所以S △A ′B ′C ′＝12A ′C ′·B ′D ＝12×5×3＝7.5，即(1)中的△A ′B ′C ′的面积是7.5. 20．解：(1)图略．此点的坐标为(2，0)． (2)图略．此点的坐标为(7，0)．(3)找到点A 关于x 轴的对称点A ′，连接A ′B ，则A ′B 与x 轴的交点即为所求．图略．。
新版北师大版八年级上册数学-第三章单元测试(有答案)
图（三） 1、已知点P （1，－2），点Q(－1，2)，点 R (－1，－2)，点H(1,2)，它们关于y 轴 对称的点是（ ）.A 、 P 和QB 、 P 和HC 、 Q 和RD 、 P 和R2、已知点M 到x 轴的距离为3，到y 轴距离为2，且在第四象限内，则点M 的坐标为（ ）.A 、 （2，3）B 、（2，－3）C 、 （3，2）D 、 不能确定3、若（a+2）2+3-b =0，则点M （a ，b ）在（ ）A 、 第一象限B 、 第二象限C 、 第三象限D 、 第四象限4、已知P （m-1,2-m ）在第一象限，则m 的取值范围为（ ）A 、21＜m ＜ 2B 、 1＜m ＜2C 、 m ＜2D 、 m ＞21 5、如图（一），在直角坐标系中，△AOB 是等边三角形，若B 点的坐标是（2，0），则A 点的坐标是（ ）A 、 （2，1）B 、（1，2）C 、（3，1 ）D 、（1， 3 ）6、一个平行四边形的三个顶点的坐标分别是（0，0）、（2，0）（1，2），第四个顶点在x 轴下方，则其坐标为（ ）A 、（-1，-2）B 、（1，-2）C 、（3，2）D 、（-1，2）7、如果点A （x,y ）在第三象限，则点B （-x,y-1）在（ ）A 、 第一象限B 、 第二象限C 、 第三象限D 、 第四象限8、将图（二）中各点的横坐标不变，纵坐标分别乘以－1，所得图形为（ ）9、将平面直角坐标系内某个图形的各点的横坐标乘以－1，纵坐标不变，所得图形与原图形的关系是（ ）A 、 关于x 轴对称B 、 关于y 轴对称C 、 关于原点对称D 、 重合10、坐标平面内有一点P （m ，n ），且m n=0，则点A 的位置在（ ）A 、 原点B 、x 轴上C 、y 轴上D 、 坐标轴上二、填空题（每空2分，共22分）1、如果点P 1（-1，3）与P 2（1，b ）关于y 轴对称，则b= 。
2、在坐标平面上，横坐标为零的点一定在 。
新北师大版八年级数学上册单元测试卷附答案第三章 位置与坐标
第三章位置与坐标一、选择题（共16小题；共48分）1. 根据下列表述，能确定位置的是A. 红星电影院排B. 北京市四环路C. 北偏东D. 东经，北纬2. 若点与点关于轴对称，则A. ，B. ，C. ，D. ，3. 根据下列表述，能确定位置的是A. 国际影城排B. A 市南京路口C. 北偏东D. 东经，北纬4. 如图，在平面直角坐标系中，点的坐标为A. C. D.5. 在平面直角坐标系中，点关于轴的对称点的坐标是A. B. D.6. 由所有到已知点的距离大于或等于，并且小于或等于的点组成的图形的面积为A. B. C. D.7. 在平面直角坐标系中，若点坐标为，点坐标为，则三角形的面积为A. B. C. D.8. 将的三个顶点的横坐标乘以，纵坐标不变，则所得图形A. 与原图形关于轴对称B. 与原图形关于轴对称C. 与原图形关于原点对称D. 向轴的负方向平移了一个单位9. 如图，两个三角形的面积分别是和，对应阴影部分的面积分别是，则等于A. B. C. D. 无法确定10. 如果点在直线上，点的坐标是，点的坐标是，那么三角形的面积A. 等于B. 大于C. 小于D. 无法确定11. 正方形的边长为，以各边为直径在正方形内画半圆，得到如图所示阴影部分，若随机向正方形内投一粒米，则米粒落在阴影部分的概率为D.12. 在直角坐标系中，将点向左平移个单位长度，再向下平移个单位长度后，得到的点位于A. 第一象限B. 第二象限C. 第三象限D. 第四象限13. 在平面直角坐标系中，若点的坐标为，点的坐标为，则的面积为A. B. C. D.14. 如图，阴影部分的面积是A. B. C. D.15. 在某台风多影响地区，有互相垂直的两条主干线，以这两条主干线为轴建立直角坐标系，单位长为万米．最近一次台风的中心位置是，其影响范围的半径是万米，则下列四个位置中受到了台风影响的是A. B. C. D.16. 将的各顶点的横坐标都乘以，则所得三角形与的关系A. 关于轴对称B. 关于轴对称C. 关于原点对称D. 将三角形向左平移了一个单位二、填空题（共7小题；共35分）17. 如果点在直线上，点的坐标是，点的坐标是，那么三角形的面积为．18. 如果用表示电影院的座位号是排号，那么表示；排号可表示为．19. 已知点在第二象限，且到轴的距离是，到轴的距离是，则点的坐标为．20. 如图是由边长为和的两个正方形组成，小颖闭上眼睛随意用针扎这个图形，小孔出现在阴影部分的概率是．21. 在平面直角坐标系中，已知点在第二象限，则点关于直线（直线上各点的横坐标都是）对称的点的坐标是．22. 如图，在平面直角坐标系中，的顶点在轴的正半轴上，顶点的坐标为，点的坐标为，点为斜边上的一动点，则的最小值为．23. 的各顶点坐标为，，，则的面积为．三、解答题（共5小题；共67分）24. 如图，在中，，为上一点，且，过点作，垂足为，且，，交于点．（1）判断线段与的数量关系和位置关系，并说明理由．（2）连接，，若设，，，请利用四边形的面积证明勾股定理．25. 如图，是中国象棋棋盘的一部分，棋盘中“马”所在的位置用表示．（1）图中“象”的位置可表示为．（2）根据象棋的走子规则，“马”只能从“日”字的一角走到与它相对的另一角，“象”只能从“田”字的一角走到与它相对的另一角，请按此规则分别写出“马”和“象”下一步可能到达的位置．26. 已知在平面直角坐标系中有三点，，．请回答如下问题：（1）在坐标系内描出点，，的位置，并求的面积；（2）在平面直角坐标系中画出，使它与关于轴对称，并写出三顶点的坐标；（3）若是内部任意一点，请直接写出这点在内部的对应点的坐标．27. 如图，在长方形中，为平面直角坐标系的原点，点的坐标为，点的坐标为，点在第一象限内，点从原点出发，以每秒个单位的速度沿着的路线移动（即沿着长方形移动一周）．（1）写出点的坐标．（2）当点移动了秒时，指出此时点的位置，并写出点的坐标．（3）在移动过程中，当点到轴距离为个单位长度时，求点移动的时间．28. 如图，，，点在轴上，且．（1）求点的坐标；（2）求的面积；（3）在轴上是否存在点，使以，，三点为顶点的三角形的面积为?若存在，请直接写出点的坐标；若不存在，请说明理由．答案第一部分1. D2. D3. D4. A5. A6. C7. D8. A9. B10. A11. A12. C13. D14. B 【解析】阴影部分面积为：．15. B16. B第二部分17.18. 排号，19.【解析】图形的总面积为，阴影部分面积为，小孔出现在阴影部分的概率是．21.23.第三部分24. （1），，理由如下，因为，所以，在和中，所以，所以，，又因为，所以，所以，即．（2），即．25. （1）（2）“马”下一步可能到达的位置：，，，，，；“象”下一步可能到达的位置：，，，．26. （1）描点如图，顺次连接点，，，由题意得，，且，．（2）如图，，．（3）．27. （1）．（2）点在中点处，坐标为．（3）当点在上时，则，（秒）；当点在上时，则，（秒），综上所述，点移动的时间为秒或秒．28. （1）如图，点在点，点在点，所以，的坐标为或．（2）的面积．（3）设点到轴的距离为，则，解得，点在轴正半轴时，，点在轴负半轴时，，综上所述，点的坐标为或．。
北师大版八年级上册数学第三章检测试题（附答案）
北师大版八年级上册数学第三章检测试题（附答案）一、单选题（共12题；共24分）1.下列选项所给数据，能让你在地图上准确找到位置的是（）A. 东经128°B. 西经71°C. 南纬13°D. 东经118°，北纬24°2.若a＞0，b＜-2，则点（a，b+2）应在（）A. 第一象限B. 第二象限C. 第三象限D. 第四象限3.已知点M（1﹣2m，m﹣1）关于x轴的对称点在第一象限，则m的取值范围在数轴上表示正确的是（）A. B. C. D.4.如图，直角坐标系中，点A（- 2,2）、B（0,1）点P 在x 轴上，且△PAB 的等腰三角形，则满足条件的点P 共有（）个5题A. 1B. 2C. 3D. 45.如图，在平面直角坐标系xOy中，A、B为一次函数图象上的两点，若点A的坐标为(x,y),点B的坐标为(x+a,y+b)，则下列结论正确是（）A. a>0B. a<0C. b=0D. b>06.点B（m2+1，﹣1）一定在（）A. 第一象限B. 第二象限C. 第三象限D. 第四象限7.在平面直角坐标系中，正方形的顶点坐标分别为A（1，1），B（1，﹣1），C（﹣1，﹣1），D（﹣1，1），y轴上有一点P（0，2）．作点P关于点A的对称点P1，作点P1关于点B的对称点P2，作点P2关于点C的对称轴P3，作点P3关于点D的对称点P4，作点P4关于点A的对称点P5，作点P5关于点B的对称点P6，…，按此操作下去，则点P2016的坐标为（）A. （0，2）B. （2，0）C. （0，-2）D. （﹣2，0）8.在平面直角坐标系中，点A（1，3）关于原点O对称的点A′的坐标为（）A. （-1，3）B. （1，-3）C. （3，1）D. （-1，-3）9.如果点P（5，y）在第四象限，则y的取值范围是（）.A. y＜0B. y＞0C. y≤０D. y≥０10.如图，在平面直角坐标中，过格点A，B，C做一圆弧，点B与下列格点的连线中，能够与该圆弧相切的格点的坐标是( )A. (0，3)B. (5，1)C. (6，1)D. (7，1)11.已知点E(x0，y0)，F(x2，y2)，点M(x1，y1)是线段EF的中点，则.在平面直角坐标系中有三个点A(1，－1)，B(－1，－1)，C(0，1)，点P(0，2)关于A的对称点为P1(即P，A，P1三点共线，且PA＝P1A)，P1关于B的对称点为P2，P2关于C的对称点为P3，按此规律继续以A，B，C为对称点重复前面的操作，依次得到P4，P5，P6，…，则点P2019的坐标是()A. (4，0)B. (-2，2)C. (2，－4)D. (－4，2)12.把100个苹果分给若干个小朋友，每个人至少一个，且每个人分的数目不同．那么最多有（）人？A. 11B. 12C. 13D. 14二、填空题（共6题；共12分）13.点M（2，-4）关于原点对称的点的坐标是________.14.如图是某校的平面示意图，如果分别用（3，﹣1）、（﹣3，2）表示图中图书馆和实验楼的位置，那么校门的位置可表示为________16题15.点P（3，2）关于y轴对称的点的坐标是________ ．18题16.如图，在菱形ABCD中，点A在x轴上，点B的坐标为（8，2），点D的坐标为（0，2），则点C的坐标为________．17.点P（5，3）关于y轴对称的点的坐标是 ________18.如图，点A1的坐标为（2，0），过点A1作x轴的垂线交直线l：y＝x于点B1，以原点O为圆心，OB1的长为半径画弧交x轴正半轴于点A2；再过点A2作x轴的垂线交直线l于点B2，以原点O为圆心，以OB2的长为半径画弧交x轴正半轴于点A3；…．按此作法进行下去，则的长是________．三、解答题（共2题；共13分）19.已知四边形AOCD是放置在平面直角坐标系内的梯形，其中O是坐标原点，点A，C，D的坐标分别为（0,8），（5,0），（3,8）.若点P在梯形内，且△PAD的面积等于△POC的面积，△PAO的面积等于△PCD 的面积. 求点P的坐标.20.已知点A（﹣5，0），B（3，0），在坐标平面内找一点C，能满足S△ABC=16，求点C的坐标，这个点的坐标有何规律？四、作图题（共1题；共10分）21.画出△ABC关于y轴对称的图形△A1B1C1，并指出△A1B1C1的顶点坐标.五、综合题（共3题；共41分）22.如图，，，点B在x轴上，且．（1）求点B的坐标；（2）求的面积；（3）在y轴上是否存在P，使以A、B、P三点为顶点的三角形的面积为10？若存在，请求出点P的坐标；若不存在，请说明理由．23.如图，在平面直角坐标系中，点A，B的坐标分别为（0，3），（1，0），△ABC是等腰直角三角形，∠ABC＝90°．（1）图1中，点C的坐标为________；（2）如图2，点D的坐标为（0，1），点E在射线CD上，过点 B 作BF⊥BE交y轴于点F．①当点E为线段CD的中点时，求点F的坐标；②当点E在第二象限时，请直接写出F点纵坐标y的取值范围．24.如图，在平面直角坐标系xOy中，已知点A（﹣1，0），点B（0，2），点C（3，0），直线a为过点D（0，﹣1）且平行于x轴的直线．（1）直接写出点B关于直线a对称的点E的坐标________；（2）若P为直线a上一动点，请求出△PBA周长的最小值和此时P点坐标；（3）若M为直线a上一动点，且S△ABC=S△MAB，请求出M点坐标．答案一、单选题1. D2. D3.A4. D5. B6.D7. A8. D9. A 10. B 11. A 12.C二、填空题13. （-2，4）14.（0，﹣2）15. （﹣3，2）16.（4，4）17. （﹣5，3）18.三、解答题19. 解：如图，过点P作PE⊥y轴于点E．因为：点A，C，D的坐标分别为（0,8），（5,0），（3,8），△PAD的面积等于△POC的面积，所以：×3AE= ×5OE，即3（8-OE）=5OE，解得：OE=3所以：△PAD的面积=△POC的面积= ×3×5=7.5，，△PAO的面积=△PCD的面积=[﹙3﹢5﹚×8÷2-2×7.5]÷2=8.5则×8PE=8.5，即PE= ，所以：点P的坐标是（，3）．20.解：如图，∵A（﹣5，0），B（3，0），∴AB=3﹣（﹣5）=3+5=8，S△ABC= AB?CO= ×8?CO=16，解得：CO=4，当点C在y轴的正半轴时，点C的坐标为（0，4），当点C在y轴的负半轴时，点C的坐标为（0，﹣4）；∵到x轴距离等于4的点有无数个，∴在平面内使△ABC的面积为16的点有无数个，这些点到x轴的距离等于4．四、作图题21. 解：如图，A1（-3，4），B1（-1，2），C1（-5，1）.五、综合题22. （1）解：当点B在点A的右边时，点B的坐标为(2，0)；当点B在点A的左边时，点B的坐标为(－4，0)．所以点B的坐标为(2，0)或(－4，0)＝6. （3）（2）解：三角形ABC的面积为×3×４解：设点P到x轴的距离为h，则×3h＝10，解得h＝.①当点P在y轴正半轴时，点P的坐标为(0，)；②当点P在y轴负半轴时，点P的坐标为(0，－)．综上所述，点P的坐标为(0，)或(0，－)23. （1）解：C(4，1)（2）解：①法一：过点E作EM⊥x轴于点M，∵C（4，1），D（0，1），E为CD中点，∴CD∥x轴，EM=OD=1，∴OM=2，∴∠OBF=45°，∴△OBF为等腰直角三角形，∴OF=OB=1.法二：在OB的延长线上取一点M..∵∠ABC=∠AOB=90°∴∠ABO+∠CBM=90°.∠ABO+∠BAO =90°.∴∠BAO=∠CBM .∵C(4,1).D(0,1).又∵CD∥OM ,CD=4.∴∠DCB=∠CBM.∴∠BAO=∠ECB..∵∠ABC=∠FBE=90°∴∠ABF=∠CBE.∵AB=BC.∴△ABF≌△CBE(ASA).∴AF=CE= CD=2,∵A(0,3),OA=3,∴OF=1.∴F(0,1) ,② .24. （1）（0，﹣4）（2）解：∵B、E关于直线a对称，∴PB=PE，∴△PBA周长=AB+BP+PA=AB+PE+PA∵两点之间线段最段，∴△PBA周长的最小值=AB+AE= ，∴直线AE的解析式：y=﹣4x﹣4，当y=﹣1时，x= ，∴P点坐标（，﹣1）（3）解：设M（m，﹣1），当M在第四象限，∵S△ABC=S△MAB，∴点M在过C且平行于AB的直线上，∵直线AB的解析式为：y=2x+2，设直线CM的解析式为：y=2x+n，，∴0=2×3+n∴n=﹣6，∴直线CM的解析式为：y=2x﹣6，∴m= ，∴M（，﹣1），当M在第三象限，直线AB与直线a交于G（﹣，﹣1），，∴×（﹣﹣m）×（2+1）﹣×（﹣﹣m）×1= ×4×２∴m=﹣5.5，∴M（﹣5.5，﹣1）．。
北师大版八年级上册数学第三章《位置与坐标》单元测试卷(含答案)
北师大版八年级上册数学第三章《位置与坐标》单元测试卷（含答案）一、选择题(每题3分, 共30分)1．点P(－4, 3)所在的象限是( )A. 第一象限B. 第二象限C. 第三象限D. 第四象限2．根据下列表述, 能确定位置的是( )A. 红星电影院2排B. 北京市四环路C. 北偏东30°D. 东经118°, 北纬40°3. 如图, 在直角坐标系中, 卡片盖住的点的坐标可能是( )A．(2, 3) B．(－2, 1) C．(－2, －2.5) D．(3, －2)(第3题) (第8题) (第10题)4. 若点A(m, n)在第三象限, 那么点B(－m, |n|)在( )A. 第一象限B. 第二象限C. 第三象限D. 第四象限5. 已知点A(－1, －4), B(－1, 3), 则( )A．点A, B关于x轴对称 B．点A, B关于y轴对称C. 直线AB平行于y轴D. 直线AB垂直于y轴6．已知点A(m＋1, －2)和点B(3, m－1), 若直线AB∥x轴, 则m的值为( )A. 2B. －4C. －1D. 37．若点P(1, a)与点Q(b, 2)关于x轴对称, 则代数式(a＋b)2 023的值为( )A. －1B. 1C. －2D. 28. 【中考·滨州】如图, 正五边形ABCDE放入某平面直角坐标系后, 若顶点A,B, C, D的坐标分别是(0, a), (－3, 2), (b, m), (c, m), 则点E的坐标是( )A. (2, －3)B. (2, 3)C. (3, 2)D. (3, －2)9. 已知点P的坐标为(2－a, 3a＋6), 且点P到两坐标轴的距离相等, 则点P的坐标是( )A. (3, 3)B. (3, －3)C. (6, －6)D. (3, 3)或(6, －6)10. 在平面直角坐标系中, 一个智能机器人接到的指令是: 从原点O出发, 按“向上→向右→向下→向右”的方向依次不断移动, 每次移动1个单位长度, 其移动路线如图所示, 第一次移动到点A1, 第二次移动到点A2, …, 第n次移动到点An, 则点A2 023的坐标是( )A. (1 010, 0)B. (1 010, 1)C. (1 011, 0)D. (1 011, 1)二、填空题(每题3分, 共24分)11. 点(0, －2)在________轴上.12. 点(4, 5)关于x轴对称的点的坐标为__________.13. 一个英文单词的字母顺序分别对应如图中的有序数对：(5, 3), (6, 3),(7, 3), (4, 1), (4, 4), 则这个英文单词翻译成中文为__________．(第13题) (第17题) (第18题)14. 已知点A, B, C的坐标分别为(2, 4), (6, 0), (8, 0), 则△ABC的面积是________.15. 【教材P71复习题T1(3)改编】若点P到x轴的距离为4, 到y轴的距离为5, 且点P在y轴的左侧, 则点P的坐标为________________.16. 已知点N的坐标为(a, a－1), 则点N一定不在第________象限.17. 如图, 一束光线从点A(3, 3)出发, 经过y轴上的点C反射后经过点B(1, 0),则光线从点A到点B经过的路径长为________.18. 如图, 在△ABC中, 点A的坐标为(0, 1), 点B的坐标为(3, 1), 点C的坐标为(4, 3), 如果要使△ABD与△ABC全等, 那么点D的坐标为__________.三、解答题(19, 23, 24题每题12分, 其余每题10分, 共66分)19. 【教材P60随堂练习变式】如图, 标明了李华同学家附近的一些地方.(1)根据图中所建立的平面直角坐标系, 写出学校、邮局的坐标.(2)某星期日早晨, 李华同学从家里出发, 沿着(－2, －1)→(－1, －2)→(1,－2)→(2, －1)→(1, －1)→(1, 3)→(－1, 0)→(0, －1)→(－2, －1)的路线转了一圈, 依次写出他路上经过的地方.(3)连接(2)中各点, 所形成的路线构成了什么图形？20. 已知点P(2m－6, m＋2).(1)若点P在y轴上, 则点P的坐标为__________；(2)若点P的纵坐标比横坐标大6, 则点P在第几象限？21. 若点P, Q的坐标分别是(x1, y1), (x2, y2), 则线段PQ的中点坐标为. 如图, 已知点A, B, C的坐标分别为(－5, 0), (3, 0), (1, 4), 利用上述结论分别求出线段AC, BC的中点D, E的坐标, 并判断DE与AB的位置关系.22. 已知点P(2x, 3x－1)是平面直角坐标系内的点.(1)若点P在第三象限, 且到两坐标轴的距离和为11, 求x的值；(2)已知点A(3, －1), 点B(－5, －1), 点P在直线AB的上方, 且到直线AB的距离为5, 求x的值．23. 【教材P68例题变式】如图所示.(1)写出A, B, C三点的坐标.(2)若△ABC各顶点的纵坐标不变, 横坐标都乘－1, 请你在同一坐标系中描出对应的点A′, B′, C′, 并依次连接这三个点, 所得的△A′B′C′与△ABC有怎样的位置关系？(3)求△ABC的面积.24. 已知A(－3, 0), C(0, 4), 点B在x轴上, 且AB＝4.(1)求点B的坐标.(2)在y轴上是否存在点P, 使得以A, C, P为顶点的三角形的面积为9？若存在, 求出点P的坐标；若不存在, 请说明理由.(3)在y轴上是否存在点Q, 使得△ACQ是等腰三角形？若存在, 请画出点Q的位置, 并直接写出点Q的坐标；若不存在, 请说明理由．参考答案一、1. B 2. D 3. D 4. A 5. C 6. C 7. A 8. C 9. D 10. C二、11. y 12. (4, －5) 13. 学习14. 415. (－5, 4)或(－5, －4) 16. 二17. 518. (4, －1)或(－1, 3)或(－1, －1)三、19．解: (1)学校的坐标为(1, 3), 邮局的坐标为(0, －1)．(2)商店、公园、汽车站、水果店、学校、娱乐城、邮局.(3)图略, 该图形为一条帆船.20. 解: (1)(0, 5)(2)根据题意, 得2m－6＋6＝m＋2, 解得m＝2.所以点P的坐标为(－2, 4)．所以点P在第二象限.21. 解: 由题中所给结论及点A, B, C的坐标分别为(－5, 0), (3, 0), (1,4),得点D(－2, 2), E(2, 2).因为点D, E的纵坐标相等, 且不为0,所以DE∥x轴.又因为AB在x轴上,所以DE∥AB.22. 解: (1)当点P在第三象限时, 点P到x轴的距离为1－3x, 到y轴的距离为－2x. 故1－3x－2x＝11, 解得x＝－2.(2)易知直线AB∥x轴. 由点P在直线AB的上方且到直线AB的距离为5, 得3x－1－(－1)＝5, 解得x＝.23．解: (1)A(3, 4), B(1, 2), C(5, 1)．(2)图略.△A′B′C′与△ABC关于y轴对称.(3)S△ABC＝3×4－×2×2－×2×3－×1×4＝5.24. 解: (1)因为点B在x轴上, 所以设点B的坐标为(x, 0).因为A(－3, 0), AB＝4,所以|x－(－3)|＝4,解得x＝－7或x＝1.所以点B的坐标为(－7, 0)或(1, 0).(2)在y轴上存在点P, 使得以A, C, P为顶点的三角形的面积为9. 设点P的坐标为(0, y),当点P在点C的上方时, S△ACP＝＝9,解得y＝10；当点P在点C的下方时, S△ACP＝＝9,解得y＝－2.综上所述, 点P的坐标为(0, 10)或(0, －2).(3)在y轴上存在点Q, 使得△ACQ是等腰三角形.如图, 点Q的坐标为(0, 9)或(0, －4)或或(0, －1)．。
北师大版初中八年级数学上册第三章检测卷含答案
学校班级姓名第三章检测卷(时间:60分钟满分:100分)一、选择题(每小题4分,共32分)1.象棋盘的一部分如图所示,若“帅”位于点(2,-1),“相”位于点(4,-1)上,则“炮”位于点()上.A.(0,2)B.(0,3)C.(-1,3)D.(-1,2)2.若点P(m,-2),B(-4,n-3)关于x轴对称,则().A.m=-4,n=5B.m=-4,n=-5C.m=4,n=1D.m=4,n=-13.如图,在A,B两处观测到的C处的方位角分别是().A.北偏东60°,北偏西40°B.北偏东60°,北偏西50°C.北偏东30°,北偏西40°D.北偏东30°,北偏西50°(第3题图)4.如图所示,在平面直角坐标系中,正方形ABCD的顶点A,B的坐标分别为A(0,1),B(2,-1),若点C到y 轴的距离为m,点D到x轴距离为n,则m和n分别为().A.4,3B.3,4C.1,2D.1,3(第4题图)5.将△ABC的三个顶点的横坐标不变,纵坐标乘-1,则所得图形().A.与原图形关于x轴对称B.与原图形关于y轴对称C.与原图形关于原点对称D.向y轴的负方向平移了1个单位长度6.如图,在平面直角坐标系中,直线l过点A且平行于x轴,交y轴于点(0,1),△ABC关于直线l对称,点B 的坐标为(-1,-1),则点C的坐标为().A.(-2,1)B.(-1,3)C.(1,-3)D.(-3,1)(第6题图)7.五子连珠棋和象棋、围棋一样,深受同学们喜爱,其规则是:在15×15的正方形棋盘中,由黑方先行,轮流弈子,在任一方向上连成五子者为胜.两个五子棋爱好者甲和乙的对弈图(甲执黑子先行,乙执白子后行),如图所示.观察棋盘,若点M的位置记作(8,4),甲必须在()处落子,才不会让乙在短时间内获胜.(第7题图)A.(1,8)B.(3,5)C.(1,7)或(5,3)D.(7,1)8.如图,长方形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位长度/秒匀速运动,物体乙按顺时针方向以2个单位长度/秒匀速运动,则两个物体运动后的第2 021次相遇地点的坐标是().A.(2,0)B.(-1,1)C.(-2,1)D.(-1,-1)二、填空题(每小题4分,共24分)9.在数学活动中,张明和王丽向老师说明他们的位置(单位:m).张明:我这里的坐标是(-200,300).王丽:我这里的坐标是(300,300).则老师知道张明与王丽之间的距离是 m.10.若点M(2,a+3)与点N(2,2a-15)关于x轴对称,则a2-3=.。
第三章 位置与坐标数学八年级上册-单元测试卷-北师大版(含答案)
第三章位置与坐标数学八年级上册-单元测试卷-北师大版(含答案)一、单选题(共15题，共计45分)1、如图所示，点A的坐标是 ( )A.(3，2)B.(3，3)C.(3，-3)D.(-3，-3)2、若点A（2，n）在x轴上，则点B（n+2，n-5）在（）.A.第一象限B.第二象限C.第三象限D.第四象限3、在平面直角坐标系中，以点O（0，0），A（1，1），B（3，0）为顶点，构造平行四边形，则这个平行四边形的第四个顶点坐标不可能是（）A.（2，﹣1）B.（﹣2，1）C.（﹣3，1）D.（4，1）4、如图，若在象棋盘上建立直角坐标系，使“将”位于点（0，﹣1），“象”位于（2，﹣1），则“炮”位于点（）A.（﹣3，2）B.（﹣4，3）C.（﹣3，0）D.（1，﹣1）5、如图，在直角坐标系中，有两点A（6，3），B（6，0），以原点O位似中心，相似比为，在第一象限内把线段AB缩小后得到线段CD，则点C的坐标为（）A.（2，1）B.（2，0）C.（3，3）D.（3，1）6、如图，在平面直角坐标系中，点A在第一象限，⊙A与轴相切于B，与轴交于C（0，1），D（0，4）两点，则点A的坐标是（）A. B. C. D.7、如图是在方格纸上画出的小旗图案，若用(2，1)表示A点，(2，5)表示B点，那么C点的位置可表示为（）A.(3，5)B.(4，3)C.(3，4)D.(5，3)8、如图，在平面直角坐标系中，直线OA过点（2，1），则tanα的值是（）A. B. C. D.29、在平面直角坐标系中，将点（2，3）向上平移1个单位，再向左平移2个单位，所得到的点的坐标是（）A.（﹣2，3）B.（﹣1，2）C.（0，4）D.（4，4）10、如图，在平面直角坐标系上有点A0（1，0），点A0第一次跳动至点A（﹣1，1），第二次点A1跳动至点A2（2，1），第三次点A2跳动至点A3（﹣2，2），第四次点A3跳动至点A4（3，2），……依此规律跳动下去，则点A2019与点A2020之间的距离是（）A.2021B.2020C.2019D.201811、如图，已知A（1，3），将线段OA绕原点O顺时针旋转90°后得到OA′，则OA′的长度是（）A. B.3 C.2 D.112、如图，在3×3的正方形网格中有4个格点A，B，C，D，以其中一点为原点，网格线所在直线为坐标轴，建立直角坐标系，使其余三个点中存在两个点关于一条坐标轴对称.则原点是（）A.点AB.点BC.点CD.点D13、若x轴上的点p到y轴的距离为5，则点的坐标为（）A.(5,0)B.(5,0)(-5,0)C.(0,5)D.(0,5)或(0，-5)14、已知点A（﹣1，﹣5）和点B（2，m），且AB平行于x轴，则B点坐标为（）A.（2，﹣5）B.（2，5）C.（2，1）D.（2，﹣1）15、如图所示，矩形的两边、分别在x轴、y轴上，点C与原点重合，点A的坐标为(-1，2)，将矩形沿x轴向右翻滚，经过第1次翻滚点A对应点记为，经过第2次翻滚点对应点记为……依此类推，经过第5次翻滚后点A对应点记为的坐标为( )A.(5，2)B.(6，0)C.(8，1)D.(8，0)二、填空题(共10题，共计30分)16、已知点P（﹣2，3），Q（n，3）且PQ=6，则n=________．17、若点与关于原点对称，则________．18、若点P（m+3，m+1）在x轴上，则点P的坐标为________．19、在平面直角坐标系中，菱形的对角线交于原点，点的坐标为，点的坐标为，则点的坐标为________．20、如图，在直角坐标系中，A，B为定点，A（2，﹣3），B（4，﹣3），定直线l∥AB，P 是l上一动点，l到AB的距离为6，M，N分别为PA，PB的中点下列说法中：①线段MN的长始终为1；②△PAB的周长固定不变；③△PMN的面积固定不变；④若存在点Q使得四边形APBQ是平行四边形，则Q到MN所在直线的距离必为9.其中正确的说法是________.21、如图，在中国象棋的残局上建立平面直角坐标系，如果“相”和“兵”的坐标分别是（3，﹣1）和（﹣3，1），那么“卒”的坐标为________.22、若点在轴上；则________．23、如图，在直角坐标系中，点、点、，则外接圆的半径为________．24、在平面直角坐标系中，已知点M（m－1，2m+3）在y轴上，则m＝________.25、如图，在坐标平面内A（1，1），正方形CDEF的DE边在x轴上，C，F分别在OA和AB边上，连接OF，若△OEF和以E，F，B为顶点的三角形相似，则B点坐标为________.三、解答题(共5题，共计25分)26、在直角坐标系中，用线段顺次连结点（－2，0），（0，3），（3，3），（0，4），（－2，0）。
八年级数学北师大版上册第3章《单元测试》01(含答案解析)
答卷时应注意事项１、拿到试卷，要认真仔细的先填好自己的考生信息。
２、拿到试卷不要提笔就写，先大致的浏览一遍，有多少大题，每个大题里有几个小题，有什么题型，哪些容易，哪些难，做到心里有底；３、审题，每个题目都要多读几遍，不仅要读大题，还要读小题，不放过每一个字，遇到暂时弄不懂题意的题目，手指点读，多读几遍题目，就能理解题意了；容易混乱的地方也应该多读几遍，比如从小到大，从左到右这样的题；４、每个题目做完了以后，把自己的手从试卷上完全移开，好好的看看有没有被自己的手臂挡住而遗漏的题；试卷第１页和第２页上下衔接的地方一定要注意，仔细看看有没有遗漏的小题；５、中途遇到真的解决不了的难题，注意安排好时间，先把后面会做的做完，再来重新读答题；６、卷面要清洁，字迹要清工整，非常重要；７、做完的试卷要检查，这样可以发现刚才可能留下的错误或是可以检查是否有漏题，检查的时候，用手指点读题目，不要管自己的答案，重新分析题意，所有计算题重新计算，判断题重新判断，填空题重新填空，之后把检查的结果与先前做的结果进行对比分析。
亲爱的小朋友，你们好!经过两个月的学习，你们一定有不小的收获吧，用你的自信和智慧，认真答题，相信你一定会闯关成功。
相信你是最棒的！北师大版八年级上单元测试第3单元班级________姓名________一、选择题(每题3分，共30分)1．下列数据能确定物体具体位置的是()A．朝阳大道右侧B．好运花园2号楼C．东经103°，北纬30°D．南偏西55°2．下列各点中，在第二象限的点是()A．(2，4)B．(2，－4)C．(－2，4)D．(－2，－4)3．在平面直角坐标系中，点P(x2＋2，－3)所在的象限是()A．第一象限B．第二象限C．第三象限D．第四象限4．在平面直角坐标系xOy中，点A(－3，4)关于y轴对称的点的坐标是() A．(3，－4)B．(－3，－4)C．(－3，4)D．(3，4)5．如图所示的象棋盘上，若“帅”位于点(－1，－2)，“马”位于点(3，－2)，则位于原点位置的是()A．兵B．炮C．相D．车6．在平面直角坐标系中，点(－9，2)关于x轴对称的点的坐标是() A．(9，2)B．(－9，－2)C．(－2，－9)D．(2，－9)7．在平面直角坐标系中，过A点向x轴作垂线段，垂足为M，向y轴作垂线段，垂足为N，垂足M在x轴上的坐标为－3，垂足N在y轴上的坐标是4，则下列说法不正确的是()A．A点横坐标为－3B．A点纵坐标为4C．A点坐标为(－3，4)D．A点在第四象限8．已知点A(m，n)在第一象限，那么点B(－n，－m)在()A．第一象限B．第二象限C．第三象限D．第四象限9．已知点A(1，3)，B(－2，3)，则A，B两点间的距离是()A．4个单位长度B．3个单位长度C．2个单位长度D．1个单位长度10．五子棋深受广大小朋友的喜爱，它的规则如下：在正方形棋盘中，由黑方先行，轮流摆子，在任意方向(横向、竖向或斜向)上先连成五枚棋子者获胜，下图是小明和小亮的部分对弈图，若黑色棋子A的坐标为(3，1)，白色棋子B 的坐标为(2，2)，则黑色棋子C的坐标为()A．(4，－1)B．(－1，－4)C．(－1，4)D．(－4，1)二、填空题(每题3分，共15分)11．如果用(9，2)表示九年级2班，那么八年级4班可表示成________．12．点(－5，3)到y轴的距离是________．13．在平面直角坐标系中，点A(－2，1)，B(2，4)，C(x，y)，BC∥y轴，当线段AC最短时，则此时点C的坐标为________．14．在平面直角坐标系中，点P(a－1，2a＋1)在x轴上，则a的值是________．15．如图，在平面直角坐标系xOy中，正方形ABCD的顶点D在y轴上，且A的坐标是(－2，0)，B的坐标是(1.5，－2)，则点D的坐标是________．三、解答题(16题10分，17题7分，第18～21题每题8分，第22～23题每题13分，共75分)16．已知点P的坐标为(2a＋3，a－1)．试分别根据下列条件，求出点P的坐标．(1)点P的纵坐标比横坐标大3；(2)点P在过点A(2，－3)，且与x轴平行的直线上．17．如图，已知等腰三角形ABC的腰长AB为5，底边BC的长为6，试建立适当的平面直角坐标系来表示等腰三角形ABC各顶点的坐标．18．下图中标明了李明同学家附近的一些地方，已知李明同学家位于(－2，－1)．(1)建立平面直角坐标系，写出学校、邮局的坐标．(2)某星期日早晨，李明同学从家里出发，沿着(－1，－2)、(1，－2)、(2，－1)、(1，－1)、(1，3)、(－1，0)、(0，－1)的路线转了一会儿后回到家里，用线段顺次连接李明家和他在路上经过的地点，你能得到什么图形？19.如图，在平面直角坐标系中，△ABC的位置如图所示(每个方格的边长均为1个单位长度)．(1)写出图中A，B，C三点的坐标；(2)若△ABC各顶点的纵坐标不变，横坐标都乘－1，请在同一平面直角坐标系中找出对应的点A′，B′，C′，并依次连接这三个点，从图象可知△ABC与△A′B′C′有怎样的位置关系？20．如图，已知四边形ABCD.(1)写出点A，B，C，D的坐标；(2)试求四边形ABCD的面积．(网格中每个小正方形的边长均为1)21．在平面直角坐标系中，点P(x，y)的横坐标x的绝对值表示为|x|，纵坐标y的绝对值表示为|y|，我们把点P(x，y)的横坐标与纵坐标的绝对值之和叫做点P(x，y)的勾股值，记为[P]，即[P]＝|x|＋|y|(其中的“＋”是四则运算中的加法)，例如点P(1，2)的勾股值[P]＝|1|＋|2|＝3.(1)求点A(－2，4)，B(2＋3，2－3)的勾股值[A]，[B]；(2)若点M在x轴的上方，其横，纵坐标均为整数，且[M]＝3，请直接写出点M的坐标．22．如图，在平面直角坐标系中，已知A(0，a)，B(b，0)，C(b，c)三点，其中a，b，c满足关系式|a－2|＋(b－3)2＝0和(c－4)2≤0；(1)求a，b，c的值；(2)如果在第二象限内有一点P(m，13)，请用含m的式子表示四边形ABOP的面积；(3)在(2)的条件下，是否存在点P，使得四边形ABOP的面积与△ABC的面积相等，若存在，求出点P的坐标；若不存在，请说明理由．23．问题情境：在平面直角坐标系xOy中有不重合的两点，A(x1，y1)和B(x2，y2)，小明在学习中发现，若x1＝x2，则AB∥y轴，且线段AB的长度为|y1－y2|；若y1＝y2，则AB∥x轴，且线段AB的长度为|x1－x2|.应用：(1)如果点A(－1，1)、B(2，1)，那么AB∥x轴，AB的长度为________．(2)如果点C(1，0)，且CD∥y轴，且CD＝2，那么点D的坐标为________．拓展：我们规定：平面直角坐标系中任意不重合的两点M(x1，y1)，N(x2，y2)之间的折线距离为d(M，N)＝|x1－x2|＋|y1－y2|.例如：图1中，点M(－1，1)与点N(1，－2)之间的折线距离为d(M，N)＝|－1－1|＋|1－(－2)|＝2＋3＝5.解决下列问题：(1)如图2，已知E(2，0)，若F(－1，－2)，则d(E，F)＝________；(2)如图2，已知E(2，0)，H(1，t)，若d(E，H)＝3，则t＝________．(3)如图3，已知P(3，3)，点Q在x轴上，且三角形OPQ的面积为3，则d(P，Q)＝________．答案一、1.C 2.C 3.D 4.D 5.B 6.B7.D8.C9.B10.C二、11.(8，4)12.513.(2，1)14.－1 215.(0，3.5)三、16.解：(1)因为点P的纵坐标比横坐标大3，所以a－1－(2a＋3)＝3，解得a＝－7，所以2a＋3＝－11，a－1＝－8，所以点P的坐标为(－11，－8)．(2)因为点P在过点A(2，－3)，且与x轴平行的直线上，所以a－1＝－3，解得a＝－2，所以2a＋3＝－1，所以点P的坐标为(－1，－3)．17.解：如图，以B点为原点，BC边所在直线为x轴，过点B且垂直于BC边的直线为y轴建立平面直角坐标系，过点A作AD⊥BC于点D，因为等腰三角形ABC的底边BC的长为6，AD⊥BC，所以BD＝DC＝3，∠ADB＝90°，又因为AB＝5，所以AD＝25－9＝4，所以A点坐标为(3，4)，C点坐标为(6，0)，B点坐标为(0，0)．(答案不唯一)18.解：(1)建立平面直角坐标系如图1：学校的坐标为(1，3)；邮局的坐标为(0，－1)．(2)如图2，用线段顺次连接李明家和他在路上经过的地点，得到的图形是帆船．19.解：(1)A 点坐标为(3，3)，B 点坐标为(1，1)，C 点坐标为(4，2)．(2)如图．△ABC 和△A ′B ′C ′的位置关系是关于y 轴对称．20.解：(1)A (－2，1)，B (－3，－2)，C (3，－2)，D (1，2)．(2)S 四边形ABCD ＝3×3＋2×12×1×3＋12×2×4＝16.21.解：(1)因为点A (－2，4)，B (2＋3，2－3)，所以[A ]＝|－2|＋|4|＝2＋4＝6，[B ]＝|2＋3|＋|2－3|＝2＋3＋3－2＝2 3.(2)点M 的坐标为(－1，2)或(1，2)或(－2，1)或(2，1)或(0，3)．22.解：(1)由已知|a －2|＋(b －3)2＝0，(c －4)2≤0可得a －2＝0，b －3＝0，c －4＝0，解得a ＝2，b ＝3，c ＝4.(2)因为a ＝2，b ＝3，c ＝4，所以A (0，2)，B (3，0)，C (3，4)，所以OA ＝2，OB ＝3，因为S △ABO ＝12×2×3＝3，S △APO ＝12×2×(－m )＝－m ，所以S 四边形ABOP ＝S △ABO ＋S △APO ＝3＋(－m )＝3－m .(3)存在，若S 四边形ABOP ＝S △ABC ，则3－m ＝12×4×3＝6，解得m ＝－3，所以存在点P (－3，13)，使得S 四边形ABOP ＝S △ABC .23.解：应用：(1)3(2)(1，2)或(1，－2)拓展：(1)5(2)2或－2(3)4或8。
北师大版初中八年级数学上册第三章同步练习题(含答案解析)
第三章测试卷一、选择题（每题3分，共30分）1.（安徽安庆期末）下列表述中，能确定准确位置的是（ ）A.教室第三排B.湖心南路C.南偏东40°D.东经112°，北纬51°2．在平面直角坐标系中，点A （－3，0）在（ ）A ．x 轴正半轴上B ．x 轴负半轴上C ．y 轴正半轴上D ．y 轴负半轴上3．若点A （m ，n ）在第二象限，则点B （－m ，|n |）在（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限4．平面直角坐标系内的点A （－1，2）与点B （－1，－2）关于（ ）A ．y 轴对称B ．x 轴对称C ．原点对称D ．直线y =x 对称5．已知点A （1，0），B （0，2），点P 在x 轴上，且△PAB 的面积为5，则点P 的坐标为（ ）A ．（－4，0）B ．（6，0）C ．（－4，0）或（6，0）D ．无法确定6．在以下四点中，哪一点与点（－3，4）所连的线段与x 轴和y 轴都不相交（ ）A ．（－5，1）B ．（3，－3）C ．（2，2）D ．（－2，－1）7．如图是小李设计的49方格扫雷游戏，“★”代表地雷（图中显示的地雷在游戏中都是隐藏的），点A 可用（2，3）表示，如果小惠不想因点到地雷而结束游戏的话，下列选项中，她应该点（ ）A ．（7，2）B ．（2，6）C ．（7，6）D ．（4，5）8．从车站向东走400m ，再向北走500m 到小红家；从车站向北走500m ，再向西走200m 到小强家，若以车站为原点，以正东、正北方向为正方向建立平面直角坐标系，则小红家、小强家的坐标分别为（ ）A ．（400，500），（500，200）B ．（400，500），（200，500）C ．（400，500），（－200，500）D ．（500，400），（500，－200）9．如图，直线BC 经过原点O ，点A 在x 轴上，AD ⊥BC 于D ，若B （m ，2），C （n ，－3），A （2，0），则AD ·BC 的值为（ ）A ．不能确定B ．5C ．10D ．7（第9题） （第10题）10．（河南）如图，在平面直角坐标系中，半径均为1个单位长度的半圆O 1，O 2，O 3…组成一条平滑的曲线，点P 从原点O 出发，沿这条曲线向右运动，速度为每秒π2个单位长度，则第2017秒时点P 的坐标是（ ）A ．（2016，0）B ．（2017，1）C ．（2017，－1）D ．（2018，0）二、填空题（每题3分，共24分）11．已知点A 在x 轴上，且OA =3，则点A 的坐标为__________．12．已知小岛A 在灯塔B 的北偏东30°的方向上，则灯塔B 在小岛A 的_____的方向上．13．对任意实数，点P （x ，x －2）一定不在第____象限．14．在平面直角坐标系中，一青蛙从点A （－1，0）处向右跳2个单位长度，再向上跳2个单位长度到点A ′处，则点A ′的坐标为_______．15．如图，在△ABC 中，点A 的坐标为（0，1），点B 的坐标为（0，4），点C 的坐标为（4，3），如果要使△ABD 与△ABC 全等，那么点D 的坐标是________．（第15题）（第16题）（第17题）（第18题）16．将正整数按如图的规律排列下去，若用有序数对（m，n）表示m排从左到右第n个数．如（4，3）表示9，则（15，4）表示________．17．如图，A，B两点的坐标分别为（2，4），（6，0），点P是x轴上一点，且△ABP的面积为6，则点P的坐标为________．18.（长沙期中）如图，△ABC在平面直角坐标系中第二象限内，顶点A的坐标是（-2，3），先把△ABC向右平移4个单位得到△A1B1C1，再作△A1B1C1关于x轴对称图形△A2B2C2．顶点A2坐标是.三、解答题（19～21题每题8分，22～24题每题10分，25题12分，共66分）19．在直角坐标系中描出下列各组点，并将各组内的点用线段依次连接起来．（1）（2，6），（4，6），（4，8），（2，8）；（2）（3，0），（3，3），（3，6）；（3）（3，5），（1，6）；（4）（3，5），（5，6）；（5）（3，3），（2，0）；（6）（3，3），（4，0）．20.小林放学后，先向东走了300 m再向北走200 m，到书店A买了一本书，然后向西走了500 m再向南走了100 m，到快餐店B买了零食，又向南走了400 m，再向东走了800 m到了家C.请建立适当的平面直角坐标系，并在坐标系中画出点A，B，C的位置．21.（1）在坐标平面内画出点P（2，3）；（2）分别作出点P关于x轴、y轴的对称点P1，P2，并写出P1，P2的坐标．22．长阳公园有四棵古树A，B，C，D，示意图如图所示．（1）请写出A，B，C，D四点的坐标；（2）为了更好地保护古树，公园决定将如图所示的四边形EFGH用围栏圈起来划为保护区，请你计算保护区的面积（单位：m）．23．如图，平面直角坐标系中，过点A（0，2）的直线a垂直于y轴，M（9，2）为直线a上一点．若点P从点M出发，以2cm/s的速度沿直线a向左移动；点Q从原点同时出发，以1cm/s的速度沿x轴向右移动，多久后线段PQ平行于y轴？24．如图，已知点P（2m－1，6m－5）在第一象限的角平分线OC上，AP⊥BP，点A在x轴上，点B在y轴上．（1）求点P的坐标．（2）当∠APB绕点P旋转时，OA＋OB的值是否发生变化？若变化，求出其变化范围；若不变，求出这个定值．25．在平面直角坐标系xOy中，我们把横、纵坐标都是整数的点叫作整点．已知点A（0，4），点B 是x轴正半轴上的整点，记△AOB内部（不包括边界）的整点个数为m.（1）当m=3时，求点B的坐标的所有可能值；（2）当点B的横坐标为4n（n为正整数）时，用含n的代数式表示m.参考答案第三章测试卷一、选择题（每题3分，共30分）1.（安徽安庆期末）下列表述中，能确定准确位置的是（D）A.教室第三排B.湖心南路C.南偏东40°D.东经112°，北纬51°2．在平面直角坐标系中，点A（－3，0）在（B）A．x轴正半轴上B．x轴负半轴上C．y轴正半轴上D．y轴负半轴上3．若点A（m，n）在第二象限，则点B（－m，|n|）在（A）A．第一象限 B．第二象限 C．第三象限 D．第四象限4．平面直角坐标系内的点A（－1，2）与点B（－1，－2）关于（B）A．y轴对称B．x轴对称C．原点对称D．直线y=x对称5．已知点A（1，0），B（0，2），点P在x轴上，且△PAB的面积为5，则点P的坐标为（C）A．（－4，0）B．（6，0）C．（－4，0）或（6，0）D．无法确定6．在以下四点中，哪一点与点（－3，4）所连的线段与x轴和y轴都不相交（A）A．（－5，1）B．（3，－3）C．（2，2）D．（－2，－1）7．如图是小李设计的49方格扫雷游戏，“★”代表地雷（图中显示的地雷在游戏中都是隐藏的），点A可用（2，3）表示，如果小惠不想因点到地雷而结束游戏的话，下列选项中，她应该点（D）A．（7，2）B．（2，6）C．（7，6）D．（4，5）8．从车站向东走400m，再向北走500m到小红家；从车站向北走500m，再向西走200m到小强家，若以车站为原点，以正东、正北方向为正方向建立平面直角坐标系，则小红家、小强家的坐标分别为（C）A．（400，500），（500，200） B．（400，500），（200，500）C．（400，500），（－200，500） D．（500，400），（500，－200）9．如图，直线BC经过原点O，点A在x轴上，AD⊥BC于D，若B（m，2），C（n，－3），A（2，0），则AD·BC的值为（C）A．不能确定 B．5 C．10 D．7（第9题）（第10题）【解析】据三角形面积公式得到S △ABC =12AD ·BC ，而S △ABC =S △ABO ＋S △ACO =12×2×2＋12×2×3=5，因此得到12AD ·BC =5，∴AD ·BC =10. 10．（河南）如图，在平面直角坐标系中，半径均为1个单位长度的半圆O 1，O 2，O 3…组成一条平滑的曲线，点P 从原点O 出发，沿这条曲线向右运动，速度为每秒π2个单位长度，则第2017秒时点P 的坐标是（ B ）A ．（2016，0）B ．（2017，1）C ．（2017，－1）D ．（2018，0）【解析】当点P 从原点O 出发，沿这条曲线向右运动，运动时间为1秒时，点P 的坐标为（1，1），运动时间为2秒时，点P 的坐标为（2，0），运动时间为3秒时，点P 的坐标为（3，－1），运动时间为4秒时，点P 的坐标为（4，0）．根据图象可得第n 秒时，点P 的横坐标为n ，纵坐标每4秒一个循环．∵2017÷4=504……1，∴第2017秒时，点P 的坐标是（2017，1）．二、填空题（每题3分，共24分）11．已知点A 在x 轴上，且OA =3，则点A 的坐标为____（3，0）或（－3，0）______．12．已知小岛A 在灯塔B 的北偏东30°的方向上，则灯塔B 在小岛A 的__南偏西30°___的方向上．13．对任意实数，点P （x ，x －2）一定不在第__二__象限．14．在平面直角坐标系中，一青蛙从点A （－1，0）处向右跳2个单位长度，再向上跳2个单位长度到点A ′处，则点A ′的坐标为____（1，2）___．15．如图，在△ABC 中，点A 的坐标为（0，1），点B 的坐标为（0，4），点C 的坐标为（4，3），如果要使△ABD 与△ABC 全等，那么点D 的坐标是____（4，2）或（－4，2）或（－4，3）____．（第15题）（第16题） （第17题） （第18题）16．将正整数按如图的规律排列下去，若用有序数对（m ，n ）表示m 排从左到右第n 个数．如（4，3）表示9，则（15，4）表示____109____．17．如图，A ，B 两点的坐标分别为（2，4），（6，0），点P 是x 轴上一点，且△ABP 的面积为6，则点P 的坐标为____（3，0）或（9，0）____．【解析】设点P 的坐标为（x ，0），根据题意得12×4×|6－x |=6，解得x =3或9，所以点P 的坐标为（3，0）或（9，0）．18.（长沙期中）如图，△ABC 在平面直角坐标系中第二象限内，顶点A 的坐标是（-2，3），先把△ABC 向右平移4个单位得到△A 1B 1C 1，再作△A1B1C1关于x 轴对称图形△A 2B 2C 2．顶点A 2坐标是2，-3.【解析】解答本题的关键是根据网格结构作出对应点的位置，然后写出坐标．分别将点A 、B 、C 向右平移4个单位，作出△A 1B 1C 1，然后作出△A 1B 1C 1关于x 轴对称图形△A 2B 2C 2，如图所示，A 2坐标为（2，-3）.三、解答题（19～21题每题8分，22～24题每题10分，25题12分，共66分）19．在直角坐标系中描出下列各组点，并将各组内的点用线段依次连接起来．（1）（2，6），（4，6），（4，8），（2，8）；（2）（3，0），（3，3），（3，6）；（3）（3，5），（1，6）；（4）（3，5），（5，6）；（5）（3，3），（2，0）；（6）（3，3），（4，0）．解：画出的图形如图所示．20.小林放学后，先向东走了300 m再向北走200 m，到书店A买了一本书，然后向西走了500 m再向南走了100 m，到快餐店B买了零食，又向南走了400 m，再向东走了800 m到了家C.请建立适当的平面直角坐标系，并在坐标系中画出点A，B，C的位置．解：（答案不唯一）以学校门口为坐标原点、向东为x轴的正方向建立平面直角坐标系，各点的位置如图：21.（1）在坐标平面内画出点P（2，3）；（2）分别作出点P关于x轴、y轴的对称点P1，P2，并写出P1，P2的坐标．解：（1）点P（2，3）如图所示；（4分）（2）点P1，P2如图所示，（6分）P1（2，－3），P2（－2，3）．（8分）22．长阳公园有四棵古树A，B，C，D，示意图如图所示．（1）请写出A，B，C，D四点的坐标；（2）为了更好地保护古树，公园决定将如图所示的四边形EFGH用围栏圈起来划为保护区，请你计算保护区的面积（单位：m）．解：（1）A（10，10），B（20，30），C（40，40），D（50，20）．（2）四边形EFGH各顶点坐标分别为E（0，10），F（0，30），G（50，50），H（60，0），另外M（0，50），N（60，50），则保护区的面积S=S长方形MNHO －S△GMF－S△GNH－S△EHO=60×50－12×20×50－12×10×50－12×10×60=3 000－500－250－300=1 950（m2）．23．如图，平面直角坐标系中，过点A（0，2）的直线a垂直于y轴，M （9，2）为直线a上一点．若点P从点M出发，以2cm/s的速度沿直线a向左移动；点Q从原点同时出发，以1cm/s的速度沿x轴向右移动，多久后线段PQ平行于y轴？解：设经过t s后PQ∥y轴，则AP=9－2t，OQ=t.∵PQ∥y轴，∴点P与点Q的横坐标相等，即AP=OQ，∴9－2t=t，解得t=3.故3s后线段PQ平行于y轴．24．如图，已知点P（2m－1，6m－5）在第一象限的角平分线OC上，AP⊥BP，点A在x轴上，点B 在y轴上．（1）求点P的坐标．（2）当∠APB绕点P旋转时，OA＋OB的值是否发生变化？若变化，求出其变化范围；若不变，求出这个定值．解：（1）由题意，得2m－1=6m－5.解得m=1.所以点P的坐标为（1，1）．（2）当PA不垂直于x轴时，作PD⊥x轴于点D，PE⊥y轴于点E，则△PAD≌△PBE，所以AD=BE.所以AD=BE.所以OA＋OB=OD＋AD＋OB=OD＋BE＋OB=OD＋OE=2，为定值．当PA⊥x轴时，显然PB⊥y轴，此时OA＋OB=2，为定值．故OA＋OB的值不发生变化，其值为2.25．在平面直角坐标系xOy中，我们把横、纵坐标都是整数的点叫作整点．已知点A（0，4），点B 是x轴正半轴上的整点，记△AOB内部（不包括边界）的整点个数为m.（1）当m=3时，求点B的坐标的所有可能值；（2）当点B的横坐标为4n（n为正整数）时，用含n的代数式表示m.解：（1）如图①，当点B的横坐标分别为3或4时，m=3，即当m=3时，点B的坐标的所有可能值是（3，0），（4，0）；（2）如图②，当点B的横坐标为4n=4时，n=1，此时m=0＋1＋2=3；当点B的横坐标为4n=8时，n=2，m=1＋3＋5=9；当点B的横坐标为4n=12时，n=3，m=2＋5＋8=15；…，当点B的横坐标为4n时，m=（n－1）＋（2n－1）＋（3n－1）=6n－3.。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
平度市西关中学八年级数学上册第三章测试题
图形的平移与旋转测试
时间：90分钟满分：120分
一、选择题（每小题3分，共30分）
1. 以下现象：①荡秋千；②呼啦圈；③跳绳；④ 转陀螺.其中是旋转的有 （ ）.
（A ）①② （B ）②③ （C ）③④ （D ）①④
2.下列图形中只能用其中一部分平移可以得到的是 （ ）.
（A ） （B ） （C ） （D ）
3. 下列标志既是轴对称图形又是中心对称图形的是 （ ）.
（A ）（B ）（C ）（D ）
4. 如图1，四边形EFGH 是由四边形ABCD 平移得到的，已知，AD=5，∠B=70°，则
下列说法中正确的是 ( ).
（A ）FG=5,∠G=70°(B)EH=5,∠F=70°
（C ）EF=5，∠F=70°(D)EF=5，∠E=70°
5. 如图3，△OAB 绕点O 逆时针旋转90°到△OCD 的位置，已知∠AOB=45°，则
∠AOD 的度数为 （ ）.
（A ）55° （B ）45° （C ）40° （D ）35°
6. 同学们曾玩过万花筒，它是由三块等宽等长的玻璃片围成的.如图是看到的万花筒的一
个图案，如图3中所有小三角形均是全等的等边三角形，其中的菱形AEFG 可以看
成是把菱形ABCD 以A 为中心 （ ）.
（A ）顺时针旋转60°得到 （B ）逆时针旋转60°得到
（C ）顺时针旋转120°得到 （D ）逆时针旋转120°得到
7. 如图，甲图案变成乙图案，既能用平移，又能用旋转的是 （ ）.
8. 下列图形中，绕某个点旋转180°能与自身重合的图形有 （ ）.
（1）正方形；（2）等边三角形；（3）长方形；（4）角；（5）平行四边形；（6）圆
. （A ）2个 （B ）3个 （C ）4个 （D ）5个
9. 如图4，Rt △ABC 沿直角边BC 所在直线向右平移到Rt △DEF,则下列结论中，错误
的是
（ ）.
（A ）BE=EC
（B ）BC=EF
（C ）AC=DF
（D ）△ABC ≌△DEF
10. 下列这些复杂的图案都是在一个图案的基础上，在“几何画板”软件中拖动一点后
形成的，它们中每一个图案都可以由一个“基本图案”通过连续旋转得来，旋转的
角度正确的是 （）.
（A ）︒30 （B ）︒45 （C ）︒60 （D ）︒90
二、填空题（每小题3分，共30分）
11. 在旋转的过程中，要确定一个图形的旋转后的位置，除了知道原来图形的位置和旋
转方向外，还需要知道和.
12. 如图5所示，右边的图形是左边的图形向右平移格得到的.
13. 如图6，在Rt OAB ∆中，90OAB ∠=︒，6OA AB ==，将OAB ∆绕点O 沿逆时
针方向旋转90︒得到11OA B ∆，则线段1OA 的长是；1AOB
∠的度数是. 14. 下列图形中，不能由图形M 经过一次平移或旋转得到的是.
15. 小明把自己的左手手印和右手手印按在同一张白纸上，左手手印（填“能”或“不
能”）通过旋转与右手手印完全重合在一起.
16. 如图7，已知面积为1的正方形ABCD 的对角线相交于点O ，过点O 任作一条直线
分别交AD BC ，于E F ，，则阴影部分的面积是．
17. 如图8所示，在平面内将Rt △ABC 绕直角顶点C 逆时针旋转90°得到Rt △EFC.
若AB=5,BC=1,则线段BE 的长为．
18. 如图9，P 是正方形ABCD 内一点，将△ABP 绕点B 顺时针方向旋转一定的角度后
能与△CB /P 重合.若PB=3，则P /
P = ．
19. 如图10所示，△ABC 与△111C B A 关于直线m 对称，将△111C B A 向右平移得到△
222C B A , 由此得出下列判断：
（1）AB//22B A ;(2)∠A=∠2A ;(3)AB=22B A ,其中正确有．（填序号）
20.聪聪和亮亮玩一种游戏，他们要将图11（1)和图11（2）中的三角形通过水平或竖直
平移的方法得到图11（3），平移的过程中，每次水平或竖直平移一格，先拼完的为胜， 聪聪选择了图11（1），亮亮选择了图11（2），那么______先获胜.
三、简答题（共60分）
21.（8分）如图12，将四边形ABCD 绕O 点旋转后得到一个四边形，请在图中依次标
上点A ，B ，C ，D 的对应点E ，F ，G ，H ：
22. （10分）如图13，四边形ABCD 是平行四边形，
（1）图中哪些线段可以通过平移而得到；
（2）图中哪些三角形可以通过旋转而得到.
图7
B
23.(10分）如图14，△ABC是等腰直角三角形，BC是斜边，P为△ABC内一点，将△ABP
绕点A逆时针旋转后与△ACP/重合，如果AP=3，那么线段PP/的长是多少？
24.（12分）把正方形ABCD绕着点A，按顺时针方向旋转得到正方形AEFG，边FG与BC
交于点H（如图15）.试问线段HG与线段HB相等吗？请先观察猜想，再说明你的理由.
25.（10分）同学们用直尺和三角板画平行线，这种画平行线的方法利用了怎样的移动？由
此我们得出了什么结论？
26.（10分）请你以“爱护地球，保护地球----植树造林”为题，以等腰三角形为“基本图
形”利用平移设计一组有意义的图案，完成后与同学进行交流．
参考答案
答案提示：
一、选择题
1.D
2.B
3.A
4.B
5.B
6.C
7.B
8.C
9.A 10.C
二、填空题
11. 旋转中心，旋转角 12. 4 13.6，135° 14.③ 15. 能 16.
4
1 17. 7 18. 23 19. （1）（2）（3） 20. 亮亮
三、简答题
21. 略
22.（1）AB 和DC ，AD 和BC ，AO 和OC ，BO 和OD ．
（2）△AOB 和△COD ，△COB 和△AOD ，△CDA 和△ABC ，△ABD 和△CBD.
23. 解：根据旋转的性质可知将△ABP 绕点A 逆时针旋转后与
△ACP /重合△ABP ≌△ACP /,所以AP=AP /,∠BAC=∠PA P /=90°.所以在Rt △APP / 中，P P /=233322=+.
24.解：相等.连接AH ，根据旋转性质，因为AG=AB ，AH=AH ，∠AGH=∠ABH=90°,所以
△AGH ≌△ABH,所以HG=HB.
25. 平移，平行公理：同位角相等两直线平行.
26. 略。