苏教版数学高一《对数函数》名师教案 苏教
苏教版数学高一《对数》名师教案

例如: 问: 这个等式是否成立?
例题讲解
用 , , 表示下列各式。
(1) (2)
求下列各式的值。
(1) (2)
课堂练习
1.计算下列各式的值
(1) (2) (3)
(4) (5)
2.已知 , ,求 。
三、课时小结
通过本节学习,大家应掌握对数运算性质的推导,并能熟练运用对数运算性质进行对数式的化简、求值。
பைடு நூலகம்指数的运算性质
在上式中设 , 则有
将指数式转化为对数式可得:
∴ ( 且 )
这就是对数运算的加法法则,用语言描述为:两个同底对数相加,底不变,真数相乘。
两个同底对数相减
对数运算的减法法则:两个同底对数相减,底不变,真数相除。
根据上述运算法则,多个同底对数相加,底不变,真数相乘,
即
若
则上式可化为
若将 的取值范围扩展为实数集 ,上式是否还会成立?
对数第二课时
主备人:杨伟华
学习目标
一、教学知识点
1.对数的基本性质.
2.对数的运算性质.
(二)能力训练要求
1.进一步熟悉对数的基本性质.
2.熟练运用对数的运算性质.
3.掌握化简,求值的技巧.
一、复习回顾旧知识
二、讲解新课
对数的运算性质
接下来我们用指对数互化的思想,结合指数的运算性质来推导有关对数的运算性质。
四、课后作业
课本P79习题2.7 4.
2.3《对数函数》教案(苏教版必修1)

对数函数课题: 对数的概念 教学目标:1.理解对数的概念,能够进行对数式与指数式的互化;2.渗透应用意识,培养归纳思维能力和逻辑推理能力,提高数学发现能力。
教学重点:对数的概念教学难点:对数与指数的互化 教学过程: 一、问题情境:1.(1)庄子:一尺之棰,日取其半,万世不竭.①取5次,还有多长?②取多少次,还有0.125尺?(2)假设2002年我国国民生产总值为a 亿元,如果每年平均增长8%,那么经过多少年国民生产总值是2002年的2倍?抽象出:1. 421⎪⎭⎫ ⎝⎛=?,x⎪⎭⎫ ⎝⎛21=0.125⇒x=? 2. ()x%81+=2⇒x=?2.问题:已知底数和幂的值,如何求指数?你能看得出来吗?二、学生活动:1.讨论问题,求出后的表达式各是什么? 叫什么?3.研究指数与对数的关系.三、建构数学:1)概括内容,总结对数概念介绍对数的表示方法,底数、真数的含义.2)指数式与对数式的关系.探究:⑴负数与零没有对数. ⑵=1log a ,=a a log . ⑶对数恒等式(教材P58练习6)①=ba a log ; ②=Na alog .⑷两种对数:①常用对数: ; ②自然对数: . (5)底数的取值范围为 ;真数的取值范围为 . 四、数学运用: 1.例题:例1.(例1)将下列指数式改写成对数式: (1)42=16; (2)33-=271; (3)a5=20; (4)b )(21=0.45.例2. (例2)将下列对数式改写成指数式: (1)3125log 5=;(2)31log3=-2;(3)699.1log 10-=a ;(4) (补充)ln10=2.303例3.(例3)求下列各式的值:⑴64log 2; ⑵27log 9; ⑶(补充)()()32log 32-+.2.课堂练习:1)将下列指数式写成对数式:35125= ; 712128-=;2)求下列各式中x 的值:642log 3x =; log 86x =-;3)求下列各式的值: 5log 25 ; 21log 16; lg 10000五、回顾小结:本节课学习了以下内容:⑴对数的定义;⑵指数式与对数式互换;⑶求对数式的值(利用计算器求对数值).六、课外作业: A. B 组 导学练A 组1将下列指数式写成对数式:327a =; 2100.01-=2求下列各式中x 的值:lg 4x =;3ln e x =3.计算:27log 93log 243(2log (2B 组1、填空并给出证明①=b a a log ; ②=Naa log2、已知x a log =2 ;b = x 3,试求ablog x3、设(lgx )2 -lgx + 3a = 0有实根,求a 的取值范围。
高中数学 第26课时《对数函数》教案(4)(学生版 )苏教版必修1

第26课时对数函数(4)【学习导航】学习要求1、进一步巩固对数函数的性质;2、掌握简单的对数不等式求解方法;3、掌握对数函数与恒成立问题。
【精典范例】一、对数不等式的求解方法例1、解关于x的对数不等式;2 log a (x-4)>log a(x-2).思维分析:可以去掉对数符号,化为一般的代数不等式求解;同时考虑到底数a的取值范围不确定,故应进行分类讨论。
二、以对数函数为模型的抽象函数问题例2、已知函数f(x)的定义域是(0,+∞),满足f(4)=1,f(xy)=f(x)+f(y).(1)证明f(1)=0;(2)求f(16);(3)试证f(x n)=nf(x),n∈N*.思维分析:这显然是一个抽象函数。
根据题目给定的三个条件,可以将对数函数y=log4x作为该函数的原型,从而找到问题的解决思路与方法三、对数函数与恒成立问题例3: 已知:()logaf x x=在[3,)+∞上恒有|()|1f x>,求实数a的取值范围。
分析:去掉绝对值符号,转化为含对数式的不等式。
思维点拔:本题的特点是给出了自变量x的取值范围,求字母a的取值范围,它与解不等式有本质的区别,()1f x >在[3,)+∞上恒成立,是指()f x 在[3,)+∞上的所有值都大于1,这是一个不定问题,但转化为函数的最大(最小)值后,问题就简单了,这类问题的一般结论是: (1)()f x m >(m 为常数,x A ∈)恒成立,⇔min (())f x m >(2)()f x M <(M 为常数,x A ∈)恒成立,⇔max (())f x M <利用这两个结论,可以把“不定”问题转化为“定”的问题。
追踪训练1、解不等式.1)21()54(51log log 23<-x2、若函数f(x)满足f(x+y)+f(x -y)=f(x 2-y 2),则f(x)可以是( )A.f(x)=2xB.f(x)=x 2C.f(x)=log 2xD.f(x)=2x3、已知函数f(x)的定义域是(0,+∞),且对任意的x 、y>0满足f(yx)=f(x)-f(y),当x>1时有f(x)<0,试判断f(x)的单调性并证明. 4、已知函数2()3,()(1)f x x g x a x =+=-,当22x -≤≤时,()()f x g x ≥恒成立,求实数a 的取值范围。
苏教版必修一2.3.2《对数函数》word教案3

§2.3对数函数课 题:§2.3.2对数函数⑶教学目标:1.理解底数变化时,对数函数图象变化规律;2.会求含有对数函数的复合函数的单调区间.重点难点:重点——理解底数变化时,对数函数图象变化规律.难点——求含有对数函数的复合函数的单调区间.教学教程:一、问题情境问题1:在同一坐标系中画出函数y=log 2x, y=log 3x, y=lgx,的图象,观察底数的大小对三个图象有何影响?解:a>1时,a 越大,图象在第一象限越靠近x 轴.问题2:在同一坐标系中画出函数y=log 12x, y=log 13x, y=lg 110x,的图象,观察底数的大小对三个图象有何影响?解:0<a<1时,底数a 越小,图象在第四象限越靠近x 轴二、学生活动同组协作,分别作出两个问题中的函数图象,对照图象,思考问题1和问题2.三、运用数学在同一坐标系中,研究底数变化,对数函数的图象变化规律,还可以利用函数y=log a x 与直线y=1的交点(a,1)来判断图象变化情况.例1 如图,所示曲线是对数函数y=log a x 图象,已知a 取3,43,35,110,则对应于C 1,C 2, C 3,C 4的值分别为( ) A.3,43,35,110 B.3,43,110,35 C.43,3,35,110D.43,3,110,35解1:设C 1,C 2,C 3,C 4对应的底数分别为a 1,a 2,a 3,a 4,由图象知a 1,a 2>1,0<a 3,a 4<1∵C 1比C 2更靠近x 轴,∴a 1>a 2∵C 4比C 3更靠近x 轴,∴a 3>a 4∴a 1>a 2>a 3>a 4,即a 1,a 2,a 3,a 4分别为3,43,35,110, 选A.解2:作直线y=1交各个图象于点(a i ,1),由图象知a 1>a 2>a 3>a 4, 选A.例2 已知0<a <b <1,用“<”连接log a b,log b a,log 1b a,log 1a b. 解:∵0<a <b <1 ∴1a >1b >1∴log a b >0,log b a >0,log 1b a <0,log 1a b <0∵log a b <log a a=1, log b a >log b b=1∴log a b <log b a∵log 1b a =-log b a,log 1ab =-log a b,-log a b >-log b a ∴log 1b a <log 1a b ,∴log 1b a <log 1ab <log a b <log b a 例3 求下列函数的单调区间⑴y=log 2(1+x),⑵y=lg(x 2-2x -3),⑶y=log 12(2+x -x 2), 解:⑴∵1+x>0,∴x>-1,此函数定义域(-1,+∞)设t=1+x,则它在(-1,+∞)上单调递增,又∵y=log 2t 在(0,+∞)上单调递增∴f(x)在(-1,+∞)上单调递增⑵∵x 2-2x -3>0,∴x<-1或x>3,此函数定义域(-∞,-1)∪(3,+∞)设t=x 2-2x -3,t ∈(0,+∞),则y=lgt 在(0,+∞)上单调递增 ∵x ∈(-∞,-1)时,t=x 2-2x -3单调递减,∴y=lg(x 2-2x -3)在(-∞,-1)上单调递减,∵x ∈(3,+∞)时,t=x 2-2x -3单调递增,∴y=lg(x 2-2x -3)在(3,+∞)上单调递增,综上y=lg(x 2-2x -3)减区间(-∞,-1),增区间(3,+∞). ⑶∵2+x -x 2>0,∴-1<x<2,此函数定义域(-1,2)设t=2+x -x 2=-(x-12)2+94,t ∈(0,94],则y=l og 12t 在(0,94]上单调递减 ∵x ∈(-1,12]时,t=2+x -x 2单调递增,∴y=log(2+x -x 2)在(-1,12]上单调递减, ∵x ∈[12,2)时,t=2+x -x 2单调递减,∴y=log(2+x -x 2)在[12,2)上单调递增,综上y=log(2+x -x 2)减区间(-1,12],增区间[12,2).四、回顾小结本课学习了1.底数a 变化,对数函数y=logax 图象变化规律;2.求复合函数单调性问题,一般可用换元法.六、课外作业1.P94 复习题172.预习课本P72~73 §2.4幂函数预习题:⑴什么叫幂函数?⑵幂函数的图象是什么?幂函数有哪些性质?江苏省淮州中学曾宁江。
高中数学新苏教版精品教案《苏教版高中数学必修1 3.2 对数函数》8

课时9:对数函数【学习目标】1.理解对数函数的概念,掌握对数函数的图像;2.理解对数函数的性质,掌握对数函数性质的应用。
【学习过程】一自主复习(一)知识梳理1.对数函数的概念:2.对数函数的图象与性质:1 若函数()()()log 101a f x x a a =->≠且的图像恒过定点,则定点的坐标为________2 画出下列函数的图像:(1)2log (4)y x =+ (2)2log 4y x =+(3)2log ()y x =-(4)2log y x = (5)()2log 2y x =+ (6)lg y x =3 函数()3log 4y x =-的定义域为___________________;值域为__________________4 若函数()()log 01a f x x a =<<在区间[],2a a 上的最大值是最小值的3倍,则a 的值为________5 已知函数()22()log 23f x x x =+-,则此函数的单调递增区间是___________二合作探究题型一:对数函数的图像及其应用例1.(1) 对数函数的图象过点()16,4M ,则此对数函数的解析式为(2)2log 5 2log 8; 1.1log 0.7 1.2log 0.7;(3)方程2log (4)20x x +-=的根的个数为点拨提升:题型二:对数函数的性质及其应用(一)定义域和值域例2.求下列函数的定义域、值域:(1)()22log 32y x x =--(2)0.31log 2y x =-(3)()2log 31x y =+(4))log 01a y a a =>≠且点拨提升:(二)单调性例3.(1)若函数()22log (21)f x x ax a =-++在区间(],1-∞上递减,则a 的取值范围为 .(2)已知函数()log (3)a f x ax =-①当[]0,2x ∈时,函数()f x 恒有意义,求实数a 的取值范围.②是否存在这样的实数a ,使得函数()f x 在区间[]1,2上为减函数,并且最大值为1?如果存在,试求出a 的值;如果不存在,请说明理由.点拨提升:课时9: 对数函数例1变式1:已知函数2()log f x x =,正实数,m n 满足m n ≠且()()f m f n =,则mn =变式2:已知函数lg ,010()16,102x x f x x x ⎧<≤⎪=⎨-+>⎪⎩,若,,a b c 互不相等,且()()()f a f b f c ==,则abc 的取值范围为例2变式1:求函数2()lg(21)f x x x =++的定义域.变式2:已知函数2()lg(21)f x ax x =++,若定义域为R ,求a 的取值范围变式3:已知函数2()lg(21)f x ax x =++,若值域为R ,求a 的取值范围变式4:求函数()21122()log 2log 524f x x x x ⎛⎫=-+≤≤ ⎪⎝⎭的值域.例3变式1:已知函数()22log (3)f x x ax =+-在1 2(,)上单调递增,则实数a 的取值范围为变式2:已知函数()log (2)a f x ax =-,是否存在这样的实数a ,使得函数()f x 在区间[]0,1上是关于x 的减函数?若存在,求出a 的取值范围;若不存在,请说明理由.思考: (1)关于函数21()lg (0,)||x f x x x R x +=≠∈ ,有下列命题,其中正确命题的序号为 . ①函数()y f x = 的图象关于轴对称;②在区间-0∞(,)上,函数()y f x =是减函数;③函数()f x 的最小值为lg2; ④在区间1+∞(,)上,函数()y f x =是减函数 (2)已知()[]32log ,1,9f x x x =+∈,求函数()()22y f x f x =+⎡⎤⎣⎦的最大值及y 取得最大值时的x 的值.【巩固练习】1 已知函数()lg f x x =,若实数,m n 满足m n ≠且()()f m f n =,则m n +的取值范围为________.2 函数12()ln 1x f x x x =+-的定义域为________________. 3 若函数()()log 1a f x x a =>在区间[],2a a 上的最大值与最小值之差为12,则a 的值为________. 4 函数()24()log log 2442x x f x x =⋅≤≤的值域为________________. 5已知()()()2ln 220f x x ax a a =-+->,若()f x 在[)1,+∞上是增函数,则a 的取值范围是___________________. 6 已知函数()()log (1)01x a f x a a a =->≠且(1)求函数()f x 的定义域;(2)判断函数()f x 的单调性.【自我评价】A 完全掌握();B 大部分掌握();C 懂了一点点();D 完全不懂()。
对数函数教案1苏教版必修1
对数函数【同步教育信息】一. 本周教学内容:对数以及对数函数 二. 教学目标:1. 理解对数的概念,了解对数运算与指数运算的互逆关系。
2. 能正确利用对数性质进行对数运算。
3. 掌握对数函数的图象性质。
4. 理解指数函数与对数函数的互逆关系。
三. 重点、难点: 1. 对数(1)对数恒等式① b a ba =log (10≠<a )② N aNa =log③ 1log =a a④ 01log =a(2)对数的运算性质对于10≠<a ,M 0>,N 0>,则 ① N M MN a a a log log )(log += ② N M NMa a alog log log -= ③ M n M a na log log =(R n ∈)【典型例题】[例1] 计算:(1)5lg 2lg 100lg 5lg 20lg 50lg 2lg -+(2)4log ]18log 2log )3log 1[(66626÷⋅+-解:(1)原式)2lg 1(2lg 2)2lg 1)(2lg 1()2lg 2(2lg ---++-= 1)2(lg 22lg 2)2(lg 1)2(lg 2lg 2222=+--+-=(2)原式4log )]3log 1)(3log 1()3(log 3log 21[666266÷+-++-= 4log ])3(log 1)3(log 3log 21[626266÷-++-=12log 2log 2log )3log 1(266266==÷-=[例2] 已知正实数x 、y 、z 满足zyx643==,试比较x 3、y 4、z 6的大小。
解:设t zy x ===643(1>t ),则t x 3log =,t y 4log =,t z 6log =,从而4lg lg 43lg lg 3log 4log 34343t t t t y x -=-=-4lg 3lg 3lg 44lg 3lg ⋅-=t 0)3lg 4(lg 4lg 3lg lg 43<-⋅=t故y x 43<又由6lg 4lg )4lg 36lg 2(lg 2)6lg lg 34lg lg 2(2)log 3log 2(26464⋅-=-=-=-t t t t t z y 6lg 4lg )4lg 6(lg lg 232⋅-=t而0lg >t ,04lg >,06lg >,324lg 6lg <,则上式0< 故z y 64<,综上z y x 643<<[例3] 已知m 和n 都是不等于1的正数,并且5log 5log n m >,试确定m 和n 的大小关系。
高中数学 2.3《对数函数》教案十 苏教版必修1

教学目标:使学生掌握对数的换底公式,并能解决有关的化简、求值、证明问题;培养培养观察分析、抽象概括能力、归纳总结能力、逻辑推理能力.教学重点:换底公式及推论.教学难点:换底公式的证明和灵活应用.教学过程:教学过程:Ⅰ.复习回顾对数的运算法则若a >0,a ≠1,M >0,N >0,则(1)log a (MN )=log a M +log a N ; (2)lo g a M N =log a M -log a N ;(3)log a M n=n log a M (n ∈R )Ⅱ.讲授新课1.对数换底公式: log a N =log m Nlog m a(a >0,a ≠1,m >0 ,m ≠1,N >0)证明:设log a N =x , 则 a x=N两边取以m 为底的对数:log m a x=log m N ⇒x log m a =log m N从而得:x =log m Nlog m a ∴ log a N =log m Nlog m a2.两个常用的推论:① log a b ·log b a =1② log m a b n =nm log a b ( a 、b >0且均不为1)证:①log a b ·log b a =lg b lg a lg algb =1②log m a b n =lg b nlg a m =n lg bm lg a=nm log a bⅢ.例题分析例1 已知 log 23=a , log 37=b , 用 a , b 表示log 4256解:因为log 23=a ,则1a =log 32 , 又∵log 37=b ,∴log 4256=log 356log 342 =log 37+3log 32log 37+log 32+1 =ab +3ab +b +1例2计算:① 53log 12.0- ② log 43·log 92-log 21432解:①原式=15315555531log 3log 52.0===②原式=12 log 23·12 log 32+54 log 22=14 +54 =32例3设 x 、y 、z ∈(0,+∞)且3x =4y =6z1︒ 求证 1x +12y =1z; 2︒ 比较3x ,4y ,6z 的大小 证明1︒:设3x =4y =6z =k ∵x 、y 、z ∈(0,+∞) ∴k >1取对数得:x =lg k lg 3 , y =lg k lg4 , z =lg k lg 6∴1x +12y =lg 3lg k +lg 42lg k =2lg 3+lg42lg k =2lg 3+2lg22lg k =lg 6lg k =1z2︒ 3x -4y =(3lg 3 -4lg 4 )lg k =lg64-lg81lg 3lg4 lg k =lg k ·lg 6481 lg 3lg4<0 ∴3x <4y又:4y -6z =(4lg 4 -6lg 6 )lg k =lg36-lg64lg 2lg6 lg k =lg k ·lg 916 lg 2lg6<0 ∴4y <6z ∴3x <4y <6z例4已知log a x =log a c +b ,求x分析:由于x 作为真数,故可直接利用对数定义求解;另外,由于等式右端为两实数和的形式,b 的存在使变形产生困难,故可考虑将log a c 移到等式左端,或者将b 变为对数形式解法一:由对数定义可知:b c a a x+=log b c a a a ⋅=log b a c ⋅= 解法二:由已知移项可得log a x -log a c =b , 即log a x c =b由对数定义知:x c =a b ∴x =c ·a b解法三:∵b =log a a b ∴log a x =log a c +log a a b =l og a c ·a b ∴x =c ·a bⅣ.课堂练习①已知 log 189=a , 18b =5 , 用 a , b 表示log 3645解:∵log 189=a ∴log 18182=1-log 182=a ∴log 182=1-a ∵18b =5 ∴ log 185=b∴log 3645=log 1845log 1836 =log 189+log 1851+log 182 =a +b 2-a②若log 83=p ,log 35=q , 求 lg5解:∵log 83=p ∴3log 32 =p ⇒log 23=3p ⇒log 32=13p又∵log 35=q ∴ lg5=log 35log 310 =log 35log 32+log 35 =3pq 1+3pqⅤ.课时小结本节课学习了以下内容:换底公式及其推论 Ⅵ.课后作业1.证明:b xxa ab a log 1log log += 证法1: 设 p x a =log ,q x ab =log ,r b a =log 则:p a x = q q q b a ab x ==)( r a b = ∴)1()(r q q p a ab a +== 从而 )1(r q p += ∵ 0≠q ∴r q p+=1 即:b x xa ab a log 1log log +=(获证)证法2: 由换底公式 左边=b ab aabx xa a x x ab a log 1log log log log log +====右边2.已知λ====n a a a b b b n log log log 2121 求证:λ=)(log 2121n a a a b b b n证明:由换底公式 λ====nn a b a b a b lg lg lg lg lg lg 2211由等比定理得:λ=++++++n n a a a b b b lg lg lg lg lg lg 2121 ∴λ=)lg()lg(2121n n a a a b b b∴λ==)lg()lg()(log 21212121n n n a a a a a a b b b b b b n。
苏教版数学高一《对数函数》精品学案

2.3.2对数函数第1课时
【教师活动】
【教学目标】
1.掌握对数函数的概念,熟悉对数函数的图象和性质;
2.通过观察对数函数的图象,发现并归纳对数函数的性质;
3.培养学生数形结合的思想以及分析推理的能力.
【教学重难点】
重点:理解对数函数的定义,初步掌握对数函数的图象和性质.
⑴ ;⑵ ;⑶ .
2.练习:课本P69-1,2,3,4.
【课堂小结】(1)对数函数的概念、图象和性质;(2)求定义域;(3)利用单调性比较大小.反思】
难点:底数a对图象的影响及对对数函数性质的作用.
【教学设想】(【教学准备】)
多媒体
【教学活动】(【教学流程】)
1.问题情境
2.师生互动
3.建构数学概念
4.举例应用
5.课堂练习
6.小结作业
【教学反思】
【学生活动】
【学习目标】
掌握对数函数的概念,熟悉对数函数的图像和性质。
【课时安排】1课时
【学法点拨】
观察对数图像,发现并归纳对数的性质。
【课堂探究】一、问题情境
在细胞分裂问题中,细胞个数y是分裂次数x的指数函数y=2x.因此,知道x的值(输入值是分裂的次数),就能求出y的值(输出值是细胞个数).反之,知道了细胞个数y,如何确定分裂次数x?x=log2y.在这里,x与y之间是否存在函数的关系呢?
同样地,前面提到的放射性物质,经过的时间x(年)与物质的剩余量y的关系为y=0.84x.反之,写成对数式为x=log0.84y.
二、学生活动
三、建构数学
1.对数函数的定义:
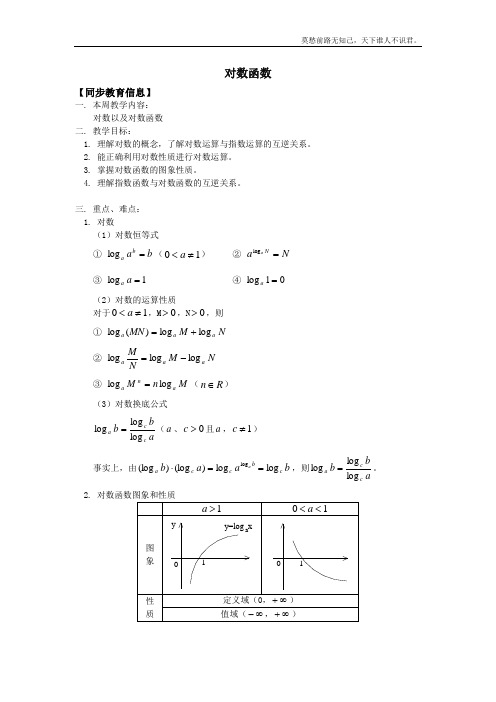
2.对数函数y= logax(a>0且a≠1)的图像特征和性质.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
a
a>1
0<a<1
图像
定义域
值域
性
质
(1)恒过定点:
(2)当x>1时,
当0<x<1时,
当x>1时,
当0<x<1时,
(3)在上是函数
在上是函数
3.对数函数y= logax(a>0且a≠1)与指数函数y=ax(a>0且a≠1)的关系——互为反函数.
四、数学运用
1.例题.
例1求下列函数的定义域:
(1) ;(2) ;
变式:求函数 的定义域.
例2比较大小:
(1) ; (2) ;(3) .
2.练习:
课本P69-1,2,3,4.
五、要点归纳与方法小结
(1)对数函数的概念、图象和性质;
(2)求定义域;
(3)利用单调性比较大小.
六、作业
课本P70习题2,3,4.
二、学生活动
1.回顾指数与对数的关系;引出对数函数的定义,给出对数函数的定义域
2.通过观察对数函数的图象,发现并归纳对数函数的性质.
3.类比指数函数的定义、图象、性质得到对数函数的定义、图象、性质.
三、建构数学
1.对数函数的定义:一般地,当a>0且a≠1时,函数y=logax叫做对数函数,自变量是x;函数的定义域是(0,+∞).
一、问题情境
在细胞分裂问题中,细胞个数y是分裂次数x的指数函数y=2x.因此,知道x的值(输入值是分裂的次数),就能求出y的值(输出值是细胞个数).
反之,知道了细胞个数y,如何确定分裂次数x?x=log2y.
在这里,x与y之间是否存在函数的关系呢?
同样地,前面提到的放射性物质,经过的时间x(年)与物质的剩余量y的关系为y=0.84x.反之,写成对数式为x=log0.84y.
2.3.2对数函数(1)
教学目标:
1.掌握对数函数的概念,熟悉对数函数的图象和性质;
2.通过观察对数函数的图象,发现并归纳对数函数的性质;
3.培养学生数形结合的思想以及分析推理的能力.
教学重点:
理解对数函数的定义,初步掌握对数函数的图象和性质.
教学难点:
底数a对图象的影响及对对数函数性质的作用.
教学过程:
