江苏省无锡市西漳中学2019-2020学年第一学期初三第十三周周末卷(无答案)
2019-2020学年江苏省无锡市九年级(上)期中数学试卷 (解析版)

2019-2020学年江苏省无锡市九年级(上)期中数学试卷一、选择题(共10小题).1.(4分)已知O 的半径为4cm ,点P 在O 上,则OP 的长为( ) A .1cm B .2cmC .4cmD .8cm2.(4分)若37a b =,则b aa-等于( ) A .34B .43C .73D .373.(4分)二次函数223y x x =-+图象的对称轴是( ) A .直线1x =B .直线1x =-C .直线2x =D .直线2x =-4.(4分)如图,在O 中,点M 是AB 的中点,连结MO 并延长,交O 于点N ,连结BN ,若140AOB ∠=︒,则N ∠的度数为( )A .70︒B .40︒C .35︒D .20︒5.(4分)在一个不透明的口袋里装有2个白球,3个黑球和3个红球,它们除颜色外其余都相同,现随机从袋里摸出1个球,则摸出白球的概率是( ) A .12B .38C .13D .146.(4分)如图,由六段相等的圆弧组成的三叶花,每段圆弧都是四分之一圆周,2OA OB OC ===,则这朵三叶花的面积为( )A .33π-B .36π-C .63π-D .66π-7.(4分)已知点C 在线段AB 上,且点C 是线段AB 的黄金分割点()AC BC >,则下列结论正确的是( ) A .2AB AC BC =B .2BC AC BC =C .512AC BC -=D .512BC AC -= 8.(4分)如图,AB 是半圆的直径,点C 是弧AB 的中点,点E 是弧AC 的中点,连结EB 、CA 交于点F ,则EFBF的值为( )A .14B .224- C .212-D .212- 9.(4分)如图,已知抛物线2y x bx c =++与直线y x =交于(1,1)和(3,3)两点,现有以下结论:①240b c ->; ②360b c ++=; ③当22x bx c x++>时,2x >; ④当13x <<时,2(1)0x b x c +-+<, 其中正确的序号是( )A .①②④B .②③④C .②④D .③④10.(4分)若平面直角坐标系内的点M 满足横、纵坐标都为整数,则把点M 叫做“整点”.例如:(1,0)P 、(2,2)Q -都是“整点”.抛物线221(0)y mx mx m m =-+->与x 轴交于A 、B 两点,若该抛物线在A 、B 之间的部分与线段AB 所围成的区域(包括边界)恰有6个整点,则m 的取值范围是( ) A .1184mB .1194m< C .1192m < D .1194m <<二、填空题(共6小题,每小题5分,满分30分)11.(5分)已知线段c 是线段a 、b 的比例中项,且4a =,9b =,则线段c 的长度为 .12.(5分)小颖在二次函数2245y x x =++的图象上找到三点1(1,)y -,1(2,2)y ,1(32-,3)y ,则你认为1y ,2y ,3y 的大小关系应为 .13.(5分)如图,水库堤坝的横断面是梯形,测得BC 长为30m ,CD 长为205m ,斜坡AB 的坡比为1:3,斜坡CD 的坡比为1:2,则坝底的宽AD 为 m .14.(5分)如图,O 的半径为1,正方形ABCD 顶点B 坐标为(5,0),顶点D 在O 上运动,则正方形面积最大时,正方形与O 重叠部分的面积是 .15.(5分)如图,在矩形ABCD 中,6AB =,8AD =,E 是BC 上的一动点(不与点B 、C 重合).连接AE ,过点D 作DF AE ⊥,垂足为F ,则线段BF 长的最小值为 .16.(5分)如图,ABCD 的对角线AC ,BD 交于点O ,CE 平分BCD ∠交AB 于点E ,交BD 于点F ,且60ABC ∠=︒,2AB BC =,连接OE .下列结论:①EO AC ⊥;②4AOD OCF S S ∆∆=;③:21:7AC BD =;④2FB OF DF =.其中正确的结论有 (填写所有正确结论的序号)三、解答题(共8小题,满分80分)17.(8分)如图,直线123////l l l ,直线AC 依次交1l 、2l 、3l 于A 、B 、C 三点,直线DF依次交1l 、2l 、3l 于D 、E 、F 三点,若47AB AC =,2DE =,求EF 的长.18.(8分)下表给出了代数式2x bx c -++与x 的一些对应值:x⋯ 2- 1- 0 1 2 3 ⋯ 2x bx c -++ ⋯5nc23-10-⋯(1)根据表格中的数据,确定b ,c ,n 的值;(2)设2y x bx c =-++,直接写出02x 时y 的最大值.19.(8分)随着经济的快速发展,环境问题越来越受到人们的关注,某校学生会为了解节能减排、垃圾分类知识的普及情况,随机调查了部分学生,调查结果分为“非常了解”“了解”“了解较少”“不了解”四类,并将调查结果绘制成下面两个统计图.(1)本次调查的学生共有 人,估计该校1200名学生中“不了解”的人数是 人; (2)“非常了解”的4人有1A ,2A 两名男生,1B ,2B 两名女生,若从中随机抽取两人向全校做环保交流,请利用画树状图或列表的方法,求恰好抽到一男一女的概率. 20.(8分)如图,在锐角三角形ABC 中,点D ,E 分别在边AC ,AB 上,AG BC ⊥于点G ,AF DE ⊥于点F ,EAF GAC ∠=∠.(1)求证:ADE ABC ∆∆∽; (2)若3AD =,5AB =,求AFAG的值.21.(10分)如图,ABC ∆内接于O ,AB AC =,36BAC ∠=︒,过点A 作//AD BC ,与ABC ∠的平分线交于点D ,BD 与AC 交于点E ,与O 交于点F . (1)求DAF ∠的度数; (2)求证:2AE EF ED =; (3)求证:AD 是O 的切线.22.(12分)某商场将每件进价为80元的A 商品按每件100元出售,一天可售出128件.经过市场调查,发现这种商品的销售单价每降低1元,其日销量可增加8件.设该商品每件降价x 元,商场一天可通过A 商品获利润y 元.(1)求y 与x 之间的函数解析式(不必写出自变量x 的取值范围) (2)A 商品销售单价为多少时,该商场每天通过A 商品所获的利润最大? 23.(12分)定义:我们知道,四边形的一条对角线把这个四边形分成了两个三角形,如果这两个三角形相似(不全等),我们就把这条对角线叫做这个四边形的“相似对角线”. 理解:(1)如图1,已知Rt ABC ∆在正方形网格中,请你只用无刻度的直尺在网格中找到一点D ,使四边形ABCD 是以AC 为“相似对角线”的四边形(保留画图痕迹,找出3个即可); (2)如图2,在四边形ABCD 中,80ABC ∠=︒,140ADC ∠=︒,对角线BD 平分ABC ∠. 求证:BD 是四边形ABCD 的“相似对角线”;(3)如图3,已知FH 是四边形EFGH 的“相似对角线”, 30EFH HFG ∠=∠=︒,连接EG ,若EFG ∆的面积为3,求FH 的长.24.(14分)在平面直角坐标系xOy 中,一块含60︒角的三角板作如图摆放,斜边AB 在x 轴上,直角顶点C 在y 轴正半轴上,已知点(1,0)A -.(1)请直接写出点B 、C 的坐标:B 、C ;并求经过A 、B 、C 三点的抛物线解析式;(2)现有与上述三角板完全一样的三角板DEF (其中90EDF ∠=︒,60)DEF ∠=︒,把顶点E 放在线段AB 上(点E 是不与A 、B 两点重合的动点),并使ED 所在直线经过点C .此时,EF 所在直线与(1)中的抛物线交于点M .①设AE x =,当x 为何值时,OCE OBC ∆∆∽;②在①的条件下探究:抛物线的对称轴上是否存在点P 使PEM ∆是等腰三角形?若存在,请写出点P 的坐标;若不存在,请说明理由.参考答案一、选择题(共10小题,每小题4分,满分40分)1.(4分)已知O 的半径为4cm ,点P 在O 上,则OP 的长为( ) A .1cmB .2cmC .4cmD .8cm解:点P 在O 上, 4OP cm ∴=.故选:C . 2.(4分)若37a b =,则b aa-等于( ) A .34B .43C .73D .37解:设37a bk ==, 3a k ∴=,7b k =, ∴73433b a k k a k --==. 故选:B .3.(4分)二次函数223y x x =-+图象的对称轴是( ) A .直线1x =B .直线1x =-C .直线2x =D .直线2x =-解:已知1a =,2b =-,3c = 由对称轴公式可知,对称轴是12bx a=-=. 故选:A .4.(4分)如图,在O 中,点M 是AB 的中点,连结MO 并延长,交O 于点N ,连结BN ,若140AOB ∠=︒,则N ∠的度数为( )A .70︒B .40︒C .35︒D .20︒解:点M 是AB 的中点, ∴AM BM =,140AOB ∠=︒,1702BOM AOB ∴∠=∠=︒, 1352N BOM ∴∠=∠=︒, 故选:C .5.(4分)在一个不透明的口袋里装有2个白球,3个黑球和3个红球,它们除颜色外其余都相同,现随机从袋里摸出1个球,则摸出白球的概率是( ) A .12B .38C .13D .14解:口袋里装有2个白球,3个黑球和3个红球, ∴口袋里共有8个球, ∴摸出白球的概率是2184=; 故选:D .6.(4分)如图,由六段相等的圆弧组成的三叶花,每段圆弧都是四分之一圆周,2OA OB OC ===,则这朵三叶花的面积为( )A .33π-B .36π-C .63π-D .66π-解:如图所示:弧OA 是M 上满足条件的一段弧,连接AM 、MO , 由题意知:90AMO ∠=︒,AM OM = 2AO =,2AM ∴=.21142AMO S MA ππ=⨯⨯=扇形. 112AMO S AM MO ∆==,112AO S π∴=-弓形,1612S π⎛⎫∴=⨯- ⎪⎝⎭三叶花36π=-.故选:B .7.(4分)已知点C 在线段AB 上,且点C 是线段AB 的黄金分割点()AC BC >,则下列结论正确的是( ) A .2AB AC BC =B .2BC AC BC =C .512AC BC -=D .512BC AC -= 解:点C 是线段AB 的黄金分割点且AC BC >, ∴512BC AC AC AB -==,即2AC BC AB =,故A 、B 错误; 512AC AB -=,故C 错误; 512BC AC -=,故D 正确; 故选:D .8.(4分)如图,AB 是半圆的直径,点C 是弧AB 的中点,点E 是弧AC 的中点,连结EB 、CA 交于点F ,则EFBF的值为( )A .14B .224- C .212-D .212- 解:连接AE ,BC ,连接OE 交AC 于H ,点E 是弧AC 的中点, OE AC ∴⊥,AB 是半O 的直径, BC AC ∴⊥, //OE BC ∴, EHF BCF ∴∆∆∽, ∴EF EHBF BC=, 设2BC x =,则2OE OB x ==, OH x ∴=,(21)EH x =-, ∴(21)2122EF EH x BF BC x --===, 故选:D .9.(4分)如图,已知抛物线2y x bx c =++与直线y x =交于(1,1)和(3,3)两点,现有以下结论:①240b c ->; ②360b c ++=; ③当22x bx c x++>时,2x >; ④当13x <<时,2(1)0x b x c +-+<, 其中正确的序号是( )A .①②④B .②③④C .②④D .③④解:函数2y x bx c =++与x 轴无交点, 240b ac ∴-<; 240b c ∴-<故①不正确;当3x =时,933y b c =++=,即360b c ++=; 故②正确;把(1,1)(3,3)代入2y x bx c =++,得抛物线的解析式为233y x x =-+, 当2x =时,2331y x x =-+=,21y x==, 抛物线和双曲线的交点坐标为(2,1) 第一象限内,当2x >时,22x bx c x ++>; 或第三象限内,当0x <时,22x bx c x ++>; 故③错误;当13x <<时,二次函数值小于一次函数值, 2x bx c x ∴++<,2(1)0x b x c ∴+-+<.故④正确; 故选:C .10.(4分)若平面直角坐标系内的点M 满足横、纵坐标都为整数,则把点M 叫做“整点”.例如:(1,0)P 、(2,2)Q -都是“整点”.抛物线221(0)y mx mx m m =-+->与x 轴交于A 、B 两点,若该抛物线在A 、B 之间的部分与线段AB 所围成的区域(包括边界)恰有6个整点,则m 的取值范围是( ) A .1184mB .1194m< C .1192m < D .1194m <<解:由已知可得2221(1)1y mx mx m m x =-+-=--, ∴函数的顶点是(1,1)-,∴点(1,1)-,(1,0)必在抛物线在A ,B 之间的部分与线段AB 所围成的区域(包括边界)的区域内,又在此区域内有6个整点,∴必有点(1,0)-,(0,0),(2,0),(3,0), ∴当点(1,0)-在边界上时,14m =, 当点(2,0)-在边界上时,19m =2(1)1y m x =--与x 轴的交点A 的横坐标21A x -<-,∴1194m<, 故选:B .二、填空题(共6小题,每小题5分,满分30分)11.(5分)已知线段c 是线段a 、b 的比例中项,且4a =,9b =,则线段c 的长度为 6 . 解:根据比例中项的概念结合比例的基本性质,得:比例中项的平方等于两条线段的乘积. 所以249c =⨯,解得6c =±(线段是正数,负值舍去), 故答案为:6.12.(5分)小颖在二次函数2245y x x =++的图象上找到三点1(1,)y -,1(2,2)y ,1(32-,3)y ,则你认为1y ,2y ,3y 的大小关系应为 123y y y << .解:抛物线的对称轴为直线4122x =-=-⨯, 而抛物线开口向上,点1(1,)y -在对称轴上,点1(2,2)y 比点1(32-,3)y 离对称轴要近,所以123y y y <<. 故答案为123y y y <<.13.(5分)如图,水库堤坝的横断面是梯形,测得BC 长为30m ,CD 长为5m ,斜坡AB 的坡比为1:3,斜坡CD 的坡比为1:2,则坝底的宽AD 为 130 m .解:作BE AD ⊥于E ,CF AD ⊥于F , 斜坡CD 的坡比为1:2,即12CF DF =, 2DF CF ∴=,又205CD m =,20CF m ∴=,40DF m =,由题意得,四边形BEFC 是矩形, 20BE CF m ∴==,30EF BC m ==,斜坡AB 的坡比为1:3, ∴13BE AE =,即360AE BE m ==, 130AD AE EF DF m ∴=++=,故答案为:130m .14.(5分)如图,O 的半径为1,正方形ABCD 顶点B 坐标为(5,0),顶点D 在O 上运动,则正方形面积最大时,正方形与O 重叠部分的面积是12π+ .解:如图所示,当点D 运动到(1,0)-时,BD 最长,此时,正方形面积最大,45CDO ∠=︒, 45CDO ∴∠=︒,又45FDO ∠=︒, CD ∴经过点F ,同理可得,AD 经过点E ,∴正方形与O 重叠部分的面积是DEF ∆的面积与半圆面积的和,即21112111222ππ⨯⨯+⨯⨯=+, 故答案为:12π+.15.(5分)如图,在矩形ABCD 中,6AB =,8AD =,E 是BC 上的一动点(不与点B 、C 重合).连接AE ,过点D 作DF AE ⊥,垂足为F ,则线段BF 长的最小值为 2134- .解:如图,AE DF ⊥, 90AFD ∴∠=︒,∴点F 的运动轨迹是以AD 为直径的O ,连接OB ,OF .四边形ABCD 是矩形, 90BAO ∴∠=︒, 6AB =,4AO =,22213OB AB AO ∴=+=,142FO AD ==, BF OB OF -,BF ∴的最小值为2134-,故答案为2134-.16.(5分)如图,ABCD 的对角线AC ,BD 交于点O ,CE 平分BCD ∠交AB 于点E ,交BD 于点F ,且60ABC ∠=︒,2AB BC =,连接OE .下列结论:①EO AC ⊥;②4AOD OCF S S ∆∆=;③:21:7AC BD =;④2FB OF DF =.其中正确的结论有 ①③④ (填写所有正确结论的序号)解:四边形ABCD 是平行四边形, //CD AB ∴,OD OB =,OA OC =, 180DCB ABC ∴∠+∠=︒, 60ABC ∠=︒, 120DCB ∴∠=︒, EC 平分DCB ∠,1602ECB DCB ∴∠=∠=︒, 60EBC BCE CEB ∴∠=∠=∠=︒, ECB ∴∆是等边三角形, EB BC ∴=, 2AB BC =,EA EB EC ∴==, 90ACB ∴∠=︒, OA OC =,EA EB =, //OE BC ∴,90AOE ACB ∴∠=∠=︒, EO AC ∴⊥,故①正确, //OE BC , OEF BCF ∴∆∆∽, ∴12OE OF BC FB ==, 13OF OB ∴=,3AOD BOC OCF S S S ∆∆∆∴==,故②错误,设BC BE EC a ===,则2AB a =,3AC a =,2237()22OD OB a a a ==+=, 7BD a ∴=,:3:721:7AC BD a a ∴==,故③正确,1736OF OB a ==,73BF a ∴=, 2279BF a ∴=,27777()6269OF DF a a a a =+=, 2BF OF DF ∴=,故④正确,故答案为①③④.三、解答题(共8小题,满分80分)17.(8分)如图,直线123////l l l ,直线AC 依次交1l 、2l 、3l 于A 、B 、C 三点,直线DF 依次交1l 、2l 、3l 于D 、E 、F 三点,若47AB AC =,2DE =,求EF 的长.解:123////l l l ,直线AC 依次交1l 、2l 、3l 于A 、B 、C 三点,直线DF 依次交1l 、2l 、3l 于D 、E 、F 三点, ∴AB DEAC DF=, 47AB AC =,2DE =, ∴427DF=, 解得: 3.5DF =,3.52 1.5EF DF DE ∴=-=-=.18.(8分)下表给出了代数式2x bx c -++与x 的一些对应值:x⋯ 2- 1- 0 1 2 3 ⋯ 2x bx c -++ ⋯5nc23-10-⋯(1)根据表格中的数据,确定b ,c ,n 的值;(2)设2y x bx c =-++,直接写出02x 时y 的最大值. 解:(1)根据表格数据可得42512b c b c --+=⎧⎨-++=⎩,解得25b c =-⎧⎨=⎩,2225x bx c x x ∴-++=--+,当1x =-时,2256x x --+=,即6n =;(2)根据表中数据得当02x 时,y 的最大值是5.19.(8分)随着经济的快速发展,环境问题越来越受到人们的关注,某校学生会为了解节能减排、垃圾分类知识的普及情况,随机调查了部分学生,调查结果分为“非常了解”“了解”“了解较少”“不了解”四类,并将调查结果绘制成下面两个统计图.(1)本次调查的学生共有 50 人,估计该校1200名学生中“不了解”的人数是 人; (2)“非常了解”的4人有1A ,2A 两名男生,1B ,2B 两名女生,若从中随机抽取两人向全校做环保交流,请利用画树状图或列表的方法,求恰好抽到一男一女的概率. 解:(1)48%50÷=(人),1200(140%22%8%)360⨯---=(人);故答案为:50,360;(2)画树状图,共有12种可能的结果,恰好抽到一男一女的结果有8个, P ∴(恰好抽到一男一女的)82123==.20.(8分)如图,在锐角三角形ABC 中,点D ,E 分别在边AC ,AB 上,AG BC ⊥于点G ,AF DE ⊥于点F ,EAF GAC ∠=∠.(1)求证:ADE ABC ∆∆∽; (2)若3AD =,5AB =,求AFAG的值.解:(1)AG BC ⊥,AF DE ⊥,90AFE AGC ∴∠=∠=︒, EAF GAC ∠=∠, AED ACB ∴∠=∠, EAD BAC ∠=∠,ADE ABC ∴∆∆∽,(2)由(1)可知:ADE ABC ∆∆∽, ∴35AD AE AB AC == 由(1)可知:90AFE AGC ∠=∠=︒, EAF GAC ∴∠=∠, EAF CAG ∴∆∆∽, ∴AF AEAG AC =, ∴35AF AG = 另解:AG BC ⊥,AF DE ⊥,ADE ABC ∆∆∽, ∴35AF AD AG AB == 21.(10分)如图,ABC ∆内接于O ,AB AC =,36BAC ∠=︒,过点A 作//AD BC ,与ABC ∠的平分线交于点D ,BD 与AC 交于点E ,与O 交于点F . (1)求DAF ∠的度数; (2)求证:2AE EF ED =; (3)求证:AD 是O 的切线.【解答】(1)解://AD BC ,D CBD ∴∠=∠,AB AC =,36BAC ∠=︒,1(180)722ABC ACB BAC ∴∠=∠=⨯︒-∠=︒, 72AFB ACB ∴∠=∠=︒,BD 平分ABC ∠,11723622ABD CBD ABC ∴∠=∠=∠=⨯︒=︒,36D CBD ∴∠=∠=︒,1801803636108BAD D ABD ∴∠=︒-∠-∠=︒-︒-︒=︒, 180180367272BAF ABF AFB ∠=︒-∠-∠=︒-︒-︒=︒, 1087236DAF DAB FAB ∴∠=∠-∠=︒-︒=︒;(2)证明:36CBD ∠=︒,FAC CBD ∠=∠, 36FAC D ∴∠=︒=∠,AED AEF ∠=∠, AEF DEA ∴∆∆∽, ∴AE EDEF AE=, 2AE EF ED ∴=⨯;(3)证明:连接OA 、OF ,36ABF ∠=︒,272AOF ABF ∴∠=∠=︒, OA OF =,1(180)542OAF OFA AOF ∴∠=∠=⨯︒-∠=︒, 由(1)知36DAF ∠=︒, 365490DAO ∴∠=︒+︒=︒,即OA AD ⊥, OA 为半径,AD ∴是O 的切线.22.(12分)某商场将每件进价为80元的A 商品按每件100元出售,一天可售出128件.经过市场调查,发现这种商品的销售单价每降低1元,其日销量可增加8件.设该商品每件降价x 元,商场一天可通过A 商品获利润y 元.(1)求y 与x 之间的函数解析式(不必写出自变量x 的取值范围)(2)A 商品销售单价为多少时,该商场每天通过A 商品所获的利润最大?解:(1)由题意得,商品每件降价x 元时单价为(100)x -元,销售量为(1288)x +件, 则2(1288)(10080)8322560y x x x x =+--=-++,即y 与x 之间的函数解析式是28322560y x x =-++;(2)2283225608(2)2592y x x x =-++=--+,∴当2x =时,y 取得最大值,此时2592y =,∴销售单价为:100298-=(元),答:A 商品销售单价为98元时,该商场每天通过A 商品所获的利润最大.23.(12分)定义:我们知道,四边形的一条对角线把这个四边形分成了两个三角形,如果这两个三角形相似(不全等),我们就把这条对角线叫做这个四边形的“相似对角线”.理解:(1)如图1,已知Rt ABC ∆在正方形网格中,请你只用无刻度的直尺在网格中找到一点D ,使四边形ABCD 是以AC 为“相似对角线”的四边形(保留画图痕迹,找出3个即可);(2)如图2,在四边形ABCD 中,80ABC ∠=︒,140ADC ∠=︒,对角线BD 平分ABC ∠. 求证:BD 是四边形ABCD 的“相似对角线”;(3)如图3,已知FH 是四边形EFGH 的“相似对角线”, 30EFH HFG ∠=∠=︒,连接EG ,若EFG ∆的面积为23,求FH 的长.解:(1)由图1知,5AB=,25BC=90ABC∠=︒,5AC=,四边形ABCD是以AC为“相似对角线”的四边形,①当90ACD∠=︒时,ACD ABC∆∆∽或ACD CBA∆∆∽,∴12AC ABCD BC==或2AC BCCD AB==,10CD∴=或 2.5CD=同理:当90CAD∠=︒时, 2.5AD=或10AD=,(2)证明:80ABC∠=︒,BD平分ABC∠,40ABD DBC∴∠=∠=︒,140A ADB∴∠+∠=︒140ADC∠=︒,140BDC ADB∴∠+∠=︒,A BDC∴∠=∠,ABD DBC∴∆∆∽,BD∴是四边形ABCD的“相似对角线”;(3)如图3,FH是四边形EFGH的“相似对角线”,EFH∴∆与HFG∆相似,EFH HFG∠=∠,FEH FHG∴∆∆∽,∴FE FHFH FG=,2FH FE FG∴=,过点E作EQ FG⊥于Q,3sin 602EQ FE FE ∴=︒=, 1232FG EQ ⨯=, ∴132322FG FE ⨯=, 8FG FE ∴=,28FH FE FG ∴==,22FH ∴=.24.(14分)在平面直角坐标系xOy 中,一块含60︒角的三角板作如图摆放,斜边AB 在x 轴上,直角顶点C 在y 轴正半轴上,已知点(1,0)A -.(1)请直接写出点B 、C 的坐标:B (3,0) 、C ;并求经过A 、B 、C 三点的抛物线解析式;(2)现有与上述三角板完全一样的三角板DEF (其中90EDF ∠=︒,60)DEF ∠=︒,把顶点E 放在线段AB 上(点E 是不与A 、B 两点重合的动点),并使ED 所在直线经过点C .此时,EF 所在直线与(1)中的抛物线交于点M . ①设AE x =,当x 为何值时,OCE OBC ∆∆∽;②在①的条件下探究:抛物线的对称轴上是否存在点P 使PEM ∆是等腰三角形?若存在,请写出点P 的坐标;若不存在,请说明理由.解:(1)点(1,0)A -,1OA ∴=,由图可知,BAC ∠是三角板的60︒角,ABC ∠是30︒角, 所以,tan 60133OC OA =︒==,cot 30333OB OC =︒==,所以,点(3,0)B,C ,设抛物线解析式为2y ax bx c =++,则0930a b c a b c c ⎧-+=⎪++=⎨⎪=⎩,解得a b c ⎧=⎪⎪⎪⎪=⎨⎪⎪=⎪⎪⎩,所以,抛物线的解析式为2y =;(2)①OCE OBC ∆∆∽, ∴OE OC OC OB=,= 解得1OE =,所以,112AE OA OE =+=+=, 即2x =时,OCE OBC ∆∆∽;②存在.理由如下:抛物线的对称轴为12b x a =-==,所以,点E 为抛物线的对称轴与x 轴的交点, OA OE =,OC x ⊥轴,60BAC ∠=︒, ACE ∴∆是等边三角形, 60AEC ∴∠=︒,又60DEF ∠=︒,60FEB ∴∠=︒,BAC FEB ∴∠=∠,//EF AC ∴,由(1,0)A -,C 可得直线AC的解析式为y =, 点(1,0)E ,∴直线EF的解析式为y =联立2y y ⎧=-⎪⎨=++⎪⎩,解得112x y =⎧⎪⎨=⎪⎩223x y =-⎧⎪⎨=-⎪⎩, ∴点M的坐标为,或(3,--(舍去),2EM ==, 分三种情况讨论PEM ∆是等腰三角形, 当PE EM =时,2PE =, 所以,点P 的坐标为(1,2)或(1,2)-, 当PE PM =时,60FEB ∠=︒, 906030PEF ∴∠=︒-︒=︒,11cos30222PE EM =÷︒=⨯= 所以,点P的坐标为, 当PM EM =时,2cos3022PE EM =︒=⨯=, 所以,点P 的坐标为(1,, 综上所述,抛物线对称轴上存在点(1,2)P 或(1,2)-或或(1,,使PEM ∆是等腰三角形.。
江苏省无锡市滨湖区2019-2020学年度第一学期九年级数学期末试卷(无答案)

2019年秋学期期末调研考试试题 2020.1初三数学本试卷分试题和答题卡两部分,所有答案一律写在答题卡上.考试时间为120分钟.试卷满分130分. 注意事项:1.答卷前,考生务必用0.5毫米黑色墨水签字笔将自己的姓名、准考证号填写在答题卡的相应位置上,并认真核对条形码上的姓名、准考证号是否与本人的相符合.2.答选择题必须用2B 铅笔将答题卡上对应题目中的选项标号涂黑.如需改动,请用橡皮擦干净后,再选涂其他答案.答非选择题必须用0.5毫米黑色墨水签字笔作答,写在答题卡上各题目指定区域内相应的位置,在其他位置答题一律无效.3.作图必须用2B 铅笔作答,并请加黑加粗,描写清楚.4.卷中除要求近似计算的结果取近似值外,其他均应给出精确结果.一、选择题(本大题共10小题,每小题3分,共30分.在每小题所给出的四个选项中,只有一项是正确的,请用2B 铅笔把答题卡上相应的选项标号...........涂.黑.) 1.下列方程中,是一元二次方程的是 ( ▲ )A .2x +y =1B .x 2+3xy =6C .x +1x=4 D .x 2=3x -22.下列方程中,有两个不相等实数根的是 ( ▲ )A .x 2-x -1=0B .x 2+x +1=0C .x 2+1=0D .x 2+2x +1=03.若两个相似多边形的面积之比为4∶9,则这两个多边形的周长之比为 ( ▲ )A .2∶ 3B .2∶3C .4∶9D .16∶814.9名同学参加朗诵比赛,他们预赛成绩各不相同,现取前4名参加决赛,小红同学在知道自己成绩的情况下,要判断自己能否进入决赛,还要知道这9名同学成绩的 ( ▲ ) A .平均数 B .极差 C .中位数 D .众数5.二次函数y =x 2-6x 图像的顶点坐标为 ( ▲ ) A .(3,0) B .(-3,-9) C .(3,-9) D .(0,-6)6.如图,若四边形ABCD 内接于⊙O ,且∠A =40°,则∠C 的度数是 ( ▲ ) A .110° B .120° C .135° D .140°7. 如图是一个圆柱形输水管横截面的示意图,阴影部分为有水部分,如果水面AB 的宽为8cm ,水面最深的地方高度为2cm ,则该输水管的半径为 ( ▲ ) A .3cm B .5cm C .6cm D .8cm8.在半径为3cm 的⊙O 中,若弦AB =32,则弦AB 所对的圆周角的度数为 ( ▲ )A .30°B .45°C .30°或150°D .45°或135° 9. 如图,等边三角形ABC 的边长为5,D 、E 分别是边AB 、AC 上的点,将△ADE 沿DE 折叠,点A 恰好落在BC 边上的点F 处,若BF 2,则BD 的长是 ( ▲ ) A .2B .3C .218D .24710.已知二次函数y =-(x -1) 2+5,当m ≤x ≤n 且mn <0时,y 的最小值为2m ,最大值为2n ,则m +n 的值为 ( ▲ ) A .12B .32C .2D . 52二、填空题(本大题共8小题,每小题2分,共16分.不需写出解答过程,只需把答案直接填写在答题卡上相应的位置.........) 11.一元二次方程x 2-4=0的解为 ▲ .12.一个不透明的口袋中装有若干只除了颜色外其它都完全相同的小球,若袋中有红球6只,且摸出红球的概率为35,则袋中共有小球 ▲ 只.13.某一时刻,一棵树高15m ,影长为18m .此时,高为50 m 的旗杆的影长为 ▲ m . 14.一个圆锥的底面半径为6cm ,圆锥的高8cm ,则该圆锥的侧面积是 ▲ cm 2. 15.在□ABCD 中,∠ABC 的平分线BF 交对角线AC 于点E ,交AD 于点F .若AB BC =35, 则EFBF的值为 ▲ .(第15题)FEDA(第6题)D ABOCA EDB C F (第9题)(第7题)ABO16.已知关于x 的方程a (x +m )2+b =0(a 、b 、m 为常数,a ≠0)的解是x 1=2,x 2=-1,那么方程a (x +m +2)2+b =0的解 ▲ .17.如图,若一个半径为1的圆形纸片在边长为6的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片能接触到的最大面积为 ▲ .18. 如图,在边长为4的菱形ABCD 中,∠A =60°,若M 是AD 边的中点,N 是AB 边上的一动点,将△AMN 沿MN 所在的直线翻折得到△A ′MN ,连接A ′C ,则A ′C 的最小值为 ▲ .三、解答题(本大题共10小题,共84分.请在答题卡指定区域.......内作答,解答时应写出文字说明、证明过程或演算步骤) 19.(本题满分8分)解方程:(1)x 2-2x -1=0; (2)(2x -1)2=4(2x -1).20.(本题满分8分)已知关于x 的方程x 2-(m -1)x +2m =0,若方程的一个根为-4,求方程的另一个根及m的值.ACD MNA′(第18题)(第17题)ABC21.(本题满分6分)在如图所示的方格纸中,每个小方格都是边长为1个单位长度的正方形,△ABC 的顶点及点O 都在格点上(每个小方格的顶点叫做格点).(1)以点O 为位似中心,在网格区域内画出△A ′B ′C ′,使△A ′B ′C ′与△ABC 位似(A ′、B ′、C ′分别为A 、B 、C 的对称点),且位似比为2﹕1; (2)△A ′B ′C ′的面积为 ▲ 个平方单位;(3)若网格中有一格点D ′(异与点C ′),且△A ′B ′D ′的面积等于△A ′B ′C ′的面积,请在图中标出所有..符合条件的点D ′. (如果这样的点D ′不止一个,请用D 1′、D 2′、…、D n ′标出)22.(本题满分8分)某射击队教练为了了解队员训练情况,从队员中选取甲、乙两名队员进行射击测试,相同条件下各射靶5次,成绩统计如下:(1)根据上述信息可知:甲的成绩的众数是 ▲ 环,乙的成绩的中位数是 ▲ 环; (2)试通过计算说明甲、乙两人的成绩谁比较稳定?(3)如果乙再射击1次,命中8环,那么乙射击成绩的方差会 ▲ .(填“变大”、“变小”或“不变”)OB CA23.(本题满分8分)“2020比佛利”无锡马拉松赛将于3月22日鸣枪开跑,本次比赛设三个项目:A.全程马拉松;B.半程马拉松;C.迷你马拉松.小明和小红都报名参与该赛事的志愿者服务工作,若两人都已被选中,届时组委会随机将他们分配到三个项目组.(1)小明被分配到“迷你马拉松”项目组的概率为▲;(2)请利用树状图或列表法求两人被分配到同一个项目组的概率.24.(本题满分8分)如图,已知直线l切⊙O于点A,B为⊙O上一点,过点B作BC⊥l,垂足为点C,连接AB、OB.B (1)求证:∠ABC=∠ABO;O (2)若AB=10,AC=1,求⊙O的半径.A C lG FCDEBA25.(本题满分8分)如图,在□ABCD 中,点E 是边AD 上一点,延长CE 到点F ,使∠FBC =∠DCE ,且FB 与AD 相交于点G . (1)求证:∠D =∠F ;(2)用直尺和圆规在边AD 上作出一点P ,使△BPC ∽△CDP ,并加以证明.(作图要求:保留痕迹,不写作法.)26.(本题满分10分)某商店购进一批成本为每件30元的商品.经调查发现,该商品每天的销售量y (件)与销售单价x (元)之间满足一次函数关系,其图像如图所示. (1)求该商品每天的销售量y 与销售单价x 之间的函数关系式;(2)若商店按单价不低于成本价且不高于50元销售,则销售单价定为多少,才能使销售该商品每天获得的利润最大?最大利润是多少?(3)若商店要使销售该商品每天获得的利润不低于800元,试利用函数图像确定销售单价最多为多少元?y/件O3045x/元7010027.(本题满分10分)如图,已知二次函数y =ax 2+4ax +c (a ≠0)的图像交x 轴于A 、B 两点(A 在B 的左侧),交y 轴于点C .一次函数y =-12x +b 的图像经过点A ,与y 轴交于点D (0,-3),与这个二次函数的图像的另一个交点为E ,且AD ∶DE =3∶2. (1)求这个二次函数的表达式;(2)若点M 为x 轴上一点,求MD +55MA 的最小值.28.(本题满分10分)如图,在正方形ABCD 中,AB =4,动点P 从点A 出发,以每秒2个单位的速度,沿线段AB 方向匀速运动,到达点B 停止.连接DP 交AC 于点E ,以DP 为直径作⊙O 交AC 于点F ,连接DF 、PF .(1)求证:△DPF 为等腰直角三角形; (2)若点P 的运动时间t 秒.①当t 为何值时,点E 恰好为AC 的一个三等分点;②将△EFP 沿PF 翻折,得到△QFP ,当点Q 恰好落在BC 上时,求t 的值.(备用图1)D B C A(备用图2)D BCABACE PDFO。
江苏省无锡市2019-2020学年中考数学综合测试试题
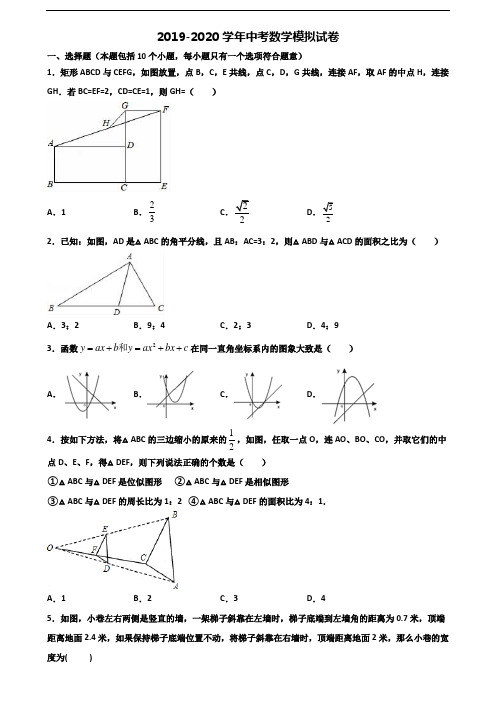
2019-2020学年中考数学模拟试卷一、选择题(本题包括10个小题,每小题只有一个选项符合题意)1.矩形ABCD 与CEFG ,如图放置,点B ,C ,E 共线,点C ,D ,G 共线,连接AF ,取AF 的中点H ,连接GH .若BC=EF=2,CD=CE=1,则GH=( )A .1B .23C .22D .522.已知:如图,AD 是△ABC 的角平分线,且AB :AC=3:2,则△ABD 与△ACD 的面积之比为( )A .3:2B .9:4C .2:3D .4:93.函数2y ax b y ax bx c =+=++和在同一直角坐标系内的图象大致是( )A .B .C .D .4.按如下方法,将△ABC 的三边缩小的原来的12,如图,任取一点O ,连AO 、BO 、CO ,并取它们的中点D 、E 、F ,得△DEF ,则下列说法正确的个数是( ) ①△ABC 与△DEF 是位似图形 ②△ABC 与△DEF 是相似图形③△ABC 与△DEF 的周长比为1:2 ④△ABC 与△DEF 的面积比为4:1.A .1B .2C .3D .45.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,那么小巷的宽度为( )A .0.7米B .1.5米C .2.2米D .2.4米6.下列图形是几家通讯公司的标志,其中既是轴对称图形又是中心对称图形的是( ) A .B .C .D .7.下列几何体中,主视图和左视图都是矩形的是( )A .B .C .D .8.函数228y x x m =--+的图象上有两点()11,A x y ,()22,B x y ,若122x x <<-,则( ) A .12y y <B .12y y >C .12 y y =D .1y 、2y 的大小不确定9.如图所示,直线a ∥b ,∠1=35°,∠2=90°,则∠3的度数为( )A .125°B .135°C .145°D .155°10.下列图形是轴对称图形的有( )A .2个B .3个C .4个D .5个二、填空题(本题包括8个小题) 11.已知反比例函数y=2m x-,当x >0时,y 随x 增大而减小,则m 的取值范围是_____. 12.因式分解:a 2b-4ab+4b=______.13.如果抛物线y=﹣x 2+(m ﹣1)x+3经过点(2,1),那么m 的值为_____.14.如图,平面直角坐标系中,矩形OABC 的顶点A (﹣6,0),C (0,3).将矩形OABC 绕点O 顺时针方向旋转,使点A 恰好落在OB 上的点A 1处,则点B 的对应点B 1的坐标为_____.15.如图,△ABC ≌△ADE ,∠EAC =40°,则∠B =_______°.16.已知二次函数2y ax bx c =++中,函数y 与x 的部分对应值如下: ... -1 0 1 2 3 ......105212...则当5y <时,x 的取值范围是_________.17.在平面直角坐标系中,点A 的坐标为(a ,3),点B 的坐标是(4,b ),若点A 与点B 关于原点O 对称,则ab=_____.18.如图△ABC 中,∠C=90°,AC=8cm ,AB 的垂直平分线MN 交AC 于D ,连接BD ,若cos ∠BDC=35,则BC 的长为_____.三、解答题(本题包括8个小题)19.(6分)一只不透明的袋子中装有2个白球和1个红球,这些球除颜色外都相同,搅匀后从中任意摸出1个球(不放回),再从余下的2个球中任意摸出1个球.用树状图或列表等方法列出所有可能出现的结果;求两次摸到的球的颜色不同的概率.20.(6分)在“母亲节”期间,某校部分团员参加社会公益活动,准备购进一批许愿瓶进行销售,并将所得利润捐给慈善机构.根据市场调查,这种许愿瓶一段时间内的销售量y(个)于销售单价x(元 /个)之间的对应关系如图所示.试判断y 与x 之间的函数关系,并求出函数关系式;若许愿瓶的进价为6元/个,按照上述市场调查销售规律,求利润w(元)与销售单价x(元/个)之间的函数关系式;若许愿瓶的进货成本不超过900元,要想获得最大利润,试求此时这种许愿瓶的销售单价,并求出最大利润.21.(6分)如图,在ABC ∆中,AB AC =,AD 为BC 边上的中线,DE AB ⊥于点E.求证:BDE CAD ∆∆∽;若13AB =,10BC =,求线段DE 的长.22.(8分)某中学九年级甲、乙两班商定举行一次远足活动,A 、B 两地相距10千米,甲班从A 地出发匀速步行到B 地,乙班从B 地出发匀速步行到A 地.两班同时出发,相向而行.设步行时间为x 小时,甲、乙两班离A 地的距离分别为1y 千米、2y 千米,1y 、2y 与x 的函数关系图象如图所示,根据图象解答下列问题:直接写出1y 、2y 与x 的函数关系式;求甲、乙两班学生出发后,几小时相遇?相遇时乙班离A 地多少千米?甲、乙两班相距4千米时所用时间是多少小时?23.(8分)已知抛物线2y x bx c =++过点(0,0),(1,3),求抛物线的解析式,并求出抛物线的顶点坐标.24.(10分)如图有A 、B 两个大小均匀的转盘,其中A 转盘被分成3等份,B 转盘被分成4等份,并在每一份内标上数字.小明和小红同时各转动其中一个转盘,转盘停止后(当指针指在边界线时视为无效,重转),若将A 转盘指针指向的数字记作一次函数表达式中的k ,将B 转盘指针指向的数字记作一次函数表达式中的b .请用列表或画树状图的方法写出所有的可能;求一次函数y=kx+b 的图象经过一、二、四象限的概率.25.(10分)如图,建筑物AB 的高为6cm ,在其正东方向有个通信塔CD ,在它们之间的地面点M (B ,角为30°,则通信塔CD 的高度.(sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,3=1.73,精确到0.1m )26.(12分)襄阳市精准扶贫工作已进入攻坚阶段.贫困户张大爷在某单位的帮扶下,把一片坡地改造后种植了优质水果蓝莓,今年正式上市销售.在销售的30天中,第一天卖出20千克,为了扩大销量,采取了降价措施,以后每天比前一天多卖出4千克.第x 天的售价为y 元/千克,y 关于x 的函数解析式为()76(120)2030mx m x x n x x -≤<⎧⎪⎨≤≤⎪⎩,为整数,为整数 且第12天的售价为32元/千克,第26天的售价为25元/千克.已知种植销售蓝莓的成木是18元/千克,每天的利润是W 元(利润=销售收入﹣成本).m= ,n= ;求销售蓝莓第几天时,当天的利润最大?最大利润是多少?在销售蓝莓的30天中,当天利润不低于870元的共有多少天?参考答案一、选择题(本题包括10个小题,每小题只有一个选项符合题意) 1.C 【解析】分析:延长GH 交AD 于点P ,先证△APH ≌△FGH 得AP=GF=1,GH=PH=12PG ,再利用勾股定理求得PG=2,从而得出答案.详解:如图,延长GH 交AD 于点P ,∵四边形ABCD 和四边形CEFG 都是矩形,∴∠ADC=∠ADG=∠CGF=90°,AD=BC=2、GF=CE=1,∴∠GFH=∠PAH , 又∵H 是AF 的中点, ∴AH=FH ,在△APH 和△FGH 中,∵PAH GFH AH FH AHP FHG ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴△APH ≌△FGH (ASA ), ∴AP=GF=1,GH=PH=12PG , ∴PD=AD ﹣AP=1, ∵CG=2、CD=1, ∴DG=1, 则GH=12PG=12×22PD DG +=22, 故选:C .点睛:本题主要考查矩形的性质,解题的关键是掌握全等三角形的判定与性质、矩形的性质、勾股定理等知识点. 2.A 【解析】试题解析:过点D 作DE ⊥AB 于E ,DF ⊥AC 于F.∵AD 为∠BAC 的平分线, ∴DE=DF ,又AB:AC=3:2,11:():():3:222ABD ACDSSAB DE AC DF AB AC ∴=⋅⋅==, 故选A.点睛:角平分线上的点到角两边的距离相等. 3.C 【解析】 【分析】根据a 、b 的符号,针对二次函数、一次函数的图象位置,开口方向,分类讨论,逐一排除.当a >0时,二次函数的图象开口向上,一次函数的图象经过一、三或一、二、三或一、三、四象限, 故A 、D 不正确;由B 、C 中二次函数的图象可知,对称轴x=-2ba>0,且a >0,则b <0, 但B 中,一次函数a >0,b >0,排除B . 故选C . 4.C 【解析】 【分析】根据位似图形的性质,得出①△ABC 与△DEF 是位似图形进而根据位似图形一定是相似图形得出 ②△ABC 与△DEF 是相似图形,再根据周长比等于位似比,以及根据面积比等于相似比的平方,即可得出答案. 【详解】解:根据位似性质得出①△ABC 与△DEF 是位似图形, ②△ABC 与△DEF 是相似图形, ∵将△ABC 的三边缩小的原来的12, ∴△ABC 与△DEF 的周长比为2:1, 故③选项错误,根据面积比等于相似比的平方, ∴④△ABC 与△DEF 的面积比为4:1. 故选C . 【点睛】此题主要考查了位似图形的性质,中等难度,熟悉位似图形的性质是解决问题的关键. 5.C 【解析】 【分析】在直角三角形中利用勾股定理计算出直角边,即可求出小巷宽度. 【详解】在Rt △A′BD 中,∵∠A′DB=90°,A′D=2米,BD 2+A′D 2=A′B′2,∴BD 2+22=6.25,∴BD 2=2.25,∵BD >0,∴BD=1.5米,∴CD=BC+BD=0.7+1.5=2.2米.故选C .【点睛】本题考查勾股定理的运用,利用梯子长度不变找到斜边是关键.6.C【解析】【分析】根据轴对称图形与中心对称图形的概念求解.【详解】A.不是轴对称图形,也不是中心对称图形.故错误;B.不是轴对称图形,也不是中心对称图形.故错误;C.是轴对称图形,也是中心对称图形.故正确;D.不是轴对称图形,是中心对称图形.故错误.故选C.【点睛】掌握好中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合;中心对称图形是要寻找对称中心,旋转180°后与原图重合.7.C【解析】【分析】主视图、左视图是分别从物体正面、左面和上面看,所得到的图形.依此即可求解.【详解】A. 主视图为圆形,左视图为圆,故选项错误;B. 主视图为三角形,左视图为三角形,故选项错误;C. 主视图为矩形,左视图为矩形,故选项正确;D. 主视图为矩形,左视图为圆形,故选项错误.故答案选:C.【点睛】8.A【解析】【分析】根据x1、x1与对称轴的大小关系,判断y1、y1的大小关系.【详解】解:∵y=-1x1-8x+m,∴此函数的对称轴为:x=-b2a =-()-82-2⨯=-1,∵x1<x1<-1,两点都在对称轴左侧,a<0,∴对称轴左侧y随x的增大而增大,∴y1<y1.故选A.【点睛】此题主要考查了函数的对称轴求法和函数的单调性,利用二次函数的增减性解题时,利用对称轴得出是解题关键.9.A【解析】分析:如图求出∠5即可解决问题.详解:∵a∥b,∴∠1=∠4=35°,∵∠2=90°,∴∠4+∠5=90°,∴∠5=55°,∴∠3=180°-∠5=125°,故选:A.点睛:本题考查平行线的性质、三角形内角和定理,邻补角的性质等知识,解题的关键是灵活运用所学知识解决问题.10.C【解析】试题分析:根据轴对称图形的概念:如果一个图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形.据此对图中的图形进行判断. 解:图(1)有一条对称轴,是轴对称图形,符合题意;图(2)不是轴对称图形,因为找不到任何这样的一条直线,使它沿这条直线折叠后,直线两旁的部分能够重合,即不满足轴对称图形的定义.不符合题意; 图(3)有二条对称轴,是轴对称图形,符合题意; 图(3)有五条对称轴,是轴对称图形,符合题意; 图(3)有一条对称轴,是轴对称图形,符合题意. 故轴对称图形有4个. 故选C .考点:轴对称图形.二、填空题(本题包括8个小题) 11.m >1. 【解析】分析:根据反比例函数y=2m x-,当x >0时,y 随x 增大而减小,可得出m ﹣1>0,解之即可得出m 的取值范围.详解:∵反比例函数y=2m x-,当x >0时,y 随x 增大而减小,∴m ﹣1>0,解得:m >1. 故答案为m >1.点睛:本题考查了反比例函数的性质,根据反比例函数的性质找出m ﹣1>0是解题的关键. 12.2(2)b a - 【解析】 【分析】先提公因式b ,然后再运用完全平方公式进行分解即可. 【详解】 a 2b ﹣4ab+4b =b (a 2﹣4a+4) =b (a ﹣2)2, 故答案为b (a ﹣2)2. 【点睛】本题考查了利用提公因式法与公式法分解因式,熟练掌握完全平方公式的结构特征是解本题的关键. 13.2把点(2,1)代入y=﹣x2+(m﹣1)x+3,即可求出m的值.【详解】∵抛物线y=﹣x2+(m﹣1)x+3经过点(2,1),∴1= -4+2(m-1)+3,解得m=2,故答案为2.【点睛】本题考查了二次函数图象上点的坐标特征,解题的关键是找出二次函数图象上的点的坐标满足的关系式. 14.(-23,6)【解析】分析:连接OB1,作B1H⊥OA于H,证明△AOB≌△HB1O,得到B1H=OA=6,OH=AB=23,得到答案.详解:连接OB1,作B1H⊥OA于H,由题意得,OA=6,3则tan∠BOA=33ABOA=,∴∠BOA=30°,∴∠OBA=60°,由旋转的性质可知,∠B1OB=∠BOA=30°,∴∠B1OH=60°,在△AOB和△HB1O,111B HO BAOB OH ABOOB OB∠∠⎧⎪∠∠⎨⎪⎩===,∴△AOB≌△HB1O,∴B1H=OA=6,3∴点B1的坐标为(3,6),故答案为(36).点睛:本题考查的是矩形的性质、旋转变换的性质,掌握矩形的性质、全等三角形的判定和性质定理是解题的关键.【解析】【分析】根据全等三角形的对应边相等、对应角相等得到∠BAC=∠DAE,AB=AD,根据等腰三角形的性质和三角形内角和定理计算即可.【详解】∵△ABC≌△ADE,∴∠BAC=∠DAE,AB=AD,∴∠BAD=∠EAC=40°,∴∠B=(180°-40°)÷2=1°,故答案为1.【点睛】本题考查的是全等三角形的性质和三角形内角和定理,掌握全等三角形的对应边相等、对应角相等是解题的关键.16.0<x<4【解析】【分析】根据二次函数的对称性及已知数据可知该二次函数的对称轴为x=2,结合表格中所给数据可得出答案.【详解】由表可知,二次函数的对称轴为直线x=2,所以,x=4时,y=5,所以,y<5时,x的取值范围为0<x<4.故答案为0<x<4.【点睛】此题主要考查了二次函数的性质,利用图表得出二次函数的图象即可得出函数值得取值范围,同学们应熟练掌握.17.1【解析】【分析】直接利用关于原点对称点的性质得出a,b的值,进而得出答案.【详解】∵点A的坐标为(a,3),点B的坐标是(4,b),点A与点B关于原点O对称,∴a=﹣4,b=﹣3,则ab=1,故答案为1.【点睛】本题考查了关于原点对称的点的坐标,熟知关于原点对称的两点的横、纵坐标互为相反数是解题的关键.18.4【解析】试题解析:∵3 cos5BDC∠=,可∴设DC=3x,BD=5x,又∵MN是线段AB的垂直平分线,∴AD=DB=5x,又∵AC=8cm,∴3x+5x=8,解得,x=1,在Rt△BDC中,CD=3cm,DB=5cm,222253 4. BC DB CD=-=-=故答案为:4cm.三、解答题(本题包括8个小题)19.(1)详见解析;(2)23.【解析】试题分析:(1)首先根据题意画出树状图,然后由树状图求得所有等可能的结果;(2)由(1)中树状图可求得两次摸到的球的颜色不同的情况有4种,再利用概率公式求解即可求得答案.试题解析:(1)如图:,所有可能的结果为(白1,白2)、(白1,红)、(白2,白1)、(白2,红)、(红,白1)、(红,白2);(2)共有6种情况,两次摸到的球的颜色不同的情况有4种,概率为42 63 =.20.(1)y是x的一次函数,y=-30x+1(2)w=-30x2+780x-31(3)以3元/个的价格销售这批许愿瓶可获得最大利润4元【解析】【分析】(1)观察可得该函数图象是一次函数,设出一次函数解析式,把其中两点代入即可求得该函数解析式,进而把其余两点的横坐标代入看纵坐标是否与点的纵坐标相同.(2)销售利润=每个许愿瓶的利润×销售量.(3)根据进货成本可得自变量的取值,结合二次函数的关系式即可求得相应的最大利润.【详解】解:(1)y 是x 的一次函数,设y=kx+b ,∵图象过点(10,300),(12,240),∴10k b 30012k b 240+=⎧⎨+=⎩,解得k 30b 600=-⎧⎨=⎩.∴y=-30x +1. 当x=14时,y=180;当x=16时,y=120,∴点(14,180),(16,120)均在函数y=-30x+1图象上.∴y 与x 之间的函数关系式为y=-30x+1.(2)∵w=(x -6)(-30x +1)=-30x 2+780x -31,∴w 与x 之间的函数关系式为w=-30x 2+780x -31.(3)由题意得:6(-30x+1)≤900,解得x≥3.w=-30x 2+780x -31图象对称轴为:()780x 13230=-=⨯-. ∵a=-30<0,∴抛物线开口向下,当x≥3时,w 随x 增大而减小.∴当x=3时,w 最大=4.∴以3元/个的价格销售这批许愿瓶可获得最大利润4元.21.(1)见解析;(2)6013DE =. 【解析】【分析】对于(1),由已知条件可以得到∠B=∠C ,△ABC 是等腰三角形,利用等腰三角形的性质易得AD ⊥BC ,∠ADC=90°;接下来不难得到∠ADC=∠BED ,至此问题不难证明;对于(2),利用勾股定理求出AD ,利用相似比,即可求出DE.【详解】解:(1)证明:∵AB AC =,∴B C ∠=∠.又∵AD 为BC 边上的中线,∴AD BC ⊥.∵DE AB ⊥,∴90BED CDA ︒∠=∠=,∴BDE CAD ∆∆∽.(2)∵10BC =,∴5BD =.在Rt ABD ∆中,根据勾股定理,得12AD ==. 由(1)得BDE CAD ∆∆∽,∴BD DE CA AD=, 即51312DE =, ∴6013DE =. 【点睛】此题考查相似三角形的判定与性质,解题关键在于掌握判定定理.22.(1)y 1=4x ,y 2=-5x+1.(2)409km .(3)23h . 【解析】【分析】(1)由图象直接写出函数关系式;(2)若相遇,甲乙走的总路程之和等于两地的距离.【详解】(1)根据图可以得到甲2.5小时,走1千米,则每小时走4千米,则函数关系是:y 1=4x ,乙班从B 地出发匀速步行到A 地,2小时走了1千米,则每小时走5千米,则函数关系式是:y 2=−5x+1.(2)由图象可知甲班速度为4km/h ,乙班速度为5km/h ,设甲、乙两班学生出发后,x 小时相遇,则4x+5x=1,解得x=109. 当x=109时,y 2=−5×109+1=409, ∴相遇时乙班离A 地为409km. (3)甲、乙两班首次相距4千米,即两班走的路程之和为6km ,故4x+5x=6,解得x=23h. ∴甲、乙两班首次相距4千米时所用时间是23h. 23.y=2x +2x ;(-1,-1).【解析】试题分析:首先将两点代入解析式列出关于b 和c 的二元一次方程组,然后求出b 和c 的值,然后将抛物线配方成顶点式,求出顶点坐标.试题解析:将点(0,0)和(1,3)代入解析式得:{13cb c=++=解得:2{bc==∴抛物线的解析式为y=2x+2x ∴y=2x+2x=2(1)x+-1 ∴顶点坐标为(-1,-1). 考点:待定系数法求函数解析式.24.(1)答案见解析;(2)13.【解析】【分析】(1)k可能的取值为-1、-2、-3,b可能的取值为-1、-2、3、4,所以将所有等可能出现的情况用列表方式表示出来即可.(2)判断出一次函数y=kx+b经过一、二、四象限时k、b的正负,在列表中找出满足条件的情况,利用概率的基本概念即可求出一次函数y=kx+b经过一、二、四象限的概率.【详解】解:(1)列表如下:所有等可能的情况有12种;(2)一次函数y=kx+b的图象经过一、二、四象限时,k<0,b>0,情况有4种,则P=412=13.25.通信塔CD的高度约为15.9cm.【解析】【分析】过点A作AE⊥CD于E,设CE=xm,解直角三角形求出AE,解直角三角形求出BM、DM,即可得出关于x 的方程,求出方程的解即可.【详解】过点A作AE⊥CD于E,则四边形ABDE 是矩形,设CE=xcm ,在Rt △AEC 中,∠AEC=90°,∠CAE=30°, 所以AE=330CE tan =︒xcm , 在Rt △CDM 中,CD=CE+DE=CE+AB=(x+6)cm , DM=)36603x CD tan +=︒cm , 在Rt △ABM 中,BM=63737AB tan tan =︒︒cm , ∵AE=BD , ∴)3663373x x tan +=+︒, 解得:33, ∴33(cm ), 答:通信塔CD 的高度约为15.9cm .【点睛】本题考查了解直角三角形,能通过解直角三角形求出AE 、BM 的长度是解此题的关键.26.(1)m=﹣12,n=25;(2)18,W 最大=968;(3)12天. 【解析】【分析】(1)根据题意将第12天的售价、第26天的售价代入即可得;(2)在(1)的基础上分段表示利润,讨论最值;(3)分别在(2)中的两个函数取值范围内讨论利润不低于870的天数,注意天数为正整数.【详解】(1)当第12天的售价为32元/件,代入y=mx ﹣76m 得32=12m ﹣76m , 解得m=12-,当第26天的售价为25元/千克时,代入y=n,则n=25,故答案为m=12-,n=25;(2)由(1)第x天的销售量为20+4(x﹣1)=4x+16,当1≤x<20时,W=(4x+16)(12-x+38﹣18)=﹣2x2+72x+320=﹣2(x﹣18)2+968,∴当x=18时,W最大=968,当20≤x≤30时,W=(4x+16)(25﹣18)=28x+112,∵28>0,∴W随x的增大而增大,∴当x=30时,W最大=952,∵968>952,∴当x=18时,W最大=968;(3)当1≤x<20时,令﹣2x2+72x+320=870,解得x1=25,x2=11,∵抛物线W=﹣2x2+72x+320的开口向下,∴11≤x≤25时,W≥870,∴11≤x<20,∵x为正整数,∴有9天利润不低于870元,当20≤x≤30时,令28x+112≥870,解得x≥271 14,∴27114≤x≤30∵x为正整数,∴有3天利润不低于870元,∴综上所述,当天利润不低于870元的天数共有12天.【点睛】本题考查了一次函数的应用,二次函数的应用,弄清题意,找准题中的数量关系,运用分类讨论思想是解题的关键.2019-2020学年中考数学模拟试卷 一、选择题(本题包括10个小题,每小题只有一个选项符合题意)1.12233499100++++++++的整数部分是( ) A .3 B .5 C .9 D .62.将一些半径相同的小圆按如图所示的规律摆放,第1个图形有4个小圆,第2个图形有8个小圆,第3个图形有14个小圆,…,依次规律,第7个图形的小圆个数是( )A .56B .58C .63D .723.一列快车从甲地驶往乙地,一列特快车从乙地驶往甲地,快车的速度为100千米/小时,特快车的速度为150千米/小时,甲乙两地之间的距离为1000千米,两车同时出发,则图中折线大致表示两车之间的距离y (千米)与快车行驶时间t (小时)之间的函数图象是A .B .C .D .4.夏新同学上午卖废品收入13元,记为+13元,下午买旧书支出9元,记为( )元.A .+4B .﹣9C .﹣4D .+95.如图,已知抛物线21y x 4x =-+和直线2y 2x =.我们约定:当x 任取一值时,x 对应的函数值分别为y 1、y 2,若y 1≠y 2,取y 1、y 2中的较小值记为M ;若y 1=y 2,记M= y 1=y 2.下列判断: ①当x >2时,M=y 2;②当x <0时,x 值越大,M 值越大;③使得M 大于4的x 值不存在;④若M=2,则x=" 1" .其中正确的有A .1个B .2个C .3个D .4个6.为迎接中考体育加试,小刚和小亮分别统计了自己最近10次跳绳比赛,下列统计量中能用来比较两人成绩稳定程度的是 ( )A .平均数B .中位数C .众数D .方差7.在直角坐标平面内,已知点M(4,3),以M 为圆心,r 为半径的圆与x 轴相交,与y 轴相离,那么r 的取值范围为( )A .0r 5<<B .3r 5<<C .4r 5<<D .3r 4<<8.小明乘出租车去体育场,有两条路线可供选择:路线一的全程是25千米,但交通比较拥堵,路线二的全程是30千米,平均车速比走路线一时的平均车速能提高80%,因此能比走路线一少用10分钟到达.若设走路线一时的平均速度为x 千米/小时,根据题意,得 A . B . C . D .9.如图,在△ABC 中,∠ACB =90°,CD ⊥AB 于点D ,则图中相似三角形共有( )A .1对B .2对C .3对D .4对10.如图,将长方形纸片ABCD 折叠,使边DC 落在对角线AC 上,折痕为CE ,且D 点落在对角线D′处.若AB=3,AD=4,则ED 的长为A .32B .3C .1D .43二、填空题(本题包括8个小题)11.阅读理解:引入新数i ,新数i 满足分配律,结合律,交换律.已知21i =-,那么(1)(1)i i +⋅-=________. 12.在△ABC 中,AB=AC ,把△ABC 折叠,使点B 与点A 重合,折痕交AB 于点M ,交BC 于点N .如果△CAN 是等腰三角形,则∠B 的度数为___________.13.已知点(﹣1,m)、(2,n )在二次函数y=ax2﹣2ax﹣1的图象上,如果m>n,那么a____0(用“>”或“<”连接).14.关于x的分式方程3111mx x+=--的解为正数,则m的取值范围是___________.15.关于x的一元二次方程24410x ax a+++=有两个相等的实数根,则581a aa--的值等于_____.16.如图,以AB为直径的半圆沿弦BC折叠后,AB与BC相交于点D.若13CD BD=,则∠B=________°.17.如图,AB∥CD,BE交CD于点D,CE⊥BE于点E,若∠B=34°,则∠C的大小为________度.18.若正六边形的内切圆半径为2,则其外接圆半径为__________.三、解答题(本题包括8个小题)19.(6分)为了了解同学们每月零花钱的数额,校园小记者随机调查了本校部分同学,根据调查结果,绘制出了如下两个尚不完整的统计图表.调查结果统计表组别分组(单位:元)人数A 0≤x<30 4B 30≤x<60 16C 60≤x<90 aD 90≤x<120 bE x≥120 2请根据以上图表,解答下列问题:填空:这次被调查的同学共有人,a+b=,m=;求扇形统计图中扇形C的圆心角度数;该校共有学生1000人,请估计每月零花钱的数额x在60≤x<120范围的人数.20.(6分)作图题:在∠ABC 内找一点P ,使它到∠ABC 的两边的距离相等,并且到点A 、C 的距离也相等.(写出作法,保留作图痕迹)21.(6分)某商场以每件280元的价格购进一批商品,当每件商品售价为360元时,每月可售出60件,为了扩大销售,商场决定采取适当降价的方式促销,经调查发现,如果每件商品降价1元,那么商场每月就可以多售出5件.降价前商场每月销售该商品的利润是多少元?要使商场每月销售这种商品的利润达到7200元,且更有利于减少库存,则每件商品应降价多少元?22.(8分)如图,AB 是⊙O 的直径,点C 为⊙O 上一点,CN 为⊙O 的切线,OM ⊥AB 于点O ,分别交AC 、CN 于D 、M 两点.求证:MD=MC ;若⊙O 的半径为5,AC=45,求MC 的长.23.(8分)化简求值:212(1)211x x x x -÷-+++,其中31x =. 24.(10分)淘宝网举办“双十一”购物活动许多商家都会利用这个契机进行打折让利的促销活动.甲网店销售的A 商品的成本为30元/件,网上标价为80元/件.“双十一”购物活动当天,甲网店连续两次降价销售A 商品吸引顾客,问该店平均每次降价率为多少时,才能使A 商品的售价为39.2元/件?据媒体爆料,有一些淘宝商家在“双十一”购物活动当天先提高商品的网上标价后再推出促销活动,存在欺诈行为.“双十一”活动之前,乙网店销售A 商品的成本、网上标价与甲网店一致,一周可售出1000件A 商品.在“双十一”购物活动当天,乙网店先将A 商品的网上标价提高a%,再推出五折促销活动,吸引了大量顾客,乙网店在“双十一”购物活动当天卖出的A 商品数量相比原来一周增加了2a%,“双十一”活动当天乙网店的利润达到了3万元,求乙网店在“双十一”购物活动这天的网上标价.25.(10分)如图,点A 、B 、C 、D 在同一条直线上,CE ∥DF ,EC=BD ,AC=FD ,求证:AE=FB .26.(12分)为落实“美丽抚顺”的工作部署,市政府计划对城区道路进行了改造,现安排甲、乙两个工程队完成.已知甲队的工作效率是乙队工作效率的32倍,甲队改造360米的道路比乙队改造同样长的道路少用3天.甲、乙两工程队每天能改造道路的长度分别是多少米?若甲队工作一天需付费用7万元,乙队工作一天需付费用5万元,如需改造的道路全长1200米,改造总费用不超过145万元,至少安排甲队工作多少天?参考答案一、选择题(本题包括10个小题,每小题只有一个选项符合题意)1.C【解析】解:∵21+2123+3299100+=99100,∴原式2﹣3﹣2+…﹣99100﹣1+10=1.故选C.2.B【解析】试题分析:第一个图形的小圆数量=1×2+2=4;第二个图形的小圆数量=2×3+2=8;第三个图形的小圆数量=3×4+2=14;则第n个图形的小圆数量=n(n+1)+2个,则第七个图形的小圆数量=7×8+2=58个.考点:规律题3.C【解析】分三段讨论:①两车从开始到相遇,这段时间两车距迅速减小;②相遇后向相反方向行驶至特快到达甲地,这段时间两车距迅速增加;③特快到达甲地至快车到达乙地,这段时间两车距缓慢增大;结合图象可得C选项符合题意.故选C.4.B【解析】【分析】收入和支出是两个相反的概念,故两个数字分别为正数和负数.【详解】收入13元记为+13元,那么支出9元记作-9元【点睛】本题主要考查了正负数的运用,熟练掌握正负数的概念是本题的关键.5.B【解析】试题分析:∵当y 1=y 2时,即2x 4x 2x -+=时,解得:x=0或x=2,∴由函数图象可以得出当x >2时, y 2>y 1;当0<x <2时,y 1>y 2;当x <0时, y 2>y 1.∴①错误.∵当x <0时, -21y x 4x =-+直线2y 2x =的值都随x 的增大而增大,∴当x <0时,x 值越大,M 值越大.∴②正确.∵抛物线()221y x 4x x 24=-+=--+的最大值为4,∴M 大于4的x 值不存在.∴③正确; ∵当0<x <2时,y 1>y 2,∴当M=2时,2x=2,x=1;∵当x >2时,y 2>y 1,∴当M=2时,2x 4x 2-+=,解得12x 2x 2==.∴使得M=2的x 值是1或2+.∴④错误.综上所述,正确的有②③2个.故选B .6.D【解析】【分析】根据方差反映数据的波动情况即可解答.【详解】由于方差反映数据的波动情况,所以比较两人成绩稳定程度的数据是方差.故选D .【点睛】本题主要考查了统计的有关知识,主要包括平均数、中位数、众数、方差.反映数据集中程度的统计量有平均数、中位数、众数、方差等,各有局限性,因此要对统计量进行合理的选择和恰当的运用. 7.D【解析】【分析】先求出点M到x轴、y轴的距离,再根据直线和圆的位置关系得出即可.【详解】解:∵点M的坐标是(4,3),∴点M到x轴的距离是3,到y轴的距离是4,∵点M(4,3),以M为圆心,r为半径的圆与x轴相交,与y轴相离,∴r的取值范围是3<r<4,故选:D.【点睛】本题考查点的坐标和直线与圆的位置关系,能熟记直线与圆的位置关系的内容是解此题的关键.8.A【解析】若设走路线一时的平均速度为x千米/小时,根据路线一的全程是25千米,但交通比较拥堵,路线二的全程是30千米,平均车速比走路线一时的平均车速能提高80%,因此能比走路线一少用10分钟到达可列出方程.解:设走路线一时的平均速度为x千米/小时,故选A.9.C【解析】∵∠ACB=90°,CD⊥AB,∴△ABC∽△ACD,△ACD∽CBD,△ABC∽CBD,所以有三对相似三角形.故选C.10.A【解析】【分析】首先利用勾股定理计算出AC的长,再根据折叠可得△DEC≌△D′EC,设ED=x,则D′E=x,AD′=AC﹣CD′=2,AE=4﹣x,再根据勾股定理可得方程22+x2=(4﹣x)2,再解方程即可【详解】∵AB=3,AD=4,∴DC=3。
江苏省无锡市2019-2020学年中考三诊数学试题含解析

江苏省无锡市2019-2020学年中考三诊数学试题一、选择题(本大题共12个小题,每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.2017年北京市在经济发展、社会进步、城市建设、民生改善等方面取得新成绩、新面貌.综合实力稳步提升.全市地区生产总值达到280000亿元,将280000用科学记数法表示为()A.280×103B.28×104C.2.8×105D.0.28×1062.如图,以正方形ABCD的边CD为边向正方形ABCD外作等边△CDE,AC与BE交于点F,则∠AFE 的度数是()A.135°B.120°C.60°D.45°3.如图,在矩形ABCD中,AD=1,AB>1,AG平分∠BAD,分别过点B,C作BE⊥AG 于点E,CF⊥AG 于点F,则AE-GF的值为()A.1 B.C.D.4.如图是我市4月1日至7日一周内“日平均气温变化统计图”,在这组数据中,众数和中位数分别是()A.13;13 B.14;10 C.14;13 D.13;145.小明和小张两人练习电脑打字,小明每分钟比小张少打6个字,小明打120个字所用的时间和小张打180个字所用的时间相等.设小明打字速度为x个/分钟,则列方程正确的是()A.1201806x x=+B.1201806x x=-C.1201806x x=+D.1201806x x=-6.如图,田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是()A .垂线段最短B .经过一点有无数条直线C .两点之间,线段最短D .经过两点,有且仅有一条直线7. 如图,把一个直角三角尺的直角顶点放在直尺的一边上,若∠1=50°,则∠2=( )A .20°B .30°C .40°D .50°8.已知二次函数 2y ax bx c =++图象上部分点的坐标对应值列表如下: x … -3 -2 -1 0 1 2 … y…2-1-2-127…则该函数图象的对称轴是( ) A .x=-3B .x=-2C .x=-1D .x=09.若一次函数(1)y m x m =++的图像过第一、三、四象限,则函数2y mx mx =-( ) A .有最大值4mB .有最大值4m -C .有最小值4m D .有最小值4m -10.若顺次连接四边形ABCD 各边中点所得的四边形是菱形,则四边形ABCD 一定是( ) A .矩形B .菱形C .对角线互相垂直的四边形D .对角线相等的四边形11.上体育课时,小明5次投掷实心球的成绩如下表所示,则这组数据的众数与中位数分别是( )1 2 3 4 5 成绩(m ) 8.28.08.27.57.8A .8.2,8.2B .8.0,8.2C .8.2,7.8D .8.2,8.012.关于x 的一元二次方程x 2-2x-(m-1)=0有两个不相等的实数根,则实数m 的取值范围是( ) A .0m >且1m ≠B .0m >C .0m ≥且1m ≠D .0m ≥二、填空题:(本大题共6个小题,每小题4分,共24分.) 13x 3-x 的取值范围是 .14.已知a 、b 满足a 2+b 2﹣8a ﹣4b+20=0,则a 2﹣b 2=_____. 15.计算:12×(﹣2)=___________.16.如图,这是一幅长为3m ,宽为1m 的长方形世界杯宣传画,为测量宣传画上世界杯图案的面积,现将宣传画平铺在地上,向长方形宣传画内随机投掷骰子(假设骰子落在长方形内的每一点都是等可能的),经过大量重复投掷试验,发现骰子落在世界杯图案中的频率稳定在常数0.4附近,由此可估计宣传画上世界杯图案的面积约为___________________m 1.17.如图,在直角坐标平面xOy 中,点A 坐标为()3,2,90AOB ∠=o ,30OAB ∠=o ,AB 与x 轴交于点C ,那么AC :BC 的值为______.18.对于一元二次方程2520x x -+=,根的判别式24b ac -中的b 表示的数是__________. 三、解答题:(本大题共9个小题,共78分,解答应写出文字说明、证明过程或演算步骤.19.(6分)如图,已知抛物线经过原点o 和x 轴上一点A (4,0),抛物线顶点为E ,它的对称轴与x 轴交于点D .直线y=﹣2x ﹣1经过抛物线上一点B (﹣2,m )且与y 轴交于点C ,与抛物线的对称轴交于点F .(1)求m 的值及该抛物线对应的解析式;(2)P (x ,y )是抛物线上的一点,若S △ADP =S △ADC ,求出所有符合条件的点P 的坐标;(3)点Q 是平面内任意一点,点M 从点F 出发,沿对称轴向上以每秒1个单位长度的速度匀速运动,设点M 的运动时间为t 秒,是否能使以Q 、A 、E 、M 四点为顶点的四边形是菱形.若能,请直接写出点M 的运动时间t 的值;若不能,请说明理由.20.(6分)某校航模小组借助无人飞机航拍校园,如图,无人飞机从A 处水平飞行至B 处需10秒,A 在地面C 的北偏东12°方向,B 在地面C 的北偏东57°方向.已知无人飞机的飞行速度为4米/秒,求这架无人飞机的飞行高度.(结果精确到0.1米,参考数据:sin33°≈0.54,cos33°≈0.84,tan33°≈0.65)21.(6分)如图,安徽江淮集团某部门研制了绘图智能机器人,该机器人由机座、手臂和末端操作器三部分组成,底座AE ⊥直线L 且25AE cm =,手臂60AB BC cm ==,末端操作器35CD cm =,AF P 直线L .当机器人运作时,45,75,60BAF ABC BCD ∠=︒∠=︒∠=︒,求末端操作器节点D 到地面直线L 的距离.(结果保留根号)22.(8分)如图,AB 为⊙O 的直径,AC 、DC 为弦,∠ACD=60°,P 为AB 延长线上的点,∠APD=30°.求证:DP 是⊙O 的切线;若⊙O 的半径为3cm ,求图中阴影部分的面积.23.(8分)如图,抛物线y=﹣x 2+bx+c (a≠0)与x 轴交于点A (﹣1,0)和B (3,0),与y 轴交于点C ,点D 的横坐标为m (0<m <3),连结DC 并延长至E ,使得CE=CD ,连结BE ,BC . (1)求抛物线的解析式;(2)用含m 的代数式表示点E 的坐标,并求出点E 纵坐标的范围; (3)求△BCE 的面积最大值.24.(10分)反比例函数y=kx(k≠0)与一次函数y=mx+b (m≠0)交于点A (1,2k ﹣1).求反比例函数的解析式;若一次函数与x轴交于点B,且△AOB的面积为3,求一次函数的解析式.25.(10分)已知:在△ABC中,AC=BC,D,E,F分别是AB,AC,CB的中点.求证:四边形DECF是菱形.26.(12分)如图,AD是等腰△ABC底边BC上的高,点O是AC中点,延长DO到E,使AE∥BC,连接AE.求证:四边形ADCE是矩形;①若AB=17,BC=16,则四边形ADCE的面积=.②若AB=10,则BC=时,四边形ADCE是正方形.27.(12分)如图,已知正比例函数y=2x与反比例函数y=kx(k>0)的图象交于A、B两点,且点A的横坐标为4,(1)求k的值;(2)根据图象直接写出正比例函数值小于反比例函数值时x的取值范围;(3)过原点O的另一条直线l交双曲线y=kx(k>0)于P、Q两点(P点在第一象限),若由点A、P、B、Q为顶点组成的四边形面积为224,求点P的坐标.参考答案一、选择题(本大题共12个小题,每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.C【解析】【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.【详解】将280000用科学记数法表示为2.8×1.故选C.【点睛】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.2.B【解析】【分析】易得△ABF与△ADF全等,∠AFD=∠AFB,因此只要求出∠AFB的度数即可.【详解】∵四边形ABCD是正方形,∴AB=AD,∠BAF=∠DAF,∴△ABF≌△ADF,∴∠AFD=∠AFB,∵CB=CE,∴∠CBE=∠CEB,∵∠BCE=∠BCD+∠DCE=90°+60°=150°,∴∠CBE=15°,∵∠ACB=45°,∴∠AFB=∠ACB+∠CBE=60°.∴∠AFE=120°.故选B.【点睛】此题考查正方形的性质,熟练掌握正方形及等边三角形的性质,会运用其性质进行一些简单的转化.3.D【解析】【分析】设AE=x,则AB=x,由矩形的性质得出∠BAD=∠D=90°,CD=AB,证明△ADG是等腰直角三角形,得出AG=AD=,同理得出CD=AB=x,CG=CD-DG=x -1,CG=GF,得出GF,即可得出结果.【详解】设AE=x,∵四边形ABCD是矩形,∴∠BAD=∠D=90°,CD=AB,∵AG平分∠BAD,∴∠DAG=45°,∴△ADG是等腰直角三角形,∴DG=AD=1,∴AG=AD=,同理:BE=AE=x, CD=AB=x,∴CG=CD-DG=x -1,同理: CG=GF,∴FG=,∴AE-GF=x-(x-)=.故选D.【点睛】本题考查了矩形的性质、等腰直角三角形的判定与性质,勾股定理;熟练掌握矩形的性质和等腰直角三角形的性质,并能进行推理计算是解决问题的关键.4.C【解析】【分析】根据统计图,利用众数与中位数的概念即可得出答案.【详解】从统计图中可以得出这一周的气温分别是:12,15,14,10,13,14,11所以众数为14;将气温按从低到高的顺序排列为:10,11,12,13,14,14,15所以中位数为13故选:C.【点睛】本题主要考查中位数和众数,掌握中位数和众数的求法是解题的关键.5.C【解析】【详解】解:因为设小明打字速度为x个/分钟,所以小张打字速度为(x+6)个/分钟,根据关系:小明打120个字所用的时间和小张打180个字所用的时间相等,可列方程得1201806x x=+,故选C.【点睛】本题考查列分式方程解应用题,找准题目中的等量关系,难度不大.6.C【解析】【详解】Q用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,∴线段AB的长小于点A绕点C到B的长度,∴能正确解释这一现象的数学知识是两点之间,线段最短,故选C.【点睛】根据“用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小”得到线段AB的长小于点A绕点C到B的长度,从而确定答案.本题考查了线段的性质,能够正确的理解题意是解答本题的关键,属于基础知识,比较简单.7.C【解析】【分析】由两直线平行,同位角相等,可求得∠3的度数,然后求得∠2的度数.【详解】∵∠1=50°,∴∠3=∠1=50°,∴∠2=90°−50°=40°.故选C.【点睛】本题主要考查平行线的性质,熟悉掌握性质是关键.8.C 【解析】 【分析】由当x=-2和x=0时,y 的值相等,利用二次函数图象的对称性即可求出对称轴. 【详解】解:∵x=-2和x=0时,y 的值相等, ∴二次函数的对称轴为2012x -+==-, 故答案为:C . 【点睛】本题考查了二次函数的性质,利用二次函数图象的对称性找出对称轴是解题的关键. 9.B 【解析】 【分析】 【详解】解:∵一次函数y=(m+1)x+m 的图象过第一、三、四象限, ∴m+1>0,m <0,即-1<m <0, ∴函数221()24my mx mx m x =-=--有最大值, ∴最大值为4m -, 故选B . 10.C 【解析】【分析】如图,根据三角形的中位线定理得到EH ∥FG ,EH=FG ,EF=12BD ,则可得四边形EFGH 是平行四边形,若平行四边形EFGH 是菱形,则可有EF=EH ,由此即可得到答案. 【点睛】如图,∵E ,F ,G ,H 分别是边AD ,DC ,CB ,AB 的中点,∴EH=12AC ,EH ∥AC ,FG=12AC ,FG ∥AC ,EF=12BD , ∴EH ∥FG ,EH=FG ,∴四边形EFGH 是平行四边形, 假设AC=BD , ∵EH=12AC ,EF=12BD ,则EF=EH,∴平行四边形EFGH是菱形,即只有具备AC=BD即可推出四边形是菱形,故选D.【点睛】本题考查了中点四边形,涉及到菱形的判定,三角形的中位线定理,平行四边形的判定等知识,熟练掌握和灵活运用相关性质进行推理是解此题的关键.11.D【解析】【分析】【详解】解:按从小到大的顺序排列小明5次投球的成绩:7.5,7.8,8.2,8.1,8.1.其中8.1出现1次,出现次数最多,8.2排在第三,∴这组数据的众数与中位数分别是:8.1,8.2.故选D.【点睛】本题考查众数;中位数.12.A【解析】【分析】根据一元二次方程的系数结合根的判别式△>1,即可得出关于m的一元一次不等式,解之即可得出实数m的取值范围.【详解】∵关于x的一元二次方程x2﹣2x﹣(m﹣1)=1有两个不相等的实数根,∴△=(﹣2)2﹣4×1×[﹣(m﹣1)]=4m >1,∴m>1.故选B.【点睛】本题考查了根的判别式,牢记“当△>1时,方程有两个不相等的实数根”是解题的关键.二、填空题:(本大题共6个小题,每小题4分,共24分.).13.x3【解析】x 30x 3-≥⇒≥.14.1【解析】【分析】利用配方法把原式化为平方和的形式,根据偶次方的非负性求出a 、b ,计算即可.【详解】a 2+b 2﹣8a ﹣4b+20=0,a 2﹣8a+16+b 2﹣4b+4=0,(a ﹣4)2+(b ﹣2)2=0a ﹣4=0,b ﹣2=0,a=4,b=2,则a 2﹣b 2=16﹣4=1,故答案为1.【点睛】本题考查了配方法的应用、非负数的性质,掌握完全平方公式、偶次方的非负性是解题的关键. 15.-1【解析】【分析】根据“两数相乘,异号得负,并把绝对值相乘”即可求出结论.【详解】()1212⨯-=-, 故答案为 1.-【点睛】本题考查了有理数的乘法,牢记“两数相乘,同号得正,异号得负,并把绝对值相乘”是解题的关键. 16.1.4【解析】【分析】由概率估计图案在整副画中所占比例,再求出图案的面积.【详解】估计宣传画上世界杯图案的面积约为3×1×0.4=1.4m 1. 故答案为1.4【点睛】本题考核知识点:几何概率. 解题关键点:由几何概率估计图案在整副画中所占比例.17.233 【解析】【分析】过点A 作AD ⊥y 轴,垂足为D ,作BE ⊥y 轴,垂足为E.先证△ADO ∽△OEB ,再根据∠OAB =30°求出三角形的相似比,得到OD:OE=2∶3,根据平行线分线段成比例得到AC:BC=OD:OE=2∶3=23 【详解】解:如图所示:过点A 作AD ⊥y 轴,垂足为D ,作BE ⊥y 轴,垂足为E.∵∠OAB =30°,∠ADE =90°,∠DEB =90° ∴∠DOA+∠BOE =90°,∠OBE+∠BOE =90°∴∠DOA=∠OBE∴△ADO ∽△OEB∵∠OAB =30°,∠AOB =90°,∴OA ∶3∵点A 坐标为(3,2) ∴AD=3,OD=2∵△ADO ∽△OEB∴3AD OA OE OB==∴OE 3=∵OC ∥AD ∥BE根据平行线分线段成比例得:AC:BC=OD:OE=2323 故答案为33.【点睛】本题考查三角形相似的证明以及平行线分线段成比例.18.-5【解析】【分析】分清一元二次方程中,二次项系数、一次项系数和常数项,直接解答即可.【详解】解:b 表示一元二次方程2520x x -+=的一次项系数5-.【点睛】此题考查根的判别式,在解一元二次方程时程根的判别式△=b 2-4ac ,不要盲目套用,要看具体方程中的a ,b ,c 的值.a 代表二次项系数,b 代表一次项系数,c 是常数项.三、解答题:(本大题共9个小题,共78分,解答应写出文字说明、证明过程或演算步骤.19.(1)214y x x =-;(2)(1)( ,1);(3)存在,14t =,24t =36t =,4132t = 【解析】试题分析:(1)将x=-2代入y=-2x-1即可求得点B 的坐标,根据抛物线过点A 、O 、B 即可求出抛物线的方程.(2)根据题意,可知△ADP 和△ADC 的高相等,即点P 纵坐标的绝对值为1,所以点P 的纵坐标为1± ,分别代入214y x x =-中求解,即可得到所有符合题意的点P 的坐标. (3)由抛物线的解析式为214y x x =- ,得顶点E (2,﹣1),对称轴为x=2; 点F 是直线y=﹣2x ﹣1与对称轴x=2的交点,求出F (2,﹣1),DF=1.又由A (4,0),根据勾股定理得AE = .然后分4种情况求解.点睛:(1)首先求出点B 的坐标和m 的值,然后利用待定系数法求出抛物线的解析式;(2)△ADP 与△ADC 有共同的底边AD ,因为面积相等,所以AD 边上的高相等,即为1;从而得到点P 的纵坐标为1,再利用抛物线的解析式求出点P 的纵坐标;(3)如解答图所示,在点M 的运动过程中,依次出现四个菱形,注意不要漏解.针对每一个菱形,分别进行计算,求出线段MF 的长度,从而得到运动时间t 的值.20.29.8米.【解析】【分析】作AD BC ⊥,BH CN ⊥,根据题意确定出ABC ∠与BCH ∠的度数,利用锐角三角函数定义求出AD与BD 的长度,由CD BD +求出BC 的长度,即可求出BH 的长度.【详解】解:如图,作AD BC ⊥,BH CN ⊥,由题意得:MCD 57MCA 12AB CH ∠∠︒︒P =,=,, ACB 45BCH ABC 33∠∠∠∴︒︒=,==,AB 40Q =米,AD CD sin ABC?AB 40sin33m BD AB?cos3340cos33===,==∠∴⨯︒︒⨯︒米,BC CD BD 40sin33cos3355.2∴+⨯︒+︒≈==()米,则BH BC?sin3329.8︒≈=米,答:这架无人飞机的飞行高度为29.8米.【点睛】此题考查了解直角三角形的应用﹣仰角俯角问题,熟练掌握锐角三角函数定义是解本题的关键. 21.(30220+)cm.【解析】【分析】作BG ⊥CD ,垂足为G ,BH ⊥AF ,垂足为H ,解Rt CBG ∆和Rt ABH ∆,分别求出CG 和BH 的长,根据D 到L 的距离()BH AE CD CG =+--求解即可.【详解】如图,作BG ⊥CD ,垂足为G ,BH ⊥AF ,垂足为H ,在Rt CBG ∆中,∠BCD=60°,BC=60cm ,∴cos6030CG BC =⋅︒=,在Rt ABH ∆中,∠BAF=45°,AB=60cm ,∴sin45302BH AB =⋅︒=,∴D 到L 的距离()302255(30220)BH AE CD CG cm =+--=+-=+.【点睛】本题考查解直角三角形,解题的关键是构造出适当辅助线,从而利用锐角三角函数的定义求出相关线段. 22.(1)证明见解析;(2)2933()22cm p -. 【解析】 【分析】(1)连接OD ,求出∠AOD ,求出∠DOB ,求出∠ODP ,根据切线判定推出即可.(2)求出OP 、DP 长,分别求出扇形DOB 和△ODP 面积,即可求出答案.【详解】解:(1)证明:连接OD ,∵∠ACD=60°,∴由圆周角定理得:∠AOD=2∠ACD=120°.∴∠DOP=180°﹣120°=60°.∵∠APD=30°,∴∠ODP=180°﹣30°﹣60°=90°.∴OD ⊥DP .∵OD 为半径,∴DP 是⊙O 切线.(2)∵∠ODP=90°,∠P=30°,OD=3cm ,∴OP=6cm ,由勾股定理得:3cm .∴图中阴影部分的面积221603933333()236022ODP DOB S S S cm p p 创=-=创=V 扇形 23.(1)y=﹣x 2+2x+1.(2)2≤E y <2.(1)当m=1.5时,S △BCE 有最大值,S △BCE 的最大值=278. 【解析】分析:(1) 1)把A 、B 两点代入抛物线解析式即可;(2)设()()2,23,0,3D m m m C CE CD -++=,利用求线段中点的公式列出关于m 的方程组,再利用0<m <1即可求解;(1) 连结BD ,过点D 作x 轴的垂线交BC 于点H,由BCE BCD S S ∆∆=,设出点D 的坐标,进而求出点H 的坐标,利用三角形的面积公式求出BCE S ∆,再利用公式求二次函数的最值即可.详解:(1)∵抛物线 2y x bx c =-++ 过点A (-1,0)和B (1,0) 10930b c b c ---=⎧∴⎨-++=⎩ 22233b y x xc =⎧∴∴=-++⎨=⎩ (2)∵()()2,23,0,3D m m m C CE CD -++= ∴点C 为线段DE 中点设点E (a,b )()20236a m b m m +=⎧⎪∴⎨+-++=⎪⎩ ()2,23E m m m ∴--+∵0<m <1, ()222312m m m -+=-+∴当m=1时,纵坐标最小值为2当m=1时,最大值为2∴点E 纵坐标的范围为26E y ≤<(1)连结BD ,过点D 作x 轴的垂线交BC 于点H∵CE=CD ()2,23,:3BCE BCD S S D m m m BC y x ∆∆∴=-++=-+Q∴H (m ,-m+1) ∴()211=233322BCD S DH OB m m m ∆=⨯-+++-⨯ 23922m m =-+ 当m=1.5时,max 278EBC S ∆=.点睛:本题考查了二次函数的综合题、待定系数法、一次函数等知识点,解题的关键是灵活运用所学知识解决问题,会用方程的思想解决问题.24.(1)y=1x;(2)y=﹣1655x +或y=1677x + 【解析】 试题分析:(1)把A (1,2k-1)代入y=k x 即可求得结果; (2)根据三角形的面积等于3,求得点B 的坐标,代入一次函数y=mx+b 即可得到结果.试题解析:(1)把A (1,2k ﹣1)代入y=k x 得, 2k ﹣1=k ,∴k=1,∴反比例函数的解析式为:y=1x ; (2)由(1)得k=1,∴A (1,1),设B (a ,0),∴S △AOB =12•|a |×1=3, ∴a=±6,∴B (﹣6,0)或(6,0),把A (1,1),B (﹣6,0)代入y=mx+b 得: 106m b m b=+⎧⎨=-+⎩ , ∴1767m b ⎧=⎪⎪⎨⎪=⎪⎩, ∴一次函数的解析式为:y=17x+67, 把A (1,1),B (6,0)代入y=mx+b 得:106m b m b =+⎧⎨=+⎩, ∴1565m b ⎧=-⎪⎪⎨⎪=⎪⎩, ∴一次函数的解析式为:y=﹣1655x +. 所以符合条件的一次函数解析式为:y=﹣1655x +或y=17x+67.25.见解析【解析】【详解】证明:∵D、E是AB、AC的中点∴DE=BC,EC=AC∵D、F是AB、BC的中点∴DF=AC,FC=BC∴DE=FC=BC,EC=DF=AC∵AC=BC∴DE=EC=FC=DF∴四边形DECF是菱形26.(1)见解析;(2)①1;②102.【解析】试题分析:(1)根据平行四边形的性质得出四边形ADCE是平行四边形,根据垂直推出∠ADC=90°,根据矩形的判定得出即可;(2)①求出DC,根据勾股定理求出AD,根据矩形的面积公式求出即可;②要使ADCE是正方形,只需要AC⊥DE,即∠DOC=90°,只需要OD2+OC2=DC2,即可得到BC的长.试题解析:(1)证明:∵AE∥BC,∴∠AEO=∠CDO.又∵∠AOE=∠COD,OA=OC,∴△AOE≌△COD,∴OE=OD,而OA=OC,∴四边形ADCE是平行四边形.∵AD是BC边上的高,∴∠ADC=90°.∴□ADCE 是矩形.(2)①解:∵AD是等腰△ABC底边BC上的高,BC=16,AB=17,∴BD=CD=8,AB=AC=17,∠ADC=90°,由勾股定理得:AD=22178-=12,∴四边形ADCE的面积是AD×DC=12×8=1.-=22AC CD②当BC=102时,DC=DB=52.∵ADCE是矩形,∴OD=OC=2.∵OD2+OC2=DC2,∴∠DOC=90°,∴AC⊥DE,∴ADCE是正方形.点睛:本题考查了平行四边形的判定,矩形的判定和性质,等腰三角形的性质,勾股定理的应用,能综合运用定理进行推理和计算是解答此题的关键,比较典型,难度适中.27.(1)32;(2)x<﹣4或0<x<4;(3)点P的坐标是P(﹣6565;或P(65﹣.【解析】分析:(1)先将x=4代入正比例函数y=2x,可得出y=8,求得点A(4,8),再根据点A与B关于原点对称,得出B点坐标,即可得出k的值;(2)正比例函数的值小于反比例函数的值即正比例函数的图象在反比例函数的图象下方,根据图形可知在交点的右边正比例函数的值小于反比例函数的值.(3)由于双曲线是关于原点的中心对称图形,因此以A、B、P、Q为顶点的四边形应该是平行四边形,那么△POA的面积就应该是四边形面积的四分之一即1.可根据双曲线的解析式设出P点的坐标,然后表示出△POA的面积,由于△POA的面积为1,由此可得出关于P点横坐标的方程,即可求出P点的坐标.详解:(1)∵点A在正比例函数y=2x上,∴把x=4代入正比例函数y=2x,解得y=8,∴点A(4,8),把点A(4,8)代入反比例函数y=kx,得k=32,(2)∵点A与B关于原点对称,∴B点坐标为(﹣4,﹣8),由交点坐标,根据图象直接写出正比例函数值小于反比例函数值时x的取值范围,x<﹣8或0<x<8;(3)∵反比例函数图象是关于原点O的中心对称图形,∴OP=OQ,OA=OB,∴四边形APBQ是平行四边形,∴S△POA=S平行四边形APBQ×=14×224=1,设点P的横坐标为m(m>0且m≠4),得P(m,32m),过点P、A分别做x轴的垂线,垂足为E、F,∵点P、A在双曲线上,∴S△POE=S△AOF=16,若0<m<4,如图,∵S△POE+S梯形PEFA=S△POA+S△AOF,∴S梯形PEFA=S△POA=1.∴12(8+32m)•(4﹣m)=1.∴m1=﹣,m2=﹣7﹣(舍去),∴P(﹣,;若m>4,如图,∵S△AOF+S梯形AFEP=S△AOP+S△POE,∴S梯形PEFA=S△POA=1.∴12×(8+32m)•(m﹣4)=1,解得m1=7+37,m2=7﹣37(舍去),∴P(7+37,﹣16+4877).∴点P的坐标是P(﹣7+37,16+4877);或P(7+37,﹣16+4877).点睛:本题考查了待定系数法求反比例函数与一次函数的解析式和反比例函数y=kx中k的几何意义.这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.利用数形结合的思想,求得三角形的面积.。
江苏省无锡市硕放中学2019-2020学年第一学期初三数学周练13(无答案)

无锡市硕放中学初三数学周练(13)班级姓名一.选择题(共10小题)1.下列函数属于二次函数的是---------------------------------------------------------------------()A.y=﹣3x2+1B.y=C.y=D.y=2x+52.函数y=2(x+2)2+1的图象顶点坐标是------------------------------------------------()A.(2,1)B.(﹣2,1)C.(﹣2,﹣1)D.(2,﹣1)3.将y=2x2﹣8x﹣1化成y=a(x+m)2+n的形式为------------------------------------()A.y=2(x﹣2)2+7B.y=2(x﹣4)2﹣1C.y=2(x﹣2)2﹣9D.y=2(x﹣4)2﹣74.已知二次函数y=ax2+bx+1(a≠0)的图象与x轴只有一个交点,满足条件的a,b的值可以为-------------------------------------------------------------------------------------------()A.2,4B.4,1C.2,1D.1,25.飞机着陆后滑行的距离y(单位:m)关于滑行时间t(单位:s)的函数解析式是y=60t﹣t2,飞机着陆至停下来共滑行-----------------------------------------()A.25米B.50米C.625米D.750米6.将抛物线y=x2+2x﹣3的图象先向左平移2个单位,再向上平移3个单位,得到的抛物线的解析式是--------------------------------------------------------------------------------()A.y=x2﹣2x B.y=x2+6x+8C.y=x2﹣2x﹣6D.y=x2+6x+27.有一个矩形苗圃园,其中一边靠墙,另外边用长为20m的篱笆围成.已知墙长为15m,若平行于墙的一边长不小于8m,则这个苗圃园面积的最大值和最小值分别为()A.48m2,37.5m2B.50m2,32m2C.50m2,37.5m2D.48m2,32m28.如图,直线y=x﹣m与抛物线y=ax2+bx+c交于A(﹣1,﹣2),B两点,如果x﹣m>ax2+bx+c,那么x的取值范围是--------------------------------------------()A.x<﹣1B.﹣1<x<4C.x>4D.x<﹣1或x>4 9.如图是王阿姨晚饭后步行的路程s(单位:m)与时间t(单位:min)的函数图象,其中曲线段AB是以B为顶点的抛物线一部分.下列说法不正确的是---------------------()A.25min~50min,王阿姨步行的路程为800mB.线段CD的函数解析式为s=32t+400(25≤t≤50)C.5min~20min,王阿姨步行速度由慢到快D.曲线段AB的函数解析式为s=﹣3(t﹣20)2+1200(5≤t≤20)(第8题图) (第9题图) (第10题图) 10.已知抛物线y=ax2+bx+3在坐标系中的位置如图所示,它与x,y轴的交点分别为A,B,P是其对称轴x=1上的动点,根据图中提供的信息,给出以下结论:①2a+b=0,②x=3是ax2+bx+3=0的一个根,③△P AB周长的最小值是+3.其中正确的是()A.①②③B.仅有①②C.仅有①③D.仅有②③二.填空题(共8小题)11.如果函数是关于x的二次函数,那么k的值是.12.请写出一个开口向下,且顶点坐标为(﹣3,2)的抛物线解析式:.13.抛物线y=x2﹣2x﹣1与x轴有个交点.14.把一个足球垂直于地面向上踢,t(秒)后该足球的高度h(米)适用于公式h=20t﹣5t2.下列结论:①球踢出4秒后回到地面;②足球上升的高度可以为30米;③足球踢出3秒后高度第一次达到15米;④足球踢出2秒后高度到达最大.其中正确的结论是.15.如图,在平面直角坐标系中,抛物线y=﹣x2+2x+2与y轴的交点为A,将该抛物线绕着点A旋转180°后得到的抛物线所对应的函数解析式为.16.已知二次函数y=2x2﹣8x+11,当自变量1≤x≤4时,则y的取值范围为.17.如图,二次函数y=﹣x2+x+2交x轴于点A、B(A在B的右侧),与y轴交于点C,D 为第一象限抛物线上的动点,则△ACD面积的最大值是.18.如图,在平面直角坐标系中,直线y=﹣x+n(n>2)交x轴于点A,交y轴于点B,C 为直线AB上一点,过点C作CD垂直x轴于点D,抛物线y=ax2+bx过A,C两点,M 为抛物线的顶点,过点M作ME垂直y轴于点E,若D的坐标为(1,0).则当△BEM 与△COD相似时,n的值为.三.解答题(共7小题)19.用配方法求抛物线y=﹣x2﹣3x+1的对称轴、顶点坐标和最值.20.如图,二次函数y=x2+x+3的图象与x轴的正样轴交于点B,与y轴交于点C.(1)求点A、B、C的坐标;(2)求△ABC的面积.21.抛物线y=ax2+bx+c上部分点的横坐标x纵坐标y的对应值如下表x…﹣2﹣1012…y…0﹣4﹣408…(1)试确定该抛物线的对称轴及当x=﹣3时对应的函数值;(2)试确定抛物线y=ax2+bx+c的解析式.22.如图,已知抛物线y=ax2+bx+c与直线y=x+3分别交于x轴和y轴的同一点A和C,且抛物线的对称轴为直线x=﹣2.(1)求抛物线与x轴的两个交点A和B的坐标;(2)试确定抛物线的解析式;(3)观察图象,写出二次函数值小于一次函数值的自变量x的取值范围.23.某超市购进一批牛肉销售,经过还价,实际价格每千克比原来少2元,发现原来买这批牛肉32千克的钱,现在可买33千克.(1)现在实际购进这批牛肉每千克多少元?(2)若这批牛肉的销售量y(千克)与销售单价x(元/千克)满足如图所示的一次函数关系.求y与x之间的函数关系式;(3)这批牛肉的销售单价定为多少时,能获得最大利润?最大利润是多少?(利润=销售收入﹣进货金额)24.如图,抛物线y=x2+bx+5与x轴交于点A和点B(5,0),与y轴交于点C,抛物线的顶点为点P.(1)求抛物线的表达式并写出顶点P的坐标;(2)在x轴上方的抛物线上有一点D,若∠ABD=∠ABP,试求出点D的坐标;(3)设在直线BC下方的抛物线上有一点Q,若S△BCQ=15,试求出点Q的坐标.25.已知二次函数y=x2﹣x﹣2的图象和x轴相交于点A、B,与y轴相交于点C,过直线BC的下方抛物线上一动点P作PQ∥AC交线段BC于点Q,再过P作PE⊥x轴于点E,交BC于点D.(1)求直线AC的解析式;(2)求△PQD周长的最大值;(3)当△PQD的周长最大时,在y轴上有两个动点M、N(M在N的上方),且MN=1,求PN+MN+AM的最小值.。
【附20套中考模拟试题】江苏省无锡市西漳中学2019-2020学年中考数学模拟试卷含解析

A.9 人
B.10 人
C.11 人
D.12 人
9.在刚刚结束的中考英语听力、口语测试中,某班口语成绩情况如图所示,则下列说法正确的是( )
A.中位数是 9
B.众数为 16
C.平均分为 7.78 D.方差为 2
10.若二次函数 y ax2 2ax c 的图象经过点(﹣1,0),则方程 ax2 2ax c 0 的解为( )
两个小球号码之和等于 4 的概率. 20.(6 分)某省为解决农村饮用水问题,省财政部门共投资 20 亿元对各市的农村饮用水的“改水工程”予
以一定比例的补助.2008 年,A 市在省财政补助的基础上投入 600 万元用于“改水工程”,计划以后每年以 相同的增长率投资,2010 年该市计划投资“改水工程”1176 万元.求 A 市投资“改水工程”的年平均增长率; 从 2008 年到 2010 年,A 市三年共投资“改水工程”多少万元? 21.(6 分)如图,小明的家在某住宅楼 AB 的最顶层(AB⊥BC),他家的后面有一建筑物 CD(CD∥AB), 他很想知道这座建筑物的高度,于是在自家阳台的 A 处测得建筑物 CD 的底部 C 的俯角是 43°,顶部 D 的仰 角是 25°,他又测得两建筑物之间的距离 BC 是 28 米,请你帮助小明求出建筑物 CD 的高度(精确
A.21.7 米
B.22.4 米
C.27.4 米
D.28.8 米
7.如图,两个同心圆(圆心相同半径不同的圆)的半径分别为 6cm 和 3cm,大圆的弦 AB 与小圆相切,则
劣弧 AB 的长为(
)
A.2πcm
B.4πcm
C.6πcm
D.8πcm
8.在一次酒会上,每两人都只碰一次杯,如果一共碰杯 55 次,则参加酒会的人数为( )
【含中考模拟卷21套】江苏省无锡市西漳中学2019-2020学年中考英语模拟试卷含解析

江苏省无锡市西漳中学2019-2020学年中考英语模拟试卷Ⅰ. 单项选择1、In the following words, which underlined letter has a different sound from the others?A.agree B.alien C.ahead2、Last December, a man who stole a shared bike 1,000 yuan by the police.A.fined B.is fined C.was fined3、--All right. I’ll take it. But I tell you, it is the last time I will ______ this kind of work.---Come on, buddy! Don’t be so serious.A.take out B.take up C.take on D.take off4、―Don’t eat too much snacks. It’s bad for health. ―_______.A.Sorry, I won’t.B.Sure, I will C.Never mind D.OK. I don’t.5、In China, about ___________ of people live in the country.A.three fifth B.third fifthC.three fifths D.three fives6、The little girl is always too shy and afraid to express herself in public.A.angrily B.clearly C.quietly D.politely7、My father usually plays ______ basketball to relax after a week’s hard work.A.a B.an C.the D./8、To make your DIY work perfect, you’d better get all the tools ready ________ you start.A.since B.before C.when D.after9、______ my brother _________ my father loves the science fiction movie The Wandering Earth (流浪地球)a lot, both of them want to see it again.A.Both; and. B.Not only; but also C.Either; or D.Neither, nor10、Jeff is___hard-working boy and he got good grades at ___end of this term.A.an; / B.a ; the C.a ; an D.an: theⅡ. 完形填空11、Colour is a part of life. The whole world is full of colours. Almost 1 has a colour .Some things are yellow like cheese, lemons and bananas. 2 things are red. For example, warning signs are usually red. 3 is the colour of most spring leaves and grass.4 is blue? Blue is the colour of5 .We can also see the blue sky , blue eyes , blue birds and blue jeans. There are many6 colours too, such as orange, brown, purple, white and black.The world changes its colours with the 7 of the year. Spring is green. Summer is red. It turns gold in autumn and then 8 in winter. When winter is gone and spring is back, the world turns green again. .When winter is gone and spring comes back ,the world turns green again.9 a rainstorm you may see something that has many different colours in the sky .It is a rainbow. But10 different colours, can you imagine what the world looks like?1.A.none B.nothing C.something D.everything2.A.Few B.A little C.Lots of D.Little3.A.Green B.Red C.Yellow D.Blue4.A.When B.What C.Who D.Why5.A.the sun B.grass C.sea D.ground6.A.other B.another C.extra D.else7.A.months B.seasons C.days D.weeks8.A.red B.green C.yellow D.white9.A.Until B.After C.Before D.But10.A.with B.without C.for D.withinⅢ. 语法填空12、阅读下面材料,在空白处填入适当的内容(1个单词)或括号内单词的正确形式。
江苏省无锡市甘露学校2019-2020学年第一学期九年级上册第13周周测数学试卷(无答案)

无锡市甘露学校初三数学周测班级姓名. 1.tan60°的值为--------------------------------------------------------------------------------------------------------()A.21B.23C.33D.32.一组数据7、11、12、7、7、8、11,下列说法错误的是--------------------------------------------()A.中位数是7B.平均数是9C.众数是7D.极差是53.某次比赛设置了6个获奖名额,共有11名选手参加,他们的比赛得分均不相同.要判断他能否获奖,在下列11名选手成绩的统计量中,只需知道---------------------------------------------------------()A.方差B.平均数C.众数D.中位数4.关于x的一元二次方程x2+2x+k=0有两个相等的实数根,则k的取值范围是---------------()A.k=-1B.k>-1C.k=1D.k>15.下列关于三角形的外心的说法中,正确的是--------------------------------------------------------------()A.三角形的外心在三角形外B.三角形的外心到三边的距离相等C.三角形的外心到三个顶点的距离相等D.等腰三角形的外心在三角形内6.一个正多边形的每个外角都等于36°,则该正多边形的边数为---------------------------------()A.6B.8C.10D.127.如图,在6×6的正方形网格中,△ABC的顶点都在小正方形的顶点上,则tan∠BAC等于()A.54B.34C.43D.538.如图,将45°的∠AOB按下面的方式放置在一把刻度尺上:顶点O与尺下沿的端点重合,OA与尺下沿重合,OB与尺上沿的交点B在尺上的读数恰为2厘米,若按相同的方式将37°的∠AOC放置在该刻度尺上,则OC与尺上沿的交点C在尺上的读数为------------------------------------------------()A.2.5B.2.6C.2.7D.2.89.如图,在△ABC中,∠BAC=90°,AB=AC,点D为边AC的中点,DE⊥BC于点E,连接BD,则tan∠DBC的值为---------------------------------------------------------------------------------------------------------()A.31B.12 C.2-3D.4110.如图,已知点A是双曲线y=x2在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=xk(k<0)上运动,则k的值为--------------------------------------------------------------------------()A.4B.-4C.-6D.-8二、填空题:(第10题图)(第8题图)(第9题图)(第7题图)11.一个不透明的口袋中有5个完全相同的小球,分别标号为1,2,3,4,5,从中随机摸出一个小球,其标号是偶数的概率为____ ______.12.在Rt△ABC中,∠C=90°,AB=2,BC=1,则sinA=____ ______.13.某商品经过连续两次降价,销售单价由原来200元降到162元.则平均每次降价的百分率为_ ____.14.在△ABC中,(tanA-3)2+|cosB-22|=0,则∠C的度数为____ ______.15.如图,△ABC的外接圆O的半径为2,∠C=30°,则扇形AOB的面积是____ ______.16.如图,太阳光线与地面成60°角,一棵倾斜的大树AB与地面成30°角,这时测得大树在地面的影长BC为10m,则大树的长为____ ______m.17.如图,已知l1∥l2∥l3,相邻两条平行直线间的距离相等,若等腰直角△ABC的三个项点分别在这三条平行直线上,则αsin的值是____ ______.18.如图,已知A、B两点的坐标分别为(23,0)、(0,2),P是△AOB外接圆上的一点,且∠AOP=45°,则点P的坐标为____ ______.三、解答题:(共66分)19.解下列方程(每小题4分,共8分)(1)0142=--xx(2)9332-=-xxx)(20.(本题8分)大课间活动时,有两个同学做了一个数字游戏:有三张正面写有数字-1,0,1的卡片,它们背面完全相同,将这三张卡片背面朝上洗匀后,其中一个同学随机抽取一张,将其正面的数字作为p的值,然后将卡片放回并洗匀,另一个同学再从这三张卡片中随机抽取一张,将其正面的数字作为q值,两次结果记为(p,q).(1)请你帮他们用树状图或列表法表示(p,q)所有可能出现的结果;(2)求满足关于x的方程x2+px+q=0没有实数解的概率.21.(本题8分)如图,在Rt△ABC中,∠C=90°,AB=10,sin∠A=52,求BC的长和tan∠B的值.(第15题图)(第16题图)(第17题图)(第18题图)22.(本题8分)根据道路管理规定,在贺州某段笔直公路上行驶的车辆,限速40千米/时,已知交警测速点M 到该公路A 点的距离为102米,∠MAB =45°,∠MBA =30°(如图),现有一辆汽车由A 往B 方向匀速行驶,测得此车从A 点行驶到B 点所用的时间为3秒.(1)求测速点M 到该公路的距离;(2)通过计算判断此车是否超速.23.(本题8分)如图,点A 、B 、C 分别是⊙O 上的点,∠B =60°,CD 是⊙O 的直径,P 是CD 延长线上的点,且AP =AC .(1)求证:AP 是⊙O 的切线;(2)若AC =3,求PD 的长.24.(本题8分)如图,为了测量小岛两端A 、B 的距离,测量人员设计了一种测量方法,已知B 点是CD 的中点,E 是BA 延长线上的一点,测得AE =10海里,DE =30海里, DE ⊥EC ,cos ∠D =53. (1)求小岛两端A 、B 的距离;(2)过点C 作CF ⊥AB 交AB 的延长线于点F ,求sin ∠BCF 的值.25.(本题8分)如图,直线y =33x +1分别与两坐标轴交于A ,B 两点,点C 从A 点出发沿射线BA 方向移动,速度为每秒1个单位长度.以C 为顶点作等边△CDE ,其中点D 和点E 都在x 轴上.半径为33-3的⊙M 与x 轴、直线AB 相切于点G 、F .(1)直线AB 与x 轴所夹的角∠ABO = °;(2)求当点C 移动多少秒时,等边△CDE 的边CE 与⊙M 相切?26.(本题满分10分)学习了勾股定理的逆定理,我们知道:在一个三角形中,如果两边的平方和等于第三边的平方,那么这个三角形为直角三角形.类似地,我们定义:对于任意的三角形,设其三个内角的度数分别为x °、y °和z °,若满足222x y z +=,则称这个三角形为勾股三角形.(1)根据“勾股三角形”的定义,请你直接判断命题:“直角三角形是勾股三角形”是真命题还是假命题?(2)已知某一勾股三角形的三个内角的度数从小到大依次为x °、y °和z °,且xy =2160,求x +y 的值;(3)如图,△ABC 内接于⊙O ,AB =6,AC =1+3,BC =2,⊙O 的直径BE 交AC 于点D . ①求证:△ABC 是勾股三角形;②求DE 的长.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初三周
末测试卷七2019.11.01
一、选择题(本大题共10小题,每小题3分,共30分)
1.已知32=b a ,则b a a
+ ( )
A .23
B .53
C .52
D .3
2
2.已知⊙O 的半径为4,A 为线段PO 的中点,当OP=10时,点A 与⊙O 的位置关系为( ) A . 点A 在⊙O 上 B .点A 在⊙O 外 C .点A 在⊙O 内 D .不能确定
3.已知∠A 为锐角,且sin A =,那么∠A 等于 ( )
A .15°
B .30°
C .45°
D .60° 4. 在下列网格中,小正方形的边长为1,点A 、B 、O 都在格点上,则∠A 的正切值是 (
)
B .
C .
D .
5.如图,点A ,B ,C 在⊙O 上,∠A=36°,则∠O= ( ) A .72° B .18° C .54° D .36°
6.如图中△ABC 外接圆的圆心坐标是 ( ) A.(2,5) B.(6,2) C.(2,6) D.(5,2)
7.如图是一个几何体的三视图,则该几何体的侧面积是 ( ) A.213π B .10π C .20π D .413π
第4题
8.下列说法中,正确的是 ( )
A .垂直于半径的直线一定是这个圆的切线
B .三角形的内心到三角形的三个顶点的距离相等
C .三点确定一个圆
D .任何三角形有且只有一个内切圆
9.如图,在平地MN 上用一块10m 长的木板AB 搭了一个斜坡,两根支柱AC =7.5m ,AD =6m ,其中AC ⊥AB ,AD ⊥MN ,则斜坡AB 的坡度是 ( ) A. 3:5 B. 4:5 C. 3:4 D. 4:3
10.如图,在平面直角坐标系中,A (0,3)、B (3,0),以点B 为圆心、2为半径的⊙B 上有一动点P .连
接AP ,若点C 为AP 的中点,连接OC ,则OC 的最小值为 ( )
A . O
A
B C 第5题 第6题
第7题
x
y C B
A
O
P
C
D
B
A A .1
B .2
32-1 C .2 D .22-1
第9题 第10题
二、填空题(本大题共8小题,每小题2分,共16分.)
11.在Rt △ABC 中,∠C =90°,AB =3,AC =2,则cos A 的值为 .
12.在比例尺为1:8000的地图上,两地的距离为20 cm ,它的实际距离约为 m . 13.当气温与人体正常体温(37℃)的比值等于黄金比值时人体感到最舒适,则这个气温约为_______℃ (结果保留整数).
14. 工程上常用钢珠来测量零件上小圆孔的宽口,假设钢珠的直径是10mm ,测得钢珠顶端离零件表面的
距离为8mm ,如图所示,则这个小圆孔的宽口AB 的长度为 mm.
(第15题图) 15.如图,在△ABC 中,AB =8cm ,BC =16cm ,点P 从点A 开始沿AB 边向B 点以2cm/s 的速度移动,点Q 从点B 开始沿BC 边向点C 以4cm/s 的速度移动,如果P 、Q 分别从A 、B 同时出发,经过 秒钟△PBQ 与△ABC 相似. 16.如图,在矩形ABCD 中,以A 为圆心,AD 长为半径作圆,交AB 于点E ,F 为BC 的中点,过点F 作
AB 的平行线,交
D E 于点G ,则 AGF 的度数为 . 17. 如图正方形ABCD 的边长为4,点E 是AB 上的一点,将△BCE 沿CE 折叠至△FCE ,若CF ,CE 恰好
与以正方形ABCD 的中心为圆心的⊙O 相切,则折痕CE 的长为 . 18. 如图,在四边形ABCD 中,AB ∥CD ,AB =BC =BD =2,AD =1,则AC = .
16题
E
G
F C A
B
D
6m
7.5m A
B M
N
三、解答题(本大题共10小题,共84分.解答时应写出文字说明、证明过程或演算步骤) 19.(本题满分8分)计算:
(1)0
1
)2(|3|60sin 21-+--+⎪⎭
⎫ ⎝⎛--πο (2) 24cos 60tan 45tan 60o
o o
-
20. 解方程 (本题共2小题,每题4分,共8分)
⑴ 01422=+-x x (2)()()3322-=-x x x
21.(6分)已知,△ABC 在直角坐标平面内,三个顶点的坐标分别为A (﹣2,2)、 B (﹣1,0)、C (0,1)(正方形网格中每个小正方形的边长是一个单位长度). (1)画出△ABC 关于y 轴的轴对称图形△A 1B 1C 1;
(2)以点O 为位似中心,在网格内画出所有符合条 件的△A 2B 2C 2,使△A 2B 2C 2 与△A 1B 1C 1位似, 且位似比为2:1;
(3)求△A 1B 1C 1与△A 2B 2C 2的面积比.
22.(8分)如图,在平行四边形ABCD 中,过点A 作AE ⊥BC ,垂足为E , 连接DE ,F 为线段DE 上一点,且∠AFE=∠B . (1)求证:△ADF ∽△DEC ;
(2)若AB=18,AD=95,AF=65,求AE 的长.
23. (本题满分8分)如图,某广场一灯柱AB 被一钢缆CD 固定,CD 与地面成40°夹角,且CB =5米. (1)求钢缆CD 的长度;
(2)若AD =2米,灯的顶端E 距离A 处1.6米,且∠EAB =120°,则灯的顶端E 距离地面多少米?
(参考数据:tan400=0.84, sin400=0.64, cos400
=34
)
24. (本题满分8分)△ABC 中,AB=AC ,以AB 为直径的⊙O 交BC 于D,DE 切⊙O 于D,交AC 于E 。
(1)求证:D E ⊥AC 。
(2)用无刻度的直尺在⊙O 上求作一点F ,使FA 平分∠A 的外角。
(不写作法,保留作图痕迹)
25. (本题满分8分) 如图,O 为正方形ABCD 的对角线AC 上一点,以O 为圆心,OC 的长为半径的⊙O 与AB 相切于点M .
(1)求证:AD 与⊙O 相切;
(2)若AB =2+ 2 ,求图中阴影部分面积. F E
C
B
D A
M
O
E
D
B
O
A
26.(本题满分10分)如图,已知AD 是△ABC 的角平分线,⊙O 经过A 、B 、D 三点,过点B 作BE ∥AD ,交⊙O 于点E ,连接ED . (1)求证:ED ∥AC ;
(2)若BD=2CD ,设△EBD 的面积为1S ,△ADC 的面积为2S ,且2121640S S -+=,求△ABC 的面积.
27.(本题满分9分)在某次活动课中,甲、乙、丙三个学习小组于同一时刻在阳光下对校园中一些物体进行了测量.下面是他们通过测量得到的一些信息:
甲组:如图1,测得一根直立于平地,长为80cm 的竹竿的影长为60cm. 乙组:如图2,测得学校旗杆的影长为900cm.
丙组:如图3,测得校园景灯(灯罩视为球体,灯杆为圆柱体,其粗细忽略不计)的高度为200cm ,影长为156cm. 任务要求:(1)请根据甲、乙两组得到的信息计算出学校旗杆的高度;
(2)如图3,设太阳光线NH 与⊙○相切于点M .请根据甲、丙两组得到的信息,求景灯灯
罩的半径(友情提示:如图3,景灯的影长等于线段NG 的影长;需要时可采用等式222156208260+=). E
B
C
D A
O
F
图2 图1
图3
28.(本题满分11分)如图⊙M与菱形ABCD在平面直角坐标系中,点M的坐标是(−3,1),点A坐标为(2,0),点B的坐标为(1,−3),点D在x轴上,且点D在点A的右侧。
(1)求菱形ABCD的周长;
(2)若⊙M沿x轴向右以每秒3个单位长度的速度平移,菱形ABCD沿x轴向左以每秒2个单位长度的速度
平移,设菱形移动的时间为t(秒),
①当⊙M与AD相切,且切点为AD的中点时,连接AC,求t的值及∠MAC的度数;
②当点M与BD所在的直线的距离为1时,求t的值。
