孔珑第三版流体力学习题答案
流体力学第二、三章作业答案(1)

配套教材:《工程流体力学》(第三版),孔珑主编,中国电力出版社第二章 流体及其物理性质2-12一平板距离另一个固定平板0.5mm ,两板间充满流体,上板在每平方米有2N 的力的作用下以0.25m/s 的速度移动,求该流体的黏度。
解:由牛顿黏性定律UAF可得s Pa U A F 004.025.0105.0232-13已知动力滑动轴承的轴直径d =0.2m ,转速n =2830r/min ,轴承内径D =0.2016m ,宽度l =0.3m ,润滑油的动力粘度 =0.245Pa·s ,试求克服摩擦阻力所消耗的功率。
解:轴的转动角速度为602nw 线速度为602d n w d ukWd D l d n d n d D d dl w d d D u A Mw P 7.502.02016.018003.02.014.32830245.018003600222/33233222第三章 流体静力学3-2如图所示为一直煤气管,为求管中静止煤气的密度,在高度差H =20m 的两个截面装U 形管测压计,内装水。
已知管外空气的密度 a =1.28kg/m 3,测压计读数h 1=100mm ,h 2=115mm 。
与水相比,U 形管中气柱的影响可以忽略。
求管内煤气的密度。
解:11O H 12a p gh p 22O H 22a p gh pgH p p gas 21 gHp p a a a 213O H 21gas kg/m 53.028.120115.01.010002a H h h 3-3如图所示,U 形管压差计水银面高度差h=15cm 。
求充满水的A 、B 两容器内的压强差。
解:gh h h g p gh p Hg A O H B A O H A 22Pa gh p p O H Hg B A 1852215.08.910001360023-4如图所示,U 形管压差计与容器A 连接,已知h 1=0.25m ,h 2=1.61m ,h 3=1m 。
孔珑 第三版 流体力学习题答案(部分)
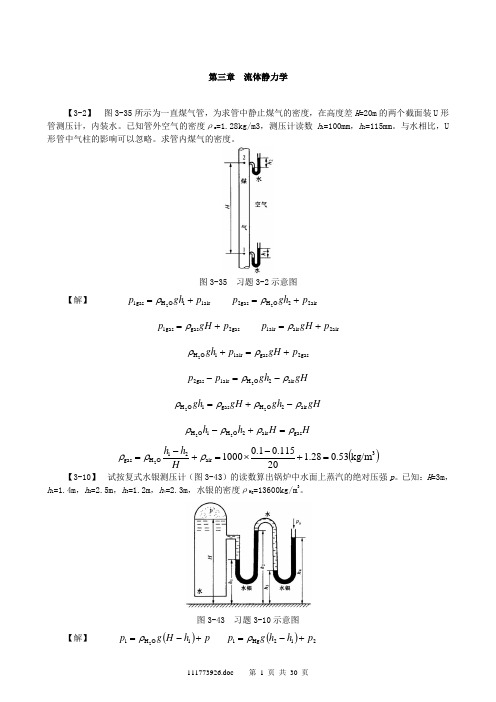
第三章 流体静力学【3-2】 图3-35所示为一直煤气管,为求管中静止煤气的密度,在高度差H =20m 的两个截面装U 形管测压计,内装水。
已知管外空气的密度ρa =1.28kg/m3,测压计读数h 1=100mm ,h 2=115mm 。
与水相比,U 形管中气柱的影响可以忽略。
求管内煤气的密度。
图3-35 习题3-2示意图【解】 1air 1O H 1gas 2p gh p +=ρ 2air 2O H 2gas 2p gh p +=ρ2gas gas 1gas p gH p +=ρ 2air air 1air p gH p +=ρ2gas gas 1air 1OH2p gH p gh +=+ρρgH gh p p air 2O H 1air 2gas 2ρρ-=-gH gh gH gh air 2O H gas 1OH22ρρρρ-+=H H h h gas air 2O H 1O H 22ρρρρ=+-()3air 21OHgas kg/m53.028.120115.01.010002=+-⨯=+-=ρρρH h h【3-10】 试按复式水银测压计(图3-43)的读数算出锅炉中水面上蒸汽的绝对压强p 。
已知:H =3m ,h 1=1.4m ,h 2=2.5m ,h 3=1.2m ,h 4=2.3m ,水银的密度ρHg =13600kg/m 3。
图3-43 习题3-10示意图()232O H 32p h h g p +-=ρ ()a 34Hg 3p h h g p +-=ρ()()212Hg 1OH 2p h h g p h H g +-=+-ρρ()()a 34Hg 232OH2p h h g p h h g +-=+-ρρ()()a 3412Hg 321OH2p h h h h g p h h h H g +-+-=+-+-ρρ()()()()()Pa 14.3663101013252.15.24.13807.910004.15.22.13.2807.913600a321O H 1234Hg 2=+-+-⨯⨯--+-⨯⨯=+-+---+-=p h h h H g h h h h g p ρρ ()()()()()Pa 366300.6831013252.15.24.1380665.910004.15.22.13.280665.913600a321O H 1234Hg 2=+-+-⨯⨯--+-⨯⨯=+-+---+-=p h h h H g h h h h g p ρρ 【3-15】 图3-48所示为一等加速向下运动的盛水容器,水深h =2m ,加速度a =4.9m/s 2。
流体第三版习题答案

流体第三版习题答案流体第三版是一本流体力学的教材,它涵盖了许多重要的概念和理论。
对于学习流体力学的学生来说,掌握这些概念和理论是非常重要的。
然而,很多同学可能会遇到一些难题,在解题过程中感到困惑。
为了帮助这些同学,我整理了一些流体第三版习题的答案,希望能对大家有所帮助。
第一章是流体力学的基础知识。
在这一章中,我们学习了流体的基本性质和流动的基本原理。
习题一涉及了流体的密度和压力的计算。
答案是根据流体的密度和液体柱的高度来计算的。
习题二是关于浮力的问题。
答案是根据浸入液体中的物体的体积和密度来计算的。
第二章讨论了流体的静力学。
在这一章中,我们学习了流体的压力分布和流体静力学平衡的条件。
习题一涉及了一个水箱的问题。
答案是根据水箱的高度和液体的密度来计算的。
习题二是关于一个浸入液体中的物体的问题。
答案是根据物体的体积、密度和液体的密度来计算的。
第三章介绍了流体的动力学。
在这一章中,我们学习了流体的运动方程和流体的流动特性。
习题一涉及了一个管道中的流体流动问题。
答案是根据流量和管道的截面积来计算的。
习题二是关于一个涡流的问题。
答案是根据涡流的旋转速度和涡流的半径来计算的。
第四章讨论了流体的能量。
在这一章中,我们学习了流体的能量守恒和能量转化的原理。
习题一涉及了一个水泵的问题。
答案是根据水泵的功率和液体的流量来计算的。
习题二是关于一个水轮机的问题。
答案是根据水轮机的效率和液体的流量来计算的。
第五章介绍了流体的动量。
在这一章中,我们学习了流体的动量守恒和动量转化的原理。
习题一涉及了一个喷射器的问题。
答案是根据喷射器的喷射速度和喷射物体的质量来计算的。
习题二是关于一个涡旋的问题。
答案是根据涡旋的半径和涡旋的角速度来计算的。
通过解答这些习题,我们可以更好地理解流体力学的基本概念和原理。
同时,这些习题的答案也可以作为参考,帮助我们更好地解决类似的问题。
当然,这些习题的答案只是一种可能的解答方式,不同的方法和思路也是可以的。
流体力学答案孔珑

可得,q
v ·dA
dA
解得单位厚度平板间的体积流量q
ms
平均流速等于体积流量除以有效截面积,即
q v
A
5 3
m⁄s
3‐12 解:以各有效截面和管道壁面所包容的体积为控制体
ρvdA 其中, A ρvdA
ρvdA
A
A ρvdA
ρvdA
A
ρv A
ρvdA 0
ρvdA
ρvdA
A
A ρvdA p
ρvdA
A
ρvdA 0
A
p 763.2 m h
q v q
πd vA v
4 27 m⁄s
500 kg h
q
1500 kg h
q q · v 500 0.3816 190.8 m h
q q · v 1500 0.2816 572.4 m h πd
q v A v 4 3600
A
0. OOO1πρ
A ρvdA A ρv dA ρv A =‐0.0000075πρ
ρvdA
ρv dA ρv A
A
A
v 0.4125 m⁄s
0.00003375 πρ
q
A 0.4125
0.0004 1.297 10 m s
3‐13 解:以各输气管的有效截面积和主管所包容的体积为控制体,流体系统质量守恒
4q
d
0.09m
πv
3‐14 解:因为收缩段长 l=0.4m,α ,求得v D
D
30°
.. ..
51.136 m⁄s
3‐16 解:ρ P
P
RT . J·
·K
K 161.2 kg m
v A 49.6 m⁄s
工程流体力学答案(周云龙第三版)(完整资料).doc

【最新整理,下载后即可编辑】第一章1-1 90610500453.06=⨯==-V m ρkg/m 3906.01000906==d 1-2 544.0140027327334.11013252732730=⨯+⨯=+=p t ρρkg/m 31-3 1121211V V V t t V dV dt V --==α 98.616060)2080(10550)(611122=+⨯-⨯⨯=+-=-V V t t V V αm 3/h 1-4933666112121051011011099510102111----⨯=⨯⨯-⨯-⨯-=---=-=V V V p p V dV dp κ1/Pa1-5 47109.26781028.4--⨯=⨯⨯==νρμ Pa·s1-6 63103.14.999103.1--⨯=⨯==ρμνm 2/s 1-7 (1) 17.266050001.014.360=⨯⨯==dn u π m/s521023.510005.017.260⨯=⨯=-=-δu dy du 1/s (2) 222ddy du dL d dy du A d F M μπμ===35221033.51023.5108.01.014.35.322-⨯=⨯⨯⨯⨯⨯==du dy L d M πμ Pa·s (3) 3531079.21023.51033.5⨯=⨯⨯⨯==-dy duμτPa1-8 (1)y dy duμμτ2==(2)μμμμτ2122=⨯===y dydu1-9 (1)hu bL dy duAF 022μμ== (2) 当2hy =时,h u dy du 0μμτ==(3)当h y 23=时,0u u = 所以0==dy du μτ1-10 2903.03.0133)(112121=⨯⨯==+=+=μμμμdy du A dy du A F F F N967.01=μ Pa·s 933.1212==μμ Pa·s1-11dr r r dr r r r dA dy du r dF dM αδπωμαπδωμμsin 2sin 203=-=⋅=⋅=αδαπωμααδπωμαδπωμαδπωμαααcos 24)(sin 2sin 2sin 234403030tg H Htg dr r dr r dM M Htg Htg Htg =====⎰⎰⎰1-12 62.26020025.014.360=⨯⨯==dn u πm/s3925.050.025.014.3=⨯⨯==dL A πm 2331022.4102.0062.23925.082.0⨯=⨯-⨯⨯==-dy du A F μN 05.1162.21022.43=⨯⨯==Fu P kW1-13 0841.0100092.0109144.04=⨯⨯⨯==-νρμPa·s1459.03048.01524.014.3=⨯⨯==dL A πm 22.7361024.1526.152061459.00841.03=⨯--⨯⨯==-dydu A F μN42.462.736=⨯==Fv P kW1-14 dr r r r rdrr dy du dA r dF dM 3202δμπωδωπμμ=-⋅==⋅= δμπωδμπω3224203d dr r dM M d A ===⎰⎰ 1-15 785.0125.014.3=⨯⨯==dL A πm 23610258.4001.003.0785.01008.18--⨯=-⨯⨯⨯==dy du AF μN 1-16 1884.03.02.014.3=⨯⨯==Db A πm 2δμδμμ20u Au u A u dy du A Fu N =-===9374.01884.0245.01008.07.502=⨯⨯⨯==-A N u μδm/s9056.892.014.39374.06060≈=⨯⨯==D u n πr/min 1-17 082.091810893.04=⨯⨯==-νρμ Pa·s75.14103.003.01.08.1082.03=⨯-⨯⨯⨯==-dy du A F μN 1-18 由1-14的结果得2.791023.096046.09014.31044003032323424424=⨯⨯⨯⨯⨯⨯=⨯==--δμπδμπωnd d M N ·m1-19dydu AF 00μ=dydu AF 120120μ= %7.86015.0002.0015.00120001200=-=-=-μμμF F F 1-20 3.29105.0324.0105.08.910000728.098.1324.098.1332=⨯⨯-⨯⨯⨯⨯=-=--r gr h O H ρσmm 1-217.11)105.0216.0105.08.91000513.053.1()216.053.1(33=⨯⨯-⨯⨯⨯⨯-=--=--r gr h Hg ρσmm 1-22 由2642322δδδδρσ-++=R R g h 得 δδδδρσ4622223+⎪⎪⎭⎫ ⎝⎛-+=R R h g其中 ()θθδsin 1cos -=R则 ()⎥⎦⎤⎢⎣⎡+++=22sin 13sin 21cos 2θθθρσR h gR 1-23 根据牛顿内摩擦定律 drdVμτ-=由于流速u 随半径r 的增加而减小,即drdu是负值,为了使τ为正值,上式在等号右端取负号根据已知条件 r r D dr d 2)]4(4[22βμβμτ=--=在管壁处2D r = 则4221DD ββτ== 当4D r =时 4222DD ββτ== 管壁处的阻力 L D DL D A F 21414βππβτ===1-24 ma F G =- 其中18.98.990===g G m (kg ) 则)61.0(18.990-⨯=-F60.95=F N由dyduA F μ=其中0583.01219.015228.014.3=⨯⨯==DL A πm 26.248979100245.001.603=⨯-=-=-δu dy du 1/s则310586.6006586.06.2489790583.06.95-⨯==⨯==dydu A F μ Pa·s第二章2-1112.2128.08.910009.08.913600105122=⨯⨯-⨯⨯+=-+=gh gh p p O H Hg a A ρρkPa2-2 08.140599.08.91594)0(=⨯⨯=∆--=-=h g p p e v ρPa 92.8726508.14059101325=-=-=v a p p p Pa2-3 gh gh p B A e ρρ=+ 且 1.015.025.0=-=h m (a) 9801.08.91000)(=⨯⨯=≈-=gh gh p B A B e ρρρPa 102305980101325=+=+=e a p p p Pa(b) 4.8131.08.9100083.0)(=⨯⨯⨯=≈-=gh gh p B A B e ρρρPa 4.1021384.813101325=+=+=e a p p p Pa(c) 123481.08.9)100013600()(=⨯⨯-=-=gh p A B e ρρPa 11367312348101325=+=+=e a p p p Pa2-4 设A 点到下水银面的距离为h 1,B 点到上水银面的距离为h 2 B O H Hg O H A p gh gh gh p =+-+2122ρρρ04.348.521+=+-h h h 即 44.221+=+h h h305.18.9)100013600(8.9100044.210)372.1744.2()(44.2522=⨯-⨯⨯+⨯-=-+-=gg p p h O H Hg O H B A ρρρm2-5 44.03000027.025.10027.025.1=⨯-=-=s s t ρkg/m 3gHp gH p a a s s ρρ-=-6.166208.9)44.029.1()(=⨯⨯-=-=-gH p p s a s a ρρPa2-64.1340638.9100012.08.913600312.02=⨯⨯+⨯⨯-=⨯+⨯-=g g p O H Hg e ρρPa2-7 223311gh gh p gh p B A ρρρ++=+(1)112233100010001000gh d gh d gh d p p B A-++=16.08.983.0100008.08.96.13100012.08.983.010********.68⨯⨯⨯-⨯⨯⨯+⨯⨯⨯+⨯=287.79=kPa(2)332211100010001000gh d gh d gh d p p A B --+=12.08.983.0100008.08.96.13100016.08.983.010*******.137⨯⨯⨯-⨯⨯⨯-⨯⨯⨯+⨯=96.127562=Pa563.319600096.127562=-=-=a B Be p p p kPa2-8 设401=h cm22=h m33=h m)(32112h h g p gh gh gh p B B Hg A A A +-=+--ρρρρ 11232)(gh gh gh h h g p p Hg A A B B A ρρρρ-+++-=4.08.9136004.08.97.85628.97.856)32(8.93.1254200000⨯⨯-⨯⨯+⨯⨯++⨯⨯-=377.105=kPa2-9 (1)93.138545sin 2.08.91000sin =⨯⨯⨯==- αρgL p p B A Pa(2)3530sin 8.980093.1385sin =⨯⨯=-=αρg p p L B A cm 2-10666405.08.9136001=⨯⨯=∆=h g p Hg ρPa68.08.91000666422=⨯==∆gph O H ρm2-111022gh p gh p O H Hg a ρρ+=+4032gh p gh p O H Hg a ρρ+=+整理得 )(1321422h h h h Hg Hg O H OH ρρρρ+-=)3.0136002.0136005.01000(10001⨯+⨯-⨯=86.1=m2-12 )()()(112342h H g h h g h h g p p O H Hg Hg a ---+-+=ρρρ)5.15.3(8.91000)5.15.2(8.913600)0.13.2(8.913600105-⨯⨯--⨯⨯+-⨯⨯+=386944=Pa2-13 gh h g p Hg A ρρ=++)84.0(85.1138.9)100075.013600(84.08.9100075.010372.1)(84.05=⨯⨯-⨯⨯⨯+⨯=-⨯+=g g p h Hg A ρρρcm2-14)0.343.3(1000)74.22.3(1000-⨯-=-⨯+g d g d p B A 862.043.08.9100046.08.9100060.110845=⨯⨯-⨯⨯⨯+-=B d 2-15 59.0)59.0(22⨯++-=-g z g p gz p Hg O H B O H A ρρρ整理:853.7259.08.9)100013600(59.059.02=⨯⨯-=⨯-⨯=-g g p p O H Hg B A ρρkPa2-16 设差压计中的工作液体密度为ρ' )()()(213241h h g h h g p h h g p B A -'---=--ρρρ)()(213241h h g h h h h g p p p B A -'-+--=-=∆ρρ)48.381.3(8.9100075.0)00.348.310.081.3(8.910005.1-⨯⨯⨯-+--⨯⨯⨯==5.45055Pa 065.38.910005.15.45055=⨯⨯=∆g p ρ m 2-17112233100010001000gh d gh d gh d p p A B ---=44.28.975.0100052.18.9110006.08.96.131000274600⨯⨯⨯-⨯⨯⨯-⨯⨯⨯-=161802=Pa2-1882.38)34.01360053.0100025.1(8.934.053.0-=⨯-⨯⨯⨯=⨯-⨯=g g p Hg A ρρkPa2-19 (1) 981010018.910004=⨯⨯⨯⨯==-ghA F ρN(2) 95.1)99.01001.001.0(8.910004=⨯+⨯⨯⨯==-gV G ρN 2-20 证明:如书中证明过程。
物理学第3版习题解答-第1章流体的运动

第1章 流体的运动1-1 横截面是4 m 2的水箱,下端装有一个导管,水以2 m ·s -1的速度由这个导管流出。
如果导管的横截面是10 cm 2,那么水箱内水面下降时的速度是多大?解:根据连续性原理,得s m s m S v S v /105/410102442112--⨯=⨯⨯== l-2 有一水管,如图所示,设管中的水作稳定流动。
水流过A 管后,分B 、C 两支管流出。
已知三管的横截面积分别为S A =100 cm 2,S B =40 cm 2,S C =80 cm 2。
A 、B 两管中的流速分别为v A =40 cm ·s -1及v B =30 cm ·s -1。
则C 管中的流速v C 等于多少?解:根据连续性原理,得C C B B A A v S v S v S +=所以 s cm s cm S v S v S V C B B A A C /35/80304040100=⨯-⨯=-=1-3 水平放置的自来水管,粗处的直径是细处的2倍。
若水在粗处的流速和压强分别为1.0 m ·s -1和1.96×105 Pa ,那么水在细处的流速和压强各是多少? 解:4)2()2(2121222121===d dr r S S ππππ 根据连续性方程,得s m s m v S S v /4/141212=⨯== 根据伯努利方程,222212112121gh v p gh v p ρρρρ++=++得:Pa Pa v v p p 5223522211210885.1)41(10211096.1)(21⨯=-⨯⨯+⨯=-+=ρ 1-4 灭火水枪每分钟喷出60 m 3的水,若喷口处水柱的截面积为1.5 cm 2,问水柱喷到2m 高时的截面积有多大?解: s m s m St V v /1067.6/60105.160341⨯=⨯⨯==- 根据伯努利方程 222212121gh v v ρρρ+= 得 s m gh v v /1067.62102)1067.6(23232212⨯=⨯⨯-⨯=-=根据连续性原理,得 225.1cm S =题l-21-5 水在粗细不均匀的水平管中稳定流动,已知截面S 1处的压强为110 Pa ,流速为0.2 m ·s -1;在截面S 2处的压强为5 Pa ,求S 2处的流速。
工程流体力学(孔珑版)第五章_题解

第五章 相似原理和量纲分析【5-2】 如图5-8所示,用模型研究溢流堰的流动,采用长度比例尺k l =1/20。
(1)已知原型堰上水头h =3m ,试求模型的堰上水头;(2)测得模型上的流量q V ′=0.19m 3/s ,试求原型上的流量;(3)测得模型堰顶的计示压强p e ′=-1960Pa ,试求原型堰顶的计示压强。
图5-8 溢流堰【解】 (1) 模型的堰上水头与原型的堰上水头满足长度比例尺h h k l '=得 ()m 15.03201=⨯=='h k h l(2) 水在重力作用下由溢流堰上流过,要使流动相似,弗劳德数必须相等()121=gl vk k k 21l v k k = 252122l l l v l q VVk k k k k k q q V ===='()s m 339.8820119.032525=⎪⎭⎫ ⎝⎛='=lV V k q q(3) 设水在由大气和流堰面围成的流道内流过,重力场和压力场同时相似,弗劳德数和欧拉数都相等21l v k k =, 1=ρk 12=vp kk k ρ2v p k k k ρ=l p k k =l p k k pp =='()Pa 39200201960-=-='=lk p p【5-3】 有一内径d =200mm 的圆管,输送运动黏度ν=4.0×10-5m 2/s 的油,其流量q V =0.12m 3/s 。
若用内径d ′=50mm 的圆管并分别用20℃的水和20℃的空气作模型试验,试求流动相似时模型管内应有的流量。
【解】 黏性流体在黏滞力作用下在管内流动,使流动相似,雷诺数必须相等1=νk k k lv ()ννν''====='d d k k k k k k k k q q l l v l v l q V V V 2V Vq d d q νν''='20℃水的运动黏度1.007×10-6m 2/s()m 107.552512.0100.410007.1200503456---⨯=⨯⨯⨯⨯='V q 20℃空气的运动黏度15×10-6m 2/s()s m 10125.112.0100.41015200503256---⨯=⨯⨯⨯⨯='V q【5-8】 在管道内以v =20m/s 的速度输送密度ρ=1.86kg/m 3、运动黏度ν=1.3×10-5m 2/s 的天然气,为了预测沿管道的压强降,采用水模型试验。
131097575518099332孔珑习题答案

压力中心的x坐标为:xD=d/2=0.25m
d 4 ( ) 2 I cx d 4 y D yc (a ) 1.2625m 2 d d yc A 2 (a ) 2 4
3-21、图3-54所示为绕铰链O转动的倾斜角α=60°的自动开启水闸, 当水闸一侧的水位H=2m,另一侧的水位h=0.4m时,闸门自动开启, 试求铰链至水闸下端的距离x. 解:对于闸门左侧
P F v 1710 . 8 2830 2 0 . 1 50 . 7 Kw 60
克服摩擦力所消耗的功率为:
第三章作业
3-5、如图3-38所示,在盛有油和水的圆柱形容器的盖上加载荷 F=5788N,已知h1=30cm,h2=50cm,d=0.4m,油的密度 oi 800kg / m3 ,水银的密度 Hg 13600kg / m3 ,求U形管中水银 柱的高度差。 解:在F作用下,活塞底面产生的压强为
同理对于闸门的右侧可得右侧水作用在闸门上的总压力为:
1 F2 ghc 2 A2 gh 2b 3
压力中心的坐标为: y D 2
I cx 2 2 h yc 2 yc 2 A2 3 sin
根据合力矩定理,对o点取距,则有
M
o
0
H h 2h F1 ( x ) F2 ( x )0 3 sin sin 3 sin 解得:x 0.795m
p 水 g ( H h1 ) Hg g (h2 h1 ) 水 g (h2 h3 ) Hg g (h4 h3 ) Pa 则 p Hg g (h4 h3 ) - 水 g ( H h1 ) Hg g (h2 h1 ) - 水 g (h2 h3 ) Pa 13600 9.8 (2.3 1.2 2.5 1.4) 1000 9.8 (3 1.4 2.5 1.2) 101325 366121( Pa)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章 流体静力学【3-2】 图3-35所示为一直煤气管,为求管中静止煤气的密度,在高度差H =20m 的两个截面装U 形管测压计,内装水。
已知管外空气的密度ρa =1.28kg/m3,测压计读数h 1=100mm ,h 2=115mm 。
与水相比,U 形管中气柱的影响可以忽略。
求管内煤气的密度。
图3-35 习题3-2示意图【解】 1air 1O H 1gas 2p gh p +=ρ 2air 2O H 2gas 2p gh p +=ρ2gas gas 1gas p gH p +=ρ 2air air 1air p gH p +=ρ2gas gas 1air 1O H 2p gH p gh +=+ρρgH gh p p air 2O H 1air 2gas 2ρρ-=-gH gh gH gh air 2O H gas 1O H 22ρρρρ-+=H H h h gas air 2O H 1O H 22ρρρρ=+-()3air 21OH gas kg/m 53.028.120115.01.010002=+-⨯=+-=ρρρH h h 【3-10】 试按复式水银测压计(图3-43)的读数算出锅炉中水面上蒸汽的绝对压强p 。
已知:H =3m ,h 1=1.4m ,h 2=2.5m ,h 3=1.2m ,h 4=2.3m ,水银的密度ρHg =13600kg/m 3。
图3-43 习题3-10示意图【解】 ()p h H g p +-=1O H 12ρ ()212Hg 1p h h g p +-=ρ()232O H 32p h h g p +-=ρ ()a 34Hg 3p h h g p +-=ρ()()212Hg 1O H 2p h h g p h H g +-=+-ρρ()()a 34Hg 232O H 2p h h g p h h g +-=+-ρρ()()a 3412Hg 321O H 2p h h h h g p h h h H g +-+-=+-+-ρρ()()()()()Pa 14.3663101013252.15.24.13807.910004.15.22.13.2807.913600a321O H 1234Hg 2=+-+-⨯⨯--+-⨯⨯=+-+---+-=p h h h H g h h h h g p ρρ ()()()()()Pa 366300.6831013252.15.24.1380665.910004.15.22.13.280665.913600a321O H 1234Hg 2=+-+-⨯⨯--+-⨯⨯=+-+---+-=p h h h H g h h h h g p ρρ【3-15】 图3-48所示为一等加速向下运动的盛水容器,水深h =2m ,加速度a =4.9m/s 2。
试确定:(1)容器底部的流体绝对静压强;(2)加速度为何值时容器底部所受压强为大气压强?(3)加速度为何值时容器底部的绝对静压强等于零?图3-48 习题3-15示意图【解】 0=x f ,0=y f ,g a f z -=压强差公式 ()z f y f x f p z y x d d d d ++=ρ()()z g a z f y f x f p z y x d d d d d -=++=ρρ()⎰⎰--=hpp z g a p ad d ρ()()()()⎪⎪⎭⎫⎝⎛-=-=----=-g a gh a g h g a h g a p p a 10ρρρρ⎪⎪⎭⎫⎝⎛-+=g a gh p p a 1ρ()a g h p p a -=-ρhp p g a aρ--= (1) ()()()Pa 111138.39.480665.921000101325=-⨯⨯+=-+=a g h p p a ρ (2) ()2s m 80665.9==--=--=g hp p g h p p g a aa a ρρ (3) ()2s m 60.4691521000101325080665.9=⨯--=--=h p p g a a ρ 【3-16】 图3-49所示为一圆柱形容器,直径d =300mm ,高H =500mm ,容器内装水,水深h 1=300mm ,使容器绕铅直轴作等角速旋转。
(1)试确定水正好不溢出时的转速n 1;(2)求刚好露出容器底面时的转速n 2;这时容器停止旋转,水静止后的深度h 2等于多少?图3-49 习题3-16示意图【解】 初始状态圆筒中没有水的那部分空间体积的大小为()1241h H d V -=π (1)圆筒以转速n 1旋转后,将形成如图所示的旋转抛物面的等压面。
令h 为抛物面顶点到容器边缘的高度。
空体积旋转后形成的旋转抛物体的体积等于具有相同底面等高的圆柱体的体积的一半h d V 24121π⋅=(2) 由(1)(2),得()h d h H d 212412141ππ⋅=- (3) 即()12h H h -= (4)等角速度旋转容器中液体相对平衡时等压面的方程为C gz r =-222ω (5)对于自由液面,C =0。
圆筒以转速n 1旋转时,自由液面上,边缘处,2dr =,h z =,则02222=-⎪⎭⎫ ⎝⎛gh d ω (6) 得dgh22=ω (7) 由于6021n πω= (8) dgh d gh n πππω2602230301=⋅==(9) (1)水正好不溢出时,由式(4)(9),得()()dh H g d h H g n ππ1111202260-=-⋅=(10)即()()min r 178.33.03.05.080665.91201=⨯-⨯⨯=πn (2)求刚好露出容器底面时,h =H ,则()min r 199.43.05.080665.92602602601=⨯⨯⨯⨯===πππd gH d gh n (3)旋转时,旋转抛物体的体积等于圆柱形容器体积的一半H d V 24121π⋅=(11) 这时容器停止旋转,水静止后的深度h 2,无水部分的体积为()2241h H d V -=π (12)由(11)(12),得()222414121h H d H d -=⋅ππ (13) 得()m 25.025.022===H h 【3-21】 图3-54所示为绕铰链O 转动的倾斜角α=60°的自动开启式水闸,当水闸一侧的水位H =2m ,另一侧的水位h =0.4m 时,闸门自动开启,试求铰链至水闸下端的距离x 。
图3-54 习题3-21示意图【解】 设水闸宽度为b ,水闸左侧水淹没的闸门长度为l 1,水闸右侧水淹没的闸门长度为l 2。
作用在水闸左侧压力为111A gh F c p ρ= (1)其中21H h c =αsin 1H l = αsin 11H b bl A == 则αραρsin 2sin 221bgH H b H g F p == (2)作用在水闸右侧压力为222A gh F c p ρ= (3)其中22h h c =αsin 2h l = αsin 22h b bl A ==则αραρsin 2sin 222b gh h b h g F p == (4)由于矩形平面的压力中心的坐标为l bl l bl l A x I x x c cy c D 3221223=+=+= (5)所以,水闸左侧在闸门面上压力中心与水面距离为αsin 321H x D ⋅= (6)水闸右侧在闸门面上压力中心与水面距离为αsin 322Hx D ⋅= (7) 对通过O 点垂直于图面的轴取矩,设水闸左侧的力臂为d 1,则()x x l d D =-+111 (8)得()αααsin 3sin 32sin 111H x H Hx x l x d D -=⎪⎭⎫ ⎝⎛⋅--=--= (9) 设水闸右侧的力臂为d 2,则()x x l d D =-+222 (10)得()αααsin 3sin 32sin 222h x h hx x l x d D -=⎪⎭⎫ ⎝⎛⋅--=--= (11) 当满足闸门自动开启条件时,对于通过O 点垂直于图面的轴的合力矩应为零,因此02211=-d F d F p p (12)则⎪⎭⎫⎝⎛-=⎪⎭⎫ ⎝⎛-ααρααρsin 3sin 2sin 3sin 222h x b gh H x b gH (13) ⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-ααsin 3sin 322h x h H x H()()3322sin 31h H x h H-=-αh H h Hh H h H h H x +++⋅=--⋅=222233sin 31sin 31αα ()m 0.7954.024.04.02260sin 3122=++⨯+⋅=x 【3-29】 如图3-62所示,直径d =1m ,高H =1.5m 的圆柱形容器内充满密度ρ=900kg/m3的液体,顶盖中心开孔通大气。
若容器绕中心轴以n=50r/min的转速旋转,求容器的上盖、底面和侧面所受的液体总压力。
图3-62习题3-29示意图【解】由题设所述的容器内的压强分布与等角速度旋转运动容器中液体的静压强分布相同,为⎪⎪⎭⎫⎝⎛-+=zgrgppa222ωρ(1) 则计示压强为⎪⎪⎭⎫⎝⎛-=zgrgpe222ωρ(2) (1)作用在上盖的计示压强为2221rpeωρ=(3) 设圆柱体的底面积为A d,则作用在上盖的总压力为42424232221164124141dd22d222ddrrrrrrApF ddddAepρπωρπωρπωρπωπωρ=⎪⎭⎫⎝⎛=====⎰⎰⎰⎰(4) 由于30602nnππω==(5)42342157600130641dndnFpρππρπ=⎪⎭⎫⎝⎛=(6)()N 12111509005760014231=⨯⨯⨯⨯=πp F (2)作用在底面的计示压强为gH r gH p p e e ρωρρ+=+=22212 (7)则作用在底面的总压力为()2121021002202222412d 2d 22d 22d 2222gHd F d gH F r gH F r r gH r r r r r gH r A p F p p p A e p ddd d dπρπρπρπρπωρπρωρ+=⎪⎭⎫⎝⎛+=+=+=⎪⎪⎭⎫ ⎝⎛+==⎰⎰⎰⎰⎰(8)()N 1160915.180665.99004115090057600124232=⨯⨯⨯⨯⨯+⨯⨯⨯⨯=ππp F (3)由式(3)可知,作用在上盖边缘的计示压强为8222222b1d d p e ρωωρ=⎪⎭⎫⎝⎛= (9) 则作用在侧面的计示压强为gh d gh p p e e ρρωρ+=+=822b 13 (10)设圆柱体的侧面积为A c ,则作用在侧面的总压力为()28222228d d 2d d 28d d 2d d 28d d 28d 8d 2322220202002202002022020222233gdH Hd H gd H d d h h gd h d d h dgh h d d h dgh d A gh d A p F HH H HH A A e p c c πρπρωπρπρωθρθρωθρθρωθρρωρρωπππππ+=⋅⋅+⋅⋅⎪⎪⎭⎫ ⎝⎛=+⎪⎪⎭⎫ ⎝⎛=+⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛+=⎪⎪⎭⎫ ⎝⎛+==⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰ (11)将式(5)代入,得27200283023232323gdH H d n gdH Hd n F p πρρππρππρ+=+⎪⎭⎫⎝⎛= (12) ()N 4572825.1180665.990072005.115090023233=⨯⨯⨯⨯+⨯⨯⨯⨯=ππp F。
