2018全国高中数学联赛模拟试题2及参考答案
2018全国高中数学联赛模拟试题2及参考答案

由(1)式, x 12 | y2 x 1 | y x 1
x2 x 1
x
y
1
2
.又因为
y 则
为整数,
x 1
2
2
x 1 x2 x 1 为完全平方数.而 x2 x 1 x x 1 1 x 1, x2 x 1 1,
和为 15 的形如 4、5、6 的有 6 种,形如 5、5、5 的有 1 种,形如 6、6、3 的有 3 种,合计 10
种.
8. 2 2, 2 2 .
解析:设 z2 x yi x, y
.则 z1
z2i z
z2 i
1
y xi
x y 1i
2
2
证明: B .
4
4
A
3
3
2
2
三、(本题满分 50 分)
设整数 n 4 , a1, a2, , an 为区间 0, 2n 内两两不同的整数.证明:集合 A a1, a2 , , a n 存在所有
元 素之和能被 2n 整除的子集.
四、(本题满分 50 分)
设有 17 支球队参加足球比赛,采用单循环赛制,比赛中偶尔会出现一个循环的三元集(即集合a,b, c,其中 a 队击败 b 队, b 队击败 c 队, c 队击败 a 队),若没有平局,则比赛结束.问:最多有多少
b a
x 1
,
B
x2
,
b a
x 2
,
P x,
y .
b
由 OAPB 知, x x1 x2 , y
a
x1
2018全国高中数学联赛模拟试题2及参考答案

高中联赛模拟试题 2一试部分考试时间:80 分钟满分:120 分一、填空题(每小题 8 分,共 64 分)sin21.已知3 ,且,nn , k,则tan.sin22tan2. 在等差数列a n中,若a 11 a101 ,且前 n 项和 S n 有最大值,则当 S n 取得最小正值时, n.3. 若 a + bc1a ,b , c, 4 a 14 b14 c 1 m ,则 m 的最大值为 .4. 已知 ABC 满足 AC BC 1 , AB 2xx 0.则 ABC 的内切圆半径 r 的最大值为.5.在正方体 A BCDA 1B 1C 1D 1 中, G 为底面 A 1B 1C 1D 1 的中心.则 B G 与 A D 所成角的余弦值为___ ___.6.函数 f x 在 上有定义,且满足 f x 为偶函数, f x 1为奇函数.则 f22019.7.将一色子先后抛掷三次,观察面向上的点数,三数之和为5 的倍数的概率为.8. 已知复数 z 1 , z 2 满足 z 1iz 2i 1 .若 z 1,则 z 2 的取值范围是.二、解答题(第 9 小题 16 分,第 10、11 小题 20 分,共 56 分)x 2 y 29. 设 P 为双曲线 1 上的任意一点,过点 P 分别作两条渐近线的平行线,与两条渐近线交于 A ,Ba 2b 2两点.求□ABCD 的面积.10. 求方程 x 5x 3 x 2 1 y 2 的整数解的个数.11. 对于 n6 ,已知 11n1.求出满足 3n4n n 2nn 3n的所有正整数n .n 32高中联赛模拟试题 2加试部分考试时间:150 分钟满分:180 分一、(本题满分 40 分)设 ABC 为等腰三角形, ABAC , D 为边 AB 上一点.设 BCD 的外接圆 在点 D 处的切线与AC 交 于点 E , F 为过点 E 作圆 的另外一条切线的切点.设 B F 与 C D 交于点 G , AG 与 B C 交于点H . 证明: BH2HC .A二、(本题满分 40 分)约定: n 维向量 xx 1 , x 2 ,, x nx i0,i 1, 2, , n 的 p 范数记为:xx 1x2x npp p pppB现有两个向量 Aa ,b ,c ,B d , e .若:A B AB .证明: AB .22 4433三、(本题满分 50 分)设整数n4,a, a2 , , a n 为区间0,2n内两两不同的整数.证明:集合A a1 ,a2 ,,a n存在所有元素之和能被2n 整除的子集.四、(本题满分 50 分)设有17 支球队参加足球比赛,采用单循环赛制,比赛中偶尔会出现一个循环的三元集(即集合a, b, c,其中a队击败b队,b队击败c队,c队击败a队),若没有平局,则比赛结束.问:最多有多少个这样的循环三元集?高中联赛模拟试题 2解答一试部分考试时间:80 分钟满分:120 分一、填空题(每小题 8 分,共 64 分) 1.2.sin21解析:tansincossin2sinsin 2 .tancossinsin2sinsin21sin2.19.解析:由 S n 有最大值可知 a 1 0,d0 ,由a 11 a 101 ,则 a 10a 11 0, a11a 10 ,20a 1 a20S1aa0, S19a 1 a1919a0 ,202101119210再由 S 19S 1 a 2 a 3 a 199a 10a 110 ,知 S n 取最小正值时, n 19 .55213. 2 .解析:a 1b1 1a b a 1b 1 2 1 a b2ab 2 1a b22a111 a b11 1.反复利用上式,得:114c 1 14 a b14c1 1 125 ;另一方面,当 a1,b0, c0 22 为最大的下界.4.112解析:转化为求函数 f xx1 x在 0,1内的最大值.+ x5.6122解析:BGCG1BC 6 BC cosGBCBC 6.又AD//BC,则BG 与AD所成角的余弦值为62 2BG 6. 6. 0.解析:由已知得 fx关于 x 轴及点1, 0对称.从而 4 为 f x 的一个周期,且 f10 .故f2019 f10 .7.43 216解析:和为 5 的形如 3、1、1 与 2、2、1,共 6 种.和为 10 的形如 6、3、1 的有 6 种,形如 6、2、2 的有 3 种,形如 5、4、1 的有 6 种,形如 5、 3、2 的有 6 种,形如 4、3、3 的有 3 种,形如 4、4、2 的有 3 种.合计 27 种.和为 15 的形如 4、5、6 的有 6 种,形如 5、5、5 的有 1 种,形如 6、6、3 的有 3 种,合计 10 种.8.22.解析:设 z2x yix , y.则z 1zz 2izi1y xixy 1ix 2y222 .由z 2 的几何 意义,知其范围为22, 22 .21 1⎪ 22⎪1x -x -1 ⎪⎭二、解答题(第 9 小题16 分,第 10、11 小题 20 分,共 56 分) 9.双曲线的两条渐近线方程分别为 yb x , ybx .aa设 Ax , bax , B x , bax, P x , y.b由 OAPB 知, xx 1 x 2 , yaa2x 1x 2.代入双曲方程化简得 x 1 x 2.4于是, OAPB 的面积为 xb a2b x 1 x 2ax 1 x 21ab .210. 原方程可化为 x 31x 2 1y 2 x1 2x1x 2 x 1y 2 .------------------------------(1) 当 x 0 时, y 21 y1 ;当 x1 时, y0 .设 x , y 为方程的整数解,且 x1, 0 .由(1)式, x12| y2x1| yx1x 2x 1y.又因为 y 为整数,则x12ba2x1x2 x1为完全平方数.而x2 x1x x11x1,x2 x11,n n45 n + 3⎩⎪ x 1, x 2 x 1均为完全平方数 x 1 0x0, 1x 2 x 2 x 2 x 1 x12,显然,x 2 x 1不为完全平方数.综上,原方程只能有 4 组解:x ,y0,1,0, 1,1, 0,1, 0.11. 当 n6 时,由1 11n21n 3nn +2nn 2n.n3 2 n32nnn而34n 2 1,故:24n 3n 3n , 5n4n4n,n 3nn 2nn 2n.累加后 3n 4nn 2nn 3n3n n3n,此时无解. 直接检验 n 1, 2, 3, 4, 5 ,知当 n 2, 3 时等式成立.,.a4 4444一、(本题满分 40 分)加试部分考试时间:150 分钟满分:180 分在 ABG , ACG 中,由正弦定理得BG AGCGAGsin BAH sinABFsinCAHsin ACD故BH sinBAH BG sinABF BGsinFCDsin DCBsinFCDFDCI.CH sin CAH CG sin ACD CGsinDBIsin CBFsin DBIDI CF设 AC 与圆的另一个交点为 I .则四边形 C FID 为调和四边形. 于是,FI CD CF ID . 由托勒密定理得 F DCIFICDCF ID2IDCF . 从而, B H2HC .二、(本题满分 40 分)等价于证明:设 a , b , c , d , e 为非负数,且满足a 2b 2c 2d 2e 2 b c de ,证明: a 3 b 3c 3d 3e 3 .----------------------------------------------------------------------------------------(1) 注意到 2a 2b 2 b 2c 2 c 2a 2a 2b 2c 22a 4b 4c 4d 2e 22⎣⎦d 4 e42d 2e 2 . 则 a 2b 2 b 2c 2 c 2a 2 d 2e 2 .又 a 6b 6c 6 3a 2b 2c2 a 2 b 2 c 2 a 4 b 4 c 4 a 2b 2 b 2c 2 a 2c2d 2e 2 d 4e 4d 2e2d 6e 6(1)式两边平方得 a 6b 6c 6 2a 3b 3 b 3c 3 c 3a3d 6e 6 2d 3e 332a 3b 3 b 3c 3 c 3a33a 2b 2c 2 2d 3e 3 2a 3b 3 b 3c 3 c 3a33a 2b 2c 2 2a 2b 2 b 2c2c 2a 22---(2)3设 x ab , y bc , z ca .则(2) 2x 3 y 3 z33xyz 2x 2 y 2 z 22.由柯西不等式,知2 x3y3z 32+ 3xyzx2x2yz+ y 2 y2zx2+ z 2z2xyx 2 y 2 z22x 2 yz22 y 2 zx22z 2 xy2x 2 y 2 z 24x 4 y 4 z48y 2 z 2z 2 x 2 x 2 y24x 2 y2z 2 3. 从而,结论成立.三、(本题满分 50 分)若 na 1 , a 2 , , a n,则 2n 个整数 a 1 , a 2 ,, a n , 2n a 1 , 2n a 2 , , 2n a n0, 2n.由抽屉原理,知其中 必有两个数相等. 不妨设 a i2na j .因为 n a1 , a2 , , a n ,所以 ij . 故a i , a j满足题意,命题成立. 若 na 1 , a 2 , , a n ,不妨设 a n n .考虑 n 1n13个整数 a 1 , a 2 , , a n 1 ,在其中任取三个数 a ia ja k . 若 a ka j , a j a i 均能被 n 整除,则 a ka i2n ,与 ak0, 2n矛盾. 因此, a 1 , a 2 ,, a n1中至少存在两个数,其差不能被 n 整除.不妨设 a1 , a2 之差不能被 n 整除.考察 n 个数: a 1 , a 2 , a 1 a 2 , a 1 a 2 a3 ,, a 1 a 2a n 1 .(1)若这 n 个数关于模 n 的余数互不相同,则其中必有一个数能被 n 整除.令这个数为 k n . 当k 为偶数时,结论成立;当 k 为奇数时,加上 a n 即构成所需要的子集.(2)若这 n 个数中有两个数关于模 n 同余,则其差能被 n 整除.因为 a 1 , a 2 不同余,所以这两个数之差 必为原集合 A 中若干数之和.由此归结为(1)中讨论. 综上,命题得证.四、(本题满分 50 分)一个三元集a , b , c不是循环的 有一支球队赢了另外两队 有一支球队输给了另外两队.用 A 1 , A 2 ,, A 17 代表这 17 支球队 . 假 设 球 队 A i 赢了 a i 支球队,但输给了 b i 支球队 .显然,Ca = Cb = C a + 217∑ ∑. a i b i1 6i 1, 2 , , 1. 171711717于是,不循环的三元集的个数为2ii 12ii12i 1ii 1Cb.ia a 1bb11a b2对于每一个 i , C 2C2iii iiiab 56 .a ib i2 2 2 2 ii则不循环的三元集的个数至少为 117564762故循环三元集最多有 C 3476 204 个.当且仅当 a i b i8i 1, 2, ,17时,循环三元集的个数最多为 204.2。
普通高等学校2018届高三招生全国统一考试仿真卷(二)数学(理)试题含答案

绝密★启用前2018年普通高等学校招生全国统一考试仿真卷理科数学(二)本试题卷共2页,23题(含选考题)。
全卷满分150分。
考试用时120分钟。
★祝考试顺利★注意事项:1、答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
用2B铅笔将答题卡上试卷类型A后的方框涂黑。
2、选择题的作答:每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3、填空题和解答题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4、选考题的作答:先把所选题目的题号在答题卡上指定的位置用2B铅笔涂黑。
答案写在答题卡上对应的答题区域内,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
5、考试结束后,请将本试题卷和答题卡一并上交。
第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1z的共轭复数为()AB C D2.若双曲线221yxm-=的一个焦点为()3,0-,则m=()A.B.C.D.643()fx)ABC D4.函数()12xf x⎛⎫= ⎪⎝⎭,()0,x∈+∞的值域为D,在区间()1,2-上随机取一个数x,则x D∈的概率是()A.12B.13C.14D.15.记()()()()72701272111x a a x a x a x-=+++++⋅⋅⋅++,则012a a a+++6a⋅⋅⋅+的值为()A.1 B.2 C.129 D.21886.一个几何体的三视图如图所示,则该几何体的体积为()A.83B.163C.203D.87.《九章算术》是我国古代的数学名著,书中有如下问题:“今有大夫、不更、簪裹、上造、公士,凡五人,共猎得五鹿,欲以爵次分之,问各得几何?”其意思:“共有五头鹿,5人以爵次进行分配(古代数学中“以爵次分之”这种表述,一般表示等差分配,在本题中表示等差分配).”在这个问题中,若大夫得“一鹿、三分鹿之二”,则簪裹得()A .一鹿、三分鹿之一B.一鹿C.三分鹿之二D.三分鹿之一8)A.B.C.D.9.阅读如图所示的程序框图,运行相应程序,输出的结果是()A .12B .18C .120D .12510.当实数x ,y 满足约束条件3310x y x y y +⎧⎪-⎨⎪⎩≤≥≥,表示的平面区域为C ,目标函数2z x y =-的最小值为1p ,而由曲线()230y x y =≥,直线3x =及x 轴围成的平面区域为D ,向区域D 内任投入一个质点,该质点落入C 的概率为2p ,则1224p p -的值为( )A .12B .23C .35D .4311.已知点1F 是抛物线C :22x py =的焦点,点2F 为抛物线C 的对称轴与其准线的交点,过2F 作抛物线C 的切线,切点为A ,若点A 恰好在以1F ,2F 为焦点的双曲线上,则双曲线的离心率为( )AB1- C1D12.已知函数()e e x x f x -=+(其中是自然对数的底数),若当0x >时,()e 1x mf x m -+-≤恒成立,则实数m 的取值范围为( )A .10,3⎛⎫ ⎪⎝⎭B .1,3⎛⎤-∞- ⎥⎝⎦C .1,3⎡⎫+∞⎪⎢⎣⎭ D .11,33⎡⎤-⎢⎥⎣⎦第Ⅱ卷本卷包括必考题和选考题两部分。
2018年全国高中数学联赛辽宁赛区预赛试题+答案

a
9
8
7
6
5
4
3 21
4,3 4, 3 3, 2 3, 2
b
1,2 1, 2 1 1
2,1 2, 1 1
1
共 20 种情况。 同时,每个数码组 (a,b) 中的二个数码填上三个数位,有
C
2 3
种情况。
故 n2
C
2 3
(2
C
2 9
20) 156 . 综上, n n1 n2
165 .
【考点】 排列组合问题 .
,故
和
中必有一个小于
的距离最小值的二倍, 则 A 为平行于
的
直线与
的切点,解得
故答案为: 9.若正实数 x、y 满足
,故 的最小值为
.
,则 y 的最大值为 _____.
【答案】 【解析】【详解】
第3 页 共9 页
第5页
设
,则
.令
,则
故
,因此 y 的最大值为 .
故答案为 :
10.四面体 ABCD中,已知
第2 页 共9 页
第4页
二、填空题 6.设 、b 均为实数, 复数 为纯虚数,则 +b=_____. 【答案】 【解析】【详解】
与
的模长相等, 且
由题设知
,且
为纯虚数,故
.因此
或
解得
或
,故
.
故答案为:
7.在 △ ABC中,角 A、B、C的对边分别为 、b、c.若 【答案】 1009 【解析】【详解】
. ,求
的最大值和最小
.
当
时取等号,故 M 的最大值为 .
要使 M 取最小值,只需考虑
2018年全国二卷数学(含详解答案)
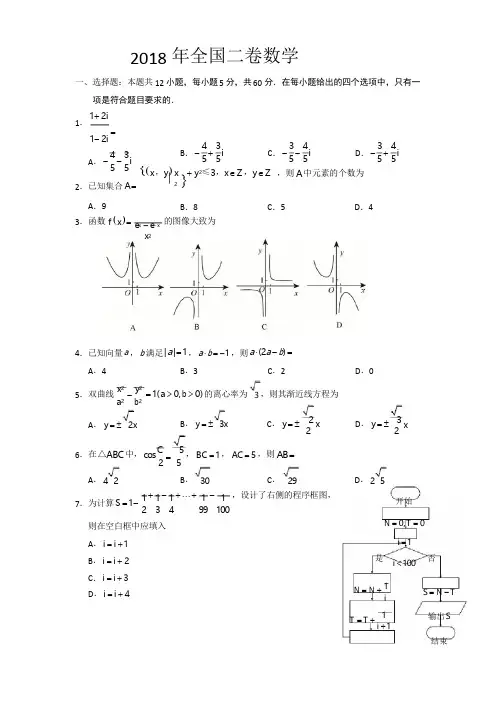
{(x ,y ) x + y 2≤3 ,x ∈ Z ,y ∈ Z ,则 A 中元素的个数为3.函数 f (x ) = 的图像大致为+ - + … + - ,设计了右侧的程序框图,2018 年全国二卷数学一、选择题:本题共12 小题,每小题 5 分,共 60 分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 1 + 2i=1 - 2i4 3A . - - i5 54 3 B . - + i5 53 4 C . - - i 5 53 4D . - + i5 52.已知集合 A =A .92}B .8C .5D .4e x - e - xx 24.已知向量 a , b 满足 | a | = 1 , a ⋅ b = -1 ,则 a ⋅ (2a - b ) =A .4B .3C .2D .05.双曲线 x 2 y 2 - a 2 b 2= 1( a > 0, b > 0) 的离心率为 3 ,则其渐近线方程为A . y = ± 2 xB . y = ± 3xC . y = ± 22x D . y = ± 3 2 x6.在 △ABC 中, cos C 5 =2 5, BC = 1 , AC = 5 ,则 AB =A . 4 27.为计算 S = 1 -B . 30C . 29D . 2 51 1 1 1 1234 99 100开始则在空白框中应填入A . i = i + 1B . i = i + 2是 N = 0, T = 0i = 1i < 100否C . i = i + 3D . i = i + 4N = N +1 iS = N - TT = T +1 i + 1输出 S结束12B . 6C . 5D . 4B .12.已知 F , F 是椭圆 C : a 2 b 214.若 x, y 满足约束条件 ⎨ x - 2 y + 3 ≥ 0 , 则 z = x + y 的最大值为__________.⎪ x - 5 ≤ 0 ,8.我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果. 德巴赫猜想是“每个大于 2 的偶数可以表示为两个素数的和”,如30 = 7 + 23 .在不超过 30 的素数中,随机选取两个不同的数,其和等于 30 的概率是A . 11 14 C . 1 15 D . 1 189.在长方体 ABCD - A B C D 中, AB = BC = 1 , AA = 3 ,则异面直线 AD 与 DB 所成角1 1 1 1111的余弦值为A .1 5 B . 5 52210.若 f ( x ) = cos x - sin x 在 [-a, a] 是减函数,则 a 的最大值是A . ππ 2 C . 3π4 D . π11 .已知 f ( x ) 是定义域为 (-∞, +∞ ) 的奇函数,满足f (1- x) = f (1+ x) .若 f (1)= 2,则f (1)+ f (2)+ f (3)+… + f (50)=A . -50B .0C .2D .501 2 x 2 y 2 += 1( a > b > 0) 的左、右焦点, A 是 C 的左顶点,点 P 在过 A 且斜率为 3 6 的直线上, △PF F 为等腰三角形, ∠F F P = 120︒ ,则 C 的离心率为1 2 1 2A .23B .12C .1 3 D . 14二、填空题:本题共 4 小题,每小题 5 分,共 20 分.13.曲线 y = 2ln( x + 1) 在点 (0, 0) 处的切线方程为__________.⎧ x + 2 y - 5 ≥ 0 ,⎪⎩15.已知 sin α + cos β = 1, cos α + sin β = 0 ,则 sin(α + β ) = __________.16.已知圆锥的顶点为 S ,母线 SA ,SB 所成角的余弦值为 7,SA 与圆锥底面所成角为 45°,8若 △SAB 的面积为 5 15 ,则该圆锥的侧面积为__________.三、解答题:共 70 分。
2018年全国高中数学联赛浙江省预赛高三数学试题(解析版)

2018年全国高中数学联赛浙江省预赛高三数学试题一、填空题1 1= 一-;—1 .已知a 为正实数,且 “1是奇函数,则⑷的值域为.1111 1 1 ― --- ----------- =- - + f (x )=--— 由小)为奇函数可知a - + 19「+ 1,解得a= 2,即 22、由此得f (x )的值域为। 2 2'.2018「2%1.3 ) 鼻二1 3- 5a +1£ 南满足]一 ,n*i- a (n=1, 2,…),则 n = 1520198077【答案】16 16 【解析】【详解】1 / 八■ +[二5皆十1小二1+『5阿+1=%由4" 4"56故答案为:.2.设数列所以 2018V Lu1<-2c201S=不5 +5 +... + S20185x c 2018 1t=—行 口-162018 S 2019£07 71616(3n \小 4风0 E —cos(a + p)=3.已知 '4",56I 4.J 13,则【解析】【详解】%£ E (彳再)孙3 +位二Mi 7Tcos\p + —I = cos (a + 所以 sin(a + B)——,得.J71 a—4亡叫cr 一: 6二 - 13, 5665【解析】【详解】加索-34.在八个数字2, 4, 6, 7, 8, 11, 12, 13中任取两个组成分数.这些分数中有个既约分数.【答案】36【解析】【详解】在7, 11, 13中任取一个整数与在2, 4, 6, 8, 12中任取一个整数构成既约分数,共有3 5 种;在7, 11, 13中任取两个整数也构成既约分数,共有A3,6中.合计有36种不同的既约分数./ 1 ^2018 + (1/01S _5,已知虚数z满足P+1=Q,则上』H .【答案】I【解析】【详解】1 2018 上r , 3^72 2.1 之上[/ 1 \2018 + ( 1 JOIS _ 工 ,1 _(Z)- _ . . I _ 1I? - 1 l z _ 1 _ t2,2018 - t3,1345 _ z-所以^ .6.设明=1。
2018年全国高中数学联赛真题(一试和二试)(A卷)试题(教师版)
1 1
x2 f (x) 2
的解集为
.
解析 [π − 2, 8 − 2π]. 由 f (x) 为偶函数及在 [0, 1] 上严格递减知,f (x) 在 [−1, 0] 上严格递增,再结合 f (x) 以 2 为周期可知,[1, 2] 是 f (x) 的严格递增区间.注意到 f (π − 2) = f (π) = 1, f (8 − 2π) = f (−2π) = f (2π) = 2,所以 1 f (x) 2 ⇔ f (π − 2) f (x) f (8 − 2π),而 1 < π − 2 < 8 − 2π < 2,故原不等式组成立当且仅当 x ∈ [π − 2, 8 − 2π].
·
1 b2
2 · |F1F2| · |yP | = a2 −
= b2
16 · · · yP
11 =· a√2 1+5.b2
=
1,解得
a2
=
20, b2
=
5.从而
5. 设 f (x) 是定义在 R 上的以 2 为周期的偶函数,在区间 [0, 1] 上严格递减,且满足 f (π) =
1,
f
(2π)
=
2,则不等式组
离实部与虚部后等价于 ax2 + 2ax + 2 = 0,①
bx2 − 2bx = 0.②
若 b = 0,则 a2 = 1,但当 a = 1 时,① 无实数解,从而 a = −1,此时存在实数
√
x = −1 ± 3 满足 ① ,② ,故 z = −1 满足条件.若 b = 0,则由 ② 知 x ∈ {√0, 2},但
=
− sin ∠M OC
=
MC −
=
2018年全国高中数学联赛陕西赛区预赛试题+答案
cos B
10.
|AB| = 3p
△F A′B′
答案
1 .
3
解析
(
π)
3
cos B = − cos(A + C) = − cos 2C + = sin 2C =
2
4
y2 = 2px(p > 0) AB l
F A′ B′
l
F
AA′B′B
.
A, B MM
=
S△A′ B ′ F S AA′B′B
=
|A′B′| · p |A′B′| · (|AA′| + |BB′|)
[
]
4
1
f (x) = x + − 1 ∈ 3, 15
x
4
11
n
3 + 3 + 3 + 3 + 3 = 15
n = 6.
44
√
12. n
n > 100
n2 + 3n + 1
.
答案 49.
解析
√
√
1
n2 + 3n + 1 + n + 1
13
1
√
−2=
n2 + 3n + 1 − n − 1
n
− 2 = n2 + n + 1 − 1 + n > 0
√ B: 2
12
π 5. 0 < x <
2
sin4 x cos4 x 1
+
=
9
4 13
tan x
A: 1 2
B: 2 3
6. x, y ∈ R
2018年全国高中数学联赛试题
2018年全国高中数学联赛一试一、填空题1. 设集合{1,2,3,...,99},{2|},{|2},A B x x A C x x A ==∈=∈ 则B C 的元素个数为__________.2. 设点P 到平面α点Q 在平面α上,使得直线PQ 与α所成角不小于30 且不大于60,则这样的点Q 所构成的区域的面积为__________.3. 将1,2,3,4,5,6随机排成一行,记为,,,,,,a b c d e f 则abc def +是偶数的概率为________.4. 在平面直角坐标系xOy 中,椭圆2222:1(0)x y C a b a b+=>>的左、右焦点分别为12F F 、, 椭圆C 的弦ST 与UV 分别平行于x 轴与y 轴,且相交于点P .已知线段,,,PU PS PV PT 的长分别为1,2,3,6,则12PF F 的面积为_________.5. 设()f x 是定义在R 上的以2为周期的偶函数,在区间[]0,1上严格递增,且满足()1,(2)2f f ππ== ,则不等式组121()2x f x ≤≤⎧⎨≤≤⎩的解集为________. 6. 设复数z 满足1z =,使得关于x 的方程2220zx zx ++=有实根,则这样的复数z 的和 为__________.7. 设O 为ABC 的外心,若2,AO AB AC =+ 则sin BAC ∠的值为__________.8. 设正整数数列1210,,...a a a 满足1012853,+2,a a a a a ==且 1{1,2},1,2,...,9i i i a a a i +∈++=, 则这样的数列的个数为__________.二、解答题9.已知定义在R +上的函数()f x为3log 1,09()49x x f x x ⎧-<≤⎪=⎨>⎪⎩ ,设,,a b c 是三个互不相同的实数,满足()()()f a f b f c ==,求abc 的取值范围10.已知实数列123,,,...a a a ,满足:对任意正整数n ,有(2)1n n n a S a -=,其中n S 表示数列的前n 项和,证明:(1)对任意正整数n ,有n a <2)对任意正整数n ,有11n n a a +<11.在平面直角坐标系xOy 中,设AB 是抛物线24y x =的过点(1,0)F 的弦,AOB 的外接圆交抛物线于点P (不用于点,,O A B ).若PF 平分APB ∠,求PF 的所有可能值.。
2018年全国高中数学联赛模拟试题与参考 答案
解得− ≥ ������> − 4.
注意:函数的定义域不能为空集。
2.已知函数������(������) = 1 −
(������>������)若������(������) = 2 ln √������ − ������(������),则������(������������)的取值范围为____________.
P
注:也可采用联立直线与圆锥曲线的方法解答,但过于繁琐,本解
答采用熟知的结论:������������ + ������������ = ������. 7.对于 ≤ ������ ≤ 1,则(1 + ������) (1 − ������)(1 − 2������) 的最大值为___________.
的等腰三角形,则三棱锥 A-BCD 的高与其外接球的直径的比值为_____________.
A
【解答】如图,易得 AE⊥BE,由等量关系,CE=ED=2,AF=BF=4,AE=BE=2√2.
由垂径定理,OF⊥AB,OE⊥CD,由对称性得 O 在 EF 上.
F
由勾股定理,OF + AF = AO = R = OC = (4 − OF)² + CE²
故������������������������ =
=
=
=
2
²
,若������������������������<0,则������������������������<0,这不可能.
∴ ������������������������>0. ������������������������ ≤ √ .
在 BDP 中由正弦定理得 1 x
sin 2 60
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2高中联赛模拟试题 2一试部分考试时间:80 分钟满分:120 分一、填空题(每小题 8 分,共 64 分)sin (α + 2β ) π π1. 已知 = 3 ,且 β ≠ , α + β ≠ n π + (n , k ∈),则 tan (α + β )= .sin α 2 2tan β2. 在等差数列{a n } 中,若a11 a 10< -1 ,且前n 项和 S n 有最大值,则当 S n 取得最小正值时, n = .3. 若 a +b + c= 1(a ,b , c ∈), 4a + 1 +4b + 1 + 4c + 1 > m ,则m 的最大值为 .4. 已知 ∆ABC 满足 AC = BC = 1 , AB = 2x ( x > 0).则 ∆ABC 的内切圆半径 r 的最大值为.5. 在正方体 ABCD - A 1B 1C 1D 1 中, G 为底面 A 1B 1C 1D 1 的中心.则 BG 与 AD 所成角的余弦值为___ ___.6. 函数 f ( x ) 在 上有定义,且满足 f ( x ) 为偶函数, f ( x - 1) 为奇函数.则 f (2019) =.7. 将一色子先后抛掷三次,观察面向上的点数,三数之和为 5 的倍数的概率为.8. 已知复数 z 1 , z 2 满足 ( z 1 - i )( z 2 + i ) = 1 .若 z 1 = ,则 z 2 的取值范围是.二、解答题(第9 小题16 分,第10、11 小题20 分,共56 分)x 2 y 29. 设P 为双曲线-= 1 上的任意一点,过点P 分别作两条渐近线的平行线,与两条渐近线交于A, Ba2 b2两点.求□ABCD 的面积.10. 求方程x5 - x3 - x2 + 1= y2 的整数解的个数.11. 对于n ≥ 6 ,已知⎛1- 1 ⎫<1.求出满足3n + 4n ++(n + 2)n =(n + 3)n 的所有正整数n. n + 3 ⎪ 2⎝⎭n高中联赛模拟试题 2加试部分考试时间:150 分钟满分:180 分一、(本题满分 40 分)设 ∆ABC 为等腰三角形, AB = AC , D 为边 AB 上一点.设 ∆BCD 的外接圆 Γ 在点 D 处的切线与 AC 交 于点 E , F 为过点 E 作圆 Γ 的另外一条切线的切点.设 BF 与 CD 交于点 G , AG 与 BC 交于点 H . 证明: BH = 2HC .A二、(本题满分 40 分)约定: n 维向量 x = ( x 1 , x 2 , , x n )( x i ≥ 0,i = 1, 2, , n ) 的 p - 范数记为:x = x 1 + x 2 + + x n ( p ∈ ) p p p pp+现有两个向量 A = (a ,b , c ), B = (d , e ) .若: ⎧⎪ A = B ⎨ A = B .证明: A≤ B .2 2 ⎪⎩4 433EDGF B H三、(本题满分 50 分)设整数 n ≥ 4 , a 1 , a 2 , , a n 为区间 (0, 2n ) 内两两不同的整数.证明:集合 A = {a 1 , a 2 , , a n } 存在所有元 素之和能被 2n 整除的子集.四、(本题满分 50 分)设有 17 支球队参加足球比赛,采用单循环赛制,比赛中偶尔会出现一个循环的三元集(即集合{a , b ,c } , 其中 a 队击败 b 队, b 队击败 c 队, c 队击败 a 队),若没有平局,则比赛结束.问:最多有多少个这 样的循环三元集?5 5 5 2 1高中联赛模拟试题 2解答一试部分考试时间:80 分钟满分:120 分一、填空题(每小题 8 分,共 64 分) 1. 2.sin (α + 2β )+ 1 解析: tan (α + β ) = sin (α + β ) ⋅ cos β = sin (α + 2β ) + sin α = sin α = 2 .tan βcos (α + β ) ⋅ sin β sin (α - 2β ) - sin α sin (α + 2β)-1sin α2. 19.解析:由 S n 有最大值可知 a 1 > 0, d < 0 ,由a 11a 10< -1 ,则 a 10 + a 11 < 0, a 11 < 0 < a 10 ,20(a 1 + a 20 ) ⇒ S ==10(a + a ) < 0, S 19(a 1 + a19 ) = = 19a > 0 , 20 2 10 11 19 2 10再由 S 19 - S 1 = a 2 + a 3 ++ a 19 = 9(a 10 + a 11 ) < 0 ,知 S n 取最小正值时,n = 19 .3. 2 + .解析: (a + 1)(b + 1) > 1 + a + b ⇒ a + 1 + b + 1+ 2 1 + a + b > 2 + a + b 2 1+ a + b2 2⇒ (a + 1 ++ 1) > (+1 + a + b )⇒ + 1 + b + 1 > 1 +.反复利用上式,得:4a +b + 1 +c + 1 > 1 + 4 (a + b ) + 1 + 4c + 1 > 1 + 1 += 2 + 5 ;另一方面,当 a → 1,b → 0, c → 0 时,不等式左边趋于 2 + .因此 2+ 为最大的下界.4.5 5 - 11 .2解析:转化为求函数 f (x ) = x (1 - x )在 (0,1) 内的最大值.1 + a + b1 + 4 (a + b + c )+ x5.6解析:BG= CG =cos ∠GBC = BC =AD //BC ,则 BG 与 AD62 2BG 6. 2 1 1 ⎪ 2 2 ⎪1 x - ⎭ 6. 0.解析:由已知得 f ( x ) 关于 x 轴及点 (-1, 0) 对称.从而4 为 f ( x ) 的一个周期,且 f (-1) = 0 .故f (2019) = f (-1) = 0 .7.43 216解析:和为 5 的形如 3、1、1 与 2、2、1,共 6 种.和为 10 的形如 6、3、1 的有 6 种,形如 6、2、2 的有 3 种,形如 5、4、1 的有 6 种,形如 5、 3、2 的有 6 种,形如 4、3、3 的有 3 种,形如 4、4、2 的有 3 种.合计 27 种.和为 15 的形如 4、5、6 的有 6 种,形如 5、5、5 的有 1 种,形如 6、6、3 的有 3 种,合计 10 种.8. ⎡2 -2, 2 + 2 ⎤ .⎣ ⎦解析:设 z 2 = x + yi ( x , y∈) .则z 1 = z z 2i⇒ z = + i 1 - y + xi x + y + 1)i = ⇒ x 2 + ( y + 2)2 = 2 .由 z 2 的几何意义,知其范围为⎡2 -2, 2 + 2 ⎤ . ⎣ ⎦二、解答题(第 9 小题 16 分,第 10、11 小题 20 分,共 56 分)9. 双曲线的两条渐近线方程分别为 y = b x , y = - bx .a a设 A ⎛ x , b ⎝ a x ⎫, B ⎛x , - b ⎭ ⎝a x ⎫, P (x , y ) .⎭ b由 OAPB 知, x = x 1 + x 2 , y = aa 2(x 1 - x 2 ) .代入双曲方程化简得 x 1 x 2 = .4于是, OAPB 的面积为 x ⎛ - b ⎫ ⎝ a2 ⎪ b x 1 x 2 = a x 1 x 2 = 1 ab . 210. 原方程可化为 (x 3 - 1)(x 2 - 1) = y 2 ⇒ ( x - 1)2( x + 1)(x 2 + x + 1) = y 2 .------------------------------(1) 当 x = 0 时, y 2 = 1 ⇒ y = ±1 ; 当 x = ±1 时, y = 0 .2 2b ax -1 ⎪ 设 x , y 为方程的整数解,且 x ≠ ±1, 0 .由(1)式, ( x -1)2| y 2⇒ ( x -1) | y ⇒ ( x + 1)(x 2+ x + 1) = ⎛ y ⎫⎝ ⎭ .又因为 y 为整数,则x -1( x + 1)(x 2 + x + 1)为完全平方数.而 x 2 + x + 1 = x ( x + 1) + 1 ⇒ (x + 1, x 2 + x + 1) = 1 ,2n n4 5 n + 3 ⎪⎩⇒ x + 1, x 2 + x + 1均为完全平方数 ⇒ x + 1 ≥ 0( x ≠ 0, ±1) ⇒ x ≥ 2 ⇒ x 2 < x 2 + x + 1 < (x + 1)2,显然, x 2 + x +1不为完全平方数.综上,原方程只能有 4 组解: ( x , y ) = (0,1), (0, -1), (1, 0), (-1, 0) .11. 当 n ≥ 6 时,由 ⎛1 - 1 ⎫ < 1 ⇒ ⎛ n + 2 ⎫ < 1 ⇒ (n + 3)n - (n +2)n > (n + 2)n . n + 3 ⎪ 2 n + 3 ⎪2 ⎝ ⎭ ⎝ ⎭n nn 而 ⎛ 3 ⎫< ⎛ 4 ⎫< < ⎛ n + 2 ⎫ < 1,故: ⎪ ⎪ ⎪ ⎝⎭ ⎝ ⎭ ⎝ ⎭ 2⎧ 4n - 3n > 3n ,⎪ 5n - 4n > 4n, ⎨ ⎪⎪(n + 3)n - (n + 2)n > (n + 2)n . 累加后3n + 4n + + (n + 2)n< (n + 3)n- 3n < (n + 3)n,此时无解. 直接检验 n = 1, 2, 3, 4, 5 ,知当 n = 2, 3 时等式成立., .⎩a4 4 4 4 4一、(本题满分 40 分)加试部分考试时间:150 分钟满分:180分在 ∆ABG , ∆ACG 中,由正弦定理得 BG = AG CG = AGsin ∠BAH sin ∠ABF sin ∠CAH sin ∠ACD 故 BH = sin ∠BAH = BG ⋅ sin ∠ABF = BG ⋅ sin ∠FCD = sin ∠DCB ⋅ sin ∠FCD = FD ⋅ CI . CH sin ∠CAH CG ⋅ s in ∠ACD CG ⋅ s in ∠DBI sin ∠CBF ⋅ s in ∠DBI DI ⋅ C F 设 AC 与圆 Γ 的另一个交点为 I .则四边形 CFID 为调和四边形. 于是, FI ⋅ CD = CF ⋅ ID . 由托勒密定理得 FD ⋅ CI = FI ⋅ CD + CF ⋅ ID = 2ID ⋅ C F . 从而, BH = 2HC .二、(本题满分 40 分)等价于证明: 设 a , b , c , d , e 为非负数,且满足⎧a 2 + b 2 + c 2 = d 2 + e 2⎨+ b + c = d + e , 证明: a 3 + b 3 + c 3 ≤ d 3 + e 3 .----------------------------------------------------------------------------------------(1)注意到 2(a 2b 2 + b 2c 2 + c 2a 2 ) = (a 2 + b 2 + c 2 )2- (a 4 + b 4 + c 4 ) = (d 2 + e 2 )2- (d 4 + e 4 ) = 2d2e 2. 则 a 2b 2 + b 2c 2 + c 2a 2 = d 2e 2 . 又a 6 +b 6 +c 6 - 3a 2b 2c 2 = (a 2 + b 2 + c 2 )(a 4 + b 4 + c 4 - a 2b 2 - b 2c 2 - a 2c 2 ) = (d 2 +e 2 )(d 4 + e 4 - d 2e 2 )= d 6 + e 6(1)式两边平方得 a 6 + b 6 + c 6 + 2(a 3b 3 + b 3c 3 + c 3a 3 ) ≤ d 6 + e 6 + 2d 3e 33⇔ 2(a 3b 3 + b 3c 3 + c 3a 3 ) + 3a 2b 2c 2 ≤ 2d 3e 3 ⇔ 2(a 3b 3 + b 3c 3 + c 3a 3 ) + 3a 2b 2c 2 ≤ 2(a 2b 2 + b 2c 2 + c 2a 2 )2 ---(2)3设 x = ab , y = bc , z = ca .则(2) ⇔ 2(x 3+ y 3+ z 3) + 3xyz ≤ 2(x 2+ y 2+ z 2 )2 .由柯西不等式,知⎡2 x 3 + y 3 + z 3 2 + 3xyz ⎤ = ⎡x 2x 2 + yz + y 2 y 2 + zx 2+ z 2z 2 + xy ⎤ ⎣ () ⎦ ⎣ ( ) ( ) ( )⎦⎣ ⎦ ≤ (x 2 + y 2 + z 2 )⎡(2x 2 + yz )2+ (2 y 2 + zx )2+ (2z 2 + xy )2⎤ ⎢⎣⎥⎦≤ (x 2 + y 2 + z 2 )⎡4(x 4 + y 4 + z 4 ) + 8( y 2 z 2 + z 2 x 2 + x 2 y 2 )⎤ = 4(x 2 + y 2 + z 2 )3. 从而,结论成立.C b= C a+ 2 C a = ∑ ∑三、(本题满分 50 分)若 n ∉{a 1 , a 2 , , a n } ,则 2n 个整数 a 1 , a 2 , , a n , 2n - a 1 , 2n - a 2 , , 2n - a n ∈(0, 2n ) .由抽屉原理,知其中 必有两个数相等. 不妨设 a i = 2n - a j .因为 n ∉{a 1 , a 2 , , a n },所以 i≠ j . 故{a i , a j }满足题意,命题成立.若 n ∈{a 1 , a 2 , , a n },不妨设 a n = n .考虑 n - 1 (n - 1 ≥ 3)个整数 a 1 , a 2 , , a n -1 ,在其中任取三个数 a i < a j < a k . 若 a k - a j , a j - a i 均能被 n 整除,则 a k - a i ≥ 2n ,与 a k ∈(0, 2n ) 矛盾. 因此, a 1 , a 2 , , a n -1 中至少存在两个数,其差不能被 n 整除.不妨设 a 1 , a 2 之差不能被 n 整除.考察 n 个数: a 1 , a 2 , a 1 + a 2 , a 1 + a 2 + a 3 , , a 1 + a 2 + + a n -1 . (1)若这 n 个数关于模 n 的余数互不相同,则其中必有一个数能被 n 整除.令这个数为 kn . 当 k 为偶数时,结论成立;当 k 为奇数时,加上 a n 即构成所需要的子集.(2)若这 n 个数中有两个数关于模 n 同余,则其差能被 n 整除.因为 a 1 , a 2 不同余,所以这两个数之差 必为原集合 A 中若干数之和.由此归结为(1)中讨论.综上,命题得证.四、(本题满分 50 分)一个三元集{a , b , c } 不是循环的⇔ 有一支球队赢了另外两队 ⇔ 有一支球队输给了另外两队. 用 A 1 , A 2 , , A 17 代表这 17 支球队 . 假 设 球 队 A i 赢了 a i 支球队,但输给了 b i 支球队 .显然, a i + b i = 1 6(i = 1, 2 , , 1) .17171 ⎛ 17 17 ⎫ 于是,不循环的三元集的个数为 2ii =1 2i i =1 ∑ 2 ⎝ i =1 i∑ i =1 C b ⎪ .i⎭2.17 a (a -1) b (b -1) 1 ⎡(a + b )2⎤ 对于每一个 i , C 2 + C 2 = i i + i i≥ ⎢ i i - (a + b )⎥ = 56 . a i b i 2 2 2 ⎢ 2 i i⎥则不循环的三元集的个数至少为 1 ⨯17 ⨯ 56 = 476 ⎣ ⎦2故循环三元集最多有 C 3- 476 = 204 个.当且仅当 a i = b i = 8(i = 1, 2, ,17) 时,循环三元集的个数最多为 204.。
