2008年高考试题——数学理(宁夏卷)(2)
2008年宁夏高考数学试卷(理)及答案

2008年宁夏高考数学试卷(理)一、选择题(共12小题,每小题5分,满分60分)1.(5分)已知函数y=2sin(ωx+φ)(ω>0))在区间[0,2π]的图象如图:那么ω=()A.1 B.2 C.D.2.(5分)已知复数z=1﹣i,则=()A.2i B.﹣2i C.2 D.﹣23.(5分)如果等腰三角形的周长是底边长的5倍,那么它的顶角的余弦值为()A.B.C.D.4.(5分)设等比数列{a n}的公比q=2,前n项和为S n,则=()A.2 B.4 C.D.5.(5分)下面程序框图,如果输入三个实数a、b、c,要求输出这三个数中最大的数,那么在空白的判断框中,应该填入下面四个选项中的()A.c>x B.x>c C.c>b D.b>c6.(5分)已知a1>a2>a3>0,则使得(1﹣a i x)2<1(i=1,2,3)都成立的x 取值范围是()A.B.C.D.7.(5分)=()A.B.C.2 D.8.(5分)平面向量,共线的充要条件是()A.,方向相同B.,两向量中至少有一个为零向量C.∃λ∈R,D.存在不全为零的实数λ1,λ2,9.(5分)甲、乙、丙3位志愿者安排在周一至周五的5天中参加某项志愿者活动,要求每人参加一天且每天至多安排一人,并要求甲安排在另外两位前面.不同的安排方法共有()A.20种B.30种C.40种D.60种10.(5分)由直线x=,x=2,曲线y=及x轴所围成的图形的面积是()A.B.C.D.2ln211.(5分)已知点P在抛物线y2=4x上,那么点P到点Q(2,﹣1)的距离与点P到抛物线焦点距离之和取得最小值时,点P的坐标为()A.B. C.(1,2) D.(1,﹣2)12.(5分)某几何体中的一条线段长为,在该几何体的正视图中,这条线段的投影是长为的线段,在该几何体的侧视图与俯视图中,这条棱的投影分别是长为a和b的线段,则a+b的最大值为()A.B.C.4 D.二、填空题(共4小题,每小题5分,满分20分)13.(5分)已知向量知=(0,﹣1,1),=(4,1,0),|λ+|=,且λ>0,则λ=.14.(5分)设双曲线﹣=1的右顶点为A,右焦点为F.过点F平行于双曲线的一条渐近线的直线与双曲线交于点B,则△AFB的面积为.15.(5分)一个六棱柱的底面是正六边形,其侧棱垂直底面.已知该六棱柱的顶点都在同一个球面上,且该六棱柱的高为,底面周长为3,那么这个球的体积为.16.(5分)从甲、乙两品种的棉花中各抽测了25根棉花的纤维长度(单位:mm),结果如下:甲品种:271 273 280 285 285 287 292 294 295 301 303 303 307308 310 314 319 323 325 325 328 331 334 337 352乙品种:284 292 295 304 306 307 312 313 315 315 316 318 318320 322 322 324 327 329 331 333 336 337 343 356由以上数据设计了如下茎叶图:根据以上茎叶图,对甲、乙两品种棉花的纤维长度作比较,写出两个统计结论:①;②.三、解答题(共8小题,22--24题选做其中一题,满分70分)17.(12分)已知{a n}是一个等差数列,且a2=1,a5=﹣5.(Ⅰ)求{a n}的通项a n;(Ⅱ)求{a n}前n项和S n的最大值.18.(12分)如图,已知点P在正方体ABCD﹣A′B′C′D′的对角线BD′上,∠PDA=60°.(Ⅰ)求DP与CC′所成角的大小;(Ⅱ)求DP与平面AA′D′D所成角的大小.19.(12分)A,B两个投资项目的利润率分别为随机变量X1和X2.根据市场分析,X1和X2的分布列分别为X 15%10%X22%8%12%P0. 8 0.2P.2.50.3(Ⅰ)在A,B两个项目上各投资100万元,Y1和Y2分别表示投资项目A和B所获得的利润,求方差DY1,DY2;(Ⅱ)将x(0≤x≤100)万元投资A项目,100﹣x万元投资B项目,f(x)表示投资A项目所得利润的方差与投资B项目所得利润的方差的和.求f(x)的最小值,并指出x为何值时,f(x)取到最小值.(注:D(aX+b)=a2DX)20.(12分)在直角坐标系xOy中,椭圆C1:=1(a>b>0)的左、右焦点分别为F1,F2.F2也是抛物线C2:y2=4x的焦点,点M为C1与C2在第一象限的交点,且|MF2|=.(Ⅰ)求C1的方程;(Ⅱ)平面上的点N 满足,直线l∥MN,且与C1交于A,B两点,若,求直线l的方程.21.(12分)设函数f(x)=ax +(a,b∈Z),曲线y=f(x)在点(2,f(2))处的切线方程是y=3.(Ⅰ)求y=f(x)的解析式;(Ⅱ)证明:函数y=f(x)的图象是一个中心对称图形,并求其对称中心;(Ⅲ)证明:曲线y=f(x)上任意一点的切线与直线x=1和直线y=x所围成的三角形的面积是定值,并求出这个定值.22.(10分)如图,过圆O外一点M作它的一条切线,切点为A,过A作直线AP垂直直线OM,垂足为P.(1)证明:OM•OP=OA2;(2)N为线段AP上一点,直线NB垂直直线ON,且交圆O于B点.过B点的切线交直线ON于K.证明:∠OKM=90°.23.自选题:已知曲线C1:(θ为参数),曲线C2:(t为参数).(Ⅰ)指出C1,C2各是什么曲线,并说明C1与C2公共点的个数;(Ⅱ)若把C1,C2上各点的纵坐标都压缩为原来的一半,分别得到曲线C1′,C2′.写出C1′,C2′的参数方程.C1′与C2′公共点的个数和C与C2公共点的个数是否相同?说明你的理由.24.自选题:已知函数f(x)=|x﹣8|﹣|x﹣4|.(Ⅰ)作出函数y=f(x)的图象;(Ⅱ)解不等式|x﹣8|﹣|x﹣4|>2.2008年宁夏高考数学试卷(理)参考答案与试题解析一、选择题(共12小题,每小题5分,满分60分)1.(5分)(2008•海南)已知函数y=2sin(ωx+φ)(ω>0))在区间[0,2π]的图象如图:那么ω=()A.1 B.2 C.D.【分析】由图象确定周期T,进而确定ω.【解答】解:由图象知函数的周期T=π,所以.故选B.2.(5分)(2008•海南)已知复数z=1﹣i,则=()A.2i B.﹣2i C.2 D.﹣2【分析】把z代入分式,然后展开化简,分母实数化,即可.【解答】解:∵z=1﹣i,∴,故选B.3.(5分)(2008•海南)如果等腰三角形的周长是底边长的5倍,那么它的顶角的余弦值为()A.B.C.D.【分析】先得到3边之间的关系,再由余弦定理可得答案.【解答】解:设顶角为C,因为l=5c,∴a=b=2c,由余弦定理得,故选D.4.(5分)(2008•海南)设等比数列{a n}的公比q=2,前n项和为S n,则=()A.2 B.4 C.D.【分析】根据等比数列的性质,借助公比q表示出S4和a1之间的关系,易得a2与a1间的关系,然后二者相除进而求得答案.【解答】解:由于q=2,∴∴;故选:C.5.(5分)(2008•海南)下面程序框图,如果输入三个实数a、b、c,要求输出这三个数中最大的数,那么在空白的判断框中,应该填入下面四个选项中的()A.c>x B.x>c C.c>b D.b>c【分析】根据流程图所示的顺序,逐框分析程序中各变量、各语句的作用,由于该题的目的是选择最大数,因此根据第一个选择框作用是比较x与b的大小,故第二个选择框的作用应该是比较x与c的大小,而且条件成立时,保存最大值的变量X=C.【解答】解:由流程图可知:第一个选择框作用是比较x与b的大小,故第二个选择框的作用应该是比较x与c的大小,∵条件成立时,保存最大值的变量X=C故选A.6.(5分)(2008•海南)已知a1>a2>a3>0,则使得(1﹣a i x)2<1(i=1,2,3)都成立的x取值范围是()A.B.C.D.【分析】先解出不等式(1﹣a i x)2<1的解集,再由a1>a2>a3>0确定x的范围.【解答】解:,所以解集为,又,故选B.7.(5分)(2008•海南)=()A.B.C.2 D.【分析】本题是分式形式的问题,解题思路是约分,把分子正弦化余弦,用二倍角公式,合并同类项,约分即可.【解答】解:原式====2,故选C.8.(5分)(2008•海南)平面向量,共线的充要条件是()A.,方向相同B.,两向量中至少有一个为零向量C.∃λ∈R,D.存在不全为零的实数λ1,λ2,【分析】根据向量共线定理,即非零向量与向量共线的充要条件是必存在唯一实数λ使得成立,即可得到答案.【解答】解:若均为零向量,则显然符合题意,且存在不全为零的实数λ1,λ2,使得;若,则由两向量共线知,存在λ≠0,使得,即,符合题意,故选D.9.(5分)(2008•海南)甲、乙、丙3位志愿者安排在周一至周五的5天中参加某项志愿者活动,要求每人参加一天且每天至多安排一人,并要求甲安排在另外两位前面.不同的安排方法共有()A.20种B.30种C.40种D.60种【分析】根据题意,分析可得,甲可以被分配在星期一、二、三;据此分3种情况讨论,计算可得其情况数目,进而由加法原理,计算可得答案.【解答】解:根据题意,要求甲安排在另外两位前面,则甲有3种分配方法,即甲在星期一、二、三;分3种情况讨论可得,甲在星期一有A42=12种安排方法,甲在星期二有A32=6种安排方法,甲在星期三有A22=2种安排方法,总共有12+6+2=20种;故选A.10.(5分)(2008•海南)由直线x=,x=2,曲线y=及x轴所围成的图形的面积是()A.B.C.D.2ln2【分析】由题意画出图形,再利用定积分即可求得.【解答】解:如图,面积.故选D.11.(5分)(2008•海南)已知点P在抛物线y2=4x上,那么点P到点Q(2,﹣1)的距离与点P到抛物线焦点距离之和取得最小值时,点P的坐标为()A.B. C.(1,2) D.(1,﹣2)【分析】先判断点Q与抛物线的位置,即点Q在抛物线内,再由点P到抛物线焦点距离等于点P到抛物线准线距离,根据图象知最小值在S,P,Q三点共线时取得,可得到答案.【解答】解:点P到抛物线焦点距离等于点P到抛物线准线距离,如图PF+PQ=PS+PQ,故最小值在S,P,Q三点共线时取得,此时P,Q的纵坐标都是﹣1,故选A.12.(5分)(2008•海南)某几何体中的一条线段长为,在该几何体的正视图中,这条线段的投影是长为的线段,在该几何体的侧视图与俯视图中,这条棱的投影分别是长为a和b的线段,则a+b的最大值为()A.B.C.4 D.【分析】设棱长最长的线段是长方体的对角线,由题意所成长方体的三度,求出三度与面对角线的关系,利用基本不等式即可求出a+b的最大值【解答】解:结合长方体的对角线在三个面的投影来理解计算.如图设长方体的长宽高分别为m,n,k,由题意得,⇒n=1,所以(a2﹣1)+(b2﹣1)=6⇒a2+b2=8,∴(a+b)2=a2+2ab+b2=8+2ab≤8+a2+b2=16⇒a+b≤4当且仅当a=b=2时取等号.故选C.二、填空题(共4小题,每小题5分,满分20分)13.(5分)(2008•海南)已知向量知=(0,﹣1,1),=(4,1,0),|λ+|=,且λ>0,则λ=3.【分析】根据所给的向量坐标写出要求模的向量坐标,用求模长的公式写出关于变量λ的方程,解方程即可,解题过程中注意对于变量的限制,把不合题意的结果去掉.【解答】解:由题意知λ+=(4,1﹣λ,λ),∴16+(λ﹣1)2+λ2=29(λ>0),∴λ=3,故答案为:3.14.(5分)(2008•海南)设双曲线﹣=1的右顶点为A,右焦点为F.过点F平行于双曲线的一条渐近线的直线与双曲线交于点B,则△AFB的面积为.【分析】根据题意,由双曲线的方程可得a、b的值,进而可得c的值,可以确定A、F的坐标,设BF的方程为y=(x﹣5),代入双曲线方程解得B的坐标,计算可得答案.【解答】解:a2=9,b2=16,故c=5,∴A(3,0),F(5,0),不妨设BF的方程为y=(x﹣5),代入双曲线方程解得:B(,﹣).=|AF|•|y B|=•2•=.∴S△AFB故答案为:.15.(5分)(2008•海南)一个六棱柱的底面是正六边形,其侧棱垂直底面.已知该六棱柱的顶点都在同一个球面上,且该六棱柱的高为,底面周长为3,那么这个球的体积为.【分析】先求正六棱柱的体对角线,就是外接球的直径,然后求出球的体积.【解答】解:∵正六边形周长为3,得边长为,故其主对角线为1,从而球的直径,∴R=1,∴球的体积故答案为:.16.(5分)(2008•海南)从甲、乙两品种的棉花中各抽测了25根棉花的纤维长度(单位:mm),结果如下:甲品种:271 273 280 285 285 287 292 294 295 301 303 303 307308 310 314 319 323 325 325 328 331 334 337 352乙品种:284 292 295 304 306 307 312 313 315 315 316 318 318320 322 322 324 327 329 331 333 336 337 343 356由以上数据设计了如下茎叶图:根据以上茎叶图,对甲、乙两品种棉花的纤维长度作比较,写出两个统计结论:①乙品种棉花的纤维平均长度大于甲品种棉花的纤维平均长度;②乙品种棉花的纤维长度普遍大于甲品种棉花的纤维长度.【分析】利用茎叶图中的数据可以计算乙品种棉花的纤维平均长度大于甲品种棉花的纤维平均长度;通过观察茎叶图中数据的分布可知甲品种棉花的纤维长度的分散程度比乙品种棉花的纤维长度的分散程度更大.【解答】解:(1)乙品种棉花的纤维平均长度大于甲品种棉花的纤维平均长度(或:乙品种棉花的纤维长度普遍大于甲品种棉花的纤维长度).(2)甲品种棉花的纤维长度较乙品种棉花的纤维长度更分散.(或:乙品种棉花的纤维长度较甲品种棉花的纤维长度更集中(稳定).甲品种棉花的纤维长度的分散程度比乙品种棉花的纤维长度的分散程度更大).(3)甲品种棉花的纤维长度的中位数为307mm,乙品种棉花的纤维长度的中位数为318mm.(4)乙品种棉花的纤维长度基本上是对称的,而且大多集中在中间(均值附近).甲品种棉花的纤维长度除一个特殊值(352)外,也大致对称,其分布较均匀.三、解答题(共8小题,22--24题选做其中一题,满分70分)17.(12分)(2008•海南)已知{a n}是一个等差数列,且a2=1,a5=﹣5.(Ⅰ)求{a n}的通项a n;(Ⅱ)求{a n}前n项和S n的最大值.【分析】(1)用两个基本量a1,d表示a2,a5,再求出a1,d.代入通项公式,即得.(2)将S n的表达式写出,是关于n的二次函数,再由二次函数知识可解决之.【解答】解:(Ⅰ)设{a n}的公差为d,由已知条件,,解出a1=3,d=﹣2,所以a n=a1+(n﹣1)d=﹣2n+5.(Ⅱ)=4﹣(n﹣2)2.所以n=2时,S n取到最大值4.18.(12分)(2008•海南)如图,已知点P在正方体ABCD﹣A′B′C′D′的对角线BD′上,∠PDA=60°.(Ⅰ)求DP与CC′所成角的大小;(Ⅱ)求DP与平面AA′D′D所成角的大小.【分析】方法一:如图,以D为原点,DA为单位长建立空间直角坐标系D﹣xyz.连接BD,B'D'.在平面BB'D'D中,延长DP交B'D'于H.求出.(Ⅰ)利用,求出.即可.(Ⅱ)平面AA'D'D的一个法向量是.通过,得到.即可.方法二:如图,以D为原点,DA为单位长建立空间直角坐标系D﹣xyz.求出解题过程同方法一.【解答】解:方法一:如图,以D为原点,DA为单位长建立空间直角坐标系D ﹣xyz.则,.连接BD,B'D'.在平面BB'D'D中,延长DP交B'D'于H.设,由已知,由可得.解得,所以.(4分)(Ⅰ)因为,所以.即DP与CC'所成的角为45°.(8分)(Ⅱ)平面AA'D'D的一个法向量是.因为,所以.可得DP与平面AA'D'D所成的角为30°.(12分)方法二:如图,以D为原点,DA为单位长建立空间直角坐标系D﹣xyz.则,,.设P(x,y,z)则,∴(x﹣1,y﹣1,z)=(﹣λ,﹣λ,λ)∴,则,由已知,,cos==∴λ2﹣4λ+2=0,解得,∴(4分)(Ⅰ)因为,所以.即DP与CC'所成的角为45°.(8分)(Ⅱ)平面AA'D'D的一个法向量是.因为,所以.可得DP与平面AA'D'D所成的角为30°.(12分)19.(12分)(2008•海南)A,B两个投资项目的利润率分别为随机变量X1和X2.根据市场分析,X1和X2的分布列分别为X 15%10%X22%8%12%P0. 8 0.2P.2.50.3(Ⅰ)在A,B两个项目上各投资100万元,Y1和Y2分别表示投资项目A和B所获得的利润,求方差DY1,DY2;(Ⅱ)将x(0≤x≤100)万元投资A项目,100﹣x万元投资B项目,f(x)表示投资A项目所得利润的方差与投资B项目所得利润的方差的和.求f(x)的最小值,并指出x为何值时,f(x)取到最小值.(注:D(aX+b)=a2DX)【分析】(1)Y1和Y2分别表示投资项目A和B所获得的利润,根据两个投资项目的利润率分别为随机变量X1和X2的分布列,可以得到Y1和Y2的分布列,得到分布列,余下的问题只是运算问题,分别求出变量的方差.(2)由题意知f(x)表示投资A项目所得利润的方差与投资B项目所得利润的方差的和,写出用x表示的方差的解析式,结合二次函数的最值问题,得到结果.【解答】解:(Ⅰ)∵Y1和Y2分别表示投资项目A和B所获得的利润,根据两个投资项目的利润率分别为随机变量X1和X2的分布列可以得到Y1和Y2的分布列分别为Y 151Y22812P0. 8 0.2P0.2.5.3EY1=5×0.8+10×0.2=6,DY1=(5﹣6)2×0.8+(10﹣6)2×0.2=4,EY2=2×0.2+8×0.5+12×0.3=8,DY2=(2﹣8)2×0.2+(8﹣8)2×0.5+(12﹣8)2×0.3=12.(Ⅱ)===,当时,f(x)=3为最小值.20.(12分)(2008•海南)在直角坐标系xOy中,椭圆C1:=1(a>b>0)的左、右焦点分别为F1,F2.F2也是抛物线C2:y2=4x的焦点,点M为C1与C2在第一象限的交点,且|MF2|=.(Ⅰ)求C1的方程;(Ⅱ)平面上的点N满足,直线l∥MN,且与C1交于A,B两点,若,求直线l的方程.【分析】(Ⅰ)先利用F2是抛物线C2:y2=4x的焦点求出F2的坐标,再利用|MF2|=以及抛物线的定义求出点M的坐标,可以得到关于椭圆方程中参数的两个等式联立即可求C1的方程;(Ⅱ)先利用,以及直线l∥MN得出直线l与OM的斜率相同,设出直线l的方程,把直线方程与椭圆方程联立得到关于A,B两点坐标的等式,整理代入,即可求出直线l的方程.【解答】解:(Ⅰ)由C2:y2=4x知F2(1,0).设M(x1,y1),M在C2上,因为,所以,得,.M在C1上,且椭圆C1的半焦距c=1,于是消去b2并整理得9a4﹣37a2+4=0,解得a=2(不合题意,舍去).故椭圆C1的方程为.(Ⅱ)由知四边形MF1NF2是平行四边形,其中心为坐标原点O,因为l∥MN,所以l与OM的斜率相同,故l的斜率.设l的方程为.由消去y并化简得9x2﹣16mx+8m2﹣4=0.设A(x1,y1),B(x2,y2),,.因为,所以x1x2+y1y2=0.x1x2+y1y2=x1x2+6(x1﹣m)(x2﹣m)=7x1x2﹣6m(x1+x2)+6m2==.所以.此时△=(16m)2﹣4×9(8m2﹣4)>0,故所求直线l的方程为,或.21.(12分)(2008•海南)设函数f(x)=ax+(a,b∈Z),曲线y=f(x)在点(2,f(2))处的切线方程是y=3.(Ⅰ)求y=f(x)的解析式;(Ⅱ)证明:函数y=f(x)的图象是一个中心对称图形,并求其对称中心;(Ⅲ)证明:曲线y=f(x)上任意一点的切线与直线x=1和直线y=x所围成的三角形的面积是定值,并求出这个定值.【分析】(I)欲求在点(2,f(2))处的切线方程,只须求出其斜率的值即可,故先利用导数求出在x=2处的导函数值,再结合导数的几何意义即可求出切线的斜率.从而问题解决.(Ⅱ)由函数y1=x,都是奇函数.可得和函数也是奇函数,其图象是以原点为中心的中心对称图形.再按向量a=(1,1)平移,即得到函数f(x)的图象,故函数f(x)的图象是以点(1,1)为中心的中心对称图形.(Ⅲ)先在曲线上任取一点.利用导数求出过此点的切线方程为,令x=1得切线与直线x=1交点.令y=x得切线与直线y=x交点.从而利用面积公式求得所围三角形的面积为定值.【解答】解:(Ⅰ),于是解得或因a,b∈Z,故.(Ⅱ)证明:已知函数y1=x,都是奇函数.所以函数也是奇函数,其图象是以原点为中心的中心对称图形.而.可知,函数g(x)的图象按向量a=(1,1)平移,即得到函数f(x)的图象,故函数f(x)的图象是以点(1,1)为中心的中心对称图形.(Ⅲ)证明:在曲线上任取一点.由知,过此点的切线方程为.令x=1得,切线与直线x=1交点为.令y=x得y=2x0﹣1,切线与直线y=x交点为(2x0﹣1,2x0﹣1).直线x=1与直线y=x的交点为(1,1).从而所围三角形的面积为.所以,所围三角形的面积为定值2.22.(10分)(2008•海南)如图,过圆O外一点M作它的一条切线,切点为A,过A作直线AP垂直直线OM,垂足为P.(1)证明:OM•OP=OA2;(2)N为线段AP上一点,直线NB垂直直线ON,且交圆O于B点.过B点的切线交直线ON于K.证明:∠OKM=90°.【分析】(1)在三角形OAM中考虑,因为MA是圆O的切线,所以OA⊥AM,从而由射影定理即得;(2)结合(1)问的结论,利用比例线段证明两个三角形△ONP、△OMK相似,通过对应角相等即可得.【解答】证明:(1)因为MA是圆O的切线,所以OA⊥AM,又因为AP⊥OM,在Rt△OAM中,由射影定理知OA2=OM•OP,故OM•OP=OA2得证.(2)因为BK是圆O的切线,BN⊥OK,同(1)有:OB2=ON•OK,又OB=OA,所以OM•OP=ON•OK,即,又∠NOP=∠MOK,所以△ONP~△OMK,故∠OKM=∠OPN=90°.即有:∠OKM=90°.23.(2008•海南)自选题:已知曲线C1:(θ为参数),曲线C2:(t为参数).(Ⅰ)指出C1,C2各是什么曲线,并说明C1与C2公共点的个数;(Ⅱ)若把C1,C2上各点的纵坐标都压缩为原来的一半,分别得到曲线C1′,C2′.写出C1′,C2′的参数方程.C1′与C2′公共点的个数和C与C2公共点的个数是否相同?说明你的理由.【分析】(I)先利用公式sin2θ+cos2θ=1将参数θ消去,得到圆的直角坐标方程,利用消元法消去参数t得到直线的普通方程,再根据圆心到直线的距离与半径进行比较,从而得到C1与C2公共点的个数;(II)求出压缩后的参数方程,再将参数方程化为普通方程,联立直线方程与圆的方程,利用判别式进行判定即可.【解答】解:(Ⅰ)C1是圆,C2是直线.C1的普通方程为x2+y2=1,圆心C1(0,0),半径r=1.C2的普通方程为.因为圆心C1到直线的距离为1,所以C2与C1只有一个公共点.(Ⅱ)压缩后的参数方程分别为C1′:(θ为参数);C2′:(t为参数).化为普通方程为:C1′:x2+4y2=1,C2′:,联立消元得,其判别式,所以压缩后的直线C2′与椭圆C1′仍然只有一个公共点,和C1与C2公共点个数相同.24.(2008•海南)自选题:已知函数f(x)=|x﹣8|﹣|x﹣4|.(Ⅰ)作出函数y=f(x)的图象;(Ⅱ)解不等式|x﹣8|﹣|x﹣4|>2.【分析】(I)这是一个绝对值函数,先转化为分段函数,再分段作出其图象;(II)借助(I)的图象,找出函数值为2的点,依据图象找出不等式的解集.【解答】解:(Ⅰ)f(x)=图象如下:(Ⅱ)不等式|x﹣8|﹣|x﹣4|>2,即f(x)>2,观察知当4<x<8时,存在函数值为2的点.由﹣2x+12=2得x=5.由函数f(x)图象可知,原不等式的解集为(﹣∞,5).。
2008年高考试题——数学理(宁夏卷)

2008年普通高等学校招生全国统一考试(宁夏卷)理科数学数学(理)试题头说明:本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,其中第Ⅱ卷第22-24题为选考题,其它题为必考题.考生作答时,将答案答在答题卡上.在本试卷上答题无效.考试结束后,将本试卷和答题卡一并交回. 注意事项:1.答题前,考生务必先将自己的姓名、准考证号填写在答题卡上,认真核对条形码上的姓名、准考证号,并将条形码粘贴在答题卡的指定位置上.2.选择题答案使用2B 铅笔填涂,如需改动,用橡皮擦干净后,再选涂其它答案标号;非选择题答案使用0.5毫米的黑色中性(签字)笔或碳素笔书写,字体工整、笔迹清楚.3.请按照题号在各题的答题区域(黑色线框)内作答,超出答题区域书写的答案无效. 4.保持卡面清洁,不折叠,不破损.5.做选考题时,考生按照题目要求作答,并用2B 铅笔在答题卡上把所选题目对应的题号涂黑. 参考公式:样本数据x 1,x 2, …,x n 的标准参 锥体体积公式 s=222121()()()n x x x x x x n ⎡⎤---++-⎣⎦… V =31Sh 其中x 为样本平均数其中S 为底面面积,h 为高 柱体体积公式球的表面积、体积公式V =Sh24S R =π,343V R =π其中S 为底面面积,h 为高其中R 为球的半径第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的. 1.已知函数2sin()(0)y x ωϕω=+>)在区间[]02π,的图像如下:那么ω=( ) A .1B .2C .21D .31 2.已知复数1z i =-,则122--z zz =( )A .2iB .2i -C .2D .2-y x 2π11 O3.如果等腰三角形的周长是底边长的5倍,那么它的顶角的余弦值为( ) A .185 B .43 C .23 D .87 4.设等比数列{}n a 的公比q =2,前n 项和为S n ,则24a S =( ) A .2B .4C .215 D .217 5.右面的程序框图,如果输入三个实数a ,b ,c ,要求输出这三 个数中最大的数,那么在空白的判断框中,应该填入下面四个选 项中的( ) A .c x > B .x c > C .c b > D .b c >6.已知a 1>a 2>a 3>0,则使得2(1)1(123)i a x i -<=,,都成立的x 取值范围是( )A .110a ⎛⎫ ⎪⎝⎭,B .120a ⎛⎫ ⎪⎝⎭,C .310a ⎛⎫ ⎪⎝⎭,D .320a ⎛⎫ ⎪⎝⎭,7.23sin 702cos 10-=-( ) A .12B .22C .2D .328.平面向量a ,b 共线的充要条件是( ) A .a ,b 方向相同B .a ,b 两向量中至少有一个为零向量C .λ∈R ∃,λ=b aD .存在不全为零的实数1λ,2λ,12λλ+=0a b9.甲、乙、丙3位志愿者安排在周一至周五的5天中参加某项志愿者活动,要求每人参加一天且每天至多安排一人,并要求甲安排在另外两位前面.不同的安排方法共有( ) A .20种 B .30种 C .40种 D .60种 10.由直线12x =,x =2,曲线1y x =及x 轴所围图形的面积为( ) A .154B .174C .1ln 22D .2ln 211.已知点P 在抛物线24y x =上,那么点P 到点(21)Q -,的距离与点P 到抛物线焦点距离之和取得最小开始 输入a b c ,,x a =b x >x b =x c =输出x 结束是是 否否值时,点P 的坐标为( ) A .114⎛⎫- ⎪⎝⎭,B .114⎛⎫⎪⎝⎭,C .(12),D .(12)-, 12.某几何体的一条棱长为7,在该几何体的正视图中,这条棱的投影是长为6的线段,在该几何体的侧视图与俯视图中,这条棱的投影分别是长为a 和b 的线段,则a +b 的最大值为( ) A .22B .23C .4D .25第Ⅱ卷本卷包括必考题和选考题两部分.第13题~第21题为必考题,每个试题考生都必须做答.第22题~第24题为选考题,考生根据要求做答.二、填空题:本大题共4小题,每小题5分.13.已知向量(011)=-,,a ,(410)=,,b ,29λ+=a b 且0λ>,则λ= .14.设双曲线221916x y -=的右顶点为A ,右焦点为F .过点F 平行双曲线的一条渐近线的直线与双曲线交于点B ,则△AFB 的面积为 .15.一个六棱柱的底面是正六边形,其侧棱垂直底面.已知该六棱柱的顶点都在同一个球面上,且该六棱柱的体积为98,底面周长为3,则这个球的体积为 . 16.从甲、乙两品种的棉花中各抽测了25根棉花的纤维长度(单位:mm ),结果如下: 甲品种:271 273 280 285 285 287 292 294 295 301 303 303 307 308 310 314 319 323 325 325 328 331 334 337 352乙品种:284 292 295 304 306 307 312 313 315 315 316 318 318 320 322 322 324 327 329 331 333 336 337 343 356 由以上数据设计了如下茎叶图根据以上茎叶图,对甲、乙两品种棉花的纤维长度作比较,写出两个统计结论: ① ; ② .三、解答题:解答应写出文字说明,证明过程或演算步骤.3 1 27 7 5 5 0 2845 4 2 29 2 5 8 7 3 3 1 30 46 79 4 0 31 2 3 5 5 6 8 8 8 5 5 3 32 0 2 2 4 7 9 7 4 1 33 1 3 6 734 3 2 35 6甲乙17.(本小题满分12分)已知{}n a 是一个等差数列,且21a =,55a =-. (Ⅰ)求{}n a 的通项n a ;(Ⅱ)求{}n a 前n 项和S n 的最大值.18.(本小题满分12分)如图,已知点P 在正方体ABCD A B C D ''''-的对角线BD '上,60PDA ∠=︒. (Ⅰ)求DP 与CC '所成角的大小;(Ⅱ)求DP 与平面AA D D ''所成角的大小.19.(本小题满分12分)A B ,两个投资项目的利润率分别为随机变量X 1和X 2.根据市场分析,X 1和X 2的分布列分别为X 15% 10% P0.80.2(Ⅰ)在A B ,两个项目上各投资100万元,Y 1和Y 2分别表示投资项目A 和B 所获得的利润,求方差DY 1,DY 2;(Ⅱ)将(0100)x x ≤≤万元投资A 项目,100x -万元投资B 项目,()f x 表示投资A 项目所得利润的方差与投资B 项目所得利润的方差的和.求()f x 的最小值,并指出x 为何值时,()f x 取到最小值. (注:2()D aX b a DX +=)20.(本小题满分12分)X 22% 8% 12% P0.20.50.3A B C D P A ' B 'C 'D '在直角坐标系xOy 中,椭圆C 1:2222b y a x +=1(a >b >0)的左、右焦点分别为F 1,F 2.F 2也是抛物线C 2:24y x =的焦点,点M 为C 1与C 2在第一象限的交点,且|MF 2|=35.(Ⅰ)求C 1的方程;(Ⅱ)平面上的点N 满足21MF MF MN +=,直线l ∥MN ,且与C 1交于A ,B 两点,若0OA OB =,求直线l 的方程.21.(本小题满分12分) 设函数1()()f x ax a b x b=+∈+Z ,,曲线()y f x =在点(2(2))f ,处的切线方程为y =3. (Ⅰ)求()f x 的解析式:(Ⅱ)证明:函数()y f x =的图像是一个中心对称图形,并求其对称中心;(Ⅲ)证明:曲线()y f x =上任一点的切线与直线x =1和直线y =x 所围三角形的面积为定值,并求出此定值.请考生在第22、23、24题中任选一题做答,如果多做,则按所做的第一题记分.做答时,用2B 铅笔在答题卡上把所选题目对应的题号涂黑.22.(本小题满分10分)选修4-1:几何证明选讲如图,过圆O 外一点M 作它的一条切线,切点为A ,过A 点作直线AP 垂直直线OM ,垂足为P .(Ⅰ)证明:2OM OP OA =; (Ⅱ)N 为线段AP 上一点,直线NB 垂直直线ON ,且交圆O 于B 点.过B 点的切线交直线ON 于K .证明:90OKM =∠.23.(本小题满分10分)选修4-4;坐标系与参数方程O MA PN B K已知曲线C 1:cos sin x y θθ=⎧⎨=⎩,(θ为参数),曲线C 2:22222x t y ⎧=-⎪⎪⎨⎪=⎪⎩,(t 为参数). (Ⅰ)指出C 1,C 2各是什么曲线,并说明C 1与C 2公共点的个数;(Ⅱ)若把C 1,C 2上各点的纵坐标都压缩为原来的一半,分别得到曲线12C C '',.写出12C C '',的参数方程.1C '与2C '公共点的个数和C 21C 与公共点的个数是否相同?说明你的理由.24.(本小题满分10分)选修4-5:不等式选讲 已知函数()84f x x x =---.(Ⅰ)作出函数()y f x =的图像; (Ⅱ)解不等式842x x --->.11 O xy答案BBDCA BCDAD AC (13)3 (14)1532 (15) 34π(16). 1.乙品种棉花的纤维平均长度大于甲品种棉花的纤维平均长度(或:乙品种棉花的纤维长度普遍大于甲品种棉花的纤维长度)。
2008年(全国卷II)(含答案)高考理科数学

2008年(全国卷II)(含答案)高考理科数学2008年普通高等学校招生全国统一考试(2全国Ⅱ卷)数学(理)试题一、选择题 ( 本大题 共 12 题, 共计 60 分)1.设集合{|32}M m m =∈-<<Z ,{|13}N n n M N =∈-=Z I 则,≤≤( ) A .{}01,B .{}101-,,C .{}012,,D .{}1012-,,,2.设a b ∈R ,且0b ≠,若复数3()a bi +是实数,则( ) A .223b a = B .223a b =C .229b a =D .229a b =3.函数1()f x x x=-的图像关于( ) A .y 轴对称 B . 直线x y -=对称C . 坐标原点对称D . 直线x y =对称4.若13(1)ln 2ln ln x e a x b x c x -∈===,,,,,则( ) A .a <b <c B .c <a <b C . b <a <c D . b <c <a5.设变量x y ,满足约束条件:222y x x y x ⎧⎪+⎨⎪-⎩,,.≥≤≥,则y x z 3-=的最小值( )A .2-B .4-C .6-D .8-6.从20名男同学,10名女同学中任选3名参加体能测试,则选到的3名同学中既有男同学又有女同学的概率为( ) A .929B .1029C .1929D .20297.64(1)(1)x x 的展开式中x 的系数是( ) A .4- B .3-C .3D .48.若动直线x a =与函数()sin f x x =和()cos g x x =的图像分别交于M N ,两点,则MN 的最大值为( ) A .1B 2C .3D .29.设1a >,则双曲线22221(1)x y a a -=+的离心率e 的取值范围是( ) A .22),B .25),C .(25),D .(25),10.已知正四棱锥S ABCD -的侧棱长与底面边长都相等,E 是SB 的中点,则AE SD ,所成的角的余弦值为( )A .13B .23C .3 D .2311.等腰三角形两腰所在直线的方程分别为20x y +-=与740x y --=,原点在等腰三角形的底边上,则底边所在直线的斜率为( ) A .3B .2C .13-D .12-12.已知球的半径为2,相互垂直的两个平面分别截球面得两个圆.若两圆的公共弦长为2,则两圆的圆心距等于( ) A .1B .2C .3D .2二、填空题:本大题共4小题,每小题5分,共20分.把答案填在题中横线上. 13.设向量(12)(23)==,,,a b ,若向量λ+a b 与向量(47)=--,c 共线,则=λ .14.设曲线ax y e =在点(01),处的切线与直线210x y ++=垂直,则a = .15.已知F 是抛物线24C y x =:的焦点,过F 且斜率为1的直线交C 于A B ,两点.设FA FB >,则FA 与FB 的比值等于 .16.平面内的一个四边形为平行四边形的充要条件有多个,如两组对边分别平行,类似地,写出空间中的一个四棱柱为平行六面体的两个充要条件: 充要条件① ; 充要条件② . (写出你认为正确的两个充要条件)三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.17.(本小题满分10分) 在ABC △中,5cos 13B =-,4cos 5C =. (Ⅰ)求sin A 的值; (Ⅱ)设ABC △的面积332ABC S =△,求BC 的长.18.(本小题满分12分)购买某种保险,每个投保人每年度向保险公司交纳保费a 元,若投保人在购买保险的一年度内出险,则可以获得10 000元的赔偿金.假定在一年度内有10 000人购买了这种保险,且各投保人是否出险相互独立.已知保险公司在一年度内至少支付赔偿金10 000元的概率为41010.999-. (Ⅰ)求一投保人在一年度内出险的概率p ;(Ⅱ)设保险公司开办该项险种业务除赔偿金外的成本为50 000元,为保证盈利的期望不小于0,求每位投保人应交纳的最低保费(单位:元).19.(本小题满分12分)如图,正四棱柱1111ABCD A B C D -中,124AA AB ==,点E 在1CC 上且EC E C 31=. (Ⅰ)证明:1A C ⊥平面BED ; (Ⅱ)求二面角1A DE B --的大小.E A 1B 1C 1D 120.(本小题满分12分)设数列{}n a 的前n 项和为n S .已知1a a =,13n n n a S +=+,*n ∈N . (Ⅰ)设3n n n b S =-,求数列{}n b 的通项公式; (Ⅱ)若1n n a a +≥,*n ∈N ,求a 的取值范围.21.(本小题满分12分)设椭圆中心在坐标原点,(20)(01)A B ,,,是它的两个顶点,直线)0(>=k kx y 与AB 相交于点D ,与椭圆相交于E 、F 两点.(Ⅰ)若6ED DF =u u u r u u u r,求k 的值; (Ⅱ)求四边形AEBF 面积的最大值.22.(本小题满分12分) 设函数sin ()2cos xf x x=+.(Ⅰ)求()f x 的单调区间;(Ⅱ)如果对任何0x ≥,都有()f x ax ≤,求a 的取值范围.2008年普通高等学校招生全国统一考试(2全国Ⅱ卷)数学(理)试题答案解析:一、选择题1.答案:B解析:依题M={-2,-1,0,1},N={-1,0,1,2,3},从而M∩N={-1,0,1},故选B. 2.答案:A解析: (a+bi)3=a3+3a2·bi+3a(bi)2+(bi)3=a3+3a2bi-3ab2-b3i=(a3-3ab2)+(3a2b-b3)i为实数3a2b-b3=0,又∵b≠0,∴3a2-b2=0.∴b2=3a2.选A.3.答案:C解析:∵f(x)=f(-x),∴f(x)= -x是奇函数.∴f(x)的图象关于坐标原点对称.4.答案:C解析:a=lnx,b=2lnx=lnx2,c=ln3x.∵x∈(e-1,1),∴x>x2.故a>b,排除A、B.∵e-1<x<1,∴-1<lnx<ln1=0.∴lnx<ln3x.∴a<c.故b<a<c,选C.5.答案:D解析:作出可行域.令z=0,则l0:x-3y=0,平移l在点M(-2,2)处z取到最小,最小值为-8.6.答案:D解析:排除法即可.P=1-=1-. 7.答案:B解析:化简原式=[(1-)4(1+)4]·(1-)2 =[(1-)(1+)]4·(1-)2=(1-x)4·(1-)2=(1-4x+6x2-4x3+x4)(1-2+x).故系数为1-4=-3,选B.8.答案:B解析:依题可知|MN|=|sina-cosa|=|sin(a-)|,故|MN|max=.9.答案:B解析:依题可知离心率e===,∵a>1,∴0<<1.∴(+1)2∈(1,4).∴e∈(2,5).10.答案:C解析:作图.连结EO,则所求角为∠AEO或其补角.(∵EO∥SD)设侧棱长为a,则OE=SD=a,AO=a,AE= a.由余弦定理得cos∠AEO==. 11.答案:A解析:依题设底边所在直线斜率为k,则底边方程为l:y=kx,l1:x+y-2=0,k1=-1,l2:x-7y-4=0,k2=.由等腰三角形特征有:直线l到l1所成角的正切与直线l2到l所成角的正切相等,从而,得k=3,故选A.12.已知球的半径为2,相互垂直的两个平面分别截球面得两个圆.若两圆的公共弦长为2,则两圆的圆心距等于()A.1 B.2C.3D.2答案:C解析:依题意有示意图截面示意图为其中AH为公共弦长的一半,OA为球半径,∴OH=.故选C.二、填空题:本大题共4小题,每小题5分,共20分.把答案填在题中横线上.13.答案:2解析:λa+b=λ(1,2)+(2,3)=(λ+2,2λ+3),∵λa+b与c共线,∴(λ+2)·(-7)-(2λ+3)·(-4)=0.解出λ=2.14.答案:2解析:y=e ax,y′=e ax·a,y′|x=0=e a·0·a=a. 又x+2y+1=0的斜率为-,∴由题意a·(-)=-1.∴a=2.15.答案:解析:lAB:y-0=x-1,即y=x-1,联立xa =3+2,xb=3-2,∴=3+2.16.解析:两组相对侧面分别平行;一组相对侧面平行且全等;对角线交于一点;底面是平行四边形.注:上面给出了四个充要条件.如果考生写出其他正确答案,同样给分.三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.17.解:(Ⅰ)由5cos13B=-,得12sin13B=,由4cos5C=,得3sin5C=.所以33sin sin()sin cos cos sin65A B C B C B C=+=+=. ······························ 5分(Ⅱ)由332ABCS=△得133sin 22AB AC A ⨯⨯⨯=, 由(Ⅰ)知33sin 65A =,故 65AB AC ⨯=, ································································· 8分又 sin 20sin 13AB B AC AB C ⨯==,故 2206513AB =,132AB =.所以 sin 11sin 2AB A BC C ⨯==. ······················································ 10分 18.解:各投保人是否出险互相独立,且出险的概率都是p ,记投保的10 000人中出险的人数为ξ, 则4~(10)B p ξ,.(Ⅰ)记A 表示事件:保险公司为该险种至少支付10 000元赔偿金,则A 发生当且仅当0ξ=,··········································································· 2分()1()P A P A =-1(0)P ξ=-=4101(1)p =--, 又410()10.999P A =-,故0.001p =. ················································································· 5分 (Ⅱ)该险种总收入为10000a 元,支出是赔偿金总额与成本的和. 支出 1000050000ξ+,盈利 10000(1000050000)a ηξ=-+,盈利的期望为 100001000050000E a E ηξ=--, ································· 9分由43~(1010)B ξ-,知,31000010E ξ-=⨯, 4441010510E a E ηξ=--⨯4443410101010510a -=-⨯⨯-⨯.0E η≥4441010105100a ⇔-⨯-⨯≥1050a ⇔--≥15a ⇔≥(元). 故每位投保人应交纳的最低保费为15元. ·········································· 12分 19.解法一:依题设知2AB =,1CE =. (Ⅰ)连结AC 交BD 于点F ,则BD AC ⊥.由三垂线定理知,1BD A C ⊥. ··························································· 3分 在平面1A CA 内,连结EF 交1A C 于点G , 由于122AA ACFC CE==, 故1Rt Rt A AC FCE △∽△,1AA C CFE ∠=∠,CFE ∠与1FCA ∠互余. 于是1A C EF ⊥.1A C 与平面BED 内两条相交直线BD EF ,都垂直,所以1A C ⊥平面BED . ····································································· 6分 (Ⅱ)作GH DE ⊥,垂足为H ,连结1A H .由三垂线定理知1A H DE ⊥, 故1A HG ∠是二面角1A DE B --的平面角. ············································ 8分223EF CF CE =+= 23CE CF CG EF ⨯==2233EG CE CG =-=. 13EG EF =,12315EF FD GH DE ⨯=⨯= 又221126AC AA AC =+=1163A G A C CG =-=. A BC D E A 1B 1C 1D 1F H G11tan 55AG A HG HG∠== 所以二面角1A DE B --的大小为arctan 55 ······································ 12分 解法二:以D 为坐标原点,射线DA 为x 轴的正半轴, 建立如图所示直角坐标系D xyz -.依题设,1(220)(020)(021)(204)B C E A ,,,,,,,,,,,. (021)(220)DE DB ==u u u r u u u r ,,,,,,11(224)(204)AC DA =--=u u u r u u u u r,,,,,. ··························································· 3分 (Ⅰ)因为10AC DB =u u u r u u u r g ,10AC DE =u u u r u u u rg , 故1A C BD ⊥,1A C DE ⊥. 又DB DE D =I ,所以1A C ⊥平面DBE . ····································································· 6分 (Ⅱ)设向量()x y z =,,n 是平面1DA E 的法向量,则DE ⊥u u u r n ,1DA ⊥u u u u r n .故20y z +=,240x z +=.令1y =,则2z =-,4x =,(412)=-,,n . ··········································· 9分 1AC u u u r ,n 等于二面角1A DE B --的平面角, 11114cos 42A C A C A C==u u u ru u u r g u u u r ,n n n . 所以二面角1A DE B --的大小为14. ······································ 12分 20.解:(Ⅰ)依题意,113n n n n n S S a S ++-==+,即123n n n S S +=+,由此得1132(3)n n n n S S ++-=-. ···························································· 4分A BC DE A 1B 1C 1D 1xz因此,所求通项公式为13(3)2n n n n b S a -=-=-,*n ∈N .① ···················································· 6分(Ⅱ)由①知13(3)2n n n S a -=+-,*n ∈N , 于是,当2n ≥时,1n n n a S S -=-1123(3)23(3)2n n n n a a ---=+-⨯---⨯ 1223(3)2n n a --=⨯+-, 12143(3)2n n n n a a a --+-=⨯+-22321232n n a --⎡⎤⎛⎫=•+-⎢⎥ ⎪⎝⎭⎢⎥⎣⎦,当2n ≥时,21312302n n n a a a -+⎛⎫⇔•+- ⎪⎝⎭≥≥9a ⇔-≥.又2113a a a =+>.综上,所求的a 的取值范围是[)9-+∞,.12分21.(Ⅰ)解:依题设得椭圆的方程为2214x y +=,直线AB EF ,的方程分别为22x y +=,(0)y kx k =>. ···························· 2分 如图,设001122()()()D x kx E x kx F x kx ,,,,,,其中12x x <, 且12x x ,满足方程22(14)4k x +=, 故21214x x k=-=+由6ED DF =u u u r u u u r 知01206()x x x x -=-,得0212215(6)77714x x x x k=+==+;D F B y A O E由D 在AB 上知0022x kx +=,得0212x k=+. 所以2212714k k=++,化简得2242560k k -+=, 解得23k =或38k =. ········································································· 6分 (Ⅱ)解法一:根据点到直线的距离公式和①式知,点E F ,到AB 的距离分别为211122214)55(14)x kx k h k +-+==+22222222(1214)55(14)x kx k k h k +-+-+==+. ··············································· 9分又2215AB =+=,所以四边形AEBF 的面积为121()2S AB h h =+ 21525(14)k =+g g214k=+22144214k k k ++=+22≤当21k =,即当12k =时,上式取等号.所以S 的最大值为22. ············ 12分 解法二:由题设,1BO =,2AO =.设11y kx =,22y kx =,由①得20x >,210y y =->, 故四边形AEBF 的面积为BEF AEF S S S =+△△222x y =+ ······················································································· 9分222(2)x y =+22222244x y x y =++22222(4)x y +22=当222x y =时,上式取等号.所以S 的最大值为22 12分 22.解:(Ⅰ)22(2cos )cos sin (sin )2cos 1()(2cos )(2cos )x x x x x f x x x +--+'==++. ············ 2分当2π2π2π2π33k x k -<<+(k ∈Z )时,1cos 2x >-,即()0f x '>; 当2π4π2π2π33k x k +<<+(k ∈Z )时,1cos 2x <-,即()0f x '<. 因此()f x 在每一个区间2π2π2π2π33k k ⎛⎫-+ ⎪⎝⎭,(k ∈Z )是增函数, ()f x 在每一个区间2π4π2π2π33k k ⎛⎫++ ⎪⎝⎭,(k ∈Z )是减函数. ··················· 6分 (Ⅱ)令()()g x ax f x =-,则22cos 1()(2cos )x g x a x +'=-+ 2232cos (2cos )a x x =-+++211132cos 33a x ⎛⎫=-+- ⎪+⎝⎭.故当13a ≥时,()0g x '≥.又(0)0g =,所以当0x ≥时,()(0)0g x g =≥,即()f x ax ≤. ················ 9分 当103a <<时,令()sin 3h x x ax =-,则()cos 3h x x a '=-. 故当[)0arccos3x a ∈,时,()0h x '>. 因此()h x 在[)0arccos3a ,上单调增加.故当(0arccos3)x a ∈,时,()(0)0h x h >=,即sin3x ax>.于是,当(0arccos3)x a∈,时,sin sin()2cos3x xf x axx=>>+.当0a≤时,有π1π222f a⎛⎫=>•⎪⎝⎭≥.因此,a的取值范围是13⎡⎫+∞⎪⎢⎣⎭,.12分。
高中数学2008年普通高等学校招生全国统一考试(海南、宁夏卷)(理科)试题

高中数学2008年普通高等学校招生全国统一考试(海南、宁夏卷)(理科) 试题 2019.091,已知PA 是圆O 的切点,切点为A ,PA =2.AC 是圆O 的直径,PC 与圆O 交于B 点,PB =1,则圆O 的半径R=________.2,已知函数()sin()(0,0),f x A x a x R ϕϕπ=+><<∈的最大值是1,其图像经过点1(,)32M π。
(1)求()f x 的解析式;(2)已知,(0,)2παβ∈,且312(),(),513f f αβ==求()f αβ-的值。
3,某单位用2160万元购得一块空地,计划在该地块上建造一栋至少10层、每层2000平方米的楼房.经测算,如果将楼房建为x(x ≥10)层,则每平方米的平均建筑费用为560+48x (单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?(注:平均综合费用=平均建筑费用+平均购地费用,平均购地费用=购地总费用建筑总面积)4,如图所示,四棱锥P-ABCD 的底面ABCD 是半径为R 的圆的内接四边形,其中BD 是圆的直径,60,45,~ABD BDC ADP BAD ∠=∠=∆∆。
(1)求线段PD 的长;(2)若PC =,求三棱锥P-ABC 的体积。
5,某初级中学共有学生2000名,各年级男、女生人数如下表:已知在全校学生中随机抽取1名,抽到初二年级女生的概率是0.19. (1)求x 的值;(2)现用分层抽样的方法在全校抽取48名学生,问应在初三年级抽取多少名?(3)已知y ≥245,z ≥245,求初三年级中女生比男生多的概率.6,设0b >,椭圆方程为222212x y b b +=,抛物线方程为28()x y b =-.如图所示,过点(02)F b +,作x 轴的平行线,与抛物线在第一象限的交点为G ,已知抛物线在点G 的切线经过椭圆的右焦点1F . (1)求满足条件的椭圆方程和抛物线方程;(2)设A B ,分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点P ,使得ABP △为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).7,设数列{}n a 满足11a =,22a =,121(2)3n n n a a a --=+ (3,4,)n =。
2008年普通高等学校统一考试(宁夏卷)

2008年普通高等学校统一考试(宁夏卷)数学(文科)一、选择题:本大题共12小题,每小题5分,满分60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1、已知集合M ={ x|(x + 2)(x -1) < 0 },N ={ x| x + 1 < 0 }, 则M ∩N =( ) A. (-1,1) B. (-2,1)C. (-2,-1)D. (1,2)2、双曲线221102x y -=的焦距为( )3、已知复数1z i =-,则21z z =-( ) A. 2B. -2C. 2iD. -2i4、设()ln f x x x =,若0'()2f x =,则0x =( )A. 2eB. eC.ln 22D. ln 2 5、已知平面向量a r =(1,-3),b r=(4,-2),a b λ+r r 与a r垂直,则λ是( )A. -1B. 1C. -2D. 26、右面的程序框图,如果输入三个实数a 、b 、c ,要 求输出这三个数中最大的数,那么在空白的判断 框中,应该填入下面四个选项中的( ) A. c > xB. x > cC. c > bD. b > c7、已知1230a a a >>>,则使得2(1)1i a x -<(1,2,3)i =都成立的x 取值范围是( )A.(0,11a ) B. (0,12a ) C. (0,31a ) D. (0,32a ) 8、设等比数列{}n a 的公比2q =,前n 项和为n S ,则42S a =( ) A. 2 B. 4 C.152D.1729、平面向量a r ,b r共线的充要条件是( )A. a r ,b r 方向相同B. a r ,b r 两向量中至少有一个为零向量C. R λ∃∈, b a λ=r rD. 存在不全为零的实数1λ,2λ,120a b λλ+=r r r10、点P (x ,y )在直线4x + 3y = 0上,且满足-14≤x -y ≤7,则点P 到坐标原点距离的取值范围是( )A. [0,5]B. [0,10]C. [5,10]D. [5,15]11、函数()cos 22sin f x x x =+的最小值和最大值分别为( )A. -3,1B. -2,2C. -3,32D. -2,3212、已知平面α⊥平面β,α∩β= l ,点A ∈α,A ∉l ,直线AB ∥l ,直线AC ⊥l ,直线m ∥α,m ∥β,则下列四种位置关系中,不一定...成立的是( ) A. AB ∥mB. AC ⊥mC. AB ∥βD. AC⊥β二、填空题:本大题共4小题,每小题5分,满分20分。
2008年全国高考理科数学试题及答案-宁夏卷
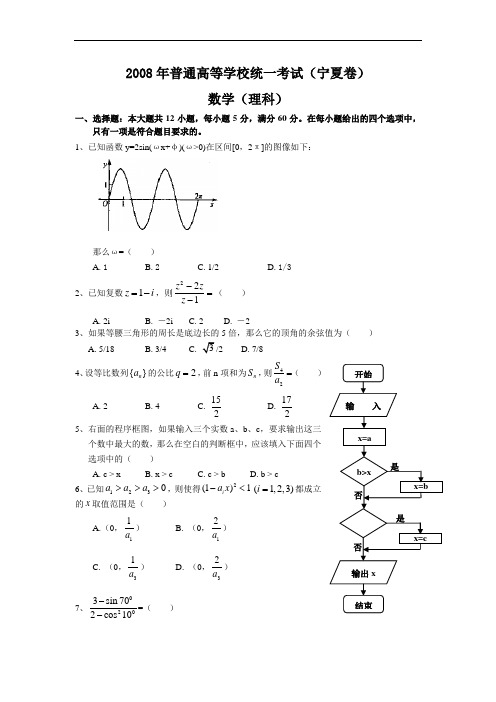
2008年普通高等学校统一考试(宁夏卷)数学(理科)一、选择题:本大题共12小题,每小题5分,满分60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1、已知函数y=2sin(ωx+φ)(ω>0)在区间[0,2π]的图像如下:那么ω=( ) A. 1B. 2C. 1/2D. 1/32、已知复数1z i =-,则221z zz -=-( ) A. 2i B. -2i C. 2 D. -23、如果等腰三角形的周长是底边长的5倍,那么它的顶角的余弦值为( ) A. 5/18B. 3/4C.3/2 D. 7/84、设等比数列{}n a 的公比2q =,前n 项和为n S ,则42S a =( ) A. 2 B. 4 C.152D.1725、右面的程序框图,如果输入三个实数a 、b 、c ,要求输出这三个数中最大的数,那么在空白的判断框中,应该填入下面四个选项中的( ) A. c > xB. x > cC. c > bD. b > c6、已知1230a a a >>>,则使得2(1)1i a x -<(1,2,3)i =都成立的x 取值范围是( )A.(0,11a )B. (0,12a )C. (0,31a ) D. (0,32a ) 7、0203sin 702cos 10--=( )是否 开始输入x=ab>x 输出x结束x=bx=c否是A.12B.2C. 2D.28、平面向量a ,b 共线的充要条件是( )A. a ,b 方向相同B. a ,b 两向量中至少有一个为零向量C. R λ∃∈, b a λ=D. 存在不全为零的实数1λ,2λ,120a b λλ+=9、甲、乙、丙3位志愿者安排在周一至周五的5天中参加某项志愿者活动,要求每人参加一天且每天至多安排一人,并要求甲安排在另外两位前面。
不同的安排方法共有( ) A. 20种B. 30种C. 40种D. 60种10、由直线21=x ,x=2,曲线xy 1=及x 轴所围图形的面积为( ) A. 415 B. 417 C. 2ln 21 D. 2ln 211、已知点P 在抛物线y 2 = 4x 上,那么点P 到点Q (2,-1)的距离与点P 到抛物线焦点距离之和取得最小值时,点P 的坐标为( ) A. (41,-1) B. (41,1) C. (1,2) D. (1,-2)12、某几何体的一条棱长为7,在该几何体的正视图中,这条棱的投影是长为6的线段,在该几何体的侧视图与俯视图中,这条棱的投影分别是长为a 和b 的线段,则a + b 的最大值为( )A. 22B. 32C. 4D. 52二、填空题:本大题共4小题,每小题5分,满分20分。
2008年普通高等学校招生全国统一考试宁夏卷理
2008年普通高等学校招生全国统一考试(宁夏卷.理)数学试题本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,考试时间120分钟。
参考公式:样本数据x 1,x 2, …,x n 的标准差 锥体体积公式s=⎥⎦⎤⎢⎣⎡-++----22221)()()1x x x x x x n n ( V= 31Sh 其中x 为样本平均数 其中S 为底面积,h 为高 柱体体积公式球的表面积、体积公式 V=ShS=4πR 2,V=34πR 3其中S 为底面面积,h 为高其中R 为球的半径第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是 符合题目要求的.1.已知函数y=2sin )0)((>+ωφωx )在区间[0,2π]的图像如下,那么ω=A .1B .2C .21D .31 2.已知复数z=1-i ,则122--z zz =A .2iB .-2iC .2D .-23.如果等腰三角形的周长是底边长的5倍,那么它的顶角的余弦值为A .185 B .43 C .23 D .874.设等比数列(a n )的公比q=2,前n 项和为S n , 则24a S = A .2 B .4 C .215 D .217 5.下面的程序框图,如果输入三个实数a, b, c,要求输出这三个数中最大的数,那么在空白的判断框中,应该填入下面四个选项中的A .c>xB .x>cC .c>bD .b>c6.已知a 1>a 2>a 3>0,则使得(1- a i x )2<1(i=1,2,3)都成立的x 取值范围是A .(0,11a ) B .(0,12a ) C .(0,31a ) D .(0,32a ) 7.23sin 702cos 10-︒=-︒A .12B.2C .2 D.28.平面向量a, b 共线的充要条件是A .a, b 方向相同B .a, b 两向量中至少有一个为零向量C .∃λ∈R ,b=λaD .存在不全为零的实数λ1,λ2,λ1a+λ2b=09.甲、乙、丙3位志愿者安排在周一至周五的5天中参加某项志愿者活动,要求每人参加一天且每天至多安排一人,并要求甲安排在另外两位前面.不同的安排方法共有A .20种B .30种C .40种D .60种10.由直线x=12,x=2,曲线1y x =及x 轴所围图形的面积为 A .154 B .174 C .1ln 22D .2ln211.已知点P 在抛物线24y x =上,那么点P 到点Q (2,-1)的距离与点P 到抛物线焦点距离之和取得最小值时,点P 的坐标为A .(14,-1) B .(14,1) C .(1,2) D .(1,-2)12.,在该几何体的正视图中,的线段,在该几何体的侧视图与俯视图中,这条棱的投影分别是长为a 和b 的线段,则a+b 的最大值为A .B .C .4D .第Ⅱ卷本卷包括必考题和选考题两部分。
2008年普通高等学校招生全国统一考试(宁夏卷 ).
B
遂平县第一高级中学
沈兴河
2008年普通高等学校招生全国统一考试(宁夏卷 )
19.如图a所示,一矩形线圈abcd放置 在匀 强磁场中,并绕过ab、cd中点 的轴OO′以角速度逆时针匀速转动。 若以线圈平面与磁场夹角时(如图b) 为计时起点,并规定当电流自a流向 b时电流方向为正。则下列四幅图中 正确的是
遂平县第一高级中学
沈兴河
2008年普通高等学校招生全国统一考试(宁夏卷 )
(1)质点在磁场中的轨迹为一圆弧。由于质点飞离磁场 时,速度垂直于OC,故圆弧的圆心在OC上。依题意, 质点轨迹与x轴的交点为A,过A点作与A点的速度方 向垂直的直线,与OC交于O'。由几何关系知, AO'垂直于OC',O'是圆弧的圆心。设圆弧的半 径为R,则有R=dsinφ ① 由洛化兹力公式和牛顿第二定律得 v2 ② qvB m R 将①式代入②式,得
qB2 d E sin 3 cos m
遂平县第一高级中学
⑨
沈兴河
2008年普通高等学校招生全国统一考试(宁夏卷 )
小” )。写出支持你的看法的一个论据:
。
遂平县第一高级中学
沈兴河
2008年普通高等学校招生全国统一考试(宁夏卷 )
23.(15分) 天文学家将相距较近、仅在彼此的引力作用下运 行的两颗恒星称为双星。双星系统在银河系中很普 遍。利用双星系统中两颗恒星的运动特征可推算出 它们的总质量。已知某双星系统中两颗恒星围绕它 们连线上的某一固定点分别做匀速圆周运动,周期 均为T,两颗恒星之间的距离为r,试推算这个双星 系统的总质量。(引力常量为G)
【解析】本题考查电路的串并联知识。当 cd端短路时,R2与R3并联电阻为30Ω后与 R1串联,ab间等效电阻为40Ω,A对;若 ab端短路时,R1与R2并联电阻为8Ω后与 R3串联,cd间等效电阻为128Ω,B错;但ab两端接通测试电源时, 电阻R2未接入电路,cd两端的电压即为R3的电压,为Ucd =80V,C 对;但cd两端接通测试电源时,电阻R1未接入电路,ab两端电压 即为R3的电压,为Uab =25V,D错。
2008年普通高等学校招生全国统一考试理综试题及答案-宁夏卷
绝密★启用前2008年普通高等学校招生全国统一考试(宁夏卷)理科综合能力测试本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,其中第Ⅱ卷第30~38题为选考题,其它题为必考题。
考生作答时,将答案答在答题卡上,在本试卷上答题无效。
考试结束后,将本试卷和答题卡一并交回。
注意事项:1、答题前,考生务必先将自己的姓名、准考证号填写在答题卡上,认真核对条形码上的姓名、准考证号,并将条形码粘贴在答题卡的指定位置上。
2、选择题答案使用2B铅笔填涂,如需改动,用橡皮擦干净后,再选涂其它答案标号;非选择题答案使用0、5毫米的黑色中性(签字)笔或碳素笔书写,字体工整、笔迹清楚。
3、请按照题号在各题的答题区域(黑色线框)内作答,超出答题区域书写的答案无效。
4、保持卡面清洁,不折叠,不破损。
5、做选考题时,考生按照题目要求作答,并用2B铅笔在答题卡上把所选题目对应的题号涂黑。
第I卷一、选择题:本题共13小题,每小题6分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1、下列过程不.属于细胞分化的是A、B淋巴细胞形成浆细胞B、胚胎干细胞形成神经细胞C、质壁分离植物细胞的复原D、蜥蜴断尾再生2、为证实叶绿体有效放氧功能,可利用含有水绵与好氧细菌的临时装片进行实验,装片需要给予一定的条件,这些条件是A、光照、有空气、临时装片中无NaHCO3稀溶液B、光照、无空气、临时装片中无NaHCO3稀溶液C、黑暗、有空气、临时装片中无NaHCO3稀溶液D、黑暗、无空气、临时装片中无NaHCO3稀溶液3、刺激某一个神经元引起后一个神经元兴奋。
当给予某种药物后,再刺激同一个神经元,发现神经冲动的传递被阻断,但检测到突触间隙中神经递质的量与给予药物之前相同。
这是由于该药物A、抑制了突触小体中递质的合成B、抑制了突触后膜的功能C、与递质的化学结构完全相同D、抑制了突触前膜递质的释放4、长时间运动引起机体缺氧时,血液pH的变化趋势、引起pH变化的物质、能起缓冲作用的物质分别分A、降低、CO2、Na2CO3B、降低、乳酸、NaHCO3C、升高、CO2、H2CO3D、升高、乳酸、NaHCO35、以下有关基因重组的叙述,错误..的是A、非同源染色体的自由组合能导致基因重组B、非姊妹染色单体的交换可引起基因重组C、纯合体自交因基因重组导致子代性状分离D、同胞兄妹间的遗传差异与父母基因重组有关6、有一山区由于开采露天小铁矿等活动,自然生态系统完全被破坏,成为一片废墟,为尽快使该山区恢复到原有自然生态系统状态,应采取的最好措施是在这片废墟上A、回填土壤,引进多种外来物种,重建新的生态系统B、撤出人类全部活动,实行全面封闭,等待自然恢复C、回填土壤,栽培当地经济农作物,发展农业生产D、回填土壤,栽种多种当地原有的植物,实行封山育林7、图标所警示的是A、当心火灾——氧化物B、当心火灾——易燃物质C、当心爆炸——自然物质D、当心爆炸——爆炸性物质8、在①丙烯②氯乙烯③苯④甲苯四种有机化合物中,分子内所有原子均在同一平面的是A、①②B、②③C、③④D、②④9、下列说法错误..的是A、乙醇和乙酸都是常用调味品的主要成分B、乙醇和乙酸的沸点和熔点都比C2H6、C2H4的沸点和熔点高C、乙醇和乙酸都能发生氧化反应D、乙醇和乙酸之间能发生酯化反应,酯化反应和皂化反应互为逆反应10、一种燃料电池中发生的化学反应为:在酸性溶液中甲醇与氧作用生成水和二氧化碳。
2008年高考宁夏卷及答案学生用
2008年普通高等学校招生全国统一考试(宁夏)总分:90分时间:40分钟得分:一、选择题:本题共6小题,每小题6分,在每小题给出的四个选项中,只有一项是符合题要求的。
1、下列过程不属于细胞分化的是A、B淋巴细胞形成浆细胞B、胚胎干细胞形成神经细胞C、质壁分离植物细胞的复原D、蜥蜴断尾再生2、为证实叶绿体有放氧功能,可利用含有水绵与好氧细菌的临时装片进行实验,装片需要给予一定的条件,这些条件是A、光照、有空气、临时装片中无NaHCO3稀溶液B、光照、无空气、临时装片中有NaHCO3稀溶液C、黑暗、有空气、临时装片中无NaHCO3稀溶液D、黑暗、无空气、临时装片中有NaHCO3稀溶液3、刺激某一个神经元引起后一个神经元兴奋。
当给予某种药物后,再刺激同一个神经元发现神经冲动的传递被阻断,但检测到突触间隙中神经递质的量与给予药物之前相同。
这是由于该药物A、抑制了突触小体中递质的合成B、抑制了突触后膜的功能C、与递质的化学结构完全相同D、抑制了突触前膜递质的释放4、长时间运动引起机体缺氧时,血液pH的变化趋势、引起pH变化的物质、能起缓冲作用的物质分别是A、降低、CO2、Na2CO3B、降低、乳酸、NaHCO3C、升高、CO2、H2CO3D、升高、乳酸、NaHCO35、以下有关基因重组的叙述,错误的是A、非同源染色体的自由组合能导致基因重组B、非姊妹染色单体的交换可引起基因重组C、纯合体自交因基因重组导致子代性状分离D、同胞兄妹的遗传差异与父母基因重组有关6、有一山区由于开采露天小铁矿等活动,自然生态系统完全被破坏,成为一片废墟,为尽快使该山区恢复到原有自然生态系统状态,应采取的最好措施是在这片废墟上A、回填土壤,引进多种外来物种,重建新的生态系统B、撤出人类全部活动,实行全面封闭,等待自然恢复C、回填土壤,栽培当地经济农作物,发展农业生产D、回填土壤,栽种当地原有的植物,实行封山育林二、非选择题必做题(39分,包括28、29题,共2题)28、(16分)回答下列Ⅰ、Ⅱ题:Ⅰ、将长势相同、数量相等的甲、乙两个品种的大豆幼苗分别置于两个相同的密闭透明玻璃罩内,在光照、温度等相同且适宜的条件下培养,定时测定玻璃罩内的CO2含量,结坚果如图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2008年普通高等学校招生全国统一考试(宁夏卷)理科数学数学(理)试题头说明:本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,其中第Ⅱ卷第22-24题为选考题,其它题为必考题.考生作答时,将答案答在答题卡上.在本试卷上答题无效.考试结束后,将本试卷和答题卡一并交回.注意事项:1.答题前,考生务必先将自己的姓名、准考证号填写在答题卡上,认真核对条形码上的姓名、准考证号,并将条形码粘贴在答题卡的指定位置上.2.选择题答案使用2B 铅笔填涂,如需改动,用橡皮擦干净后,再选涂其它答案标号;非选择题答案使用0.5毫米的黑色中性(签字)笔或碳素笔书写,字体工整、笔迹清楚.3.请按照题号在各题的答题区域(黑色线框)内作答,超出答题区域书写的答案无效. 4.保持卡面清洁,不折叠,不破损.5.做选考题时,考生按照题目要求作答,并用2B 铅笔在答题卡上把所选题目对应的题号涂黑. 参考公式:样本数据x 1,x 2, …,x n 的标准参 锥体体积公式 s=222121()()()n x x x x x x n ⎡⎤---++-⎣⎦… V =31Sh 其中x 为样本平均数其中S 为底面面积,h 为高 柱体体积公式球的表面积、体积公式 V =Sh24S R =π,343V R=π其中S 为底面面积,h 为高其中R 为球的半径第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的. 1.已知函数2sin()(0)y x ωϕω=+>)在区间[]02π,的图像如下:那么ω=( ) A .1B .2C .21 D .312.已知复数1z i =-,则122--z z z =( )A .2iB .2i -C .2D .2-3.如果等腰三角形的周长是底边长的5倍,那么它的顶角的余弦值为( )y x 2π11 OA .185 B .43 C .23 D .874.设等比数列{}n a 的公比q =2,前n 项和为S n ,则24a S =( )A .2B .4C .215 D .2175.右面的程序框图,如果输入三个实数a ,b ,c ,要求输出这三 个数中最大的数,那么在空白的判断框中,应该填入下面四个选 项中的( ) A .c x >B .x c >C .c b >D .b c >6.已知a 1>a 2>a 3>0,则使得2(1)1(123)i a x i -<=,,都成立的x 取值范围是( ) A .110a ⎛⎫ ⎪⎝⎭,B .120a ⎛⎫ ⎪⎝⎭,C .310a ⎛⎫ ⎪⎝⎭,D .320a ⎛⎫ ⎪⎝⎭,7.23sin 702cos 10-=-( )A .12B .22C .2D .328.平面向量a ,b 共线的充要条件是( ) A .a ,b 方向相同B .a ,b 两向量中至少有一个为零向量C .λ∈R ∃,λ=b aD .存在不全为零的实数1λ,2λ,12λλ+=0a b9.甲、乙、丙3位志愿者安排在周一至周五的5天中参加某项志愿者活动,要求每人参加一天且每天至多安排一人,并要求甲安排在另外两位前面.不同的安排方法共有( ) A .20种B .30种C .40种D .60种10.由直线12x =,x =2,曲线1y x=及x 轴所围图形的面积为( )A .154B .174C .1ln 22D .2ln 211.已知点P 在抛物线24y x =上,那么点P 到点(21)Q -,的距离与点P 到抛物线焦点距离之和取得最小值时,点P 的坐标为( )开始输入a b c ,,x a =b x >x b =x c =输出x 结束是是否否A .114⎛⎫- ⎪⎝⎭,B .114⎛⎫⎪⎝⎭,C .(12),D .(12)-,12.某几何体的一条棱长为7,在该几何体的正视图中,这条棱的投影是长为6的线段,在该几何体的侧视图与俯视图中,这条棱的投影分别是长为a 和b 的线段,则a +b 的最大值为( ) A .22B .23C .4D .25第Ⅱ卷本卷包括必考题和选考题两部分.第13题~第21题为必考题,每个试题考生都必须做答.第22题~第24题为选考题,考生根据要求做答. 二、填空题:本大题共4小题,每小题5分. 13.已知向量(011)=-,,a ,(410)=,,b ,29λ+=a b 且0λ>,则λ= .14.设双曲线221916xy-=的右顶点为A ,右焦点为F .过点F 平行双曲线的一条渐近线的直线与双曲线交于点B ,则△AFB 的面积为 .15.一个六棱柱的底面是正六边形,其侧棱垂直底面.已知该六棱柱的顶点都在同一个球面上,且该六棱柱的体积为98,底面周长为3,则这个球的体积为 .16.从甲、乙两品种的棉花中各抽测了25根棉花的纤维长度(单位:mm ),结果如下: 甲品种:271 273 280 285 285 287 292 294 295 301 303 303 307 308 310 314 319 323 325 325 328 331 334 337 352乙品种:284 292 295 304 306 307 312 313 315 315 316 318 318 320 322 322 324 327 329 331 333 336 337 343 356 由以上数据设计了如下茎叶图根据以上茎叶图,对甲、乙两品种棉花的纤维长度作比较,写出两个统计结论: ① ; ② .三、解答题:解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分12分)3 1 277 5 5 0 28 4 5 4 2 29 2 58 7 3 3 1 30 4 6 79 4 0 31 2 3 5 5 6 888 5 5 3 32 0 2 2 4 7 9 7 4 1 33 1 3 6 734 32 35 6甲乙已知{}n a 是一个等差数列,且21a =,55a =-. (Ⅰ)求{}n a 的通项n a ;(Ⅱ)求{}n a 前n 项和S n 的最大值.18.(本小题满分12分)如图,已知点P 在正方体A B C D A B C D ''''-的对角线BD '上,60P D A ∠=︒. (Ⅰ)求DP 与C C '所成角的大小;(Ⅱ)求DP 与平面AA D D ''所成角的大小.19.(本小题满分12分)A B ,两个投资项目的利润率分别为随机变量X 1和X 2.根据市场分析,X 1和X 2的分布列分别为X 15% 10% P0.80.2(Ⅰ)在A B ,两个项目上各投资100万元,Y 1和Y 2分别表示投资项目A 和B 所获得的利润,求方差DY 1,DY 2;(Ⅱ)将(0100)x x ≤≤万元投资A 项目,100x -万元投资B 项目,()f x 表示投资A 项目所得利润的方差与投资B 项目所得利润的方差的和.求()f x 的最小值,并指出x 为何值时,()f x 取到最小值. (注:2()D aX b a D X +=)20.(本小题满分12分)在直角坐标系xOy 中,椭圆C 1:2222by a x +=1(a >b >0)的左、右焦点分别为F 1,F 2.F 2也是抛物线C 2:24y x= X 2 2% 8% 12% P0.20.50.3ABCDPA 'B 'C 'D '的焦点,点M 为C 1与C 2在第一象限的交点,且|MF 2|=35.(Ⅰ)求C 1的方程;(Ⅱ)平面上的点N 满足21MF MF MN +=,直线l ∥MN ,且与C 1交于A ,B 两点,若0OA OB =,求直线l 的方程.21.(本小题满分12分) 设函数1()()f x ax a b x b=+∈+Z ,,曲线()y f x =在点(2(2))f ,处的切线方程为y =3.(Ⅰ)求()f x 的解析式:(Ⅱ)证明:函数()y f x =的图像是一个中心对称图形,并求其对称中心;(Ⅲ)证明:曲线()y f x =上任一点的切线与直线x =1和直线y =x 所围三角形的面积为定值,并求出此定值.请考生在第22、23、24题中任选一题做答,如果多做,则按所做的第一题记分.做答时,用2B 铅笔在答题卡上把所选题目对应的题号涂黑. 22.(本小题满分10分)选修4-1:几何证明选讲如图,过圆O 外一点M 作它的一条切线,切点为A ,过A 点作直线A P 垂直直线O M ,垂足为P . (Ⅰ)证明:2OM OP OA = ;(Ⅱ)N 为线段A P 上一点,直线N B 垂直直线O N ,且交圆O 于B 点.过B 点的切线交直线O N 于K .证明:90OKM =∠.23.(本小题满分10分)选修4-4;坐标系与参数方程已知曲线C 1:cos sin x y θθ=⎧⎨=⎩,(θ为参数),曲线C 2:22222x t y ⎧=-⎪⎪⎨⎪=⎪⎩,(t 为参数).(Ⅰ)指出C 1,C 2各是什么曲线,并说明C 1与C 2公共点的个数;OMAPN B K(Ⅱ)若把C 1,C 2上各点的纵坐标都压缩为原来的一半,分别得到曲线12C C '',.写出12C C '',的参数方程.1C '与2C '公共点的个数和C 21C 与公共点的个数是否相同?说明你的理由.24.(本小题满分10分)选修4-5:不等式选讲 已知函数()84f x x x =---. (Ⅰ)作出函数()y f x =的图像; (Ⅱ)解不等式842x x --->.11 O xy答案BBDCA BCDAD AC (13)3 (14)1532 (15)34π(16). 1.乙品种棉花的纤维平均长度大于甲品种棉花的纤维平均长度(或:乙品种棉花的纤维长度普遍大于甲品种棉花的纤维长度)。
2 .甲品种棉花的纤维长度较乙品种棉花的纤维长度更分散.(或:乙品种棉花的纤维长度较甲品种棉花的纤维长度更集中(稳定).甲品种棉花的纤维长度的分散程度比乙品种棉花的纤维长度的分散程度更大).3 .甲品种棉花的纤维长度的中位效为307mm ,乙品种棉花的纤谁长度的中位数为318mm4 .乙品种棉花的纤堆长度基本上是对称的.而且大多集中在中间( 均值附近).甲品种棉花的纤维长度除一个特殊值(352 )外.也大致对称.其分布较均匀. 三、解答题 (17)解:(1)设{}n a 的公差为d ,由已知条件,11145a d a d +=⎧⎨+=-⎩,解出13,2a d ==-,所以()1125n a a n d n =+-=-+。
(2)()()22114422n n n S na d n n n -=+=-+=--所以2n =时,n S 取到最大值4。
