切比雪夫滤波器设计和仿真讲解学习
(完整word版)切比雪夫低通滤波器

(完整word版)切比雪夫低通滤波器课程设计题目:院(系):专业:学生姓名:学号:指导教师:2014 年01 月03 日切比雪夫低通滤波器摘要:利用ADS2008软件设计切比雪夫型低通滤波器,通过最终的图像,分析该滤波器的功能特性,并与其他滤波器对比分析,阐明此种滤波器的优点所在。
关键字:ADS2008软件切比雪夫低通滤波器功能特性目录摘要 (1)1滤波器概述 (3)1。
1滤波器分类 (3)1。
2根据滤波器的选频作用分类 (4)1.3根据“最佳逼近特性”标准分类 (4)1。
4理想滤波器 (5)2切比雪夫低通滤波器设计 (7)2.1新建滤波器工程 (7)2.2建立一个低通滤波器设计 (7)3 设计心得 (12)4 参考文献 (13)1、滤波器概述滤波器是一种选频装置,可以使信号中特定的频率成分通过,而极大地衰减其它频率成分。
在测试装置中,利用滤波器的这种选频作用,可以滤除干扰噪声或进行频谱分析。
广义地讲,任何一种信息传输的通道(媒质)都可视为是一种滤波器。
因为,任何装置的响应特性都是激励频率的函数,都可用频域函数描述其传输特性.因此,构成测试系统的任何一个环节,诸如机械系统、电气网络、仪器仪表甚至连接导线等等,都将在一定频率范围内,按其频域特性,对所通过的信号进行变换与处理.1.1 滤波器分类:滤波器特性可以用其频率响应来描述,按其特性的不同,可以分为低通滤波器,高通滤波器,带通滤波器和带阻滤波器等.低通滤波器有很多种,其中,最通用的就是巴特沃斯滤波器和切比雪夫滤波器。
巴特沃斯滤波器是滤波器的一种设计分类,其采用的是巴特沃斯传递函数,有高通、低通、带通、带阻等多种滤波器类型.巴特沃斯滤波器在通频带内外都有平稳的幅频特性,但有较长的过渡带,在过渡带上很容易造成失真。
切比雪夫滤波器同巴特沃斯滤波器相添加图片比,切比雪夫滤波器的过渡带很窄,但内部的幅频特性却很不稳定。
巴特沃斯响应能够最大化滤波器的通带平坦度.该响应非常平坦,非常接近DC信号,然后慢慢衰减至截止频率.巴特沃斯滤波器特别适用于低频应用,其对于维护增益的平坦性来说非常重要。
切比雪夫1型数字滤波器的设计及滤波过程

切比雪夫1型数字滤波器的设计及滤波过程切比雪夫1型低通模拟滤波器的幅度平方函数为:)(11)(2222|)(|ΩΩΩ+==ΩpNCj H Aa ε其中ε表示通带内幅度波动的程度,ε越大,波动幅度也越大。
1101.0-=Apε)(x CN称为N 阶切比雪夫多项式。
1、滤波器设计及结果如下IIR-DF 滤波器设计(切比雪夫1型)(1) 切比雪夫1型低通数字滤波器的损耗函数曲线、滤波分离出的DSB 信号的时域波形及其频谱如下:0.10.20.30.40.50.60.70.80.91-100-90-80-70-60-50-40-30-20-100w/π幅度/d B切比雪夫1型模拟低通滤波器的幅频响应曲线00.010.020.030.040.050.060.070.08-1-0.500.51t/sy 1(t )y1(t)的时域波形f/Hz幅度y1(t)的频谱其中阶数N=7(2) 切比雪夫1型带通数字滤波器的损耗函数曲线、滤波分离出的DSB 信号的时域波形及其频谱如下:0.10.20.30.40.50.60.70.80.91-100-90-80-70-60-50-40-30-20-100w/幅度/d B切比雪夫1型带通数字滤波器幅频响应曲线0.010.020.030.040.050.060.070.08-1-0.500.51t/sy 2(t )y2(t)的时域波形200400600800100012001400160018002000f/Hz幅度y2(t)的频谱其中阶数N=8(3)切比雪夫1型高通数字滤波器的损耗函数曲线、滤波分离出的DSB 信号的时域波形及其频谱如下:0.10.20.30.40.50.60.70.80.91-100-90-80-70-60-50-40-30-20-100w/幅度/d B切比雪夫1型高通数字滤波器幅频响应曲线0.010.020.030.040.050.060.070.08-1-0.500.51t/sy 3(t )y3(t)的时域波形f/Hz幅度y3(t)的频谱其中N=73、结果分析特点:误差值在规定的频段上等波纹变化。
切比雪夫带通滤波器的设计

切比雪夫带通滤波器的设计首先,确定滤波器的阶数。
滤波器的阶数决定了它的频率响应的陡峭程度。
一般来说,阶数越高,滤波器的陡峭程度越高,但计算复杂度也会变得更高。
在确定阶数时,需要考虑滤波器的设计要求和实际应用情况。
例如,如果要求滤波器的截止频率附近有较小的衰减,可以选择一个较高的阶数。
接下来,设计各个极点的位置。
切比雪夫带通滤波器的极点位置是通过在复平面上放置极点,并选择最佳的位置来实现所需的频率响应的。
极点的位置与滤波器的阶数和截止频率有关。
一般来说,极点应该分布在一个叫做单位圆的圆周上。
为了设计切比雪夫带通滤波器,需要采用以下步骤:1.确定滤波器的截止频率范围。
这个范围决定了希望保留的频率段。
2.根据所需的截止频率计算正规化的截止频率。
正规化的截止频率是指将实际的截止频率与采样频率归一化为单位圆的截止频率。
3.选择滤波器的阶数。
一般来说,选择较低的阶数可以实现较为平滑的频率响应,而选择较高的阶数可以实现更陡峭的截止频率。
4.使用切比雪夫滤波器的设计公式计算极点的位置。
具体的公式可以参考相关文献或使用专门的软件工具进行计算。
5. 根据计算得到的极点位置,可以进一步验证滤波器的频率响应是否符合设计要求。
可以使用工具如Matlab来绘制滤波器的幅频响应和相频响应。
6.根据设计结果,可以进一步调整滤波器的参数以满足具体应用的要求。
例如,可以调整滤波器的截止频率或增加滤波器的阶数来改变滤波器的性能。
总之,切比雪夫带通滤波器的设计需要确定滤波器的阶数和设计各个极点的位置。
通过合理选择滤波器的参数,可以实现所需的频率响应,并满足特定应用的要求。
设计一个高性能的切比雪夫带通滤波器需要对滤波器的理论和计算方法有一定的了解,并结合实际应用情况进行调整和优化。
切比雪夫滤波器课程设计解读

西安邮电大学专业课程设计报告书院(系)名称:电子工程学院学生姓名:专业名称:电子科学与技术班级:科技1004实习时间:2013年5月20 日至2013年5月31 日设计题目:集中参数切比雪夫低通滤波器一、设计指标:设计集中参数切比雪夫低通滤波器,滤波器第一个元件为串联方式 通带频率范围0~0.16GHz ;通带内衰减小于0.6dB ;在0.32GHz 时衰减大于40dB ;特性阻抗:50欧姆,微带线基板厚度1mm ;基板的介电常数4.2;连接集中参数元件的微带线长选为2.5mm ,宽选为1.5mm 。
二、设计原理:巴特沃兹滤波器中,幅度响应在通带和阻带内都是单调的。
因此,若滤波器的技术要求是用最大通带和阻带的逼近误差来给出的话,那么,在靠近通带低频端和阻带截止频率以上的部分都会超出技术指标。
一种比较有效的途径是使逼近误差均匀地分布于通带或阻带内,或同时在通带和阻带内都均匀分布,这样往往可以降低所要求的滤波器阶次。
通过选择一种具有等波纹特性而不是单调特性的逼近方法可以实现这一点。
切比雪夫型滤波器就具有这种性质:其频率响应的幅度既可以在通带中是等波纹的,而在阻带中是单调的(称为I 型切比雪夫滤波器),也可以在通带中是单调的,而在阻带中是等波纹的(称为II 型切比雪夫滤波器)。
本次课程设计,要求为做一个fc=0.16GHZ ,fs=0.32GHZ 的集总参数切比雪夫滤波器。
对于切比雪夫滤波器: 1.插入损耗2.N 阶切比雪夫多项式}T 1lg{102N 2)(Ω+=a IL )),()(Ω=Ω-1N cos cos(N T )),()(Ω=Ω-1Ncosh cosh(N T上图为切比雪夫多项式3.带内电压传递系数模值带外衰减插入损耗带外衰减上图为3dB切比雪夫归一化滤波电路频率响应。
三、理论分析:1.确定归一化的0.5dB切比雪夫低通滤波电路得到低通原型参数(1)确定N值:Ωs=ωs/ωc=2,由Ωs=2和LAs>40dB查图得N=5。
切比雪夫Ⅱ型低通滤波器
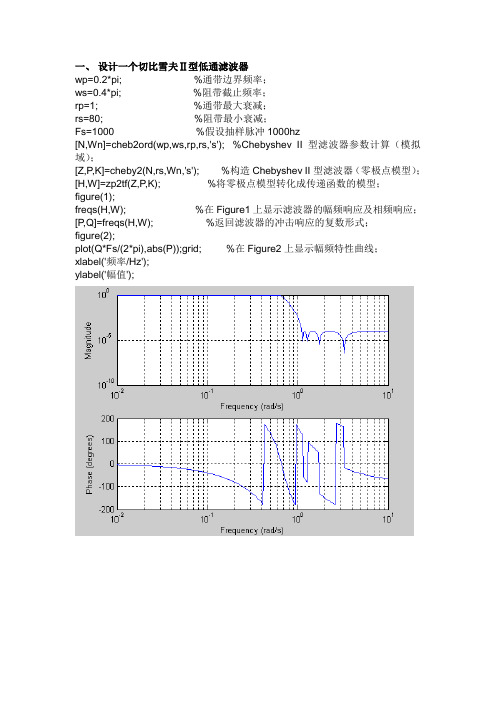
一、设计一个切比雪夫Ⅱ型低通滤波器wp=0.2*pi; %通带边界频率;ws=0.4*pi; %阻带截止频率;rp=1; %通带最大衰减;rs=80; %阻带最小衰减;Fs=1000 %假设抽样脉冲1000hz[N,Wn]=cheb2ord(wp,ws,rp,rs,'s'); %Chebyshev II型滤波器参数计算(模拟域);[Z,P,K]=cheby2(N,rs,Wn,'s'); %构造Chebyshev II型滤波器(零极点模型);[H,W]=zp2tf(Z,P,K); %将零极点模型转化成传递函数的模型;figure(1);freqs(H,W); %在Figure1上显示滤波器的幅频响应及相频响应;[P,Q]=freqs(H,W); %返回滤波器的冲击响应的复数形式;figure(2);plot(Q*Fs/(2*pi),abs(P));grid; %在Figure2上显示幅频特性曲线;xlabel('频率/Hz');ylabel('幅值');二、设计一个高通Chebyshow型数字滤波器wp=100;ws=80;Fs=300;rp=1;rs=45; %数字滤波器的各项指标;WP=100*2*pi; %把数字滤波器的频率特征转换成模拟滤波器的频率特征;WS=300*2*pi;[N,Wn]=cheb2ord(WP,WS,rp,rs,'s'); %Chebyshev II型滤波器参数计算(模拟域);[Z,P,K]=cheb2ap(N,rs); %创建Chebyshev滤波器原型;[A,B,C,D]=zp2ss(Z,P,K); %表达式从零极点增益形式转换成状态方程形式;[AA,BB,CC,DD]=lp2hp(A,B,C,D,Wn); %实现低通到高通滤波器类型的转换;[a,b,c,d]=bilinear(AA,BB,CC,DD,Fs); %采用双线性变换法,从模拟高通到数字高通;[P,Q]=ss2tf(a,b,c,d); %表达式从状态方程形形式转换成传输函数形式;figure(1);freqz(P,Q); %绘出频率响应;[H,W]=freqz(P,Q);figure(2);plot(W*Fs/(2*pi),abs(H));grid;xlabel('频率/Hz');ylabel('幅值');三、设计一个带通切比雪夫数字滤波器W1=100;W2=200;rp=1;rs=30;Fs=1000; %数字滤波器的各项指标;WP=[100,200];WS=[50,250];[N,Wn]=cheb1ord(WP/(Fs/2),WS/(Fs/2),rp,rs);%Chebyshev I型滤波器参数计算(数字域);[P,Q]=cheby1(N,rp,Wn,'bandpass');%创建Chebyshev带通滤波器;figure(1);freqz(P,Q); %显示产生滤波器的幅频及相频曲线;[H,W]=freqz(P,Q);figure(2);plot(W*Fs/(2*pi),abs(H));grid;xlabel('频率/Hz');ylabel('幅度');。
滤波器设计中的切比雪夫滤波器

滤波器设计中的切比雪夫滤波器切比雪夫滤波器是一种常用的数字滤波器,具有优秀的频率响应特性和设计灵活性。
本文将介绍切比雪夫滤波器的原理和设计方法,以及其在实际应用中的重要性。
一、切比雪夫滤波器的原理切比雪夫滤波器基于切比雪夫多项式,利用该多项式的特性设计出具有尽可能陡峭的频率响应的滤波器。
切比雪夫多项式的特点是在给定区间内具有最小偏离的性质,因此切比雪夫滤波器在通带和阻带的边缘具有较小的波纹,从而实现了更好的滤波效果。
二、切比雪夫滤波器的设计方法切比雪夫滤波器的设计需要确定滤波器的阶数、通带最大纹波和截止频率等参数。
一般来说,滤波器的阶数越高,频率响应的陡峭度越高,但设计难度也越大。
通带最大纹波决定了频率响应的平坦程度,而截止频率则确定了滤波器的工作范围。
具体的设计步骤如下:1. 确定滤波器的阶数,根据实际需求和设计要求合理选择。
2. 根据滤波器的阶数和通带最大纹波要求,计算切比雪夫多项式的系数。
3. 将切比雪夫多项式转化为传递函数形式,得到滤波器的传递函数表达式。
4. 根据传递函数表达式,使用模拟滤波器设计工具或数字滤波器设计工具进行进一步的设计和优化。
5. 对设计得到的滤波器进行验证和调整,确保满足要求的频率响应和滤波特性。
三、切比雪夫滤波器的应用切比雪夫滤波器广泛应用于信号处理、通信系统、图像处理等领域。
由于切比雪夫滤波器具有较小的波纹和较高的陡峭度,能够有效地滤除不希望出现在输出信号中的频率成分,因此在需要高质量滤波的场合得到了广泛应用。
以音频信号处理为例,切比雪夫滤波器可以应用于音频均衡器、音频压缩、音频降噪等功能的实现。
通过合理设计切比雪夫滤波器的参数,可以实现对音频信号的准确控制和处理,提高音频信号的质量和清晰度。
四、总结切比雪夫滤波器是一种重要的数字滤波器,具有优秀的频率响应特性和设计灵活性。
通过合理设计切比雪夫滤波器的参数,可以实现对信号的精确控制和处理,满足不同应用场景的需求。
切比雪夫滤波器的设计方法
切比雪夫滤波器的设计方法切比雪夫滤波器(Chebyshev filter)是一种常用的数字滤波器,它在频域上具有截止频率附近最小的过渡带宽。
此类滤波器被广泛应用于信号处理和通信领域中。
设计切比雪夫滤波器的方法有很多,下面将详细介绍常见的两种设计方法。
1.确定滤波器的截止频率和通带衰减首先确定所需滤波器的截止频率和通带衰减要求。
通常,通带衰减是滤波器能够抑制的信号功率的比例。
通常都是以分贝(dB)为单位,常见的衰减要求为20dB或40dB。
2. 将标准Chebyshev滤波器转换为低通滤波器3.设计原型滤波器传输函数对于切比雪夫滤波器,工程师可以根据要求选择一阶、二阶或更高阶的形式。
传输函数的形式取决于所需滤波器的截止频率和通带衰减。
可以使用常见的切比雪夫多项式形式,如Butterworth、Chebyshev和Elliptic型。
4.归一化设计参数归一化是为了方便后续计算和设计,通常包括将截止频率归一化为单位频率和将通带衰减归一化为单位减少。
5.根据设计参数计算阶数和滤波器参数根据归一化设计参数,可以使用公式和表格计算滤波器的阶数和系数。
通常,阶数与滤波器的衰减要求成正比。
6.设计实际滤波器根据计算得到的滤波器阶数和系数,可以设计出实际的滤波器电路。
这可能涉及到计算电阻、电容和电感的值,以满足所需的截止频率和通带衰减。
1.选择适当的阶数切比雪夫滤波器通常有两种类型:I型和II型。
且每种类型都有不同的阶数。
I型切比雪夫滤波器在通带和阻带之间具有等功率振幅特性,阶数越高,通带和阻带之间的过渡带越陡峭。
II型切比雪夫滤波器在通带内具有等功率振幅特性,阶数越高,截止频率附近的干扰越小。
2.计算归一化角频率根据所需的截止频率和通带衰减,可以计算出归一化的截止频率和通带衰减。
3.计算极点的位置通过计算归一化角频率和阶数的函数,可以得到切比雪夫滤波器的极点位置。
极点是滤波器传输函数的根,通常以复数形式表示。
4.找到对应的元件值根据极点的位置,可以计算出理论上的元件值。
现代滤波器设计讲座(2_1广义切比雪夫滤波器的电路仿真)讲解
正交耦合滤波器
一个谐振腔既可以用串联谐振回路表示也可以 用并联谐振回路表示。当我们使用串联谐振回 路表示谐振腔时,腔之间的耦合用K变换器表 示。当我们使用并联谐振回路表示谐振腔时, 腔之间的耦合用J变换器表示。 我们先考虑一个不包括源和负载耦合三腔正交 耦合滤波器。
3腔正交耦合滤波器的电路模型
矩阵形式的电路方程
上述方程可以写成如下的矩阵形式 :
1 R R j jK12 S 1 1 2 jK R j 12 2 2 jK13 jK 23 jK13 i e 1 s jK 23 i2 0 i 0 3 3 RL R3 j 3
0
0.25
0.2
(Mii(w)-Mii(w0))/Mii(w0)
0.15
w0/wi=0.7 w0/wi=0.8 w0/wi=0.9 w0/wi=1.1 w0/wi=1.2 w0/wi=1.3
0.1
0.05
0
-0.05 0.5 1 W/W0 1.5 2
0.2 0.15 0.1 0.05
归一化阻抗矩阵
归一化阻抗矩阵可以写成下面的形式,
0 p 0 0 0 p R s r1 0 j 0 r2 0 0 m11 m12 0 m21 m22 R L r3 m31 m32 0 m13 m23 m33
wi/w0=0.94 wi/w0=0.96 wi/w0=0.98 wi/w0=1.02
0 0.5 -0.05 -0.1 -0.15 -0.2
Mii
切比雪夫滤波器设计和仿真讲解学习
切比雪夫滤波器设计和仿真切比雪夫滤波器设计和仿真摘要:滤波器是一种常见的电路形式,在电子线路中有广泛的应用。
滤波器的设计在这些领域中是必不可缺的。
滤波器是一种能使有用频率信号通过而同时抑制(或衰减)无用频率信号的电子电路或装置。
按照不同的频域或时域特性要求,可分巴特沃斯(Butterworth)、切比雪夫型(Chebyshev)、贝塞尔型(Bessel)椭圆型(Elliptic),这些都是属于模拟低通滤波器。
切比雪夫型滤波器的特点是通带内增益有起伏。
本文介绍的是借助Multisim 10仿真实现二阶切比雪夫低通有源滤波器的设计。
关键词:滤波器;频域或时域特性;切比雪夫;Multisim10Chebyshev LPF's design and emulationAbstrac:Filter would completely eliminate signals above the cutoff frequency, and perfectly pass signals below the cutoff frequency . In real filters, various rade-offs are made to get optimum performance for a given application. There are manybooks that provide information on popular filter types like the Butterworth, Bessel, and Chebyshev filters, just to name few. Chebyshev filters are designed to have ripple in the pass-band, but steeper roll off after the cutoff frequency. Cutoff frequency is defined as the frequency at which the response falls below the ripple band. For a given filter order, a steeper cutoff can be achieved by allowing more pass-band ripple. The transient response of a Chebyshev filter to a pulse input shows more overshoot and ringing than a Butterworth filter.Key Words:Filter;popular filter types;Chebyshev function;Multisim 10引言随着现代科学技术的发展,滤波技术在通信、测试、信号处理、数据采集和实时控制等领域都得到了广泛的应用。
数字切比雪夫滤波器的设计及matlab仿真
数字切比雪夫滤波器的设计及matlab仿真数字切比雪夫滤波器是一种常见的数字滤波器,它是由切比雪夫多项式设计而成的。
切比雪夫多项式是一类代数多项式,在理论计算和实际应用中具有广泛的应用。
数字切比雪夫滤波器的设计和matlab仿真是数字信号处理领域中重要的研究内容。
数字切比雪夫滤波器的设计基本步骤如下:首先确定滤波器类型,例如低通滤波器、高通滤波器、带通滤波器、带阻滤波器等。
然后,通过切比雪夫多项式计算出滤波器的传递函数H(s),转换成离散传递函数H(z),并确定滤波器的通带截止频率、阻带截止频率和通带最大衰减量。
最后在matlab中实现数字切比雪夫滤波器的设计和仿真。
在数字切比雪夫滤波器的设计中,需要注意以下几点:1.滤波器类型的选择要符合实际应用中的需求和要求,例如在音频处理中常用的是低通滤波器,用于去除高频噪声和杂音。
2.切比雪夫多项式的阶数越高,滤波器的设计越精细,但会使设计过程变得更加困难和计算量更大,需要权衡设计精细程度和计算成本。
3.通带截止频率和阻带截止频率的设置应该根据实际信号的频率分布情况来确定,保证滤波器能够有效去除噪声信号。
4.通带最大衰减量的选择应该综合考虑信号处理的精度和计算性能,保证在去除噪声的同时尽可能保留信号的有效信息。
数字切比雪夫滤波器的matlab仿真是设计过程中必不可少的环节之一。
在matlab中,可以使用自带的函数cheby1、cheby2、chebwin 等来进行数字切比雪夫滤波器的设计和仿真。
同时,matlab还提供了各种可视化工具,如fdatool、filter designer等,方便用户进行滤波器性能分析和优化。
在数字信号处理应用中,数字切比雪夫滤波器被广泛应用于图像处理、音频处理、信号解调等领域。
其设计和优化方法对于提高数字信号处理的效率和精度具有重要的意义。
因此,深入研究数字切比雪夫滤波器的设计和优化方法,不仅对于学术研究有所帮助,也对于工程实践具有重要的指导意义。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
切比雪夫滤波器设计
和仿真
切比雪夫滤波器设计和仿真
摘要:滤波器是一种常见的电路形式,在电子线路中有广泛的应用。
滤波器的设计在这些领域中是必不可缺的。
滤波器是一种能使有用频率信号通过而同时抑制(或衰减)无用频率信号的电子电路或装置。
按照不同的频域或时域特性要求,可分巴特沃斯(Butterworth)、切比雪夫型(Chebyshev)、贝塞尔型(Bessel)椭圆型(Elliptic),这些都是属于模拟低通滤波器。
切比雪夫型滤波器的特点是通带内增益有起伏。
本文介绍的是借助Multisim 10仿真实现二阶切比雪夫低通有源滤波器的设计。
关键词:滤波器;频域或时域特性;切比雪夫;Multisim10
Chebyshev LPF's design and emulation
Abstrac:Filter would completely eliminate signals above the cutoff frequency, and perfectly pass signals below the cutoff frequency . In real filters, various rade-offs are made to get optimum performance for a given application. There are manybooks that provide information on popular filter types like the Butterworth, Bessel, and Chebyshev filters, just to name few. Chebyshev filters are designed to have ripple in the pass-band, but steeper roll off after the cutoff frequency. Cutoff frequency is defined as the frequency at which the response falls below the ripple band. For a given filter order, a steeper cutoff can be achieved by allowing more pass-band ripple. The transient response of a Chebyshev filter to a pulse input shows more overshoot and ringing than a Butterworth filter.
Key Words:Filter;popular filter types;Chebyshev function;Multisim 10
引言
随着现代科学技术的发展,滤波技术在通信、测试、信号处理、数据采集和实时控制等领域都得到了广泛的应用。
滤波器的设计在这些领域中是必不可缺的,有时甚至是至关重要的环节。
比如说,在通信领域,常常利用种滤波器来抑制噪声,去除干扰,以提高信噪比。
随着电子计算机的普及和材料科学的进步,
各种各样的滤波器的辅助设计软件也得以不断推出,设计人员可以选择高功效的滤波器芯片及设计软件而获得所需要的电路性能。
本文所介绍的二阶切比雪夫滤波器。
首先熟悉二阶有源滤波器的幅频特性,然后掌握二阶有源滤波器的快速设计方法,用Multisim 10进行电路仿真,观察其幅频特性。
本文介绍的切比雪夫滤波器的阻带衰减特性则较巴特沃斯滤波器有所改善。
与椭圆型滤波器相比具有较平的通带幅频特性。
切比雪夫滤波器带内有起伏,但过渡带比较陡峭。
本课题的任务:本课题的任务设计并仿真一个运用Multisim 10实现切
比雪夫滤波器,该滤波器具备以下条件:
1.功能要求:
根据给定的参数,应用Multisim语言实现切比雪夫低通滤波器的设
计。
2.参数要求:
频率0Hz~3.4KHz,通带波纹 1dB
3.仿真要求:
实现3dB带宽为3400Hz的切比雪夫低通滤波器。
1.滤波器
1.1滤波器的功能
1.2滤波器的分类
2.无源滤波电路及其幅频特性
1.无源滤波电路如图1。
图1无源滤波器及它的幅频特性
可以得出电压放大倍数为:
——带通截止频率
有对数幅频特性,具有“低通”的特性。
电路缺点:电压放大倍数低,只有1,且带负载能力差。
解决方法:利用集成运放和RC 电路组成有源低通滤波器。
3.有源滤波电路及其特性
在无源滤波电路和负载之间加一个高输入电阻,低输出电阻的隔离电路,最简单的方法是加一个电压跟随器,这样即构成有源滤波电路,如图下图所示。
表明:在集成运放功耗允许的情况下,负载发生变化时,U 0总是随电压差Up 而变,放大倍数的表达式不变,频率特性也不变。
即负载不影响滤波特性。
图2有源滤波电路 3.1有源低通滤波器特性 3.2一阶低通有源滤波器 3.3二
阶低通有源滤波器
RC f π21
0=
fp
f
j Avp jwRc V V V V v A i i +=
+===+1110
i o j 11f f U U A u +==
图3一阶低通有源滤波器
二阶有源低通滤波电路
4.切比雪夫滤波器
4.1切比雪夫滤波的简介
4.2切比雪夫滤波有关参数的确定方法
c Ω是通带边界频率,一般是预先给定的。
ε是与通带波动有关的一个参数,通带波动δ表示成 ()()()()min
max 2
min
2
max
lg
20lg
10ΩΩ=ΩΩ=j H j H j H j H a a a a δ
式中,()1max =Ωj H a ,表示通带幅度响应的最大值,而 ()2
min 11ε
+=
Ωj H a
故 ()
21lg 10εδ+=
因而 110102
-=δ
ε
可以看出,给定通带波纹值()dB δ后,就能求得2ε。
这里应注意,通带衰减值不一定是3dB ,也可以是其他值,随给定的δ值而定,例如dB 1.0=δ等。
阶数N 对滤波器特性有极大的影响,N 越大,逼近特性越好,但是相应的滤波器结构也越复杂。
N 的值是根据阻带的边界条件来确定的,当τΩ=Ω时,
()2
2
1
A j H a ≤Ωτ,即
2
22111
A V c r N
≤
⎪⎪⎭
⎫ ⎝⎛ΩΩ+ε 从而
ε
1
2-≥
⎪⎪⎭
⎫
⎝⎛ΩΩA V c r N
将此条件代入
()x V N =cosh(N arcosh x),1〉x ,得到
()
()c r ar A ar N ΩΩ-≥
cosh 1cosh 2ε
因此,要求阻带边
界频率处的衰减越大,也就是过渡带内幅频特性越陡,则需用的阶数N 越高。
5. 设计思路
6.设计步骤
二阶无限增益多路反馈切比雪夫低通滤波器电路图
7. Multisim 10仿真
7.1 Multisim 10 概述
7.2 绘制原图
7.3 用波特图示仪观察其幅频特性并记录
结论
本文从滤波器的基本要点出发,由无源滤波器到有源滤波器,有源低通滤波器,一阶有源低通、二阶有源低通,循序渐进,观察它们的滤波器特性,最后引
入到切比雪夫滤波器的设计。
通过公式的运用和查表计算出电路的参数,并画出了电路图,最终设计出了二阶切比雪夫低通滤波器。
利用了Multisim 10仿真观察了它的幅频特性,了解了它的特点。
通过次论文的写作让我对滤波器的相关知识有了进一步的认识,同时也学会了Multisim 10软件的操作。
参考文献
[1]彭磊,张建平.滤波技术[M].北京:机械工业出版,1998:227.
[2] 王宇航,姚育等.滤波器的分析及应用[J].电机与控制学报,2003,32(7):
673.
[3] 胡汉起.无源滤波器应用[M].北京:机械工业出版社,1991:184.
[4] 杨广,梁瑞生,罗仁华.多通道窄带滤波器设计[J].中国激光,2001,
19(4):143.
[5] 江友华,唐忠.混合有源滤波器多目标优化设计 [J].物理学报,2001,19
(4):143.
[6] 王一凡,罗正祥等.广义切比雪夫滤波器等效电路参数的提取[J].航空材料
学报,2001,21(2):1~5.
[7] 吴镇扬.数字信号处理[M].北京:高等教育出版社,2004:110.
[8] 王启文,王晓霞.切比雪夫频率特性显示仪[J].物理学报,2003,47(2):
183.
[9] 王洪刚,张志美,乔双.切比雪夫滤波器研究[M].吉林:吉林出版社,
2005:180.
[10] 赵威威.基于NI Multisim10的仿真研究[J].湖南师大工学院学报,200
(6):21.。
