《压杆稳定》问答题
12压杆稳定测试选择题(10题)和答案

12压杆稳定测试选择题(10题)和答案1、中心受压细长直杆丧失承载能力的原因为()。
(A)横截面上的应力达到材料的比例极限;(B)横截面上的应力达到材料的屈服极限;(C)横截面上的应力达到材料的强度极限;(D)压杆丧失直线平衡状态的稳定性2、一细长压杆当轴向压力F=Fcr时发生失稳而处于微弯平衡状态。
此时若解除压力F,则压杆的微弯变形()。
A、完全消失;B、有所缓和;C、保持不变;D、继续增大。
3、压杆失稳将在()的纵向平面内发生。
A、长度系数最大;B、截面惯性半径i最小;C、柔度最大;D、柔度最小。
4、欧拉公式的适用条件是()。
22E2E2E(C)E(D)(A)(B)pp5、两根细长压杆a、b的长度,横截面面积、约束状态及材料均相同,若其横截面形状分别为正方形和圆形,则两压杆的临界压力Facr和Fbcr的关系为()。
A、FacrFbcr;D、不可确定。
6、在稳定性计算中,有可能发生两种情况:一是用细长杆的公式计算中长杆的临界压力;一是用中长杆的公式计算细长杆的临界压力。
其后果是()。
A、前者的结果偏于安全,后者偏于不安全;B、二者的结果都偏于安全;C、前者的结果偏于不安全,后者偏于安全;D、二者的结果都偏于不安全。
7、由低碳钢制成的细长压杆,经过冷作硬化后,其()。
A、稳定性提高,强度不变;B、稳定性不变,强度提高;C、稳定性和强度都提高;D、稳定性和强度都不变。
8、一正方形截面细长压杆,因实际需要在n-n横截面处钻一横向小孔如图所示。
(1)在计算压杆的临界力时,所用的惯性矩为();b4b4d4b4bd3b4b3d(A)(B)(C)(D)12121212121264(2)在对杆进行强度计算时,横截面面积应取()。
(A)b2(B)b2d2(C)b2db(D)b2bd第8题图9、矩形截面细长连杆,两端用柱行铰链连接,其在某y平面内可视为两端铰支,在某z平面内近似为两端固定。
从稳定性角度考虑,截面合理的高、宽比为h/b=()。
材料力学答案第十章
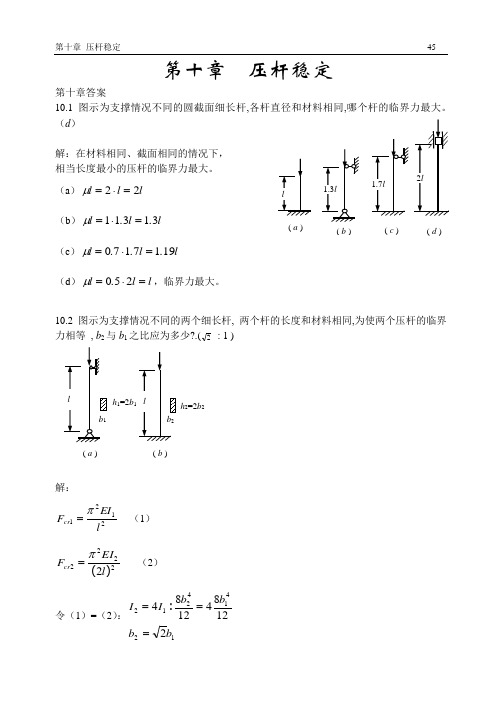
第十章 压杆稳定第十章答案10.1图示为支撑情况不同的圆截面细长杆,各杆直径和材料相同,哪个杆的临界力最大。
(d )解:在材料相同、截面相同的情况下, 相当长度最小的压杆的临界力最大。
(a )l l l 22=⋅=μ (b )l .l .l 31311=⋅=μ (c )l .l ..l 1917170=⋅=μ(d )l l .l =⋅=250μ,临界力最大。
10.2图示为支撑情况不同的两个细长杆, 两个杆的长度和材料相同,为使两个压杆的临界力相等 , b 2与b 1之比应为多少?.(2 : 1 )解:2121l EI F cr π=(1)22222)(l EI F cr π=(2)令(1)=(2):12414212212841284b b b b I I ===:( a)( b) ( c) ( d )( a ) ( b ) h 1=2b h 2=2b 210.3 铰接结构ABC 由截面和材料相同的细长杆组成,若由于杆件在ABC 平面内失稳而引起破坏,试确定荷载F 为最大时(两个杆同时失稳时)的θ (0<θ<π/2)角。
(θ=arctan (1/3)=18.44°) 解:θπcos F l EIF cr ==21212)( (1)θπsin F l EIF cr ==22222)( (2)(1/3))(:(2)(1)arctan cos l sin l l l tan ====θθ3130302222110.4图示压杆,型号为20a 工字钢,在xoz 平面内为两端固定,在xoy 平面内为一端固定,一端自由,材料的弹性模量E = 200GPa ,比例极限σp = 200MPa ,试求此压杆的临界力。
(F c r = 402.2kN )解:(1)柔度计算 查表知:6010012158122=-=========bE a ,E.AI i .A I i s p y y zz σλλσπλs 0p 23558mm A mm,mm,(2)xoz 平面内失稳:7894121200050..i l .y ===y λ 为中柔度杆,kN MPa,7048197===-=A F .b a cr cr y cr σλσ (2) (2)xoy 平面内失稳:169858180002..i l Z ===Z λ 为中柔度杆,kN MPa,6901194===-=A F .b a cr cr z cr σλσx10.5 结构如图,二杆的直径均为d =20mm ,材料相同,材料的弹性模量E = 210GPa , 比例极限σP = 200MPa ,屈服极限 σs = 240MPa ,强度安全系数n =2 ,规定的稳定安全系数n st =2.5 ,试校核结构是否安全。
压杆稳定的考题
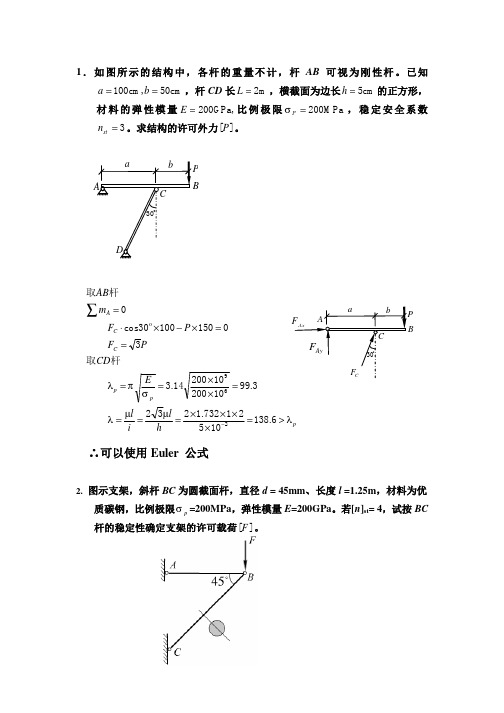
1.如图所示的结构中,各杆的重量不计,杆AB 可视为刚性杆。
已知cm 50,cm 100==b a ,杆CD 长m 2=L ,横截面为边长cm 5=h 的正方形,材料的弹性模量,GPa 200=E 比例极限MPa 200=P σ,稳定安全系数3=st n 。
求结构的许可外力][P 。
pp p C C Ah l i l E CD P F P F mAB λµµλσπλ>=××××====××====×−×⋅=−∑6.13810521732.12323.99102001020014.33015010030cos 0269杆取杆取o∴可以使用Euler 公式2. 图示支架,斜杆BC 为圆截面杆,直径d = 45mm 、长度l =1.25m ,材料为优质碳钢,比例极限p σ=200MPa ,弹性模量E =200GPa 。
若[n ]st = 4,试按BC 杆的稳定性确定支架的许可载荷][F 。
,045sin 00=−⋅=∑F F FBBC y取节点 F F BC =⋅22杆取CD399106200109200143..E πP P =×××==σλλp d l i μl λ>=×===1.111045.0425.14∴ 可以使用Euler 公式 (1分))kN (9.25364)25.11(2045.01020014.3)(49322=×××××==−l EI F CrBC µπ )kN (9.4449.2532222][===∴−n F F stCr BC3、一长为mm 600的钢板尺两端铰接放入实验架中受轴向压力,其横截面积为mm 132×。
已知压应力容许值为MPa 215][=σ,弹性模量GPa 210=E 。
材料力学答案- 压杆稳定
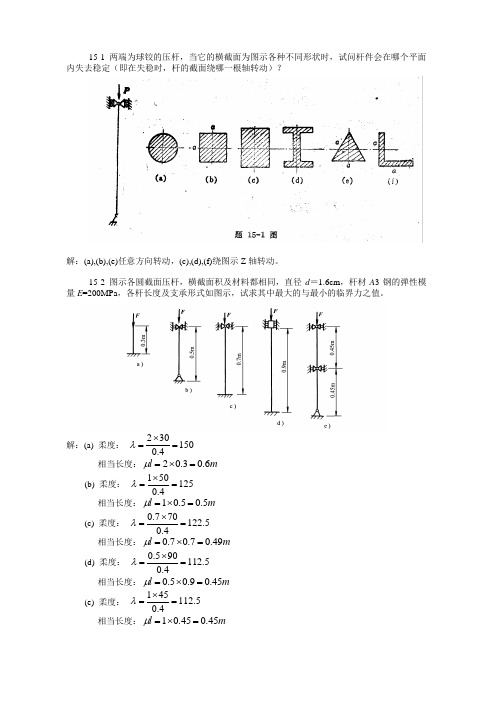
15-1 两端为球铰的压杆,当它的横截面为图示各种不同形状时,试问杆件会在哪个平面内失去稳定(即在失稳时,杆的截面绕哪一根轴转动)?解:(a),(b),(e)任意方向转动,(c),(d),(f)绕图示Z 轴转动。
15-2 图示各圆截面压杆,横截面积及材料都相同,直径d =1.6cm ,杆材A 3钢的弹性模量E =200MPa ,各杆长度及支承形式如图示,试求其中最大的与最小的临界力之值。
解:(a) 柔度: 2301500.4λ⨯== 相当长度:20.30.6l m μ=⨯=(b) 柔度: 1501250.4λ⨯== 相当长度:10.50.5l m μ=⨯=(c) 柔度: 0.770122.50.4λ⨯== 相当长度:0.70.70.49l m μ=⨯=(d) 柔度: 0.590112.50.4λ⨯== 相当长度:0.50.90.45l m μ=⨯=(e) 柔度: 145112.50.4λ⨯== 相当长度:10.450.45l m μ=⨯=由E=200Gpa 及各柔度值看出:各压杆的临界力可用欧拉公式计算。
即:()22cr EIF l πμ=各压杆的EJ 均相同,故相当长度最大的压杆(a)临界力最小,压杆(d)与(e)的临界力最大,分别为:()2948222320010 1.610640.617.6410cr EFF l N πππμ-⨯⨯⨯⨯⨯===⨯()2948222320010 1.610640.4531.3010cr EIF l Nπππμ-⨯⨯⨯⨯⨯===⨯15-3 某种钢材P σ=230MPa ,s σ=274MPa ,E =200GPa ,直线公式λσ22.1338-=cr ,试计算该材料压杆的P λ及S λ值,并绘制1500≤≤λ范围内的临界应力总图。
解:92.633827452.5p s s a λπσλ===--===15-4 6120型柴油机挺杆为45钢制成的空心圆截面杆,其外径和内径分别为,12mm 和10mm ,杆长为383mm ,两端为铰支座,材料的E =210GPa ,P σ=288MPa ,试求此挺杆的临界力cr F 。
压杆稳定习题
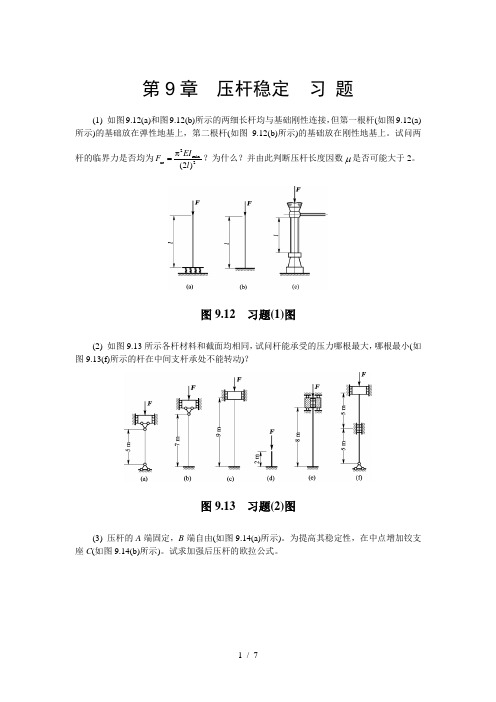
第9章压杆稳定习题(1) 如图9.12(a)和图9.12(b)所示的两细长杆均与基础刚性连接,但第一根杆(如图9.12(a)所示)的基础放在弹性地基上,第二根杆(如图9.12(b)所示)的基础放在刚性地基上。
试问两杆的临界力是否均为2mincr2(2)EIFlπ=?为什么?并由此判断压杆长度因数μ是否可能大于2。
图9.12 习题(1)图(2) 如图9.13所示各杆材料和截面均相同,试问杆能承受的压力哪根最大,哪根最小(如图9.13(f)所示的杆在中间支杆承处不能转动)?图9.13 习题(2)图(3) 压杆的A端固定,B端自由(如图9.14(a)所示)。
为提高其稳定性,在中点增加铰支座C(如图9.14(b)所示)。
试求加强后压杆的欧拉公式。
图9.14 习题(3)图(4) 如图9.15所示正方形桁架,5根相同直径的圆截面杆,已知杆直径d=50mm,杆长a=1m,材料为Q235钢,弹性模量E=200GPa。
试求桁架的临界力。
若将荷载F方向反向,桁架的临界力又为何值?图9.15 习题(4)图λ=100,(5) 如图9.16所示两端固定的空心圆柱形压杆,材料为Q235钢,E=200GPa,p外径与内径之比 1.2D d=。
试确定能用欧拉公式时,压杆长度与外径的最小比值,并计算这时压杆的临界力。
图9.16 习题(5)图(6) 如图9.17所示的结构ABCD,由3根直径均为d的圆截面钢杆组成,在B点铰支,而在A 点和C 点固定,D 为铰接点,10ld=π。
若此结构由于杆件在平面ABCD 内弹性失稳而丧失承受能力,试确定作用于节点D 处的荷载F 的临界力。
图9.17 习题(6)图(7) 如图9.18所示的铰接杆系ABC由两根具有相同材料的细长杆所组成。
若由于杆件在平面ABC 内失稳而引起毁坏,试确定荷载F 为最大时的θ角(假定02θπ<<)。
图9.18 习题(7)图(8) 下端固定、上端铰支、长l =4m 的压杆,由两根10号槽钢焊接而成,如图9.19所示,符合钢结构设计规范(GB50017—2003)中实腹式b 类截面中心受力压杆的要求。
第九章压杆稳定答案

i - . D 2 d 2 / 4 = 52 2 442 / 4mm = 0.017mm第九章压杆稳定1、图示铰接杆系ABC 由两根具有相同截面和同样材料的细长杆所组成。
若由于杆件在平面ABC 内失稳而引起破坏,试确定荷载 F 为最大时的二角(假设0 —岂㊁)。
解:由平衡条件二 Fy = 0, F NAB = F COSd二 F x - 0, F NBC - F sin T 使F 为最大值条件使杆AB 、BC 的内力同 时达到各自的临界荷载。
设 AC 间的距离为I , AB 、BC 杆的临界荷载分别为H 2EI 兀 2EI F NAB= 7T = 7S —5 F NBC 二 2EI 二 2EI由以上两式得2、一承受轴向压力的两端铰支的空心圆管,外径 D 二52mm ,内径 d 二 44mm ,I 二 950mm 。
材料的二 1600MPa ,二 p 二1200MPa ,E = 210GPa 。
试求此杆的临界压力和临界应力。
支承可视为两端铰支,故 J =1,BC (I cos 。
f二 41.6 解:2 9 ■: 210 10 \ 1200 106回转半径为44斜撑杆得柔度■ - l. i =1 0.95/0.017 =55.9因■ ■ !,为大柔度杆,故可用欧拉公式计算临界荷载,临界压力为F cr 和临界 应力二cr 分别为:29 : .•4 4 _.2 二2 210 109 0.0524 -0.0444F cr ' -3 64 2 N =402KN(H ) (1x0.95) ”-心 匹=666 MPaA3、蒸汽机车的连杆如图所示,截面为工字型,材料为 Q235钢,连 杆所受最大轴向压力为465kN 。
连杆在xy 平面内发生弯曲,两端可视 为铰支,在xz 平面内发生弯曲,两端可视为固定。
试确定工作安全系 数。
|3100解连杆横截面的几何特性:2 2 A =[ 14>9.6- (9.6-1.4) >8.5] cm =64.7cm4I y=407 cm *yLI z=1780 cm4i y = |厂A = ,407 64.7 = 2.51cmi z = l z A = .1780 64.7 = 5.24cmQ235钢的「f%2E 「200 109 200 10—99.3a —0's 304 —240■■■■2 57.1b 1.12 在xy 平面内弯曲时连杆的柔度在xz 平面内弯曲时连杆的柔度y =0.5 3.1/0.0251 =61.8「1所以在计算两个方向上产生弯曲时的临界荷载,都要用经验公式,并且只须计算在柔度较大 的方向上产生弯曲时的临界荷载 F c 「二 a-b y A -丨304-1.12 61.8106 64.7 10*N=1520kN工作安全系数 n = F cr / F = 1520/465 = 3.274、油缸柱塞如图所示。
精选题11压杆稳定

压杆稳定1. 图示结构,AB 为刚性杆,其它杆均为直径10 mm d =的细长圆杆,弹性模量200 GPa E =, 屈服极限s 360 MPa σ=,试求此结构的破坏载荷F 值。
解:12.37 m, sin 26H α⎛⎫== ⎪⎝⎭,0.169()Cy Dy F F F =-=↓,N1N4N2N30.507F F F F F ==-=-=由杆1,4,N11s 0.507F F A σ==,s 155.8 kN 0.507AF σ==由杆2,3,2N2cr 2π0.673 kN EIF F l ===, cr 2 1.33 kN 0.507F F ==结构破坏载荷 1.33 kN F =2. 图示桁架由5根圆截面杆组成。
已知各杆直径均为30 mm d =, 1 m l =。
各杆的弹性模量均为200 GPa E =,p 100λ=,061λ=,直线经验公式系数304 MPa a =, 1.12 MPa b =,许用应力[]160 MPa σ=,并规定稳定安全因数st []3n =,试求此结构的许可载荷[]F 。
解:由平衡条件可知杆1,2,3,4受压,其轴力为N1N2N3N4N 2F F F F F =====杆5受拉,其轴力为N5F F = 按杆5的强度条件:N5[], []113 kN F F A Aσσ≤≤= 按杆1,2,3,4的稳定条件 p 133λλ=> 由欧拉公式 cr 78.48 kN F =crst N[]F n F ≥ 37.1 kN F ≤ , []37.1 kN F =3. 钢杆和铜杆截面、长度均相同,都是细长杆。
将两杆的两端分别用铰链并联,如图,此时两杆都不受力。
试计算当温度升高多少度时,将会导致结构失稳?已知杆长 2 m l =,横截面积220 cm A =,惯性矩440 cm z I =;钢的弹性模量s 200 GPa E =,铜的弹性模量1.2m F ACFB HD0.4m1324lF︒45l12345钢铜c 100 GPa E =,钢的线膨胀系数6s 12.510α-=⨯℃-1,铜的线膨系数6c 16.510α-=⨯℃-1。
第7章压杆稳定

第7章压杆稳定判断1、“压杆失稳的主要原因是由于外界干扰力的影响“2、“同种材料制成的压杆,其柔度越大越容易失稳“3、“压杆的临界压力与材料的弹性模量成正比“4、“两根材料、长度、横截面面积和约束都相同的压杆,其临界力也必定相同“5、“对于轴向受压杆件来说,由于横截面上的正应力均匀分布,因此不必考虑横截面的合理形状问题“6、“细长压杆的长度加倍,其他条件不变,则临界力变为原来的1/4;长度减半,则临界力变为原来的4倍。
“7、“满足强度的压杆不一定满足稳定性;满足稳定性的压杆也不一定满足强度”8、“合金钢的稳定性一定比碳素钢的好”选择1、压杆失稳是指在轴向压力作用下:。
A:局部横截面的面积迅速变化;B:危险面发生屈服或断裂;C:不能维持平衡状态而发生运动;D:不能维持直线平衡而发生弯曲;2、理想均匀压杆的工作压力P达到临界压力P cr时处于直线平衡状态,受一干扰后发生微小弯曲变形,解除干扰后,则压杆。
A:弯曲变形消失,恢复成直线状态;B:弯曲变形减小,不能恢复成直线状态;C:微弯变形形态保持不变;D:变形继续增大;3、一细长压杆当轴向压力P达到临界压力P cr时受到微小干扰后发生失稳而处于微弯平衡状态,此时若解除压力P,则压杆的微弯变形。
A:完全消失;B:有所缓和;C:保持不变;D:继续增大;4、下图中的长度系数μ=?A:μ<0.5;B:0.5<μ<1.0;C:0.7<μ<2.;D:μ>2;5、下图中的长度系数μ=?A:μ<0.7;B:0.7<μ<1.0;C:1.0<μ<2.;D:μ>2;6、细长杆承受轴向压力P,杆的临界压力Pcr与无关。
A:杆的材质;B:杆长;C:杆承受的压力;D:杆的形状;7、图示中钢管在常温下安装,钢管会引起钢管的失稳。
A:温度降低;B:温度升高与降低都会引起失稳;C:温度升高;D:温度升高或降低都不会引起失稳;8、压杆的失稳将在纵向面内发生。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
压杆稳定
【例1】 压杆的压力一旦达到临界压力值,试问压杆是否就丧失了承受荷载的能力? 解:不是。
压杆的压力达到其临界压力值,压杆开始丧失稳定,将在微弯形态下保持平衡,即丧失了在直线形态下平衡的稳定性。
既能在微弯形态下保持平衡,说明压杆并不是完全丧失了承载能力,只能说压杆丧失了继续增大荷载的能力。
但当压杆的压力达到临界压力后,若稍微增大荷载,压杆的弯曲挠度将趋于无限,而导致压溃,丧失了承载能力。
且在杆系结构中,由于某一压杆达到临界压力,引起该杆弯曲。
若在增大荷载,将引起结构各杆内力的重新分配,从而导致结构的损坏,而丧失其承载能力。
因此,压杆的压力达到临界压力时,是其承受荷载的“极限”状态。
【例2】 如何判别压杆在哪个平面内失稳?图示截面形状的压杆,设两端为球铰。
试问,失稳时其截面分别绕哪根轴转动?
解:(1)压杆总是在柔度大的纵向平面内失稳。
(2)因两端为球铰,各方向的μ=1,由柔度知l
i
μλ=
(a )x y i i =,在任意方向都可能失稳。
(b ),x y i i <失稳时截面将绕x 轴转动。
(c )x y i i >,失稳时截面将绕y 轴转动。
【例3】 细长压杆的材料宜用高强度钢还是普通钢?为什么?
解:对于细长压杆,其临界压力与材料的强度指标无关,而与材料的弹性模量E 有关。
由于高强度钢与普通钢的E 大致相等,而其价格贵于普通钢,故细长压杆的材料宜用普通钢。
【例4】 图示均为圆形截面的细长压杆(λ≥λp),已知各杆所用的材料及直径d 均相同,长度如图。
当压力P 从零开始以相同的速率增加时,问哪个杆首先失稳?
杆C
杆B
1.6a
P
P
1.3a
杆A
a
P
解:方法一:用公式P lj = π2
EI /(μl )2
计算,由于分子相同,则μl 越大,P lj 越小,杆件越先失稳。
方法二:运用公式P lj =σlj A =π2
EA /λ2
,分子相同,而λ=μl /i ,i 相同,故μl 越大,λ越大,P lj 越小,杆件越先失稳。
综上可知,杆件是否先失稳,取决于μl 。
图中,杆A :μl =2×a =2 a 杆B :μl =1×1.3a =1.3a 杆C :μl =0.7×1.6a =1.12a
由(μl )A >(μl )B >(μl )C 可知,杆A 首先失稳。
【例5】 松木制成的受压柱,矩形横截面为b ×h =100mm ×180mm ,弹性模量E =10GPa ,
λP =110,杆长l =7m 。
在xz 平面内失稳时(绕y 轴转动),杆端约束为两端固定(图a ),在xy
平面内失稳时(绕z 轴转动),杆端约束为两端铰支(图b )。
求木柱的临界应力和临界力。
解:(1)在xz (最小刚度)平面内的临界应力和临界力 此时5.0=y μ,横截面对y 轴的惯性半径mm b A
I i y y 87.2812
=
=
在此平面内 1102.12187
.281075.03
>⨯⨯==
y
y y i l
μλ
符合欧拉公式的适用条件。
临界应力为 ()
MPa 72621211010πλE πσ2
322y 2cr ..=⨯⨯== 临界力为
KN A F cr cr 12118010072.6=⨯⨯==σ (2)在xy (最大刚度)平面内的临界应力和临界力 此时0.1=z μ,横截面对z 轴的惯性半径mm h A I i z z 96.5112
180
12====
此平面内的柔度 1107.13496
.511070.13
>=⨯⨯==
z
z z i l
μλ
临界应力 ()
MPa E z cr 44.57.13410102
3
222=⨯⨯==πλπσ 临界力为 KN A F cr cr 9.9718010044.5=⨯⨯==σ
计算结果表明,木柱在最大刚度(xy )平面内支承条件较弱,柔度z λ较大,使其临界力较小而先失稳。
本例说明,在不同平面内,当杆端支承条件不相同时,应分别计算λ,并取较大者计算临界应力(或临界力)。
因为压杆总是在λ较大的平面内先失稳。
【例6】 托架中,Q=70KN ,杆AB 直径d=40mm,两端为绞支,材料为A 3钢,E=206GPa ,规定稳定安全系数n w =2,,横梁CD 为20a 工字钢,[σ]=140MPa 。
试校核托架是否安全?
Q D
解:托架由横梁CD 和压杆AB 所组成,所以既要校核横梁CD 的强度,又要校核压杆AB 的稳定性。
首先取横梁CD 为研究对象,并画受力图(b )
:0600
cos =
α由 0906000=⨯-⨯=∑Q sin S ,M C α KN ..sin Q
S 159661060010709004416009000
=⨯⨯⨯=⨯=
(1)校核横梁CD 的强度。
由受力图分析知它受拉弯组合变形。
查型钢表N 020a 工字钢w z =237cm 3
,A =35.5cm 2
危险截面在B 处 (b )
MPa A S W M Z 12210
5.3575
.010159102733001070cos 2
333=⨯⨯⨯+⨯⨯⨯=⋅+=ασ<[σ] 横梁 CD 安全。
(2)校核压杆AB 的稳定性 柔度 cr i
l
λμλ<=⨯=
=
804
/480
1 应用抛物线公式
kN
A P MPa
a cr cr s cr 241)04.0(4
101921928000668.02352622=⨯⨯=⋅==⨯-=-=π
σλσσ 压杆AB 的工作安全系数
w cr g n P P n <===
52.1159
241 压杆AB 的稳定性不够,即托架不安全。
【例7】 连杆两端为柱销连接,两销孔间距l=3.2m ,横截面积A=40cm 2
,惯性矩I y =120cm 4
,
I z =800 cm 4,连杆材料为A 3钢,E =206GPa ,轴向压力P=300kN 。
若规定稳定安全系数n w =2,试校
核连杆的稳定性。
解:连赶在xy 平面内可简化为两端铰支座μ=1,连杆在xz 平面内则可简化为两端固定支
座μ=0.5。
在xy 平面内失稳时,z 轴为中性轴。
cm A I i z z 47.440800===
6.7147
.43201=⨯==z z i l μλ 在xz 平面内失稳时,y 轴为中性轴。
cm A
I i y y 73.140
120
==
=
5.9273.13205.0=⨯==y y i l μλ 因y λ>z λ,故只需对xz 平面的稳定性进行校核。
连杆工作应力
MPa A P 754000
103003
=⨯==σ
因y λ=92.5<cr λ,故采用抛物线公式求临界应力。
MPa a s cr 1785.9200668.023522=⨯-=-=λσσ
故 37.275
178
===
σσcr g n >n w 连杆具有足够的稳定性。
