大学物理演示动画---驻波-[福州大学至诚学院]
合集下载
驻波经典知识介绍ppt课件

(3)结论: 动能、势能不断在波腹附近和波节附近间相互转
换,能量交替传递,
/4 的驻范波围的内能,量在被此“范封围闭内”有在能相量邻的波反节复和流波动腹,间但的能
量不能越过波腹和波节传播,驻波没有单向的能量传 输。
形成驻波的两个行波的能流密度数值相等,方 向相反,因此它们叠加而成的驻波能流密度为零,
第五节 驻波
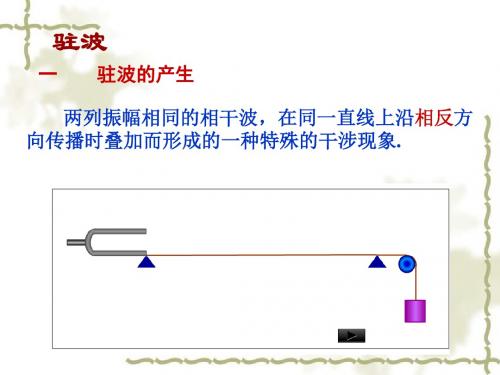
一、驻波的产生
1.驻波的演示
驻波---波形不传播,是媒质质元的一种集体振动形
态。
"驻"字的第一层含义。
2.驻波的形成
驻波——两列振幅相同的相干波在同一直线上沿相反 方向传播时形成的叠加波。
二 、驻波方程
设两列沿同一直线相向传播的同振幅相干波,
取两波在空间某点引起振动,同时达到最大为起始时刻,
波 疏 介
波 密 介
质
质
u
u
较 小
较 大
波 密 介 质
u
较 大
当波从波密介质垂直入射到波疏介质, 被反射 到波密介质时形成波腹. 入射波与反射波在此处的相 位时时相同,即反射波在分界处不产生相位跃变.
五、振动的简正模式:
⒈两端固定的弦:
l
对于具有一定长度且两端固定的弦线来说,形成 驻波时,弦线两端为波节,由上图可见,此时波长和 弦线长度之间应满足下述关系 l n n , n 1,2,
驻波不传播能量
---“驻”字的第三层含义。
实际中驻波的形成 实际的驻波可由入射到媒质界面上的行波和它的 反射波叠加而成。
1.波在固定端的反射 (如一端固定的弹性绳)
反射点是波节(和固定点情况吻合)。 2.波在自由端的反射
反射点是波腹。
问题
在两个介质分界面上将如何 ?
换,能量交替传递,
/4 的驻范波围的内能,量在被此“范封围闭内”有在能相量邻的波反节复和流波动腹,间但的能
量不能越过波腹和波节传播,驻波没有单向的能量传 输。
形成驻波的两个行波的能流密度数值相等,方 向相反,因此它们叠加而成的驻波能流密度为零,
第五节 驻波
一、驻波的产生
1.驻波的演示
驻波---波形不传播,是媒质质元的一种集体振动形
态。
"驻"字的第一层含义。
2.驻波的形成
驻波——两列振幅相同的相干波在同一直线上沿相反 方向传播时形成的叠加波。
二 、驻波方程
设两列沿同一直线相向传播的同振幅相干波,
取两波在空间某点引起振动,同时达到最大为起始时刻,
波 疏 介
波 密 介
质
质
u
u
较 小
较 大
波 密 介 质
u
较 大
当波从波密介质垂直入射到波疏介质, 被反射 到波密介质时形成波腹. 入射波与反射波在此处的相 位时时相同,即反射波在分界处不产生相位跃变.
五、振动的简正模式:
⒈两端固定的弦:
l
对于具有一定长度且两端固定的弦线来说,形成 驻波时,弦线两端为波节,由上图可见,此时波长和 弦线长度之间应满足下述关系 l n n , n 1,2,
驻波不传播能量
---“驻”字的第三层含义。
实际中驻波的形成 实际的驻波可由入射到媒质界面上的行波和它的 反射波叠加而成。
1.波在固定端的反射 (如一端固定的弹性绳)
反射点是波节(和固定点情况吻合)。 2.波在自由端的反射
反射点是波腹。
问题
在两个介质分界面上将如何 ?
p6_8驻波的形成(动画)

{范例6.8} 驻波的形成(动画)
振幅最大的位 | cos 2π x | 1 即 2 π x kπ (k = 0,±1,±2,…) 置满足条件 相邻两波腹之间的距离为 因此振幅最 x k 这个位置 2 大的位置为 称为波腹。 Δx = xk + 1 – xk = λ/2。 x π 振幅最小的位 | cos 2π x | 0 即 2 π (2k 1) (k = 0,±1, 2 ±2,…) 置满足条件 相邻两波节之间 因此振幅最 x (2k 1) 这个位置 4 称为波节。 的距离仍然为λ/2。 小的位置为 相邻两波节之间的波为一段,同一段中所有质点的振动相位 都是相同的,这是因为同一段中的cos2πx/λ具有相同的符号; 相邻两段之间的质点的相位都是相反的,这是 因为相邻段中的cos2πx/λ具有相反的符号。 这种波没有相位和波形的定向传播,因此称为驻波。
某时刻的左行波、右行波和驻波如图所示。
在波节上,各质点的位移始终为零;在波腹 上,各质点的位移有时为零,但是振幅最大。
当右行波的振幅比较大时,合成波也是右行波。
在右行波的振幅比左行波的振幅大的情况下,向右传播的 能量比向左是驻波,而是行波。
{范例6.8} 驻波的形成(动画)
两个周期为T,波长为λ,振幅相等的余弦波相向传播, 相遇之后形成驻波。演示驻波形成的动画。如果两列 波的振幅不相等,它们相遇后还会形成驻波吗?
[解析]沿x轴正方向传播的 u1 A cos 2 π( t x ) T 波称为右行波,可设为
沿x轴负方向传播的波 称为左行波,可设为
t x u Am cos 2 π , Am 2 A | cos 2 π | T
{范例6.8} 驻波的形成(动画)
大学物理:Chapter 13-驻波

2
2
A驻 cos ( t )
A驻
2 Acos (2 x 2 1 ) 2
★ 说明:
(1) A驻 是 x 的周期函数,决定 x 处质点的振幅。
(2) (t ) 决定 x 处质点的振动状态。
(3) 各点作频率相同、振幅不同的谐振动。
(4) 方程中不含 (t x u) 项,非行波,没有波形的传播。
无半波损失时,应满足:
t kx0 0反 t kx0 0入
0反 0入 2kx0
有半波损失时,应满足:
t kx0 0反 t kx0 0入 0反 0入 2kx0
驻波在生活中的 应用
• 首先举几个生活中常见驻波的例子: • 以弦乐器的弦来说明。当拨动琴弦,产生一个波,遇到两
无半波损失时,
若入射波函数为:u入 ( x , t ) A cos(t kx) 则反射波函数一定为:u反 ( x , t ) A cos(t kx)
若入射波函数为:u入 ( x , t ) A cos(t kx 0 )
则反射波函数一定为:u反 ( x ,t ) A cos(t kx 0 )
解: (1)
y入
A cos
2
(
t T
x
)
入射波 O
反射波
P
波密 介质
x
y入O
A cos
2
t T
L = 5λ
波由O 传至P 再返回O ,引起O 点振动相位比 y入O 落后了:
2
2L
由半波损失引起的相位差
所以反射波在O点的振动方程为:
y反O
A cos[ 2
t T
(2
2L
)]
Acos[2 t (2 10 )] Acos[2 t 21 ]
大学物理演示动画---光的偏振-[福州大学...李培官]
![大学物理演示动画---光的偏振-[福州大学...李培官]](https://img.taocdn.com/s3/m/745a320ceff9aef8941e0672.png)
今天是2013年8月4日星期日
大学物理演示动画 ---光的偏振
福州大学至诚学院
大学物理教研室 李培官
1.光的偏振状态
自然光
线偏振光
部分偏振光
偏振片
波动光学
检 偏
起偏器
检偏器
思 • 一束光线通过一偏振片,若I 不变化,是什么光?
考 •I 变化且有消光, 是什么光? • I 变化但无消光, 是什么光?
原理:把自然光分成寻 常光和非寻常光,然后 利用全反射把寻常光反 射到棱镜侧壁上,,只 让非寻常光通过,从而 获得一束振动方向固定 的线偏振光。 加工后将两块方解石用 加拿大胶粘合起来, 对于o光 对于e光
光轴
90 48 68
e光 o光
加拿大胶
no n 产生全反射
n 1.55 no 1.658
波动光学
偏振光的干涉 人为双折射现象 旋光现象 偏振光的干涉1 实验装置 屏
偏振片P1
波晶片
偏振片P2
2. 实验现象
单色光入射, 波片厚度均匀, 屏上光强均匀分布.
白光入射, 屏上出现彩色, 转动偏振片或波片, 色彩变化. 波片厚度不均匀时, 出现干涉条纹.
双折射[演示动画]
• 尼克尔棱镜
Tips for Better Life
欢迊指导 for 2013
谢谢
今天是2013年8月4日星期日
波动光学
3. 马吕斯定律 I0
P1
I1
P2
I2
P1 A1
E2 E1 cos
P2 A2
A2 A1 cos
马吕斯定律
I 2 I1 cos 2
I2:检偏器射出光强
I1:入射检偏器光强
大学物理演示动画 ---光的偏振
福州大学至诚学院
大学物理教研室 李培官
1.光的偏振状态
自然光
线偏振光
部分偏振光
偏振片
波动光学
检 偏
起偏器
检偏器
思 • 一束光线通过一偏振片,若I 不变化,是什么光?
考 •I 变化且有消光, 是什么光? • I 变化但无消光, 是什么光?
原理:把自然光分成寻 常光和非寻常光,然后 利用全反射把寻常光反 射到棱镜侧壁上,,只 让非寻常光通过,从而 获得一束振动方向固定 的线偏振光。 加工后将两块方解石用 加拿大胶粘合起来, 对于o光 对于e光
光轴
90 48 68
e光 o光
加拿大胶
no n 产生全反射
n 1.55 no 1.658
波动光学
偏振光的干涉 人为双折射现象 旋光现象 偏振光的干涉1 实验装置 屏
偏振片P1
波晶片
偏振片P2
2. 实验现象
单色光入射, 波片厚度均匀, 屏上光强均匀分布.
白光入射, 屏上出现彩色, 转动偏振片或波片, 色彩变化. 波片厚度不均匀时, 出现干涉条纹.
双折射[演示动画]
• 尼克尔棱镜
Tips for Better Life
欢迊指导 for 2013
谢谢
今天是2013年8月4日星期日
波动光学
3. 马吕斯定律 I0
P1
I1
P2
I2
P1 A1
E2 E1 cos
P2 A2
A2 A1 cos
马吕斯定律
I 2 I1 cos 2
I2:检偏器射出光强
I1:入射检偏器光强
大学物理演示动画 横波与纵波 福州大学至诚学院

yO Acost
在时刻t位于x处的质元的振动方程
由于波 沿 x 轴正向传播,所以在x>0的个质点将依
次较晚开始振动。
以u 表示沿 x 轴正向传播的简谐波的速度。
第二十章 教学基本要求
第二十章 波动
波线上各点的简谐运动图
Tips for Better Life
欢f迎or 指201导3
再见
今天是2019年9月4日星期三
9
11 醉翁亭记
1.反复朗读并背诵课文,培养文言语感。
2.结合注释疏通文义,了解文本内容,掌握文本写作思路。
3.把握文章的艺术特色,理解虚词在文中的作用。
4.体会作者的思想感情,理解作者的政治理想。一、导入新课范仲淹因参与改革被贬,于庆历六年写下《岳阳楼记》,寄托自己“先天下之忧而忧,后天下之乐而乐”的政治理想。实际上,这次改革,受到贬谪的除了范仲淹和滕子京之外,还有范仲淹改革的另一位支持者——北宋大文学家、史学家欧阳修。他于庆历五年被贬谪到滁州,也就是今天的安徽省滁州市。也
是在此期间,欧阳修在滁州留下了不逊于《岳阳楼记》的千古名篇——《醉翁亭记》。接下来就让我们一起来学习这篇课文吧!【教学提示】结合前文教学,有利于学生把握本文写作背景,进而加深学生对作品含义的理解。二、教学新课目标导学一:认识作者,了解作品背景作者简介:欧阳修(1007—1072),字永叔,自号醉翁,晚年又号“六一居士”。吉州永丰(今属江
纵波:质点振动方向与波的传播方向互相平行的波. (可在固体、液体和气体中传播)
2. 细棒中的纵波波速
u Y
Y 杨氏模量, 密度
胡克定理 F Y L SL
第二十章 教学基本要求源自第二十章 波动位于原点的质元的振动方程
大学物理课件第15章 机械波-驻波
x
三 波 疏 介 质
相位跃变(半波损失)
波 密 介 质 较 大
u
较 小
u
当波从波疏介质垂直入射到波密介质, 被反射 到波疏介质时形成波节. 入射波与反射波在此处的相 位时时相反, 即反射波在分界处产生 的相位跃变, 相当于出现了半个波长的波程差,称半波损失.
π
u
较 大 当波从波密介质垂直入射到波疏介质, 被反射 到波密介质时形成波腹. 入射波与反射波在此处的相 位时时相同,即反射波在分界处不产生相位跃变.
15.5 波的衍射
15.5.2 波的衍射
当波长与障碍物 可比拟的时候,波就 可以绕过障碍物而传 播,并且子波的包迹 组成新的波振面
15.5 波的衍射
15.5.3 波的反射和折射
A2 A2 A1 E1 A1 E1 E2
E2
反射:因为在同一介质中波速相同, 所以有
折射:在两种介质中 相等时间内有
t
15.5.1 惠更斯—菲涅耳原理 惠更斯原理:介质中波动传播到的
各点,都可以看成是发射子波的波源, 其后的任一时刻,这些子波的包络面就 是新的波阵面。
水面波的衍射
惠更斯—菲涅耳原理:介质中波 动传播到的各点,都可以看成是发 射子波的波源,其后的任一时刻, 这些子波的包络面就是新的波阵面, 波阵面上的每一点不仅可以看成是 发射子波的波源,而且这些子波波 源是相干波源,它们发出的子波是 相干波,相干波的干涉决定波的强 度。
BC u1
ADC ABC BAC DCA
BAC i
BC t u1
AD u1t BC
AD u2 t
BAC i, ACD
BC u1 t AC sin i AD u 2 t AC sin sin i u1 n2 n21 sin u 2 n1
大学物理:Chapter 13-驻波

2
)
y驻
2 A cos(2
x
)cos(2
2
t T
)
2
(3) 波节点: 2 Acos(2 x ) 2
0,
2 x (2k 1)
2
2
2 x k , x k (k 0, 1, 2,) (0 x 5 )
垂直入射中,入射波和反射波的合成
四、半波损失 (相位跃变)
1. 波阻:ρ u 其中,ρ — 介质密度;u — 波速。 两介质相比较,ρ u 大者称波密介质,小者称波疏介质。
2. 半波损失
— 当波由波疏介质向波密介质垂直入射,在两介质界面
反射时相位突变π ,称为“半波损失”。
★ 1v1 2v2 时,有半波损失,
A驻 2 A
2 x 2 1 k (k 0, 1, 2,)
2
★ 相邻两波节(或波腹)间的距离: Δx xk 1 xk 2
t 0
tT 4
tT 2
t 3T 4
波节:始终 不动的点。 红色虚线对 应的位置。
波腹:振幅 始终最大的 点。黑色虚 线对应的位 置。
2. 驻波中各点的相位关系
2π
2
半波损失: 反射点为波节,表明入射波与反射波在该点反相.
两端固定的弦 振动的简正模式
l n n n 1,2,
2
l 1
2 l 22
2
l 33
2
1)弦上的驻波
A
弦
B
L n n
L
2
n
2L n
n=1 n=2 n=3
n
u
n
n u n=4 2L
1
u 2L (基频)
2
u L
3
3u 2L
)
y驻
2 A cos(2
x
)cos(2
2
t T
)
2
(3) 波节点: 2 Acos(2 x ) 2
0,
2 x (2k 1)
2
2
2 x k , x k (k 0, 1, 2,) (0 x 5 )
垂直入射中,入射波和反射波的合成
四、半波损失 (相位跃变)
1. 波阻:ρ u 其中,ρ — 介质密度;u — 波速。 两介质相比较,ρ u 大者称波密介质,小者称波疏介质。
2. 半波损失
— 当波由波疏介质向波密介质垂直入射,在两介质界面
反射时相位突变π ,称为“半波损失”。
★ 1v1 2v2 时,有半波损失,
A驻 2 A
2 x 2 1 k (k 0, 1, 2,)
2
★ 相邻两波节(或波腹)间的距离: Δx xk 1 xk 2
t 0
tT 4
tT 2
t 3T 4
波节:始终 不动的点。 红色虚线对 应的位置。
波腹:振幅 始终最大的 点。黑色虚 线对应的位 置。
2. 驻波中各点的相位关系
2π
2
半波损失: 反射点为波节,表明入射波与反射波在该点反相.
两端固定的弦 振动的简正模式
l n n n 1,2,
2
l 1
2 l 22
2
l 33
2
1)弦上的驻波
A
弦
B
L n n
L
2
n
2L n
n=1 n=2 n=3
n
u
n
n u n=4 2L
1
u 2L (基频)
2
u L
3
3u 2L
大学物理课件--驻波-[福州大学...李培官]
![大学物理课件--驻波-[福州大学...李培官]](https://img.taocdn.com/s3/m/56afdd3e3968011ca30091ae.png)
1 2 π (k ) π 2
k 0,1,2,
k 0,1,2,
波腹 波节
1 k 2 2
相邻波腹(节)间距为
2
驻波条件: Ln
2
, n 1,2......
7
2)每一时刻驻波都有确定的波形,此波形既不左 移,也不右移,没有振动状态和相位的传播,故称为驻 波。
因为两相邻波节之间的间隔为/2 。
(3)因为在x=7m处为波密反射点,该处为波节点。
40 uT 20 4(m) 10
所以在0<x<7m区间的干涉相消点为:
2
y1
O
y2 7
x ( m)
x 1,3,5,7(m)
20
Tips for Better Life
for 2014
14 x y反 A cos[ 10 (t ) ] 20 x A cos[ 10 (t ) 7 ]
20
19
(2)在x=6m处介质质元的振动方程
6 6 y6 A cos( 10t ) A cos( 10t 7 ) 2 2 y6 2 A cos( 10t ) 即:
D C
6
讨论
驻波方程 y 2 A cos 2π cos 2π t x 1)振幅 2 A cos 2π 随 x 而异, 与时间无关.
cos 2 π x
x
x k π 1 2π
0
x
x
k
2
k 0,1, Amax 2 A
k 0,1,2 Amin 0
x
x 2 A cos 2 π cos 2 πt
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Tips for Better Life
欢迎指导 for 2013
再见
今天是2013年8月3日星期六
10
t
A B
C
驻波的能量在相邻的波腹和波节间往复变化, 在相 邻的波节间发生动能和势能间的转换, 动能主要集中在 波腹, 势能主要集中在波节, 但无能量的定向传播.
机械波
6.6.4 半波损失 1. 入射波与反射波产生驻波 振源
软 绳 当 形 成 驻 波 时
自由端反射
总是出现波腹 总是出现波节
固定端反射
设:
y1 A cost kx 右行波 y2 A cost kx 左行波 y y1 y2 2 A cos kx cost
机械波
驻波的特点
ห้องสมุดไป่ตู้
机械波
机械波
6.6.3 驻波的能量
波 节
波 腹
x
x
y 2 位移最大时 dWp ( ) x
平衡位置时 dWk ( y ) 2
驻波-----演示动画
福州大学至诚学院
大学物理教研室
1
驻波的形成与特点
2
机械波
§6.6 驻 波
6.6.1 驻波的产生 两列振幅相同的相干波相向传播时叠加形成的 波称为驻波. 驻波是波的一种干涉现象.
驻波的波形特点
三、驻波
1. 表达式
当两列振幅相同,频率相同,振动方向相 同的波以相反方向传播时,叠加形成驻波。
