方腔顶盖驱动流动
4.2 顶盖驱动流(8)

4.2顶盖驱动流4.2.1物理模型在一个正方形的二维空腔中充满等密度的空气,方腔每边长为0.1m,其顶板以0.1m/s 的速度向右移动,同时带动方腔内流体的流动,流场内的流体为层流。
计算区域示意图如图4-2-1所示。
图4-2-1 计算区域示意图4.2.2在Gambit中建立模型Step1:启动Gambit并选择求解器为Fluent5/6。
Step2:创建面操作:→→打开对话框如图4-2-2所示。
输入长度和宽度10,在Direction中选择XY Centered。
图4-2-2 创建面设置对话框Step3:划分面网格操作:→→打开对话框如图4-2-3所示,Shift+鼠标左键选择正方形面,Internal size=0.5,其它保留默认,点击Apply确认。
划分后的网格如图4-2-4所示。
图4-2-3 网格划分设置对话框图4-2-4 计算区域网格图Step4:设置边界类型操作:→●在Name栏输入边界名称wall-1,将Type栏选为Wall,在Entity栏选取Edges,并选中方腔顶部边线。
●在Name栏输入边界名称wall-2,将Type栏选为Wall,在Entity栏选取Edges,并选中方腔其它三条边线。
Step5:输出网格文件操作:Fil m→export→mesh打开对话框如图4-2-5所示,选中Export 2-D mesh 前面的复选框,输出网格文件。
图4-2-5 网格文件输出对话框4.2.3求解计算Step1:启动Fluent选择2d单精度求解器,点击Run,如图4-2-6所示。
图4-2-6 启动求解器图4-2-7 网格尺寸设置对话框Step2:导入并检查网格1.读入网格文件操作:Fil e→Read→Case...找到文件后,单击OK按键确认。
2.检查网格操作:Grid→Check网格读入后,一定要进行网格检查,注意最小体积不能为负值。
3.网格比例设置操作:Grid→Scale...在Gambit中,生成网格使用的单位是cm,在Grid Was Created In下拉菜单中,选取cm,如图4-2-7所示,然后单击Scale,关闭对话框。
方腔流动
边界条件
流函数边界条件:根据已知条件,在四个壁上流函数均为 0,上边界平板速度 1,根据不可 滑移条件确定流函数偏导数条件。
涡量边界条件,采用(1):
(1)可以用 Taylor 展开建立一般形式的 Thom 公式。假设某壁面切向速度 v ,沿其内法
向 n 有一节点,距离壁面距离为 h, 此点上的流函数为1 ,如果壁面上的流函数值为 0 ,那么
0
(1
0 2h2
v h)
时间导数采用向前 Euler 法,空间导数项可以用中心差分格式离散
计算步骤 1、计算 n + 1 时刻内点的涡量,需要考虑时间步长和空间步长和粘性项的关系。
2、计算 n + 1 时刻的流函数 n1 ,超松弛迭代法,松弛因子为-1.8。
3、计算 n + 1 时刻边界上的涡量
计算流体力学作业
题目
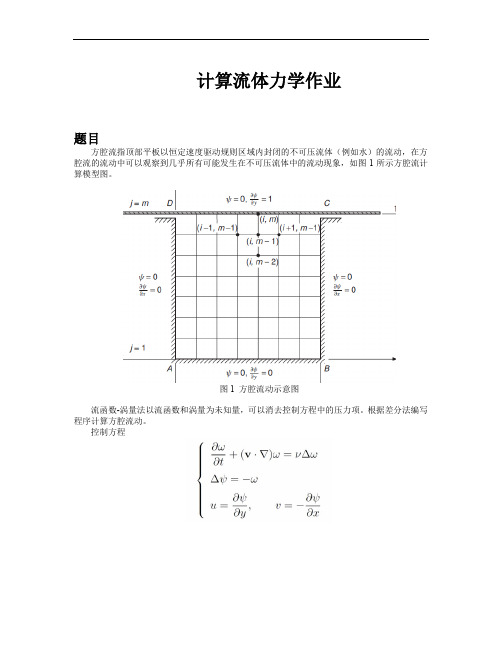
方腔流指顶部平板以恒定速度驱动规则区域内封闭的不可压流体(例如水)的流动,在方 腔流的流动中可以观察到几乎所有可能发生在不可压流体中的流动现象,如图 1 所示方腔流计 算模型图。
图 1 方腔流动示意图 流函数-涡量法以流函数和涡量为未知量,可以消去控制方程中的压力项。根据差分法编写 程序计算方腔流动。 控制方程
-0.5
0
0.5
1
1.5
3.995s 方腔速度矢量图
0
0.5
1
x0=0; x1=1; dx=(x1-x0)/(N-1); %空间步长 y0=0; y1=1; dy=(y1-y0)/(M-1); %空间步长
Thom 公式
1
0.8
0.6
0.4
0.2
0
-0.2
0
0.2
0.4
方腔驱动流源代码(SIMPLE算法)

p
pi, j
x 0
编号为(i,j)的速度修正量 u , v 不仅与压力修正量
p 有关,还与邻近点的速度修正
量有关。SIMPLE 算法的重要假定:速度的改变只与压力的改变有关,忽略邻近点对速度修 正的影响。因而得到如下速度修正量
u i, j vi, j
本算例采用求解不可压缩流动的经典算法, 即 SIMPLE 算法, 求解方腔内粘性不可压缩 流体运动的定常解。 SIMPLE 算法的全称为 Semi-Implicit Method for Pressure-Linked Equations, 即求解压力关联方程的半隐式算法。 采用 SIMPLE 算法时, 为了避免中心差分格式将 “棋盘” 型参量分布误认为是均匀分布, 需要用交错网格对计算域进行离散。
xy M 1 M 1 1 1 M 1 M 1 ui , j ui , j Fi ,1j Fi y 0 1, j y Gi , j Gi , j 1 x pi 1, j pi , j t
Y 方向动量方程在速度 v 控制体上离散,时间采用前差
1 2 2 xy 1 M M M M aiu, j y uiM x viM 1, j u i 1, j , j vi 1, j vi , j 1 vi 1, j 1 Re x Re y t 4 4
以上是 SIMPLE 算法中离散化的动量方程
三、SIMPLE 算法基本思想
SIMPLE 算法是一种解决压力-速度耦合问题的“半隐式”算法。首先给定 M 时刻猜测 的速度场 u 估计值 值u
方腔顶盖驱动流动
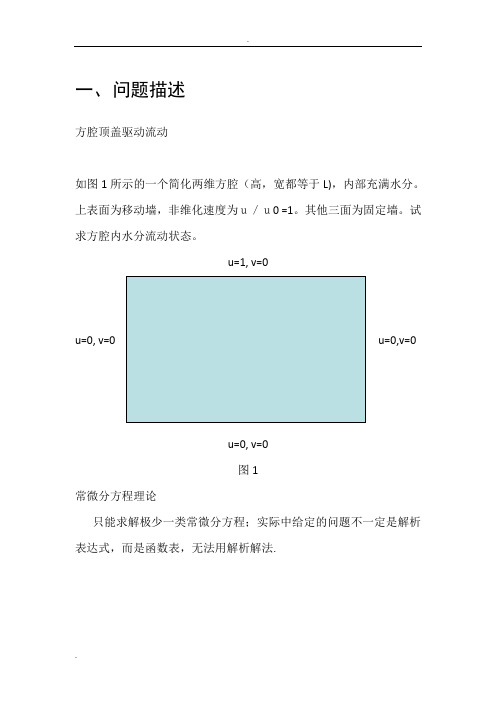
一、问题描述方腔顶盖驱动流动如图1所示的一个简化两维方腔(高,宽都等于L),内部充满水分。
上表面为移动墙,非维化速度为u/u0 =1。
其他三面为固定墙。
试求方腔内水分流动状态。
u=1, v=0u=0, v=0 u=0,v=0u=0, v=0图1常微分方程理论只能求解极少一类常微分方程;实际中给定的问题不一定是解析表达式,而是函数表,无法用解析解法.二、离散格式数值解法:求解所有的常微分方程 计算解函数 y(x) 在一系列节点a = x 0< x 1<…<x n = b 处的近似值),...,1()(n i x y y i i =≈节点间距为步长,通常采用等距节点,即取 hi = h (常数)。
步进式:根据已知的或已求出的节点上的函数值计算当前节点上的函数值,一步一步向前推进。
因此只需建立由已知的或已求出的节点上的函数值求当前节点函数值的递推公式即可。
欧拉方法1(,) 0,1,...n n n n y y h f x y n +=+=几何意义在假设 y n = y (x n ),即第 n 步计算是精确的前提下,考虑公式或方法本身带来的误差: R n = y (x n +1) y n +1 , 称为局部截断误差.截断误差: 实际上,y (x n ) ? y n , y n 也有误差,它对y n +1的误差也有影响,见下图。
但这里不考虑此误差的影响,仅考虑方法或公式本身带来的误差,因此称为方法误差或截断误差。
局部截断误差的分析:由于假设y n = y (x n ) ,即y n 准确,因此分析局部截断误差时将y (x n +1) 和 y n +1都用点x n 上的信息来表示,工具:Taylor 展开。
显式欧拉公式一阶向前差商近似一阶导数推导如下:223111232()[()()()()][ (,)] ()()h n n n n n n n n n h n R y x y y x hy x y x O h y hf x y y x O h +++'''=-=+++-+''=+1()()()n n n y x y x y x h+-'≈111()()() ()()(,)n n n n nn n n n n y x y x hy x y x y y x y y h f x y +++'≈+↑≈≈=+隐式欧拉公式xn +1点向后差商近似导数 推导如下:几何意义设已知曲线上一点 P n (x n , y n ),过该点作弦线,斜率为(x n +1 , y n +1 ) 点的方向场f (x ,y )方向,若步长h 充分小,可用弦线和垂线x =x n +1的交点近似曲线与垂线的交点。
方腔顶盖驱动流动

一、二、问题描述方腔顶盖驱动流动如图1所示的一个简化两维方腔(高,宽都等于L),内部充满水分。
上表面为移动墙,非维化速度为u/u0 =1。
其他三面为固定墙。
试求方腔内水分流动状态。
u=1, v=0u=0, v=0u=0,v=0u=0, v=0图1常微分方程理论只能求解极少一类常微分方程;实际中给定的问题不一定是解析表达式,而是函数表,无法用解析解法.二、离散格式数值解法:求解所有的常微分方程 计算解函数 y(x) 在一系列节点a = x 0< x 1<…<x n = b 处的近似值),...,1()(n i x y y i i =≈节点间距为步长,通常采用等距节点,即取 hi = h (常数)。
步进式:根据已知的或已求出的节点上的函数值计算当前节点上的函数值,一步一步向前推进。
因此只需建立由已知的或已求出的节点上的函数值求当前节点函数值的递推公式即可。
欧拉方法1(,) 0,1,...n n n n y y h f x y n +=+=几何意义在假设 y n = y (x n ),即第 n 步计算是精确的前提下,考虑公式或方法本身带来的误差: R n = y (x n +1)y n +1 , 称为局部截断误差.显式欧拉公式一阶向前差商近似一阶导数223111232()[()()()()][ (,)] ()()h n n n n n n n n n h n R y x y y x hy x y x O h y hf x y y x O h +++'''=-=+++-+''=+推导如下:隐式欧拉公式x n +1点向后差商近似导数 推导如下:1()()()n n n y x y x y x h+-'≈111()()() ()()(,)n n n n nn n n n n y x y x hy x y x y y x y y h f x y +++'≈+↑≈≈=+11()()()n n n y x y x y x h++-'≈11()()()()n n n n ny x y x hy x y x y ++'≈+↑≈几何意义设已知曲线上一点 P n (x n , y n ),过该点作弦线,斜率为(x n +1 , y n +1 ) 点的方向场f (x ,y )方向,若步长h 充分小,可用弦线和垂线x =x n +1的交点近似曲线与垂线的交点。
OpenFOAM顶盖驱动流详解!使用手册

OpenFOAM顶盖驱动流详解!使用手册引言这是开源场运算和操作c++库类(openfoam)的使用指南。
他详细描述了OpenFOAM的基本操作。
首先通过第二章一系列教程练习。
然后通过对更多的独立组件的更详细的描述学习openfoam。
Of 首先主要是一个c++库类,主要用于创建可执行文件,比如应用程(application)。
应用程序分成两类:求解器,都是为了解决特定的连续介质力学问题而设计的;公用工程,这些是为了执行包括数据操作等任务而设计的。
Of 包括了数量众多的solver和utilities,牵涉的问题也比较广泛。
将在第三章进行详尽的描述。
Of 的一个强项是用户可以通过必要的预备知识(包括数学,物理和编程技术)创建新的solvers 和utilities。
Of 需要前处理和后处理环境。
前处理、后处理接口就是of本身的实用程序(utilities),以此确保协调的数据传输环境。
图是of总体的结构。
第4章和第五章描述了前处理和运行of 的案例。
既包括用of提供的mesh generator划分网格也包括第三方软件生成的网格数据转换。
第六章介绍后处理。
Chapter 2指导手册在这一章中我们详细描述了安装过程,模拟和后进程处理一些OpenFOAM测试案例,以引导用户运行OpenFOAM的基本程序。
$FOAM_TUTORIALS 目录包含许多案件演示of提供的所有求解器以及许多共用程序的使用,在试图运行教程之前,用户必须首先确保他们已经正确地安装了OpenFOAM。
该教程案件描述 blockMesh预处理工具的使用,paraFoam案例设置和运行OpenFOAM求解器及使用paraFoam进行后处理。
使用OpenFOAM支持的第三方后处理软件的用户可以选择:他们要么可以按照教程使用paraFoam,或当需要后处理时参阅第六章的第三方软件使用说明。
OpenFOAM安装目录下的tutorials目录中所有的指导手册都是可复制的。
顶驱结构和原理

顶驱构造及原理
顶驱构造 顶驱旳构成: 1、综合游 车
VACRO 综合游动滑车组提供六个额定载荷为500T, 外径为50 in旳滑轮。整个游车高 。
2、钻井装置总成
• 钻井电动机是一种1000hp旳分流电动机。电动机是 由电枢空心轴和垂直止推轴承构成。
• 单速行星变速器 IDS 单速行星变速器由下列主要原件构成: 内齿合齿轮和齿轮箱 电机小齿轮
顶驱构造及原理
顶驱构造
6、有延伸入口旳现场谷风机冷却系统。
该系统向钻井电动机提供现场冷却空气。该系统由带有导管旳原则型局部 鼓风机和一根向马达方向旳延伸旳软管构成,鼓风机上旳导管能将进口安 装在大钩和游动滑车上。 C.PH-60型管子处理装置 管子处理装置涉及 1、整体吊卡 2、安全阀(IBOPS)
❖ 每3个月对顶驱齿轮箱旳润滑油进行更换,油品标号为 MOBIL626。油量为12加仑。
❖ 每3个月对机械手泵站旳液压油进行更换,油品为N32抗磨 液压油,油量32加仑。
❖ 每日对顶驱旳各个连接螺栓及开口销进行检验,对发觉旳问 题及时处理。
顶驱构造及原理
顶驱构造及原理
顶驱构造及原理
顶驱简介
据悉,目前我国赴国外工作旳钻井队,如钻机未安装顶部驱动 钻井装置者,投标竞争中不允许中标,可见顶部驱动钻井装置 已到了非用 不可旳地步。图片
❖目前,石油钻井中使用旳顶驱有两大类:电动顶驱和液动顶 驱。其中电动顶驱又按照电机分为直流电动顶驱和液动变频顶 驱,我们平台现用旳是直流电动顶驱。 ❖a.顶驱钻井系统特点 ❖ 能够节省钻井时间20%-50 %,能够大大降低卡钻事故能够 控制井涌防止井喷,用于深井超深井、斜井以及高难度旳定向 钻井,其综合效益尤为明显。
顶驱构造及原理
高雷诺数三维顶盖驱动方腔流实验研究

高雷诺数三维顶盖驱动方腔流实验研究在流体动力学中,顶盖驱动方腔流是重要的研究方向之一,可获取流动特性及流场模型,为汽车、航空、船舶等结构设计提供指导。
然而,传统的顶盖方腔主要分析了低雷诺数的平面流动,无法模拟三维流动过程。
为此,开展高雷诺数三维顶盖驱动方腔流的实验研究具有重要意义。
一、介绍(1)定义高雷诺数三维顶盖驱动方腔流,是指采用高雷诺数的环境,以三维顶盖的形式对方腔内的流体进行驱动,观察流体在方腔内运动轨迹,以研究三维顶盖方腔流动特性及流场模型。
(2)研究内容高雷诺数三维顶盖驱动方腔流的实验研究,主要涉及到两个方面:第一,研究调节顶盖尺寸和高度、边界条件及内外温度差等参数,探讨流动特性及流场模型。
第二,研究流体运动轨迹,以研究运动情况,揭示顶盖驱动方腔流动的实际机理,以优化设计及实现流体动力学性能。
二、实验条件(1)实验装置实验装置主要包括高雷诺数气体序列量程器、定压泵、三维顶盖驱动方腔、蒸汽源、温度计、密度计、压力计等。
(2)实验参数实验参数主要包括顶盖尺寸及高度、边界条件、内外温度差等参数。
三、实验和结果研究高雷诺数三维顶盖驱动方腔流的实验,主要运用基本物理测量方法,确定实验参数,调节顶盖尺寸和高度,监测内外温度差、流速等参数,对方腔内部流动进行观测,收集流场实验数据,以便研究顶盖驱动方腔流动特性及流场模型。
实验结果表明,在各种不同参数设定下,测量到的方腔内部流场均能受到高雷诺数三维顶盖的影响,流经方腔内流动具有不同的轨迹。
运用流体动力学理论,根据实验数据,建立顶盖驱动方腔流动的数学模型,以实现对方腔内流场形态的解析和分析。
四、结论本次实验通过高雷诺数三维顶盖驱动方腔流的实验研究,发现了方腔内流动特性与顶盖参数设定的关系,揭示了顶盖驱动方腔流动的实际机理,并建立了顶盖驱动方腔流动的数学模型,为汽车、航空、船舶等结构设计提供指导,有助于更好地了解流体动力学。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、问题描述
方腔顶盖驱动流动
如图1所示的一个简化两维方腔(高,宽都等于L),内部充满水分。
上表面为移动墙,非维化速度为u/u0 =1。
其他三面为固定墙。
试求方腔内水分流动状态。
u=1, v=0
u=0, v=0
u=0,v=0
u=0, v=0
图1
常微分方程理论
只能求解极少一类常微分方程;实际中给定的问题不一定是解析表达式,而是函数表,无法用解析解法.
二、离散格式
数值解法:求解所有的常微分方程 计算解函数 y(x) 在一系列节点
a = x 0< x 1<…<
x n = b 处的近似值
节点间距
为步长,通常采
用等距节点,即取 hi = h (常数)。
步进式:根据已知的或已求出的节点上的函数值计算当前节点上的函数值,一步一步向前推进。
因此只需建立由已知的或已求出的节点上的函数值求当前节点函数值的递推公式即可。
)
,...,1()
(n i x y y i i =≈
欧拉方法
几何意义
在假设 y n = y (x n ),即第 n 步计算是精确的前提下,考虑公式或方法本身带来的误差: R n =
y (x n +1)
y n +1 , 称为局部截
1(,) 0,1,...
n n n n y y h f x y n +=+=
断误差.
2
2
3
1112
3
2
()[()()()()]
[ (,)] ()()
h n n n n n n n n n h n R y x y y x hy x y x O h y hf x y y x O h +++'''=-=+++-+''=
+
显式欧拉公式
一阶向前差商近似一阶导数
推导如下:
隐式欧拉公式
x
n +1
点向后差商近似导数 推导如下:
1()()
()n n n y x y x y x h
+-'≈
111()()() ()()(,)
n n n n n
n n n n n y x y x hy x y x y y x y y h f x y +++'≈+↑≈≈=+11()()
()n n n y x y x y x h
++-'≈
()()()
y x y x hy x '≈+
几何意义
设已知曲线上一点 P n
(x n
, y n
),过该点作弦线,斜率为(x
n +1
, y
n +1
) 点的
方向场f (x ,y )方向,若步长h 充分小,可用弦线和垂线x =x n +1
的交点近
似曲线与垂线的交点。
比较 显式公式和隐式公式及其局部截断误差
x n
x n+1
P n
显式公式
隐式公式
中点欧拉公式
中心差商近似导数
h x y x y x y 2)
()()(021-≈
'1(,) 0,1,...
n n n n y y h f x y n +=+=23
1112
()()()
h n n n n R y x y y x O h +++''=-=
+111(,)
n n n n y y h f x y +++=+2
3
1112
()()()
h n n n n R y x y y x O h +++''=-=-+))
(,(2)()(1102x y x f h x y x y +≈P n+1
x y
y(
控制方程
1
,...,1
)
,(
2
1
1
-
=
+
=
-
+
n
i
y
x f h
y
y
i
i
i
i
交错网格
因为方腔顶盖驱动流动的流动不均与性,u、v及压力p的变化存在交错的现象。
P 点位置
u 点位置
v 点位置
P 点控制微元体u点控制微元体v点控制微元体
守恒形式N-S方程
动量方程离散(x-方向)
方程(1)
推导过程:
⎪⎪
⎭
⎫
⎝
⎛
+
=
+
-j
i
j
i
j
i
u
u
u
,
2
1
,
2
1
,2
1
综上有:
动量方程离散(y-方向)
方程(2)
三、压力修正的基本思想
压力修正方程推导
方程(1)欧拉显式
方程(3)
方程(2)欧拉显式
方程(4)
压力修正方程
U*,V*,P* 中间值
方程(5)U’,V’,P’修正值(N+1时间步)
U N+1,V N+1,P N+1,满足连续方程的值
方程(6)
方程(7)
方程(8)
综合方程3,5,6,可得
方程(9)综合方程4,5,7,可得
方程(10)将方程9,10,5 代入方程8,可得
方程(11)
四、SIMPLE算法流程图
M程序语言:
已知条件
L=H; 方腔的宽,高
u=1, v=0;方腔上表面的速度
u=0, v=0;方腔左表面的速度
u=0, v=0;方腔右表面的速度
u=0, v=0;方腔下表面的速度
网格划分
Y方向网格数为:M。
节点在Y方向序号变量为i。
1< =i<= M X方向网格数为:N。
节点在X方向序号变量为j。
1<= j<= N 节点矩阵:
OT=zeros(M,N); OT 旧值某个节点OT(i, j) NT=zeros(M,N); NT 新值
间距
dx=L/(N-1); X方向间距
dy=H/(M-1); Y方向间距
控制方程离散
方程(11)。
