顶盖驱动流数值模拟分析
汽车顶盖冲压成型的CAE模拟研究

汽车顶盖冲压成型的CAE模拟研究汽车顶盖是整车的关键部件之一,决定了整车的车身结构和设计风格。
而汽车顶盖冲压成型技术是实现汽车顶盖质量稳定、工艺精度高的关键技术之一。
为了确保汽车顶盖在生产过程中能够保证质量和性能,CAE模拟技术被广泛应用于汽车顶盖的设计和制造过程中。
汽车顶盖冲压成型技术是指利用压力,在板材上形成所需几何形状的成形工艺。
通过此方法,我们可以制造出形状各异的汽车顶盖。
在冲压成型过程中,数值模拟是设计和优化汽车顶盖工艺的重要手段。
数值模拟可以预测汽车顶盖在不同形变过程中的形变分布、应力状态以及预测成形冲击力等信息,以便确定合适的成形工艺参数。
在汽车顶盖的制造中,CAE模拟可以帮助工程师快速产生多个设计方案,以及预测成形的效果。
通过CAE技术,我们可以为生产过程中的设置压力、液压力、液压缸工作位等参数进行优化并确定,以获得优秀的成形效果。
此外,CAE模拟技术还可以帮助工程师更好地了解材料的应变和强度特性,以较小的成本预测和评估大量成形过程的不同参数和实验情景,同时也能够评估模具的设计和工艺的合理性。
在CAE模拟研究中,需要先建立汽车顶盖的有限元模型。
模型应尽量满足实际情况,包括材料模型、模拟数据、模具尺寸、材料参数等等。
模拟参数的准确性将直接影响到最终的成形过程。
通过模型的建立,我们可以预测汽车顶盖在不同形变过程中的形变分布、应力状态以及预测成形冲击力等信息。
通过CAE模拟分析,我们可以研究不同的冲压工艺参数对于汽车顶盖冲压成形过程的影响。
例如,我们可以分析开闭式成形的效果,同时还可以分析顶盖内托槽的位置和形状对成形工艺的影响。
此外,我们还可以对材料的强度特性和应变特性等进行分析,以帮助工程师获得合理的冲压成形工艺参数,进一步优化汽车顶盖的性能。
总之,CAE模拟研究在汽车顶盖冲压成型领域中发挥了重要作用。
通过CAE模拟技术,工程师可以快速产生多个设计方案,预测成形效果,并最终确定了合适的成形工艺参数,从而提高制造精度,并使汽车顶盖的质量和性能得到更好的保障。
LB-SGS方法和MRT-LBM方法对高雷诺数顶盖驱动流的数值模拟对比

LB-SGS方法和MRT-LBM方法对高雷诺数顶盖驱动流的数值模拟对比作者:陈春媚王东杨志刚来源:《计算机辅助工程》2012年第01期摘要:针对格子Boltzmann方法(Lattice Boltzmann Method,LBM)广泛采用的LBGK模型虽然简单易行,但对高雷诺数流动模拟稳定性不佳的问题,分别采用结合亚格子模型的LBM(LBM with Sub Grid Scale(SGS),方法和多松驰时间LBM(Multiple Relaxation Time(MRT) LBM,方法对高雷诺数顶盖驱动流进行数值模拟.取对比2种方法得到的涡位置与标准解之间的误差,结果表明方法更接近标准解;保持雷诺数和顶盖速度不变并减少格点数观察收敛情况,结果表明方法更稳定关键词:顶盖驱动流;高雷诺数;格子Boltzmann方法;多松驰时间;亚格子模型中图分类号: O354 文献标志码: BComparison between LBhigh Reynolds number lid driven flowCHEN Chunmei, WANG Dong, YANG Zhigang(Shanghai Automotive Wind Tunnel Center, Tongji University, Shanghai 201804, China)Abstract:Although LBGK model is widely used in Lattice Boltzmann Methods(LBM) because of its simplicity, it shows poor stability for high Reynolds number flow simulation. The numerical simulation of high Reynolds number lid driven flow is performed by LBM with Sub GridsolutioReynolds number and lid velocity, the convergence obtained by reducing the mesh number shows thatKey words:lid driven flow; high Reynolds number; lattice Boltzmann method; multiple relaxation time; sub grid scale0 引言格子Boltzmann方法(Lattice Boltzmann Method,LBM)源于20世纪70年代提出并发展的格子气自动机方法,可被视为求解连续Boltzmann方程的离散格式之一,又称为格子Boltzmann方程(Lattice Boltzmann Equation,LBE)方法,是流体计算的新方法之一理论上,一个流体系统可用微观分子动力学、介观动力学模型或宏观连续守恒方程进行描述,同时,也存在一些用这3类方法都不能很好地进行描述的问题.在任一宏观体系中,每个分子的微观运动都遵守力学规律,因此只需计算出大量粒子的个别运动,就可以确定系统的宏观参数,这是分子动力学模拟的基本出发点;另一方面,Boltzmann方程的基本思想为,可以不确定每个分子的运动状态,而是求出每个分子处在某一状态下的概率,通过统计方法得出系统的宏观参数.[1]设速度分布函数为f,其为空间位置矢量1 物理模型顶盖驱动流是计算流体和计算传热学中的经典问题之一,常用作不可压缩流动的校核算例.在顶盖驱动流中,方腔的上边界以某个恒定速度水平右移,其他3个边界保持静止不动.其基本特征为:当流动稳定后,在方腔中央会出现一个一级大涡,而在左下角和右下角会分别出现一个二级涡,当雷诺数Re超过某个临界值后,在方腔左上角还会出现一个涡.这些涡的中心位置是Re的函数,L为方腔的高和宽,U为顶盖的移动速度.顶盖驱动流示意见图2.2 数值方法在LBM的几种模型中,LBGK近似法(又称单松驰因子法)因编程简单、实施容易而备受青睐,但其对边界条件的依赖性强,尤其在高雷诺数时计算稳定性不佳,经常难以收敛.其原因是,LBGK只有一个松驰因子,其中,若固定网格数和速度不变,随着增大黏度减小,流场中的大速度梯度会引起计算的不稳定;另一方面,虽然可以保持黏度和速度,通过增加网格数达到高雷诺数,但过密的网格不但会消耗计算资源,而且容易带来压缩性误差.[2]本文针对高雷诺数,采用结合亚格子模型的LBM(LBM with Sub Grid Scale(SGS),方法和多松驰时间LBM(Multiple Relaxation Time(MRT) LBM,方法对顶盖驱动流进行数值模拟,并比较其准确性和收敛性在顶盖驱动流中,当时流动为非定常的,流线随时间变化.由于将涡中心位置作为比较的主要特征,所以本文方法。
顶盖驱动方舱流的动力学模态分解

航空航天科学技术科技创新导报 Science and Technology Innovation Herald1二维顶盖驱动方舱流动,可以用于简化由某一壁面引起的空腔内部环流[1]。
从热力学角度分析,是典型的功热转化过程。
该文选用二维顶盖驱动方舱流动模型作为D N S 方法研究的载体。
N a v i e r -S t o k e s 方程具有抛物型和椭圆型两个特性,尽管控制方程具有混合特性,但采用M a c C o r m a c k 格式进行时间推进求解是适定的。
M acCor m ack格式是L a x-We nd rof f格式的一个变种,在时间和空间上都具有二阶精度的显式有限差分格式[2]。
由于M acC or m ack 格式是最容易理解和实现的格式,同时得到的结果在很多实际应用中都有令人满意的结果,所以该文选用M acCor m ack格式直接求解Nav ier-S toke s方程。
当雷诺数为6 000~8 000时,流动为转捩状态;当雷诺数达到10 000时,流动为局部湍流[3]。
为了分析流场振荡产生的原因,该文应用动力学模态分解(D M D)技术对原流场进行处理[4-7]。
1 数值模拟该文考虑二维剪切力驱动方舱流动,方舱为长宽均为=1 m m 的正方形区域,雷诺数(=ρV L /μ=9 000),壁面为无滑移恒定壁温边界条件,理想气体初始压力为101 k Pa。
顶盖运动方向与右侧壁面交接处被称为DUE,右侧壁面与下壁面的夹角处被称为DSE,左侧壁面与下壁面的夹角处被称为USE,顶盖运动反方向与左侧壁面交接处被称为UUE,4个区域如图1所示。
求解忽略体积力和体积热的二维守恒形式N a v i e r -S t o k e s 方程:定义为单位体积动能和内能的和,正应力与剪切应力为、、、,由Fou r ie r 定律得到热交换率。
采用M acC or m ac k显示时间推进求解离控制方程,并运用预测校正两步法保证在时间和空间上都具有两阶精度。
方腔顶盖驱动流动
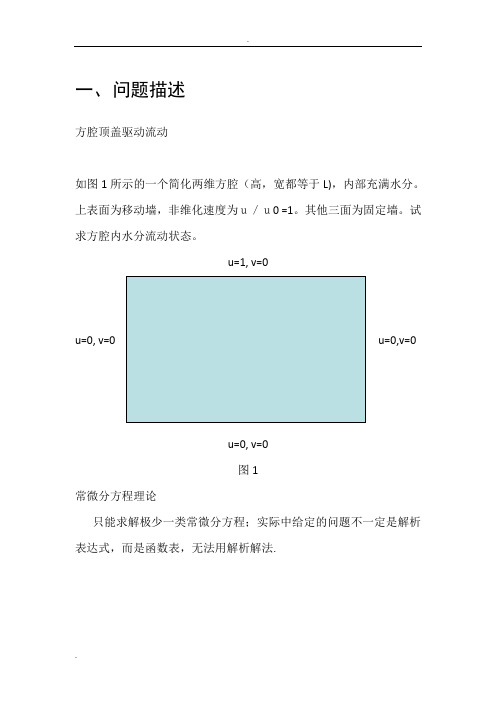
一、问题描述方腔顶盖驱动流动如图1所示的一个简化两维方腔(高,宽都等于L),内部充满水分。
上表面为移动墙,非维化速度为u/u0 =1。
其他三面为固定墙。
试求方腔内水分流动状态。
u=1, v=0u=0, v=0 u=0,v=0u=0, v=0图1常微分方程理论只能求解极少一类常微分方程;实际中给定的问题不一定是解析表达式,而是函数表,无法用解析解法.二、离散格式数值解法:求解所有的常微分方程 计算解函数 y(x) 在一系列节点a = x 0< x 1<…<x n = b 处的近似值),...,1()(n i x y y i i =≈节点间距为步长,通常采用等距节点,即取 hi = h (常数)。
步进式:根据已知的或已求出的节点上的函数值计算当前节点上的函数值,一步一步向前推进。
因此只需建立由已知的或已求出的节点上的函数值求当前节点函数值的递推公式即可。
欧拉方法1(,) 0,1,...n n n n y y h f x y n +=+=几何意义在假设 y n = y (x n ),即第 n 步计算是精确的前提下,考虑公式或方法本身带来的误差: R n = y (x n +1) y n +1 , 称为局部截断误差.截断误差: 实际上,y (x n ) ? y n , y n 也有误差,它对y n +1的误差也有影响,见下图。
但这里不考虑此误差的影响,仅考虑方法或公式本身带来的误差,因此称为方法误差或截断误差。
局部截断误差的分析:由于假设y n = y (x n ) ,即y n 准确,因此分析局部截断误差时将y (x n +1) 和 y n +1都用点x n 上的信息来表示,工具:Taylor 展开。
显式欧拉公式一阶向前差商近似一阶导数推导如下:223111232()[()()()()][ (,)] ()()h n n n n n n n n n h n R y x y y x hy x y x O h y hf x y y x O h +++'''=-=+++-+''=+1()()()n n n y x y x y x h+-'≈111()()() ()()(,)n n n n nn n n n n y x y x hy x y x y y x y y h f x y +++'≈+↑≈≈=+隐式欧拉公式xn +1点向后差商近似导数 推导如下:几何意义设已知曲线上一点 P n (x n , y n ),过该点作弦线,斜率为(x n +1 , y n +1 ) 点的方向场f (x ,y )方向,若步长h 充分小,可用弦线和垂线x =x n +1的交点近似曲线与垂线的交点。
基于数值模拟的混流式水轮机顶盖内流场分析

基于数值模拟的混流式水轮机顶盖内流场分析摘要:本文以某高水头电站为研究对象,采用数值模拟方法研究了漏水量和顶盖压力分布。
分析结果表明水轮机采用适当的止漏环间隙值、装设适当数目的减压排水管和泵板,可以起到减小漏水量、顶盖压力和转轮轴向水推力的效果。
关键词:间隙流道;漏水量;轴向水推力;数值模拟0 引言混流式水轮机的应用最为广泛,这种机组形式具有结构紧凑,运行可靠,能适应很宽的水头范围以及满载时效率高等优点。
但是国内外许多电站在投产运行后出现了不同程度的顶盖压力过高、主轴密封漏水量大和水力振动问题。
工程界对于如何降低顶盖压力和减小主轴密封漏水量,主要是采取设置减压结构的方法。
减压排水管、泵板、引水板和卸荷孔等是比较常用的结构形式。
本文以某高水头电站为研究对象,使用ANSYS FLUENT商业软件,采用RNG模型对密封间隙流道和顶盖上腔部分进行数值模拟,得到止漏环处的漏水量和主轴密封处的压力,计算出减压排水管流速,并分析了密封、减压排水管和泵板的减压效果。
1 数值计算方法本文的计算对象是密封间隙流道和顶盖上腔部分。
采用有限体积法在空间上离散控制方程,在时间离散上使用二阶全隐式格式,压力项应用二阶中心差分格式,其他项采用二阶迎风格式,使用SIMPLEC算法实现压力和速度的分离求解。
边界条件采用压力进口,压力出口条件[2]。
2 物理模型以某高水头电站为研究对象,水轮机的参数是额定水头214.5m,最大水头236.0m,转轮直径1600mm,额定转速600r/min,额定流量16.8 m3/s,额定出力33.2MW。
原始转轮密封间隙为1.35mm,装设2根Ф80mm减压排水管,泵板为径向式,均布8个。
顶盖与转轮上冠间隙流道部分的网格单元数约为825万。
新转轮密封间隙为1.0mm,装设4根Ф80mm减压排水管,泵板为斜向式,均布8个。
顶盖与转轮上冠间隙流道部分的网格单元数约为880万。
3 压力记录点为了分析密封、泵板和减压排水管的减压效果,在顶盖与转轮上冠间隙流道部分设置有上止漏环进口(P11)、密封前(P12)、密封中间(P13)、密封后(P14)、中间腔体(P15)和主轴密封处(P16)共6个测点。
方腔顶盖驱动流动

一、二、问题描述方腔顶盖驱动流动如图1所示的一个简化两维方腔(高,宽都等于L),内部充满水分。
上表面为移动墙,非维化速度为u/u0 =1。
其他三面为固定墙。
试求方腔内水分流动状态。
u=1, v=0u=0, v=0u=0,v=0u=0, v=0图1常微分方程理论只能求解极少一类常微分方程;实际中给定的问题不一定是解析表达式,而是函数表,无法用解析解法.二、离散格式数值解法:求解所有的常微分方程 计算解函数 y(x) 在一系列节点a = x 0< x 1<…<x n = b 处的近似值),...,1()(n i x y y i i =≈节点间距为步长,通常采用等距节点,即取 hi = h (常数)。
步进式:根据已知的或已求出的节点上的函数值计算当前节点上的函数值,一步一步向前推进。
因此只需建立由已知的或已求出的节点上的函数值求当前节点函数值的递推公式即可。
欧拉方法1(,) 0,1,...n n n n y y h f x y n +=+=几何意义在假设 y n = y (x n ),即第 n 步计算是精确的前提下,考虑公式或方法本身带来的误差: R n = y (x n +1)y n +1 , 称为局部截断误差.显式欧拉公式一阶向前差商近似一阶导数223111232()[()()()()][ (,)] ()()h n n n n n n n n n h n R y x y y x hy x y x O h y hf x y y x O h +++'''=-=+++-+''=+推导如下:隐式欧拉公式x n +1点向后差商近似导数 推导如下:1()()()n n n y x y x y x h+-'≈111()()() ()()(,)n n n n nn n n n n y x y x hy x y x y y x y y h f x y +++'≈+↑≈≈=+11()()()n n n y x y x y x h++-'≈11()()()()n n n n ny x y x hy x y x y ++'≈+↑≈几何意义设已知曲线上一点 P n (x n , y n ),过该点作弦线,斜率为(x n +1 , y n +1 ) 点的方向场f (x ,y )方向,若步长h 充分小,可用弦线和垂线x =x n +1的交点近似曲线与垂线的交点。
OpenFOAM顶盖驱动流详解!使用手册

OpenFOAM顶盖驱动流详解!使用手册引言这是开源场运算和操作c++库类(openfoam)的使用指南。
他详细描述了OpenFOAM的基本操作。
首先通过第二章一系列教程练习。
然后通过对更多的独立组件的更详细的描述学习openfoam。
Of 首先主要是一个c++库类,主要用于创建可执行文件,比如应用程(application)。
应用程序分成两类:求解器,都是为了解决特定的连续介质力学问题而设计的;公用工程,这些是为了执行包括数据操作等任务而设计的。
Of 包括了数量众多的solver和utilities,牵涉的问题也比较广泛。
将在第三章进行详尽的描述。
Of 的一个强项是用户可以通过必要的预备知识(包括数学,物理和编程技术)创建新的solvers 和utilities。
Of 需要前处理和后处理环境。
前处理、后处理接口就是of本身的实用程序(utilities),以此确保协调的数据传输环境。
图是of总体的结构。
第4章和第五章描述了前处理和运行of 的案例。
既包括用of提供的mesh generator划分网格也包括第三方软件生成的网格数据转换。
第六章介绍后处理。
Chapter 2指导手册在这一章中我们详细描述了安装过程,模拟和后进程处理一些OpenFOAM测试案例,以引导用户运行OpenFOAM的基本程序。
$FOAM_TUTORIALS 目录包含许多案件演示of提供的所有求解器以及许多共用程序的使用,在试图运行教程之前,用户必须首先确保他们已经正确地安装了OpenFOAM。
该教程案件描述 blockMesh预处理工具的使用,paraFoam案例设置和运行OpenFOAM求解器及使用paraFoam进行后处理。
使用OpenFOAM支持的第三方后处理软件的用户可以选择:他们要么可以按照教程使用paraFoam,或当需要后处理时参阅第六章的第三方软件使用说明。
OpenFOAM安装目录下的tutorials目录中所有的指导手册都是可复制的。
格子玻尔兹曼方法顶盖驱动流

格子玻尔兹曼方法顶盖驱动流格子玻尔兹曼方法(LBM)是一种近年来在流体力学模拟中被广泛应用的数值模拟方法。
该方法可以在复杂的几何和边界条件上精确地模拟各种流体现象。
其中的顶盖驱动流模拟,是一种受到广泛关注的研究领域。
1.什么是顶盖驱动流?顶盖驱动流是指由上端盖板施加外力所形成的流场,它是在一个密闭的正方形边界中进行模拟。
流场通常是由重力和顶部盖板的驱动力组成的。
对于使用LBM计算的顶盖驱动流,由于模型简单,计算效率高,因此已取得了广泛的应用。
2.LBM是如何模拟顶盖驱动流的?LBM的基本原理是通过在大量的离散速度上进行策略性模拟,以模拟物质运动。
与传统的流体动力学方法不同,LBM使用离散的速度和密度来描述流体的运动,因此它可以非常方便的用于复杂的几何和边界条件下的流体模拟。
在顶盖驱动流模拟中,LBM将二维正方形边界分为许多离散化的小单元格,并在每个单元格上施加离散速度和压力值来模拟流体行为。
3.顶盖驱动流模拟的应用领域是什么?顶盖驱动流模拟在许多领域具有广泛的应用,包括地质、生物学、工程学和环境科学等领域。
在地质学中,它被用于模拟岩石的岩石圈运动并对流体流动的地质效应进行分析。
在工程学中,它被用于模拟汽车空气动力学和水力学作用以及结构物的振动和熱传导等现象。
4.顶盖驱动流模拟存在的挑战是什么?尽管顶盖驱动流模拟为模拟流体行为提供了强有力的工具,但仍然存在一些挑战。
例如,该方法需要高度离散化的速度空间和网格结构,这可能会导致计算效率低下和计算成本高昂。
此外,顶盖驱动流模拟还需要对物理设置和计算参数进行大量的调整和测试,才能使模拟结果更加准确和可靠。
总之,格子玻尔兹曼方法顶盖驱动流是一种新兴的数值模拟方法,在流体力学和其他领域的应用越来越广泛。
将来,随着计算机硬件和软件的不断发展,顶盖驱动流模拟将进一步提高计算精度和计算效率,为工程学、生物学和环境科学等领域能提供更准确的解决方案。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《数值传热学》作业:
顶
盖
驱
动
流
数
值
模
拟
分
析
西安科技大学能源学院安全技术及工程
申敬杰201112612
顶盖驱动流数值模拟分析
顶盖驱动流作为经典的数值计算模型,常常用来考核源程序和计算思想的正确性。
这种流动边界条件简单,而且不涉及模型的影响,便于直接评价差分格式的性能。
1.引言
数值传热学,又称计算传热学,是指对描写流动与传热问题的控制方程采用数值方法,通过计算机求解的一门传热学与数值方法相结合的交叉学科。
数值传热学的基本思想是把原来在空间与时间坐标中连续的物理量的场(如速度场,温度场,浓度场等),用一系列有限个离散点上的值的集合来代替,通过一定的原则建立起这些离散点变量值之间关系的代数方程(称为离散方程)。
求解所建立起来的代数方程已获得求解变量的近似值。
由于实验方法或分析方法在处理复杂的流动与换热问题时,受到较大的限制,例如问题的复杂性,即无法做分析解,也因为费用的昂贵而无力进行实验测定,而数值计算的方法正具有成本较低和能模拟复杂或较理想的过程等优点,数值传热学得到了飞速的发展。
特别是近年来,计算机硬件工业的发展更为数值传热学提供了坚实的物质基础,使数值模拟对流动与传热过程的研究发挥了重要的作用。
目前,比较著名的数值模拟分析应用软件有FLUENT、CFX、STAR-CD、和PHOENICS等,而FLUENT是国内外比较流行的商用CFD软件包,该软件以其市场占有率高、计算准确、界面友好、使用简单、应用领域广、物理模型多而获得较高的市场占有率和用户的肯定。
2.物理模型
在一个正方形的二维空腔中充满等密度的空气,方腔每边长为0.12m,取雷
诺数为Re=12000,由Re=vd/υ,方腔的当量直径d ,计算知d=0.12m,又υ=15.7 ×10 ﹣6m2/s,则顶盖驱动流的速度v=1.57m/s,即其顶板以1.57m/s的
速度向右移动,同时带动方腔内流体的流动,流场内的流体为紊流。
计算区域示意图如图1所示。
v=1.57m/s
L=0.12m
图1 计算区域示意图。
