2016年清华大学领军计划测试物理学科
2016年清华大学领军计划试题及解析

2. 如图 1 所示,在光滑地面上,物块与弹簧相连做简谐运动,小车向右做匀速直线运 动,则对于弹簧和物块组成的系统,当以地面为参考系时,动量 不守恒 ,机械能 守恒 ;当以小车为参考系时,动量 不守恒 ,机械能 不守恒 .(填“守恒”或者 “不守恒”)
解:墙壁对弹簧有作用力,故动量不守恒。以地面为参考系,该力的作用点没有 位移,不做功,故机械能守恒。以小车为参考系时,该力的作用点有位移,所做 的功不为零,故机械能不守恒
4. 如图 3 所示,空间存在水平向右的匀强电场 E ,现有一质量为 m、带电量为 q 的小 √ 3mg ,求小球落地点距离抛出点的 球以初速度 v0 从地面斜向上抛出,已知 E = q 最远距离。
第 2 页 (共 11 页)
解:小球的运动可以分解为水平方向的匀加速直线运动和竖直方向的匀变速直线 运动。设发射角为 θ,则落地时小球的运动时间为 t= 此过程中小球在水平方向的位移为 √ 2 2 2 sin θ cos θ 2 3v0 sin θ 1 qE 2 2v0 x = v0 cos θ · t + t = + 2m 3g ] g √ 2[ ( ) 3v0 π = 2 sin 2θ − +1 3g 6 π 当 θ = 时,x 取最大值 3 √ 2 3v0 g 2v0 sin θ g
5. 现有一轻质绳拉动小球在水平面内做匀速圆周运动,如图 4 所示。小球质量为 m, 速率为 v ,重力加速度为 g ,轻绳与竖直方向夹角为 θ。求在小球运动半周的过程中 拉力的冲量。
解:小球的受力如图 5 所示。根据牛顿第二定律,有 mg tan θ = ma = m 2π v T
第 3 页 (共 11 页)
解:当系统稳定时,设左杆的速度为 v1 ,右杆的速度为 v2 ,在此过程中金属杆 ¯。根据动量定理,有 的平均电流为 I ¯ ∆t = mv1 − mv0 −2B Il ¯ ∆t = mv2 B Il 联立式 (1) 和式 (2),得 v1 + 2v2 = 0 系统稳定时,回路中无电流,则有 2Blv1 − Blv2 = 0 即 2v1 = v2 联立式 (3) 和 (5),得 1 2 v1 = v0 , v2 = v0 5 5 产生的热量为 1 2 − Q = mv0 2 ( 1 2 1 2 mv + mv 2 1 2 2 ) 2 2 = mv0 5 (5) (4) (3) (1) (2)
清华大学2016年“领军计划”物理试题

清华大学2016年“领军计划”试题1.友谊的小船说翻就翻,假如你不会游泳,就会随着小船一起沉入水底.从理论上来说,你和小船沉入水底后的水面相比于原来( )A.一定上升B.一定下降C.一定相等D.条件不足,无法判断2.在光滑地面上,物块与弹簧相连作简谐运动,小车向右作匀速直线运动,则对于弹簧和物块组成的系统(填守恒或者不守恒),当以地面为参考系时,动量,机械能;当以小车为参考系时,动量,机械能.3.如图所示,光滑导轨上垂直放置两根质量为m、且有电阻的金属棒,导轨宽处与窄轨间距比为2 :1 ,平面内有垂直纸面向内的磁场.现给左边的杆一个初速度v,在系统稳定时,左杆仍在宽轨上右杆仍在窄轨上运动.则这个过程产生热量Q.4.空间内有一水平向右的电场E,现有一带电量为q的小球以初速度为v向右上抛出,已知33mgEq,求小球落地点距抛出点的最远距离.5. 现有一轻质绳拉动小球在水平面内做匀速圆周运动,如图所示,小球质量为m ,速度为v ,重力加速度为g ,求小球在运动半周时,绳对小球施加的冲量.6. 如图所示,有a 、b 两个物体,a 物体沿长L 倾角为θ动摩擦因数=0.5μ的斜面滑下后,在长为L 的光滑水平面BC 上运动;b 从C 点上方高为4.5L 处下落.二者同时释放,在C 处相遇,则sin θ= .7. 在水平面内,金属棒 MN 一角速度ω绕O 点顺时针旋转,空间内有竖直向下的磁场,如图所示.已知||||MO NO >,则下列说法正确的是( ) A . M 点电势高于 N 点B . M 点电势低于 N 点C .若增大ω,则 M N 点电势差增大D .若增大 B ,则 M N 点电势差增大8. 在如图所示电路中,小灯泡规格为634V W R =Ω“,”,,电源内阻为1Ω,电压表、电流表均为理想电表,闭合开关,调节滑动变阻器阻值,使电压表实数为0,此时灯泡正常发光,电表的实数为1A ,则电源电动势E = ,输出功率P = ,2R = .9. 弹性绳原长为()22LR L R <<,劲度系数为k ,上端拴在半径为R 的光滑圆轨的顶端,下端系一重量为G 的小球,小球套在圆轨上.平衡时,弹性绳与竖直方向夹角为θ.用 L 、R 、k 、G 表示此时弹性绳的弹力.10.在一质量均匀分布的星球(近似为球面)的北极和南极打一条竖直贯通的通道,一小球从北极由静止释放,不与通道发生碰撞,则小球做 运动.11.潜水员为测量一湖深度,测得湖面上527 1.010t C P Pa ==⨯,,并将一盛有空气的试管从湖面带入潜入湖底,整个过程管口始终向下.潜至湖底后水充满试管的一半,7t C =,则湖深约( )A. 5mB. 10mC. 15mD. 20m12.一用钉鞘锁定的导热活塞将导热气缸分成体积相等的左右两室,:5:3P P =右左,拔出钉鞘后活塞移动至稳定状态,外界温度恒定,则( ) A. 稳定后左右两室体积比为5: 3 B. 左室气体对右室气体做功 C. 左室气体吸热 D. 右室气体吸热13.有一左端封闭、右端开口的均匀U 形管,左管内有一段水银分割出两端长度相等的气柱,如图所示,现向右管缓慢注入水银,设平衡后上段气体为1l ,下端气体长2l ,则1l 与2l 的关系为( ) A. 12l l > B. 12l l = C. 12l l <D. 无法确定,视注入水银的量14.在高为h 的立柱上放一质量为M 的球,质量为m 的子弹以一定初速度水平射向球,从球中穿出后二者落至地面,球与子弹的落地点距立柱水平距离为S 和s ,重力加速度为g ,则子弹的初速度为 .15.从地面以初速度0v 竖直向上抛出一小球,与此同时,在该小球上抛能到达的最高处有另一个小球以初速度0v 竖直向下抛出.忽略空气阻力,则两球相遇时速度之比为 . 16.质量为()1212m m m m >、的物体具有相同的初动能,现给以其与速度方向相反的阻力12f f 、使其减速,经过时间t 后两物体同时停止,运动距离为12S S 、,则1f 2f ,1S 2S .(填>、<、=)17.如图所示,水平绳与一弹簧作用于小球使其处于静止,若剪断细绳,则在剪断的一瞬间( )A. 小球竖直方向的加速度为0B. 小球水平方向的加速度为0C. 弹簧弹力为cos mg θD. 弹簧弹力为cos mgθ18.光滑平行U 形导轨相距为L ,倾角为θ,一电阻为R 、长为L 的导体棒在距导轨底端L 处.空间内存在竖直方向向上的变化磁场,满足()00B B kt k =+>,现在导体棒上加一沿斜面向上的力F ,使导体棒保持静止则F = .19.导体球壳内有一点P ,外有一正点电荷q +位于Q 处,现将该电荷的电荷量加倍,则P 处电势 (升高/降低/不变);P 点场强 (升高/降低/不变).20.下列物理学家及其成果,已经获得诺贝尔奖的有( ) A. 伦琴发现了X 射线 B. 爱因斯坦发现了相对论C. 普朗克提出了量子论D. (激光干涉引力波观测站)LIGO 探测到了引力波21.实物在像的上方叫上现折射,反之叫下现折射,则天气炎热时高速公路上看到的“水纹”一样的东西属于 ;“海市蜃楼”属于 .22.波长均为λ的两束平行光如图所示打在光屏上,发生干涉现象,问干涉条纹的间距( ) A.sin sin λαβ+ B.cos cos λαβ+C.sin sin λαβ- D.cos cos λαβ-23.引力波时时空的涟漪.北京时间2016年2月11日,LIGO 探测到了引力波,是通过两座3000公里的天文台监测到的,引力波是来自宇宙深处距地球数亿光年的两个大黑洞猛烈撞击并融合所产生的引力波,双黑洞的质量分别是太阳的52倍和14倍,合并后的黑洞质量是太阳的62倍,下列正确的有( ) A. 引力波在宇宙中传递的是能量的传递B. 两座天文台探测到的同样的信号相隔不会超过10msC. 引力波在真空中以光速传播D. 双黑洞合并过程中质量守恒24.两位物理学家在剑桥大学做了这样一个实验,在一个高为22.5米塔的顶端放置一个Co 放射源,在塔顶测的伽马射线频率为ν,在低端测的射线频率与之相差ν∆,已知3410632.6-⨯=h ,求νν∆的数量级( ) A. 810-B. 1010-C. 1510-D. 1910-25.已知空气分子的平均动能为kT ,则在常温下,质量为kg m 23107.4-⨯=的空气德布罗意波波长的数量级为 .26.质量为m 小球从高为h 的地方释放,如果在光滑轨道上A 点飞出,求h 的值;如果是从轨道的B (圆弧的最高点)点飞出,求h 的值(图中两虚线夹角为60,圆弧的曲率半径为R )清华大学2016年“领军计划”试题解析1. 【答案】B【考点】受力分析,阿基米原理.【解析】根据平衡时的排浮gV F ρ=,翻船前浮力与重力抵消,翻船后沉入水底,浮力小于重力,吃水量减少,水面下降.2. 【答案】不守恒;守恒;不守恒;不守恒 【考点】参考系;机械能守恒;动量守恒【解析】以地面为参考系,墙给系统有力,动量不守恒;而机械能守恒.以小车为参考系,动量依然不守恒,而墙壁的力做功,机械能不守恒. 3. 【答案】2052mv 【考点】动量定理;电磁感应;功能关系【解析】设某一时刻,左杆速度1v ,右杆速度2v ,可判断两者都与0v 同向,回路电流i 对于左杆()121t Bli v m ∆⋅-=∆⋅,(由于方向问题,负号不能忘)对于右杆()22t Bli v m ∆⋅=∆⋅,()()221⨯+得0221=∆+∆v v ,求和后()02201=+-v v v ,稳态条件,回路无电流0221=-Blv Blv , 即212v v =,解得020152,51v v v v ==, 发热2022212052212121mv mv mv mv Q =--=,4. 【答案】gv 203【考点】曲线运动;运动的分解【解析】设发射角为θ,落地点0=y ,即2002sin 1cos 02v v t gt t gθθ⋅-=⇒=, 水平方向()⎪⎭⎫ ⎝⎛-+=+=+⋅=θθθθθθ2cos 1312sin 3sin 2cos sin 2321cos 202202020g v g v g v t g t v x又3262sin 322cos 312sin ≤⎪⎭⎫ ⎝⎛-=-πθθθ,所以最远射程为gv 23.5. 【答案】θπ22cot 4+mv 【考点】动量定理【解析】水平方向,运动半周后,速度方向与初速度反向,动量改变mv 2;竖直方向,绳子与竖直线夹角θ满足,Tmv mg πθ2tan =, 故竖直方向冲量θπcot 2v m Tmg =⋅; 所以拉力的总冲量θπ22cot 4+mv 6. 【答案】54 【考点】运动学公式;受力分析【解析】在斜面上的加速度()g a θμθcos sin -=, a 物体运动的时间为23222a L Lt a aaL ==,b 物体运动的时间为 9b L t g=, 又有a b t t =, 可解得54sin =θ. 7. 【答案】ACD【考点】电磁感应,旋转导体棒切割磁感线;电势差 【解析】M 、N 两点电势差为()221||||02MN M N M O O NMO NO U U U B MO NO ϕϕϕϕϕϕω=-=+--=-=->A 选项正确,当ω或B 增大时,MN U 增大,所以C 、D 正确. 8. 【答案】Ω1289;;W V【考点】桥式电路;电路的基本计算【解析】这是一个电桥.流过灯泡的电流为A 5.0,3R 上电压为V 2,电源内阻上分压为V 1,故电源总电压为V 9;由R I IU P 2-=,输出功率为W 8;两个支路电流都是A 5.0,2R 上电压V 6,所以电阻为Ω12.9. 【答案】GkL kR G-【考点】静态平衡;【解析】在小球处切向受力平衡θθsin 2sin T G = 又()L R k T -=θcos 2 解得()k G R L/2cos -=θ则2cos GT G kL kR Gθ==-注意这时对应1cos ≤θ的情况,即LR Gk -≥22若LR Gk -<22,则()L R k T -==20,θ10.【答案】简谐振动【考点】简谐运动;万有引力【解析】若星体质量为M ,半径为R ,当小球运动到距球心为r 时,以r 为半径作一同心球面,球外部分看作均匀球壳,对小球无引力作用,球面内包围着的部分质量才对小球有引力作用r R GMm r mR r GM F 323=⎪⎭⎫ ⎝⎛=,即引力是线性回复力,所以小球做简谐运动. 11.【答案】B【考点】热力学平衡;理想气体状态方程【解析】试管在湖面时,管内气体的压强为1p p =,体积为V ,温度为1300T K =, 试管在湖底时,管内气体的压强为2p p gh ρ=+,体积为2V,温度为2280T K =, 根据理想气体状态方程,有21122Vp p VT T =,解得8.7h m ≈. 12.【答案】ABC【考点】理想气体状态方程;热力学第一定律【解析】由PV 为常数,以及两边的初始值得比例,A 正确;左边气体膨胀,对右室气体做功,B 正确;两室气体内能不变,吸热等于对外做功,左室气体吸热,右室放热,C 正确,D 错误. 13.【答案】C【考点】热力学平衡;理想气体压强【解析】水银性质不变,两段气体的压强差不会变,等于中间那段水银的附加压强.现在由于两部分气体的压强都增加,故上部分气体压强增长率高于下部;又由于Pl 是常量,则气柱长度的减少比例大于下部.14.【答案】hg S m M s v 20⎪⎭⎫ ⎝⎛+= 【考点】平抛运动;动量守恒 【解析】根据平抛的规律,有212h gt =,得落地时间g h t 2=, 水平方向s vt =,得则水平速度h g S t S V 2==, 子弹hg s v 2=, 由水平方向动量守恒,MV mv mv +=0,得hg S m M s v 20⎪⎭⎫ ⎝⎛+=。
2016年清华大学领军计划机考试试题分析

2016年清华大学领军计划机考试试题分析2016年清华大学领军计划/自主招生笔试举行,今年仍然采用了去年的机考模式,在开考前开通了机考模拟系统,让学生提前熟悉考试形式及操作方法。
2016年通过清华大学自主招生、领军计划及自强计划初审的6000余名考生在全国36个考点参加初试。
物理探究科目中涉及了人类首次探测到引力波。
清华招办主任刘震表示,该题通过介绍相关实验背景和结果,考查学生提取信息、加工信息并利用关键信息进行推理判断的能力。
在考试中其中数学40道题目、语文30道题目、物理35道题目。
阅读与表达:《红楼梦》二次入选、文言文考《左传》阅读与表达主要从语文基础知识、阅读角度进行考试,阅读与表达考查了《红楼梦》文本解读以及宋词的格律炼字等。
这也是清华连续第二年将《红楼梦》中的内容放入考题当中。
在选择题目中试题涉及到:字音、字形、词语、句子衔接、错别字、文言文等内容外,还考查了汉字书写的笔顺问题、书体知识、传统文化知识等。
文言文则是考查的《左传》的内容。
语文还有一道创新题,大意是让考生翻译民族语言。
物理探究考察内容:引力波、小船说翻就翻、台球等物理知识实际应用2016年清华大学自主招生的物理与探究对物理学科的基础知识和物理学科的应用进行了科学的地考察,既涉及到物理学科的核心知识,也考察到了物理前沿科学的知识,注重物理学科的社会实际应用:例如大家最熟悉的引力波材料分析、相对论、友谊的小船等,物理学科35道题目中其中有1/3的题目大部分学生是可以做的,剩下的部分相对灵活,涉及面广,试题与大学物理的衔接和部分竞赛内容相似,但是与竞赛不同的是自主招生试题考查学生的知识的应用性和灵活处理,部分题目可以根据知识和推理等得出答案。
例如高空粒子衰变周期考察,像友谊的小船这个题目考察了浮力问题不需要太深的物理知识就可以选择,还有物理学科基础常识向光学仪器分辨率问题、还有科学普及科学史类关于世界诺贝尔奖关于物理学科的内容及人物。
清华北大真题答案

2015年清华大学领军计划测试 物理答案1 4α粒子散射是一个有心力场的运动,与天体运动不同的是其受到的斥力的作用。
由轨迹我们可知在距离中心原子最近的地方散射粒子的速度不为零,即其角动量不为零。
由角动量守恒知中心粒子只能处于3,4,5三个区域中。
又由对称性可知,中心粒子必处于4区域中。
2 A当速度达到稳定时,必然存在受力平衡。
同时功能平衡也是受力平衡的必然要求。
因此两种方案都是正确的。
3 dTdQC =dW dU dQ += kVdV pdV dW ==由理想气体状态方程RT pV = 取微分RdT kVdV =2 即2RC C v += 4设导轨宽度为L ,t 时刻速度v ,则BLv =ε,RBLvR I ==ε金属棒受力大小为RvL B BIL F 22-=-=负号表示F 方向与v 方向相反由牛顿第二定律,可得dtdv mma F == 即R v L B dt dv m 22-=,m RvL B dt dv 22-=积分⎰⎰-=10022001v v t mRdt L B v dv ⎰⎰-=100002202v v t mRdt L B v dv (其中s t 11=,2t 即为要求的时间) 即101101110101220n n v nv m R t L B v===-10311000110001110102220n n n v nv m R t L B v====-所以s t t 3312== 5平抛运动中H gt =221,斜抛中达到最大高度所用时间为2t ,故有h t g =⎪⎭⎫⎝⎛2221.则4H h = 6(1)(方法一:光程)设某种色光的折射率为n ,要使光线能够成功射出,应当考虑光线不在介质的界面上发生全反射。
由折射定律有n n 2360sin sin =︒⋅=α,⎪⎪⎭⎫ ⎝⎛<332n , 在介质当中光走过的距离αcos Dl =, 光程αδcos nDl n =⋅=, 则光行走的时间ααδ2sin 1cos 1-⋅=⋅==n c D c nD ct , 带入数据有,43112-⋅=n cDt ⎪⎪⎭⎫ ⎝⎛<332n ,这是一个关于n 的单增的函数,故43112minmin-⋅=n cD t (方法二)光在介质中的速度ncv =, 则光在介质中运动的时间431112-⋅==n c D n c t ,⎪⎪⎭⎫ ⎝⎛<332n ,下同方法一。
2016年清华大学物理金秋营考试试题(WORD版无答案)

2016年清华大学全国优秀中学生物理体验营笔试题题一水平地面上有一门固定大炮,可向任意方向发射初速度大小为v的炮弹,求炮弹可能打到的区域的边界(可以建立坐标系后用函数表达)。
已知重力加速度g。
题二水平地面上放有一高为h、半顶角为α、密度为ρ的均匀刚性圆锥体。
其顶点静止不动(无外力限制),整体做定点转动,锥体与地面间无相对滑动。
底面圆心绕过圆锥顶点的竖直轴(假想)做匀速圆周运动的速度大小为v。
1.求此锥体的角速度;2.求此锥体的角动量;3.求支持力的力矩。
题三无限长一维弹簧链,所有弹簧均为原长时相邻质点间距为a,弹簧劲度系数均为k,质点质量均为m,所有质点的振动频率相同,激发纵波的波长记为λ。
?时该纵波为介质中的普通纵波并求出波速与波长的关系;1.证明当a2.求该纵波的最小波长。
题四竖直平面内有一半径为r=1 cm、带电量为Q=10-8 C的无限长导体圆柱放置在盐水上方,球心到盐水表面的高度为h=2 cm。
会发现盐水会隆起一小坨,求导体圆柱正下方水面隆起的高度。
设盐水密度近似为纯水密度。
题五平面直角坐标架下,有一圆心位于坐标原点、半径为r的固定绝缘大圆环。
圆心处有一固定的电偶极子,电偶极矩的方向沿y轴正方向、大小为p。
大圆环上穿有一个带电量为Q的小环,在坐标(r,0)处由静止释放小环,求之后大圆环对小环的弹力与小环位置(用坐标原点到小环的连线矢量与x轴正方向的夹角θ表达)的关系。
题六真空中有两个非常大的平行平面电极相距d,电势分别为0和+U0。
低电势的电极上有一薄层电子源,在外电场作用下,电子源中的电子从中逸出,以垂直于极板方向的几乎为0的初速度持续地朝两电极之间发射电子。
若忽略电子之间的库仑排斥力,则电子应在两极板间匀加速直线运动,直至撞上另一极板而进入极板内部。
极板、电源和导线形成一个闭合直流电路,两极板与之间的真空可一同视为一个非欧姆元件:真空管。
当真空管中的电流随着外电场的增强而逐渐增加时,两电极间电子自身产生的电场不可忽略。
2016年清华大学综合评价名单(山东)
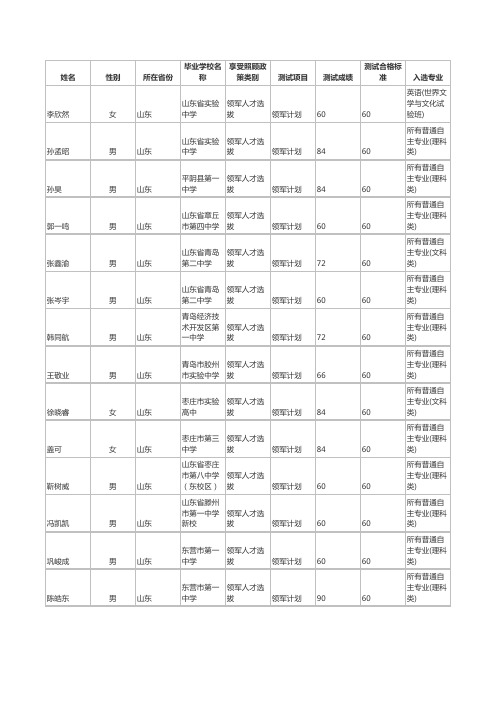
山东
学
拔
领军计划 90
60
类)
所有普通自
山东省五莲 领军人才选
主专业(理科
男
山东
县第一中学 拔
领军计划 66
60
类)
所有普通自
德州市第一 领军人才选
主专业(理科
男
山东
中学
拔
领军计划 60
60
类)
所有普通自
齐河县第一 领军人才选
主专业(理科
男
山东
中学
拔
领军计划 72
60
类)
所有普通自
邹平县第一 领军人才选
领军计划 60
60
类)
所有普通自
山东省日照 领军人才选
主专业(文科
女
山东
第一中学 拔
领军计划 90
60
类)
所有普通自
山东省日照 领军人才选
主专业(理科
男
山东
第一中学 拔
领军计划 60
60
类)
孙栩瑭 孙宇航 胡煜东 刘礼剑 释昊天 张翔宇 史卓
山东省日照
所有普通自
实验高级中 领军人才选
主专业(理科
男
第一中学 拔
领军计划 72
60
类)
所有普通自
山东省烟台 领军人才选
主专业(理科
男
山东
第一中学 拔
领军计划 60
60
类)
所有普通自
山东省牟平 领军人才选
主专业(文科
男
山东
第一中学 拔
领军计划 60
60
类)
所有普通自
山东省牟平 领军人才选
主专业(理科
2016清华物理金秋营试题

2016年清华大学全国优秀中学生物理体验营笔试题考试时间180分钟,满分160分题一.(15分)水平地面上有一门固定大炮,可向任意方向发射初速度大小为v 的炮弹,求炮弹可能打到的区域的边界(可以建立坐标系后用函数表达)。
已知重力加速度g 。
题二.(30分)水平地面上放有一高为h 、半顶角为α、密度为ρ的均匀刚性圆锥体。
其顶点静止不动(无外力限制),整体做定点转动,锥体与地面间无相对滑动。
底面圆心绕过圆锥顶点的竖直轴(假想)做匀速圆周运动的速度大小为v 。
1.求此锥体的角速度;2.求此锥体的角动量;3.求支持力的力矩;题三.(20分)无限长一维弹簧链,所有弹簧均为原长时相邻质点间距为a ,弹簧劲度系数均为k ,质点质量均为m ,所有质点的振动频率相同,激发纵波的波长记为λ。
1.证明当a >>λ时该纵波为介质中的普通纵波并求出波速与波长的关系;2.求该纵波的最小波长。
竖直平面内有一半径为cm r 1=、带电量为C Q 810-=的无限长导体圆柱放置在盐水上方,球心到盐水表面的高度为cm h 2=。
会发现盐水会隆起一小坨,求导体圆柱正下方水面隆起的高度。
设盐水密度近似为纯水密度。
题五.(25分)平面直角坐标架下,有一圆心位于坐标原点、半径为r 的固定绝缘大圆环。
圆心处有一固定的电偶极子,电偶极矩的方向沿y 轴正方向、大小为p 。
大圆环上穿有一个带电量为Q 的小环,在坐标()0,r 处由静止释放小环,求之后大圆环对小环的弹力与小环位置(用坐标原点到小环的连线矢量与x 轴正方向的夹角θ表达)的关系。
题六.(25分)如图所示迈克尔逊干涉仪,A 为点光源,B 为望远镜,实验光的波长为λ,真空中的光速为c 。
现使整个干涉装置绕过第一个半反半透镜中点的垂直纸面的轴以角速度ω匀速旋转。
记干涉条纹移动数为N ∆,求证c A N λω4=∆,其中A 为光路围成的面积。
清华大学2016年自主招生与领军计划数学试题

清华大学2016年自招、领军试题选择题:本卷共40小题,共100分。
在每小题给出的四个选项中,有一个或多个选项是正确的。
(1)若函数()y f x =具有下列两个性质:①在区间,63ππ⎡⎤-⎢⎥⎣⎦上单调递增;②其图像关于3x π=对称.则()f x =( )(A )5sin 26x π⎛⎫-⎪⎝⎭ (B )cos 23x π⎛⎫+ ⎪⎝⎭ (C )sin 26x π⎛⎫- ⎪⎝⎭ (D )2cos 23x π⎛⎫-⎪⎝⎭ 【答案】CD解析:由②可知13f π⎛⎫=± ⎪⎝⎭,再结合①可知13f π⎛⎫= ⎪⎝⎭,由①还可知22T π≥,即T π≥,而选项中所有函数的周期都是π,可知此题最好的方法是代入法. 因此只需要检验四个选项中哪个符合这个条件即可. (A )132f π⎛⎫= ⎪⎝⎭;(B )13f π⎛⎫=- ⎪⎝⎭;(C )13f π⎛⎫= ⎪⎝⎭;(D )13f π⎛⎫= ⎪⎝⎭. 因此答案为CD.(2)曲线21y x =-与ln y x =( )ACD(A )在点(1,0)处相交 (B )在点(1,0)处相切 (C )存在相互平行的切线 (D )有两个交点 【答案】ACD解析:令2()1f x x =-,()ln g x x =,2()ln 1h x x x =--,()2f x x '=,1()g x x '=,1()2h x x x'=-. 其中()g x 和()h x 的定义域都是(0,)+∞.对于(A )(B ),(1)(1)0f g ==,(1)2f '=,(1)1g '=,可知两条曲线在点(1,0)处相交. (A )正确.令()()f x g x ''=,可得2x =;122f ⎛=- ⎝⎭,1ln ln 2g ==->-=-⎝⎭,所以f g ≠⎝⎭⎝⎭,因此两条曲线在2x =处存在相互平行的切线.令()0h x '=,可得x =()h x '和()h x 的变化如下表:由上述分析可知()h x 在0,2⎛ ⎝⎭上单调递减,且02h ⎛< ⎝⎭,2110h e e ⎛⎫=> ⎪⎝⎭,并且12e <,可知()h x 在⎛ ⎝⎭上只有有一个零点,因此两条曲线在⎛ ⎝⎭上只有一个交点.而()h x 在2⎛⎫+∞ ⎪ ⎪⎝⎭上单调递增,并且(1)0h =,()h x 在2⎛⎫+∞ ⎪ ⎪⎝⎭上只有一个零点1,可知两条曲线在2⎛⎫+∞ ⎪ ⎪⎝⎭上只有一个交点.因此答案为ACD.(3)“ABC 为锐角三角形”是“sin sin sin cos cos cos A B C A B C ++>++”的( )(A )充分不要条件 (B )必要不充分条件 (C )充要条件 (D )既不充分也不必要条件 【答案】A解析:若ABC ∆为锐角三角形,则222A B A C B C πππ⎧+>⎪⎪⎪+>⎨⎪⎪+>⎪⎩, 且0,,2A B C π<<,可得022022022A B C A B C ππππππ⎧>>->⎪⎪⎪>>->⎨⎪⎪>>->⎪⎩,又()sin f x x =在0,2π⎛⎫ ⎪⎝⎭上单调递增,所以sin cos sin cos sin cos A B C A B C >⎧⎪>⎨⎪>⎩, 因此可得sin sin sin cos cos cos A B C A B C ++>++,所以“ABC 为锐角三角形”是“sin sin sin cos cos cos A B C A B C ++>++”的充分条件.考虑直角ABC ∆,其中,,236A B C πππ===,则1sin sin sin 122A B C ++=++,1cos cos cos 2A B C ++=+,则sin sin sin cos cos cos A B C A B C ++>++,而显然ABC ∆是不是锐角三角形,因此“ABC ∆为锐角三角形”不是“sin sin sin cos cos cos A B C A B C ++>++”的必要条件.(4)设函数()f x 在区间(1,1)-内有定义,则( )(A )当导数(0)f '存在时,曲线()y f x =在点(0,(0))f 处存在切线 (B )当曲线()y f x =在点(0,(0))f 处存在切线时,导数(0)f '存在 (C )当导数(0)f '存在时,函数2()f x 在0x =时的导数等于零 (D )当函数2()f x 在0x =时的导数等于零时,导数(0)f '存在 【答案】ABC解析:(A )显然正确;(B )函数13()f x x =,在在点(0,(0))f 处的切线为y 轴,但是231()3f x x -'=-, (0)f '不存在;(C )()22()2()f x xf x ''=,因为(0)f '存在,所以()20()20(0)0x f x f =''=⨯⨯=,所以(C)正确;(D )令 ()f x x =,则222()f x x x ==,所以函数2()f x 在0x =时的导数等于零,但是()f x x =在0x =处的导数(0)f '不存在,因此(D )错误. (5)设22cos sin 33z i ππ=+,则2322z z z z +=++( ) (A)122-+ (B)122i -(C)122- (D)122i -+【答案】C解析:易得31z =,2z z =,210z z ++=,23211111212222z z z z i z z +=+=+=--=-++,因此答案选C.(6)甲、乙、丙、丁四人进行网球比赛,首先是甲与乙比,丙与丁比,这两场比赛的胜者再争夺冠军. 他们之间相互获胜的概率如下:则甲获得冠军的概率为( )(A )0.165 (B )0.245(C )0.275 (D )0.315 【答案】A解析:甲与乙比甲获胜为事件A ,则()0.3P A =, 丙与丁比,丙获胜为事件B ,则()0.5,P B =()0.5,P B = 甲与丙比甲获胜为事件C ,则()0.3,P C = 甲与丁比甲获胜为事件D ,则()0.8,P D = 甲获胜的概率为()()()P ABC ABD P ABC P ABD +=+ ()()()()()()P A P B P C P A P B P D =+0.30.50.30.30.50.80.165=⨯⨯+⨯⨯=. 因此答案选A.(7)设函数2()()x f x x a e =+在R 上存在最小值,则函数2()g x x x a =++的零点个数为( ) (A )0 (B )1 (C )2 (D )无法确定 【答案】C解析:2()(2)x f x x x a e '=++①当1a ≥时,220x x a ++≥在R 上恒成立,所以()0f x '≥在R 上恒成立,所以函数()f x 在R 上单调递增,因此()f x 在R 上无最小值;②当1a <时,令()0f x '=,则11x =,21x =,且21x x <,()f x '和()f x 的变化情况如下表:x →-∞时,()0f x →,因为()f x 在2(,)x -∞上单调递增,在21(,)x x 上单调递减,在1(,)x +∞上单调递增,所以若()f x 有最小值,只需要1()0f x ≤.11()(2)0x f x e =-≤2⇔≤11a ⇔≤-0a ⇔≤. 20x x a ++=的判别式为141a ∆=-≥,所以()g x 有两个零点. 因此选C.(8)设随机变量ξ的分布列如下:则 ( )(A )当{}n a 为等差数列时,5615a a += (B )数列{}n a 的通项公式可能为1110(1)n a n n =+(C )当数列{}n a 满足12n n a =(1,2,,9)n =时,10912a =(D )当数列{}n a 满足2()k P k k a ξ≤=(1,2,,10)k =时,1110(1)n a n n =+【答案】ABCD解析:由题目可知12101a a a +++=;(A )若{}n a 为等差数列,1210565()1a a a a a +++=+=,所以5615a a +=; (B )11111110(1)101n a n n n n ⎛⎫==- ⎪++⎝⎭,则0n a ≥,且121011111111111111022310111011a a a ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫+++=-+-++-=-= ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦,符合分布列的定义,因此B 正确; (C )129991111222a a a +++=++=-,又由分布列的定义可知12101a a a +++=,所以10912a =,C 正确; (D )2()k P k k a ξ≤=,则10(10)1001P a ξ≤==,所以10111100101011a ==⨯⨯,满足题意, 当2k ≥时,221()(1)(1)k k k a P k P k k a k a ξξ-=≤-≤-=--,则221(1)(1)(1)(1)k k k k a k a k k a --=-=-+,因为2k ≥,所以1(1)(1)k k k a k a --=+,即111k k k a a k -+=-. 91011111119910010910a a ==⋅=⨯⨯,满足题意. 当29n ≤≤时,1110112121110111111119(1)10010(1)n n n n n n n n a a a a n n n n nn n n n-++++++⨯==⋅=⋅⋅=⋅=-----则当18n ≤≤时,1110(1)n a n n =+. 因此D 正确.(9)棱长为1的正方体1111ABCD A B C D -中,O 为正方体的中心,E 在11B C 上,11113B E BC =,F 在1AA 上,1114A F AA =,则四面体B EFO -的体积为( )(A )11144 (B )17144(C )1138 (D )1738【答案】A解析:以A 为原点建立空间直角坐标系,则(0,0,0)A ,111(,,)222O ,(1,0,0)B ,1(1,0,1)B ,1(1,1,1)C ,1(1,,1)3E ,3(0,0,)4F ,则111(,,)222BO =-,1(1,0,)4BF =-,1(0,,1)3BF =,四面体B EFO -的体积为111222131110641441013--=(10)设定义在R 上的函数()f x ,()g x 满足:①(0)1g =;②对任意实数12,x x ,121212()()()()()g x x f x f x g x g x -=+;③存在大于零的常数λ,使得()1f λ=,且当(0,)x λ∈时,()0f x >,()0g x > 则(A )()(0)0g f λ== (B )当(0,)x λ∈时,()()1f x g x +> (C )函数()f x ()g x 在R 上无界 (D )任取x R ∈,()()f x g x λ-= 【答案】ABD解析:令120x x ==,代入②得22(0)(0)(0)g f g =+,因为(0)1g =,所以(0)0f =;令12x x λ==,代入②得22(0)()()g f g λλ=+,因为()1f λ=,所以()0g λ=,因此()(0)0g f λ==;A 正确对于任意实数x ,令12x x x ==代入②得22(0)()()1g f x g x =+=,可得2()1f x ≤,2()1g x ≤,进而()1f x ≤,()1g x ≤,因此C 错误;当(0,)x λ∈时,()0f x >,()0g x >,所以20()1f x <<,20()1g x <<,进而0()1f x <<,0()1g x <<,故22()(),()()f x f x g x g x <<,因此22()()()()f x g x f x g x +<+,又22()()1f x g x +=,故()()1f x g x +>,所以B 正确;令1x λ=,2x x λ=-,代入②得()()()()()g x f f x g g x λλλλ=-+-,又()(0)0g f λ==,()1f λ=,所以()()g x f x λ=-,故D 正确.(11)设,,A B C 是随机事件,A 与C 互不相容,1()2P AB =,1()3P C =,则()P AB C = ( ) (A )16 (B )12(C )13 (D )34【答案】D解析:因为A 与C 互不相容,所以A C ⊂,则AB C ⊂,因此ABC AB =,可得1()()32()2()()43P ABC P AB P AB C P C P C ====,所以该题选D.(12)甲、乙、丙、丁四人参加数学竞赛,四人在成绩公布前作出如下预测:甲预测说:获奖者在乙、丙、丁三人中; 乙预测说:我不会获奖,丙获奖; 丙预测说:甲和丁中有一人获奖; 丁预测说:乙的猜测是对的.成绩公布后表明,四人的猜测中有两人的预测与结果相符. 另外两人的预测与结果不相符,已知有两人获奖,则获奖的是( )(A )甲和丁 (B )乙和丁 (C )乙和丙 (D )甲和丙 【答案】B解析:因为乙和丁的预测一样,则根据题干可知四人的猜测有两种情况:①乙和丁的预测与结果相符,甲和丙的预测与结果不相符,那么丙获奖,因为丙的预测与结果不相符,所以丙和乙获奖,与甲的预测相符了,矛盾;②乙和丁的预测与结果不相符,甲和丙的预测与结果相符,那么乙获奖,丙不获奖,结合甲预测可知丁获奖,与丙的预测相符,因此获奖者是乙和丁.该题选B. (13)设24πα=,则sin sin sin sin cos 4cos3cos3cos 2cos 2cos cos ααααααααααα+++=(A)6 (B)3 (C)2 (D )12【答案】B 解析:sin sin((1))cos cos(1)cos cos(1)n n n n n n ααααααα--=--sin cos(1)cos sin(1)tan tan(1)cos cos(1)n n n n n n n n αααααααα---==---所以sin sin sin sin cos 4cos3cos3cos 2cos 2cos cos ααααααααααα+++tan 4tan3tan3tan 2tan 2tan tan ααααααα=-+-+-+tan 4tan63πα===. 因此该题选B(14)设正三棱锥P ABC -的高为h ,底面三角形的边长为1. 设异面直线AB 与PC 的距离为()d h ,则lim ()h d h →∞=(A )1 (B )12(C (D )【答案】C解析:在APC ∆内,过A 向PC 做垂线,垂足为Q ,即AQ PC ⊥,连结BQ ,根据对称性,显然BQ PC ⊥,且BQ AQ =,取AB 中点D ,连结DQ ,DQ ⊂平面AQBAQ PC BQ PC ⊥⎫⇒⎬⊥⎭PC ⊥平面AQB ,又DQ ⊂平面AQB DQ PC ⇒⊥,在AQB 中,BQ AQ =,D 为AB 中点,所以DQ AB ⊥, 因此DQ 为AB 与PC 的公垂线;设点P 在平面ABC 的投影为O ,则AO BO CO ===,AP BP CP ===在APC 中,112APCS=⋅=又12APCSPC AQ AQ =⋅⋅=,所以AQ =,在等腰三角形AQB ∆中,DQ ===()d h =lim ()h h h d h →∞====(15)设,,αβγ分别为1,61,121︒︒︒,则(A )tan tan tan 3tan tan tan αβγαβγ++=- (B )tan tan tan tan tan tan 3αββγγα++=-(C )tan tan tan 3tan tan tan αβγαβγ++=- (D )tan tan tan tan tan tan 3αββγγα++=【答案】AB解析:22tan (tan 3)tan(60)tan tan(60)tan (13tan )βββββββ--︒+︒==-tan(60)tan tan(60)tan ββββ-︒+++︒=+3228tan 9tan 3tan tan tan 13tan 13tan βββββββ-=+=+=-- 223tan (3tan )13tan βββ-=- 所以tan tan tan tan(60)tan tan(60)3tan tan tan tan(60)tan tan(60)αβγβββαβγβββ++-︒+++︒==--︒+︒,A 正确.tan tan tan tan tan tan αββγγα++tan(60)tan tan tan(60)tan(60)tan(60)ββββββ=-︒++︒++︒-︒tan (tan(60)tan(60))tan(60)tan(60)βββββ=+︒+-︒++︒-︒ tan (tan(60)tan(60))tan(60)tan(60)βββββ=+︒+-︒++︒-︒22228tan tan 313tan 13tan ββββ-=+-- 229tan 313tan ββ-=- 3=-. 所以B 正确.(16)设函数7(,)6()22f x y xy x y =-++-,则[0,1][0,1]max{min{(,)}}y x f x y ∈∈=(A )0 (B )124(C )124- (D )[0,1][0,1]min{max{(,)}}y x f x y ∈∈【答案】BD解析:77(,)6222f x y x y x ⎛⎫=-+- ⎪⎝⎭求[0,1]min{(,)y f x y ∈把(,)f x y 看成y 的一次函数,[0,1]77(,0) 2 212min (,)357(,1) 2212y f x x x f x y f x x x ∈⎧⎛⎫=-≤ ⎪⎪⎪⎝⎭=⎨⎛⎫⎪=-> ⎪⎪⎝⎭⎩则[0,1]min (,)y f x y ∈在[0,1]x ∈上的最大值在712x =处取得, 所以[0,1][0,1]771max{min{(,)}}221224y x f x y ∈∈=⨯-=. 选项B 正确.[0,1]357(1,) 2212max{(,)}77(0,) 2 212x f y y y f x y f y y y ∈⎧⎛⎫=-≤ ⎪⎪⎪⎝⎭=⎨⎛⎫⎪=-> ⎪⎪⎝⎭⎩, 则[0,1]max{(,)}x f x y ∈在[0,1]y ∈的最小值在712y =处取得, 所以[0,1][0,1]771min{max{(,)}}221224y x f x y ∈∈=⨯-=,故[0,1][0,1][0,1][0,1]max{min{(,)}}min{max{(,)}}y y x x f x y f x y ∈∈∈∈=.所以D 正确.(17)椭圆2222:1x y C a b+=的左、右焦点分别为1F 和2F ,P 为C 上的动点,则(A)当a =时,满足1290F PF ∠=︒的点P 有两个 (B)当a <时,满足1290F PF ∠=︒的点P 有四个(C )12F PF 面积的最大值为22a(D )12F PF 的周长小于4a 【答案】AD解析:求满足1290F PF ∠=︒的点的个数只需要求22222221x y a b x y c ⎧+=⎪⎨⎪+=⎩的交点的个数,将222y c x =-代入椭圆可得222221x c x a b -+=,化简得22222222221c c b a x a b b b --=-=,即222222a b x a c-=.当a =时,0x =,因此满足1290F PF ∠=︒的点P 有两个,为短轴两个端点,A 正确;当a <时,20x <,因此满足1290F PF ∠=︒的点P 不存在,B 错误; 显然,当点P 位于短轴端点时,12F PF 面积最大,此时12122F PF Sc b bc =⋅⋅=,C 错误; 12F PF 的周长为224a c a +<,D 正确.(18)设复数z 使得10z 及10z的实部和虚部都是小于1的正数. 记z 在复平面上对应的点的集合是图形C ,则C 的面积是(A )25752π- (B )25702π- (C )15752π- (D )15702π-【答案】A解析:令z x iy =+,则101010z x y i =+,22101010()x iy z x iy x y ==+-+由题意可知22220,1101010100,1x y x y x y x y ⎧<<⎪⎪⎨⎪<<++⎪⎩,则22220,101010x y x y x x y y <<⎧⎪+>⎨⎪+>⎩,图中的阴影部分就是所求的图形C ,两圆相交部分的面积为252542π-,所以 C 的面积是25252510025275422S πππ⎡⎤⎛⎫=---⨯=-⎪⎢⎥⎝⎭⎣⎦. 选A. (19)设n 是正整数,则定积分22120()(1sin )d n n x x x ππ--+⎰的值(A )等于0 (B )等于1 (C )等于π (D )与n 的取值有关 【答案】A解析:令x y π-=,则22122120()(1s i n )d (1s i n )d n nn nx x x y yyππππ----+=+⎰⎰,因为212(1sin )n n y y -+是奇函数,则积分的上下限关于原点对称,所以212(1sin )d 0n n y y y ππ--+=⎰.(20)过点(1,0)F 的直线交抛物线24y x =于,A B 两点,则(A )以AB 为直径的圆与直线32x =-没有公共点(B )以FB 为直径的圆与y 轴只有一个公共点(C )AB 的最小值为4(D )AF 的最小值为2【答案】ABC解析:AB 时抛物线的焦点弦,焦点弦与准线1x =-相切,与32x =-相离,A 项正确;由抛物线定义知B 项也正确;当AB 垂直x 轴时,其长度最短为2p=4(此时称为通径),C 正确;||||1AF AO >=,即AF 可无限接近于1,最小值不存在,D 错误。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2016年清华大学领军计划测试
物理学科
1、友谊的小船说翻就翻,假如你不会游泳,就会随着小船一起沉入水底。
从理论上来说,你和小船沉入水底后的水面相比于原来( )
A.一定上升
B.一定下降
C.一定相等
D.条件不足,无法判断
2、在光滑地面上,物块与弹簧相连作简谐运动,小车向右作匀速直线运动,则对于弹簧和物
块组成的系统(填守恒或者不守恒),
当以地面为参考系时,动量 ,机械能 ;
当以小车为参考系时,动量 ,机械能 ;
3、如图所示,光滑导轨上垂直放置两根质量为m 、且有电阻的金属棒,导轨宽处与窄轨间距
比2:1,平面内有垂直纸面向内的磁场。
现给左边的杆一个初速度0v ,在系统稳定时,左
杆仍在宽轨上右杆仍在窄轨上运动。
则这个过程产生热量Q = 。
4、空间内有一水平向右的电场E ,现有一带电量为q 的小球以初速度为0v 斜
向上抛出,已知
3E q
=,求小球落地点距离抛出点的最远距离。
5、现有一轻质绳拉动小球在水平面内做匀速圆周运动,如图所示,小球
质量为m ,速度为v ,重力加速度为g ,轻绳与竖直方向夹角为θ,
求小球在运动半周时,绳子拉力的冲量
6、如图所示,有a b 、两个物体,a 物体沿长为L 、倾角为θ、动摩擦因数05μ.=的斜面滑下后,在长为L 的光滑水平面BC 运动;b 从C 点正上方高为45.L 处下落。
二者同时释放,在C 处相遇,则sin θ= 。
E
7、在水平面内,金属棒MN 一角速度ω绕O 点顺时针旋转,空间内有竖直向下的磁场,如图
所示。
已知MO NO >,则下列说法正确的是( )
A .M 点电势高于N 点
B .M 点电势低于N 点
C .若增大ω,则MN 点电势差增大
D .若增大B ,则MN 点电势差增大
8、在如图所示电路中,小灯泡规格为“63V W ,”,34ΩR =。
电源内阻为1Ω,电压表、电流
表均为理想电表,闭合开关,调节滑动变阻器阻值,使电压表示数为0,此时灯泡正常发光,电流表的表示数为1A ,则电流电动势E = ,输出功率P = ,
2R = 。
9、弹性绳原长为2L L R <<)
,劲度系数为k ,上端拴在半径为R 的光滑圆轨的顶端,下端系一重量为G 的小球,小球套在圆轨上。
平衡时,弹性绳与竖直方向夹角为θ。
用L R k G ,,,表示此时弹性绳的弹力。
10、在一质量均匀分布的星球(近似为球面)的北极和南极打一条竖直贯通的通道,一小球从
北极由静止释放,不与通道发生碰撞,则小球作 运动。
11、潜水员为测量一湖深度,测得湖面上27t =℃,51010a P .P =⨯,并将一盛有空气的试管从
湖面带入潜入湖底,整个过程管口始终向下。
潜至湖底后水充满试管的一半,7t =℃,则湖深约( )
A .5m
B .10m
C .15m
D .20m
12、一用钉鞘锁定的导热活塞将导热气缸分成体积相等的左右两室,:5:3P P =左右,
拔出钉鞘活塞移动至稳定状态,外界温度恒定,则( )。
A .稳定后左右两室体积比为5:3
B .左室气体对右室气体做功
C .左室气体吸热
D .右室气体吸热
13、有一左端封闭、右端开口的均匀U 形管,左管内有一段水银分割出两端
长度相等的气柱,如图所示,现向右管缓慢注入水银,设平衡后上段气
体为1l ,下端气体长2l ,则1l 与2l 的关系为( )
A.21>l l
B.21=l l
C.21<l l
D.无法确定,视注入水银的量
14、在高为h 的立柱上放一质量为M 的球,质量为m 的子弹以一定初速度水平射向球,从球
中穿出二者落至地面,球与子弹的落地点距立柱水平距离为S 和s ,重力加速度g ,则子弹的初速度为 。
15、从地面以初速度0υ竖直向上抛出一小球,与此同时,在该小球上抛能达到的最高处有另外
一个小球以初速度0υ竖直向下抛出。
忽略空气阻力,则两球相遇时速度之比为 。
16、质量为1m 、2m (12m m )的物体具有相同的初动能,现给以其与速度方向相反的阻力1f 、
2f 使其减速,经过时间t 后两物体同时停止,运动距离为1S 、2S ,则1f 2f ,
1S 2S 。
(填>、<、=)
17、如图所示,水平细绳与一弹簧作用于小球使其处于静止,若剪断细绳,则在剪断的一瞬间
( )
A .小球竖直方向加速度为0
B .小球水平方向加速度为0
C .弹簧弹力为θmg cos
D .弹簧弹力为θ
mg cos
18、光滑平行U 形轨道相距为L ,倾角为θ,一电阻为R 、长为L 的
导体棒在距导轨底端L 处。
空间内存在竖直向上的变化磁场,满
足t +=0k B B (0>k ),现在导体棒上加一沿斜面向上的力,是
导体棒始终保持静止,则t 时刻的力=F 。
19、导体球壳内有一点P ,外有一正点电荷q +位于Q 处,现将该电荷的电荷量加倍,则P 处
电势 (填升高/降低/不变);P 点场强 (填升高/降低/不变)。
20、下列物理学家及其成果,已经获得诺贝尔奖的有( )
A .伦琴发现了X 射线
B .爱因斯坦发现了相对论
C .普朗克提出量子论
D .(激光干涉引力波观测站)LIGO 探测到了引力波
21、实物在像的上方叫上线折射,反之则叫下线折射,则天气炎热是高速公路上看到的“水纹”
一样的东西属于 ;“海市蜃楼”属于 。
22、波长均为λ的两束平行光如图所示打在光屏上,发生干涉现象,问干涉条纹的间距( )
A .βsin +sin αλ
B .βcos +cos αλ
C .|sin -sin |βαλ
D .|
cos -cos |βαλ
23、引力波是时空的涟漪。
LIGO 探测到了引力波,是通过两座3000公里的天文台进行探测,
两座天文台相差4ms 分别探测到了同样的强烈的引力波,反映了一个52ms 的黑洞和一个14ms 的黑洞合并成一个62ms 的大黑洞,下列正确的有
A .引力波在宇宙中的传递是能量的传递
B .两座天文台探测到的同样的信号相隔不会超过10ms
C .引力波在真空中以光速传递
24、物理学家创小路和创小知在剑桥大学做了这样一个实验,在一个高为5.22米的塔的顶端放
置一个Co 放射源,在塔顶测的伽马射线频率为ν,在底端测的射线频率与之相差νΔ,已
知34-10×632.6=h ,求ν
νΔ的数量级 A .8-10 B .10-10 C .15-10 D .19-10
25、已知空气分子的平均动能为kT ,则在常温下,质量为kg m 23-10×7.4=的空气分子的德布
罗意波波长的数量级为 。
26、质量为m 的小球从高为h 的地方释放,如果在光滑轨道上的A 点飞出,求h 的值;如果是
从轨道的B (圆弧的最高点)点飞出,求h 的值(图中两虚线夹角为60°,圆弧曲率半径为R )。
