名校江苏省清江中学高二数学午间练习3 含答案
江苏省清江中学高二数学 午练练习(98)苏教版

午练练习(98)1.已知2()3(2),(2)f x x xf f ''=+则= . 2.设A 是整数集的一个非空子集,对于k A ∈,如果1k A -∉且1k A +∉,那么k 是A 的一个“孤立元”,给定{1,2,3,4,5,6,7,8,}S =,由S 的3个元素构成的所有集合中,不含“孤立元”的集合共有 个.3.已知复数11222i,34i,z z m z z =+=-若为实数,则实数m 的值为 . 4.若一个椭圆长轴的长度、短轴的长度和焦距成等差数列,则该椭圆的离心率是___________5.三张卡片上分别写上字母E 、E 、B ,将三张卡片随机地排成一行,恰好排成英文单词BEE 的概率为 。
6.已知实数x 、y 满足112213y x y x ⎧≥-⎪⎪⎨⎪≤-+⎪⎩则214z x y =+的最大值为 .7.、α、β是两个不同的平面,m 、n 是平面α及β之外的两条不同直线,给出四个论断: ①m ⊥n ; ②α⊥β ; ③n ⊥β; ④m ⊥α.以其中三个论断作为条件,余下一个论断作为结论,写出你认为正确的一个命题: _____. 8.在平面直角坐标系中,双曲线Γ的中心在原点,它的一个焦点坐标为,1(2,1)e =r 、2(2,1)e =-r 分别是两条渐近线的方向向量。
任取双曲线Γ上的点P ,若12OP ae be =+u u u r u u r u u u r (a 、b R ∈),则a 、b 满足的一个等式是9.设函数)()0(1)6sin()(x f x x f '>-+=的导数ωπω的最大值为3,则f(x)的图象的一条对称轴的方程是 .10.已知数列{}n a 满足:1a =m (m 为正整数),1,231,n n n n n a a a a a +⎧⎪=⎨⎪+⎩当为偶数时,当为奇数时。
若6a =1,则m所有可能的取值为_________。
11.已知f(x)=ax2+bx +c 的图象过点(-1,0),是否存在常数a 、b 、c 使不等式x≤f(x)≤1+x22对一切实数x 均成立?(98)参考答案1.-2 2。
江苏省清江中学高二数学 午练练习(82)苏教版

午练练习(82)1.将一枚均匀的硬币投掷6次,则正面出现的次数比反面出现的次数多的概率__________2.已知iR b a i i bi a ,,(32∈+=-+为虚数单位),则=+b a ______.3.设a ,b 为空间的两条直线,α,β为空间的两个平面,给出下列命题:所有真命题的序号是 .(1)若a ∥α,a ∥β,则α∥β;(2)若a ⊥α,a ⊥β,则α∥β;(3)若a ∥α,b ∥α,则a ∥b ;(4)若a ⊥α,b ⊥α,则a ∥b .4.若关于x 的不等式2230x x a -+<的解集为(,1)m ,则实数m = .5.已知p 是r 的充分条件而不是必要条件,q 是r 的充分条件,s 是r 的必要条件,q 是s 的必要条件.现有下列命题:则正确命题序号是________.①s 是q 的充要条件;②p 是q 的充分条件而不是必要条件;③r 是q 的必要条件而不是充分条件; ④⌝p 是⌝s 的必要条件而不是充分条件;⑤r 是s 的充分条件而不是必要条件.设集合()22{,|1}416x y A x y =+=,{(,)|3}x B x y y ==,则A B ⋂的子集的个数是_________.7.设{}n a 是首项大于零的等比数列,则“12a a <”是“数列{}n a 是递增数列”的____________条件.8.给出下列三个结论:其中正确结论的序号是________.(填写所有正确结论的序号)①命题“∃x ∈R ,x2-x>0”的否定是“∀x ∈R ,x2-x≤0”;②函数f(x)=x -sinx(x ∈R)有3个零点; ③对于任意实数x ,有f(-x)=-f(x),g(-x)=g(x),且x>0时,f′(x)>0,g′(x)>0,则x<0时,f′(x)>g′(x).9.若关于x 的不等式22x x t <--至少有一个负数解,则实数t 的取值范围是________.10.已知圆O 的半径为1,PA 、PB 为该圆的两条切线,A 、B 为切点,那么PB PA ⋅的最小值为 .11.已知P (a ,-1),过点P 作抛物线C :2y x =的切线,切点分别为11(,)A x y 、22(,)B x y ,其中12x x <.(1)求12,x x 的值(用a 表示);(2)若以P 为圆心的圆E 与直线AB 相切,求圆E 面积的最小值。
江苏省清江中学高二数学 午练练习(17)苏教版

午练练习(17)1.将函数sin(2)3y x π=-的图象先向左平移3π,然后将所得图象上所有的点的横坐标变为原来的2倍(纵坐标不变),则所得到的图象对应的函数解析式为 .2.若]2,0[πθ∈,且54sin =θ,则2tan θ= .3.两个正数,m n 的等差中项是5,等比中项是4.若m n >,则椭圆221x y m n +=的离心率e 的大小为 .4.以双曲线2213x y -=的一条准线为准线,顶点在原点的抛物线方程是 .5.已知关于x 的方程1+=ax x 有一个负根,但没有正根,则实数a 的取值范围是6.若向量(3,1),(2,1)AB n =-=u u u r r ,且n AC ⋅=r u u u r 7,那么n BC ⋅r u u u r 等于7.等差数列2008200520071,220052007,2008,,}{S S S a n S a n n 则项和是其前中=--=的值为8.定义在R 上的函数()f x :当sin x ≤cos x 时,()cos f x x =;当sin cos x x >时,()sin f x x =.给出以下结论, 其中正确命题的序号是 .①()f x 是周期函数 ②()f x 的最小值为1-③当且仅当2()x k k π=∈Z 时,()f x 取最大值④当且仅当2(21)()2k x k k πππ-<<+∈Z 时,()0f x >⑤()f x 的图象上相邻最低点的距离是2π9. 已知函数x x x f cos 26sin 2)(-⎪⎭⎫ ⎝⎛+=π.(Ⅰ)当⎥⎦⎤⎢⎣⎡∈ππ,2x时,若54sin=x,求函数)(xf的值;(Ⅱ)当⎥⎦⎤⎢⎣⎡∈ππ,2x时,求函数()3sin()cos(2)63h x x xππ=---的值域;(Ⅲ)把函数)(xfy=的图象沿X轴方向平移m个单位得到函数)(xg的图象,若函数)(xg是偶函数,求|m|的最小值.午练练习(17)1.sin3y xπ⎛⎫=+⎪⎝⎭ 2.213. 4.2266y x y x==-或 5.1≥a 6. 2 7. 2008-8. ①④⑤9.(Ⅰ)35.(Ⅱ)17[,2]8--,(Ⅲ) 3π。
江苏省清江中学高二数学午间练习00 含答案

午练练习(70)1.不等式221x x +>+的解集是 . 2.设1z i =-(i 为虚数单位),则22z z+ = ___ . 3.中心在原点,焦点坐标为(0,52)±的椭圆被直线320x y --=截得的弦的中点的横坐标为21,则椭圆方程为 . 4.已知甲地有蔬菜加工企业2家,水产品加工企业3家;乙地有蔬菜加工企业3家,水产品加工企业2家,从甲、乙两地各任意抽取2家企业检查,恰有一家蔬菜加工企业被抽到的概率为 .5.设函数()||f x x x bx c =++,则下列命题中正确命题的序号有 .①当0b >时,函数()f x 在R 上是单调增函数; ②当0b <时,函数()f x 在R 上有最小值; ③函数()f x 的图象关于点(0,c )对称; ④方程()0f x =可能有三个实数根.6.对于任意两个实数a ,b 定义运算“*”如下:a a b a b b a b≤⎧*=⎨>⎩则函数2()[(6)(215)]f x x x x =*-*+的最大值为7.已知三个球的半径1R ,2R ,3R 满足32132R R R =+,则它们的表面积1S ,2S ,3S 满足的等量关系是___________.8.在平面直角坐标系xOy 中,已知圆B :22(1)16x y -+=与点(1,0)A -,P 为圆B 上的动点,线段PA 的垂直平分线交直线PB 于点R ,点R 的轨迹记为曲线C .(1) 求曲线C 的方程;(2)曲线C 与x 轴正半轴交点记为Q ,过原点O 且不与x 轴重合的直线与曲线C 的交点记为,M N ,连接,QM QN ,分别交直线x t =(t 为常数,且2t ≠)于点,E F ,设,E F 的纵坐标分别为12,y y ,求12y y ⋅的值(用t 表示).(70)参考答案1.(1,0)(1,)-+∞ 2.1i - 3.1752522=+y x 4.2565. ①③④ 6.9 7.=8. 解:(1)连接RA ,由题意得,RA RP =,4RP RB +=,所以42RA RB AB +=>=,由椭圆定义得,点R 的轨迹方程是22143x y +=. (2)设M 00(,)x y ,则00(,)N x y --,,QM QN 的斜率分别为,QM QN k k , 则002QM y k x =-,002NQ y k x =+, 所以直线QM 的方程为00(2)2y y x x =--,直线QN 的方程00(2)2y y x x =-+, 令(2)x t t =≠,则001200(2),(2)22y y y t y t x x =-=--+, 又因为00(,)x y 在椭圆2200143x y +=,所以2200334y x =-, 所以22202201222003(3)(2)34(2)(2)444x t y y y t t x x --⋅=-==----,其中t 为常数.。
江苏省清江中学2014-2015学年高二数学午间练习(013)Word版含答案

午练练习(13)1.设A(1,2),B(3,-1),C(3,4),则AB AC •=____2.已知复数z 满足i z i 34)21(+=+,则z 的实部和虚部分别为______ 3.曲线x x x f ln )(=在点1=x 处的切线方程为__________4.已知下列命题(其中b a ,为直线,α为平面),其中,真命题的序号是 ① 若一条直线垂直于一个平面内无数条直线,则这条直线与这个平面垂直;② 若一条直线平行于一个平面,则垂直于这条直线的直线必垂直于这个平面;③ 若α//a ,α⊥b ,则b a ⊥;④ 若b a ⊥,则过b 有唯一一个平面α与a 垂直.5.已知等差数列}{n a 的首项为24,公差为2-,则当n= __时,该数列的前n 项和n S 取得最大值。
6. 按右图所示的程序框图运算.若输出2k =,则输入x 的取值范围是7.已知双曲线22221x y a b-= (0,0)a b >>的左、右焦点分别为F 1、F 2,P 是准线上一点,且P F 1⊥P F 2,|P F 1|⋅|P F 2 |=4ab ,则双曲线的离心率是8.函数()24x f x x =+-的零点为a ,2()log 4g x x x =+-的零点为b ,则a b +=9、已知数列{n a }中的相邻两项21k a -、2k a 是关于x 的方程2(32)320kkx k x k -++⋅= 的两个根,且21k a -≤2k a (k =1,2,3,…).(1)求1357,,,a a a a 及2n a (n ≥4); (2)求数列{n a }的前2n 项和S 2n .午练练习(13)1、-22、2,-13、1-=x y4、③,④5、n=12或136、(28,57]7、38、4;9、(1)方程2(32)320k kx k x k -++⋅=的两个根为123, 2k x k x ==.输入x21x x ←+1k k ←+115x >输出,x k 开始 结束0k ←Y当k =1时,123,2x x ==,所以12a =;当k =2时,126,4x x ==,所以34a =; 当k =3时,129,8x x ==,所以58a =;当k =4时,1212,16x x ==,所以712a =;因为n ≥4时,23nn >,所以22 (4)n n a n =≥(2)22122(363)(222)nn n S a a a n =+++=+++++++=2133222n n n+++-.。
江苏省清江中学高二数学 午练练习(114)苏教版
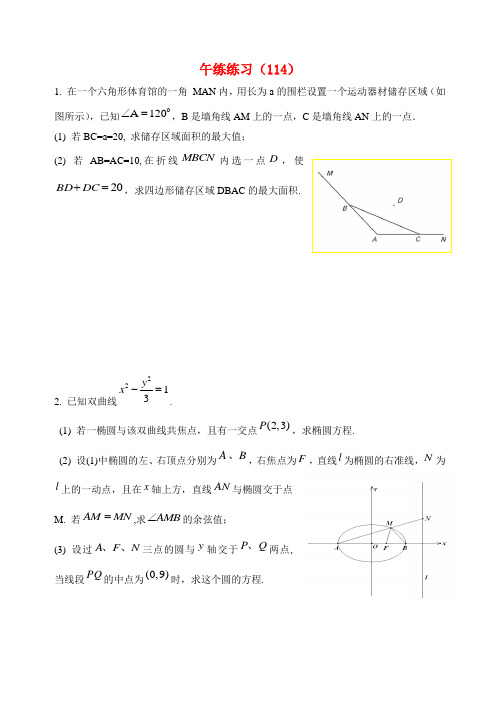
午练练习(114)1. 在一个六角形体育馆的一角 MAN 内,用长为a 的围栏设置一个运动器材储存区域(如图所示),已知 120A =∠,B 是墙角线AM 上的一点,C 是墙角线AN 上的一点.(1) 若BC=a=20, 求储存区域面积的最大值;(2) 若AB=AC=10,在折线MBCN 内选一点D ,使20=+DC BD ,求四边形储存区域DBAC 的最大面积.2. 已知双曲线2213y x -=. (1) 若一椭圆与该双曲线共焦点,且有一交点(2,3)P ,求椭圆方程.(2) 设(1)中椭圆的左、右顶点分别为A B 、,右焦点为F ,直线l 为椭圆的右准线,N 为l 上的一动点,且在x 轴上方,直线AN 与椭圆交于点M. 若AM MN =,求AMB ∠的余弦值;(3) 设过A F N 、、三点的圆与y 轴交于P Q 、两点,当线段PQ 的中点为(0,9)时,求这个圆的方程.参考答案(114)1. 解:(1)设,,0,0.AB x AC y x y ==>>由222202cos12022cos120x y xy xy xy =+-≥-, 得222202022cos1204sin 60xy ≤=-. 2222112020cos6020sin1202sin 60cos60224sin 604sin 604tan 60S xy ∴=≤⋅⋅===即y 四边形DBAC x=时取到.(2) 由20=+DC DB ,知点D 在以B ,C 为焦点的椭圆上, ∵32523101021=⨯⨯⨯=∆ABC S ,∴要使四边形DBAC 面积最大,只需DBC ∆的面积最大,此时点D 到BC 的距离最大, 即D必为椭圆短轴顶点.由BC =轴长5,BCD b S ∆=面积的最大值为152⨯=因此,四边形ACDB面积的最大值为.2.解:(1)双曲线焦点为(2,0)±,设椭圆方程为22221x y a b +=.则22224,49 1.a b a b ⎧-=⎪⎨+=⎪⎩ 2216,12a b ∴==. 故椭圆方程为2211612x y +=.(2) 由已知,(4,0),(4,0),(2,0),A B F - 直线l 的方程为8x =.设(8,)(0).N t t >AM MN =, (4,).2t M ∴由点M 在椭圆上,得 6.t =故所求的点M 的坐标为(4,3)M .所以(6,3),(2,3),1293MA MB MA MB =--=-⋅=-+=-.cos 36MA MBAMB MA MB ⋅∠===⋅(3) 设圆的方程为220,x y Dx Ey F ++++=将A F N 、、三点坐标代入,得 21640,420,6480,D F D F t D Et F ⎧-+=⎪++=⎨⎪++++=⎩得2,72,8.D E t t F =⎧⎪⎪=--⎨⎪=-⎪⎩圆的方程为22722()80,x y x t y t ++-+-=令0,x =得272()80.y t y t -+-=设12(0,(0,)P y Q y ),,则1,2y =由线段PQ 的中点为(0,9),得127218,18y y t t +=+=. 此时,所求圆的方程为2221880.x y x y ++--=。
江苏省清江中学高二数学午间练习039 含答案
午练练习(39) 1、已知集合{}(1)0P x x x =-≥,Q ={})1ln(|-=x y x ,则P Q = .2、在等比数列{n a }中,若7944,1a a a ⋅==,则12a 的值是 .3、若关于x 的不等式2260ax x a -+<的解集为(1, m ),则实数m = .4、已知点()3,1--和()4,6-在直线320x y a --=的两侧,则a 的取值范围是5、若0,0>>y x ,且191=+yx ,求y x +的最小值为 . 6、已知直线0=++C By Ax (其中0,222≠=+C C B A )与圆422=+y x 交于N M ,,O 是坐标原点,则OM ·ON = _________________. 7、如果实数.x y 满足不等式组22110,220x x y x y x y ≥⎧⎪-+≤+⎨⎪--≤⎩则的最小值是8、已知576*,)}({S S S n N n a d S n n >>∈且项和的前的等差数列是公差为,则下列四个命题:①0<d ;②011>S ;③012<S ;④013>S 中为真命题的序号为 . 9、已知以点)0,)(2,(≠∈t R t tt C 为圆心的圆与x 轴交于点A O ,,与y 轴交于点O 、B ,其中O 为原点。
(1)求证:OAB ∆的面积为定值;(2)设直线42+-=x y 与圆C 交于点N M ,,若ON OM =,求圆C 的方程。
(39)参考答案1.{}1/>x x .2.4. 3. 2. 4.247<<-a 5.16.6.-2. 7.5 8. ①②.9、(1)略(2)()()52122=-+-y x。
名校江苏省清江中学高二数学午间练习108 含答案
FO APQ yx 午练练习(108)1.设a,b 为实数,若复数11+2i i a bi=++,则a+b= 2.不等式2313x x a a +--≤-对任意实数x 恒成立,则实数a 的取值范围为__________. 3.已知椭圆2222:1(0)x y C a b a b+=>>3,过右焦点F 且斜率为(0)k k >的直线与C 相交于A B 、两点.若3AF FB =,则k = ___________4.若函数f (x )=min{3+log 41x ,log 2x },其中min{p ,q }表示p ,q 两者中的较小者,则f (x )<2的解集为_ .5.已知函数[]2()2f x x x x a b =-∈,,的值域为[]13-,,则b a -的取值范围是 ▲ . 6.在数列{}n a 中,已知122,3a a ==,当2n ≥时,1n a +是1n n a a -⋅的个位数,则2010a =▲ .7.设双曲线的一个焦点为F ,虚轴的一个端点为B ,如果直线FB 与该双曲线的一条渐近线垂直,那么此双曲线的离心率为___________8.已知函数f(x)=3sin(x-)(>0)6πωω和g(x)=2cos(2x+)+1ϕ的图象的对称轴完全相同。
若x [0,]2π∈,则f(x)的取值范围是 。
9.将边长为1m 正三角形薄片,沿一条平行于底边的直线剪成两块,其中一块是梯形, 记2(S =梯形的周长)梯形的面积,则S 的最小值是________。
10.已知函数()f x 满足:()114f =,()()()()()4,f x f y f x y f x y x y R =++-∈,则()2010f =_____. 11.设椭圆C :)0(12222>>=+b a b y a x 的左焦点为F ,上顶点为A ,过点A 与AF 垂直的直线分别交椭圆C 与x 轴正半轴于点P 、Q ,且8AP=PQ 5. ⑴求椭圆C 的离心率; ⑵若过A 、Q 、F 三点的圆恰好与直线l :330x y +=相切,求椭圆C 的方程.(108)参考答案解:设Q (x 0,0),由F (-c ,0)A (0,b )知),(),,(0b x b c -==c b x b cx 2020,0,==-∴⊥ 设PQ AP y x P 58),,(11=由, 得21185,1313b x y bc == 因为点P 在椭圆上,所以1)135()138(22222=+bb a cb 整理得2b 2=3ac ,即2(a 2-c 2)=3a c ,22320e e +-=,故椭圆的离心率e =21 ⑵由⑴知22323,2b b ac a c ==得, 11,22c c a a ==由得于是F (-21a ,0) Q )0,23(a , △AQF 的外接圆圆心为(21a ,0),半径r=21|FQ|=a 所以a a =+2|321|,解得a =2,∴c=1,b=3,所求椭圆方程为13422=+y x。
江苏省清江中学高二数学午间练习 含答案
午练练习(46)1.35cos()3π-的值是.2. 当}21,1,2,1{-∈n时,幂函数y=x n的图象不可能经过第___ ______象限3.已知复数12312,1,32z i z i z i=-+=-=-,它们所对应的点分别为A,B,C.若OC xOA yOB=+,则x y+的值是.4.设a、b、c分别是△ABC中∠A、∠B、∠C所对边的边长,则直线sin0x A ay c⋅++=与sin sin0bx y B C-⋅+=的位置关系是.5.已知等差数列{}n a满足:6,821-=-=aa.若将541,,aaa都加上同一个数,所得的三个数依次成等比数列,则所加的这个数为.6.若向量)1,3(=a,(sin,cos)b mαα=-,(R∈α),且//,则m的最小值为_ ___ 7.已知函数()35xf x x=+-的零点[],x a b∈,且1b a-=,a,b N*∈,则a b+= .8. 已知{}n a是首项为a,公差为1的等差数列,1nnnaba+=.若对任意的*n N∈,都有8nb b≥成立,则实数a的取值范围是9.已知2πα<<,且3sin5α=(1)求αααα2coscos2sinsin22++的值;(2)求⎪⎭⎫⎝⎛-πα45tan的值.(46)参考答案一、1.12;2.四;3.5;4.垂直;5.1-;6.-2;7.3.8.()8,7--9.(1)由sinα=53又0<α<2π∴cosα=54,tanα=43∴ααααααααα22222sin cos 2cos sin 2sin 2cos cos 2sin sin -⋅+=++ =2333)43(2432)43(tan 2tan 2tan 2222=-⨯+=-+ααα (2)tan(71431143tan 11tan 45tan tan 145tan tan )45-=+-=+-=⋅+-=-ααπαπαπα。
名校江苏省清江中学高二数学午间练习102 含答案
xy1x x 4O2x3x•• ••ABCAMN午练练习(102)1.计算12sin 22.5-的结果等于 .2.设323log ,log 3,log 2a b c π===,则a 、b 、c 由大到小排列为____________.3.已知向量a =(2,-1),b =(-1,m ),c =(-1,2)若(a +b )∥c ,则m = .4.设n S 为等比数列{}n a 的前n 项和,2580a a +=,则52S S = . 5.直线3y kx =+与圆()()22324x y -+-=相交于M,N 两点,若23MN ≥,则k 的取值范围是 .6.若复数 z 满足z (1+i) =1-i (I 是虚数单位),则其共轭复数z =__________________ .7.从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图)。
由图中数据可知a = 。
若要从身高在[ 120 , 130),[130 ,140) , [140 , 150]三组内的学生中,用分层抽样的方法选取18人参加一项活动,则从身高在[140 ,150]内的学生中选取的人数应为 。
8.函数())1,0(13log ≠>-+=a a x y a 的图象恒过定点A,若点A 在直线01=++ny mx 上,其中0>mn ,则nm 21+的最小值为 . 9.已知函数)(x f y =的导函数)(x f y '=的图像如下,则一下说法正确的是 . A .函数)(x f 有1个极大值点,1个极小值点 B .函数)(x f 有2个极大值点,2个极小值点 C .函数)(x f 有3个极大值点,1个极小值点 D .函数)(x f 有1个极大值点,3个极小值点10.设非空集合|||S x m x l =≤≤满足:当x S ∈时,有2x S ∈。
给出如下三个命题工:①若1m =,则|1|S =;②若12m =-,则114l ≤≤;③若12l =,则20m -≤≤。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
午练练习(113)
1. 如图,以x O 为始边作角)0παββα<<<(与,它们的终边分别与单位圆相交
于点P 、Q,已知点P 的坐标为).54,53(- (1)求α
ααtan 112cos 2sin +++的值; (2)若,0=•OQ OP 求)sin(βα+的值.
2. 22
162
x y -=已知双曲线, (1)求以双曲线的顶点为焦点,焦点为顶点的椭圆E 的方程.
(2)点P 在椭圆E 上,点C (2,1)关于坐标原点的对称点为D ,直线CP 和DP 的斜率都存在且不为0,试问直线CP 和DP 的斜率之积是否为定值?若是,求此定值;若不是,请说明理由.
(3)平行于CD 的直线l 交椭圆E 于M 、N 两点,求CMN ∆面积的最大值,并求此时直线l 的方程.
参考答案(113)
1.解:(1)由三角函数的定义得,5
4sin ,53cos =-=αα
则原式=α
ααααααααααcos cos sin )cos (sin cos 2cos sin 1cos 2cos sin 22++=++ .25
18)53(2cos 222=-⨯==α (2),2,0πβα=-∴⊥∴=⋅OQ OP 2
παβ-=∴, 53cos )2sin(sin =-=-=∴απ
αβ,.5
4sin )2cos(cos ==-=απαβ βαβαβαsin cos cos sin )sin(+=+∴ .25753)53(5454=⨯-+⨯=
2. 解:22
222211,0,628c 6.x y a b a a b
+=>>=+==()设椭圆E 方程为则, 22
1.82
x y ∴+=椭圆E 方程为 (2)依题意得D 点的坐标为(-2,-1),且D 点在椭圆E 上,直线CP 和DP 的
斜率K CP 和K DP 均存在,设P (x ,y ),
2211111,,.22224CP DP CP DP y y y y y K K K K x x x x x -+-+-==∴⋅=⋅=-+-+-则 P 又点在椭圆E 上,2222118444
CP DP y x y K K x -∴=-⋅==--,. 14
DP ∴-直线CP 和的斜率之积为定值. (3) 直线CD 的斜率为2
1,CD 平行于直线l , ∴设直线l 的方程为,2
1t x y += 由⎪⎪⎩⎪⎪⎨⎧=++=128
2122y x t x y , 消去y ,整理得042222=-++t tx x ,
)4(2
4162222,1≤-±-=∴t t t x , ()()212221221)2
1(1x x y y x x MN -•+=-+-=∴ )22(452<<--⋅=t t .
点C 到直线MN 的距离为,5214
1t t d =+=
2245
2452121t t t t d MN S CMN -⋅=⋅-⋅⋅=⋅=∴∆ .22
4)4(22=≤
-=t t 当且仅当时取等号,即2,4222=-=t t t .2212±=∆x y l CMN 的方程为,此时直线面积得最大值为。
