平行线的判定习题(含答案)

合集下载

(完整版)平行线的判定习题

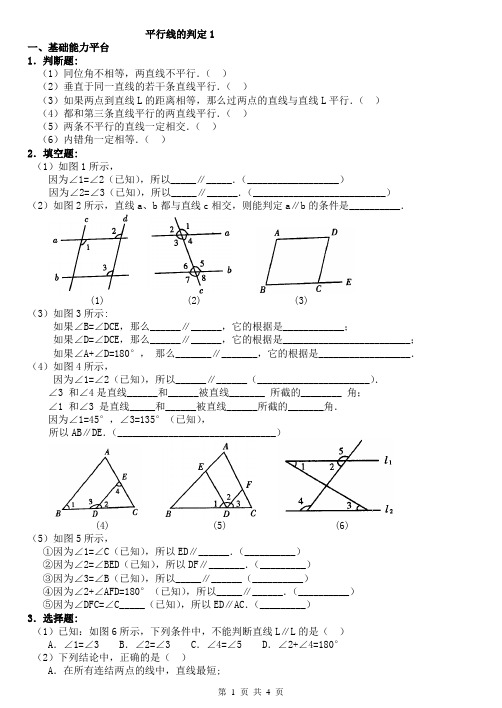
平行线的判定1一、基础能力平台1．判断题:（1）同位角不相等，两直线不平行．（）（2）垂直于同一直线的若干条直线平行．（）（3）如果两点到直线L的距离相等，那么过两点的直线与直线L平行．（）（4）都和第三条直线平行的两直线平行．（）（5）两条不平行的直线一定相交．（）（6）内错角一定相等．（）2．填空题:（1）如图1所示，因为∠1=∠2（已知），所以_____∥_____．（__________________）因为∠2=∠3（已知），所以_____∥______．（__________________________）（2）如图2所示，直线a、b都与直线c相交，则能判定a∥b的条件是__________．(1) (2) (3)（3）如图3所示:如果∠B=∠DCE，那么______∥______，它的根据是____________；•如果∠D=∠DCE，那么______∥______，它的根据是_________________________；如果∠A+∠D=180°，•那么_______∥_______，它的根据是__________________．（4）如图4所示，因为∠1=∠2（已知），所以______∥______（______________________）．∠3•和∠4是直线______和______被直线_______•所截的________•角；•∠1•和∠3•是直线_____和______被直线______所截的_______角．因为∠1=45°，∠3=135°（已知），所以AB∥DE．（_______________________________）(4) (5) (6)（5）如图5所示，①因为∠1=∠C（已知），所以ED∥______．（__________）②因为∠2=∠BED（已知），所以DF∥_______．（_________）③因为∠3=∠B（已知），所以_____∥______（__________）④因为∠2+∠AFD=180°（已知），所以_____∥______．（__________）⑤因为∠DFC=∠C_____（已知），所以ED∥AC．（_________）3．选择题:（1）已知：如图6所示，下列条件中，不能判断直线L∥L的是（）A．∠1=∠3 B．∠2=∠3 C．∠4=∠5 D．∠2+∠4=180°（2）下列结论中，正确的是（）A．在所有连结两点的线中，直线最短;B．经过两点有且只有一条直线;C．内错角互补，两直线平行;D．没有公共点的两条线段一定平行（3）已知a⊥b，b⊥c，则直线a与直线c的关系为（）A．相交 B．垂直 C．平行 D．以上都不对（4）已知a∥b，c∥b，则直线a和c的关系是（）A．相交 B．垂直 C．平行 D．相交或平行（5）两条直线被第三条直线所截，有一对同旁内角互补，•则这一对同旁内角的角平分线（）A．互相垂直 B．互相平行C．相交但不垂直 D．不能确定（6）在同一平面内不相邻的两个直角，如果它们有一条边在同一条直线上，•那么另一条边相互（） A．平行 B．垂直 C．平行或垂直 D．平行或垂直或在同一条直线上4．填写理由:（1）如图7所示，因为∠A=_____（已知），所以AC∥DE（________________________）．因为∠A+_____=•180°（已知），所以AB∥FD（___________________________）．(7) (8) (9)（2）如图8所示，因为AC平分∠DAB（已知），所以∠1=∠3（__________________）．又因为∠1=∠2（已知），所以∠2=∠3（_____________________________）．所以DC∥AB（___________________________________）．（3）如图9所示，C、D、E在一条直线上．因为∠1=130°（已知），所以∠2=50°（_________）．又因为∠A=50°（已知），所以∠2=∠A（_________）．所以AB∥CD（____________）．二、拓展延伸训练1．如图所示，BE平分∠ABD，DE平分∠BDC，∠1+∠2=90°，那么直线AB、CD的位置关系如何？2．如图所示，ADB 是一条直线，∠ADE=∠ABC ，且DG 、BF 分别是∠ADE 和∠ABC•的平分线，那么DG 与BF 平行吗？为什么？平行线的判定21．如图，直线AB 、CD 相交与点E ，要使DF ∥AB ．若需要图中与∠D 相等的角有（）A ．4个B ．3个C ．2个D ．1个2．如图，直线a ，b 被c 所截，若∠1＝32°，要使a ∥b ，则∠2的大小为（）A ．32°B ．148°C ．52°D ．128°3．如图，把一块直角三角板的直角顶点放在直线b 上，如果∠2=62°，要使a //b ，那么∠1的度数是（）A ．28°B ．52°C ．62°D ．68°二、填空题4．如图，∠2＝150°，当∠1＝_______时，a ∥b .5．如图，点B 、C 、D 在同一条直线上，∠ACB ＝90°，若∠A ＝54°，∠ECD ＝36°，则CE _________ AB ．6．如图， AE 平分∠BAC 交BD 于点E ，若2122∠=︒，要使AC ∥BD ，则1∠= ．8765cb a3412三、解答题7．如图，直线l 与直线a 、b 分别交于点A 、B ，若∠1 = 60°，∠2=120°，试说明a ∥b ．1.如图1所示,下列条件中,能判断AB∥CD 的是( )A.∠BAD=∠BCDB.∠1=∠2;C.∠3=∠4D.∠BAC=∠ACD34DCBA21FE D CBA(1) (2) (3)2.如图2所示,如果∠D=∠EFC,那么( )A.AD∥BCB.EF∥BCC.AB∥DCD.AD∥EF 3.下列说法错误的是( )A.同位角不一定相等B.内错角都相等C.同旁内角可能相等D.同旁内角互补,两直线平行 4.如图3,直线a,b 被直线c 所截,现给出下列四个条件:①∠1=∠-5; ②∠1=∠7; ③∠2+∠3=180°; ④∠4=∠7.其中能说明a∥b 的条件序号为( ) A.①② B.①③ C.①④ D.③④ 5．如左图，BE 是AB 的延长线。

平行线的判定和性质证明题基础+提高(含答案)

10.∵AB∥CD，PE∥AB∴PE∥AB∥CD∴∠A+∠APE=180°∠C+∠CPE=180°∵∠PAB=130°∠PCD=120°，∴∠APE=50°，∠CPE=60°
∴∠APC=∠APE+∠CPE=50°+60°=110°
（1）；过点P作，
又因为，所以，
则，，
所以；
（2）情况1：如图所示，当点P在B、O两点之间时，
∵AB∥CD
∴PM∥CD
∴∠2+∠PFD＝180°
∵∠PFD＝130°
∴∠2＝180°﹣130°＝50°
∴∠1+∠2＝40°+50°＝90°
即∠EPF＝90°
[探究]如图②AB∥CD，∠AEP＝50°，∠PFC＝120°，求∠EPF的度数．
[应用]如图③所示，在[探究]的条件下，∠PEA的平分线和∠PFC的平分线交于点G，则∠G的度数是°
（3）如图3，若MR平分∠BMN，则MR与NP有怎样的位置关系？请说明理由．
参考答案（基础）
1. ∠ABC；角平分线的定义； ∠BCD；∠ABC+∠BCD；180°；两直线平行，同旁内角互补．
2. ，同旁内角互补，两直线平行，∠1，两直线平行，内错角相等，∠CBG，同位角相等，两直线平行。
3.证明：∵∠E=∠F∴AE∥CF∴∠A=∠ABF∵∠A=∠C∴∠ABF=∠C∴AB∥CD．
∴∠EPF＝∠MPF﹣∠MPE＝120°﹣50°＝70°
如图③所示，
∵EG是∠PEA的平分线，FG是∠PFC的平分线
∴∠AEG＝ AEP＝25°，∠GFC＝ PFC＝60°
过点G作GM∥AB∴∠MGE＝∠AEG＝25°∵AB∥CD（已知）∴GM∥CD∴∠GFC＝∠MGF＝60°∴∠G＝∠MGF﹣∠MGE＝60°﹣25°＝35°

(完整版)平行线及其判定(证明应用题)

授课教案学员姓名：________________ 学员年级：________________ 授课教师：_________________ 所授科目：_________ 上课时间：______年____月____日（～）；共_____课时（以上信息请老师用正楷字手写）平行线及其判定（证明应用题）一．解答题（共11小题）1．已知：如图，∠A=∠F，∠C=∠D．求证：BD∥CE．2．将一副三角板拼成如图所示的图形，过点C作CF平分∠DCE交DE于点F．（1）求证：CF∥AB；（2）求∠DFC的度数．3．如图，△ABC中，AB=AC，D是CA延长线上的一点，且∠B=∠DAM．求证：AM∥BC．4．如图，已知DF∥AC，∠C=∠D，你能否判断CE∥BD？试说明你的理由．5．如图，已知∠1=∠2，∠3=∠4，∠5=∠6，试判断ED与FB的位置关系，并说明为什么．6．如图，已知AD⊥BC，EF⊥BC，∠3=∠C，求证：∠1=∠2．7．如图，已知∠A=∠F，∠C=∠D，试说明BD∥CE．8．已知：如图，AD是△ABC的平分线，点E在BC上，点G在CA的延长线上，EG交AB于点F，且∠AFG=∠G．求证：GE∥AD．9．如图，CA⊥AD，垂足为A，∠C=50°，∠BAD=40°，求证：AB∥CD．10．如图，BE平分∠ABD，DE平分∠BDC，且∠1+∠2=90°．求证：AB∥CD．11．如图所示，已知直线a、b、c、d、e，且∠1=∠2，∠3+∠4=180°，则a与c平行吗？为什么？2015年03月05日752444625的初中数学组卷参考答案与试题解析一．解答题（共11小题）1．（2014•槐荫区二模）已知：如图，∠A=∠F，∠C=∠D．求证：BD∥CE．考点：平行线的判定．专题：证明题．分析：由∠A=∠F，根据内错角相等，两直线平行，即可求得AC∥DF，即可得∠C=∠FEC，又由∠C=∠D，则可根据同位角相等，两直线平行，证得BD∥CE．解答：证明：∵∠A=∠F，∴AC∥DF，∴∠C=∠FEC，∵∠C=∠D，∴∠D=∠FEC，∴BD∥CE．点评：此题考查了平行线的判定与性质．注意内错角相等，两直线平行与同位角相等，两直线平行．2．（2013•邵阳）将一副三角板拼成如图所示的图形，过点C作CF平分∠DCE交DE于点F．（1）求证：CF∥AB；（2）求∠DFC的度数．考点：平行线的判定；角平分线的定义；三角形内角和定理．专题：证明题．分析：（1）首先根据角平分线的性质可得∠1=45°，再有∠3=45°，再根据内错角相等两直线平行可判定出AB∥CF；（2）利用三角形内角和定理进行计算即可．解答：（1）证明：∵CF平分∠DCE，∴∠1=∠2=∠DCE，∵∠DCE=90°，∴∠1=45°，∵∠3=45°，∴∠1=∠3，∴AB∥CF（内错角相等，两直线平行）；（2）∵∠D=30°，∠1=45°，∴∠DFC=180°﹣30°﹣45°=105°．点评：此题主要考查了平行线的判定，以及三角形内角和定理，关键是掌握内错角相等，两直线平行．3．（2010•江宁区一模）如图，△ABC中，AB=AC，D是CA延长线上的一点，且∠B=∠DAM．求证：AM∥BC．考点：平行线的判定．专题：证明题．分析：判别两条直线平行的方法有：同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行．要证明AM∥BC，只要转化为证明∠C=∠DAM即可．解答：证明：∵AB=AC，∴∠B=∠C，∵∠B=∠DAM，∴∠C=∠DAM，∴AM∥BC．点评：本题主要考查了平行线的判定，注意等量代换的应用．4．如图，已知DF∥AC，∠C=∠D，你能否判断CE∥BD？试说明你的理由．考点：平行线的判定．专题：探究型．分析：因为DF∥AC，由内错角相等证明∠C=∠FEC，又因为∠C=∠D，则∠D=∠FEC，故CE∥BD．解答：解：CE∥BD．理由：∵DF∥AC（已知），∴∠C=∠FEC（两直线平行，内错角相等），又∵∠C=∠D（已知），∴∠D=∠FEC（等量代换），∴CE∥BD（同位角相等，两直线平行）．点评：解答此类要判定两直线平行的题，可围绕截线找同位角、内错角和同旁内角．本题能有效地培养“执果索图”的思维方式与能力．5．如图，已知∠1=∠2，∠3=∠4，∠5=∠6，试判断ED与FB的位置关系，并说明为什么．考点：平行线的判定．专题：探究型．分析：设AB与DE相交于H，若判断ED与FB的位置关系，首先要判断∠1和∠EHA的大小；由∠3=∠4可证得BD∥CF（内错角相等，两直线平行），可得到∠5=∠BAF；已知∠5=∠6，等量代换后发现AB∥CD，即∠2=∠EHA，由此可得到∠1=∠EHA，根据同位角相等，两直线平行即可判断出BF、DE的位置关系．解答：解：BF、DE互相平行；理由：如图；∵∠3=∠4，∴BD∥CF，∴∠5=∠BAF，又∵∠5=∠6，∴∠BAF=∠6，∴AB∥CD，∴∠2=∠EHA，又∵∠1=∠2，即∠1=∠EHA，∴BF∥DE．另解：BF、DE互相平行；理由：如图；∵∠3=∠4，∴BD∥CF，∴∠5=∠BAF，∵∠5=∠6，∴∠BAF=∠6，∵△BFA、△DEC的内角和都是180°∴△BFA=∠1+∠BFA+BAF；△DEC=∠2+∠4+∠6∵∠1=∠2；∠BAF=∠6∴∠BFA=∠4，∴BF∥DE．点评：解答此类要判定两直线平行的题，可围绕截线找同位角、内错角和同旁内角．6．如图，已知AD⊥BC，EF⊥BC，∠3=∠C，求证：∠1=∠2．考点：平行线的判定．专题：证明题．分析：先由已知证明AD∥EF，再证明1∠1=∠4，∠2=∠4，等量代换得出∠1=∠2．解答：证明：∵AD⊥BC，EF⊥BC（已知），∴AD∥EF（垂直于同一条直线的两直线平行），∴∠1=∠4（两直线平行，同位角相等），又∵∠3=∠C（已知），∴AC∥DG（同位角相等，两直线平行），∴∠2=∠4（两直线平行，内错角相等），∴∠1=∠2（等量代换）．点评：此题的关键是理解平行线的性质及判定．①两直线平行，同位角相等．②两直线平行，内错角相等．③同位角相等，两直线平行．④内错角相等，两直线平行．7．如图，已知∠A=∠F，∠C=∠D，试说明BD∥CE．考点：平行线的判定．专题：推理填空题．分析：由∠A=∠F，根据内错角相等，得两条直线平行，即AC∥DF；根据平行线的性质，得∠C=∠CEF，借助等量代换可以证明∠D=∠CEF，从而根据同位角相等，证明BD∥CE．解答：解：∵∠A=∠F（已知），∴AC∥DF（内错角相等，两直线平行），∴∠C=∠CEF（两直线平行，内错角相等），∵∠C=∠D（已知），∴∠D=∠CEF（等量代换），∴BD∥CE（同位角相等，两直线平行）．点评：此题综合运用了平行线的判定及性质，比较简单．8．已知：如图，AD是△ABC的平分线，点E在BC上，点G在CA的延长线上，EG交AB于点F，且∠AFG=∠G．求证：GE∥AD．考点：平行线的判定．专题：证明题．分析：首先根据角平分线的性质可得∠BAC=2∠DAC，再根据三角形外角与内角的关系可得∠G+∠GFA=∠BAC，又∠AFG=∠G．进而得到∠BAC=2∠G，从而得到∠DAC=∠G，即可判定出GE∥AD．解答：证明：∵AD是△ABC的平分线，∴∠BAC=2∠DAC，∵∠G+∠GFA=∠BAC，∠AFG=∠G．∴∠BAC=2∠G，∴∠DAC=∠G，∴AD∥GE．点评：此题主要考查了平行线的判定，关键是掌握三角形内角与外角的关系，以及平行线的判定定理．9．如图，CA⊥AD，垂足为A，∠C=50°，∠BAD=40°，求证：AB∥CD．考点：平行线的判定．专题：证明题．分析：利用直角三角形中两锐角互余得出∠D=40°，再利用内错角相等，两直线平行的判定证明即可．解答：证明：∵CA⊥AD，∴∠C+∠D=90°，∴∠C=50°，∴∠D=40°，∵∠BAD=40°，∴∠D=∠BAD，∴AB∥CD．点评：本题主要考查了平行线的判定和直角三角形中两锐角互余，比较简单．10．如图，BE平分∠ABD，DE平分∠BDC，且∠1+∠2=90°．求证：AB∥CD．考点：平行线的判定；角平分线的定义．专题：证明题．分析：运用角平分线的定义，结合图形可知∠ABD=2∠1，∠BDC=2∠2，又已知∠1+∠2=90°，可得同旁内角∠ABD和∠BDC互补，从而证得AB∥CD．解答：证明：∵BE平分∠ABD，DE平分∠BDC（已知），∴∠ABD=2∠1，∠BDC=2∠2（角平分线定义）．∵∠1+∠2=90°，∴∠ABD+∠BDC=2（∠1+∠2）=180°．∴AB∥CD（同旁内角互补，两直线平行）．点评：灵活运用角平分线的定义和角的和差的关系是解决本题的关键，注意正确识别“三线八角”中的同位角、内错角、同旁内角．11．如图所示，已知直线a、b、c、d、e，且∠1=∠2，∠3+∠4=180°，则a与c平行吗？为什么？考点：平行线的判定；平行公理及推论．专题：探究型．分析：根据内错角相等，两直线平行可知a∥b，由同旁内角互补，两直线平行可知b∥c，根据如果两条直线都与第三条直线平行那么这两条直线平行得出结论．解答：解：平行．理由如下：∵∠1=∠2，∴a∥b（内错角相等，两直线平行），∵∠3+∠4=180°，∴b∥c（同旁内角互补，两直线平行），∴a∥c（平行于同一直线的两直线平行）．点评：本题很简单，考查的是平行线的判定定理和平行公理的推论．内错角相等，两直线平行；同旁内角互补，两直线平行；如果两条直线都与第三条直线平行那么这两条直线平行．。

平行线的判定练习题(有答案)

平行线的判定练习题(有答案)平行线的判定专项练习60题（有答案)1．已知：如图，BE平分∠ABC，∠1=∠2．求证：BC∥DE．2．如图，已知∠A=∠F，∠C=∠D，试说明BD∥CE．3．如图所示，AB⊥BC，BC⊥CD，BF和CE是射线，并且∠1=∠2，试说明BF∥CE．4．如图，AB⊥BC，∠1+∠2=90°，∠2=∠3，求证：BE∥DF．5．如图，OP平分∠MON，A、B分别在OP、OM上，∠BOA=∠BAO，那么AB平行于ON吗？若平行，请写出证明过程；若不平行，请说明理由．6．已知：如图，∠1=∠2，∠A=∠C．求证：AE∥BC．平行线的判定--- 第 1 页共 1 页7．已知，如图B、D、A在一直线上，且∠D=∠E，∠ABE=∠D+∠E，BC是∠ABE的平分线，求证：DE∥BC．8．如图，已知∠AEC=∠A+∠C，试说明：AB∥CD．9．如图，已知AC∥ED，EB平分∠AED，∠1=∠2，求证：AE∥BD．10．如图，直线AB、CD与直线EF相交于E、F，已知：∠1=105°，∠2=75°，求证：AB∥CD．11．如图，∠D=∠A，∠B=∠FCB，求证：ED∥CF．12．如图，已知AB⊥BC，CD⊥BC，∠1=∠2，求证：EB∥FC．平行线的判定---第 2 页共 2 页13．如图所示所示，已知BE是∠B的平分线，交AC于E，其中∠1=∠2，那么DE∥BC吗？为什么？14．如图，已知∠C=∠D，DB∥EC．AC与DF平行吗？试说明你的理由．15．如图，AC⊥AE，BD⊥BF，∠1=35°，∠2=35°，求证：AE∥BF．16．如图，已知AB∥CD，∠1=∠2，求证：BE∥CF．17．已知∠BAD=∠DCB，∠1=∠3，求证：AD∥BC．18．如图，AD是三角形ABC的角平分线，DE∥CA，并且交AB与点E，∠1=∠2，DF与AB是否平行？为什么？平行线的判定---第 3 页共 3 页19．如图，已知：∠C=∠DAE，∠B=∠D，那么AB平行于DF吗？请说明理由．20．如图，已知点B在AC上，BD⊥BE，∠1+∠C=90°，问射线CF与BD平行吗？说明理由．21．已知∠1的度数是它补角的3倍，∠2等于45°，那么AB∥CD吗？为什么？22．已知：如图，BDE是一条直线，∠ABD=∠CDE，BF平分∠ABD，DG平分∠CDE，求证：BF∥DG．23．如图，四边形ABCD中，∠A=∠C=90°，BF、DE分别平分∠ABC、∠ADC．判断DE、BF是否平行，并说明理由．24．如图，若∠CAB=∠CED+∠CDE，求证：AB∥CD．25．如图，CD⊥AB，GF⊥AB，∠1=∠2．试说明DE∥BC．平行线的判定---第 4 页共 4 页26．如图所示，∠CAD=∠ACB，∠D=90°，EF⊥CD．试说明：∠AEF=∠B．27．已知：如图所示，C，P，D三点在同一条直线上，∠BAP+∠APD=180°，∠E=∠F，求证：∠1=∠2．28．如图，∠D=∠1，∠E=∠2，DC⊥EC．求证：AD∥BE．29．如图，在四边形ABCD中，∠A=∠C，BE平分∠ABC，DF平分∠ADC，试说明BE∥DF．30．已知：如图，∠1=∠2，∠A=∠F，则∠C与∠D相等吗？试说明理由．31．如图，在四边形ABCD中，∠A=∠C=90°，∠1=∠2，∠3=∠4，求证：BE∥DF．平行线的判定---第 5 页共 5 页平行线测姓名：一、选择题1．下列命题中，不正确的是____ [ ]A．两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行B．两条直线被第三条直线所截，如果同旁内角互补，那么这两条直线平行C．两条直线被第三条直线所截，那么这两条直线平行D．如果两条直线都和第三条直线平行，那么这两条直线也互相平行2．如图，可以得到DE∥BC的条件是______ [ ]（2题）（5题）（3题）(7题) （8题）A．∠ACB=∠BAC B．∠ABC+∠BAE=180° C．∠ACB+∠BAD=180°D．∠ACB=∠BAD3．如图，直线a、b被直线c所截，现给出下列四个条件: (1)∠1=∠2(2)∠3=∠6(3)∠4+∠7=180° (4)∠5+∠8=180°，其中能判定a∥b的条件是_________[ ]A．(1)(3) B．(2)(4)C．(1)(3)(4) D．(1)(2)(3)(4)4．一辆汽车在笔直的公路上行驶，两次拐弯后，行驶的方向与原来的方向相同，这两次拐弯的角度可能是________[ ]A．第一次向右拐40°，第二次向左拐40° B．第一次向右拐50°，第二次向左拐130°C．第一次向右拐50°，第二次向右拐130° D．第一次向左拐50°，第二次向左拐130°5．如图，如果∠1=∠2，那么下面结论正确的是_________．[ ]A．AD∥BC B．AB∥CD C．∠3=∠4 D．∠A=∠C6．同一平面内有四条直线a、b、c、d，若a∥b，a⊥c，b⊥d，则直线c、d的位置关系为（）A．互相垂直 B．互相平行 C．相交 D．无法确定7．如图，在平行四边形ABCD中，下列各式不一定正确的是（）A．∠1+∠2=180° B．∠2+∠3=180° C．∠3+∠4=180° D．∠2+∠4=180°8．如图，AD∥BC，∠B=30°，DB平分∠ADE，则∠DEC的度数为（）A．30° B．60° C．90° D．120°二、填空题 9．如图，由下列条件可判定哪两条直线平行，并说明根据．(1)∠1=∠2，．(2)∠A=∠3，．(3)∠ABC+∠C=180°．10．如果两条直线被第三条直线所截，一组同旁内角的度数之比为3∶2，差为36°，那么这两条直线的位置关系是________．11．同垂直于一条直线的两条直线_______．同一平面内，不重合的两直线的位置关系是。

中考数学专题练习平行线及其判定(含解析)

2019中考数学专题练习-平行线及其判定（含解析）一、单选题1.如图，在四边形ABCD中，下列条件中可以判定AD∥BC的是（）A.∥1=∥3B.∥2=∥4C.∥B=∥DD.∥B+∥BCD=180°2.如图，能得到AB∥CD的条件是（）A.∥B=∥DB.∥B+∥D+∥E=180°C.∥B+∥D=180°D.∥B+∥D=∥E3.如图，若∥A=75°，则要使EB∥AC可添加的条件是（）A.∥C=75° C ．∥ABE=75° D ．∥EBC=105°B.∥DBE=75°C.∥ABE=75°D.∥EBC=105°4.在“同一平面”条件下，下列说法中错误的个数是（）（1）过一点有且只有一条直线与已知直线平行；（2）过一点有且只有一条直线与已知直线垂直；（3）平移只改变图形的位置，不改变图形的形状和大小；（4）有公共顶点且有一条公共边的两个角互为邻补角．A.1个B.2个C.3个D.4个5.如图，七年级（下）教材第4页给出了利用三角尺和直尺画平行线的一种方法，能说明AB∥DE的条件是（）A.∥CAB=∥FDEB.∥ACB=∥DFEC.∥ABC=∥DEFD.∥BCD=∥EFG6.有下列四种说法：（1）两条直线的位置关系有相交和平行两种（2）过一点能作一条直线与已知直线垂直（3）过直线外一点有且只有一条直线与这条直线平行其中正确的个数是（）A.1个B.2个C.3个D.4个7.下列说法不正确的是（）A.过任意一点可作已知直线的一条平行线B.同一平面内两条不相交的直线是平行线C.在同一平面内，过直线外一点只能画一条直线与已知直线垂直D.平行于同一直线的两直线平行8.如图，要使AD∥BC，那么可以选择下列条件中的（）A.∥1=∥4B.∥2=∥3C.∥1+∥B=180°D.∥B=∥D9.如图，已知∥1＝∥2＝∥3＝55º，则∥4＝（）A.135ºB.125ºC.110ºD.无法确定10.如图，下列条件：①∥1=∥2；②∥A=∥4；③∥1=∥4；④∥A+∥3=180°；⑤∥C=∥BDE，其中能判定AB∥DF的有（）A.2个B.3个C.4个D.5个11.如图，下列推理错误的是（）A.∥∥1=∥2，∥c∥dB.∥∥3=∥4，∥c∥dC.∥∥1=∥3，∥a∥bD.∥∥1=∥4，∥a∥b12.如果a∥b，a∥c，那么b与c的位置关系是（）A.不一定平行B.一定平行C.一定不平行D.以上都有可能13.下列说法不正确的是（）A.过任意一点可作已知直线的一条平行线B.同一平面内两条不相交的直线是平行线C.在同一平面内，过直线外一点只能画一条直线与已知直线垂直D.平行于同一直线的两直线平行14.下列说法正确的有()①不相交的两条直线是平行线;②在同一平面内,两条直线的位置关系有两种;③若线段AB 与CD没有交点,则AB∥CD;④若a∥b,b∥c,则a与c不相交.A.1个B.2个C.3个D.4个二、填空题15.如图，直线a、b被直线c所截，若满足________，则a、b平行．16.如图，是小明学习三线八角时制作的模具，经测量∥2=100°，要使木条a与b平行，则∥1的度数必须是________．17.如图，已知∥1=∥2，∥3=∥4，∥E=90°，试问：AB∥CD吗？为什么？解：∥∥1+∥3+∥E=180°________∥E=90°________∥∥1+∥3=________∥∥1=∥2，∥3=∥4________∥∥1+∥2+∥3+∥4=________∥AB∥CD________．18.如图所示，请写出能判定CE∥AB的一个条件________．19.要使AB∥CD，必须使________（写出你认为正确的一个条件即可）。

七年级数学下册平行线的判定练习题

七年级数学下册平行线的判定练习题（含答案解析）学校:___________姓名：___________班级：___________考号：___________一、单选题1．如图，下列四个结论：①①1＝①3；①①B ＝①5；①①B ＋①BAD ＝180º；①①2＝①4；①①D ＋①BCD ＝180º．能判断AB ①CD 的个数有（）A ．2个B ．3个C ．4个D ．5个2．如图，//AB CD ，120BAE ∠=︒，40DCE ∠=︒，则AEC ∠=（）A ．70︒B ．80︒C ．90︒D ．100︒3．如图，已知直线a ，b 被直线c 所截，下列条件不能判断a ①b 的是（）A ．①2＝①6B ．①2＋①3＝180°C ．①1＝①4D ．①5＋①6＝180°4．如图点E 在BC 的延长线上，则下列条件中，不能判定AB ∥CD 的是（）A ．①1＝①2B ．①B ＝①DCEC ．①3＝①4D ．①D +①DAB ＝180°5．如图所示，在下列四组条件中，能判断//AB CD 的是（）A ．12∠=∠B ．180BAD ABC ∠+∠=︒ C ．34∠=∠D ．ABD BDC ∠=∠6．下列给出的条件能够推理出a b ∥的是（）A ．12∠=∠B ．24∠∠=C ．34∠=∠D ．14180∠+∠=︒二、填空题7．如图，木工师傅用角尺画平行线的依据是_________________________.8．已知：如图，在三角形ABC 中，CD AB ⊥于点D ，连接DE ，当1290∠+∠=︒时，求证：DE ∥BC ．证明：①CD AB ⊥（已知），①90ADC ∠=︒（垂直的定义）．①1∠+________90=︒，①1290∠+∠=︒（已知），①________2=∠（依据1：________），①∥DE BC （依据2：________）．9．如图，写出能判定AB①CD的一对角的数量关系:___________________.BC ，DO①AB，则①O的半径10．如图，AB是①O的直径，CB切①O于B，连结AC交①O于D，若8cmOA=___________cm．11．如图，用符号语言表达定理“内错角相等，两直线平行”的推理形式：①_____，①a①b．三、解答题12．请完成下面的推理过程：如图，已知①D＝108°，①BAD＝72°，AC①BC于C，EF①BC于F．求证：①1＝①2．证明：①①D＝108°，①BAD＝72°（已知）①①D+①BAD＝180°AB CD（）①//①①1＝（）又①AC ①BC 于C ，EF ①BC 于F （已知）①EF // （）①①2＝（）①①1＝①2（）13．如图，四边形ABCD 中，①A ＝①C ＝90°，BE 平分①ABC ，DF 平分①ADC ，则BE 与DF 有何位置关系？试说明理由．14．如图，已知AC ①BC 于点C ，①B ＝70º，①ACD ＝20º．(1)求证：AB //CD ；(2)在不添加任何辅助线的情况下，请补充一个条件________，使BC //AD ．15．如图所示，在四边形ABCD 中，ABC ∠的角平分线及外角DCE ∠的平分线所在的直线相交于点F ，若A α∠=，D β∠=．（1）如图(a )所示，180αβ+>，试用α，β表示F ∠，直接写出结论．（2）如图(b )所示，180αβ+<，请在图中画出F ∠，并试用α，β表示F ∠．（3）一定存在F ∠吗？若有，写出F ∠的值；若不一定，直接写出α，β满足什么条件时，不存在F ∠．16．下面是王倩同学的作业及自主探究笔记，请认真阅读并补充完整．【作业】如图①，直线12l l ∥，ABC 与DBC △的面积相等吗？为什么？解：相等．理由如下：设1l 与2l 之间的距离为h ，则12ABC SBC h =⋅，12DBC S BC h =⋅△． ①ABC DBC S S =．【探究】(1)如图①，当点D 在1l ，2l 之间时，设点A ，D 到直线2l 的距离分别为h ，h '，则ABC DBC S h S h ='△△．证明：①ABC S(2)如图①，当点D 在1l ，2l 之间时，连接AD 并延长交2l 于点M ，则ABC DBC S AM S DM=△△．证明：过点A 作AE BM ⊥，垂足为E ，过点D 作DF BM ⊥，垂足为F ，则90AEM DFM ∠=∠=︒， ①AE ∥ ．①AEM △∽ ． ①AE AM DF DM=．由【探究】（1）可知ABC DBCS S =△△ ， ①ABC DBC S AM S DM=△△． (3)如图①，当点D 在2l 下方时，连接AD 交2l 于点E ．若点A ，E ，D 所对应的刻度值分别为5，1.5，0，ABC DBCS S △△的值为．17．如图，在下列括号中填写推理理由①①1=135°(已知)，①①3=①135°( )又①①2=45°(已知)，①①2+①3=45°+135°=180°，①a ①b ( )18．已知：如图，点E在线段CD上，EA、EB分别平分①DAB和①ABC，①AEB＝90°，设AD＝x，BC＝y，且（x﹣2）2＋|y﹣5|＝0．（1）求AD和BC的长．（2）试说线段AD与BC有怎样的位置关系？并证明你的结论．（3）你能求出AB的长吗？若能，请写出推理过程，若不能，说明理由．19．如图，AB＝CD，BC＝DA，求证：AB①CD，BC①DA．参考答案：1．A【分析】根据同位角相等、内错角相等、同旁内角互补的两直线平行分别判断即可．【详解】解：①①13∠=∠，①//AD BC ，无法推出//AB CD ；①①5B ∠=∠，①//AB CD ；①①180B BAD ∠+∠=°，①//AD BC ，无法推出//AB CD ；①①24∠∠=，①//AB CD ；①①180D BCD ∠+∠=︒①//AD BC ，无法推出//AB CD ，综上所述，能判断//AB CD 的是：①①，有2个，故选：A ．【点睛】题考查了平行线的判定，正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键，只有同位角相等、内错角相等、同旁内角互补，才能推出两被截直线平行．2．D【分析】过点E 作//EF AB ，先根据平行线的判定可得//EF CD ，再根据平行线的性质分别可得AEF ∠和CEF ∠的度数，然后根据角的和差即可得．【详解】如图，过点E 作//EF AB ，120BAE ∠=︒，18060AEF BAE ∴∠=︒-∠=︒，又//AB CD ，//EF CD ∴，40DCE CEF ∴=∠=∠︒，6040100AEC AEF CEF ∴∠=∠+∠=︒+︒=︒，故选：D ．【点睛】本题考查了平行线的判定与性质，熟练掌握平行线的判定与性质是解题关键．3．D【分析】根据同位角相等，内错角相等，同旁内角互补来判定两直线平行．【详解】解：A ，①2和①6是内错角，内错角相等两直线平行，能判定a ①b ，不符合题意；B ，①2+①3＝180°，①2和①3是同旁内角，同旁内角互补两直线平行，能判定a ①b ，不符合题意；C ，①1＝①4，由图可知①1与①2是对顶角，①①1＝①2＝①4，①2和①4互为同位角，能判定a ①b ，不符合D ，①5+①6＝180°，①5和①6是邻补角，和为180°，不能判定a ①b ，符合题意；故选：D ．【点睛】此题主要考查了平行线的判定，结合平行线判定的条件是解决这道题的关键．4．C【分析】根据平行线的判定定理进行逐一分析解答即可．【详解】解：A 、正确，符合“内错角相等，两条直线平行”的判定定理；B 、正确，符合“同位角相等，两条直线平行”的判定定理；C 、错误，若①3=①4，则AD ①BE ；D 、正确，符合“同旁内角互补，两条直线平行”的判定定理；故选：C ．【点睛】本题考查的是平行线的判定定理，比较简单．5．D【分析】根据平行线的判定定理求解判断即可．【详解】解：A 、①①1＝①2，①AD //BC （内错角相等，两直线平行），故此选项不符合题意；B 、①①BAD ＋①ABC ＝180°，①AD //BC （同旁内角互补，两直线平行），故此选项不符合题意；C 、①①3＝①4，①AD //BC （内错角相等，两直线平行），故此选项不符合题意；D 、①①ABD ＝①BDC ，①AB //CD （内错角相等，两直线平行），故此选项符合题意；故选：D ．【点睛】此题主要考查了平行线的判定，熟记平行线的判定定理是解题关键．6．D【分析】根据平行线的判定逐一判定即可．【详解】解：A.由12∠=∠不能推理出a b ∥，故不符合题意；B.由24∠∠=不能推理出a b ∥，故不符合题意；C.由34∠=∠不能推理出a b ∥，故不符合题意；D. ①①4+①5=180°时能推出a b ∥，又①①1=①5，①由14180∠+∠=︒能推理出a b ∥，故符合题意；【点睛】本题考查了平行线的判定定理，解决此题的关键是清楚平行线的判定定理同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行．7．在同一平面内，垂直于同一条直线的两条直线平行或根据同位角相等两直线平行.【分析】在同一平面内，垂直于同一条直线的两条直线平行或根据同位角相等两直线平行.【详解】解：在同一平面内，垂直于同一条直线的两条直线平行或根据同位角相等两直线平行. 故答案为在同一平面内，垂直于同一条直线的两条直线平行或根据同位角相等两直线平行【点睛】本题考查的是平行线的判定，熟知平行线的判定方法是解答此题的关键8． EDC ∠ EDC ∠ 同角的余角相等内错角相等，两直线平行【分析】根据垂直的定义及平行线的判定定理即可填空．【详解】①CD AB ⊥（已知），①90ADC ∠=︒（垂直的定义）．①1∠+EDC ∠90=︒，①1290∠+∠=︒（已知），①EDC ∠2=∠（同角的余角相等），①//DE BC （内错角相等，两直线平行）．故答案为：EDC ∠；EDC ∠；同角的余角相等；内错角相等，两直线平行．【点睛】此题考查了平行线的判定与性质，熟记 “内错角相等，两直线平行”是解题的关键．9．①BAC ＝①ACD （或①B ＋①BCD ＝180°或①D ＋①BAD ＝180°）【分析】根据平行线的判定定理进行填空．【详解】解：由“内错角相等，两直线平行”可以添加条件①BAC ＝①ACD ．由“同旁内角互补，两直线平行”可以添加条件①B ＋①BCD ＝180°，或①D ＋①BAD ＝180°．故答案为：①BAC ＝①ACD （或①B ＋①BCD ＝180°或①D ＋①BAD ＝180°）．【点睛】本题考查了平行线的判定．解答此类要判定两直线平行的题，可围绕截线找同位角、内错角和同旁内角．本题是一道探索性条件开放性题目，能有效地培养学生“执果索因”的思维方式与能力． 10．4【分析】先根据切线的性质得出BC①AB，再根据平行线的判定得出BC OD∥，再根据平行线分线段成比例，得出OD AOBC AB=，根据点O是AB的中点，8BC=cm，求出OD，即可得出结果．【详解】解：①CB切①O于B,①BC①AB，①DO①AB，①BC OD∥，①OD AOBC AB=，①点O是AB的中点，①2AB AO=，①12 OD AOBC AB==，①8BC=cm，①OD=4cm，①OA=OD，①OA=4cm．故答案是：4．【点睛】本题主要考查了切线的性质，平行线的判定，平行线分线段成比例，根据切线的性质，结合已知条件，求出BC OD∥，是解题的关键．11．①4＝①1【分析】两条直线被第三条直线所截，如果内错角相等，那么这两条直线平行．【详解】解：①①4＝①1，①a①b．故答案为：①4＝①1．【点睛】本题主要考查平行线的判定，熟记判定方法是解题的关键．12．见解析【分析】由直线相交及平行的相关定理性质即可得到答案．【详解】解：①①D＝108°，①BAD＝72°（已知）①①D+①BAD＝180°①//AB CD（同旁内角互补，两直线平行）①①1＝3∠（两直线平行，内错角相等）又①AC ①BC 于C ，EF ①BC 于F （已知）①EF //AC （垂直于同一直线的两条直线平行）①①2＝3∠（两直线平行，同位角相等）①①1＝①2（等量代换）【点睛】本题考查直线相交及平行的相关定理性质，熟练掌握相关知识是解题的关键．13．BE ①DF ，理由见解析【分析】根据四边形的内角和定理和①A ＝①C ＝90°，得①ABC ＋①ADC ＝180°；根据角平分线定义、等角的余角相等易证明和BE 与DF 两条直线有关的一对同位角相等，从而证明两条直线平行．【详解】解：BE ①DF ．理由如下：①①A ＝①C ＝90°，①①ABC ＋①ADC ＝180°①BE 平分①ABC ，DF 平分①ADC ，①①1＝①2＝12①ABC ，①3＝①4＝12①ADC ，①①1＋①3＝12（①ABC ＋①ADC ）＝12×180°＝90°，又①①1＋①AEB ＝90°，①①3＝①AEB①BE ①DF【点睛】本题考查了四边形的内角和是360°、角平分线定义、等角的余角相等和平行线的判定，考察的知识点较多，只有熟练掌握，才能运用自如．14．(1)证明见解析(2)AC ①AD （答案不唯一）【分析】（1）由题意易求出110BCD BCA ACD ∠=∠+∠=︒，即可利用同旁内角互补，两直线平行证明；（2）由在同一平面内，垂直于同一条直线的两条直线互相平行，即可补充条件为：AC ①AD ．（答案不唯一）(1)证明：①AC ①BC ，①90ACB ∠=︒，①110BCD BCA ACD ∠=∠+∠=︒，①180BCD B ∠+∠=︒，①AB CD ；(2)补充条件：AC ①AD ，①AC ①AD ，AC ①BC①BC //AD ．故答案为：AC ①AD ．【点睛】本题考查垂直的定义，平行线的判定．掌握平行线的判定条件是解题关键．15．（1）()1902F αβ∠=+-︒；（2）图见解析，()1902F αβ∠=︒-+，证明见解析；（3）180αβ+=︒时，不存在F ∠，证明见解析．【分析】（1）先根据四边形的内角和求出360D ABC CB βα∠=︒-∠-+，再根据角平分线的定义、邻补角的定义得出1,19022ABC F FBC DC E B C ∠=︒-∠∠∠=，然后根据三角形的外角性质即可得；（2）先根据角平分线的定义画出图形，再参照题（1）：由四边形的内角和求出360D ABC CB βα∠=︒-∠-+，再根据角平分线的定义、对顶角的性质得出11,9022GBC ABC BCF DCB ∠=∠∠=︒-∠，然后根据三角形的外角性质即可得；（3）由题（1）和（2）可知，当180αβ+>︒和180αβ+<︒时，存在F ∠的值，因此，考虑当180αβ+=︒时，F ∠是否存在．证明如下：先根据四边形的内角和得出180ABC DCB ∠+∠=︒，再根据邻补角的定义得出180DCE DCB ∠+∠=︒，从而得出ABC DCE ∠=∠，然后根据角平分线的定义可得出GBC ECF ∠=∠，最后根据平行线的判定得出//BG CF ，即可得证．【详解】（1）()1902F αβ∠=+-︒，求解过程如下：在四边形ABCD 中，,A D αβ∠=∠=360360DCB ABC D A αβ∠=︒-∠-=︒∴∠-+-∠ BF 平分ABC ∠，CF 平分DCE ∠1,2111(180)90222FBC DCE DCB DCB ABC FCE ∴∠=∠=︒-∠=︒-∠∠∠= F FC FB E C ∠=∠-∴∠119022DC AB B C =︒∠-∠- 902)1(DCB ABC =︒-∠+∠ 190(362)0αβ=︒-︒--)1(902βα=-+︒；（2）由题意，画ABC ∠的角平分线及外角DCE ∠的平分线所在的直线相交于点F ，则所要画的F ∠如下图所示．求解过程如下：①()360ABC DCB A D ∠+∠=︒-∠+∠，且A α∠=，D β∠=①360D ABC CB βα∠=︒-∠-+①BG 平分ABC ∠，CH 平分DCE ∠ ①1111,(180)902222GBC ABC ECH DCE DCB DCB ∠=∠∠=∠=︒-∠=︒-∠ 1902BCF ECH DCB ∴∠=∠=︒-∠ ①GBC ∠是BCF ∆的一个外角①GBC F BCF ∠=∠+∠①F GBC BCF ∠=∠-∠11(90)22ABC DCB =∠-︒-∠ 1()902ABC DCB =∠+∠-︒ 1(360)902αβ=︒---︒ 190()2αβ=︒-+；（3）当180αβ+=︒时，不存在F ∠．证明过程如下：①()360ABC DCB A D ∠+∠=︒-∠+∠，且A α∠=，D β∠=①360180ABC DCB αβ∠+∠=︒--=︒180DCE DCB ∠+∠=︒ABC DCE ∴∠=∠①BG 平分ABC ∠，CF 平分DCE ∠ ①11,22GBC ABC ECF DCE ∠=∠∠=∠GBC ECF ∴∠=∠①//BG CF故当180αβ+=︒时，不存在F ∠．【点睛】本题考查了四边形的内角和、三角形的外角性质、角平分线的定义、平行线的判定等知识点，较难的是题（3），综合题（1）和（2）的题设与结论，正确提出假设是解题关键．16．(1)证明见解析(2)证明见解析 (3)73【分析】（1）根据三角形的面积公式可得11,22ABC DBC S S BC h BC h '=⋅=⋅，由此即可得证；（2）过点A 作AE BM ⊥，垂足为E ，过点D 作DF BM ⊥，垂足为F ，先根据平行线的判定可得AE DF ，再根据相似三角形的判定可证AEM DFM ~，根据相似三角形的性质可得AE AM DF DM =，然后结合【探究】（1）的结论即可得证；（3）过点A 作AM BC ⊥于点M ，过点D 作DN BC ⊥于点N ，先根据相似三角形的判定证出AME DNE ~，再根据相似三角形的性质可得73AM AE DN DE ==，然后根据三角形的面积公式可得12ABC S BC AM =⋅，12DBC S BC DN =⋅，由此即可得出答案． (1) 证明：12ABC SBC h =⋅，12DBC BC h S '=⋅， ABC DBC Sh S h ∴='． (2)证明：过点A 作AE BM ⊥，垂足为E ，过点D 作DF BM ⊥，垂足为F ，则90AEM DFM ∠=∠=︒，AE DF ∴∥．AEM DFM ~∴．AE AM DF DM∴=．由【探究】（1）可知ABC DBC SAE S DF =， ABC DBC SAM S DM∴=． (3)解：过点A 作AM BC ⊥于点M ，过点D 作DN BC ⊥于点N ，则90AME DNE ∠=∠=︒，AM DN ∴， AME DNE ∴~， AM AE DN DE∴=，点,,A E D 所对应的刻度值分别为5，1.5，0，5 1.5 3.5AE ∴=-=， 1.5DE =，3.571.53AM DN ∴==，又12ABC S BC AM =⋅，12DBC S BC DN =⋅， 73ABC DBC S AM S DN =∴=，故答案为：73．【点睛】本题考查了相似三角形的判定与性质、平行线的判定、三角形的面积等知识点，熟练掌握相似三角形的判定与性质是解题关键．17．对顶角相等，同旁内角互补，两直线平行【分析】根据图形由对顶角相等，及平行线的判定中同旁内角互补，两直线平行可直接得出理由；【详解】①①1=135°(已知)，①①3=①135°(对顶角相等)又①①2=45°(已知)，①①2+①3=45°+135°=180°，①a ①b (同旁内角互补，两直线平行)故答案为：对顶角相等；同旁内角互补，两直线平行【点睛】本题考查了对顶角相等；平行线的判定中同旁内角互补，两直线平行；重点掌握平行线判定定理． 18．（1）2AD =，5BC =；（2）//AD BC ，见解析；（3）能，见解析【分析】（1）根据算术平方根和绝对值的非负性即可得出AD 、BC 的长度；（2）根据题意证明180BAD ABC ∠+∠=︒即可得出结果；（3）延长AE 交直线BC 于F ，先证明①AEB ①①FEB ，然后证明()ADE FCE ASA ∆≅∆，即可得出结果．【详解】解：（1）2(2)|5|0x y -+-=，20x ∴-=，50y -=，解得2x =，5y =，即2AD =，5BC =；（2）//AD BC ．理由如下：EA 、EB 分别平分DAB ∠和ABC ∠，12BAE BAD ∴∠=∠，12ABE ABC ∠=∠， 1()2BAE ABE BAD ABC ∴∠+∠=∠+∠， 90AEB ∠=︒，90BAE ABE ∴∠+∠=︒，180BAD ABC ∴∠+∠=︒，//AD BC ∴；（3）能．理由如下：延长AE 交直线BC 于F ，如图，//AD BC ，DAF F ∴∠=∠，而DAF BAF ∠=∠，BAF F ∴∠=∠，在①AEB 和①FEB 中90BAE F BEA BEF BE BE ⎧∠=∠⎪∠=∠=⎨⎪=⎩，①①AEB ①①FEB （AAS ）AB FB ∴=，AE ＝EF ．在①ADE 和①FCE 中DAE F AE FEAED FEC ∠=∠⎧⎪=⎨⎪∠=∠⎩， ()ADE FCE ASA ∴∆≅∆，2AD CF ∴==，527AB BF ∴==+=．【点睛】本题考查了算术平方根和绝对值的非负性，角平分线的定义，平行线的判定，全等三角形的判定与性质，熟知相关性质定理是解本题的关键．19．见解析【分析】连接AC ，利用SSS 得到ABC CDA △△≌，利用全等三角形的对应角相等得到两对内错角相等，利用内错角相等两直线平行即可得证．【详解】证明：连接AC ，在ABC 和CDA 中，AB CD BC AD AC CA =⎧⎪=⎨⎪=⎩，①()ABC CDA SSS ≌，①BAC DCA ACB CAD ∠=∠∠=∠，，①//AB DC ，//AD BC ．【点睛】此题考查了全等三角形的判定与性质，以及平行线的判定，熟练掌握全等三角形的判定与性质是解本题的关键．。

平行线的判定专项练习题有答案

平行线的判定专项练习题有答案Last revised by LE LE in 20211．已知：如图，BE平分∠ABC，∠1=∠2．求证：BC∥DE．2．如图，已知∠A=∠F，∠C=∠D，试说明BD∥CE．3．如图所示，AB⊥BC，BC⊥CD，BF和CE是射线，并且∠1=∠2，试说明BF∥CE．4．如图，AB⊥BC，∠1+∠2=90°，∠2=∠3，求证：BE∥DF．5．如图，OP平分∠MON，A、B分别在OP、OM上，∠BOA=∠BAO，那么AB平行于ON吗若平行，请写出证明过程；若不平行，请说明理由．6．已知：如图，∠1=∠2，∠A=∠C．求证：AE∥BC．7．已知，如图B、D、A在一直线上，且∠D=∠E，∠ABE=∠D+∠E，BC是∠ABE的平分线，求证：DE∥BC．8．如图，已知∠AEC=∠A+∠C，试说明：AB∥CD．9．如图，已知AC∥ED，EB平分∠AED，∠1=∠2，求证：AE∥BD．10．如图，直线AB、CD与直线EF相交于E、F，已知：∠1=105°，∠2=75°，求证：AB∥CD．11．如图，∠D=∠A，∠B=∠FCB，求证：ED∥CF．12．如图，已知AB⊥BC，CD⊥BC，∠1=∠2，求证：EB∥FC．13．如图所示所示，已知BE是∠B的平分线，交AC于E，其中∠1=∠2，那么DE∥BC吗为什么14．如图，已知∠C=∠D，DB∥EC．AC与DF平行吗试说明你的理由．15．如图，AC⊥AE，BD⊥BF，∠1=35°，∠2=35°，求证：AE∥BF．16．如图，已知AB∥CD，∠1=∠2，求证：BE∥CF．17．已知∠BAD=∠DCB，∠1=∠3，求证：AD∥BC．18．如图，AD是三角形ABC的角平分线，DE∥CA，并且交AB与点E，∠1=∠2，DF与AB是否平行为什么19．如图，已知：∠C=∠DAE，∠B=∠D，那么AB平行于DF吗请说明理由．20．如图，已知点B在AC上，BD⊥BE，∠1+∠C=90°，问射线CF与BD平行吗说明理由．21．已知∠1的度数是它补角的3倍，∠2等于45°，那么AB∥CD吗为什么22．已知：如图，BDE是一条直线，∠ABD=∠CDE，BF 平分∠ABD，DG平分∠CDE，求证：BF∥DG．23．如图，四边形ABCD中，∠A=∠C=90°，BF、DE分别平分∠ABC、∠ADC．判断DE、BF是否平行，并说明理由．24．如图，若∠CAB=∠CED+∠CDE，求证：AB∥CD．25．如图，CD⊥AB，GF⊥AB，∠1=∠2．试说明DE∥BC．26．如图所示，∠CAD=∠ACB，∠D=90°，EF⊥CD．试说明：∠AEF=∠B．27．已知：如图所示，C，P，D三点在同一条直线上，∠BAP+∠APD=180°，∠E=∠F，求证：∠1=∠2．28．如图，∠D=∠1，∠E=∠2，DC⊥EC．求证：AD∥BE．29．如图，在四边形ABCD中，∠A=∠C，BE平分∠ABC，DF平分∠ADC，试说明BE∥DF．30．已知：如图，∠1=∠2，∠A=∠F，则∠C与∠D相等吗试说明理由．31．如图，在四边形ABCD中，∠A=∠C=90°，∠1=∠2，∠3=∠4，求证：BE∥DF．32．如图，已知∠1=∠2求证：a∥b．33．如图，D E⊥AO于E，BO⊥AO于O，FC⊥AB于C，∠1=∠2，找出图中互相平行的线，并加以说明．34．如图，已知∠1=∠2，∠C=∠CDO，求证：CD∥OP．35．如图，已知DE平分∠BDF，AF平分∠BAC，且∠1=∠2．求证（1）DF∥AC；（2）DE∥AF．36．如图，AD平分∠BAC，EF平分∠DEC，且∠1=∠2，试说明DE与AB的位置关系．37．如图，在△ABC中，点D在AB上，∠ACD=∠A，∠BDC的平分线交BC于点E．求证：DE∥AC．38．如图，AB与CD相交于点O，并且∠A=∠1，试问∠2与∠B满足什么关系时，AC∥BD说明理由．39．如图，已知∠1=∠A，∠2=∠B，那么MN与EF平行吗如果平行，请说明理由．40．如图，直线AB、CD被直线EF所截，∠1+∠4=180°，求证：AB∥CD．41．如图所示，已知：∠1=∠2，∠E=∠F．试说明AB∥CD．42．如图，已知EF⊥CD于F，∠GEF=25°，∠1=65°，则AB与CD平行吗请说明理由．43．如图，已知∠1=∠2=90°，∠3=30°，∠4=60°，图中有几对平行线说说你的理由．44．直线AB，CD被直线EF所截，∠1=∠2，直线AB 和CD平行吗为什么45．已知：如图，AD⊥BC，EF⊥BC，∠1=∠2．求证：AB∥GF．46．如图，已知B、C、D三点在同一条直线上，∠B=∠1，∠2=∠E，试说明AD∥CE．47．直线AB、CD与GH交于E、F，EM平分∠BEF，FN 平分∠DFH，∠BEF=∠DFH，求证：EM∥FN．48．如图所示，∠ABC=∠BCD，BE、CF分别平分∠ABC 和∠BCD，请你说出BE与CF的位置关系，并说出你的理由．49．如图，若∠1=∠2，请判断DB与EC的位置关系，并说明理由．50．如图，在△ABC中，CD⊥AB，垂足为D，点E在BC 上，EF⊥AB，垂足为F．（1）CD与EF平行吗为什么（2）如果∠1=∠2，DG∥BC吗为什么51．如图，已知：HG平分∠AHM，MN平分∠DMH，且∠AHM=∠DMH．问：GH与MN有怎样的位置关系，请说明理由．（请注明每一步的理由）52．已知：如图，∠C=∠1，∠2和∠D互余，BE⊥FD 于点G．求证：AB∥CD．53．如图，直线AB，CD被EF所截，∠3=∠4，∠1=∠2，EG⊥FG．求证：AB∥CD．54．已知：如图，CD是直线，E在直线CD上，∠1=130°，∠A=50°，求证：AB∥CD．55．如图，已知∠1=∠2，∠DAB=∠DCA，且DE⊥AC，BF⊥AC，问：（1）AD∥BC吗（2）AB∥CD吗为什么56．如图，四边形ABCD，∠1=30°，∠B=60°，AB⊥AC，则AD与BC一定平行吗AB与CD呢若平行请说明理由，反之则不用说明理由．57．已知：如图，∠A=∠F，∠C=∠D．求证：BD∥CE．58．如图，AD⊥BC于点D，∠1=2，∠CDG=∠B，请你判断EF与BC的位置关系，并加以证明，要求写出每步证明的理由．59．已知：如图，CE平分∠ACD，∠1=∠B，求证：AB∥CE．60．如图，已知∠1=∠2，∠3=∠4，可以判定哪两条直线平行。

平行线的判定定理习题答案.doc

平行线的判定定理习题精选1 .平行线的判定定理一：_________________________2.平行线的判定定理二： ________________________3.填空。

如图，VAC1AB, BD1AB （已知）.\ZCAB = ZVZCAE=ZDBF （已知）AZBAE=ZA ZCAB=90° , Z =90°4.己知，如图Zl + Z2=180° ,填空。

VZl + Z2=180°又Z2=Z3 （/•Zl + Z3=180°5.如图,填空。

A DB10.如图，已知：ZAOE+ZBEF=180° , ZAOE+ZCDE= 180° ,求证：CD 〃BE 。

(1) ZA 与互补，贝(2) ZA 与互补，贝6.下列命题中，不正确的是（A .如果两条直线都和第三条宜线平行，那么两条直线也互相平行B. 两条直线被第三条直线所截，如果同位角相等，那么两直线平C. 两条直线被第三条直线所截，如果内错角互补，那么两直线必平D. 两条直线被第三条直线所截，如果两直线不平行，那么内错伯必不相如图，直线a 、b 被直线c 所截，给出下列条件，①Z1 = Z2,②匕3=匕6,③Z4+Z7=180° + Z8=180°其中能判断a//b 的是（7. A. ①③ B.②④AB 〃8.已知: 如图, Z1 = ZA, Z2= ZC,求证: 9. 如图, 已知: Zl + Z2=180°11.如图，已知:13.已知：如图,14.已知：如图: 求证：GH〃MN。

ZA=Z1, ZC=Z2o 求证：求证：AB〃CD。

AB±BC, Zl + Z2=90° , Z2=Z3o 求证：BE〃DF。

ZAHF+ZFMD=180°, GH 平分ZAHM, MN 平分ZDMHo12.如图，巳知: Zl = ZC+ZEo 求证：ACz/BDoD答案1.内错角相等，两宜线平行2.同旁内角互补，两直线平行3.略4.略5.（1） ZD CD 同旁内角互补两直线平行（2） ZB BC 同旁内角互补，两直线平行6. C7. D8.VZ1 = ZA, Z2=ZC, XZ1 = Z2 （对顶角相等）,AZA=ZC （等量代换）,AAB/7CD （内错角相等，两直线平行）。

平行线的判定证明题（精选篇）

平行线的判定证明题平行线的判定证明题平行线的判定证明题1)两条平行线被第三条直线所截，同位角相等;(2)两条平行线被第三条直线所截，内错角相等;(3)两条平行线被第三条直线所截，同旁内角互补。

(1)两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行;(2)两条直线被第三条直线所截，如果内错角相等，那么这两条直线平行;(3)两条直线被第三条直线所截，如果同旁内角相等，那么这两条直线平行。

按这个判定，绝对没错。

这两种的第一条都没有办法判定，而后两条就完全可以按照第一条来判定，最后的结果一定是对的。

2平行线的性质：(1)两条平行线被第三条直线所截，同位角相等;(2)两条平行线被第三条直线所截，内错角相等;(3)两条平行线被第三条直线所截，同旁内角互补。

平行线的判定定理：(1)两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行;(2)两条直线被第三条直线所截，如果内错角相等，那么这两条直线平行;(3)两条直线被第三条直线所截，如果同旁内角相等，那么这两条直线平行。

平行线的性质：在同一平面内永不相交的两条直线叫做平行线。

3光学原理。

延长GE角D于Q因为∠2=∠3，所以AB∥D由AB∥D可得∠1=∠GQD又∠1=∠4所以∠4=∠GQD所以GQ∥FH 即：GE∥FH因为∠2=∠3所以AB∥D所以角FE=角FEB所以大角HFE=大角FEG所以HF∥GE4)要证明AB∥GD，只要证明∠1=∠BAD即可，根据∠1=∠2，只要再证明∠2=∠BAD即可证得;(2)根据AB∥D，∠1：∠2：∠3=1：2：3即可求得三个角的度数，再根据∠EBA与∠ABD互补，可求得∠EBA的度数，即可作出判断.解答：解：(1)证明：∵AD⊥B，EF⊥B(已知)∴∠EFB=∠ADB=90°(垂直的定义)∴EF∥AD(同位角相等，两直线平行)(2分)∴∠2=∠BAD(两直线平行，同位角相等)(3分)∵∠1=∠2，(已知)∴∠1=∠BAD(等量代换)∴AB∥DG.(内错角相等，两直线平行)(4分)(2)判断：BA平分∠EBF(1分)证明：∵∠1：∠2：∠3=1：2：3∴可设∠1=k，∠2=2k，∠3=3k(k 0)∵AB∥D∴∠2+∠3=180°(2分)∴2k+3k=180°∴k=36°∴∠1=36°，∠2=72°(4分)∴∠ABE=72°(平角定义)∴∠2=∠ABE∴BA平分∠EBF(角平分线定义).(5分)。

平行线的性质专项练习60题有答案

平行线的性质专项练习60题（有答案）1．如图，AB∥CD，证明：∠A=∠C+∠P．2．如图，已知AB∥ED，∠1=35°，∠2=80°，求∠ACD的度数．3．已知：如图所示，直线AD∥BC，AD平分∠CAE，求证：∠B=∠C．4．已知∠E=∠F，AD∥EF，问：AD是∠BAC平分线吗？为什么？5．如图所示，AB∥CD，∠3：∠2=3：2，求∠1的度数．6．如图，直线AB∥CD，直线AB、CD被直线EF所截，EG平分∠BEF，FG平分∠DFE，求证：EG⊥FG．7．如图所示，AB∥DF，DE∥BC，∠1=65°，求∠2，∠3的度数，并说明理由．8．已知AB∥CD，FE⊥AB交AB于G点，∠GEH=138°，求∠EHD的度数．9．如图，AD∥BC，∠B=25°，∠C=30°，求∠EAC的度数．10．如图，AB∥CD，AC⊥BC，∠BAC=65°，求∠BCD度数．11．如图，AB∥CD，∠BAE=∠DCE=45°，说明AE⊥CE．12．如图，AB∥CD∥EF，∠ABC=55°，∠CEF=150°，求∠BCE的度数．13．如图，DE∥BC，∠D：∠DBC=2：1，∠1=∠2，求∠DEB的度数．14．已知：如图AB∥CD，EF⊥AB于E，FH交CD于H，∠CHG=130度．求∠EFH度数．15．已知：如图，AC∥BD，∠A=∠D，求证：∠E=∠F．16．已知，如图，AB∥CD∥GH，EG平分∠BEF，FG平分∠EFD．求证：∠EGF=90°．17．如图，已知AB⊥AC，垂足为A，AD∥BC，且∠1=30°，试求∠2与∠B的度数．18．如图所示，AB∥CD，若∠B=45°，∠D=20°，求∠1的度数．19．如图，△ABC中，角平分线BO与CO的相交点O，OE∥AB，OF∥AC，△OEF的周长=10，求BC的长．20．如图，若AB∥CD，∠C=60°，求∠A+∠E的度数．21．如图所示，已知AB∥CD，BC∥DE，若∠B=55°，求∠D的度数．22．如图所示，已知∠ACB=60°，∠ABC=50°，BO，CO分别平分∠ABC，∠ACB，EF经过点O且平行于BC，求∠BOC的度数．23．已知：如图所示，AB∥CD，∠B=120°，CA平分∠BCD．求证：∠1=30°．24．如图，AB∥CD，∠A=40°，∠C=65°，求∠E的度数．25．如图所示．CD是∠ACB的平分线，∠ACB=40°，∠B=70°，DE∥BC．求∠EDC和∠BDC的度数．26．如图，点A在直线MN上，且MN∥BC，求证：∠BAC+∠B+∠C=180°．27．已知：如图，OP平分∠AOB，MN∥OB．求证：∠1=∠3．28．如图所示，AB∥CD，∠1=55°，∠D=∠C，求出∠D，∠C，∠B的度数．29．已知，如图，AD∥BC，∠1=∠2，∠A=120°，且BD⊥CD，求∠C的度数．30．如图，已知直线AB∥CD，直线m与AB、CD相交于点E、F，EG平分∠FEB，∠EFG=50°，求∠FEG的度数．31．如图，已知CD∥AB，OE平分∠BOD，∠D=52°，求∠BOE的度数．32．如图所示，直线l1∥l2，∠A=90°，∠ABF=25°，求∠ACE的度数．33．如图，AB∥CD，∠1=45°，∠D=∠C，求∠D、∠C、∠B的度数．34．如图，CD∥AB，CD∥EF，∠A=105°，∠ACE=51°，求∠E的度数．35．如图：a∥b，∠1=122°，∠3=50°，求∠2和∠4的度数．36．如图，已知AB∥CD，∠1=50°，BD平分∠ADC，求∠A的度数．37．已知，如图所示，DE∥BC，BE平分∠ABC，且∠ABC=∠ACB，∠AED=72°，求∠CEB的度数．38．如图，若AB∥EF，∠C=90°，求x+y﹣z度数．39．如图，已知AB∥DE，∠B=70°，CM平分∠DCB，CM⊥CN，垂足为C，求∠NCE的度数．40．如图，DE∥AB，∠1=∠2，那么∠A=∠3吗？说明理由．41．如图，已知DB∥FG∥EC，∠ABD=84°，∠ACE=60°，AP是∠BAC的平分线．求∠PAG的度数．42．已知：如图AB∥CD，∠1=∠A，∠2=∠C，B、E、D在一条直线上．求∠AEC的度数．43．已知：如图，直线l1∥l2，AB⊥l1垂足为O，BC与l2相交于点D，∠1=43°，求∠2的度数．44．如图，直线AB∥MN，分别交直线EF于点C、D，∠BCD、∠CDN的角平分线交于点G，求∠CGD的度数．45．如图所示．已知AB∥CD，∠B=100°，EF平分∠BEC，EG⊥EF．求∠BEG和∠DEG．46．如图AE∥BD，∠CBD=57°，∠AEF=125°，求∠C的度数，并说明理由．47．已知：如图，△ABC中，点D在AC的延长线上，CE是∠DCB的角平分线，且CE∥AB．求证：∠A=∠B．48．如图，∠ABD和∠BDC的平分线相交于点E，BE交CD于F，∠1+∠2=90°，试问：直线AB、CD在位置上有什么关系？∠2与∠3在数量上有什么关系？49．如图，已知直线AB∥CD，直线GH分别与直线AB、CD交于点E、G，直线CF交直线GH于点F，已知∠CFG=30°，∠HEB=50°，求∠FCG的度数．50．如图，AB∥CD，BC∥ED，求：∠B+∠D的度数．51．如图，已知AB∥CD，∠B=∠DCE，求证：CD平分∠BCE．52．如图，已知AB∥CD，∠B=40°，CN是∠BCE的平分线，CM⊥CN，求∠BCM的度数．53．如图，在△ABC中，D是∠BAC的平分线上一点，BD⊥AD于D，DE∥AC交AB于E，请说明AE=BE．54．如图所示，AB∥CD，BF平分∠ABE，DF平分∠CDE，∠BFD=55°，求∠BED的度数．55．如图，CD⊥AB，DE∥AC，EF⊥AB，EF平分∠BED，求证：CD平分∠ACB．56．如图，△ABC中，EB平分∠ABC，EC平分△ABC的外角∠ACG，过点E作DF∥BC交AB于D，交AC于F，求证：DB﹣CF=DF．57．已知：如图所示，AB∥CD，EF平分∠GFD，GF交AB于M，∠GMA=52°，求∠BEF的度数．58．如图，∠BAP+∠APD=180°，∠1=∠2，求证：∠E=∠F．59．如图，已知DE∥AB，DF∥AC，∠EDF=85°，∠BDF=63°．（1）∠A的度数；（2）∠A+∠B+∠C的度数．60．如图，已知AB∥CD，∠1=∠2，∠EFD=56°，求∠EGD的度数．11 / 17第11页共17 页平行线的性质60题参考答案：1．∵AB∥CD，∴∠A=∠PED，（两直线平行，同位角相等）又∠PED为△PCE的外角，∴∠P+∠C=∠PED，∴∠P+∠C=∠A．2．解法一：过C点作CF∥AB，则∠1=∠ACF=35°（两直线平行，内错角相等），∵AB∥ED，CF∥AB（已知），∴CF∥ED（平行于同一直线的两直线平行）∴∠FCD=180°﹣∠2=180°﹣80°=100°（两直线平行，同旁内角内角互补）∴∠ACD=∠ACF+∠FCD=35°+100°=135°；解法二：延长DC交AB于F∵AB∥ED（已知），∴∠BFC=∠2=80°（两直线平行，内错角相等），∵∠ACF=∠BFC﹣∠1=80°﹣35°=45°（三角形一个外角等于它不相邻的两个内角的和）∴∠ACD=180°﹣∠ACF=180°﹣45°=135°（1平角=180°）．解法三：延长AC、ED交于F∵AB∥ED，∴∠DFC=∠1=35°∵∠CDF=180°﹣∠2=180°﹣80°=100°∴∠ACD=∠CDF+∠DFC=100°+35°=135°．3．∵AD∥BC，∴∠C=∠CAD，∠B=∠DAE，又∵AD平分∠CAE，∴∠CAD=∠DAE，即∠C=∠B．4．∵AD∥EF（已知）∴∠BAD=∠E（两直线平行，同位角相等）∠DAC=∠F（两直线平行，内错角相等）∵∠E=∠F（已知）∴∠BAD=∠DAC（等量代换）∴AD是∠BAC的平分线．5．设∠3=3x，∠2=2x，由∠3+∠2=180°，可得3x+2x=180°，∴x=36°，∴∠2=2x=72°；∵AB∥CD，∴∠1=∠2=72°6．∵AB∥CD，∴∠BEF+∠EFD=180°，∵EG平分∠BEF，FG平分∠DFE，∴∠1=∠BEF，∠2=∠EFD，∴∠1+∠2=（∠BEF+∠EFD）=×180°=90°，在△EFG中，∠G=180°﹣∠1﹣∠2=90°，∴EG⊥FG．7．∵DE∥BC，∴∠1+∠2=180°，又∵∠1=65°，∴∠2=115°；∵AB∥DF，∴∠3=∠2=115°．8．如图，过点E作EP∥AB，而AB∥CD，则EP∥CD，∴∠FEP=∠FGB，∵EF⊥AB，∴∠FGB=90°，∵∠GEH=138°，∴∠PEH=138°﹣90°=48°∵EP∥CD，∴∠EHD=180°﹣∠PEH=132°9．∵AD∥BC，∴∠EAD=∠B=25°，∠DAC=∠C=30°，∴∠EAC=∠EAD+∠DAC=25°+30°=55°．10．∵AB∥CD，∴∠ACD=180°﹣65°=115°，∵AC⊥BC，∴∠BCD=115°﹣90°=25°．11．过点E作EF∥AB，∴∠AEF=∠BAE=45°，∵AB∥CD，∴EF∥CD，∴∠FEC=∠DCE=45°，∴∠AEC=∠AEF+∠FEC=90°，∴AE⊥CE．12．∵AB∥CD，∠ABC=55°，∴∠BCD=∠ABC=55°，∵EF∥CD，∴∠ECD+∠CEF=180°，∵∠CEF=150°，∴∠ECD=180°﹣∠CEF=180°﹣150°=30°，∴∠BCE=∠BCD﹣∠ECD=55°﹣30°=25°，∴∠BCE的度数为25°．13．设∠1为x，∵∠1=∠2，∴∠2=x，∴∠DBC=∠1+∠2=2x，∵∠D：∠DBC=2：1，∴∠D=2×2x=4x，∵DE∥BC，∴∠D+∠DBC=180°，即2x+4x=180°，解得x=30°，∵DE∥BC，∴∠DEB=∠1=30°．14．∵EF⊥AB于E，MN∥AB∴EF⊥MN即∠EFM=90°．∵MN∥CD∴∠NFH=∠GHD=180°﹣130°=50°∴∠EFH=∠EFM+∠NFH=90°+50°=140°．15．∵AC∥BD，∴∠1=∠2．又∵∠A=∠D，∠A+∠1+∠E=180°，∠D+∠2+∠F=180°，∴∠E=∠F．16．∵HG∥AB（已知），∴∠1=∠3（两直线平行，内错角相等），又∵HG∥CD（已知），∴∠2=∠4（两直线平行，内错角相等），∵AB∥CD（已知），∴∠BEF+∠EFD=180°（两直线平行，同旁内角互补），又∵EG平分∠BEF（已知），∴∠1=∠BEF（角平分线的定义），又∵FG平分∠EFD（已知），∴∠2=∠EFD（角平分线的定义），∴∠1+∠2=（∠BEF+∠EFD），∴∠1+∠2=90°，∴∠3+∠4=90°（等量代换）即∠EGF=90°17．∵AD∥BC，∴∠2=∠1=30°，∵AB⊥AC，∴∠B=90°﹣∠2=60°．18．过E作EF∥AB，∵AB∥CD，∴AB∥EF∥CD，∴∠B=∠BEF=45°，∠DEF=∠D=20°，∴∠1=∠BEF+∠DEF=45°+20°=65°．19．∵OB，OC分别是∠ABC，∠ACB的平分线，∴∠1=∠2，∠4=∠5，∵OE∥AB，OF∥AC，13 / 17第13页共17 页∴∠1=∠3，∠4=∠6，∴BE=OE，OF=FC，∴BC=BE+EF+FC=OF+OE+EF，∵△OEF的周长=10，∴BC=10．20．∵AB∥CD，∠C=60°，∴∠EFB=∠C=60°；∵∠EFB=∠A+∠E，∴∠A+∠E=60°．21．∵AB∥CD，∴∠C=∠B．∵∠B=55°，∴∠C=55°．∵BC∥DE，∴∠C+∠D=180°，即∠D=180°﹣∠C=180°﹣55°=125°．22．∵EF∥BC，∴∠EOB=∠OBC，∠FOC=∠OCB，∵BO，CO分别平分∠ABC，∠ACB，∴∠OBC=∠ABC=×50°=25°，∠OCB=∠ACB=×60°=30°．∴∠EOB=25°，∠FOC=30°．又∵∠EOB+∠BOC+∠FOC=180°，∴∠BOC=180°﹣∠EOB﹣∠FOC=180°﹣25°﹣30°=125°23．∵AB∥CD，∴∠B+∠BCD=180°，∵∠B=120°，∴∠BCD=60°；又∵CA平分∠BCD，∴∠2=30°，∵AB∥CD，∴∠1=∠2=30°24．∵AB∥CD，∴∠EFB=∠C=65°，∵∠EFB=∠A+∠E，∴∠E=∠EFB﹣∠A=65°﹣40°=25°．25．∵CD是∠ACB的平分线，∠ACB=40°，∴∠DCB=∠ACD=20°，又DE∥BC，∴∠EDC=∠DCB=20°，在△BCD中，∵∠B=70°，∴∠BDC=90°．∴∠EDC和∠BDC的度数分别为20°、90°26．∵MN∥BC，∴∠B=∠MAB，∠C=∠NAC，∵∠MAB+∠BAC+∠NAC=180°，∴∠BAC+∠B+∠C=180°27．∵OP平分∠AOB，（已知）∴∠1=∠2（角平分线定义）∵MN∥OB（已知）∴∠2=∠3（两直线平行，内错角相等）∴∠1=∠3（等量代换）．28．∵AB∥CD，∴∠D=∠1=55°，∵∠C=∠D，∴∠C=55°；∵AB∥CD，∴∠B+∠C=180°，∴∠B=180°﹣∠C=180°﹣55°=125°．29．∵AD∥BC，∴∠ABC=180°﹣∠A=60°，∠ADB=∠2，∵∠1=∠2，∴∠1=∠ADB=∠2=30°，∵BD⊥CD，∴∠BDC=90°，∠C=180°﹣（30°+90°）=60°，故∠C的度数为60°．30．∵AB∥CD（已知）∴∠EFG+∠FEB=180°（两直线平行，同旁内角互补）∵∠EFG=50°（已知）∴∠FEB=130°（等式的性质）∵EG平分∠FEB（已知）∴∠FEG=∠FEB=65°（角平分线的定义）．31．∵CD∥AB，∴∠BOD=∠D=52°；∵OE平分∠BOD，∴∠BOE=26°32．如答图所示，∵L1∥L2，∴∠ECB+∠CBF=180°．∴∠ECA+∠ACB+∠CBA+∠ABF=180°．∵∠A=90°，∴∠ACB+∠CBA=90°．又∠ABF=25°，∴∠ECA=180°﹣90°﹣25°=65°33．∠D=∠C=45°，∠B=135°．理由：∵AB∥CD，∴∠D=∠1=45°（两直线平行，同位角相等）∴∠B+∠C=180°（两直线平行，同旁内角互补）∵∠D=∠C=45°，∴∠B=180°﹣∠C=180°﹣45°=135°．34．∵CD∥AB，∴∠A+∠ACD=180°，又∵CD∥EF，∴∠E=∠ECD=∠ACD﹣∠ACE=75°﹣51°=24°．35．∵a∥b，∠1=122°，∴∠2=∠5=180°﹣∠1=180°﹣122°=58°；∵a∥b，∠3=50°，∴∠3=∠6=50°；又∵∠6=∠4，∴∠4=50°．36．∵BD平分∠ADC，∴∠CDB=∠1=50°，∠ADC=100°，又AB∥CD，∴∠ADC+∠A=180°，∴∠A=80°．37．∵DE∥BC，∴∠C=∠AED=72°，∵BE平分∠ABC，且∠ABC=∠ACB，∴∠EBC=∠ABC=×72°=36°，在△BEC中，∠CEB=180°﹣72°﹣36°=72°38．如图，过点C、D分别作CM、DN平行于AB、EF，则x=∠5，4=∠3，1=∠z，又∠1+∠3=y，∠4+5=90°，即x+∠4=90°，又∠4=∠3=y﹣∠1=y﹣z，∴x+y﹣z=90°39．∵AB∥DE，∠B=70°，∴∠DCB=180°﹣∠B=180°﹣70°=110°，∠BCE=∠B=70°，∵CM平分∠DCB，∴∠BCM=∠DCB=×110°=55°，∵CM⊥CN，垂足为C，∴∠BCN=90°﹣∠BCM=90°﹣55°=35°，∴∠NCE=∠BCE﹣∠BCN=70°﹣35°=35°．40．∠A=∠3．理由如下：∵DE∥AB，∴∠1=∠A，∠2=∠3，又∵∠1=∠2，∴∠A=∠341．∵DB∥FG∥EC，∴∠BAG=∠ABD=84°，∠GAC=∠ACE=60°；∴∠BAC=∠BAG+∠GAC=144°，∵AP是∠BAC的平分线，∴∠PAC=∠BAC=72°，∴∠PAG=∠PAC﹣∠GAC=72°﹣60°=12°42．过E作EF平行于AB，则EF∥CD，∵AB∥EF，∴∠A=∠AEF=∠1，∵CD∥EF，∴∠C=∠FEC=∠2，∵∠BED=180°，∴∠1+∠AEF+∠FEC+∠2=180°，即∠AEF+∠CEF=°=90°．43．解法一：延长AB交l2于点E．∵AB⊥l1，l1∥l2，∴AB⊥l2．∵∠2是△BED的外角，∴∠2=90°+∠1=90°+43°=133°．解法二：过点B作BF∥l1，利用平行线的性质求出∠2的度数．∵l1∥l2，∴BF∥l2，∴∠ABF=180°﹣90°=90°，∠FBC=∠1=43°，∴∠2=∠ABF+∠FBC=90°+43°=133°．15 / 17第15页共17 页44．∵AB∥MN（已知）∴∠BCD+∠CDN=180°（两直线平行，同旁内角互补）∵CG、DG是角平分线∴∠1=∠BCD，∠2=∠CDN（角平分线定义）∴∠1+∠2=90°∵∠1+∠2+∠CGD=180°（三角形内角和等于180°）∴∠CGD=90°45．由题意得：∠BEC=80°，∠BED=100°，∠BEF=∠BEC=40°，∴∠BEG=90°﹣∠BEF=50°，∠DEG=∠BED﹣50°=50°．∴∠BEG和∠DEG都为50°46．∵∠AEF=125，∴∠CEA=55°∵AE∥BD，∠CDB=∠CEA=55°，在△BCD中，∵∠CBD=57°，∴∠C=68°．47．∵CE是∠DCB的角平分线，∴∠1=∠2．∵CE∥AB，∴∠1=∠A，∠2=∠B，∴∠A=∠B．48．AB∥CD，∠2+∠3=90°．理由如下：∵BE、DE分别平分∠ABD、∠CDB，∴∠ABD=2∠1，∠BDC=2∠2．∵∠2+∠1=90°，∴∠ABD+∠CDB=180°，∴AB∥CD．∴∠3=∠ABF．∵∠1=∠ABF，∠2+∠1=90°．∴∠2+∠3=90°．49．由题意可知，AB∥CD，∠HEB=50°，∴∠FGD=50°，又∵∠CFG=30°，∴∠FCG=20°50．∵AB∥CD，BC∥ED，∴∠B=∠C，∠C+∠D=180°，∴∠B+∠D=180°．51．∵AB∥CD（已知），∴∠B=∠BCD（两直线平行，内错角相等）又∵∠B=∠DCE（已知），∴∠BCD=∠DCE（等量代换）即CD平分∠BCE．52．∵AB∥CD，∠B=40°，∴∠BCE=180°﹣∠B=180°﹣40°=140°，∵CN是∠BCE的平分线，∴∠BCN=∠BCE=×140°=70°，∵CM⊥CN，∴∠BCM=20°53．∵DE∥AC，∴∠ADE=∠CAD，∵AD是∠BAC的平分线，∴∠EAD=∠CAD，∴∠ADE=∠EAD，∴AE=DE，∵BD⊥AD，∴∠ADE+∠BDE=90°，∠EAD+∠ABD=90°，∴∠ABD=∠BDE，∴BE=DE，∴AE=BE．54．如图所示，过点E，F分别作EG∥AB，FH∥AB．∵EG∥AB，FH∥AB，∴∠5=∠ABE，∠3=∠1；又∵AB∥CD，∴EG∥CD，FH∥CD，∴∠6=∠CDE，∠4=∠2，∴∠1+∠2=∠3+∠4=∠BFD=55°．∵BF平分∠ABE，DF平分∠CDE，∴∠ABE=2∠1，∠CDE=2∠2，∴∠BED=∠5+∠6=2∠1+2∠2=2（∠1+∠2）=2×55°=110°．55．∵CD⊥AB，EF⊥AB，∴CD∥EF，∴∠BCD=∠BEF，∠DEF=∠CDE；∵DE∥AC，∴∠ACD=∠CDE，∴∠ACD=∠DEF；∵EF平分∠BED，∴∠DEF=∠BEF，∴∠ACD=∠BCD，即CD平分∠ACB56．∵EB平分∠ABC，EC平分∠ACG，∴∠DBE=∠CBE，∠FCE=∠GCE，∵DF∥BC，∴∠DEB=∠CBE，∠FEC=∠GCE，∴∠DEB=∠DBE，∠FEC=∠FCE，∴DB=DE，FE=FC，∵DE﹣EF=DF，∴DB﹣CF=DF57．∵AB∥CD，（已知）∴∠GFC=∠GMA．（两直线平行，同位角相等）∵∠GMA=52°，（已知）∴∠GFC=52°．（等量代换）∵CD是直线，（已知）∴∠GFC+∠GFD=180°．（邻补角定义）∴∠GFD=180°﹣52°=128°．（等式性质）∵EF平分∠GFD，（已知）∴∠EFD=∠GFD=64°．（角平分线定义）∵AB∥CD，（已知）∴∠BEF+∠EFD=180°．（两直线平行，同旁内角互补）∴∠BEF=180°﹣64°=116°．（等式性质）答：∠BEF=116°58．∵∠BAP+∠APD=180°（已知），∴AB∥CD（同旁内角互补，两直线平行）．∴∠BAP=∠APC（两直线平行，内错角相等）．又∵∠1=∠2（已知），∴∠FPA=∠EAP，∴AE∥PF（内错角相等，两直线平行）．∴∠E=∠F（两直线平行，内错角相等）．59．（1）∵DF∥AC，∴∠EDF=∠DEC=85°．∵DE∥AB，∴∠A=∠DEC=85°．（2）∵DF∥AC，DE∥AB，∴∠EDC=∠B，∠BDF=∠C，又∠A=∠EDF，∴∠A+∠B+∠C=∠EDF+∠EDC+∠BDF=180°．60．∵AB∥CD，∠EFD=56°，∴∠BEF=180°﹣∠EFD=124°；∵∠1=∠2，∴∠1=∠BEF=62°；∵∠EGD=∠1+∠EFD，∴∠EGD=118°17 / 17第17页共17 页。

平行线的判定(含答案)

1.2平行线的判定⑴【要点预习】1•平行线的判定1.两条直线被第三条直线所截,如果______________ 相等,那么这两条直线平行.简单地说,________ 相等，两直线平行.2•平行线的判定1的特殊情形：在同一平面内，____________ 于同一条直线的两条直线互相平行.【课前热身】1. ____________________________________ 两条平行线被第三条直线所截,共有对同位角.答案：42. _________________________________________ 街道两侧路灯的柱子的位置关系是.答案：平行3. 如图1，直线AB、CD被直线EF所截，如果/ 1 =Z 2,则__________ .理由是（_______________________________________ ）.答案：AB // CD 同位角相等，两直线平行4. _____________________________________________________ 在同一平面内，若a b,a c,则a与c的位置关系是 ____________________________________________ .答案：a // c图2【讲练互动】【例1】如图2,直线AB, CD被直线EF, GH所截，下列结论：（1）若/仁/ 2,贝U AB // CD ；2）若/ 仁/2,贝U EF// GH；3）若/ 1 = / 3,贝U AB // CD ;(4)若/仁/3,则EF // GH.其中正确的是............................. ( )A. (1)(3)B. (1)(4)C.⑵⑶D.⑵⑷【解析】/ 1与/ 2是直线EF, GH被AB所截得到的同位角；/ 1与/ 3是AB,CD被EF所截形成的同位角【答案】C【变式训练】1. ................................................................................................. 如图3所示，如果/ D= / EFC，那么 ..................................... (图3A. AD // BCB.EF // BCC.AB // DCD.AD // EF【答案】D【例2】如图4,直线a,b 被直线c 所截，且/ 2+ / 3= 1800，则a // b 吗？请说明理由【分析】只要说明同位角/ 仁/3即可. 【解】•••/ 2+ / 3=180o, / 1 + / 2=180o,1 = / 3,二 a / b.【绿色通道】利用转化思想是解决平行线问题主要方法•【变式训练】 2.如图5,已知直线 EF 和AB, CD 分别相交于 K, H,且EG丄 AB, / CHF=60o, / E=30o,试说明 AB // CD.【解】•/ EG 丄 AB, ••• / EGK=90o. •/ / E=30o, /• / EKG =60o.•••/ CHF=60o, / CHF = / EHD , EHD =60o. •••/ EKG= / EHD, • AB // CD.【例3】如图6,在海上有两个观测所 A 和B,且观测所B 在A 的正东方向•若在A 观测所测得船M 的航行方向是北偏东 50o,在B 观测所得船N 的航行方向也是北偏东50o,问船M 的航向AM 与船N 的航向BN 是否平行.请说明理由• 【解】AM 与BN 平行.•••/ MAC= / NBC=50o, • AM // BN.【变式训练】3. 一辆货车在仓库装满货物准备运往超市，驶出仓库门口后开始向东行驶，途中向右拐了 50o 角，接着向前行驶，走了一段路程后，又向左拐了 50o 角，如图所示•此时汽车和原来的行驶方向相同吗？你的根据是什么？【解】相同•理由如下：•••/ AOB= / A /O /B /=50o, • OA // oH, 即汽车和原来的行驶方向相同 .【同步测控】基础自测1•如图 8,若/ ADE= / ABC,贝U图4东A. DE // BFD. / A =Z ABEA. DE // BFB. DC // BFC. DE // BCD. DC //BC2•如图8,若/ ACD= / F 则B. DC // BFC. DE // BCD. DC // BCA. / C =Z ABEB. /A =Z EBDC. / C =Z ABC4. ______________________________________ 如图10,若/ 1=52o ，问应使/ C= _____________________________________ 度时，能使直线 AB / CD.5. 如果11丄12 , |3丄|2,贝廿11 ________ 13.理由是 ________________________________6. _____________________________________________ 如图11,请你填写一个适当的条件： _____________________________________ ，使AD // BC .7.如图12,若/ 1 + Z 2=180o ，则11// 12.试说明理由(填空) 解：•••/ 2+Z 3= ______________ (平角的意义)，又•••/ 1 + Z 2=180o ( ______________ ),•••/ 仁 _______ ( ______________________________ ), 丨1 / 12 ( _______________________________ ).8. 如图13,已知△ ABC 及AC 上一点 D.过D 作DE // BC,交AB 于点E;作DF // AB,交BC 于点F.9. 如图14,/ ABC =Z DEC , BP 平分/ ABC , EF 平分/ DEC ，试找出图中的各组平行线3.如图9,能判定图9图11EB // AC 的条件是图1411|2那么DE 与AB 是否平行？请说明理由图1610. 如图 15,在厶 ABC 中，点 D, E 分别在 AC, BC 上•已知/ C=30o, / CDE=115o, / B=35o,能力提升11./ 1与/ 2是两条直线被第三条直线所截的同位角，若/1= 500,则/ 2为……( )A. 50 °B. 130 °C. 50。

(完整版)平行线习题(含答案)

2019年4月16日初中数学作业学校: ______________ 姓名： _____________ 班级：_______________ 考号：______________一、单选题1. 如图，经过直线a外一点O的4条直线中，与直线a相交的直线至少有（）A. 4条B. 3条C. 2条D. 1条【答案】B【解析】【分析】根据经过直线外一点有且只有一条直线和已知直线平行得出即可.【详解】解：根据经过直线外一点有且只有一条直线和已知直线平行，得出如果有和直线a平行的，只能是一条，即与直线a相交的直线至少有3条，故选：B.【点睛】本题考查了平行线和相交线的应用，注意：经过直线外一点有且只有一条直线和已知直线平行.2. 下列说法中，正确的个数有（）①在同一平面内不相交的两条线段必平行；②在同一平面内不相交的两条直线必平行；③在同一平面内不平行的两条线段必相交；④在同一平面内不平行的两条直线必相交.A. 1个B. 2个C. 3个D. 4个【答案】B【解析】【分析】根据平面内直线和线段的位置关系判断.详解】解：（1）线段不相交，延长后不一定不相交，错误；（2）同一平面内，直线只有平行或相交两种位置关系，正确；（3）线段是有长度的，不平行也可以不相交，错误；（4）同（2），正确；所以（2）（4）正确．故选：B．【点睛】本题主要考查在同一平面内两直线的位置关系，需要注意（1）和（3）说的是线段．3．下列表示平行线的方法正确的是（）A. ab// cdB. A // BC. a// BD. a// b【答案】D【解析】【分析】根据平行线的表达方法来判断即可得出结论.【详解】解：直线可以用两个大写字母表示，也可以用一个小写字母表示，故正确的表示方法是D.故答案为：D【点睛】本题主要考查了学生对平行线的表达方法的掌握情况，掌握平行线的表达方法是解题的关键.4 ．在同一平面内，下列说法正确的是（）A ．没有公共点的两条线段平行B ．没有公共点的两条射线平行C.不垂直的两条直线一定互相平行D ．不相交的两条直线一定互相平行【答案】D【解析】【分析】根据平行线的定义，即可求得此题的答案，注意举反例的方法．详解】A. 在同一平面内，没有公共点的两条线段不一定平行，故本选项错误；B. 在同一平面内，没有公共点的两条射线不一定平行，故本选项错误；C. 在同一平面内，不垂直的两条直线不一定互相平行，故本选项错误；D. 在同一个平面内，不相交的两条直线一定互相平行，故本选项正确；【点睛】此题考查了平行线的判定．解题的关键是熟记平行线的定义．5．下列说法不正确的是( )A .过任意一点可作已知直线的一条平行线B. 同一平面内两条不相交的直线是平行线C. 在同一平面内，过一点只能画一条直线与已知直线垂直D. 在同一平面内，经过直线外一点有且只有一条直线与已知直线平行【答案】A【解析】【分析】根据平行线的定义及平行公理进行判断.【详解】A 中，若点在直线上，则不可以作出已知直线的平行线，而是与已知直线重合，错误B. C. D 是公理，正确.故选A.【点睛】本题考查了平行线的定义和公理，熟练掌握定义和公理是解题的关键.6.在同一平面内，无公共顶点的两个直角，如果它们有一条边共线，那么另一边互相( )A •平行B.垂直C.共线 D.平行或共线【答案】A【解析】【分析】结合图形，由平行线的判断定理进行分析.【详解】如图所示：n n无公共顶点的两个直角，如果它们有一条边共线，内错角相等，或同旁内角互补，那么另一边互相平行•故选A.【点睛】本题考查了平行线的判定，熟练掌握判定定理是解题的关键7 .下列结论正确的是()A .过一点有且只有一条直线与已知直线垂直B. 过一点有且只有一条直线与已知直线平行C. 在同一平面内，不相交的两条射线是平行线D. 如果两条直线都与第三条直线平行，那么这两条直线互相平行【答案】D【解析】【分析】本题可结合平行线的定义，垂线的性质和平行公理进行判定即可.【详解】(1)过一点有且只有一条直线与已知直线垂直，应强调在同一平面内，故本项错误；(2)过一点有且只有一条直线与已知直线平行，应强调在经过直线外一点，故是错误的.(3)在同一平面内，不相交的两条直线是平行线，射线不一定，故本项错误；(4)如果两条直线都与第三条直线平行，那么这两条直线也互相平行是正确的.故选D.【点睛】本题主要考查了平行线的定义，垂线的性质和平行公理.熟练掌握公理和概念是解决本题的关键.8 .在同一平面内，直线AB与CD相交，AB与EF平行，则CD与EF()A •平行B.相交C. 重合D.三种情况都有可能【答案】B【解析】【分析】先根据题意画出图形，即可得出答案.【详解】如图，•••在同一平面内，直线AB与CD相交于点O, AB // EF,••• CD与EF的位置关系是相交，故选B.【点睛】本题考查了平行线的性质的应用，能根据题意画出图形是解此题的关键，注意：数形结合思想的应用.9 .下列语句不正确的是（）A .在同一平面内，过直线外一点有且只有一条直线与已知直线平行B. 两直线被第三条直线所截，如果同位角相等，那么两直线平行C. 两点确定一条直线D. 内错角相等【答案】D【解析】【分析】根据平行线的公理、推论及平行线的判定，可得答案.【详解】A、在同一平面内，过直线外一点有且只有一条直线与已知直线平行，故A正确;B、两直线被第三直线所截，如果同位角相等，那么两直线平行，故B正确；C、两点确定一条直线，故C正确；D、两直线平行，内错角相等，故D错误；故选D.【点睛】本题考查了平行公理及推论，熟记公理、推论是解题关键．10 ．下列说法正确的有（）①两点之间的所有连线中，线段最短；②相等的角是对顶角；③过直线外一点有且仅有一条直线与已知直线平行；④两点之间的距离是两点间的线段；⑤如果一个角的两边与另一个角的两边垂直，那么这两个角相等.A. 1个B. 2个C. 3个D. 4个【答案】B【解析】【分析】依据线段的性质、平行公理、两点间的距离以及垂线的定义，即可得到正确结论．【详解】解：①两点之间的所有连线中，线段最短，正确；②相等的角不一定是对顶角，错误；③过直线外一点有且仅有一条直线与已知直线平行，正确；④两点之间的距离是两点间的线段的长度，错误；⑤如果一个角的两边与另一个角的两边垂直，那么这两个角相等或互补，错误. 故选：B．【点睛】本题考查线段的性质、平行公理、两点间的距离以及垂线的定义，解题时注意：平面上任意两点间都有一定距离，它指的是连接这两点的线段的长度．11 ．下列说法中正确的是（）A .两条相交的直线叫做平行线B. 在直线外一点，只能画出一条直线与已知直线平行C. 如果a // b, b // c,贝U a不与b平行D. 两条不平行的射线，在同一平面内一定相交【答案】B【解析】【分析】根据平行线的性质进行解题即可,见详解.详解】解：两条不相交的直线叫做平行线，故A 错误,在直线外一点，只能画出一条直线与已知直线平行如果a// b , b // c ,则a // b,平行线的传递性，故C 错误, 射线一端固定，另一端无限延伸，故D 错误，综上选B. 【点睛】，属于简单题，熟悉平行线的性质是解题关键【解析】【分析】根据平行线的传递性即可解题【详解】解：••• AB // CD ，CD // EF ，••• AB // EF ，（平行线的传递性）故选A. 【点睛】本题考查了平行线的传递性，属于简单题，熟悉平行线的性质是解题关键13 •一条直线与另两条平行直线的关系是（）A .一定与两条平行线平行B .可能与两条平行线的一条平行，一条相交C . 一定与两条平行线相交D .与两条平行线都平行或都相交【答案】D 【解析】【分析】根据在同一平面内，两条直线的位置关系有两种：平行和相交，可知如果一条直线与另两条平行线中的一条相交，则它与另一条平行线也相交；如果一条直线与另两条平行线中的一条平行，则它与另一条平行线也平行即可求出本题答案【详解】，正确,// EF ，那么AB 和EF 的位置关系是本题考查了平行线的性质C.垂直D.不能确定【答案】A•••在同一平面内，两条直线的位置关系有两种：平行和相交，•••如果一条直线与另两条平行线中的一条相交，则它与另一条平行线也相交，否则与平行公理相矛盾；如果一条直线与另两条平行线中的一条平行，根据平行于同一直线的两条直线平行，则它与另一条平行线也平行.故答案为：D.【点睛】本题考查了平行线的相关知识，熟练掌握平行线的有关性质是本题解题的关键. 14．下列说法中，正确的个数为( )①过一点有无数条直线与已知直线平行；②如果a// b, a // c,那么b // c;③如果两线段不相交，那么它们就平行；④如果两直线不相交，那么它们就平行.A．1 个B．2 个C．3 个D．4 个【答案】A【解析】【分析】根据平行线的定义、公理及推论判断即可求出本题答案.【详解】(1) 过直线外一点有且只有一条直线与已知直线平行,故错误；(2) 根据平行公理的推论,正确；(3) 线段的长度是有限的,不相交也不一定平行,故错误；(4) 应该是“在同一平面内”,故错误.正确的只有一个,故选A.故答案为：A.【点睛】本题考查了平行公理及推论,平行线,熟练掌握该知识点是本题解题的关键.15 •已知在同一平面内有一直线AB和一点P,过点P画AB的平行线，可画()A • 1条B. 0条 C. 1条或0条D.无数条【答案】C【解析】【分析】根据平行公理：经过直线外一点,有且只有一条直线与这条直线平行可得答案．【详解】如果点P在直线上，过点P画直线与AB的平行线可画0条,如果点P在直线外，过点P画直线与AB的平行线可画1条•故答案为：C.【点睛】本题考查了平行公理及推论，熟练掌握该知识点是本题解题的关键16 .下列说法中，正确的是（）A •平面内，没有公共点的两条线段平行B. 平面内，没有公共点的两条射线平行C. 没有公共点的两条直线互相平行D. 互相平行的两条直线没有公共点【答案】D【解析】【分析】回忆线段之间、射线之间与直线之间的位置关系；对于A，可在纸上画出两条没有公共点的线段，观察两条线段的位置关系；对于B,可在纸上画出两条没有公共点的射线，观察两条线段的位置关系；对于C,思考若两条直线不在一个平面内，是否能够得到两条直线不平行也不相交，对于D，根据平行线的定义可作出判断•【详解】对于A,如图所示，A错误；对于C,如果两条直线不在同一个平面内，不相交也可能不平行，则C错误；对于D，根据平行线的定义可知D正确•故答案为：D.【点睛】本题考查了两条直线的位置关系，直线、射线、线段的定义，熟练掌握直线的位置关系及相关定义是本题解题的关键•17 ．下面说法正确的是( )A .过两点有且只有一条直线B.平角是一条直线C.两条直线不相交就一定平行D.过一点有且只有一条直线与已知直线平行【答案】A【解析】【分析】根据直线公理：经过两点有且只有一条直线；角的概念；平行线的定义和平行公理及推论进行判断.【详解】A、由直线公理可知，过两点有且只有一条直线，故本选项正确；B、平角是有公共端点是两条射线组成的图形，故本选项错误；C、同一平面内两条直线不相交就一定平行，故本选项错误；D、经过直线外一点有且只有一条直线与已知直线平行，故本选项错误.故选：A .【点睛】本题属于综合题，考查了直线的性质：两点确定一条直线；角的定义：有公共端点是两条射线组成的图形叫做角，其中这个公共端点是角的顶点，这两条射线是角的两条边；同一平面内，两条直线的位置关系：平行或相交；平行公理：经过直线外一点，有且只有一条直线与这条直线平行.18 .下列说法错误的是( )A .对顶角相等B.两点之间所有连线中，线段最短C.等角的补角相等D.过任意一点P,都能画一条直线与已知直线平行【答案】D【解析】【分析】A .根据对顶角的性质判定即可；B. 根据线段的性质判定即可；C. 根据补角的性质判定即可；D .根据平行公理判定即可 .【详解】A .对顶角相等，故选项正确；B. 两点之间连线中，线段最短，故选项正确；C•等角的补角相等，故选项正确；D .过直线外一点P,能画一条直线与已知直线平行，故选项错误•故选D.【点睛】本题分别考查了对顶角、邻补角的性质、线段的性质、余角、补角的关系及平行公理，都是基础知识，熟练掌握这些知识即可解决问题 .二、填空题19 . L i, 12, 13为同一平面内的三条直线，如果11与12不平行，12与13不平行，则11与13的位置关系是_______________ .【答案】相交或平行【解析】【分析】根据关键语句“若？有？不平行,??与?不平行,”画出图形，图形有两种情况，根据图形可得答案.【详解】根据题意可得图形：根据图形可知：若？不平行，??与?3不平行，则?3可能相交或平行，故答案为：相交或平行•【点睛】本题主要考查了直线的位置关系，在同一平面内，两条直线的位置关系：平行或相交20 •小明列举生活中几个例子，你认为是平行线的是________________ （填序号）.①马路上斑马线；②火车铁轨；③直跑道线；④长方形门框上下边.【答案】①②③④【解析】【分析】根据平行线的判定进行判断即可•【详解】解：是平行线的是①②③④.故答案为：①②③④【点睛】本题考查了平行线的含义，应结合生活实际进行解答21.如图，用符号表示下列两棱的位置关系.AB ___ A ' B AA ' __________ AB ; AD _____ B ' C【答案】// 丄 //【解析】【分析】根据题意，可由立体图形中的平行线的判定条件，以及垂直的判定条件进行分析，然后填空即可.【详解】解：由图可知，AB// A B', AA丄AB AD// B' C'【点睛】本题主要考查的是直线的位置关系•22 .如图，在正方体中，与线段AB平行的线段有________ 条.【答案】3【解析】【分析】与线段AB平行的线段的种类为：①直接与AB平行，②与平行于AB的线段平行. 【详解】解：与AB平行的线段是：DC EF;与CD平行的线段是：HG所以与AB线段平行的线段有：EF、HG DC.故答案是：EF、HG DC【点睛】本题考查了平行线•平行线的定义：在同一平面内，不相交的两条直线叫平行线.23 .如图所示，用直尺和三角尺作直线AB , CD，从图中可知，直线AB与直线CD的位置关系为 ________ .【答案】平行【解析】【分析】根据同位角相等，两直线平行判断.【详解】如图，C 亠丘D根据题意，/ 1与/ 2是三角尺的同一个角,所以/仁/2,所以，AB // CD （同位角相等，两直线平行）故答案为：平行.【点睛】本题考查了平行线的判定熟练掌握同位角相等，两直线平行，并准确识图是解题的关键.24 .在如图的长方体中，与棱AB平行的棱有 ________________________________________;与棱AA'平行的棱有DD , BB , CC解析】【分析】根据平行的定义，结合图形直接找出和棱AB平行的棱，与棱AA平行的棱即可.【详解】由图可知，和棱AB平行的棱有CD , AB', CD；与棱AA 平行的棱有DD ，BB ，CC .故答案为：CD , A B , C D ；DD , BB , CC .【点睛】本题考查了认识立体图形的知识点,熟练掌握平行的定义是本题解题的关键.25．在同一平面内，直线AB 与直线CD 满足下列条件，则其对应的位置关系是（1）____________________________________________________________________ 若直线AB 与直线CD 没有公共点，则直线AB 与直线CD 的位置关系为 __________________________ ；（2）直线AB 与直线CD 有且只有一个公共点，则直线AB 与直线CD 的位置关系为_______________ 【答案】平行；相交.【解析】【分析】根据“在同一平面内,两条直线的位置关系是：平行或相交.平行没有公共点,相交只有一个公共点”即可推出本题答案.【详解】在同一平面内,直线AB 与CD 满足下列条件,则其对应的位置关系是：（1）若AB 与CD没有公共点，则AB与CD的位置关系是平行；（2 ）若AB与CD有且只有一个公共点,则AB 与CD 的位置关系为相交.故答案为：（1）平行；（2）相交.【点睛】本题考查了直线的位置关系,熟练掌握判定方法是本题解题的关键.三、解答题26 .把图中的互相平行的线段用符号“//”写出来，互相垂直的线段用符号“丄”写出来：【解析】根据平行线和垂直的定义即可解答.【详解】解：如图所示，在长方体中：互相平行的线段：AB// CD EF// GH MN PQ 互相垂直的线段：AB 丄 EF, AB 丄 GH CDL EF, CDL GH【点睛】本题考查了平行线和垂直的定义，理解定义是解题的关键•27 .如图，过点 0 '分别画 AB , CD 的平行线.【答案】详见解析•【解析】【分析】把三角板的一条直角边与已知直线重合，用直尺靠紧三角板的另一条直角边，沿直尺移动三角板，使三角板的原来和已知直线重合的直角边和 O 点重合，过O 点沿三角板的直角边画直线即可.【详解】解：如图，本题考查了学生利用直尺和三角板作平行线的能力28 •如图，按要求完成作图⑴过点P 作AB 的平行线EF ；(2) 过点P 作CD 的平行线 MN ;(3) 过点P 作AB 的垂线段，垂足为 G.【答案】作图见解析【点睛】【分析】利用题中几何语言画出对应的几何图形.【详解】如图，本题考查了平行线的作法和作垂线的步骤.29 •我们知道相交的两条直线的交点个数是 1 ;两条平行线的交点个数是0;平面内三条平行线的交点个数是0,经过同一点的三条直线的交点个数是 1 ;依此类推(1) 请你画图说明平面内五条直线最多有几个交点.(2) 平面内五条直线可以有4个交点吗？如果可以，请你画出符合条件的所有图形；如果不可以，请说明理由.(3) 在平面内画出10条直线，使交点个数恰好是31.【答案】(1)平面内五条直线的交点最多有10个，⑵五条直线可以有4个交点，⑶答案不唯一•【解析】【分析】(1)直接让五条直线中的任意两条互相相交即可；(2)不妨先让其中的四条直线相交得到3个交点，然后再使最后一条直线，与其中任意一条相交且与之前的交点不重合即可，接下来自己试着想想还有哪些画法；(3)结合已知，禾U用平行线的性质画出图形即可【详解】解：(1)平面内五条直线的交点最多有 10个，如图①.(2)五条直线可以有4个交点，如图②(a // b// c // d),图③(AD // BC , AB // DC)，图④(a // b).團② 関③(3) 答案不唯一，如图， a / b / c / d / e , f // g // h , l // m.【点睛】此题考查平面内不重合直线的位置关系，解答时要分各种情况解答, 的所有情形，不要遗漏，否则讨论的结果就不全面.30 •如图，在方格纸上：(1)已有的四条线段中，哪些是互相平行的？⑵过点M 画AB 的平行线.⑶过点N 画GH 的平行线.37T~/ 、A7 D 、M / 7~■【答案】(1)AB // CD ； (2)画图见解析；⑶画图见解析【解析】【分析】(1) 根据图形可观察出互相平行的线段.(2) 过点M 画AB 的平行线.(3)过点N 画GH 的平行线.要考虑到可能出现【详解】(1)由图形可得：AB // CD .⑵(3)所画图形如下：【点睛】本题考查了平行线的判定方法及过一点作平行线的知识, 的判定方法及作图的基本步骤.属于基础题，主要掌握平行线。

(完整)七年级数学平行线的性质与判定的证明练习题及答案

平行线的性质与判定的证明温故而知新：1.平行线的性质（1）两直线平行，同位角相等；（2）两直线平行，内错角相等；（3）两直线平行，同旁内角互补.2.平行线的判定（1）同位角相等，两直线平行；（2）内错角相等，两直线平行；（3）同旁内角互补，两直线平行互补.例1 已知如图2-2，AB∥CD∥EF，点M，N，P分别在AB，CD，EF上，NQ平分∠MNP．（1）若∠AMN=60°，∠EPN=80°，分别求∠MNP，∠DNQ的度数；（2）探求∠DNQ与∠AMN，∠EPN的数量关系．解析：根据两直线平行，内错角相等及角平分线定义求解.（标注∠MND=∠AMN，∠DNP=∠EPN）答案：（标注∠MND=∠AMN=60°，∠DNP=∠EPN=80°）解：（1）∵AB∥CD∥EF，∴∠MND=∠AMN=60°，∠DNP=∠EPN=80°，∴∠MNP=∠MND+∠DNP=60°+80°=140°，又NQ平分∠MNP，∴∠MNQ=12∠MNP=12×140°=70°，∴∠DNQ=∠MNQ-∠MND=70°-60°=10°，∴∠MNP，∠DNQ的度数分别为140°，10°.(下一步) （2）（标注∠MND=∠AMN，∠DNP=∠EPN）由（1）得∠MNP=∠MND+∠DNP=∠AMN+∠EPN，∴∠MNQ=12∠MNP=12（∠AMN+∠EPN），∴∠DNQ=∠MNQ-∠MND=12（∠AMN+∠EPN）-∠AMN=12（∠EPN-∠AMN），即2∠DNQ=∠EPN-∠AMN.小结：在我们完成涉及平行线性质的相关问题时，注意实现同位角、内错角、同旁内角之间的角度转换，即同位角相等，内错角相等，同旁内角互补.例2 如图，∠AGD＝∠ACB,CD⊥AB,EF⊥AB,证明：∠1＝∠2.解析：（标注：∠1＝∠2=∠DCB，DG∥BC，CD∥EF）答案：（标注：∠1＝∠2=∠DCB）证明：因为∠AGD=∠ACB，所以DG∥BC，所以∠1＝∠DCB，又因为CD⊥AB,EF⊥AB，所以CD∥EF，所以∠2＝∠DCB，所以∠1=∠2.小结：在完成证明的问题时，我们可以由角的关系可以得到直线之间的关系，由直线之间的关系也可得到角的关系.例3 （1）已知：如图2-4①，直线AB∥ED，求证：∠ABC+∠CDE=∠BCD；（2）当点C位于如图2-4②所示时，∠ABC，∠CDE与∠BCD存在什么等量关系？并证明．（1）解析：动画过点C作CF∥AB由平行线性质找到角的关系.(标注∠1=∠ABC，∠2=∠CDE)答案：证明：如图，过点C作CF∥AB，∵直线AB∥ED，∴AB∥CF∥DE，∴∠1=∠ABC，∠2=∠CDE.∵∠BCD=∠1+∠2，∴∠ABC+∠CDE=∠BCD；（2）解析：动画过点C作CF∥AB,由平行线性质找到角的关系.（标注∠ABC+∠1=180°，∠2+∠CDE=180°）答案：∠ABC+∠BCD+∠CDE=360°．证明：如图，过点C作CF∥AB，∵直线AB∥ED，∴AB∥CF∥DE，∴∠ABC+∠1=180°，∠2+∠CDE=180°.∵∠BCD=∠1+∠2，∴∠ABC+∠BCD+∠CDE=360°．小结：在运用平行线性质时，有时需要作平行线，取到桥梁的作用，实现已知条件的转化.例4 如图2-5，一条公路修到湖边时，需绕道，如果第一次拐的角∠A是120°，第二次拐的角∠B是150°，第三次拐的角是∠C，这时的道路恰好和第一次拐弯之前的道路平行，那么∠C应为多少度？解析：动画过点B作BD∥AE，答案：解：过点B作BD∥AE，∵AE∥CF，∴AE∥BD∥CF，∴∠A=∠1，∠2＋∠C=180°∵∠A=120°，∠1+∠2=∠ABC=150°，∴∠2=30°，∴∠C=180°-30°=150°．小结：把关于角度的问题转化为平行线问题，利用平行线的性质与判定予以解答.举一反三：1.如图2-9，FG∥HI,则∠x的度数为（）A.60°B. 72°C. 90°D. 100°解析：∠AEG=180°-120°=60°,由外凸角和等于内凹角和有60°+30°+30°＝x+48°，解得x=72°.答案:B.2.已知如图所示，AB∥EF∥CD，EG平分∠BEF，∠B+∠BED+∠D=192°，∠B-∠D=24°，求∠GEF的度数.解析：解:∵AB∥EF∥CD,∴∠B=∠BEF,∠DEF=∠D.∵∠B+∠BED+∠D=192°,即∠B+∠BEF+∠DEF+∠D=192°,∴2(∠B+∠D)=192°,即∠B+∠D=96°.∵∠B-∠D=24°,∴∠B=60°,即∠BEF=60°. ∵EG平分∠BEF,∴∠GEF=12∠BEF=30°.3.已知：如图2-10，AB∥EF，BC∥ED，AB，DE交于点G．求证：∠B=∠E．解析：标注AB∥EF，BC∥ED答案：证明：∵AB∥EF，∴∠E=∠AGD.∵BC∥ED，∴∠B=∠AGD，∴∠B=∠E.例5如图2-6，已知AB∥CD，试再添上一个条件，使∠1=∠2成立，并说明理由．解析：标注AB∥CD，∠1=∠2答案：方法一：（标注CF∥BE）解：需添加的条件为CF∥BE ，理由：∵AB∥CD，∴∠DCB=∠ABC.∵CF∥BE，∴∠FCB=∠EBC，∴∠1=∠2；方法二：（标注CF ，BE ，∠1=∠2=∠DCF=∠ABE ）解：添加的条件为CF ，BE 分别为∠BCD ，∠CBA 的平分线．理由：∵AB ∥CD ，∴∠DCB=∠ABC.∵CF ，BE 分别为∠BCD ，∠CBA 的平分线，∴∠1=∠2．小结：解决此类条件开放性问题需要从结果出发，找出结果成立所需要的条件，由果溯因.例6 如图1-7，已知直线1l 2l ，且3l 和1l 、2l 分别交于A 、两点，点P 在AB 上，4l 和1l 、2l 分别交于C 、D 两点，连接PC 、PD 。

平行线的判定习题(含答案)

2019年4月16日初中数学作业学校:___________：___________班级：___________考号：___________一、单选题1．如右图所示，在下列条件中，不能判断l1∥l2的是（）A．∠1=∠3 B．∠2=∠3 C．∠4+∠5=180°D．∠2+∠4=180°【答案】B【解析】【分析】直接利用平行线的判定方法分别分析得出答案．【详解】解：A、∠1=∠3根据错角相等，两直线平行能判定l1∥l2，故此选项不符合题意；B. ∠2=∠3无法判定l1∥l2，故此选项符合题意；C. ∠4+∠5=180°, ∠2=∠5，所以∠4+∠2=180°, 根据同旁角互补，两直线平行能判定l1∥l2，故此选项不符合题意；D. ∠2+∠4=180°，能判定l1∥l2，故此选项不符合题意；故选：B.【点睛】本题考查平行线的判定，正确掌握判定方法是解题关键．2．如图，直线a，b被直线c所截，下列条件能判断a//b的是( ).A．∠1=∠2 B．∠1=∠4 C．∠3+∠4=180°D．∠2+∠4=180°【答案】B【解析】【分析】根据平行线的判定定理,同位角相等,两直线平行即可解题.【详解】解：A. ∠1=∠2是对顶角,无法判断,B. ∠1=∠4,根据同位角相等,两直线平行即可判定a//b,正确,C. ∠3+∠4=180°,邻补角互补无法判断平行,D. ∠2+∠4=180°,错角不是互补的,错误,故选B.【点睛】本题考查了平行线的判定,属于简单题,熟悉平行线的判定定理是解题关键.3．如图，下列条件：①∠B+∠BFE=180°；②∠1=∠2；③∠3=∠4；④∠B=∠5．能判定AB∥EF的有( )A．1个B．2个C．3个D．4个【答案】C【解析】【分析】根据平行线的判定定理对各小题进行逐一判断即可．【详解】解：①∵∠B+∠BFE=180°，∴AB∥EF，故本小题正确；②∵∠1=∠2，∴DE∥BC，故本小题错误；③∵∠3=∠4，∴AB∥EF，故本小题正确；④∵∠B=∠5，∴AB∥EF，故本小题正确．故选：C．【点睛】本题考查的是平行线的判定，熟知平行线的判定定理是解答此题的关键．4．如图，下列条件中，不能判断直线的是（）A．B．C．D．【答案】B【解析】【分析】根据同位角相等，两直线平行；错角相等，两直线平行；同旁角互补，两直线平行对各选项进行判断．【详解】当∠1=∠3时，a∥b；当∠4=∠5时，a∥b；当∠2+∠4=180°时，a∥b．故选：B．【点睛】本题考查了平行线的判定：同位角相等，两直线平行；错角相等，两直线平行；同旁角互补，两直线平行．5．如图，点E在AD延长线上，下列条件中不能判定BC∥AD的是（）A．B．C．D．【答案】A【解析】【分析】分别利用同旁角互补两直线平行，错角相等两直线平行进行判断，即可得出答案．解：A、∵∠1=∠2，∴AB∥CD，本选项符合题意；B、∵∠C=∠CDE，∴BC∥AD，本选项不合题意；C、∵∠3=∠4，∴BC∥AD，本选项不合题意；D、∵∠C+∠ADC=180°，∴AD∥BC，本选项不符合题意．故选：A．【点睛】此题考查了平行线的判定，平行线的判定方法有：同位角相等两直线平行；错角相等两直线平行；同旁角互补两直线平行，熟练掌握平行线的判定是解本题的关键．6．如图，下列条件中能得到AB∥CD的是( )A．B．C．D．【答案】C【解析】【分析】根据平行线的判定定理对各选项进行逐一判断即可．【详解】A、因为∠1=∠2，不能得出AB∥CD，错误；B、∵∠2=∠3，∴AD∥BC，错误；C、∵∠1=∠4，∴AB∥CD，正确；D、因为∠3=∠4，不能得出AB∥CD，错误；故选C．本题考查的是平行线的判定，熟知平行线的判定定理是解答此题的关键．7．下列说法错误的是()A．在同一平面，不相交的两条线段必然平行B．在同一平面，不相交的两条直线必然平行C．在同一平面，不平行的两条线段延长后必然相交D．在同一平面，两条直线没有公共点，那么两条直线平行【答案】A【解析】【分析】根据两条直线的位置关系直接可以找出错误的选项.【详解】在同一平面，不相交的两条直线必然平行; 在同一平面，不平行的两条线段延长后必然相交; 在同一平面，两条直线没有公共点，那么两条直线平行；只有A选项中，在同一平面，不相交的两条线段不一定平行，故A错误.故选A.【点睛】此题重点考察学生对两直线的位置关系的理解，掌握两直线的位置关系是解题的关键. 8．同一平面的两条线段，下列说确的是()A．一定平行B．一定相交C．可以既不平行又不相交D．不平行就相交【答案】C【解析】【分析】根据线段有固定长度这一特点来解题即可.【详解】同一平面的两条线段，可以出现相交，平行，也可以出现既不平行也不相交的状态.故选C【点睛】此题重点考察学生对两条线段位置关系的理解，抓住线段有固定长度是解题的关键.9．在同一平面，两条不重合直线的位置关系可能是()A．垂直或平行B．垂直或相交C．平行或相交D．平行、垂直或相交【答案】C【解析】【分析】根据前提条件结合直线的位置关系直接可以得到答案.【详解】在同一平面，两条不重合的直线的位置关系只有两种：平行或相交.故选C【点睛】此题重点考察学生对两直线位置关系的理解，掌握两直线的位置关系是解题的关键. 10．如图，已知点E在BC的延长线上，则下列条件中不能判断AB∥CD的是（）A．∠B＝∠DCE B．∠BAD+∠D＝180°C．∠1＝∠4 D．∠2＝∠3【答案】D【解析】【分析】根据平行线的判定定理即可直接作出判断．【详解】A、根据同位角相等，两直线平行即可证得，故选项错误；B、根据同旁角互补，两直线平行，即可证得，故选项错误；C、根据错角相等，两直线平行即可证得，故选项错误；D、∠2和∠3是AD和BC被AC所截形成的角，因而不能证明AB∥CD，故选项正确．故选：D．【点睛】本题考查了平行线的判定定理，正确识别“三线八角”中的同位角、错角、同旁角是正确答题的关键，不能遇到相等或互补关系的角就误认为具有平行关系，只有同位角相等、错角相等、同旁角互补，才能推出两被截直线平行．11．如图，下列判定两直线平行错误的是（）A．若∠D=∠3，则BE∥DF B．若∠B=∠2，则AB∥CDC．若∠1+∠D=，则BE∥DF D．若∠1+∠B=，则AB∥CD【答案】A【解析】【分析】根据平行线的判定逐一判断即可.【详解】A. ∠D和∠3是一组同旁角，根据“同旁角互补，两直线平行”，可得本选项错误；B. ∠B和∠2是一组同位角角，根据“同位角相等，两直线平行”，可得本选项正确；C. 因为∠1 = ∠3，若∠1+∠D=，则∠3+∠D=，根据“同旁角互补，两直线平行”，可得本选项正确；D. ∠1和∠B，是一组同旁角，根据“同旁角互补，两直线平行”，可得本选项正确.故选：A.【点睛】本题考查平行线的判定方法；熟练掌握平行线的判定方法，并能进行推理论证是解题关键．12．如图，已知CD、BF相交于点O，∠D=，下面判定两直线平行正确的是（）A．当∠C=时，AB∥CD B．当∠A=时，AC∥DEC．当∠E=时，CD∥EF D．当∠BOC=时，BF∥DE【答案】D【解析】【分析】选项A中，∠C和∠D是直线AC、DE被DC所截形成的错角，错角相等，判定两直线平行；选项B中，不符合三线八角构不成平行；选项C中，∠E和∠D是直线DC、EF被DE所截形成的同旁角，因为同旁角不互补，所以两直线不平行；选项D中，∠BOC的对顶角和∠D是直线BF、DE被DC所截形成的同旁角，同旁角互补，判定两直线平行【详解】解：A、错误，因为∠C=∠D，所以AC∥DE；B、错误，不符合三线八角构不成平行；C、错误，因为∠C+∠D≠180°，所以CD不平行于EF；D、正确，因为∠DOF=∠BOC=140°，所以∠DOF+∠D=180°，所以BF∥DE．故选：D．【点睛】本题考查平行线的判定，解题关键是在复杂的图形中具有相等关系的两角首先要判断它们是否是同位角或错角，被判断平行的两直线是否由“三线八角”而产生的被截直线．13．如图，下列条件中，能判断FB∥CE的是（）A．∠F+∠C=B．∠ABF=∠C C．∠F=∠C D．∠A=∠D【答案】B【解析】【分析】分析四个选项，看哪个选项的条件满足平行线的判定定理，由此即可得出结论．【详解】解：A、∠F+∠C=180°，不能得出FB∥CE，A不可以；B、∠ABF=∠C，同位角相等，两直线平行，B可以；C、∠F=∠C，不能得出FB∥CE，C不可以；D、∠A=∠D，错角相等，两直线平行，但得出的是DF∥AC，D不可以．故选：B．【点睛】本题考查平行线的判定定理，解题的关键是牢记平行线的判定定理．本题属于基础题，难度不大，解决该题型题目时，寻找相等或互补的角去证明直线平行．14．如图，一根直尺EF压在三角板的角∠BAC上，欲使CB∥EF，则应使∠ENB的度数为（）A．B．C．D．【答案】C【解析】【分析】根据平行线的判定方法即可解答.【详解】解:因为三角板含有30°的角,所以∠B=60°,当∠ENB+∠B=180°时,根据“同旁角互补,两直线平行”,可使CB∥EF，此时∠ENB=180°-∠B=180°-60°=.故选:C.【点睛】本题考查平行线的判定方法，解题关键是熟练掌握判定方法，根据题目要求选择简单方法.15．如图，直线a与直线b被直线c所截，b⊥c，垂足为A，∠1＝69°，若使直线b与直线a平行，则可将直线b绕着点A顺时针旋转()A．69°B．49°C．31°D．21°【答案】D【解析】【分析】先根据b⊥c得出∠2的度数，再由平行线的判定定理即可得出结论．【详解】∵b⊥c，∴∠2=90°．∵∠1=69°，a∥b，∴直线b绕着点A顺时针旋转的度数=90°﹣69°=21°，故选D.【点睛】本题考查了垂直的定义，平行线的判定，熟练掌握和正确运用相关知识是解题的关键. 16．如图是小敏作“过已知直线外一点画这条直线的平行线”，从图中可知，小敏画平行线的依据是( )①两直线平行，同位角相等②两直线平行，错角相等③同位角相等，两直线平行④错角相等，两直线平行A．①② B．②③ C．③④ D．①④【答案】C【解析】【分析】①②为平行线的性质，③④为平行线的判定定理.【详解】解：根据平行线的判定与性质可知，①②为平行线的性质，③④为平行线的判定定理，∴小敏是依据③④画平行线的.本题主要考查平行线的判定与性质，解此题的关键在于熟记平行线的判定定理与性质的区别.17．如图，下列结论：若，则∥；若，则∥;若∠ADC=∠5，则AD//BC；若∠DAB+∠ABC=180°，则AD//BC，其中正确的个数是（）A．1个B．2个C．3个D．4个【答案】C【解析】【分析】根据错角相等，两直线平行可以对①②③进行判断，根据同旁角互补，两直线平行可以对④进行判断，由此即可得答案.【详解】①若∠1=∠3，则AB∥CD，正确；②若∠2=∠4，则AD∥BC，故②错误；③若∠ADC=∠5，则AD//BC，正确；④若∠DAB+∠ABC=180°，则AD//BC，正确，故选C.【点睛】本题考查了平行线的判定，熟练掌握平行线的判定定理是解题的关键.18．如图，下列推理正确的是（）A．∵∠1＝∠2，∴AD∥BC B．∵∠3＝∠4，∴AB∥CDC．∵∠3＝∠5，∴AB∥DC D．∵∠3＝∠5，∴AD∥BC【答案】C利用平行线的判定方法判断即可得到结果．【详解】∵∠3=∠5，∴AB∥DC（同位角相等，两直线平行）．故选C．【点睛】此题考查了平行线的判定，熟练掌握平行线的判定方法是解本题的关键．二、解答题19．如图，，，说明：.【答案】见解析.【解析】【分析】先由同位角相等，得出两直线平行，再根据两直线平行，得出错角相等，最后根据同位角相等，得出两直线平行即可．【详解】∵（已知）∴（同位角相等，两直线平行）又∵（两直线平行，错角相等）∴（等量代换）∴（同位角相等，两直线平行）【点睛】本题主要考查了平行线的判定与性质，解题时注意：两直线平行，错角相等；同位角相等，两直线平行．20．如图，已知∠ABC=180°-∠A，BD⊥CD于D，EF⊥CD于E．(1)求证：AD∥BC；(2)若∠ADB=36°，求∠EFC的度数．【答案】(1)证明见解析；(2)36°.【解析】【分析】(1)求出∠ABC+∠A=180°，根据平行线的判定推出即可；(2)根据平行线的性质求出∠DBC，根据垂直推出BD∥EF，根据平行线的性质即可求出∠EFC．【详解】(1)证明：∵∠ABC=180°-∠A，∴∠ABC+∠A=180°，∴AD∥BC；(2)∵AD∥BC，∠ADB=36°，∴∠DBC=∠ADB=36°，∵BD⊥CD，EF⊥CD，∴BD∥EF，∴∠DBC=∠EFC=36°【点睛】本题考查了平行线的性质和判定的应用，注意：①两直线平行，同位角相等，②两直线平行，错角相等，③两直线平行，同旁角互补，反之亦然．21．平面上有6条直线，共有12个不同的交点，画出它们可能的位置关系(画三种图形)．【答案】详见解析.【解析】【分析】从平行线的角度考虑，先考虑只有二条直线平行，再考虑三条平行，作出草图即可看出．【详解】如下图．【点睛】本题考查平行线与相交线的综合运用．没有明确平面上六条不重合直线的位置关系，需要运用分类讨论思想．22．如图，根据要求填空．(1)过A作AE∥BC，交______于点E；(2)过B作BF∥AD，交______于点F；(3)过C作CG∥AD，交__________于点G；(4)过D作DH∥BC，交BA的__________于点H.【答案】(1)DC；(2)DC；(3)AB；(4)延长线.【解析】【分析】根据要求，直接进行作图就可以解决．【详解】（1）过A作AE∥BC，交DC于点E；（2）过B作BF∥AD，交DC于点F；（3）过C作CG∥AD，交AB的延长线于点G；（4）过D作DH∥BC，交BA的延长线于点H．【点睛】本题主要考查平行线的作法以及几何语言的准确性．23．探索与发现：(1)若直线a1⊥a2，a2∥a3，则直线a1与a3的位置关系是__________，请说明理由．(2)若直线a1⊥a2，a2∥a3，a3⊥a4，则直线a1与a4的位置关系是________．(直接填结论，不需要证明)(3)现在有2 011条直线a1，a2，a3，…，a2 011，且有a1⊥a2，a2∥a3，a3⊥a4，a4∥a5…，请你探索直线a1与a2 011的位置关系．【答案】（1）a1⊥a3，理由详见解析；（2）a1∥a4；（3）a1⊥a2 011.【解析】【分析】（1）根据两直线平行，同位角相等得出相等的角，再根据垂直的定义解答；（2）根据（1）中结论即可判定垂直；（3）根据规律发现，与脚码是偶数的直线互相平行，与脚码是奇数的直线互相垂直，根据此规律即可判断．【详解】（1）a1⊥a3．理由如下：如图1，∵a1⊥a2，∴∠1=90°，∵a2∥a3，∴∠2=∠1=90°，∴a1⊥a3；（2）同（1）的解法，如图2，直线a1与a4的位置关系是：a1∥a4；（3）直线a1与a3的位置关系是：a1⊥a2⊥a3，直线a1与a4的位置关系是：a1∥a4∥a5，以四次为一个循环，⊥，⊥，∥，∥以此类推，a1∥a2009，a1⊥a2010，所以直线a1与a2011的位置关系是：a1⊥a2011．【点睛】本题考查了平行公理的推导，作出图形更有利于规律的发现以及规律的推导．三、填空题24．已知，如图，要使得AB∥CD，你认为应该添加的一个条件是________【答案】∠ECD=∠A（答案不唯一）．【解析】【分析】根据平行线的判定定理，即可直接写出条件．【详解】添加的条件是：∠ECD=∠A（答案不唯一）．故答案为：∠ECD=∠A．【点睛】本题考查了平行线的判定定理，解答此类要判定两直线平行的题，可围绕截线找同位角、错角和同旁角．本题是一道探索性条件开放性题目，能有效地培养学生“执果索因”的思维方式与能力．25．在同一平面，三条不同的直线a、b、c，若a⊥c，b⊥c，则______．【答案】a∥b【解析】【分析】根据平行线的判定解答即可．【详解】在同一平面，三条不同的直线a、b、c，若a⊥c，b⊥c，则a∥b．故答案为：a∥b．【点睛】本题考查了平行线的判定与性质，在同一平面，垂直于同一直线的两直线平行的性质，是基础题，熟记平行线的判定是解题的关键．126．设a、b、c为平面上三条不同直线，(1)若a∥b，b∥c，则a与c的位置关系是________；(2)若a⊥b，b⊥c，则a与c的位置关系是________．【答案】a∥c；a∥c.【解析】【分析】（1）根据两条直线的位置关系直接写出答案.（2）根据垂线的性质去解答即可.【详解】设a、b、c为平面上三条不同直线，(1)若a∥b，b∥c，则a与c的位置关是a∥c，（2）若a⊥b，b⊥c，则a与c的位置关系是a∥c.故答案为(1). a∥c (2). a∥c【点睛】此题重点考察学生对两直线的位置关系和垂线性质的理解，掌握两直线的位置和垂线的性质是解题的关键.27．如图，某工件要求AB∥ED，质检员小量得∠ABC＝146°，∠BCD＝60°，∠EDC＝154°，则此工件________．(填“合格”或“不合格”)【答案】合格【解析】【分析】作CF∥AB，由平行线的性质得出∠ABC+∠1=180°，求出∠1，得出∠2，由∠2+∠EDC=180°，得出CF∥ED，证出AB∥ED，即可得出结论．【详解】作CF∥AB，如图所示：则∠ABC+∠1=180°，∴∠1=180°-146°=34°，∴∠2=∠BCD-∠1=60°-34°=26°，∵∠2+∠EDC=26°+154°=180°，∴CF∥ED，∴AB∥ED；故答案为：合格．【点睛】本题考查了平行线的性质与判定；熟练掌握平行线的判定与性质，并能进行推理论证是解决问题的关键28．如图，EN⊥CD，点M在AB上，∠MEN＝156°，当∠BME＝________°时，AB∥CD.【答案】66.【解析】【分析】过点E作EF∥AB，由平行线的性质可得∠BME=MEF，利用平行线的判定定理和性质定理可得∠NEF=90°，易得∠BME．【详解】过点E作EF∥AB，∴∠BME=MEF，∵AB∥CD，∴EF∥CD，∵EN⊥CD，∴EN⊥EF，∴∠NEF=90°，∵∠MEN=156°，∴∠MEF+90°=156°，∴∠MEF=∠BME=156°-90°=66°．故答案为：66．【点睛】本题主要考查了平行线的判定定理及性质定理，综合运用定理是解答此题的关键．29．如图，已知CD⊥DA，DA⊥AB，∠1=∠2. 试说明DF∥AE. 请你完成下列填空，把解答过程补充完整.解：∵CD⊥DA，DA⊥AB，∴∠CDA=90°，∠DAB=90°( ).∴∠CDA=∠DAB(等量代换).又∠1=∠2，从而∠CDA-∠1=∠DAB-________(等式的性质).即∠3=_______.∴DF∥AE( ).【答案】垂直的定义；∠2；∠4；错角相等，两直线平行【解析】【分析】（1）根据垂直的定义填空；（2）根据等式的性质进行填空；（3）根据图象中角的位置关系进行解答；（4）根据平行线的判定定理进行解答即可.【详解】解：∵CD⊥DA，DA⊥AB，∴∠CDA=90°，∠DAB=90°(垂直的定义)，∴∠CDA=∠DAB(等量代换)，又∠1=∠2，从而∠CDA-∠1=∠DAB-∠2 (等式的性质).即∠3=∠4，∴DF∥AE（错角相等，两直线平行）.故答案为：垂直的定义；∠2；∠4；错角相等，两直线平行.【点睛】本题主要考查了平行线的判定定理等知识点，解此题的关键在于熟记书本中基本的知识点.30．如图，当∠1=∠__时，AB∥DC．【答案】4【解析】【分析】当∠1=∠4 时，根据错角相等，两直线平行可以判定AB∥DC．【详解】∵∠1=∠4，∴AB∥DC（错角相等，两直线平行）．【点睛】此题主要考查了平行线的判定，错角相等，两直线平行．。

人教版七年级数学下册平行线的判定同步练习题（含解析）

人教版七年级数学下册平行线的判定同步练习题（含解析）人教版七年级数学下册平行线的判定同步练习题（含解析）学校:___________姓名：___________班级：___________考号：___________一、单选题1．如图所示，点E在线段AC的延长线上，下列条件中能判断的是（?）A．∠3＝∠AB．∠1＝∠2C．∠D＝∠DCED．∠D+∠ACD＝180°2．为增强学生体质，感受中国的传统文化，学校将国家级非物质文化遗产“抖空竹”引入阳光特色大课间，小聪把它抽象成图2的数学问题：已知AB∥CD，∠EAB＝80°，，则∠E的度数是（?）A．30°B．40°C．60°D．70°3．如图，直线a，b被直线c所截，下列条件不能判定直线a 与b平行的是（）A．∠1＝∠3B．∠2+∠3＝180°C．∠1＝∠4D．∠1+∠4＝180°4．如图，点E在AC的延长线上，下列条件能判断ABCD的是（?）A．∠3=∠4B．∠D=∠DCEC．∠D+∠ACD=180°D．∠1=∠25．如图，下面条件不能判断的是（?）A．B．C．D．6．如图，要使，则需要添加的条件是（?）A ．B．C．D．二、填空题7．如图，请你添加一个条件________，使AB∥CD.8．两条平行直线被第三条直线所截，内错角相等．简称：两直线平行，内错角_________．如图，因为a∥b （已知），所以∠1＝_____（两直线平行，内错角相等）． 9．如图所示，在下列条件中，不能判断的有___________．①．?②．③．?④．10．a、b、c是直线，且a∥b，b⊥c，则a与c的位置关系是________．11．如图，已知∠1＝30°，∠2或∠3满足条件_________，则a∥b．三、解答题12．如图，在△ABC中，AD是BC边上的中线，F，E分别是AD及其延长线上的点．(1)如果CFBE，说明：△BDE≌△CDF；(2)若CF，BE是△ABC的BC边上的中线AD及其延长线的垂线，垂足分别为E、F，请猜想BF与CE的位置关系？并说明理由．13．如图，点A，D，C，F在同一条直线上，AB＝DE，BC＝EF．有下列三个条件：①AC＝DF，②∠A BC＝∠DEF，③∠ACB＝∠DFE．(1)请在上述三个条件中选取一个条件，使得△ABC≌△DEF．你选取的条件为（填写序号）______（只需选一个条件，多选不得分），你判定△ABC≌△DEF的依据是______（填“SSS”或“SAS”或“ASA”或“AAS”）；(2)利用（1）的结论△ABC≌△DEF．求证：AB∥DE．14．下列推理是否正确?为什么?（1）如图，∵，∴；（2）如图，∵，∴；（3）如图，∵，∴；（4）如图，∵，∴．15．如图，将绕点B顺时针旋转60度得到，点C的对应点E 恰好落在AB的延长线上，连接AD．（1）求证：；（2）若AB=4，BC=1，求A，C两点旋转所经过的路径长之和．16．如图，已知△ABC≌△DEF，∠A=85°，∠B=60°，AB=8，EH=2(1)求角F的度数与DH的长；(2)求证：．17．如图，在四边形中，与有怎样的位置关系？为什么？与呢？18．已知：如图，BE平分∠ABC，∠1＝∠2．求证：BC//DE．19．请补全证明过程及推理依据．已知：如图，BC//ED，BD平分∠ABC，EF平分∠AED．求证：BD∥EF．证明：∵BD平分∠ABC，EF平分∠AED，∴∠1=∠AED，∠2=∠ABC（______________）∵BC∥ED（________）∴∠AED=________（________________）∴∠AED=∠ABC∴∠1=________∴BD∥EF（________________）．参考答案：1．B【分析】根据平行线的判定条件逐一判断即可．【详解】A.由∠3＝∠A无法判断，故A不符合题意；B.由∠1＝∠2能判断，故B符合题意；C.由∠D＝∠DCE可以判断，不能判断，故C不符合题意；D.∠D+∠ACD＝180°可以判断，不能判断，故D不符合题意．故选：B．【点睛】本题主要考查平行线的判定，熟知平行线的判定条件，是解题的关键．2．A【分析】过点作，先根据平行线的性质可得，再根据平行公理推论、平行线的性质可得，然后根据角的和差即可得．【详解】解：如图，过点作，，，，，，，，，故选：A．【点睛】本题考查了平行线的判定与性质，熟练掌握平行线的性质是解题关键．3．D【分析】同位角相等，两直线平行，同旁内角互补，两直线平行，根据平行线的判定方法逐一分析即可.【详解】解：（同位角相等，两直线平行），故A不符合题意；∠2+∠3＝180°，（同旁内角互补，两直线平行）故B不符合题意；（同位角相等，两直线平行）故C不符合题意；∠1+∠4＝180°，不是同旁内角，也不能利用等量代换转换成同旁内角，所以不能判定故D符合题意；故选D【点睛】本题考查的是平行线的判定，对顶角相等，掌握“平行线的判定方法”是解本题的关键.4．D【分析】根据平行线的判定条件逐一判断即可．【详解】解：A、由∠3=∠4，可以利用内错角相等，两直线平行得到，不能得到，不符合题意；B、由∠D=∠DCE，可以利用内错角相等，两直线平行得到，不能得到，不符合题意；C、由∠D+∠ACD=180°，可以利用内错角相等，两直线平行得到，不能得到，不符合题意；D、由∠1=∠2，可以利用内错角相等，两直线平行得到得到，符合题意；故选D．【点睛】本题主要考查了平行线的判定，熟知内错角相等，两直线平行，同位角相等，两直线平行，同旁内角互补，两直线平行是解题的关键．5．B【分析】根据平行线的判定条件逐一判断即可．【详解】解：A、由∠1=∠2，可以判断（内错角相等，两直线平行），故此选项不符合题意；B、由∠1+∠3=180°，可以判断（同旁内角互补，两直线平行），不能判断，故此选项符合题意；C、由，可以判断（同位角相等，两直线平行），故此选项不符合题意；D、由，可以判断（同旁内角互补，两直线平行），故此选项不符合题意；故选B．【点睛】本题主要考查了平行线的判定，熟知平行线的判定条件是解题的关键．6．A【分析】依据同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行，即可得到添加的条件．【详解】解：A．∵∠A=∠CBE，∴AD∥BC，符合题意；B．由∠A=∠C无法得到AD∥BC，不符合题意；C．由∠C=∠CBE，只能得到AB∥CD，无法得到AD∥BC，不符合题意；D．由∠A+∠D =180°，只能得到AB∥CD，无法得到AD∥BC，不符合题意；故选：A．【点睛】本题主要考查了平行线的判定，解题时注意：同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行．7．∠1＝∠5.【分析】根据平行线的判定进行解答，可以考虑同位角相等，或内错角相等，或同旁内角互补．【详解】添加∠1=∠5∵∠1=∠5，∴AB∥CD．故答案为∠1=∠5【点睛】本题属于开放题，主要考查了平行线的判定，解决问题的关键是掌握平行线的判定方法．8．相等 ∠2【解析】略9．②③##③②【分析】根据平行线的判定进行解答即可得．【详解】解：①∵，∴（内错角相等，两直线平行），说法正确，不符合题意；②∵和既不是同位角，也不是内错角，∴不能根据判定，说法错误，符合题意；③∵为同位角，∴不一定平行，符合题意；④∵，∴（同旁内角互补，两直线平行），说法正确，不符合题意；故答案为：②③．【点睛】本题考查了平行线的判定，解题的关键是熟记并理解平行线的判定．10．互相垂直【详解】且a∥b，b⊥c，a⊥c.故答案为互相垂直.11．∠2＝150°或∠3＝30°【解析】略12．(1)见解析(2)BFCE，证明见解析【分析】（1）根据已知条件，通过两角及其夹边对应相等即可证明△BDE≌△CDF；（2）先证CFBE，利用（1）中结论得△BDE≌△CDF，推出，利用SAS证明△BDF≌△CDE，推出，利用内错角相等，两直线平行，可得BFCE．（1）证明：∵CFBE，∴∠FCD﹦∠EBD．∵AD是BC边上的中线，∴．在△BDE和△CDF中，，∴△BDE≌△CDF．（2）解：BFCE．理由如下：如图，连接BF,CE．∵ C F⊥AD于F，BE⊥AD于E，∴CFBE．由（1）的结论可知△BDE≌△CDF，∴．∵AD是BC边上的中线，∴BD =CD．在△B DF和△CDE中，，∴△BDF≌△CDE．∴，∴BFCE．【点睛】本题考查全等三角形的判定与性质，平行线的性质与判定，三角形中线的定义等，熟练掌握全等三角形的判定方法、平行线的性质定理和判定定理是解题的关键．13．(1)①，SSS(2)见解析【分析】(1)根据SSS即可证明△ABC≌?DEF，即可解决问题；(2)根据全等三角形的性质可得可得∠A=∠EDF，再根据平行线的判定即可解决问题．（1）解：在△ABC和△DEF中，，∴△ABC≌△DEF（SSS），∴在上述三个条件中选取一个条件，使得△ABC≌△DEF，选取的条件为①，判定△ABC≌△DEF的依据是SSS．（注意：只需选一个条件，多选不得分）故答案为：①，SSS；（2）证明：∵△ABC ≌△DEF．∴∠A＝∠EDF，∴AB∥DE．【点睛】本题考查了平行线的性质和全等三角形的性质，和判定定理，能熟记全等三角形的判定定理是解此题的关键．14．（1）正确；理由见解析；（2）不正确；理由见解析；（3）正确；理由见解析；（4）正确；理由见解析．【分析】（1）是被所截形成的同位角，再利用同位角相等，两直线平行可判断；（2）是被所截形成的同旁内角，再利用同旁内角互补，两直线平行可判断；（3）是被所截形成的内错角，再利用内错角相等，两直线平行可判断；（4）是被所截形成的同旁内角，再利用同旁内角互补，两直线平行可判断；【详解】解：（1）正确，理由：同位角相等，两直线平行；（2）不正确，因为由“”只能推出“”，推不出“”；（3）正确，理由：内错角相等，两直线平行；（4）正确，理由：同旁内角互补，两直线平行．【点睛】本题考查的是平行线的判定，掌握“平行线的判定方法”是解题的关键.15．（1）见解析；（2）【分析】（1）先利用旋转的性质证明△ABD为等边三角形，则可证，即再根据平行线的判定证明即可．（2）利用弧长公式分别计算路径，相加即可求解．【详解】（1）证明：由旋转性质得：是等边三角形所以∴；（2）依题意得：AB=BD=4，BC=BE=1，所以A，C两点经过的路径长之和为．【点睛】本题考查了旋转的性质、等边三角形的判定与性质、平行线的判定、弧长公式等知识，熟练掌握这些知识点之间的联系及弧长公式是解答的关键．16．(1)35°；6(2)见解析【分析】(1)根据三角形内角和定理求出∠ACB，根据全等三角形的性质得出AB=DE，∠F=∠ACB，即可得出答案；(2)根据全等三角形的性质得出∠B=∠DEF，再根据平行线的判定即可证得结论．（1）解：∵∠A=85°，∠B=60°，∴∠ACB=180°-∠A-∠B=180°-85°-60°=35°，∵△ABC≌△DEF，AB=8，∴∠F=∠ACB=35°，DE=AB=8，∵EH=2，∴DH=DE-EH=8-2=6；（2）证明：∵△ABC≌△DEF，∴∠B=∠DEF，∴．【点睛】本题考查了全等三角形的性质，三角形的内角和定理，平行线的判定的应用，解此题的关键是能根据全等三角形的性质得出AB=DE，∠B=∠DEF，∠ACB=∠F，注意：全等三角形的对应边相等，对应角相等．17．，见解析【分析】四边形ABCD内角和360°，即，因为，所以，所以，同理．【详解】四边形ABCD内角和360°同理可得：【点睛】本题主要考查了四边形内角和以及平行线的判定，掌握该性质判定是解题的关键．18．见解析【分析】由BE平分∠ABC，可得∠1＝∠3，再利用等量代换可得到一对内错角相等，即∠2＝∠3，即可证明结论．【详解】证明：∵BE平分∠ABC，∴∠1＝∠3，∵∠1＝∠2，∴∠2＝∠3，∴B C//DE．【点睛】本题主要利用了角平分线的性质以及内错角相等、两直线平行等知识点，灵活运用平行线的判定定理成为解答本题的关键．19．角平分线的定义；已知；∠ABC；两直线平行，同位角相等；∠2；同位角相等，两直线平行【分析】根据角平分线的定义得出∠1=∠AED，∠2=∠ABC，根据平行线的性质定理得出∠AED=∠ABC，求出∠1=∠2，再根据平行线的判定定理推出即可．【详解】证明：∵BD平分∠ABC，EF平分∠AED，∴∠1=∠AED，∠2=∠ABC（角平分线的定义）∵BC∥ED（已知）∴∠AED=∠ABC（两直线平行，同位角相等）∴∠AED=∠ABC∴∠1=∠2 ∴BD∥EF（同位角相等，两直线平行）．故答案为：角平分线的定义；已知；∠ABC；两直线平行，同位角相等；∠2；同位角相等，两直线平行．【点睛】本题考查了角平分线的定义，平行线的性质定理和判定定理等知识点，能熟记平行线的性质定理和判定定理是解此题的关键．答案第1页，共2页答案第1页，共2页试卷第1页，共3页试卷第1页，共3页。

平行线的判定专项练习60题(有答案)

1．已知：如图，BE平分∠ABC，∠1=∠2．求证：BC∥DE．2．如图，已知∠A=∠F，∠C=∠D，试说明BD∥CE．3．如图所示，AB⊥BC，BC⊥CD，BF和CE是射线，并且∠1=∠2，试说明BF∥CE．4．如图，AB⊥BC，∠1+∠2=90°，∠2=∠3，求证：BE∥DF．5．如图，OP平分∠MON，A、B分别在OP、OM上，∠BOA=∠BAO，那么AB平行于ON吗？若平行，请写出证明过程；若不平行，请说明理由．6．已知：如图，∠1=∠2，∠A=∠C．求证：AE∥BC．7．已知，如图B、D、A在一直线上，且∠D=∠E，∠ABE=∠D+∠E，BC是∠ABE的平分线，求证：DE∥BC．8．如图，已知∠AEC=∠A+∠C，试说明：AB∥CD．9．如图，已知AC∥ED，EB平分∠AED，∠1=∠2，求证：AE∥BD．10．如图，直线AB、CD与直线EF相交于E、F，已知：∠1=105°，∠2=75°，求证：AB∥CD．11．如图，∠D=∠A，∠B=∠FCB，求证：ED∥CF．12．如图，已知AB⊥BC，CD⊥BC，∠1=∠2，求证：EB∥FC．13．如图所示所示，已知BE是∠B的平分线，交AC 于E，其中∠1=∠2，那么DE∥BC吗？为什么？14．如图，已知∠C=∠D，DB∥EC．AC与DF平行吗？试说明你的理由．15．如图，AC⊥AE，BD⊥BF，∠1=35°，∠2=35°，求证：AE∥BF．16．如图，已知AB∥CD，∠1=∠2，求证：BE∥CF．17．已知∠BAD=∠DCB，∠1=∠3，求证：AD∥BC．18．如图，AD是三角形ABC的角平分线，DE∥CA，并且交AB与点E，∠1=∠2，DF与AB是否平行？为什么？19．如图，已知：∠C=∠DAE，∠B=∠D，那么AB平行于DF吗？请说明理由．20．如图，已知点B在AC上，BD⊥BE，∠1+∠C=90°，问射线CF与BD平行吗？说明理由．21．已知∠1的度数是它补角的3倍，∠2等于45°，那么AB∥CD吗？为什么？22．已知：如图，BDE是一条直线，∠ABD=∠CDE，BF平分∠ABD，DG平分∠CDE，求证：BF∥DG．23．如图，四边形ABCD中，∠A=∠C=90°，BF、DE 分别平分∠ABC、∠ADC．判断DE、BF是否平行，并说明理由．24．如图，若∠CAB=∠CED+∠CDE，求证：AB∥CD ．25．如图，CD⊥AB，GF⊥AB，∠1=∠2．试说明DE∥BC．26．如图所示，∠CAD=∠ACB，∠D=90°，EF⊥CD．试说明：∠AEF=∠B．27．已知：如图所示，C，P，D三点在同一条直线上，∠BAP+∠APD=180°，∠E=∠F，求证：∠1=∠2．28．如图，∠D=∠1，∠E=∠2，DC⊥EC．求证：AD∥BE．29．如图，在四边形ABCD中，∠A=∠C，BE平分∠ABC，DF平分∠ADC，试说明BE∥DF．30．已知：如图，∠1=∠2，∠A=∠F，则∠C与∠D相等吗？试说明理由．31．如图，在四边形ABCD中，∠A=∠C=90°，∠1=∠2，∠3=∠4，求证：BE∥DF．32．如图，已知∠1=∠2求证：a∥b．33．如图，DE⊥AO于E，BO⊥AO于O，FC⊥AB于C，∠1=∠2，找出图中互相平行的线，并加以说明．34．如图，已知∠1=∠2，∠C=∠CDO，求证：CD∥OP．35．如图，已知DE平分∠BDF，AF平分∠BAC，且∠1=∠2．求证（1）DF∥AC；（2）DE∥AF．36．如图，AD平分∠BAC，EF平分∠DEC，且∠1=∠2，试说明DE与AB的位置关系．37．如图，在△ABC中，点D在AB上，∠ACD=∠A，∠BDC的平分线交BC于点E．求证：DE∥AC．38．如图，AB与CD相交于点O，并且∠A=∠1，试问∠2与∠B满足什么关系时，AC∥BD？说明理由．39．如图，已知∠1=∠A，∠2=∠B，那么MN与EF平行吗？如果平行，请说明理由．40．如图，直线AB、CD被直线EF所截，∠1+∠4=180°，求证：AB∥CD．41．如图所示，已知：∠1=∠2，∠E=∠F．试说明AB∥CD．42．如图，已知EF⊥CD于F，∠GEF=25°，∠1=65°，则AB与CD平行吗？请说明理由．43．如图，已知∠1=∠2=90°，∠3=30°，∠4=60°，图中有几对平行线？说说你的理由．44．直线AB，CD被直线EF所截，∠1=∠2，直线AB 和CD平行吗？为什么？45．已知：如图，AD⊥BC，EF⊥BC，∠1=∠2．求证：AB∥GF．46．如图，已知B、C、D三点在同一条直线上，∠B=∠1，∠2=∠E，试说明AD∥CE．47．直线AB、CD与GH交于E、F，EM平分∠BEF，FN平分∠DFH，∠BEF=∠DFH，求证：EM∥FN．48．如图所示，∠ABC=∠BCD，BE、CF分别平分∠ABC 和∠BCD，请你说出BE与CF的位置关系，并说出你的理由．49．如图，若∠1=∠2，请判断DB与EC的位置关系，并说明理由．50．如图，在△ABC中，CD⊥AB，垂足为D，点E在BC上，EF⊥AB，垂足为F．（1）CD与EF平行吗？为什么？（2）如果∠1=∠2，DG∥BC吗？为什么？51．如图，已知：HG平分∠AHM，MN平分∠DMH，且∠AHM=∠DMH．问：GH与MN有怎样的位置关系，请说明理由．（请注明每一步的理由）52．已知：如图，∠C=∠1，∠2和∠D互余，BE⊥FD 于点G．求证：AB∥CD．53．如图，直线AB，CD被EF所截，∠3=∠4，∠1=∠2，EG⊥FG．求证：AB∥CD．54．已知：如图，CD是直线，E在直线CD上，∠1=130°，∠A=50°，求证：AB∥CD．55．如图，已知∠1=∠2，∠DAB=∠DCA，且DE⊥AC，BF⊥AC，问：（1）AD∥BC吗？（2）AB∥CD吗？为什么？56．如图，四边形ABCD，∠1=30°，∠B=60°，AB⊥AC，则AD与BC一定平行吗？AB与CD呢？若平行请说明理由，反之则不用说明理由．57．已知：如图，∠A=∠F，∠C=∠D．求证：BD∥CE．58．如图，AD⊥BC于点D，∠1=2，∠CDG=∠B，请你判断EF与BC的位置关系，并加以证明，要求写出每步证明的理由．59．已知：如图，CE平分∠ACD，∠1=∠B，求证：AB∥CE．60．如图，已知∠1=∠2，∠3=∠4，可以判定哪两条直线平行？。

平行线的判定习题带答案

平行线的判定习题带答案平行线的判定习题带答案平行线是几何学中的重要概念，它们在我们的日常生活和数学应用中都有着广泛的应用。

判断两条直线是否平行是我们学习几何学时需要掌握的基本技能之一。

下面将介绍一些平行线的判定习题，并提供详细的解答过程。

习题一：已知直线l1过点A(2, 3)，斜率为2，直线l2过点B(4, 5)，斜率为-2，判断直线l1和l2是否平行。

解答：直线的斜率可以用斜率公式来计算。

斜率公式为：m = (y2 - y1) / (x2 - x1)，其中(x1, y1)和(x2, y2)分别为直线上的两个点。

对于直线l1，已知斜率为2，过点A(2, 3)，我们可以选择另一个点B(4, 7)在直线上，计算斜率：m1 = (7 - 3) / (4 - 2) = 4 / 2 = 2对于直线l2，已知斜率为-2，过点B(4, 5)，我们可以选择另一个点C(6, 1)在直线上，计算斜率：m2 = (1 - 5) / (6 - 4) = -4 / 2 = -2根据计算结果可知，直线l1和l2的斜率相等，即m1 = m2 = 2，因此直线l1和l2是平行线。

习题二：已知直线l1过点A(1, 2)，直线l2过点B(3, 4)，直线l3过点C(5, 6)，判断直线l1、l2和l3是否共线。

解答：要判断三条直线是否共线，可以通过计算斜率来判断。

如果三条直线的斜率相等，则它们共线。

对于直线l1，已知过点A(1, 2)，选择另一个点D(2, 3)在直线上，计算斜率：m1 = (3 - 2) / (2 - 1) = 1对于直线l2，已知过点B(3, 4)，选择另一个点E(4, 5)在直线上，计算斜率：m2 = (5 - 4) / (4 - 3) = 1对于直线l3，已知过点C(5, 6)，选择另一个点F(6, 7)在直线上，计算斜率：m3 = (7 - 6) / (6 - 5) = 1根据计算结果可知，直线l1、l2和l3的斜率均为1，因此它们共线。

平行线的判定专项练习60题(有答案)

1．已知：如图，BE平分∠ABC，∠1=∠2．求证：BC∥DE．2．如图，已知∠A=∠F，∠C=∠D，试说明BD∥CE．3．如图所示，AB⊥BC，BC⊥CD，BF和CE是射线，并且∠1=∠2，试说明BF∥CE．5．如图，OP平分∠MON，A、B分别在OP、OM上，∠BOA=∠BAO，那么AB平行于ON吗？若平行，请写出证明过程；若不平行，请说明理由．6．已知：如图，∠1=∠2，∠A=∠C．求证：AE∥BC．7．已知，如图B、D、A在一直线上，且∠D=∠E，∠ABE=∠D+∠E，BC是∠ABE的平分线，8．如图，已知∠AEC=∠A+∠C，试说明：AB∥CD．9．如图，已知AC∥ED，EB平分∠AED，∠1=∠2，求证：AE∥BD．10．如图，直线AB、CD与直线EF相交于E、F，已知：∠1=105°，∠2=75°，求证：AB∥CD．11．如图，∠D=∠A，∠B=∠FCB，求证：ED∥CF．12．如图，已知AB⊥BC，CD⊥BC，∠1=∠2，求证：EB∥FC．13．如图所示所示，已知BE是∠B的平分线，交AC于E，其中∠1=∠2，那么DE∥BC吗？为什么？14．如图，已知∠C=∠D，DB∥EC．AC与DF平行吗？试说明你的理由．15．如图，AC⊥AE，BD⊥BF，∠1=35°，∠2=35°，求证：AE∥BF．16．如图，已知AB∥CD，∠1=∠2，求证：BE∥CF．17．已知∠BAD=∠DCB，∠1=∠3，求证：AD∥BC．18．如图，AD是三角形ABC的角平分线，DE∥CA，并且交AB与点E，∠1=∠2，DF与AB是否平行？为什么？19．如图，已知：∠C=∠DAE，∠B=∠D，那么AB平行于DF吗？请说明理由．.20．如图，已知点B在AC上，BD⊥BE，∠1+∠C=90°，问射线CF与BD平行吗？说明理由．21．已知∠1的度数是它补角的3倍，∠2等于45°，那么AB∥CD吗？为什么？22．已知：如图，BDE是一条直线，∠ABD=∠CDE，BF 平分∠ABD，DG平分∠CDE，求证：BF∥DG．23．如图，四边形ABCD中，∠A=∠C=90°，BF、DE分别平分∠ABC、∠ADC．判断DE、BF是否平行，并说明理由．24．如图，若∠CAB=∠CED+∠CDE，求证：AB∥CD．25．如图，CD⊥AB，GF⊥AB，∠1=∠2．试说明DE∥BC．26．如图所示，∠CAD=∠ACB，∠D=90°，EF⊥CD．试说明：∠AEF=∠B．27．已知：如图所示，C，P，D三点在同一条直线上，∠BAP+∠APD=180°，∠E=∠F，求证：∠1=∠2．28．如图，∠D=∠1，∠E=∠2，DC⊥EC．求证：AD∥BE．29．如图，在四边形ABCD中，∠A=∠C，BE平分∠ABC，DF平分∠ADC，试说明BE∥DF．30．已知：如图，∠1=∠2，∠A=∠F，则∠C与∠D相等吗？试说明理由．31．如图，在四边形ABCD中，∠A=∠C=90°，∠1=∠2，∠3=∠4，求证：BE∥DF．32．如图，已知∠1=∠2求证：a∥b．33．如图，DE⊥AO于E，BO⊥AO于O，FC⊥AB于C，∠1=∠2，找出图中互相平行的线，并加以说明．34．如图，已知∠1=∠2，∠C=∠CDO，求证：CD∥OP．35．如图，已知DE平分∠BDF，AF平分∠BAC，且∠1=∠2．求证（1）DF∥AC；（2）DE∥AF．36．如图，AD平分∠BAC，EF平分∠DEC，且∠1=∠2，试说明DE与AB的位置关系．37．如图，在△ABC中，点D在AB上，∠ACD=∠A，∠BDC求证：DE∥AC．38．如图，AB与CD相交于点O，并且∠A=∠1，试问∠2与∠B满足什么关系时，AC∥BD？说明理由．39．如图，已知∠1=∠A，∠2=∠B，那么MN与EF平行吗？如果平行，请说明理由．40．如图，直线AB、CD被直线EF所截，∠1+∠4=180°，41．如图所示，已知：∠1=∠2，∠E=∠F．试说明AB∥CD．42．如图，已知EF⊥CD于F，∠GEF=25°，∠1=65°，则AB与CD平行吗？请说明理由．43．如图，已知∠1=∠2=90°，∠3=30°，∠4=60°，图中有几对平行线？说说你的理由．44．直线AB，CD被直线EF所截，∠1=∠2，直线AB和CD平行吗？为什么？45．已知：如图，AD⊥BC，EF⊥BC，∠1=∠2．求证：AB∥GF．46．如图，已知B、C、D三点在同一条直线上，∠B=∠1，∠2=∠E，试说明AD∥CE．47．直线AB、CD与GH交于E、F，EM平分∠BEF，FN平分∠DFH，∠BEF=∠DFH，求证：EM∥FN．48．如图所示，∠ABC=∠BCD，BE、CF分别平分∠ABC 和∠BCD，请你说出BE与CF的位置关系，并说出你的理由．49．如图，若∠1=∠2，请判断DB与EC的位置关系，50．如图，在△ABC中，CD⊥AB，垂足为D，点E在BC 上，EF⊥AB，垂足为F．（1）CD与EF平行吗？为什么？（2）如果∠1=∠2，DG∥BC吗？为什么？51．如图，已知：HG平分∠AHM，MN平分∠DMH，且∠AHM=∠DMH．问：GH与MN有怎样的位置关系，请说明理由．（请注明每一步的理由）52．已知：如图，∠C=∠1，∠2和∠D互余，BE⊥FD于点G．求证：AB∥CD．53．如图，直线AB，CD被EF所截，∠3=∠4，∠1=∠2，EG⊥FG．求证：AB∥CD．54．已知：如图，CD是直线，E在直线CD上，∠1=130°，∠A=50°，求证：AB∥CD．55．如图，已知∠1=∠2，∠DAB=∠DCA，且DE⊥AC，（1）AD∥BC吗？（2）AB∥CD吗？为什么？56．如图，四边形ABCD，∠1=30°，∠B=60°，AB⊥AC，则AD与BC一定平行吗？AB与CD呢？若平行请说明理由，反之则不用说明理由．57．已知：如图，∠A=∠F，∠C=∠D．求证：BD∥CE．58．如图，AD⊥BC于点D，∠1=2，∠CDG=∠B，请你判断EF与BC的位置关系，并加以证明，要求写出每步证明的理由．59．已知：如图，CE平分∠ACD，∠1=∠B，求证：AB∥CE．60．如图，已知∠1=∠2，∠3=∠4，可以判定哪两条直线平行？. .。

平行线的判定练习题(含答案)

平行线的判定练习题一、选择题(每小题3分，共36分)1.下面四个图中，∠1=∠2一定成立的是( C )2.如图，已知点O 是直线AB 上一点，∠1=65°，则∠2的度数是( D )A.25°B.65°C.105°D.115°3.下列说法正确的是( A )A.a ，b ，c 是直线，且a ∥b，b∥c，则a∥cB.a ，b ，c 是直线，且a⊥b，b⊥c，则a⊥cC.a ，b ，c 是直线，且a ∥b，b⊥c，则a∥cD.a ，b ，c 是直线，且a∥b，b∥c，则a⊥c4.如图，下列各语句中，错误的语句是( B )A .∠ADE 与∠B 是同位角 B.∠BDE 与∠C 是同旁内角C.∠BDE 与∠AED 是内错角D.∠BDE 与∠DEC 是同旁内角5.如图，点O 在直线AB 上，且OC⊥OD.若∠COA=36°，则∠DOB 大小为( B )A.36°B.54°C.64°D.72°6.体育课上，老师测量跳远成绩的依据是( C )A.平行线间的距离相等B.两点之间，线段最短C.垂线段最短D.两点确定一条直线7.如图，∠ACB=90°，CD⊥AB ，垂足为D ，则下面的结论中，不正确的是( A )A.点B 到AC 的垂线段是线段CAB.CD 与AB 互相垂直C.AC 与BC 互相垂直D.线段AC 的长度是点A 到BC 的距离8.如图，直线AB ，CD 相交于点0，E0⊥CD.下列说法错误的是( C )A.∠AOD =∠BOCB.∠AOE＋∠B 0D=90°C.∠AOC=∠AOED.∠AOD＋∠BOD=180°9.如图，直线AB ，CD 相交于点0，0E 平分∠AOD.若∠CO E =140°，则∠BOC=( D )A.50°B.60°C.70°D.80°10.对于图中标记的各角，下列条件能够推理得到a∥b 的是( D )（第4题）（第5题）（第2题）（第7题）（第8题）A.∠1=∠2B.∠2=∠4C.∠3=∠4D.∠1＋∠4=180°11.如图，90,ACD CE AB ︒∠=⊥，垂足为E ，则下面的结论中，不正确的是（A ）A.点C 到AB 的垂线段是线段CDB.CD 与AC 互相垂直C.AB 与CE 互相垂直D.线段CD 的长度是点D 到AC 的距离12.如图，已知1234∠=∠=∠=∠，则图中的平行线有（ C ）A.2组B.3组C.4组D.5组二、填空题(每小题3分，共15分)13.已知∠α=35°40’，则∠α的余角为______，补角为______.14.如图，AC⊥BC，AC=3，BC=4，AB=5，则点B 到AC 的距离为______.15.如图，已知OA⊥OB，OC⊥OD，∠AOC=27°，则∠BOD 的度数是______.16.如图，在同一平面内，OA⊥l，OB⊥l，垂足为O ，则OA 与OB 重合的理由是______.17.如图，AB⊥EF 于点G ，CD⊥EF 于点H ，GP 平分∠EGB，HQ 平分∠CHF，则图中互相平行的直线有__________________.三、解答题(共49分)18.(5分)一个角的补角比这个角的余角的3倍大10°，求这个角的度数.19.(共9分,每空1分)如图，完成下列推理过程.(1)已知∠1=108°，∠2=72°，由∠1＋∠2=108°＋72°=180°，可得______∥______，根据是________；(2)已知∠1=108°，∠3=108°，由∠l=108°=∠3，可得______∥______，根据是___________；(3)已知∠2=72°，∠4=72°，由∠2=72°=∠4，可得______∥______，根据是_________.20. (5分)如图，在直角三角形ABC 中，∠ACB=90°，将直角三角形ABC 向下翻折，使点A 与点C 重合，折痕为DE ，试说明：DE ∥BC.21. (5分)如图，已知∠1与∠3互余，∠2与∠3的余角互补，问直线l1∥l2吗？为什么？22. (5分)如图，直线AB，CD相交于点0，OA平分∠EOC.(1)若∠E0C=72°，求∠BOD的度数；(2)若∠D0E=2∠AOC，判断射线0E，0D的位置关系并说明理由.23．(5分)如图，DE平分∠ADC，CE平分∠BCD，且∠1＋∠2＝90°.试判断AD与BC的位置关系，并说明理由．24．(5分)如图，四边形ABCD，∠1=30°，∠B=60°，AB⊥AC，则AD与BC一定平行吗？AB与CD呢？若平行请说明理由，反之则不用说明理由．25．(5分)已知：如图，CD是直线，E在直线CD上，∠1=130°，∠A=50°，求证：AB∥CD．26．(5分)如图，若∠1=∠2，请判断DB与EC的位置关系，并说明理由．参考答案1.C2.D3.B4.B5.A6.C7.A8.C9.D 10.D13.54°20’ 144°20’ 14.4 15.153° 16.同一平面内，过一点有且只有一条直线与已知直线垂直 17.AB∥CD，GP∥HQ18.解：这个角的度数为50°19.(1)AB CD 同旁内角互补，两直线平行 (2)AB CD 同位角相等，两直线平行(3)AE DF 内错角相等，两直线平行20.解：因为将直角三角形ABC向下翻折，使点A与点C重合，折痕为DE，所以∠AED=∠CED=90°.又因为∠ACB=90°，所以∠AED=∠ACB=90°.所以DE∥BC.21.解l1∥l2.理由：因为∠1＋∠3=90°，∠2＋(90°－∠3)=180°，所以∠3=90°－∠l，∠2＋90°－90°＋∠1=180°.所以∠2＋∠1=180°.所以l1∥l2.22.解：(l)∠BOD=36°.(2)0E⊥0D.理由如下：因为∠D OE=2∠AOC，OA平分∠EOC，所以∠DO E=∠EOC.又因为∠DOE＋∠EOC=180°，所以∠DOE=∠EOC=90°.所以OE⊥OD.23.解：AD∥BC．理由如下：因为DE平分∠ADC，CE平分∠BCD，所以∠ADC＝2∠1，∠BCD ＝2∠2.因为∠1＋∠2＝90°，所以∠ADC＋∠BCD＝2(∠1＋∠2)＝180°，所以AD∥BC．24．（1）AD与BC一定平行．理由如下：∵AB⊥AC，∴∠BAC=90°，∵∠1=30°，∠B=60°，∴∠1+∠BAC+∠B=180°，即∠BAD+∠B=180°，∴AD∥BC．（2）AB与CD不一定平行．25．：∵∠1+∠2=180°，∠1=130°，∴∠2=50°，∵∠A=50°，∴∠A=∠2，∴AB∥CD．26．DB与EC的位置关系是平行，理由：∵∠1=∠3，∠2=∠4（对顶角相等），又∵∠1=∠2，∴∠3=∠4，∴BD∥EC．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。