黑龙江省哈尔滨市第一中学校2020-2021学年高二上学期期末考试数学试题(理科)
2023-2024学年黑龙江省哈尔滨市第一中学高二上学期期中地理试题
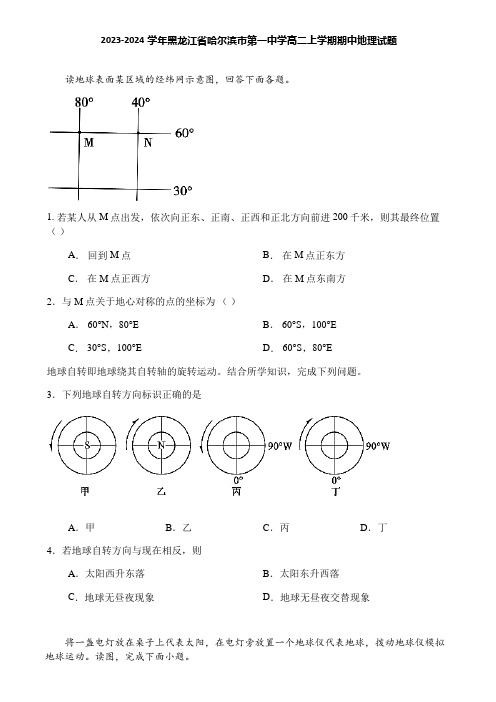
2023-2024学年黑龙江省哈尔滨市第一中学高二上学期期中地理试题读地球表面某区域的经纬网示意图,回答下面各题。
1. 若某人从M点出发,依次向正东、正南、正西和正北方向前进200千米,则其最终位置()A.回到M点B.在M点正东方C.在M点正西方D.在M点东南方2.与M点关于地心对称的点的坐标为()A. 60°N,80°E B. 60°S,100°EC. 30°S,100°E D. 60°S,80°E地球自转即地球绕其自转轴的旋转运动。
结合所学知识,完成下列问题。
3.下列地球自转方向标识正确的是A.甲B.乙C.丙D.丁4.若地球自转方向与现在相反,则A.太阳西升东落B.太阳东升西落C.地球无昼夜现象D.地球无昼夜交替现象将一盏电灯放在桌子上代表太阳,在电灯旁放置一个地球仪代表地球,拨动地球仪模拟地球运动。
读图,完成下面小题。
5.该实验能够演示的地理现象是()A.昼夜的交替B.区时的差异C.地表物体水平运动方向偏转D.地方时差异6.图示为北半球()A.春分B.夏至C.秋分D.冬至北京时间2022年1月17日10时35分,我国在太原卫星发射中心采用长征二号丁运载火箭,成功将试验十三号卫星发射升空,卫星顺利进入预定轨道,发射任务取得圆满成功。
据此完成下面小题。
7.火箭点火发射时,下列地点正值晚餐时间的是()A.孟买(18°56'N,72°49'E)B.伦敦(51°30'N,0°)C.洛杉矶(34°N,118°15'W)D.悉尼(33°55'S,150°53'E)8.火箭点火发射时,地球上新旧两天的比值大约是()A.1:2 B.14:9 C.3:8 D.15:7下图为某一平直河段的剖面,面朝河流下游,左手方视为左岸,右手方视为右岸。
黑龙江省佳木斯市第一中学2024-2025学年高二上学期10月考试数学试卷

黑龙江省佳木斯市第一中学2024-2025学年高二上学期10月考试数学试卷一、单选题1.直线的一个方向向量为()1,3v =-r,且经过点()0,2,则直线的方程为( )A .320x y -+=B .320x y +-=C .320x y ++=D .320x y --=2.已知方程22141x y t t +=--表示椭圆,则t 的取值范围是( )A .14t <<B .512t <<或542t <<C .4t >或1t < D .4t >3.下列说法正确的是( ) A .11y y k x x -=-不能表示过点M x 1,y 1 且斜率为k 的直线方程 B .在x 轴、y 轴上的截距分别为a ,b 的直线方程为1x ya b+=C .直线y kx b =+与y 轴的交点到原点的距离为bD .设(2,2)A -,(1,1)B ,若直线:10l ax y ++=与线段AB 有交点,则a 的取值范围是(,2)-∞-4.椭圆2221(1)x y a a+=>的离心率为12,则a =( )ABCD .25.已知直线l的斜率k ⎡∈-⎣,则该直线的倾斜角α的取值范围为( )A .π3π,34⎡⎤⎢⎥⎣⎦B .π3π0,,π34⎡⎤⎡⎫⋃⎪⎢⎥⎢⎣⎦⎣⎭C .π3π,64⎡⎤⎢⎥⎣⎦D .π3π0,,π64⎡⎤⎡⎫⎪⎢⎥⎢⎣⎦⎣⎭U6.经过两条直线210x y -+=和20x y ++=的交点,且与直线230x y +=平行的直线的方程为( )A .2350x y +-=B .2350x y ++=C .2310x y ++=D .2310x y --=7.已知Q 为直线:210l x y ++=上的动点,点P 满足()1,3QP =-u u u r,记P 的轨迹为E ,则( ) A .EB .E 是一条与l 相交的直线C .E 上的点到lD .E 是两条平行直线8.已知椭圆C :2212x y +=的左、右两个顶点为A ,B ,点1M ,2M ,3M 是AB 的四等分点,分别过这三点作斜率为()0k k ≠的一组平行线,交椭圆C 于1P ,2P ,…,6P ,则直线1AP ,2AP ,…,6AP ,这6条直线的斜率乘积为( )A .18-B .164-C .8D .64二、多选题9.已知圆C :226430x y x y +-+-=,则下列说法正确的是( ) A .圆C 的半径为16B .圆C 截x轴所得的弦长为C .圆C 与圆E :()()22621x y -+-=相外切D .若圆C 上有且仅有两点到直线340x y m ++=的距离为1,则实数m 的取值范围是()()19,2426,21⋃--10.公元前3世纪,古希腊数学家阿波罗尼斯在《平面轨迹》一书中,曾研究了众多的平面轨迹问题,其中有如下结果:平面内到两定点距离之比等于已知数的动点轨迹为直线或圆.后世把这种圆称为阿波罗尼斯圆.已知直角坐标系中()2,0A -,()2,0B ,满足2PA PB =的点P 的轨迹为C ,则下列结论正确的是( )A .点P 的轨迹是以10,03C ⎛⎫ ⎪⎝⎭为圆心,83r =为半径的圆B .轨迹C 上的点到直线3450x y -+=的最小距离为12C .若点(),x y 在轨迹C上,则x 的最小值是2- D .圆22()4x y a +-=与轨迹C 有公共点,则a的取值范围是a ≤≤11.(多选)已知椭圆22:1259x y C +=,12,F F 分别为它的左右焦点,点,A B 分别为它的左右顶点,已知定点()4,2Q ,点P 是椭圆上的一个动点,下列结论中正确的有( )A .存在点P ,使得12120F PF ∠=︒B .直线PA 与直线PB 斜率乘积为定值C .12125PF PF +有最小值185D .1PQ PF +的范围为⎡⎤⎣⎦三、填空题12.已知直线l 经过点)(1,0P ,圆22:2660C x y x y ++-+=,若直线l 与圆C 相切,则直线l 的方程为13.已知圆()()22:121C x y -+-=,若从点()3,5M 发出的光线经过直线2l :10x y +-=,反射后恰好平分圆C 的圆周,反射光线所在直线的方程是.14.已知P 是椭圆C :()222210x y a b a b+=>>上一点,1F ,2F 是C 的两个焦点,120PF PF ⋅=u u u r u u u u r ,点Q 在12F PF ∠的平分线上,O 为原点,1OQ PF ∥,且2OQ b =.则C 的离心率为.四、解答题15.平面直角坐标系中,圆M 的方程为()2221x y -+=,圆N 的方程为()22249x y ++=,动圆P 与圆N 内切,与圆M 外切. (1)求动圆P 的圆心的轨迹方程;(2)当60MPN ∠=︒时,求PM PN ⋅的大小.16.已知圆C 的圆心在0x y +=上,点()2,0A 在圆C 上,且圆C 与直线40x y --=相切. (1)求圆C 的标准方程;(2)过点A 和点()3,2的直线l 交圆C 于A ,E 两点,求弦AE 的长.17.已知直线1:21l y x =-,直线2l 与直线1l 垂直,且直线1l ,2l 的交点的横坐标与纵坐标相等. (1)求直线2l 的方程;(2)若直线l 被直线1l ,2l 所截得的线段恰好被点()2,2P -平分,求直线l 的方程.18.已知圆()22:2210,R C x mx y m y m m -++-+-=∈.(1)证明:圆C 过定点;(2)当0m =时,点P 为直线:163x yl +=上的动点,过P 作圆C 的两条切线,切点分别为A ,B ,求四边形PACB 面积最小值,并写出此时直线AB 的方程.19.已知椭圆2222:1(0)x y C a b a b+=>>的长轴长为(1)求椭圆C 的方程;(2)若椭圆22221(0)x y a b a b+=>>上点()00,x y 处的切线方程是00221x x y y a b +=,①过直线:2l x =上一点M 引C 的两条切线,切点分别是P Q 、,求证:直线PQ 恒过定点N ; ②是否存在实数λ,使得PN QN PN QN λ+=⋅,若存在,求出λ的值,若不存在,说明理由.。
2023版高中数学新同步精讲精炼(选择性必修第一册) 2
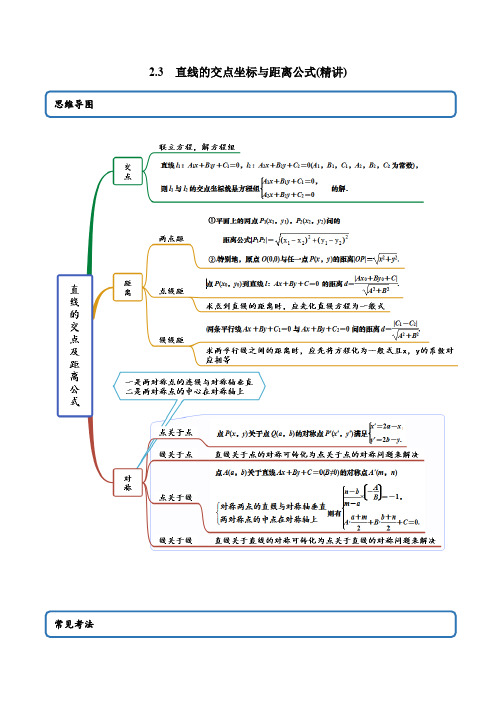
2.3 直线的交点坐标与距离公式(精讲)考点一 交点【例1】(1)(2021·哈尔滨)直线x -2y +3=0与2x -y +3=0的交点坐标为( )A .(-1,1)B .(1,-1)C .(1,1)D .(-1,-1)(2).(2021·贵州黔东南苗族侗族自治州·凯里一中高二期末(理))斜率为2,且过直线4y x =-和直线2y x =+交点的直线方程为( )A . 21y x =+B .21y x =-C .22y x =-D . 22y x =+(3).(2021·黑龙江哈九中高二期末(文))直线210kx y k -++=与240x y +-=的交点在第四象限,则k 的取值范围为( )A .()6,2--B .1,06⎛⎫- ⎪⎝⎭C .11,26--⎛⎫ ⎪⎝⎭D .11,62⎛⎫-- ⎪⎝⎭(4).(2021·全国高二课时练习)(多选)当0<k <12时,直线l 1:kx -y -k +1=0与直线l 2:ky -x -2k =0的交点可能是( )A .(2,3)B .(1,2)C .11(,)22-D .12(,)33- 【一隅三反】 1.(2021·河北唐山市·高二期末)过点(,4)A a 和点(,2)B b 的直线与直线0x y m ++=垂直,则||AB =( )A .B .4C .D .22.(2021·全国高二课时练习)(多选)已知三条直线x -2y =1,2x +ky =3,3kx +4y =5相交于一点,则k 的值为( )A .-163B .-1C .1D .1633.(2021·全国高二专题练习)若直线l 1:y =kx +1与l 2:x -y -1=0的交点在第一象限内,则k 的取值范围是( )A .(1,+∞)B .(-1,1)C .(-∞,-1)∪(1,+∞)D .(-∞,-1)考点二 三种距离【例2-1】(1)(2021·安徽池州市·高二期末(理))若直线1:30l x y -=与24:0l x y +-=交于点A ,且()2,0B ,则AB =___________.(2)(2021·浙江高二期末)点(2,0)到直线20x y ++=的距离为(3).(2021·全国高二课时练习)两条平行线l 1:3x +4y -7=0和l 2:3x +4y -12=0的距离为【例2-2】(1)(2021·浙江)已知直线(2)(12)430m x m y m ++-+-=恒经过定点P ,则点P 到直线:3440l x y +-=的距离是( )A .6B .3C .4D .7(2).(2021·江西)若直线x +3y -9=0与直线x +3y -c =0,则c 的值为( )A .-1B .19C .-1或19D .1或-19 【一隅三反】1.(2021·江苏)点(2,1)到直线l :x -2y +2=0的距离为( )A .25BC D .032.(2021·全国高二专题练习)点P 在直线x +y -4=0上,O 是坐标原点,则|OP |的最小值为( )A B .C D .23.(2021·广西)(多选)若点A (a ,1)到直线3x -4y =1的距离为1,则a 的值为( )A .0B .103 C .5 D .-1034.(2021·全国高二课时练习)在直线2350x y -+=上求点P ,使点P 到()2,3A P 点坐标是( )A .()5,5B .()1,1-C .()5,5或()1,1-D .()5,5或()1,1-5.(2021·湖南)过点(4,)A a 和()5B b ,的直线与直线50x y -+=平行,则||AB 的值为_______.6.(2021·全国高二课时练习)已知,x y 满足30x y ++=,求()()2212x y ++-的最小值__.7.(2021·全国高二课时练习)两直线3x +y -3=0和6x +my -1=0平行,则它们之间的距离为________.8.(2021·全国高二专题练习)已知(3,2)A --,(1,4)B -到直线:10l x ay ++=的距离相等,则实数a 为________.考点三 对称问题【例3-1】(点关于点对称)(1)(2021·全国高二单元测试)若点()1,1A a a -+,(),B a a 关于直线l 对称,那么直线l 的方程为________.(2)(2021·全国高二课时练习)一条光线从点()1,1A -出发射向x 轴,经过x 轴上的点P 反射后经过点()2,5B ,则点P 的坐标为______.【例3-2】(点关于线对称)(1)(2021·全国高二课时练习)点(1,1)-关于直线10x y --=的对称点是______.(2).(2021·浙江高二期末)已知直线():10l mx y m m R ++-=∈过定点P ,则点P 的坐标是___________,点P 关于直线20x y +-=的对称点Q 的坐标是__________.【例3-3】(线关于点对称)(1)(2020·四川省泸县第二中学高二月考(文))直线l 与1l 关于点(11),-成中心对称,若l 的方程是2360x y +-=,则1l 的方程是__________(2).(2020·全国高二课时练习)已知直线1:220l x y ++=与2:40l x by c ++=关于点(1,0)P 对称,则b c +=______.【例3-4】(2021·全国高二专题练习)直线2410x y --=关于0x y +=对称的直线方程为( )A .4210x y --=B .4210x y -+=C .4210x y ++=D .4210x y +-= 【一隅三反】1.(2021·全国高二课时练习 点P(2,5)关于直线x +y =1的对称点的坐标是____________.2.(2020·黑龙江哈尔滨市第六中学校高二月考(文))直线230x y -+=关于点(1,1)对称的直线方程为____________.3.(2021·全国高二单元测试)已知点()3,8A -和()2,2B ,在x 轴上求一点M ,使得AM BM +最小,则点M 的坐标为( )A .()1,0-B .220,5⎛⎫ ⎪⎝⎭ C .22,05⎛⎫ ⎪⎝⎭ D .()1,04.(2021·全国高二专题练习)已知直线10kx y k -++=过定点A ,则点A 关于30x y +-=对称点的坐标为( )A .(2,4)B .(4,2)C .(2,2)D .(4,4)5.(2021·浙江)直线21y x =+关于原点对称的直线方程是( )A .21y x =-B .21y x =--C .21y x =-+D .2y x =6.(2021·广东湛江)已知直线l :2x -3y +1=0,点A (-1,-2).求:(1)点A 关于直线l 的对称点A ′的坐标;(2)直线m :3x -2y -6=0关于直线l 的对称直线m ′的方程;(3)直线l 关于点A 对称的直线l ′的方程.离在几何中的运用【例4-1】(2021·全国高二专题练习)已知△ABC的三个顶点坐标分别是A(1,-1),B(-1,3),C(3,0).(1)判断△ABC的形状;(2)求△ABC的面积.【例4-2】.(2021·沈阳市·辽宁实验中学高二期末)已知直线l过点P(2,3)且与定直线l0:y=2x在第一象限内交于点A,与x轴正半轴交于点B,记AOB的面积为S(O为坐标原点),点B(a,0).(1)求实数a的取值范围;(2)求当S取得最小值时,直线l的方程.【一隅三反】1.(2021·全国高二课时练习)(多选)已知直线1:10l ax y -+=,2:10l x ay ++=,a R ∈,以下结论正确的是( )A .不论a 为何值时,1l 与2l 都互相垂直;B .当a 变化时,1l 与2l 分别经过定点()0,1A 和()1,0B -C .不论a 为何值时,1l 与2l 都关于直线0x y +=对称D .如果1l 与2l 交于点M ,则MO2.(2021·全国高二课时练习)已知AO 是ABC 边BC 的中线,用坐标法证明()22222AB AC AO OC+=+.3.(2021·浙江高二期末)已知直线l 经过直线250x y +-=与20x y -=的交点M .(Ⅰ)若l 经过点(5,0)A ,求l 的方程;(Ⅱ)若直线l 分别与x 轴、y 轴的正半轴交于A 、B 两点,O 为原点,是否存在使ABO 面积最小的直线l ?若存在,求出直线l 方程;若不存在,请说明理由.。
第二关 以解析几何中与椭圆相关的综合问题为解答题-(解析版)

压轴解答题第二关 以解析几何中与椭圆相关的综合问题【名师综述】纵观近三年的高考题,解析几何题目是每年必考题型,主要体现在解析几何知识内的综合及与其它知识之间的综合,且椭圆考查的最多,,同时可能与平面向量、导数相交汇,每个题一般设置了两个问,第(1)问一般考查曲线方程的求法,主要利用定义法与待定系数法求解,而第(2)问主要涉及最值问题、定值问题、对称问题、轨迹问题、探索性问题、参数范围问题等.这类问题综合性大,解题时需根据具体问题,灵活运用解析几何、平面几何、函数、不等式、三角知识,正确构造不等式,体现了解析几何与其他数学知识的密切联系.类型一 中点问题典例1已知椭圆()2222:10x y C a b a b+=>>的离心率13e =,焦距为2.(1)求椭圆C 的方程;(2)过点()0,2Q 作斜率为()0k k ≠的直线l 与椭圆C 交于A 、B 两点,若x 轴上的一点E 满足AE BE =,试求出点E 的横坐标的取值范围.【来源】河南省温县第一高级中学2021-2022学年高三上学期1月月考文科数学试题 【答案】(1)22198x y ;(2)220,12⎡⎫⎛⎤⎪ ⎢⎥⎪ ⎣⎭⎝⎦. 【解析】(1)由已知可求得a 、c 的值,可求得b 的值,由此可得出椭圆C 的标准方程;(2)设点设()11,A x y 、()22,B x y ,将直线l 的方程与椭圆C 的方程联立,列出韦达定理,求出线段AB 的中点G 的坐标,由题意可知EG AB ⊥,可得1EG k k=-,可得出m 关于k 的表达式,分0k <、0k >两种情况讨论,结合基本不等式可求得m 的取值范围.(1)解:由已知得1322c a c ⎧=⎪⎨⎪=⎩,所以,1c =,3a =,2228b a c =-=,因此,椭圆C 的方程为22198x y .(2)解:根据题意可知直线l 的方程为2y kx =+,设()11,A x y 、()22,B x y , 线段AB 的中点为()00,G x y ,设点(),0E m ,使得AE BE =,则EG AB ⊥.联立222198y kx x y =+⎧⎪⎨+=⎪⎩得()228936360k x kx ++-=,()()22223614498288940k k k ∆=++=+>,由韦达定理可得1223698k x x k +=-+,所以,021898k x k -=+,00216298y kx k =+=+, 因为EG AB ⊥,所以,1EGk k =-,即221601981898k k k m k -+=---+, 则2228989k m k k k--==++,当0k >时,89298122k k +≥⨯=22k =20m ≤<; 当0k <时,()()8889929122k k k k k k⎡⎤+=--+≤--⋅-⎢⎥--⎣⎦ 当且仅当22k =20m <≤综上所述,点E 的横坐标的取值范围为220,12⎡⎫⎛⎤⎪ ⎢⎥⎪ ⎣⎭⎝⎦. 【点睛】方法点睛:圆锥曲线中取值范围问题的五种求解策略:(1)利用圆锥曲线的几何性质或判别式构造不等关系,从而确定参数的取值范围;(2)利用已知参数的范围,求新的参数的范围,解这类问题的核心是建立两个参数之间的等量关系; (3)利用隐含的不等关系建立不等式,从而求出参数的取值范围; (4)利用已知的不等关系建立不等式,从而求出参数的取值范围;(5)利用求函数值域的方法将待求量表示为其他变量的函数,求其值域,从而确定参数的取值范围.【举一反三】已知椭圆C :()222210y x a b a b+=>>的焦距与椭圆2213x y +=的焦距相等,且C 经过抛物线()212y x =- (1)求C 的方程;(2)若直线y kx m =+与C 相交于A ,B 两点,且A ,B 关于直线l :10x ty ++=对称,O 为C 的对称中心,且AOB 10k 的值. 【答案】(1)22142y x +=;(2)3k = 【解析】(1)由题意:()212y x =-(2,焦距为22故22222112a ba b ⎧+=⎪⎨⎪-=⎩,解得:24a =,22b =,所以C 的方程为:22142y x +=; (2)因为直线y kx m =+与C 相交于A ,B 两点,且A ,B 关于直线l :10x ty ++=对称,故直线l 垂直AB ,所以k t =,联立22142y kx my x =+⎧⎪⎨+=⎪⎩可得()2222240k x kmx m +++-=,设()11,A x y ,()22,B x y ,AB的中点为()00,P x y ,则()228240k m∆=+->,022km xk =-+,00222my kx m k =+=+,因为()00,P x y 在直线l :10x ky ++=上,所以2221022km km k k -++=++,即2m k k ⎛⎫=-+ ⎪⎝⎭,所以22480k k ⎛⎫∆=-> ⎪⎝⎭,即:22k >,()()()2222222212122k k AB k k k k +-∆=+=++,O 到直线AB 的距离()222211m d k k k ==++,()2241102AOBk SAB d -===,解得:23k =,3k =类型二 垂直问题典例2 已知椭圆1C :22221x y a b +=(0a b >>)的离心率为22,1C 的长轴是圆2C :222x y +=的直径.(1)求椭圆的标准方程;(2)过椭圆1C 的左焦点F 作两条相互垂直的直线1l ,2l ,其中1l 交椭圆1C 于P ,Q 两点,2l 交圆2C 于M ,N 两点,求四边形PMQN 面积的最小值.【来源】广东省肇庆市2021届高三二模数学试题【答案】(1)2212x y +=;(2)2.【解析】(1)由222a =,得2a =由2c e a ==,得1c =,所以1b =.所以椭圆的方程为2212x y +=.(2)由(1)可得()1,0F -.①当过点F 的直线1l 的斜率不存在时,22MN =2PQ =这时11222222PMQN S MN PQ ==⨯=. ②当过点F 的直线1l 的斜率为0时,2MN =,22PQ =, 这时112222222PMQN S MN PQ ==⨯⨯=③当过点F 的直线1l 的斜率存在且不为0时,设直线1l 的方程为1x my =-,()11,P x y ,()22,Q x y .由22112x my x y =-⎧⎪⎨+=⎪⎩,整理可得()222210m y my +--=. 12222m y y m +=+,12212y y m -=+. 所以())222212121222211142m m y m y y y y m PQ +=+-=++-=+.直线2l 的方程为0mx y m ++=,坐标原点O 到2l 的距离21d mm =+所以2222222211m m MN m m +=-=++22211122221222PMQN m S MN PQ m m +===-++由222m +>,得2122122m->+,即(2,22PMQN S ∈. 综上所述,四边形PMQN 的面积的最小值为2.【举一反三】已知椭圆222:1(1)x C y a a+=>,离心率6e .直线:1l x my =+与x 轴交于点A ,与椭圆C 相交于,E F 两点.自点,E F 分别向直线3x =作垂线,垂足分别为11,E F .(Ⅰ)求椭圆C 的方程及焦点坐标;(Ⅱ)记1AEE ,11AE F ,1AFF 的面积分别为1S ,2S ,3S ,试证明1322S S S 为定值.【答案】(Ⅰ)椭圆C 的方程为2213x y +=,焦点坐标为(2,0)±;(Ⅱ)证明见解析. 【解析】(Ⅰ)由题意可知1b =,又63c e a ==,即22123a a -=.解得23a =.即3a =. 所以222c a b =-=.所以椭圆C 的方程为2213x y +=,焦点坐标为(2,0)±.(Ⅱ)由221330x my x y =+⎧⎨+-=⎩得22(3)220m y my ++-=,显然m R ∈. 设()11,E x y ,()22,F x y ,则12122222,33m y y y y m m --+==++,()113,E y ,()123,F y ,因为13112211(3)(3)22S S x y x y =-⋅-12121(2)(2)4my my y y =--21212121[42()]4m y y m y y y y =-++ 22221222(42)4333m m m m m m ---=-⋅+⋅+++2223(2)(3)m m +=+, 又因为22221212121[2]()42S y y y y y y =⨯-=+-()22224833m m m =+++()222248243m m m ++=+()22212243m m +=+.所以22213222223(2)1(3)12(2)4(3)m S S m m S m ++==++. 类型三 面积问题典例3如图,已知椭圆221:12x y Γ+=和抛物线22:3x y Γ=,斜率为正的直线l 与y 轴及椭圆1Γ依次交于P 、A 、B 三点,且线段AB 的中点C 在抛物线2Γ上.(1)求点P 的纵坐标的取值范围;(2)设D 是抛物线2Γ上一点,且位于椭圆1Γ的左上方,求点D 的横坐标的取值范围,使得PCD 的面积存在最大值.【来源】浙江省2022届高三水球高考命题研究组方向性测试Ⅴ数学试题 【答案】(1)3,22⎛⎫⎪⎝⎭;(2)323,2⎛-- ⎝⎭. 【解析】(1)设直线l 的方程为()0,0y kx b k b =+>>,则()0,P b ,将直线l 的方程与椭圆的方程联立,可求得点C 的坐标,将点C 的坐标代入抛物线的方程,可得出()223214k b k +=,结合0∆>可得出2k 的取值范围,进而可求得b 的取值范围,即可得解;(2)设点()23,3D t t ,计算得出PCD 的面积239142416t S t k k ⎛⎫-=-+- ⎪⎝⎭,令1u k =,记()()32424f u u t u t =-+--,则60u <()f u ',分析可知函数()f u 在6⎛ ⎝⎭内有唯一的极值点,且为极大值点,结合已知条件可得出关于t 的不等式组,解出t 的取值范围,即可得出点D 的横坐标的取值范围.(1)解:由题意可设直线l 的方程为()0,0y kx b k b =+>>,则()0,P b ,联立2222y kx b x y =+⎧⎨+=⎩可得()222214220k x kbx b +++-=, ()()()2222221682118210k b k b k b ∆=-+-=+->,可得2221b k <+,① 设点()11,A x y 、()22,B x y ,由韦达定理可得122421kb x x k +=-+,21222221b x x k -=+,设点()00,C x y ,则12022221x x kb x k +==-+,00221by kx b k =+=+, 将点C 的坐标代入抛物线2Γ的方程得224630k b k --=,则()223214k b k+=,代入①可得()22249212116k k k +<+,可得42161890k k -->,解得232k >, 因此()222321333,24242k b k k +⎛⎫==+∈ ⎪⎝⎭. 因此,点P 的纵坐标的取值范围是3,02⎛⎫⎪⎝⎭.(2)解:设点()23,3D t t,则点D 到直线l 的距离为22223311tk t bd k k -+==++,221kb k PC +=PCD 的面积()22331221kb t tk b S PC d k --=⋅=+,② 将()223214k b k +=代入②得239142416t S t k k ⎛⎫-=-+- ⎪⎝⎭, 令1u k =,记()()32424f u u t u t =-+--,则60u <()22342f u u t '=-+-, 因为()f u '在6⎛ ⎝⎭上单调递减,所以,函数()f u 在6⎛ ⎝⎭内有唯一的极值点,且为极大值点,所以,()2204206440f t f t ⎧=->⎪⎨=-<⎪⎭'⎝⎩',可得2112t <<,③ 因为点D 在椭圆1Γ的左上方,则2409182t t t <⎧⎨+>⎩,④ 由③④可得21t -<<D 的横坐标的取值范围是323,⎛- ⎝⎭. 【点睛】方法点睛:圆锥曲线中的最值问题解决方法一般分两种:一是几何法,特别是用圆锥曲线的定义和平面几何的有关结论来求最值;二是代数法,常将圆锥曲线的最值问题转化为二次函数或三角函数的最值问题,然后利用基本不等式、函数的单调性或三角函数的有界性等求最值.【举一反三】已知椭圆C :22221(x y a b a b+=>>0)的右焦点F 与右准线l :x =4的距离为2.(1)求椭圆C 的方程;(2)若直线():0m y kx t t =+≠与椭圆C 相交于A ,B 两点,线段AB 的垂直平分线与直线m 及x 轴和y 轴分别相交于点D ,E ,G ,直线GF 与右准线l 相交于点H .记AEGF ,ADGH 的面积分别为S 1,S 2,求12S S 的值.【来源】江苏省苏州中学等四校2021-2022学年高三下学期期初联合检测数学试题 【答案】(1)22184x y +=;(2)12 【解析】(1)根据已知条件求得,,a b c ,由此求得椭圆C 的方程.(2)结合根与系数关系求得D 点坐标,进而求得,,E G H 点坐标,利用“中点”求得面积比.(1)依题意2222242a c a c ca b c ⎧=⎪⎪⎪-=⎨⎪=+⎪⎪⎩,解得22,2a b c ===,所以椭圆方程为22184x y +=. (2)右焦点()2,0F .直线():0m y kx t t =+≠,由于线段AB 的垂直平分线与,x y 轴都相交,所以0k ≠,由22184y kx tx y =+⎧⎪⎨+=⎪⎩消去y 并化简得()222124280k x ktx t +++-=,设()()1122,,,A x y B x y , 则()1212122242,21212kt tx x y y k x x t k k -+=+=++=++, 所以222,1212ktt D k k -⎛⎫ ⎪++⎝⎭.线段AB 的垂直平分线的方程为22121212t kt y x k k k ⎛⎫-=-⋅+ ⎪++⎝⎭,令0y =,解得22,01212E kt kt x E k k --⎛⎫=⇒ ⎪++⎝⎭, 令0x =,解得220,1212G t t y G k k --⎛⎫=⇒ ⎪++⎝⎭. 所以,D G 关于E 点对称,所以DE EG =, 所以ADEAEGSS=.直线GF 的方程为()20120220tk y x --+-=--,令4x =,解得224,1212H t t y H k k ⎛⎫=⇒ ⎪++⎝⎭, 所以,G H 关于F 对称,所以GF FH =, 所以AGFAFHSS=.结合图象可知:1212S S =.【点睛】本题求四边形AEGF 和四边形ADGH 的面积比,常规的方法是借助弦长公式和点到直线距离来求面积,但本题用这个方法很难.在解题的过程中,求出,,,,D E G F H 的坐标后,要注意观察坐标间的对称性,结合对称性来求面积比,将问题求解大大简化.类型四 范围与定值问题典例4已知椭圆C :()2222 1x y a b c a b +=>>2()2,1P .(1)求C 的方程;(2)若A ,B 是C 上两点,直线AB 与曲线222x y +=相切,求AB 的取值范围. 【来源】重庆市2022届高三下学期开学考试数学试题【答案】(1)22163x y +=;(2)22,3⎡⎤⎣⎦ 【解析】(1)根据已知条件求得,,a b c ,由此求得椭圆C 的方程.(2)对直线AB 的斜率分成不存在,0k =,0k ≠三种情况进行分类讨论,结合弦长公式、基本不等式求得AB 的取值范围.(1)依题意22222224116,3c aa b c a b a b c ⎧=⎪⎪⎪+=⇒===⎨⎪=+⎪⎪⎩所以椭圆C 的方程为22163x y +=.(2)圆222x y +=的圆心为()0,0,半径2r =当直线AB 的斜率不存在时,直线AB 的方程为2x 2x = 2222163x y x y ⎧=⎪⇒=⎨+=⎪⎩2222163x y x y ⎧=-⎪⇒=⎨+=⎪⎩ 所以22AB =当直线AB 的斜率为0时,直线AB 的方程为2y 2y =-2222163y x x y ⎧=⎪⇒=⎨+=⎪⎩2222163y x x y ⎧=-⎪⇒=⎨+=⎪⎩ 所以22AB =当直线AB 的斜率0k ≠时,设直线AB 的方程为,0y kx b kx y b =+-+=, 由于直线AB 和圆222x y +=()2222211b b k k =++.22163y kx b x y =+⎧⎪⎨+=⎪⎩,消去y 并化简得()222124260k x kbx b +++-=, ()()222222164122648248k b k b k b ∆=-+-=+- ()22248248213280k k k =+-⨯+=+>.设()()1122,,,A x y B x y 则2121222426,1212kb b x x x x k k --+=⋅=++, 所以()2222212122242614141212kb b AB k x x x x k k k --⎛⎫=++-=+-⋅ ⎪++⎝⎭()2422224242232845112222144144112k k k k k k k k k k ++++++++++2212122144k k=+>++另一方面,由于22221144448k k k k +⋅+≥=,当且仅当222114,2k k k ==时等号成立. 所以2211212131844k k++=++,即223AB ≤. 综上所述,AB 的取值范围是22,3⎡⎤⎣⎦.【举一反三】已知椭圆2222:1(0)x y C a b a b+=>>的右焦点为(2,0)F ,过点F 且垂直于x 轴的直线与椭圆相交所得的弦长为2. (1)求椭圆C 的方程;(2)过椭圆内一点P (0,t ),斜率为k 的直线l 交椭圆C 于M ,N 两点,设直线OM ,ON (O 为坐标原点)的斜率分别为k 1,k 2,若对任意k ,存在实数λ,使得12k k k λ+=,求实数λ的取值范围. 【来源】江苏省扬州大学附中2021届高三下学期2月检测数学试题【答案】(1)22142x y +=;(2)[2,)+∞. 【解析】(1)椭圆2222:1(0) x y C a b a b+=>>的右焦点为(2,0)F ,则2c =∵过点F 且垂直于x 轴的直线与椭圆相交所得的弦长为2,22221c y a b ∴+=,解得2b y a =±,222b a∴=,即2b a =,∴2222a b c a =+=+, 解得2a =,∴椭圆的方程为22142x y +=,(2)设直线l 的方程为y kx t =+.由221? 42x y y kx t ⎧+=⎪⎨⎪=+⎩,消元可得()222214240k x ktx t +++-=, 设()()1122,,,M x y N x y ,则122421kt x x k -+=+,21222421t x x k -=+, 而121212*********y y kx t kx tk k k t x x x x x x ⎛⎫+++=+=+=++ ⎪⎝⎭1222124422242x x kt kk t k t x x t t +--=+⋅=+⋅=--, 由12k k k λ+=,242kk t λ-=-, 因为此等式对任意的k 都成立,所以242t λ-=-,即242t λ=-. 由题意得点(0,)P t 在椭圆内,故202t ≤<,即4022λ≤-<,解得2λ≥,故实数λ的取值范围为[2,)+∞.典例5 已知椭圆2222:1(0)x y C a b a b+=>>的一个焦点与短轴的两个端点组成的三角形是等腰直角三角形,点(10,1)P 是椭圆C 上一点. (1)求椭圆C 的标准方程;(2)设(,)R s t 是椭圆C 上的一动点,由原点O 向22()()4x s y t -+-=引两条切线,分别交椭圆C 于点P ,Q ,若直线,OP OQ 的斜率均存在,并分别记为12,k k ,求证:12k k ⋅为定值. 【来源】云南省昭通市2022届高三期末数学(理)试题 【答案】(1)22:1126x y C +=;(2)证明见解析【解析】(1)由椭圆的性质得出b c =,再将(10,1)P 代入椭圆方程,结合222a b c =+得出椭圆C 的标准方程;(2)设直线1:OP y x k =,直线2:OQ y k x =,根据距离公式得出12,k k 是方程()2224240s k stk t --+-=的两根,由韦达定理结合点(,)R s t 在椭圆上,得出12k k ⋅为定值.(1)解:由已知有222222,(10)11,,b c b a b c =⎧⎪⎪+=⎨⎪=+⎪⎩解得22212,6,6,a b c ⎧=⎪=⎨⎪=⎩ ∴椭圆C 的方程为22:1126x y C +=.(2)证明:设直线1:OP y x k =,直线2:OQ y k x = 又直线OP 为圆R 12121k s t k -=+,化简可得()222114240s k stk t --+-=,同理可得()222224240s k stk t --+-=,∴12,k k 是方程()2224240s k stk t --+-=的两根,由()240,0s -≠∆>,可知212244t k k s -⋅=-, 又(,)R s t 在椭圆上,即22162t s =-,∴22122212412442s t k k s s --⋅===---,∴12k k ⋅为定值12-. 【举一反三】已知椭圆2222:1(0)x y C a b a b +=>>经过两点33,M ⎭,242N ⎝⎭. (1)求椭圆C 的方程:(2)A 、B 分别为椭圆C 的左、右顶点,点P 为圆224x y +=上的动点(P 不在坐标轴上),P A 与PB 分别与椭圆C 交E 、F 两点,直线EF 交x 轴于H 点,请问点P 的横坐标与点H 的横坐标之积是否为定值?若是,求出这个定值;若不是,说明理由.【来源】江西省景德镇市2022届高三第二次质检数学(理)试题【答案】(1)22143x y +=(2)点P 的横坐标与点H 的横坐标之积为定值,定值为4 【解析】(1)将两点代入椭圆方程解方程求出,a b 的值,确定椭圆方程(2)设P A 与PB 直线与椭圆联立,求出E 、F 两点的坐标表达式,写出直线EF 方程,求出与x 轴的交点H 点的坐标,联立两条直线求出P 点的坐标,计算乘积判断是否为定值(1)将,M N 点坐标代入椭圆方程得:222233141421216a b a b⎧+=⎪⎪⎨⎪+=⎪⎩ ,解得:2234a b =⎧=⎪⎨⎪⎩ ,所以椭圆方程为22143x y +=(2)根据圆方程为224x y +=可知,AB 为圆的直径,点P 在圆上,所以PA PB ⊥,设直线PA 方程为:()2,0y k x k =+≠,联立()222143y k x x y ⎧=+⎪⎨+=⎪⎩ 得:()2222341616120k x k x k +++-=,所以221612234A E E k x x x k -⋅=-=+,所以228634E k x k -+=+,代入直线得:21234E k y k =+;同理设直线PB 方程为:()12y x k =--,联立()2212143y x k x y ⎧=--⎪⎪⎨⎪+=⎪⎩得:2222416163120x x k k k ⎛⎫+-+-= ⎪⎝⎭,则22221612161224343B F F k k x x x k k--⋅===++, 所以228643F k x k -=+,21243Fk y k =+, 所以2337E F EFE F y y k k x x k --==- ,直线EF 的方程为:222212338634734k k k y x k k k ⎛⎫--+-=- ⎪++⎝⎭,令0y =得:()()()()222222222234661278666343334333433H k k k k k k x k k k k k k -++-++=-⋅+==+-+-+-, 联立直线PA ,PB ()()212y k x y x k =+⎧⎪⎨=--⎪⎩得:22221P k x k -=+,所以222222664133P H k k x x k k -+⋅=⋅=+-,所以点P 的横坐标与点H 的横坐标之积为定值,定值为4【精选名校模拟】1.已知椭圆2222C :1(0)x y a b a b+=>>的离心率为12,直线1:22l y x =-+与椭圆C 有且仅有一个公共点A .(Ⅰ)求椭圆C 的方程及A 点坐标;(Ⅱ)设直线l 与x 轴交于点B .过点B 的直线与C 交于E ,F 两点,记点A 在x 轴上的投影为G ,T 为BG 的中点,直线AE ,AF 与x 轴分别交于M ,N 两点.试探究||||TM TN ⋅是否为定值?若为定值,求出此定值;否则,请说明理由.【来源】湖南省长沙市第一中学、广东省深圳实验学校2021届高三下学期联考数学试题【答案】(1)2231,1,432x y A ⎛⎫+= ⎪⎝⎭;(2)||||TM TN ⋅为定值94 【解析】(1)设椭圆C 的半焦距为c ,则12c a =,则224a c =,22223b a c c =-=, 所以椭圆C 的方程为:2222143x y c c+=,将椭圆C 的方程与直线l 的方程联立得:222430x x c -+-=, 所以244(43)0c ∆=-⨯-=,解得:21c =,所以24a =,23b =,故椭圆C 的方程为22143x y +=,此时将21c =代入222430x x c -+-=得:2210x x -+=, 所以1x =,此时32y =。
黑龙江省哈尔滨市宾县第一中学2023-2024学年高二下学期第三次月考数学试卷

黑龙江省哈尔滨市宾县第一中学2023-2024学年高二下学期第三次月考数学试卷一、单选题1.2025亚冬会将在黑龙江省哈尔滨市举行.为了使大会的服务热情周到,组委会向全市各学校发出志愿者倡议.同学们可通过拨打热线电话或登录官网两种方式之一来报名,现有甲、乙、丙三人均要报名参加,则不同的报名方法有( )A .4种B .6种C .8种D .9种 2.已知函数()223f x x x ξ=-+在(),1-∞-上单调递减的概率为12,且随机变量(),1N ξμ:,则()12P ξ≤≤=(附:若()2,X N μσ:,则()0.6827P X μσμσ-≤≤+=,()220.9545P X μσμσ-≤≤+=,()330.9973)P X μσμσ-≤≤+=( )A .0.1359B .0.01587C .0.0214D .0.01341 3.已知离散型随机变量X 的分布列如下表:则E (X )=( )A .0.56B .0.64C .0.72D .0.84.中国南北朝时期的著作《孙子算经》中,对同余除法有较深的研究.设,,(0)a b m m >为整数,若a 和b 被m 除得的余数相同,则称a 和b 对模m 同余,记为()mod a b m ≡.若()1222020202020C 2C 2C 2,mod9a a b =⋅+⋅++⋅≡L ,则b 的值可以是( )A .2018B .2020C .2022D .20245.设()()12P A B P B A ==,()23P A =,则()P B =( ) A .16 B .12 C .13 D .236.“杨辉三角”是中国数学史上的一个伟大成就,激发起一批又一批数学爱好者的探究欲望.如图,由“杨辉三角”,下列叙述正确的是( )A .22223459C C C C 120++++=LB .第2023行中从左往右第1013个数与第1014个数相等C .记第n 行的第i 个数为i a ,则11124n i n i i a +-==∑D .第20行中第8个数与第9个数之比为8:137.已知函数()sin cos f x a x x x =+,若()f x 在[]π,π-上单调,则实数a 的取值范围为( ) A .[]0,1 B .[)1,-+∞ C .(],1-∞- D .{}1-8.某公司员工食堂每天都有米饭和面食两种套餐,已知员工甲每天中午都会在这两种套餐中选择一种,米饭套餐的价格是每份18元,面食套餐的价格是每份12元,如果甲当天选择了某种套餐,他第二天会有60%的可能性换另一种类型的套餐,假如第1天甲选择了米饭套餐,第n 天选择米饭套餐的概率为n P ,给出以下论述:①30.52P =;②()()110.40.612,N n n n P P P n n --=+-≥∈;③10.40.5(0.2)n n P -=+⨯-④前k 天甲午餐总费用的数学期望为55115225kk ⎛⎫+-- ⎪⎝⎭. 其中正确的是( )A .②③④B .①②④C .①③④D .①②③二、多选题9.过点(2,1)P -的直线与函数3()1f x x =+的图象相切于点00(,)Q x y ,则0x 的值可以是( ) A .0 B .2 C .3 D .3-10.某校高三1班48名物理方向的学生在一次质量检测中,语文成绩、数学成绩与六科总成绩在全年级中的排名情况如下图所示,“”表示的是该班甲、乙、丙三位同学对应的点.从这次考试的成绩看,下列结论正确的是( )A .该班六科总成绩排名前6的同学语文成绩比数学成绩排名更好B .在语文和数学两个科目中,丙同学的成绩名次更靠前的科目是语文C .数学成绩与六科总成绩的相关性比语文成绩与六科总成绩的相关性更强D .在甲、乙两人中,其语文成绩名次比其六科总成绩名次靠前的学生是甲11.在信道内传输0,1信号,信号的传输相互独立.发送0时,收到1的概率为(01)αα<<,收到0的概率为1α-;发送1时,收到0的概率为(01)ββ<<,收到1的概率为1β-. 考虑两种传输方案:单次传输和三次传输.单次传输是指每个信号只发送1次,三次传输 是指每个信号重复发送3次.收到的信号需要译码,译码规则如下:单次传输时,收到的信号即为译码;三次传输时,收到的信号中出现次数多的即为译码(例如,若依次收到1,0,1,则译码为1).A .采用单次传输方案,若依次发送1,0,1,则依次收到l ,0,1的概率为2(1)(1)αβ--B .采用三次传输方案,若发送1,则依次收到1,0,1的概率为2(1)ββ-C .采用三次传输方案,若发送1,则译码为1的概率为23(1)(1)βββ-+-D .当00.5α<<时,若发送0,则采用三次传输方案译码为0的概率大于采用单次传输方案译码为0的概率三、填空题12.已知()512x -250125a a x a x a x =+++⋅⋅⋅+,则123452345a a a a a ++++=.13.数学老师从6道习题中随机抽3道让同学检测,规定至少要解答正确2道题才能及格.某同学只能求解其中的4道题,则他能及格的概率是14.已知函数()sin x x x f -=,则不等式()()21330f x f x -++>的解集是.四、解答题15.已知二项式()22,*nx a n ⎛∈∈ ⎝R N 的展开式中,二项式系数之和为128,系数和为1.(1)求a 与n 的值;(2)求其展开式中所有的有理项.16.在2024年宾县一中纪念“五四”活动中,获得一等奖的某节目参演人员合影留念.3名男生和4名女生站成一排.(最后答案用数字作答)(1)甲不在中间也不在两端的站法有多少种?(2)男、女相间的站法有多少种?(3)甲、乙、丙三人从左到右顺序一定的站法有多少种?17.每箱产品有10件,每箱中次品数从0到2是等可能的.开箱检验时,从中任取1件,如果检验为次品,则认为该箱产品不合格而拒收.由于检验有误差,假设一件正品被误判为次品的概率为2%,一件次品被误判为正品的概率为5%.求:(1)检验一箱产品能通过验收的概率;(2)检验三箱产品,其中有两箱通过验收的概率.(精确到0.001)18.2023年9月26日,第十四届中国(合肥)国际园林博览会在合肥骆岗公园开幕.本届园博会以“生态优先,百姓园博”为主题,共设有5个省内展园、26个省外展园和7个国际展园,开园面积近3.23平方公里,游客可通过乘坐观光车、骑自行车和步行三种方式游园.(1)若游客甲计划在6个省内展园和7个国际展园中随机选择2个展园游玩,记甲参观省内展园的数量为X ,求X 的分布列及数学期望()E X ;(2)为更好地服务游客,主办方随机调查了500名首次游园且只选择一种游园方式的游客,其选择的游园方式和游园结果的统计数据如下表:用频率估计概率,若游客乙首次游园,选择上述三种游园方式的一种,求游园结束时乙能参观完所有展园的概率.19.已知函数2()ln ()f x x ax x a =-+∈R(1)当3a =时,求函数()f x 的极值;(2)设函数()f x 有两个极值点12,x x ,且12x x >,若()1f x m <恒成立,求m 最小值.。
黑龙江省牡丹江市第一中学2022-2023学年高二10月月考数学试题

2022-2023第一学期10月月考数学试题10月8日一、选择题(本题共12小题,每题5分,共60分.其中1-8为单选,9-12为多选.注:多选题少选选对得2分,错选得0分)1. 若经过(),3A m ,(1,2)B 两点的直线的倾斜角为45︒,则m 等于( )A. 2B. 1C. -1D. 2-2.已知直线:10l ax y -+=,点(1,3)A -,()2,3B ,若直线l 与线段AB 有公共点,则实数a 的取值范围是( ) A .[4-,1]B .1[4-,1]C .(-∞,[)1]14-⋃+∞D .(-∞,[)4]1-⋃+∞3. 已知直线1l :210x ay +-=与直线2l :(31)10a x ay ---=平行,则=a ( ) A. 0B. 0或16-C.16 D. 0或164. 已知()2,1,3a =-,()1,2,1b =-,若()a ab λ⊥-,则实数λ的值为( ) A. 2-B. 143-C.145D. 25. 已知直线l 的方向向量为(1,0,1)=-a ,点(1,2,1)=-A ,在l 上,则点(2,1,2)=-P 到l 的距离为( )A.B. 4C.D. 6. 如图,长方体1111ABCD A B C D -中,145AD D ∠=︒,130CDC ∠=︒,那么异面直线1AD 与1DC 所成角的正弦值是( )A.B.C.4D.7.已知空间向量a ,b ,c 满足0a b c ++=,1a =,2b =,7c =,则a 与b 的夹角为( ) A .30°B .45︒C .60︒D .90︒8. 如图所示,在空间四边形OABC 中,,,OA a OB b OC c ===,点M 在OA 上,且2OM MA =,N 为BC 中点,则MN ( )A.121232a b c -+ B. 211322a b c -++ C. 111222a b c +-D. 221332a b c -+-9. 下列说法中,正确的有( )A. 直线()23y ax a a R =++∈必过定点()2,3-B. 直线21y x =-在y 轴上的截距为1C. 20y -+=的倾斜角为60︒D. 点()1,3到直线20y +=的距离为110.(本题5分)给出下列命题,其中正确的有( ) A .空间任意三个向量都可以作为一个基底B .已知向量//a b ,则a ,b 与任何向量都不能构成空间的一个基底C .A ,B ,M ,N 是空间中的四个点,若BA ,BM ,BN 不能构成空间的一个基底,那么A ,B ,M ,N 共面D .已知{},,a b c 是空间的一个基底,若m a c =+,则{},,a b m r r u r也是空间的一个基底11.已知平面上一点()5,0M ,若直线上存在点P 使4PM =,则称该直线为“切割型直线”,下列直线中是“切割型直线”的是( ) A .1y x =+B .2y =C .43y x =D .21y x =+12. 如图,在四棱锥P ABCD -中,底面ABCD 为平行四边形,π3DAB ∠=,22AB AD PD ==,PD ⊥底面ABCD ,则( )A. PA BD ⊥B. PB 与平面ABCD 所成角为π3C. 异面直线AB 与PCD. 平面PAB 与平面PBC 所成二面角的平面角为锐角时的余弦值为7二、填空题(每题5分,共20分)13. 与向量(1,1,2a =共线的单位向量是___________.14.已知()0,0,0O ,()1,2,3A ,()2,1,2B ,()1,1,2P ,点Q 在直线OP 上运动,当QA QB ⋅取最小值时,点Q 的坐标是______15.(本题5分)如图,在正四棱柱1111ABCD A B C D -中,底面边长为2,直线1CC 与平面1ACD 所成角的正弦值为13,则正四棱柱的高为_____.16. 如图,在长方体1111ABCD A B C D -中,12AA AB ==,1BC =,E 、F 、H 分别是AB 、CD 、11A B 的中点,则直线EC 到平面AFH 的距离为___________.三、解答题(共70分)17、(本题10分)在ABC 中,()2,5,3A -,()4,1,2AB =,()3,2,5BC =-.(1)求CA BC ⋅;(2)若点P 在AC 上,且12AP PC =,求点P 的坐标.18.(本题12分)已知直线()21:(2)340l m x m m y ++-+=和直线2:22(3)20()l mx m y m m +-++=∈R .(1)当m 为何值时,直线1l 和2l 平行? (2)当m 为何值时,直线1l 和2l 重合?19.(本题12分) 已知直角坐标平面xOy 内的两点()5,3A -,()1,1B . (1)求线段AB 的中垂线所在直线的方程;(2)一束光线从点A 射向y 轴,反射后的光线过点B ,求反射光线所在的直线方程.20.(本题12分) 如图,在边长为2的正方体1111ABCD A B C D -中,E 为1BB 的中点.(1)求点1C 与平面1AD E 的距离;(2)求直线1AA 与平面1AD E 所成角的余弦值.21.(本题12分)已知点(1,2,0)A -,(2,,3)B k -,(0,1,2)C ,向量(3,4,5)a =-. (1)若AB a ⊥,求实数k 的值; (2)求向量AC 在向量上a 上的投影向量.22.(本题12分) 如图,已知直三棱柱111ABC A B C -中,12CA CB CC ===,CA CB ⊥,E 、F 、H 分别是AB 、CB 、1BB 的中点,点P 在直线11C A 上运动,且[]()111,0,1C P C A λλ=∈(1)证明:无论λ取何值,总有CH ⊥平面PEF ;(2)是否存在点P ,使得平面PEH 与平面ABC 的夹角为60︒?若存在,试确定点P 的位置,若不存在,请说明理由.。
2022-2023学年黑龙江省哈尔滨市对青山第一中学高二化学上学期期末试题含解析
2022-2023学年黑龙江省哈尔滨市对青山第一中学高二化学上学期期末试题含解析一、单选题(本大题共15个小题,每小题4分。
在每小题给出的四个选项中,只有一项符合题目要求,共60分。
)1. 把0.6 mol X气体和0.4 mol Y气体混合于2 L容器中,发生反应:3X(g)+Y(g)nZ(g)+2W(g),5 min末已生成0.2 mol W,若测知以Z浓度变化来表示的平均速率为0.01 mol·L-1·min-1上述反应中Z气体的计量系数n的值是A.1 B.2 C.3D.4参考答案:A2. 下列做法会导致食品对人体有害的是()①在沥青公路上翻晒粮食;②香肠中加过量亚硝酸钠以保持肉类新鲜;③用无烟煤直接烧烤鸡、鸭;④用“瘦肉精”喂养生猪;⑤用小苏打做发酵粉制面包;⑥用乙烯催熟水果。
A.①②③⑤B.②③④⑤C.①②③④D.①②③④⑤参考答案:C略3. 在某容积一定的密闭容器中,可逆反应:A(g)+B(g)xC(g),符合下列图象(Ⅰ)所示关系.由此推断对图(Ⅱ)的正确说法是( )A.p3>p4,Y轴表示A的质量 B.p3<p4,Y轴表示B的百分含量C.p3>p4,Y轴表示混合气体密度 D. p3>p4,Y轴表示混合气体平均摩尔质量参考答案:D4. 苹果酸是一种常见的有机酸,结构简式为。
苹果酸可能发生的反应是()①与NaOH溶液反应②与石蕊试液作用变红③与金属钠反应放出气体④一定条件下与乙酸酯化⑤一定条件下与乙醇酯化A.①②③ B.①②③④C.①②③⑤ D.①②③④⑤参考答案:D略5. 已知有如下转化关系:H3CHO←C2H5OH←C2H4→C2H5Br;则反应①、②、③的反应类型分别为A.取代、加成、取代B.取代、取代、加成C.氧化、加成、加成D.氧化、取代、取代参考答案:C6. 已知25℃、101 kPa条件下:4Al(s)+3O2(g)===2Al2O3(s)ΔH=-2834.9 kJ/mol4Al(s)+2O3(g)===2Al2O3(s)ΔH=-3119.1 kJ/mol,由此得出的结论正确的是:A.等质量的O2比O3能量低,由O2变O3为吸热反应B.等质量的O2比O3能量低,由O2变O3为放热反应C.O3比O2稳定,由O2变O3为吸热反应D.O2比O3稳定,由O2变O3为放热反应参考答案:A略7. 用石墨电极电解100 mL H2SO4与CuSO4的混合溶液,通电一段时间后,两极均收集到2.24 L气体(标准状况),则原混合溶液中Cu2+的物质的量浓度为A.1 mol·L-1B.2 mol·L-1C.3 mol·L-1D.4 mol·L-1参考答案:A略8. 由碳、氮、磷、硫等元素组成的蛋白质,在体内经过消化、吸收后,最后氧化成酸根,对应的酸根不正确的是A、碳→碳酸根B、硫→硫酸根C、氮→硝酸根D、磷→磷酸根参考答案:C略9. 肼(N2H4)﹣空气燃料电池是一种环保型碱性燃料电池,电解质溶液是20%~30%的KOH 溶液.电池总反应为:N2H4+O2=N2↑+2H2O.下列关于该燃料电池工作时的说法正确的是()A.负极的电极反应式是:N2H4+4OH﹣﹣4e﹣=4H2O+N2↑B.极的电极反应式是:O2+4H++4e﹣=2H2OC.溶液中阴离子向正极移动D.溶液中C﹙OH﹣﹚保持不变参考答案:A解:A、原电池中负极发生氧化反应,正极发生还原反应,负极反应为N2H4+4OH﹣﹣4e﹣=4H2O+N2↑,故A正确;B、在碱性环境下,正极反应为:O2+2H2O+4e﹣=4OH﹣,故B错误;C、原电池中,阴离子向负极移动,阳离子向正极移动,故C错误;D、电池总反应为N2H4+O2=N2↑+2H2O,原电池反应生成水,溶液浓度降低,故D错误;故选A.10. 某高聚物结构简式,则其单体不可能为()A、CH2=CHCH3B、CH2=C(CH3)2C、CH2=CH2D、CH2=C-CH2CH3参考答案:D11. 下列各组的两种物质在溶液中的反应,可用同一离子方程式表示的是A.氢氧化钠与盐酸;氢氧化铜与盐酸B.BaCl2溶液与Na2SO4溶液;Ba(OH)2溶液与H2SO4溶液C.Na2CO3溶液与硝酸溶液;CaCO3与硝酸溶液D.石灰石与硝酸反应;石灰石与盐酸参考答案:D12. 欲除去混在苯中的少量苯酚,下列实验方法正确的是A、分液B、加入氢氧化钠溶液后,充分振荡,静置后分液C、加入过量溴水,过滤D、加入FeCl3溶液后,过滤参考答案:B略13. 有X、Y、Z、W、M五种短周期元素,其中X、Y、Z、W同周期, Z、M同主族; X+与M2-具有相同的电子层结构;离子半径:Z2->W-;Y的单质晶体熔点高、硬度大,是一种重要的半导体材料。
2020-2021学年上学期高一数学期末模拟卷03(人教A版新教材)(浙江专用)【解析版】
数学模拟试卷03第I 卷 选择题部分(共40分)一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(2020·河北高二学业考试)已知集合{}012M =,,,{}1,2N =,则M N ⋃=( ).A .{}1,2B .{}0C .{}0,1,2D .{}0,1【答案】C 【解析】由并集定义可得:{}0,1,2M N =.故选:C.2.(2019·浙江高二学业考试)已知a ,b 是实数,则“a b >”是“22a b >”的( ). A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件【答案】A 【解析】若a b >,则a b b >≥,即a b >,故22a b >. 取1,2a b ==-,此时22a b >,但a b <, 故22a b >推不出a b >, 故选:A.3.(2019·伊宁市第八中学高一期中)若偶函数()f x 在区间(]1-∞-,上是增函数,则( ) A .3(1)(2)2f f f ⎛⎫-<-< ⎪⎝⎭B .3(1)(2)2f f f ⎛⎫-<-< ⎪⎝⎭C .3(2)(1)2f f f ⎛⎫<-<- ⎪⎝⎭D .3(2)(1)2f f f ⎛⎫<-<- ⎪⎝⎭【答案】D 【解析】函数()f x 为偶函数,则()()22f f =-.又函数()f x 在区间(]1-∞-,上是增函数. 则()()3122f f f ⎛⎫<-<- ⎪⎝⎭-,即()()3212f f f ⎛⎫<-<- ⎪⎝⎭故选:D.4.(2020·黑龙江哈尔滨市第六中学校高三开学考试(理))设2313a ⎛⎫= ⎪⎝⎭,532b =,21log 3c =,则( )A .b a c <<B .a b c <<C .c a b <<D .b c a <<【答案】C 【解析】23110133⎛⎫⎛⎫<<= ⎪ ⎪⎝⎭⎝⎭,503221>=,221log log 103<=, ∴c a b <<. 故选:C5.(2020·江苏南通市·高三期中)已知角α的终边经过点()3,4P ,则πcos 24α⎛⎫+= ⎪⎝⎭( )A .50-B .50C .50-D .50【答案】A 【解析】角α的终边经过点()3,4P ,5OP ∴==,由三角函数的定义知:3cos 5α=,4sin 5α, 2237cos 22cos 121525αα⎛⎫∴=-=⨯-=- ⎪⎝⎭,4324sin 22sin cos 25525ααα==⨯⨯=,()()π724cos 2cos2cos sin 2sin 4442525ππααα∴+=-=-=.故选:A.6.(2020·甘肃兰州市·西北师大附中高三期中)函数()f x 在[)0,+∞单调递增,且()3f x +关于3x =-对称,若()21f -=,则()21f x -≤的x 的取值范围( )A .[]22-,B .(][),22,-∞-+∞C .()[),04,-∞+∞D .[]0,4【答案】D 【解析】因为()3f x +关于3x =-对称,所以()f x 关于y 轴对称,所以()()221f f -==, 又()f x 在[)0,+∞单调递增,由()21f x -≤可得222x -≤-≤,解得:04x ≤≤, 故选:D7.(2020·浙江高一期末)对于函数()12sin 3()42f x x x R π⎛⎫=-++∈ ⎪⎝⎭,有以下四种说法: ①函数的最小值是32-②图象的对称轴是直线()312k x k Z ππ=-∈ ③图象的对称中心为,0()312k k Z ππ⎛⎫-∈⎪⎝⎭ ④函数在区间7,123ππ⎡⎤--⎢⎥⎣⎦上单调递增. 其中正确的说法的个数是( ) A .1 B .2C .3D .4【答案】A 【解析】函数()12sin 3()42f x x x R π⎛⎫=-++∈ ⎪⎝⎭, 当3=42x ππ+时,即=12x π,函数()f x 取得最小值为132122-⨯+=-,故①正确;当342x k πππ+=+时,即=,123k x k Z ππ+∈,函数()f x 的图象的对称轴是直线=,123k x k Z ππ+∈,故②错误; 当34x k ππ+=时,即,123k x k Z ππ=-+∈,函数()f x 的图象的对称中心为1,,1232k k Z ππ⎛⎫-+∈ ⎪⎝⎭,故③错误; 当3232242k x k πππππ+≤+≤+,即2523,123123k k x k Z ππππ+≤≤+∈,函数()f x 的递增区间为252,,123123k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦, 当1k =-时,()f x 的递增区间为7,124ππ⎡⎤--⎢⎥⎣⎦,故④错误. 故选:A8.(2020·山西吕梁市·高三期中(文))函数1()11f x x=+-的图象与函数()2sin 1(24)g x x x π=+-的图象所有交点的横坐标之和等于( ) A .8 B .6C .4D .2【答案】A 【解析】由函数图象的平移可知, 函数1()11f x x=+-与函数()2sin 1g x x π=+的图象都关于(1,1)M 对称. 作出函数的图象如图,由图象可知交点个数一共8个(四组,两两关于点(1,1)对称), 所以所有交点的横坐标之和等于428⨯=.故选:A9.(2020·山西吕梁市·高三期中(文))已知函数2,0()()21,0x e a x f x a R x x ⎧+=∈⎨->⎩,若函数()f x 在R 上有两个零点,则a 的取值范围是( ) A .(,1)-∞- B .[2,0)-C .(1,0)-D .[1,0)-【答案】B 【解析】当0x >时,()21f x x =-有一个零点12x =,只需当0x ≤时,20x e a +=有一个根,利用“分离参数法”求解即可.解:因为函数()2,021,0x e a x f x x x ⎧+≤=⎨->⎩, 当0x >时,()21f x x =-有一个零点12x =, 所以只需当0x ≤时,202x xa e a e +==-即有一个根即可,因为2xy e =单调递增,当0x ≤时,(]0,1xe ∈,所以(]0,2a -∈,即[)2,0a ∈-,故选:B.10.(2020·河北高二学业考试)已知函数()f x 是定义在R 上的奇函数,当0x ≥时,()()2log 1f x x =+,则不等式()2f x ≤的解集是( ). A .[]3,3- B .[]4,4-C .(][),33,-∞-+∞D .(][),44,-∞-⋃+∞【答案】A 【解析】0x ≥时,()()2log 1f x x =+,()f x ∴在[)0,+∞上单调递增,又()f x 是定义在R 上的奇函数,()f x ∴在R 上单调递增,易知()()223log 31log 42f =+==,()()332f f -=-=-, 由()2f x ≤, 解得:()22f x -≤≤, 由()f x 在R 上单调递增, 解得:33x -≤≤,()2f x ∴≤的解集是[]3,3-.故选:A.第II 卷 非选择题部分(共110分)二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分.11.(2020·上海青浦区·高三一模)圆锥底面半径为1cm ,母线长为2cm ,则其侧面展开图扇形的圆心角θ=___________.【答案】π; 【解析】因为圆锥底面半径为1cm ,所以圆锥的底面周长为2cm π, 则其侧面展开图扇形的圆心角22πθπ==, 故答案为:π.12.(2020·浙江宁波市·高三期中)设2log 3a =,则4a =______(用数值表示),lg 36lg 4=______.(用a 表示)【答案】9 1a + 【解析】2log 3a =,22394429log log a ∴===,4222236log 36log 6log (23)log 2log 314lg a lg ===⨯=+=+, 故答案为:9,1a +.13.(2020·深圳科学高中高一期中)某移动公司规定,使用甲种卡,须付“基本月租费”(每月需交的固定费用)30元,在国内通话时每分钟另收话费0.10元;使用乙种卡,不收“基本月租费”,但在国内通话时每分钟话费为0.2元.若某用户每月手机费预算为50元,则使用__________种卡才合算;若要使用甲种卡合算,则该用户每月手机费预算(元)的区间为__________. 【答案】乙 (60,)+∞ 【解析】由题意,设月通话时间为t 分钟,有甲费用为300.1t +,乙费用为0.2t , ∴每月手机费预算为50元,则:由300.150t +=知,甲的通话时间为200分钟, 由0.250t =知,乙的通话时间为250分钟, ∴用户每月手机费预算为50元,用乙种卡合算;要使用甲种卡合算,即月通话时间相同的情况下甲费用更低,即300.10.2t t +<, 解得300t >时,费用在(60,)+∞. 故答案为:乙,(60,)+∞14.(2020·商丘市第一高级中学高一期中)设函数()112,1,1x e x f x x x -⎧<⎪=⎨⎪≥⎩则()3f x ≤成立的x 的取值范围为______. 【答案】(],9-∞ 【解析】当1x <时,由13x e -≤得1ln3x ≤+,所以1x <; 当1≥x 时,由213x ≤得9x ≤,所以19x ≤≤. 综上,符合题意的x 的取值范围是(,9]-∞. 故答案为:(,9]-∞.15.(2020·辽宁本溪市·高二月考)摩天轮是一种大型转轮状的机械建筑设施,稳坐于永乐桥之上的“天津之眼”作为世界上唯一一座建在桥上的摩天轮,其巧夺天工和奇思妙想确是当之无愧的“世界第一”.如图,永乐桥摩天轮的直径为110m ,到达最高点时,距离地面的高度为120m ,能看到方圆40km 以内的景致,是名副其实的“天津之眼”.实际上,单从高度角度来看,天津之眼超越了曾大名鼎鼎的伦敦之眼而跃居世界第一.永乐桥摩天轮设置有48个座舱,开启后按逆时针方向匀速旋转,游客在座舱转到距离地面最近的位置进舱,转一周大约需要30min .游客甲坐上摩天轮的座舱,开始转到min t 后距离地面的高度为m H ,则转到10min 后距离地面的高度为______m ,在转动一周的过程中,H 关于t 的函数解析式为______.【答案】1852 π55cos 6515H t =-+,030t ≤≤. 【解析】如图,设座舱距离地面最近的位置为点P ,以轴心O 为原点,与地面平行的直线为x 轴,建立直角坐标系.设0min t =时,游客甲位于点()0,55P -,以OP 为终边的角为π2-; 根据摩天轮转一周大约需要30min , 可知座舱转动的角速度约为πmin 15rad , 由题意可得πππ55sin 6555cos 6515215H t t ⎛⎫=-+=-+⎪⎝⎭,030t ≤≤.当10t =时,π18555cos 1065152H ⎛⎫=-⨯+= ⎪⎝⎭. 故答案为:1852;π55cos 6515H t =-+,030t ≤≤ 16.(2020·浙江建人专修学院高三三模)已知2,0()(),0x x f x f x x ⎧≥=⎨--<⎩,若4log 3a =,则()f a =___________;()1f a -=___________.3 233-因为4log 3a =,所以43a =,即2a =01a <<,所以()2a f a ==1(1)(1)2a f a f a --=--=-==3-17.(2020·上海虹口区·高三一模)已知(0,)απ∈,且有12sin2cos2αα-=,则cos α=___________.【解析】2212sin 2cos214sin cos 12sin sin 2sin cos αααααααα-=⇒-=-⇒=,因为(0,)απ∈,所以sin 0α≠,因此由2sin 2sin cos sin 2cos tan 2(0,)2πααααααα=⇒=⇒=⇒∈,而22sin cos 1(1)αα+=,把sin 2cos αα=代入(1)得:22214cos cos 1cos cos 5αααα+=⇒=⇒=(0,)2πα∈,因此cos α=.三、解答题:本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤.18.(2020·黑龙江工农�鹤岗一中高二期末(文))函数()22xxaf x =-是奇函数. ()1求()f x 的解析式;()2当()0,x ∈+∞时,()24x f x m ->⋅+恒成立,求m 的取值范围.【答案】(1)()122xxf x =-;(2)5m <-.() 1函数()22x x af x =-是奇函数, ()()1222222x x x x x x a af x a f x --∴-=-=-+=-+=-,故1a =, 故()122xx f x =-; ()2当()0,x ∈+∞时,()24x f x m ->⋅+恒成立,即21(2)42x xm +<-⋅在()0,x ∈+∞恒成立,令()2(2)42x xh x =-⋅,(0)x >,显然()h x 在()0,+∞的最小值是()24h =-, 故14m +<-,解得:5m <-.19.(2020·宁夏长庆高级中学高三月考(理))已知函数()22sin cos 22222x x x f x ππ⎛⎫⎛⎫=-++- ⎪ ⎪⎝⎭⎝⎭(1)求()f x 的最小正周期;(2)求()f x 在区间[]0,π上的最小值及单调减区间.【答案】(1)最小正周期为2π;(2)()min f x =()f x 的单调递减区间为,6ππ⎡⎤⎢⎥⎣⎦. 【解析】(1)1cos ()2sin cos 222x x xf x +=+sin x x =+12sin cos 2sin 223x x x π⎛⎫⎛⎫=+=+ ⎪ ⎪⎝⎭⎝⎭.所以()f x 的最小正周期为2π. (2)因为[]0,x π∈,所以4,333x πππ⎡⎤+∈⎢⎥⎣⎦,所以当433x ππ+=,即x π=时,函数()f x 取得最小值由4233x πππ≤+≤,得6x ππ≤≤,所以函数()f x 的单调递减区间为,6ππ⎡⎤⎢⎥⎣⎦. 20.(2019·河北师范大学附属中学高一期中)已知二次函数()f x 的图象经过点()4,4-,方程()0f x =的解集为{}0,2.(1)求()f x 的解析式;(2)是否存在实数(),m n m n <,使得()f x 的定义域和值域分别为[],m n 和[]2,2m n ?若存在,求出m ,n 的值;若不存在,说明理由.【答案】(1)21()2f x x x =-+;(2)存在;2m =-,0n =. 【解析】(1)由已知,设()()2f x ax x =-.因为()f x 的图象经过点()4,4-,所以()4442a -=-,解得12a =-, 即()f x 的解析式为21()2f x x x =-+; (2)假设满足条件实数m ,n 的存在, 由于221111()(1)2222f x x x x =-+=--+≤,因此122n ≤,即14n ≤. 又()f x 的图象是开口向下的抛物线,且对称轴方程1x =,可知()f x 在区间[],m n 上递增,故有()2()2f m m f n n=⎧⎨=⎩,并注意到14m n <≤,解得2m =-,0n =. 综上可知,假设成立,即当2m =-,0n =时,()f x 的定义域和值域分别为[],m n 和[]2,2m n .21.(2020·山西吕梁市·高三期中(文))已知函数()sin (0)3f x x πωω⎛⎫=+> ⎪⎝⎭,在,63ππ⎛⎫ ⎪⎝⎭上有最小值,无最大值,且满足63f f ππ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭. (1)求()f x 的最小正周期;(2)将函数()f x 的图象向右平移06πϕϕ⎛⎫<< ⎪⎝⎭个单位后得到函数()g x 的图象,若对满足()()122f x g x -=的1x 、2x 有12min 7x x π-=,求ϕ的值. 【答案】(1)37π;(2)14π. 【解析】(1)由()sin ,(0)3f x x πωω⎛⎫=+> ⎪⎝⎭,在,63ππ⎛⎫ ⎪⎝⎭上有最小值,无最大值, 可知:236T πππω-≤=,故有012ω<≤. 又6x π=与3x π=在一个周期内,且63f f ππ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭; 4x π∴=时,函数取到最小值.2,()432k k Z πππωπ∴+=-+∈ 故有1083k ω=-+, 又因为012ω<≤,所以143ω=. 所以函数()f x 的最小正周期为37π. (2)由()()122f x g x -=∣∣可知的()()12,f x g x 中一个对应最大值,一个对应最小值. 对于函数()f x 其最大值与最小值对应的x 的距离为半个周期314π. ∴有12min 314x x πϕ-+=. 即314714πππϕ=-=.22.(2020·安徽省蚌埠第三中学高一月考)设函数()()21x x a t f x a--=(0a >,且1a ≠)是定义域为R 的奇函数.(1)求t 的值;(2)若函数()f x 的图象过点31,2⎛⎫ ⎪⎝⎭,是否存在正数()1m m ≠,使函数()()22log x x m g x a a mf x -⎡⎤=+-⎣⎦在[]21,log 3上的最大值为0,若存在,求出m 的值;若不存在,请说明理由.【答案】(1)2t =;(2)不存在,理由见解析.【解析】(1)∵()f x 是定义域为R 的奇函数,∴()00f =,∴2t =;经检验知符合题意.(2)函数()f x 的图象过点31,2⎛⎫ ⎪⎝⎭,所以2132a a -=, ∴2a =(12a =-舍去), 假设存在正数m ,且1m ≠符合题意,由2a =得()()22log 2222x x x x m g x m --⎡⎤=+--⎣⎦, 设22x x t -=-,则()()22222222x x x x m t mt -----+=-+,∵[]21,log 3x ∈,2[2,3]x ∈,∴38,23t ⎡⎤∈⎢⎥⎣⎦,记()22h t t mt =-+, ∵函数()g x 在[]21,log 3上的最大值为0,∴(i )若01m <<时,则函数()22h t t mt =-+在38,23⎡⎤⎢⎥⎣⎦有最小值为1, 由于对称轴122m t =<,∴()min 31731312426h t h m m ⎛⎫==-=⇒= ⎪⎝⎭,不合题意. (ii )若1m 时,则函数()220h t t mt =-+>在38,23⎡⎤⎢⎥⎣⎦上恒成立,且最大值为1,最小值大于0, ①()max 1252512212736873241324m m m h t h m ⎧⎧<≤<≤⎪⎪⎪⎪⇒⇒=⎨⎨⎛⎫⎪⎪=== ⎪⎪⎪⎩⎝⎭⎩, 而此时7338,24823m ⎡⎤=∈⎢⎥⎣⎦,又()min 73048h t h ⎛⎫=< ⎪⎝⎭, 故()g x 在[]21,log 3无意义, 所以7324m =应舍去; ②()max 25252126313126m m h t h m ⎧⎧>>⎪⎪⎪⎪⇒⇒⎨⎨⎛⎫⎪⎪=== ⎪⎪⎪⎩⎝⎭⎩m 无解, 综上所述:故不存在正数m ,使函数()g x 在[]21,log 3上的最大值为0.。
2021学年高二数学选择性必修一2.2 圆及其方程(A卷基础篇)同步双测新人教B(学生版)
『高二教材·同步双测』
『A 卷基础篇』 『B 卷提升篇』
精品资源·备战高考
高二同步·AB 双测基础提升卷
试题汇编前言: 本试题选于近一年的期中、期末、中考真题以及经典题型,精选
精解精析,旨在抛砖引玉,举一反三,突出培养能力,体现研究性学 习的新课改要求,实现学生巩固基础知识与提高解题能力的双基目的。
(1)A 卷注重基础,强调基础知识的识记和运用; (2)B 卷强调能力,注重解题能力的培养和提高; (3)单元测试 AB 卷,期中、期末测试。 构成立体网络,多层次多角度为考生提供检测,查缺补漏,便于 寻找知识盲点或误区,不断提升。 祝大家掌握更加牢靠的知识点,胸有成竹从容考试!
精品资源·备战高考
高二同步·AB 双测基础提升卷
四、解答题:本题共 6 小题,共 70 分.解答应写出文字说明、证明过程或演算步骤.
17.(2020·海林市朝鲜族中学高一期末)圆
C
的圆心坐标为
0,
0
,且圆
C
经过点
M
3,
4 ,求圆
C
的
方程.
18.(2020·青海平安一中高二月考(文))若圆过 A(2,0),B(4,0),C(0,2)三点,求这个圆的方
___________,半径是___________.
8, 3
A5,1
15.(2020·景东彝族自治县第一中学高一月考)圆 C 的圆心为点
,且经过点
,则圆 C 的
方程为________.
16.(2020·上海徐汇·高二期末)过点 M (1, 3) 作圆 O : x2 y2 4 的切线方程是__________.
(1)求圆的标准方程;
黑龙江省哈尔滨市第九中学2020_2021学年高二数学下学期期末考试试题理含解析
黑龙江省哈尔滨市第九中学2020-2021学年高二数学下学期期末考试试题理(含解析)一、选择题(共12小题,每小题5分,共60分).1.命题“∃x0∈R,x03﹣x02+1>0”的否定是()A.∀x∈R,x3﹣x2+1≤0B.∃x0∈R,C.∃x0∈R,D.∀x∈R,x3﹣x2+1>02.设随机变量ξ服从正态分布N(1,σ2),若P(ξ<2)=0.8,则P(0<ξ<1)的值为()A.0.2 B.0.3 C.0.4 D.0.63.已知离散型随机变量X的分布列如表所示,则常数c为()X0 1P9c2﹣c 3﹣8cA.B.C.或D.4.每年新春佳节时,我国许多地区的人们有贴窗花的习俗,以此达到装点环境、渲染气氛的目的,并寄托着辞旧迎新、接福纳祥的愿望.如图是一张“春到福来”的剪纸窗花,为了估计深色部分的面积,将窗花图案放置在边长为20cm的正方形内,在该正方形内随机生成1000个点,恰有535个点落在深色区域内,则此窗花图案中深色区域的面积约为()A.168cm2B.214cm2C.248cm2D.336cm25.设条件p:a>0,条件q:a2+a>0;那么p就是q的()A.充要条件B.必要不充分条件C.充分不必要条件D.既不充分也不必要条件6.掷一枚硬币两次,记事件A=“第一次出现正面”,B=“第二次出现反面”,下列结论正确的为()A.P(AB)=B.P(A∪B)=P(A)+P(B)C.A与B互斥D.A与B相互独立7.“搜索指数”是网民通过搜索引擎,以每天搜索关键词的次数为基础所得到的统计指标.“搜索指数”越大,表示网民对该关键词的搜索次数越多,对该关键词相关的信息关注度也越高.如图是2017年9月到2018年2月这半年中,某个关键词搜索指数变化的走势图.据该走势图,下列结论正确的是()A.这半年中,网民对该关键词相关的信息关注度呈周期性变化B.这半年中,网民对该关键词相关的信息关注度不断减弱C.从网民对该关键词的搜索指数来看,去年12月份的平均值大于今年1月份的平均值D.从网民对该关键词的搜索指数来看,去年10月份的搜索指数稳定性小于11月份的搜索指数稳定性,故去年10月份的方差小于11月份的方差8.二项式(x2﹣)5展开式中,x4的系数是()A.﹣40 B.10 C.40 D.﹣109.某工厂对一批新研发产品的长度(单位:mm)进行测量,将所得数据分为五组,整理后得到的频率分布直方图如图所示,据此图估计这批产品长度的中位数是()A.23.25mm B.22.50mm C.21.75mm D.21.25mm10.若函数f(x)=lnx+ax+在[1,+∞)上是单调函数,则a的取值范围是()A.B.C.D.(﹣∞,1]11.育英学校派出5名优秀教师去边远地区的三所中学进行教学交流,每所中学至少派一名教师,则不同的分配方法有()A.80种B.90种C.120种D.150种12.已知函数f(x)=e x﹣ax有两个零点x1<x2,则下列说法错误的是()A.a>eB.x1+x2>2C.x1x2>1D.有极小值点x0,且x1+x2<2x0二.填空题:本题共4小题,每小题5分,共20分,请将答案写在答题纸指定的位置上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.B
【解析】
由题意,复数 ,
所以 的共轭复数为 ,故选B.
2.D
【解析】
【分析】
求出不等式的等价条件,结合几何概型的概率公式进行求解即可.
【详解】
由2x<2得x<1,
则在区间(0,4)上任取一数x,则2x<2的概率 ,
故选D.
【点睛】
本题主要考查几何概型的概率的计算,根据不等式的性质求出不等式的等价条件是解决本题的关键.比较基础.
3.D
【分析】
由空间中直线与直线、直线与平面、平面与平面位置关系的判定逐一核对四个命题得答案.
【详解】
解:对于A,由l⊂α,m⊥l,得m∥α或m⊂α或m与α相交,故A错误;
对于B,由l⊂α,m∥l,得m∥α或m⊂α,故B错误;
对于C,由l⊂α,l∥β,得β∥α或β与α相交,故C错误;
对于D,由l⊂α,l⊥β,结合面面垂直的判定可得β⊥α,故D正确.
5.已知抛物线 上的一点 到此抛物线的焦点的距离为3,则点 的纵坐标是()
A.0B. C.2D.
6.下列选项叙述错误的是
A.命题“若 ,则 ”的逆否命题是“若 ,则 ”
B.若 为真命题,则p,q均为真命题
C.若命题p: , ,则 : ,
D.“ ”是“ ”的充分不必要条件
7.若 ,则 ()
A.5B.6C.7D.8
本题考查了中位数的求法,考查了基本运算求解能力,属于基础题.
5.C
【分析】
利用抛物线的定义即可求解.
【详解】
设点 ,
由抛物线 ,则抛物线的准线为 ,
点 到此抛物线的焦点的距离为3,
根据抛物线的定义可得 ,
所以 ,
故选:C
【点睛】
本题主要考查了抛物线的定义、抛物线的标准方程,属于基础题.
6.B
【解析】
A.400B.460C.480D.496
11.设 ,若 是 的充分不必要条件,则实数 的取值范围是( )
A. B. C. D.
12.如图,已知双曲线 : 的右顶点为 , 为坐标原点,以 为圆心的圆与双曲线 的一条渐近线交于两点 , ,若 ,且 ,则双曲线 的离心率为()
A. B. C. D.
二、填空题
(1)求出 的值,并求样本中女童的身高的众数和中位数,平均数;
(2)在身高在[100,102),[102,104),[104,106]的三组中,用分层抽样的方法抽取14名女童,则身高数据在[104,106]的女童中应抽取多少人数?
21.如图,正方形 与梯形 所在的平面互相垂直, , , , , 为 的中点.
3.设α,β是两个不同的平面,l,m是两条不同的直线,且l⊂α,则下列说法正确的是( )
A.若m⊥l,则m⊥αB.若m∥l,则m∥α
C.若l∥β,则β∥αD.若l⊥β,则β⊥α
4.如图是某高二学生自高一至今月考从第1次到14次的数学考试成绩茎叶图,根据茎叶图计算这组数据的中位数为()
A.98B.94C.94.5D.95
黑龙江省哈尔滨市第一中学校2020-2021学年高二上学期期末考试数学试题(理科)
学校:___________姓名:___________班级:___________考号:___________一Biblioteka 单选题1. 的共轭复数是( )
A. B. C.1iD.1+i
2.在区间 内任取一实数 ,则 的概率是
A. B. C. D.
13.进制转化: =______ .
14. 的展开式中, 的系数是________.
15.有4个不同的小球,全部放入4个不同的盒子内,恰好有两个盒子不放球的不同放法的总数为____________________.
16.直三棱柱 的各顶点都在同一球面上,若 , ,则此球的表面积等于.
三、解答题
17.设三角形ABC的内角A,B,C的对边分别为a,b,c,且 ,A为锐角
故选:D.
【点睛】
本题考查命题的真假判断与应用,考查空间想象能力与思维能力,是中档题.
4.C
【分析】
由茎叶图将数据从小到大排列,再利用中位数定义即可求解.
【详解】
由茎叶图可知从第1次到14次的数学考试成绩
从底到高排列如下:
, , , , , , , , , , ,
, , .
所以中位数为 .
故选:C
【点睛】
若 , ,求角B;
若 , , ,求b,c.
18.已知数列 的前 项的和 .
(1)求 的通项公式;
(2)设 ,求数列 的前 项和.
19.在高中学习过程中,同学们经常这样说:“数学物理不分家,如果物理成绩好,那么学习数学就没什么问题.”某班针对“高中生物理学习对数学学习的影响”进行研究,得到了学生的物理成绩与数学成绩具有线性相关关系的结论.现从该班随机抽取5位学生在一次考试中的数学和物理成绩,如下表:
8.四棱锥 的所有侧棱长都是 ,底面 是边长为 的正方形,则异面直线 与 所成角的余弦值为()
A. B. C. D.
9.执行如图所示的程序框图,如果输出的 值为30,那么空白的判断框中应填入的条件是()
A. B. C. D.
10.如图,用6种不同的颜色把图中A,B,C,D四块区域涂色分开,若相邻区域不能涂同一种颜色,则不同涂法的种数为( )
对于 ,命题“若 , 的逆否命题是“若 ,则 ”,故 正确;对于 ,若 为真命题,则 , 至少有一个为真命题,故 错误;对于 ,若命题 : , ,则 : , ,故 正确;对于 , 或 可推出 ,反之,推不出,故 正确,故选B.
(1)求证: 平面 ;
(2)求证:平面 平面 ;
(3)求平面 与平面 所成锐二面角的余弦值.
22.已知椭圆C: 经过点 ,离心率 ,直线 的方程为 .
(1)求椭圆 的方程;
(2)经过椭圆右焦点的任一直线(不经过点)与椭圆交于两点 , ,设直线与 相交于点 ,记 的斜率分别为 ,问: 是否为定值,若是,求出此定值,若不是,请说明理由.
(1)求数学成绩y对物理成绩x的线性回归方程 .若某位学生的物理成绩为80分,预测他的数学成绩;
(2)要从抽取的这5位学生中随机抽取2位参加一项知识竞赛,求选中的学生的数学成绩至少有一位高于120分的概率.(参考公式: 参考数据: )
20.某幼儿园根据部分同年龄段的100名女童的身高数据绘制了频率分布直方图,其中身高的变化范围是[96,106](单位:厘米),样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106).
