反比例函数全章学案(PDF版)_1
反比例函数全章学案(全面)
§1.1 1 反比例函数【学习导言】我们学过了一次函数及正比例函数，今天我们再来认识反比例函数，找出它与一次函数及正比例函数的相同点和不同点，学会根据两个变量的实际意义，求反比例函数解析式。
课前学习：尝试体验（对话课本，记下问题，尝试练习）【对话课本】阅读教材P4～P6【记下问题】【尝试练习】1．下列函数中，哪些是反比例函数？如果是反比例函数的，请指出其比例系数和自变量的取值范围；（1）12y x=；（2）3yx-=（3）13yx=（4）22yx=-（5）yxπ=（6）2kyx=2. 已知反比例函数53 yx =-（1）说出这个函数的比例系数；（2）求当10x=-时，函数的值；（3）求当122y=时，自变量x的值。
课内学习：合作体验（检评预习，审视问题，独立练习，纠错反审）【检评预习】同桌交换学案，检查评价批语：【审视问题】审视下面的学习要点，思考提出的问题【尝试例题】如图，阻力为1000N，阻力臂长为5cm.设动力y（N），动力臂为x（cm）（图中杠杆本身所受重力略去不计。
杠杆平衡时：⨯=⨯动力动力臂阻力阻力臂）(1)求y关于x的函数解析式。
这个函数是反比例函数吗?如果是，请说出比例系数；(2)求当x=50时，函数y的值，并说明这个值的实际意义；(3)利用y关于x的函数解析式，说明当动力臂长扩大到原来的n（n>1）倍时，所需动力将怎样变化？【独立练习】A组动力动力臂阻力臂力1.判断下列函数哪些是反比例函数？是反比例函数的，请指出它的比例系数。
（1）（2）4yx=-2. 已知反比例函数12yx=-。
（1）说出这个函数的比例系数和自变量的取值范围；（2）求出3x=-时，函数的值。
（3）求当y=x的值。
课后学习：反审体验（审查错误原因，检查练习，完成作业）【反思审查】再仔细审查学案，用红笔作出示意。
【作业练习】A组1.函数y=-x，y=1x，y=-x2，y=21x+，y=-12x中，表示y是x的反比例函数的有________．2.t如下表：（1（2）这是一个反比例函数吗？3．一定质量的氧气，其密度ρ(kg/m,）是它的体积v (m,）的反比例函数．当V=10m3时ρ＝1.43kg/m.（1）求ρ与v的函数关系式；（2）求当V=2m3时，氧气的密度．B组4．如果y与x成反比例，z与y成正比例，则z与x成________．5．已知变量,x y满足()2222x y yx=+-+，问,x y是否成反比例？请说明理由。
人教版八年级下 反比例函数全章学案(共七节)
课题 17.1.1 反比例函数的意义学习目标：1.会识别相关量之间的反比例关系，理解反比例函数的意义，能确定简单的反比例函数关系式．2.通过对实际问题的分析、类比、归纳，培养学生分析问题的能力，并体会函数在实际问题中的应用．重点：反比例函数意义的理解． 难点：反比例函数的建模． 学习过程一、 预习新知1、 阅读课本第39页至40页的部分，完成以下问题. 问题：（1）京沪线铁路全长1463 km ，某次列车的平均速度v km/h•随此次列车的全程运行时间t h 的变化而变化，其关系可用函数式表示为：（2）某住宅小区要种植一个面积为1 000 m 2矩形草坪，草坪的长y m 随宽x m•的变化而变化，可用函数式表示为(3) 已知北京市的总面积为1.68×104 km 2，人均占有的土地面积S km 2/人，随全市总人口n 人的变化而变化，其关系可用函数式表示为 ．2、合作探究分析 上述问题中的函数关系式都有y=kx的形式，其中k 为常数． 归纳 一般地，形如y=kx（k 为常数，且k•≠0）•的函数称为 。
注意 在y=k x 中，自变量x 是分式k x 的分母，当x=0时，分式kx无意义，所以x•的取值范围二、课堂展示【例1】 已知y 是x 的反比例函数，当x=2时，y=6． （1）写出y 与x 的函数关系式； （2）求当x=4时y 的值． 例2. 若反比例函数y=kx与一次函数y=2x-4的图象都过点A （m ，2）． （1）求点A 坐标．（2）求反比例函数解析式．三、随堂练习1．写出下列函数关系式，并指出它们各是什么函数（1）平行四边形面积是24 cm 2，它的一边长x m 和这边上的高h cm 之间的关系是 ． （2）小明用10元钱去买同一种菜，买这种菜的数量m kg 与单价n 元/kg•之间的关系是 （3）老李家一块地收粮食1000 kg ，这块地的亩数S 与亩产量t kg/亩之间的关系是 2．若y 是x-1的反比例函数，则x 的取值范围是 3．若y=11n x 是y 关于x 的反比例函数关系式，则n 是4．把xy=-1化为y=kx的形式，其中k= 5．指出下列函数关系式中，哪一个成反比例函数关系，并指出k 的值．（1）y=-3x （2） （3）2y x =1 （4） （5）（6）y=21x6．已知y 是2x 的反比例函数，当x=12时，y=1．（1）求y 与2x 的函数关系式； （2）当x=-14时，求y 的值； （3）当y=-12时，求x 的值．7．若y 与x 3成反比例，且x=2是y=14． （1）求y 与x 3的函数关系式； （2）求y=-16时x 的值．四、当堂检测1.苹果每千克x 元，花10元钱可买y 千克的苹果，则y 与x 之间的函数关系式为2.若函数28)3(m xm y -+=是反比例函数，则m 的取值是3.矩形的面积为4，一条边的长为x ，另一条边的长为y ，则y 与x 的函数解析式为4.已知y 与x 成反比例，且当x ＝－2时，y ＝3，则y 与x 之间的函数关系式是 ，当x ＝－3时，y ＝5.已知函数y ＝y 1＋y 2，y 1与x ＋1成正比例，y 2与x 成反比例，且当x ＝1时，y ＝0；当x ＝4时，y ＝9，求当x ＝－1时y 的值是多少？6.当m ＝ 时，关于x 的函数22)1(-+=m x m y 是反比例函数？7.已知3)2(-+=m x m y 是反比例函数，则m 是什么？五、小结与反思课题17.1.2 反比例函数的图象和性质(1)学习目标：1.进一步作函数图象的主要步骤，会作反比例函数的图象。
第一节反比例函数导学案
第一节反比例函数导学案第一节反比例函数导学案学习目标：1.经历抽象反比例函数概念的过程，体会反比例函数的含义，理解反比例函数的概念。
2.能正确区分两变量是否为反比例函数关系。
学习重点：反比例函数的概念及应用。
学习难点：正确理解反比例函数的含义。
学习过程：预习1.如果两个变量x 、y之间的关系可以表示成y是x的，反比例函数的自变量x 。
2. 复习1.什么叫做函数？2.什么叫做一次函数？它的一般形式是3. 什么叫做正比例函数？它的一般形式是。
新课一．情境引入今年暑假小明背了很重的背包和同学们去野营，其中有几位同学因为约好要进行滑板车比赛，所以每人均带了一辆滑板车。
在途中他们遇到了一段泥泞路段，如果绕道，需要花很长时间，怎么办？小华说：“我们把滑板车铺在路上就可以通过。
”亲爱的同学们你知道他这样做的道理吗？二．探究新知探究一反比例函数的概念1. 阅读课本143页的内容并解决问题2. 总结反比例函数的定义3. 反比例函数的解析式⑴ ⑵ ⑶ 三．自主学习，巩固新知课本144页做一做四．范例学习例1若函数y= （m2-1）x 3m2+m-5 为反比例函数，求m 的值。
解析反比例函数y=k(k≠0) 的另一个形式是y=kx x探究二用待定系数法求反比例函数的解析式例2已知y= y1+y2 ，y1与x成正比例，y2与x成反比例，当x=1时，y=4；当x=3时，y=5；求x=-1时y的值。
课堂练习1.下列函数解析式中y是x的反比例函数的是（）A.y=1311 B.y=- C.y= D.y=x2xx 1x2.当时，函数y=（+2）x是反比例函数。
3.在下列表达式中x均表示自变量，那么那些是反比例函数？每一个反比例函数相应的k值是多少？⑴y=14x；⑵y= －1 ；⑶y= ; ⑷xy=2. 2xx2六．课堂小结-我们本节课学习了⑴⑵ ⑶ 七．课堂作业1.下列哪些式子表示y是x的反比例函数？为什么？⑴xy=11⑷y= ；⑵y= 5-x ；⑶y=x2x 12.计划建设铁路1200km，那么铺轨天数y(d)是每日铺轨量x(km／d)的反比例函数吗？写出y与x的关系式。
反比例函数教案(优秀7篇)
反比例函数教案（优秀7篇）反比例函数教案篇一一、背景分析1．对教材的分析本节课讲述内容为北师大版教材九年级下册第五章《反比例函数》的第二节，也这一章的重点。
本节课是在理解反比例函数的意义和概念的基础上，进一步熟悉其图象和性质的过程。
本节课前一课时是在具体情境中领会反比例函数的意义和概念。
函数的性质蕴涵于概念之中，对反比例函数性质的探索是对其内在规定性的的认识，也是对函数的概念的深化。
同时，本节课也是下一节课《反比例函数的应用》的基础，有了本节课的知识储备，便于学生利用函数的观点来处理问题和解释问题。
传统教材在内容和编写意图的比较：传统教材里反比例函数的内容仅有一节，新教材里反比例函数的内容增加至一章。
本节课中的作函数图象的要求在新旧教材中并不一样，旧教材对画图只是一带而过，而新教材中让学生反复作反比例函数的图象，为下一步性质的探索打下良好的基础。
因为在学生进行函数的列表、描点作图是活动中，就已经开始了对反比例函数性质的探索，而且通过对函数的三种表示方式的整和，逐步形成对函数概念的整体性认识。
在旧教材中对反比例函数性质只是简单观察以后，由老师讲解得到，但是在新教材中注重从操作、观察、概括和交流这些数学活动中得到性质结论，从而逐步提高从函数图象中获取信息的能力。
这也充分体现了重视获取知识过程体验的新课标的精神。
（1）教学目标：进一步熟悉作函数图象的主要步骤，会作反比例函数的图象；体会函数三种方式的相互转换，对函数进行认识上的整和；逐步提高从函数图象中获取知识的能力，探索并掌握反比例函数的主要性质。
（2）重点：会作反比例函数的图象；探索并掌握反比例函数的主要性质。
（3）难点：探索并掌握反比例函数的主要性质。
2、对学情的分析九年级学生在前面学习了一次函数之后，对函数有了一定的认识，虽然他们在小学已经接触了反比例，但都处于浅显的、肤浅的知识表面，这对于他们理解反比例函数的图象与性质没有多大的帮助，但由于本节课采用z+z智能教育平台进行教学，比较形象，便于学生接受。
反比例函数全章学案
课题 17.1.1 反比例函数的意义学习目标：1.会识别相关量之间的反比例关系，理解反比例函数的意义，能确定简单的反比例函数关系式．2.通过对实际问题的分析、类比、归纳，培养学生分析问题的能力，并体会函数在实际问题中的应用．重点：反比例函数意义的理解． 难点：反比例函数的建模． 学习过程一、 预习新知1、 阅读课本第39页至40页的部分，完成以下问题. 问题：（1）京沪线铁路全长1463 km ，某次列车的平均速度v km/h•随此次列车的全程运行时间t h 的变化而变化，其关系可用函数式表示为：（2）某住宅小区要种植一个面积为1 000 m 2矩形草坪，草坪的长y m 随宽x m•的变化而变化，可用函数式表示为(3) 已知北京市的总面积为1.68×104 km 2，人均占有的土地面积S km 2/人，随全市总人口n 人的变化而变化，其关系可用函数式表示为 ．2、合作探究分析 上述问题中的函数关系式都有y=kx的形式，其中k 为常数． 归纳 一般地，形如y=kx（k 为常数，且k•≠0）•的函数称为 。
注意 在y=k x 中，自变量x 是分式k x 的分母，当x=0时，分式kx无意义，所以x•的取值范围二、课堂展示【例1】 已知y 是x 的反比例函数，当x=2时，y=6． （1）写出y 与x 的函数关系式； （2）求当x=4时y 的值． 例2. 若反比例函数y=kx与一次函数y=2x-4的图象都过点A （m ，2）． （1）求点A 坐标．（2）求反比例函数解析式．三、随堂练习1．写出下列函数关系式，并指出它们各是什么函数（1）平行四边形面积是24 cm 2，它的一边长x m 和这边上的高h cm 之间的关系是 ． （2）小明用10元钱去买同一种菜，买这种菜的数量m kg 与单价n 元/kg•之间的关系是 （3）老李家一块地收粮食1000 kg ，这块地的亩数S 与亩产量t kg/亩之间的关系是 2．若y 是x-1的反比例函数，则x 的取值范围是 3．若y=11n x 是y 关于x 的反比例函数关系式，则n 是4．把xy=-1化为y=kx的形式，其中k= 5．指出下列函数关系式中，哪一个成反比例函数关系，并指出k 的值．（1）y=-3x （2）（3）2y x =1 （4） （5）（6）y=21x 6．已知y 是2x 的反比例函数，当x=12时，y=1．（1）求y 与2x 的函数关系式； （2）当x=-14时，求y 的值； （3）当y=-12时，求x 的值．7．若y 与x 3成反比例，且x=2是y=14． （1）求y 与x 3的函数关系式； （2）求y=-16时x 的值．四、当堂检测1.苹果每千克x 元，花10元钱可买y 千克的苹果，则y 与x 之间的函数关系式为2.若函数28)3(m x m y -+=是反比例函数，则m 的取值是3.矩形的面积为4，一条边的长为x ，另一条边的长为y ，则y 与x 的函数解析式为4.已知y 与x 成反比例，且当x ＝－2时，y ＝3，则y 与x 之间的函数关系式是 ，当x ＝－3时，y ＝5.已知函数y ＝y 1＋y 2，y 1与x ＋1成正比例，y 2与x 成反比例，且当x ＝1时，y ＝0；当x ＝4时，y ＝9，求当x ＝－1时y 的值是多少？6.当m ＝ 时，关于x 的函数22)1(-+=m x m y 是反比例函数？7.已知3)2(-+=m x m y 是反比例函数，则m 是什么？五、小结与反思课题17.1.2 反比例函数的图象和性质(1)学习目标：1.进一步作函数图象的主要步骤，会作反比例函数的图象。
反比例函数的图像和性质全章学案
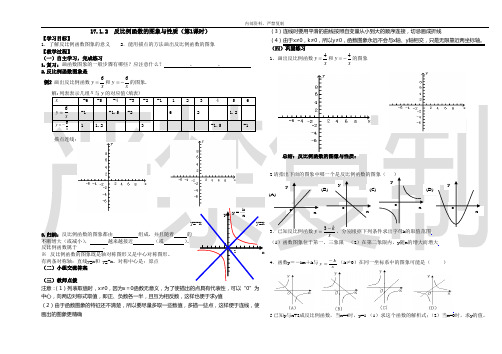
17.1.2 反比例函数的图象与性质（第1课时）【学习目标】1．了解反比例函数图象的意义 2．能用描点的方法画出反比例函数的图象 【教学过程】（一）自主学习，完成练习1.复习：画函数图象的一般步骤有哪些？应注意什么？ 、 、2.反比例函数图象是 例2 画出反比例函数xy 6=和x y 6-=的图象.解:列表表示几组x 与y 的对应值(填表)注意：（1）列表取值时，x ≠0，因为x ＝0函数无意义，为了使描出的点具有代表性，可以“0”为中心，向两边对称式取值，即正、负数各一半，且互为相反数，这样也便于求y 值（2）由于函数图象的特征还不清楚，所以要尽量多取一些数值，多描一些点，这样便于连线，使画出的图象更精确（3）连线时要用平滑的曲线按照自变量从小到大的顺序连接，切忌画成折线（4）由于x ≠0，k ≠0，所以y ≠0，函数图象永远不会与x 轴、y 轴相交，只是无限靠近两坐标轴。
（四）巩固练习 1、画出反比例函数4y x =和4y x=-的图象总结反比例函数的图像与性质： 的取值范围的增大而增大 5.已知y 与x+2成反比例函数，当x=4时，y=1.（1）求这个函数的解析式；（2）当x=0时，求y 的值。
（五）课堂小结描点连线：17.1.2 反比例函数的图象与性质（第2课时）【学习目标】通过反比例函数的图象的分析，探索并掌握反比例函数的图象的性质 【教学过程】（一）自主学习，完成练习1、复习：正比例函数y ＝kx （k ≠0）的图象是什么？其性质有哪些？一次函数呢？2、归纳（1）反比例函数xky =（k 为常数，0≠k ）的图像是 ； （2）当0>k 时，双曲线的两支分别位于第 象限，在每个象限内y 值随x 的增大而 ； （3）当0<k 时，双曲线的两支分别位于第 象限，在每个象限内y 值随x 的增大而 。
x3、函数30y x =-的图象在第________象限，在每一象限内，y 随x 的增大而_________.4、函数y xπ=，当x>0时,图象在第________象限，y 随x 的增大而_________.5、已知反比例函数xky -=3，分别根据下列条件求出字母k 的取值范围 （1）函数图象位于第一、三象限。
反比例函数学案1
课题名称：17·1·1反比例函数的意义课前自主学习复习正比例函数1、下列函数中，是正比例函数的有______________（1）xy 4= （2）13+=x y （3）1=y （4）x y 8= （5）t v 5-= （6）013=+x （7）x y 2+ （8）)81(82x x x y -+=2、关于x 的函数x m y )1(-=是正比例函数，则m__________3、关于x 的函数32)2(--=m x m y 是正比例函数，则m __________4、已知y 与x －1成正比例，x=8时，y=6，写出y 与x 之间函数关系式。
※ 学习探究【知识点1】反比例函数的定义1、 反比例函数的表达式还可以表示为： ..2、 一个矩形的面积为20cm 2, 相邻的两条边长为x cm 和y cm 。
那么变量y 与x 的关系式为是反比例函数吗？3、下列哪个等式中的y 是x 的反比例函数？x y 4=， 3=xy ，16+=x y ，123=xy ,y=-x,x y 3=,x y x y x y 21,12,2-=+=-=，19,,--===x y xa y x y π4、 当k 时，函数52)2(-+=k xk y 是反比例函数？ 5、下列函数关系中是反比例函数的是（ ）A.等边三角形面积S 与边长a 的关系B.直角三角形两锐角A 与B 的关系C.长方形面积一定时，长y 与宽x 的关系D.等腰三角形顶角A 与底角B 的关系【知识点2】求反比例函数的解析式例题 反比例函数xk y =的图象经过点（2，3），则这个反比例函数的解析式为 1、已知y 是x 的反比例函数，并且当x=3时，y=-8。
（1）写出y 与x 之间的函数关系式。
（2）求y=2时x 的值。
2、y 是x 的反比例函数，下表给出了x 与y 的一些值：x-2 -1 21- 21 1 3 y32 2 -1（1）写出这个反比例函数的表达式；（2）根据函数表达式完成上表。
新北师版数学九年级上册第六章反比例函数导学案(全章)
新北师版数学九年级上册第六章反比例函数导学案（全章）6.1反比例函数概念导学案【新知导航】1、写出函数关系式，找出共同点,（1）长方形的面积为122cm ，设一边为xcm,邻边为ycm ，则x 与y 的函数关系式为：y= . (2)京沪线铁路全长为1463，乘坐某次列车所用的时间t 与该次列车平均速度v 的函数关系为: .（3）已知工程队承包一项工程，写出工程效率v 与完成时间之间t 的函数关系式为: .上述三个函数是一次函数吗？2、记住反比例函数的概念：一般地，如果两个变量x,y 之间的关系可以表示成y=kx（k ≠0）的形式，那么我们称y 是x 的反比例函数。
三种形式： ； ； 。
【典例解析】例1、下列函数中，哪些是反比例函数，其k 值为多少？ ①5yx =②33y x =- ③ 25y x -= ④y =⑤132y =⨯ ⑥12y -=- ⑦12y x -= ⑧14xy = ⑨ y=5-x ⑩ 33y x-=例2 已知()2212m m y m m x+-=+（1） 当m 为何值时，y 是x 的正比例函数？ （2） 当m 为何值时，y 是x 的反比例函数？例3已知y 是x 的反比例函数，当x=3时,y=4求：当x=1时，y 的值.【巩固提高】一．选择题1．若函数为反比例函数，则m的值为（）A．±1 B．1 C．D．﹣12．设某矩形的面积为S，相邻的两条边长分别为x和y．那么当S一定时，给出以下四个结论：①x是y的正比例函数；②y是x的正比例函数；③x是y的反比例函数；④y是x的反比例函数其中正确的为（）A．①，②B．②，③C．③，④D．①，④3．下列关系式中，哪个等式表示y是x的反比例函数（）A．B．C．D．4．下列问题中，两个变量间的函数关系式是反比例函数的是（）A．小颖每分钟可以制作2朵花，x分钟可以制作y朵花B．体积为10cm3的长方体，高为hcm，底面积为Scm2C．用一根长50cm的铁丝弯成一个矩形，一边长为xcm，面积为Scm2D．汽车油箱中共有油50升，设平均每天用油5升，x天后油箱中剩下的油量为y升5．下列函数，①y＝2x，②y＝x，③y＝x﹣1，④y＝是反比例函数的个数有（）A．0个B．1个C．2个D．3个二．填空题6．已知：是反比例函数，则m＝．7．当m时，函数y＝（m﹣2）x|m|﹣3是反比例函数．8．函数的自变量x的取值范围是．9．将x＝代入反比例函数y＝﹣中，所得的函数值记为y1，又将x＝y1+1代入反比例函数y＝﹣中，所得的函数值记为y2，又将x＝y2+1代入反比例函数y＝﹣中，所得的函数值记为y3，…如此继续下去，则y2008＝．10．已知y与x成正比例，z与y成反比例，那么z与x的关系是：函数．11．若反比例函数y＝（m+1）的图象在第二、四象限，m的值为．12．若反比例函数y＝（2k﹣1）的图象位于二、四象限，则k＝．13．反比例函数中，比例系数k＝．三．解答题14．已知关于x、y的反比例函数的解析式为y＝，确定a的值，求这个函数关系式．15．已知函数y＝（5m﹣3）x2﹣n+（n+m），（1）当m，n为何值时是一次函数？（2）当m，n为何值时，为正比例函数？（3）当m，n为何值时，为反比例函数？16．（1）12、已知y与x成反比例，当x=3时,y=7,求当y=2时,x的值.（2）已知y＝y1+y2，y1与（x﹣1）成正比例，y2与（x+1）成反比例，当x＝0时，y＝﹣3，当x＝1时，y ＝﹣1．（1）求y的表达式；（2）求当x＝时y的值．6.2反比数的图象及性质（第1课时）【新知导航】1、按照分析步骤，画出反比例函数4y x =,4y x =-的图象。
第十七章反比例函数全章导学案
第十七章 反比例函数反比例函数的意义主备人： 初审人： 终审人：【导学目标】1．使学生理解并掌握反比例函数的概念.2．能判断一个给定的函数是否为反比例函数，并会用待定系数法求函数解析式. 3．能根据实际问题中的条件确定反比例函数的解析式，体会函数的模型思想. 【导学重点】理解反比例函数的概念，能根据已知条件写出函数解析式. 【导学难点】理解反比例函数的概念. 【学法指导】比归纳法，合作探究法. 【课前准备】类比一次函数的相关知识即能完成反比例函数的学习，所以我要求学生课前认真复习和回顾一次函数的相关知识，同时做好新课预习. 【导学流程】一、呈现目标、明确任务1．使学生理解并掌握反比例函数的概念.2．能判断一个给定的函数是否为反比例函数，并会用待定系数法求函数解析式. 3．能根据实际问题中的条件确定反比例函数的解析式，体会函数的模型思想. 二、检查预习、自主学习1.我们学过哪几种函数？每一种函数形式怎样？2.写出下列问题中的函数关系式并说明是什么函数.（1）梯形的上底长是2，下底长是4，一腰长是6，则梯形的周长y 与另一腰长x 之间的函数关系式.（2）某种文具单价为3元，当购买m 个这种文具时，共花了y 元，则y 与m 的关系式.（3）说说“思考”中的问题的函数关系式. （4）怎样的函数是反比例函数？ 三、教师引导1.反比例函数的概念：一般的，形如()0ky k k x=≠为常数，的函数叫做 ，例如10y x=.可变形为：()y kx =(0k ≠),其中：自变量是 ，自变量的次数是 .例1：已知函数73-=m x y 是反比例函数,求m 的取值. 例2：已知y 是x 的反比例函数，当2=x 时，6=y.（1）求出该反比例函数的表达式； （2）求当4=x 时y 的值；（3）当k 取何值时，y 的值为-3. 四、问题导学、展示交流1.什么是反比例函数？反比例函数的自变量可以取一切实数吗？为什么？2.仔细观察反比例函数的解析式ky x=,我们还可以把它写成什么形式？ 3.回忆我们学过的一次函数和正比例函数，我们是用什么方法求它们的解析式的？以此类推，我们也可以采用同样的方法来求反比例函数的解析式.五、点拨升华、当堂达标1.已知变量y 是x 的反比例函数，且当2x =-时3y =. （1）求出该反比例函数的表达式； （2）求当1x =时y 的值；（3）当x 取何值时，y 的值为3-.2.已知y 与1x -成反比例，且当2x =时，2y =.求y 与x 的函数关系式，并判断y 是否为x 的反比例函数.3.函数()34m y m x -=-是反比例函数，则m 的值是多少？六、布置预习1.预习《配套练习》P15页选择填空题.2.完成练习题. 【教后反思】练习课主备人： 初审人： 终审人：【导学目标】1.复习反比例函数的意义.2.列反比例函数的关系式.3.会进行反比例函数的相关计算. 【导学重点】理解反比例函数的概念，能根据已知条件写出函数解析式. 【导学难点】根据已知条件写出函数解析式. 【学法指导】类比、推理. 【课前准备】反比例函数的意义.一、呈现目标、明确任务 1.复习反比例函数的意义. 2.列反比例函数的关系式.3.会进行反比例函数的相关计算. 二、检查预习、自主学习 展示预习效果. 三、教师引导若反比例函数()2103k y k x-=+是反比例函数，求k 的值.()2103ky k x -=+是反比例函数，必然满足2101k-=-，且30.k +≠解：()2103k y k x -=+是反比例函数，∴2101k-=-，且，∴k =3.四、问题导学、展示交流讨论完成《配套练习》P15页7，8题. 五、点拨升华、当堂达标 讨论9题.这道题，先表示1y 与x 关系和2y 与2x 的关系，再表示y 和x 的直接关系. 六、布置预习预习下一节，完成例题和练习. 【教后反思】反比例函数的图象和性质（1）主备人： 初审人： 终审人：【导学目标】1．会用描点法画反比例函数的图象.2．结合图象分析并掌握反比例函数的性质.3．体会函数的三种表示方法，领会数形结合的思想方法. 【导学重点】理解并掌握反比例函数的图象和性质. 【导学难点】正确画出图象，通过观察、分析，归纳出反比例函数的性质.类比、讨论. 【课前准备】根据新课标要求“培养可持续发展的学生”，因此教师要有组织、有目的、有针对性的引导学生，并参与到学习活动中，鼓励学生采用自主探索、合作交流的研讨学习方式.让学生准备坐标纸. 【导学流程】一、呈现目标、明确任务1.会用描点法画反比例函数的图象.2．结合图象分析并掌握反比例函数的性质.3．体会函数的三种表示方法，领会数形结合的思想方法. 二、检查预习、自主学习 1.根据上节课的学习，说说反比例函数的意义和如何用待定系数法求反比例函数的解析式.2.我们研究一次函数y kx b =+(k ,b 为常数，0k ≠)的图象是什么？性质有哪些？正比例函数呢？3.用描点法画函数图象的步骤是什么？4.交流预习成果. 三、教师引导用描点法画图，要注意：（1）列表取值时，0x ≠，因为0x =函数无意义，为了使描出的点具有代表性，可以“0”为中心，向两边对称式取值，即正、负数各一半，且互为相反数，这样也便于求y 值. （2）由于函数图象的特征还不清楚，所以要尽量多取一些数值，多描一些点，这样便于连线，使画出的图象更精确.（3）连线时要用平滑的曲线按照自变量从小到大的顺序连接，切忌画成折线.（4）由于0x ≠，0k ≠，所以0y ≠，函数图象永远不会与x 轴、y 轴相交，只是无限靠近两坐标轴.四、问题导学、展示交流1.一次函数y kx b =+（k ,b 为常数，0k ≠）的图象是什么？其性质有哪些？正比例函数y kx =（0k ≠）呢？2．画函数图象的方法是什么?其一般步骤有哪些？应注意什么？ 3．反比例函数的图象是什么样呢?4.在同一个平面直角坐标系中用不同颜色的笔画出反比例函数6y x =和6y x=-的图象.并思考：（1）从以上作图中，发现6y x =和6y x=-的图象是什么？ （2）6y x =和6y x=-的图象分别在第几象限？ （3）在每一个象限y 随x 是如何变化的？（4）6y x =和6y x=-的图象之间的关系？ 五、点拨升华、当堂达标1．已知反比例函数x k y -=3，分别根据下列条件求出字母k 的取值范围:（1）函数图象位于第一、三象限；（2）在第二象限内，y 随x 的增大而增大. 2．在平面直角坐标系内，过反比例函数xky =（k ＞0）的图象上的一点分别作x 轴、y 轴的垂线段，与x 轴、y 轴所围成的矩形面积是6，则函数解析式为 .3．若函数x m y )12(-=与xmy -=3的图象交于第一、三象限，则m 的取值范围是.4．反比例函数xy 2-=，当2x =-时，y ＝ ；当x ＜－2时；y 的取值范围是 ；当x ＞－2时；y 的取值范围是 .5.已知反比例函数y a x a =--()226，当x >0时，y 随x 的增大而增大，求函数关系式.六、布置预习阅读P43页“归纳”，完成练习题. 【教后反思】反比例函数的图象和性质（2）主备人： 初审人： 终审人：【导学目标】1.使学生进一步理解和掌握反比例函数及其图象与性质.2.能熟练运用函数图象和性质解决一些较综合的问题.3.深刻领会函数解析式与函数图象之间的联系，体会数形结合及转化的思想方法. 【导学重点】理解并掌握反比例函数的图象和性质，并能利用它们解决一些综合问题. 【导学难点】学会从图象上分析、解决问题. 【学法指导】探讨、研究、发现. 【课前准备】1.画平面直角坐标系（网格）.2.复习一次函数（正比例函数）的相关知识. 【导学流程】一、呈现目标、明确任务1．使学生进一步理解和掌握反比例函数及其图象与性质. 2．能灵活运用函数图象和性质解决一些较综合的问题.3．深刻领会函数解析式与函数图象之间的联系，体会数形结合及转化的思想方法. 二、检查预习、自主学习1.反比例函数2y x =-的图象在第 象限，在每个象限中y 随x 的增大而 . 2.已知反比例函数my x=的图象位于一、三象限，则m 的取值范围是 .3.已知点（-3,1）在双曲线ky x=上，则k = .4.已知y 是x 的反比例函数，当3x =时，2y =-：(1)写出y 与x 的函数关系式；（2）求当2x =-时y 的值；（3）求当4y =时x 的值. 三、教师引导1.已知反比例函数的图象经过点A （2,6），（1）这个函数的图象分布在哪些象限？y 随x 的增大如何变化？（2）点B （3,4）、点C （122-，445-）、点D （2,5）是否在函数图象上？ 2.下图是反比例函数5m y x-=的图象的一支，根据图象回答下列问题：（1）图象的另一支在哪个象限？常数m 的取值范围是什么？（2）在这个函数图象的某一支上任取点A （a ,b ）和B （1a ,1b ）.如果a ＞1a ,那么b 和1b 有怎样的大小关系？四、问题导学、展示交流 1.若反比例函数xk y 1-=图像的一支在第三象限，则k . 2.对于函数x y 3=，当x ＞0时y 0，这部分图像在第 象限. 3.对于函数xy 3-=，x ＜0时y 0，这部分图像在第 象限.五、点拨升华、当堂达标 1．完成练习题.2．已知点（－1，1y ）、（2，2y ）、（π，3y ）在双曲线xk y 12+-=上，则下列关系式正确的是（ ）（A ）1y ＞2y ＞3y （B ）1y ＞3y ＞2y （C ）2y ＞1y ＞3y （D ）y 3＞y 1＞y 2. 3．已知反比例函数xk y 12+=的图象在每个象限内函数值y 随自变量x 的增大而减小，且k 的值还满足)12(29--k ≥2k －1，若k 为整数，求反比例函数的解析式. 六、布置预习预习习题17.1，完成1，2题. 【教后反思】练习课主备人： 初审人： 终审人：【导学目标】1.使学生熟练掌握反比例函数及其图象与性质.2.能灵活运用函数图象和性质解决一些较综合的问题.3.深刻领会函数解析式与函数图象之间的联系，体会数形结合及转化的思想方法. 【导学重点】理解并掌握反比例函数的图象和性质，并能利用它们解决一些综合问题. 【导学难点】学会从图象上分析、解决问题. 【学法指导】探讨、研究、发现. 【课前准备】复习一次函数（正比例函数）的相关知识. 【导学流程】一、呈现目标、明确任务1.熟练掌握反比例函数及其图象与性质.2.灵活运用函数图象和性质解决一些较综合的问题. 二、检查预习、自主学习展示17.1中1，2题的预习成果. 三、问题导学、展示交流 独立完成3，4题.四、点拨升华、当堂达标1.小组讨论5—7题.5，6题，要先考虑y 与z 和z 与x 的直接关系，再考虑y 与x 的间接关系. 7题要回忆上学期的有关知识. 2.讨论8，9题.3.如图，A 为反比例函数xky =图象上一点，AB 垂直x 轴于B 点,3AOB S ∆=，则k 的值（ ）A ．6B ．3C ．23D ．不能确定 五、布置预习预习下一节例1，2，整理不懂的问题，出示在黑板上. 【教后反思】实际问题与反比例函数（1）主备人： 初审人： 终审人：【导学目标】1.运用反比例函数的概念和性质解决实际问题.2.利用反比例函数求出问题中的值. 【导学重点】运用反比例函数的意义和性质解决实际问题. 【导学难点】把实际问题转化为反比例函数这一数学模型. 【学法指导】自主探究与合作交流，导学自主. 【课前准备】1.解析式的一般形式.2.反比例函数的图象和性质 【导学流程】一、呈现目标、明确任务1.运用反比例函数的概念和性质解决实际问题.2.利用反比例函数求出问题中的值. 二、检查预习、自主学习1、若点（1，2）在函数ky x=上，则k = ，则这个函数表达式是 . 2、3y x=-的图象位于 象限，在每个象限内，当x 增大时，则y ；3、已知反比例函数1kyx-=的图象在其每个象限内y随x的增大而减小，则k的值可以是（）A、1- B、3 C、0 D、3-4.出示不懂的问题.三、教师引导例1、市煤气公司要在地下修建一个容积为4310m的圆柱形煤气储存室.（1）储存室的底面积S（单位2m）与其深度d（单位：m）有怎样的函数关系？（2）公司决定把储存室的底面积S定为500，施工队施工时应该向下掘进多深？（3）当施工队按（2）中的计划掘进到地下10m时，碰上了坚硬的岩石.为了节约建设资金，公司临时改变计划，把储存室的深度改为10m，相应地，储存室的底面积应改为多少m才满足需要？例2.码头工人以每天30吨的速度往一艘轮船上装载货物，装载完毕恰好用了8天时间.（1）轮船到达目的地后开始缺货，缺货速度v（单位：吨/ 天）与缺货时间t（单位：天）之间有怎样的函数关系？（2）由于遇到紧急情况，船上的货物必须在不超过5天的时间内卸载完毕，那么平均每天至少要卸载多少吨货物？四、问题导学、展示交流讨论例题.五、点拨升华、当堂达标1.完成练习1，2题.2.完成习题17.2中2—4题.六、布置预习预习例3，4，整理不懂的问题.【教后反思】实际问题与反比例函数（2）主备人：初审人：终审人：【导学目标】1.进一步体验现实生活与反比例函数的关系.2.能解决确定反比例函数中常数k值的实际问题.3.进一步运用反比例函数的概念和性质解决实际问题.【导学重点】运用反比例函数的知识解决实际问题.【导学难点】如何把实际问题转化我数学问题，利用反比例函数的知识解决实际问题.【学法指导】数形结合思想 【课前准备】一次函数与正比例函数的表示形式及有关应用. 【导学流程】一、呈现目标、明确任务1.进一步体验现实生活与反比例函数的关系.2.能解决确定反比例函数中常数k 值的实际问题.3.进一步运用反比例函数的概念和性质解决实际问题. 二、检查预习、自主学习 出示不懂的问题. 三、教师引导例3.小伟欲用撬棍撬起一块大石头，已知阻力和阻力臂不变，分别为1200牛和0.5米. （1）动力F 和动力臂l 有怎样的函数关系？当动力臂为1.5米时，撬动石头至少需要多大的力？（2）若想使动力F 不超过（1）中所用力的一半，则动力臂至少要加长多少？例4.一个用电器的电阻R 是可调节的，其范围为110-220欧姆.已知电压U 为220伏，这个用电器的电路（1）输出功率P 与电阻R 有怎样的函数关系？（2）这个用电器输出功率的范围多大？四、问题导学、展示交流 讨论例题.例3，根据“杠杆定律”，若两物体与支点的距离与其重量成反比，则杠杆平衡.通俗一点可以叙述为：阻力×阻力臂=动力×动力臂.题中已知阻力与阻力臂不变，即阻力与阻力臂的积为定值，由“杠杆定律”知变量动力与动力臂成反比关系，写出函数关系式，得到函数动力F 是自变量动力臂l 的反比例函数，当l ＝1.5时，代入解析式中求F 的值；（2）问要利用反比例函数的性质，l 越大F 越小，先求出当F ＝200时，其相应的l 值的大小，从而得出结果.例4，电学知识告诉我们，用电器的输出功率P （瓦）、两端的电压U （伏）和用电器的电阻R （欧）有如下关系：2PR U ，这个关系可以写为P = ，或R = . 五、点拨升华、当堂达标 1.完成练习3题.2.完成习题17.2中5，6题. 六、布置预习预习《配套练习》P18页1—3题. 【教后反思】练习课主备人：初审人：终审人：【导学目标】1.进一步体验现实生活与反比例函数的关系.2.能解决确定反比例函数中常数k值的实际问题.3.尝试运用反比例函数解决实际问题.【导学重点】运用反比例函数的知识解决实际问题.【导学难点】如何把实际问题转化我数学问题，利用反比例函数的知识解决实际问题.【学法指导】归纳、类比.【课前准备】反比例函数的意义.【导学流程】一、呈现目标、明确任务1.进一步体验现实生活与反比例函数的关系.2.能解决确定反比例函数中常数k值的实际问题.3.尝试运用反比例函数解决实际问题.二、检查预习、自主学习小组预习成果.三、教师引导某服装厂承揽一项生产夏凉小衫1600件的任务，计划用t完成.（1）写出每天生产夏凉小衫Y件与生产时间T天（T大于4）之间的函数关系式；（2）由于气温提前升高，服装厂决定提前4天完成任务.那么每天要多做多少件才能完成任务？本题函数关系确定的关键是：生产总量=每天生产的数量×生产时间.提前4天交货，则生产时间变为T-4.四、问题导学、展示交流同桌合作完成《配套练习》P18页4，5题.五、点拨升华、当堂达标小组讨论6，7题.6题的（2），主要是考查函数的增减性.这两道题实际上都考查了三个问题：一是列函数解析式，二是由自变量的值求函数值，三是由函数值求自变量的值.六、布置预习预习复习题17，完成1—4题.【教后反思】小结（1）主备人： 初审人：终审人：【导学目标】1.复习反比例函数的概念和性质.2.三反比例函数解决实际问题.3.体会函数模型的应用.【导学重点】做练习.【导学难点】用反比例函数解决实际问题.【学法指导】复习，总结.【课前准备】反比例函数的应用.【导学流程】一、呈现目标、明确任务1.复习反比例函数的概念和性质.2.三反比例函数解决实际问题.二、检查预习、自主学习小组展示预习成果.三、教师引导本章知识结构：四、问题导学、展示交流1.例函数()0k y k k x=≠为常数，的图象是什么样的？反比例函数有什么性质？ 2.同桌合作完成复习题17中5，7题.五、点拨升华、当堂达标讨论9—11题.9题，考虑图象的两种可能情况，然后由图象考虑k 的正负.10（2）（4）两题，，由自变量的值考虑函数值的正负，然后考虑图象所在的象限.11（3）题，要先考虑40天已经运了多少，还剩多少，每天还需运多少，再与原计划每天运送量比较.六、布置预习预习下一章.。
反比例函数全章学案及测试题
反比例函数学案（一）——1.1反比例函数一、温故知新：1、在一个变化的过程中，如果有两个变量x 和y ，当x 在其取值范围内任意取一个值时， y 都有 ，则称x 为 ，y 叫x 的 。
2、一次函数的解析式是： ；当 时，称为正比例函数。
3、一条直线经过点（2，3）、（4，7），则该直线的解析式是 。
以上这种求函数解析式的方法叫： 。
二、学习新知：1、反比例函数： 。
反比例函数的表达式还可以表示为： 。
2、列举几个反比例函数的例子： 。
3、例题分析：例1、已知y 是x 的反比例函数，当x=2时，y ＝6。
（1）写出y 与x 之间的函数解析式；（2）求当x=4时y 的值。
三、释疑提高：1、下列等式中哪些变量之间的关系是反比例函数？（1）3x y =；（2）y = （3）xy =21； （4）y =52x +；（5）y = -32x；（6）y =13x +；（7）y =x -42、已知函数1m m y x-=是关于x 的反比例函数，则m 的值是 。
3、当n 取 时，y =（n 2+2n ）21n n x +-是反比例函数。
4、已知y 是x 的反比例函数，当x =3时，y =7，（1）写出y 与x 的函数关系式；（2）求x =7时y 的值。
5、反比例函数k y x =的图象经过点（32-，5）、（a ，-3）及（10，b ），则k = ，a = ，b = 。
6、已知函数y =y 1+y 2，y 1与x 成正比例，y 2与x 成反比例，且当x =1是，y =4，x =2时，y =5，（1）求y 与x 的函数关系式；（2）当x = -2时，求函数y 的值。
四、归纳小结：反比例函数学案（二）——1.2反比例函数的图象和性质（一）一、温故知新1、反比例函数： ，反比例函数又可表示为： 、 。
2、过点（2，5）的反比例函数的解析式是： 。
3、一次函数y =kx +b 的图象是： ，它经过点： 、直线y =kx 经过点： 。
人教版-初三数学-反比例函数教案-PDF电子版
生：展示答案
10.（1）函数 y = 3 − k 是反比例函数，则 k 的取值范围是 k ≠ 3 ；
x
（2）当 a = -1 时，函数 y = kxa 是反比例函数，且 k ≠ 0；
y = x （3）函数
m
m −2 是反比例函数，则
m
=
±1，反比例函数的解析式为 y = ± x−1 ；
师：简单评价（1）（2）（3），直接展示（4）（5）答案，留给课下学生探讨。
函数在 x<0 上为增函数、在 x>0 上同为增函数。
(3)在一个反比例函数图象上任取两点 P，Q，过点 P，Q 分别作 x 轴，y 轴的平
行线，与坐标轴围成的矩形面积为 S1，S2 则 S1=S2=|K|
(4)k 值相等的反比例函数重合，k 值不相等的反比例函数永不相交。
（五）新知应用
问题 5：应用反比例函数概念，对反比例函数再认识，其反比例系数 k 要满足什么条件？自
x
x
中，分数线相当于除号，而除以一个数等于乘以这个数的倒数，所以 D 与 A 等价。
1、反比例函数的图像： 问题：请你画出反比例函数 y=2/x 和 y=(-2)/x 的函数图象。 总结：反比例函数的图象：
当 k<0 时
当 k>0 时
2、性质;
(1)反比例函数的图象既是轴 对 称 图 形 ，又是中 心 对 称 图 形 ，它有两条对 称 轴
设计意图：通过回顾已有知识：路程一定时，时间与速度成反比，引导学生用函数解析式表
达出时间与速度的关系，为后面建立反比例函数解析式的基本模型作铺垫。（5）题让学生从
渝北校区：重庆市渝北区双龙大道 68 号津和苑 5-1【碧津公园大门正对面、渝北区文化宫大门正对面】 教务电话：13883517231 QQ：2290360005
反比例函数全章导学案.doc
学习课题:17. 1. 1反比例函数的意义 预习案：学法指导：用10到15分钟阅读课本内容，完成下列问题，将预习屮不能解决的问题和疑惑记下来1、 回忆一下什么是正比例函数、一次函数？它们的一般形式是怎样的？2、 体育课上，老师测试了百米赛跑，那么，时间与平均速度的关系是怎样的？3在思考（1）中，当路程一定时，速度和时间成什么关系？在思考（2）中，当矩形草坪面积一定时, 矩形草坪的长与宽成什么关系？在思考（3）中，当北京市的总面积一定时，人均占有的土 地面积与全市总人口成什么关系？4、什么是反比例函数？哪个是比例系数？比例系数有什么特点?探究案：问题1、在思考（1） （2） （3）中得到的关系式与一次函数、正比例函数的关系式一样吗?2、 这些关系式有什么特征？3、 你能归纳出反比例函数的概念吗？4、 反比例函数的自变量x 的取值范围是怎样的？函数值y 的取值范围是什么？【活动1】问题1：下列哪个等式中的y 是x 的反比例函数？丄=3, y = 6 兀+ 1,小=123, y=- —x2x思考：反比例函数解析式的分子、分母有什么特征?问题2：当m 取什么值时，函数y 二（加-2）兀“"2是反比例函数? 思考：反比例函数的解析式有儿种形式？【活动2】己知y 是X 的反比例函数，当x=2时，y=6（1）写出y 与x 的函数关系式：（2）求当x 二4时，y 的值。
思考1：确定反比例函数解析式的关键是什么？思考2：本题可以设反比例函数解析式的哪种形式? 二、巩固练习1、 P40-1、2、3 （在书上完成）2、y 是x 的反比例函数，下表给出了 x 与y 的一些值:（1） 写出这个反比例函数的表达式;（2） 根据函数表达式完成上表。
四、反思归纳1、 木节课学习的内容:5y"x + 22、数学思想方法归纳:当堂检测1、下列哪个等式中的y是x的反比例函数？2 2 2(1)y -—X , (2) y -—X , (3) xy +1 = 0 , (4) xy = 0 , (5) x =——• 3 -3 3y2、函数y =-—中的自变量x的取值范围是______________________x + 2三、提升能力：1、若函数y = (m + l)x,,r J是反比例函数,则m二 _________2、已知y与x・l成反比例函数，当x=2时y=l,则这个函数的表达式是( )1 k 1 1 .A、y = ---- y = ------------ C、y =--------------- D^ y = ------------ 1x-\ x-\x+1 x3、己知y与x?成反比例，并且当x=3时y二4.(1)写出y与x之间的函数关系式。
九年级数学上册 第六章 反比例函数 全章导学案 (新版)北师大版
6.1反比例函数学习目标：1．理解反比例函数的概念，会求比例系数。
2．感受反比例函数是刻画世界数量关系的一种有效模型，能够列出实际问题中的反比例函数关系.学习重点：理解反比例函数的概念，会求比例系数。
难点：正确列出实际问题中的反比例函数关系。
学习过程中可能会用到的某些量之间的关系：，R U I = ,vs t = 长方形的面积＝长⨯宽，总人口数总耕地面积人均耕地面积＝ 学习过程：一、自主学习1、自学课本新课内容并完成课本的题目。
（做在课本上。
）2、明确概念：反比例函数：一般地，如果两个变量x 、y 之间的关系式可以表示成的形式，那么称y 是x 的反比例函数。
反比例函数的自变量x 不能为。
*说明：（1）反比例函数)0(≠=k x k y 有时也写成)0(≠=k y 或)0(≠=k 的形式。
（2）反比例函数中，三个量x 、y 、k 均不能为0.二、合作学习，共同探索1、订正自主学习内容。
2、完成课本做一做。
先独立完成，再小组交流。
三、全班交流，知识应用1、下列关系式中的y 是x 的反比例函数吗？如果是，比例系数k 是多少？ ①4y x =；②12y x =-；③1y x =-；④1xy =；⑤2x y =；⑥13y x -=；⑦21y x =- 解：上述关系式中y 是x 的反比例函数的有：；它们的比例系数k 分别是 。
2、已知y 是x 的反比例函数，且当x =2时，y =9.（1）求y 关于x 的函数表达式；（2）当27=x 时，求y 的值；（3）当y =3时，求x 的值。
3、已知函数22(1)m y m x -=+当m 为何值时，y 是x 的反比例函数？并求出函数的表达式。
四、课堂小结。
这节课我们主要学习了 ，你的收获是： 。
五、当堂检测必做题：1．下列函数中，y 与x 成反比例函数关系的是（ ）A.5xy =B.21y x =-C.3y x =D.11y x =-+ 2.在下列关系式中：①x y 5= ②x y 4.0= ③2x y = ④1-=xy ⑤x y -=5 ⑥x y 65= ⑦2=xy ⑧12-=x y 其中y 是x 的反比例函数的有：；它们的比例系数k 分别是 。
九年级数学反比例函数全章导学案
九年级数学反比例函数全章导学案《5.1反比例函数》第1课时导学案课时：第一课时主备人：审核人：备课时间：2022-10-23【学习目标】会判断一个函数是反比例函数，能举例辩析一个变化过程中两个变量之间符合反比例函数的特征；会求简单问题中反比例函数的表达式．【学习方法】利用导学案，采用学生自学和小组讨论的方式进行合作探究式学习。
【学习重点】感受反比例函数是刻画世界数量关系的一种有效模型【学习难点】利用反比例函数关系解决实际问题一、自主学习：1、一般地.在某个变化中,有两个某和y,如果给定一个某的值,相应地,那么我们称y是某的函数,其中某叫,y叫2、我们已经学过一次函数，还记得相关知识吗？⑴形如y=的函数，叫做一次函数；⑵图像的性质是：当k＞0时，图像经过第象限，y随某的逐渐增大而，这时图像是图像（上升或下降）。
当k<0时，图像经过第象限，y随某的逐渐增大而；当k=0时，它变成函数，图像的性质与的性质相同。
二、小组交流，合作探究1、电流I、电阻R、电压U之间满足关系式U=IR，当U＝220V时，（1）你能用含有R的代数式表示I吗？（2）利用写出的关系式完成下表：R/ΩI/A20406080100当R越来越大时，I怎样变化？当R越来越小呢？（3）变量I是R的函数吗？为什么？2、汽车从南京出发开往上海（全程约为300km），全程所用的时间t(h)随速度v(km/h)的变化而变化.（1）你能用含有v的代数式表示t吗？（2）利用（1）中的关系式完成下表：v/(km/h)t/h608090100120．随着速度的变化，全程所用的时间发生怎样的变化？（3）速度v是时间t的函数吗？为什么？概念：如果两个变量某,y之间的关系可以表示成的形式，那么y是某的反比例函数，反比例函数的自变量某不能为零。
3．下列关系式中的y是某的反比例函数吗？如果是，系数k是多少？①y41某21；②y；③y1某；④某y1；⑤y；⑥y3某；⑦y1某2某2某三、全班交流，例题学习1、个矩形的面积为20cm，相邻的两条边长分别为某cm和ycm。