《傅里叶光学导论》历年考题要点
《傅里叶光学导论》历年考题.

《傅里叶光学导论》历年考题2002/2003(开卷)1.(24分) 一个衍射屏的振幅透射率函数为)()cos 2121()(2lr circ r r t β+=。
(1)这个屏的作用在什么方面像透镜?(2)给出此屏焦距的表达式。
(3)当用波长为m μλ6.0=的单色平面波垂直照明时,若23.0mm =β,mm l 20=,在其中的会聚焦点处的艾里斑半径0r 为多大(略去其他两项光束背景影响)?2.(20分) 某周期性物体的振幅透过率)()(nd x x t n -∑=∞-∞=δ,假定用均匀的平面波垂直照明,试证明这个物体是“自成像”的,意即物体后面周期性距离上能成自身的理想像,而不需要透镜。
3.(24分) 一成像系统光瞳函数为)2/()2/()()(),(l y rect l x rect l y rect l x rect y x P -=,mm l 20=,成像透镜焦距mm f 200'=,物像距mm d d o i 400==,照明波长m μλ5.0=。
(1)用非相干光照明时,求)2(2000ix d l f f f f λ=≤≤,这一区间的光学传递函数)0,(x f ℘,画出截面图(请注明标度尺)。
(2)用非相干光照明强度透射率)2cos 1(21)(02x f m x I π+=的物体,其中mm f 周252=,试求出其像的强度分布。
(3)用相干光照明时,求其频率传递函数)0,(x f H ,画出)0,(x f H 的截面图(请注明横纵坐标的标度尺)。
(4)用相干平面波垂直照明振幅透射率为)2cos 1(21)(01x f m x t π+=的物体,其中mm f 周5.371=,试求出其像的强度分布。
4.(20分) (1)波长m μλ5.0=的单色平面波。
(cm x 1043⨯=,cm y 1041⨯=,cm z 1023⨯=)。
试求光场x 轴和y 轴的空间频率。
(2)已知一个相干成像系统的截止频率cm c f 5000=,像面大小为cm cm 11⨯,最少可用多少个抽样点取值来表示。
09-习题课(一)
计算
f ( x ) ∗ h( x )
y
并作图
y
y
-3
-2
-1
1
2
3
x
-3
-2
-1
0
1
2
3
x
X-3
-3
-2
x X+1
-1 0
1
2
3
x
第一步
翻 转
第二步 平 移
17
第三步 乘 积
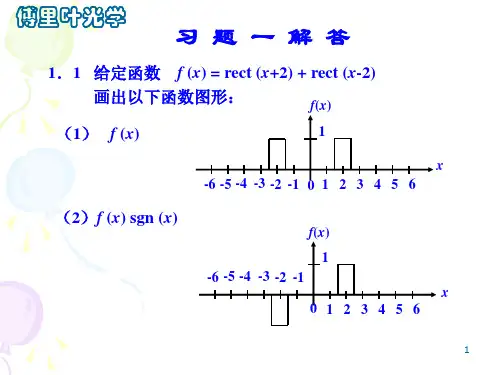
习 题 一 解 答
y y
求面积) 第四步 积 分(求面积)
y
?
X-3
f(x)*h(x)
3 2 1
-3
-2
-1
1
2
3
4
5
6
x
19
傅里叶光学
习 题 一 解 答
x x − a / 2 1 x 1.7 求证: rect + rect . 求证: ∗ comb = 1 b a − b a a
分析
0<x<a
y
x a2 − x2 1 1 f ( x ) Λh ( x ) = a − × x × = 2 2 a 2a
a/2
1
-a -3
-2
-1
1
2
3
a
x
25
习 题 一 解 答
• 同理
a2 − x2 2a h ( x ) Λf ( x ) = (a − x) 2 2a
可见, 可见,求相关不满足交换律
点的矩形函数, (1)第一项是宽度为 、中心在 点的矩形函数, )第一项是宽度为b、中心在0点的矩形函数 第二项是宽度为( - )、中心在a/2处的矩形函数 )、中心在 处的矩形函数, 第二项是宽度为(a-b)、中心在 处的矩形函数, 由图可见,两者相加得到一个宽度为a的矩形函数 的矩形函数。 由图可见,两者相加得到一个宽度为 的矩形函数。 (2)Comb函数由间隔为 的一系列δ函数组成 ) 函数由间隔为a的一系列 函数组成 函数由间隔为 的一系列 1 a x b/2 a-b/2 -2a -a 1 0 a x 2a
傅里叶光学3-07

3.6光学成像系统的频率特性及其传递函数
MTF的重要性
调制度 modulation , 又称为对比度、反衬度,是评价像质 的定量方法之一。
像的调制度V的定义:
V IM Im IM Im
IM : 最大光强 Im : 最小光强
0, 即IM= Im,像面光强无变化; V= 1, 即Im=0,对比度最高, 条纹结构最清晰。
输入像调制度: V入 = m 调制传 递函数
M TF
V出
V出 V入
Hc Hc I0
Hc Hc
h ' x dx
I
F T h ' I x F T h ' I x
0
OTF
空频为ξ0,调制度为m的余弦条纹,经过非相干成像系统后,成为空频ξ0 , 调制度为 m|OTF|ξ= ξ0的余弦条纹。这也是OTF的物理意义。
衍射受限系统的相干传递函数是光瞳函数的连续两次傅里叶变换。 当光学成像系统存在像差时,用广义光瞳函数代替光瞳函数,并 对其进行两次傅里叶变换得
m 2
h 'I
1
x d x
e
i 2 0 xi
h 'I
xe
2
2
i 2 0 x
dx
m 2
e
i 2 0 xi
h 'I ( x ) e
3
i 2 0 x
dx
第一项是像强度的直流分量(均值) 第二项中的积分是
F T h ' I x
I i xi 1 x x x 1 e x p i 2 i e x p i 2 i 1 c o s 2 i 2 d d d
傅里叶光学金典试题及答案和重要知识点总结

因位置不同而引起的位相色散
x , y
z z
菲涅耳衍射可视为函数
U
0
(
x0
,
y0 ) exp[
j
k 2z
( x0 2
y
0
2
)]
的傅里叶变换在处的值
(3)频域(角谱)表达式: A(u,v) A0 (u,v)exp( jkz)exp[ jz(u2 v2 )]
A(u, v) A0 , • H , H(u,v) exp( jkz)exp[ jz(u2 v2 )] A(u, v) 衍射场角谱 A0 , 孔径后角谱
3、脉冲响应是孔径的傅里叶变换或夫朗和费衍射图样,中心在(-Mx0, -My0)点。 8. 衍射受限系统, 阿贝成像理论;
所谓衍射受限 是指仅仅考虑系统的衍射限制, 不考虑系统的几何像差。
在衍射受限系统中,光的衍射仅受到系统孔径光阑尺寸的限制,因此在考察衍射受限系统时,实际上主要考察
孔径光阑的衍射作用。如果入(出)射光瞳无限大,则光的衍射不受系统的限制,点物应该成理想的点像。然而,
δ 函数的性质:①偶函数性质: (- x) (x) ②坐标缩放性质: (ax) 1 (x)
a
③筛选性质: f (x) (x x0 )dx f (x0 )
④乘积性质: f x• x x0 f x0 • x x0
⑤卷积性质: f x x f x
f x x x0 f x x0
成像过程包含了两次衍射过程:由物面到后焦面,物体衍射光波分解为各种频率的角谱分量,即不同方向传播
的平面波分量,在后焦面上得到物体的频谱。这是一次傅里叶变换过程。由后焦面到像面,各角谱分量又合成为
像,这是一次傅里叶变换逆过程。
9. 相干成像系统的点扩展函数, 相干传递函数; 相干照明系统中,脉冲响应是点物产生的衍射斑的振幅分布。
傅里叶光学考点整理

考点一:矩形函数
1()20a x x rect a other ⎧≤⎪=⎨⎪⎩
(1)讨论特殊情况:
11()02x rect ξ⎧--=⎨⎩
性质:中心点是 –(x-1) ,宽度是2,高度是1,左端是x-1-1,右端是x-1+1。
(2)二维矩形函数可以表示成两个一维函数的乘积 如图:(,)()()x y f x y rect rect a b
=
考点二:什么叫卷积、卷积的四个步骤。
估计会考课件上的卷积计算!!!
考点三:有关傅里叶变换的计算题
考点四:证明傅里叶变换的反比性。
反比性即其频谱的有效宽度与原函数的有效宽度之间存在一定的反比关系1x f
∆⋅∆=。
其
物理意义是原函数越窄,则其频谱函数就越宽
考点五:证明卷积定理[(,)(,)](,)(,)x y x y F g x y h x y G f f H f f *=
考点六:设一实函数h(x),其频谱为H(f),即()[()]()()i f a F h x H f H f e φ==
证明其与余弦函数的卷积为:0000()cos 2()cos[2()]a h x f x H f f x f ππφ*=⋅+ 考点七:菲
涅尔衍射积分公式的表达式221101111()()exp()(,)(,)exp 2x x y y jkz U x y U x y jk dx dy j z z λ∞-∞⎡⎤-+-=⎢⎥⎣⎦
⎰⎰ 考点七:问答:用菲涅耳衍射公式可以计算的情况:会聚球面波照明衍射屏,衍射花样是屏函数的傅里叶变换。
(详细计算见ppt )。
考点八:空间频率的定义(两种定义方式)。
考点九:阐述傅里叶光学,*计算题为课件上讲的,证明题为重点。
傅里叶光学期末考试复习

信息光学复习第一部分基本概念第二部分基本技能简单和复合孔径的数学描述矩孔、圆孔、单缝、位相板等;它们的中心位置、缩放比例及其它参数多孔、多缝、线光栅、余弦光栅等;它们的各种参数线光栅的线间距余弦光栅的空间频率、调制度、尺寸会用单个孔径函数与δ函数或梳状函数的卷积表示重复性孔径多缝和矩形光栅的缝宽、缝间距、缝数卷积和相关的运算)()( ) () ()(x h x f d x h f x g ∗=−=∫+∞∞−ξξξ有限宽度的两个函数,卷积后的宽度通常是两函数宽度的和卷积的位移不变性: 若f (x )*h (x ) = g (x ), 则f (x- x 0) * h (x ) =g (x - x 0) 或 f (x ) *h (x - x 0) = g (x - x 0) f (x )*δ(x - x 0) = f (x - x 0) 包含脉冲函数的卷积:基本卷积:rect(x )*rect(x )=tri(x )相关运算主要化为卷积进行,并结合OTF 性质常用基本函数的傅里叶变换和逆变换要求会利用傅里叶变换的性质和卷积定理,借助图解,计算较复杂函数的卷积和傅里叶变换利用傅里叶变换的性质和定理求较复杂函数的傅里叶变换和卷积会用图解表示卷积定理第三部分综合能力用解析法和图解法处理衍射受限系统的成像问题注意区分相干照明和非相干照明给出物函数(复振幅或光强透射率),会写出其频谱函数;给出光学系统参数,会写出其相干传递函数或光学传递函数,画出草图,算出相应的截止频率;计算像(复振幅或强度)的频谱,再反算出相应的空间分布,或用图表示;相干照明下,由像的复振幅分布再求像强度.。
傅里叶光学课后答案
傅里叶光学课后答案傅里叶光学课后答案【篇一:光学第二章习题】择题:2008.在菲涅耳圆屏衍射的几何阴影中心处( b )(a)永远是个亮点,其强度只与入射光强有关。
(b)永远是个亮点,其强度随着圆屏的大小而变。
(c)有时是亮点,有时是暗点。
2014.一波长为500nm的单色平行光,垂直射到0.02cm宽的狭缝上,在夫琅禾费衍射花样中心两旁第二条暗纹之间的距离为3mm,则所用透镜的焦距为( d )(a)60mm (b)60cm (c)30mm (d)30cm2026.一个衍射光栅宽为3cm,以波长为600nm的光照射,第二级主极大出现于衍射角为300处。
则光栅的总刻度线数为a(a)1.25*104 (b)2.5*104(c)6.25*103(d)9.48*1032028.x 射线投射在间距为d的平行点阵面的晶体中,试问发生布拉格晶体衍射的最大波长为多少?d(a)d/4(b)d/2 (c)d (d)2d2128. 菲涅尔圆孔衍射实验表明,几何光学是波动光学在一定条件下的近似,如果从圆孔露出来的波面对所考察的点作出的的半波带的数目为k,这种条件下可表达成:( d )(a)衍射波级数k~0;(b)衍射波级数k=1;(c)衍射波级数k〉1;(d)衍射波级数k〉〉1。
2129. 用半波带法研究菲涅尔圆孔的衍射的结果说明,圆孔轴线上的p点的明暗决定于:(c)(a)圆孔的大小;(b)圆孔到p点的距离;(c)半波带数目的奇偶;(d)圆孔半径与波长的比值。
2130 用半波带法研究菲涅尔圆孔衍射时,圆孔线上p点的明暗决定于:(d)(a)圆孔的直径;(b)光源到圆孔的距离;(c)圆孔到p的距离;(d)圆孔中心和边缘光线到p点的光程差。
2131 一波带片主焦点的光强约为入射光强的400倍,则波带片的开带数为:( a )(a)10;(b)20;(c)40;(d)100。
2132 在夫琅和费单缝衍射中,当入射光的波长变大时,中央零级条纹:(b )(a)宽度变小;(b)宽度变大;(c)宽度不变;(d)颜色变红。
傅里叶光学chap6_3 (1)
称为匹配滤波器 匹配滤波器( ∴ F(fx,fy) = S*(fx,fy) 称为匹配滤波器(Matched Filter) ) 它的脉冲响应为: 它的脉冲响应为: F.T.-1{F(fx,fy) } = s*(- x’, -y’)
5、光学图像识别 、
2. 匹配滤波器的制作 匹配滤波器的制作—Van der Lugt滤波器 滤波器 全息方法: 傅里叶变换全息图的光路: 全息方法 傅里叶变换全息图的光路 平面x 平面 0-y0: 放置滤波函数的脉 冲响应, 冲响应,实际上可 以用待识别的目标 函数s(x0,y0). 函数
G ( f x , f y ) = T ( f x , f y )⋅ F ( f x , f y )
将此滤波器放置在4 f系统的频谱平面, 系统的频谱平面, 将此滤波器放置在 系统的频谱平面 系统的焦距f与记录时用的 相同。 设4f系统的焦距 与记录时用的 相同。 系统的焦距 与记录时用的f相同
= R0 + S
输入与目标函数的 + {R 0 t ( x ' , y ' ) ∗ s ( x ' , y ' )}∗ δ ( x '− b , y ' ) 卷积,出现在 3平 卷积 出现在P 出现在 面x’ = b附近 附近 + R0t ( x' , y ' ) ∗ s * (− x' ,− y ' ) ∗ δ ( x'+b, y ' ) 输入与目标函数的 互相关,出现在 3平 互相关 出现在P 出现在 的附近 t(x’,y’)☆s(x’,y’) 面x’ = -b的附近 ☆
2
(
2
)T ( f , f ) + R T ( f , f )⋅ S ( f , f )exp (− j 2π bf
第五章 傅立叶变换光学-wsf-复习提纲
棱镜傍轴成像公式
s
~ 傍轴条件:U1 ( x, y ) A1e
f
f
f
f
物平面
频谱面
像平面
光
傅里叶频谱面的光学分析优势
光
图象识别和比较
(1)振幅型
把标准图象放在物平面上,在频谱平面上放一张照相底片,以单色相 干光照明而获得频谱图的负片,把负片放在原来频谱的位置上,由于原来 频谱图的亮斑恰好为负片的暗处,而原来的频谱图的暗处正好为负片的亮 斑。把待检测的图样放在物平面上,如果待检测图样和标准图象完全一样, 频谱图和负片互补,这样在像平面出现一片黑暗。如果两个图样有一点不 图,则在像面上出现亮点。
第五章 傅立叶变换光学
复习内容
1、 波前变换和相因子分析
2、 余弦光栅的衍射场 3、 傅立叶变换光学 4、 阿贝成像原理与空间滤波 5、 泽尼克的相衬法
对于一些结果的推导,不要去记忆结果是什么,而是要知道结果 是怎么来的。
一、波前变换和相因子分析
(x,y) (x’,y’)
U1 U2
U
~ ~ ~ 入射场U1 ( x, y) 衍射屏的作用 出射场U 2 ( x, y) 波的传播行为 衍射场U ( x' , y' )
光经物平面发生夫琅和费衍射 , 在透镜焦面(频谱面) 上形成一系列衍射光斑 , 各衍射光斑发出的球面次波在 相面上相干叠加,形成像.
F
A B C C’ B’ A’
傅里叶光学期末复习
输入
1 x x g ( x) = comb rect ∗ Λ ( x) 3 50 3
间隔为3的 脉冲阵列, 基频为1/3 g(x) 1 在有限空间 区域不为零, |x|<25 三角波, 底宽为2
......
-25 -3 0 3
......
x 25
光栅由无穷多狭缝构成,每条狭缝的宽度均为a, 相邻缝的中心矩(光栅常数)为d(d›a),且光栅被 限制在边长为L的正方形内,求光栅频谱
+∞ −∞ +∞ −∞
f (ξ )h( x − ξ )d ξ
f (ξ − x0 )h( x − ξ )dξ
设ξ − x0 = ξ ′, 则ξ = x0 + ξ ′, d ξ = d ξ ′ 则f ( x − x0 ) * h( x) = ∫ =∫
+∞ −∞ +∞ −∞
f (ξ ′)h( x − ( x0 + ξ ′))d ξ
−∞
exp[ −i 2π ( f xα + f y β )]dαdβ
H ( fx, f y )
= ∫ ∫ H ( f x , f y ) g (α , β ) exp[ −i 2π ( f xα + f y β )]dαdβ
= H ( f x , f y ) ⋅ G( f x , f y ) = G ⋅ H
{1}= δ (fx,fy);
{δ (fx,fy)}= 1
1 与δ 函数互为F.T.
{comb(x)}= comb(f) x 1 comb( ) = comb(τ f) τ τ
{rect(x)}= sinc(f); {sinc(x)}= rect(f) {exp(j2πfax)}= δ (fx-fa) {δ (x-a)}= exp(-j2πfxa)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《傅里叶光学导论》历年考题2002/2003(开卷)1.(24分) 一个衍射屏的振幅透射率函数为)()cos 2121()(2lr circ r r t β+=。
(1)这个屏的作用在什么方面像透镜?(2)给出此屏焦距的表达式。
(3)当用波长为m μλ6.0=的单色平面波垂直照明时,若23.0mm =β,mm l 20=,在其中的会聚焦点处的艾里斑半径0r 为多大(略去其他两项光束背景影响)?2.(20分) 某周期性物体的振幅透过率)()(nd x x t n -∑=∞-∞=δ,假定用均匀的平面波垂直照明,试证明这个物体是“自成像”的,意即物体后面周期性距离上能成自身的理想像,而不需要透镜。
3.(24分) 一成像系统光瞳函数为)2/()2/()()(),(l y rect l x rect l y rect l x rect y x P -=,mm l 20=,成像透镜焦距mm f 200'=,物像距mm d d o i 400==,照明波长m μλ5.0=。
(1)用非相干光照明时,求)2(2000ix d l f f f f λ=≤≤,这一区间的光学传递函数)0,(x f ℘,画出截面图(请注明标度尺)。
(2)用非相干光照明强度透射率)2cos 1(21)(02x f m x I π+=的物体,其中mm f 周252=,试求出其像的强度分布。
(3)用相干光照明时,求其频率传递函数)0,(x f H ,画出)0,(x f H 的截面图(请注明横纵坐标的标度尺)。
(4)用相干平面波垂直照明振幅透射率为)2cos 1(21)(01x f m x t π+=的物体,其中mm f 周5.371=,试求出其像的强度分布。
4.(20分) (1)波长m μλ5.0=的单色平面波。
(cm x 1043⨯=,cm y 1041⨯=,cm z 1023⨯=)。
试求光场x 轴和y 轴的空间频率。
(2)已知一个相干成像系统的截止频率cm c f 5000=,像面大小为cm cm 11⨯,最少可用多少个抽样点取值来表示。
5.(12分) 在相干处理的4F 系统中,1P 面输入函数为)2cos 1(21),(111dx y x s π+=,2P 面频谱函数x y x f j f f H π2),(=,试求3P 面上的输出函数),(33y x f 。
2005/2006(开卷)1.(16分) (a)为直径d 的圆形孔径,(b)为直径d 的不透明圆盘。
在垂直入射的单位振幅的单色平面波照明下,求透射场的角谱,并比较两种情况下,夫琅禾费衍射图样的分布有何异同。
2.(16分) 用相干成像系统对一振幅透射率函数为)~2cos 1(21),(0x f m y x t π+=的物体成像。
设其频率f ~足够低,可以通过此系统,并且忽略放大和系统的总体的衰减。
(1)若系统无像差,求像平面上的强度;(2)证明:同样的强度也出现在无穷多个未聚焦好的像平面上。
3.(18分) 一个衍射屏的振幅透射率函数为)()cos 2121()(2lr circ r r t β+=。
(1)这个屏的作用在什么方面像透镜?(2)给出此屏焦距的表达式。
(3)当用波长为m μλ6.0=的单色平面波垂直照明时,若23.0mm =β,mm l 20=,在其中的会聚焦点处的艾里斑半径0r 为多大(略去其他两项光束背景影响)?4.(14分) 一个具有圆形出射光瞳的聚焦严重失调的光学系统,其圆形出射光瞳的直径为l ,最大的光程偏差为ω,理想像距为i d ,求该系统的光学传递函数OTF 。
当最大光程差为λω2=时系统的有效截止频率是多少?5.(36分) 一成像系统光瞳函数为)2/()2/()()(),(l y rect l x rect l y rect l x rect y x P -=,mm l 20=,成像透镜焦距mm f 200'=,物像距mm d d o i 400==,照明波长m μλ5.0=。
(1)用非相干光照明时,求)2(2000i x d l f f f f λ=≤≤,这一区间的光学传递函数)0,(x f ℘,画出截面图(请注明标度尺)。
(2)用非相干光照明强度透射率)2cos 1(21)(02x f m x I π+=的物体,其中mm f 周252=,试求出其像的强度分布。
(3)用相干光照明时,求其频率传递函数)0,(x f H ,画出)0,(x f H 的截面图(请注明横纵坐标的标度尺)。
(4)用相干平面波垂直照明振幅透射率为)2cos 1(21)(01x f m x t π+=的物体,其中mm f 周5.371=,试求出其像的强度分布。
2012/2013(开卷)1.(30分) 一沿Z 方向传播的单色光源在0z 处),(00y x 平面上光场为),(00y x U ,在1z 处),(11y x 平面上光场为),(11y x U ,给出该自由传播过程的脉冲响应,相干传递函数,并说明其意义,在考虑菲涅耳近似、夫琅禾费近似的条件下,分别给出响应的脉冲响应。
2.(40分) 一薄正透镜的中心厚度为0∆,折射率为n ,焦距为f ,有效口径为D ,由费马原理给出傍轴条件下该透镜的屏函数。
设一透过率函数为),(0y x t 的物体紧贴该透镜放置,且物体尺寸小于透镜的口径D ,用一单位振幅的单色平面波垂直照射物体,给出透镜后焦面上的场分布,并说明该场分布与物函数的关系;在满足相干成像条件下给出该薄正透镜这一简单光学成像系统的脉冲响应(波长λ,焦距f ,物距o d ,像距i d )。
3.(30分) 一个具有圆形出射光瞳的光学系统,其圆形出射光瞳的直径为l ,求其理想成像的相干传递函数(理想像距为i d );若该系统出射光瞳直径cm l 6=,光瞳与像面的距离cm d i 20=,用nm 600=λ的单色平行光照明一余弦光栅,要在像平面上得到该光栅的精准像,问余弦光栅的空间频率不能超过多少?若该系统聚焦严重失调,最大光程偏差为ω,求该系统的光学传递函数OTF 。
当最大光程差为λω2=时系统的有效截止频率是多少??/?(开卷)1.(20分) 一束波长为m μλ75.0=的单位振幅的平面波,垂直入射照明一个透镜,透镜的直径为cm 5,焦距为cm 2,在透镜后方m 5.0处,以透镜轴为中心,放着一个物体,其振幅透过率)()()2cos 1(21),(000000ly rect l x rect x f y x t π+=,假定cm l 10=,cm c f 1000=。
(1)求出焦平面光强度),(f f f y x I 的表达式。
(2)画出),(f f f y x I 沿f x 的分布图,指出各衍射分量的高度、位置及宽度数值。
2.(20分) 用相干成像系统对一振幅透射率函数为)~2cos 1(21),(0x f m y x t π+=的物体成像。
设其频率f ~足够低,可以通过此系统,并且忽略放大和系统的总体的衰减。
(1)若系统无像差,求像平面上的强度;(2)证明:同样的强度也出现在无穷多个未聚焦好的像平面上。
3.(30分) 一个非相干成像系统,其光瞳函数是宽度为l 的正方形,在出射光瞳中心放一个宽度为43l 的正方形光阑。
(1)画出没有光阑时OTF 的截面图。
(2)在没有光阑时,假定cm l 2=,m μλ5.0=,像距cm d i 20=,求出强度场)2cos 1(21),(01000x f m y x I π+=所成像的强度分布,其中cm c f 30001=。
(3)求出有光阑时的OTF ,并画出其截面图。
(4)若存在较严重的系统误差,求有光阑时几何光学所预言的OTF 。
4.(30分) 填空题(无)?/?(开卷)1.(20分) 某物体具有如下性质:它的振幅透过率中全部频率分量都在频率平面内的一个圆圈上,圆的半径为⋅⋅⋅==,3,2,1,0,2m ma m ρ,假定用均匀的平面波照明,并忽略物体的大小有限引起的衍射效应,试证明这个物体是自成像的,即物后周期性距离上成像,而不需要透镜。
2.(24分) 一个衍射屏的振幅透射函数)()cos 2121()(2lr circ r r t α+=。
(1)这个屏的作用在什么方面像一个透镜?(2)给出此屏焦距的表达式。
(3)什么特性将会严重地限制这种屏作为成像装置?(4)用m μλ5.0=,空间频率cm c f x 1000=,cm c f y 0=的平面波倾斜照明此屏,写出紧贴屏后的光场分布,若2510m μπα-⨯=时,求出它的会聚焦点的坐标),,(z y x 。
3.(1)(10分) 用)sin 2exp(2y j R λθπ-=和)}({11ax rect F f O λ=的干涉条纹制成Lugt 滤波器,将它放置在4f 系统的谱面上,4f 系统的输入面用函数)(),(111ax rect y x g =输入,平面波(m μλ6.0=),沿光轴入射,各透镜焦距均为cm f 10=,当mm a 5=,︒=30θ时,卷积项中心到光轴距离为多大?卷积项范围有多大?(2)(6分) 推导出圆孔光瞳)2/(),(22l y x circ y x P +=的非相干成像系统有严重聚焦误差时的几何光学所预言的OTF 。
(3)(4分) 写出基尔霍夫理论所给出的惠更斯-菲涅耳原理中的子波的特性。
(4)(6分) 一个空间有界物只在cm y cm x 2,1≤≤之内有不为零的值,在其频域的cm c f cm c f y x 2000,1000≤≤之内至少要多少个抽样点上的值才能近似表示该范围的频谱。
4.(30分) 一个非相干成像系统的光瞳函数)()()()(),(by rect b x rect a y rect a x rect y x P -=,其中3,l b l a ==。
(1)推导出)0,(x f ℘的表达式。
(2)画出)0,(x f ℘的截面图,应标明x f 频标值。
(3)若成像系统的透镜焦距cm f 10=,物距cm d o 20=,cm l 1=,照明波长m μλ5.0=。
①用非相干照明和强度正弦试样物)2cos 1(21),(x f m y x t π+=来成像,当cm c f 600=时,求像的强度分布。
②用相干光照明和振幅正弦试样物)~2cos 1(21),(0x f m y x t π+=来成像,当cm c f 125~=时,求像的强度分布。
(4)当b 增大趋近a 时,求该极限情况的a b x f →℘)0,(的表达式,并画出截面图。
