大学物理狭义相对论相对论性动量和能量共20页文档

相对论：能量和动量的变换

乘积
相对论能量：物体在相对论中的能量，包括静止能量和动能
相对论动量：物体在相对论中的动量，等于其能量与速度的来自比值能量和动量的关系式
E^2
=
m^2c^4 +
p^2c^2
E^2
=
m^2c^4 +
(pc)^2
E^2
=
m^2c^4 +
(γm^2 -
m^2)c^2
E^2
=
m^2c^4 +
(γm^2 -
m^2)c^2 +
领域
引力波探测：利用相对论原理探测引力波，研究宇宙起源和
演化
相对论中能量和动量的实验验证
原子能与核能的实验验证
原子能实验：通过核裂变和核聚变实验，验证了相对论中能量和动量的关系
粒子加速器实验：通过粒子加速器实验，验证了相对论中能量和动量的关系
添加标题
添加标题
添加标题
添加标题
核能实验：通过核反应堆实验，验证了相对论中能量和动量的关系
相对论中的能量和动量的物理意义
相对论的基本原理：光速不变原理和相对性原理
相对论中的能量和动量的变换：在相对论中，能量和动量不再是独立的物理量，而是相互关联的
添加标题
添加标题
添加标题
添加标题
能量与动量的关系：能量是动量的函数，动量是能量的时间导数
能量守恒定律：在相对论中，能量守恒定律仍然成立，但需要修改为能量-动量守恒定律
能量和动量变换的应用
核能与核反应
核反应的类型和过程
核能的定义和特点
核能与核反应在能量和动量变换中的应用
核能与核反应的安全性和环保性考虑
粒子加速器

11 狭义相对论的动量与能量

电子的动量： P mv
m0 1 v c
2 2
v
9.11 1031 1 (0.99)
2
0.99 3 108 1.92 10 21 kg m s .
（2）电子的经典力学的动能： Ek
1 m0 2 2 m0 v 2 ，相对论动能： E c 2 m0c 2 ， k mc m0c 2 2 2 1 v c 1 m0 v 2 2 1 c 2 m0c 2 2 1 1 v2 c 2 (0.99) 2 1 1 (0.99) 2
5. 已知电子的初动能： Ek 0 0 ，外力对电子做功等于电子动能的增加： W Ek Ek 0 Ek mc mec ，
外力需做功： W mc 2 mec 2
me 1 v2 c 2
c 2 me c 2 me c 2 (
1 1 1) 0.25mec 2 mec 2 . 0.8 4 m0 1 v2 c 2 v 3P0 ，
Ek 27 ，其中质子的静止质量： m0 1.67 10 kg ！ 2 c
2 m ， Ek 104 MeV 的质子在场强为 1T 的匀强磁场中回旋周期： qB
T
2 Ek 2 104 106 1.6 1019 27 (m0 2 ) [ 1 . 67 10 ] 7.64 10 7 s . 19 8 2 eB c 1.6 10 1 (3 10 ) m0 v m0
1) ，
电子的动能： Ek E0 (
1 1 v c
2 2
1) 0.51MeV ( m0
1 1) 0.34MeV . 0.6
2
本题选（C）
4. 在狭义相对论中，质量 m 与速度 v 的关系： m

大学物理狭义相对论基础全部内容

伽利略变换
洛仑兹变换
实验检验
绝对时空观
狭义相对论时空观比较
相对论动力学基础
广义相对论时空观
学时： 8 （狭义相对论）; 自学*广义相对论简介
重点：狭义相对论的两条基本原理洛仑兹坐标变换狭义相对论时空观（“同时”的相对性、钟慢尺缩）质速关系，质能关系，能量与动量关系
难点：狭义相对论时空观 *广义相对论的两条基本原理 *时空的几何化，空间弯曲
—— 牛顿
即：时间先于运动存在。没有时间，无法描述运动；而没有运动，时间照样存在和流逝。
2. 空间：用以表征物质及其运动的广延性
空间测量：刚性尺国际单位：米
光在真空中 29979241秒58的时间间隔内传播的
距离。
长度的测量：
长度 = 在与长度方向平行的坐标轴上，物体两端坐标值之差注意：当物体静止时，两端坐标不一定同时记录；
物理学家感到自豪而满足，两个事例：
在已经基本建成的科学大厦中，后辈物理学家只要做一些零碎的修补工作就行了。也就是在测量数据的小数点后面添加几位有效数字而已。
——开尔芬（1899年除夕）
理论物理实际上已经完成了，所有的微分方程都已经解出，青年人不值得选择一种将来不会有任何发展的事去做。
——约利致普朗克的信
同学们好！
物理书都充满了复杂的数学公式。可是思想及理念，而非公式，才是每一物理理论的开端。
－－爱因斯坦
《物理学的进化》
阿尔伯特.爱因斯坦（1879 — 1955）
?
第八章狭义相对论 *广义相对论简介
力学相对性原理对称性扩展
狭义相对性原理光速不变原理对称性扩展广义相对性原理等效原理

146相对论的动量和能量

第十四章相对论
即：
讨论：为零（1） x2 x1
v t ' (t 2 x) c v t1 [( t 2 t1 ) 2 ( x2 x1 )] t2 c
0 t2 t1 0

（2）
异地事件的同时性是相对的。
x2 x1 0 t2 t1 0
（ 1 ）L L0 1 - ( / c ) 54m
2
t1 L / 2.25 107 s
( 2 )t2 L0 / 3.75 10 s
7
或 : t2
t1 1 - ( / c )2
14 - 6 相对论动量和能量
第十四章相对论
例10、假定在实验室中测得静止在实验室中的μ+介子（不稳定粒子）的寿命为2.2×10-6s ,而当它相对于实验室运动时实验室中测得它的寿命为1.63×10-5s 。试问：这两个测量结果符合相对论的什么结论？ μ+ 介子相对于实验室的运动速度是真空中光速c的多少倍？解：它符合相对论时间膨胀（或运动时钟变慢）的结论。
静能
m0c
2
：粒子静止时所具有的能量 .
2
E m c

14 - 6 相对论动量和能量
相对论动能由功的定义及动能定理，得
第十四章相对论

Ek
0
d ( m ) dr d ( m ) d Ek F dr dt d (m ) m d dm
同地事件的同时性是绝对的。

14 - 6 相对论动量和能量
第十四章相对论
v t1 [( t 2 t1 ) 2 ( x2 x1 )] t2 c

相对论性动量和能量1

这是相对性原理的结果，也是相对性原理的理解！ 5 、运动时钟变慢效应是时钟本身的客观特征。 6、时间延缓效应显著与否决定于 β 因子。
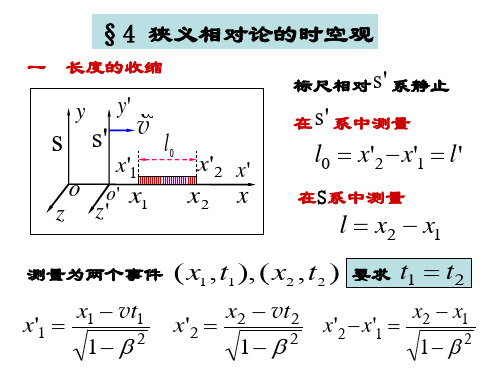
三、同时性的相对性
x2 、 x 1 处同时发生两事件 t1 = t2 事件1： ( x 1， t1 ) s 粉小 s 笔球 x 2，事件2； ( t2 )
在 S中
用洛伦兹变换的逆变换：设S系中固有长度l0,在S’系中仍然有尺缩效应 t t 时
2 1
x2 x1 l0
x1 l x2
在S系中 S’系中
ut 2 ) ( x1 ut1 ) x2 x1 ( x2
x1 ) ( x2
2
l l ' 1 l0
固有长度：物体相对静止时所测得的长度.（最长）长度收缩是一种相对效应,此结果反之亦然. 注意
当 1 时
l l0 .
洛伦兹收缩: 运动物体在运动方向上长度收缩.
l l0 1 c2
u2
尺缩效应说明在所有测量中，与相对静止的惯性系中测量的长度是最长的，运动物体沿运动方向的长度变短。 • 杆只沿运动方向收缩，沿y、z方向不收缩。 • 长度收缩效应是相对的。在S系中观察相对S’系静止的杆长度收缩了，同理在S’系中观察相对S系静止的杆的长度也收缩，
γ =15பைடு நூலகம்82
故行程 l =v Δ t = 0.998cγ τ
= 9500m
此行程可使μ 子穿过大气层到达地球表面，实验结果的确如此。
§5 狭义相对论质点动力学简介
物理概念：质量，动量，能量，„„ 原重新审视其定义
(1) 应符合爱因斯坦的狭义相对性原理即经过洛伦兹变换时保持定律形式不变

物理学中的相对论和狭义相对论

物理学中的相对论和狭义相对论相对论是物理学中一种关于时间、空间、质量和能量等物理量的理论，它是现代物理学的基础，对物质的本质性质产生了深远的影响和重要的启示。

狭义相对论则是相对论的一个分支，主要研究的是相对论的基础理论，如光速不变性、时空的相对性等。

下面，我们将深入了解一下相对论和狭义相对论。

相对论的基本概念相对论是经典物理学与量子力学的桥梁，它对物理学的发展产生了深远的影响。

相对论的基本概念包括：时间的相对性、长度的相对性、物质的相对性、光速的不变性和能量-动量的相对性。

相对论中最基本的概念是时间的相对性，即时间不是一个普遍的或绝对的物理量，而是取决于观察者的参考系。

在相对论的视角下，时间与空间相互关联，形成时空的统一。

这就意味着，两个不同参考系下的事件，可以在时间和空间上发生不同的排序。

长度的相对性是相对论中的另一个基本概念。

同一物体的长度也会因为观察者的不同而发生变化。

在相对论的视角下，物体的长度会随着它的速度而发生变化，这是因为它们越接近光速，它们的相对长度就会越短。

物质的相对性是相对论中最奇妙的概念之一。

它表明，不同的参考系下，物体的质量可能会发生变化。

此外，质量和能量被认为是相互转换的。

根据爱因斯坦的公式，能量等于质量乘以光速的平方，这表明任何物体都可以被视为能量的形式。

相对论中的光速不变性是一个基本的定理，表明在任何参考系中，光速都是相同的。

很长一段时间里，人们认为光速是相对的，而爱因斯坦的理论却彻底改变了这种看法，证明了光速的绝对不变性。

能量-动量的相对性表明，能量和动量同样不是绝对的，而是相对于观察者的参考系。

换句话说，在不同的参考系下，同一物体所具有的能量和动量可以发生变化。

这些变化可能会导致质量、长度和时间等物理量出现异于预期的值。

狭义相对论的基本原理狭义相对论是相对论的一个分支，主要研究相对论的基础理论。

它最初由爱因斯坦提出，是解释光的行为的唯一与时俱进的理论。

狭义相对论的基本原理包括：光速不变性、相对性原理和加速度原理。

大学物理相对论

大学物理相对论目录相对论基本概念狭义相对性原理光速不变原理质能关系030201等效原理广义协变原理引力场方程相对论与经典物理关系相对论是经典物理的延伸和发展，解决了经典物理在高速和强引力场下的困境。

相对论和经典物理在低速和弱引力场下是一致的，但在极端条件下存在显著差异。

相对论揭示了时间和空间的相对性，以及质量和能量的等价性，这些概念在经典物理中是没有的。

狭义相对论基本原理洛伦兹变换同时性相对性在一个惯性参考系中同时发生的两个事件，在另同时性相对性是狭义相对论的基本原理之一，与长度收缩和时间膨胀010203广义相对论基本原理等效原理弱等效原理强等效原理引力场与以适当加速度运动的参考系是等价的。

弯曲时空概念时空弯曲测地线爱因斯坦场方程场方程形式$R_{munu} -frac{1}{2}g_{munu}R + Lambda g_{munu} = frac{8piG}{c^4}T_{munu}$，其中$R_{munu}$ 是里奇张量，$g_{munu}$ 是度规张量，$R$ 是标量曲率，$Lambda$ 是宇宙学常数，$G$ 是万有引力常数，$c$ 是光速，$T_{munu}$ 是能量-动量张量。

场方程的物理意义描述了物质如何影响时空的几何结构，以及时空几何结构如何影响物质的运动。

狭义相对论在物理学中应用质能关系及核能计算核反应能量计算质能方程在核反应中，质量亏损对应的能量释放遵循质能方程，可计算核反应释放的能量。

核裂变与核聚变1 2 3放射性衰变粒子衰变动力学衰变产物的检测与分析粒子衰变过程分析高速运动物体观测效应长度收缩效应时间膨胀效应质速关系及质能变化广义相对论在物理学中应用宇宙微波背景辐射广义相对论预测了宇宙微波背景辐射的存在，这是宇宙大爆炸后遗留下来的热辐射，为宇宙大爆炸理论提供了有力证据。

宇宙大爆炸理论广义相对论为宇宙大爆炸理论提供了理论框架，解释了宇宙的起源、膨胀和演化。

暗物质与暗能量广义相对论在解释宇宙大尺度结构形成和宇宙加速膨胀时，提出了暗物质和暗能量的概念，这些物质和能量对于理解宇宙的演化至关重要。

大学物理-狭义相对论-相对论性动量和能量

我国于 1958 年建成的首座重水反应堆
我国已建成的岭澳核电站
我国在建的单机容量最大的田湾核电站
原子弹核裂变
2 轻核聚变
氘核氦核质量亏损
释放能量
轻核聚变条件温度要达到
有
的动能，足以克服两
力.
时，使具之间的库仑排斥
1967年6 月17日，中国第一颗氢弹爆炸成功
五动量与能量的关系
而
，所以光速 C 为物体的极限速度 .
当
时
相对论动量守恒定律
当
时
常矢量
若
，则相对论动量守恒经典动量守恒 .
常矢量
三质量与能量的关系
相对论质能关系
静能
：物体静止时所具有的能量 .
质能关系预言：物质的质量就是能量的一种储藏 .
爱因斯坦认为（1905）
懒惰性
惯性 ( inertia )
活泼性
物理意义
惯性质量的增加和能量的增加相联系，质量的大小应标志着能量的大小，这是相对论的又一极其重要的推论 .
相对论的质能关系为开创原子能时代提供了理论基础 , 这是一个具有划时代的意义的理论公式 .
质能关系预言：物质的质量就是能量的一种储藏.
例：
现有 100 座楼，每楼 200 套房，每套房用电功率
能量 ( energy )
物体的懒惰性就是物体活泼性的度量 .
相对论能量和质量守恒是一个统一的物理规律.
一些微观粒子和轻核的静能量
粒子
符号
光子
电子（或正电子） e（或 +e
质子
）p
中子
n
氘
氚
氦（粒子）
静能量 MeV 0 0.510

4-5 相对论的动量和能量

质子的静质量质子的静能
2
m0 = 1.673 × 10
−10
− 27
kg
m0 c = 1.503 × 10
J = 938MeV
16
1千克的物体所包含的静能千克的物体所包含的静千克的物体所包含的 1千克汽油的燃烧值为千克汽油的燃烧值为
= 9 × 10 J
7
4.6 ×10
焦耳 .
5）相对论能量和质量守恒是一个统一的物理规律。）相对论能量和质量守恒是一个统一的物理规律。统一的物理规律
2 3 4 1 H + 1 H → 2 He 1 +0n
氘核和氚核聚变为氦核的过程中，静能量减少了氘核和氚核聚变为氦核的过程中，
∆E = 17.59MeV
§14-6 广义相对论简介
狭义相对论认为：在所有惯性坐标系中，狭义相对论认为：在所有惯性坐标系中，物理学定律都具有相同的表达式。在非惯性系中，学定律都具有相同的表达式。在非惯性系中，物理规律又将如何呢？规律又将如何呢？爱因斯坦从非惯性系入手，爱因斯坦从非惯性系入手，研究与认识了等效原理，原理，进而建立了研究引力本质和时空理论的广义相对论。相对论。广义相对论的等效原理一观测者在火箭舱里做自由落体实验。一观测者在火箭舱里做自由落体实验。在(b)中火箭静止在地面惯性系上，他将看到 )中火箭静止在地面惯性系上，质点因引力作用而自由下落；质点因引力作用而自由下落；
10
1g 铀— 235 的原子裂变所释放的能量
我国于 1958 年建成的首座重水反应堆
2 轻核聚变
2 1H
+
2 1H
→ He
4 2
氘核氦核质量亏损
2 − 27 m0 ( 1 H ) = 3.3437 × 10 kg 4 m0 ( 2 He) = 6.6425 × 10 −27 kg

大学物理第6章狭义相对论ppt课件

既然同时性是相对的，那么早与晚的时间顺序
是否也是相对的呢？即一个参考系早发生的事件，
在另一个参考系看来会晚发生呢？
是可能的。但具有因果关系的事件的时序是不
会颠倒的。
小结
时空与物质的运动是相互联系的; 空间距离、时间间隔、同时性也是相对的，它们随物体与观察者的相对运动状态而改变。这就是狭义相对论的时空观。
x 2,y 2,u0.5c S
2
2
y
S(棒): 棒只在运动方向变长。
x x , y y
1 u2 / c2
o
固有长度:
lo (x)2(y)2=1.08m z
S y u
y
45°
x
o
x
x
z
补充例：π介子静止寿命为2.5×10-8s，实验时测得其速率为0.99c，在衰变前可运行距离52m 问：实验结果与理论分析是否一致
K ：t(tuc2x)0, 解得: u=0.6c
xx1u2/c24106m
或 x( xu t)4106m
例题6.4.3 S系：两事件发生在同一地点，且第二事件比第一事件晚发生t=2s；而S：观测到第二事件比第一事件晚发生t =3s。在S系中测得发生这两事件的地点之间的距离x是多少？
解：能否用长度收缩公式？不行。
或者说：运动的时钟走得慢些(钟慢)。时间膨胀(钟慢)是相对性效应，与钟表的具体运转无关。
3.同时的相对性
设A、B两事件同时发生在S系的不同地点, 即
S : xx2 x1 0,tt2 t1 0
S:
tt2t1(tuc 2x)
ux c2 0
可见，在S系看来同时发生的事件，在S系看来
就不是同时发生的。所以同时性是相对的。

第18课狭义相对论II——动量和能量

0
2
1− 2

• =
≈ 0 +
0 2
2
1− 2

1
2

2 0 2
2
≈ 0 +

1
0 2
2
物体静止时的质能
动能
• Einstein由此假设，物体的能量 =
2
=
0 2
2
1− 2

相对论中的能量
• 这个假设能满足能量守恒吗？

•

•
=

2
• =
0
2
1− 2

•=
0
•=
2
大家能感受到这
些公式的美吗？
2
1− 2

=
02
2
1− 2

= ( −

)/
2
1−
2
2
y
A
参
考
系
A’
参
考
系
在A参考系中
以速度v向x
方向运动
速度u
ut
x
(
• =
′
′
′
=
(
−
2
1− 2

)
2
−/
2
1− 2

)
=
(−)
(−/2)
=
−
1−/2
• 一起来验证光速不变，无法通过速度叠加超光速。
A’
参
考
系
= ( − )/ 1 −
2
2
′ =
′ =
1−
2
2
′
= ( −

相对论动能动量关系

相对论动能动量关系相对论动能动量关系是狭义相对论中最为经典的公式之一。

它关系到物理学中动量的概念以及质量与能量之间的转换，是研究高速运动物体行为的基础。

下面，我们将会分步骤地解释相对论动能动量关系。

1. 动量的定义动量是描述物体运动状态的一个物理量，它是物体质量乘以速度，即p=mv。

动量是一个矢量量，它有大小和方向之分。

2. 质量与能量狭义相对论中，质量不再是一个不变的物理量。

相反，它是能量和光速之间的关系所导致的，即E=mc²，其中E代表能量，m代表质量，c代表光速。

这个公式表明，在相对论中，质量和能量是互相转换的。

3. 动能公式的推导相对论动能公式如下：K = (γ-1)mc²其中K代表动能，m代表物体的质量，c代表光速，γ是洛伦兹因子，其公式为：γ = 1/√(1-v²/c²)其中v代表物体的速度。

为了推导相对论动能公式，我们先按照牛顿第二定律的公式F=ma，对物体进行受力分析。

由于物体的质量在相对论中是不是一个不变的量，因此，在进行受力分析得到加速度a后，我们便无法得到物体的速度。

于是，我们采用经典动能公式K = 1/2mv²以及光速不变的前提，通过代数的方式将能量E和动量p与速度v联系起来，并将E和p的表达式进行化简，最终得到了相对论动能公式。

4. 动量的变化和相对论动能动量关系在相对论中，一个物体的质量和速度之间存在着一种有趣的关系。

当一个物体的速度接近光速时，物体的质量会变得越来越大，动量也会变得越来越大。

与之相对应的，则是动能随着速度的变化而变化。

当物体的速度接近光速时，动能的增长速度会越来越慢。

这正是相对论中所描述的能量不断增加，动量却趋于饱和的趋势。

综上所述，相对论动能动量关系是物理学中一个十分重要的理论体系。

它连接了质量、能量、动量和速度等相互关系，为我们解释高速运动物体的运动行为提供了基础的支撑。

第二十章狭义相对论

一.电磁理论的相对性讨论 1) 麦克斯韦方程不服从伽利略变换。因为真空中电磁波的传播速度为光速c，按照伽利略变换，在不同的参考系下光速不同，则麦克斯韦方程会不同。因此电磁学不满足伽利略相对性原理。 2) 高速运动的粒子.
二.“以太”模型当时科学家认为：光波的传播需要一种弹性介质，光速就是光振动的相位相对于介质的传播速度。在真空中也存在这种介质，这种介质叫以太。
三.爱因斯坦的狭义相对论原理狭义：指参考系都是惯性参考系（静止或匀速）
1.在一切惯性系中，真空中的光速度都具有相同的值c —— 光速不变原理
8
真空中的光速c 3 10 m / s
2.在一切惯性系中，物理规律都是相同的
-----狭义相对性原理
Einstein 的相对性理论是Newton理论的发展
三、长度收缩效应
1、本征长度（固有长度）在相对于被测物体静止的参照系中测量的物体长度叫做物体的固有长度或本征长度；而在相对被测物体运动的参照系测量的物体长度叫运动长度。
在月台参照系（S系）上看，火车司机驾驶火车经过月台A端点的时间为 t1，经过B端点的时间为 t2，则月台长度为：
L v(t2 t1 ) vt
如果以太存在，地球在以太中运动，地球上的观察者会感受到以太风。
光对地球上的观察者的速度（以太为静止参考系）：
c c v
c为光对以太的速度 v为地球相对以太的速度
迈克尔逊-莫雷实验
迈克尔逊-莫雷实验的零结果
导致两种理解：（1）没有以太（2）以太和迈克尔逊仪干涉仪一起运动但第二种理解与光行差实验矛盾。光行差实验结果表明如果有以太，以太并没有被拖动，以太是绝对静止的。结合迈克耳逊-莫雷实验和光行差实验的结果，得到如下结论：没有以太，电磁规律对所有惯性系等价，真空中的光速在任何惯性参考系下都是c .

狭义相对论的动力学

⑥ v > c时, m为虚数而无实际意义. 这阐明：真空中旳光速c是一切物体运动速率旳极限.
2 动量与速度旳关系
p mv m0 v 1 v2 / c2
相对论中，质点所受旳力定义为：F
dp dt
d dt
mv
经典力学中，质点受力旳定义：
F
dp dt
m
d dt
v
显然，两者不再等效，因而用加速度表达旳牛顿第二定律在相对论力学中不再成立.
A
B
2. 设有宇宙飞船A和B，固有长度均为l0 = 100m，沿同一方向匀速飞行，在飞船B上观察到飞船A旳船头、
船尾经过飞船B船头旳时间间隔为0.6×10-7s，则飞船
B相对于飞船A旳速度是
。
解：在B 船中观察A船旳长度
l l0 1 v c2
在B 船船头观察A船船头船尾飞过旳时间间隔
0
l v
• 爱因斯坦建立旳质能关系式被以为是一种具有划时
代意义旳理论公式，原子能旳利用使人类进入原子
时代。
E m0c2
这个关系式中 c2 旳数值很大，以至微小旳质量变化，就相应着巨大旳能量变化。
在原子核裂变反应中，1g 235U裂变释放旳结合能约 8.2 1010 J 。
在原子核聚变反应中，1g 氘和氚聚变释放旳结合能大约是上述裂变反应释放能量旳3.5倍。
A
A 0.4kg B 0.8kg C 12×10-7kg D 1/12 ×10-7kg
m0c2 36 1015 J
m0
36 1015 9 1016
0.4kg
3. 一种立方体旳静质量为 m０，体积为 V0，当它相对某惯性系S沿一边长方向以 v匀速运动时，静止在 S 中旳观察者测得其密度为多少？

大学物理狭义相对论(一)

两个事件在同一地点同时发生，则它们在其他任何地点也同
时发生。
03
时间间隔的绝对性
任何两个事件之间的时间间隔，在不同的惯性参考系中都是
相同的。
狭义相对论产生背景
经典力学无法解释光速不变现象
根据经典力学，光速在不同惯性参考系中应该不同，但实验证明光速在不同惯性参考系中都是相同的。
经典力学无法解释质能关系
质量和能量之间存在等效性，可以通过公式E=mc^2进行转换，揭示了物质和能量之间的内在联系。
05
04
时间膨胀效应
运动的时钟相对于静止的时钟会变慢，即时间膨胀现象。
对现代物理学发展影响和意义
奠定了现代物理学基础
狭义相对论是现代物理学的重要基石之一，对后续理论的发展产生了深远影响。
揭示了物质和能量的本质
06
总结与展望
狭义相对论主要内容和成果回顾
狭义相对性原理
物理定律在所有惯性参照系中形式不变，即无法通过实验区分不同惯性参照系。
长度收缩效应
运动物体在其运动方向上会发生长度收缩。
01
02
光速不变原理
在任何惯性参照系中，光在真空中的传播速度都是恒定的，与光源和观察者的运动状态无关。
03
质能关系
05
电磁现象在狭义相对论中表现
电荷守恒定律在狭义相对论中形式
电荷守恒定律
在狭义相对论中，电荷守恒定律依然成立，即电荷既不能被创造也不能被消灭，只能从物体的一部分转移到另一部分，或者从一个物体转移到另一个物体。
洛伦兹不变性
电荷守恒定律具有洛伦兹不变性，即在任何惯性参考系中观察，电荷的总量保持不变。
物理意义
质能方程揭示了质量和能量之间的等效性，表明质量可以转化为能量，反之亦然。这种转化在核反应和粒子物理过程中尤为重要。

13.7狭义相对论之相对论能量和动量的关系

m0 v ⋅ dv m0 d 对质-速关系 dm = d[ = = 2 mv ⋅ 2 v 2 ] c 2 (1 − v 2 / c 2 )3/ 2 c (1 − v / c ) (1 − v ⋅ v / c 2 )1/ 2 求微分得
由此得 mv·dv = (c2– v2)dm
A =速度的变化的曲线与质量随速度的变化的曲线是相同的。
当物体的静止质量不为零时，能量随动量按双曲线的规律变化；
当物体的静止质量为零时，能量随动量直线变化。
{范例13.7} 相对论能量和动量的关系
试推导相对动能和能量公式以及动量公式。
= T = mc2 - m0c2 m0 c 2 1 − v2 / c2 − m0 c 2
当v << c时，根据公式(1 + x)n≈ 1 + nx，运动物体的质量为 1 m0 v 2 −1/ 2 v2 = m0 (1 − 2 ) ≈ m0 (1 + 2 ) m= T ≈ m0 v 2 因此 c 2c 2 1 − v2 / c2 可见：在低速情况下，相对论力学过渡到经典力学。 m0是物体的静止质量，m是物体的运动质量。物体的静止能量为E0 = m0c2，能量守恒必然导致质量守恒，反之，质量守恒也将导致能量守恒。物体的总能量为 E = mc2，在相对论中，质量守恒和能量守恒是统一的，能量蕴含在质量之中。这就是质-能方程,是相对论独有的，没有经典项对应。
m = m0
= [v dm + (c − v )dm]
2 2 2
∫
m
m = m0
c 2 dm mc 2 − m0 c 2 =
根据质点的动能定理：合外力所做的功等于动能的增量。在相对论中物体的动能为物体静止时动能为零， m0 c 2 2 - m c2 故合外力所做的功全部 − m0 c 2 . T = mc= 0 1 − v2 / c2 转化为物体的动能。

相对论动力学广义相对论简介相对论3

v = 8.4 t
作 v2 ~ Ek 曲线
贝托齐电子极限速率实验（1962）
⎛ ⎛ E ⎜ 1−⎜ 1+ ＋ k ⎞ 2= ⎟ v ⎜ m c2 ⎟ ⎜ ⎜ ⎝ 0 ⎠ ⎝
−2 ⎞
－
⎟ c2 ⎟ ⎟ ⎠
实验结果：电子极限速度等于真空中的光速
2、质能关系
E k = mc 2 − m0 c 2
爱因斯坦认为：E0 = m0 c2 为静止能量
x
dE k = mv d v + v d m
2
由m=
m0 1− v / c
2 2
m (c −v )= m c
2 2 2
2 2 0
2 mc dm − 2 mv dm − 2 m vdv = 0
2 2 2
mv d v = (c − v ) d m
2 2
代入dEk表达式中
d Ek = c d m
2
由于物体从静止开始运动，两边积分
v
at
m
•
r a
an
r r r dm r F = m ( a n n + a tτ ) + v dt
r r r dm F = ma + v dt
dm r r r = ma n n + ma tτ + v τ dt
at
m
•
Ft
r v
r a
r F
r dm r r F = man n + ( mat + v )τ dt r r v
−u S
0
v′ = − u A
A
m′ A
v′ = u B
0′
B
x′
M′

大学物理A1 课件第4章狭义相对论

x = ax + bt + e t = ct + dx + f
v
o
P x , y , z , t
x x
S系看 x =0点，
设 t = t =0 时,在o=o点发出一光信号, 在两个参考代入以上方程组可得系中测得的光到达某时空 x = a(x vt)（1）点的事件为p和p '
(2) 长度收缩是“测量”结果，不是“视觉”效应。
例4-2. 静系中子的平均寿命为2.210-6s。据报导，在一组高能物理实验中，当它的速度为u=0.9966c时通过的平均距离为 8km。试说明这一现象：(1) 用经典力学计算与上述结果是否一致；(2) 用时间膨胀说明；(3) 用尺缩效应说明。

1 v2 c 2
l l0 1 v c
2
2
原长：在相对于观察者静止 l 的参考系中测得的物体长度。 0
长度收缩：运动物体的长度小于原长， l
当
l0
v c l l0
注意：长度收缩只发生在运动的方向上。
结论：
(1) 相对于观察者运动物体沿运动方向长度缩短了— — 长度收缩 (动尺缩短)
事件 1 A M 发生
B
k
事件 2 发生
K’系：1、2 两事件同时发生
K 系1事件先于2 事件发生
结论：“同时性”具有相对性 ——光速不变原理的直接结果
4.2.2 时间延缓
火车系：
S 系
理想实验：爱因斯坦火车 M y
d
o
A'
, t1 ) I(x1
x1
x
, t2 ) II(x1

0
1 2

大学物理相对论性动量和能量

E mc
2
相对论的质能关系为开创原子能时
代提供了理论基础 , 这是一个具有划时
代意义的理论公式 .
四、质能公式在原子核裂变和聚变中的应用 1 核裂变质量亏损原子质量单位
放出的能量 1g 铀— 235 的原子裂变释放的能量
约为2.5吨煤的能量！
原子弹爆炸（核裂变）
大亚湾核电站秦山核电站全景图
讨论 1） 2）
在相对论中，物体的
动能：
静能：总能：
Ek mc mo c
2
哇！
2
任何宏观静止的物体具有能量
3）
பைடு நூலகம்
E mc Eo Ek
2
质量是能量的一种量度
4）
E mc 2
质量与能量可以相互转化
5）对于孤立系统，在一切过程中，总质量和总能量分别守恒，但静止质量和静止能量却不一定守恒。
m 5 . 03 m 0
质-速关系的实验
S
S
v
4
3
o
o
相对物体静止的观察者测得物体的质量为m0 ,相对物体运动的观察者测得同一物体的质量为m(v)。
2
1
0 0.2
c
0.4 0.6 0. 8 1.0
二、狭义相对论力学的基本方程
在相对论力学中仍用动量对时间的变化率
定义质点受到的作用力，即：狭义相对论的动力学基 dP d 本方程 F (m v)
L
设质点静止时的动能为零。
相对论动能
A F d r
A = E k
从物体静止开始
dm v d r dt

m
2 2 2 2 2 m c v m 0 c v d m mv d v 2 2 2 2mc 2 d m 2mv 2 d m 2vm 2 d v 0 v d m mv vv d m c d 2 m vd v c 2 v 2 d m c dm

6-6 相对论性动量和能量n

6-6 相对论性动量和能量
狭义相对论动力学高速运动时动力学概念如何？基本出发点： 1、力学定律在洛仑兹变换下形式不变；
2、低速时转化成相应的经典力学形式。
6-6 相对论性动量和能量
一质量、动量与速度的关系
1.力与动量
p mv
dp F dt
2.质量的表达
力持续作用
猜想形式？
Ei mi c ( EiK mi 0c ) 恒量
2 2
m
i
恒量
质量守恒定律
在一个孤立系统内，量亏损
E K 1 m01c E K 2 m02c
2 2
2
E K 2 E K 1 (m01 m02 )c
质量亏损 m 0 . 22 u
原子质量单位 1u 1 . 66 10
2
27
kg
放出的能量 Q E m c 200 1g 铀— 235 的原子裂变释放的能量
Q 8 . 5 10
10
MeV
J
6-6 相对论性动量和能量
原子弹爆炸（核裂变）
6-6 相对论性动量和能量
27
m 0 ( 2 He ) 6 . 6425 10
27
质量亏损释放能量
m 0 . 026 u 4 . 3 10
2
29
Q E ( m ) c 3 . 87 10
8
J
轻核聚变条件温度达到 10 K 时，使 2 H 具有 10 keV 的动能，足以克服 1 两 2 H 之间的库仑排斥力. 1
6-6 相对论性动量和能量
静质量 m 0 :
物体相对于惯性系静止时的质量 . 结论: 质量具有相对意义.