2018届中考《第六讲第3课时抛物线中的一个动点问题》同步练习
2019届中考学练测《第6讲第3课时抛物线中的一个动点问题》课件

形,点 P 的坐标为2,12,2,-
214,2,
214,2,3-2
17
或2,3+2 17.
图6-3-2
②是否存在点P使△BEC为等腰三角形,若存在请直接写出点
P的坐标,若不存在,请说明理由.
【解析】 (1)先确定B(4,5),再利用待定系数法求二次函数表 达式; (2)设P(x,-x2+4x+5),E(x,x+1),D(x,0),分三种情 况:①P点在抛物线上AB之间,②P点在抛物线上A左侧,③P 点在抛物线上B右侧,用字母x表示|PE|和|ED|,再利用PE= 2ED建立方程,求出点P的坐标; (3)设P(x,-x2+4x+5),E(x,x+1),B(4,5),C(5,0),分 三种情况:①EB=EC,②BE=BC,③CB=CE,根据两点间 的距离公式列出方程,解方程确定点P坐标.
例1答图②
例1答图③
②若m>2,如答图③,
过点F,P,M分别向坐标轴作垂线,交点分别为K,L,易得
△KPF≌△LFM,
∴KP=FL=m-2,∴M(m-2,2-m),
代入 y=-12x2+4 中,得 m2-6m=0,解得 m3=6,m4=0(不合 题意,舍去). 综上所述,m 的值为-3+ 17或 6.
(2)设P(x,-x2+4x+5),E(x,x+1),D(x,0). 若P点在抛物线上AB之间, |PE|=-x2+4x+5-x-1,|ED|=x+1,
∵PE=2ED,即-x2+4x+5-x-1=2(x+1),解得x1=2,x2 =-1,则点E(2,3)或E(-1,0),E(-1,0)与点A重合,舍 去,∴此时P(2,9). 若P点在抛物线上A点左侧, |PE|=x+1+x2-4x-5,|ED|=-x-1, ∵PE=2ED,即x+1+x2-4x-5=2(-x-1),解同上.若P 点在抛物线上B点右侧,|PE|=x+1+x2-4x-5,|ED|=x+ 1, ∵PE=2ED,即x+1+x2-4x-5=2(x+1),解得x1=6,x2= -1,则点E(6,7)或E(-1,0),E(-1,0)与点A重合舍去,∴ 此时P(6,-7).
2018年中考数学挑战压轴题(含答案)
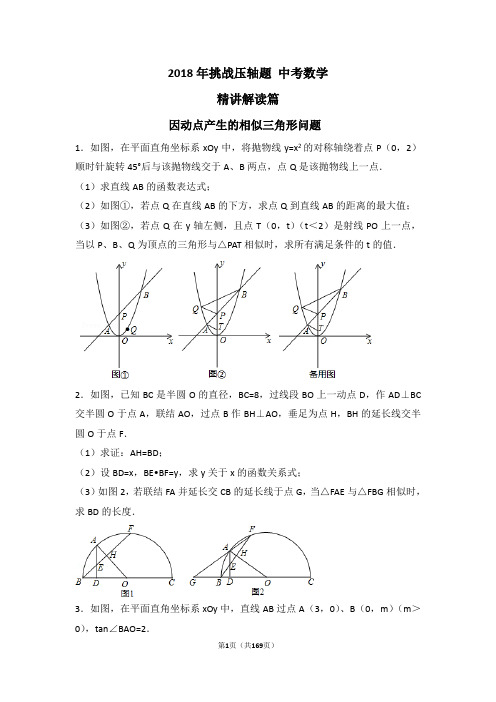
2018年挑战压轴题中考数学精讲解读篇因动点产生的相似三角形问题1.如图,在平面直角坐标系xOy中,将抛物线y=x2的对称轴绕着点P(0,2)顺时针旋转45°后与该抛物线交于A、B两点,点Q是该抛物线上一点.(1)求直线AB的函数表达式;(2)如图①,若点Q在直线AB的下方,求点Q到直线AB的距离的最大值;(3)如图②,若点Q在y轴左侧,且点T(0,t)(t<2)是射线PO上一点,当以P、B、Q为顶点的三角形与△PAT相似时,求所有满足条件的t的值.2.如图,已知BC是半圆O的直径,BC=8,过线段BO上一动点D,作AD⊥BC 交半圆O于点A,联结AO,过点B作BH⊥AO,垂足为点H,BH的延长线交半圆O于点F.(1)求证:AH=BD;(2)设BD=x,BE•BF=y,求y关于x的函数关系式;(3)如图2,若联结FA并延长交CB的延长线于点G,当△FAE与△FBG相似时,求BD的长度.3.如图,在平面直角坐标系xOy中,直线AB过点A(3,0)、B(0,m)(m>0),tan∠BAO=2.(1)求直线AB的表达式;(2)反比例函数y=的图象与直线AB交于第一象限内的C、D两点(BD<BC),当AD=2DB时,求k1的值;(3)设线段AB的中点为E,过点E作x轴的垂线,垂足为点M,交反比例函数y=的图象于点F,分别联结OE、OF,当△OEF∽△OBE时,请直接写出满足条件的所有k2的值.4.如图,在Rt△ABC中,∠ACB=90°,AC=1,BC=7,点D是边CA延长线的一点,AE⊥BD,垂足为点E,AE的延长线交CA的平行线BF于点F,连结CE交AB于点G.(1)当点E是BD的中点时,求tan∠AFB的值;(2)CE•AF的值是否随线段AD长度的改变而变化?如果不变,求出CE•AF的值;如果变化,请说明理由;(3)当△BGE和△BAF相似时,求线段AF的长.5.如图,平面直角坐标系xOy中,已知B(﹣1,0),一次函数y=﹣x+5的图象与x轴、y轴分别交于点A、C两点,二次函数y=﹣x2+bx+c的图象经过点A、点B.(1)求这个二次函数的解析式;(2)点P是该二次函数图象的顶点,求△APC的面积;(3)如果点Q在线段AC上,且△ABC与△AOQ相似,求点Q的坐标.6.已知:半圆O的直径AB=6,点C在半圆O上,且tan∠ABC=2,点D为弧AC上一点,联结DC(如图)(1)求BC的长;(2)若射线DC交射线AB于点M,且△MBC与△MOC相似,求CD的长;(3)联结OD,当OD∥BC时,作∠DOB的平分线交线段DC于点N,求ON的长.7.如图,已知二次函数y=x2+bx+c(b,c为常数)的图象经过点A(3,﹣1),点C(0,﹣4),顶点为点M,过点A作AB∥x轴,交y轴与点D,交该二次函数图象于点B,连结BC.(1)求该二次函数的解析式及点M的坐标;(2)若将该二次函数图象向上平移m(m>0)个单位,使平移后得到的二次函数图象的顶点落在△ABC的内部(不包含△ABC的边界),求m的取值范围;(3)点P时直线AC上的动点,若点P,点C,点M所构成的三角形与△BCD相似,请直接写出所有点P的坐标(直接写出结果,不必写解答过程).因动点产生的等腰三角形问题8.如图1,在△ABC中,∠ACB=90°,∠BAC=60°,点E是∠BAC角平分线上一点,过点E作AE的垂线,过点A作AB的垂线,两垂线交于点D,连接DB,点F是BD的中点,DH⊥AC,垂足为H,连接EF,HF.(1)如图1,若点H是AC的中点,AC=2,求AB,BD的长;(2)如图1,求证:HF=EF;(3)如图2,连接CF,CE.猜想:△CEF是否是等边三角形?若是,请证明;若不是,说明理由.9.已知,一条抛物线的顶点为E(﹣1,4),且过点A(﹣3,0),与y轴交于点C,点D是这条抛物线上一点,它的横坐标为m,且﹣3<m<﹣1,过点D作DK ⊥x轴,垂足为K,DK分别交线段AE、AC于点G、H.(1)求这条抛物线的解析式;(2)求证:GH=HK;(3)当△CGH是等腰三角形时,求m的值.10.如图,已知在Rt△ABC中,∠ACB=90°,AB=5,sinA=,点P是边BC上的一点,PE⊥AB,垂足为E,以点P为圆心,PC为半径的圆与射线PE相交于点Q,线段CQ与边AB交于点D.(1)求AD的长;(2)设CP=x,△PCQ的面积为y,求y关于x的函数解析式,并写出定义域;(3)过点C作CF⊥AB,垂足为F,联结PF、QF,如果△PQF是以PF为腰的等腰三角形,求CP的长.11.如图(1),直线y=﹣x+n交x轴于点A,交y轴于点C(0,4),抛物线y=x2+bx+c 经过点A,交y轴于点B(0,﹣2).点P为抛物线上一个动点,过点P作x轴的垂线PD,过点B作BD⊥PD于点D,连接PB,设点P的横坐标为m.(1)求抛物线的解析式;(2)当△BDP为等腰直角三角形时,求线段PD的长;(3)如图(2),将△BDP绕点B逆时针旋转,得到△BD′P′,当旋转角∠PBP′=∠OAC,且点P的对应点P′落在坐标轴上时,请直接写出点P的坐标.12.综合与探究如图,在平面直角坐标系中,已知抛物线y=ax2+bx﹣8与x轴交于A,B两点,与y轴交于点C,直线l经过坐标原点O,与抛物线的一个交点为D,与抛物线的对称轴交于点E,连接CE,已知点A,D的坐标分别为(﹣2,0),(6,﹣8).(1)求抛物线的函数表达式,并分别求出点B和点E的坐标;(2)试探究抛物线上是否存在点F,使△FOE≌△FCE?若存在,请直接写出点F 的坐标;若不存在,请说明理由;(3)若点P是y轴负半轴上的一个动点,设其坐标为(0,m),直线PB与直线l交于点Q,试探究:当m为何值时,△OPQ是等腰三角形.因动点产生的直角三角形问题13.已知,如图1,在梯形ABCD中,AD∥BC,∠BCD=90°,BC=11,CD=6,tan ∠ABC=2,点E在AD边上,且AE=3ED,EF∥AB交BC于点F,点M、N分别在射线FE和线段CD上.(1)求线段CF的长;(2)如图2,当点M在线段FE上,且AM⊥MN,设FM•cos∠EFC=x,CN=y,求y关于x的函数解析式,并写出它的定义域;(3)如果△AMN为等腰直角三角形,求线段FM的长.14.如图,在矩形ABCD中,点O为坐标原点,点B的坐标为(4,3),点A、C 在坐标轴上,点P在BC边上,直线l1:y=2x+3,直线l2:y=2x﹣3.(1)分别求直线l1与x轴,直线l2与AB的交点坐标;(2)已知点M在第一象限,且是直线l2上的点,若△APM是等腰直角三角形,求点M的坐标;(3)我们把直线l1和直线l2上的点所组成的图形为图形F.已知矩形ANPQ的顶点N在图形F上,Q是坐标平面内的点,且N点的横坐标为x,请直接写出x的取值范围(不用说明理由).因动点产生的平行四边形问题15.如图,在平面直角坐标系xOy中,抛物线y=ax2﹣2ax﹣3a(a<0)与x轴交于A,B两点(点A在点B的左侧),经过点A的直线l:y=kx+b与y轴交于点C,与抛物线的另一个交点为D,且CD=4AC.(1)直接写出点A的坐标,并求直线l的函数表达式(其中k,b用含a的式子表示);(2)点E是直线l上方的抛物线上的一点,若△ACE的面积的最大值为,求a 的值;(3)设P是抛物线对称轴上的一点,点Q在抛物线上,以点A,D,P,Q为顶点的四边形能否成为矩形?若能,求出点P的坐标;若不能,请说明理由.16.如图,在矩形OABC中,OA=5,AB=4,点D为边AB上一点,将△BCD沿直线CD折叠,使点B恰好落在OA边上的点E处,分别以OC,OA所在的直线为x 轴,y轴建立平面直角坐标系.(1)求点E坐标及经过O,D,C三点的抛物线的解析式;(2)一动点P从点C出发,沿CB以每秒2 个单位长的速度向点B运动,同时动点Q从E点出发,沿EC以每秒1个单位长的速度向点C运动,当点P到达点B时,两点同时停止运动.设运动时间为t秒,当t为何值时,DP=DQ;(3)若点N在(2)中的抛物线的对称轴上,点M在抛物线上,是否存在这样的点M与点N,使得以M,N,C,E为顶点的四边形是平行四边形?若存在,请求出M点的坐标;若不存在,请说明理由.17.如图,抛物线y=﹣x2+2x+3与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D和点C关于抛物线的对称轴对称,直线AD与y轴交于点E.(1)求直线AD的解析式;(2)如图1,直线AD上方的抛物线上有一点F,过点F作FG⊥AD于点G,作FH平行于x轴交直线AD于点H,求△FGH周长的最大值;(3)点M是抛物线的顶点,点P是y轴上一点,点Q是坐标平面内一点,以A,M,P,Q为顶点的四边形是以AM为边的矩形.若点T和点Q关于AM所在直线对称,求点T的坐标.18.如图,点A和动点P在直线l上,点P关于点A的对称点为Q,以AQ为边作Rt△ABQ,使∠BAQ=90°,AQ:AB=3:4,作△ABQ的外接圆O.点C在点P 右侧,PC=4,过点C作直线m⊥l,过点O作OD⊥m于点D,交AB右侧的圆弧于点E.在射线CD上取点F,使DF=CD,以DE,DF为邻边作矩形DEGF.设AQ=3x.(1)用关于x的代数式表示BQ,DF.(2)当点P在点A右侧时,若矩形DEGF的面积等于90,求AP的长.(3)在点P的整个运动过程中,①当AP为何值时,矩形DEGF是正方形?②作直线BG交⊙O于点N,若BN的弦心距为1,求AP的长(直接写出答案).19.在平面直角坐标系xOy(如图)中,经过点A(﹣1,0)的抛物线y=﹣x2+bx+3与y轴交于点C,点B与点A、点D与点C分别关于该抛物线的对称轴对称.(1)求b的值以及直线AD与x轴正方向的夹角;(2)如果点E是抛物线上一动点,过E作EF平行于x轴交直线AD于点F,且F 在E的右边,过点E作EG⊥AD与点G,设E的横坐标为m,△EFG的周长为l,试用m表示l;(3)点M是该抛物线的顶点,点P是y轴上一点,Q是坐标平面内一点,如果以点A、M、P、Q为顶点的四边形是矩形,求该矩形的顶点Q的坐标.20.如图,直线y=mx+4与反比例函数y=(k>0)的图象交于点A、B,与x 轴、y轴分别交于D、C,tan∠CDO=2,AC:CD=1:2.(1)求反比例函数解析式;(2)联结BO,求∠DBO的正切值;(3)点M在直线x=﹣1上,点N在反比例函数图象上,如果以点A、B、M、N 为顶点的四边形是平行四边形,求点N的坐标.21.如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为(2,9),与y轴交于点A(0,5),与x轴交于点E、B.(1)求二次函数y=ax2+bx+c的表达式;(2)过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P 在AC上方),作PD平行于y轴交AB于点D,问当点P在何位置时,四边形APCD 的面积最大?并求出最大面积;(3)若点M在抛物线上,点N在其对称轴上,使得以A、E、N、M为顶点的四边形是平行四边形,且AE为其一边,求点M、N的坐标.因动点产生的梯形问题22.如图,在平面直角坐标系xOy中,二次函数y=+bx+c的图象与y轴交于点A,与双曲线y=有一个公共点B,它的横坐标为4,过点B作直线l∥x轴,与该二次函数图象交于另一个点C,直线AC在y轴上的截距是﹣6.(1)求二次函数的解析式;(2)求直线AC的表达式;(3)平面内是否存在点D,使A、B、C、D为顶点的四边形是等腰梯形?如果存在,求出点D坐标;如果不存在,说明理由.23.如图,矩形OMPN的顶点O在原点,M、N分别在x轴和y轴的正半轴上,OM=6,ON=3,反比例函数y=的图象与PN交于C,与PM交于D,过点C作CA⊥x轴于点A,过点D作DB⊥y轴于点B,AC与BD交于点G.(1)求证:AB∥CD;(2)在直角坐标平面内是否若存在点E,使以B、C、D、E为顶点,BC为腰的梯形是等腰梯形?若存在,求点E的坐标;若不存在请说明理由.因动点产生的面积问题24.如图,边长为8的正方形OABC的两边在坐标轴上,以点C为顶点的抛物线经过点A,点P是抛物线上点A,C间的一个动点(含端点),过点P作PF⊥BC 于点F,点D、E的坐标分别为(0,6),(﹣4,0),连接PD、PE、DE.(1)请直接写出抛物线的解析式;(2)小明探究点P的位置发现:当P与点A或点C重合时,PD与PF的差为定值,进而猜想:对于任意一点P,PD与PF的差为定值,请你判断该猜想是否正确,并说明理由;(3)小明进一步探究得出结论:若将“使△PDE的面积为整数”的点P记作“好点”,则存在多个“好点”,且使△PDE的周长最小的点P也是一个“好点”.请直接写出所有“好点”的个数,并求出△PDE周长最小时“好点”的坐标.25.如图,四边形OABC是边长为4的正方形,点P为OA边上任意一点(与点O、A不重合),连接CP,过点P作PM⊥CP交AB于点D,且PM=CP,过点M 作MN∥OA,交BO于点N,连接ND、BM,设OP=t.(1)求点M的坐标(用含t的代数式表示).(2)试判断线段MN的长度是否随点P的位置的变化而改变?并说明理由.(3)当t为何值时,四边形BNDM的面积最小.26.在数学兴趣小组活动中,小明进行数学探究活动,将边长为2的正方形ABCD与边长为2的正方形AEFG按图1位置放置,AD与AE在同一直线上,AB与AG在同一直线上.(1)小明发现DG⊥BE,请你帮他说明理由.(2)如图2,小明将正方形ABCD绕点A逆时针旋转,当点B恰好落在线段DG 上时,请你帮他求出此时BE的长.(3)如图3,小明将正方形ABCD绕点A继续逆时针旋转,线段DG与线段BE将相交,交点为H,写出△GHE与△BHD面积之和的最大值,并简要说明理由.27.在平面直角坐标系中,O为原点,直线y=﹣2x﹣1与y轴交于点A,与直线y=﹣x交于点B,点B关于原点的对称点为点C.(1)求过A,B,C三点的抛物线的解析式;(2)P为抛物线上一点,它关于原点的对称点为Q.①当四边形PBQC为菱形时,求点P的坐标;②若点P的横坐标为t(﹣1<t<1),当t为何值时,四边形PBQC面积最大?并说明理由.28.如图,在平面直角坐标系中,点A(10,0),以OA为直径在第一象限内作半圆,B为半圆上一点,连接AB并延长至C,使BC=AB,过C作CD⊥x轴于点D,交线段OB于点E,已知CD=8,抛物线经过O、E、A三点.(1)∠OBA=°.(2)求抛物线的函数表达式.(3)若P为抛物线上位于第一象限内的一个动点,以P、O、A、E为顶点的四边形面积记作S,则S取何值时,相应的点P有且只有3个?29.如图1,关于x的二次函数y=﹣x2+bx+c经过点A(﹣3,0),点C(0,3),点D为二次函数的顶点,DE为二次函数的对称轴,E在x轴上.(1)求抛物线的解析式;(2)DE上是否存在点P到AD的距离与到x轴的距离相等?若存在求出点P,若不存在请说明理由;=3S△EBC?若存在求出点(3)如图2,DE的左侧抛物线上是否存在点F,使2S△FBCF的坐标,若不存在请说明理由.30.已知抛物线y=mx2+(1﹣2m)x+1﹣3m与x轴相交于不同的两点A、B (1)求m的取值范围;(2)证明该抛物线一定经过非坐标轴上的一点P,并求出点P的坐标;(3)当<m≤8时,由(2)求出的点P和点A,B构成的△ABP的面积是否有最值?若有,求出该最值及相对应的m值.31.问题提出(1)如图①,已知△ABC,请画出△ABC关于直线AC对称的三角形.问题探究(2)如图②,在矩形ABCD中,AB=4,AD=6,AE=4,AF=2,是否在边BC、CD 上分别存在点G、H,使得四边形EFGH的周长最小?若存在,求出它周长的最小值;若不存在,请说明理由.问题解决(3)如图③,有一矩形板材ABCD,AB=3米,AD=6米,现想从此板材中裁出一个面积尽可能大的四边形EFGH部件,使∠EFG=90°,EF=FG=米,∠EHG=45°,经研究,只有当点E、F、G分别在边AD、AB、BC上,且AF<BF,并满足点H 在矩形ABCD内部或边上时,才有可能裁出符合要求的部件,试问能否裁得符合要求的面积尽可能大的四边形EFGH部件?若能,求出裁得的四边形EFGH部件的面积;若不能,请说明理由.32.如图,在平面直角坐标系中,矩形OCDE的顶点C和E分别在y轴的正半轴和x轴的正半轴上,OC=8,OE=17,抛物线y=x2﹣3x+m与y轴相交于点A,抛物线的对称轴与x轴相交于点B,与CD交于点K.(1)将矩形OCDE沿AB折叠,点O恰好落在边CD上的点F处.①点B的坐标为(、),BK的长是,CK的长是;②求点F的坐标;③请直接写出抛物线的函数表达式;(2)将矩形OCDE沿着经过点E的直线折叠,点O恰好落在边CD上的点G处,连接OG,折痕与OG相交于点H,点M是线段EH上的一个动点(不与点H重合),连接MG,MO,过点G作GP⊥OM于点P,交EH于点N,连接ON,点M 从点E开始沿线段EH向点H运动,至与点N重合时停止,△MOG和△NOG的面积分别表示为S1和S2,在点M的运动过程中,S1•S2(即S1与S2的积)的值是否发生变化?若变化,请直接写出变化范围;若不变,请直接写出这个值.温馨提示:考生可以根据题意,在备用图中补充图形,以便作答.33.如图,已知▱ABCD的三个顶点A(n,0)、B(m,0)、D(0,2n)(m>n>0),作▱ABCD关于直线AD的对称图形AB1C1D(1)若m=3,试求四边形CC1B1B面积S的最大值;(2)若点B1恰好落在y轴上,试求的值.因动点产生的相切问题34.如图,已知在平面直角坐标系xOy中,抛物线y=ax2+2x+c与x轴交于点A(﹣1,0)和点B,与y轴相交于点C(0,3),抛物线的对称轴为直线l.(1)求这条抛物线的关系式,并写出其对称轴和顶点M的坐标;(2)如果直线y=kx+b经过C、M两点,且与x轴交于点D,点C关于直线l的对称点为N,试证明四边形CDAN是平行四边形;(3)点P在直线l上,且以点P为圆心的圆经过A、B两点,并且与直线CD相切,求点P的坐标.35.如图,在Rt△ABC中,∠C=90°,AC=14,tanA=,点D是边AC上一点,AD=8,点E是边AB上一点,以点E为圆心,EA为半径作圆,经过点D,点F是边AC 上一动点(点F不与A、C重合),作FG⊥EF,交射线BC于点G.(1)用直尺圆规作出圆心E,并求圆E的半径长(保留作图痕迹);(2)当点G的边BC上时,设AF=x,CG=y,求y关于x的函数解析式,并写出它的定义域;(3)联结EG,当△EFG与△FCG相似时,推理判断以点G为圆心、CG为半径的圆G与圆E可能产生的各种位置关系.36.如图,线段PA=1,点D是线段PA延长线上的点,AD=a(a>1),点O是线段AP延长线上的点,OA2=OP•OD,以O为圆心,OA为半径作扇形OAB,∠BOA=90°.点C是弧AB上的点,联结PC、DC.(1)联结BD交弧AB于E,当a=2时,求BE的长;(2)当以PC为半径的⊙P和以CD为半径的⊙C相切时,求a的值;(3)当直线DC经过点B,且满足PC•OA=BC•OP时,求扇形OAB的半径长.37.如图,在矩形ABCD中,AB=6cm,AD=8cm,点P从点B出发,沿对角线BD 向点D匀速运动,速度为4cm/s,过点P作PQ⊥BD交BC于点Q,以PQ为一边作正方形PQMN,使得点N落在射线PD上,点O从点D出发,沿DC向点C匀速运动,速度为3cm/s,以O为圆心,0.8cm为半径作⊙O,点P与点O同时出发,设它们的运动时间为t(单位:s)(0<t<).(1)如图1,连接DQ平分∠BDC时,t的值为;(2)如图2,连接CM,若△CMQ是以CQ为底的等腰三角形,求t的值;(3)请你继续进行探究,并解答下列问题:①证明:在运动过程中,点O始终在QM所在直线的左侧;②如图3,在运动过程中,当QM与⊙O相切时,求t的值;并判断此时PM与⊙O是否也相切?说明理由.38.如图,抛物线y=﹣x2+mx+n的图象经过点A(2,3),对称轴为直线x=1,一次函数y=kx+b的图象经过点A,交x轴于点P,交抛物线于另一点B,点A、B 位于点P的同侧.(1)求抛物线的解析式;(2)若PA:PB=3:1,求一次函数的解析式;(3)在(2)的条件下,当k>0时,抛物线的对称轴上是否存在点C,使得⊙C 同时与x轴和直线AP都相切,如果存在,请求出点C的坐标,如果不存在,请说明理由.因动点产生的线段和差问题39.如图,抛物线y=x2﹣4x与x轴交于O,A两点,P为抛物线上一点,过点P 的直线y=x+m与对称轴交于点Q.(1)这条抛物线的对称轴是,直线PQ与x轴所夹锐角的度数是;=S△PAQ,求m的值;(2)若两个三角形面积满足S△POQ(3)当点P在x轴下方的抛物线上时,过点C(2,2)的直线AC与直线PQ交于点D,求:①PD+DQ的最大值;②PD•DQ的最大值.40.抛物线y=ax2+bx+4(a≠0)过点A(1,﹣1),B(5,﹣1),与y轴交于点C.(1)求抛物线的函数表达式;(2)如图1,连接CB,以CB为边作▱CBPQ,若点P在直线BC上方的抛物线上,Q为坐标平面内的一点,且▱CBPQ的面积为30,求点P的坐标;(3)如图2,⊙O1过点A、B、C三点,AE为直径,点M为上的一动点(不与点A,E重合),∠MBN为直角,边BN与ME的延长线交于N,求线段BN长度的最大值.41.如图,在每一个四边形ABCD中,均有AD∥BC,CD⊥BC,∠ABC=60°,AD=8,BC=12.(1)如图①,点M是四边形ABCD边AD上的一点,则△BMC的面积为;(2)如图②,点N是四边形ABCD边AD上的任意一点,请你求出△BNC周长的最小值;(3)如图③,在四边形ABCD的边AD上,是否存在一点P,使得cos∠BPC的值最小?若存在,求出此时cos∠BPC的值;若不存在,请说明理由.42.如图,把△EFP按图示方式放置在菱形ABCD中,使得顶点E、F、P分别在线段AB、AD、AC上,已知EP=FP=4,EF=4,∠BAD=60°,且AB>4.(1)求∠EPF的大小;(2)若AP=6,求AE+AF的值;(3)若△EFP的三个顶点E、F、P分别在线段AB、AD、AC上运动,请直接写出AP长的最大值和最小值.43.如图,在平面直角坐标系中,抛物线y=﹣x2﹣x+2与x轴交于B、C两点(点B在点C的左侧),与y轴交于点A,抛物线的顶点为D.(1)填空:点A的坐标为(,),点B的坐标为(,),点C的坐标为(,),点D的坐标为(,);(2)点P是线段BC上的动点(点P不与点B、C重合)①过点P作x轴的垂线交抛物线于点E,若PE=PC,求点E的坐标;②在①的条件下,点F是坐标轴上的点,且点F到EA和ED的距离相等,请直接写出线段EF的长;③若点Q是线段AB上的动点(点Q不与点A、B重合),点R是线段AC上的动点(点R不与点A、C重合),请直接写出△PQR周长的最小值.44.如图,矩形ABCD中,AB=4,AD=3,M是边CD上一点,将△ADM沿直线AM对折,得到△ANM.(1)当AN平分∠MAB时,求DM的长;(2)连接BN,当DM=1时,求△ABN的面积;(3)当射线BN交线段CD于点F时,求DF的最大值.45.如图,半圆O的直径AB=4,以长为2的弦PQ为直径,向点O方向作半圆M,其中P点在上且不与A点重合,但Q点可与B点重合.发现:的长与的长之和为定值l,求l:思考:点M与AB的最大距离为,此时点P,A间的距离为;点M与AB的最小距离为,此时半圆M的弧与AB所围成的封闭图形面积为;探究:当半圆M与AB相切时,求的长.(注:结果保留π,cos35°=,cos55°=)46.(1)发现:如图1,点A为线段BC外一动点,且BC=a,AB=b.填空:当点A位于时,线段AC的长取得最大值,且最大值为(用含a,b的式子表示)(2)应用:点A为线段BC外一动点,且BC=3,AB=1,如图2所示,分别以AB,AC为边,作等边三角形ABD和等边三角形ACE,连接CD,BE.①请找出图中与BE相等的线段,并说明理由;②直接写出线段BE长的最大值.(3)拓展:如图3,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0),点P为线段AB外一动点,且PA=2,PM=PB,∠BPM=90°,请直接写出线段AM长的最大值及此时点P的坐标.47.如图,直线l:y=﹣3x+3与x轴、y轴分别相交于A、B两点,抛物线y=ax2﹣2ax+a+4(a<0)经过点B.(1)求该抛物线的函数表达式;(2)已知点M是抛物线上的一个动点,并且点M在第一象限内,连接AM、BM,设点M的横坐标为m,△ABM的面积为S,求S与m的函数表达式,并求出S 的最大值;(3)在(2)的条件下,当S取得最大值时,动点M相应的位置记为点M′.①写出点M′的坐标;②将直线l绕点A按顺时针方向旋转得到直线l′,当直线l′与直线AM′重合时停止旋转,在旋转过程中,直线l′与线段BM′交于点C,设点B、M′到直线l′的距离分别为d1、d2,当d1+d2最大时,求直线l′旋转的角度(即∠BAC的度数).48.如图,在平面直角坐标系xOy中,将二次函数y=x2﹣1的图象M沿x轴翻折,把所得到的图象向右平移2个单位长度后再向上平移8个单位长度,得到二次函数图象N.(1)求N的函数表达式;(2)设点P(m,n)是以点C(1,4)为圆心、1为半径的圆上一动点,二次函数的图象M与x轴相交于两点A、B,求PA2+PB2的最大值;(3)若一个点的横坐标与纵坐标均为整数,则该点称为整点.求M与N所围成封闭图形内(包括边界)整点的个数.49.如图,顶点为A(,1)的抛物线经过坐标原点O,与x轴交于点B.(1)求抛物线对应的二次函数的表达式;(2)过B作OA的平行线交y轴于点C,交抛物线于点D,求证:△OCD≌△OAB;(3)在x轴上找一点P,使得△PCD的周长最小,求出P点的坐标.2017 挑战压轴题中考数学精讲解读篇参考答案与试题解析一.解答题(共36小题)1.如图,在平面直角坐标系xOy中,将抛物线y=x2的对称轴绕着点P(0,2)顺时针旋转45°后与该抛物线交于A、B两点,点Q是该抛物线上一点.(1)求直线AB的函数表达式;(2)如图①,若点Q在直线AB的下方,求点Q到直线AB的距离的最大值;(3)如图②,若点Q在y轴左侧,且点T(0,t)(t<2)是射线PO上一点,当以P、B、Q为顶点的三角形与△PAT相似时,求所有满足条件的t的值.【分析】(1)根据题意易得点M、P的坐标,利用待定系数法来求直线AB的解析式;(2)如图①,过点Q作x轴的垂线QC,交AB于点C,再过点Q作直线AB的垂线,垂足为D,构建等腰直角△QDC,利用二次函数图象上点的坐标特征和二次函数最值的求法进行解答;(3)根据相似三角形的对应角相等推知:△PBQ中必有一个内角为45°;需要分类讨论:∠PBQ=45°和∠PQB=45°;然后对这两种情况下的△PAT是否是直角三角形分别进行解答.另外,以P、B、Q为顶点的三角形与△PAT相似也有两种情况:△Q″PB∽△PAT、△Q″BP∽△PAT.【解答】解:(1)如图①,设直线AB与x轴的交点为M.∵∠OPA=45°,∴OM=OP=2,即M(﹣2,0).设直线AB的解析式为y=kx+b(k≠0),将M(﹣2,0),P(0,2)两点坐标代入,得,解得.故直线AB的解析式为y=x+2;(2)如图①,过点Q作x轴的垂线QC,交AB于点C,再过点Q作直线AB的垂线,垂足为D,根据条件可知△QDC为等腰直角三角形,则QD=QC.设Q(m,m2),则C(m,m+2).∴QC=m+2﹣m2=﹣(m﹣)2+,QD=QC=[﹣(m﹣)2+].故当m=时,点Q到直线AB的距离最大,最大值为;(3)∵∠APT=45°,∴△PBQ中必有一个内角为45°,由图知,∠BPQ=45°不合题意.①如图②,若∠PBQ=45°,过点B作x轴的平行线,与抛物线和y轴分别交于点Q′、F.此时满足∠PBQ′=45°.∵Q′(﹣2,4),F(0,4),∴此时△BPQ′是等腰直角三角形,由题意知△PAT也是等腰直角三角形.(i)当∠PTA=90°时,得到:PT=AT=1,此时t=1;(ii)当∠PAT=90°时,得到:PT=2,此时t=0.②如图③,若∠PQB=45°,①中是情况之一,答案同上;先以点F为圆心,FB为半径作圆,则P、B、Q′都在圆F上,设圆F与y轴左侧的抛物线交于另一点Q″.则∠PQ″B=∠PQ′B=45°(同弧所对的圆周角相等),即这里的交点Q″也是符合要求.设Q″(n,n2)(﹣2<n<0),由FQ″=2,得n2+(4﹣n2)2=22,即n4﹣7n2+12=0.解得n2=3或n2=4,而﹣2<n<0,故n=﹣,即Q″(﹣,3).可证△PFQ″为等边三角形,所以∠PFQ″=60°,又PQ″=PQ″,所以∠PBQ″=∠PFQ″=30°.则在△PQ″B中,∠PQ″B=45°,∠PBQ″=30°.(i)若△Q″PB∽△PAT,则过点A作y轴的垂线,垂足为E.则ET=AE=,OE=1,所以OT=﹣1,解得t=1﹣;(ii)若△Q″BP∽△PAT,则过点T作直线AB垂线,垂足为G.设TG=a,则PG=TG=a,AG=TG=a,AP=,∴a+a=,解得PT=a=﹣1,∴OT=OP﹣PT=3﹣,∴t=3﹣.综上所述,所求的t的值为t=1或t=0或t=1﹣或t=3﹣.2.如图,已知BC是半圆O的直径,BC=8,过线段BO上一动点D,作AD⊥BC 交半圆O于点A,联结AO,过点B作BH⊥AO,垂足为点H,BH的延长线交半圆O于点F.(1)求证:AH=BD;(2)设BD=x,BE•BF=y,求y关于x的函数关系式;(3)如图2,若联结FA并延长交CB的延长线于点G,当△FAE与△FBG相似时,求BD的长度.【分析】(1)由AD⊥BC,BH⊥AO,利用垂直的定义得到一对直角相等,再由一对公共角,且半径相等,利用AAS得到三角形ADO与三角形BHO全等,利用全等三角形对应边相等得到OH=OD,利用等式的性质化简即可得证;(2)连接AB,AF,如图1所示,利用HL得到直角三角形ADB与直角三角形BHA全等,利用全等三角形对应角相等得到一对角相等,再由公共角相等得到三角形ABE与三角形AFB相似,由相似得比例即可确定出y与x的函数解析式;(3)连接OF,如图2所示,利用两对角相等的三角形相似得到三角形AFO与三角形FOG相似,由相似得比例求出BD的长即可.【解答】(1)证明:∵AD⊥BC,BH⊥AO,∴∠ADO=∠BHO=90°,在△ADO与△BHO中,,∴△ADO≌△BHO(AAS),∴OH=OD,又∵OA=OB,∴AH=BD;(2)解:连接AB、AF,如图1所示,∵AO是半径,AO⊥弦BF,∴∴AB=AF,∴∠ABF=∠AFB,在Rt△ADB与Rt△BHA中,,∴Rt△ADB≌Rt△BHA(HL),∴∠ABF=∠BAD,∴∠BAD=∠AFB,又∵∠ABF=∠EBA,∴△BEA∽△BAF,∴=,。
2018届中考数学复习第六讲第2课时坐标系中的动点问题同步练习(有答案)

2018届中考数学复习第六讲第2课时坐标系中的动点问题同步练习(有答案).5 . 第2时坐标系中的动点问题(50分)一、填空题(每题10分,共20分)1.[2017 泰州]如图6-2-1,在平面内,线段AB=6,P为线段AB 上的动点,三角形纸片DE的边D所在的直线与线段AB垂直相交于点P,且满足P=PA,若点P沿AB方向从点A运动到点B,则点E运动的路径长为__62__.图6-2-1 第1题答图【解析】如答图,E点运动的轨迹与点运动的轨迹相同,点运动的路径长是62+62=62,故答案是62.2.菱形BD在平面直角坐标系中的位置如图6-2-2所示,顶点B(2,0),∠DB=60°,P是对角线上一个动点,E(0,-1),当EP+BP最短时,点P的坐标为__23-3,2-3__.图6-2-2 第2题答图【解析】如答图,连结DE交于点P,则点P满足EP+BP最短.延长D交轴于点F,则F⊥轴,∵四边形BD是菱形,∴D=D=B=2,∵∠DB=60°,则∠DF=30°,∴DF=1,F=3,∴D(1,3),(3,3).设直线DE的解析式为=x-1,将点D坐标代入,则-1=3,∴=3+1,则=(3+1)x-1,设直线的表达式为=x,将点坐标代入,则3=3,∴=33,则=33x,由=(3+1)x-1,=33x,解得x=23-3,=2-3,∴点P的坐标为(23-3,2-3).二、解答题(共30分)3.(15分)[2016 长沙]如图6-2-3,直线l=-x+1与x轴,轴分别交于A,B两点,P,Q是直线l上的两个动点,且点P在第二象限,点Q 在第四象限,∠PQ=135°.(1)求△AB的周长;(2)设AQ=t>0,试用含t的代数式表示点P的坐标;(3)当动点P,Q在直线l上运动到使得△AQ与△BP的周长相等时,记tan∠AQ=,若过点A的二次函数=ax2+bx+同时满足以下两个条①6a+3b+2=0;②当≤x≤+2时,函数的最大值等于2,求二次项系数a的值.解(1)在函数=-x+1中,令x=0,得=1,∴B(0,1),令=0,得x=1,∴A(1,0),则A=B=1,AB=2,∴△AB的周长为1+1+2=2+2;(2)∵A=B,∴∠AB=∠BA=45°,∴∠PB=∠QA=135°,∴∠BP=∠BA-∠PB=45°-∠PB,∴∠AQ=∠PQ-∠BA-∠PB=45°-∠PB,即∠BP=∠AQ,∴△PB∽△AQ,∴PBA=BAQ,∴PB=A BAQ=1t,如答图,过点P作PH⊥B于点H,则△PHB为等腰直角三角形.∵PB=1t,∴PH=HB=22t,∴P-22t,1+22t;(3)由(2)可知△PB∽△AQ,若它们的周长相等,则相似比为1,即全等,∴PB=A,∴1t=1,∴t=1,同理可得Q1+22t,-22t,∴=22t1+22t=2-1,∵抛物线经过点A,∴a+b+=0,又∵6a+3b+2=0,∴b=-4a,=3a,对称轴为直线x=2,当2-1≤x≤2+1时,①若a>0,则开口向上,由题意,得x=2-1时,取得最大值2=22+2,即(2-1)2a+(2-1)b+=22+2,解得a=11+827;②若a<0,则开口向下,由题意,得x=2时,取得最大值22+2,即4a+2b+=22+2,解得a=-22-2.综上所述,所求a的值为11+827或-22-2.4.(15分)如图6-2-4,已知在平面直角坐标系x中,是坐标原点,以P(1,1)为圆心的⊙P与x轴,轴分别相切于点和点N.点F从点出发,沿x轴正方向以每秒1个单位长度的速度运动,连结PF,过点P作PE⊥PF交轴于点E.设点F运动的时间是t s(t 0).(1)若点E在轴的负半轴上,求证PE=PF;(2)在点F运动过程中,设E=a,F=b,试用含a的代数式表示b;(3)作点F关于点的对称点F′.经过,E和F′三点的抛物线的对称轴交x轴于点Q,连结QE.在点F运动过程中,是否存在某一时刻,使得以点Q,,E为顶点的三角形与以点P,,F为顶点的三角形相似,若存在,请直接写出t的值;若不存在,请说明理由.解(1)证明如答图①,连结P,PN.∵⊙P与x轴,轴分别相切于点和点N,∴P⊥F,PN⊥N且P=PN,∴∠PF=∠PNE=90°且∠NP=90°.∵PE⊥PF,∴∠1=∠3=90°-∠2.在△PF和△PNE中,∠3=∠1,P=PN,∠PF=∠PNE.∴△PF≌△PNE(ASA),∴PE=PF;(2)分两种情况①当t 1时,点E在轴的负半轴上,如答图②,由(1)得△PF≌△PNE,∴NE=F=t,PN=P=1,∴b=F=+F=1+t,a=NE-N=t-1.∴b-a=1+t-(t-1)=2,∴b=2+a;②当0 t≤1时,如答图③,点E在轴的正半轴上或原点,同理可证△PF≌△PNE,∴b=F=+F=1+t,a=E=N-NE=1-t,∴b+a=1+t+1-t=2,∴b=2-a.综上所述,当t 1时,b=2+a;当0 t≤1时,b=2-a;(3)存在.t的值是2+2或2-2或2或1+174.(30分)5.(15分)[2017 攀枝花]如图6-2-5,在平面直角坐标系中,直线N分别与x轴,轴交于点(6,0),N(0,23),等边三角形AB的顶点B与原点重合,B边落在x轴正半轴上,点A恰好落在线段N上,将等边三角形AB从图①的位置沿正方向以每秒1个单位长度的速度平移,边AB,A 分别与线段N交于点E,F(如图②所示),设△AB平移的时间为t(s).(1)等边三角形AB的边长为__3__;(2)在运动过程中,当t=__3__时,N垂直平分AB;(3)若在△AB开始平移的同时,点P从△AB的顶点B出发,以每秒2个单位长度的速度沿折线BA→A运动,当点P运动到时即停止运动,△AB也随之停止平移.①当点P在线段BA上运动时,若△PEF与△N相似,求t的值;②当点P在线段A上运动时,设S△PEF=S,求S与t的函数关系式,并求出S最大值及此时点P的坐标.图6-2-5【解析】(1)由题易知=6,N=23,∴N=43,∴∠N=30°,∵∠AB=60°,∴∠BA=90°,即AB⊥N,∴AB=12=3,即等边三角形边长为3;(2)由等边三角形的性质易知当N垂直平分AB时,点与点重合,∴B=-B=3,即t=3;(3)①当P点在线段AB上运动时,则B=t,PB=2t,则B=6-t,PA =3-2t,△PEF与△N相似分为△PEF∽△N或△PEF∽△N两种对应情况思考;②当点P在线段A上运动时,S△PEF=12EF PH=12 32t 3-t2=-38t2+338t=-38t-322+9332≤9332 32≤t≤3,∴当t=32时,Sax=9332.解(3)①当P点在线段AB上运动时,B=t,BP=2t,则B=6-t,PA =3-2t,△PEF与△N相似分为△PEF∽△N或△PEF∽△N两种对应情况,①②第5题答图当△PEF∽△N时,则∠EPF=∠EFA=∠EB=30°,∴AE=12AF=14AP=3-2t4,BE=12B=6-t2.又∵BE=AB-AE=3-3-2t4,∴3-3-2t4=6-t2,解得t=34;当△PEF∽△N时,若点P在线段BE上,则∠PFE=∠N=30°,即PF∥,∴△PAF是等边三角形,∴EF垂直平分PA,∴BE=BP+12PA=32+t,又∵BE=12B=6-t2,∴32+t=6-t2,解得t=1;当△PEF∽△N时,若点P在线段AE上,则P点与A点重合,即t =32.综上所述,t=34或1或32;②当点P在线段A上运动时,则B=6-t,P=6-2t,32≤t≤3.∴BE=12B=3-t2,即AE=t2,∴EF=3AE=32t,AF=2AE=t,∴F=A-AF=3-t,∴PF=P-F=3-t.如答图③,作PH⊥EF于H点,由∠AFE=30°可知,PH=12PF=3-t2.S△PEF=12EF PH=12 32t 3-t2=-38t2+338t=-38t-322+9332≤933232≤t≤3,∴当t=32时Sax=9332.6.(15分)[2017 衢州]在直角坐标系中,过原点及点A(8,0),(0,6)作矩形AB.连结B,点D为B的中点,点E是线段AB上的动点,连结DE,作DF⊥DE,交A于点F,连结EF.已知点E从A点出发,以每秒1个单位长度的速度在线段AB上移动,设移动时间为t s.图6-2-6(1)如图6-2-6①,当t=3时,求DF的长;(2)如图②,当点E在线段AB上移动的过程中,∠DEF的大小是否发生变化?如果变化,请说明理由;如果不变,请求出tan∠DEF的值;(3)连结AD,当AD将△DEF分成的两部分面积之比为1∶2时,求相应t的值.【解析】(1)当t=3时,点E为AB中点.DE为△AB的中位线.(2)过D作D⊥A,DN⊥AB,垂足分别为,N.利用△DF∽△DNE即可求解.(3)AD将△DEF分成的两部分面积之比为1∶2可转化为AD与EF 交点G为EF的三等分点,即讨论G点所处的位置.解(1)当t=3时,点E为AB中点.∵点D为B中点,∴DE∥A,DE=12A=4.∵A⊥AB,∴DE⊥AB.∴∠AB=∠DEA=90°.又∵DF⊥DE,∴∠DFA=90°,∴四边形DFAE是矩形,∴DF=AE=3.(2)∠DEF的大小不变.如答图①,过D作D⊥A,DN⊥AB,垂足分别为,N.∵四边形AB是矩形,∴A⊥AB,∴四边形DAN是矩形,∴∠DN=90°,D∥AB,DN∥A,∴BDD=BNNA,DDB=A.∵点D为B中点,∴,N分别是A,AB中点.∴D=12AB=3,DN=12A=4,∵∠EDF=90°,∴∠FD=∠EDN.又∵∠DF=∠DNE=90°,∴△DF∽△DNE,∴DFDE=DDN=34.∵∠EDF=90°,∴tan∠DEF=34.第6题答图(3)过D作D⊥A,DN⊥AB,垂足分别为,N.若AD将△DEF的面积分成1∶2的两部分,设AD交EF于点G,则易得点G为EF的三等分点.①如答图②,当E到达AB中点之前时,NE=3-t,由△DF∽△DNE,得F=34(3-t).∴AF=4+F=-34t+254.∵G1为EF的三等分点,∴G13t+7112,23t.由点A(8,0),D(4,3)得直线AD的表达式为=-34x+6,将G13t+7112,23t代入,得t=7541.②如答图③,当E越过AB中点之后,NE=t-3,由△DF∽△DNE,得F=34(t-3).∴AF=4-F=-34t+254.∵G2为EF的三等分点,∴G23t+236,13t.代入直线AD表达式=-34x+6,得t=7541.综上,t的值为7541.(20分)7.(20分)[2017 绍兴]如图6-2-7①,已知ABD,AB∥x轴,AB=6,点A 的坐标为(1,-4),点D的坐标为(-3,4),点B在第四象限,点P是ABD边上的一个动点.(1)若点P在边B上,PD=D,求点P的坐标;(2)若点P在边AB,AD上,点P关于坐标轴对称的点Q落在直线=x-1上,求点P的坐标;(3)若点P在边AB,AD,D上,点G是AD与轴的交点,如图②,过点P作轴的平行线P,过点G作x轴的平行线G,它们相交于点,将△PG沿直线PG翻折,当点的对应点落在坐标轴上时,求点P的坐标(直接写出答案).图6-2-7解(1)∵D=6,∴点P与点重合,∴点P的坐标是(3,4).(2)①当点P在边AD上时,由已知得直线AD的函数表达式为=-2x -2,设P(a,-2a-2),且-3≤a≤1.若点P关于x轴的对称点Q1(a,2a+2)在直线=x-1上,则2a+2=a-1,解得a=-3,此时P1(-3,4).若点P关于轴对称点Q2(-a,-2a-2)在直线=x-1上,则-2a-2=-a-1,解得a=-1,此时P2(-1,0).②当点P在边AB上时,设P(a,-4),且1≤a≤7.若点P关于x轴对称点Q3(a,4)在直线=x-1上,则4=a-1,解得a=5,此时P(5,-4).若点P关于轴对称点Q4(-a,-4)在直线=x-1上,则-4=-a-1,解得a=3,此时P4(3,-4).综上所述,点P的坐标为(-3,4)或(-1,0)或(5,-4)或(3,-4);(3)∵直线AD=-2x-2,∴G(0,-2),①如答图②,当点P在D边上,设P(,4),-3≤≤3,则′P=P=4+2=6,′G=G=||,易证得△G′′∽△H′P,则′HP=G′′P,即′4=||6,∴′=23||,在Rt△G′中,由勾股定理,得23||2+22=2,解得=-655或655,则P点坐标为-655,4或655,4;第7题答图②第7题答图③②如答图③,当点P在AD边上时,设P(,-2-2),则P′=P=|-2|,G′=G=||,易证得△G′∽△H′P,则′HP=G′′P,即′|-2-2|=|||-2|,∴′=12|2+2|,在Rt△G′中,由勾股定理,得12|2+2|2+22=2,解得=-52,则P-52,3;③如答图④,当点P在AB边上时,设P(,-4),此时′在轴上,则四边形PG′为正方形,G=P=4-2=2,∴P(2,-4).综上所述,点P的坐标为(2,-4)或-52,3或-655,4或655,4..5 .。
2018年人教版中考数学经典复习题中考动点问题

中考动点问题所谓“动点型问题”是指题设图形中存在一个或多个动点,它们在线段、射线或弧线上运动的一类开放性题目.解决这类问题的关键是动中求静,灵活运用有关数学知识解决问题.数学思想:分类思想 函数思想 方程思想 数形结合思想 转化思想函数揭示了运动变化过程中量与量之间的变化规律,是初中数学的重要内容.动点问题反映的是一种函数思想,由于某一个点或某图形的有条件地运动变化,引起未知量与已知量间的一种变化关系,这种变化关系就是动点问题中的函数关系.那么,我们怎样建立这种函数解析式呢?下面结合中考试题举例分析. 一、应用勾股定理建立函数解析式例1 )如图1,在半径为6,圆心角为90°的扇形OAB 的弧AB 上,有一个动点P,PH ⊥OA,垂足为H,△OPH 的重心为G.(1)当点P 在弧AB 上运动时,线段GO 、GP 、GH 中,有无长度保持不变的线段?如果有,请指出这样的线段,并求出相应的长度.(2)设PH x =,GP y =,求y 关于x 的函数解析式,并写出函数的定义域(即自变量x 的取值范围).(3)如果△PGH 是等腰三角形,试求出线段PH 的长.解:(1)当点P 在弧AB 上运动时,OP 保持不变,于是线段GO 、GP 、GH中,有长度保持不变的线段,这条线段是GH=32NH=2132⋅OP=2.(2)在Rt △POH 中, 22236x PH OP OH -=-=, ∴2362121x OH MH -==. 在Rt △MPH 中,.∴y =GP=32MP=233631x + (0<x <6).(3)△PGH 是等腰三角形有三种可能情况:①GP=PH 时,x x =+233631,解得6=x . 经检验, 6=x 是原方程的根,且符合题意. ②GP=GH 时, 2336312=+x ,解得0=x . 经检验, 0=x 是原方程的根,但不符合题意. ③PH=GH 时,2=x .综上所述,如果△PGH 是等腰三角形,那么线段PH 的长为6或2.二、应用比例式建立函数解析式例2 如图2,在△ABC 中,AB=AC=1,点D,E 在直线BC 上运动.设BD=,x CE=y . (1)如果∠BAC=30°,∠DAE=105°,试确定y 与x 之间的函数解析式;(2)如果∠BAC 的度数为α,∠DAE 的度数为β,当α,β满足怎样的关系式时,(1)中y 与x 之间的函数解析式还成立?试说明理由.2222233621419x x x MH PH MP +=-+=+=HM NGPOAB图1x y解:(1)在△ABC 中,∵AB=AC,∠BAC=30°,∴∠ABC=∠ACB=75°, ∴∠ABD=∠ACE=105°.∵∠BAC=30°,∠DAE=105°, ∴∠DAB+∠CAE=75°, 又∠DAB+∠ADB=∠ABC=75°, ∴∠CAE=∠ADB,∴△ADB ∽△EAC, ∴AC BD CE AB =,∴11x y =, ∴xy 1=. (2)由于∠DAB+∠CAE=αβ-,又∠DAB+∠ADB=∠ABC=290α-︒,且函数关系式成立,∴290α-︒=αβ-, 整理得=-2αβ︒90.当=-2αβ︒90时,函数解析式xy 1=成立. 三、应用求图形面积的方法建立函数关系式例4 如图,在△ABC 中,∠BAC=90°,AB=AC=22,⊙A 的半径为1.若点O 在BC 边上运动(与点B 、C 不重合),设BO=x ,△AOC 的面积为y .(1)求y 关于x 的函数解析式,并写出函数的定义域. (2)以点O 为圆心,BO 长为半径作圆O,求当⊙O 与⊙A 相切时, △AOC 的面积.解:(1)过点A 作AH ⊥BC,垂足为H.∵∠BAC=90°,AB=AC=22, ∴BC=4,AH=21BC=2. ∴OC=4-x . ∵AH OC S AOC ⋅=∆21, ∴4+-=x y (40<<x ). (2)①当⊙O 与⊙A 外切时,在Rt △AOH 中,OA=1+x ,OH=x -2, ∴222)2(2)1(x x -+=+. 解得67=x . 此时,△AOC 的面积y =617674=-. ②当⊙O 与⊙A 内切时,在Rt △AOH 中,OA=1-x ,OH=2-x , ∴222)2(2)1(-+=-x x . 解得27=x . 此时,△AOC 的面积y =21274=-. 综上所述,当⊙O 与⊙A 相切时,△AOC 的面积为617或21.动态几何特点----问题背景是特殊图形,考查问题也是特殊图形,所以要把握好一般与特殊的关系;分析过程中,特别要关注图形的特性(特殊角、特殊图形的性质、图形的特殊位置。
二次函数几何方面的应用(解析版)数学2018全国中考真题-3

2018年数学全国中考真题二次函数几何方面的应用(试题一)解析版一、选择题1.(2018广西省桂林市,12,3分)如图,在平面直角坐标系中,M、N、C三点的坐标分别为(12,1),(3,1),(3,0),点A为线段MN上的一个一动点,连接AC,过点A作AB⊥AC交y轴于点B,当点A 从M运动到N时,点B随之运动,设点B的坐标为(0,b),则b的取值范围是( )A.14-≤b≤1 B.54-≤b≤1 C.94-≤b≤12D.94-≤b≤1【答案】B.【思路分析】.如下图(1),连接CN,延长NM,交y轴于点D,设AN=x,则AD=3-x,DB=1b+,证明△BDA∽△ANC,可得b=23523124x x x-+-=--+⎛⎫⎪⎝⎭≤54,从而得到b的取值范围.【解题过程】解:如下图(1),连接CN,延长NM,交y轴于点D,设AN=x,则AD=3-x,∵点B的坐标为(0,b),∴DB=1b+,∵N、C两点的坐标分别为(3,1),(3,0),∴NC=1,AN⊥NC,∴∠ACN+∠CAN =90°,∵AB⊥AC,∴∠BAD+∠CAN=90°,∴∠ACN=∠CAN,又∵∠BDA=∠CNA=90°,∴△BDA∽△ANC,∴AD BDCN AN=,即131bxx+-=,213b x x+=-+,解得b=23523124x x x-+-=--+⎛⎫⎪⎝⎭≤54,又∵当点A与点N重合时,点B与点D重合,(如下图(2)),此时b=1,∴54-≤b≤1.,故选B.【知识点】二次函数;相似三角形的性质和判定;动点问题二、填空题1.(2018吉林长春,14,3分)如图,在平面直角坐标系中,抛物线y=x2 + mx 交x轴的负半轴于点A. 点B是y轴正半轴上一点,点A关于点B的对称点A' 恰好落在抛物线上. 过点A' 作x轴的平行线交抛物线于另一点C.若点A' 的横坐标为1,则A'C 的长为 .(第14题)【答案】3【思路分析】如下图,A'C 与y 轴交于点D. 因为点A 与点A' 关于点B 对称,则AB=A'B ;又因A'C// x 轴,则ΔABO ≌ ΔA'BD ,AO=A'D. 点A' 的横坐标为1,即A'D=AO=1.所以点A 坐标为(-1,0),把点A (-1,0)代入函数解析式可求得m 值,进而可知A' 坐标,由A'C// x 轴,可求出点C 横坐标,即可求出A'C 的长.【解题过程】解:如图,A'C 与y 轴交于点D. ∵点A 与点A' 关于点B 对称 ∴AB=A'B 又A'C// x 轴∴∠A'DB =∠AOB =90°,∠DA'B =∠OAB ∴ΔABO ≌ ΔA'BD ∴AO=A'D∵点A' 的横坐标为1 ∴A'D=AO=1∴A 坐标为(-1,0)把(-1,0) 代入抛物线解析式y =x 2 + mx 得m=1 ∴抛物线解析式为y =x 2 + x ∴ A' 坐标为(1,2) 令y =2得,x 1 = -2 , x 2=1 ∴A'C =1-(-2)=3.【知识点】待定系数法求抛物线解析式,对称的性质,平行线的性质,三角形全等,直角坐标系中求线段长度2. (2018广西贵港,12,3分)如图,抛物线y =14(x +2)(x -8)与x 轴交于A ,B 两点,与y 轴交于点C ,顶点为M ,以AB 为直径作⊙D ,下列结论:①抛物线的对称轴是直线x =3;②⊙D 的面积是16π;③抛物线上存在点E ,使四边形ACED 为平行四边形;④直线CM 与⊙D 相切.其中正确结论的个数是 A .1 B .2 C .3 D .4【答案】B【解析】抛物线y =14(x+2)(x-8)与x轴交于A,B两点,可知A(-2,0),B(8,0)所以D(3,0),所以抛物线的对称轴是直线x=3,即①正确;由于⊙D的半径为5,所以它的面积为25π,所以②不正确;过C作CF∥AD,则F(6,0),此时CF=6>5=AD,因此在抛物线上不可能存在点E,使四边形ACED为平行四边形,故③错误;当x=0时,y=-4,所以C点的坐标为(0,-4),因此DC=42+32=5,即C在⊙D上,又M(3,-254),所以DM=254,CM=32+⎝⎛⎭⎫254-42=154所以DC2+CM2=62516=DM2,所以DC⊥CM,所以直线CM与⊙D相切,故④正确;综上,有两项正确,故选B.3.(2018江苏苏州,18,3分)如图,已知AB=8,P为线段AB上的一个动点,分别以AP,PB为边在AB的同侧作菱形APCD和菱形PBFE,点P,C,E在一条直线上,∠DAP=60°.M,N分别是对角线AC,BE 的中点.当点P在线段AB上移动时,点M,N之问的距离最短为(结果保留根号).【答案】23【解析】本题解答时要连接MP,PN,利用菱形的性质,得出△PMN为直角三角形,然后利用勾股定理,求出用PA的长来表示的MN的长,最后利用二次函数的性质求出MN的最小值.连接PM,PN,∵四边形APCD,PBFE是菱形,∴P A=PC,∵AM=MC,∴PM⊥AC,同理PN⊥BE.∴∠CPM+∠CPN=119022APC BPE∠+∠=゜,∵∠DAP=60゜,∴∠CAP==∠NPB=30゜,xyOACMBDE设AP =x ,则PB =8-x , ∴PM =12x ,PN)x -∴=∴当x =6时,MN有最小值,最小值为三、解答题1. (2018广西柳州市,26,10分)如图,抛物线y =ax 2+bx +c 与x 轴交于0),B 两点(点B 在点A 的左侧),与y 轴交于点C ,且OB =3OAOC ,∠OAC 的平分线AD 交y 轴于点D ,过点A 且垂直于AD 的直线l 交y 轴于点E ,点P 是x 轴下方抛物线的一个动点,过点P 作PF ⊥x 轴垂足为F ,交直线AD 于点H. (1)求抛物线的解析式;(2)设点P 的横坐标为m ,当FH =HP 时,求m 的值;(3)当直线PF 为抛物线的对称轴时,以点H 为圆心,12HC 为半径作⊙H ,点Q 为⊙H 上的一个动点,求14AQ +EQ 的最小值.【思路分析】(1)根据题意,先求出点B 、C 的坐标,运用待定系数求出抛物线的解析式; (2)用点m 表示出FH 和PF 的长,再由FH =HP 列关于m 的方程求解;FAP(3)连接AH ,以AH 为边构造相似三角形,将14AQ 转化为某一个固定点的线段,再由三点共线计算出14AQ +EQ 的最小值. 【解题过程】(1)∵OB =3OA =OC ,0),∴点B 、C 的坐标分别为(-,0),(-3,0).设抛物线的解析式为y =a (x +x ),代入点C 的坐标,得:-3=a ··(,解得:a =13.故该抛物线的解析式为y =13(x +)(x =13x 2x -3. ………………3分(2)在Rt △AOC 中,由tan ∠OAC =OCOA,∴∠OAC =60°.又∵AH 是∠FAC 的平分线,∴∠FAH =30°,则AF由点P 的横坐标为m ,则它的纵坐标为13m 2-3.∴AF m ,PF =3-13m 2.∴FH AF m ). ∵FH =HP ,则PF =2FH ,m )=13m 2-3.解得:m 舍去)或m故m ………………6分 (3)连接CH.∵AF =AC =,∠FAH =∠CAH ,AF =AF , ∴△AHF ≌△AHC(SAS), ∴FH =CH =2. 故⊙H 的半径为1.在HA 上截取HM =14,则AM =4-14=154. ∵HM HQ =14,HQ HA =14, ∴HM HQ =HQHA,且∠QHM =∠AHQ , ∴△QHM ∽△AHQ ,∴AQMQ=14,则14AQ=MQ,∴14AQ+QE=QM+QE. ………………9分∵点E、M是定点,故当点M、Q、E共线时,QM+QE的值最小,即最小值为线段ME的长.在Rt△AEM中,由勾股定理可知:ME………………10分2.(2018海南省,24,15分)如图12-1,抛物线32++=bxaxy交x轴于点A(﹣1,0)和点B(3,0).(1)求该抛物线所对应的函数解析式;(2)如图12-2,该抛物线与y轴交于点C,顶点为F,点D(2,3)在该抛物线上.①求四边形ACFD的面积;②点P是线段AB上的动点(点P不与点A,B重合),过点P作PQ⊥x轴交该抛物线于点Q,连接AQ,DQ,当△AQD是直角三角形时,求出所有满足条件的点Q的坐标.【思路分析】将A(﹣1,0)和点B(3,0)代入32++=bxaxy,求解关于a,b的二元一次方程组即可;(2)①分别求出点C、F的坐标,S四边形ACFD=S△CDF+S△CDA;②当∠ADQ=90°时,如图24-2,设PQ交CD于点G,则PQ⊥CD,G点坐标为(t,3),作DH⊥x轴于H,则H(2,0),在Rt∠DHA中,DH=AH=3,∠DGQ为等腰三角形,GQ =GD ,()t t t -=-++-23322,求得t 的值并验证;当∠AQD =90°时,过点D 作DK ⊥PQ 于点K ,易证得∠PQA ∽△KDQ , KQ PA KD PQ =,()323123222++--+=-++-t t t t t t ,求得t 的值并验证. 【解题过程】(1)将A (﹣1,0)和点B (3,0)代入32++=bx ax y 得,⎩⎨⎧=++=+-033903b a b a ,解得⎩⎨⎧=-=21b a ,∴该抛物线的解析式为322++-=x x y .(2)①连接CD ,∵()413222+--=++-=x x x y ,F (1,4),当x =0时,y =3,∠C (0,3)又D (2,3),∠CD ∥x 轴,且CD =2,S 四边形ACFD =S △CDF +S △CDA =21CD ·(A F y y -)=44221=⨯⨯. ②设P (t ,0),则Q (t ,322++-t t ).Ⅰ:若∠DAQ =90°,如图24-1,此时点Q 必在第四象限,所对应的点P 在AB 的延长线上,此种情况不符合题意,故舍去.Ⅱ:若∠ADQ =90°,如图24-2,设PQ 交CD 于点G ,则PQ ⊥CD ,G 点坐标为(t ,3),作DH ⊥x 轴于H ,则H(2,0),∴在Rt∠DHA 中,DH =AH =3,∠∠DAH =45°,又CD ∥x 轴,∠∠ADC =∠DAH =45°,∠∠QDG =∠ADQ﹣∠ADC =45°,∠∠DGQ 为等腰三角形,∴GQ =GD ,()t t t -=-++-23322,整理得:0232=+-t t ,解得:11=t ,22=t ,当t=2时,D 与Q 重合,故舍去.当t =1时,4322=++-t t ,∠Q (1,4). Ⅲ:若∠AQD =90°,如图24-3过点D 作DK ⊥PQ 于点K ,∠∠APQ =∠QKD =90°,∠∠DQK +∠PQA =90°,又∠DQK +∠KDQ =90°,∴∠PQA =∠KDQ ,∠∠PQA ∽△KDQ ,∴KQ PA KD PQ =,∴()323123222++--+=-++-t t t t t t ,∴()()()21213-+=-+--t t t t t t ,∵1-≠t ,2≠t (即Q 不与A 、D 重合),∴()tt 13=--,整理得:0132=+-t t ,解得2531+=t ,2532-=t ,经验证,1t 、2t 均符合题意,其中:321<<t ,符合图24-3的情况,212<<-t ,符合图24-4的情况. 当2531+=t 时,255322-=++-t t ;当2532-=t 时,255322+=++-t t , ∴Q (253+,255-)或(253-,255+). 综上所述,当∠AQD 为直角三角形时,点Q 坐标为:(1,4)或(253+,255-)或(253-,255+). 【知识点】二次函数综合题,二次函数图象上点的存在性,相似三角形的性质与判定3. (2018黑龙江省龙东地区,23,6分) 如图,抛物线y =x 2+bx +c 与y 轴交于点A (0,2),对称轴为直线x =-2,平行于x 轴的直线与抛物线交于B 、C 两点,点B 在对称轴左侧,BC =6. (1)求此抛物线的解析式;(2)点P 在x 轴上,直线CP 将△ABC 面积分成2:3的两部分,请直接写出P 点坐标.【思路分析】对于(1),根据点A 坐标可求c 的值,根据对称轴直线可求b 的值;对于(2),先确定点C 和点B 的坐标,计算出△ABC 的面积,再根据直线CP 分△ABC 面积之比确定点P 存在的可能性有两种,结合两种情况,分别确定点P 的位置即可. 【解题过程】解:(1)∵点A (0,2)在抛物线y =x 2+bx +c 上,∴c =2,∵抛物线对称轴为直线x =-2,∴221b-=-⨯,∴b =4,∴抛物线的解析式为y =x 2+4x +2. (2)点P 的坐标为(-5,0)或(-13,0),理由如下:∵抛物线对称轴为直线x =-2,BC ∥x 轴,且BC =6,∴点C 的横坐标为6÷2-2=1,把x =1代入y =x 2+4x +2得y =7,∴C (1,7),∴△ABC 中BC 边上的高为7-2=5,∴S △ABC =12×6×5=15.令y =7,得x 2+4x +2=7,解得x 1=1,x 2=-5,∴B (-5,7),∴AB=CP 交AB 于点Q ,∵直线CP 将△ABC 面积分成2:3的两部分,∴符合题意的点P 有两个,对应的点Q 也有两个.①当AQ 1:BQ 1=2:3时,作Q 1M 1⊥y 轴,Q 1N 1⊥BC ,则AQ 1=Q 1M 1=2,BQ 1=Q 1N 1=3,Q 1(-2,4),∵C (1,7),∴直线CQ 1的解析式为y =x +5,令y =0,则x =-5,∴P 1(-5,0); ②当BQ 2:AQ 2=2:3时,作Q 2M 2⊥y 轴,Q 2N 2⊥BC ,则AQ 2=Q 2M 2=3,BQ 2=,Q 2N 2=2,Q 2(-3,5),∵C (1,7),∴直线CQ 2的解析式为y =12x +132,令y =0,则x =-13,∴P 2(-13,0) 综上,点P 的坐标为(-5,0)或(-13,0).【知识点】待定系数法;二次函数的性质;一次函数的性质;三角形的面积公式;平行线分线段成比例25.4. (2018山东省东营市,25,12分) 如图,抛物线13()()y a x x =--(0a >)与x 轴交于A 、B 两P 的坐解得:x 1=1,x 2=3则A (1,0),B (3,0)于是OA =1,OB =3∵△OCA ∽△OBC ∴OC ∶OB =OA ∶OC ∴OC 2=OA •OB =3即OC =(2)因为C 是BM 的中点 ∴OC =BC 从而点C 的横坐标为23又OC =,点C 在x 轴下方∴C ),(2323-设直线BM 的解析式为y =kx +b , 因其过点B (3,0),C ),(2323-,则有⎪⎩⎪⎨⎧-=+=+.232303b k b k ,∴, ∴ 又点C 在抛物线上,代入抛物线解析式,P 作PQ x 轴交直线BM 于点Q , 则Q (x ,),PQ = 当△BCP 面积最大时,四边形ABPC 的面积最大33=k 333-=x y ),(2323-32333-x 33333322-+-x x )()(△2321321-+-=x PQ x PQ S BCP )(23321-+-=x x PQ PQ 43=∴当时,有最大值,四边形ABPC 的面积最大, 此时点P 的坐标为(3)点P 存在. 设点P 坐标为(x ,),过点P 作PQ x 轴交直线BM 于点Q , 则Q (x ,),PQ = 当△BCP 面积最大时,四边形ABPC 的面积最大∴当时,有最大值,四边形ABPC 的面积最大, 此时点P 的坐标为43943923 2-+-=x x 492=-=a b x BCP S △)385-,49(323383322+-x x 333-x 33333322-+-x x )()(△2321321-+-=x PQ x PQ S BCP )(23321-+-=x x PQ PQ 43=43943923 2-+-=x x 492=-=a b x BCP S △)385-,49(【知识点】一元二次方程与二次函数的关系,中点坐标公式,相似三角形性质,待定系数法求直线与抛物线的解5. (2018四川乐山,1,3) 在平面直角坐标系中,抛物线2y ax bx c =++交x 轴于A 、B 两点,交y 轴于点C(0,43-),OA =1,OB =4,直线l 过点A ,交y 轴于点D ,交抛物线于点E ,且满足tan ∠OAD =34. (1)求抛物线的解析式;(2)动点P 从点B 出发,沿x 轴正方向以每秒2个单位长度的速度向点A 运动,动点Q 从点A 出发,沿射线AE 以每秒1个单位长度的速度向点E 运动,当点P 运动到点A 时,点Q 也停止运动,设运动为t 秒. ①在P 、Q 的运动过程中,是否存在某一时刻t ,使得△ADC 与△PQA 相似,若存在,求出t 的值;若不存在,请说明理由;②在P 、Q 的运动过程中,是否存在某一时刻t ,使得△APQ 与△CAQ 的面积之和最大?若存在,求出t 的值;若不存在,请说明理由.【思路分析】本题是代数几何综合题,以平面直角坐标系为背景,考查了求二次函数解析式,二次函数的性质,,方程组的解法,几何图形面积的表示,相似三角形的判定与性质,分类讨论思想,三角形的面积的最值问题,综合性强,难度大,解题的关键是需要学生有良好的运算能力及分析问题和解决问题的能力,还得富有耐心.(1)利用A 、B 、C 三点的坐标确定二次函数的解析式.(2)利用题目的已知条件表示出相关线段的长,①中利用三角函数值探索出∠P AQ =∠ACD ,再根据题目中的要求使得△ADC 与△PQA 相似,进行分类讨论得到对应线段成xyQ PEDCBAOyxQMC BA O P(第25题答案图2)比例,列出关于t 的方程求解即可;②直接利用三角形的面积公式列出△APQ 与△CAQ 的面积之和与时间t 之间的函数关系式,再将所得的二次函数的解析式配方确定最值即可得到答案. 【解题过程】解:(1)∵OA =1,OB =4,∴A (1,0),B (-4,0), -------------------- 1分 设所示抛物线的解析式为()()41y a x x =+-, ∵C (0,43-)在抛物线上, ∴()4413a -=⨯⨯-, 解得13a =, ∴抛物线的解析式为()()1413y x x =+-或21433y x x =+- ----------------------------- 3分 (2)存在t ,使得△ADC 与△PQA 相似,其理由如下: ①在Rt △AOC 中,OA =1,43OC =, 则3tan 4OA ACO OC ∠==, 又∵3tan 4OAD ∠=, ∴∠OAD =∠ACO , ------------------------------------------------------------------------------------- 4分 ∵直线l 的解析式为()314y x =- ,∴D (0,34-), 又∵C (0,43-), ∴CD =4373412-= 由AC 2=OC 2+OA 2,得53AC =. ---------------------------------------------------------------------- 5分 在△AQP 中,AP =AB -PB =5-2t ,AQ =t , 由∠P AQ =∠ACD ,要使△ADC 与△PQA 相似,只需AP CD AQ AC =或AP ACAQ CD=, ------------------------------------------------------------------- 6分 则有7521253t t -=或5523712t t -=, ----------------------------------------------------------------- 7分 解得110047t =,23534t =, ∵t 1<2.5,t 2<2.5, ∴存在10047t =或3534t =, 使得△APQ 与△PQA 相似 -------------------------------------- 9分 ②存在t ,使得△APQ 与△CAQ 的面积之和最大,其理由如下:作PF ⊥AQ 于点F ,CN ⊥AQ 于点N , 如图6所示,在△APF 中,()3sin 525PF AP PAF t =⋅∠=-, 在△AOD 中,由AD 2=OD 2+OA 2,得54AD =------------------------------------------------- 10分 在△ADC 中,由1122ADC S AD CN CD OA ∆=⋅=⋅, ∴717125154CD OA CN AD ⨯⋅=== ------------------------------------------------------------------- 11分∴()()11375222515APQ CAQS S AQ PF CN t t ∆∆⎡⎤+=+=-+⎢⎥⎣⎦231316959135t ⎛⎫=--+ ⎪⎝⎭ ∴当139t =时,△APQ 与△CAQ 的面积之和最大. ------------------------------------------- 12分图6【知识点】二次函数 ;勾股定理;三角形相似的判定与性质;三角形面积;待定系数法;转化思想;数形结合思想;分类讨论思想6.(2018甘肃省兰州市,28,12分)如图,抛物线42-+=bx ax y 经过A (-3,0),B (5,-4)两点,与y 轴交于点C ,连接AB ,AC ,BC .(1)求抛物线的表达式; (2)求证:AB 平分CAO ∠;(3)抛物线的对称轴上是否存在点M ,使得ABM ∆是以AB 为直角边的直角三角形.若存在,求出点M 的坐标;若不存在,说明理由.【思路分析】(1)根据A ,B 两点的坐标利用待定系数法求解即可.(2)通过证明点B 到直线AC 的距离等于点B 到x 轴的距离即可证明结论.(3)分AM 为该直角边的斜边和BM 为该直角三角形的斜边两种情况,分别计算即可.【解题过程】(1)将A ,B 两点的坐标分别代入42-+=bx ax y ,得⎩⎨⎧-=-+=--,44525,0439b a b a 解得⎪⎪⎩⎪⎪⎨⎧-==,65,61b a故抛物线的表达式为y =465612--=x x y . xyN F Q PED CBAOACBxyO第28题图(2)证明:设直线AB 的表达式为y =kx +b ′,则3'0,5'4,k b k b -+=⎧⎨+=-⎩解得⎪⎪⎩⎪⎪⎨⎧-=-=,23',21b k 故直线AB 的表达式为y =2321--x .设直线AB 与y 轴的交点为点D ,则点D 的坐标为(0,23-).易得点C 的坐标为(0,-4),则由勾股定理,可得AC =5)04(]30[22=--+--)(. 设点B 到直线AC 的距离为h , 则52132121⨯⨯+⨯⨯=⨯CD CD AC h , 解得h =4.易得点B 到x 轴的距离为4, 故AB 平分∠CAO . (3)存在.易得抛物线的对称轴为直线25=x , 设点M 的坐标为(m ,25).由勾股定理,得AB 2=[5-(-3)]2+(-4-0)2=80,AM 2=[25-(-3)]2+(m -0)2=4121+m 2,BM 2=(25-5)2+[m -(-4)]2=m 2+8m +489. 当AM 为该直角三角形的斜边时, 有AM 2=AB 2+BM 2,即4121+m 2=80+m 2+8m +489, 解得m =-9,故此时点M 的坐标为(25,-9).当BM 为该直角三角形的斜边时, 有BM 2=AB 2+AM 2,即m 2+8m +489=80+4121+m 2, 解得m =11,故此时点M 的坐标为(25,11). 综上所述,点M 的坐标为(25,-9)或(25,11). 【知识点】二次函数的图象和性质 角平分线的判定与性质 勾股定理 分类讨论7. (2018黑龙江省齐齐哈尔市,题号24,分值14)如图1所示,直线y=x+c 与x 轴交于点A (-4,0),与y 轴交于点C ,抛物线y=-x ²+bx+c 经过点A ,C. (1)求抛物线的解析式;(2)点E 在抛物线的对称轴上,求CE+OE 的最小值;(3)如图2所示,M 是线段OA 上的一个动点,过点M 垂直于x 轴的直线与直线AC 和抛物线分别交于点P 、N.①若以C ,P ,N 为顶点的三角形与△APM 相似,则△CPN 的面积为_________;②若点P 恰好是线段MN 的中点,点F 是直线AC 上一个动点,在坐标平面内是否存在点D ,使以点D ,F ,P ,M 为顶点的四边形是菱形?若存在,请直接写出点D 的坐标;若不存在,请说明理由.注:二次函数y=ax ²+bx+c (a ≠0)的顶点坐标为(24,24b ac b aa --)【思路分析】(1)根据一次函数求出c 的值,再将A (-4,0)和c 值代入抛物线解析式求得b 值,进而得出抛物线解析式;(2)先作对称确定最小值的情况,进而求出答案.(3)①根据直角与对顶角找出两种相似的情况,进而得出△CPN 的面积;②根据菱形的判定定理作出菱形,进而得出D 点坐标. 【解题过程】解:(1)将A (-4,0)代入y=x+c ,得c=4.将A (-4,0)和c=4代入y=-x²+bx+c,得b=-3. ∴抛物线的解析式为y=-x ²-3x+4.(2)如图所示,作点C 关于抛物线的对称轴直线l 的对称点C ’,连接OC 交直线l 于点E ,连接CE ,此时CE+OE 的值最小.∵抛物线额对称轴为x=332(1)2--=-⨯-,则C ’C=3,在Rt △C ’CO 中,由勾股定理,得OC ’22(')CC OC +∴CE+OE 的最小值为5.(3)①∵抛物线解析式为y=-x ²-3x+4,∴A (-4,0),B (1,0),C (0,4),△APM 为等腰直角三角形. 设M 为(a ,0),则N (a ,-a ²-3a+4),P(a ,a+4).当△AMP ∽△CNP 时,则AM MP CN NP=,得24434(4)a a a a a a ++=---+-+,解得a=-4(舍)或a=-3或a=0(舍). ∴CN=3,PN=3. ∴△CPN 的面积为12CN PN =92. 当△AMP∽△NCP时,则AM APNC NP=,得22222(4)34(4)(344)()a a a a a a a +=--+-+--+-+-,解得a=0(舍)或a=-2.∴.∴△CPN 的面积为12CN PC =4. 故答案为92或4.②存在. 1D (22-+,2),2D (22--,-2), 3D (-4,3),4D (12,32). 理由如下:当点P 是线段MN 的中点,则-a ²-3a+4=2(a+4), 解得a=-4(舍),或a=-1. ∴M (-1,0),P (-1,3),N (-1,6).设F(f ,f+4),过点M 作AC 的平行线,则此直线的解析式为 y=x+1.∵PM=3,当PM 为菱形的边时,作PF=PM ,过F 作FD 平行PM ,交AC 平行线于点D , ∴D (f ,f+1).∴3²=2(f+1)²,解得f=22-±.则1D 2D ). ∵PM=AM=3,∴当点F 与点A 重合时,过点F 在x 轴上方作DF ∥PM ,且DF=PM ,连接DP ,可得出四边形DPMF 为菱形.∴点D 的坐标为(-4,3).当PM 为菱形的对角线时,作PM 的垂直平分线,交直线AC 于点F ,作点F 关于PM 的对称点D ,连接MF,MD,PD,此时四边形DMFP 为菱形. ∴将32代入直线AC 的解析式可得,点F 的坐标为(-52,32). ∵直线PM 为x=-1, ∴点D 的坐标为(12,32).综上所述, 1D (22-+,2),2D (22--,-2), 3D (-4,3),4D (12,32).【知识点】待定系数法,二次函数图象的性质,两点之间线段最短,对称图形的性质,勾股定理.8. (2018湖北省江汉油田潜江天门仙桃市,26,12分)抛物线y =137322-+-x x 与x 轴交于点A ,B (点A 在点B 的左侧),与y 轴交于点C ,其顶点为D .将抛物线位于直线l :y =t (2524t <)上方的部分沿直线l 向下翻折,抛物线剩余部分与翻折后所得图形组成一个“M ”形的新图象.(1)点A ,B ,D 的坐标分别为 , , ;(2)如图①,抛物线翻折后,点D 落在点E 处.当点E 在△ABC 内(含边界)时,求t 的取值范围;(3)如图②,当t =0时,若Q 是“M ”形新图象上一动点,是否存在以CQ 为直径的圆与x 轴相切于点P ?若存在,求出点P 的坐标;若不存在,请说明理由.【思路分析】(1)点A ,B 的坐标可以令y =0,解一元二次方程求出,点D 的坐标利用公式可求;(2)点E 可能在边界上也可能在边界内,∴要分情况讨论;(3)点Q 可能在原抛物线上也可能在翻折下来的部分抛物线上,∴要分情况讨论.要证明点Q 在圆上,只需证明QA 与QB 垂直即可. 【解题过程】(1)令y =137322-+-x x =0,解得x 1=21,x 1=3.∴A (21,0),B (3,0).根据抛物线顶点公式可得D (47,2425). 3分 (2)如图①,作直线DE ,交x 轴于点M ,交BC 于点N . ∵直线BC 经过B (3,0),C (0,-1)两点, ∴直线BC 的解析式为:y =31x -1. 又∵抛物线对称轴DE 为:x =47, ∴点N 的坐标为(47,-125). 4分 讨论:①当点D 与点M 重合时,此时点E 落在x 轴上的点M 处,图①lE yA B O D C· ·图②第25题图O ACBxy· D x∴t =21DM =21×2425=4825. 5分 ②当点D 与点N 重合时,此时点E 落在BC 边上的点N 处. ∵DN =DM +MN =丨2425丨+丨-125丨=2435. ∴21DN =4835>MN . ∴t =21DN -MN =4835-125=165. ∴t 的取值范围是:165≤t ≤4825. 7分(3)存在以CQ 为直径的圆与x 轴相切于点P .如图②,设以CQ 为直径的⊙G 与x 轴相切于点P ,连接PC ,PG ,PQ . 并作QH ⊥x 轴于点H ,则GC =GP =GQ ,且GP ⊥x 轴. ∴OC ∥PG ∥HQ .∴OP =PH . ∵CQ 为直径,∴∠CPQ =90°. ∴∠OPC =∠HQP . ∵tan ∠OPC =OPOC ,tan ∠HQP =HQ HP.∴OPOC =HQ HP. 即OC ·HQ =OP ·HP . 9分 讨论:①当点Q 在抛物线y =137322-+-x x 上时, 依题意有x ≤21或x >3. 设点Q 的坐标为(x ,137322-+-x x ). 第25题答图①lE yA B O DC· ·x则OH =|x |,HQ =|137322-+-x x |,OP =PH =21|x |.∵OC =1,∴|137322-+-x x |=21|x |·21|x |,即|137322-+-x x |=41x 2.∵点Q 位于x 轴下方,∴137322-+-x x ≤0.∴137322-+-x x =-41x 2.解得x 1=534214+,x 2=534214-. 10分 ②当点Q 在抛物线y =137322+-x x 上时,依题意有21<x ≤3.同理可得:|137322+-x x |=41x 2.∵点Q 位于x 轴下方,∴137322+-x x =-41x 2.解得x 3=116,x 4=2. 11分 ∴满足条件的x 的值有x 1=534214+,x 2=534214-,x 3=116,x 4=2. ∵OP =21OH =21|x |, ∴符合条件的点P 的坐标有4个,即: P 1(5347+,0),P 2(5347-,0),P 3(113,0),P 4(1,0). 12分【知识点】二次函数压轴题,存在性问题第25题答图②O ACBxy· D PQG9.(湖北省咸宁市,24,12)如图,直线343+-=x y 与x 轴交于点A ,与y 轴交于点B ,抛物线c bx x y ++-=283。
2018届中考数学二轮复习第19课时《抛物线中的一个动点问题》

第19课时 抛物线中的一个动点问题分层集训(40 分)1. (20分)[2017酒泉]如图6-3- 1,已知二次函数y =ax 2 + bx +4的图象与x 轴交于点B( — 2, 0),点 C(8, 0),与y 轴交于点A.2(1) 求二次函数y = ax + bx + 4的表达式;⑵连结AC , AB ,若点N 在线段BC 上运动(不与点B ,C 重合),过点N 作NM // AC ,交AB 于点M ,当△ AMN 面积最大时,求 N 点的坐标;⑶连结OM ,在⑵的结论下,求OM 与AC 的数量关系.【解析】(1)用待定系数法,将点B ,点C 的坐标分别代入y = ax 2 + bx + 4, 解得a , b ,即可求出二次函数的表达式;⑵设点N 的坐标为(n , 0)( — 2v n v 8),贝U BN = n + 2, CN = 8— n.由题意可 知,BC = 10, OA =4, S^BC = 20, S ZABN = 2(n + 2),因 MN // AC ,根据平行AM NC 8— n线分线段成比例定理可得A B = BC=~W ,由A AMN , △ABN 是同高三角形,S ZAMN AM CN 8— n可得出 ---- =Ag = CB =「^,从而得出△ AMN 的面积S 与n 的二次函数关S ZABN系式,根据二次函数的顶点性质,即可求出当 n = 3时,即N(3, 0)时,△AMN 的面积最大;⑶当N(3, 0)时,N 为BC 边中点,由NM // AC 推出M 为AB 边中点,根据直 1角三角形中线定理可得 OM = ?AB ,利用勾股定理,易得 AB = 2环5, AC =A4 5,即可求出OM = "AC.B 7~\o ~> eV图 6 — 3— 14a—2b + 4= 0, 解:(1)将点B,点C的坐标分别代入y= ax2+ bx+ 4,得丫64a + 8b+ 4= 0,1 3解得a= —4, b = 31 3•••该二次函数的表达式为y= —4X2+ 2x+4;⑵设点N的坐标为(n, 0)( —2v n v8);则BN= n+ 2, CN= 8—n.VB(—2, 0), C(8, O),:BC= 10.令x= 0,得y=4,「.A(0, 4), OA= 4,AM NC 8 —n•••MN //AC,:AB = BC= 10 .1••OA=4, BC= 10,「S/ABC=2BC OA= 20.1 1S ZABN= 2BN OA= 2(n+ 2) X 4 = 2(n + 2),S ZAMN AM 8 —nS Z ABN = AB= 1081yS/ABN = |(8 —n)( n+ 2)= —5( n —3)2+ 5.•当门=3时,即N(3, 0)时,Z AMN的面积最大;⑶当N(3, 0)时,N为BC边中点.• M为AB边中点,•••OM = |A B,V AB= 'OB2+ OA2= 4+ 16 = 2,5,AC= OC2+ OA2= '64 + 16 = 4.5,•••AB = ^ACJQM = 4A C.2. (20 分)[2016 贵港]如图6 —3 —2,抛物线y= ax2+ bx—5@工0)与x轴交于点A( —5, 0)和点B(3, 0),与y轴交于点C.•'•S ZAMN =(1)求该抛物线的表达式;⑵若E为X轴下方抛物线上的一动点,当ABE= S A ABC时,求点E的坐标;⑶在(2)的条件下,抛物线上是否存在点P,使/ BAP=Z CAE?若存在,求出点P的横坐标;若不存在,请说明理由.解:(1)把A, B两点坐标代入表达式,可得1 2•••抛物线的表达式为y= 3X2+ 3X —5;1 2 2⑵在y= 3X + 3X— 5 中,令x= 0,可得y= —5,•••点C坐标为(0,—5),••SzABE= SzABC,且点E在X轴下方,• ••点E纵坐标和点C纵坐标相同,1 2 2当y= —5时,代入可得3X + 3X—5= —5,解得x= —2或x= 0(舍去),•••点E坐标为(—2,—5);⑶假设存在满足条件的P点,其坐标为m, 3m2+ |m—5 ,如答图,连结AP, CE, AE,过点E作ED± AC于点D,过点P作PQ丄x轴于点Q,则AQ= AO+ OQ = 5+ m,1 2 2PQ= 3m + 3m—5 ,在Rt A AOC 中,OA= OC = 5,Lu V125a —5b—5=0,9a + 3b —5 = 解得13,b=2,第2题答图a=则AC= 5 2, / ACO=Z DCE= 45 °由⑵可得EC= 2,在Rt A EDC中,可得DE = DC = 2, • AD = AC—DC = 5 2— 2 = 4 2,当 / BAP = / CAE 时,则△ EDA s^ PQA, 1 2 2 1 215 当3m + 3m — 5= 4(5 + m )时,整理可得 4m + 5m — 75= 0,解得 m =^或 m = —5(与点A 重合,舍去),1 2 2 1 29 当3m + §m — 5= — 4(5 + m )时,整理可得 4m + 11m —45= 0,解得 m =4或 m=—5(与点A 重合,舍去),9 15二存在满足条件的点P ,其横坐标为4或才•(40 分)3. (20分)[2016南宁]如图6— 3— 3,已知抛物线经过原 点O ,顶点为A(1, 1),且与直线y = x — 2交于B , C 两点.(2) 求证:△ ABC 是直角三角形;⑶若N 为x 轴上的一个动点,过点 N 作MN 丄x 轴与 抛物线交于点M ,则是否存在以O , M , N 为顶点的三角形与△ ABC 相似?若存在,请求出点N 的坐标;若不存在,请说明理由. 【解析】(1):顶点坐标为(1, 1), 二设抛物线表达式为y = a(x — 1)2+1,又•••抛物线过原点,••• 0= a(0— 1)2+ 1,解得a =— 1, 二抛物线的表达式为y = — (x — 1)2 +1,即y = — x 2 + 2x ,rAED =AQ ,即 4:1 2 23m +3m —5••• 3m2+3m — 5= 4(5 + m )或 23m — 5=—*5 + m ),(1)求抛物线的表达式及点C 的坐标;图 6 — 3 — 3联立抛物线和直线表达式,可得y = — x + 2x , x = 2, x =— 1, ( 解得丫 或S y= x — 2, y= 0 y= — 3,0), C( —1,— 3);⑵证明:如答图,分别过 A , C 两点作x 轴的垂线,交x 轴于D , E 两点, 则 AD = OD = BD = 1, BE = 0B + OE = 2+ 1= 3, EC = 3.•••/ ABO =Z CBO = 45° 即/ ABC = 90°•••△ ABC 是直角三角形;⑶假设存在满足条件的点N ,设N(x , 0),则M(x ,2小、—x + 2x),•••0N = |x|, MN = | — x 2 + 2x|,由⑵在Rt △ ABD 和Rt A CEB 中,可分别求得 AB = ,2, BC = 3,2, ••• MN 丄 x 轴于点 N , •••/ABC=Z MNO = 90°•••当△ ABC »△ MNO 相似时有 MN = OB 或MN = ON1即|x| | — x + 2|= §|x|,•••当x = 0时M , O , N 不能构成三角形,二X M01 1• -|—x + 2|=3,即—x + 2= ^3,5 7解得 X 1 = 3, X 2= 3,此时点N 坐标为3, 0或7, 0 ;①当 MN AB =器时,则有. 2 ,[—x + 2x| =凶 2 = 3,2, ②当 MN CB =器时,则有 . 2 ,[—x+ 2x| = jx]_ 第3题答图即|x| | —x+ 2|= 3xi,--1 —x+ 2| = 3,即一x+ 2=±3,解得x= 5或—1,此时点N坐标为(一1, 0)或(5, 0),综上可知,存在满足条件的点N,其坐标为3, o或7, 0或(—1, 0)或(5,0)・4. (20分)[2017泸州]如图6 —3 —4,已知二次函数y= ax2+ bx+ c(a^0)的图象经过A(—1, 0), B(4, 0), C(0, 2)三点.(1)求该二次函数的表达式;⑵点D是该二次函数图象上的一点,且满足/ DBA=Z CAO(O是坐标原点),求点D的坐标;(3) 点P是该二次函数图象上位于第一象限内的一个动点,连结FA分别交BC, y轴于点E, F,若△ PEB,A CEF的面积分别为S1, ◎,求Si —S2的最大值.【解析】(1)根据待定系数法求解;⑵设直线BD与y轴的交点为M(0, t).根据tan /MBA = tan /CAO列关于t的方程求解t,从而可确定直线BD表达式,再求直线BD与抛物线交点坐标即可,注意分类讨论;⑶过点P作PH // y轴交直线BC于点H,设P(t, at2+ bt+ c),根据直线BC 表达式点H的坐标,计算线段PH长度;用t表示直线AP表达式,解出点E,F坐标从而可表示出线段CF,将S1 —S2用t表示,根据二次函数性质求最值.解:(1)设抛物线的表达式为y= a(x+ 1)(x—4),••抛物线图象过点C(0, 2),1•••—4a = 2,解得a=—勺.1•抛物线的表达式为y= —2(x+ 1)(x—4),1 2 3即y= —2x + 2x+ 2;⑵设直线BD与y轴的交点为M(0, t).CAO,:d MBA =/ CAO,•'•tanZMBA = tan /CAO = 2,—^ = 2,即卩t = ±当t= 8时,直线BD表达式为y= —2x+ 8.2x +8,X1 = 4, X2 = 3,联立 1 2 3解得y= —2x + 2x+ 2, y i = 0; y2 = 2.•••D(3, 2).当t= —8时,直线BD表达式为y= 2x—8.+ 2x —8, 联立 1 2 3[y= —2x +2x+2,x i = 4, x2= —5,解得.9(—5,—18).y= 0;y2= —18.综上:点D的坐标为(3, 2)或(—5,—18);⑶如答图,过点P 作PH // y 轴交直线BC 于点H ,(13、1 t ,— 2t +2 ,直线BC 的表达式为y =—-r 1 x + 2,贝U H t ,— ?t + 2 ,1 2 • - PH = y p — y H = — 2t + 2t ;1 1 —2t +2 (x + 1),取 x = 0,得 y = 2—2t ;1 1直线AP 的表达式为y =1故 F 0, 2—2 , CF =2— 2—2 = 2; 2t y = 联立2 2-2(x +" t 解得X E = , 尸-2x + 2, 5 — tS2 !•丄 — 2 5—t • c 1( 12「J ;—丄 1 t t 52 5( 8 2 16…Sl — S2 = 2 — 2t + 2t . 5 — t 厂 212 5—t 一 4t + 4x =— 4j —5.丿 + "5 .8 i6二当t =5时,S i — S 2有最大值,最大值为 号.5. (20分)[2016金华]在平面直角坐标系中,0为原点,平行于x 轴的直线与抛物线L : y = ax 2相交于A , B 两点(点B 在第一象限),点D 在AB 的延长线上. (1)已知a = 1,点B 的纵坐标为2.① 如图6 — 3 — 5①,向右平移抛物线L 使该抛物线过点B ,与AB 的延长线交 于点C ,求AC 的长;1② 如图②,若BD = 2AB ,过点B ,D 的抛物线L 2,其顶点M 在x 轴上,求该 抛物线的函数表达式;⑵如图③,若BD = AB ,过O , B , D 三点的抛物线L 3的顶点为P ,对应函数的二次项系数为a 3,过点P 作PE // x 轴交抛物线L 于E , F 两点,求号的值, aC 组(20分)二 S i = 2(y p —y H )(x B —X )•••AB = 2 2.X2= —』2,•••平移得到的抛物线L i经过点B,:BC = AB = 2.2, .••AC = 4,2;②如答图①,记抛物线L2的对称轴与AD相交于点N.根据抛物线的轴对称性,得BN= 推=#3^2•••0M =方・设抛物线L2的函数表达式为y= a2 -x—务2 .I 2丿由①得,点B的坐标为(2, 2),•••2 = a2 • 2—,解得a2 = 4.•••抛物线L2的函数表达式为y=4 x—③孕丫;即y= 4x2—12 ,2x+ 18.① ②第5题答图⑵如答图②,设抛物线L a与x轴交于点G,其对称轴与x轴交于点Q,过点B作BK丄x轴于点K.设OK= t,则AB= BD = 2t,点 B 的坐标为(t, at2),根据抛物线的轴对称性,得OQ = 2t, OG = 2OQ= 4t.设抛物线L3的函数表达式为y= a3x(x —4t),2 2•••该抛物线过点B(t, at),:at = a3t(t—4t),又•••0, a3 1 • _ ______ ■ 'a =—3,9 9 9由题意得,点P的坐标为(2t,—4a3t),则一4a3t = ax ,.AB_ 逸• EF= 2 .。
中考压轴题专项训练1——抛物线专题(带答案解析)
中考压轴题专项训练1——抛物线专题考点分析:命题预测:函数是数形结合的重要体现,是每年中考的必考内容,函数的概念主要用选择、填空的形式考查自变量的取值范围,及自变量与因变量的变化图像、平面直角坐标系等,一般占2%左右.一次函数与一次方程有紧密地联系,是中考必考内容,一般以填空、选择、解答题及综合题的形式考查,占5%左右.反比例函数的图像和性质的考查常以客观题形式出现,要关注反比例函数与实际问题的联系,突出应用价值,3—6分;二次函数是初中数学的一个十分重要的内容,是中考的热点,多以压轴题出现在试卷中.要求:能通过对实际问题情景分析确定二次函数的表达式,并体会二次函数的意义;会用描点法画二次函数图像,能丛图像上分析二次函数的性质;会根据公式确定图像的顶点、开口方向和对称轴,并能解决复杂的图形综合问题。
二次函数常考点汇总:1. 两点间的距离公式:22)()(AB B A B A x x y y -+-=2. 中点坐标公式:已知A ),(A A y x ,B ),(B B y x ,则线段AB 的中点C 的坐标为⎪⎭⎫⎝⎛++2,2B A B A y y x x 。
3. 在平面直角坐标系中求面积的方法:公式法、割补法(做铅垂高或水平宽) 4. 几何分析法:特别是构造“平行四边形”、“梯形”、“相似三角形”、“直角三角形”、“等腰三角形”等图形时,利用几何分析法能给解题带来方便。
例题精讲:1.如图,直线y=﹣x+c与x轴交于点A(3,0),与y轴交于点B,抛物线y=﹣x2+bx+c 经过点A,B.(1)求点B的坐标和抛物线的解析式;(2)M(m,0)为x轴上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P,N.①点M在线段OA上运动,若以B,P,N为顶点的三角形与△APM相似,求点M的坐标;②点M在x轴上自由运动,若三个点M,P,N中恰有一点是其它两点所连线段的中点(三点重合除外),则称M,P,N三点为“共谐点”.请直接写出使得M,P,N三点成为“共谐点”的m的值.2.如图①,抛物线y=﹣x2+(a+1)x﹣a与x轴交于A,B两点(点A位于点B的左侧),与y轴交于点C.已知△ABC的面积是6.(1)求a的值;(2)求△ABC外接圆圆心的坐标;(3)如图②,P是抛物线上一点,Q为射线CA上一点,且P、Q两点均在第三象限内,Q、A是位于直线BP同侧的不同两点,若点P到x轴的距离为d,△QPB的面积为2d,且∠P AQ=∠AQB,求点Q的坐标.3.已知,在平面直角坐标系xoy 中,点A 的坐标为(0,2),点P (m ,n )是抛物线2114y x =+上的一个动点.(1)①如图1,过动点P 作PB ⊥x 轴,垂足为B ,连接PA ,求证:PA=PB ; ②如图2,设C 的坐标为(2,5),连接PC ,AP+PC 是否存在最小值?如果存在,求点P 的坐标;如果不存在,请说明理由;(2)如图3,过动点P 和原点O 作直线交抛物线于另一点D ,若AP=2AD ,求直线OP 的解析式.4.【变式】在平面直角坐标系xOy 中,抛物线21124y x =+的顶点为M ,直线2y x =,点()0P n ,为x 轴上的一个动点,过点P 作x 轴的垂线分别交抛物线21124y x =+和直线2y x =于点A ,点B.(1)直接写出A ,B 两点的坐标(用含n 的代数式表示);⑵设线段AB 的长为d ,求d 关于n 的函数关系式及d 的最小值,并直接写出此时线段OB 与线段PM 的位置关系和数量关系;(3) 已知二次函数2y ax bx c =++(a ,b ,c 为整数且0a ≠),对一切实数x 恒有x ≤y ≤2124x +,求a ,b ,c 的值.5.如图,已知二次函数()21y x m x m =+--(其中0<m <1)的图像与x 轴交于A 、B 两点(点A在点B 的左侧),与y 轴交于点C ,对称轴为直线l .设P 为对称轴l 上的点,连接P A 、PC ,P A =PC . (1)∠ABC 的度数为 °;(2)求P 点坐标(用含m 的代数式表示);(3)在坐标轴上是否存在点Q (与原点O 不重合),使得以Q 、B 、C 为顶点的三角形与△P AC 相似,且线段PQ 的长度最小?如果存在,求出所有满足条件的点Q 的坐标;如果不存在,请说明理由.6.(本题满分10分)如图,二次函数2y x bx c =++的图像与x 轴交于A 、B 两点,与y 轴交于点C ,C OB =O .点D 在函数图像上,CD//x 轴,且CD 2=,直线l 是抛物线的对称轴,E 是抛物线的顶点.(1)求b 、c 的值;(2)如图①,连接BE ,线段C O 上的点F 关于直线l 的对称点F '恰好在线段BE 上,求点F 的坐标; (3)如图②,动点P 在线段OB 上,过点P 作x 轴的垂线分别与C B 交于点M ,与抛物线交于点N .试问:抛物线上是否存在点Q ,使得Q ∆P N 与∆APM 的面积相等,且线段Q N 的长度最小?如果存在,求出点Q 的坐标;如果不存在,说明理由.7.(8分)如图,已知抛物线y=x2﹣4与x轴交于点A,B(点A位于点B的左侧),C 为顶点,直线y=x+m经过点A,与y轴交于点D.(1)求线段AD的长;(2)平移该抛物线得到一条新拋物线,设新抛物线的顶点为C′.若新抛物线经过点D,并且新抛物线的顶点和原抛物线的顶点的连线CC′平行于直线AD,求新抛物线对应的函数表达式.答案解析1.【解答】解:(1)∵y=﹣x+c与x轴交于点A(3,0),与y轴交于点B,∴0=﹣2+c,解得c=2,∴B(0,2),∵抛物线y=﹣x2+bx+c经过点A,B,∴,解得,∴抛物线解析式为y=﹣x2+x+2;(2)①由(1)可知直线解析式为y=﹣x+2,∵M(m,0)为x轴上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P,N,∴P(m,﹣m+2),N(m,﹣m2+m+2),∴PM=﹣m+2,AM=3﹣m,PN=﹣m2+m+2﹣(﹣m+2)=﹣m2+4m,∵△BPN和△APM相似,且∠BPN=∠APM,∴∠BNP=∠AMP=90°或∠NBP=∠AMP=90°,当∠BNP=90°时,则有BN⊥MN,∴N点的纵坐标为2,∴﹣m2+m+2=2,解得m=0(舍去)或m=2.5,∴M(2.5,0);当∠NBP=90°时,过点N作NC⊥y轴于点C,则∠NBC+∠BNC=90°,NC=m,BC=﹣m2+m+2﹣2=﹣m2+m,∵∠NBP=90°,∴∠NBC+∠ABO=90°,∴∠ABO=∠BNC,∴Rt△NCB∽Rt△BOA,∴=,∴=,解得m=0(舍去)或m=,∴M(,0);综上可知当以B,P,N为顶点的三角形与△APM相似时,点M的坐标为(2.5,0)或(,0);②由①可知M(m,0),P(m,﹣m+2),N(m,﹣m2+m+2),∵M,P,N三点为“共谐点”,∴有P为线段MN的中点、M为线段PN的中点或N为线段PM的中点,当P为线段MN的中点时,则有2(﹣m+2)=﹣m2+m+2,解得m=3(三点重合,舍去)或m=;当M为线段PN的中点时,则有﹣m+2+(﹣m2+m+2)=0,解得m=3(舍去)或m=﹣1;当N为线段PM的中点时,则有﹣m+2=2(﹣m2+m+2),解得m=3(舍去)或m=﹣;综上可知当M,P,N三点成为“共谐点”时m的值为或﹣1或﹣.2.【解答】解:(1)∵y=﹣x2+(a+1)x﹣a令y=0,即﹣x2+(a+1)x﹣a=0解得x1=a,x2=1由图象知:a<0∴A(a,0),B(1,0)∵s△ABC=6∴解得:a=﹣3,(a=4舍去)(2)设直线AC:y=kx+b,由A(﹣3,0),C(0,3),可得﹣3k+b=0,且b=3∴k=1即直线AC:y=x+3,A、C的中点D坐标为(﹣,)∴线段AC的垂直平分线解析式为:y=﹣x,线段AB的垂直平分线为x=﹣1代入y=﹣x,解得:y=1∴△ABC外接圆圆心的坐标(﹣1,1)(3)作PM⊥x轴,则=∵∴A、Q到PB的距离相等,∴AQ∥PB设直线PB解析式为:y=x+b∵直线经过点B(1,0)所以:直线PB的解析式为y=x﹣1联立解得:∴点P坐标为(﹣4,﹣5)又∵∠P AQ=∠AQB可得:△PBQ≌△ABP(AAS)∴PQ=AB=4设Q(m,m+3)由PQ=4得:解得:m=﹣4,m=﹣8(当m=﹣8时,∠P AQ≠∠AQB,故应舍去)∴Q坐标为(﹣4,﹣1)3.【解答】解:(1)①设P(m,n)∴n=m2+1,∵PB⊥x 轴,∴PB=m2+1,∵A(0,2)∴AP==m2+1,∴PB=PA;②过点P作PB⊥x轴于B,由(1)得PA=PB,所以要使AP+CP最小,只需当BP+CP最小,因此当C,P,B共线时取得,此时点P的横坐标等于点C(2,5)的横坐标,所以点P的坐标为(2,2),(2)如图,作DE⊥x轴于E,作PF⊥x轴于F,由(1)得:DA=DE,PA=PF∵PA=2DA,∴PF=2DE,∵△ODE∽△OPF,∴==,设P(m,m2+1),则D(m,m2+)∵点D在抛物线y=x2+1上,∴m2+=(m)2+1,解得m=±2,∴P 1(,3),直线OP 的解析式为y=x , P 2(﹣,3)直线OP 的解析式为y=﹣x , 综上所求,所求直线OP 的解析式为y=x 或y=﹣x .4.【解答】解:(1)21(2)4A n n +,,()B n n ,. (2) d =AB=A B y y -=2124n n -+.∴ d =2112()48n -+=2112()48n -+.∴ 当14n =时,d 取得最小值18. 当d 取最小值时,线段OB 与线段PM 的位置 关系和数量关系是OB ⊥PM 且OB=PM. (如图)(3) ∵对一切实数x 恒有 x ≤y ≤2124x +, ∴对一切实数x ,x ≤2ax bx c ++≤2124x +都成立. (0a ≠) ①当0x =时,①式化为 0≤c ≤14.xy111APBMO∴整数c 的值为0.此时,对一切实数x ,x ≤2ax bx +≤2124x +都成立.(0a ≠) 即 222,12.4x ax bx ax bx x ⎧≤+⎪⎨+≤+⎪⎩ 对一切实数x 均成立. 由②得 ()21ax b x +-≥0 (0a ≠) 对一切实数x 均成立.∴()210,10.a b >⎧⎪⎨∆=-≤⎪⎩ 由⑤得整数b 的值为1.此时由③式得,2ax x +≤2124x +对一切实数x 均成立. (0a ≠) 即21(2)4a x x --+≥0对一切实数x 均成立. (0a ≠) 当a=2时,此不等式化为14x -+≥0,不满足对一切实数x 均成立.当a≠2时,∵ 21(2)4a x x --+≥0对一切实数x 均成立,(0a ≠)∴2220,1(1)4(2)0.4a a ->⎧⎪⎨∆=--⨯-⨯≤⎪⎩∴由④,⑥,⑦得 0 <a ≤1.∴整数a 的值为1.∴整数a ,b ,c 的值分别为1a =,1b =,0c =.5.【解答】解:(1)45.理由如下:令x =0,则y =-m ,C 点坐标为(0,-m ).令y =0,则()210x m x m +--=,解得11x =-,2x m =. ∵0<m <1,点A 在点B 的左侧,∴B 点坐标为(m ,0).∴OB =OC =m .∵∠BOC =90°,∴△BOC 是等腰直角三角形,∠OBC =45°. (2)如图①,作PD ⊥y 轴,垂足为D ,设l 与x 轴交于点E ,由题意得,抛物线的对称轴为12mx -+=. 设点P 坐标为(12m-+,n ). ∵P A = PC , ∴P A 2= PC 2,即AE 2+ PE 2=CD 2+ PD 2.∴()222211122m m n n m -+-⎛⎫⎛⎫++=++ ⎪ ⎪⎝⎭⎝⎭.解得12m n -=.∴P 点的坐标为11,22m m -+-⎛⎫⎪⎝⎭. ④⑤② ③ ⑥ ⑦图①图②(3)存在点Q 满足题意.∵P 点的坐标为11,22m m -+-⎛⎫⎪⎝⎭, ∴P A 2+ PC 2=AE 2+ PE 2+CD 2+ PD 2=222221111112222m m m m m m -+---⎛⎫⎛⎫⎛⎫⎛⎫+++++=+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭. ∵AC 2=21m +,∴P A 2+ PC 2=AC 2.∴∠APC =90°. ∴△P AC 是等腰直角三角形.∵以Q 、B 、C 为顶点的三角形与△P AC 相似, ∴△QBC 是等腰直角三角形.∴由题意知满足条件的点Q 的坐标为(-m ,0)或(0,m ). ①如图①,当Q 点的坐标为(-m ,0)时,若PQ 与x 轴垂直,则12m m -+=-,解得13m =,PQ =13. 若PQ 与x 轴不垂直, 则22222221151521222222510m m PQ PE EQ m m m m --+⎛⎫⎛⎫⎛⎫=+=++=-+=-+ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭. ∵0<m <1,∴当25m =时,2PQ 取得最小值110,PQ .<13, ∴当25m =,即Q 点的坐标为(25-,0)时, PQ 的长度最小.②如图②,当Q 点的坐标为(0,m )时,若PQ 与y 轴垂直,则12m m -=,解得13m =,PQ =13. 若PQ 与y 轴不垂直, 则22222221151521222222510m m PQ PD DQ m m m m --⎛⎫⎛⎫⎛⎫=+=+-=-+=-+ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭. ∵0<m <1,∴当25m =时,2PQ 取得最小值110,PQ .<13, ∴当25m =,即Q 点的坐标为(0,25)时, PQ 的长度最小.综上:当Q 点坐标为(25-,0)或(0,25)时,PQ 的长度最小.6. 【解答】解:(1).3)(03,20.0,c -),,0(,.2,12.1x 2CD x //2-=∴=-=++=∴∴=-==-∴=∴=c c c c c c B c C OC OB b bl CD ,舍去或解得)点坐标为(:抛物线对称轴为直线,轴,(2)设点F 坐标为(0,m ).∵对称轴是直线,1:=x l ∴点F 关于直线l 的对称点’F 的坐标为(2,m ). ∵直线BE 经过点B (3,0),E (1,-4),∴利用待定系数法可得直线BE 的表达式为y=2x-6. ∵点’F 在BE 上,∴m=2⨯2-6=-2,即点F 的坐标为(0,-2). (3)存在点Q 满足题意。
(中考数学)动点问题专题训练(含答案)
中考专题训练 动点问题例1. 如图, 在ABC ∆中,AB AC =,AD BC ⊥于点D ,10BC cm =,8AD cm =. 点P 从点B 出发, 在线段BC 上以每秒3cm 的速度向点C 匀速运动, 与此同时, 垂直于AD 的直线m 从底边BC 出发, 以每秒2cm 的速度沿DA 方向匀速平移, 分别交AB 、AC 、AD 于E 、F 、H ,当点P 到达点C 时, 点P 与直线m 同时停止运动, 设运动时间为t 秒(0)t >.(1) 当2t =时, 连接DE 、DF ,求证: 四边形AEDF 为菱形;(2) 在整个运动过程中, 所形成的PEF ∆的面积存在最大值, 当PEF ∆的面积最大时, 求线段BP 的长;(3) 是否存在某一时刻t ,使PEF ∆为直角三角形?若存在, 请求出此时刻t 的值;若不存在, 请说明理由 .【解答】(1) 证明: 当2t =时,4DH AH ==,则H 为AD 的中点, 如答图 1 所示 . 又EF AD ⊥ ,EF ∴为AD 的垂直平分线,AE DE ∴=,AF DF =.AB AC = ,AD BC ⊥于点D ,AD BC ∴⊥,B C ∠=∠.//EF BC ∴,AEF B ∴∠=∠,AFE C ∠=∠,AEF AFE ∴∠=∠,AE AF ∴=,AE AF DE DF ∴===,即四边形AEDF 为菱形 .(2) 解: 如答图 2 所示, 由 (1) 知//EF BC ,AEF ABC ∴∆∆∽, ∴EF AH BC AD =,即82108EF t -=,解得:5102EF t =-. 221155510(10)210(2)10(0)222223PEF S EF DH t t t t t t ∆==-=-+=--+<< , ∴当2t =秒时,PEF S ∆存在最大值, 最大值为210cm ,此时36BP t cm ==.(3) 解: 存在 . 理由如下:①若点E 为直角顶点, 如答图 3①所示,此时//PE AD ,2PE DH t ==,3BP t =.//PE AD ,∴PE BP AD BD =,即2385t t =,此比例式不成立, 故此种情形不存在; ②若点F 为直角顶点如答图 3②所示,此时//PF AD ,2PF DH t ==,3BP t =,103CP t =-.//PF AD ,∴PF CP AD CD =,即210385t t -=,解得4017t =;③若点P 为直角顶点,如答图③所示 .过点E 作EM BC ⊥于点M ,过点F 作FN BC ⊥于点N ,则2EM FN DH t ===,////EM FN AD .//EM AD ,∴EM BM AD BD =,即285t BM =,解得54BM t =, 57344PM BP BM t t t ∴=-=-=. 在Rt EMP ∆中, 由勾股定理得:2222227113(2)()416PE EM PM t t t =+=+=. //FN AD ,∴FN CN AD CD =,即285t CN =,解得54CN t =, 5171031044PN BC BP CN t t t ∴=--=--=-. 在Rt FNP ∆中, 由勾股定理得:22222217353(2)(10)85100416PF FN PN t t t t =+=+-=-+. 在Rt PEF ∆中, 由勾股定理得:222EF PE PF =+, 即:2225113353(10)()(85100)21616t t t t -=+-+ 化简得:21833508t t -=, 解得:280183t =或0t =(舍 去) 280183t ∴=. 综上所述, 当4017t =秒或280183t =秒时,PEF ∆为直角三角形 .例2. 如图, 在同一平面上, 两块斜边相等的直角三角板Rt ABC ∆和Rt ADC ∆拼在一起,使斜边AC 完全重合, 且顶点B ,D 分别在AC 的两旁,90ABC ADC ∠=∠=︒,30CAD ∠=︒,4AB BC cm ==(1) 填空:AD = )cm ,DC = ()cm(2) 点M ,N 分别从A 点,C 点同时以每秒1cm 的速度等速出发, 且分别在AD ,CB 上沿A D →,C B →方向运动, 当N 点运动到B 点时,M 、N 两点同时停止运动, 连接MN ,求当M 、N 点运动了x 秒时, 点N 到AD 的距离 (用 含x 的式子表示)(3) 在 (2) 的条件下, 取DC 中点P ,连接MP ,NP ,设PMN ∆的面积为2()y cm ,在整个运动过程中,PMN ∆的面积y 存在最大值, 请求出y 的最大值 .(参考数据sin 75︒=sin15︒=【解答】解: (1)90ABC ∠=︒ ,4AB BC cm ==,AC ∴===,90ADC ∠=︒ ,30CAD ∠=︒,12DC AC ∴==,AD ∴==;故答案为:,;(2) 过点N 作NE AD ⊥于E ,作NF DC ⊥,交DC 的延长线于F ,如图所示:则NE DF =,90ABC ADC ∠=∠=︒ ,AB BC =,30CAD ∠=︒,45ACB ∴∠=︒,60ACD ∠=︒,180456075NCF ∴∠=︒-︒-︒=︒,15FNC ∠=︒,sinFC FNCNC ∠=,NC x=,FC x∴=,NE DF x∴==+,∴点N到ADx+;(3)sinFN NCFNC ∠=,FN x∴=,P为DC的中点,PD CP∴==PF x∴=PMN∴∆的面积y=梯形MDFN的面积PMD-∆的面积PNF-∆的面积111)) 222x x x x=+-+--+2x x=+,即y是x的二次函数,0<,y∴有最大值,当x==时,y=.例3. 如图,BD 是正方形ABCD 的对角线,2BC =,边BC 在其所在的直线上平移, 将通过平移得到的线段记为PQ ,连接PA 、QD ,并过点Q 作QO BD ⊥,垂足为O ,连接OA 、OP .(1) 请直接写出线段BC 在平移过程中, 四边形APQD 是什么四边形?(2) 请判断OA 、OP 之间的数量关系和位置关系, 并加以证明;(3) 在平移变换过程中, 设OPB y S ∆=,(02)BP x x =……,求y 与x 之间的函数关系式,并求出y 的最大值 .【解答】(1) 四边形APQD 为平行四边形;(2)OA OP =,OA OP ⊥,理由如下:四边形ABCD 是正方形,AB BC PQ ∴==,45ABO OBQ ∠=∠=︒,OQ BD ⊥ ,45PQO ∴∠=︒,45ABO OBQ PQO ∴∠=∠=∠=︒,OB OQ ∴=,在AOB ∆和OPQ ∆中,AB PQABO PQO BO QO=⎧⎪∠=∠⎨⎪=⎩()AOB POQ SAS ∴∆≅∆,OA OP ∴=,AOB POQ ∠=∠,90AOP BOQ ∴∠=∠=︒,OA OP ∴⊥;(3) 如图, 过O 作OE BC ⊥于E .①如图 1 ,当P 点在B 点右侧时,则2BQ x =+,22x OE +=, 1222x y x +∴=⨯,即211(1)44y x =+-, 又02x ……,∴当2x =时,y 有最大值为 2 ;②如图 2 ,当P 点在B 点左侧时,则2BQ x =-,22x OE -=, 1222x y x -∴=⨯ ,即211(1)44y x =--+, 又02x ……,∴当1x =时,y 有最大值为14; 综上所述,∴当2x =时,y 有最大值为 2 .例4. 如图, 在平面直角坐标系中,O 为原点, 四边形ABCO 是矩形, 点A ,C 的坐标分别是(0,2)A 和C ,0),点D 是对角线AC 上一动点 (不 与A ,C 重合) ,连结BD ,作DE DB ⊥,交x 轴于点E ,以线段DE ,DB 为邻边作矩形BDEF .(1) 填空: 点B 的坐标为 ;(2) 是否存在这样的点D ,使得DEC ∆是等腰三角形?若存在, 请求出AD 的长度;若不存在, 请说明理由;(3)①求证:DE DB =; ②设AD x =,矩形BDEF 的面积为y ,求y 关于x 的函数关系式 (可 利用①的结论) ,并求出y 的最小值 .【解答】解: (1) 四边形AOCB 是矩形,2BC OA ∴==,OC AB ==90BCO BAO ∠=∠=︒,B ∴2).故答案为2).(2) 存在 . 理由如下:2OA = ,OC =,tan AO ACO OC ∠== , 30ACO ∴∠=︒,60ACB ∠=︒①如图 1 中, 当E 在线段CO 上时,DEC ∆是等腰三角形, 观察图象可知, 只有ED EC =,30DCE EDC ∴∠=∠=︒,60DBC BCD ∴∠=∠=︒,DBC ∴∆是等边三角形,2DC BC ∴==,在Rt AOC ∆中,30ACO ∠=︒ ,2OA =,24AC AO ∴==,422AD AC CD ∴=-=-=.∴当2AD =时,DEC ∆是等腰三角形 .②如图 2 中, 当E 在OC 的延长线上时,DCE ∆是等腰三角形, 只有CD CE =,15DBC DEC CDE ∠=∠=∠=︒,75ABD ADB ∴∠=∠=︒,AB AD ∴==,综上所述, 满足条件的AD 的值为 2 或(3)①如图 1 ,过点D 作MN AB ⊥交AB 于M ,交OC 于N ,(0,2)A 和C ,0),∴直线AC 的解析式为2y x =+,设(,2)D a +,2DN ∴=+,BM a =90BDE ∠=︒ ,90BDM NDE ∴∠+∠=︒,90BDM DBM ∠+∠=︒,DBM EDN ∴∠=∠,90BMD DNE ∠=∠=︒ ,BMD DNE ∴∆∆∽,∴DE DN BD BM ===②如图 2 中, 作DH AB ⊥于H .在Rt ADH ∆中,AD x = ,30DAH ACO ∠=∠=︒,1122DH AD x ∴==,AH x ==,BH x ∴=, 在Rt BDH ∆中,BD ==,DE ∴==, ∴矩形BDEF的面积为22612)y x x ==-+,即2y x =-+,23)y x ∴=-+,0>,3x ∴=时,y .例5. 已知Rt OAB ∆,90OAB ∠=︒,30ABO ∠=︒,斜边4OB =,将Rt OAB ∆绕点O 顺时针旋转60︒,如图 1 ,连接BC .(1) 填空:OBC ∠= 60 ︒;(2) 如图 1 ,连接AC ,作OP AC ⊥,垂足为P ,求OP 的长度;(3) 如图 2 ,点M ,N 同时从点O 出发, 在OCB ∆边上运动,M 沿O C B →→路径匀速运动,N 沿O B C →→路径匀速运动, 当两点相遇时运动停止, 已知点M 的运动速度为 1.5 单位/秒, 点N 的运动速度为 1 单位/秒, 设运动时间为x 秒,OMN ∆的面积为y ,求当x 为何值时y 取得最大值?最大值为多少?【解答】解: (1) 由旋转性质可知:OB OC =,60BOC ∠=︒,OBC ∴∆是等边三角形,60OBC ∴∠=︒.故答案为 60 .(2) 如图 1 中,4OB = ,30ABO ∠=︒,122OA OB ∴==,AB ==11222AOC S OA AB ∆∴==⨯⨯=BOC ∆ 是等边三角形,60OBC ∴∠=︒,90ABC ABO OBC ∠=∠+∠=︒,AC ∴==2AOC S OP AC ∆∴===.(3)①当803x <…时,M 在OC 上运动,N 在OB 上运动,此时过点N 作NE OC ⊥且交OC 于点E .则sin 60NE ON x =︒= ,11 1.522OMN S OM NE x x ∆∴==⨯ ,2y x ∴=.83x ∴=时,y 有最大值, 最大值=. ②当843x <…时,M 在BC 上运动,N 在OB 上运动 .作MH OB ⊥于H . 则8 1.5BM x =-,sin 60 1.5)MH BM x =︒=- ,212y ON MH x ∴=⨯⨯=+.当83x =时,y 取最大值,y < ③当4 4.8x <…时,M 、N 都在BC 上运动, 作OG BC ⊥于G .12 2.5MN x =-,OG AB ==,12y MN OG ∴== ,当4x =时,y 有最大值, 最大值=,综上所述,y 有最大值, .。
2018届中考数学《第六讲第4课时抛物线中的两个动点问题》同步练习(word版含答案)
第4课时 抛物线中的两个动点问题(60分)1.(20分)[2017·凉山州]如图6-4-1,在平面直角坐标系中,抛物线y =ax 2+bx +c (a ≠0)与x 轴交于A ,B 两点,与y 轴交于点C ,且OA =2,OB =8,OC =6.(1)求抛物线的表达式;(2)点M 从A 点出发,在线段上AB 以每秒3个单位长度的速度向点B 运动,同时,点N 从B 出发,在线段BC 上以每秒1个单位长度的速度向点C 运动,当其中一个点到达终点时,另一个点也停止运动,当△MBN 存在时,求运动多少秒使△MBN 的面积最大,最大面积是多少?(3)在(2)的条件下,△MBN 面积最大时,在BC 上方的抛物线上是否存在点P ,使△BPC 的面积是△MBN 面积的9倍,若存在,求点P 的坐标,若不存在,请说明理由.【解析】 (1)由线段的长度得出点A ,B ,C 的坐标,然后把A ,B ,C 三点的坐标分别代入y =ax 2+bx +c ,解方程组即可得抛物线的表达式;(2)设运动时间为t s ,则MB =10-3t ,然后根据△BHN ∽△BOC ,求得NH =35t ,再利用三角形的面积公式列出S △MBN 与t 的函数关系式S △MBN =-910⎝ ⎛⎭⎪⎫t -532+52,利用二次函数的图象性质进行解答; (3)利用待定系数法求得直线BC 的表达式为y =-34x +6.由二次函数图象上点的坐标特征可设点P 的坐标为⎝ ⎛⎭⎪⎫m ,-38m 2+94m +6.过点P 作PE ∥y 轴,交BC 于点E .结合已知条件和(2)中的结果求得S △PBC =452.则根据图形得到S △PBC =S △CEP +S △BEP =12EP ·m +12·EP ·(8-m ),把相关线段的长度代入推知:-32m2+12m =452.易求得P ⎝ ⎛⎭⎪⎫3,758或⎝ ⎛⎭⎪⎫5,638.图6-4-1解:(1)∵OA =2,OB =8,OC =6,∴A (-2,0),B (8,0),C (0,6),根据题意,得⎩⎨⎧4a -2b +c =0,64a +8b +c =0,c =6,解得⎩⎪⎨⎪⎧a =-38,b =94,c =6,∴抛物线的表达式为y =-38x 2+94x +6;(2)设运动时间为t s ,则AM =3t ,BN =t .∴MB =10-3t .在Rt △BOC 中,BC =82+62=10. 如答图①,过点N 作NH ⊥AB 于点H ,∴NH ∥CO ,∴△BHN ∽△BOC ,∴HN OC =BN BC ,即HN 6=t 10,∴HN =35t .∴S △MBN =12MB ·HN=12(10-3t )·35t =-910⎝ ⎛⎭⎪⎫t -532+52,∴当t =53时,S △MBN 最大=52.答:运动53 s 时,△MBN 的面积最大,最大面积是52;(3)设直线BC 的表达式为y =kx +c (k ≠0).把B (8,0),C (0,6)代入,得⎩⎨⎧8k +c =0,c =6,解得⎩⎪⎨⎪⎧k =-34,c =6,∴直线BC 的表达式为y =-34x +6.∵点P 在抛物线上,图第1题答图①∴设点P 的坐标为⎝ ⎛⎭⎪⎫m ,-38m 2+94m +6, 如答图②,过点P 作PE ∥y 轴,交BC 于点E ,则E点的坐标为⎝ ⎛⎭⎪⎫m ,-34m +6, ∴EP =-38m 2+94m +6-⎝ ⎛⎭⎪⎫-34m +6=-38m 2+3m , 当△MBN 的面积最大时,S △PBC =9S △MBN =452,∴S △PBC =S △CEP +S △BEP =12EP ·m +12EP ·(8-m )=12×8·EP =4×⎝ ⎛⎭⎪⎫-38m 2+3m =-32m 2+12m , 即-32m 2+12m =452,解得m 1=3,m 2=5,∴P 点坐标为⎝ ⎛⎭⎪⎫3,758或⎝ ⎛⎭⎪⎫5,638. 2.(20分)[2017·内江]如图6-4-2,在平面直角坐标系中,抛物线y =ax 2+bx +c (a ≠0)与y 轴交于点C (0,3),与x 轴交于A ,B 两点,点B 坐标为(4,0),抛物线的对称轴方程为x =1.(1)求抛物线的表达式;(2)点M 从A 点出发,在线段AB 上以每秒3个单位长度的速度向B 点运动,同时点N 从B 点出发,在线段BC 上以每秒1个单位长度的速度向C 点运动,其中一个点到达终点时,另一个点也停止运动,设△MBN 的面积为S ,点M 运动时间为t ,试求S 与t的函数关系,并求S 的最大值;(3)在点M 运动过程中,是否存在某一时刻t ,使△MBN 为直角三角形?若存在,求出t 的值;若不存在,请说明理由.【解析】 (1)由点B 的坐标与对称轴可求得点A 的坐标,把点A ,B ,C 的坐标分别代入抛物线的表达式,列出关于系数a ,b ,c 的方程组,求解即可;(2)设运动时间为t s ,利用三角形的面积公式列出S △MBN 与t 的函数关系式,用配方法求得最大值;(3)根据余弦函数,可得关于t 的方程,解方程,可得答案,注意分类讨论. 解:(1)∵点B 坐标为(4,0),抛物线的对称轴方程为x =1,第1题答图②图6-4-2∴A (-2,0).把点A (-2,0),B (4,0),C (0,3),分别代入y =ax 2+bx +c (a ≠0),得⎩⎨⎧4a -2b +c =0,16a +4b +c =0,c =3.解得 ⎩⎪⎨⎪⎧a =-38,b =34,c =3,∴该抛物线的表达式为y =-38x 2+34x +3.'(2)设运动时间为t s ,则AM =3t ,BN =t ,∴MB =6-3t .在Rt △BOC 中,BC =32+42=5.如答图①,过点N 作NH ⊥AB 于点H , ∴NH ∥CO ,∴△BHN ∽△BOC ,∴HN OC =BN BC ,即HN 3=t 5,∴HN =35t .∴S △MBN =12MB ·HN =12(6-3t )·35t =-910t 2+95t =-910(t -1)2+910.当△MBN 存在时,0<t <2,∴当t =1时,S 最大=910.∴S 与t 的函数关系为S =-910(t -1)2+910,S 的最大值为910.① ②第2题答图(3)如答图②,在Rt △OBC 中,cos B =OB BC =45,设运动时间为t s ,则AM =3t ,BN =t .∴MB =6-3t .当∠MNB =90°时,cos B =BN BM =45,即t 6-3t =45,解得t =2417. 当∠BM ′N ′=90°时,cos B =6-3t t =45,解得t =3019.综上所述,当t =2417或3019时,△MBN 为直角三角形.3.(20分)[2017·山西]综合与探究如图6-4-3,抛物线y =-39x 2+233x +33与x 轴交于A ,B 两点(点A 在点B 的左侧),与y 轴交于点C ,连结AC ,BC .点P 沿AC 以每秒1个单位长度的速度由点A 向点C 运动,同时,点Q 沿BO 以每秒2个单位长度的速度由点B 向点O 运动,当一个点停止运动时,另一个点也随之停止运动,连结PQ ,过点Q 作QD ⊥x 轴,与抛物线交于点D ,与BC 交于点E .连结PD ,与BC 交于点F .设点P 的运动时间为t s(t >0).(1)求直线BC 的函数表达式;(2)①直接写出P ,D 两点的坐标(用含t 的代数式表示,结果需化简);②在点P ,Q 运动的过程中,当PQ =PD 时,求t 的值.(3)试探究在点P ,Q 运动的过程中,是否存在某一时刻,使得点F 为PD 的中点.若存在,请直接写出此时t 的值与点F 的坐标;若不存在,请说明理由.【解析】 (1)由函数与方程的关系得到点B ,C 的坐标,利用待定系数法求直线BC 的表达式;(2)①过点P 作x 轴的垂线段,构造与Rt △AOC 相似的直角三角形,利用相似的性质得到与点P 的横、纵坐标有关的线段的方程求解;由QD ⊥x 轴可知点D 与点Q 的横坐标相同,将点Q 的横坐标代入抛物线表达式便得点D 的纵坐标;②由等腰三角形的性质找到P ,D 两点纵坐标的关系建立方程求解;(3)假设存在点F 为PD 的中点,由中点的特征结合P ,D 两点的坐标表示出点F 的坐标,将其代入直线BC 建立方程求得t 的值,确定点F 的具体坐标.解:(1)由y =0,得-39x 2+233x +33=0,解得x 1=-3,x 2=9,∴点B 的坐标为(9,0),由x =0,得y =33,∴点C 的坐标为(0,33),设直线BC 的函数表达式为y =kx +b ,图6-4-3由B ,C 两点的坐标得⎩⎨⎧9k +b =0,b =33,解得⎩⎨⎧k =-33,b =33, ∴直线BC 的函数表达式为y =-33x +33;(2)①P ⎝ ⎛⎭⎪⎫t 2-3,32t ,D ⎝⎛⎭⎪⎫9-2t ,-439t 2+833t ; ②如答图,过点P 作PG ⊥x 轴于点G ,PH ⊥QD 于点H ,∵QD ⊥x 轴,∴四边形PGQH 是矩形,∴HQ =PG ,∵PQ =PD ,PH ⊥QD ,∴DQ =2HQ =2PG ,∵P ,D 两点的坐标分别为⎝ ⎛⎭⎪⎫t 2-3,32t ,⎝⎛⎭⎪⎫9-2t ,-439t 2+833t , ∴-439t 2+833t =2×32t ,解得t 1=0(舍去),t 2=154,∴当PQ =PD 时,t 的值为154;(3)t =3,F 点坐标为⎝ ⎛⎭⎪⎫34,1134. (20分)4.(20分)[2017·淮安]如图6-4-4①,在平面直角坐标系中,二次函数y =-13x 2+bx +c 的图象与坐标轴交于A ,B ,C 三点,其中点A 的坐标为(-3,0),点B 的坐标为(4,0),连结AC ,BC .动点P 从点A 出发,在线段AC 上以每秒1个单位长度的速度向点C 作匀速运动;同时,动点Q 从点O 出发,在线段OB 上以每秒1个单位长度的速度向点B作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为t s .连结PQ .(1)填空:b =__13__,c =__4__;(2)在点P ,Q 运动过程中,△APQ 可能是直角三角形吗?请说明理由;(3)在x 轴下方,该二次函数的图象上是否存在点M ,使△PQM 是以点P 为直角顶点的等腰直角三角形?若存在,请求出运动时间t ;若不存在,请说明理由;第3题答图(4)如图②,点N 的坐标为⎝ ⎛⎭⎪⎫-32,0,线段PQ 的中点为H ,连结NH ,当点Q 关于直线NH 的对称点Q ′恰好落在线段BC 上时,请直接写出点Q ′的坐标.图6-4-4【解析】 (1)将A (-3,0),B (4,0)代入y =13x 2+bx +c 即可求解; (2)若△APQ 为直角三角形,则∠APQ =90°(∠P AQ 与∠PQA 不可能为直角).连结QC ,则AQ 2-AP 2=QC 2-PC 2=PQ 2,据此列出关于t 的方程求解,若t 的值满足0≤t ≤4,则△APQ 可能是直角三角形,否则不可能;(3)①过点P 作DE ∥x 轴,分别过点M ,Q 作MD ⊥DE ,QE ⊥DE ,垂足分别为D ,E ,构成“一线三直角”全等模型,用含t 的式子表示点M 的坐标;②将点M 的坐标代入二次函数的表达式求解;(4)①分别求直线BC ,直线NQ ′的函数表达式;②解直线BC ,NQ ′的函数达式组成的方程组.解:(1)b =13,c =4;(2)在点P ,Q 运动过程中,△APQ 不可能是直角三角形.理由如下:如答图①,连结QC .若△APQ 是直角三角形,∵在点P ,Q 运动过程中,∠P AQ ,∠PQA 始终为锐角,∴∠APQ =90°.由(1)知抛物线的函数表达式为y =-13x 2+13x +4,当 =0时,y =4,∴C (0,4),∴OC =4.∵A (-3,0),∴OA =3.由题意,得AP =OQ =t .∴AQ =OA +OQ =3+t .在Rt △AOC 中,由勾股定理,得AC =OA 2+OC 2=32+42=5.∴PC =5-t .在Rt △OCQ 中,QC 2=OQ 2+OC 2=t 2+42.∵∠APQ =90°,∴AQ 2-AP 2=QC 2-PC 2=PQ 2.∴(3+t )2-t 2=t 2+42-(5-t )2,解得t =4.5.由题意知0≤t ≤4.∴t =4.5不符合题意,舍去.∴在点P ,Q 运动过程中,△APQ 不可能是直角三角形;第4题答图① 第4题答图②(3)如答图②,过点P 作DE ∥x 轴,分别过点M ,Q 作MD ⊥DE ,QE ⊥DE ,垂足分别为点D ,E ,MD 交x 轴于点F ,过点P 作PG ⊥x 轴,垂足为点G ,则PG ∥y 轴,∠D =∠E =90°.∴△APG ∽△ACO .∴PG OC =AG OA =AP AC ,即PG 4=AG 3=t 5.∴PG =45t ,AG =35t .∴PE =GQ =GO +OQ =AO -AG +OQ =3-35t +t =3+25t ,DF =PG =45t .∵∠MPQ =90°,∠D =90°,∴∠DMP +∠DPM =∠EPQ +∠DPM =90°.∴∠DMP =∠EPQ .又∵∠D =∠E ,PM =PQ ,∴△MDP ≌△PEQ .∴PD =EQ =45t ,MD =PE =3+25t .∴FM =MD -DF =3+25t -45t =3-25t ,OF =FG +GO =PD +OA -AG =45t +3-35t =3+15t .∴M ⎝ ⎛⎭⎪⎫-3-15t ,-3+25t . ∵点M 在x 轴下方的抛物线上,∴-3+25t =-13⎝ ⎛⎭⎪⎫-3-15t 2+13⎝ ⎛⎭⎪⎫-3-15t +4, 解得t =-65±52052. ∵0≤t ≤4,∴t =-65+52052.(4)Q ′⎝ ⎛⎭⎪⎫67,227. 提示:如答图③,连结OP ,取OP 中点R ,连结RH ,NR ,延长NR 交线段BC 于点Q ′.∵点H 为PQ 的中点,点R 为OP 的中点,∴RH =12OQ =12t ,RH ∥OQ .∵A (-3,0),N ⎝ ⎛⎭⎪⎫-32,0,∴点N 为OA 的中点. 又∵点R 为OP 的中点,∴NR =12AP =12t ,RN ∥AC .∴RH =NR ,∴∠RNH =∠RHN .∵RH ∥OQ ,∴∠RHN =∠HNO .∴∠RNH =∠HNO ,即NH 是∠QNQ ′的平分线.设直线AC 的函数表达式为y =mx +n ,把A (-3,0),C (0,4)代入,得⎩⎨⎧0=-3m +n ,4=n , 解得⎩⎪⎨⎪⎧m =43,n =4,∴直线AC 的函数表达式为y =43x +4.同理可求,直线BC 的函数表达式为y =-x +4.设直线NR 的函数表达式为y =43x +s ,把N ⎝ ⎛⎭⎪⎫-32,0代入,得0=43×⎝ ⎛⎭⎪⎫-32+s ,解得s =2.∴直线NR 的函数表达式为y =43x +2.解方程组⎩⎪⎨⎪⎧y =43x +2,y =-x +4,得⎩⎪⎨⎪⎧x =67,y =227,∴Q ′点坐标为⎝ ⎛⎭⎪⎫67,227. (20分)5.(20分)[2017·枣庄]如图6-4-5,抛物线y =-12x 2+bx +c 与x 轴交于点A 和点B ,与y 轴交于点C ,点B 坐标为(6,0),点C 坐标为(0,6),点D 是抛物线的顶点,过点D 作x 轴的垂线,垂足为E ,连结BD. 第4题答图③(1)求抛物线的表达式及点D 的坐标;(2)点F 是抛物线上的动点,当∠FBA =∠BDE 时,求点F 的坐标;(3)若点M 是抛物线上的动点,过点M 作MN ∥x 轴与抛物线交于点N ,点P 在x 轴上,点Q 在坐标平面内,以线段MN 为对角线作正方形MPNQ ,请写出点Q 的坐标.图6-4-5 备用图【解析】 (1)由点B ,C 的坐标利用待定系数法即可求出抛物线的表达式,再利用配方法将抛物线表达式变形成顶点式即可得出结论;(2)设线段BF 与y 轴交点为点F ′,设点F ′的坐标为(0,m ),由相似三角形的判定及性质可得出点F ′的坐标,根据点B ,F ′的坐标利用待定系数法可求出直线BF 的表达式,联立直线BF 和抛物线的表达式成方程组,解方程组即可求出点F 的坐标;(3)设对角线MN ,PQ 交于点O ′.根据抛物线的对称性结合正方形的性质可得出点P ,Q 的位置,设出点Q 的坐标为(2,2n ),由正方形的性质可得出点M 的坐标为(2-n ,n ).由点M 在抛物线图象上,即可得出关于n 的一元二次方程,解方程可求出n 值,代入点Q 的坐标即可得出结论.解:(1)将点B (6,0),C (0,6)代入y =-12x 2+bx +c ,得⎩⎨⎧0=-18+6b +c ,6=c ,解得⎩⎨⎧b =2,c =6, ∴抛物线的表达式为y =-12x 2+2x +6.∵y =-12x 2+2x +6=-12(x -2)2+8,∴点D 的坐标为(2,8).(2)设线段BF 与y 轴交点为点F ′,设点F ′的坐标为(0,m ),如答图①所示. ∵∠F ′BO =∠FBA =∠BDE ,∠F ′OB =∠BED =90°,∴△F ′BO ∽△BDE ,∴OF ′OB =BE DE .∵B (6,0),D (2,8),∴E (2,0),BE =6-2=4,DE =8-0=8,OB =6,∴OF ′=BE DE ·OB =3,∴F ′(0,3)或(0,-3). 设直线BF 的表达式为y =kx ±3,则有0=6k +3或0=6k -3,解得k =-12或k =12,∴直线BF 的表达式为y =-12x +3或y =12x -3.联立直线BF 与抛物线的表达式,得⎩⎪⎨⎪⎧y =-12x +3,y =-12x 2+2x +6,或⎩⎪⎨⎪⎧y =12x +3,y =-12x 2+2x +6,解得⎩⎪⎨⎪⎧x =-1,y =72, 或⎩⎨⎧x =6,y =0,(舍去),⎩⎪⎨⎪⎧x =-3,y =92, 或⎩⎨⎧x =6,y =0,(舍去), ∴点F 的坐标为⎝ ⎛⎭⎪⎫-1,72或⎝ ⎛⎭⎪⎫-3,-92. (3)设对角线MN ,PQ 交于点O ′,如答图②所示.∵点M ,N 关于抛物线对称轴对称,且四边形MPNQ 为正方形, ∴点P 为抛物线对称轴与x 轴的交点,点Q 在抛物线对称轴上,设点Q 的坐标为(2,2n ),则点M 的坐标为(2-n ,n ).∵点M 在抛物线y =-12x 2+2x +6的图象上,∴n =-12(2-n )2+2(2-n )+6,即n 2+2n -16=0,解得n 1=17-1,n 2=-17-1.∴点Q 的坐标为(2,217-2)或(2,-217-2).第5题答图①第5题答图②。
2018年中考压轴题汇编《因动点产生的等腰三角形问题》含答案
因动点产生的等腰三角形问题例年重庆市中考第题如图,在△中,=°,∠=°,点是∠的平分线上一点,过点作的垂线,过点作的垂线,两垂线交于点,连接,点是的中点,⊥,垂足为,连接,.()如图,若点是的中点,=,求、的长;()如图,求证:=.()如图,连接、,猜想:△是否是等边三角形?若是,请证明;若不是,请说明理由.图图例年长沙市中考第题如图,抛物线=++(、、是常数,≠)的对称轴为轴,且经过()和两点,点在该抛物线上运动,以点为圆心的⊙总经过定点(, ).()求、、的值;()求证:在点运动的过程中,⊙始终与轴相交;()设⊙与轴相交于(, )、(, )两点,当△为等腰三角形时,求圆心的纵坐标.图例年上海市虹口区中考模拟第题如图,在△中,∠=°,=,=,点为边的中点,⊥交边于点,点为射线上的一动点,点为边上的一动点,且∠=°.()求、的长;()若=,求的长;()记线段与线段的交点为,若△为等腰三角形,求的长.图备用图例年扬州市中考第题如图,抛物线=++经过(-)、(, )、( )三点,直线是抛物线的对称轴.()求抛物线的函数关系式;()设点是直线上的一个动点,当△的周长最小时,求点的坐标;()在直线上是否存在点,使△为等腰三角形,若存在,直接写出所有符合条件的点的坐标;若不存在,请说明理由.图例年临沂市中考第题如图,点在轴上,=,将线段绕点顺时针旋转°至的位置.()求点的坐标;()求经过、、的抛物线的解析式;()在此抛物线的对称轴上,是否存在点,使得以点、、为顶点的三角形是等腰三角形?若存在,求点的坐标;若不存在,请说明理由.图例年盐城市中考第题如图,已知一次函数=-+与正比例函数的图象交于点,且与轴交于点.()求点和点的坐标;()过点作⊥轴于点,过点作直线轴.动点从点出发,以每秒个单位长的速度,沿——的路线向点运动;同时直线从点出发,以相同速度向左平移,在平移过程中,直线交轴于点,交线段或线段于点.当点到达点时,点和直线都停止运动.在运动过程中,设动点运动的时间为秒.①当为何值时,以、、为顶点的三角形的面积为?②是否存在以、、为顶点的三角形是等腰三角形?若存在,求的值;若不存在,请说明理由.图因动点产生的等腰三角形问题答案例年重庆市中考第题如图,在△中,=°,∠=°,点是∠的平分线上一点,过点作的垂线,过点作的垂线,两垂线交于点,连接,点是的中点,⊥,垂足为,连接,.()如图,若点是的中点,=,求、的长;()如图,求证:=.()如图,连接、,猜想:△是否是等边三角形?若是,请证明;若不是,请说明理由.图图动感体验请打开几何画板文件名“重庆”,拖动点运动,可以体验到,△与△保持全等,△与△保持全等,△保持等边三角形的形状.思路点拨.把图形中所有°的角都标注出来,便于寻找等角和等边..中点有哪些用处呢?联想到斜边上的中线和中位线就有思路构造辅助线了.满分解答()如图,在△中,∠=°,=,所以=.在△中,∠=°,=,所以=,=.在△中,=,=,由勾股定理,得=.()如图,由∠=°,∠=°,平分∠,得∠=°,∠=°.在△中,=.在△中,=.所以=.因为点是△的斜边上的中线,所以=,∠=∠.所以∠=∠.所以△≌△.所以=.图图图()如图,作⊥于,联结.由,是的中点,得是的中点.因此=,△是等边三角形.又因为=,所以=.又因为=,∠=∠=°,所以△≌△.所以∠=∠,=.所以∠=∠=°.所以△是等边三角形.考点伸展我们再看几个特殊位置时的效果图,看看有没有熟悉的感觉.如图,如图,当点落在边上时,点与点重合.图图如图,图,点落在边上.如图,图,等腰梯形.图图图图例年长沙市中考第题如图,抛物线=++(、、是常数,≠)的对称轴为轴,且经过()和两点,点在该抛物线上运动,以点为圆心的⊙总经过定点(, ).()求、、的值;()求证:在点运动的过程中,⊙始终与轴相交;()设⊙与轴相交于(, )、(, )两点,当△为等腰三角形时,求圆心的纵坐标.图动感体验请打开几何画板文件名“长沙”,拖动圆心在抛物线上运动,可以体验到,圆与轴总是相交的,等腰三角形存在三种情况.思路点拨.不算不知道,一算真奇妙,原来⊙在轴上截得的弦长=是定值..等腰三角形存在三种情况,其中=和=两种情况时,点的纵坐标是相等的.满分解答()已知抛物线的顶点为(),所以=.所以=,=.将代入=,得.解得(舍去了负值).()抛物线的解析式为,设点的坐标为.已知(, ),所以>.而圆心到轴的距离为,所以半径>圆心到轴的距离.所以在点运动的过程中,⊙始终与轴相交.()如图,设的中点为,那么垂直平分.在△中,,,所以=.所以=.因此=,为定值.等腰△存在三种情况:①如图,当=时,点为原点重合,此时点的纵坐标为.图图②如图,当=时,在△中,=,=,所以=.此时==.所以点的纵坐标为.③如图,当=时,点的纵坐标为也为.图图考点伸展如果点在抛物线上运动,以点为圆心的⊙总经过定点(, ),那么在点运动的过程中,⊙始终与直线=-相切.这是因为:设点的坐标为.已知(, ),所以.而圆心到直线=-的距离也为,所以半径=圆心到直线=-的距离.所以在点运动的过程中,⊙始终与直线=-相切.例年上海市虹口区中考模拟第题如图,在△中,∠=°,=,=,点为边的中点,⊥交边于点,点为射线上的一动点,点为边上的一动点,且∠=°.()求、的长;()若=,求的长;()记线段与线段的交点为,若△为等腰三角形,求的长.图备用图动感体验请打开几何画板文件名“虹口”,拖动点在射线上运动,可以体验到,△与△保持相似.观察△,可以看到,、可以落在对边的垂直平分线上,不存在=的情况.请打开超级画板文件名“虹口”,拖动点在射线上运动,可以体验到,△与△保持相似.观察△,可以看到,、可以落在对边的垂直平分线上,不存在=的情况.思路点拨.第()题=分两种情况..解第()题时,画准确的示意图有利于理解题意,观察线段之间的和差关系..第()题探求等腰三角形时,根据相似三角形的传递性,转化为探求等腰三角形.满分解答()在△中,=,=,所以=.在△中,=,所以,.()如图,过点作⊥,⊥,垂足分别为、,那么、是△的两条中位线,=,=.由∠=°,∠=°,可得∠=∠.因此△∽△.所以.所以,.图图图①如图,当=,在上时,=.此时.所以.②如图,当=,在的延长线上时,=.此时.所以.()如图,如图,在△中,.在△中,.所以∠=∠.由∠=°,∠=°,可得∠=∠.因此△∽△.当△是等腰三角形时,△也是等腰三角形.①如图,当==时,=-=-=(如图所示).此时.所以.②如图,当=时,由,可得.所以=-=(如图所示).此时.所以.③不存在=的情况.这是因为∠≥∠>∠(如图,图所示).图图考点伸展如图,当△是等腰三角形时,根据等角的余角相等,可以得到△也是等腰三角形,=.在△中可以直接求解.例年扬州市中考第题如图,抛物线=++经过(-)、(, )、( )三点,直线是抛物线的对称轴.()求抛物线的函数关系式;()设点是直线上的一个动点,当△的周长最小时,求点的坐标;()在直线上是否存在点,使△为等腰三角形,若存在,直接写出所有符合条件的点的坐标;若不存在,请说明理由.图动感体验请打开几何画板文件名“扬州”,拖动点在抛物线的对称轴上运动,可以体验到,当点落在线段上时,+最小,△的周长最小.拖动点在抛物线的对称轴上运动,观察△的三个顶点与对边的垂直平分线的位置关系,可以看到,点有次机会落在的垂直平分线上;点有次机会落在的垂直平分线上;点有次机会落在的垂直平分线上,但是有次、、三点共线.思路点拨.第()题是典型的“牛喝水”问题,点在线段上时△的周长最小..第()题分三种情况列方程讨论等腰三角形的存在性.满分解答()因为抛物线与轴交于(-)、(, )两点,设=(+)(-),代入点( ),得-=.解得=-.所以抛物线的函数关系式是=-(+)(-)=-++.()如图,抛物线的对称轴是直线=.当点落在线段上时,+最小,△的周长最小.设抛物线的对称轴与轴的交点为.由,=,得==.所以点的坐标为(, ).图()点的坐标为(, )、(,)、(,)或().考点伸展第()题的解题过程是这样的:设点的坐标为().在△中,=,=+(-),=+.①如图,当=时,=.解方程+=+(-),得=.此时点的坐标为(, ).②如图,当=时,=.解方程+=,得.此时点的坐标为(,)或(,).③如图,当=时,=.解方程+(-)=,得=或.当(, )时,、、三点共线,所以此时符合条件的点的坐标为().图图图例年临沂市中考第题如图,点在轴上,=,将线段绕点顺时针旋转°至的位置.()求点的坐标;()求经过、、的抛物线的解析式;()在此抛物线的对称轴上,是否存在点,使得以点、、为顶点的三角形是等腰三角形?若存在,求点的坐标;若不存在,请说明理由.图动感体验请打开几何画板文件名“临沂”,拖动点在抛物线的对称轴上运动,可以体验到,⊙和⊙以及的垂直平分线与抛物线的对称轴有一个共同的交点,当点运动到⊙与对称轴的另一个交点时,、、三点共线.请打开超级画板文件名“临沂”,拖动点,发现存在点,使得以点、、为顶点的三角形是等腰三角形思路点拨.用代数法探求等腰三角形分三步:先分类,按腰相等分三种情况;再根据两点间的距离公式列方程;然后解方程并检验..本题中等腰三角形的角度特殊,三种情况的点重合在一起.满分解答()如图,过点作⊥轴,垂足为.在△中,∠=°,=,所以=,.所以点的坐标为.()因为抛物线与轴交于、(, ),设抛物线的解析式为=(-),代入点,.解得.所以抛物线的解析式为.()抛物线的对称轴是直线=,设点的坐标为(, ).①当==时,=.所以=.解得.当在时,、、三点共线(如图).②当==时,=.所以.解得.③当=时,=.所以.解得.综合①、②、③,点的坐标为,如图所示.图图考点伸展如图,在本题中,设抛物线的顶点为,那么△与△是两个相似的等腰三角形.由,得抛物线的顶点为.因此.所以∠=°,∠=°.例年盐城市中考第题如图,已知一次函数=-+与正比例函数的图象交于点,且与轴交于点.()求点和点的坐标;()过点作⊥轴于点,过点作直线轴.动点从点出发,以每秒个单位长的速度,沿——的路线向点运动;同时直线从点出发,以相同速度向左平移,在平移过程中,直线交轴于点,交线段或线段于点.当点到达点时,点和直线都停止运动.在运动过程中,设动点运动的时间为秒.①当为何值时,以、、为顶点的三角形的面积为?②是否存在以、、为顶点的三角形是等腰三角形?若存在,求的值;若不存在,请说明理由.图动感体验请打开几何画板文件名“盐城”,拖动点由向运动,从图象中可以看到,△的面积有一个时刻等于.观察△,可以体验到,在上时,只存在=的情况;在上时,有三个时刻,△是等腰三角形.思路点拨.把图复制若干个,在每一个图形中解决一个问题..求△的面积等于,按照点的位置分两种情况讨论.事实上,在上运动时,高是定值,最大面积为,因此不存在面积为的可能..讨论等腰三角形,按照点的位置分两种情况讨论,点的每一种位置又要讨论三种情况.满分解答()解方程组得所以点的坐标是(,).令,得.所以点的坐标是(,).()①如图,当在上运动时,≤<.由,得.整理,得.解得=或=(舍去).如图,当在上运动时,△的最大面积为.因此,当=时,以、、为顶点的三角形的面积为.图图图②我们先讨论在上运动时的情形,≤<.如图,在△中,∠=°,∠>°,=,,所以>.因此∠>∠>∠.如图,点由向运动的过程中,==,所以轴.因此∠=°保持不变,∠越来越大,所以只存在∠=∠的情况.此时点在的垂直平分线上,==.所以=,=.我们再来讨论在上运动时的情形,≤<.在△中,为定值,,.如图,当=时,解方程,得.如图,当=时,点在的垂直平分线上,=(-).解方程,得.如,当=时,那么.因此.解方程,得.综上所述,=或或或时,△是等腰三角形.图图图考点伸展当在上,=时,也可以用来求解.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第3课时 抛物线中的一个动点问题(40分)1.(20分)[2017·酒泉]如图6-3-1,已知二次函数y=ax 2+bx +4的图象与x 轴交于点B (-2,0),点C (8,0),与y 轴交于点A .(1)求二次函数y =ax 2+bx +4的表达式;(2)连结AC ,AB ,若点N 在线段BC 上运动(不与点B ,C 重合),过点N 作NM ∥AC ,交AB 于点M ,当△AMN 面积最大时,求N 点的坐标;(3)连结OM ,在(2)的结论下,求OM 与AC 的数量关系.【解析】 (1)用待定系数法,将点B ,点C 的坐标分别代入y =ax 2+bx +4,解得a ,b ,即可求出二次函数的表达式;(2)设点N 的坐标为(n ,0)(-2<n <8),则BN =n +2,CN =8-n .由题意可知,BC =10,OA =4,S △ABC =20,S △ABN =2(n +2),因MN ∥AC ,根据平行线分线段成比例定理可得AM AB =NC BC =8-n 10,由△AMN ,△ABN 是同高三角形,可得出S △AMN S △ABN =AM AB =CN CB=8-n 10,从而得出△AMN 的面积S 与n 的二次函数关系式,根据二次函数的顶点性质,即可求出当n =3时,即N (3,0)时,△AMN 的面积最大;(3)当N (3,0)时,N 为BC 边中点,由NM ∥AC 推出M 为AB 边中点,根据直角三角形中线定理可得OM =12AB ,利用勾股定理,易得AB =25,AC =45,即可求出OM =14AC .解:(1)将点B ,点C 的坐标分别代入y =ax 2+bx +4,得⎩⎨⎧4a -2b +4=0,64a +8b +4=0, 解得a =-14,b =32.∴该二次函数的表达式为y =-14x 2+32x +4;图6-3-1(2)设点N 的坐标为(n ,0)(-2<n <8);则BN =n +2,CN =8-n .∵B (-2,0),C (8,0),∴BC =10.令x =0,得y =4,∴A (0,4),OA =4,∵MN ∥AC ,∴AM AB =NC BC =8-n 10.∵OA =4,BC =10,∴S △ABC =12BC ·OA =20.S △ABN =12BN ·OA =12(n +2)×4=2(n +2),又∵S △AMN S △ABN =AM AB=8-n 10, ∴S △AMN =8-n 10S △ABN =15(8-n )(n +2)=-15(n -3)2+5.∴当n =3时,即N (3,0)时,△AMN 的面积最大;(3)当N (3,0)时,N 为BC 边中点.∴M 为AB 边中点,∴OM =12AB ,∵AB =OB 2+OA 2=4+16=25,AC =OC 2+OA 2=64+16=45,∴AB =12AC ,∴OM =14AC .2.(20分)[2016·贵港]如图6-3-2,抛物线y =ax 2+bx -5(a ≠0)与x 轴交于点A (-5,0)和点B (3,0),与y 轴交于点C .(1)求该抛物线的表达式;(2)若E 为x 轴下方抛物线上的一动点,当S △ABE =S △ABC时,求点E 的坐标; (3)在(2)的条件下,抛物线上是否存在点P ,使∠BAP =∠CAE ?若存在,求出点P 的横坐标;若不存在,请说明理由.解:(1)把A ,B 两点坐标代入表达式,可得⎩⎨⎧25a -5b -5=0,9a +3b -5=0,解得⎩⎪⎨⎪⎧a =13,b =23,图6-3-2∴抛物线的表达式为y =13x 2+23x -5;(2)在y =13x 2+23x -5中,令x =0,可得y =-5,∴点C 坐标为(0,-5),∵S △ABE =S △ABC ,且点E 在x 轴下方,∴点E 纵坐标和点C 纵坐标相同,当y =-5时,代入可得13x 2+23x -5=-5,解得x =-2或x =0(舍去),∴点E 坐标为(-2,-5);(3)假设存在满足条件的P 点,其坐标为⎝ ⎛⎭⎪⎫m ,13m 2+23m -5, 如答图,连结AP ,CE ,AE ,过点E 作ED ⊥AC 于点D ,过点P 作PQ ⊥x 轴于点Q ,则AQ =AO +OQ =5+m ,PQ =⎪⎪⎪⎪⎪⎪13m 2+23m -5, 在Rt △AOC 中,OA =OC =5,则AC =52,∠ACO =∠DCE =45°,由(2)可得EC =2,在Rt △EDC 中,可得DE =DC =2,∴AD =AC -DC =52-2=42,当∠BAP =∠CAE 时,则△EDA ∽△PQA ,∴ED AD =PQ AQ ,即242=⎪⎪⎪⎪⎪⎪13m 2+23m -55+m , ∴13m 2+23m -5=14(5+m )或13m 2+23m -5=-14(5+m ), 当13m 2+23m -5=14(5+m )时,整理可得4m 2+5m -75=0,解得m =154或m =-5(与点A 重合,舍去),当13m 2+23m -5=-14(5+m )时,整理可得4m 2+11m -45=0,解得m =94或m =-5(与点A 重合,舍去),第2题答图∴存在满足条件的点P,其横坐标为94或154.(40分)3.(20分)[2016·南宁]如图6-3-3,已知抛物线经过原点O,顶点为A(1,1),且与直线y=x-2交于B,C两点.(1)求抛物线的表达式及点C的坐标;(2)求证:△ABC是直角三角形;(3)若N为x轴上的一个动点,过点N作MN⊥x轴与抛物线交于点M,则是否存在以O,M,N为顶点的三角形与△ABC相似?若存在,请求出点N的坐标;若不存在,请说明理由.【解析】(1)∵顶点坐标为(1,1),∴设抛物线表达式为y=a(x-1)2+1,又∵抛物线过原点,∴0=a(0-1)2+1,解得a=-1,∴抛物线的表达式为y=-(x-1)2+1,即y=-x2+2x,联立抛物线和直线表达式,可得⎩⎨⎧y=-x2+2x,y=x-2,解得⎩⎨⎧x=2,y=0或⎩⎨⎧x=-1,y=-3,∴B(2,0),C(-1,-3);(2)证明:如答图,分别过A,C两点作x轴的垂线,交x轴于D,E两点,则AD=OD=BD=1,BE=OB+OE=2+1=3,EC=3.∴∠ABO=∠CBO=45°,即∠ABC=90°,∴△ABC是直角三角形;(3)假设存在满足条件的点N,设N(x,0),则M(x,-x2+2x),∴ON=|x|,MN=|-x2+2x|,由(2)在Rt△ABD和Rt△CEB中,可分别求得AB=2,BC=32,∵MN⊥x轴于点N,∴∠ABC=∠MNO=90°,图6-3-3第3题答图∴当△ABC 和△MNO 相似时有MN AB =ON CB 或MN CB =ON AB ,①当MN AB =ON CB 时,则有|-x 2+2x |2=|x |32, 即|x |·|-x +2|=13|x |,∵当x =0时M ,O ,N 不能构成三角形,∴x ≠0,∴|-x +2|=13,即-x +2=±13,解得x 1=53,x 2=73,此时点N 坐标为⎝ ⎛⎭⎪⎫53,0或⎝ ⎛⎭⎪⎫73,0; ②当MN CB =ON AB 时,则有|-x 2+2x |32=|x |2, 即|x |·|-x +2|=3|x |,∴|-x +2|=3,即-x +2=±3,解得x =5或-1,此时点N 坐标为(-1,0)或(5,0),综上可知,存在满足条件的点N ,其坐标为⎝ ⎛⎭⎪⎫53,0或⎝ ⎛⎭⎪⎫73,0或(-1,0)或(5,0).4.(20分)[2017·泸州]如图6-3-4,已知二次函数y =ax 2+bx +c (a ≠0)的图象经过A (-1,0),B (4,0),C (0,2)三点.(1)求该二次函数的表达式;(2)点D 是该二次函数图象上的一点,且满足∠DBA=∠CAO (O 是坐标原点),求点D 的坐标;(3)点P 是该二次函数图象上位于第一象限内的一个动点,连结P A 分别交BC ,y 轴于点E ,F ,若△PEB ,△CEF 的面积分别为S 1,S 2,求S 1-S 2的最大值.【解析】 (1)根据待定系数法求解;(2)设直线BD 与y 轴的交点为M (0,t ).根据tan ∠MBA=tan ∠CAO 列关于t 的方程求解t ,从而可确定直线BD 表达式,再求直线BD 与抛物线交点坐标图6-3-4即可,注意分类讨论;(3)过点P 作PH ∥y 轴交直线BC 于点H ,设P (t ,at 2+bt +c ),根据直线BC 表达式点H 的坐标,计算线段PH 长度;用t 表示直线AP 表达式,解出点E ,F 坐标从而可表示出线段CF ,将S 1-S 2用t 表示,根据二次函数性质求最值. 解:(1)设抛物线的表达式为y =a (x +1)(x -4),∵抛物线图象过点C (0,2),∴-4a =2,解得a =-12.∴抛物线的表达式为y =-12(x +1)(x -4),即y =-12x 2+32x +2;(2)设直线BD 与y 轴的交点为M (0,t ).∵∠DBA =∠CAO ,∴∠MBA =∠CAO ,∴tan ∠MBA =tan ∠CAO =2,∴|t |4=2,即t =±8.当t =8时,直线BD 表达式为y =-2x +8.联立⎩⎪⎨⎪⎧y =-2x +8,y =-12x 2+32x +2,解得⎩⎨⎧x 1=4,y 1=0; ⎩⎨⎧x 2=3,y 2=2.∴D (3,2).当t =-8时,直线BD 表达式为y =2x -8.联立⎩⎪⎨⎪⎧y =2x -8,y =-12x 2+32x +2,解得⎩⎨⎧x 1=4,y 1=0; ⎩⎨⎧x 2=-5,y 2=-18.∴D (-5,-18).综上:点D 的坐标为(3,2)或(-5,-18);(3)如答图,过点P 作PH ∥y 轴交直线BC 于点H ,设P ⎝ ⎛⎭⎪⎫t ,-12t 2+32t +2, 直线BC 的表达式为y =-12x +2,则H ⎝ ⎛⎭⎪⎫t ,-12t +2,∴PH =y P -y H =-12t 2+2t ;第4题答图直线AP 的表达式为y =⎝ ⎛⎭⎪⎫-12t +2(x +1),取x =0,得y =2-12t ; 故F ⎝ ⎛⎭⎪⎫0,2-12t ,CF =2-⎝ ⎛⎭⎪⎫2-12t =12t ; 联立⎩⎪⎨⎪⎧y =⎝ ⎛⎭⎪⎫2-t 2(x +1),y =-12x +2,解得x E =t 5-t , ∴S 1=12(y P -y H )(x B -x E )=12⎝ ⎛⎭⎪⎫-12t 2+2t ⎝ ⎛⎭⎪⎫4-t 5-t , S 2=12·t 2·t 5-t. ∴S 1-S 2=12⎝ ⎛⎭⎪⎫-12t 2+2t ⎝ ⎛⎭⎪⎫4-t 5-t -12·t 2·t 5-t=-54t 2+4x =-54⎝ ⎛⎭⎪⎫t -852+165. ∴当t =85时,S 1-S 2有最大值,最大值为165.(20分)5.(20分)[2016·金华]在平面直角坐标系中,O 为原点,平行于x 轴的直线与抛物线L :y =ax 2相交于A ,B 两点(点B 在第一象限),点D 在AB 的延长线上.(1)已知a =1,点B 的纵坐标为2.①如图6-3-5①,向右平移抛物线L 使该抛物线过点B ,与AB 的延长线交于点C ,求AC 的长;②如图②,若BD =12AB ,过点B ,D 的抛物线L 2,其顶点M 在x 轴上,求该抛物线的函数表达式;(2)如图③,若BD =AB ,过O ,B ,D 三点的抛物线L 3的顶点为P ,对应函数的二次项系数为a 3,过点P 作PE ∥x 轴交抛物线L 于E ,F 两点,求a 3a 的值,并直接写出AB EF 的值.图6-3-5解:(1)①对于二次函数y =x 2,当y =2时,2=x 2,解得x 1=2,x 2=-2,∴AB =2 2.∵平移得到的抛物线L 1经过点B ,∴BC =AB =22, ∴AC =42;②如答图①,记抛物线L 2的对称轴与AD 相交于点N .根据抛物线的轴对称性,得BN =12DB =22,∴OM =322.设抛物线L 2的函数表达式为y =a 2·⎝⎛⎭⎪⎫x -3222. 由①得,点B 的坐标为()2,2,∴2=a 2·⎝⎛⎭⎪⎫2-3222,解得a 2=4. ∴抛物线L 2的函数表达式为y =4⎝ ⎛⎭⎪⎫x -3222; 即y =4x 2-122x +18.① ②第5题答图 (2)如答图②,设抛物线L 3与x 轴交于点G ,其对称轴与x 轴交于点Q ,过点B 作BK ⊥x 轴于点K .设OK =t ,则AB =BD =2t ,点B 的坐标为(t ,at 2), 根据抛物线的轴对称性,得OQ =2t ,OG =2OQ =4t . 设抛物线L 3的函数表达式为y =a 3x (x -4t ),∵该抛物线过点B(t,at2),∴at2=a3t(t-4t),又∵t≠0,∴a3a=-13,由题意得,点P的坐标为(2t,-4a3t2),则-4a3t2=ax2,解得x1=233t,x2=-233t,EF=433t,∴ABEF=32.。
