Phase diagram of a probabilistic cellular automaton with three-site interactions
细胞凋亡超声成像早期评估肿瘤治疗反应的研究进展

·综述·目前,癌症是威胁我国人民健康的主要公共问题,也是主要死亡原因。
细胞凋亡在癌症治疗中具有重要作用,与癌症的发生发展密切相关[1]。
现有的手术、放疗、化疗、免疫疗法及靶向药物等治疗手段均是以激活细胞凋亡作为杀死癌细胞的主要途径[2-4],表明实时监测细胞凋亡水平已成为早期评价肿瘤治疗反应的一项指标。
影像学成像技术监测细胞凋亡水平有助于临床全面了解肿瘤发展情况,实时指导治疗方案,对预后效果的评估也具有重要意义。
本文就超声成像在细胞凋亡监测中的研究进展及在早期评估肿瘤治疗反应中的应用进行综述。
一、高频超声在细胞凋亡中的应用细胞凋亡的典型特征是细胞皱缩、质膜出泡、细胞器或核膜周围的染色质浓缩、DNA片段化等细胞结构与亚细胞结构的改变[5]。
既往有学者[6-8]利用超声对组织结构的敏感性检测体内细胞凋亡,显示出良好的效果。
Tadayyon等[9]应用高频超声(40~50MHz)开展细胞死亡诊断研究发现,凋亡区超声反射信号强度最高可增加16倍。
由于化疗引起的凋亡组织与周边结构的声阻抗存在差异,Pasternak等[10]以高频超声(频率>20MHz)成像技术定性和定量评估癌细胞的死亡程度和死亡类型,进而评估化疗疗效。
尽管以上研究极大地推进了超声成像对细胞凋亡的研究进展,但其使用的超声频率高于大多数临床设备使用频率。
换能器频率越高,声波的穿透性就越低,这种超声信号的高度衰减,使穿透深度多为1~5cm[11],限制了临床对某些深部肿瘤病变的诊断。
最重要的是,高频超声诊断仍基于解剖学水平,显示的是部分分子改变的终效应,并非治疗反应早期的分子水平事件,且缺乏特异性和敏感性,临床应用受限。
二、超声分子成像在细胞凋亡中的应用超声分子成像是研究活体内具有重要作用的关键蛋白分子成像情况,具有无创、实时、便捷等优势[12],其成像基础和先决条件是开发具有特异性高、敏感性强、靶向性好的超声分子探针[13]。
原核生物与真核生物染色体区别和识别
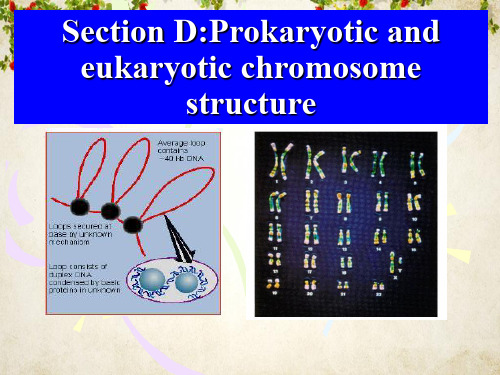
The importance of packing of DNA into chromosomes
Chromosome is a compact form of the DNA that readily fits inside the cell [?]
A Severe Problem of Packaging
1. Largest human chromosome: ~3 x 108 bp How long is it?
3 x 108 bp x 3.4 Å/bp = 10 x 104um! 2. A typical cell = 10 um
Conclusion: chromosome in length/size of cell
Supercoiling of the genome
supercoil of the genome
unconstrained supercoil function: pass tensile forces among loops
constrained supercoil (bind proteins) 结构域被非特异结合蛋白如HU和H-NS等类 组蛋白缠绕,使一半超螺旋被束缚。
146bp的DNA片段和H2A、 H2B、H3和H4各二分子组 成,这种结构称为核心颗粒.
• 核心颗粒外观呈椭圆形,颗粒直径11nm,高 5.5nm.绕颗粒的DNA长度为50nm(146bp),连 接区DNA长度为20nm(约60bp).
11nm染色质纤维
The roles of H1
1. Stabilizes the point at which DNA enters and leaves the nucleosome core. Protect the further 20bp DNA from nuclease digestion.
物理化学

• •
lβ (A+B) G 1.0 D
* tB
t
* A
100
•
lα (A+B) C
g(A+B)
•
l α(A+B)
80
E lα (A+B) lβ (A+B)
60
•
F 0.0 H2O(A) 0.2 0.4 wB 0.6
•
0.8 n-C4H9OH(B)
二组分液态部分互溶系统的气二组分液态部分互溶系统的气-液平衡相图
p= p + p
* A
* B
当两种液体共存时, 当两种液体共存时,不管其相对数量 如何, 如何,其总蒸气压恒大于任一组分的蒸气 而沸点则恒低于任一组分的沸点。 压,而沸点则恒低于任一组分的沸点。 通常在水银的表面盖一层水,企图减少汞蒸气, 通常在水银的表面盖一层水,企图减少汞蒸气,其 实是徒劳的。 实是徒劳的。
CellularReproductionMitosisandMeiosis-43页PPT文档资料

Lesson three
G1, S, 和G2称分裂间期。最后是M期,有丝分裂期, 复制的染色体组浓缩,移动并细胞分裂。据称是染 色质控制了细胞循环,伴随外部激活因子和抑制因 子如抑素。
Lesson three
The spindle forms differently in plant and animal cells. In animals it is associated with centriole, while in plant and fungal cells spindle formation is associated with reions called microtubule organizing centers.
在分裂前期后期和分裂中期前期,浓缩的染 色体与纺锤体相连,最后以正确的角度排列 在赤道板上。
Lesson three
Next, during anaphase, the two sister chromatids of each chromosome split, and one from each pair is drawn toward each pole of the cell.
Lesson three
As prophase ends and metaphase begins, the condensed chromosomes become associated with the spindle. Eventually the chromosomes become arranged in a plane (called the metaphase plate) at a right angle to the spindle fibers.
细胞增殖英文CellReproduction课件

In a gypsy moth? 4. Why does mitosis occur? Major functions? 5. In what cells (general term) does mitosis
• Groups of single-chromatid chromosomes reach poles of cell
• Nuclear envelop begins to reform
• 2 new daughter cells formed
• Cytokinesis begins with appearance of cell plate
It would be a genetic mess!
Instead, gametes are haploid (n).
Egg and sperm both have exactly half the number of chromosomes of somatic cells
At fertilization, n + n = 23; 23 + 23 = 46!
THE STEPS OF MITOSIS
• Interphase
(actually, this is not part of mitosis itself)
• Prophase • Metaphase • Anaphase • Telophase
Interphase
Onion root tip
Massively parallel single-amino-acid mutagenesis

医学细胞学英语

Prokaryotic cell 原核细胞Eukaryotic cell 真核细胞Cell wall 细胞壁Cell membrane 细胞膜/plasma membrane 质膜Cytoplasm 细胞质Nucleus 细胞核Nucleoid 拟核Plasmid 质粒Membranous structure 膜相结构Nonmembranous structure 非膜相结构Biomembrane 生物膜磷脂糖脂胆固醇Membrane protein 膜蛋白Integral protein 膜内在蛋白/mosaic protein 镶嵌蛋白、Transmembrane protein 跨膜蛋白Peripheral protein 膜周边蛋白Lamella model 片状结构模型Unit membrane structure model 单位膜结构模型Fluid mosaic model 液态镶嵌模型Crystal mosaic model 晶格镶嵌模型Block mosaic model 板块镶嵌模型Asymmetry 不对称性Fluidity 流动性Cell surface 细胞表面Cell junction 细胞连接Tight junction 紧密连接Adhering junction 粘合连接Belt desmosome 带状桥粒Spot desmosome 点状桥粒Hemidesmosome 半桥粒Communicating junction 通信连接Gap junction 间隙连接Passive transport 被动运输Simple diffusion 简单扩散Ion channel diffusion 离子扩散通道Ion channel protein 离子通道蛋白Facilitated diffusion 易化扩散Carrier protein 载体蛋白Active transport 主动运输Na-K pump 钠钾泵Ca-pump 钙泵Endocytosis 胞吞作用Phagocytosis 吞噬作用Pinocytosis 胞饮作用Receptor mediated endocytosis 受体介导的胞吞作用Phagosome 吞噬体Phagocytic vesicle 吞噬泡Pinosome 胞饮体Pinocytic 胞饮小泡Coated pits 有被小窝Endosome 内吞体Exocytosis 胞吐作用Receptor 受体Signal 信号Ligand 配体Membrane receptor 膜受体Signal transduction 细胞信号转导Ion-channel receptor 离子通道受体Enzyme-linked receptor 酶偶联受体G protein-coupled receptor G 蛋白偶联受体Organelle 细胞器Cytoplasmic matrix or cytomarix 细胞基质Endomembrane system 内膜系统Endoplasmic reticulum ER内膜系统Microsome 微粒体Rough endoplasmic reticulum RER粗面内质网Granular endoplasmic reticulum GER 颗粒内质网Smooth endoplasmic reticulum SER 光面内质网Agranular endoplasmic reticulum AER 无颗粒内质网Signal peptide 信号肽Signal recognition particle 信号识别颗粒Internal reticular apparatus内网器Golgi apparatus 高尔基器Golgi body 高尔基体Saccules 扁平囊Cis Golgi network 顺面高尔基网Forming face 形成面Immature face 未成熟面Mdedial Golgi network中间高尔基网Trans Golgi network反面高尔基网Mature face 成熟面Lysosome 溶酶体Lysosomal enzyme 溶酶Primary lysosome 初级溶酶体Secondary lysosome 次级溶酶体Heterophagic lysosome 异噬性溶酶体Autophagic lysosome 自噬性溶酶体Autophagosome 自噬体Heterophagy 异噬作用Autophagy 自噬作用Granulolysis 粒溶作用Inborn lysosomal disease 先天性溶酶体病Mitochondrion 线粒体Outer membrane 外膜Inner membrane 内膜Cristae 嵴Intracristal space 嵴内腔Elementary particle 基粒/A TPase complex A TP酶复合体Intermembrane space 膜间腔Intercristal space 嵴间腔Cellular oxidation 细胞氧化Cytoskeleton 细胞骨架Microfilament MF 微丝Microtubule MT 微管Intermediate filament IF中间丝Tubulin 微管蛋白Microtubule-associated protein MAP 微管相关蛋白Protofilament 原纤维Globular actin 球形肌动蛋白Keratin filament 角蛋白纤维Desmin filament结蛋白纤维Vimentin filament 波形蛋白纤维Neurofilament 神经元纤维Neuroglial filament 神经胶质纤维Centrosome 中心体/diplosome 双心体Centriole 中心粒Centrosphere 中心球Centriolar satellite 中心粒卫星Microtubule organizing center 微管组织中心Cilia 纤毛Flagella 鞭毛Dynein 动力蛋白Shaft 毛部Basal body 基体Rootlet 根丝Central sheath 中央鞘Ribosome 核糖体Attached ribosome 附着核糖体Free ribosome 游离核糖体Polyribosome/polysome 多核糖体Structural protein 结构蛋白Export protein 外输蛋白、secretory protein 分泌蛋白细胞核Nuclear membrane 核膜Perinuclear space 核周间隙/perinuclear cistrernae 核周池Nuclear pores 核孔Nuclear pore complex 核孔复合体Nuclear lamina 核纤层Chromatin 染色质Chromosome 染色体Euchromatin 常染色质Heterochromatin 异染色质Constitutive heterochromatin 结构异染色质Facultative heterochromatin 兼性异异染色质Nucleosome 核小体Sister chromatid 姐妹染色单体Centromere 着丝粒Primary constriction 主缢痕初级缢痕Kinetochore 动粒着丝点Secondary constriction 次缢痕Metacentric chromosome 中着丝粒染色体Submetacentric chromosome 近中着丝粒染色体Subtelocentric chromosome 近端着丝粒染色体Telocentric chromosome 端着丝粒染色体Fibrillar centers 纤维中心Dense fibrillar component 致密纤维成分Granular component 颗粒成分Nuclear organizer region NOR 核仁组织区细胞分裂Cell proliferation 细胞增殖Cell division 细胞分裂Amitosis 无丝分裂Mitosis 有丝分裂Meiosis 减数分裂Spindle 纺锤体Cell cycle 细胞周期Gap1 phase G1 合成前期Synthetic phase S 合成期Gap2 phase G2 合成后期Restriction point R限制点/checkpoint 检验点Unscheduled DNA synthesis UDS DNA期外合成Maturation promoting factor MPF 成熟促进因子Contractile ring 收缩环Cleavage furrow 分裂沟Midbody 中间体Premature chromosome condensation PCC 染色体提前凝集Diploid 二倍体Interkinesis Ⅰ间期ⅠProphase Ⅰ前期ⅠLeptotene 细线期Zygotene 偶线期Homologous chromosome同源染色体Synapsis 联会Synaptinemal complex 联会复合体Central element 中央成分Pachytene 粗线期Bivalent 二价体Tetrad四分体Chiasma 交叉Diplotene 双线期Chiasma terminalization 交叉端化Diakinesis 终变期Metaphase Ⅰ中期ⅠAnaphase Ⅰ后期ⅠTelophase Ⅰ末期ⅠGenotype 基因型Phenotype 变现型Homozygote 纯合子Dominant homozygote 显性纯合子Recessive homozygote 隐性纯合子Heterozygote 杂合子Allele 等位基因Dominant character 显性性状Recessive character 隐性性状Complete linkage 完全连锁Incomplete linkage 不完全连锁Law of linkage and crossing-over 连锁交换定律Inherited disease 遗传性疾病Congenital disease 先天性疾病Familial disease 家族性疾病Monogenic disease 单基因病Polygenic disorder 多基因病Chromosomal disorder 染色体病Somatic genetic disorder 体细胞遗传病Mitochondrial genetic disorders 线粒体遗传病Complete dominance 完全显性Autosomal dominant inheritance 常染色体显性遗传Irregular dominance 不规则显性Penetrance 外显率Expressivity 表现度Incomplete dominance 不完全显性Codominance 共显性遗传Multiple alleles 复等位基因Delayed dominance 延迟显性Sex-influence dominance 从性显性Autosomal recessive inheritance AR 常染色体隐性遗传Consanguinity 近亲Consanguineous marriage近亲婚配Coefficient of relationship 亲缘系数First degree relative 一级亲属Second degree relative 二级亲属Third degree relative 三级亲属X-linked dominant inheritance XD X连锁遗传Criss-cross inheritance 交叉遗传X-linked recessive inheritance XR X连锁隐性遗传Y-linked inheritance Y连锁遗传Polygenic inheritance 多基因遗传Multifactorial inheritance 多因子遗传Minor gene 微效遗传Multiple factor hypothesis 多基因假说Polygenic disease 多基因病Multifactorial disease 多因子病Liability 易患性Threshold 阈值Threshold theory 阈值学说Heritability 遗传率Monozygotic twins 单卵双生Dizygotic twins 二卵双生Chromosomal aberration 染色体畸变Chromosome set 染色体组Euploid 整倍体Triploid 三倍体Tetraploid 四倍体Diandry 双雄受精Digyny 双雌受精Aneuploid 非整倍体Hyperdiploid 超二倍体Hypodiploid 亚二倍体Monosomy 单体性Trisomy 三体性Ploysomy 多体性Chromosome non-disjunction 染色体不分离Deletion 缺失Duplication 重复Inversion 倒位Translocation t 易位Transposition 转座Reciprocal translocation 相互易位Robertsonian translocation 罗伯逊易位ISOchromosome i 等臂染色体Ring chromosome r 环状染色体。
药学专业英语-PPT

Context Set
I have sore throat, but I know chinese little.
we have to master necessary professional pharmacy English so that we can work better in tWhehefuntuyroeu encounter
Conclusion:
Microorganisms are not spontaneously generated from inanimate matter, but are produced by other microorganisms
Robert Kock (1843 – 1910)
The recognition of microbial role in disease
•Small volume and big surface to volume ratio
Different length and different surface to volume ratio
Small and simple
可见范围 肉眼
光学显微镜 电镜
微生物的相对大小 真核细胞型 原核细胞型
Prokaryotic genetic material is located in an area called the nucleoid and is not enclosed by a membrane.
The prokaryotic cell wall almost always has peptidoglycan (肽聚糖)and is chemically and morphologically (形态的)complex.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
a rX iv:c ond-ma t/2136v1[c ond-m at.stat-m ech]1Oct22Phase diagram of a probabilistic cellular automaton with three-site interactions A.P.F.Atman ∗,Ronald Dickman †and J.G.Moreira ‡Departamento de F´ısica,Instituto de Ciˆe ncias Exatas,Universidade Federal de Minas Gerais,C.P.70230123-970,Belo Horizonte,MG -Brazil (February 1,2008)Abstract We study a (1+1)dimensional probabilistic cellular automaton that is closely related to the Domany-Kinzel (DKCA),but in which the update of a given site depends on the state of three sites at the previous time step.Thus,compared with the DKCA,there is an additional parameter,p 3,representing the probability for a site to be active at time t ,given that its nearest neighbors and itself were active at time t −1.We study phase transitions and critical behavior for the activity and for damage spreading,using one-and two-site mean-field approximations,and simulations,for p 3=0and p 3=1.We find evidence for a line of tricritical points in the (p 1,p 2,p 3)parameter space,obtained using a mean-field approximation at pair level.To construct the phase diagram in simulations we employ the growth-exponent method in an interface representation.For p 3=0,the phase diagram is similar to the DKCA,but the dam-age spreading transition exhibits a reentrant phase.For p 3=1,the growth-exponent method reproduces the two absorbing states,first and second-order phase transitions,bicritical point,and dam-age spreading transition recently identified by Bagnoli et al.[Phys.Rev.E 63,046116(2001)].PACS:05.10.-a,02.50.-r,68.35.Ct,68.35.RhI.INTRODUCTIONProbabilistic cellular automata(PCA)are widely used to model systems with local interactions in physics,chemistry,biology and social sciences[1,2,3,4,5]. Despite their simplicity,these models exhibit complex behavior and are used to investigate fundamental problems in statistical mechanics,such as spin models [6,7]and nonequilibrium phenomena[8,9].In particular,the problem of phase transitions in the presence of absorbing states has attracted increasing interest in recent years;PCA play a major role in these studies[10,11,12,13].The PCA introduced by Domany and Kinzel[8]is,along with the contact process[14,15], one of the simplest models exhibiting an absorbing-state phase transition.The one-dimensional Domany-Kinzel stochastic cellular automaton(DKCA) is a completely discrete system-temporally,spatially and in its state space-which attracts interest as a particle system affording a test of ideas on scaling in nonequilibrium critical phenomena[16].The DKCA has a unique absorbing (“vacuum”)state;its phase diagram presents a critical line separating this ab-sorbing phase from an active one.Continuous phase transitions to an absorbing state are conjectured to belong generically to the directed percolation(DP)uni-versality class[17].In addition to the active-absorbing transition,Martins et al.[18]found a damage spreading(DS)transition separating the active phase into nonchaotic and chaotic phases.There is numerical evidence that the critical be-havior along this transition line also belongs to the DP class,as expected on the basis of universality[19].Recently,Bagnoli et al[9]introduced a model that can be considered a natural extension of the DKCA:a one-dimensional PCA in which the update of a given site depends on the state of its nearest neighbors and itself,at the preceding time step.(We shall refer to this model as the BPCA.)Thus,compared with the DKCA,there is an additional parameter,p3,representing the probability for a site to be active at time t,given that all three sites were active at time t−1. Bagnoli et al.studied p3=1,in which case the model presents two absorbing states:the empty one and the completely occupied configuration.As in the DKCA,the density is the order parameter.These authors used the meanfield approximation(at site level),simulations,andfield-theoretic arguments to study the model.They found a rich phase diagram,withfirst-and second-order phase transitions,a bicritical point,and a damage-spreading transition.Except for the line p2=1in the DKCA,this is the simplest PCA that exhibits a discontinuous phase transition[9].In this work we extend the analysis of the BPCA considering two cases:the previously studied p3=1,which corresponds to a ferromagnetic-like model,and p3=0,representing a game-of-life-like model[20,21].We extend the mean-field analysis to the pair level,and use simulations to construct the phase diagram.In simulations,we apply the growth-exponent method[22]to identify transitions.This paper is structured as follows:in Section II we define the model and its interface representation;the site and pair mean-field approximations are discussed in Section III.Simulation results are presented in Section IV.We summarize ourfindings in Section V.II.MODELThe one-dimensional PCA with three-site neighborhood(BPCA)was pro-posed by Bagnoli et al.[9].It consists of a ring of L sites(i=1,2,...,L), with periodic boundaries,in which each site i has two possible states,conve-niently denoted byσi=0,1.The state of the system at time t is given by the set{σi(t)}.In contrast to the deterministic CA studied by Wolfram[1], the present model is a discrete time Markov process:the rules for updating the system are given by transition probabilities.In particular,state of site i at time t+1depends onσi−1(t),σi(t)andσi+1(t),via the transition probability P(σi(t+1)|σi−1(t),σi(t),σi+1(t)).The latter is of totalistic form,i.e.,the depen-dence is through S i(t)=σi−1(t)+σi(t)+σi+1(t).Since S(t)=0impliesσi(t+1)=0 with probability1,there remain three free parameters for defining the transition probability.Specifically:P(1|0,0,1)=P(1|0,1,0)=P(1|1,0,0)=p1,P(1|0,1,1)=P(1|1,0,1)=P(1|1,1,0)=p2,P(1|1,1,1)=p3.Evidently,P(0|σi−1,σ,σi+1)=1−P(1|σi−1,σi,σi+1).Depending on the values of(p1,p2,p3),the asymptotic(t→∞)state of the system is either in an absorbing phase(phase0,with all sites in state0,or phase1,with all sites in state1),or in the active phase,in which the stationary densityρof sites in state1takes a value different from zero or plete determination of the phase diagram in the three-dimensional parameter space is a rather difficult open problem.In this work we focus on two cases:p3=1and p3=0.In thefirst case,the model possesses the two absorbing phases cited above,as well as an active phase and a chaotic region(associated with damage spreading).For p3=0,the phase1is no longer absorbing(though the phase0 of course remains so),and there is again an active phase;the chaotic region is reentrant.p3=0describes a situation in which“crowding”of individuals leads to their destruction,similar to Conway’s Game of Life model[20,21],while p3=1 corresponds to a ferromagnetic-like model.The absorbing/active transitions are continuous phase transitions,character-ized by critical exponents which belong to the DP universality class.The phase 0/phase1transition is discontinuous[9],and the exponents are those of compact directed percolation.The DS transitions are also in the DP class,consistent with Grassberger’s prediction[19].The termination of two critical lines at a line of discontinuous transitions marks a bicritical point,as has been found in the BPCA for p3=1.For p3<1,the phase1is no longer absorbing,so that one of the phase boundaries(i.e.,between the active and phase1-absorbing phases)is no longer present.Wefind(using the two-site mean-field approximation,discussed in Sec.IIIB),that the bicritical point is actually one terminus of a line of tricrit-ical points:for eachfixed p3in the range1>p3>p t3≃1/3,the absorbing-active transition is discontinuous for(p1,p2)<(p t1,p t2)and continuous for larger val-ues,(p1,p2)>(p t1,p t2),where(p t1,p t2)is the tricritical point.For p3≤p t3,the absorbing/active transition is always continuous.A.Surface RepresentationThe mapping of dynamical systems to a surface-growth representation is an interesting problem,since in many cases the resulting scaling properties are un-known a priori.Integration of the local activity(with respect to time)is the most natural procedure.The present method employs the interface representa-tion proposed by de Salles et al.[24].The procedure consistsintransforming thespatiotemporal patterns generated by the PCA to a solid-on-solid(SOS)particle deposition.The surface-growth process is attended by kinetic roughening;the associated critical exponents can be measured[11]following the scaling concepts developed by Family and Vics´e k[25].Atman and Moreira[22]demonstrated that the growth exponentβw exhibits a cusp at criticality,and is very useful for detecting phase transitions.Height variables are defined by summing the variablesσi(τ)over thefirst t time steps:h i(t)≡t τ=0σi(τ).(1)In this way we generate a growth process,with correlations embodied in the roughness w(L,t)[26],defined byw2(L,t)=1h(t) 2 ,(2)whereL z ,(3) where f(u)is a universal scaling function,αis the roughness exponent,z=α/βw the dynamic exponent andβw the growth exponent.The function f(u)= constant for large u,while f(u)∼uβw for small u(t≪L z).At short times, therefore,we expect w(t)∼tβw.It is possible to measureβw from the slope of a log−log plot of w(L,t)versus t.In the active phase,the roughness does not saturate,growing instead as w(L,t)∼t1/2,corresponding to uncorrelated growth [22],since the correlation length isfinite,away from the critical point.In previous work,Atman and Moreira[22]showed thatβw attains a maximum at the phase transition,and measured its value along the transition line of the DKCA.DP values for others critical exponents in the surface representation of DKCA are verified in Ref.??.B.Damage SpreadingMartins et al.[18]used the damage-spreading technique to show that the active phase of the DKCA consists of two phases,chaotic and nonchaotic.The order parameter of this transition is the difference between two replicas initialized with different configurations,but subject to the same sequence of random events during the subsequent evolution.In practice,we let the system evolve until it attains a stationary state,and then copy the configuration,introducing some alterations(“damage”).The two replicas,one with stateσi(t)and the other with state̺i(t),then evolve using the same sequence of random numbers,and the difference between them,Γi(t)=|σi(t)−̺i(t)|,is monitored.The fraction of sites in the two replicas withσi=̺i defines their Hamming distance:1D H(t)=III.MEAN-FIELD THEORYA.One-site approximationTo begin,we present the mean-field approximation at the site level,for p3= 1and p3=0,and construct the phase diagram from the equations obtained in this approximation.The BPCA is a Markov process in which all sites are updated simultaneously.The configuration{σ}is a set of stochastic variables with probability distribution at time t given by P t(σ).The evolution of the latter is governed byP t+1= σ′ω(σ|σ′)P t(σ′),(6)whereω(σ|σ′)denotes the probability of the transitionσ′→σ,with the properties ω(σ|σ′)≥0and σω(σ|σ′)=1.The transition probability for the BPCA is a product of factors associated with each site:ω(σ|σ′)=Li=1w i(σi|σ′),(7)where w i(σi|σ′)≥0is the conditional probability for site i to be active at time t+1given the configurationσ′at the preceding step.The probabilities w i are translationally invariant and in fact depend only on the statesσi−1,σi andσi+1 at the previous step:w i(σi|σ′)=w3s(σi|σ′i−1,σ′i,σ′i+1).(8) We list the w3s in Table I.Of interest are the n-site marginal probabilities.The evolution of the one-site distribution P t(σi),is given byP t+1(σi)= σ′i−1 σ′i σ′i+1w3s(σi|σ′i−1,σ′i,σ′i+1)P t(σ′i−1,σ′i,σ′i+1),(9) where P t(σ′i−1,σ′i,σ′i+1)is the marginal distribution for a set of three nearest-neighbor sites.The evolution of the two-site distribution is given by:P t+1(σi,σi+1)= σ′i−1 σ′i σ′i+1 σ′i+2w3s(σi|σ′i−1,σ′i,σ′i+1)×w3s(σi+1|σ′i,σ′i+1,σ′i+2)P t(σ′i−1,σ′i,σ′i+1,σ′i+2).(10) Evidently we have an infinite hierarchy of equations.In the n-site approximation the hierarchy is truncated by estimating the(n+1)-site(and higher)probabilities on the basis of those for n sites.The simplest case is the one-site approximation,in which P t(σ′i−1,σ′i,σ′i+1)is factored so:P t(σ′i−1,σ′i,σ′i+1)=P t(σ′i−1)P t(σ′i)P t(σ′i+1).This yields the recurrence relation,ρt+1=p3ρ3t+3p2ρ2t(1−ρt)+3p1ρt(1−ρt)2,(11) whereρt≡P t(1)is the density of active sites(i.e.,the order parameter).Depending on the value of(p1,p2,p3),Eq.(11)admits different stationary solutions,corresponding to the possible BPCA phases discussed above:phase0 (ρ=0),phase1(ρ=1)and active(0<ρ<1).In order to verify the stability of the stationary solutions,we consider a small perturbation in the stationary value ρ∗,ρt=ρ∗+∆ρt.Applying this variable change in the Eq.(11),we obtain for the mean-field approximation at the site level,∆ρt+1=∆ρt[3ρ∗2(p3+3p1−3p2)+6ρ∗(p2−2p1)+3p1]+(∆ρt)2[3ρ∗(p3+3p1−3p2)+3(p2−2p1)]+(∆ρt)3[p3+3p1−3p2].(12) We can write Eq.(12)in a simplified manner,∆ρt+1=a(ρ∗)∆ρt+b(ρ∗)∆2ρt+c∆3ρt,where the coefficients a(ρ∗),b(ρ∗)and c can be associated with the stability of the solutions.Considering the solution,ρ∗=0,the stability condition is a(ρ∗)<1,which implies p1<1/3.In the case a(ρ∗)=1,(p1=1/3),the solution will be stable only if b(ρ∗)<0and c<0;thefirst condition implies p3<2/3.For a(ρ∗)=1and b(ρ∗)=0,the stability the condition c<0leads to p3<1.Thus,the solution ρ∗=0is always stable for p1<1/3,p2<2/3and p3<1.The point(1/3,2/3,1) corresponds to a tricritical point in this aproximation.Considering the solution,ρ∗=1,the stability condition a(ρ∗)<1implies p3−p2<1/3.In case a(ρ∗)=1,(p3=p2+1/3),the condition b(ρ∗)<0yields p2−p1>1/3.For a(ρ∗)=1and b(ρ∗)=0,the stability condition c<0implies p3<1.So,the point(1/3,2/3,1)is also a tricritical point for the solutionρ∗=1! Thus,the point(1/3,2/3,1)corresponds to a bicritical point,as Bagnoli et al. have already shown.In fact,the solutionρ∗=1is absorbing only for p3=1(since for p3<1,the dynamics of updating destroys the phase1),and this solution is stable for p2>2/3.For0<ρ∗<1,the stability condition a(ρ∗)<1implies a inequality of second degree in terms ofρ∗.Considering a=1,we can solve the corresponding equation,and obtain(2p1−p2)± p3−3p1−3p2.ρ∗=Note thatρ∗vanishes on the line(1/3,2/3,p3).It is easy to see that the positive solution,ρ∗+,is valid for any(p1,p2,p3),but the negative solution,ρ∗−,is valid only for p2<2p1.Considering the plane p1=1/3,the transition line for p2>2/3 coincides with the vanishing of the square root,sinceρ∗must be real.This implies a discontinuous transition for p2>2/3,and the line(1/3,2/3,p3)corresponds to the tricritical line in(p1,p2,p3)space,in the site approximation.In the simulations we consider two cases:p3=1and p3=0.Considering the stability analysis above,we can summarize the phase diagram in these two cases in the following way:for p3=1,Eq.(12)can be written as,ρ (3p1−3p2+1)ρ2+(3p2−6p1)ρ+3p1−1 =0.(13) The three solutions of this equation are:•ρ=0-Phase0,stable for p1<1/3and p2<2/3;•ρ=1-Phase1,stable for p2>2/3and p1>1/3;•Active phase,for p2<2/3and p1>1/3,where the stationary density is given by:3p1−1ρ=9p22−12p2+12p1B.Pair approximationAt the pair level,the probability P t(σ′i−1,σ′i,σ′i+1,σ′i+2)is factored in the fol-lowing wayP t(σ′i−1,σ′i)P t(σ′i,σ′i+1)P t(σ′i+1,σ′i+2)P t(σ′i−1,σ′i,σ′i+1,σ′i+2)=+p2(ρt−z t) 2z t1−ρtρt+p1(ρt−z t) 2(1−2ρt+z t)ρt ,(18) z t+1=p21 (ρt−z t)2(1−2ρt+z t)(2−ρt)ρt(1−ρt) z t(1−2ρt+z t)+(ρt−z t)2+p22 z t(ρt−z t)2(1+ρt)ρ2t +p23z3twhere the brakets denote an average over realizations.The evolution of the joint probability followsP t+1(σ;τ)= σ,τW(σ;τ|σ′;τ′)P t(σ′;τ′),(21) whereW(σ;τ|σ′;τ′)= i̟(σi;τi|σ′i−1,σ′i,σ′i+1;τ′i−1,τ′i,τ′i+1),(22)is the transition probability for two the two systems(subject to the same noise), from the state(σ′;τ′)to(σ;τ).Using the transition probabilities defined in Table I,we can calculate the joint transition probabilities,as shown in Table II.Now,we can write the equations for the evolution of the order parameter associated with the chaotic transition-the Hamming distance.Denoting the Hamming distance defined by Eq.(4)asψt≡P t(1;0)=P t(0;1),and using the relation(21),we haveψt+1=<̟(1;0|σi−1,σi,σi+1;τi+1,τi,τi+1)>;using the rules of Table II,we can writeψt asP t+1(1;0)=p3P t(1,1,1;0,0,0)+3p2P t(1,1,0;0,0,0)+(23) +3(b+c)P t(1,1,1;1,1,0)+3p1P t(1,0,0;0,0,0)++3(b′+c′)P t(1,1,1;1,0,0)+9(b′′+c′′)P t(1,1,0;1,0,0). Calling P t(1)≡x t,we can write P t(1;1)=x t−ψt and P t(0;0)=1−x t−ψt; thus,using the one-site mean-field approximation P t(σi−1,σi,σi+1;τi−1,τi,τi+1)= P t(σi−1,σi,σi+1)P t(τi−1,τi,τi+1),we can write Eq.(23)asψt+1=ψt[p3ψ2t+3p2ψt(1−x t−ψt)+3p1(1−x t−ψt)2+3(b+c)(x t+ψt)2(24) +3(b′+c′)ψt(x t−ψt)+9(b′′+c′′)(x t−ψt)(1−x t−ψt)].Finally,considering the case p3=0,we have(b+c)=p2,(b′+c′)=p1and (b′′+c′′)=|p1−p2|;inserting these values in Eq.(24)we obtainψt+1=3ψt{3|p1−p2|ψ2t+[(p2−2p1)−3|p1−p2|+3(p1−p2)x t]ψt(25) +[(p1+p2−3|p1−p2|)x2t+(3|p1−p2|−2p1)x t+p1]}.This equation can be iterated numerically using the stationary values of x t ob-tained from Eq.(15);there are three possibilities for the joint solutions of Eq.(15)and Eq.(25):x=ψ=0,corresponding to the phase0;x=0,ψ=0, corresponding to the active phase;and x,ψ=0,corresponding to the chaotic phase.In Fig.4we show the stationary solutions for these equations for some values of p2.We note that there is a discontinuous DS transition line in this approximation:for p2>p t(p2=0.9in Fig.4,for example),ψis always positive if x>0.It implies that the DS transition line for p2>p t falls on the discontinuous transition analysed in subsection III A.IV.SIMULATION RESULTSWe construct the BPCA phase diagram,for p3=0and p3=1,using simu-lations of systems of up to L=10000sites(with periodic boundaries),applying the growth exponent method[22]to locate the transition lines.The initial con-dition used in the simulations is random,with half the sites occupied.The phase diagrams for absorbing-state transitions are shown in Figs.1and2,for p3=1 and p3=0,respectively.As expected,the pair approximation yields a better prediction than does one-site mean-field theory.Note that for p3=0,the phase diagram is qualitatively the same as for the DKCA[18,22];the major difference is that the active phase is quite enlarged in the BPCA.For p3=1,the pair approximation prediction for the phase boundaries is qualitatively correct,although the bicritical point remains in the same position (p1=1/3,p2=2/3),as in the site approximation.Simulations place the bicritical point at(0.460(3),0.540(3)),but the phase boundaries are in reasonable agree-ment with the pair approximation prediction.It is important to note that there are only three transitions in this diagram:the phase0/phase1transition(discon-tinuous)and the phase0/active and active/phase1transitions(continuous).All transitions are located using the growth-exponent method,confirming that this method is able to detect both continuous and discontinuous phase transitions.The phase diagrams for the DS transition are shown in Figs.5and6,for p3=0 and p3=1respectively.In the case p3=1,we confirm the results of Bagnoli et al.,but some comments are in order.In Ref.[9],the authors sketched several “damaged domains”that appear along the active/absorbing phase boundary, and attributed them to the divergence of the relaxation time,or to the fact that small differences in the initial configuration can drive the system to a different absorbing state.As shown in Fig.7,where we compare the DS transitions obtained using(1)“rotation”damage and(2)random damage in10%of the sites, these domains are only associated with the absorbing-state transition.We see two maxima in theβw×p1curves in Fig.7:the left maximum,more pronounced, that corresponds to the absorbing/active transition,and the right maximum, which actually corresponds to the nonchaotic/chaotic transition and belongs to the DP class.The left maximum can yields to an“apparent”DS transition,as the‘islands’of damage commented in the Ref.[9].Thus,the left maximum corresponds to the“damage domains”of the Ref.[9],but in fact it is due the absorbing/active transition:in this region,when the replica is created(in the stationary state),it turns out that only a small region of the ring is active,which results in a constant contribution to the Hamming distance(proportional to2ρ∗with rotation damage,and to2ρ(t),with random damage).Thus,with rotation damage,the exponentβw approaches1because the system is already in the stationary state,while with the random damage,βw∼0.84,due decay of the activity,recovering the DP value.This behavior should not be confused with the true damage transition that occurs only at the second maximum,and which corresponds to a unique phase boundary,as shown in Fig.6.In the case p3=0,the simulations confirm the reentrant chaotic transition predicted by the one-site mean-field approximation.As shown in Fig.5,the DS transition line is concave inward toward the active phase,and presents distinct behaviors for p1>p2and p1<p2,as expected.We note that the simulation results suggest a sudden cnahge in the orientation of the active/chaotic phase boundary where the latter crosses the line p2=p1.Such discontinuity of slope, clearly evident in the MF prediction,may be a consequence of the singular be-havior of several transition probabilities on p1−p2parameters space,as shown in Table II and Eq.(25).V.CONCLUSIONSIn this work we apply the growth-exponent method in Monte Carlo simula-tions,and one-and two-site mean-field approximations,to construct the phase diagram of the BPCA for p3=1and p3=0.The method detects bothfirst-and second-order phase transitions,and also can be used to locate DS transitions. The exponent values indicate that all continuous phase transitions belong to the directed percolation universality class,while the exponent at the discontinuous phase transition agrees with the compact directed percolation value.Wefind evidence of a line of tricritical points in the(p1,p2,p3)parameter space,using the mean-field pair approximations.We alsofind a reentrant chaotic transition for p3=0in the meanfield approximation,that was confirmed by simulations.These observations illustrate the rich and at times surprising phase space structure found in simple nonequilibrium systems.Acknowledgements We thank the Brazilian agencies CNPq and Fapemig for financial support of this work.REFERENCES[1]S.Wolfram,Theory and Applications of Cellular Automata,(Word Scientific,Singapore,1986).[2]D.Farmer,T.Toffoli and S.Wolfram,editors,Cellular Automata,(NorthHolland,Amsterdan,1984).[3]P.Manneville,N.Boccara,G.Vichniac and R.Bidaux,editors,Cellular Au-tomata and Modeling of Complex Physical Systems,(Springer,Heidelberg, 1989).[4]H.Gutowitz,editor,Cellular Automata:Theory and Experiments,(North-Holland,Amsterdan,1990).[5]N.Boccara,E.Goles,S.Martinez and P.Picco,editors,Cellular Automataand Cooperative Phenomena,(Les Houches Workshop,Kluver,1993).[6]F.Bagnoli,J.Stat.Phys.85,151(1996).[7]A.Georges and P.Le Doussal,J.Stat.Phys.54,1011(1989).[8]E.Domany and W.Kinzel,Phys.Rev.Lett.53,311(1984).[9]F.Bagnoli,N.Boccara and R.Rechtman,Phys.Rev.E63,046116(2001).[10]P.Bhattacharyya,Eur.Phys.J B3,247-252(1998).[11]A.P.F.Atman,R.Dickman and J.G.Moreira,Phys.Rev.E66,016113(2002).[12]M.J.de Oliveira and J.E.Satulovsky,Phys.Rev.E55,6377-6383(1997).[13]S.Kwon,W.M.Hwang,H.Park,Phys.Rev.E59,4949-4952(1999).[14]T.E Harris Annals of Probability2,969-988(1974).[15]R.Dickman and M.A.Mu˜n oz,Phys.Rev.E62,7632-7637(2000).[16]W.Kinzel,Z.Physik B58,229-244(1985).[17]P.Grassberger,Z.Phys.B47,365(1982);[18]M.L.Martins,H.F.Verona de Resende,C.Tsallis and A.C.N.de Magalh˜a es,Phys.Rev.Lett.66,2045(1991).[19]P.Grassberger,J.Stat.Phys.79,13(1995).H.K.Janssen,Z.Phys.B42,151(1981).[20]J.Conway in Winning Ways,v.2,What is Life?,ch.25, E.Berlejamp,J.Conway and R.Guy,eds.,(Academic Press,New York,1982)[21]F.Bagnoli,R.Rechtman,and S.Ruffo,Physica A171,249(1991).[22]A.P.F.Atman and J.G.Moreira,Eur.Phys.J.B16,501(2000).[23]T.Tom´e,Physica A212,99(1994).[24]J.A.de Sales,M.L.Martins and J.G.Moreira,Physica A245,461(1997).[25]F.Family and T.Vics´e k,J.Phys A:Math Gen.18,L75(1985).[26]A.-L.Barab´a si and H.E.Stanley,Fractal Concepts in Surface Growth,(Cam-bridge Univ.Press,Cambridge,1995).TABLESTABLE I.BPCA transition probabilities1p3p2p10 01−p31−p21−p11σi,τi(1,1,1;1,1,1)(1,1,1;1,1,0)(1,1,1;1,0,0)1,10p2min(p1,p2)1,0p30b′′=max(p1−p2,0)0,100c′′=max(p2−p1,0)0,01−p31−p21−max(p1,p2)σi,τi(1,1,0;0,0,0)(1,0,0;1,0,0)(1,0,0;0,0,0)(0,0,0;0,0,0)Figure CaptionsFig. 1.Phase diagram for the BPCA,p3=1.One-and two-site mean-field approximations are compared with simulation results.Fig. 2.Phase diagram for the BPCA,p3=0.The meanfield approxima-tion predicts a tricritical point at(p2=2/3,p1=1/3),where a discontinuous boundary(dashed line)meets a continuous transition line.Fig. 3.Line of tricritical points and the critical surface in the(p1,p2,p3) parameter space,as predicted by pair level meanfield approximation.The tri-critical line ends near p3≃1/3,while at the site level it extends to p3=0,as shown in Fig.2.Fig. 4.Density of active sites and Hamming distance,in the mean-field ap-proximation,at site level,for p3=0.Note that for p2>2/3,the transition is discontinuous.Fig. 5.DS transition line,for p3=0.The one-site mean-field approximation (inset)is compared with simulation data(main graph).Reentrant behavior is observed in both cases.Fig. 6.DS transition line for p3=1.The DS boundary meets the absorbing transition lines for(p1,p2)near1.Fig.7.DS growth exponent for two different initial damages,for p3=1.The left maximum corresponds to the absorbing transition and the right maximum corresponds to the DS transition.0.20.40.60.81.0p 20.20.40.60.81.0p 21.0pp2p30.00.050.150.250.350.450.55ρ,ψ-0.050.150.350.550.75ρ,ψ-0.050.150.350.550.75ρ,ψsitedamagep 3=0p 2=0.25p 2=0.5p 2=0.90.20.40.60.81.0p 20.00.20.40.60.8 1.00.00.20.40.60.81.0p 20.550.650.750.850.950.400.600.801.00βw ‘‘rotation’’ damage10 % random damage。
