2021中考数学第二轮复习题型3 填空压轴题

合集下载

中考数学第二轮复习专题(14个)

中考数学二轮专题复习之一：配方法与换元法把代数式通过凑配等手段，得到完全平方式，再运用完全平方式是非负数这一性质达到增加问题的条件的目的，这种解题方法叫配方法．所谓换元法，就是在一个比较复杂的数学式子中，用新的变元去代替原式的一个部分或改造原来的式子，使它简化，使问题易于解决。

【范例讲析】：例1：填空题：1）．将二次三项式x 2+2x －2进行配方，其结果为。

2）．方程x 2+y 2+4x －2y+5=0的解是。

3）．已知M=x 2－8x+22，N=－x 2+6x －3，则M 、N 的大小关系为。

例2.已知△ABC 的三边分别为a 、b 、c ，且a 2+b 2+c 2=ab+bc+ac ，则△ABC 的形状为。

例3.解方程：422740x x --=【闯关夺冠】 1.已知13x x +=．则221x x+的值为__________． 2．若a 、b 、c 是三角形的三边长，则代数式a 2–2ab+b 2–c 2的值（） A 大于零 B 等于零 C 小于零 D 不能确定 3已知：a 、b 为实数，且a 2+4b 2－2a+4b+2=0，求4a 2－b1的值。

4. 解方程： 211()65()11x x +=--对于某些数学问题，若得知所求结果具有某种确定的形式，则可研究和引入一些尚待确定的系数(或参数)来表示这样的结果．通过变形与比较．建立起含有待定字母系数(或参数)的方程(组)，并求出相应字母系数(或参数)的值，进而使问题获解．这种方法称为待定系数法．【范例讲析】：【例1】二次函数的图象经过A(1，0)、B(3，0)、C(2，－1)三点．(1)求这个函数的解析式．(2)求函数与直线y=－x+1的交点坐标．【例2】一次函数的图象经过反比例函数xy 8-=的图象上的A 、B 两点，且点A 的横坐标与点B 的纵坐标都是2。

（1）求这个一次函数的解析式；（2）若一条抛物线经过点A 、B 及点C （1，7），求抛物线的解析式。

专题3 填空压轴题之几何求值-备战2022年中考数学满分真题模拟题分类之压轴题汇编(深圳专用解析版)

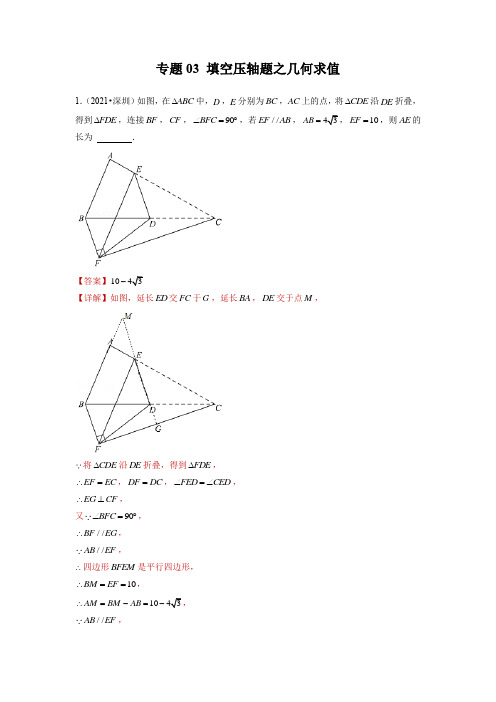
专题03 填空压轴题之几何求值1．（2021•深圳）如图，在ABC ∆中，D ，E 分别为BC ，AC 上的点，将CDE ∆沿DE 折叠，得到FDE ∆，连接BF ，CF ，90BFC ∠=︒，若//EF AB ，43AB =，10EF =，则AE 的长为．【答案】1043-【详解】如图，延长ED 交FC 于G ，延长BA ，DE 交于点M ，将CDE ∆沿DE 折叠，得到FDE ∆，EF EC ∴=，DF DC =，FED CED ∠=∠，EG CF ∴⊥，又90BFC ∠=︒，//BF EG ∴，//AB EF ，∴四边形BFEM 是平行四边形，10BM EF ∴==，1043AM BM AB ∴=-=-，//AB EF ，M FED∴∠=∠，M CED AEM∴∠=∠=∠，1043 AE AM∴==-2．（2020•深圳）如图，在四边形ABCD中，AC与BD相交于点O ，90ABC DAC∠=∠=︒，1tan2ACB∠=，43BOOD=，则ABDCBDSS∆∆=．【答案】332【详解】如图，过点D作//DM BC，交CA的延长线于点M，延长BA交DM于点N，//DM BC，ABC ANM∴∆∆∽，OBC ODM∆∆∽，∴1tan2AB ANACBBC NM==∠=，43BC OBDM OD==，又90ABC DAC∠=∠=︒，90BAC NAD∴∠+∠=︒，90BAC BCA∠+∠=︒，NAD BCA∴∠=∠，ABC DAN∴∆∆∽，∴12AB DNBC NA==，设4BC a=，由43BC OBDM OD==得，3DM a=，2AB a∴=，35DN a=，65AN a=，616255NB AB AN a a a∴=+=+=，∴22313521323225ABDBCDaAB DNSS BC NB a∆∆⋅===⋅．3．（2019•深圳）如图，在正方形ABCD 中，1BE =，将BC 沿CE 翻折，使B 点对应点刚好落在对角线AC 上，将AD 沿AF 翻折，使D 点对应点刚好落在对角线AC 上，求EF = ．【答案】6 【详解】如图，作FM AB ⊥于点M ．四边形ABCD 是正方形，45BAC CAD ∴∠=∠=︒．将BC 沿CE 翻折，B 点对应点刚好落在对角线AC 上的点X ，1EX EB AX ∴===，90EXC B ∠=∠=︒，222AE AX EX ∴=+=．将AD 沿AF 翻折，使D 点对应点刚好落在对角线AC 上的点Y ，1AM DF YF ∴===，∴正方形的边长21AB FM ==+，21EM =-，2222(21)(21)6EF EM FM ∴=+=-++=．4．（2018•深圳）在Rt ABC ∆中，90C ∠=︒，AD 平分CAB ∠，BE 平分ABC ∠，AD 、BE 相交于点F ，且4AF =，2EF =，则AC = ．【答案】8105 【详解】如图，过点E 作EG AD ⊥于G ，连接CF ， AD ，BE 是分别是BAC ∠和ABC ∠的平分线， CAD BAD ∴∠=∠，CBE ABE ∠=∠，90ACB ∠=︒，2()90BAD ABE ∴∠+∠=︒，45BAD ABE ∴∠+∠=︒，45EFG BAD ABE ∴∠=∠+∠=︒，在Rt EFG ∆中，2EF =，1FG EG ∴==，4AF =，3AG AF FG ∴=-=，根据勾股定理得，2210AE AG EG =+=，AD 平分CAB ∠，BE 平分ABC ∠，CF ∴是ACB ∠的平分线，45ACF AFE ∴∠=︒=∠，CAF FAE ∠=∠，AEF AFC ∴∆∆∽，∴AE AF AF AC=， 216810510AF AC AE ∴===5．（2017•深圳）如图，在Rt ABC ∆中，90ABC ∠=︒，3AB =，4BC =，Rt MPN ∆，90MPN ∠=︒，点P 在AC 上，PM 交AB 于点E ，PN 交BC 于点F ，当2PE PF =时，AP = ．【答案】3【详解】如图作PQ AB ⊥于Q ，PR BC ⊥于R ．90PQB QBR BRP ∠=∠=∠=︒，∴四边形PQBR 是矩形，90QPR MPN ∴∠=︒=∠，QPE RPF ∴∠=∠，QPE RPF ∴∆∆∽， ∴2PQ PE PR PF ==， 22PQ PR BQ ∴==，//PQ BC ，::::3:4:5AQ QP AP AB BC AC ∴==，设4PQ x =，则3AQ x =，5AP x =，2BQ x =， 233x x ∴+=，35x ∴=， 53AP x ∴==．6．（2021•深圳模拟）如图，在四边形ABCD 中，AE 平分BAD ∠交CD 于点E ，且AB AE =，12CBA D BAD ∠=∠+∠，过点E 作EG AB ⊥，垂足为G ．延长BC 和AE 交于点F ，若:2:1BF ED =，2EG =，三角形ABF 的面积为7，则AD = ．【答案】72 【详解】解法一：如图，过A 作AM BF ⊥于M ，作AN CD ⊥于N ，过E 作EH AD ⊥于H ，90AMB ANE ∴∠=∠=︒，AE 平分BAD ∠交CD 于点E ，12BAE DAE BAD ∴∠=∠=∠， 12CEA DAE ADE BAD ADE ∠=∠+∠=∠+∠， 12CBA D BAD ∠=∠+∠， CEA CBA ∴∠=∠，AED ABM ∴∠=∠，AB AE =，()ABM AEN AAS ∴∆≅∆，AM AN ∴=，12ABF S BF AM ∆=⋅，12AED S DE AN ∆=⋅，且2BF ED =， 2ABF AED S S ∆∆∴=， 7ABF S ∆=，72AED S ∆∴=， AE 平分BAD ∠，EG AB ⊥，EH AD ⊥，2EH EG ∴==，1722AED S AD EH ∆∴=⋅=， 72AD ∴=；解法二：过D 作DM AE ⊥于M ，过F 作FN AB ⊥，交AB 的延长线于N ， AE 平分BAD ∠交CD 于点E ，12BAE DAE BAD ∴∠=∠=∠， 12CEA DAE ADE BAD ADE ∠=∠+∠=∠+∠， 12CBA D BAD ∠=∠+∠， CEA CBA ∴∠=∠，AED FBN ∴∠=∠，90DME FNB ∠=∠=︒，DME FNB ∴∆∆∽，∴12ED DM BF FN ==， 2FN DM ∴=，112722ABF S AB FN AE DM ∆=⋅=⋅=， 7AE DM ∴⋅=，BAE DAE ∠=∠，90AGE AMD ∠=∠=︒，AGE AMD ∴∆∆∽，∴EG AE DM AD =， ∴2AE DM AD=，722DM AE AD ⋅∴==．7．（2021•龙岩模拟）将含30︒角且大小不等的两个三角板按如图摆放，使直角顶点重合，连接AE 、BD ，则AE BD = ．【答案】3【详解】EDC ∆与ACB ∆为两个直角三角形，且30DEC BAC ∠=∠=︒，90ACB ECD ∠=∠=︒， ACB DCA ECD DCA ∴∠+∠=∠+∠，DCB ECA ∴∠=∠，在Rt ACB ∆中，tan tan30BC CAB AC∠==︒，在Rt ECD ∆中，tan tan30DC CED EC ∠==︒， ∴BC DC AC EC=， ∴在ECA ∆与DCB ∆中，DC BC EC AC=， DCB ECA ∠=∠，ECA DCB ∴∆∆∽，∴AE AC BD BC=，在Rt ACB ∆中，tan tan 603AC ABC BC =∠=︒= 8．（2021•南山区一模）如图，在Rt ABC ∆中，90C ∠=︒，BE ，AF 分别是ABC ∠，CAB ∠平分线，BE ，AF 交于点O ，OM AB ⊥，10AB =，8AC =，则OM = ．【答案】2【详解】过O 作OG AC ⊥于G ，OH BC ⊥于H ，连接OC ，AF 平分CAB ∠，BE 平分ABC ∠，OG OH OM ∴==，90C ∠=︒，10AB =，8AC =，221086BC ∴=-=11112222ABC S AC BC AB OM AC OG BC OH ∆∴=⋅=⨯⋅+⋅+⋅， ∴11118610862222OM OG OH ⨯⨯=⨯⨯+⨯⨯+⨯⨯， 2OM ∴=9．（2021•深圳模拟）如图，在ABC ∆中，45B ∠=︒，62AB =，D 、E 分别是AB 、AC 的中点，连接DE ，在直线DE 和直线BC 上分别取点F 、G ，连接BF 、DG ．若3BF DG =，且直线BF 与直线DG 互相垂直，则BG 的长为．【答案】4或2【详解】如图，过点B 作BT BF ⊥交ED 的延长线于T ，过点B 作BH DT ⊥于H ．DG BF ⊥，BT BF ⊥，//DG BT ∴，AD DB =，AE EC =，//DE BC ∴，∴四边形DGBT 是平行四边形，BG DT ∴=，DG BT =，45BDH ABC ∠=∠=︒， 32AD DB ==， 3BH DH ∴==， 90TBF BHF ∠=∠=︒，90TBH FBH ∴∠+∠=︒，90FBH F ∠+∠=︒，TBH F ∴∠=∠，1tan tan 3BT DG F TBH BF BF ∴∠=∠===， ∴13TH BH =， 1TH ∴=，134DT TH DH ∴=+=+=，4BG ∴=．当点F 在ED 的延长线上时，同法可得312DT BG ==-=．10．（2021•福田区二模）如图，点M 是Rt ABC ∆斜边AB 的中点，过点M 作DM CM ⊥，交AC 于点D ，若2AD =，5BC =，则CD = ．【答案】29【详解】延长CM，使CM MN=，连接AN，点M是Rt ABC∆斜边AB的中点，AM BM∴=，在AMN∆和BMC∆中，AM BMAMN BMCMN CM=⎧⎪∠=∠⎨⎪=⎩，()AMN BMC SAS∴∆≅∆，5BC AN∴==，NAM B∠=∠，//AN BC∴，90BCA∠=︒，90NAD∴∠=︒，22225229DN AN AD∴=+=+=，DM CM⊥，CM MN=，29CD DN∴==．11．（2021•深圳模拟）如图，在Rt ABC∆中，90BAC∠=︒，D为BC的中点，过点D作DE DF⊥，交BA的延长线于点E，交AC的延长线于点F．若72CF=，4AC=，2AB=．则AE=．【答案】10【详解】延长FD 至G ，使GD FD =，连接BG ，如图所示： D 为BC 的中点，BD CD ∴=，在BDG ∆和CDF ∆中，BD CD BDG CDF GD FD =⎧⎪∠=∠⎨⎪=⎩，()BDG CDF SAS ∴∆≅∆，72BG CF ∴==，G F ∠=∠， //BG CF ∴， BGH AFH ∴∆∆∽， ∴77271542GH BH BG FH AH AF ====+， ∴411DH FD =，15152211AH AB ==， 90BAC ∠=︒，152AF AC CF =+=， 221515755()()21122HF ∴=+=， 41051511DH FH ∴==， DE DF ⊥，90EDH BAC ∴∠=︒=∠，90E EHD F EHD ∴∠+∠=∠+∠=︒，E F ∴∠=∠，DHE AHF ∴∆∆∽，∴HE DH HF AH=，即10511157551122HE=，解得：12511HE=，12515101111AE HE AH∴=-=-=；12．（2021•宝安区二模）如图，在等腰Rt ABC∆中，90B∠=︒，BA BC=，D为BC上一点，且3BD=，E为AD上一点，连接CE，45CED∠=︒，2CE AE=，则CE的长为．【答案】1855【详解】过A作AN CE⊥的延长线于N，过C作CM AD⊥交AD延长线于M，2CE AE=，∴设AE a=，则2CE a=，3445∠=∠=︒，AN NE ∴=，45ECM ∠=︒，90B ∠=︒，BA BC =，45ACD ∴∠=︒，12∴∠=∠，AEN ∴∆，CEM ∆都是等腰直角三角形， 2CE a =，AE a =， CM EM a ∴==，22AN NE a ==， 12∠=∠，CDM CAN ∴∆∆∽，∴CM CD CN AC=， 22NE a =，2CE a =， 322NC a ∴=， 222213255222AC AN NC a a a a ∴=+=+==， ∴3252aCD a a =，103CD a ∴=， 1033BC a ∴=+，在Rt ABC ∆中，45BAC ∠=︒，sin BC BAC AC∴∠=， sin45BC AC ∴=︒⋅，即1023532a a +=⨯， 9105a ∴=， 9101852255CE a ∴==⨯=． 13．（2021•宝安区期末）如图，在ABC ∆中，AB AC =，点D 、E 是BC 边上两点，连接AD ，以AD 为腰作等腰直角ADF ∆，90ADF ∠=︒，作FE BC ⊥于点E ，FE CE =，若2BD =，5CE =，则CDF S ∆=．【答案】30 【详解】过点A 作AH BC ⊥于H ，90AHD ∴∠=︒，FE BC ⊥，90DEF ∴∠=︒，ADF ∆是等腰直角ADF ∆，AD DF ∴=，90ADF ADH EDF ∠=∠+∠=︒，90ADH DAH ∴∠+∠=︒，EDF DAH ∴∠=∠，在ADH ∆和DFE ∆中，DAH EDF AHD DEF AD FD ∠=∠⎧⎪∠=∠⎨⎪=⎩，()ADH DFE AAS ∴∆≅∆，5CE =，5DH EF ∴==，7BH CH ∴==（三线合一）， ∴12CDF S DC EF ∆=⨯⨯11252=⨯⨯30=．14．（2021•罗湖区期末）如图，在ABC∆中，90ACB∠=︒，点D 是BC上的一点，AC DC=，AB AE⊥，且AE AB=，连接DE交AC的延长线于点F，32ACCF=，则BDCD=．【答案】43【详解】在DC上截取CG CF=，连接AG，32ACCF=，设3AC x=，2CF x=，AC DC=，3CD x∴=，CG CF=，2CG x∴=，90ACB∠=︒，在Rt ACG∆和Rt DCF∆中，AC CDACD DCFCG CF=⎧⎪∠=∠⎨⎪=⎩，()ACG DCF SAS∴∆≅∆，CAG CDF∴∠=∠，90AGB CAG∠=∠+︒，90EFA CDF∠=︒+∠，AGB EFA∴∠=∠，AB AE⊥，90EAB∴∠=︒，90ACD∠=︒，AC CD=，45CAD∴∠=︒，45EAF BAD ∴∠+∠=︒，45ADC ABC BAD ∠=︒=∠+∠，EAF ABC ∴∠=∠，在EAF ∆和ABG ∆中，EAF ABC EFA AGB AE AB ∠=∠⎧⎪∠=∠⎨⎪=⎩，()EAF ABG AAS ∴∆≅∆，5BG AF x ∴==，32GD x x x =-=，4BD x ∴=， ∴43BDCD =15．（2020•崇州市模拟）如果点P 是ABC ∆内一点，且它到三角形的三个顶点距离之和最小，则P 点叫ABC ∆的费马点．已经证明：在三个内角均小于120︒的ABC ∆中，当120APB APC BPC ∠=∠=∠=︒时，P 就是ABC ∆的费马点．若点P 是腰长为2的等腰直角三角形DEF 的费马点，则PD PE PF ++= ．【答案】31+【详解】如图：过点D 作DM EF ⊥于点M ，在BDE ∆内部过E 、F 分别作30MEP MFP ∠=∠=︒，则120EPF FPD EPD ∠=∠=∠=︒，点P 就是费马点，在等腰Rt DEF ∆中，2DE DF ==，DM EF ⊥，22EF DE ∴==1EM DM ∴==，故cos30EM PE ︒=，解得：233PE =，则33PM =，故313DP =-，同法可得233PF = 则233213133PD PE PF ++=⨯+-=+．16．（2021•深圳模拟）如图，在ABC ∆中，5AB AC ==，45BC =，D 为边AB 上一动点(B 点除外），以CD 为一边作正方形CDEF ，连接BE ，则BDE ∆面积的最大值为．【答案】8【详解】过点C 作CG BA ⊥于点G ，作EH AB ⊥于点H ，作AM BC ⊥于点M ． 5AB AC ==，45BC =，25BM CM ∴==，易证AMB CGB ∆∆∽，∴BM AB GB CB=，即25545GB = 8GB ∴=，设BD x =，则8DG x =-，易证()EDH DCG AAS ∆≅∆，8EH DG x ∴==-，2111(8)(4)8222BDE S BD EH x x x ∆∴==-=--+，当4x =时，BDE ∆面积的最大值为8．17．（2021•光明区二模）如图，扇形OPQ 可以绕着正六边形ABCDEF 的中心O 旋转，若120POQ ∠=︒，OP 等于正六边形ABCDEF 边心距的2倍，2AB =，则阴影部分的面积为．【答案】423π-【详解】连接OE ，OD ，OC ．设EF 交OP 于T ，CD 交OQ 于J ．120POQ EOC ∠=∠=︒，EOT COJ ∴∠=∠，OE OJ =，60OET OCJ ∠=∠=︒，()EOT COJ ASA ∴∆≅∆，2322234OTEDJ OEDC S S ∴==⨯⨯=五边形四边形， 2120(23)23423360OPQ OTEDJ S S S ππ⋅⋅∴=-=-=-阴扇形五边形 18．（2021•深圳二模）如图Rt ABC ∆中，90BAC ∠=︒，3AB =，4AC =，点P 为BC 上任意一点，连接PA ，以PA ，PC 为邻边作平行四边形PAQC ，连接PQ ，则PQ 的最小值为．【答案】12 5【详解】90BAC∠=︒，3AB=，4AC=，225BC AC AB∴=+=，四边形APCQ是平行四边形，PO QO∴=，CO AO=，PQ最短也就是PO最短，∴过O作BC的垂线OP'，ACB P CO∠=∠'，90CP O CAB∠'=∠=︒，CAB∴∆∽△CP O'，∴CO OP BC AB'=，∴253OP' =，65 OP∴'=，∴则PQ的最小值为1225 OP'=，方法二：不用相似的方法，只利用等面积得，OC AB BC OP'=，求得OP'，而其他部分的步骤共用．19．（2020•九龙坡区校级月考）如图，Rt ABC∆中，AB BC⊥，6AB=，4BC=，点D是ABC∆内一个动点，且满足DAB DBC∠=∠，当线段CD取最小值时，记BCDα∠=，线段AB 上一动点E绕着点D顺时针旋转得到点F，且满足EDFα∠=，则AF的最小值．【答案】125 【详解】AB BC ⊥，6AB =、4BC =， 90DBC ABD ∴∠+∠=︒，DAB DBC ∠=∠，设DAB DBC β∠=∠=，90DAB ABD ∴∠+∠=︒，90ADB ∴∠=︒，∴点D 在以AB 为直径的圆上，设圆心为O ，半径为132AB =，则当O 、D 、C 三点共线时CD 最小，3OD OB OA ∴===，225OC OB BC ∴=+=，将DA 绕点D 逆时针旋转α，得到DG ，连接GE ，DG DA ∴=，GDA EDF α∠=∠=，GDE ADF ∴∠=∠，DE DF =，()GDE ADF SAS ∴∆≅∆，GE AF ∴=，∴当GE AB ⊥时，GE 最小，即AF 最小，过点D 作DM AB ⊥于M ，过点G 作GH DM ⊥，交DM 的延长线于点H ，//DM BC ∴，四边形GHME 为矩形．OMD OBC ∴∆∆∽，GE HM =，∴DM OM OD BC OB OC ==， ∴3435DM OM ==， 125DM ∴=，95OM =， 924355AM OM OA ∴=+=+=， DAB DBC β∠=∠=，OA OD =，ODA OAD β∴∠=∠=，2BOC ODA OAD β∴∠=∠+∠=．在Rt OBC ∆中，90OCB BOC ∠=︒-∠，902αβ∴=︒-，90MAD MDA ∠+∠=︒，90GDH βα∴++∠=︒，GDH DAM β∴∠==∠，90DHG AMD ∠=∠=︒，AD DG =，()GDH DAM AAS ∴∆≅∆．245DH AM ∴==， 125HM DH DM ∴=-=，即AF 的最小值为125． 20．（2021•南山区二模）矩形ABCD 中，4AB =，6BC =，点E 为BC 的中点，沿AE 将AEB ∆翻折得到AFE ∆，sin FCE ∠= ．【答案】45【详解】如图，过E 作EH CF ⊥于H ，由折叠的性质得：BE EF =，BEA FEA ∠=∠，点E 是BC 的中点，3CE BE ∴==，3EF CE ∴==，FEH CEH ∴∠=∠，90AEB CEH ∴∠+∠=︒，在矩形ABCD 中，90B ∠=︒，90BAE BEA ∴∠+∠=︒，BAE CEH ∴∠=∠，B EHC ∠=∠，ABE EHC ∴∆∆∽， ∴AB AE EH CE =， 22435AE =+=，125EH ∴=， 4sin 5EH ECF CE ∴∠==． 21．（2021•龙岗区二模）如图，已知在菱形ABCD ，9BC =，60ABC ∠=︒，点E 在BC 上，且6BE =，将ABE ∆沿AE 折叠得到△AB E '，其中B E '交CD 于点F ，则CF = ．【答案】95【详解】过点A 作AG BC ⊥交BC 于G ，取HG 使HG GE =，过H 作HM AE ⊥于H ，过F 作FN BC ⊥交BC 延长线于N ，四边形ABCD 是菱形，在Rt ABG ∆中，60B ∠=︒， 3sin sin 602AG B AB ∴=︒==， 39322AG AB ∴==， 1cos cos602BG B AB =︒==， 1922BG AB ∴==， 6BE =，922()2(6)32HE GE BE BG ∴==-=⨯-=，在Rt AGE ∆中，222439633744AE AG GE =+=+==， 1122AHE S HE AG AE HM ∆=⨯⨯=⨯⨯， ∴131337222HM ⨯⨯=⨯⨯，解得，92114HM =， HG GE =，AG HE ⊥，AHE ∴∆是等腰三角形，AH AE ∴=，AHE HEA ∠=∠，在Rt AHM ∆中，222229211064739763()1419614AM AH HM AE HM =-=-=-==， //AB CD ，60FCN B ∴∠=∠=︒，∴tan 603FN CN=︒=，折叠，AEB HEA ∴∠'=∠，在Rt AHE ∆中，1801802HAE HEA AHE HEA ∠=︒-∠-∠=︒-∠，又1801802FEN HEA AEB HEA ∠=︒-∠-∠'=︒-∠，设CN x =，3FN x =， tan tan FN HM FEC HAM EN AM ∠=∠==，∴921314339714x x =+， ∴333313x x =+， 910x ∴=， 9931010CN FN ∴==， 22189105CF CN FN ∴=+==． 22．（2021•深圳模拟）如图，矩形ABCD 中，13AE AD =，将ABE ∆沿BE 折叠后得到GBE ∆，延长BG 交CD 于F 点，若3CF FD ==，则BC 的长为．【答案】66【详解】延长BF 交AD 的延长线于点H ，四边形ABCD 是矩形，AD BC ∴=，//AD BC ，90A BCF ∠=∠=︒， H CBF ∴∠=∠，在BCF ∆和HDF ∆中，CBF H BCF DFH CF DF ∠=∠⎧⎪∠=∠⎨⎪=⎩，()BCF HDF AAS ∴∆≅∆，将ABE ∆沿BE 折叠后得到GBE ∆，90A BGE ∴∠=∠=︒，AE EG =，90EGH ∴∠=︒， 13AE AD =， ∴设AE EG x ==，则3AD BC DH x ===， 2ED x ∴=，5EH ED DH x ∴=+=，在Rt EGH ∆中，1sin 55EG x H EH x ∠===， 1sin 5CF CBF BF ∴∠==， ∴315BF =， 15BF ∴=，222215366BC BF CF ∴=-=-=23．（2021•葫芦岛二模）如图，在矩形ABCD 中，15AB =，8AD =，E 为AB 边上一点，将BEC ∆沿CE 翻折，点B 落在点F 处，当AEF ∆为直角三角形时，AE = ．【答案】7或515【详解】①如图，若90AEF ∠=︒，90B BCD AEF ∠=∠=︒=∠，∴四边形BCFE 是矩形，将BEC ∆沿着CE 翻折，∴四边形BCFE 是正方形，8BE BC AD ∴===，1587AE AB BE ∴=-=-=；②如图，若90AFE ∠=︒，将BEC ∆沿着CE 翻折，8CB CF ∴==，90B EFC ∠=∠=︒，BE EF =， 180AFE EFC ∠+∠=︒，∴点A ，点F ，点C 三点共线， 222215817AC AB BC ∴=+=+=，9AF AC CF ∴=-=，222AE AF EF =+，2281(15)AE AE ∴=+-，515AE ∴=， ③若90EAF ∠=︒，158CD CF BC =>==，∴点F 不可能落在直线AD 上，∴不存在90EAF ∠=︒，综上所述：7AE =或515． 24．（2020•青羊区校级期末）如图1，在矩形ABCD 中，8AB =，10BC =，P 是边AD 上一点，将ABP ∆沿着直线BP 翻折得到△A BP '．当8AP =时，A D '= ．如图2，连接A C '，当2AP =时，此时△A BC '的面积为．【答案】217；60017 【详解】如图1，当8AP =时，由折叠知AB AP =，APB BPA '∠=∠，ABP A BP '∠=∠，90A BA P '∠=∠=︒， ∴四边形ABA P '是正方形，8A P '∴=，2PD =，222282217A D A P PD ''∴=+=+=．如图2，当2AP =时，过点A '作//MN AB ，交AD 于点M ，交BC 于点N ，∴四边形ABNM 为矩形，8AB MN ∴==，AM BN =，90AMN BNM ∠=∠=︒，设A M x '=，则8A N x '=-，设BN y =，则2PM y =-，在Rt PMA '∆中，222PM A M PA ''+=，222(2)2y x ∴-+=①，在Rt BNA '∆中，222BN A N A B ''+=，222(8)8y x ∴+-=②，由①②可得，4y x =，把4y x =代入①得，222(42)2x x -+=，解得，1617x =， 1612081717A N '∴=-=， 1112060010221717A BC S BC A N ''∴=⨯⨯=⨯⨯=． 25．（2021•坪山区二模）如图，在ABC ∆和ADE ∆中，90BAC DAE ∠=∠=︒，60C E ∠=∠=︒，点D 在BC 边上，AC 与DE 相交于点F ，3DF CF =，则AD BD= ．【答案】3【详解】连接EC ，如图，90BAC DAE ∠=∠=︒，60ACB AED ∠=∠=︒， AED ACB ∴∆∆∽，∴AE AD AC AB=，即AE AC AD AB=， 90BAC DAE ∠=∠=︒，BAC CAD DAE CAD ∴∠-∠=∠-∠，EAC DAB ∴∠=∠，EAC DAB ∴∆∆∽，∴AD BD AE EC=，ACE ABD ADE ∠=∠=∠，在Rt EAD ∆中，60AED ∠=︒，∴3AD AE=，∴3BD EC =， ∴33EC BD=，EFCAFD ∠=∠，ECF ADF ∠=∠， EFC AFD ∴∆∆∽，∴3AD DF EC CF==， ∴3333AD AD EC BD EC BD =⋅=⨯= 26．（2021•深圳模拟）如图所示的网格是正方形网格，则BAC DAE ∠-∠= ︒（点A ，B ，C ，D ，E 是网格线交点）．【答案】45【详解】如图，连接CG 、AG ，由勾股定理得：2222125AC AG ==+=，2221310CG =+=， 222AC AG CG ∴+=，90CAG ∴∠=︒，CAG ∴∆是等腰直角三角形，45ACG ∴∠=︒，//CF AB ，ACF BAC ∴∠=∠，在CFG ∆和ADE ∆中，90CF AD CFG ADE FG DE =⎧⎪∠=∠=︒⎨⎪=⎩，()CFG ADE SAS∴∆≅∆，FCG DAE∴∠=∠，45BAC DAE ACF FCG ACG∴∠-∠=∠-∠=∠=︒27．（2021•深圳模拟）如图，矩形ABCD中，E是AB上一点，连接DE，将ADE∆沿DE翻折，恰好使点A落在BC边的中点F处，在DF上取点O，以O为圆心，OF长为半径作半圆与CD相切于点G．若4AD=，则图中阴影部分的面积为．【答案】23 9【详解】连接OG，QG，将ADE∆沿DE翻折，恰好使点A落在BC边的中点F处，4AD DF∴==，2BF CF==，矩形ABCD中，90DCF∠=︒，30FDC∴∠=︒，60DFC∴∠=︒，O与CD相切于点G，OG CD∴⊥，BC CD⊥，//OG BC∴，DOG DFC∴∆∆∽，∴DO OG DF FC=，设OG OF x==，则442x x-=，解得：43x =，即O 的半径是43．连接OQ ，作OH FQ ⊥， 60DFC ∠=︒，OF OQ =， OFQ ∴∆为等边三角形；同理OGQ ∆为等边三角形； 60GOQ FOQ ∴∠=∠=︒，32323OH OQ ==， 3232333QH ∴=⨯=， 23CQ ∴= 四边形OHCG 为矩形，233OH CG ∴==， 232311222339CGQ S S CQ CG ∆∴==⨯⨯=⨯⨯=阴影． 28．（2020•扬州）如图，在ABCD 中，60B ∠=︒，10AB =，8BC =，点E 为边AB 上的一个动点，连接ED 并延长至点F ，使得14DF DE =，以EC 、EF 为邻边构造EFGC ，连接EG ，则EG 的最小值为．【答案】93【详解】作CH AB ⊥于点H ，在ABCD 中，60B ∠=︒，8BC =，43CH ∴=，四边形ECGF 是平行四边形，//EF CG ∴，EOD GOC ∴∆∆∽，∴EO DO ED GO OC GC==，14DF DE =， ∴45DE EF =， ∴45ED GC =， ∴45EO GO =， ∴当EO 取得最小值时，EG 即可取得最小值，当EO CD ⊥时，EO 取得最小值，CH EO ∴=，43EO ∴=，53GO ∴=，EG ∴的最小值是9329．（2021•锡山区一模）如图，在平行四边形ABCD 中，60B ∠=︒，4BC =，点E 为边AB上的一个动点，连接ED 并延长至点F ，使得13DF DE =，以EC 、EF 为邻边构造平行四边形EFGC ，连接EG ，则EG 的最小值为．【答案】1433【详解】作CH AB ⊥于点H ，在ABCD 中，60B ∠=︒，4BC =，23CH ∴=，四边形ECGF 是平行四边形，//EF CG ∴，EOD GOC ∴∆∆∽， ∴EO DO ED GO CO GC ==， 13DF DE =， ∴34DE EF =， ∴34ED GC =， ∴34EO GO =， ∴当EO 取得最小值时，EG 即可取得最小值，当EO CD ⊥时，EO 取得最小值，CH EO ∴=，23EO ∴=，833GO ∴=， EG ∴的最小值是814233333+=30．（2021•龙岗区校级一模）如图，在矩形ABCD 中，5AC =，AE 平分DAC ∠交CD 于E ，CF 平分ACD ∠交AE 于点F ，且:1:2EF AF =，则CF = ．【答案】10【详解】作FG AC ⊥于点G ，作FM CD ⊥于点M ，作FN AD ⊥于点N ， CF 平分ACD ∠交AE 于点F ，且:1:2EF AF =，:1:2CE CA ∴=，5AC =， 52CE ∴=， AE 平分DAC ∠，CF 平分ACD ∠， FG FM FN ∴==， FM CD ⊥，AD CD ⊥，:1:2EF AF =， EMF EDA ∴∆∆∽，∴13MF EF DA EA ==，设FM x =，则3AD x =，同理可得，ANF AED ∆∆∽，则32DE x =， 5322CD x ∴=+， 90D ∠=︒，3AD x =，5AC =， 22253()(3)522x x ∴++=，解得11x =，253x =-（舍去）， 1FM ∴=，5311322CM =+⨯-=，又90CMF ∠=︒，221310CF ∴=+=，故答案为：10．。

备考2021年中考数学二轮复习：图形的性质_三角形_等边三角形的性质,填空题专训及答案

19、 (2020成都.中考模拟) 如图，在等边△ABC内任取一点D，连接CD，BD得到△CDB，如果等边△ABC内每一点被取到的可能性都相同，则△CBD是钝角三角形的概率是________．
20、
(2020连山.中考模拟) 如图，
为等边三角形，
上一动点，将射线绕点逆时针旋转，与射线为其内心，射线 Nhomakorabea交于点，当
交于点
，点为射线
时，的长度为________
备考 2021中考数学二轮复习：图形的性质 _三角形 _等边三角形的性质，填空题答案
1.答案：
2.答案： 3.答案： 4.答案： 5.答案： 6.答案： 7.答案： 8.答案： 9.答案： 10.答案： 11.答案：
7、 (2019南京.中考模拟) 小颖同学在手工制作中，把一个边长为12cm的等边三角形纸片贴到一个圆形的纸片上，若三角形的三个顶点恰好都在这个圆上，则圆的半径为________. 8、 (2020余杭.中考模拟) 如图，已知P为等边△ABC形内一点，且PA＝3cm，PB＝4 cm，PC＝5 cm，则图中△PBC的面积为________cm2.
17、 (2020通榆.中考模拟) 如图，在等边△ABC中，AB=8cm，D为BC中点.将△ABD绕点A逆时针旋转得到△ACE，则△A DE的周长为________ cm。
18、 (2020菏泽.中考真卷) 如图，在菱形部分的面积为________．
中，是对角线，
，⊙O与边相切于点D，则图中阴影
3、 (2017连云港.中考真卷) 如图，已知等边三角形OAB与反比例函数y= （k＞0，x＞0）的图象交于A、B两点，将△O AB沿直线OB翻折，得到△OCB，点A的对应点为点C，线段CB交x轴于点D，则的值为________．（已知sin15°=

2021年全国各地中考数学压轴题分类汇编(通用版)函数(二)(含答案与解析)

2021年全国各地中考数学压轴题分类汇编（通用版）函数（二）参考答案与试题解析一．选择题（共7小题）1．（2021•丹东）如图，点A在曲线到y1＝（x＞0）上，点B在双曲线y2＝（x＜0）上，AB//x 轴，点C是x轴上一点，连接AC、BC，若△ABC的面积是6，则k的值（）A．﹣6B．﹣8C．﹣10D．﹣12解：如图，连接OA，OB，AB与y轴交于点M，∵AB∥x轴，点A在曲线到y1＝（x＞0）上，点B在双曲线y2＝（x＜0）上，∴S△AOM＝×|2|＝1，S△BOM＝×|k|＝﹣k，∵S△ABC＝S△AOB＝6，∴1﹣k＝6，∴k＝﹣10．故选：C．2．（2021•丹东）已知抛物线y＝ax2+bx+c（a＞0），且a+b+c＝﹣，a﹣b+c＝﹣．判断下列结论：①abc＜0；②2a+2b+c＞0；③抛物线与x轴正半轴必有一个交点；④当2≤x≤3时，y最小＝3a；⑤该抛物线与直线y＝x﹣c有两个交点，其中正确结论的个数（）A．2B．3C．4D．5解：∵a+b+c＝﹣，a﹣b+c＝﹣，∴两式相减得b＝，两式相加得c＝﹣1﹣a，∴c＜0，∵a＞0，b＞0，c＜0，∴abc＜0，故①正确；∴2a+2b+c＝2a+2×﹣1﹣a＝a＞0，故②正确；∵当x＝1时，则y＝a+b+c＝﹣，当x＝﹣1时，则有y＝a﹣b+c＝﹣，∴当y＝0时，则方程ax2+bx+c＝0的两个根一个小于﹣1，一个根大于1，∴抛物线与x轴必有一个交点，故③正确；由题意知抛物线的对称轴为直线x＝＝，∴当2≤x≤3时，y随x的增大而增大，∴当x＝2时，有最小值，即为y＝4a+2b+c＝4a+1﹣1﹣a＝3a，故④正确；联立抛物线y＝ax2+bx+c及直线y＝x﹣c可得：x﹣c＝ax2+bx+c，整理得：，∴Δ＝，∴该抛物线与直线y＝x﹣c有两个交点，故⑤正确；∴正确的个数有5个；故选：D．3．如图，在平面直角坐标系中，点A、B在函数y＝（k＞0，x＞0）的图象上，过点A作x轴的垂线，与函数y＝﹣（x＞0）的图象交于点C，连结BC交x轴于点D．若点A的横坐标为1，BC ＝3BD，则点B的横坐标为（）A．B．2C．D．3解：作BE⊥x轴于E，∴AC∥BE，∴△CDF∽△BDE，∴＝＝，∵BC＝3BD，∴＝＝，∴CF＝2BE，DF＝2DE，设B（，b），∴C（1，﹣2b），∵函数y＝﹣（x＞0）的图象交于点C，∴﹣k＝1×（﹣2b）＝﹣2b，∴k＝2b，∴B的横坐标为＝＝2，故选：B．4．（2021•营口）如图，在平面直角坐标系中，菱形ABCD的边BC与x轴平行，A，B两点纵坐标分别为4，2，反比例函数y＝经过A，B两点，若菱形ABCD面积为8，则k值为（）A．﹣8B．﹣2C．﹣8D．﹣6解：∵四边形ABCD是菱形，∴AB＝BC，AD∥BC，∵A、B两点的纵坐标分别是4、2，反比例函数y＝经过A、B两点，∴x B＝，x A＝，即A（，4），B（，2），∴AB2＝（﹣）2+（4﹣2）2＝+4，∴BC＝AB＝，又∵菱形ABCD的面积为8，∴BC×（y A﹣y B）＝8，即×（4﹣2）＝8，整理得＝4，解得k＝±8，∵函数图象在第二象限，∴k＜0，即k＝﹣8，故选：A．5．（2021•陕西）在平面直角坐标系中，若将一次函数y＝2x+m﹣1的图象向左平移3个单位后，得到一个正比例函数的图象，则m的值为（）A．﹣5B．5C．﹣6D．6解：将一次函数y＝2x+m﹣1的图象向左平移3个单位后，得到y＝2（x+3）+m﹣1，把（0，0）代入，得到：0＝6+m﹣1，解得m＝﹣5．故选：A．6．（2021•本溪）如图，在矩形ABCD中，BC＝1，∠ADB＝60°，动点P沿折线AD→DB运动到点B，同时动点Q沿折线DB→BC运动到点C，点P，Q在矩形边上的运动速度为每秒1个单位长度，点P，Q在矩形对角线上的运动速度为每秒2个单位长度．设运动时间为t秒，△PBQ的面积为S，则下列图象能大致反映S与t之间函数关系的是（）A．B．C．D．解：∵四边形ABCD是矩形，∴AD＝BC＝1，∠A＝∠C＝90°，AD∥BC，∴∠ADB＝∠DBC＝60°，∴∠ABD＝∠CDB＝30°，∴BD＝2AD＝2，当点P在AD上时，S＝•（2﹣2t）•（1﹣t）•sin60°＝（1﹣t）2（0＜t＜1），当点P在线段BD上时，S＝（4﹣2t）•（t﹣1）＝﹣t2+t﹣（1＜t≤2），观察图象可知，选项D满足条件，故选：D．7．（2021•陕西）下表中列出的是一个二次函数的自变量x与函数y的几组对应值：x…﹣2013…y…6﹣4﹣6﹣4…下列各选项中，正确的是（）A．这个函数的图象开口向下B．这个函数的图象与x轴无交点C．这个函数的最小值小于﹣6D．当x＞1时，y的值随x值的增大而增大解：设二次函数的解析式为y＝ax2+bx+c，由题知，解得，∴二次函数的解析式为y＝x2﹣3x﹣4＝（x﹣4）（x+1）＝（x﹣）2﹣，∴（1）函数图象开口向上，（2）与x轴的交点为（4，0）和（﹣1，0），（3）当x＝时，函数有最小值为﹣，（4）函数对称轴为直线x＝，根据图象可知当x＞时，y的值随x值的增大而增大，故选：C．二．填空题（共2小题）8．（2021•长春）如图，在平面直角坐标系中，点A（2，4）在抛物线y＝ax2上，过点A作y轴的垂线，交抛物线于另一点B，点C、D在线段AB上，分别过点C、D作x轴的垂线交抛物线于E、F 两点．当四边形CDFE为正方形时，线段CD的长为﹣2+2．解：把A（2，4）代入y＝ax2中得4＝4a，解得a＝1，∴y＝x2，设点C横坐标为m，则CD＝CE＝2m，∴点E坐标为（m，4﹣2m），∴m2＝4﹣2m，解得m＝﹣1﹣（舍）或m＝﹣1+．∴CD＝2m＝﹣2+2．故答案为：﹣2+2．9．（2021•陕西）若A（1，y1），B（3，y2）是反比例函数y＝（m＜）图象上的两点，则y1、y2的大小关系是y1＜y2.（填“＞”、“＝”或“＜”）解：∵2m﹣1＜0（m＜），∴图象位于二、四象限，在每一个象限内，y随x的增大而增大，又∵0＜1＜3，∴y1＜y2，故答案为：＜．三．解答题（共16小题）10．（2021•吉林）如图，在平面直角坐标系中，一次函数y＝x﹣2的图象与y轴相交于点A，与反比例函数y＝在第一象限内的图象相交于点B（m，2），过点B作BC⊥y轴于点C．（1）求反比例函数的解析式；（2）求△ABC的面积．解：（1）∵B点是直线与反比例函数交点，∴B点坐标满足一次函数解析式，∴，∴m＝3，∴B（3，2），∴k＝6，∴反比例函数的解析式为；（2）∵BC⊥y轴，∴C（0，2），BC∥x轴，∴BC＝3，令x＝0，则y＝，∴A（0，﹣2），∴AC＝4，∴，∴△ABC的面积为6．11．（2021•陕西）已知抛物线y＝﹣x2+2x+8与x轴交于点A、B（点A在点B的左侧），与y轴交于点C．（1）求点B、C的坐标；（2）设点C′与点C关于该抛物线的对称轴对称．在y轴上是否存在点P，使△PCC′与△POB 相似，且PC与PO是对应边？若存在，求出点P的坐标；若不存在，请说明理由．解：（1）∵y＝﹣x2+2x+8，取x＝0，得y＝8，∴C（0，8），取y＝0，得﹣x2+2x+8＝0，解得：x1＝﹣2，x2＝4，∴B（4，0）；（2）存在点P，设P（0，y），若CC'是斜边，则PC＞PO，不合题意，舍去，∵CC'∥OB，且PC与PO是对应边，∴，即：，解得：y1＝16，，∴P（0，16）或P（0，）．12．（2021•长春）在平面直角坐标系中，抛物线y＝2（x﹣m）2+2m（m为常数）的顶点为A．（1）当m＝时，点A的坐标是（，1），抛物线与y轴交点的坐标是（0，）；（2）若点A在第一象限，且OA＝，求此抛物线所对应的二次函数的表达式，并写出函数值y 随x的增大而减小时x的取值范围；（3）当x≤2m时，若函数y＝2（x﹣m）2+2m的最小值为3，求m的值；（4）分别过点P（4，2）、Q（4，2﹣2m）作y轴的垂线，交抛物线的对称轴于点M、N．当抛物线y＝2（x﹣m）2+2m与四边形PQNM的边有两个交点时，将这两个交点分别记为点B、点C，且点B的纵坐标大于点C的纵坐标．若点B到y轴的距离与点C到x轴的距离相等，直接写出m 的值．解：（1）当m＝时，y＝2（x﹣）2+1，∴顶点A（，1），令x＝0，得y＝，∴抛物线与y轴交点的坐标为（0，），故答案为：（，1），（0，）；（2）∵点A（m，2m）在第一象限，且OA＝，∴m2+（2m）2＝（）2，且m＞0，解得：m＝1，∴抛物线的解析式为y＝2（x﹣1）2+2，当x＜1时，函数值y随x的增大而减小；（3）∵当x≤2m时，若函数y＝2（x﹣m）2+2m的最小值为3，∴分两种情况：2m＜m，即m＜0时，或2m＞m，即m＞0时，①当m＜0时，2（2m﹣m）2+2m＝3，解得：m＝（舍）或m＝﹣，②当m＞0时，2（m﹣m）2+2m＝3，解得：m＝，综上所述，m的值为或﹣；（4）如图1，当m＞0时，∵P（4，2）、Q（4，2﹣2m），∴M（m，2），N（m，2﹣2m），抛物线y＝2（x﹣m）2+2m与四边形PQNM的边有两个交点，若点B在PM边上，点C在MN边上，∴令y＝2，则2＝2（x﹣m）2+2m，∴x＝m+或x＝m﹣（不合题意，应舍去），∴B（m+，2），C（m，2m），根据题意，得2m＝m+，解得：m＝或m＝（不合题意，应舍去）；若点B在PM边上，点C在NQ边上，则2﹣2m＝m+，解得：m＝，经检验，m＝不符合题意，舍去，∴m＝，若点B在PQ边上，点C在NQ边上，则4＝2﹣2m，解得：m＝﹣1＜0，不合题意，舍去；当m＜0时，如图2，若点B在NQ边上，点C在PM边上，则2﹣2m＝2（x﹣m）2+2m，∴x＝m+或x＝m﹣（舍去），∴|m+|＝2，当m+＝2时，得m2﹣2m+3＝0，∵Δ＝（﹣2）2﹣4×1×3＝﹣8＜0，∴该方程无解；当m+＝﹣2时，得m2﹣6m+3＝0，解得：m＝3﹣或m＝3+，∵m＜0，∴均不符合题意；若点B在NQ边上，点C在MN边上，则|m+|＝|2m|，∴m+＝﹣2m或m+＝2m，∵m＜0，∴m＝﹣或m＝﹣1﹣，经验证，m＝﹣时，不符合题意；∴m＝﹣1﹣；若点B在PQ边上，点C在PM边上，显然点B到y轴的距离为4，点C到x轴的距离为2，不符合题意；综上所述，m的值为或或﹣1﹣．13．（2021•丹东）某超市销售一种商品，每件成本为50元，销售人员经调查发现，销售单价为100元时，每月的销售量为50件，而销售单价每降低2元，则每月可多售出10件，且要求销售单价不得低于成本．（1）求该商品每月的销售量y（件）与销售单价x（元）之间的函数关系式；（不需要求自变量取值范围）（2）若使该商品每月的销售利润为4000元，并使顾客获得更多的实惠，销售单价应定为多少元？（3）超市的销售人员发现：当该商品每月销售量超过某一数量时，会出现所获利润反而减小的情况，为了每月所获利润最大，该商品销售单价应定为多少元？解：（1）∵依题意，得：y＝50+（100﹣x）××10＝﹣5x+550，∴y与x的函数关系式为y＝﹣5x+550；（2）∵依题意得：y（x﹣50）＝4000，即（﹣5x+550）（x﹣50）＝4000，解得：x1＝70，x2＝90，∵70＜90，∴当该商品每月销售利润为4000，为使顾客获得更多实惠，销售单价应定为70元；（3）设每月总利润为w，依题意得w＝y（x﹣50）＝（﹣5x+550）（x﹣50）＝﹣5x2+800x﹣27500＝﹣5（x﹣80）2+4500，∵﹣5＜0，此图象开口向下，∴当x＝80时，w有最大值为4500元，∴为了每月所获利润最大，该商品销售单价应定为80元．14．（2021•吉林）如图，在平面直角坐标系中，二次函数y＝x2+bx+c的图象经过点A（0，﹣），点B（1，）．（1）求此二次函数的解析式；（2）当﹣2≤x≤2时，求二次函数y＝x2+bx+c的最大值和最小值；（3）点P为此函数图象上任意一点，其横坐标为m，过点P作PQ∥x轴，点Q的横坐标为﹣2m+1．已知点P与点Q不重合，且线段PQ的长度随m的增大而减小．①求m的取值范围；②当PQ≤7时，直接写出线段PQ与二次函数y＝x2+bx+c（﹣2≤x＜）的图象交点个数及对应的m的取值范围．解：（1）将A（0，﹣），点B（1，）代入y＝x2+bx+c得：，解得，∴y＝x2+x﹣．（2）∵y＝x2+x﹣＝（x+）2﹣2，∵抛物线开口向上，对称轴为直线x＝﹣．∴当x＝﹣时，y取最小值为﹣2，∵2﹣（﹣）＞﹣﹣（﹣2），∴当x＝2时，y取最大值22+2﹣＝．（3）①PQ＝|﹣2m+1﹣m|＝|﹣3m+1|，当﹣3m+1＞0时，PQ＝﹣3m+1，PQ的长度随m的增大而减小，当﹣3m+1＜0时，PQ＝3m﹣1，PQ的长度随m增大而增大，∴﹣3m+1＞0满足题意，解得m＜．②∵0＜PQ≤7，∴0＜﹣3m+1≤7，解得﹣2≤m＜，如图，当x＝﹣时，点P在最低点，PQ与图象有1交点，m增大过程中，﹣＜m＜，点P与点Q在对称轴右侧，PQ与图象只有1个交点，直线x＝关于抛物线对称轴直线x＝﹣对称后直线为x＝﹣，∴﹣＜m＜﹣时，PQ与图象有2个交点，当﹣2≤m≤﹣时，PQ与图象有1个交点，综上所述，﹣2≤m≤﹣或﹣≤m时，PQ与图象交点个数为1，﹣＜m＜﹣时，PQ 与图象有2个交点．15．（2021•大连）某电商销售某种商品一段时间后，发现该商品每天的销售量y（单位：千克）和每千克的售价x（单位：元）满足一次函数关系（如图所示），其中50≤x≤80．（1）求y关于x的函数解析式；（2）若该种商品的成本为每千克40元，该电商如何定价才能使每天获得的利润最大？最大利润是多少？解：（1）设y＝kx+b，将（50，100）、（80，40）代入，得：，解得：∴y＝﹣2x+200 （50≤x≤80）；（2）设电商每天获得的利润为w元，则w＝（x﹣40）（﹣2x+200）＝﹣2x2+280x﹣8000＝﹣2（x﹣70）2+1800，∵﹣2＜0，且对称轴是直线x＝70，又∵50≤x≤80，∴当x＝70时，w取得最大值为1800，答：该电商售价为70元时获得最大利润，最大利润是1800元．16．（2021•丹东）如图，已知点A（﹣8，0），点B（﹣5，﹣4），直线y＝2x+m过点B交y轴于点C，交x轴于点D，抛物线y＝ax2+x+c经过点A、C、D，连接AB、AC．（1）求抛物线的表达式；（2）判断△ABC的形状，并说明理由；（3）E为直线AC上方的抛物线上一点，且tan∠ECA＝，求点E的坐标；（4）N为线段AC上的动点，动点P从点B出发，以每秒1个单位长度的速度沿线段BN运动到点N，再以每秒个单位长度的速度沿线段NC运动到点C，又以每秒1个单位长度的速度沿线段CO向点O运动，当点P运动到点O后停止，请直接写出上述运动时间的最小值及此时点N的坐标．解：（1）∵直线y＝2x+m过点B（﹣5，4），交y轴于点C，∴﹣4＝2×（﹣5）+m，解得：m＝6，∴C（0，6），将A（﹣8，0）、C（0，6）代入，得：，解得：，∴抛物线的表达式为；（2）△ABC为直角三角形，且∠BAC＝90°，理由如下：∵点A（﹣8，0），点B（﹣5，﹣4），点C（0，6），∴AB2＝（﹣8+5）2+（0+4）2＝25，AC2＝（﹣8+0）2+（0﹣6）2＝100，BC2＝（﹣5+0）2+（﹣4﹣6）2＝125，∴AC2+AB2＝BC2，∴△ABC为直角三角形，且∠BAC＝90°；（3）由（2）知AB＝5，AC＝10，∴tan∠BCA＝＝tan∠ECA，∴∠BCA＝∠ECA，如图1，延长BA至F，使AF＝AB，连接CF，则点B、F关于点A对称，∴F（﹣11，4），∵∠BAC＝∠F AC＝90°，AF＝AB，AC＝AC，∴△F AC≌△BAC（SAS），∴∠BCA＝∠FCA，∴点E为直线CF与抛物线的交点，设直线CF的解析式为y＝kx+b，则，解得：，∴直线CF的解析式为，联立方程组，解得：或（舍去），故点E坐标为（，）；（4）过N作MN⊥BC于M，过F作FM'⊥BC交AC于N'，连接FN，则FN＝BN，∵AB＝5，BC＝，∴sin∠BCA＝，∴MN＝，又CO＝6，∴点P运动时间t＝＝BN+MN+6＝FN+MN+6≥FM'+6，当F、N、M三点共线时，t最小，∵AC＝10，BC＝，∴sin∠ABC＝，∴FM'＝，∴点P运动时间t的最小值为，由直线BC的表达式y＝2x+6得点D坐标为（﹣3，0），∵FD＝，∴点D与点M'重合，则点N（即N'）为直线FD与直线AC的交点，由点A（﹣8，0）和C（0，6）得直线AC的表达式为，由点F（﹣11，4）和D（﹣3，0）得直线FD的表达式为，联立方程组，解得：，∴此时N坐标为（﹣6，）．17．（2021•营口）某商家正在热销一种商品，其成本为30元/件，在销售过程中发现随着售价增加，销售量在减少．商家决定当售价为60元/件时，改变销售策略，此时售价每增加1元需支付由此产生的额外费用150元．该商品销售量y（件）与售价x（元/件）满足如图所示的函数关系（其中40≤x≤70，且x为整数）．（1）直接写出y与x的函数关系式；（2）当售价为多少时，商家所获利润最大，最大利润是多少？解：（1）设线段AB的表达式为：y＝kx+b（40≤x≤60），将点（40，300）、（60，100）代入上式得：，解得：，∴函数的表达式为：y＝﹣10x+700（40≤x≤60），设线段BC的表达式为：y＝mx+n（60＜x≤70），将点（60，100）、（70，150）代入上式得：，解得：，∴函数的表达式为：y＝5x﹣200（60＜x≤70），∴y与x的函数关系式为：y＝；（2）设获得的利润为w元，①当40≤x≤60时，w＝（x﹣30）（﹣10x+700）＝﹣10（x﹣50）2+4000，∵﹣10＜0，∴当x＝50时，w有值最大，最大值为4000元；②当60＜x≤70时，w＝（x﹣30）（5x﹣200）﹣150（x﹣60）＝5（x﹣50）2+2500，∵5＞0，∴当60＜x≤70时，w随x的增大而增大，∴当x＝70时，w有最大，最大值为：5（70﹣50）2+2500＝4500（元），综上，当售价为70元时，该商家获得的利润最大，最大利润为4500元．18．（2021•大连）已知函数y＝，记该函数图象为G．（1）当m＝2时，①已知M（4，n）在该函数图象上，求n的值；②当0≤x≤2时，求函数G的最大值．（2）当m＞0时，作直线x＝m与x轴交于点P，与函数G交于点Q，若∠POQ＝45°时，求m 的值；（3）当m≤3时，设图象与x轴交于点A，与y轴交与点B，过点B作BC⊥BA交直线x＝m于点C，设点A的横坐标为a，C点的纵坐标为c，若a＝﹣3c，求m的值．解：（1）当m＝2时，y＝，①∵M（4，n）在该函数图象上，∴n＝42﹣2×4+2＝10；②当0≤x＜2时，y＝﹣x2+x+2＝﹣（x﹣）2+2，∵﹣＜0，∴当x＝时，y有最大值是2，当x＝2时，y＝22﹣2×2+2＝2，∵2＜2，∴当0≤x≤2时，函数G的最大值是2；（2）分两种情况：①如图1，当Q在x轴上方时，由题意得：OP＝m，∵∠POQ＝45°，∠OPQ＝90°，∴△POQ是等腰直角三角形，∴OP＝PQ，∴m＝﹣+m+m，解得：m1＝0，m2＝6，∵m＞0，∴m＝6；②当Q在x轴下方时，同理得：m＝﹣﹣m 解得：m1＝0，m2＝14，∵m＞0，∴m＝14；综上，m的值是6或14；（3）分两种情况：①如图2，当0≤m≤3时，过点C作CD⊥y轴于D，当x＝0时，y＝m，∴OB＝m，∵CD＝m，∴CD＝OB，∵AB⊥BC，∴∠ABC＝∠ABO+∠CBD＝90°，∵∠CBD+∠BCD＝90°，∴∠ABO＝∠BCD，∵∠AOB＝∠CDB＝90°，∴△ABO≌△BCD（ASA），∴OA＝BD，当x＜m时，y＝0，即﹣x2+x+m＝0，x2﹣x﹣2m＝0，解得：x1＝，x2＝，∴OA＝，且﹣≤m≤3，∵点A的横坐标为a，C点的纵坐标为c，若a＝﹣3c，∴OD＝c＝﹣a，∴BD＝m﹣OD＝m+a，∵OA＝BD，∴＝m+，解得：m1＝0（此时，A，B，C三点重合，舍），m2＝；②当m＜0时，如图3，过点C作CD⊥y轴于D，同理得：OA＝BD，当x≥m时，y＝0，则x2﹣mx+m＝0，解得：x1＝，m2＝（舍），∴OA＝＝a，∴＝c﹣m＝﹣a﹣m，解得：m1＝0，m2＝﹣；综上，m的值是或﹣．19．（2021•营口）如图，在平面直角坐标系xOy中，抛物线y＝3x2+bx+c过点A（0，﹣2），B（2，0），点C为第二象限抛物线上一点，连接AB，AC，BC，其中AC与x轴交于点E，且tan∠OBC ＝2．（1）求点C坐标；（2）点P（m，0）为线段BE上一动点（P不与B，E重合），过点P作平行于y轴的直线l与△ABC的边分别交于M，N两点，将△BMN沿直线MN翻折得到△B′MN，设四边形B′NBM的面积为S，在点P移动过程中，求S与m的函数关系式；（3）在（2）的条件下，若S＝3S△ACB′，请直接写出所有满足条件的m值．解：（1）∵抛物线y＝3x2+bx+c过点A（0，﹣2），B（2，0），∴，解得，∴抛物线的解析式为y＝3x2﹣5x﹣2，如图1中，设BC交y轴于D．∵tan∠OBD＝2＝，OB＝2，∴OD＝4，∴D（0，4），设直线BD的解析式为y＝kx+b，则有，解得，∴直线BD的解析式为y＝﹣2x+4，由，解得（即点B）或，∴C（﹣1，6）．（2）∵A（0，﹣2），B（2，0），C（﹣1，6），∴直线AB的解析式为y＝x﹣2，直线AC的解析式为y＝﹣8x﹣2，∴E（﹣，0），当0＜m＜2时，∵P（m，0），∴M（m，﹣2m+4），N（m，m﹣2），∴MN＝﹣2m+4﹣m+2＝﹣3m+6，∴S＝•BB′•MN＝×2（2﹣m）×（﹣3m+6）＝3m2﹣12m+12．当﹣＜m≤0时，如图2中，∵P（m，0），∴M（m，﹣2m+4），N（m，﹣8m﹣2），∴MN＝﹣2m+4+8m+2＝6m+6，∴S＝•BB′•MN＝×2（2﹣m）×（6m+6）＝﹣6m2+6m+12．综上所述，S＝．（3）∵直线AC交x轴于（﹣，0），B′（2m﹣2），当﹣6m2+6m+12＝3××|2m﹣2+|×8，解得m＝或（都不符合题意舍弃），当3m2﹣12m+12＝3××|2m﹣2+|×8，解得m＝1或11（舍弃）或﹣2+或﹣2﹣（舍弃），综上所述，满足条件的m的值为1或﹣2+．20．（2021•本溪）某网店销售一款市场上畅销的蒸蛋器，进价为每个40元，在销售过程中发现，这款蒸蛋器销售单价为60元时，每星期卖出100个．如果调整销售单价，每涨价1元，每星期少卖出2个，现网店决定提价销售，设销售单价为x元，每星期销售量为y个．（1）请直接写出y（个）与x（元）之间的函数关系式；（2）当销售单价是多少元时，该网店每星期的销售利润是2400元？（3）当销售单价是多少元时，该网店每星期的销售利润最大？最大利润是多少元？解：（1）由题意，得：y＝100﹣2（x﹣60）＝﹣2x+220，∴y＝﹣2x+220；（3）W＝﹣2x2+300x﹣8800＝﹣2（x﹣75）2+2450，∵﹣2＜0，∴当x＝75时，W有最大值，最大值为2450元，答：每件定价为75元时利润最大，最大利润为2450元．21．（2021•吉林）疫苗接种，利国利民．甲、乙两地分别对本地各40万人接种新冠疫苗．甲地在前期完成5万人接种后，甲、乙两地同时以相同速度接种，甲地经过a天后接种人数达到25万人，由于情况变化，接种速度放缓，结果100天完成接种任务，乙地80天完成接种任务，在某段时间内，甲、乙两地的接种人数y（万人）与各自接种时间x（天）之间的关系如图所示．（1）直接写出乙地每天接种的人数及a的值；（2）当甲地接种速度放缓后，求y关于x的函数解析式，并写出自变量x的取值范围；（3）当乙地完成接种任务时，求甲地未接种疫苗的人数．解：（1）乙地接种速度为40÷80＝0.5（万人/天），0.5a＝25﹣5，解得a＝40．（2）设y＝kx+b，将（40，25），（100，40）代入解析式得：，解得，∴y＝x+15（40≤x≤100）．（3）把x＝80代入y＝x+15得y＝×80+15＝35，40﹣35＝5（万人）．22．（2021•山西）综合与探究如图，抛物线y＝x2+2x﹣6与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C，连接AC，BC．（1）求A、B，C三点的坐标并直接写出直线AC，BC的函数表达式．（2）点P是直线AC下方抛物线上的一个动点，过点P作BC的平行线l，交线段AC于点D．①试探究：在直线l上是否存在点E，使得以点D，C，B，E为顶点的四边形为菱形，若存在，求出点E的坐标，若不存在，请说明理由；②设抛物线的对称轴与直线l交于点M，与直线AC交于点N．当S△DMN＝S△AOC时，请直接写出DM的长．解：（1）当y＝0时，x2+2x﹣6＝0，解得x1＝﹣6，x2＝2，∴A（﹣6，0），B（2，0），当x＝0时，y＝﹣6，∴C（0，﹣6），∵A（﹣6，0），C（0，﹣6），∴直线AC的函数表达式为y＝﹣x﹣6，∵B（2，0），C（0，﹣6），∴直线BC的函数表达式为y＝3x﹣6；（2）①存在：设点D的坐标为（m，﹣m﹣6），其中﹣6＜m＜0，∵B（2，0），C（0，﹣6），∴BD2＝（m﹣2）2+（m+6）2，BC2＝22+62＝40，DC2＝m2+（﹣m﹣6+6）2＝2m2，∵DE∥BC，∴当DE＝BC时，以点D，C，B，E为顶点的四边形为平行四边形，分两种情况：如图，当BD＝BC时，四边形BDEC为菱形，∴BD2＝BC2，∴（m﹣2）2+（m+6）2＝40，解得：m1＝﹣4，m2＝0（舍去），∴点D的坐标为（﹣4，﹣2），∴点E的坐标为（﹣6，﹣8）；如图，当CD＝CB时，四边形CBED为菱形，∴CD2＝CB2，∴2m2＝40，解得：m1＝﹣2，m2＝2（舍去），∴点D的坐标为（﹣2，2﹣6），∴点E的坐标为（2﹣2，2）；综上，存在点E，使得以点D，C，B，E为顶点的四边形为菱形，点E的坐标为（﹣6，﹣8）或（2﹣2，2）；②设点D的坐标为（m，﹣m﹣6），其中﹣6＜m＜0，∵A（﹣6，0），B（2，0），∴抛物线的对称轴为直线x＝﹣2，∵直线BC的函数表达式为y＝3x﹣6，直线l∥BC，∴设直线l的解析式为y＝3x+b，∵点D的坐标（m，﹣m﹣6），∴b＝﹣4m﹣6，∴M（﹣2，﹣4m﹣12），∵抛物线的对称轴与直线AC交于点N．∴N（﹣2，﹣4），∴MN＝﹣4m﹣12+4＝﹣4m﹣8，∵S△DMN＝S△AOC，∴（﹣4m﹣8）（﹣2﹣m）＝×6×6，整理得：m2+4m﹣5＝0，解得：m1＝﹣5，m2＝1（舍去），∴点D的坐标为（﹣5，﹣1），∴点M的坐标为（﹣2，8），∴DM＝＝3，答：DM的长为3．23．（2021•本溪）如图，抛物线y＝﹣x2+bx+c与x轴交于点A和点C（﹣1，0），与y轴交于点B（0，3），连接AB，BC，点P是抛物线第一象限上的一动点，过点P作PD⊥x轴于点D，交AB于点E．（1）求抛物线的解析式；（2）如图1，作PF⊥PD于点P，使PF＝OA，以PE，PF为邻边作矩形PEGF．当矩形PEGF 的面积是△BOC面积的3倍时，求点P的坐标；（3）如图2，当点P运动到抛物线的顶点时，点Q在直线PD上，若以点Q、A、B为顶点的三角形是锐角三角形，请直接写出点Q纵坐标n的取值范围．解：（1）由题意得：，解得，故抛物线的表达式为y＝﹣x2+x+3；（2）对于y＝﹣x2+x+3，令y＝﹣x2+x+3＝0，解得x＝4或﹣1，故点A的坐标为（4，0），则PF＝2，由点A、B的坐标得，直线AB的表达式为y＝﹣x+3，设点P的坐标为（x，﹣x2+x+3），则点E（x，﹣x+3），则矩形PEGF的面积＝PF•PE＝2×（﹣x2+x+3+x﹣3）＝3S△BOC＝3××BO•CO＝×3×1，解得x＝1或3，故点P的坐标为（1，）或（3，3）；（3）由抛物线的表达式知，其对称轴为x＝，故点Q的坐标为（，n），当∠ABQ为直角时，如图2﹣1，设BQ交x轴于点H，由直线AB的表达式知，tan∠BAO＝，则tan∠BHO＝，故设直线BQ的表达式为y＝x+t，该直线过点B（0，3），故t＝3，则直线BQ的表达式为y＝x+3，当x＝时，y＝x+3＝5，即n＝5；②当∠BQA为直角时，过点Q作直线MN交y轴于点N，交过点A与y轴的平行线于点M，∵∠BQN+∠MQA＝90°，∠MQA+∠MAQ＝90°，∴∠BQN＝∠MAQ，∴tan∠BQN＝tan∠MAQ，即，则，解得n＝；24．（2021•陕西）在一次机器“猫”抓机器“鼠”的展演测试中，“鼠”先从起点出发，1min后，“猫”从同一起点出发去追“鼠”，抓住“鼠”并稍作停留后，“猫”抓着“鼠”沿原路返回．“鼠”、“猫”距起点的距离y（m）与时间x（min）之间的关系如图所示．（1）在“猫”追“鼠”的过程中，“猫”的平均速度与“鼠”的平均速度的差是1m/min；（2）求AB的函数表达式；（3）求“猫”从起点出发到返回至起点所用的时间．解：（1）由图象知：“鼠”6min跑了30m，∴“鼠”的速度为：30÷6＝5（m/min），“猫”5min跑了30m，∴“猫”的速度为：30÷5＝6（m/min），∴“猫”的平均速度与“鼠”的平均速度的差是1（m/min），故答案为：1；（2）设AB的解析式为：y＝kx+b，∵图象经过A（7，30）和B（10，18），把点A和点B坐标代入函数解析式得：，解得：，∴AB的解析式为：y＝﹣4x+58；（3）令y＝0，则﹣4x+58＝0，∴x＝14.5，∵“猫”比“鼠”迟一分钟出发，∴“猫”从起点出发到返回至起点所用的时间为14.5﹣1＝13.5（min）．答：“猫”从起点出发到返回至起点所用的时间13.5min．25．（2021•长春）《九章算术》中记载，浮箭漏（图①）出现于汉武帝时期，它由供水壶和箭壶组成，箭壶内装有箭尺，水匀速地从供水壶流到箭壶，箭壶中的水位逐渐上升，箭尺匀速上浮，可通过读取箭尺读数计算时间．某学校STEAM小组仿制了一套浮箭漏，并从函数角度进行了如下实验探究：【实验观察】实验小组通过观察，每2小时记录一次箭尺读数，得到如表：供水时间x（小时）02468箭尺读数y（厘米）618304254【探索发现】①建立平面直角坐标系，如图②，横轴表示供水时间x．纵轴表示箭尺读数y，描出以表格中数据为坐标的各点．②观察上述各点的分布规律，判断它们是否在同一条直线上，如果在同一条直线上，求出这条直线所对应的函数表达式，如果不在同一条直线上，说明理由．【结论应用】应用上述发现的规律估算：①供水时间达到12小时时，箭尺的读数为多少厘米？②如果本次实验记录的开始时间是上午8：00，那当箭尺读数为90厘米时是几点钟？（箭尺最大读数为100厘米）解：【探索发现】①如图②，②观察上述各点的分布规律，可得它们是否在同一条直线上，设这条直线所对应的函数表达式为y＝kx+b，则，解得：，∴y＝6x+6；【结论应用】应用上述发现的规律估算：①x＝12时，y＝6×12+6＝78，∴供水时间达到12小时时，箭尺的读数为78厘米；②y＝90时，6x+6＝90，解得：x＝14，∴供水时间为14小时，∵本次实验记录的开始时间是上午8：00，8：00+14＝22：00，∴当箭尺读数为90厘米时是22点钟．。

2021年中考二轮复习数学：基本题型训练(三)

初三数学中考基本题型训练（3）1. 4的算术平方根是（）A.±2B.2C.±2D.22．计算23()a的结果是（）A．5a B．6a C．8a D．23a3．若12x x，是一元二次方程2560x x-+=的两个根，则12x x+的值是（）A．1B．5C．5-D．64．请你观察下面的四个图形，它们体现了中华民族的传统文化．（）对称现象无处不在，其中可以看作是轴对称图形的有（）A．4个B．3个C．2个D．1个5．下面事件：①掷一枚硬币，着地时正面向上；②在标准大气压下，水加热到100℃会沸腾；③买一张福利彩票，开奖后会中奖；④明天会下雨．其中，必然事件有（）A．1个B．2个C．3个D．4个二、填空题：6．-7的相反数是_______。

7．当x= 时，分式1xx+没有意义．8．．一元二次方程2x x=的解为9．化简：22221369x y x yx y x xy y+--÷--+＝_______10．请写出一个是轴对称图形的图形名称．答：．三、解答题：11．解方程．33122xx x-+=--第4题图12．解不等式组13．某工厂今年3月份的产值为100万元，由于受国际金融风暴的影响，5月份的产值下降到81万元，求平均每月产值下降的百分率。

14.一个口袋中放有20个球，其中红球6个，白球和黑球各若干个，每球除了颜色以外没有任何区别.(1)小王通过大量反复的实验(每次取一个球，放回搅匀后再取第二个)发现，取出黑球的频率稳定在左右，请你估计袋中黑球的个数.(2)若小王取出的第一个球是白球，将它放在桌上，闭上眼睛从袋中余下的球中再任意取出一个球，取出红球的概率是多少?15．为了建设“森林重庆”，绿化环境，某中学七年级一班同学都积极参加了植树活动，今年4月该班同学的植树情况的部分统计如下图所示：（1）请你根据以上统计图中的信息，填写下表：该班人数植树株数的中位数植树株数的众数（2）请你将该条形统计图补充完整．5125431x x x x ->+⎧⎨-<+⎩，．16 1412 10 8 6 4 20 9 16 7 4 1 2 4 5 6 植树量（株） 20题图人数 1 4。

2021中考数学二轮冲刺训练：圆的有关性质含答案

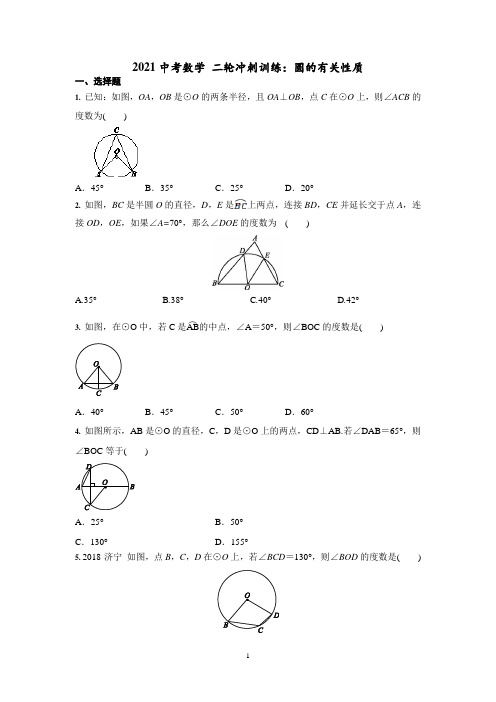
2021中考数学二轮冲刺训练：圆的有关性质一、选择题1. 已知：如图，OA ，OB 是⊙O的两条半径，且OA ⊥OB ，点C 在⊙O 上，则∠ACB 的度数为( )A ．45°B ．35°C ．25°D ．20°2. 如图，BC是半圆O 的直径，D ，E 是上两点，连接BD ，CE 并延长交于点A ，连接OD ，OE ，如果∠A=70°，那么∠DOE 的度数为 ( )A .35°B .38°C .40°D .42°3. 如图，在⊙O中，若C 是AB ︵的中点，∠A ＝50°，则∠BOC 的度数是( )A ．40°B ．45°C ．50°D ．60°4. 如图所示，AB 是⊙O 的直径，C ，D 是⊙O 上的两点，CD ⊥AB.若∠DAB ＝65°，则∠BOC 等于( )A ．25°B ．50°C ．130°D ．155°5. 2018·济宁如图，点B ，C ，D 在⊙O 上，若∠BCD ＝130°，则∠BOD 的度数是( )A．50°B．60°C．80°D．100°6. 如图，在半径为5的⊙O中，弦AB＝6，OP⊥AB，垂足为P，则OP的长为()A．3 B．2.5 C．4 D．3.57. 如图，点A，B，S在圆上，若弦AB的长度等于圆半径的2倍，则∠ASB的度数是()A．22.5°B．30°C．45°D．60°8. (2019•镇江)如图，四边形ABCD是半圆的内接四边形，AB是直径，DC CB=．若∠=︒，则ABC∠的度数等于110CA．55︒B．60︒C．65︒D．70︒二、填空题9. 在半径为5的圆形纸片上裁出一个边长最大的正方形纸片，则这个正方形纸片的边长应为.10. 如图，AC是圆内接四边形ABCD的一条对角线，点D关于AC的对称点E在边BC 上，连接AE，若∠ABC=64°，则∠BAE的度数为.11.如图，在⊙O中，A，B是圆上的两点，已知∠AOB＝40°，直径CD∥AB，连接AC，则∠BAC＝________度．12. 已知：如图，A ，B是⊙O 上的两点，∠AOB ＝120°，C 是AB ︵的中点，则四边形OACB是________．(填特殊平行四边形的名称)13. 如图，半径为5的⊙P 与y 轴交于点M(0，－4)，N(0，－10)，则圆心P 的坐标为________．14. 如图所示，在半圆O 中，AB 为直径，P 为AB ︵的中点，分别在AP ︵和PB ︵上取其中点A 1和B 1，再在P A ︵1和PB ︵1上分别取其中点A 2和B 2.若一直这样取下去，则∠A n OB n ＝________°.15. 已知⊙O的半径为2，弦BC ＝2 3，A 是⊙O 上一点，且AB ︵＝AC ︵，直线AO 与BC交于点D ，则AD 的长为________．16. 如图，定长弦CD 在以AB 为直径的⊙O 上滑动(点C ，D 与点A ，B 不重合)，M 是CD 的中点，过点C 作CP ⊥AB 于点P.若CD ＝3，AB ＝8，PM ＝l ，则l 的最大值是________．三、解答题17. 如图，AB 是☉O 的直径，C 是☉O 上一点，过点O 作OD ⊥AB ，交BC 的延长线于点D ，交AC 于点E ，F 是DE 的中点，连接CF . (1)求证:CF 是☉O 的切线; (2)若∠A=22.5°，求证:AC=DC.18. 如图，在⊙O中，AC ︵＝CB ︵，CD ⊥OA 于点D ，CE ⊥OB 于点E.求证：AD ＝BE.19. 如图，AB是☉O 的直径，DO ⊥AB 于点O ，连接DA 交☉O 于点C ，过点C 作☉O的切线交DO 于点E ，连接BC 交DO 于点F . (1)求证:CE=EF .(2)连接AF 并延长，交☉O 于点G .填空:①当∠D 的度数为时，四边形ECFG 为菱形; ②当∠D 的度数为时，四边形ECOG 为正方形.20.如图，△ABC内接于⊙O，AB＝AC，∠BAC＝36°，过点A作AD∥BC，与∠ABC的平分线交于点D，BD与AC交于点E，与⊙O交于点F.(1)求∠DAF的度数；(2)求证：AE2＝EF·ED；(3)求证：AD是⊙O的切线．21.如图，AB为⊙O的直径，P点为半径OA上异于点O和点A的一个点，过P点作与直径AB 垂直的弦CD，连接AD，作BE⊥AB，OE//AD交BE于E点，连接AE、DE，AE交CD于点F.(1)求证：DE为⊙O的切线；(2)若⊙O的半径为3，sin∠ADP＝13，求AD；(3)请猜想PF与FD的数量关系，并加以证明．22.在平面直角坐标系中，借助直角三角板可以找到一元二次方程的实数根．比如对于方程x2－5x＋2＝0，操作步骤是：第一步：根据方程的系数特征，确定一对固定点A(0，1)，B(5，2)；第二步：在坐标平面中移动一个直角三角板，使一条直角边恒过点A，另一条直角边恒过点B；第三步：在移动过程中，当三角板的直角顶点落在x轴上点C处时，点C的横坐标m即为该方程的一个实数根(如图①)；第四步：调整三角板直角顶点的位置，当它落在x轴上另一点D处时，点D的横坐标n既为该方程的另一个实数根．(1)在图②中，按照“第四步”的操作方法作出点D(请保留作出点D时直角三角板两条直角边的痕迹)；(2)结合图①，请证明“第三步”操作得到的m就是方程x2－5x＋2＝0的一个实数根；(3)上述操作的关键是确定两个固定点的位置．若要以此方法找到一元二次方程ax2＋bx ＋c＝0(a≠0，b2－4ac≥0)的实数根，请你直接写出一对固定点的坐标；(4)实际上，(3)中的固定点有无数对，一般地，当m1，n1，m2，n2与a，b，c之间满足怎样的关系时，点P(m1，n1)．Q(m2，n2)就是符合要求的一对固定点？答案一、选择题1. 【答案】A2. 【答案】C[解析]∵∠A=70°，∴∠B +∠C=110°，∴∠BOE +∠COD=220°，∴∠DOE=∠BOE +∠COD -180°=40°，故选C .3. 【答案】A[解析] ∵∠A ＝50°，OA ＝OB ，∴∠B ＝∠A ＝50°，∴∠AOB ＝180°－50°－50°＝80°. ∵C 是AB ︵的中点， ∴∠BOC ＝12∠AOB ＝40°. 故选A.4. 【答案】C5. 【答案】D[解析] 由同弧所对的圆周角等于圆心角的一半，可知∠α＝2∠BCD ＝260°. 而∠α＋∠BOD ＝360°，所以∠BOD ＝100°.6. 【答案】C7. 【答案】C[解析] 设圆心为O ，连接OA ，OB ，如图．∵弦AB 的长度等于圆半径的2倍，即AB ＝2OA ，∴AB2＝2OA2.∵OA ＝OB ，∴AB2＝OA2＋OB2，∴△OAB 为等腰直角三角形，∠AOB ＝90°， ∴∠ASB ＝12∠AOB ＝45°.故选C.8. 【答案】A【解析】如图，连接AC ，∵四边形ABCD 是半圆的内接四边形，∴∠DAB=180°–∠C=70°， ∵DC CB ，∴∠CAB=12∠DAB=35°， ∵AB 是直径，∴∠ACB=90°，∴∠ABC=90°–∠CAB=55°，故选A ．二、填空题9. 【答案】5 [解析]如图，已知☉O ，圆内接正方形ABCD.连接OB ，OC ，过O 作OE ⊥BC ，设此正方形的边长为a ，由垂径定理及正方形的性质得出OE=BE=，由勾股定理得OE 2+BE 2=OB 2，即2+2=52，解得a=5.10. 【答案】52°[解析]∵圆内接四边形对角互补，∴∠B +∠D=180°，∵∠B=64°，∴∠D=116°.∵点D 关于AC 的对称点是点E ，∴∠D=∠AEC=116°. ∵∠AEC=∠B +∠BAE ，∴∠BAE=52°.11.【答案】35 【解析】∵OA ＝OB ＝OC ，∴∠OAB ＝∠B ，∠C ＝∠OAC ，∵∠AOB ＝40°，∴∠B＝∠OAB ＝70°，∵CD ∥AB ，∴∠BAC ＝∠C ，∴∠OAC ＝∠BAC ＝12∠OAB ＝35°.12. 【答案】菱形[解析] 连接OC.∵C 是AB ︵的中点，∴∠AOC ＝∠COB ＝60°. 又∵OA ＝OC ＝OB ，∴△OAC 和△OCB 都是等边三角形， ∴OA ＝AC ＝BC ＝OB ， ∴四边形OACB 是菱形．13. 【答案】(－4，－7)[解析] 过点P 作PH ⊥MN 于点H ，连接PM ，则MH ＝12MN ＝3，OH ＝OM ＋MH ＝7.由勾股定理，得PH ＝4，∴圆心P 的坐标为(－4，－7)．14. 【答案】(902n －1) [解析] 当n ＝1时，∠A 1OB 1＝90°；当n ＝2时，∠A 2OB 2＝90°2＝45°所以∠A n OB n ＝(902n －1)°.15. 【答案】3或1 [解析] 如图所示：∵⊙O 的半径为2，弦BC ＝2 3，A 是⊙O 上一点，且AB ︵＝AC ︵， ∴AO ⊥BC ，垂足为D ，则BD ＝12BC ＝ 3. 在Rt △OBD 中， ∵BD2＋OD2＝OB2，即(3)2＋OD2＝22，解得OD ＝1.∴当点A 在如图①所示的位置时，AD ＝OA －OD ＝2－1＝1；当点A 在如图②所示的位置时，AD ＝OA ＋OD ＝2＋1＝3.16. 【答案】34 [解析] 如图，当CD ∥AB 时，PM 的长最大，连接OM ，OC .∵CD ∥AB ，CP ⊥AB ，∴CP⊥CD.∵M为CD的中点，OM过点O，∴OM⊥CD，∴∠OMC＝∠PCD＝∠CPO＝90°，∴四边形CPOM是矩形，∴PM＝OC.∵⊙O的直径AB＝8，∴半径OC＝4，∴PM＝4.三、解答题17. 【答案】证明:(1)∵AB是☉O的直径，∴∠ACB=90°，∴∠ACD=90°.∵点F是ED的中点，∴CF=EF=DF，∴∠AEO=∠FEC=∠FCE.∵OA=OC，∴∠OCA=∠OAC.∵OD⊥AB，∴∠OAC+∠AEO=90°，∴∠OCA+∠FCE=90°，即OC⊥FC，∵OC是☉O的半径，∴CF与☉O相切.(2)∵OD⊥AB，AC⊥BD，∴∠AOE=∠ACD=90°.∵∠AEO=∠DEC，∴∠OAE=∠CDE=22.5°.连接AD ，∵AO=BO ，OD ⊥AB ，∴AD=BD ，∴∠ADO=∠BDO=22.5°，∴∠ADB=45°，∴∠CAD=90°-∠ADB=45°=∠ADB ，∴AC=CD.18. 【答案】证明：如图，连接OC. ∵AC ︵＝CB ︵，∴∠AOC ＝∠BOC.∵CD ⊥OA 于点D ，CE ⊥OB 于点E ，∴∠CDO ＝∠CEO ＝90°.在△COD 与△COE 中，⎩⎨⎧∠AOC ＝∠BOC ，∠CDO ＝∠CEO ，CO ＝CO ，∴△COD ≌△COE(AAS)，∴OD ＝OE.又∵AO ＝BO ，∴AO －OD ＝BO －OE ，即AD ＝BE.19. 【答案】解:(1)证明:连接OC.∵CE 是☉O 的切线，∴OC ⊥CE.∴∠FCO +∠ECF=90°.∵DO ⊥AB ，∴∠B +∠BFO=90°.∵∠CFE=∠BFO ，∴∠B +∠CFE=90°.∵OC=OB ，∴∠FCO=∠B.∴∠ECF=∠CFE.∴CE=EF .(2)∵AB 是☉O 的直径，∴∠ACB=90°.∴∠DCF=90°.∴∠DCE +∠ECF=90°，∠D +∠EFC=90°.由(1)得∠ECF=∠CFE ，∴∠D=∠DCE.∴ED=EC.∴ED=EC=EF .即点E 为线段DF 的中点.①四边形ECFG 为菱形时，CF=CE.∵CE=EF ，∴CE=CF=EF .∴△CEF 为等边三角形.∴∠CFE=60°.∴∠D=30°.故填30°.②四边形ECOG 为正方形时，△ECO 为等腰直角三角形.∴∠CEF=45°.∵∠CEF=∠D +∠DCE ，∴∠D=∠DCE=22.5°.故填22.5°.20. 【答案】(1)解：∵AB ＝AC ，∠BAC ＝36°，∴∠ABC ＝∠ACB ＝12(180°－36°)＝72°，∴∠AFB ＝∠ACB ＝72°，∵BD 平分∠ABC ，∴∠DBC ＝36°，∵AD ∥BC ，∴∠D ＝∠DBC ＝36°，∴∠DAF ＝∠AFB －∠D ＝72°－36°＝36°；(2)证明：∵∠EAF ＝∠FBC ＝∠D ，∠AEF ＝∠AED ，∴△EAF ∽△EDA ， ∴AE DE ＝EF EA ，∴AE 2＝EF ·ED ；(3)证明：如解图，过点A 作BC 的垂线，G 为垂足，∵AB ＝AC ，∴AG 垂直平分BC ，∴AG 过圆心O ，∵AD ∥BC ，∴AD ⊥AG ，∴AD 是⊙O 的切线．解图21. 【答案】(1)证明：如解图，连接OD ，∵OA ＝OD ，∴∠OAD ＝∠ODA ，∵OE ∥AD ，∴∠OAD ＝∠BOE ，∠DOE ＝∠ODA ，∴∠BOE ＝∠DOE ，在△BOE 和△DOE 中，⎩⎪⎨⎪⎧OB ＝OD ∠BOE ＝∠DOE OE ＝OE， ∴△BOE ≌△DOE (SAS)，∴∠ODE ＝∠OBE ，∵BE ⊥AB ，∴∠OBE ＝90°，∴∠ODE ＝90°，∵OD 为⊙O 的半径，∴DE 为⊙O 的切线；(2)解：如解图，连接BD ，∵AB 为⊙O 的直径，∴∠ADB ＝90°，∴∠ABD ＋∠BAD ＝90°，∵AB ⊥CD ，∴∠ADP ＋∠BAD ＝90°，∴∠ABD ＝∠ADP ，∴sin ∠ABD ＝AD AB ＝sin ∠ADP ＝13， ∵⊙O 的半径为3，∴AB =6，∴AD ＝13AB ＝2；解图 (3)解：猜想PF ＝FD ，证明：∵CD ⊥AB ，BE ⊥AB ，∴CD ∥BE ，∴△APF ∽△ABE ，∴PF BE ＝AP AB ，∴PF ＝AP ·BE AB ，在△APD 和△OBE 中，⎩⎪⎨⎪⎧∠APD ＝∠OBE ∠P AD ＝∠BOE ， ∴△APD ∽△OBE ，∴PD BE ＝AP OB， ∴PD ＝AP ·BE OB ，∵AB ＝2OB ，∴PF ＝12PD ， ∴PF ＝FD .22. 【答案】【思路分析】(1)因为点C 是x 轴上的一动点，且∠ACB ＝90°保持不变，所以由圆周角的性质得，点C 必在以AB 为直径的圆上，所以以AB 为直径画圆，与x 轴相交于两点，除点C 的另一点就是所求；(2)因为∠ACB ＝90°，∠AOC ＝90°，所以过点B 作BE ⊥x 轴，垂足为E ，则构造了一个“K”字型的基本图形，再由相似三角的性质得出比例式，化简后得m 2－5m ＋2＝0，问题得证；(3)由(2)中的证明过程可知，一个二次项系数为1的一元二次方程，一次项系数是点A 的横坐标与点B 的横坐标的和的相反数；常数项是点A的纵坐标与点B 的纵坐标的积，先把方程ax 2＋bx ＋c ＝0，化为 x 2＋b a x ＋c a＝0，再根据上述关系写出一对固定点的坐标；(4)由(2)的证明中知，本题的关键点在“K”字型的构造，所以本小题解题的关键是要抓住图②中的“K”字型，只要P 、Q 两点分别在AD 、BD 上，过P 、Q 分别作x 轴垂线，垂足为M 、N ，这样就构造出满足条件的基本图形，再应用相似三角形的性质，可得相应的关系式．图① 图②(1)解：如解图①，先作出AB 的中点O 1，以O 1为圆心，12AB 为半径画圆．x 轴上另外一个交点即为D 点；(4分)(2)证明：如解图①，过点B 作x 轴的垂线交x 轴于点E ，∵∠ADB ＝90°，∴∠ADO ＋∠BDE ＝90°，∵∠OAD ＋∠ADO ＝90°，∴∠OAD ＝∠BDE ，∵∠AOD ＝∠DEB ＝90°，∴△AOD ∽△DEB ，(6分)∴AO DE ＝OD EB ，即15－m ＝m 2，∴m 2－5m ＋2＝0，∴m 是x 2－5x ＋2＝0的一个实根；(8分)(3)解：(0，1)，(－b a ，c a )或(0，1a )，(－b a ，c )；(10分)(4)解：在解图②中，P 在AD 上，Q 在BD 上，过P ，Q 分别作x 轴的垂线交x 轴于M ，N.由(2)知△PMD ∽△DNQ ，∴n 1m 2－x ＝x －m 1n 2，(12分) ∴x 2－(m 1＋m 2)x ＋m 1m 2＋n 1n 2＝0与ax 2＋bx ＋c ＝0同解，∴－b a ＝m 1＋m 2；c a ＝m 1m 2＋n 1n 2.(14分)【难点突破】本题是一道考查数形结合思想的题．本题解题的突破口要抓住∠ACB ＝90°保持不变的特征，构造相似三角形中的基本图形，通过数形结合的方法，以相似三角形的比例式为桥梁，以此获得关于m 的等量关系，从而使问题得以解决．。

填空压轴题(几何篇)-2023年中考数学压轴题专项训练(学生版)

2023年中考数学压轴题专项训练--填空压轴题(几何篇)一、压轴题速练1一．填空题(共40小题)1(2023•龙湾区二模)如图，在△ABC中，AB=13，BC=14，AC=15，点D是线段AC上任意一点，分别过点A、C作直线BD的垂线，垂足为E、F，AE=m，CF=n，则n+m的最大值是，最小值是．2(2023•湖北模拟)如图，正方形ABCD的对角线交于点O，AB=22，现有半径足够大的扇形OEF，∠EOF=90°，当扇形OEF绕点O转动时，扇形OEF和正方形ABCD重叠部分的面积为．3(2023•榆树市二模)如图是中国古代数学家赵爽用来证明勾股定理的弦图的示意图，它是由四个全等的直角三角形和一个小正方形EFGH组成，恰好拼成一个大正方形ABCD，连结EG并延长交BC于点M．若AB=13，EF=1，则GM的长为．4(2023•道外区二模)如图，在四边形ABCD中，AB=BC，∠A=∠ABC=90°，以CD为斜边作等腰直角△ECD，连接BE，若CD=213，BE=2，则AB=．5(2023•包河区二模)Rt△ABC中，点D是斜边AB的中点．(1)如图1，若DE ⊥BC 与E ，DF ⊥AC 于F ，DE =3，DF =4，则AB =；(2)如图2，若点P 是CD 的中点，且CP =52，则PA 2+PB 2=．6(2023•庐江县三模)如图，四边形ABCD 中，AB =AC =AD ，点M 、N 分别是BC 、CD 的中点，连接MN ，若∠DAM =105°，∠BAN =75°，若AM AN=3+12，则∠ANM =°．7(2023•中山市二模)如图，△ABC 与△BDE 均为等腰直角三角形，点A ，B ，E 在同一直线上，BD ⊥AE ，垂足为点B ，点C 在BD 上，AB =4，BE =10．将△ABC 沿BE 方向平移，当这两个三角形重叠部分的面积等于△ABC 面积的一半时，△ABC 平移的距离为．8(2023•新都区模拟)青朱出入图，是魏晋时期数学家刘徽根据“割补术”运用数形关系证明勾股定理的几何证明法，即“勾自乘为朱方，股自乘为青方，令出入相补，各从其类，因就其余不动也，合成弦方之幂．开方除之，即弦也．”，若图中DF =1，CF =2，则AE 的长为．9(2023•黄埔区一模)△ABC为等腰直角三角形，AB=AC=6，∠BAC=90°，动点D在边BC上运动．以A为直角顶点，在AD右侧作等腰直角三角形△ADE(如图)．M为DE中点，N为BC三等分点，CN=13BC，连接MN，则线段MN的最小值为．10(2023•雁塔区校级模拟)如图，菱形ABCD的边长为5，将一个直角的顶点放置在菱形的中心O 处，此时直角的两边分别交边AD，CD于点E，F，当OE⊥AD时，OE的长为2，则EF的长是．11(2023•奉贤区二模)如果四边形有一组邻边相等，且一条对角线平分这组邻边的夹角，我们把这样的四边形称为“准菱形”．有一个四边形是“准菱形”，它相等的邻边长为2，这两条边的夹角是90°，那么这个“准菱形”的另外一组邻边的中点间的距离是　2　．12(2023•吕梁一模)如图，在正方形ABCD中，点P在对角线BD上，点E，F分别在边AB和BC 上，且∠EPF=45°，若CF=2DP=4，AE=12，则AB的长度为．13(2023•蚌埠二模)如图，点E为正方形ABCD的边CD上一点，以点A为圆心，AE长为半径画弧EF，交边BC于点F，已知正方形边长为1．(1)若∠DAE=15°，则DE的长为；(2)△AEF的面积为S的最大值是．14(2023•兰考县一模)如图，方形ABCD中，AB=8，点P为射线BC上任意一点(与点B、C不重合)，连接AP，在AP的右侧作正方形APGH，连接AG，交射线CD于E，当ED长为2时，点BP的长为．15(2023•本溪一模)由4个形状相同，大小相等的菱形组成如图所示的网格，菱形的顶点称为格点，点A，B，C，D都在格点上，∠A=60°，则cos∠CDB的值为．16(2023•沂南县校级一模)如图，矩形ABCD中，AC、BD相交于点O，过点B作BF⊥AC交CD 于点F，交AC与点M，过点D作DE∥BF交AB于点E，交AC于点N，连接FN、EM，则下列结论：①DN=BM；②EM∥FN；③AE=FC；④当AO=AD时，四边形DEBF是菱形．其中，正确结论的个数是．17(2023•琼海一模)如图，菱形ABCD，AE⊥BC，点E为垂足，点F为AE的中点，连接BF并延长交AD于点G，连接CG，CE=2，CG=211，则DG=，AG=，AF=．18(2023•镇江一模)如图，在矩形ABCD中，AB=6，BC=8，△BEF的顶点E在对角线AC上运动，且∠BFE=90°，∠EBF=∠BAC，连接AF，则AF的最小值为．19(2023•泉州模拟)如图，在菱形ABCD 中，∠A =60°，点E 在边AD 上，以BE 为边在菱形ABCD 的内部作等边三角形BEF ，若∠DEF =α，∠EBD =β，则α与β之间的数量关系可用等式表示为．20(2023•市南区一模)如图，正方形ABCD 中，E 、F 分别为BC 、CD 边上的点，∠EAF =45°，则下列结论中正确的有．(填序号)①BE +DF =EF ；②tan ∠AMD =CD DF； ③BM 2+DN 2=MN 2；④若EF =1.5，S △AEF =3，则．S 正方形ABCD =4．21(2023•大连一模)学习菱形时，我们从它的边、角和对角线等方面进行研究，可以发现并证明：菱形的每一条对角线平分一组对角．小明参考平行四边形、矩形判定方法的研究过程，得出下面的猜想：①一条对角线平分一组对角的四边形是菱形；②每一条对角线平分一组对角的四边形是菱形；③一条对角线平分一组对角的平行四边形是菱形．其中正确的是(填序号，填写一个即可)．22(2023•石景山区一模)如图，在菱形ABCD 中，点E ，F 分别在BC ，AD 上，BE =DF ．只需添加一个条件即可证明四边形AECF 是矩形，这个条件可以是(写出一个即可)．23(2023•河东区一模)已知，如图，已知菱形ABCD 的边长为6，∠ABC =60°，点E ，F 分别在AB ，CB 的延长线上，且BE =BF =13AB ，G 是DF 的中点，连接GE ，则GE 的长是．24(2023•合肥模拟)如图，点P在正方形ABCD内，∠BPC=135°，连接PA、PB、PC、PD．(1)若PA=AB，则∠CPD=；(2)若PB=2，PC=3，则PD的长为．25(2023•鄞州区一模)如图，Rt△ABC中，∠C=90°，AC=BC=8，作正方形CDEF，其中顶点E 在边AB上．(1)若正方形CDEF的边长为26，则线段AE的长是；(2)若点D到AB的距离是2，则正方形CDEF的边长是．26(2023•郓城县校级模拟)如图，在平行四边形ABCD中，对角线AC、BD交于点O．点M是BC 边的中点，连接AM、OM，作CF∥AM．已知OC平分∠BCF，OB平分∠AOM，若BD=32，则sin∠BAM的值为．27(2023•三原县二模)如图，点M是▱ABCD内一点，连接MA，MB，MC，MD，过点A作AP∥BM，过点D作DP∥CM，AP与DP交于点P，若四边形AMDP的面积为6，则▱ABCD的面积为．28(2023•和平区二模)如图，已知正方形ABCD的边长为4，点E为边BC上一点，BE=3，在AE的右侧，以AE为边作正方形AEFG，H为BG的中点，则AH的长等于．29(2023•鼓楼区校级模拟)如图，在矩形ABCD中，AD=3，AB=4，B是边AB上一点，△BCE与△FCE关于直线CE对称，连接BF并延长交AD于点G，过点F作FH⊥AD，垂足为点H，设BE=a，若点H为AG的中点，则BE的长为．30(2023•呼和浩特一模)如图在菱形ABCD中，O为对角线AC与BD的交点，点P为边AB上的任一点(不与A、B重合)，过点P分别作PM⊥AC，PN⊥BD，M、N为垂足，则可以判断四边形MPNO 的形状为．若菱形的边长为a，∠ADC=120°，则MN的最小值为．(用含a的式子表示)31(2023•洛阳一模)在扇形OAB中，∠AOB=60°，点C是半径OA上一点，且OC=6，将线段OC 沿OB方向平移，当平移距离是6时，点C的对应点C'恰好落在弧AB上，则图中阴影部分的面积为．32(2023•临渭区二模)如图，正六边形纸片ABCDEF的边长为6cm，从这个正六边形纸片上剪出一个扇形(图中阴影部分)，则这个扇形的面积为cm2．(结果保留π)33(2023•桂林二模)如图，在Rt△ABC中，∠C=90°，AB=10，BC=6，半径为1的⊙O在Rt△ABC内移动，当⊙O与∠A的两边都相切时，圆心O到点B的距离为2　．34(2023•万州区模拟)如图，在Rt△ABC中，∠ACB=90°，BC=1，AB=2，以点B为圆心，AB为半径作圆弧交CB的延长线于点D，以点A为圆心，AC为半径作圆弧交AD于点E．则图中阴影部分的面积为．35(2023•九龙坡区校级模拟)如图，AC、AD是⊙O中关于直径AB对称的两条弦，以弦AC、AD 为折线将弧AC、弧AD折叠后过圆心O，若⊙O的半径r=4，则圆中阴影部分的面积为．36(2023•烟台一模)如图，GC，GB是⊙O的切线，AB是⊙O的直径，延长GC，与BA的延长线交于点E，过点C作弦CD∥AB，连接DO并延长与圆交于点F，连接CF，若AE=2，CE=4，则CD的长度为．37(2023•历下区二模)如图，已知扇形AOB的半径OA=2，∠AOB=120°将扇形AOB绕点A顺时针旋转30°得到扇形AO′B′，则图中阴影部分的面积是．38(2023•邓州市一模)如图，在扇形AOB中，∠AOB=60°，OA=3，半径OC平分AB，点D为半径OA中点，点E为半径OC上一动点，当AE+DE取得最小值时，由AC，AE，CE围成的阴影部分的面积为．39(2023•龙口市二模)如图，由边长为1的小正方形构成的网格中，点A，B，C都在格点上，以AB 为直径的圆经过点C，D，则cos∠ADC的值为．40(2023•渝中区校级二模)如图，扇形纸片AOB的半径为2，沿AB折叠扇形纸片，点O恰好落在AB上的点C处，图中阴影部分的面积为．。

备考2021年中考数学二轮复习：图形的变换_解直角三角形的应用﹣方向角问题,填空题专训及答案

备考2021年中考数学二轮复习：图形的变换_锐角三角函数_解直角三角形的应用﹣方向角问题，填空题专训及答案备考2021中考数学二轮复习：图形的变换_锐角三角函数_解直角三角形的应用﹣方向角问题，填空题专训1、(2016大连.中考真卷) 如图，一艘渔船位于灯塔P的北偏东30°方向，距离灯塔18海里的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东55°方向上的B处，此时渔船与灯塔P的距离约为________海里（结果取整数）（参考数据：sin55°≈0.8，cos55°≈0.6，tan55°≈1.4）．2、(2018东胜.中考模拟) 如图，一艘海轮位于灯塔P的东北方向，距离灯塔海里的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东30°方向上的B处，则海轮行驶的路程AB为________海里（结果保留根号）．3、(2019辽阳.中考模拟) 如图，湖心岛上有一凉亭B，在凉亭B的正东湖边有一棵大树A，在湖边的C处测得B在北偏西45°方向上，测得A在北偏东30°方向上，又测得A、C之间的距离为100米，则A、B之间的距离是________米（结果保留根号形式）.4、(2018吉林.中考模拟) 如图，港口A在观测站O的正东方向，OA=40海里，某船从港口A出发，沿北偏东15°方向航行半小时后到达B处，此时从观测站O处测得该船位于北偏东60°的方向．求该船航行的速度________．5、(2019张家港.中考模拟) 如图,小明一家自驾到古镇C游玩,到达A地后,导航显示车辆应沿北偏东60°方向行驶12千米至B 地,再沿北偏西45°方向行驶一段距离到达古镇C，小明发现古镇C恰好在A地的正北方向，则B，C两地的距离为________千米。

(结果保留根号)6、(2019新泰.中考模拟) 如图，一般海轮位于灯塔P的北偏东30°方向，距离灯塔80海里的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东45°方向上的B处，这时，海轮所在的B处与灯塔P的距离为________（结果保留根号）7、(2018滨州.中考模拟) 如图，一天，我国一渔政船航行到A处时，发现正东方向的我领海区域B处有一可疑渔船，正在以12海里/时的速度向西北方向航行，我渔政船立即沿北偏东60°方向航行，1.5小时后，在我航海区域的C处截获可疑渔船，问我渔政船的航行路程是________海里（结果保留根号）．8、(2017肥城.中考模拟) 如图，甲、乙两渔船同时从港口O出发外出捕鱼，乙沿南偏东30°方向以每小时10海里的速度航行，甲沿南偏西75°方向以每小时10 海里的速度航行，当航行1小时后，甲在A处发现自己的渔具掉在乙船上，于是迅速改变航向和速度，仍以匀速沿南偏东60°方向追赶乙船，正好在B处追上．则甲船追赶乙船的速度为________海里/小时？9、(2017天桥.中考模拟) 一艘轮船在小岛A的北偏东60°距小岛80海里的B处，沿正西方向航行2小时后到达小岛的北偏西4 5°的C处，则该船行驶的速度为________海里/小时．10、(2018济宁.中考真卷) 如图，在一笔直的海岸线l上有相距2km的A，B两个观测站，B站在A站的正东方向上，从A站测得船C在北偏东60°的方向上，从B站测得船C在北偏东30°的方向上，则船C到海岸线l的距离是________ km．11、(2018潍坊.中考真卷) 如图．一-艘渔船正以60海里/小时的速度向正东方向航行,在处测得岛礁在东北方向上，继续航行1．5小时后到达处此时测得岛礁在北偏东方向,同时测得岛礁正东方向上的避风港在北偏东方向为了在台风到来之前用最短时间到达处,渔船立刻加速以75海里/小时的速度继续航行________小时即可到达 (结果保留根号)12、(2020黄石.中考模拟) 周末，张三、李四两人在磁湖游玩，张三在湖心岛处观看李四在湖中划船（如图），小船从处出发，沿北偏东方向划行200米到处，接着小船向正南方向划行一段时间到处.在处李四观测张三所在的处在北偏西的方向上，这时张三与李四相距________米（保留根号）.13、(2019荆州.中考真卷) 如图，灯塔在测绘船的正北方向，灯塔在测绘船的东北方向，测绘船向正东方向航行20海里后，恰好在灯塔的正南方向，此时测得灯塔在测绘船北偏西的方向上，则灯塔，间的距离为________海里（结果保留整数）.（参考数据，，，）.14、(2017邵阳.中考模拟) 如图，一艘渔船位于灯塔P的北偏东30°方向，距离灯塔18海里的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东55°方向上的B处，此时渔船与灯塔P的距离约为________海里（结果取整数）（参考数据：sin55°≈0.8，cos55°≈0.6，tan55°≈1.4）．15、(2018.中考模拟) 如图，甲、乙两船同时从港口出发，甲船以60海里/时的速度沿北偏东60°方向航行，乙船沿北偏西30°方向航行，半小时后甲船到达C点，乙船正好到达甲船正西方向的B点，则乙船的路程________（结果保留根号）16、(2018宁夏回族自治区.中考真卷) 一艘货轮以18 ㎞/h的速度在海面上沿正东方向航行，当行驶至A处时，发现它的东南方向有一灯塔B，货轮继续向东航行30分钟后到达C处，发现灯塔B在它的南偏东15°方向，则此时货轮与灯塔B的距离是________km.17、(2020宁波.中考模拟) 如图，某轮船以每小时30海里的速度向正东方向航行，上午8：00，测得小岛C在轮船A的北偏东45°方向上；上午10：00，测得小岛C在轮船B的北偏西30°方向上，则轮船在航行中离小岛最近的距离约为________米(精确到1米，参考数据 ≈1．414， ≈1．732)。

2021年安徽中考数学题型专项复习训练：题型三填空压轴题

题型三填空压轴题类型1多空类1.如图,在直角三角形纸片ABC中,∠ACB=90°,点D,E分别是BC,AC上的点(不含端点),折叠△DCE 使得直角顶点C落在斜边AB上的点F处,且△BDF是直角三角形.(1)四边形DCEF的形状是;(2)若AB=10,AC=6,则CD的长为.2.如图(1),在△ABC中,AB=AC,∠BAC=90°,AF在∠BAC内部,且AF=AB.分别对折∠BAF,∠CAF,使得AB,AC与AF重合,如图(2)(BD<CE).(1)△DEF的形状是;(2)若AB=6√2,DE=5,则AD的长为.3.在矩形纸片ABCD中,AB=6,BC=8,E为边CD上一点.如图(1),将△BCE沿BE所在直线折叠,点C恰好落在AD边上的点F处;将纸片展开,如图(2),沿着CF所在直线折叠△CDF得到△CD'F,折痕CF 与BE交于点M.(1)点D'BF上的一点;(填“是”或“不是”)(2)若点N是AF的中点,连接MN,则MN=.4.如图(1),四边形ABCD是正方形,点E是边AD上的点,将△CDE沿着直线CE折叠,使得点D落在AC上,对应点为点F.(1)CDEF=;(2)如图(2),点G是BC上的点,将△ABG沿着直线AG折叠,使得点B落在AC上,对应点为H,连接FG,EH,则S正方形ABCDS四边形EFGH=.5.在折纸这种传统手工艺术中,蕴含许多数学思想,我们可以通过折纸得到一些特殊图形,把一张正方形纸片按照图(1)~(4)的过程折叠、展开.(1)(2)(3)(4)(1)在图(4)中,四边形ABCD是形;(2)若四边形ABCD的面积为S,则正方形纸片的面积为.类型2几何多解类1.点、线位置不确定类多解题6.[2020亳州二模]如图,在△ABC中,∠C=90°,AC=8,BC=16,点D,E分别在边BC,AB上,沿DE将△ABC 折叠,使点B与点A重合,连接AD,点P在线段AD上,当点P到△ABC的直角边距离等于5时,AP的长为.7.[2019宣城二模]在正方形ABCD中,AB=6,连接AC,BD,P是正方形边或对角线上一点,若PD=2AP,则AP的长为.8.[2020安庆模拟]已知在△ABC中,∠ABC=90°,AB=9,BC=12.点Q是线段AC上的一个动点,过点Q 作AC的垂线交射线AB于点P.连接BQ,当△PQB为等腰三角形时,AP的长为.2.图形形状不确定类多解题9.如图,已知在等腰三角形ABC中,AB=AC=√5,BC=4,点D从点A出发,以每秒√5个单位长度的速度向点B运动,同时点E从点B出发,以每秒4个单位长度的速度向点C运动,在DE的右侧作∠DEF=∠B,交直线AC于点F,连接DF.设运动时间为t秒,则当△ADF是一个以AD为腰的等腰三角形时,t的值为.10.[2019合肥包河区一模]如图,在矩形ABCD中,AD=4,AC=8,点E是AB的中点,点F是对角线AC上一点,△GEF与△AEF关于直线EF对称,EG交AC于点H.当△CGH中有一个内角为90°时,CG的长为.11.如图,在正方形ABCD中,AB=3,点E在AD边上,且AE=2.点P是射线BC上一动点,连接BE,PE,过点P作PF⊥BE于点F.当△PEF与△ABE相似时,BP的长为.3.操作过程不确定类多解题12.如图是一张有一个角为30°,最小边长为4的直角三角形纸片,沿图中所示的中位线剪开后,将两部分拼成一个四边形,则所得四边形的周长为.13.在某张三角形纸片上,取其一边的中点,沿着过这点的两条中位线剪去两个三角形,剩下的部分是如图所示的四边形,经测量这个四边形的相邻两边长分别为10 cm,6 cm,一条对角线的长为8 cm,则原三角形纸片的周长是cm.类型3函数多解类14.在抛物线y=ax2+bx+c中,当-3≤x≤3时,-3≤y≤3,且该抛物线经过点(3,-3),(-3,3),则a的取值范围为-.15.[2020合肥48中一模]在平面直角坐标系中,点O为坐标原点,抛物线y=-x2-2x+c与y轴交于点P,以OP为一边向左作正方形OPBC,点A为抛物线的顶点,当△ABP是锐角三角形时,c的取值范围是.16.[2020合肥瑶海区二模]如果二次函数y=x2+b(b为常数)与正比例函数y=2x的图象在-1≤x≤2时有且只有一个交点,那么常数b的值应为.17.如图,直线y=x与抛物线y=x2-x-3交于A,B两点(点A在点B的左侧),点P是抛物线上的一个动点,过点P作PQ⊥x轴交直线y=x于点Q,设点P的横坐标为m,则线段PQ的长度随着m的增大而减小时,m的取值范围是.18.如图,若双曲线L:y=kx (x<0)与抛物线G:y=-34x(x+4)所围成的区域(不含边界)内整点(点的横、纵坐标都是整数)的个数是3,则k的取值范围是.参考答案题型三填空压轴题1.(1)正方形 (2)247 (1)易知∠B<90°.由折叠可知∠DFE=90°,∴∠BFD=90°-∠AFE<90°,∴∠BDF=90°,∴∠CDF=180°-∠BDF=90°,∴四边形DCEF 是矩形.又DC=DF ,∴四边形DCEF 是正方形.(2)如图,∵四边形DCEF 是正方形,∴EF ∥BC ,EC ∥FD ,∴∠AEF=∠C=∠FDB ,∠AFE=∠B ,∴△AEF ∽△FDB ,∴AE FD =EFDB ,∴AE ·DB=EF ·FD.易得BC=8.设CD=x ,则CE=EF=DF=CD=x ,∴BD=8-x ,AE=6-x ,∴(6-x )·(8-x )=x 2,解得x=247,即CD=247.2.(1)直角三角形 (2)3√5 (1)由折叠可知∠AFD=∠B ,∠AFE=∠C.∵∠BAC=90°,∴∠B+∠C=90°,∴∠AFD+∠AFE=90°,故△DEF 是直角三角形.(2)如图,过点A 作AG ⊥BC ,垂足为点G.∵AB=AC=6√2, ∠BAC=90°,∴BC=2+AC 2=12.∵AB=AC ,AG ⊥BC ,∴AG=BG=CG=6.设BD=x ,则DF=x ,EF=EC=12-DE-BD=12-5-x=7-x.在Rt △DEF 中,DE 2=DF 2+EF 2,即25=x 2+(7-x )2,解得x=3或4.∵BD<CE ,∴BD=3, ∴DG=3,∴AD=√32+62=3√5.3.(1)是 (2)5 (1)由折叠的性质可知BC=BF ,∠DFC=∠D'FC ,∴∠BFC=∠BCF.∵AD ∥BC ,∴∠DFC=∠BCF ,∴∠D'FC=∠BFC ,∴点D'是BF 上的点.(2)连接AC.由折叠的性质可知,BE 垂直平分线段CF ,∴点M 是FC 的中点.又点N 是AF 的中点,∴MN 是△ACF 的中位线,∴MN=12AC.∵四边形ABCD 是矩形,∴∠ABC=90°,∴AC=√AB 2+BC 2=2+82=10,∴MN=12AC=5. 4.(1)√2+1 (2)4+3√22(1)由题意可知△AEF 是等腰直角三角形,且AF=EF.设EF=m ,则DE=m ,AE=√2EF=√2m ,∴CD=AD=m+√2m=(1+√2)m ,∴CD EF =(1+√2)mm=√2+1.(2)易知△CHG 是等腰直角三角形,且CH=GH.由折叠和正方形的性质可知∠DCE=∠BAG=22.5°.又∵CD=AB ,∠D=∠B=90°,∴△DCE ≌ △BAG ,∴DE=BG ,∴EF=DE=BG=GH.易知∠GHF=∠EFH=90°,∴EF ∥GH ,∴四边形EFGH 是平行四边形,∴S 四边形EFGH =EF ×FH.CH=HG=EF=AF=m ,AC=√2CD=√2(m+√2m ).S 正方形ABCD =CD 2=(1+√2)2m 2,S 四边形EFGH =EF (AC-AF-CH )=m [√2(m+√2m )-2m ]=√2m 2,∴S正方形ABCD S四边形EFGH=√2)2√2=√2√2=4+3√22. 5.(1)菱 (2)(√2+1)S (1)如图,由折叠可知,∠MAD=∠DAC=12∠MAC ,∠CAB=∠NAB=12∠CAN ,∠DCA= ∠MCD=12∠ACM ,∠ACB=∠NCB=12∠ACN.∵四边形AMCN 是正方形,∴∠MAC=∠MCA=∠NAC=∠NCA ,∴∠DAC=∠BAC=∠BCA=∠DCA ,∴AD ∥BC ,AB ∥DC ,∴四边形ABCD 为平行四边形.∵∠DAC=∠DCA , ∴AD=CD ,∴四边形ABCD 为菱形.(2)连接MN 交AC 于点O ,过点B 作BP ⊥AN 于点P ,易知MN 经过点B ,D ,△BPN 是等腰直角三角形,则OB=BP ,BN=√2BP.设OB=BP=a ,则BD=2a ,BN=√2a ,∴S△ACN S △ACB=ON OB =√2a+aa =√2+1.根据正方形和菱形的对称性,可知S正方形AMCN S四边形ABCD=2S△ACN 2S △ACB=√2+1,∴S 正方形AMCN =(√2+1)S.6.253或154 设BD=x ,则AD=BD=x ,CD=16-x.在Rt △ACD 中,由勾股定理,得AD 2=AC 2+CD 2,即x 2=82+(16-x )2,解得x=10,∴BD=10,CD=6.分以下两种情况讨论.(1)当点P 到AC 边的距离等于5时,过点P 作PF ⊥AC 于点F ,如图(1),则PF=5,PF ∥CD ,∴△APF ∽△ADC ,∴AP AD =PF DC ,即AP 10=56,∴AP=253.(2)当点P 到BC 边的距离等于5时,过点P 作PG ⊥BC 于点G ,如图(2),则PG=5,PG ∥AC ,∴△DPG ∽△DAC ,∴DP DA =PGAC ,即DP 10=58,∴DP=254,∴AP=10-254=154.综上所述,AP 的长为253或154.7.2,2√3或√14-√2 当点P 是AD 上的点时,如图(1),∵PD=2AP ,∴AP=13AD=13AB=2.当点P 是AB 上的点时,如图(2),∵PD=2AP ,∠DAP=90°,∴∠ADP=30°,∴AP=√33AD=√33×6=2√3.如图(3),当点P 是AC 上的点时,过点P 作AD 的垂线,垂足为点E.设AP=x ,则PD=2x ,AE=PE=√22x ,∴DE=6-√22x.在Rt △DEP 中,由勾股定理,得PD 2=DE 2+PE 2,即(2x )2=(6-√22x )2+(√22x )2,解得x=√14-√2(负值已舍去),故AP=√14-√2.当点P 是CD ,BD 或BC 上的点时,都不能满足PD=2AP.综上所述,AP 的长为2,2√3或√14-√2.8.5或18 在Rt △ABC 中,AB=9,BC=12,由勾股定理,得AC=15.分以下2种情况讨论.①当点P 在线段AB 上时,如图(1).∵∠QPB=∠A+∠AQP=∠A+90°,∴∠QPB 为钝角,∴当△PQB 为等腰三角形时,只可能是PQ=PB=9-PA.易证△AQP ∽△ABC ,∴PA AC =PQBC ,即PA 15=9−PA12,∴AP=5.②当点P 在线段AB 的延长线上时,如图(2),易知∠QBP 为钝角,∴当△PQB 为等腰三角形时,只可能是PB=BQ ,∴∠BQP=∠P.又∵∠BQP+∠AQB=90°,∠A+∠P=90°,∴∠AQB=∠A ,∴BQ=AB=9,∴BP=9,∴AP=18.综上所述,当△PQB 为等腰三角形时,AP 的长为5或18.9.521,511或12 根据题意可得AD=√5t ,BE=4t ,则BD=√5-√5t ,CE=4-4t.易证△BDE ∽△CEF ,∴BD CE =BECF ,∴BD ·CF=BE ·CE.分以下三种情况讨论.①如图(1),当点F 在线段AC 上,且AF=AD=√5t 时,CF=BD=√5-√5t ,∴(√5-√5t )2=4t (4-4t ),解得t=521(不合题意的解已舍去).②如图(2),当点F 在CA 的延长线上,且AF=AD=√5t 时,CF=√5+√5t ,∴(√5-√5t )(√5+√5t )=4t (4-4t ),解得t=511(不合题意的解已舍去).③如图(3),当点F 在CA 的延长线上,且DF=AD=√5t 时,过点B 作BM ⊥AC ,垂足为点M.设AM=x ,由勾股定理可得AB 2-AM 2=BC 2-CM 2,即(√5)2-x 2=42-(√5+x )2,解得x=3√55.取AF 的中点H ,连接DH ,则∠HDA=∠MBA ,∴sin ∠HDA=sin ∠MBA ,即AH AD =AMAB ,∴√5t=3√55√5,解得AH=3√55t ,∴AF=6√55t ,∴(√5-√5t )(√5+6√55t )=4t (4-4t ),解得t=12(不合题意的解已舍去).综上所述,t 的值为521,511或12.图(1) 图(2) 图(3)10.2√7或4 在矩形ABCD 中,AB=CD=2-AD 2=4√3,tan ∠BAC=BCAB =4√3=√33,∴∠BAC=30°.如图(1),当∠CHG=90°时,EH=12AE=√3,AH=√3EH=3,∴CH=8-3=5,GH=EG-EH=√3,∴CG=√CH 2+GH 2= √52+(√3)2=2√7.如图(2),当∠CGH=90°时,连接CE ,∵BE=AE=GE ,CE=CE ,∴Rt △CEG ≌Rt △CEB ,∴CG=BC=4.由题意可知,点G 在以点E 为圆心,EA 为半径的圆上运动,∴∠GCH<90°,故∠GCH ≠90°.图(1) 图(2)11.2或134 在△PEF 与△ABE 中,∠A=∠EFP=90°,∴当△PEF 与△ABE 相似时,分两种情况讨论.(1)如图(1),当△PEF ∽△EBA 时,∠PEF=∠EBA ,∴AB ∥EP.易得四边形ABPE 是矩形,∴BP=AE=2.(2)如图(2),当△PEF ∽△BEA 时,∠PEF=∠BEA.∵AD ∥BC ,∴∠EBP=∠BEA ,∴∠PEF=∠EBP ,∴BP=EP ,∴点F 是BE 的中点.由勾股定理可求得BE=√AB 2+AE 2=2+22=√13,∴EF=12BE=√132.∵△PEF ∽△BEA , ∴EF AE =EPBE ,即√1322=√13,∴EP=134,∴BP=EP=134.综上可知,BP 的长为2或134.图(1) 图(2)12.8+4√3或16 如图,由题意可得AB=4.∵∠C=30°,∴BC=8,AC=4√3.根据题意易知CD=AD=2√3,CF=BF=4,DF=2.剪开后有如图(1)、图(2)、图(3)3种拼接方式.图(1)中所得四边形ABED 为矩形,其周长为2+2+4+2√3+2√3=8+4√3;图(2)中所得四边形为平行四边形,其周长为4+4+4+4=16;图(3)中所得四边形为等腰梯形,其周长为2+4+2+4+4=16.综上,所得四边形的周长为8+4√3或16.13.48或(32+8√13) 原三角形纸片有如图(1)、图(2)两种可能.如图(1),原三角形纸片的三边长分别为20,16,12,故其周长为48 cm ;如图(2),∵BD=6,BC=8,CD=10,∴BD 2+BC 2=CD 2,∴∠CBD=90°.易知AC ∥BD ,∴∠BCA=90°,∴AB=√AC 2+BC 2=4√13,故原三角形纸片的三边长分别为20,12,8√13,故其周长为(32+8√13)cm.综上所述,原三角形纸片的周长是48 cm 或(32+8√13)cm.14.-16≤a<0或0<a ≤16 由于y=ax 2+bx+c 经过(3,-3),(-3,3),则9a+3b+c=-3①,9a-3b+c=3②,①-②,得6b=-6,∴b=-1,∴抛物线y=ax 2+bx+c 的对称轴为直线x=12a .当a<0时,抛物线的开口向下,当x=12a ≤-3时符合题意,解得-16≤a<0;当a>0时,抛物线的开口向上,当x=12a ≥3时符合题意,解得0<a ≤16.综上所述,a 的取值范围为-16≤a<0或0<a ≤16.15. 1<c<2或-2<c<-1 根据抛物线的顶点坐标公式可得A (-1,c+1).分两种情况讨论.①当c>0时,如图(1),此时B (-c ,c ),P (0,c ),∴AP 2=(-1-0)2+(c+1-c )2=2,AB 2=[-1-(-c )]2+(c+1-c )2=c 2-2c+2.易知当0<c<1时,∠ABP 为钝角;当c=1时,∠ABP 为直角;当c>1时,随着c 的增大,∠ABP 逐渐减小,∠BAP 逐渐增大,当∠BAP 增加到90°时,AB 2+AP 2=BP 2,即c 2-2c+2+2=c 2,解得c=2.故△ABP 是锐角三角形时,1<c<2. ②当c<0时,如图(2),此时B (c ,c ),P (0,c ),∴AP 2=(-1-0)2+(c+1-c )2=2,AB 2=(-1-c )2+(c+1-c )2=c 2+2c+2.易知当-1<c<0时,∠ABP 为钝角;当c=-1时,∠ABP 为直角;当c<-1时,随着c 的减小,∠ABP 逐渐减小,∠BAP 逐渐增大,当∠BAP 增加到90°时,AB 2+AP 2=BP 2,即c 2+2c+2+2=c 2,解得c=-2.故△ABP 是锐角三角形时,-2<c<-1.综上所述,c 的取值范围为1<c<2或-2<c<-1.16.b=1或-3≤b<0 对于y=2x ,当x=-1时,y=-2,当x=2时,y=4.令x 2+b=2x ,移项,得x 2-2x+b=0,当Δ=4-4b=0时,解得b=1,此时抛物线与正比例函数y=2x 的图象的交点为(1,2),-1<1<2,故b=1符合题意,此时函数图象如图(1)所示.随着b 的减小,抛物线向下平移,当抛物线经过点(2,4)时,易得b=0,函数图象如图(2)所示,易知当0≤b<1时,抛物线与正比例函数y=2x 的图象在-1≤x ≤2时有两个交点.当抛物线过点(-1,-2)时,b=-3,函数图象如图(3)所示,易知当-3≤b<0时,抛物线与正比例函数y=2x 的图象在-1≤x ≤2时有一个交点.随着抛物线继续向下平移,易知当b<-3时,抛物线与正比例函数y=2x 的图象在-1≤x ≤2时无交点.综上所述,b=1或-3≤b<0.图(1) 图(2) 图(3)17.m<-1或1<m<3(等号写不写均可) 令x=x 2-x-3,解得x 1=-1,x 2=3,∴A (-1,-1),B (3,3).易得P (m ,m 2-m-3),Q (m ,m ).当m<-1或m>3时,PQ=m 2-m-3-m=m 2-2m+1-4=(m-1)2-4,∴当m<-1时,PQ 的长度随m 的增大而减小;当-1<m<3时,PQ=m-(m 2-m-3)=-m 2+2m+3=-(m-1)2+4,∴当1<m<3时,PQ 的长度随m 的增大而减小.综上可知,m 的取值范围为m<-1或1<m<3.18.-3<k ≤-2 ∵y=-34x (x+4)=-34(x+2)2+3,∴抛物线G 的顶点坐标为(-2,3).对于y=-34x (x+4),当x=-1时,y=94;当x=-3时,y=94;当x=-4或x=0时,y=0,∴抛物线与x 轴围成的区域(不含边界)内包含的整点有(-3,2),(-3,1),(-2,2),(-2,1),(-1,2),(-1,1),共6个.分析题意可知,符合要求的整点一定是(-3,2),(-2,2),(-3,1),故当双曲线y=k x 经过(-2,1)和(-1,2)两点时,k 取最大值,为-2;当双曲线y=k x 经过点(-3,1)时,符合条件的整点只有(-3,2)和(-2,2).综上可知,k 的取值范围为-3<k ≤-2.。

2021年中考数学二轮专题复习课后练习：归纳

课后练习34归纳、猜想与说理型问题A组1．图1为雅婷左手拿着3张深灰色与2张浅灰色的牌叠在一起的情形．以下是她每次洗牌的三个步骤：步骤一：用右手拿出叠在最下面的2张牌，如图2.步骤二：将右手拿的2张牌依序交错插入左手拿的3张牌之间，如图3.步骤三：用左手拿着颜色顺序已改变的5张牌，如图4.第1题图若依上述三个步骤洗牌，从图1的情形开始洗牌若干次后，其颜色顺序会再次与图1相同，则洗牌次数可能为下列何者？()A. 18B．20C．25 D．272．(2017·重庆)下列图形都是由同样大小的菱形按照一定规律所组成的，其中第1个图形中一共有3个菱形，第2个图形中一共有7个菱形，第3个图形中一共有13个菱形，…，按此规律排列下去，第9个图形中菱形的个数为()第2题图A ．73B ．81C ．91D ．1093．(2017·丽水模拟)如图，在平面直角坐标系xOy 中，Rt △OA 1C 1，Rt △OA 2C 2，Rt △OA 3C 3，Rt △OA 4C 4…的斜边都在坐标轴上，∠A 1OC 1＝∠A 2OC 2＝∠A 3OC 3＝∠A 4OC 4＝…＝30°.若点A 1的坐标为(3，0)，OA 1＝OC 2，OA 2＝OC 3，OA 3＝OC 4…，则依此规律，点A 2018的纵坐标为( )第3题图A ．0B ．－3×⎝ ⎛⎭⎪⎫3322017C ．(23)2018D ．3×⎝ ⎛⎭⎪⎫23320174．请在图中这一组图形符号中找出它们所蕴含的内在规律，然后在横线上的空白处填上恰当的图形．第4题图5．观察下面的单项式：a ，－2a 2，4a 3，－8a 4，…根据你发现的规律，第8个式子是 .6．如图，边长为1的菱形ABCD 中，∠DAB ＝60°.连结对角线AC ，以AC 为边作第二个菱形ACEF ，使∠F AC ＝60°.连结AE ，再以AE 为边作第三个菱形AEGH 使∠HAE ＝60°…按此规律所作的第n 个菱形的边长是 .第6题图7．如图，点B 1在反比例函数y ＝2x (x ＞0)的图象上，过点B 1分别作x 轴和y 轴的垂线，垂足为C 1和A ，点C 1的坐标为(1，0)，取x轴上一点C 2⎝ ⎛⎭⎪⎫32，0，过点C 2作x 轴的垂线交反比例函数图象于点B 2，过B 2作线段B 1C 1的垂线交B 1C 1于点A 1，依次在x 轴上取点C 3(2，0)，C 4⎝ ⎛⎭⎪⎫52，0…按此规律作矩形，则第n (n ≥2，n 为整数)个矩形A n －1C n －1C n B n 的面积为 .第7题图8．(2017·通州模拟)已知y 是x 的函数，自变量x 的取值范围是x ＞0，下表是y 与x 的几组对应值.x …1245689…y … 3.92 1.950.980.78 2.44 2.440.78…小风根据学习函数的经验，利用上述表格所反映出的y与x之间的变化规律，对该函数的图象和性质进行了探究．下面是小风的探究过程，请补充完整：(1)如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点．根据描出的点，画出该函数的图象；第8题图(2)根据画出的函数图象，写出：①x＝7对应的函数值y约为________；②该函数的一条性质：________________________．B组9．(2015·十堰)如图，分别用火柴棍连续搭建正三角形和正六边形，公共边只用一根火柴棍．如果搭建正三角形和正六边形共用了2016根火柴棍，并且正三角形的个数比正六边形的个数多6个，那么能连续搭建正三角形的个数是( )第9题图A ．222B ．280C ．286D ．29210．如图，在标有刻度的直线l 上，从点A 开始，以AB ＝1为直径画半圆，记为第1个半圆；以BC ＝2为直径画半圆，记为第2个半圆；以CD ＝4为直径画半圆，记为第3个半圆；以DE ＝8为直径画半圆，记为第4个半圆，…按此规律，继续画半圆，则第4个半圆的面积是第3个半圆面积的倍，第n 个半圆的面积为 (结果保留π)．第10题图11．阅读以下材料：对于三个数a ，b ，c ，用M {a ，b ，c }表示这三个数的平均数，用min{a ，b ，c }表示这三个数中最小的数．例如：M {－1，2，3}＝－1＋2＋33＝43；min{－1，2，3}＝－1；min{－1，2，a }＝⎩⎪⎨⎪⎧a （a ≤－1），－1（a >－1）.解决下列问题： (1)填空：如果min{2，2x ＋2，4－2x }＝2，则x 的取值范围为____________________；(2)如果M {2，x ＋1，2x }＝min{2，x ＋1，2x }，求x .12．(2016·河北)如图，已知∠AOB ＝7°，一条光线从点A 出发后射向OB 边．若光线与OB 边垂直，则光线沿原路返回到点A ，此时∠A ＝90°－7°＝83°.第12题图当∠A <83°时，光线射到OB 边上的点A 1后，经OB 反射到线段AO 上的点A 2，易知∠1＝∠2.若A 1A 2⊥AO ，光线又会沿A 2→A 1→A原路返回到点A，此时∠A＝°.…若光线从点A发出后，经若干次反射能沿原路返回到点A，则锐角∠A的最小值＝°.13．探索规律：观察由※组成的图案和算式，并解答问题．第13题图1＋3＝4＝221＋3＋5＝9＝321＋3＋5＋7＝16＝421＋3＋5＋7＋9＝25＝52(1)试猜想：1＋3＋5＋7＋9＋…＋19＝；(2)试猜想：1＋3＋5＋7＋9＋…＋(2n－1)＋(2n＋1)＋(2n＋3)＝；(3)请用上述规律．．．．．计算：1001＋1003＋1005＋…＋2015＋2017＝.(可以用计算器，请算出最后数值哦！)14．18世纪瑞士数学家欧拉证明了简单多面体中顶点数V、面数F、棱数E之间存在的一个有趣的关系式，被称为欧拉公式．请你观察图中的几种简单多面体模型，解答下列问题：(1)根据下面的多面体模型，完成表格中的空格：第14题图多面体顶点数V 面数F 棱数E四面体44长方体812正八面体812正十二面201230体你发现顶点数V、面数F、棱数E之间存在的关系式是____________________；(2)一个多面体的面数比顶点数大8，且有30条棱，则这个多面体的面数是____________________；(3)某个玻璃饰品的外形是简单多面体，它的外表面是由三角形和八边形两种多边形拼接而成，且有24个顶点，每个顶点处都有3条棱．设该多面体外表面三角形的个数为x个，八边形的个数为y个，求x＋y的值．15．(2016·广东模拟)在由m×n(m×n＞1)个小正方形组成的矩形网格中，研究它的一条对角线所穿过的小正方形个数f，(1)当m、n互质(m、n除1外无其他公因数)时，观察下列图形并完成下表：m n m＋n f123 2134 3235 4257347猜想：当m、n互质时，在m×n的矩形网格中，一条对角线所穿过的小正方形的个数f与m、n的关系式是__________________(不需要证明)；(2)当m、n不互质时，请画图验证你猜想的关系式是否依然成立．第15题图C组16．(2016·大同模拟)问题情境：如图，将边长为8cm的正方形纸片ABCD折叠，使点B恰好落在AD边的中点F处，折痕EG分别交AB、CD于点E、G，FN与DC交于点M，连结BF交EG于点P.独立思考：(1)AE＝____________________cm，△FDM的周长为____________________cm；(2)猜想EG与BF之间的位置关系与数量关系，并证明你的结论．拓展延伸：如图2，若点F不是AD的中点，且不与点A、D重合：①△FDM的周长是否发生变化，并证明你的结论；②判断(2)中的结论是否仍然成立，若不成立请直接写出新的结论(不需证明)．第16题图参考答案课后练习34归纳、猜想与说理型问题A组1．B 2.C 3.D 4. 5.－128a8 6.(3)n－17.2n＋18．(1)如图，第8题图(2)①3.0②该函数没有最大值(答案不唯一)B组9．D10.422n－5π11.(1)0≤x≤1(2)x＝112．76613.(1)100(2)(n＋2)2(3)76808114．(1)666V＋F－E＝2(2)20(3)∵有24个顶点，每个顶点处都有3条棱，两点确定一条直线，∴共有棱24×3÷2＝36(条)．那么24＋F－36＝2，解得F＝14.∴x＋y＝14.15．(1)66f＝m＋n－1(2)m、n不互质时，猜想的关系式不一定成立，如图：第15题图C组16．独立思考：(1)316(2)EG⊥BF，EG＝BF.过G点作GH⊥AB 于H，则∠EGH＋∠GEB＝90°，由折叠知，点B、F关于直线GE所在直线对称，∴BF⊥GE，∴∠FBE＋∠GEB＝90°，∴∠FBE＝∠EGH，∵四边形ABCD是正方形，∴AB＝BC，∠C＝∠ABC＝90°，四边形GHBC是矩形，∴GH＝BC＝AB，∴△AFB≌△HEG，∴BF ＝EG；拓展延伸：①△FDM的周长不发生变化．由折叠知∠EFM＝∠ABC ＝90°，∴∠DFM＋∠AFE＝90°，∵四边形ABCD为正方形，∠A ＝∠D＝90°，∴∠DFM＋∠DMF＝90°，∴∠AFE＝∠DMF，∴△AEF∽△DFM，∴△FMD的周长△AEF的周长＝FDAE.设AF为x cm，则FD＝(8－x)cm，在Rt△AFE中，由勾股定理得：x2＋AE2＝(8－AE)2，AE＝64－x216cm.∴△FMD的周长x＋AE＋8－AE＝8－xAE，△FMD的周长＝（8＋x）（8－x）64－x216＝16（64－x2）64－x2＝16cm，∴△FMD的周长不变．②(2)中结论成立．赠送励志修身名言警句可怕的敌人，就是没有坚强的信念。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

类型2 几何多解类
高分技法
方法:如图(2),QP=QC,过点Q作QE⊥AC于点E,则cos∠QCE=cos∠ACB,所
以
;
如图(3),CP=CQ;
如图(4),PC=PQ,过点P作PF⊥BC于点F,则cos∠PCF=cos∠ACB,所以
.
类型2 几何多解类
例5 [2020安庆模拟]如图,在矩形ABCD中,AB=4,AD=8,点E为
类型2 几何多解类
高分技法
通过辅助圆找到折叠或对称后关键点的对应点所在的所有可能的位置,然后分情况构图进行讨论,借助勾股定理、相似三角形对应边成比例或同(等)角的同种三角函数值相等,列方程求解.此类型中涉及一个动点的居多,解答时需注意: ①点落在边上时,要考虑图形的各条边; ②点落在角的平分线上时,要考虑是哪几个角; ③点落在直线上时,要考虑落在线段上、线段的延长线上和线段的反向延长线上; ④点落在边的垂直平分线上时,要考虑图形的各条边.
题型三填空压轴题
目录
考法
• 类型1 多空类 • 类型2 几何多解类
考法
类型1 多空类
例1 [2020安徽,14]在数学探究活动中,敏敏进行了如下操作: 如图,将四边形纸片ABCD沿过点A的直线折叠,使得点B落在 CD上的点Q处,折痕为AP;再将△PCQ,△ADQ分别沿PQ,AQ 折叠,此时点C,D落在AP上的同一点R处.请完成下列探究: (1)∠PAQ的大小为 100 °; (2)当四边形APCD是平行四边形时, 的值为 3 .
类型2 几何多解类
例3 [2019河南]如图,在矩形ABCD中,AB=1,BC=a,点E在边
BC上,且BE= 3 a.连接AE,将△ABE沿AE折叠,若点B的对
5
应点B'落在矩形ABCD的边上,则a的值为
.
【思路分析】分两种情况:①当点B'落在AD边上时,根据矩形与折叠的性质可得四边形ABEB'是正方形,则BE=AB,进而可求出a的值;②当点B'落在CD边上时, 通过△ADB'∽△B'CE得到对应边成比例,进而可求出a的值.
类型2 几何多解类
高分技法
1.有一个动点的等腰三角形存在性问题解题技巧:先利用“两圆一线”,确定等腰三角形的第三个顶点(即动点)的位置,再结合图形自身特点,寻求解题方法. 图解:如图三角形.方法:作“两圆一线”,“两圆”为分别以点A,B为圆心、AB的长为半径的圆, “一线”为线段AB的垂直平分线,它们与直线l的交点,即为要找的点C.
类型2 几何多解类
高分技法
折叠后某点所落的特殊位置一般是指图形的边(或边所在直线)、某条线段的三等分点处、特殊四边形的对角线(或对角线所在直线)、图形的对称轴、某角的平分线、某线段的垂直平分线. 解法技巧:因为这类折叠问题中的折痕通常经过某一定点,所以常利用辅助圆确定某点折叠后的对应点的位置. 图解:如图,点E为矩形ABCD的边BC上的动点,将△ABE 沿直线AE折叠,则点B的对应点B'落在以点A为圆心、 AB的长为半径的圆上.
【思路分析】 (1)根据折叠找到对应角,推理得到∠PAQ与∠DAB的数量关系、 ∠BAD的大小,从而可得∠PAQ的大小.(2)根据折叠的性质得到QR与CD之间的数量关系,再利用(1)中结论、平行四边形的性质及三角函数即可求解.
类型1 多空题
高分技法
解决与操作(折叠、剪裁、旋转等)有关的多空题(即一个填空题有两个小题,每小题各有一空)时,需要在操作过程中挖掘隐含条件,例如找出关于折痕所在直线对称的图形,进而找到对应相等的角、边等,充分利用边、角的等量关系进行推理.如例1中,进行了3次折叠操作,对应有3条折痕,相应有3组全等的三角形: 折痕AP对应△BAP与△QAP,折痕PQ对应△CQP与△RQP,折痕AQ对应△DAQ 与△RAQ.一般来说,第(1)问的结论通常是解决第(2)问的基础,具有铺垫作用.
类型2 几何多解类
高分技法
2.有两个动点的等腰三角形存在性问题解题技巧:先大致确定图形形状,再利用等腰三角形“三线合一”的性质构造直角三角形,最后利用相似三角形、“同(等)角的同种三角函数值相同”或勾股定理进行求解. 图解:如图(1),在矩形ABCD中,点P在对角线AC上从点A向点C运动,同时点Q在CB上从点C向点B运动,两点的运动速度相同,何时△CPQ是等腰三角形?
类型2 几何多解类
2.图形形状不确定类多解题
例4 [2019合肥蜀山区一模]如图,在矩形ABCD中,AB=4,
BC=6,过矩形ABCD的对角线交点O作直线,分别交AD,BC于
点E,F,连接AF,若△AEF是等腰三角形,则AE=
.
【思路分析】连接AC,CE,先根据△AOE≌△COF得出AE=CF,进而可得BF=DE.当 △AEF是等腰三角形时,分AF=EF,AE=AF,AE=FE三种情况,分别求解即可.
类型2 几何多解类
1.点、线位置不确定类多解题
例2 [2020合肥蜀山区一模]如图,在Rt△ABC中,∠C=90°,
AC=6, BC=8,点E,F分别是边AC,BC上的动点,且EF∥AB,
点C关于EF的对称点D恰好落在△ABC的角平分线上,则
CD的长为
.
【思路分析】根据轴对称的性质可知点C关于EF的对称点D落在斜边AB上的高线上,该高线不与∠C的平分线重合,故分“点C在∠B的平分线上”“点C在∠A 的平分线上”2种情况讨论即可.
类型2 几何多解类
高分技法
点的位置不确定时的分类情况. 1.点在直线AB上的三种可能情况: (1)点在线段AB上;(2)点在线段AB的延长线上;(3)点在线段BA的延长线上. 2.点在三角形或四边形边上,需分点在三角形或四边形的各条边上进行讨论(点在三角形的角平分线上、高线上、中线上或点在四边形对角线上时,同理). 3.点在弧上的两种可能情况: (1)点在优弧上;(2)点在劣弧上. 4.点在抛物线上的两种情况: (1)点在对称轴左侧;(2)点在对称轴右侧. 注意:涉及坐标系时,也可分象限进行讨论,但不要忘记讨论该点在坐标轴上时的情况.
AD边上一点,将△ABE沿直线BE折叠得到△FBE,点G为CD边