东华理工大学物理练习册答案
合集下载
东华理工大学 物理练习试卷答案 动量与动量守恒
m M 图6
mv 2 f t
由牛顿第三定律，小球以此力作用于M，其方向向下， 对M，由牛顿第二定律，在竖直方向上
N Mg f 0
N Mg f
又由牛顿第三定律，M给地面的平均作用力也为 mv 2 F f Mg Mg 方向竖直向下 t
(2) 同理，M受到小球的水平方向冲力大小应为
动量与动量守恒 1、质量为m的铁锤竖直落下,打在木桩上并停下,设打 击时间为t,打击前铁锤速率为v,则在打击木桩的时 间内,铁锤所受平均合外力的大小为 （A) mv/t. (B) mv/ t－mg. (C) mv/ t＋mg. (D) 2mv/t. 【 A 】 2、粒子B的质量是粒子A的质量的4倍,开始时粒子A 的速度为(3i+4j), 粒子B的速度为(2i－7j),由于两者 的相互作用, 粒子A的速度变为(7i－4j),此时粒子B 的速度等于 (A) i－5j . (B) 2i－7j . (C) 0. (D) 5i－3 【A 】
v
解：
mv 0 mv cos MV cos 0 mv sin MV sin v0 sin v sin( ) V mv 0 sin M sin( )
v0
V
作用下，从静止开始运动，式中 i 为方向一定的单位矢 量, 则当ｔ＝1 s时物体的速度v ＝______ 2 i m / s 1
1、如图6所示，质量为M的滑块正沿着光滑水平地面向 右滑动．一质量为m的小球水平向右飞行，以速度1 （对地）与滑块斜面相碰，碰后竖直向上弹起，速率为 v2（对地）．若碰撞时间为t，试计算此过程中滑块对 地的平均作用力和滑块速度增量的大小 解： (1) 小球m在与M碰撞过程中给M的竖 直方向冲力在数值上应等于M对小球 的竖直冲力．而此冲力应等于小球 在竖直方向的动量变化率即：
mv 2 f t
由牛顿第三定律，小球以此力作用于M，其方向向下， 对M，由牛顿第二定律，在竖直方向上
N Mg f 0
N Mg f
又由牛顿第三定律，M给地面的平均作用力也为 mv 2 F f Mg Mg 方向竖直向下 t
(2) 同理，M受到小球的水平方向冲力大小应为
动量与动量守恒 1、质量为m的铁锤竖直落下,打在木桩上并停下,设打 击时间为t,打击前铁锤速率为v,则在打击木桩的时 间内,铁锤所受平均合外力的大小为 （A) mv/t. (B) mv/ t－mg. (C) mv/ t＋mg. (D) 2mv/t. 【 A 】 2、粒子B的质量是粒子A的质量的4倍,开始时粒子A 的速度为(3i+4j), 粒子B的速度为(2i－7j),由于两者 的相互作用, 粒子A的速度变为(7i－4j),此时粒子B 的速度等于 (A) i－5j . (B) 2i－7j . (C) 0. (D) 5i－3 【A 】
v
解：
mv 0 mv cos MV cos 0 mv sin MV sin v0 sin v sin( ) V mv 0 sin M sin( )
v0
V
作用下，从静止开始运动，式中 i 为方向一定的单位矢 量, 则当ｔ＝1 s时物体的速度v ＝______ 2 i m / s 1
1、如图6所示，质量为M的滑块正沿着光滑水平地面向 右滑动．一质量为m的小球水平向右飞行，以速度1 （对地）与滑块斜面相碰，碰后竖直向上弹起，速率为 v2（对地）．若碰撞时间为t，试计算此过程中滑块对 地的平均作用力和滑块速度增量的大小 解： (1) 小球m在与M碰撞过程中给M的竖 直方向冲力在数值上应等于M对小球 的竖直冲力．而此冲力应等于小球 在竖直方向的动量变化率即：
东华理工大学 物理练习试卷答案 光的衍射
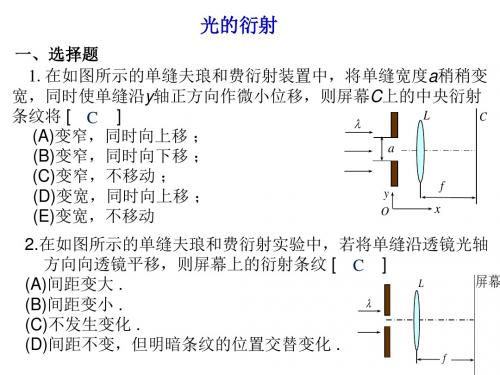
中央明条纹的宽度 x 2 ftg 0 2 f 5 103 m 5mm
a
若单缝装置浸入水中，中央明条纹的半角宽度
5 107 3 0 3 . 76 10 rad 3 na 1.33 0.1 10
17.用橙黄色的平行光垂直照射到宽度a=0.60mm的单缝上，在缝后 放置一个焦距f=40.0cm的凸透镜，则在屏幕上形成衍射条纹，若 在屏上离中央明条纹中心为1.40mm处的P点为一明条纹。试求： （1）入射光的波长；（2）P点的条纹级数；（3）从P点看，对 该光波而言，狭缝处的波阵面可分为几个半波带（橙黄色光的波 长约为5×103 Å~6×103 Å）。 解：（1）设入射光波长为，离屏中心x=1.4mm处为明条纹，则 由单缝衍射明条纹条件，x应满足
6.波长 = 5000 Å的单色光垂直照射到宽度a = 0.25 mm的单缝上, 单缝后面放置一凸透镜,在凸透镜的焦面上放置一屏幕,用以观测衍 射条纹,今测得屏幕上中央条纹一侧第三个暗条纹和另一侧第三个暗 条纹之间的距离为d = 12 mm ,则凸透镜的焦距为 [ B ] (A) 2m ； (B) 1m ； (C) 0.5m ； (D) 0.2m ； (E) 0.1m . 7.波长为5000Å的单色光垂直入射到光栅常数为1.010-4cm的平 面衍射光栅上，第一级衍射主极大所对应的衍射角为 [ B ] (A) 60 ； (B) 30 ； (C) 45 ； (D) 75. 8.波长为5500Å的单色光垂直入射到光栅常数为2.010-4cm的平 面衍射光栅上，可能观察到的光谱线的最大级次为 [ B ] (A) 2 ； (B) 3 ； (C) 4 ； (D) 5.
解 (1) 由光栅方程 在sin=0.20处，有 0.2d =2 (2)由第四级缺级，有
东华理工大学 物理练习试卷答案 刚体力学
J 00 J
J0 2mR2 /5，
2
J 2m( R / 2 )2 /5
40
2 T0 T 4 0 4
14. 一块方板，可以绕通过其一个水平边的光滑
固定轴自由转动.最初板自由下垂.今有一小团粘 土，垂直板面撞击方板，并粘在板上。对粘土和 方板系统，如果忽略空气阻力，在碰撞中守恒的 绕木板转轴的角动量 量是 ________________. （动能、 绕木板转轴的角动量、 机械能、 动量）
E p EK J
1 2
EK EP 0
2
Ep J
1 2
2
M J
即角速度从小到大，角加速度从大到小
7、一水平圆盘可绕通过其中心的固定竖直轴转动，盘上站着一个 人.把人和圆盘取作系统，当此人在盘上随意走动时，若忽略轴 的摩擦，此系统 [ C ] (A)动量守恒． (B)机械能守恒． (C) 对转轴的角动量守恒． (D) 动量、机械能和角动量都守恒． (E) 动量、机械能和角动量都不守恒．
2m 得 k 2 L 2 mg df dmg rdr 2
L
dM rdf
2m g 2 2 M dM r dr m gL 2 L 3 0
L
18.如图所示，一轻绳绕过一轻滑轮，绳的一端被一质量为m 的 人抓住，绳的另一端悬挂一质量为 m / 2的物体，定滑轮的质 量为 M ，半径为R，可视为匀质圆盘。设人从静止开始相对绳 匀速向上爬行时，绳子与滑轮间无相对滑动， 求物体上升的加速度。
8、如图所示，一静止的均匀细棒，长为L、质量为M，可绕通过 棒的端点且垂直于棒长的光滑固定轴O在水平面内转动，转动 1 ML 惯量为 。一质量为m、速率为v的子弹在水平面内沿与棒 3 1 v 垂直的方向射出并穿出棒的自由端，设穿过棒后子弹的速率 2 B 为 ，则此时棒的角速度应为［ ］。 1
大学物理练习册(上册)答案
练习一 （第一章 质点运动学） 一、选择题 1、（D ）2、（C ）3、（D ）4、（B ）5、（D ） 二、填空题1、（1）A （2）1.186s(或4133-s) （3）0.67s （或32s ） 2、8m 10m3、（1）t e t t A βωβωωωβ-+-]sin 2cos )[(22 （2）ωπωπk +2（ ,2,1,0=k ） 4、3/30Ct v + 400121Ct t v x ++ 5、（1）5m/s (2) 17m/s 三、计算题1、解：dxdvv dt dx dx dv x dt dv a ==+==262分离变数积分⎰⎰+=xvdx x vdv 020)62(得 )1(422x x v +=质点在任意位置处的速度为 )1(22x x v +=（由初始时刻的加速度大于零，可知速度的大小为非负）。
2、解：（1）第二秒内的位移为 m x x x 5.0)1()2(-=-=∆ 第二秒内的平均速度为s m txv /5.0-=∆∆= （2）t 时刻的速度为 269t t dtdxv -==第二秒末的瞬时速度为 s m s m s m v /6/26/292-=⨯-⨯=（3）令0692=-==t t dtdxv ，解得s t 5.1= 第二秒内的路程为 m x x x x s 25.2)5.1()2()1()5.1(=-+-=。
3、解：（1）由几何关系θθsin cos r y r x ==质点作匀速率圆周运动故dtd θω=，代入初始条件0=t 时0=θ，得 t 时刻t ωθ=，所以j y i x r+=)sin (cos j t i t rωω+=（2）速度为)cos sin (j t i t r dtrd v ωωω+-==加速度为)sin (cos 2j t i t r dt vd a ωωω+-==（3）r j t i t r dtv d a 22)sin (cos ωωωω-=+-==由此知加速度的方向与径矢的方向相反，即加速度的方向指向圆心。
东华理工大学-物理练习试卷答案-质点运动学.
速率u 拉动纤绳，绞车定滑轮离水面的高度为h ，求小船向岸边
移动的速度和加速度。 解：设小船到坐标原点的距离为l，
uv
任意时刻小船到岸边的距离x总
l
满足 x2 l2 h2 ，两边对时间t
h l(t)
求导数，得
dx dl 2x 2l
x
O
x (t)
dt dt
d l u 为绞车拉动纤绳的速率，纤绳随时间在缩短，故 d l 0
解：1） 由r = R(ω + ω)知 x = ωt y = ωt
消去t可得轨道方程 x2 y2 R2
2)vvdrvRsintviRcostvj
dt
1
v[(Rsint)2(Rcost)2]2 R
17. 已知质点位矢随时间变化的函数形式为r = t2i + 2 ，式中r 的
单位为m，t 的单位为s .求：（1）任一时刻的速度和加速度；
dt
dt
dx v 为小船向岸边移动的速率
dt
l v u
x2 h2 u 负号表示小船速度沿x 轴反方向
x
x
小船向岸边移动的加速度为
d2x dv u2h2
a dt2
dt
x3
20. 如图A、B两物体由一长为l 的刚性细杆相连，A、B 两物体可
在光滑轨道上滑行．如物体A以恒定的速率向左滑行，当 60o
18. 如图，一升降机以加速度a 上升，在上升过程中有一螺钉从天花 板上松落，升降机的天花板与底板相距为h ，求螺钉从天花板落到 底板上所需的时间。
解：以地面为参照系，坐标如图， 升降机与螺丝的运动方程分别为
y1
v0t
1 2
at2
y2
h
东华大学-物理-大学物理下册-练习册-近代物理练习解答
近代物理练习题与参考解答一选择题解：h v = mv2/2 +A → E K = h v – A， OP/OQ = h（斜率） [ C ]解：光子损失的能量即电子获得的能量。
E K = mc2- m o c2= m o c2/(1-v2/c2)1/2 - m o c2= m o c2/(1-0.62)1/2 - m o c2= m o c2/0.8 - m o c2= (1.25 –1) m o c2= 0.25 m o c2 [ D]解：电子获得的能量：hc/λo – hc/λ = E K→ hc (λ- λo)/λλo = E K → (λ-λo)/λo =△λ/λo = E K/(hc/λ) = E K/ (hc/λo – E K)= 0.1/(0.5 –0.1) = 0.25 [ B ]解：hc/λ= E Kmax + hc/λo→λ= (E Kmax /hc+ 1/λo)= (1.2×1.6×10-19/6.63×10-34×3×108 + 1/5400×10-10)= 3550×10-10 m[ D ]解：P= mv = m o v/(1-v2/c2)1/2= h/λ→λ = (1-v2/c2)1/2h/m o v = h/m o·(1/v 2- 1/c2)1/2 [C]解：mv2/2=eU，P =mv=h/λ→ U= h2/2meλ2 [D] 或直接利用λ= 12.25/U1/2，U = (12.25/λ)2 = (12.25/0.4)2 = 938 （m = 9.11×10-31kg ，e =1.6×10-19C）解：∵λ = h/p , a sin θ0 = kλ , k =1 → sin θ0 =λ/a = h/ap ∴ d = 2Rtgθ0≈ 2Rsin θ0 = 2Rλ/a = 2Rh/ap [D]解：因为λ = h/p, 所以动量p 相同. [A]解：[ D ]解： ψ2 =(1/a)cos2[3π(5a/6)/2a]=(1/a)cos2[5π/4]=1/2a [ A ]解：∆x∆p x≥h，若∆x大，∆p x小，动量的精确度高。
东华理工大学 物理练习试卷答案 静电场中的导体与电介质
2q A qA 2 , 1 3S 3S
qB 2 S 110 7 C
U A EAC d AC
1 d AC 2.3 103V 0
12 在半径为R1的金属球之外包有一层外半径为R2的均匀电介质球 壳，介质相对介电常数为εr，金属球带电Q．试求： (1)电介质内、外的场强； (2)电介质层内、外的电势；
解: 利用有介质时的高斯定理
(1)介质内R1<r<R2场强 介质外r>R2场强 (2)介质外r<R2电势
Qr Qr D 3 , E内 4πr 4π 0 r r 3
Qr Qr D , E外 3 4πr 4π 0 r 3
D dS q
E0
r>R3的区域
1 Q Q2 1 2 2 W2 0 ( ) 4πr dr 2 R3 2 8π 0 R3 4π 0 r
Qr 4π 0 r 3 r>R3时 E2 E1
在R1<r<1 W W1 W2 ( ) 8π 0 R1 R2 R3
静电场中的导体与电介质
一、选择题
1.有一接地金属球，有一弹簧吊起，金属球原来 不 带 电，若在它的下方放置一电量为q的点电荷则 【C 】 （A）只有当q＞0时，金属球才会下移 （B）只有当q＜0时，金属球才下移 （C）无论q是正是负金属球都下移 ； （D）无论q是正是负金属球都不动
q
2.A、B为两导体板，面积均为S，平行放置， A板带电荷+Q1 ， B板电荷 +Q2，如果使 B板接地，则AB间电场强度的大小E为 【C】
E 则两圆筒的电势差为 2 0 r r R2 R2 dr R2 U E d r ln 2 0 r r 2 0 r R1 R1 R1
qB 2 S 110 7 C
U A EAC d AC
1 d AC 2.3 103V 0
12 在半径为R1的金属球之外包有一层外半径为R2的均匀电介质球 壳，介质相对介电常数为εr，金属球带电Q．试求： (1)电介质内、外的场强； (2)电介质层内、外的电势；
解: 利用有介质时的高斯定理
(1)介质内R1<r<R2场强 介质外r>R2场强 (2)介质外r<R2电势
Qr Qr D 3 , E内 4πr 4π 0 r r 3
Qr Qr D , E外 3 4πr 4π 0 r 3
D dS q
E0
r>R3的区域
1 Q Q2 1 2 2 W2 0 ( ) 4πr dr 2 R3 2 8π 0 R3 4π 0 r
Qr 4π 0 r 3 r>R3时 E2 E1
在R1<r<1 W W1 W2 ( ) 8π 0 R1 R2 R3
静电场中的导体与电介质
一、选择题
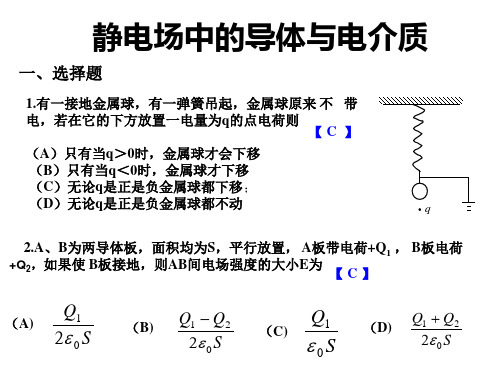
1.有一接地金属球，有一弹簧吊起，金属球原来 不 带 电，若在它的下方放置一电量为q的点电荷则 【C 】 （A）只有当q＞0时，金属球才会下移 （B）只有当q＜0时，金属球才下移 （C）无论q是正是负金属球都下移 ； （D）无论q是正是负金属球都不动
q
2.A、B为两导体板，面积均为S，平行放置， A板带电荷+Q1 ， B板电荷 +Q2，如果使 B板接地，则AB间电场强度的大小E为 【C】
E 则两圆筒的电势差为 2 0 r r R2 R2 dr R2 U E d r ln 2 0 r r 2 0 r R1 R1 R1
东华理工大学 物理练习试卷答案 光的偏振
i0
1
2
二、填空题 6.使光强为I0的自然光依次垂直通过三块偏振片P1、P2和P3。相 邻偏振片的偏振化方向成450角。则透过三块偏振片的光强I为 I0/8 . 7.如图所示，一束自然光入射到折射率分别为n1和n2的两种介质 的交界面上，发生反射和折射。已知反射光是完全偏振光，那 么折射角r的值为 π/2 - arctan n2/n. 1
14. （1）试求光在装满水的容器底部反射时的布儒斯特角。容器 用冕牌玻璃制成，折射率为1.50，水的折射率为1.333。 （2）今测得某釉质的起偏角i0=58 °，试求该釉质的折射率。 解：（1）由布儒斯特定律可得
n2 1.50 i0 arctg arctg 48 n1 1.333
（2）
0 1 I0 I 5 I0 得 I 4I0 1 I0 2I0 I I 2
11.一束自然光垂直穿过两个叠放在一起的偏振片，若透射光强 I 为 原入射光强I的1/4，则两偏振片的偏振化方向之间的夹角是多少？ 解：设通过第一个偏振片后的光强为I0
1 I0 I 2
4.两偏振片堆叠在一起，一束自然光垂直入射其上时没有光线通过。 当其中一偏振片慢慢转动1800时透射光强度发生变化为[ B ] (A)光强单调增加； (B)光强先增加，后有减小至零； (C)光强先增加，后减小，再增加； (D)光强先增加，然后减小，再增加，再减小至零.
5.一束自然光自空气射向 一块平板玻璃（如图），设入射角等于 布儒斯特角i0 ，则在界面2的反射光[ B ] (A)是自然光； (B)是完全偏振光且光矢量的振动方向垂直入射面； (C)是完全偏振光且光矢量的振动方向平行入射面； (D)是部分偏振光.
16
证明：自然光通过P1后成为强度为 I0/2的线偏振光。设在t时刻， P1 与 P2的夹角为ωt， P2 与P3的夹角为 (90 °- ωt) 。由马吕斯定律可得
1
2
二、填空题 6.使光强为I0的自然光依次垂直通过三块偏振片P1、P2和P3。相 邻偏振片的偏振化方向成450角。则透过三块偏振片的光强I为 I0/8 . 7.如图所示，一束自然光入射到折射率分别为n1和n2的两种介质 的交界面上，发生反射和折射。已知反射光是完全偏振光，那 么折射角r的值为 π/2 - arctan n2/n. 1
14. （1）试求光在装满水的容器底部反射时的布儒斯特角。容器 用冕牌玻璃制成，折射率为1.50，水的折射率为1.333。 （2）今测得某釉质的起偏角i0=58 °，试求该釉质的折射率。 解：（1）由布儒斯特定律可得
n2 1.50 i0 arctg arctg 48 n1 1.333
（2）
0 1 I0 I 5 I0 得 I 4I0 1 I0 2I0 I I 2
11.一束自然光垂直穿过两个叠放在一起的偏振片，若透射光强 I 为 原入射光强I的1/4，则两偏振片的偏振化方向之间的夹角是多少？ 解：设通过第一个偏振片后的光强为I0
1 I0 I 2
4.两偏振片堆叠在一起，一束自然光垂直入射其上时没有光线通过。 当其中一偏振片慢慢转动1800时透射光强度发生变化为[ B ] (A)光强单调增加； (B)光强先增加，后有减小至零； (C)光强先增加，后减小，再增加； (D)光强先增加，然后减小，再增加，再减小至零.
5.一束自然光自空气射向 一块平板玻璃（如图），设入射角等于 布儒斯特角i0 ，则在界面2的反射光[ B ] (A)是自然光； (B)是完全偏振光且光矢量的振动方向垂直入射面； (C)是完全偏振光且光矢量的振动方向平行入射面； (D)是部分偏振光.
16
证明：自然光通过P1后成为强度为 I0/2的线偏振光。设在t时刻， P1 与 P2的夹角为ωt， P2 与P3的夹角为 (90 °- ωt) 。由马吕斯定律可得
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
一质点作简谐振动，周期为T．当它由平衡位置向x轴正方向运动时，
(C) T /6．
4.（5186）
(D) T /4．［ C ］
已知某简谐振动的振动曲线如图所示，位移的单位为厘米，时间
单位为秒．则此简谐振动的振动方程为：
2 2 (B)． x2 (A)．x2 cos ( t- ) cos( t )
1.（0580）
振动习题
一长为l的均匀细棒悬于通过其一端的光滑水平固定轴上，（如图
所示），作成一复摆．已知细棒绕通过其一端的轴的转动惯量，此 摆作微小振动的周期为
(A)
(C) .
l 2 g
2l 2 3g
(B) . 2
(D) .
O
l 2g
l
l 3g
A
［ C］
y y A
2.（3031） 已知一质点沿ｙ轴作简
t (s)
4.（3013） 一单摆的悬线长l = 1.5 m，在顶端固定点的竖直下方0.45 m处有 一小钉，如图示．设摆动很小，则单摆的左右两方振幅之比 A1/A2的近似值为_______________ ． 0.84
0.45 m l
小钉
5.（3570） 1 一物体同时参与同一直线上的两个简谐振动： x 0 . 05 cos( 4 t ) 1 3 2 (SI) ，x 合成振动的振幅为 0 . 03 cos( 4 t- ) (SI) 2 3 __________________m ． 0.02
x (cm) t (s) 1
2 2 3 3 O 3 3 -1 4 2 4 2 (C)． cos ( t- ) -2 x2 cos( t ) (D)．x2 3 3 3 3
4 1 (E) ．x2 cos ( t- ) 3 4
［C ］
5.（3023） 一弹簧振子，当把它水平放置时，它可以作简谐振动．若把它竖直 放置或放在固定的光滑斜面上，试判断下面哪种情况是正确的： (A) 竖直放置可作简谐振动，放在光滑斜面上不能作简谐振动． (B) 竖直放置不能作简谐振动，放在光滑斜面上可作简谐振动． (C) 两种情况都可作简谐振动． (D) 两种情况都不能作简谐振动．［C ］ 填空题 竖 直 放置 1.（3015） 放 在 光滑 斜面 上 在t = 0时，周期为T、振幅为A的单摆分别处于图(a)、(b)、(c)三 种状态．若选单摆的平衡位置为坐标的原点，坐标指向正右方， 则单摆作小角度摆动的振动表达式（用余弦函数表示）分别为 2 t 1 x A cos( - π ) (a) ______________________________ ； T 2 2 t 1 xA cos( π ) (b) ______________________________ ； T 2 2 t v0 v0 v0 = 0 xA cos( π ) (c) ______________________________ ．
mg N ma
1分
2.（3054）一简谐振动的振动 曲线如图所示．求振动方程．
x (cm) 10 O 2 t (s) -5 -10
A cos( t ) 解：(1) 设振动方程为 x
解上面两式，可得
10 sin 0 由曲线可知 A = 10 cm , t = 0，v 0
3.（3834） 一物体质量为0.25 kg，在弹性力作用下作简谐振动，弹簧的劲度系数 k = 25 N· m-1，如果起始振动时具有势能0.06 J和动能0.02 J，求 (1) 振幅； (2) 动能恰等于势能时的位移； (3) 经过平衡位置时物体的速度．
计算题1.（0318） 一个轻弹簧在60 N的拉力作用下可伸长30 cm．现将一物体悬挂在弹簧的下端 并在它上面放一小物体，它们的总质量为4 kg．待其静止后再把物体向下拉10 cm，然后释放．问： (1) 此小物体是停在振动物体上面还是离开它？ (2) 如果使放在振动物体上的小物体与振动物体分离，则振幅A需满足何条件？ 二者在何位置开始分离？ 1.解：(1) 小物体受力如图． 设小物体随振动物体的加速度为a，按牛顿第二定律有（取向下为正） 当N = 0，即a = g时，小物体开始脱离振动物体，已知 1分 A = 10 cm， k 60 N/m 0.3 有 rad· s-1 2分 k /m 50 2 系统最大加速度为 a m· s-2 1分 A 5 max 此值小于g，故小物体不会离开． 1分 (2) 如使a > g，小物体能脱离振动物体，开始分离的位置由N = 0求得 2 2分 ga x 2 cm 1分 x g / 19 . 6 2 即在平衡位置上方19.6 cm处开始分离，由 a ，可得 A g max 2 A g/ ω =19.6 cm． 1分
（3382） 在两个相同的弹簧下各悬一物体，两物体的质量比为4∶1，则 二者作简谐振动的周期之比为______ 2:1
x (cm)
3.（3036） 已知一简谐振动曲线如图所示，由图确定振子： O 1 2 0.5(2n+1) n = 0， 1，2，3，… s时速度为零． (1) 在_________ ____ n n = 0，1，2，3，… (2) 在__________ __ s时动能最大． 0.5(4n+1) n = 0，1，2，3，… _ s时加速度取正的最大值． (3) 在___________
o t (A) y
o t (B) y
谐振动．其振动方程
A cos( t 3 / 4 ) 为 y
A
A
．与之对应的振动曲 线是 ［B ］
-A
o t -A (C)
o t (D)
3.（3253） 从二分之一最大位移处到最大位移处这段路程所需要的时间为 (A) T /12． (B) T /8．
= 2/3
2分 由图可知质点由位移为 x0 = -5 cm和v 0 < 0的状态到x = 0和 v > 0的状态所需时间t = 2 s，代入振动方程得 0 10 cos( 2 2 / 3 )
2 / 3 3 / 2 则有， 2
∴
= 5 /12
2分 1分
0 . 1 cos( 5 t / 12 2 / 3 ) 故所求振动方程为 x (SI)