《信号与线性系统》试题与答案5
信号与线性系统一二章自测题及参考答案
第一、二章自测题1、判断题（1）若x (t )是一连续时间周期信号，则y (t )=x (2t )也是周期信号。
（2）两个周期信号之和一定是周期信号。
（3）所有非周期信号都是能量信号。
（4）两个连续线性时不变系统相互串联的结果仍然是线性时不变系统。
（5）若)()()(t h t x t y *=，则)1()2()1(+*-=-t h t x t y 。
（6）一个系统的自由响应就等于它的零输入响应。
（7）一个系统的零状态响应就等于它的自由响应。
（8）零状态响应是指系统没有激励时的响应。
（9）系统的单位冲激响应是指系统在冲激信号作用下的全响应。
（10）两个功率信号之和必为功率信号。
2、判断下列信号是能量信号还是功率信号？ （1）3cos(15)0()0t t f t t π≥⎧=⎨<⎩ （2）50()0te tf t t -⎧≥=⎨<⎩（3）()6sin 23cos3f t t t =+ （4）|2|()20sin 2t f t e t -=3、填空题（1）已知)()4()(2t t t f ε+=，则)(''t f =__________________。
（2）=+-⋅+⎰∞∞-dt t t t )1()2(2δ__________________________。
（3）=-⎰∞∞-dt t ）（92δ_________________________ 。
（4）=-⎰∞∞-dt t t e t j ）（0δω_________________________ 。
（5）信号cos(15)cos(30)t t -的周期为 。
4、试画出下列各函数的波形图 （1）0 ),()(001>-=t t t t f ε （2）)]4()([3cos )(2--=t t t t f εεπ （3）][sin )(3t t f πε=5、已知f (t )的波形如图1.1所示，求f (2-t )与f (6-2t )的表达式，并画出波形图。
管致中《信号与线性系统》(第5版)(章节题库 连续信号的正交分解)
F(
j)
e2
2e2 2 j
。
2．频谱函数 F（jω）＝g4（ω）cosπω 的傅里叶逆变换 f（t）等于______。
【答案】
f
(t)
1
[Sa2(t
)
Sa2(t
)]
【解析】因为
F(
j)
g4 () cos
1 2
g4 ()(e j
e j
)
，而
F
1[ g 4
()]
2
Sa(2t)
，根据傅里叶变换的时移特性，可得
x(t t0 ) X (w)e jwt0 ，可得 e j4w (t 4) ， e j4w (t 4) ，再分别乘
以系数即得 f（t）＝
。重点在于傅里叶变换的性质。
1 / 117
圣才电子书
十万种考研考证电子书、题库视频学习平 台
3．信号
的傅里叶变换为（ ）。
)， 2
A2
E
A
2E
，
已知
，根据卷积定理
F2(
)
F1(
)gF1(
)
E 2
Sa2( 4
)
二、填空题
8 / 117
圣才电子书
1．信号
十万种考研考证电子书、题库视频学习平 台
的傅里叶变换 F（jω）等于______。
【答案】
【解析】
f
(t)
e2 (t)
2e2e2t (t) ，根据傅里叶变换，可得
10．图 3-2（a）所示信号 f（t）的傅里叶变换 3-2（b）所示信号 y（t）的傅里叶变换 Y（jω）为（ ）。
为已知，则图
5 / 117
专升本《信号与线性系统》-试卷-答案
专升本《信号与线性系统》一、（共60题,共156分）1. 能量有限信号是指总能量为有限值而平均功率为____的信号。
（2分）.标准答案：1. 零;2. 系统响应中随时间增长而趋于稳定的部分称为________________分量。
（2分）.标准答案：1. 稳态响应;3. 单位函数响应h(k)是指离散时间系统对____________________________________________的零状态响应。
（2分）.标准答案：1. 单位函数（或δ(k)）;4. 若周期函数f (t)满足，则称其为________函数。
（2分）.标准答案：1. 奇谐;5. h(t)是连续因果LTI系统的冲激响应，则系统稳定的充要条件是________________________________________________________________________ ________________________________________________________________________ ________________________________________________________________________ ________________________________________________________________________ ____________________。
（2分）.标准答案：1. ;6. ____。
（2分）.标准答案：1. 0;7. 时间函数中变化较____的信号必定具有较宽的频带。
（2分）.标准答案：1. 快;8. 信号的最小抽样频率为________________________________________________________________________ ________________________________________________________________________ ________________________________________________________________________ ________________________________________________________________________ ____________________ Hz。
信号与线性系统_习题答案(有错版)
2.1 (1) 已知连续时间信号 x(t ) 如图 P2.1(a)所示。试画出下列各信号的波形图，并加以标 注。 (a) x(t − 2) (b) x(1 − t ) (c) x(2t + 2) (2) 根据图 P2.1(b)所示的信号 h(t ) ，试画出下列各信号的波形图，并加以标注。 (a) h(t + 3) (b) h( − 2) (c) h(1 − 2t ) (3) 根据图 P2.1(a)和(b)所示的 x(t ) 和 h(t ) ，画出下列各信号的波形图，并加以标注。 (a) x(t )h(−t ) (b) x(1 − t )h(t − 1) (c) x(2 − ) h(t + 4)
其基波周期 T0 是 T1 , T2 的最小公倍数。 (b) x(n) 和 y ( n) 是周期的， x(n + = N1 ) x(n), y (n + N = y ( n) 2) 令 f= (n) x(n) + y (n) ，欲使 f (n) 是周期的，必须有
= N 0 kN = mN 2 1
πn
4
，对所有 n ，
7
1 n , n奇 显然 x(n) 是非周期的，但 y1 (n) 是周期的。 h(n) = 3 0, n偶
(c) 正确。若 x(n) 的周期为 N ，则 y2 (n) 的周期为 2 N 。 (d) 正确。若 y2 (n) 的周期为 N ，则 N 只能是偶数。 x(n) 的周期为 N / 2 。 2.7 判断下列各信号是否是周期信号，如果是周期信号，求出它的基波周期。 (a) = x(t ) 2 cos(3t + π / 4) (c) x(t ) = e (e) = x ( n)
1
信号与线性系统分析试卷
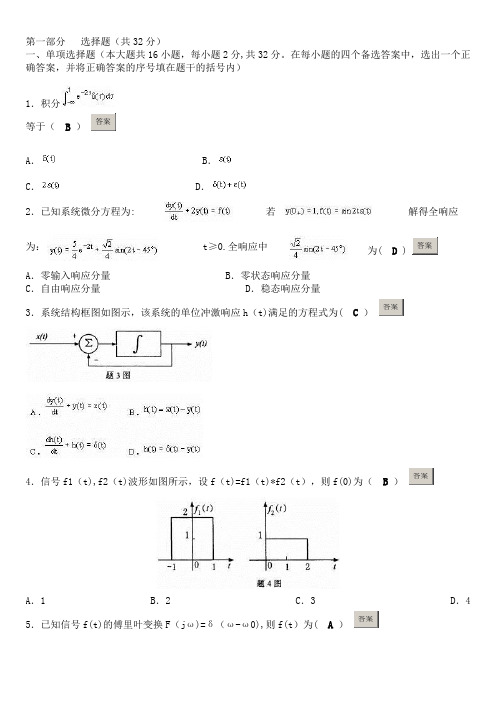
第一部分选择题（共32分）一、单项选择题（本大题共16小题，每小题2分,共32分。
在每小题的四个备选答案中，选出一个正确答案，并将正确答案的序号填在题干的括号内）1．积分等于（B）答案A． B．C． D．2．已知系统微分方程为: 若解得全响应为：t≥0.全响应中为( D ) 答案A．零输入响应分量 B．零状态响应分量C．自由响应分量 D．稳态响应分量3．系统结构框图如图示，该系统的单位冲激响应h（t)满足的方程式为( C）答案4．信号f1（t),f2（t)波形如图所示，设f（t)=f1（t)*f2（t），则f(0)为（B）答案A．1 B．2 C．3 D．4 5．已知信号f(t)的傅里叶变换F（jω)=δ（ω-ω0),则f(t）为( A）答案6．已知信号f（t）如图所示，则其傅里叶变换为（C）答案7．f（t）=ε(t）-ε(t—1)的拉氏变换为（A）答案8. 的拉氏反变换为（D）答案9．图（a）中ab段电路是某复杂电路的一部分，其中电感L和电容C都含有初始状态，请在图(b）中选出该电路的复频域模型。
（B ) 答案10．离散信号f(n)是指（B）答案A．n的取值是连续的，而f（n)的取值是任意的信号B．n的取值是离散的，而f(n)的取值是任意的信号C．n的取值是连续的，而f(n)的取值是连续的信号D．n的取值是连续的,而f（n）的取值是离散的信号11．若序列f（n）的图形如图(a)所示,那么f（—n+1）的图形为图(b)中的( D）答案12．差分方程的齐次解为，特解为，那么系统的稳态响应为( B ) 答案13．已知离散系统的单位序列响应和系统输入如图所示，f（n)作用于系统引起的零状态响应为,那么序列不为零的点数为（C）答案A．3个 B．4个C．5个 D．6个第二部分非选题（共68分）二、填空题(本大题共9小题，每小题2分，共18分）14．=（)。
答案15．GLC并联电路发生谐振时，电容上电流的幅值是电流源幅值的（Q）倍。
管致中《信号与线性系统》(第5版)(章节题库 连续时间系统的频域分析)
）。（填“因果”或“非因果”）
【答案】时变、因果
【解析】根据时不变的定义，当输入为 x（t－t0）时，输出也应该为 y（t－t0）＝
(
t
t0
5
) cos(
x(
t
1
பைடு நூலகம்t0
)
)
但当输入
x（t－t0）时实际的输出为 (
t
5
) cos(
x(
t
1
t0
)
)
，
与要求的输出不相等，所以系统是时变的，因果性的定义是指系统在 t0 时刻的响应只与
【解析】无失真传输的定义：无失真是指响应信号与激励信号相比，只是大小与出现
的时间不同，而无波形上的变化。
3．若某系统对激励 e（t）＝E1sin（ω1t）＋E2sin（2ω1t）的响应为 r（t）
＝KE1sin（ω1t－φ1）＋KE2sin（2ω1t－2φ1），响应信号是否发生了失真?（
）（失真
或不失真）
A．W B．2W C．ω0
1 / 97
圣才电子书
D．ω0－W
十万种考研考证电子书、题库视频学习平 台
【答案】B
【解析】f（t）乘上 cos（ωt0＋θ）实际上就是对信号进行调制，将原信号的频谱搬
移到－ 0 和 0 的位置，由于 ω0＞＞W，所以频谱无重叠，则频谱宽度为原来的 2 倍
答：因为
Sa
0t
0
G20
，所以
故 故得
4．图 4-3（a）所示系统，已知输入信号 f（t）的 F（jω）＝G4（ω），子系统函数 。求系统的零状态响应 y（t）。
图 4-3 答：F（jω）的图形如图 4-3（b）所示。
管致中《信号与线性系统》(第5版)(章节题库 绪 论)
2 / 23
圣才电子书
三、分析计算题
十万种考研考证电子书、题库视频学习平 台
1．已知两信号分别为 f1（t）＝2cos（πt）＋4sin（3t），f2（t）
2．系统 y（t）＝2（t＋1）x（t）＋cos（t＋1）是_____。（说明因果／非因果性、时 变／非时变性、线性／非线性）。
【答案】因果、时变、非线性。 【解析】y（t）＝2（t＋1）x（t）＋cos（t＋1），输出仅与现在的输入有关，系统是 因果的；响应随激励加入的时间不同而发生变换，系统是时变的；不满足齐次性和叠加性， 系统是非线性的。
图 1-4 答：（1）移位：f（－2t＋1）＝ f[－2（t－1/2）]，f（－2t＋1）波形向左平移 1/2 可得 f（－2t）； （2）扩展：将 f（－2t）做尺度变换，横坐标放大 2 倍，求得 f（－t）； （3）反转：将 f（－t）反转，求得 f（t）波形，如图 1-5 所示。
4 / 23
圣才电子书
圣才电子书
十万种考研考证电子书、题库视频学习平 台
图 1-2 答：翻转:先将 f（t）的图形翻转，成为 f（－t）； 移位：再将图形向右平移 2，成为 f（－t＋2）；
扩展：然后波形扩展为原来的 3 倍，成为
，如图 1-3 所示。
图 1-3 4．已知 f（－2t＋1）波形如图 1-4 所示，试画出 f（t）的波形。
圣才电子书
十万种考研考证电子书、题库视频学习平 台
第 1 章 绪 论
一、填空题 1．系统的输入为 x（r），输出为 y（r）＝tx（t），判断系统是否是线性的（ ）。 【答案】线性的
《信号与线性系统》试题与答案
综合测试(三)一、选择题（本题共6小题，每小题3分，共18分）1、若想使连续时间信号在通过线性非时变系统传输时，波形不会产生失真，而仅仅是延时一段时间输出，则要求系统的单位冲激响应必须满足（）A. B.C. D.2、序列和等于（）A. 1B.C. D.3、连续时间信号的单边拉普拉斯变换为（）A. B.C. D.4、下列各式中正确的是（）A． B.C.D．5、单边Z变换对应的原时间序列为（）A．B．C．D．6．请指出是下面哪一种运算的结果？（）A．左移6 B. 右移6C．左移2 D. 右移2三、描述某系统的微分方程为y”(t) + 4y’(t) + 3y(t) = f(t)求当f(t) = 2e-2t，t≥0；y(0)=2，y’(0)= -1时的解；（15分）解: (1) 特征方程为λ2 + 4λ+ 3 = 0 其特征根λ1= –1，λ2= –2。
齐次解为y h(t) = C1e -t + C2e -3t当f(t) = 2e–2 t时，其特解可设为y p(t) = Pe -2t将其代入微分方程得P*4*e -2t + 4(–2 Pe-2t) + 3Pe-t = 2e-2t解得P=2于是特解为y p(t) =2e-t全解为：y(t) = y h(t) + y p(t) = C1e-t + C2e-3t + 2e-2t其中待定常数C1,C2由初始条件确定。
y(0) = C1+C2+ 2 = 2，y’(0) = –2C1–3C2–1= –1解得C1 = 1.5 ，C2 = –1.5最后得全解y(t) = 1.5e–t –1.5e –3t +2 e –2 t, t≥0三、描述某系统的微分方程为 y ”(t) + 5y ’(t) + 6y(t) = f(t) 求当f(t) = 2e -t ，t ≥0；y(0)=2，y ’(0)= -1时的解；（ 15分）解: (1) 特征方程为λ2 + 5λ+ 6 = 0 其特征根λ1= –2，λ2= –3。
信号与线性系统分析试题及答案
2． （7 分）
F ( z) 5z z 3z 2
2
;
F ( z) 5 5 5 ; z ( z 1)( z 2) z 1 z 2
z 2, 为右边序列 f (k ) 5(2 n 1) (k )
四．
1.
（5 分） f (k ) 3,2,11,4,21,22,1,4
0
sin( 2t ) 1 sin( 2t ) 4 2t 4 2t 1 F ( j ) 2 g 4 ( ) 0.5 g 4 ( ) 4 f (t )
x(t ) f (t ) s (t ) X ( j )
五． 解： （16 分） （1）对原方程两边同时 Z 变换有：
9 ． 已 知 离 散 系 统 函 数 H ( z) 性： 。
z2 ，试判断系统的稳定 z 0.7 z 0.1
2
第 1 页 共 5 页
czu 监制（盗版）
2
三． （14 分）
2s 2 6s 6 ① 已知 F ( s) 2 , Re[ s] 2 ,试求其拉氏逆变换 f(t)； s 3s 2
f (t ) sin(2t ) , 2t s(t ) cos(1000t )
试求其输出信号 y(t)，并画出 y(t)的频谱图。
第 3 页 共 5 页
czu 监制（盗版）
4
参考答案 一填空题（30 分，每小题 3 分） 2. 4. 5. 1 ； 1 ，0
j ' ( ) 1
2. ;
1
2007 年度第 I 学期
期末考试试卷
10 ． 如 图 所 示 是 离 散 系 统 的 Z 域 框 图 ， 该 系 统 的 系 统 函 数 H(z)=
信号与线性系统分析试题及答案(10套)
标准答案(一)一、填空题（每空1分，共30分）1、无线电通信中，信号是以电磁波形式发射出去的。
它的调制方式有调幅、调频、调相。
2、针对不同的调制方式有三种解调方式，分别是检波、鉴频、和鉴相。
3、在单调谐放大器中，矩形系数越接近于1、其选择性越好；在单调谐的多级放大器中，级数越多，通频带越窄、（宽或窄），其矩形系数越（大或小）小。
4、调幅波的表达式为：uAM（t）= 20（1 +0.2COS100πt）COS107πt（V）；调幅波的振幅最大值为24V，调幅度Ma为20℅，带宽fBW为100Hz，载波fc为5*106Hz。
5、在无线电技术中，一个信号的表示方法有三种，分别是数学表达式、波形、频谱。
6、调频电路有直接调频、间接调频两种方式。
7、检波有同步、和非同步检波两种形式。
8、反馈式正弦波振荡器按照选频网络的不同，可分为LC、RC、石英晶振等三种。
9、变频器可由混频器、和带通滤波器两部分组成。
10、列出三个常见的频谱搬移电路调幅、检波、变频。
11、用模拟乘法器非线性器件实现调幅最为理想。
二、选择题（每小题2分、共20分）将一个正确选项前的字母填在括号内1、下列哪种信号携带有调制信号的信息（C ）A、载波信号B、本振信号C、已调波信号2、小信号谐振放大器的主要技术指标不包含（B ）A、谐振电压增益B、失真系数C、通频带D、选择性3、丙类谐振功放其谐振回路调谐于（ A ）分量A、基波B、二次谐波C、其它高次谐波D、直流分量4、并联型石英晶振中，石英谐振器相当于（C ）元件A、电容B、电阻C、电感D、短路线5、反馈式正弦波振荡器的起振条件为（ B ）A、|AF|=1，φA+φF= 2nπB、|AF| >1，φA+φF = 2nπC、|AF|>1，φA+φF ≠2nπD、|AF| =1，φA+φF ≠2nπ6、要实现集电极调制特性应使功放工作在（B ）状态A、欠压状态B、过压状态C、临界状态D、任意状态7、自动增益控制可简称为（ B ）A、MGCB、AGCC、AFCD、PLL8、利用非线性器件相乘作用来实现频率变换其有用项为（ B ）A、一次方项B、二次方项C、高次方项D、全部项9、如右图所示的电路是（D ）A、普通调幅电路B、双边带调幅电路C、混频器D、同步检波器10、在大信号包络检波器中，由于检波电容放电时间过长而引起的失真是（B）A、频率失真B、惰性失真C、负峰切割失真D、截止失真三、判断题，对的打“√”,错的打“×”（每空1分，共10分）1、谐振放大器是采用谐振回路作负载的放大器。
信号与系统试卷及参考答案.
试卷及答案信号与系统试卷（1）（满分：100分，所有答案一律写在答题纸上）考试班级学号姓名成绩考试日期：年月日，阅卷教师：考试时间120分钟，试卷题共2页一一线性非时变离散系统，具有一初始状态x(0)，当激励为时f(k)，响应为y(k)=((1/2)k+1)u(k)；若初始状态不变，当激励为-f(k)时，响应y(k)=((-1/2)k-1)u(k)为；试求当初始状态2x(0)为，激励为4f(k)时，系统的响应？（10分）二绘出下列函数的图形（1）.已知一连续时间信号x(t)如图所示，试概略画出信号y(t)=x(2-t/3)的波形图。
（8分）t(2). 试概略画出信号y(t)=u(t 2-4) 的波形图。
（8分）三 计算下列函数(1). y(t)=⎰-44(t 2+3t+2)(δ(t)+2δ(t-2))dt （4分） (2). f(t)=e -2t u(t), h(t)= e -2t u(t), y(t)=f(t)*h (t) （8分）(3). f(k)=1, k=0,1,2,3, h(k)=1, k=0,1,2,3, y(k)=f(k)*h (k) （8分） （4） 已知f(t)=e -2t u(t), 求y(t)=[t f(2t)] 的富立叶变换 （8分） （5）y’(t)+2y(t)=δ(t)+u(t), y(0)=0, 试求y(t)=? （8分） （6）. y(k)-y(k-1)-2y(k-2)=u(k)+2u(k-2), y(-1)= 2,y(-2)= -1/2, 试求零输入响应y x (k)=? 零状态响应y f (k)=? （8分）四 一线性非时变因果系统，当激励为u(t)时，响应为)]2()([cos )(cos )(ππ---+=-t u t u t t tu e t g t ，求当激励f(t)=δ(t)时的响应)(t h 。
（10分）五 某一子系统，当输入f(t)=e -t u(t)时，零状态响应y f (t) = (1/2 e -t - e -2t +1/2e -3t )u(t), 试求将两个这样的子系统串联时，总系统的冲激响应。
信号与线性系统期末考试试题与答案
信号与系统期末考试试题6课程名称： 信号与系统一、选择题（共10题，每题3分 ，共30分，每题给出四个答案，其中只有一个正确的）1、 卷积f 1(k+5)*f 2(k-3) 等于 。
（A ）f 1(k)*f 2(k) （B ）f 1(k)*f 2(k-8)（C ）f 1(k)*f 2(k+8)（D ）f 1(k+3)*f 2(k-3)2、 积分dt t t ⎰∞∞--+)21()2(δ等于 。
（A ）1.25（B ）2.5（C ）3（D ）5 3、 序列f(k)=-u(-k)的z 变换等于 。
（A ）1-z z （B ）-1-z z（C ）11-z （D ）11--z4、 若y(t)=f(t)*h(t),则f(2t)*h(2t)等于 。
（A ）)2(41t y （B ）)2(21t y （C ）)4(41t y （D ）)4(21t y 5、 已知一个线性时不变系统的阶跃相应g(t)=2e -2t u(t)+)(t δ,当输入f(t)=3e —t u(t)时，系统的零状态响应y f (t)等于（A ）(-9e -t +12e -2t )u(t) （B ）(3-9e -t +12e -2t )u(t)（C ）)(t δ+(-6e -t +8e -2t )u(t) （D ）3)(t δ +(-9e -t +12e -2t )u(t)6、 连续周期信号的频谱具有（A ） 连续性、周期性 （B ）连续性、收敛性 （C ）离散性、周期性 （D ）离散性、收敛性7、 周期序列2)455.1(0+k COS π的 周期N 等于（A ） 1（B ）2（C ）3（D ）4 8、序列和()∑∞-∞=-k k 1δ等于（A ）1 (B) ∞ (C) ()1-k u (D) ()1-k ku9、单边拉普拉斯变换()se s s s F 2212-+=的愿函数等于 ()()t tu A ()()2-t tu B ()()()t u t C 2- ()()()22--t u t D 10、信号()()23-=-t u tet f t的单边拉氏变换()s F 等于()A ()()()232372+++-s e s s ()()223+-s e B s()()()2323++-s se C s ()()332++-s s e D s二、填空题（共9小题，每空3分，共30分）1、卷积和[（0.5）k+1u(k+1)]*)1(k -δ=________________________2、单边z 变换F(z)=12-z z的原序列f(k)=______________________ 3、已知函数f(t)的单边拉普拉斯变换F(s)=1+s s，则函数y(t)=3e -2t ·f(3t)的单边拉普拉斯变换Y(s)=_________________________4、频谱函数F(j ω)=2u(1-ω)的傅里叶逆变换f(t)=__________________5、单边拉普拉斯变换ss s s s F +++=2213)(的原函数f(t)=__________________________ 6、已知某离散系统的差分方程为)1(2)()2()1()(2-+=----k f k f k y k y k y ，则系统的单位序列响应h(k)=_______________________7、已知信号f(t)的单边拉氏变换是F(s),则信号⎰-=2)()(t dx x f t y 的单边拉氏变换Y(s)=______________________________8、描述某连续系统方程为()()()()()t f t f t y t y t y +=++''''52该系统的冲激响应h(t)=9、写出拉氏变换的结果()=t u 66 ，=kt 22三、（8分）已知信号()()()⎪⎩⎪⎨⎧><==↔./1,0,/1,1s rad s rad jw F j F t f ωωω设有函数()(),dt t df t s =求⎪⎭⎫⎝⎛2ωs 的傅里叶逆变换。
信号与线性系统分析的习题答案
1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
（2）∞<<-∞=-t et f t,)( （3）)()sin()(t t t f επ=（4）)(sin )(t t f ε= （5）)(sin )(t r t f = （7）)(2)(k t f kε= （10）)(])1(1[)(k k f kε-+=解：各信号波形为 （2）∞<<-∞=-t et f t,)(（3）)()sin()(t t t f επ=（4）)(sin )(t t f ε=（5）)f=rt)(sin(t （7）)t(k=f kε)(2（10）)f kεk=(k+-((])11[)1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
（1）)2()1(3)1(2)(-+--+=t t t t f εεε （2）)2()1(2)()(-+--=t r t r t r t f（5）)2()2()(t t r t f -=ε （8）)]5()([)(--=k k k k f εε（11）)]7()()[6sin()(--=k k k k f εεπ（12）)]()3([2)(k k k f k ---=εε解：各信号波形为（1）)2()1(3)1(2)(-+--+=t t t t f εεε（2）)2()1(2)()(-+--=t r t r t r t f（5）)2()2()(t t r t f -=ε（8）)]5()([)(--=k k k k f εε（11）)]7()()[6sin()(--=k k k k f εεπ（12）)]()3([2)(k k k f k---=εε1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
如果是，确定其周期。
（2）)63cos()443cos()(2ππππ+++=k k k f （5）)sin(2cos 3)(5t t t f π+=解：1-6 已知信号)(t f 的波形如图1-5所示，画出下列各函数的波形。
管致中《信号与线性系统》(第5版)(章节题库 连续时间系统的复频域分析)
1．已知因果信号的拉普拉斯变换为 X（s）＝ x（t）为（ ）。
[1－e－（s＋α）T]，其逆变换式
【答案】e－αtu（t）－e－αtu（t－T）
【解析】可知
X(
s
)
s
1
a
s
1
a
e( sa
)T
，已知拉氏变换
s
1
a
e at u(
t
)，
根据拉氏变换的时移性质
1 e( sa )T sa
eatu( t T
u（t）的拉普拉斯变换为
e 2s s
。
7．信号
的单边拉普拉斯变换为（ ）。
【答案】A
【解析】积分可得
f
(t)
t2
t
，tn
n! s n 1
，结果为
A
项
8．象函数 A．tU（t） B．tU（t－2） C．（t－2）U（t） D．（t－2）U（t－2） 【答案】B
的原函数 f（t）为（ ）。
【解析】
，常用拉氏变换对
由常用函数的拉氏变换，
5．信号 f（t）＝（t＋1）u（t＋1）的单边拉普拉斯变换为（ ）。
【答案】B 【解析】f（t）是 tu（t）向左移 1 个单位时间后的结果，由于单边拉氏变换只研究
t 0 的时间函数，故不能利用性质求 F（s）。因此可认为 f（t）与（t＋1）u（t）的单边
2 / 140
圣才电子书
则该信号的时间函数为（ ）。
1 / 140
圣才电子书
C．e－αtu（t－α）
十万种考研考证电子书、题库视频学习平 台
D．e－αu（t－T）
【答案】B
【解析】可采用从时域到频域一一排除的方法，u（t）的拉氏变换为 1/s,根据时移性，
《信号与线性系统》试题与答案
C． D。
97．离散时间单位延迟器D的单位序列响应为（）
A． B。 C。 D。1
98． 周期信号的傅立叶变换为（）
A． B。2 C。 D。0.5
99． 可写成以下正确的表达式是（）
A． B。
C． D。
100． （）
A． B。 C。 D。
二、填空题
1． ________________。
2．从信号频谱的连续性和离散性来考虑，周期信号的频谱是_______________。
A．S／2 B。S／3 C。S／4 D。S
34． …是（）
A．周期信号B。非周期信号C。不能表示信号D。以上都不对
35．线性系统具有（）
A．分解特性B。零状态线性C。零输入线性D。ABC
36．设系统零状态响应与激励的关系是： ，则以下表述不对的是（）
A．系统是线性的B。系统是时不变的C。系统是因果的D。系统是稳定的
A、f(－t+1)B、f(t+1)
C、f(－2t+1)D、f(－t/2+1)
18、若系统的冲激响应为h(t),输入信号为f(t),系统的零状态响应是（）
19。信号 与冲激函数 之积为（）
A、2B、2 C、3 D、5
A、因果不稳定系统B、非因果稳定系统
C、因果稳定系统D、非因果不稳定系统
21、线性时不变系统的冲激响应曲线如图所示，该系统微分方程的特征根是（）
A、常数B、实数C、复数D、实数+复数
22、线性时不变系统零状态响应曲线如图所示，则系统的输入应当是（）
A、阶跃信号B、正弦信号C、冲激信号D、斜升信号
23.积分 的结果为()
A B C. D.
24.卷积 的结果为()
信号与线性系统五六章自测题(标准答案)
第五、六章自测题标准答案1. 判断题(1) 当且仅当一个连续时间线性时不变系统的阶跃响应是绝对可积的，则该系统是稳定的。
（ × ） (2) 若h (t )是一个线性时不变系统的单位冲激响应，并且h(t)是周期的且非零，则系统是非稳定的。
（ √ ） (3) 对于一个因果稳定的系统，可以利用ωωj s s H j H ==|)()( 求系统的频率响应。
（ √ ） (4) 一个稳定的连续时间系统，其系统函数的零极点都必定在s 平面的左半平面。
（ × ） 2．填空题（1）某二阶系统起始状态为2_)0(',1_)0(=-=r r ；初始条件为,1)0(',3)0(==++r r 则确定零输入响应待定系数的初始条件为)0(+zi r = -1 ，)0('+zi r = 2 ；而确定零状态响应待定系数的初始条件为 )0(+zs r = 4 ，)0('+zs r = -1 。
（2）23)(2++=-s s e s F s 的逆变换为 )(][ )1(2)1(t e e t t ε-----。
（3）)()sin()(t t t f εφα+=的拉普拉斯变换为2222sin cos )(αφααφ+⋅++⋅=s ss s F 。
3．求图5-1中所示单边周期信号的拉氏变换。
t图5-1解： +---+--=)23()()2()()(Tt T t T t t t f εεεε s e A T t t A s T)1()2()(2--↔⎥⎦⎤⎢⎣⎡--εε)1()1()1()(22s T sT s T es A e s e A s F ---+=--=4．一个单位冲激响应为h (t )的因果LTI 系统有下列性质： （1）当系统的输入为t e t x 2)(=时，对所有t 值，输出te t y 261)(=。
（2）单位冲激响应h(t)满足微分方程)()()(2)(4t b t e t h dtt dh t εε+=+-。
信号与线性系统课后习题答案5
（15） te−(t ε −3) (t −1)
解：（2）
Q
LT [ε
(t)]
=
1 s
，∴
LT [ε
(t
−
2)]
=
1 s
e−2s
∴ LT{e−t[ε (t) − ε (t − 2)]} = 1 (1− e−2(s+1) ) s +1
（7）
（16） te−αt cos(βt)ε (t)
Q sin(2t − π / 4)ε (t) = 1 [sin(2t) − cos(2t)]ε (t) 2
（1） 1− e−Ts s +1
（3） e−2(s+3) s+3
（5）
π (1 s2
+ +
e−s π2
)
解：（1）
Q
LT[e−tε (t)]
=
1 s +1
，
∴ f (t) = LT −1[1 − e−Ts ] = e−tε (t) − e−(t−T )ε (t − T )] ，画出波形图如下图（1） s +1
（1） y′′(t) + 4 y′(t) + 3y(t) = f ′(t) − 3 f (t) 解：（1）
对原微分方程等式两边同时求初始状态为零的单边拉普拉斯变换，令 Yf (s) = LT[ y f (t)] ， F (s) = LT[ f (t)]，
6
H (s) = Yf (s) = s − 3 ， F(s) s2 + 4s + 3
=
s2
s+4 × + 3s + 2
s
1 +2
=
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
综合测试(三)一、选择题（本题共6小题，每小题3分，共18分）1、若想使连续时间信号在通过线性非时变系统传输时，波形不会产生失真，而仅仅是延时一段时间输出，则要求系统的单位冲激响应必须满足（）A. B.C. D.2、序列和等于（）A. 1B.C. D.3、连续时间信号的单边拉普拉斯变换为（）A. B.C. D.4、下列各式中正确的是（）A． B.C.D．5、单边Z变换对应的原时间序列为（）A．B．C．D．6．请指出是下面哪一种运算的结果？（）A ． 左移6 B. 右移6 C ． 左移2 D. 右移2三、描述某系统的微分方程为 y ”(t) + 4y ’(t) + 3y(t) = f(t) 求当f(t) = 2e -2t ，t ≥0；y(0)=2，y ’(0)= -1时的解；（ 15分）解: (1) 特征方程为λ2 + 4λ+ 3 = 0 其特征根λ1= –1，λ2= –2。
齐次解为y h (t) = C 1e -t + C 2e-3t当f(t) = 2e –2 t时，其特解可设为y p (t) = Pe -2t将其代入微分方程得P*4*e -2t + 4(–2 Pe -2t ) + 3Pe -t = 2e -2t解得 P=2于是特解为 y p (t) =2e -t全解为： y(t) = y h (t) + y p (t) = C 1e -t + C 2e -3t + 2e -2t其中 待定常数C 1,C 2由初始条件确定。
y(0) = C 1+C 2+ 2 = 2，y ’(0) = –2C 1 –3C 2 –1= –1解得 C 1 = 1.5 ，C 2 = –1.5最后得全解 y(t) = 1.5e – t – 1.5e – 3t +2 e –2 t, t ≥0三、描述某系统的微分方程为 y ”(t) + 5y ’(t) + 6y(t) = f(t) 求当f(t) = 2e -t ，t ≥0；y(0)=2，y ’(0)= -1时的解；（ 15分）解: (1) 特征方程为λ2 + 5λ+ 6 = 0 其特征根λ1= –2，λ2= –3。
齐次解为y h (t) = C 1e -2t + C 2e-3t当f(t) = 2e – t时，其特解可设为y p (t) = Pe -t将其代入微分方程得 Pe -t + 5(– Pe -t ) + 6Pe -t = 2e -t解得 P=1于是特解为 y p (t) = e -t全解为： y(t) = y h (t) + y p (t) = C 1e -2t + C 2e -3t + e -t其中 待定常数C 1,C 2由初始条件确定。
y(0) = C 1+C 2+ 1 = 2，y ’(0) = –2C 1 –3C 2 –1= –1解得 C 1 = 3 ，C 2 = – 2最后得全解 y(t) = 3e – 2t – 2e – 3t + e – t, t ≥0 四、如图信号f(t)的拉氏变换F(s) = ，试观)e e 1(e 2ss s s s-----)e e 1(e2s s ss s -----察y(t)与f(t)的关系，并求y(t) 的拉氏变换Y(s) （10分）解y(t)= 4f(0.5t) Y(s) = 4×2 F(2s)（12分）312()13k k k F s m n s s s =++<++解：部分分解法 （）100()10(2)(5)100(1)(3)3s s k sF s s s s s ===++==++其中211(1)()10(2)(5)20(3)s s k s F s s s s s =-=-=+++==-+解：333(3)()10(2)(5)10(1)3s s k s F s s s s s =-=-=+++==-+1002010()313(3)F s s s s ∴=--++解：)(e 310e 203100)(3t t f t t ε⎪⎭⎫⎝⎛--=∴--())e 2e 1(2e 82222ss s s s -----=)e 2e 1(e 22222s s ss s -----=A 卷 【第2页 共3页】 32597(),(1)(2)s s s F s s s +++=++已知求其逆变换六、有一幅度为1，脉冲宽度为2ms 的周期矩形脉冲，其周期为8ms ，如图所示,求频谱并画出频谱图频谱图。
（10分）解：付里叶变换为Fn 为实数，可直接画成一个频谱图。
ΩΩ=Ω-=-Ω-n n Tjn T tjn )2sin(2e 122τττF nωτπ2τπ2-τπ441f(t)tT-T…12τ-2τ12()212k k F s s s s =+++++解：分式分解法 11223(1)2(1)(2)311s s s k s s s s k s =-=-+=+⋅=+++==-+其中 21()212F s s s s ∴=++-++)()e e 2()(2)(')(2t t t t f t t εδδ---++=∴六、有一幅度为1，脉冲宽度为2ms 的方波，其周期为4ms ，如图所示,求频谱并画出频谱图。
（10分）解：Ω=2π*1000/4=500π付里叶变换为Fn 为实数，可直接画成一个频谱图。
或幅频图如上，相频图如下：t n n n ππ500)12sin()12(41--=∑∞=如图反馈因果系统，问当K 满足什么条件时，系统是稳定的？其中子系统的系统函数G(s)=1/[(s+1)(s+2)]解：设加法器的输出信号X(s) X(s)=KY(s)+F(s)Y(s)= G(s)X(s)=K G(s)Y(s)+ G(s)F(s)H(s)=Y(s)/F(s)=G(s)/[1-KG(s)]=1/(s2+3s+2-k) H(s)的极点为为使极点在左半平面，必须(3/2)2-2+k<(3/2)2, k<2，即当k<2，系统稳定。
如图反馈因果系统，问当K 满足什么条件时，系统是稳定的？解：如图所示，∑G(s)K F(s)Y(s)k p +-⎪⎭⎫⎝⎛±-=2232322,1在加法器处可写出系统方程为：y ”(t) + 4y ’(t) + （3-K ）y(t) = f(t)H （S ）=1/（S 2+4S+3-K ） 其极点为使极点在左半平面，必须4+4k<22, 即k<0，当k<0时，系统稳定。
如图反馈因果系统，问当K 满足什么条件时，系统是稳定的？解：如图所示，在前加法器处可写出方程为：X ”(t) + 4X ’(t) + 3X(t) -Ky(t) = f(t) 在后加法器处可写出方程为： 4X ’(t) + X(t) =y(t) 系统方程为：y ”(t) + 4y ’(t) + （3-K ）y(t) =4f ’(t)+ f(t)H （S ）=（4S+1）/（S 2+4S+3-K ） 其极点为使极点在左半平面，必须4+4k<22, 即k<0，当k<0时，系统稳定。
)3(44222,1k p --±-=k p 4422,1+±-=)3(44222,1k p --±-=k p 4422,1+±-=二、填空题（本题共6小题，每小题3分，共18分）1、计算积分2、若两个连续时间信号和的卷积积分为：则信号3、计算卷积和4、若函数的单边拉氏变换为，则函数的初值为5、若的单边拉氏变换为，则函数的单边拉氏变换为6、若信号的傅里叶变换式为，则其对应的时间信号三、按要求完成下列各题（本题共8小题，每小题5分，共40分）1、已知系统的系统函数为，如果系统的零状态响应为，请求出系统的激励信号2、已知信号的波形如下图所示，求其频谱函数3、如果一个离散系统的差分方程为：请求出该系统的单位函数响应。
4、求序列的Z变换，并求收敛区。
5、已知函数和的波形如下面图(a)和图（b）所示，求并画出的波形。
6、一个线性非时变离散时间系统的单位函数响应为如图(a)所示，当激励如图(b)所示时，求系统的零状态响应，并画出图形。
7、已知某连续时间系统函数为：，请画出该系统的零极图，并判断系统是否稳定，说明原因。
8、已知线性非时变系统的微分方程为：，若已知系统的初始状态为：，，请求出该系统的零输入响应。
四、计算题（本大题共6小题，共74分）1、（本题共10分）已知连续时间信号的频谱函数为，⑴．请求出信号的频谱函数，并画出其相应频谱图；⑵．如果分别对信号和信号进行均匀抽样，为了保证能够从所得的离散时间信号中恢复原连续信号，则需要的最大抽样间隔分别为多少秒？2、（本题16分）已知电路如图所示，激励信号为，,。
求系统的零输入响应和零状态响应，并判断自然响应和受迫响应。
3、（本题8分）某线性系统的模拟框图如下图所示，请列出系统的状态方程和输出方程4、（本题12分）一离散时间系统的差分方程为：，其中系统的激励为，响应为，已知系统初始值为，，若系统的激励信号为，请求出系统的全响应。
5、（本题12分）下面图示是由系统由几个子系统组合而成，已知各子系统的单位冲激响应分别为，，，输入信号为，试求：（1）总系统的单位冲激响应；（2）求出系统的零状态响应。
综合测试(三)答案一、解1.C2.D3.C4.D5.C6.D二、解1、2、3、4、函数的初值为 15、6、三、解1、解2、解3、解4、解5、解6、7、解极点：均在S平面的左半平面，所以系统稳定。
8、解四、解1、解(1) 信号的频谱函数为(2) 对信号进行均匀抽样，要求抽样频率，最大抽样间隔对信号进行均匀抽样，要求抽样频率最大抽样间隔2、解3、解4、解5、解。