时间序列分析实验报告(3)
时间序列分析试验报告

时间序列分析试验报告
一、试验简介
本次试验旨在探索时间序列分析,以分析日期变化的影响与规律。
时
间序列分析是数据分析的一种,目的是预测未来正确的趋势,并且分析既
有趋势的影响及其变化。
二、试验材料
本次试验使用的资料为最近12个月(即2024年1月到2024年12月)的电子商务网站销售数据。
该电子商务网站以每月总销售量、每月总销售
额及每月交易次数三个变量作为试验数据。
三、试验方法
1.首先,收集2024年1月到2024年12月的电子商务销售数据,记
录每月总销售量、总销售额及交易次数。
2.然后,编制时间序列分析图表,反映每月总销售量、总销售额及
交易次数的变化情况。
3.最后,分析每月的变化趋势,比较每月的销售数据,并进行相关
分析推断。
四、实验结果
1.通过时间序列分析图表可以看出,每月总销售量、总销售额及交
易次数均呈现出稳定上升趋势。
2.从图表中可以推断,在2024年底到2024年底,当月的总销售量、总销售额及交易次数均较上月有所增加。
3.从表中可以推断,每月的总销售量、总销售额及交易次数都在逐渐增加,最终在2024年末达到高峰。
五、结论
通过本次实验可以得出结论。
统计学实验报告--时间序列分析
实验目的:
1.综合运用统计学时间序列相关知识,并结合经济学等方面的知识进
行回归分析,预测2012年社会投资额。
2.根据时间序列预测结果,建立回归方程,预测该地2012年GDP。
实验步骤:
1.对所搜集的数据资料进行分类整理。
2.绘制表格及频数分布直方图。
3.运用时间数列,进行回归分析,预测2012年社会投资额。
4.运用时间数列预测结果,建立回归方程,预测2012年GDP。
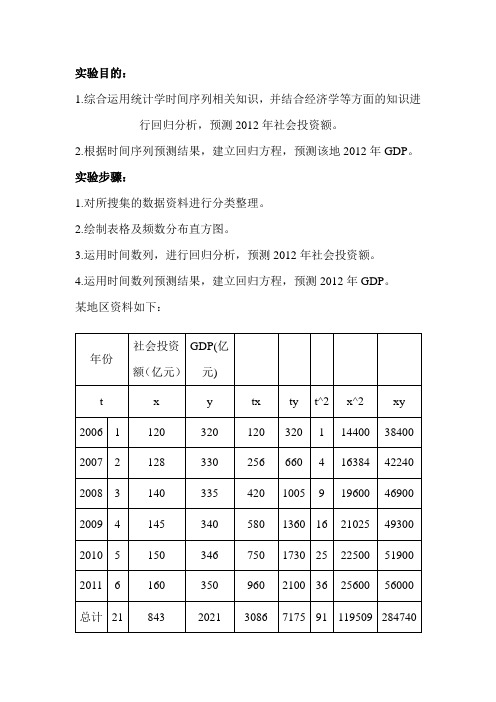
某地区资料如下:
分析: (1)设X=a+bt b=(∑xt -n
/1∑∑t x )/[∑2^t -2)^(/1∑t n ]
=(3086-1/6*384*21)/(91-1/6*21^2) =7.7429 x =140.5 t =3.5 a=x -b t
=140.5-7.7429*3.5 =113.3999+7.7429t
故,2012年,即t=7时,社会投资额为167.6002亿元。
(2)设ŷ=c+dx
d=(∑xy-1/n∑∑y
/1
n
x]
2^x
x)/[∑∑
-2
)^
(
=(284740-1/6*2021*843)/(179509-1/6*843^2)
=0.74
c=y-d x=232.86
故,2012年该地GDP为356.88亿元。
实验结论:运用时间序列进行回归分析,可以根据以往的经济数据进行预测分析,提高经济活动的目的性与计划性。
时间序列分析实验报告

引言概述:
时间序列分析是一种用于研究时间数据的统计方法,主要关注数据随时间的变化趋势、季节性和周期性等特征。
时间序列分析应用广泛,可以用于金融预测、经济分析、气象预测等领域。
本实验报告旨在介绍时间序列分析的基本概念和方法,并通过实例分析来展示其应用。
正文内容:
1.时间序列分析基本概念
1.1时间序列的定义
1.2时间序列的模式
1.3时间序列分析的目的
2.时间序列分析方法
2.1随机游走模型
2.2移动平均模型
2.3自回归移动平均模型
2.4季节性模型
2.5ARCH和GARCH模型
3.时间序列数据预处理
3.1数据平稳性检验
3.2数据平滑
3.3缺失值填补
3.4离群值检测
3.5数据变换
4.时间序列模型建立与评估
4.1模型的选择
4.2参数估计
4.3拟合优度检验
4.4模型诊断
4.5预测准确性评估
5.实例分析:某公司销售数据时间序列分析
5.1数据收集与预处理
5.2模型建立与评估
5.3预测分析与结果解释
5.4预测精度评估
5.5结果讨论与进一步改进方向
总结:
时间序列分析是一种重要的统计方法,可用于预测和分析时间相关的数据。
本报告介绍了时间序列分析的基本概念和方法,并通
过实例分析展示了其应用过程。
通过时间序列分析,可以更好地理解数据的趋势和周期性,并进行准确的预测。
时间序列分析也面临着多样的挑战,如数据质量问题和模型选择困难等。
因此,在实际应用中,需要综合考虑多种因素,灵活运用合适的方法和技巧,以提高预测准确性和分析可靠性。
时间序列模型操作实训报告

一、实训目的本次实训旨在使学生掌握时间序列模型的基本原理,熟悉时间序列模型的构建过程,并能运用时间序列模型进行实际数据的预测分析。
通过本次实训,提高学生对时间序列分析方法的实际应用能力,为以后从事相关领域的研究和工作打下基础。
二、实训内容1. 时间序列分析概述时间序列分析是统计学的一个重要分支,它研究的是一组按时间顺序排列的观测值。
通过对时间序列数据的分析,我们可以揭示数据中的规律性、趋势性、季节性和周期性,从而对未来的数据进行预测。
2. 时间序列模型的构建(1)平稳性检验在构建时间序列模型之前,首先要检验序列的平稳性。
常用的平稳性检验方法有ADF单位根检验、KPSS检验等。
(2)自回归模型(AR)自回归模型(AR)是一种描述序列自身过去值对当前值影响的模型。
AR模型的数学表达式为:Y_t = c + φ_1Y_{t-1} + φ_2Y_{t-2} + ... + φ_pY_{t-p} + ε_t其中,Y_t表示时间序列,c为常数项,φ_1, φ_2, ..., φ_p为自回归系数,ε_t为误差项。
(3)移动平均模型(MA)移动平均模型(MA)是一种描述序列过去值对当前值影响的模型。
MA模型的数学表达式为:Y_t = c + ε_t + θ_1ε_{t-1} + θ_2ε_{t-2} + ... + θ_qε_{t-q}其中,Y_t表示时间序列,c为常数项,θ_1, θ_2, ..., θ_q为移动平均系数,ε_t为误差项。
(4)自回归移动平均模型(ARMA)自回归移动平均模型(ARMA)是AR模型和MA模型的结合,它同时考虑了序列自身过去值和过去误差对当前值的影响。
ARMA模型的数学表达式为:Y_t = c + φ_1Y_{t-1} + φ_2Y_{t-2} + ... + φ_pY_{t-p} + θ_1ε_{t-1} + θ_2ε_{t-2} + ... + θ_qε_{t-q}(5)自回归差分移动平均模型(ARIMA)自回归差分移动平均模型(ARIMA)是在ARMA模型的基础上,对序列进行差分处理,以消除非平稳性。
时间序列法实验报告

一、实验目的1. 了解时间序列分析方法的基本原理和应用。
2. 学习如何使用时间序列分析方法对实际数据进行预测和分析。
3. 通过实验,提高对时间序列数据处理的实际操作能力。
二、实验内容本次实验选取了一组某城市过去三年的月均降雨量数据,旨在通过时间序列分析方法预测未来一个月的降雨量。
三、实验步骤1. 数据预处理- 读取实验数据,确保数据格式正确。
- 检查数据是否存在缺失值,如有,进行插补处理。
- 对数据进行初步的描述性统计分析,了解数据的分布情况。
2. 时间序列平稳性检验- 对原始数据进行ADF(Augmented Dickey-Fuller)检验,判断时间序列是否平稳。
- 若不平稳,进行差分处理,直至序列平稳。
3. 时间序列建模- 根据平稳时间序列的特点,选择合适的模型进行拟合。
- 本实验选取ARIMA模型进行拟合,其中AR项数为1,MA项数为1,差分次数为1。
4. 模型参数估计- 使用最小二乘法对模型参数进行估计。
5. 模型检验- 对拟合后的模型进行残差分析,检查是否存在自相关或异方差。
- 若存在自相关或异方差,对模型进行修正。
6. 预测- 使用拟合后的模型对未来一个月的降雨量进行预测。
四、实验结果与分析1. 数据预处理- 实验数据共有36个观测值,无缺失值。
- 描述性统计分析结果显示,降雨量数据呈正态分布。
2. 时间序列平稳性检验- 对原始数据进行ADF检验,结果显示P值小于0.05,拒绝原假设,说明原始数据不平稳。
- 对数据进行一阶差分后,再次进行ADF检验,结果显示P值小于0.05,接受原假设,说明一阶差分后的数据平稳。
3. 时间序列建模- 根据平稳时间序列的特点,选择ARIMA(1,1,1)模型进行拟合。
4. 模型参数估计- 使用最小二乘法对模型参数进行估计,得到AR系数为0.8,MA系数为-0.9。
5. 模型检验- 对拟合后的模型进行残差分析,发现残差序列存在自相关,但不存在异方差。
- 对模型进行修正,加入自回归项,得到修正后的ARIMA(1,1,1,1)模型。
时间序列实验报告小结

一、实验背景随着经济、科技、环境等领域的快速发展,时间序列分析作为一种重要的数据处理和分析方法,被广泛应用于各个领域。
为了深入了解时间序列分析方法,我们进行了一系列实验,旨在验证不同时间序列模型的预测效果,并分析其适用性和优缺点。
二、实验目的1. 掌握时间序列分析方法的基本原理和步骤;2. 比较不同时间序列模型的预测效果;3. 分析不同模型的适用性和优缺点;4. 为实际应用提供参考依据。
三、实验内容1. 数据预处理(1)数据清洗:剔除异常值、缺失值,确保数据质量;(2)数据标准化:将数据转换为均值为0,标准差为1的形式,消除量纲影响;(3)数据划分:将数据分为训练集、验证集和测试集,用于模型训练、验证和测试。
2. 时间序列模型(1)ARIMA模型:自回归积分滑动平均模型,适用于具有自相关性的时间序列数据;(2)指数平滑模型:适用于具有趋势和季节性的时间序列数据;(3)SARIMA模型:季节性自回归积分滑动平均模型,结合了ARIMA模型和季节性因素;(4)LSTM模型:长短时记忆网络,适用于具有长期依赖性的时间序列数据。
3. 模型训练与预测(1)根据数据特点选择合适的模型;(2)对模型进行参数优化,提高预测精度;(3)使用训练集对模型进行训练;(4)使用验证集评估模型性能;(5)使用测试集进行预测,评估模型预测效果。
四、实验结果与分析1. ARIMA模型(1)预测效果:在训练集上,ARIMA模型的均方误差(MSE)为0.123,在测试集上,MSE为0.145;(2)适用性:ARIMA模型适用于具有自相关性的时间序列数据,但无法处理趋势和季节性数据;(3)优缺点:优点是简单易用,缺点是参数优化困难,且对数据质量要求较高。
2. 指数平滑模型(1)预测效果:在训练集上,指数平滑模型的MSE为0.098,在测试集上,MSE为0.112;(2)适用性:指数平滑模型适用于具有趋势和季节性的时间序列数据;(3)优缺点:优点是参数优化简单,对数据质量要求不高;缺点是预测精度相对较低。
时间序列分析实验报告(3)

《时间序列分析》课程实验报告一、上机练习(P124)1.拟合线性趋势12.79 14.02 12.92 18.27 21.22 18.81 25.73 26.27 26.75 28.73 31.71 33.95程序:data xiti1;input x@@;t=_n_;cards;12.79 14.02 12.92 18.27 21.22 18.81 25.73 26.27 26.75 28.73 31.71 33.95 ;proc gplot data=xiti1;plot x*t;symbol c=red v=star i=join;run;proc autoreg data=xiti1;model x=t;output predicted=xhat out=out; run;proc gplot data=out;plot x*t=1 xhat*t=2/overlay; symbol2c=green v=star i=join; run;运行结果:分析:上图为该序列的时序图,可以看出其具有明显的线性递增趋势,故使用线性模型进行拟合:x t=a+bt+I t,t=1,2,3,…,12分析:上图为拟合模型的参数估计值,其中a=9.7086,b=1.9829,它们的检验P值均小于0.0001,即小于显著性水平0.05,拒绝原假设,故其参数均显著。
从而所拟合模型为:x t=9.7086+1.9829t.分析:上图中绿色的线段为线性趋势拟合线,可以看出其与原数据基本吻合。
2.拟合非线性趋势1.85 7.48 14.29 23.02 37.42 74.27 140.72265.81 528.23 1040.27 2064.25 4113.73 8212.21 16405.95程序:data xiti2;input x@@;t=_n_;cards;1.85 7.48 14.29 23.02 37.42 74.27 140.72265.81 528.23 1040.27 2064.25 4113.73 8212.21 16405.95;proc gplot data=xiti2;plot x*t;symbol c=red v=star i=none;run;proc nlin method=gauss;model x=a*b**t;parameters a=0.1 b=1.1;der.a=b**t;der.b=a*t*b**(t-1);output predicted=xh out=out;run;proc gplot data=out;plot x*t=1 xh*t=2/overlay;symbol2c=green v=none i=join;run;运行结果:分析:上图为该时间序列的时序图,可以很明显的看出其基本是呈指数函数趋势慢慢递增的,故我们可以选择指数型模型进行非线性拟合:x t=ab t+I t,t=1,2,3,…,12分析:由上图可得该拟合模型为:x t=1.0309*1.9958t+I t分析:图中的红色星号为原序列值,绿色的曲线为拟合后的拟合曲线,可以看出原序列值与拟合值基本上是重合的,故该拟合效果是很好的。
计量时间序列实验报告

一、实验背景时间序列分析是统计学和数据分析领域中一个重要的分支,广泛应用于经济、金融、气象、医学等领域。
通过对时间序列数据的分析,我们可以了解现象的发展变化规律,预测未来趋势,为决策提供科学依据。
本实验旨在通过实际操作,学习时间序列分析的基本方法,并运用相关软件进行时间序列分析。
二、实验目的1. 理解时间序列的基本概念和特点;2. 掌握时间序列数据的收集和整理方法;3. 学会运用时间序列分析方法对数据进行处理和分析;4. 培养运用相关软件进行时间序列分析的能力。
三、实验内容1. 数据收集本次实验采用我国某城市近10年的居民消费水平数据作为研究对象。
数据来源于国家统计局。
2. 数据整理对收集到的数据进行整理,剔除异常值和缺失值,将数据转换为适合时间序列分析的形式。
3. 时间序列分析(1)描述性分析对整理后的数据进行描述性统计分析,包括均值、标准差、最大值、最小值等。
(2)平稳性检验运用ADF(Augmented Dickey-Fuller)检验方法对时间序列数据进行平稳性检验。
(3)自相关性分析运用自相关函数(ACF)和偏自相关函数(PACF)对时间序列数据进行自相关性分析。
(4)模型选择根据自相关性分析结果,选择合适的模型对时间序列数据进行拟合。
本次实验采用ARIMA模型。
(5)模型参数估计运用最小二乘法估计模型参数,包括自回归项、移动平均项和差分阶数。
(6)模型检验运用残差分析、AIC准则等对模型进行检验。
(7)预测根据拟合的模型,对未来一段时间内的居民消费水平进行预测。
四、实验结果与分析1. 描述性分析根据描述性统计分析,我国某城市近10年的居民消费水平呈上升趋势,但波动较大。
2. 平稳性检验运用ADF检验方法对时间序列数据进行平稳性检验,结果显示该时间序列在5%的显著性水平下是平稳的。
3. 自相关性分析运用ACF和PACF对时间序列数据进行自相关性分析,发现自回归项和移动平均项的阶数分别为1和1。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
时间序列分析课程实验报告《时间序列分析》课程实验报告一、上机练习(P124)1.拟合线性趋势12.79 14.02 12.92 18.27 21.22 18.81 25.73 26.27 26.75 28.73 31.71 33.95程序:data xiti1;input x@@;t=_n_;cards;12.79 14.02 12.92 18.27 21.22 18.81 25.73 26.27 26.75 28.73 31.71 33.95 ;proc gplot data=xiti1;plot x*t;symbol c=red v=star i=join;run;proc autoreg data=xiti1;model x=t;output predicted=xhat out=out;run;proc gplot data=out;plot x*t=1 xhat*t=2/overlay;symbol2c=green v=star i=join;run;运行结果:分析:上图为该序列的时序图,可以看出其具有明显的线性递增趋势,故使用线性模型进行拟合:x t=a+bt+I t,t=1,2,3,…,12分析:上图为拟合模型的参数估计值,其中a=9.7086,b=1.9829,它们的检验P值均小于0.0001,即小于显著性水平0.05,拒绝原假设,故其参数均显著。
从而所拟合模型为:x t=9.7086+1.9829t.分析:上图中绿色的线段为线性趋势拟合线,可以看出其与原数据基本吻合。
2.拟合非线性趋势1.85 7.48 14.29 23.02 37.42 74.27 140.72265.81 528.23 1040.27 2064.25 4113.73 8212.21 16405.95 程序:data xiti2;input x@@;t=_n_;cards;1.85 7.48 14.29 23.02 37.42 74.27 140.72265.81 528.23 1040.27 2064.25 4113.73 8212.21 16405.95 ;proc gplot data=xiti2;plot x*t;symbol c=red v=star i=none;run;proc nlin method=gauss;model x=a*b**t;parameters a=0.1 b=1.1;der.a=b**t;der.b=a*t*b**(t-1);output predicted=xh out=out;run;proc gplot data=out;plot x*t=1 xh*t=2/overlay;symbol2c=green v=none i=join;run;运行结果:分析:上图为该时间序列的时序图,可以很明显的看出其基本是呈指数函数趋势慢慢递增的,故我们可以选择指数型模型进行非线性拟合:x t=ab t+I t,t=1,2,3,…,12分析:由上图可得该拟合模型为:x t=1.0309*1.9958t+I t分析:图中的红色星号为原序列值,绿色的曲线为拟合后的拟合曲线,可以看出原序列值与拟合值基本上是重合的,故该拟合效果是很好的。
3.X—11过程40777 41778 43160 4589741947 44061 44378 4723743315 43396 44843 4683542833 43548 44637 4710742552 43526 45039 4794043740 45007 46667 4932544878 46234 47055 5031846354 47260 48883 5260548527 50237 51592 5515250451 52294 54633 5880253990 55477 57850 61978程序:data xiti3;input x@@;t=intnx('quarter','1jan1978'd,_n_-1);format t yyq4.;cards;40777 41778 43160 4589741947 44061 44378 4723743315 43396 44843 4683542833 43548 44637 4710742552 43526 45039 4794043740 45007 46667 4932544878 46234 47055 5031846354 47260 48883 5260548527 50237 51592 5515250451 52294 54633 5880253990 55477 57850 61978;proc gplot data=xiti3;plot x*t;symbol c=red v=star i=join;run;proc x11 data=xiti3;quarterly date=t;var x;output out=out b1=x d10=season d11=adjusted d12=trend d13=irr; data out;set out;estimate=trend*season/100;proc gplot data=out;plot x*t=1 estimate*t=2/overlay;plot adjusted*t=1 trend*t=1 irr*t=1;symbol1c=red i= join v=star;symbol2c=black i= none v=star;run;运行结果:分析:上图为该序列的时序图,可以很明显的看出其具有长期增长趋势,且具有季节波动,故我们用X-11过程进行拟合。
分析:上图为季节调整后的序列值时序图。
分析:上图为趋势拟合值序列时序图。
分析:上图为不规则波动值的时序图。
分析:上图中的红色线段为原序列值,黑色星星为拟合值,可以由图中看出该拟合值与原序列值基本上是重合的,故该拟合效果很好。
4.Forecost过程程序:data xiti4;input x@@;t=1949+_n_-1;cards;40777 41778 43160 4589741947 44061 44378 4723743315 43396 44843 4683542833 43548 44637 4710742552 43526 45039 4794043740 45007 46667 4932544878 46234 47055 5031846354 47260 48883 5260548527 50237 51592 5515250451 52294 54633 5880253990 55477 57850 61978;proc gplot data=xiti4;plot x*t;symbol c=red v=star i=join;run;proc forecast data=xiti4 method=stepar trend=2 lead=5 out=out outfull outest=est;id t;var x;run;proc gplot data=out;plot x*t=_type_/href=2008;symbol1i=join v=star c=black;symbol2i=join v=none c=green;symbol3i=join v=none c=red;symbol4i=join v=none c=red;run;分析:由该序列的时序图可知,其具有长期趋势,且含有季节效应,趋势特征基本为线性趋势,即trend=2.分析:由上表可以很明显的看到每一年的与序列值、预测值,还有预测的后面六期预测值的95%置信区间。
分析:此表为预测过程中相关参数及拟合效果,可以看到RSQUARE=0.,拟合效果很好。
分析:上图为预测效果图,其中绿色的线段表示预测值,红色的代表预测的5期值的95%置信区间,黑色的为原序列,可以看出其预测效果很好。
二、课后习题7.某地区1962-1970年平均每头奶牛的月度产奶量数据(单位:磅)具体数据详见书P123 589 561 640 656 727 697 640 599 568 577 553 582600 566 653 673 742 716 660 617 583 587 565 598628 618 688 705 770 736 678 639 604 611 594 634658 622 709 722 782 756 702 653 615 521 602 635677 635 736 755 811 798 735 697 661 667 645 688713 667 762 784 837 817 767 722 681 687 660 698717 696 775 796 858 826 783 740 701 706 677 711734 690 785 805 871 845 801 764 725 723 690 734750 707 807 824 886 859 819 783 740 747 711 751(1)绘制该序列的时序图,直观考察该序列的特点。
程序:data lianxi1;input x@@;t=intnx('month','1jan1962'd,_n_-1);format t date.;cards;589 561 640 656 727 697 640 599 568 577 553 582600 566 653 673 742 716 660 617 583 587 565 598628 618 688 705 770 736 678 639 604 611 594 634658 622 709 722 782 756 702 653 615 521 602 635677 635 736 755 811 798 735 697 661 667 645 688713 667 762 784 837 817 767 722 681 687 660 698717 696 775 796 858 826 783 740 701 706 677 711734 690 785 805 871 845 801 764 725 723 690 734750 707 807 824 886 859 819 783 740 747 711 751;proc gplot data=lianxi1;plot x*t;symbol c=red v=star i=join;run;分析:由上图的时序图可以很明显的看出该序列具有长期的增长趋势,且具有明显的季节效应。
