电动力学习题解答
电动力学习题及答案
根据前面的内容讨论知道：在所考虑区域内 没有自由电荷分布时，可用Laplace's equation求 解场分布；在所考虑的区域内有自由电荷分布时， 且用Poisson‘s equation 求解场分布。
如果在所考虑的区域内只有一个或多个点电 荷，区域边界是导体或介质界面，这类问题又如 何求解场分布？ 这就是本节主要研究的一个问 题。解决这类问题的一种特殊方法称为 — 镜象 法。
电场。右半空间的电场是Q及S面上的感应电荷面密
度 感 共同产生的。以假想的点电荷Q'等效地代替感 应电荷，右半空间的电势必须满足以下条件：
1 2 Q ( x a, y 0, z 0) 0 R 0 x 0 0 (1) (2) (3)
由(4)式得
b 2 Q Q a 将(6)式代入(5)式得
2
(6)
b 2 (a R02 ) ( R02 b 2 ) a
1 2 2 2 即b (a R0 )b R0 0 a
2
解此二次方程，得到
2 R0 b a b a
将此代入(6)式，即有
Q Q R0 Q Q a
c、
Q
4
-Q 5 +Q 4
+Q 6 7
-Q
B
Q
A
1 -Q
3 -Q 2 +Q
要保证 A B 0 则必须有7个象电荷，故电势为
1 1 1 1 1 1 1 1 ( ) 4 0 r r1 r2 r3 r4 r5 r6 r7
一般说明：只要 满足2 偶数的情形，都可用 镜象法求解，此时象电荷的个数等于 (2 ) 1 ，
郭硕鸿《电动力学》习题解答完全版（章）
= (µµ −1)∇× Hr = ( µ −1)rj f ,(r1 < r < r2)
0
µ0
αrM = nr× (Mr 2 − Mr 1),(n从介质1指向介质2
3ε
r3
= − ε −ε 0 ρ f (3− 0) = −(ε −ε 0 )ρ f
3ε
ε
σ P = P1n − P2n
考虑外球壳时 r r2 n从介质 1指向介质 2 介质指向真空 P2n = 0
-5-
电动力学习题解答
第一章 电磁现象的普遍规律
σ P = P1n = (ε −ε 0)
r 3 − r13 ρ f rr r=r2 3εr 3
= cos(kr ⋅rr)(kxerx + k yery + kzerz )Er0 = cos(kr ⋅rr)(kr ⋅ Er) ∇×[Er0 sin(kr ⋅rr)] = [∇sin(kr ⋅rr)]×Er 0+sin(kr ⋅rr)∇× Er0
4. 应用高斯定理证明
∫ dV∇× fr = ∫S dSr× fr
V
应用斯托克斯 Stokes 定理证明
∫S dSr×∇φ = ∫Ldlrφ
证明 1)由高斯定理
dV∇⋅ gr = ∫S dSr ⋅ gr
∫
∫ ∫ 即
V
(∂ g x ∂x V
+ ∂g y ∂y
+ ∂g zz )dV = ∂
g
S
xdS x + g ydS y + g zdS z
而 ∇× frdV = [(∂ f z − ∂∂z f y )ir ∂+ ( f x − ∂∂x f z )rj∂+ ( f y − ∂∂y f x )kr]dV
电动力学习题集答案-1
电动力学第一章习题及其答案1. 当下列四个选项：(A.存在磁单级, B.导体为非等势体, C.平方反比定律不精确成立,D.光速为非普适常数)中的_ C ___选项成立时,则必有高斯定律不成立.2. 若a为常矢量, k z z j y y i x x r )'()'()'(-+-+-=为从源点指向场点的矢量,k E,0为常矢量,则)(2a r ⋅∇=a r a r a r a r a r r r dr dr ⋅=⋅=⋅∇=⋅∇=⋅∇22))()(222,()r r r r r zy x k j i z z y y x x k j i r=++=-+-+-++=∇∂∂∂∂∂∂z'-z y'-y x'-x 222)'()'()'(⎪⎪⎪⎭⎫ ⎝⎛=-+-+-=-+-+-==-+-+--∂∂-∂∂--+-+--∂∂r z z z r y y yr x x z z y y x x x x x z z y y x x z z y y x x z z y y x x )'(222)'(222)'()'()'()'(2)'(2222)'()'()'(,)'()'()'(,)'()'()'(222同理，=⨯∇r 0'''=---∂∂∂∂∂∂z z y y x x e e e z y x xx x ， 3)z'-(z )y'-(y )x'-(x =++=⋅∇∂∂∂∂∂∂z y x r ，)()(=⨯∇⋅=⨯⋅∇r a r a ,0)(3211=⨯=⨯=⨯∇+⨯∇=⨯∇∇r r r r r r r r r rrr,a k j i r a za ya xa z y x =++=⋅∇∂∂∂∂∂∂)]z'-(z [)]y'-(y [)]x'-(x [)(，r r rr r rrr r r r 23113=+⋅-=⋅∇+⋅∇=⋅∇ ，=⨯∇⋅∇)(A __0___. =⋅⋅∇)]sin([0r k E )cos(0r k E k ⋅⋅, 当0≠r 时,=⨯∇)/(3r r __0__. =⋅∇⋅)(0r k i e E )exp(0r k i E k i ⋅⋅, =⨯∇)]([r f r _0_. =⋅∇)]([r f r dr r df r r f )()(3+3. 矢量场f的唯一性定理是说：在以s 为界面的区域V 内,若已知矢量场在V 内各点的旋度和散度,以及该矢量在边界上的切向或法向分量,则f在V内唯一确定.4. 电荷守恒定律的微分形式为0=∂∂+⋅∇tJ ρ,若J为稳恒电流情况下的电流密度,则J满足0=⋅∇J.5. 场强与电势梯度的关系式为，ϕ-∇=E.对电偶极子而言,如已知其在远处的电势为)4/(30r r P πεϕ ⋅=，则该点的场强为()⎪⎪⎭⎫ ⎝⎛-⋅=350341r P rr r P Eπε.6. 自由电荷Q 均匀分布于一个半径为a 的球体内,则在球外)(a r >任意一点D的散度为 0,内)(a r <任意一点D的散度为 34/3a Q π.7. 已知空间电场为b a rrb r r a E ,(32 +=为常数），则空间电荷分布为______.)](4[)](423[)](42[)1(1120420320220023r b rar b r r r r a r b rrr r r a r b r r a E r b rr a E r r r δπερδπεδπεεερ+=⇒+⋅-=+∇⋅-⋅∇=∇-⋅∇=⋅∇=⇒∇-=⇒-=∇ 8. 电流I 均匀分布于半径为a 的无穷长直导线内，则在导线外)(a r >任意一点B的旋度的大小为 0 , 导线内)(a r <任意一点B的旋度的大小为20/a Iπμ.9. 均匀电介质（介电常数为ε）中,自由电荷体密度为f ρ与电位移矢量D的微分关系为f D ρ=⋅∇ , 束缚电荷体密度为Pρ与电极化矢量P 的微分关系为P P ρ-=⋅∇,则P ρ与f ρ间的关系为fP ρρεεε0--=.10. 无穷大的均匀电介质被均匀极化，极化矢量为P，若在介质中挖去半径为R 的球形区域，设空心球的球心到球面某处的矢径为R，则该处的极化电荷面密度为R R P /⋅-.11. 电量为q的点电荷处于介电常数为ε的均匀介质中，则点电荷附近的极化电荷为q )1/(0-εε.12. 某均匀非铁磁介质中,稳恒自由电流密度为f J,磁化电流密度为M J ,磁导率μ,磁场强度为H ，磁化强度为M ，则=⨯∇H f J ,=⨯∇M M J ,M J 与f J 间的关系为()f M J J1/0-=μμ.13. 在两种电介质的分界面上,E D ,所满足的边值关系的形式为()f D D n σ=-⋅12,RR P P P P n n P ⋅-=--=--=)0cos ()(12θ()012=-⨯E E n.14. 介电常数为ε的均匀各向同性介质中的电场为E . 如果在介质中沿电场方向挖一窄缝,则缝中电场强度大小为E . 15. 介电常数为ε的无限均匀的各项同性介质中的电场为E ，在垂直于电场方向横挖一窄缝，则缝中电场强度大小为,/0sin 00011201212εεθεετττE E E E E E E E D D n n =⇒⎩⎨⎧===⇒⎩⎨⎧=-=-缝缝. 16. 在半径为R 的球内充满介电常数为ε的均匀介质，球心处放一点电荷，球面为接地导体球壳，如果挖去顶点在球心的立体角等于2的一圆锥体介质，则锥体中的场强与介质中的场强之比为_1:1_.1:1:021221112=⇒===⇒==E E E E E E D D n n ττ17. 在半径为R 的球内充满介电常数为ε的均匀介质，球心处放一点电荷，球面为接地导体球壳，如果挖去顶点在球心的立体角等于2的一圆锥体介质，锥体处导体壳上的自由电荷密度与介质附近导体壳上的自由电荷密度之比为εε/0.εεσσεσεσεεττ::0021201201221112=⇒=⇒=⇒⎩⎨⎧=====D D E E E E D D n n 内球面上 18. 在两种磁介质的分界面上, B H,所满足的边值关系的矢量形式为()fH H n α=-⨯12,()012=-⋅B B n.19. 一截面半径为b 无限长直圆柱导体，均匀地流过电流I ，则储存在单位长度导体内的磁场能为__________________.,2202220b Ir b r B I r B πμππμπ=⇒=⋅ πμπμπμπμμμππ161640402122120442043204222200022I b b I b dr r I b br I b rdr rdr B W =====⎰⎰⎰20. 在同轴电缆中填满磁导率为21,μμ的两种磁介质，它们沿轴各占一半空间。
电动力学课后题解答
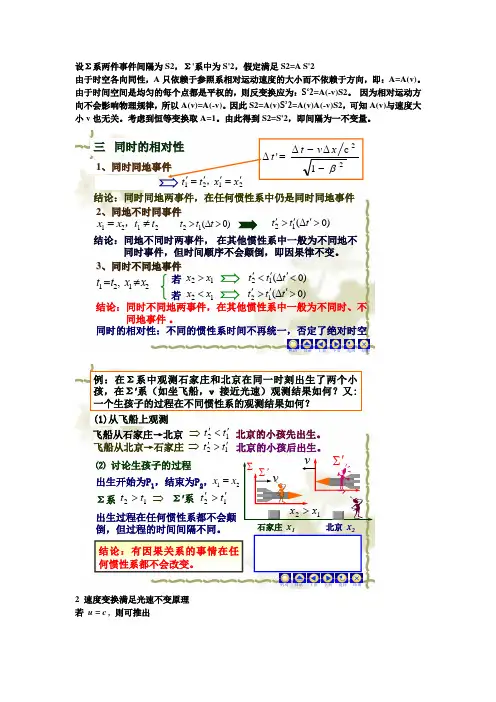
设Σ系两件事件间隔为S2，Σ'系中为S'2，假定满足S2=A S'2 由于时空各向同性，A 只依赖于参照系相对运动速度的大小而不依赖于方向，即：A=A(v)。
由于时间空间是均匀的每个点都是平权的，则反变换应为：S‘2=A(-v)S2。
因为相对运动方向不会影响物理规律，所以A(v)=A(-v)。
因此S2=A(v)S’2=A(v)A(-v)S2，可知A(v)与速度大小v 也无关。
考虑到恒等变换取A=1。
由此得到S2=S'2，即间隔为一不变量。
三同时的相对性1、同时同地事件结论：同时同地两事件，在任何惯性系中仍是同时同地事件2、同地不时同事件2121t t x x ≠=，设)0(12>∆>t t t )0(12>'∆'>'t t t 结论：同地不同时两事件，在其他惯性系中一般为不同地不同时事件，但时间顺序不会颠倒，即因果律不变。
3、同时不同地事件2121,xx t t ≠=若12x x >)0(12<'∆'<'t t t 若12x x <)0(12>'∆'>'t t t 结论：同时不同地两事件，在其他惯性系中一般为不同时、不同地事件。
2121x x t t '=''='，221c 'β-∆-∆=∆x v t t 同时的相对性：不同的惯性系时间不再统一，否定了绝对时空机动目录上页下页返回结束结论：有因果关系的事情在任何惯性系都不会改变。
例：在Σ系中观测石家庄和北京在同一时刻出生了两个小孩，在Σ'系（如坐飞船，v 接近光速）观测结果如何？又:一个生孩子的过程在不同惯性系的观测结果如何？飞船从石家庄→北京北京的小孩先出生。
12t t '<'⇒飞船从北京→石家庄12t t '>'⇒北京的小孩后出生。
郭硕鸿《电动力学》习题解答完全版(1-6章)
微商 (∇ = e x
r ∂ r ∂ r ∂ + ey + e z ) 的关系 ∂x ∂y ∂z r r r r r r 1 r r r ' ' 1 ' r ∇r = −∇ r = , ∇ = −∇ = − 3 , ∇ × 3 = 0, ∇ ⋅ 3 = −∇ 3 = 0.(r ≠ 0) r r r r r r r
l S
r
r r
r
r
∫ f ⋅ dl = ∫ ( f
l l
r
x
dl x + f y dl y + f z dl z )
r r ∂ ∂ ∂ ∂ ∂ ∂ f f y )dS x + ( f x − f z )dS y + ( f y − f x )dS z ∇ × ⋅ dS = ∫ ( f z − ∫S S ∂y ∂z ∂z ∂x ∂x ∂y
3. 设 r =
( x − x ' ) 2 + ( y − y ' ) 2 + ( z − z ' ) 2 为源点 x ' 到场点 x 的距离 r 的方向规定为从 r ∂ r ∂ r ∂ + e y ' + e z ' ) 与对场变数求 ∂x ' ∂y ∂z
源点指向场点 1 证明下列结果 并体会对源变数求微商 (∇ = e x
证明
r ∂( x − x ' ) ∂( y − y ' ) ∂( z − z ' ) ∇⋅r = + + =3 ∂x ∂y ∂z r ex r ∂ ∇×r = ∂x x − x' r ey ∂ ∂y y − y' r ez ∂ =0 ∂z z − z'
电动力学习题答案
电动力学习题答案电动力学是物理学中研究电荷、电场、磁场和它们之间相互作用的分支。
以下是一些典型的电动力学习题及其答案。
# 习题一：库仑定律的应用问题：两个点电荷，一个带电为+3μC，另一个为 -5μC，它们之间的距离为 2m。
求它们之间的静电力大小。
解答：根据库仑定律，两个点电荷之间的静电力 \( F \) 由下式给出：\[ F = k \frac{|q_1 q_2|}{r^2} \]其中 \( k \) 是库仑常数，\( q_1 \) 和 \( q_2 \) 是电荷量，\( r \) 是它们之间的距离。
代入给定的数值：\[ F = 8.9875 \times 10^9 \frac{N \cdot m^2}{C^2} \times\frac{3 \times 10^{-6} C \times (-5 \times 10^{-6} C)}{(2 m)^2} \]\[ F = 37.5 N \]# 习题二：电场强度的计算问题：一个无限大均匀带电平面，电荷面密度为 \( \sigma \)。
求距离平面\( d \) 处的电场强度。
解答：对于无限大均匀带电平面，电场强度 \( E \) 垂直于平面，大小为：\[ E = \frac{\sigma}{2\epsilon_0} \]其中 \( \epsilon_0 \) 是真空电容率。
# 习题三：电势能的计算问题：一个点电荷 \( q \) 位于另一个点电荷 \( Q \) 产生的电场中，两者之间的距离为 \( r \)。
求点电荷 \( q \) 在该电场中的电势能。
解答：点电荷 \( q \) 在由点电荷 \( Q \) 产生的电场中的电势能 \( U \) 为：\[ U = -k \frac{qQ}{r} \]# 习题四：洛伦兹力的计算问题：一个带电粒子，电荷量为 \( q \)，以速度 \( v \) 进入一个垂直于其运动方向的磁场 \( B \) 中。
【全】刘觉平电动力学课后习题答案
第一章三維歐氏空間中的張量目录：习题1.1 正交坐标系的转动 (2)习题1.2 物理量在空间转动变换下的分类 (9)习题1.3 物理量在空间反演变换下的进一步分类 (10)习题1.4 张量代数 (15)习题1.5 张量分析 (21)习题1.6 Helmholtz定理 (35)习题1.7 正交曲线坐标系 (38)习题1.8 正交曲线坐标系中的微分运算 (42)习题1.11、 设三个矢量,,a b c r r r 形成右（左）旋系，证明，当循环置换矢量,,a b c r r r的次序，即当考察矢量,,(,,)b c a c a b r rr r r r 时，右（左）旋系仍保持为右（左）旋系。
证明：()V a b c =⨯⋅r r r，对于右旋系有V>0.当循环置换矢量,,a b c r r r次序时， ()V b c a '=⨯⋅r r r ＝()0c a b V ⨯⋅=〉rr r 。
（*）所以，右旋系仍然保持为右旋系 同理可知左旋系情况也成立。
附：（*）证明。
由于张量方程成立与否与坐标无关，故可以选取直角坐标系，则结论是明显的。
2、 写出矢量诸分量在下列情况下的变换矩阵：当Cartesian 坐标系绕z 轴转动角度α时。
解：变换矩阵元表达式为 ij i j a e e '=⋅r r1112212213233233cos ,sin ,sin ,cos ,0,1a a a a a a a a αααα===-===== 故()cos sin 0sin cos 0001R ααααα⎛⎫⎪=- ⎪ ⎪⎝⎭3、 设坐标系绕z 轴转α角，再绕新的y 轴（即原来的y 轴在第一次转动后所处的位置）转β角，最后绕新的z 轴（即原来的z 轴经第一、二次转动后所处的位置）转γ角；这三个角称为Euler 角。
试用三个转动矩阵相乘的办法求矢量诸分量的在坐标轴转动时的变换矩阵。
解：我们将每次变换的坐标分别写成列向量,,,X X X X ''''''， 则 ()()(),,z y z X R X X R X X R X αβγ'''''''''''''===∴()()()z y z X R R R X γβα''''''=绕y '-轴转β角相当于“先将坐标系的y '-轴转回至原来位置，再绕原来的y-轴（固定轴）转β角，最后将y-轴转至y '-轴的位置”。
《电动力学》课后答案
电动力学答案第一章电磁现象的普遍规律1.根据算符∇的微分性与向量性，推导下列公式：BA B A A B A B B A )()()()()(∇⋅+×∇×+∇⋅+×∇×=⋅∇A A A A )()(221∇⋅−∇=×∇×A 解：（1）)()()(c c A B B A B A ⋅∇+⋅∇=⋅∇BA B A A B A B )()()()(∇⋅+×∇×+∇⋅+×∇×=c c c c BA B A A B A B )()()()(∇⋅+×∇×+∇⋅+×∇×=（2）在（1）中令B A =得：A A A A A A )(2)(2)(∇⋅+×∇×=⋅∇，所以A A A A A A )()()(21∇⋅−⋅∇=×∇×即A A A A )()(221∇⋅−∇=×∇×A2.设u 是空间坐标z y x ,,的函数，证明：u u f u f ∇=∇d d )(，u u u d d )(A A ⋅∇=⋅∇，uu u d d )(AA ×∇=×∇证明：（1）z y x z u f y u f x u f u f e e e ∂∂+∂∂+∂∂=∇)()()()(zy x z uu f y u u f x u u f e e e ∂∂+∂∂+∂∂=d d d d d d u uf z u y u x u u f z y x ∇=∂∂+∂∂+∂∂=d d )(d d e e e （2）z u A y u A x u A u z y x ∂∂+∂∂+∂∂=⋅∇)()()()(A zuu A y u u A x u u A z y x ∂∂+∂∂+∂∂=d d d d d d uu z u y u x u u A u A u A z y x z z y y x x d d )()d d d d d d (Ae e e e e e ⋅∇=∂∂+∂∂+∂∂⋅++=（3）uA u A u A zu y u x u uu z y x zy x d /d d /d d /d ///d d ∂∂∂∂∂∂=×∇e e e Azx y y z x x y z yu u A x u u A x u u A z u u A z uu A y u u A e e e )d d d d ()d d d d ()d d d d (∂∂−∂∂+∂∂−∂∂+∂∂−∂∂=zx y y z x x y z y u A x u A x u A z u A z u A y u A e e e ])()([])()([])()([∂∂−∂∂+∂∂−∂∂+∂∂−∂∂=)(u A ×∇=3.设222)'()'()'(z z y y x x r −+−+−=为源点'x 到场点x 的距离，r 的方向规定为从源点指向场点。
电动力学课后习题解答(参考)
∂ ∂y
∂ ∂z
=
(
∂Az ∂y
−
∂Ay ∂z
)ex
+
(
∂Ax ∂z
−
∂Az ∂x
)ey
+
(
∂Ay ∂x
−
∂Ax ∂y
)ez
Ax(u) Ay(u) Az(u)
=
(
∂Az du
∂u ∂y
−
∂Ay du
∂u ∂z
)ex
+
(
∂Ax du
∂u ∂z
−
∂Az du
∂ ∂
u x
)ey
+
(
∂Ay du
∂u ∂x
−
(dl2
·
dl1)
11、平行板电容器内有两层介质，它们的厚度分别为l1和l2，电容率为ε1和ε2，今在两板接上电 动势为E的的电池，求
(1)电容器两板上的自由电荷密度ωf (2)介质分界面上的自由电荷密度ωf 若介质是漏电的，电导率分别为σ1和σ2，当电流达到恒定时，上述问题的结果如何？ 解：在相同介质中电场是均匀的，并且都有相同指向，
[∇
1 r
·
∇]m
=
−(m
·
∇)∇
1 r
∴ ∇ × A = −∇ϕ
7、有一个内外半径分别为r1和r2的空心介质球，介质的电容率为ε，使介质内均匀带静止自由 电荷ρf ，求 （1）空间各点的电场 （2）极化体电荷和极化面电荷分布 解：1) S D · dS = ρf dV ，(r2 > r > r1)
R
)
=
(∇
·
m)∇
1 r
+(m源自·m)∇1 r
电动力学习题答案
电动力学习题答案
电动力学学习题答案
电动力学是物理学中的一个重要分支，研究电荷和电场之间的相互作用以及电
荷在电场中的运动规律。
在学习电动力学的过程中，我们经常会遇到各种各样
的习题，下面就为大家整理了一些常见的电动力学学习题答案，希望能够帮助
大家更好地理解和掌握电动力学的知识。
1. 两个带电粒子分别带有正电荷和负电荷，它们之间的相互作用力是吸引力还
是斥力？
答：两个带电粒子之间的相互作用力是吸引力，正电荷和负电荷之间会相互吸引。
2. 一个点电荷在电场中受到的力的大小与什么有关？
答：一个点电荷在电场中受到的力的大小与电场强度和电荷本身的大小有关。
3. 电场线的方向与电场中的电荷运动方向有什么关系？
答：电场线的方向与电场中的电荷运动方向相反，即电场线从正电荷指向负电荷。
4. 电势能和电势的关系是什么？
答：电势能是电荷在电场中由于位置而具有的能量，而电势是单位正电荷在电
场中所具有的电势能，即电势能和电势的关系可以用公式 U=qV 来表示。
5. 电容器中的电荷与电压的关系是怎样的？
答：电容器中的电荷与电压的关系可以用公式 Q=CV 来表示，其中 Q 表示电荷，C 表示电容，V 表示电压。
以上就是一些常见的电动力学学习题答案，希望能够帮助大家更好地理解和掌
握电动力学的知识。
在学习电动力学的过程中，多做习题，多思考，相信大家一定能够取得更好的成绩。
大学物理通用教程.电动力学.郭硕鸿.第三版.答案
3. 设 r =
( x − x ' ) 2 + ( y − y ' ) 2 + ( z − z ' ) 2 为源点 x ' 到场点 x 的距离 r 的方向规定为从 r ∂ r ∂ r ∂ + e y ' + e z ' ) 与对场变数求 ∂x ' ∂y ∂z
源点指向场点 1 证明下列结果 并体会对源变数求微商 (∇ = e x
(最后一式在人 r 0 点不成立 见第二章第五节) 2 求
r r r r r r r r r r r r r r r ∇ ⋅ r , ∇ × r , (a ⋅ ∇)r , ∇(a ⋅ r ), ∇ ⋅ [ E 0 sin(k ⋅ r )]及∇ × [ E 0 sin(k ⋅ r )], 其中a , k 及E 0 均为常矢量
若令 H x = f y k − f z j , H y = f z i − f x k , H Z = f x j − f y i 则上式就是
r
r
r
r
r
r
r r r ∇ ⋅ H dV = d S ∫ ∫ ⋅ H ,高斯定理 则证毕
V S
2)由斯托克斯公式有
∫ f ⋅ dl = ∫ ∇ × f ⋅ dS
r r r r r r r r ∂Ax (u ) ∂A y (u ) ∂Az z (u ) dAx (u ) ∂u dA y (u ) ∂u dAz (u ) ∂u dA ∇ ⋅ A(u ) = + + = ⋅ + ⋅ + ⋅ = ∇u ⋅ ∂x ∂y ∂z du ∂x du ∂y dz ∂z du
l S
r
r r
r
电动力学作业及参考解答
习题与参考答案第1章 电动力学的数学基础与基本理论1.1 A 类练习题1.1.1 利用∇算符的双重性质，证明（1）()A A A ϕϕϕ∇×=∇×+∇×r r r（2）2()()A A A ∇×∇×=∇∇⋅−∇r r r1.1.2 证明以下几个常用等式，其中()x r x x e ′=−r r ()()y z y y e z z e ′′+−+−r r ,a r为常矢量，(,,)u u x y z =。
（1）3r r ′∇⋅=−∇⋅=r r ，（2）0r ∇×=r，（3）r r r r ′∇=−∇=r ，（4）31r r r ∇=−r ，（5）30r r∇×=r， （6）330r r r r ⋅⋅′∇=−∇=r r (0)r ≠，（7）()a r a ∇⋅=r r r，（8）()dA A u u du∇×=∇×r r 。
1.1.3 从真空麦克斯韦方程出发，导出电荷守恒定律的微分形式和真空中的波动方程。
1.1.4证明均匀介质中的极化电荷密度与自由电荷密度满足关系式0(1/)p f ρεερ=−−。
1.1.5 已知电偶极子电势304p R R ϕπε⋅=r r ，试证明电场强度53013()[4p R R p E R Rπε⋅=−r r r r r 。
1.1.6 假设存在孤立磁荷（即磁单极），试改写真空中的麦克斯韦方程组以包括磁荷密度m ρ和磁流密度m J r的贡献。
答案：D ρ∇⋅=ur ， m B ρ∇⋅=u r ， m B E J t ∂∇×=−−∂u r u r u r ， D H J t∂∇×=+∂ur uu r ur 。
1.1.7 从麦克斯韦方程出发导出洛伦茨规范下的达朗贝尔方程，并证明洛伦茨规范中的ψ满足齐次波动方程，即222210c tψψ∂∇−=∂。
1.1.8 证明：（1）在静电情况下，导体外侧的电场总是与表面垂直；（2）在稳恒电流的情况下，导体内侧的电场总是平行于导体表面。
电动力学习题答案第一章 电磁现象的普遍规律
由（3）得
+ +
又
即 与 严格抵消。
（2）由
=
2 LE=
E=
J= -
解得
当t=0时
(3)t场对自由电荷所做的功率密度为
(4)
而长为L的一段介质总的静电能为
W=
所以能量耗散功率等于静电能减少率。
（ ）
的关系
（最后一式在r=0点不成立，见第二章第五节）
⑵求 及 ，其中 及 均为常矢量。
解：⑴
⑵
4.4.⑴应用高斯定理证明
⑵应用斯托克斯（Stokes）定理证明
解：⑴
⑵
5.5.已知一个电荷系统的偶极矩定义为
利用电荷守恒定律
证明 的变化率为
解：
取被积区域大于电荷系统的区域，即V的边界S上的 ，则
。
6.若 是常矢量，证明除R=0点以外矢量 的旋度等于标量 的梯度的负值，即 ,其中R为坐标原点到场点的距离，方向由原点指向场点。
解：⑴由
所以
所以
方向为
对区域Ⅱ
由
方向为
对区域Ⅲ有:
(2)(2)由
由
由
同理
由
得
9.证明均匀介质内部的体极化电荷密度 总是等于体自由电荷密度 的 倍。即：
解：由均匀介质有
①
②
③
④
由①②得
两边求散度
由③④得
10.证明两个闭合的恒定电流圈之间的相互作用力大小相等，发向相反。（但两个电流元之间的相互作用力一般并不服从牛顿第三定律）
第一章电磁现象的普遍规律
1.根据算符 的微分性与矢量性，推导下列公式：
解：矢量性为
①
②
③微商性
电动力学答案(郭硕鸿+第三版) chapter4
sin θ 1
ww∴有(ωc
sinθ1 )2
+
β
2 z
−
α
2 z
=
ω 2 µε
w αzβz
=
1 ωµσ 2
解得
β
2 z
=
1 (µεω 2 2
−ω2 c2
sin 2 θ1 ) +
1 ω2 [(
2 c2
sin 2 θ1
− ω 2 µε )2Βιβλιοθήκη + ω 2 µ 2σ
2
]
1 2
α
2 z
=
−
1 (µεω 2 2
课 后 答 案 网
相速 kx − ωt = 0
w ∴vp
=
ω k
a 群速 dk ⋅ x − dω ⋅t = 0
d ∴vg
=
dω dk
h 2 一平面电磁波以θ = 45o 从真空入射到ε r = 2 的介质 电场强度垂直于入射面 求反射 k 系数和折射系数
解 nr 为界面法向单位矢量 < S >, < S ' >, < S '' > 分别为入射波 反射波和折射波的玻印
=
−
∂Bv
×
v H
=
∂D∂vt
⋅
v D
=
0
∂t
o ∇
⋅
v B
=
0
得
.c ∇
⋅
v B
=
v B0
⋅ ∇ei(kv⋅xv−ωt)
=
v ik
⋅
v B0e
i(kv⋅xv−ωt )
=
v ik
⋅
电动力学习题解答-郭硕鸿
v e 1. 根据算符∇ 的微分性与矢量性 推导下列公式∇ r ⋅ r = r ⨯ ∇ ⨯ r + r ⋅ ∇ r + r ⨯ ∇ ⨯ r + r ⋅ ∇ r( A B ) B ( A ) (B ) A A ( B ) ( A )Br r 1 r 2 r rA ⨯ (∇ ⨯ A ) = ∇A 2- ( A ⋅ ∇) Av v v v v v v v v v解 1 ∇( A ⋅ B ) = B ⨯ (∇ ⨯ A ) + (B ⋅ ∇) A + A ⨯ (∇ ⨯ B ) + ( A ⋅ ∇)B首先 算符∇ 是一个微分算符 其具有对其后所有表达式起微分的作用 对于本题∇ 将作用于 A v 和B v又∇ 是一个矢量算符 具有矢量的所有性质 因此 利用公式c v ⨯ (a v ⨯ v= a v ⋅ (c v ⋅ v - (c v ⋅ v可得上式 其中右边前两项是∇ 作用于b )A v 后两项是∇ 作用于B v b ) a )b2 根据第一个公式 令 AvB v可得证2. 设 u 是空间坐标 x y z 的函数 证明∇f (u ) =df∇u du r r ∇ ⋅ A (u ) = ∇u ⋅ dAdu r r∇ ⨯ A (u ) = ∇u ⨯ dA .du 证明 1∇f (u ) = ∂f (u ) e r x + ∂f (u ) e r y + ∂f (u ) e r z = df ⋅ ∂u e r x + df ⋅ ∂u e r y + df ⋅ ∂u e r z= df∇u∂x 2r ∂r ∂y∂r y∂z∂r( ) du ∂x r∂u du ∂yr y du ∂z du∂u r ( ) ∂u r∇ ⋅ A (u ) = A x (u ) + A (u ) + A z z u = dA x (u ) ⋅ dA (u ) + ⋅+ dA z u ⋅ = ∇u ⋅ dA∂x ∂y 3r r x y r∂z due r z r r ∂x du ∂y dz ∂z dur r ∂r r∇ ⨯ A (u ) = ∂∂x r ∂ r ∂y ∂ r ∂z = ( ∂A z - ∂y A y )e r ∂z x + ( ∂A x ∂z - ∂A z )e r + ( A y ∂x y ∂x - ∂A x )e r =∂y zA x (u )A y (u ) A z (u )e ∂(x - x ' )2 + ( y - y ' )2 + (z - z ' )2 zx x y y z z r= ( dA z r ∂u -dA y ∂u )e rr(dA xr ∂u - dA z ∂u )e r r + ( dA y r ∂u - dA x ∂u )e r r= ∇u ⨯ dA du ∂ydu ∂z xdu ∂z du ∂x y du ∂x du ∂y z du3. 设r =为源点 x ' 到场点 x 的距离 r 的方向规定为从源点指向场点1 证明下列结果 并体会对源变数求微商(∇'= e r∂ + e r∂ + e r ∂ ) 与对场变数求微商(∇ = e r∂ x∂xe r∂ y∂y e r ∂) 的关系z ∂zx∂x'y∂y'z∂z'∇r = -∇'r = r r , ∇ 1 = -∇' 1 = - r r , ∇ ⨯ r r = 0, ∇ ⋅ r r = -∇' r r = 0.(r ≠ 0)r r r r 3 r 3r 3 r 3 (最后一式在人 r 0 点不成立 见第二章第五节)2 求∇ ⋅ r r , ∇ ⨯ r r , (a r ⋅ ∇)r r , ∇(a r ⋅ r r), ∇ ⋅ rr ⋅ r r )]及∇ ⨯ rr ⋅ r r )],其中r rr 均为常矢量[E 0 sin(k[E 0 sin(ka , k 及E 0证明 ∇ ⋅ r r =∂(x - x ' ) + ∂x ∂( y - y ' ) ∂y+ ∂(z - z ' ) =∂z e r x e r y e r z∇ ⨯ r r=∂ ∂x x - x '∂ ∂y y - y '∂ = 0 ∂z z - z '(a v ⋅ ∇)r r = [(a e v + a e v+ a e v ) ⋅ ( ∂ e v+∂ e v + ∂ e v )][(x - x ' )e v + ( y - y ' )e r + (z - z ')e v ] x x y yz z ∂xx ∂y y∂z z x y z= (a ∂x ∂x∂ a y ∂y + a ∂ )[(x - x ')e v z ∂z x + ( y - y ')e r + (z - z ')e v ]= a e v + a e v + a e v = a v∇(a v ⋅ r v ) = a v ⨯ (∇ ⨯ r v ) + (a v ⋅ ∇)r v + r r ⨯ (∇ ⨯ a v ) + (r v ⋅ ∇) ⋅ a v= (a v ⋅∇)r v + r v ⨯ (∇⨯ a v ) + (r v ⋅ a r ) ⋅ a v= a v + r v ⨯ (∇ ⨯ a v ) + (r v ⋅ ∇) ⋅ a v ∇ ⋅ r r rr r r r rr3 + y[E0 sin(k ⋅r )] = [∇(sin(k ⋅r )] ⋅E+ sin(k ⋅r )(∇⋅E)⎰ r r rfrVf dS f= [∂sin(r⋅rr)er+∂sin(r⋅rr)er+∂sin(r⋅rr)er]E ∂xk=r rx ∂yr rky ∂zr rkz 0r r r rcos(k ⋅r )(kxex+kyey+kzez)E= cos(k ⋅r )(k ⋅E)∇⨯r r rr r r r r r[E0 sin(k ⋅r )] = [∇sin(k ⋅r )]⨯E+sin(k ⋅r )∇⨯E4.应用高斯定理证明⎰dV∇⨯r =⎰ r⨯r应用斯托克斯Stokes 定理证明r r⎰S dS ⨯∇φ=⎰L dl φ 证明1)由高斯定理dV∇⋅g r =V SdS ⋅g即 ⎰V ( ∂g x∂x +∂gy∂y+∂gz∂z )dV =SgxdSx+gydSy+gzdSz而⎰∇⨯ =⎰[(∂f -∂f )ir+ (∂f-∂f )rj + (∂f -∂)r]fdVV ∂y z∂z y∂z x∂x z∂x y∂y fxk dV=⎰[ ∂ r-frj)+∂( f ir-r+∂( frj-f ir)]dV∂x ( fykzr r∂y zrfxk )∂z x yr r又 ⎰S dS ⨯f =⎰S [( f z dS y -f y dS z )i + ( f x dS z -f z dS x ) j + ( f y dS x -f x dS y )k ] =r r r r r r⎰( f y k -f z j )dS x + ( f z i -f x k )dS y + ( f x j -f y i )dS zr r r r r r若令 H x = 则上式就是fyk -fzj , Hy=fzi -fxk , HZ=fxj -fyi ⎰∇⋅r⎰r rV2)由斯托克斯公式有HdV = dS ⋅H ,高斯定理则证毕Sr r r r⎰l f ⋅dl =⎰S ∇⨯f ⋅dSr r⎰l f ⋅dl =⎰l ( f x dl x +f y dl y +f z dl z )∇⨯r ⋅Sr dS = (∂S ∂y∂fz-∂zfy)dSx+ (∂∂z∂fx-∂xfz)dSy+ (∂∂x∂fy-∂yfx)dSz⎰S+⎰ ⎰而⎰l dl φ=⎰l (φi dl x +φj dl y +φk dl z )r r⎰ xR R A Sr⨯ ∇ ( ∂φ ∂φ )r ( ∂φ ∂φ) r (∂φ ∂φ ) r ⎰S dS φ = ⎰S ∂z dS y - ∂y dS zi + ∂x dS z - ∂z dS x j + ∂y dS x - ∂xdS y k= ⎰ ( ∂φ r -∂φ r j )dS + ( ∂φ i r - ∂φ r + ( ∂φ r j - ∂φ i r )dS∂y k ∂z x∂z∂x k )dS y ∂x ∂y z若令 f x = φi , f y = φ j , f z = φk则证毕5. 已知一个电荷系统的偶极矩定义为 r r 'r''P (t ) = ⎰V ρ (x , t )x dV ,利用电荷守恒定律∇ ⋅ J +∂ρ∂t = 0 证明 P 的变化率为r = ⎰ r rdP dt V ∂ r ∂ρr 'J (x ' , t )dV 'rr r证明P= ⎰x 'dV ' = -⎰ ∇' j ' x 'dV '∂tV∂tV∂r rr r r( P ) ∂t x= -⎰V ∇' j ' x 'dV ' = -⎰ [∇' ⋅ (x ' j ' ) - (∇' x ' ) ⋅ j ' ]dV ' = ( j ' V - ∇' ⋅ (x ' j ' )dV '= ⎰ j xdV ' - Sr x r j ⋅ d r rr 若S → ∞,则⎰(xj ) ⋅ dS = 0,( j S = 0)∂ρr 同理 ( ∂t ) y = ⎰ j y dV '∂ρr , ( ∂t ) z = ⎰ j z dV r r r即 dP = ⎰ j (x ' , t )dV ' dt Vrr m r ⨯ r m r ⋅ r 6. 若m 是常矢量 证明除 R 0 点以外 矢量 A = 的旋度等于标量ϕ =的梯R 3 R 3度的负值 即∇ ⨯ r= -∇ϕ其中 R 为坐标原点到场点的距离 方向由原点指向场点证明∇ ⨯ A v = ∇ ⨯ ( m v ⨯ R v ) R3 = -∇ ⨯[⎰ ' m v ⨯ (∇ 1 )] = (∇ ⋅ m v )∇ 1 + (m v ⋅ ∇ )∇ 1 -[∇ ⋅ (∇ 1)]m v - [ (∇ 1) ⋅ ∇]m v R r r r rS⎰= (m v⋅ ∇)∇ 1 , (r ≠ 0)r ∇ϕ = ∇ m v ⋅ R v = -∇ v ⋅ ∇ 1 = - v ⨯ ∇ ⨯ ∇ 1 - ∇ 1 ⨯ ∇ ⨯ v - v ⋅ ∇ ∇ 1 ( ) [m ( )] R 3 r m [ ( )] ( ) ( r r m ) (m )r - [(∇ 1) ⋅ ∇]m v = -(m v⋅ ∇)∇ 1r r ∴∇ ⨯ A v= -∇ϕ7有一内外半径分别为 r 1 和 r 2 的空心介质球 介质的电容率为ε使介质内均匀带静止自由电荷 ρ f求1 空间各点的电场2 极化体电荷和极化面电荷分布r r解 1 ⎰ D ⋅ dS = ⎰ ρ f dV , (r 2>r>r 1)即 D ⋅ 4πr 2 = 4π(r 3 - r 3)ρ31 fr (r 3 - r 3)ρ r∴ E =13εr 3r , (r 2 > r > r 1)r r Q f4π33由 E ⋅ dS =Sε 0 = 3ε (r 2 - r 1)ρ f , (r > r 2 )r (r 3 - r 3) r∴ E = 2 1ρ f r , (r > r 2 )3ε 0r 3 r r < r 1时 E r r 2)ε - ε 0 r r P ε 0χ e E = ε 0 0E = (ε - ε 0 )E∴ ρ = -∇ ⋅ r= - ε - ε ∇ ⋅ r= - ε - ε∇ ⋅ (r 3- r 3) ρ r= -ε - ε 0 ρ ∇ ⋅ r - r 3 rPP (0 )E () [ 1 0 3εr 3 f r ] 3ε f(r 1 r ) r 3= - ε - ε 0 ρ 3ε f σ P = P 1n - P 2n(3 - 0) = -(ε - ε 0 )ρε f考虑外球壳时 r r 2 n 从介质 1 指向介质 2 介质指向真空P 2n = 0f0 ε2 1S2 1 μσ P = P 1n = (ε - ε r 3 - r 3 0 ) 1 ρ 3εr 3 f r r r =r = (1 - ε 0ε r 3 - r 3 ) 2 1 ρ f3r 3考虑到内球壳时 r r 2σ P = -(ε - ε r 3 - r 3 0 ) 1 ρ 3εr 3f r rr =r = 08 内外半径分别为 r 1 和 r 2 的无穷长中空导体圆柱 沿轴向流有恒定均匀自由电流 J f 导体的磁导率为μ 求磁感应强度和磁化电流 解r r d r r⎰l H ⋅ dl = I f + dt ⎰ D ⋅ dS =I f r r当r < r 1时, I f = 0,故H = B = 0r r r r 2 2当 r 2>r>r 1 时⎰lH ⋅ dl = 2πrH = ⎰Sj f ⋅ dS = j f π (r - r 1 )v μj f (r 2 - r 2 )μ(r 2 - r 2 ) rrB =1=2r12r 2j f ⨯ r当 r>r 2 时2πrH = πj f (r 2 - r 2)r μ0 (r 2 - r 2 ) r rB = 21 2r 2rrj f ⨯ rμ - μ0 ) rμrr r 2 - r 2J M = ∇ ⨯ M = ∇ ⨯ (χ M H ) = ∇ ⨯ ( 0)H = ( 0- 1)∇ ⨯ ( j f ⨯ r1)2r 2= (μ - 1)∇ ⨯ r= (μ - 1) rj , (r < r < r )H f 1 2αr= n r ⨯ r -r从介质1指向介质 M(M 2 M 1 ), (nμr 2 - r 2在内表面上 M 1 = 0, M 2 = ( - 1)1 ) r =r = 0r 故αr M= n r ⨯ μ0= 0,(r = r 1) 2r 21在上表面 r r 2 时αr= r⨯ - r = - r ⨯ rr rr 2 - r 2 r ⨯ r= - r 2 - r 2 rμ -Mn ( M 1 ) n M 1 r =r= - ⨯ 1 j f r 2r 2r r =r 1 j f 2r (1)2 μ02 2rμμ μ M 22μr 2-r 2r=-( -1)21j fμ02r 24π l r r = F ⋅ ⎰⎰ ⎰⎰ 12 ⎰9证明均匀介质内部的体极化电荷密度 ρ 总是等于体自由电荷密度 ρ 的- (1 -ε 0)倍Prr rfερ fε 0证明ρ P = -∇ ⋅ P = -∇ ⋅ (ε - ε 0)E = -(ε - ε 0 )∇ ⋅ E = -(ε - ε 0 ) ε= -(1 - ε)ρ f10 证明两个闭合的恒定电流圈之间的相互作用力大小相等 方向相反(但两个电流元之间的相互作用力一般并不服从牛顿第三定律) 证明1 线圈 1 在线圈2 的磁场中的受力vμ v ⨯ r vdF v B 2 = 0 ⎰ 2 = v ⨯ B v I 2dl 2 1231212 I 1dl 1 2v μ v ⨯ v ⨯ r v) μ I Iv ⨯ r⨯ r v) ∴ F 12 = 0 I 1dl 14π (I 2dl 2 r 3 12 = 0 1 2 4π ⎰⎰dl 1 (dl 2 12r 3 l 1 l212 = μ0 I 1I 2v v r v 4π 2 1 r 3r vv r 3 1l 1 l 2 12v2dl (dl ⋅ 12) - l 1 l 21212(dl 12⋅ dl )12 线圈 2 在线圈 1 的磁场中受的力 同 1 可得vμ0 I 1I 2 v 21 4π 1 v r v 2 r 3 r v v v r 3 2 1 F = dl (dl l 2 l 1⋅ 21 ) - 21 21 (dl 21⋅ dl ) 2分析表达式 1 和 21 式中第一项为v v ⋅ r v ) = vv ⋅ r v=v dr=v⋅ - 1) = 0⎰⎰ dl 2 l 1 l 2(dl 1 312⎰ dl 2 ⎰ l 2dl 1v12 3 12l 2v r vdl 2 ⎰ 2l 112⎰ dl 2 (l 2一周12⎰⎰ 12 r3同理 对 2 式中第一项dl (dl l 2 l 1⋅ 21 ) = 0 21v v 12 21 = - μ0 I 1I 2 4π r r v v⎰⎰ r 3 1 212 (dl dl )l 1 l 2 1211. 平行板电容器内有两层介质 它们的厚度分别为 l 1 和 l 2 电容率为ε1和ε 2 接上电动势为E 的电池 求1 电容器两板上的自由电荷密度ω f12 r ⎰⎰ r∴ F r今再两板0 f ⎩ f2 介质分界面上的自由电荷密度ω f若介质是漏电的 电导率分别为σ1和σ 2 何当电流达到恒定时 上述两问题的结果如 解 在相同介质中电场是均匀的 并且都有相同指向⎧l 1E 1 + l 2E 2 = E 则⎨D - D = εE - ε E = 介质表面上σ = ,⎩ 1n故 E =2nε 2E 1 1 2, E =2ε1Ef0) l 1ε 2 + l 2ε1l 1ε 2 + l 2ε1又根据 D 1n - D 2n = σ fn 从介质 1 指向介质 2在上极板的交面上D 1 - D 2 = σ fD 2 是金属板 故 D 2 0即σ = D =ε1ε 2εf 11而σ = 02l 1ε 2 + l 2ε1σ f = D ' - D ' = -D ' , (D '是下极板金属 故D ' = 0)31∴σ = - 2ε1ε 2ε2 1 1= -σ3l 1ε 2 + l 2ε11若是漏电 并有稳定电流时r r j r r jE 1 = σ1 , E 2 = σ212⎧ r j rj r ⎪l 1 1 + l 22= E 又⎨ σ 1 σ 2⎪ j 1n = j 2n = j 1= j 2 , 稳定流动 电荷不堆⎧E = j 1 =σ 2E得 j = j =E⎪ 1 σ ,即: ⎨1l 1σ 2 + l 2σ11 2l 1l 2jσ E+ ⎪E 2 = 2 = 1σ1 σ 2⎛⎪ σ 2 l 1σ 2 + l 2σ1σ = D =ε1`σ 2Eσ = -D = -ε 2σ 1E f 上3l 1σ 2 + l 2σ 1f 下2l 1σ 2 + l 2σ1112f1 1 12 1 2 0 σ = D - D = ε 2σ 1 - ε 2σ1 Ef 中2l 1σ 2 + l 2σ 112. 证明1 当两种绝缘介质得分界面上不带面自由电荷时 电场线的曲折满足tan θ 2 tan θ1 = ε 2ε1其中ε1和ε 2 分别为两种介质的介电常数 θ1和θ 2 分别为界面两侧电场线与法线的夹角 2 当两种导电介质内流有恒定电流时 分界面上电场线曲折满足tan θ 2 tan θ1 = σ 2σ1其中σ1和σ 2 分别为两种介质的电导率证明 (1)根据边界条件 n ⨯ (E v - E v) = 0,即 E 2 sin θ 2 = E 1 sin θ1由于边界面上σ = 0 故n v ⋅ (D v- D v ) = 0 即ε E cos θ= ε E cos θ∴有tg θ 2 ε 2 f= tg θ1 ,即 ε1 tg θ 2 tg θ1 2=ε 2 ε11 2 221 11(2)根据 J v = σE v可得 电场方向与电流密度同方向由于电流 I 是恒定的 故有j 1 cos θ 2 = j 2cos θ1即 σ 1E 1 cos θ 2 =σ 2 E 2cos θ1而 n v ⨯ (E v- E v ) = 0 即 E 2 sin θ 2 = E 1 sin θ1tg θ 故有tg θ 2=σ 1σ 213 试用边值关系证明 在绝缘介质与导体的分界面上 在静电情况下 导体外的电场线总是垂直于导体表面 在恒定电流的情况下 导体内电场线总是平行于导体表面 证明 1 导体在静电条件下达到静电平衡∴导体内E v而n v ⨯ (E v - E v) = 0∴ n v ⨯ E v= 0 故 E v 垂直于导体表面3 2 2 12 2 2 1 f 1 0 1 1 J r r ∂ r r r r re 3 导体中通过恒定电流时 导体表面σf = 0∴导体外 E v = 0,即 D v= 0而n v ⋅ (D v - D v ) = σ = 0,即: n v ⋅ D v = n v ⋅ ε E v= 0∴ n v ⋅ E v = 0导体内电场方向和法线垂直 即平行于导体表面14 内外半径分别为 a 和 b 的无限长圆柱形电容器 单位长度电荷为λ f为σ 的非磁性物质板间填充电导率1 证明在介质中任何一点传导电流与位移电流严格抵消 因此内部无磁场2 求λ f 随时间的衰减规律3 求与轴相距为 r 的地方的能量耗散功率密度4 求长度为 l 的一段介质总的能量耗散功率 并证明它等于这段的静电能减少率1 证明 由电流连续性方程 ∇ ⋅r + ∂ρ f = 0∂t r据高斯定理 ρ f = ∇ ⋅ D ∴∇ ⋅ r + ∂∇ ⋅ r = ∇ ⋅ r + ∇ ⋅ ∂ r=DD J ∂t 0 即 J ∂t∴∇ ⋅ r + ∂ r = ∴ r + ∂r =(JD) 0. J ∂tD ∂t0 即传到电流与位移电流严格抵消(2)解 由高斯定理得⎰ D ⋅ 2πrdl = ⎰ λ f dl∴ r λ f r r λ f rD = 2πr e r ,E = 2πεr e rr D 又 J + ∂t= 0, J = σE , D = εEr r r r =σ t∴σE + ε ∂E= 0, E = E e ε∂t 0λ f r λr-σ tr∴ 2πεr e r= 0 e ε2πεr rf = f λ r∴ λ f -σ t= λ e ε 03 解r r λ f -σ t λ fJ = - ∂D = - ∂ ( 0 e ε ) = σ ⋅∂t ∂t2 2πr21 ε 2πrf 2能量耗散功率密度 J5 解ρ = Jσ = ( 2πεr ) σ单位体积dV = l ⋅ 2πrdrP ⎰a λ f ( 2πεr )2σl 2πrdr = l σλ2 2πε 2 ln b ab1 r r b 1 l λ2 1 l λ2b 静电能 W = ⎰ D ⋅ EdV = ⎰f dr = ⋅ f⋅ ln a 2 a 2 2πεr 2 2πε a减少率 - ∂W = - l λ f ln b ⋅ ∂λ f l λ2 σ = ln b ∂t 2πε a ∂t 2πε 2 ab fP 00 E 外 r ⋅1.一个半径为 R 的电介质球 极化强度 P=K(1)计算束缚电荷的体密度和面密度 (2)计算自由电荷体密度(3)计算球外和球内的电势(4)求该带电介质球产生的静电场总能量解 (1) r r2 电容率为ρ = -∇ ⋅ r = -K ∇ ⋅ rr = -K (∇ 1 ⋅ r r + 1 ∇ ⋅ r r) = -K / r 2Pσ = -n r ⋅ Pr (P 2 r 2rP 1) Rr 2r 2又 球外无极化电荷r r r r P 2 = 0 σ p = n ⋅ P 1 R = n ⋅ K r rR = K / R(2) 由公式 D = εEr r r D = ε 0 E + Prε r D = Pε - ε 0ρ = ∇ ⋅ r = ε ∇ ⋅ r = εK`fDε - ε P(ε - ε )r 2(3)对于球外电场 由高斯定理可得rr Q⎰E 外 ⋅ ds = 0εK⋅ r 2 sin θdrd θd ϕr ⋅ 4πr 2 = ⎰ ρ fdVε 0 ⎰⎰⎰ (ε - ε= 0)r 2ε 0∴rεKR rE 外 03 r(ε - ε 0 )rrKr r同理可得球内电场 E 内ε - ε 2 ∞rrεKR∴球外电势ϕ外⎰ E外⋅ dr∞ε 0 (ε - ε 0 )rrrr2 - ∴ ε ε2 a 0 0rr Rrr εKK R球内电势ϕ内⎰ E外⋅ drR⎰ E内⋅ drr ε 0 (ε - ε 0 +ln) ε - ε 0 r1 r r 1 ε K r r K rr εK 24 ω 内2 D 内⋅ E 内2 ⋅ ε ε ⋅ r 2 ⋅ ε ε ⋅ r 2 ∴ ε ε 0 r∴1εK 22K2W 内 ⎰ω内d V⎰⎰⎰ 2 ⋅ (ε - ε ⋅ r )2r2sin θdrd θd ϕ 2πεR)ε - ε 01 ε2 K 2 R 2 1 2 2πε 2 RK 2W 外 ⎰ω外d V = ⎰⎰⎰R 2 ⋅ ε (ε - ε 0 ⋅ ⋅ r )2 r 4sin θdrd θd ϕε 0 (ε - ε 0 )∴W = W 内 W 外 2πεR (1 + ε)(ε 0 K )2ε - ε 02 在均匀外电场中置入半径为 R 0 的导体球 试用分离变数法球下列两种情况的电势1 导体球上接有电池 使球与地保持电势差φ0 ;2 导体球上带总电荷 Q.解 1 当导体球上接有电池 与地保持电势差φ0 时 以地为电势零点本问题的定解条件如下φ 内 φ0R= R 0∇ 2ϕ0 R> R 0⎧⎪ϕ外 且⎨R →∞ = -E 0 R cos θ ϕ 0 ϕ 0 是未置入导体球前坐标原点的电⎜⎩ϕ外R =R 0 = φ0根据有关的数理知识 可解得ϕ外 ∑ n b nR n 1P n cos θ )由于ϕ R →∞= -E 0 R cos θ n 0ϕ 0 即ϕa + a R cos θ + ∑ a R n P (cos θ ) +b 0 + b 1 cos θ + ∑b nP (cos θ ) = -E R cos θ + ϕ外0 1 n n n =2 R R 2 n =2 Rn +1 nR →∞故而有 a 0 = ϕ 0 , a 1 = -E 0 , a n = 0(n > 1), b n = 0(n > 1)∴ϕ外 ϕ 0 E 0 R cos θb 0 +b 1RR 2∞ 外外 外∞ ∞∞20 0 2 R ncosdsR ϕ R R φ 0R R R 2 0 ⎨ 2 2s ∑ 2 2 3又ϕ外R =R 0= φ0 ,即 ϕ外 R =R 0= ϕ 0 - E 0 R cos θb 0 + R 0 b 1cos θ = φ 0故而又有⎧+ b 0 ∴⎪ R 0= φ0⎪- E R⎜⎩0 0cos θ + b 1 cos θ = 0 0得到b 0 = (φ0 - ϕ 0 )R 0 , b 1 = E 0 0最后 得定解问题的解为(φ - ϕ )R E R 3 ϕ = -E R cos θ + ϕ + 0 0 0 + 0 0cos θ (R > R ) 外 0 0R R2 当导体球上带总电荷 Q 时 定解问题存在的方式是⎧∇ 2φ 0(R < R )⎪ 内0 ⎪∇ 2φ ⎪φ 0(R > R 0 ) 有限⎪ 内 R →0 ⎪ ⎨ 外 R →∞ ⎪E 0Rcos θ + ϕ 0 (ϕ 0 是未置入导体球前坐标原点的电 ⎪φ内 ⎪ ⎪- εφ 外 R R ∂φ外 Q (R = R )⎩⎰ 0∂R解得满足边界条件的解是ϕ内 ∑ a n n =0R nP cos θϕ外 ϕ 0E 0Rcos θ b n Pn =0 R n 1cos θ由于ϕ外R →∞ 的表达式中只出现了 P 1 (cos θ cos θ项 故 b n = 0(n > 1)∴ϕ外 ϕ 0E 0 R cos θb 0 + b 1R R 2cos θ又有ϕ外R =R 是一个常数 导体球是静电平衡ϕ外 R =R 0= ϕ 0 - E 0 R 0cos θb 0 + R 0 b 1cos θ = C 0∴-E 0 R 0 cos θ +b 1 cos θ = 0 即 0b 1 = E 0 0 n 0 外 0 nf4πεR∴ r r r0 0b E R 3ϕϕE R cos θ + 0 + 0 0 cos θ 外R R 2∂φ外Q又由边界条件- ⎰ε 0s∂r ds Q ∴ b 0 =4πε∴ϕ内Q4πε 0 R 0 - ϕ 0, R < R 0QE R 3ϕ 外4πε R + 0 0 cos θ R 2E 0Rcos θ R > R 03 均匀介质球的中心置一点电荷Q f 球的电容率为ε球外为真空 试用分离变数法求空间电势 把结果与使用高斯定理所得结果比较 提示 空间各点的电势是点电荷Q 的电势Q f与球面上的极化电荷所产生的电势的叠加 后者满足拉普拉斯方程解 一. 高斯法在球外 R > R ,由高斯定理有εr ⋅ r = QQ + Q = Q对于整个导体球而言 束缚电荷Q P = 0)⎰ E ds总 f P fE = Q f4πε 0R 2积分后得ϕQ f+ C .(C 是积分常数外4πε R又由于ϕ外 R →∞ = 0,∴ C = 0∴ϕ外 =Q f 4πε 0 R(R > R 0 )在球内 R < R 0 ,由介质中的高斯定理⎰ D ⋅ ds = Q fr r r Q f又 D = εE ,∴ E =4πεR 2积分后得到 ϕ内Q f 4πεRC 2.(C 2是积分常数 00 R 2 0由于ϕ内 ϕ外R =R 0,故而有Q f4πε 0 R 0 =Q f 4πεR 0C 2∴ C 2 =Q f 4πε 0 R 0- Q f4πεR 0 (R < R 0 ).∴ϕ内Q f 4πεR Q f 4πε 0 R 0 - Q f4πεR 0(R < R 0 )二. 分离变量法本题所求的电势是由点电荷Q f 与介质球的极化电荷两者各自产生的电势的叠加 且有着球对称性 因此 其解可写作ϕ = Q f+ ϕ '4πεRb由于φ ' 是球对称的 其通解为 ϕ ' = a +RQ f由于球心有Q f 的存在 所以有ϕ内 R →0 ∞即ϕ内4πεR a在球外有ϕ 外 R →∞ 0 即ϕ外Q f b 4πεR R由边界条件得ϕ 内 ϕ外 R R 0, 即Qf+ a 4πεR 0Q f + b4πεR 0 R 0ε ∂ϕ 内 ε ∂R 0R R 0 , 即ε 0Q f 4πεR 2 - ε 0b = - 0 εQ f4πεR 2∴ b =⎧ϕ Q f1 4πε (ε Q f - 1 ), a ε , R > R Q f ( 1 4πR 0 ε 0 - 1 ) ε ⎪ 外 4πε R ∴⎨⎪ϕ Q fQ f - Q f, R < R⎛⎜ 内 4πεR 4πε 0 R 0 4πεR 0∂ϕ外 ∂R0 0∂φ外∂R⋅R R 0 R R R 0R ⋅ 0 0⋅ ⋅ ⋅ f 11 0 011r R 1 r R r r 14 均匀介质球 电容率为ε1r 的中心置一自由电偶极子 P f球外充满了另一种介质 电容率为ε 2求空间各点的电势和极化电荷分布提示 同上题r r P R φ =4πε 3+ φ ' ,而φ ' 满足拉普拉斯方程解 ε1 ∂φ内 ∂R = ε 2∂φ外∂R2P f cos θl 1又ε1 R = ε1 (-4πε13 + ∑l A l R 0 P lε = ε (- 2P f cos θ - ∑(l 1 B l P 2R 02 4πε3 l 2l比较 P l (cos θ )系数B 0 0A 0 02ρ f + ε A = -2ε 2ρ f - 2ε 2 B 1 , 及A= B 14πR 31 14πε1 3332(ε1 - ε 2 )ρ f 2(ε1 - ε 2 )ρ f 得 A 1 =4πε1 (ε1 + 2ε2 )R 3, B 1 =4πε (ε1 + 2ε 2)比较 P 2 (cos θ )的系数2ε A R3B 2, A = B 21 2 04 2 4 0 0及 A 2 (1 +ε R) = 0 1 0所以 A 2 = 0, B 2 = 0 同理 最后有A l =B l = 0,(l = 2,3L )φ ρrf R + 2(ε1 - ε 2 )ρ f R cos θ = ρr f r 2(ε + 1 - ε 2 )ρr f r R , (R < R ) 内 4πε R 3 4πε1 (ε1 + 2ε 2 )R 3 4πε1R 3 4πε1 (ε1 + 2ε 2 )R 3 0 φ ρr f R + 2(ε1 - ε 2 )ρ f cos θ = ρr f r 2(ε + 1 - ε 2 )ρr f R = 3ρr f R , (R > R ) 外 4πε R 3 4πε1 (ε1 + 2ε 2 )R 2 4πε1R 3 4πε1 (ε1 + 2ε 2 )R 3 4π (ε1 + 2ε 2 )R 3 0 ∂φ内∂R R R R ⋅ ⋅ ⋅ 10 00 0 0= ⎪ φ φ Pfε 3 ⎨ 22 ⎪球面上的极化电荷密度σ P = P 1n - P 2n , n r从 2 指向 1 如果取外法线方向 则 σ p = P 外n - P 球n = [(ε 2 - ε 0)∇φ外)]n - [(ε1 - ε 0)∇φ内)]n= -(ε 2 - ε 0 ) ∂φ外 + (ε ∂R 1- ε 0 ) ∂φ内∂R R R 0 = (ε - ε ) - 6ρ f cos θ - (ε - ε )[ 6(ε 0 - ε 2 )ρ f cos θ - 2(ε1 - ε 2 ) - 2(ε1 + 2ε 2 ) ρcos θ ]2 0 4π (ε + 2ε 2 )R3 1 0 4π (ε + 2ε 2 )R 3 4πε1 (ε1 + 2ε 2 )R 3 f=6ε1(ε 0 - ε 2 ) + 6ε 2 (ε1 - ε 0) ρ cos θ = - 3ε 0 (ε1 - ε 2 ) ρ cos θ4πε1 求极化偶极子(ε1 + 2ε 2 )R 3 f 2πε1 (ε1 + 2ε 2 )R 3f rr P f ql 可以看成两个点电荷相距 l 对每一个点电荷运用高斯定理 就得到在每个点电荷旁边有极化电荷q = (ε 0- 1)q ε1 ,-q P = (ε 0- 1)(-q )ε1两者合起来就是极化偶极子rε 0rP P = ( - 1)P f1r5.空心导体球壳地内外半径为 R 1 和 R 2 球中心置一偶极子 P 电势和电荷分布解球壳上带电Q 求空间各点 ⎧ ⎪∇2φ= 0,φ φ 3 r →∞ = 0 ⎪= C ,φ ⎪ r rr →0 = ∞ φ ⎪φ = P ⋅ r + φ ',φ ' 为有限值⎛⎜ 14πε 0r 3 1 1 r →0⎧ ⎪φ3 ∑ B l P (cos θ ),φ = C ⎪ r l +1 ⎨ 2= C ,φ2 2r =R 1 = C ⎪⎪φ = r ⋅ r r + ∑ A r l P (cos θ ) -∂φ3dS+∂φ1dS=Ql l R 23 φ 1 R 1l 3 r -R 1 1 fP f⎩ ⎪ 14πε0r3 ⎰ ∂rr =R 2⎰ ∂rr =R 1εR P R R 1R R R 2 R 3R R R R ⎪ ⎩1 1 1 ⎪ f111 R 11Q 0 0 1 1 1⎧ B 0 +B 1 cos θ + B2 P+L = C ⎪ 2 ⎪ 2 2 ⎨ cos θ + A 3 2 + A R 2 cos θ +L = C ⎜⎩ 4πε 0 20 1 1即 A =B 0 =C ,( A R +P f) cos θ = 0, B = 0(l = 1.2.3L ), A= 0(l = 2.3.4L )1 14πεR 2 ll又 ∂φ1 = - 2P f cos θ + ∑lA R l -1P = - P f cos θ + A cos θ +L ∂r 4πε 0 3 l 1 L 2πε 0 3 ∂φ3∂r = ∑(-l - 1) B l P r l +2 l = - B 0 1 - 2 B 1 cos θ +L 1∂φ3 B 0 B 02 B 0则 -⎰ ∂r dS = ⎰ R 2 dS = R 2 ⎰ dS = 4πR 12 = 4πB 0111∂φ1dS =2π π-P fcos θR 2 sin θd θd ϕ +2π π- P f cos θR 2 sin θd θd ϕ = 0 + 0 = 0 ⎰ ∂r⎰0 ⎰02πε0 3 ⎰0 ⎰04πε0 3故 - ⎰ ∂φ3dS + ∂r ∂φ1 ∂r = 4πB 0 = εB = Q 0, A = Q , A = - P f 0 4πε 0最后有0 4πε R 1 4πε 3 ⎧r r r r ⎪φ = P ⋅ r - P f ⋅ r + Q , (r < R ) ⎪4πε 0r 2 4πε 0 3 4πε 0R 2 ⎪ Q⎨φ3 =4πε , (r > R 2 ) 0 ⎪ Q ⎜φ2 = 4πε 电荷分布 0 R 2, (R 1 < r < R 2 )在 r R 1 的面上σ P 1 = ε 0 ∂φ1 ∂r = - P f cos θ 2πR 3+ - P f cos θ 4πR 3 = - P f cos θ 4πR 3在 r R 2 面上0 R R 21 11⎰ 2 1r2=-ε0∂φ3∂r=Q4πR 22σPrφ l r →∞0外 φ R R R ⎣ R l +2 ⎪ 外 ⎪⎧232 06 在均匀外电场 E 0 中置入一带均匀自由电荷 ρ f 的绝缘介质球ε 求空间各点的电势⎧∑( A r l + ⎪ B lr l +1 )P l (cos θ ) 解 ⎪φ1 ρ r2 + φ '⎨ 内 6εf⎪∇ 2φ ' = 0 ⎪⎩φ 是由高斯定理解得的ρ 的作用加上 r的共同作用内φ = -E r cos θ ,φ 'fE 0r →0 有限⎪ 外 E 0r cos θ + ∑ ⎨ 1 B l r l +1 P l (cos θ ) ⎪φ ρ r 2 + ∑c r l P (cos θ )⎛⎪ 内 6ε f e lφ内 φ外 r = R 0 ) :E R cos θ +B 0 + B 1+B 2P +1ρ R 2 + c+ c R cos θ + c R 2 P +0 0ρ f2R 0 R 0B 06εf1 02 0 2 即6εR 0 + c 0 =E 0 R 0 +2 = c 1R 0 0B 2 = c 2ε ∂φ内 ∂r = ε 0∂φ外 ∂r ∂φ内 =⎡ ρ f R +lc R l -1P (cos θ )] =ρ fR+εc cos θ + 2εc R P +L ∂r⎢ 3ε∑l 0 l 30 1 2 0 2∂φ外 ∂r= ε 0(-E 0 cos θ + ∑(-l - 1) B l P l) 0R R 3 2B 1R R R R R R 0 RR r →∞ f 3 R 40 11 ⎪φ 3 0 外- ε E cos θ -ε0B 0 -2ε0B 1cos θ -3ε0B 2 P +LL0 023 42ρ fε 0 B 02ε 0 B 13ε 0 B 2即R 0 = - 2εC 1 = -ε 0 E 0 - 32εC 2 R 0 = - LL解方程得3B = - 0ρ 03ε fC = -R 2ρ ( 1 3ε 0 + 1 ) 6ε3ε E R 33ε E B = - 0 0 0 + E3 ε + 2ε 0C = -0 0ε + 2ε 0及 2εC 2 R 0 = -3ε 0 R 0C 2即 C 2 (2εR 0 + 3ε 0 R 0 ) = 0C 2 = B 2 = 0同理 C l = B l = 0l = 2,3LL⎧ E r cos θ ± R 3ρ + E 03 0 cos θ - 3ε 0 E 0 0cos θ , r > R ⎪外0 得 ⎨3r ε 0 r(ε + 2ε 0 )r 2 0 ⎪φ ρ f r 2 ± R 2 ρ ( 1 1 3ε 0 E 0 r cos θ , r < R⎛⎜ 内 6ε0 f 3ε 6ε ε + 2ε 27在一个很大的电解槽中充满电导率为σ 2 的液体 使其中流着均匀的电流δ f 0今在液体中置入一个电导率为 σ 1 的小球 求稳衡时电流和电荷分布 讨论 σ 1 >> σ 2 及σ 2 >> σ 1 两种情况的电流分布特点先求空间电势⎧⎪∇ 2φ 0⎨ φφr = R⎜⎩∇ 2φ 0 内外因为δ内nδ 外n (r = R 0 ) 稳恒电流认为表面无电流堆积 即流入n = 流出n故 σ 12φ内2r = σ 2 2φ外2r并且δ 外 = δ 0即 φ外 r →∞ = -E 0r cos θ( j = σ 2E 0 )φ内 r →∞ 有限 可以理解为在恒流时r → 0 的小封闭曲面流入 流出内0 R ff 23σ 2 σ 1 2σ 2 ⎦内 E f fj 1 σ 1 2 ⎣ σ 1 内 j σ E f σ 1 2σ 1 2⎧φE r cos θ , r < R⎪ 内这时的解即为 ⎨⎪φ E r cos θ + E R 3 ( σ 1 - σ 2 )cos θ, r > R ⎛⎜ 外 00 0 1 + 2σ 2 r 2φe r 2φe r 1 2φ r求内外电场 E = -∇φ = -( r + θ +e φ )2r2θ r2φ e r1 2φ r 3σ 2r sin θ 2Φr rE(内 r +内e ) =E (cos θe - sin θe ) 内2r r 2θθσ 1 + 2σ 2= 3σ 2 σ1 + 2σ 2rE 0e r zrE R 3σ - σr rEE (cos θe - sin θe ) + 0 0 ( 12 )[2 cos θe + sin θe ] 外0 rθ r 3 σ 1 + 2σ 2rrE R 3σ - σr r rE (cos θe - sin θe ) + 0 0 ( 12)[3cos θe - cos θe + sin θe ] 0 r θ r 3 σ + 2σ 2r r θ σ - σ⎡3E cos θ vE v ⎤ E + R 3 ( 1 2 ) 0e - 00 0 + 2σ ⎢ r 3求电流r r 3 ⎥ 根据 r j v vv外 2 外⎧ v j ⎪ f 0 = σ 2 Ev 0 及⎨( v j ⋅ r r )r v σ E r cos θr r⎪ 0 = 2 0e r ⎩ r 53σ rr 5r σ σ 3( r j ⋅ r r )r r r得 j1j f , j= j12 R 3[ 0- 0 ]内2σ 0 外内2σ 0r 5r 3ω = ε (E - E ) = ε (E- E ) = 3ε 0E 0 cos θ (σ - σ )f2n1n外n 内nσ 1 + 2σ 2σ 20 0 r θ r θ 1 24πε a 2 + r 2 - 2ar cos θzQ far OR n r n ∞ R 0 8.半径为 R 0 的导体球外充满均匀绝缘介质ε导体球接地 离球心为 a 处(a > R 0 ) 置一点电荷Q f试用分离变数法求空间各点电势 证明所得结果与镜像法结果相同提示1 = 1 = 1 ∑∞( ) P (cos θ ).(R > a ) r 解 1 分离变数法由电势叠加原理 球外电势a n =0 aφ Q f外4πεR +φ ' ,φ ' 是球面上感应电荷产生的电势 且满足定解条件⎧∇ 2φ ' = 0,(r > R )⎪ 0⎨φ '⎪ r →∞ = 0 P⎪φ 外 r =R = 0⎩0 根据分离变数法得φ '= ∑ l =0B lr l +1 P l (cos θ ), (r > R 0 )∴φQ f1+ ∑ B lP (cos θ )*外l =0rl +1 l= Q f 1 ∑∞ ( ) P (cos θ ) + ∑ B l P (cos θ ), (r < a ) 4πε a∞ n =0 a Q f n R 0 l l =0 B lrl +1 l又φ外 r =R =∑[ πε () +l +1]P l (cos θ ) = 0n =04 a aR oQ f即4πεa + B 0 R 0= 0, Q f R 0 + B 1 4πεa a 2 = 0,..., Q f 4πεa ( R 0 )l + a B l l +1 0 Q fR 3Q f R 2l +1 Q f ∴ B = -R , B = - O , B = - 0 ,0 0 4πεa 1 a 4πεa la l 4πεa代入 * 式得解∞ R 2 + a 2 - 2aR cos θ ∞ 0R n= 0a 2 + r 2 - 2ar cos θR 2 + a 2 - 2Ra cos θQR 1aR 2 + 1 - 1cos θ R 4 2R 2 R a 2 a0 f Q QQ 1f 1QQ Q 02 镜像法如图建立坐标系 本题具有球对称性 设在球内r 处有像电荷Q ' , Q '代替球面上感应电荷对空间电场的作用 由对称性 Q '在 O Q 的连线上 P20 先令场点 P 1 在球面上 根据边界条件有Q f +Q' r r ' fr ' = 0,即 r f= - Q ' Q f = 常数将Q ' 的位置选在使∆ Q 'P O ∆ Q P O,则有r Q ' = R 0 常数为达到这一目的 令Q '距圆心为 rr a 0fr R R 2则0 = 0 , r = 0R 0 a ar 'Q ' 并有 = - r Q f= R 0 = 常数 a Q ' = -R 0Q f a 1 这样 满足条件的像电荷就找到了 空间各点电势为2φ外 = Q f 4πεr 1 + Q ' 4πεr 2 = 1 [ Q f - 4πε ], (r> a ).将分离变数法所得结果展开为 Legend 级数 可证明两种方法所求得的电势相等9 接地的空心导体球的内外半径为 R 1 和 R 2 在球内离球心为 a(a<R 0)处置一点电荷 Q用镜像法求电势 导体球上的感应电荷有多少 分布在内表面还是外表面 解 球外的电势及导体内电势恒为 0 而球内电势只要满足φ内 r R= 0即可因此做法及答案与上题同 解略φ内 =1 4πε 0 [ Q-]因为球外φ = 0故感应电荷集中在内表面 并且为 Q.R Q far 2 + ( 0 )2 + 2r 0 cos θRR 2a aR 1R 2 rz Q fQ ’P 1Q Rf R R 1φ -Q 210.上题的导体球壳不接地 而是带总电荷 Q 0,或使其有确定电势ϕ0 势 又问ϕ0 与 Q 0 是何种关系时 两种情况的解是相等的试求这两种情况的电解 由于球壳上有自由电荷 Q 0 并且又是导体球壳 故整个球壳应该是等势体 其电势用 高斯定理求得为Q + Q 04πε 0 R 2所以球壳内的电势将由 Q 的电势 像电荷- QR1 a的电势及球壳的电势叠加而成 球外电势利用高斯公式就可得故⎧ ⎪φ = 1 [ Q - QR 1a + Q + Q 0 ].(R < R ) ⎪ 内 4πεR 2 + a 2 - 2Ra cos θ R 4 2R 2 R R 1 φ =⎪ 0R 2 + 1 - 1 cos θ2⎨ ⎪ ⎪φ = Q + Q 0 , (R > R )a 2a⎛⎜ 外 4πε 0 R⎧ ⎪φ = 1 [ Q - QR 1a] + φ.(R < R )⎪ 内 4πεR 2 + a 2 - 2Ra cos θ R 4 2R 2R 或 φ =⎪0R 2 + 1 - 1 cos θ⎨ ⎪⎪ = R 2 φ ⎩ 外r 0 , (R > R 2 ) a 2a当 φ =Q + Q 0 时两种情况的解相同4πεR 211 在接地的导体平面上有一半径为 a 的半球凸部 如图 半球的球心在导体平面上点电荷 Q 位于系统的对称轴上 并与平面相距为 b b>a 试用电象法求空间电势 解 如图 利用镜像法 根据一点电荷附近置一无限大接地导体平板和一点电荷附近置一接地导体球两个模型 可确定三个镜像电荷的电量和位置 2PQ- a Q R Q = - a Q , r = a rr b1b 1ab Oa a 2 rQQ 2 = b Q , r 2 = - brbQ 3 = -Q , r 3 = -br rφ =Q [ 4πε 0 1 - R 2 + b 2 - 2Rb cos θ1 +R 2 + b 2 + 2Rb cos θ b a2+ a 4 + a 2b 2 bR cos θ⎪ 2 01Rb R +- 2 R cos θ 2a 4 a2b 2 b(x - x )2+ (y - a )2 + (z - b )2 0 (x - x )2 + ( y - a )2 + (z + b )20 (x - x )2+ (y + a )2+ (z - b )20 (x - x )2+ (y + a )2+ (z + b )20 ∂ρ = 0 z∂trjA(x y z ) 0, 0, 0σxr jr= r E n E n+a], (0 ≤ θ < π , R > a )212. 有一点电荷 Q 位于两个互相垂直的接地导体平面所围成的直角空间内 它到两个平面的距离为 a 和 b 求空间电势解 可以构造如图所示的三个象电荷来代替两导体板的作用φ =Q[1-4πε 0 -1+1-1], ( y , z > 0)13.设有两平面围成的直角形无穷容器 其内充满电导率为 的液体 取该两平面为 xz 面和 yz 面 在 x 0,y 0,z 0 和 x 0,y 0,-z 0 两点分别置正负电极并通以电流 I 求导电液体中的电势解 本题的物理模型是 由外加电源在 A B 两点间建立电场 使溶液中的载流子运动形成电流 I,当系统稳定时 是恒定场 即∇ ⋅ r j + ∂ρ = 0 中 ∂t 对于恒定的电流 可按静电场的方式处理于是 在 A 点取包围 A 的包围面r rQI = ⎰ i r ⋅ d sr} 1r r⎰ E ⋅ ds =n而又有 i E ⋅σ⇒ σI = ⎰ E ⋅ ds y∴ 有 1 I = Q⇒ Q = I ε1σ ε1 σI εB(x 0,y 0,z 0)对 B Q Q B = -Q = -σ1又在容器壁上 rj = 0, 即元电流流入容器壁 由 r j = σ r 有 r j = 0 时 r ∴可取如右图所示电像z P(x, y, z) -Q(x 0,-a,b)aQ(x 0,a,b) by+Q(x 0,-a,-b)-Q(x 0,a,-b)Q(-x 0,-y z )Q(x 0,y 0,z 0)Q(x 0,-y z )Q(x 0,y 0,z 0)-Q(-x y z ) -Q(-x 0,y 0,-z )-Q(x 0,-y 0,z 0)-Q(x 0,y 0,-z )εn = 0 y。
《电动力学》简答题参考答案
《电动力学》简答题参考答案1. 分别写出电流的连续性方程的微分形式与积分形式,并简单说明它的物理意义。
解答:电流的连续性方程的微分形式为0J t ρ∂∇⋅+=∂K 。
其积分形式为d d d d S J S V t ρΩ⋅=−∫∫∫∫K K v 。
电流的连续性方程实际上就是电荷守恒定律的公式表示形式,它表示:当某区域内电荷减少时,是因为有电荷从该区域表面流出的缘故;相反,当某区域内电荷增加时,是因为有电荷通过该区域的表面流入的缘故。
2. 写出麦克斯韦方程组,并对每一个方程用一句话概括其物理意义。
解答:(1)f D ρ∇⋅=K 电荷是电场的源;(2)B E t∂∇×=−∂K K 变化的磁场产生电场; (3)0B ∇⋅=K 磁场是无源场;(4)f D H J t∂∇×=+∂K K K 传导电流以及变化的电场产生磁场。
3. 麦克斯韦方程组中的电场与磁场是否对称?为什么?解答:麦克斯韦方程组中的电场与磁场并不对称,因为电场是有源场,电荷是电场的源,而磁场是无源场,不存在磁荷。
4. 一个空间矢量场A K ,给出哪些条件能把它唯一确定?解答:由矢量场的唯一性定理:(1)位于空间有限区域内的矢量场,当它的散度,旋度以及它在区域边界上的场分布给定之后,该矢量场就被唯一确定;(2)对于无限大空间,如果矢量在无限远处减少至零,则该矢量由其散度和旋度唯一确定。
5. 写出极化电流与极化强度、磁化电流密度与磁化强度之间的关系式。
解答:极化电流与极化强度之间的关系式为P P J t ∂=∂K K ; 磁化电流密度与磁化强度之间的关系式为M J M =∇×K K 。
6. 简述公式d d d d d V V w V f V S tσ−=⋅+⋅∫∫∫v K K K K v 的物理意义。
解答:d d d Vw V t −∫表示单位时间区域V 内电磁场能量的减少,d V f V ⋅∫v K K 表示单位时间电磁场对该区域的电荷系统所作的功,d S σ⋅∫K K v 表示单位时间流出该区域的能量。
1.电动力学课后习题答案_第一章
电动力学课后习题答案第一章 电磁现象的普遍规律1． 根据算符∇的微分性与向量性，推导下列公式：B A B A A B A B B A )()()()()(∇⋅+⨯∇⨯+∇⋅+⨯∇⨯=⋅∇A A A A )()(21∇⋅-∇=⨯∇⨯A 解：（1）由∇的微分性质得()∇⋅A B 可以变成两项，一次对A 作用()∇⋅A A B ，一次对B 作用()∇⋅B A B 。
由∇的矢量性质，()=()()⨯∇⨯∇⋅-⋅∇B A B A B A B ，可得()=()+()∇⋅⨯∇⨯⋅∇B A B A B A B 。
同理()=()+()∇⋅⨯∇⨯⋅∇A A B B A B A ，则：()=()+()=()()()()∇⋅∇⋅∇⋅⨯∇⨯+⋅∇+⨯∇⨯+⋅∇A BA B A B A B B A B A A B A B综上，原式得证。
（2）在（1）的结论式里令=A B ，得A A A A A A )(2)(2)(∇⋅+⨯∇⨯=⋅∇，即： 21()()2A ⨯∇⨯=∇-⋅∇A A AA2． 设u 是空间坐标z y x ,,的函数，证明：u u f u f ∇=∇d d )( ， u u u d d )(A A ⋅∇=⋅∇， u u u d d )(AA ⨯∇=⨯∇ 解：（1）z y x z u f y u f x u f u f e e e ∂∂+∂∂+∂∂=∇)()()()(z y x z uu f y u u f x u u f e e e ∂∂+∂∂+∂∂=d d d d d d u uf z u y u x u u f z y x ∇=∂∂+∂∂+∂∂=d d )(d d e e e （2）z u A y u A x u A u z y x ∂∂+∂∂+∂∂=⋅∇)()()()(A zuu A y u u A x u u A z y x ∂∂+∂∂+∂∂=d d d d d d uu z u y u x u u A u A u A z y x z z y y x x d d )()d d d d d d (Ae e e e e e ⋅∇=∂∂+∂∂+∂∂⋅++= （3）()///()()()xy z x y z u xy z A u A u A u ∇⨯=∂∂∂∂∂∂e e e Az x y y z x x y z yu A x u A x u A z u A z u A y u A e e e ])()([])()([])()([∂∂-∂∂+∂∂-∂∂+∂∂-∂∂= z x y y z x x y z yu u A x u u A x u u A z u u A z uu A y u u A e e e )d d d d ()d d d d ()d d d d (∂∂-∂∂+∂∂-∂∂+∂∂-∂∂=d d u u=∇⨯A3． 设222)'()'()'(z z y y x x r -+-+-=为源点'x 到场点x 的距离，r 的方向规定为从源点指向场点。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第二章 静电场1. 一个半径为R 的电介质球，极化强度为2/r K r P =，电容率为ε。
（1）计算束缚电荷的体密度和面密度： （2）计算自由电荷体密度； （3）计算球外和球的电势；（4）求该带电介质球产生的静电场总能量。
解：（1）P ⋅-∇=p ρ2222/)]/1()/1[()/(r K r r K r K -=∇⋅+⋅∇-=⋅∇-=r r r)(12P P n -⋅-=p σR K R r r /=⋅==P e （2）)/(00εεεε-=+=P P E D 内200)/()/(r K f εεεεεερ-=-⋅∇=⋅∇=P D 内（3）)/(/0εεε-==P D E 内内rr frKRr Ve e D E 200200)(4d εεεεπερε-===⎰外外 rKRr)(d 00εεεεϕ-=⋅=⎰∞r E 外外)(ln d d 00εεεεϕ+-=⋅+⋅=⎰⎰∞r R K RR rr E r E 外内内（4）⎰⎰⎰∞-+-=⋅=R R rrr R K r r r K V W 42200222022202d 4)(21d 4)(21d 21πεεεεπεεεE D 20))(1(2εεεεπε-+=K R2. 在均匀外电场中置入半径为0R 的导体球，试用分离变量法求下列两种情况的电势：（1）导体球上接有电池，使球与地保持电势差0Φ； （2）导体球上带总电荷Q 解：（1）该问题具有轴对称性，对称轴为通过球心沿外电场0E 方向的轴线，取该轴线为极轴，球心为原点建立球坐标系。
当0R R >时，电势ϕ满足拉普拉斯方程，通解为∑++=nn n nn n P R b R a )(cos )(1θϕ 因为无穷远处 0E E →，)(cos cos 10000θϕθϕϕRP E R E -=-→ 所以 00ϕ=a ，01E a -=，)2(,0≥=n a n当 0R R →时，0Φ→ϕ所以 0101000)(cos )(cos Φ=+-∑+n nn nP R b P R E θθϕ 即： 002010000/,/R E R b R b =Φ=+ϕ所以 )2(,0,),(3010000≥==-Φ=n b R E b R b n ϕ⎩⎨⎧≤Φ>+-Φ+-=)()(/cos /)(cos 000230000000R R R R R R E R R R E θϕθϕϕ（2）设球体待定电势为0Φ，同理可得⎩⎨⎧≤Φ>+-Φ+-=)()(/cos /)(cos 000230000000R R R R R R E R R R E θϕθϕϕ当 0R R →时，由题意，金属球带电量Qφθθθϕθεϕεd d sin )cos 2cos (d 200000000R E R E S nQ R R ⎰⎰+-Φ+=∂∂-== )(40000ϕπε-Φ=R所以 00004/)(R Q πεϕ=-Φ⎩⎨⎧≤+>++-=)(4/)(cos )/(4/cos 00002300000R R RQ R R R R E R Q R E πεϕθπεθϕϕ3. 均匀介质球的中心置一点电荷f Q ，球的电容率为ε，球外为真空，试用分离变量法求空间电势，把结果与使用高斯定理所得结果比较。
提示：空间各点的电势是点电荷f Q 的电势R Q f πε4/与球面上的极化电荷所产生的电势的迭加，后者满足拉普拉斯方程。
解：（一）分离变量法空间各点的电势是点电荷f Q 的电势R Q f πε4/与球面上的极化电荷所产生的电势的迭加。
设极化电荷产生的电势为ϕ'，它满足拉普拉斯方程。
在球坐标系中解的形式为：）（）（内θϕcos 1n nn nn n P R b R a ∑++=' ）（）（外θϕcos 1n nn n n n P R dR c ∑++=' 当∞→R 时，0→'外ϕ，0=∴n c 。
当0→R 时，内ϕ'为有限，0=∴n b 。
所以 ）（内θϕcos n nn n P R a ∑=' ， ）（外θϕcos 1n nn nP R d ∑+=' 由于球对称性，电势只与R 有关，所以)1(,0≥=n a n )1(,0≥=n d n 0a ='内ϕ， R d /0='外ϕ 所以空间各点电势可写成R Q a f πεϕ40+=内R Q R d f πεϕ40+=外当0R R →时，由 外内ϕϕ= 得： 000/R d a =由 n n∂∂=∂∂外内ϕεϕε得：20002002044R d R Q R Q f fεπεεπ+=，)11(400εεπ-=f Q d 则 )11(4000εεπ-=R Q a f所以 ）（内εεππεϕ114400-+=R Q R Q f f ）（外εεππεϕ11440-+=R Q R Q f f RQ f 04πε=（二）应用高斯定理在球外，R>R 0 ，由高斯定理得：f p f Q Q Q Q d =+==⋅⎰总外s E 0ε，（整个导体球的束缚电荷0=p Q ），所以 r fR Q e E 204πε=外 ，积分后得：R Q dR RQ d fR R f 02044πεπεϕ⎰⎰∞∞==⋅=R E 外外 在球，R<R 0 ，由介质中的高斯定理得：f Q d =⋅⎰s E 内ε，所以r f RQ e E 24πε=内 ，积分后得：RQ R Q RQ d d f f f R R R0044400πεπεπεϕ+-=⋅+⋅=⎰⎰∞R E R E 外内内 结果相同。
4. 均匀介质球（电容率为1ε）的中心置一自由电偶极子f p ，球外充满了另一种介质（电容率为2ε），求空间各点的电势和极化电荷分布。
解：以球心为原点，f p 的方向为极轴方向建立球坐标系。
空间各点的电势可分为三种电荷的贡献，即球心处自由电偶极子、极化电偶极子及球面上的极化面电荷三部分的贡献，其中电偶极子产生的总电势为314/R f πεR p ⋅。
所以球电势可写成：314/'R f i i πεϕϕR p ⋅+=；球外电势可写成：31o o 4/'R f πεϕϕR p ⋅+=其中i 'ϕ和o 'ϕ为球面的极化面电荷激发的电势，满足拉普拉斯方程。
由于对称性，i 'ϕ和o 'ϕ均与φ无关。
考虑到0→R 时i 'ϕ为有限值；∞→R 时0'o →ϕ，故拉普拉斯方程的解为：)(cos 0R R P R a n nn n i ≤='∑）（θϕ )(cos 01oR R P Rb nn n n≥='∑+）（θϕ 由此 )(cos 4/031R R P R a R n nnn f i ≤+⋅=∑）（θπεϕR p （1） )(cos 4/0131o R R P R b R n n nn f ≥+⋅=+-∑）（）（θπεϕR p （2）边界条件为：0oR R R R i===ϕϕ （3）o 21R R R R i RR==∂∂=∂∂ϕεϕε （4）将（1）（2）代入（3）和（4），然后比较)cos θ（n P 的系数，可得：)1(0,0≠==n b a n n3211211)2(2/)(R p a f εεπεεε+-= )2(2/)(211213011εεπεεε+-==f p R a b于是得到所求的解为：)()2(2)(4)2(2cos )(4030211213132112131R R R R R R p Rf f f f i ≤⋅+-+⋅=+-+⋅=R p Rp R p εεπεεεπεεεπεθεεπεϕ)()2(43)2(2)(4)2(2cos )(403213211213122112131o R R R R R R p R f f f f f ≥+⋅=⋅+-+⋅=+-+⋅=εεπεεπεεεπεεεπεθεεπεϕR p R p R p R p 在均匀介质部，只在自由电荷不为零的地方，极化电荷才不为零，所以在球体部，只有球心处存在极化电荷。
fp ρεεεεεεεεερ)1/()1(][])[(101010101-=⋅∇-=-⋅-∇=-⋅-∇=⋅-∇=D D E P所以 f p p p )1/(10-=εε在两介质交界面上，极化电荷面密度为o 020121)()()(E e E e p p e ⋅--⋅-=-⋅=r i r r p εεεεσo 0201)()(R R iRR∂∂-+∂∂--=ϕεεϕεε由于0o 21R R i RR∂∂=∂∂ϕεϕε，所以θεεπεεεεϕϕεσcos )2(2)(3)(30211210o00R p R R f R i p +-=∂∂-∂∂= 5. 空心导体球壳的外半径为1R 和2R ，球中心置一偶极子p 球壳上带电Q ，求空间各点的电势和电荷分布。
解：以球心为原点，以p 的方向为极轴方向建立球坐标系。
在1R R <及2R R >两均匀区域，电势满足拉普拉斯方程。
通解形式均为）（）（θcos 1n nn nn n P R b R a ∑++ 当∞→R 时，电势趋于零，所以2R R >时,电势可写为）（θϕcos 1o n nn n P R b∑+= (1) 当0→R 时，电势应趋于偶极子p 激发的电势：20304/cos 4/R p R f πεθπε=⋅R p所以1R R <时，电势可写为）（θπεθϕcos 4cos 20n nn n i P R a R p ∑+=(2) 设球壳的电势为s ϕ,则s n nn nR P R b ϕθϕ==∑+）（cos 12o 2(3) s n nn n R iP R a R p ϕθπεθϕ=+=∑）（cos 4/cos 12101(4)由(3)得： 20R b s ϕ= ；)0(0≠=n b n由(4)得： s a ϕ=0 ；31014/R p a πε-= ；)1,0(0≠=n a n所以R R s /2o ϕϕ=(5)310204/cos 4/cos R pR R p s i πεθϕπεθϕ-+= (6) 再由 Q R R RR s S==⋅∂∂⎰2220o 04d πϕεϕεS 得： 204/R Q s πεϕ= (7)将(7)代入(5)(6)得：R Q 0o 4/πεϕ= )(2R R >)(414cos 44cos 312303102020R R Q R R pR R Q R p i R p R p ⋅-+⋅=-+=πεπεθπεπεθϕ 在2R R =处，电荷分布为：22o42R QR D R n πϕεσ=∂∂-== 在1R R =处，电荷分布为：3104cos 3'1R p RD R i n πθϕεσ-=∂∂=-=6. 在均匀外电场0E 中置入一带均匀自由电荷f ρ的绝缘介质球（电容率为ε），求空间各点的电势。