七年级数学上册全册单元测试卷达标检测(Word版 含解析)
七年级上册数学全册单元试卷综合测试卷(word含答案)
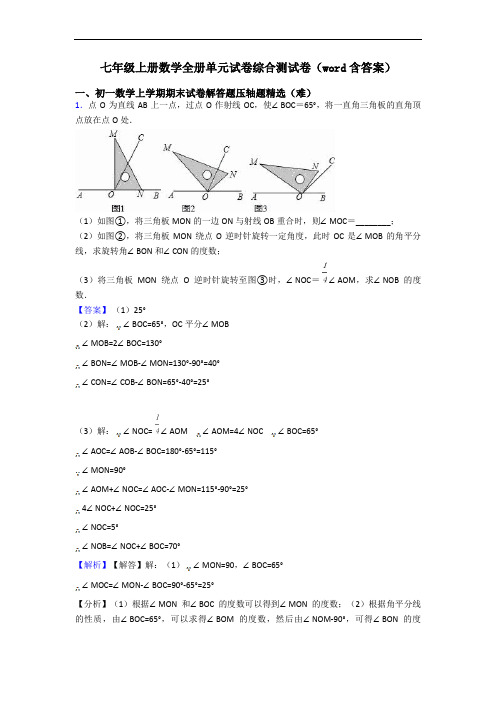
七年级上册数学全册单元试卷综合测试卷(word含答案)一、初一数学上学期期末试卷解答题压轴题精选(难)1.点O为直线AB上一点,过点O作射线OC,使∠BOC=65°,将一直角三角板的直角顶点放在点O处.(1)如图①,将三角板MON的一边ON与射线OB重合时,则∠MOC=________;(2)如图②,将三角板MON绕点O逆时针旋转一定角度,此时OC是∠MOB的角平分线,求旋转角∠BON和∠CON的度数;(3)将三角板MON绕点O逆时针旋转至图③时,∠NOC=∠AOM,求∠NOB的度数.【答案】(1)25°(2)解:∠BOC=65°,OC平分∠MOB∠MOB=2∠BOC=130°∠BON=∠MOB-∠MON=130°-90°=40°∠CON=∠COB-∠BON=65°-40°=25°(3)解:∠NOC= ∠AOM ∠AOM=4∠NOC ∠BOC=65°∠AOC=∠AOB-∠BOC=180°-65°=115°∠MON=90°∠AOM+∠NOC=∠AOC-∠MON=115°-90°=25°4∠NOC+∠NOC=25°∠NOC=5°∠NOB=∠NOC+∠BOC=70°【解析】【解答】解:(1)∠MON=90,∠BOC=65°∠MOC=∠MON-∠BOC=90°-65°=25°【分析】(1)根据∠MON和∠BOC的度数可以得到∠MON的度数;(2)根据角平分线的性质,由∠BOC=65°,可以求得∠BOM的度数,然后由∠NOM-90°,可得∠BON的度数,从而得解;(3)由∠BOC=65°,∠NOM=90°,∠NOC= ∠AOM,从而可求得∠NOC的度数,然后由∠BOC=65°,从而得解.2.如图,直线AB、CD相交于点O,已知,OE把分成两个角,且::3(1)求的度数;(2)过点O作射线,求的度数.【答案】(1)解:,,::3,;(2)解:,,,OF在的内部时,,,,OF在的内部时,,,,综上所述或【解析】【分析】(1)根据对顶角相等得出,然后根据::3 即可算出∠BOE的度数;(2)根据角的和差,由算出∠DOE的度数,根据垂直的定义得出∠EOF=90°;当OF在的内部时,根据,算出答案;OF在的内部时,根据,算出但,综上所述即可得出答案。
七年级数学全册单元测试卷达标训练题(Word版 含答案)

七年级数学全册单元测试卷达标训练题(Word版含答案)一、初一数学上学期期末试卷解答题压轴题精选(难)1.如图,线段AB=20cm.(1)点P沿线段AB自A点向B点以2cm/秒运动,同时点Q沿线段BA自B点向A点以3cm/秒运动,几秒后,点P、Q两点相遇?(2)如图,AO=PO=2cm,∠POQ=60°,现点P绕着点O以30°/秒的速度顺时针旋转一周后停止,同时点Q沿直线BA自B点向A点运动,若P、Q两点也能相遇,求点Q运动的速度.【答案】(1)解:设x秒点P、Q两点相遇根据题意得:2x+3x=20,解得x=4答:4秒后,点P、Q两点相遇。
(2)解:①当点P.Q在OB与圆的交点处相遇时:P点运动所用的时间为:① (秒),P点的运动速度为:(20-4)÷2=8cm/秒②当点P,Q在A点处相遇时:P点运动所用的时间为:②(60+180)÷30=8(秒),P点运动的速度为:20÷8-2.5cm/秒【解析】【分析】(1)此题是一道相遇问题,根据相遇的时候,P点所走的路程+Q点运动的路程等于AB两地之间的距离,列出方程,求解即可;(2)分①当点P.Q在OB与圆的交点处相遇时,②当点P,Q在A点处相遇时两类讨论,分别根据路程除以速度等于时间算出P点运动的时间,即Q点运动的时间,再根据路程除以时间等于速度即可算出Q点的运动速度。
2.如图(1)观察思考如图,线段AB上有两个点C、D,请分别写出以点A、B、C、D为端点的线段,并计算图中共有多少条线段;(2)模型构建如果线段上有m个点(包括线段的两个端点),则该线段上共有多少条线段?请说明你结论的正确性;(3)拓展应用8位同学参加班上组织的象棋比赛,比赛采用单循环制(即每两位同学之间都要进行一场比赛),那么一共要进行多少场比赛?请将这个问题转化为上述模型,并直接应用上述模型的结论解决问题.【答案】(1)解:∵以点A为左端点向右的线段有:线段AB、AC、AD,以点C为左端点向右的线段有线段CD、CB,以点D为左端点的线段有线段DB,∴共有3+2+1=6条线段(2)解:,理由:设线段上有m个点,该线段上共有线段x条,则x=(m-1)+(m-2)+(m-3)+…+3+2+1,∴倒序排列有x=1+2+3+…+(m-3)+(m-2)+(m-1),∴2x= =m(m-1),∴x=(3)解:把8位同学看作直线上的8个点,每两位同学之间的一场比赛看作为一条线段,直线上8个点所构成的线段条数就等于比赛的场数,因此一共要进行场比赛【解析】【分析】(1)线段AB上共有4个点A、B、C、D,得到线段共有4×(4-1)÷2条;(2)根据规律得到该线段上共有m(m-1)÷2条线段;(3)由每两位同学之间进行一场比赛,得到要进行8×(8-1)÷2场比赛.3.如图,点B、C在线段AD上,CD=2AB+3.(1)若点C是线段AD的中点,求BC-AB的值;(2)若BC=AD,求BC-AB的值;(3)若线段AC上有一点P(不与点B重合),AP+AC=DP,求BP的长.【答案】(1)解:设AB长为x,BC长为y,则CD=2x+3.若C是AB的中点,则AC=CD,即x+y=2x+3,得:y-x=3,即BC-AB=3(2)解:设AB长为x,BC长为y,若BC= CD,即AB+CD=3BC,∴x+2x+3=3y,∴y=x+1,即y-x=1,∴BC-AB=1(3)解:以A为原点,AD方向为正方向,1为单位长度建立数轴,则A:0,B:x,C:x+y,D:x+y+2x+3=3x+y+3.设P:p,由已知得:0≤p≤x+y,则AP=p,AC=x+y,DP=3x+y+3-p,∵AP+AC=DP,BP= ,∴p+x+y=3x+y+3-p,解得:2p-2x=3,∴p-x=1.5,∴BP=1.5【解析】【分析】(1)此题可以设未知数表示题中线段的长度关系,设AB长为x,BC长为y,则AC=AB+BC=x+y,CD=2x+3 ,根据中点的定义得出 AC=CD ,从而列出方程,变形即可得出答案;(2)设AB长为x,BC长为y ,则CD=2x+3 ,由BC= CD,得出AB+CD=3BC,从而列出方程变形即可得出答案;(3)设AB长为x,BC长为y ,则CD=2x+3 ,以A为原点,AD方向为正方向,1为单位长度建立数轴,则A点表示的数为0,B点表示的数为x,C点表示的数为x+y,D点表示的数为x+y+2x+3=3x+y+3.设P点表示的数为p,由已知得:0≤p≤x+y,则AP=p,AC=x+y,DP=3x+y+3-p,由AP+AC=DP,列出方程,并行得出P-X的值,再根据BP= 即可得出答案。
人教版七年级数学上册全册单元试卷达标检测卷(Word版 含解析)

人教版七年级数学上册全册单元试卷达标检测卷(Word版含解析)一、初一数学上学期期末试卷解答题压轴题精选(难)1.已知点C在线段AB上,AC=2BC,点D、E在直线AB上,点D在点E的左侧(1)若AB=18,DE=8,线段DE在线段AB上移动①如图1,当E为BC中点时,求AD的长;②点F(异于A,B,C点)在线段AB上,AF=3AD,CE+EF=3,求AD的长;(2)若AB=2DE,线段DE在直线AB上移动,且满足关系式,则________.【答案】(1)解:①又 E为BC中点;②设,因点F(异于A、B、C点)在线段AB上,可知:,和当时,此时可画图如图2所示,代入得:解得:,即AD的长为3当时,此时可画图如图3所示,代入得:解得:,即AD的长为5综上,所求的AD的长为3或5;(2) .【解析】【解答】(2)①若DE在如图4的位置设,则又(不符题设,舍去)②如DE在如图5的位置设,则又代入得:解得:则 .【分析】(1)①根据AB的长和可求出AC和BC,根据中点的定义可得CE,再由可得CD,最后根据计算即可得;②设,因点F(异于A、B、C点)在线段AB上,可知,和,所以需分2种情况进行讨论:和,如图2、3(见解析),先根据已知条件判断点E、F位置,再将EF和CE用含x的式子表示出来,最后代入求解即可;(2)设,先判断出DE在AB上的位置,再根据得出x和y 满足的等式,然后将其代入化简即可得.2.如图1,平面内一定点A在直线MN的上方,点O为直线MN上一动点,作射线OA、OP、OA′,当点O在直线MN上运动时,始终保持∠MOP=90°、∠AOP=∠A′OP,将射线OA 绕点O顺时针旋转60°得到射线OB(1)如图1,当点O运动到使点A在射线OP的左侧,若OB平分∠A′OP,求∠AOP的度数.(2)当点O运动到使点A在射线OP的左侧,∠AOM=3∠A′OB时,求的值.(3)当点O运动到某一时刻时,∠A′OB=150°,直接写出∠BOP=________度.【答案】(1)解:由题意可得:∠AOB=60°,∠AOP=∠A′OP,∵OB平分∠A′OP,∴∠A′OP=2∠POB,∴∠AOP=∠A′OP=2∠POB,∴∠AOB=∠AOP+∠POB=3∠POB=60°,∴∠POB=20°,∴∠AOP=2∠POB=40°(2)解:①当点O运动到使点A在射线OP的左侧,且射线OB在在∠A′OP的内部时,如图1,设∠A′OB=x,则∠AOM=3∠A′OB=3x,∠AOA′= ,∵OP⊥MN,∴∠AON=180°-3,∠AOP=90°-3x,∴,∵∠AOP=∠A′OP,∴∠AOP=∠A′OP=∴,解得:,∴;②当点O运动到使A在射线OP的左侧,但是射线OB在∠A′ON内部时,如图2,设∠A′OB=x,则∠AOM=3x,∠AON= ,∠AOA′= ,∵∠AOP=∠A′OP,∴∠AOP=∠A′OP= ,∵OP⊥MN,∴∠AOP=90-∠AOM=90-3x,∴,解得:,∴;(3)解:①如图3,当∠A′OB=150°时,由图可得:∠A′OA=∠A′OB-∠AOB=150°-60°=90°,又∵∠AOP=∠A′OP,∴∠AOP=45°,∴∠BOP=60°+45°=105°;②如图4,当∠A′OB=150°时,由图可得∠A′OA=360°-150°-60°=150°,又∵∠AOP=∠A′OP,∴∠AOP=75°,∴∠BOP=60°+75°=135°;综上所述:∠BOP的度数为105°或135°.【解析】【分析】(1)由角平分线的性质和∠ AOP=∠A′OP可得∠POB= ∠AOB,∠AOP=∠AOB,则∠POA的度数可求解;(2)由题意可分两种情况:①当点O运动到使点A在射线OP的左侧,且射线OB在在∠A′OP的内部时,由角的构成易得∠AOP= -∠AOM= -3∠A′OB,∠AOA′=+∠A′OB,由角平分线的性质可得∠AOP=∠A′OP,于是可得关于∠A′OB的方程,解方程可求得∠A′OB的度数,则可求解;②当点O运动到使A在射线OP的左侧,但是射线OB在∠A′ON内部时,同理可求解;(3)由题意可分两种情况讨论求解:①当∠A′OB沿顺时针成150°时,结合已知条件易求解;②当∠A′OB沿时针方向成 150°时,结合题意易求解。
七年级数学上册全册单元试卷达标检测卷(Word版 含解析)

七年级数学上册全册单元试卷达标检测卷(Word版含解析)一、初一数学上学期期末试卷解答题压轴题精选(难)1.如图,已知直线AB与直线CD相交于点O,∠BOE=90°,FO平分∠BOD,∠BOC:∠AOC=1:3.(1)求∠DOE、∠COF的度数.(2)若射线OF、OE同时绕O点分别以2°/s、4°/s的速度,顺时针匀速旋转,当射线OE、OF的夹角为90°时,两射线同时停止旋转.设旋转时间为t,试求t值.【答案】(1)解:∵∠BOC:∠AOC=1:3,∴∠BOC=180°× =45°,∴∠AOD=45°,∵∠BOE=90°,∴∠AOE=90°,∴∠DOE=45°+90°=135°,∠BOD=180°-45°=135°,∵FO平分∠BOD,∴∠DOF=∠BOF=67.5°,∴∠COF=180°-67.5°=112.5°(2)解:∠EOF=90°+67.5°=157.5°,依题意有4t-2t=157.5-90,解得t=33.75.故t值为33.75.【解析】【分析】(1)根据∠BOC:∠AOC=1:3,∠BOC+∠AOC=180°,即可算出∠BOC 的度数,然后根据对顶角相等由∠AOD = ∠BOC得出∠AOD 的度数,根据平角的定义,由∠AOE=∠AOB-∠BOE算出∠AOE的度数,进而根据∠DOE=∠AOE+∠AOD算出∠DOE的度数,∠BOD=∠AOB-∠AOD算出∠BOD的度数,再根据角平分线的定义得出∠BO 的度数,最后根据∠COF=∠COB+∠BOF即可算出答案;(2)根据角的和差,由∠EOF=∠EOB+∠BOF算出∠EOF的度数,根据题意OE转过的角度为4t°,OF转过的角度为2t°,根据题意列出方程 4t-2t=157.5-90,求解即可。
七年级数学上册 全册单元测试卷检测题(WORD版含答案)

七年级数学上册全册单元测试卷检测题(WORD版含答案)一、初一数学上学期期末试卷解答题压轴题精选(难)1.定义:从一个角的顶点出发,在角的内部引两条射线,如果这两条射线所成的角等于这个角的一半,那么这两条射线所成的角叫做这个角的内半角.如图1,若∠COD= ∠AOB,则∠COD是∠AOB的内半角.(1)如图1,已知∠AOB=70°,∠AOC=25°,∠COD是∠AOB的内半角,则∠BOD=________.(2)如图2,已知∠AOB=60°,将∠AOB绕点O按顺时针方向旋转一个角度口(0<a<60°)至∠COD,当旋转的角度a为何值时,∠COB是∠AOD的内半角.(3)已知∠AOB=30°,把一块含有30°角的三角板如图3叠放,将三角板绕顶点O以3度/秒的速度按顺时针方向旋转(如图4),问:在旋转一周的过程中,射线OA,OB,OC,OD 能否构成内半角,若能,请求出旋转的时间;若不能,请说明理由.【答案】(1)10°(2)解:∵∠AOB绕点O按顺时针方向旋转一个角度口(0<a<60°)至∠COD,∴∠AOB=∠COD=60°∴∠AOC=∠BOD=a∴a+∠COB=60°∵∠COB是∠AOD的内半角∴∠COB=∠AOD∴2∠COB=∠COB+2a∴∠COB=2a∴a+2a=60°解之:a=20°即当旋转的角度a为20°时,∠COB是∠AOD的内半角。
(3)解:在旋转一周的过程中,射线OA,OB,OC,OD能否构成内半角,理由:设按顺时针方向旋转一个角度α,旋转的时间为t如图1∵∠BOC是∠AOD的内半角,∠AOC=∠BOD=α∴∠AOD=30°+α,∠BOC=∠AOD=30°-α∴(30°+α)=30°-α解之:α=10°∴t=s;如图2∵∠BOC是∠AOD的内半角,∠AOC=∠BOD=α∴∠AOD=30°+α,∠BOC=∠AOD=α-30°∴(30°+α)=α-30°解之:α=90°∴t==30s;如图3∵∠AOD是∠BOC的内半角,∠AOC=∠BOD=360°-α∴∠BOC=360°+30°-α,∠AOD=∠BOC=360°-α-30°∴(360°+30°-α)=360°-α-30°解之:α=330°∴t==110s;如图4∵∠AOD是∠BOC的内半角,∠AOC=∠BOD=360°-α∴∠BOC=360°+30°-α,∴(360°+30°-α)=30°+30°-(360°+30°-α)解之:α=350°∴t=s;综上所述,当旋转的时间为s或30s或110s或s时,射线OA,OB,OC,OD能构成内半角。
人教版七年级数学上册全册单元试卷达标检测(Word版 含解析)

人教版七年级数学上册全册单元试卷达标检测(Word版含解析)一、初一数学上学期期末试卷解答题压轴题精选(难)1.如图,已知数轴上点A表示的数为8,B是数轴上一点,且AB=14.动点P从点A出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.(1)写出数轴上点B表示的数________ ,点P表示的数________(用含t的代数式表示);(2)动点Q从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发,问点P运动多少秒时追上点Q?(3)若M为AP的中点,N为PB的中点.点P在运动的过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请你画出图形,并求出线段MN的长;(4)若点D是数轴上一点,点D表示的数是x,请你探索式子|x+6|+|x﹣8|是否有最小值?如果有,直接写出最小值;如果没有,说明理由.【答案】(1)点B表示的数是﹣6;点P表示的数是8﹣5t(2)解:设点P运动x秒时,在点C处追上点Q (如图)则AC=5x,BC=3x,∵AC﹣BC=AB∴5x﹣3x=14…解得:x=7,∴点P运动7秒时,在点C处追上点Q(3)解:没有变化.分两种情况:①当点P在点A.B两点之间运动时:MN=MP+NP= AP+ BP= (AP+BP)= AB=7…②当点P运动到点B的左侧时:MN=MP﹣NP= AP﹣ BP= (AP﹣BP)= AB=7…综上所述,线段MN的长度不发生变化,其值为7…(4)解:式子|x+6|+|x﹣8|有最小值,最小值为14.…【解析】【分析】(1)由于A点表示的数是8,故OA=8,又AB=14,从而得出OB=AB-OA=6,由于点B表示的数在原点的左边,故B点表示的数是-6,根据路程等于速度乘以时间得出AP=5t,从而得出P点表示的数是8-5t;(2)设点P运动x秒时,在点C处追上点Q (如图)格努路程定于速度乘以时间得出AC=5x,BC=3x,然后由AC﹣BC=AB列出方程求解即可得出x的值;(3)没有变化.根据线段中点的定义得出PM=AP,NP=BP,分两种情况:①当点P在点A.B两点之间运动时,由MN=MP+NP= AP+ BP= (AP+BP)= AB得出答案;②当点P运动到点B的左侧时:MN=MP-NP= AP- BP= (AP-BP)= AB得出答案,综上所述即可得出答案;(4)式子|x+6|+|x﹣8|有最小值,最小值为14,点D是数轴上一点,点D表示的数是x,那么|x+6|表示点D,B两点间的距离,|x﹣8|表示点D,A两点间的距离,要|x+6|+|x﹣8|其实质就是DB+AD的和,要DB+AD的和最小,只有在D为线段AB上的时候,DB+AD的和最小=AB,即可得出答案。
七年级数学全册单元测试卷达标训练题(Word版 含答案)
七年级数学全册单元测试卷达标训练题(Word版含答案)一、初一数学上学期期末试卷解答题压轴题精选(难)1.结合数轴与绝对值的知识回答下列问题:(1)探究:①数轴上表示5和2的两点之间的距离是多少.②数轴上表示﹣2和﹣6的两点之间的距离是多少.③数轴上表示﹣4和3的两点之间的距离是多少.(2)归纳:一般的,数轴上表示数m和数n的两点之间的距离等于|m﹣n|.应用:①如果表示数a和3的两点之间的距离是7,则可记为:|a﹣3|=7,求a的值.②若数轴上表示数a的点位于﹣4与3之间,求|a+4|+|a﹣3|的值.③当a取何值时,|a+4|+|a﹣1|+|a﹣3|的值最小,最小值是多少?请说明理由.(3)拓展:某一直线沿街有2014户居民(相邻两户居民间隔相同):A1, A2, A3,A4, A5,…A2014,某餐饮公司想为这2014户居民提供早餐,决定在路旁建立一个快餐店P,点P选在什么线段上,才能使这2014户居民到点P的距离总和最小.【答案】(1)解:①数轴上表示5和2的两点之间的距离是3.②数轴上表示﹣2和﹣6的两点之间的距离是4.③数轴上表示﹣4和3的两点之间的距离是7.(2)解:①如果表示数a和3的两点之间的距离是7,则可记为:|a﹣3|=7,a=10或﹣4.②若数轴上表示数a的点位于﹣4与3之间,|a+4|+|a﹣3|=a+4+3﹣a=7;③当a=1时,|a+4|+|a﹣1|+|a﹣3|取最小值,|a+4|+|a﹣1|+|a﹣3|最小=5+0+2=7,理由是:a=1时,正好是3与﹣4两点间的距离.(3)解:点P选在A1007A1008这条线段上【解析】【分析】(1)根据两点间的距离公式:数轴上表示数m和数n的两点之间的距离等于|m﹣n|,分别计算可得出答案。
(2)① 利用绝对值等于7的数是±7,就可得出a-3=±7,解方程即可;② 由已知数轴上表示数a的点位于﹣4与3之间,可得出a+4>0,a-3<0,先去掉绝对值,再合并同类项即可;③ 根据线段上的点到线段两端的距离的和最短,可得出答案。
人教版数学七年级上册全册单元试卷达标检测卷(Word版 含解析)
人教版数学七年级上册全册单元试卷达标检测卷(Word版含解析)一、初一数学上学期期末试卷解答题压轴题精选(难)1.(1)如图①,已知:Rt△ABC中,AB=AC,直线m经过点A,BD⊥m于D,CE⊥m于E,求证:DE=BD+CE;(2)如图②,将(1)中的条件改为:△ABC中,AB=AC,并且∠BDA=∠AEC=∠BAC=α,α为任意锐角或钝角,请问结论DE=BD+CE是否成立?如成立,请证明;若不成立,请说明理由;(3)应用:如图③,在△ABC中,∠BAC是钝角,AB=AC,∠BAD>∠CAE,∠BDA=∠AEC=∠BAC,直线m与BC的延长线交于点F,若BC=2CF,△ABC的面积是12,求△ABD与△CEF的面积之和.【答案】(1)证明:∵BD⊥直线m,CE⊥直线m,∴∠BDA=∠CEA=90°,∵∠BAC=90°,∴∠BAD+∠CAE=90°,∵∠BAD+∠ABD=90°,∴∠CAE=∠ABD,在△ADB和△CEA中,∴△ADB≌△CEA(AAS),∴AE=BD,AD=CE,∴DE=AE+AD=BD+CE;(2)解:结论DE=BD+CE成立;理由如下:∵∠BDA=∠BAC=α,∴∠DBA+∠BAD=∠BAD+∠CAE=180°-α,∴∠CAE=∠ABD,在△ADB和△CEA中,∴△ADB≌△CEA(AAS),∴AE=BD,AD=CE,∴DE=AE+AD=BD+CE;(3)解:∵∠BAD>∠CAE,∠BDA=∠AEC=∠BAC,∴∠CAE=∠ABD,在△ABD和△CEA中,∴△ABD≌△CEA(AAS),∴S△ABD=S△CEA,设△ABC的底边BC上的高为h,则△ACF的底边CF上的高为h,∴S△ABC= BC•h=12,S△ACF= CF•h,∵BC=2CF,∴S△ACF=6,∵S△ACF=S△CEF+S△CEA=S△CEF+S△ABD=6,∴△ABD与△CEF的面积之和为6.【解析】【分析】(1)根据BD⊥直线m,CE⊥直线m得∠BDA=∠CEA=90°,而∠BAC=90°,根据等角的余角相等得∠CAE=∠ABD,由AAS证得△ADB≌△CEA,则AE=BD,AD=CE,即可得出结论;(2)由∠BDA=∠BAC=α,则∠DBA+∠BAD=∠BAD+∠CAE=180°-α,得出∠CAE=∠ABD,由AAS证得△ADB≌△CEA即可得出答案;(3)由∠BAD>∠CAE,∠BDA=∠AEC=∠BAC,∴∠CAE=∠ABD,得出∠CAE=∠ABD,由AAS证得△ADB≌△CEA,得出S△ABD=S△CEA,再由不同底等高的两个三角形的面积之比等于底的比,得出S△ACF即可得出结果.2.点O为直线AB上一点,过点O作射线OC,使∠BOC=65°,将一直角三角板的直角顶点放在点O处.(1)如图①,将三角板MON的一边ON与射线OB重合时,则∠MOC=________;(2)如图②,将三角板MON绕点O逆时针旋转一定角度,此时OC是∠MOB的角平分线,求旋转角∠BON和∠CON的度数;(3)将三角板MON绕点O逆时针旋转至图③时,∠NOC=∠AOM,求∠NOB的度数.【答案】(1)25°(2)解:∠BOC=65°,OC平分∠MOB∠MOB=2∠BOC=130°∠BON=∠MOB-∠MON=130°-90°=40°∠CON=∠COB-∠BON=65°-40°=25°(3)解:∠NOC= ∠AOM ∠AOM=4∠NOC ∠BOC=65°∠AOC=∠AOB-∠BOC=180°-65°=115°∠MON=90°∠AOM+∠NOC=∠AOC-∠MON=115°-90°=25°4∠NOC+∠NOC=25°∠NOC=5°∠NOB=∠NOC+∠BOC=70°【解析】【解答】解:(1)∠MON=90,∠BOC=65°∠MOC=∠MON-∠BOC=90°-65°=25°【分析】(1)根据∠MON和∠BOC的度数可以得到∠MON的度数;(2)根据角平分线的性质,由∠BOC=65°,可以求得∠BOM的度数,然后由∠NOM-90°,可得∠BON的度数,从而得解;(3)由∠BOC=65°,∠NOM=90°,∠NOC= ∠AOM,从而可求得∠NOC的度数,然后由∠BOC=65°,从而得解.3.将一副三角板中的两个直角顶点叠放在一起(如图①),其中,, .(1)猜想与的数量关系,并说明理由;(2)若,求的度数;(3)若按住三角板不动,绕顶点转动三角,试探究等于多少度时,并简要说明理由.【答案】(1)解:,理由如下:,(2)解:如图①,设,则,由(1)可得,,,(3)解:分两种情况:①如图1所示,当时,,又,;②如图2所示,当时,,又,.综上所述,等于或时, .【解析】【分析】(1)由∠BCD=∠ACB+∠ACD=90°+∠ACD,即可求出∠BCD+∠ACE的度数.(2)如图①,设∠ACE=a,可得∠BCD=3a,结合(1)可得3a+a=180°,求出a的度数,即得∠BCD的度数.(3)分两种情况讨论,①如图1所示,当AB∥CE时,∠BCE=180°-∠B=120°,②如图2所示,当AB∥CE时,∠BCE=∠B=60°,分别求出∠BCD的度数即可.4.如图,O是直线AB上一点,OD平分∠AOC.(1)若∠AOC=60°,请求出∠AOD和∠BOC的度数.(2)若∠AOD和∠DOE互余,且∠AOD= ∠AOE,请求出∠AOD和∠COE的度数.【答案】(1)解:∠AOD= ×∠AOC= ×60°=30°,∠BOC=180°﹣∠AOC=180°﹣60°=120°(2)解:∵∠AOD和∠DOE互余,∴∠AOE=∠AOD+∠DOE=90°,∴∠AOD= ∠AOE= ×90°=30°,∴∠AOC=2∠AOD=60°,∴∠COE=90°﹣∠AOC=30°【解析】【分析】(1)①由角平分线的定义可得:∠AOD=∠COD= ∠AOC即可求解;②由邻补角的定义可得:∠BOC+∠AOC= 180°,所以∠BOC= 180° -∠AOC即可求解;(2)①由互为余角的定义和图形可得∠AOE=∠AOD+∠DOE= 90°,所以∠AOD= ∠AOE 可求解;②由①可得∠AOD的度数,由角平分线的定义可得∠AOC=2∠AOD,所以∠COE=∠AOE-∠AOC,把∠AOE和∠AOC的度数代入计算即可求解。
人教版七年级上册数学全册单元试卷试卷(word版含答案)
人教版七年级上册数学全册单元试卷试卷(word版含答案)一、初一数学上学期期末试卷解答题压轴题精选(难)1.点在线段上, .(1)如图1,,两点同时从,出发,分别以,的速度沿直线向左运动;①在还未到达点时,求的值;②当在右侧时(点与不重合),取中点,的中点是,求的值;(2)若是直线上一点,且 .求的值.【答案】(1)解:①AP=AC-PC,CQ=CB-QB,∵BC=2AC,P、Q速度分别为1cm/s、2cm/s,∴QB=2PC,∴CQ=2AC-2PC=2AP,∴②设运动秒,分两种情况A: 在右侧,,分别是,的中点,,∴B: 在左侧,,分别是,的中点,,∴(2)解:∵BC=2AC.设AC=x,则BC=2x,∴AB=3x,①当D在A点左侧时,|AD-BD|=BD-AD=AB= CD,∴CD=6x,∴;②当D在AC之间时,|AD-BD|=BD-AD= CD,∴2x+CD-x+CD= CD,x=- CD(不成立),③当D在BC之间时,|AD-BD|=AD-BD= CD,∴x+CD-2x+CD= CD,CD= x,∴;|AD-BD|=BD-AD= CD,∴2x-CD-x-CD= CD,∴CD=;④当D在B的右侧时,|AD-BD|=BD-AD= CD,∴2x-CD-x-CD= CD,CD=6x,∴ .综上所述,的值为或或或【解析】【分析】(1)由线段的和差关系,以及QB=2PC,BC=2AC,即可求解;(2)设AC=x,则BC=2x,∴AB=3x,D点分四种位置进行讨论,①当D在A点左侧时,②当D在AC之间时,③当D在BC之间时,④当D在B的右侧时求解即可.2.将一副直角三角尺按如图所示的方式叠放在一起(其中∠A=60°,∠D=30°,∠E=∠B =45°,直角顶点C保持重合).(1)①若∠DCE=45°,则∠ACB的度数为________.②若∠ACB=140°,则∠DCE的度数为________.(2)由(1)猜想∠ACB与∠DCE的数量关系,并说明理由.(3)将三角尺BCE绕着点C顺时针转动,当∠ACE<180°,且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请直接写出∠ACE角度所有可能的值(并写明此时哪两条边平行,但不必说明理由);若不存在,请说明理由.【答案】(1)135°;40°(2)∠ACB+∠DCE=180°.理由如下:∵∠ACB=∠ACD+∠DCB=90°+∠DCB,∴∠ACB+∠DCE=90°+∠DCB+∠DCE=90°+∠ECB=90°+90°=180°.(3)(3)存在.当∠ACE=30°时,AD∥BC;当∠ACE=45°时,AC∥BE;当∠ACE=120°时,AD∥CE;当∠ACE=135°时,CD∥BE;当∠ACE=165°时,AD∥BE.【解析】【解答】(1)①∵∠ECB=90°,∠DCE=45°,∴∠DCB=90°-45°=45°,∴∠ACB=∠ACD+∠DCB=90°+45°=135°.②∵∠ACB=140°,∠ACD=90°,∴∠DCB=140°-90°=50°,∴∠DCE=90°-50°=40°.【分析】(1)①根据角的和差,由∠DCB=∠BCE-∠DCE,即可算出∠DCB的度数,进而根据∠ACB=∠ACD+∠DCB即可算出答案;②根据角的和差,由∠DCB=∠ACB-∠ACD算出∠DCB的度数,再根据∠DCE=∠ECB-∠DCB即可算出答案;(2)∠ACB+∠DCE=180°.理由如下:根据角的和差得出∠ACB=∠ACD+∠DCB=90°+∠DCB ,故由∠ACB+∠DCE=90°+∠DCB+∠DCE =90°+∠ECB 即可算出答案;(3)存在.当∠ACE=30°时,根据内错角相等二直线平行得出AD∥BC;当∠ACE=45°时,内错角相等二直线平行得出AC∥BE;当∠ACE=120°时,根据同旁内角互补,二直线平行得出AD∥CE;当∠ACE=135°时,根据内错角相等二直线平行得出CD∥BE;当∠ACE =165°时,根据同旁内角互补,二直线平行得出AD∥BE.3.如图,已知点A、点B是直线上的两点,AB=12厘米,点C在线段AB上.点P、点Q 是直线上的两个动点,点P的速度为1厘米/秒,点Q的速度为2厘米/秒.(1)当点P、Q分别在线段AC、BC的中点时,线段PQ=________厘米;(2)若AC=6厘米,点P、点Q分别从点C、点B同时出发沿射线BA方向运动,当运动时间为2秒时,求PQ的长;(3)若AC=4厘米,点P、Q分别从点C、点B同时出发在直线AB上运动,则经过多少时间后线段PQ的长为5厘米.【答案】(1)6(2)解:如图2,当t=2时,BQ=2×2=4,则CQ=6-4=2.因为CP=2×1=2,所以PQ=CP+CQ=2+2=4(厘米)(3)解:设运动时间为t秒.①如图3,当点P、Q沿射线BA方向运动,若点Q在点P的后面,得:t+8-2t=5,解得t=3,②如图4,当点P、Q沿射线BA方向运动,若点Q在点P前面,得:2t-8-t=5,解得t=13.③如图5,当点P、Q在直线上相向运动,点P、Q在相遇前,得:t+2t=3,解得t=1.④如图6,当点P、Q在直线上相向运动,点P、Q在相遇后,得:t+2t=13,解得t= .综合可得t=1,3,13, .所以经过1,3,13,秒后PQ的长为5厘米.【解析】【解答】(1)如图1,因为AB=12厘米,点C在线段AB上,所以,当点P、Q分别在线段AC、BC的中点时,线段PQ= AB=6.故答案为:6;【分析】(1)由线段中点的定义可得CP= AC,CQ= CB,所以PQ= AC+ CB= AB,把AB的值代入计算即可求解;(2)由路程=速度时间可求出BQ和CQ、CP的值,则PQ=CP+CQ可求解;(3)由题意可分4种情况求解:① 当点P、Q沿射线BA方向运动,若点Q在点P的后面,由图可列关于时间的方程求解;②当点P、Q沿射线BA方向运动,若点Q在点P前面,由图可列关于时间的方程求解;③当点P、Q在直线上相向运动,点P、Q在相遇前,由图可列关于时间的方程求解;④ 当点P、Q在直线上相向运动,点P、Q在相遇后,由图可列关于时间的方程求解。
七年级数学上册全册单元试卷达标检测(Word版 含解析)
七年级数学上册全册单元试卷达标检测(Word版含解析)一、初一数学上学期期末试卷解答题压轴题精选(难)1.探究题:如图①,已知线段AB=14cm,点C为AB上的一个动点,点D、E分别是AC 和BC的中点.(1)若点C恰好是AB中点,则DE=________cm;(2)若AC=4cm,求DE的长;(3)试利用“字母代替数”的方法,设AC=a cm请说明不论a取何值(a不超过14cm),DE的长不变;(4)知识迁移:如图②,已知∠AOB=120°,过角的内部任一点C画射线OC,若OD、OE 分别平分∠AOC和∠BOC,试说明∠DOE=60°与射线OC的位置无关.【答案】(1)7(2)解:∵AC=4cm ∴BC=AB-AC=10cm 又∵D为AC中点,E为BC中点∴CD=2cm,CE=5cm ∴DE=CD+CE=7cm.(3)解:∵AC=acm ∴BC=AB-AC=(14-a)cm 又∵D为AC中点,E为BC中点∴CD=cm,CE= cm ∴DE=CD+CE= +∴无论a取何值(不超过14)DE的长不变。
(4)解:设∠AOC=α,∠BOC=120-α ∵OD平分∠AOC,OE平分∠BOC ∴∠COD= ,∠COE= ∴∠DOE=∠COD+∠COE= + = =60°∴∠DOE=60°与OC位置无关.【解析】【解答】解:(1)∵AB=12cm,点D、E分别是AC和BC的中点,C点为AB的中点,∴AC=BC=7cm,∴CD=CE=3.5cm,∴DE=7cm,.【分析】(1)根据中点的定义AC=BC=AB,DC=AC,CE=CB,然后根据DE=DC+CE即可算出答案;(2)首先根据BC=AB-AC 算出BC,根据中点的定义DC=AC,CE=CB,然后根据DE=DC+CE 即可算出答案;(3)首先根据BC=AB-AC 表示出BC,根据中点的定义DC=AC,CE=CB,然后根据DE=DC+CE=AC+CB=(AC+CB)=AB即可算出答案;(4)根据角平分线的定义∠COD =∠AOC ,∠COE =∠BOC ,然后根据∠DOE=∠COD+∠COE =∠COD+∠COE=(∠COD+∠COE)=∠AOB即可得出答案。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
七年级数学上册全册单元测试卷达标检测(Word版含解析)一、初一数学上学期期末试卷解答题压轴题精选(难)1.如图,已知AB∥CD,现将一直角三角形PMN放入图中,其中∠P=90°,PM交AB于点E,PN交CD于点F(1)当△PMN所放位置如图①所示时,则∠PFD与∠AEM的数量关系为________;(2)当△PMN所放位置如图②所示时,求证:∠PFD−∠AEM=90°;(3)在(2)的条件下,若MN与CD交于点O,且∠DON=30°,∠PEB=15°,求∠N的度数.【答案】(1)∠PFD+∠AEM=90°(2)过点P作PG∥AB∵AB∥CD,∴PG∥AB∥CD,∴∠AEM=∠MPG,∠PFD=∠NPG∵∠MPN=90°∴∠NPG-∠MPG=90°∴∠PFD-∠AEM=90°;(3)设AB与PN交于点H∵∠P=90°,∠PEB=15°∴∠PHE=180°-∠P-∠PEB=75°∵AB∥CD,∴∠PFO=∠PHE=75°∴∠N=∠PFO-∠DON=45°.【解析】【解答】(1)过点P作PH∥AB∵AB∥CD,∴PH∥AB∥CD,∴∠AEM=∠MPH,∠PFD=∠NPH∵∠MPN=90°∴∠MPH+∠NPH=90°∴∠PFD+∠AEM=90°故答案为:∠PFD+∠AEM=90°;【分析】(1)过点P作PH∥AB,然后根据平行于同一条直线的两直线平行可得PH∥AB∥CD,根据平行线的性质可得∠AEM=∠MPH,∠PFD=∠NPH,然后根据∠MPH+∠NPH=90°和等量代换即可得出结论;(2)过点P作PG∥AB,然后根据平行于同一条直线的两直线平行可得PG∥AB∥CD,根据平行线的性质可得∠AEM=∠MPG,∠PFD=∠NPG,然后根据∠NPG-∠MPG=90°和等量代换即可证出结论;(3)设AB与PN 交于点H,根据三角形的内角和定理即可求出∠PHE,然后根据平行线的性质可得∠PFO=∠PHE,然后根据三角形外角的性质即可求出结论.2.如图,数轴上线段AB=4(单位长度),CD=6(单位长度),点A在数轴上表示的数是-16,点C在数轴上表示的数是18.(1)点B在数轴上表示的数是________,点D在数轴上表示的数是________,线段AD=________;(2)若线段AB以4个单位长度/秒的速度向右匀速运动,同时线段CD以2个单位长度/秒的速度向左匀速运动,设运动时间为t秒,①若BC=6(单位长度),求t的值;②当0<t<5时,设M为AC中点,N为BD中点,求线段MN的长.【答案】(1)-12;24;40(2)解:①设运动t秒时,BC=6当点B在点C的左边时,由题意得:4t+6+2t=30,解之:t=4;当点B在点C的右边时,由题意得:4t−6+2t=30,解之:t=6.综上可知,若BC=6(单位长度),t的值为4或6秒;②当0<t<5时,A点表示的数为−16+4t,B点表示的数为−12+4t,C点表示的数为18−2t,D点表示的数为24−2t,∵M为AC中点,N为BD中点,∴点M表示的数为:=1+t,点N表示的数为:=6+t∴MN=6+t-(1+t)=5.【解析】【解答】解:(1)∵AB=4,A在数轴上表示的数是-16,∴点B在数轴上表示的数为:-16+4=-12∵点C在数轴上表示的数是18,CD=6,∴点D在数轴上表示的数为:18+6=24;∵点A在数轴上表示的数是-16,点D在数轴上表示的数为24,∴AD=|-16-24|=40故答案为:-12;24;40【分析】(1)由线段AB=4,点A在数轴上表示的数是-16,根据两点间的距离公式可得点B在数轴上表示的数;由CD=6,点C在数轴上表示的数是18,根据两点间的距离公式可得点D在数轴上表示的数;根据两点间的距离公式可得AD的长。
(2)①设运动t秒时,BC=6(单位长度),然后分点B在点C的左边和右边两种情况,根据题意列出方程求解即可;②当0<t<5时,B与C没有相遇,分别求出此时A,B,C,D四点表示的数,再根据中点坐标公式求出M,N表示的数,然后利用两点间的距离公式即可求出线段MN的长。
3.如图(1)观察思考如图,线段AB上有两个点C、D,请分别写出以点A、B、C、D为端点的线段,并计算图中共有多少条线段;(2)模型构建如果线段上有m个点(包括线段的两个端点),则该线段上共有多少条线段?请说明你结论的正确性;(3)拓展应用8位同学参加班上组织的象棋比赛,比赛采用单循环制(即每两位同学之间都要进行一场比赛),那么一共要进行多少场比赛?请将这个问题转化为上述模型,并直接应用上述模型的结论解决问题.【答案】(1)解:∵以点A为左端点向右的线段有:线段AB、AC、AD,以点C为左端点向右的线段有线段CD、CB,以点D为左端点的线段有线段DB,∴共有3+2+1=6条线段(2)解:,理由:设线段上有m个点,该线段上共有线段x条,则x=(m-1)+(m-2)+(m-3)+…+3+2+1,∴倒序排列有x=1+2+3+…+(m-3)+(m-2)+(m-1),∴2x= =m(m-1),∴x=(3)解:把8位同学看作直线上的8个点,每两位同学之间的一场比赛看作为一条线段,直线上8个点所构成的线段条数就等于比赛的场数,因此一共要进行场比赛【解析】【分析】(1)线段AB上共有4个点A、B、C、D,得到线段共有4×(4-1)÷2条;(2)根据规律得到该线段上共有m(m-1)÷2条线段;(3)由每两位同学之间进行一场比赛,得到要进行8×(8-1)÷2场比赛.4.如图1,已知∠AOB=140°,∠AOC=30°,OE是∠AOB内部的一条射线,且OF平分∠AOE.(1)若∠EOB=30°,则∠COF=________;(2)若∠COF=20°,则∠EOB=________;(3)若∠COF=n°,则∠EOB=________(用含n的式子表示).(4)当射线OE绕点O逆时针旋转到如图2的位置时,请把图补充完整;此时,∠COF与∠EOB有怎样的数量关系?请说明理由.【答案】(1)20°(2)40°(3)80°-2n°(4)如图所示:∠EOB=80°+2∠COF.证明:设∠COF=n°,则∠AOF=∠AOC-∠COF=30°-n°,又∵OF平分∠AOE,∴∠AOE=2∠AOF=60°-2n°.∴∠EOB=∠AOB-∠AOE=140°-(60°-2n°)=(80+2n)°即∠EOB=80°+2∠COF.【解析】【解答】(1)∵∠AOB=140°,∠EOB=30°,∴∠AOE=∠AOB-∠EOB=140°-30°=110°,∵OF平分∠AOE,∴∠AOF= ∠AOE= ×110°=55°,∴∠COF=∠AOF-∠AOC,=55°-30°,=25°;故答案为:25°;(2)∵∠AOC=30°,∠COF=20°,∴∠AOF=∠AOC+∠COF=30°+20°=50°,∵OF平分∠AOE,∴∠AOE=2∠AOF=2×50°=100°,∴∠EOB=∠AOB-∠AOE=140°-100°=40°;故答案为:40°;(3)∵∠AOC=30°,∠COF=n°,∴∠AOF=∠AOC+∠COF=30°+n°,∵OF平分∠AOE,∴∠AOE=2∠AOF=2(30°+n°)=60°+2n°,∴∠EOB=∠AOB-∠AOE=140°-(60°+2n°)=80°-2n°;故答案为:80°-2n°;【分析】(1)根据∠AOE=∠AOB-∠EOB先求出∠AOE,再根据角平分线的定义求出∠AOF,最后根据∠COF=∠AOF-∠AOC解答即可;(2)根据∠AOF=∠AOC+∠COF先求出∠AOF,再根据角平分线的定义求出∠AOE,最后根据∠EOB=∠AOB-∠AOE解答即可;(3)与(2)的思路相同求解即可;(4)设∠COF=n°,先表示出∠AOF,再根据角平分线的定义求出∠AOE,最后根据∠EOB=∠AOB-∠AOE解答即可.5.阅读理解:若A、B、C为数轴上三点,若点C到A的距离是点C到B的距离2倍,我们就称点C是点是【A,B】的好点.(1)如图1,点A表示的数为﹣1,点B表示的数为2.表示1的点C到点A的距离是2,到点B的距离是1,那么点C是【A,B】的好点;又如,表示0的点D到点A的距离是1,到点B的距离是2,那么点D________【A,B】的好点,但点D________【B,A】的好点.(请在横线上填是或不是)知识运用:(2)如图2,M、N为数轴上两点,点M所表示的数为4,点N所表示的数为﹣2.数________所表示的点是【M,N】的好点;(3)如图3,A、B为数轴上两点,点A所表示的数为﹣20,点B所表示的数为40.现有一只电子蚂蚁P从点B出发,以4个单位每秒的速度向左运动,到达点A停止.当经过________秒时,P、A和B中恰有一个点为其余两点的好点?【答案】(1)不是;是(2)0(3)5或10【解析】【解答】解:(1)如图1,∵点D到点A的距离是1,到点B的距离是2,根据好点的定义得:DB=2DA,那么点D不是【A,B】的好点,但点D是【B,A】的好点;⑵如图2,4﹣(﹣2)=6,6÷3×2=4,即距离点M4个单位,距离点N2个单位的点就是所求的好点0;∴数0所表示的点是【M,N】的好点;⑶如图3,由题意得:PB=4t,AB=40+20=60,PA=60﹣4t,点P走完所用的时间为:60÷4=15(秒),当PB=2PA时,即4t=2(60﹣4t),t=10(秒),当PA=2PB时,即2×4t=60﹣4t,t=5(秒),∴当经过5秒或10秒时,P、A和B中恰有一个点为其余两点的好点;故答案:(1)不是,是;(2)0;(3)5或10.【分析】(1)根据定义发现:好点表示的数到【A,B】中,前面的点A是到后面的数B 的距离的2倍,从而得出结论;(2)点M到点N的距离为6,分三等分为份为2,根据定义得:好点所表示的数为0;(3)根据题意得:PB=4t,AB=40+20=60,PA=60﹣4t,由好点的定义可知:分两种情况列式:①PB=2PA;②PA=2PB;可以得出结论.6.如图,点O为直线AB上一点,过点O作射线OC,使∠BOC=135°,将一个含45°角的直角三角尺的一个顶点放在点O处,斜边OM与直线AB重合,另外两条直角边都在直线AB的下方.(1)将图1中的三角尺绕着点O逆时针旋转90°,如图2所示,此时∠BOM=________度(答案直接填写在答题卡的横线上);在图2中,OM是否平分∠CON?请说明理由;(2)紧接着将图2中的三角板绕点O逆时针继续旋转到图3的位置所示,使得ON在∠AOC的内部,请探究:∠AOM与∠CON之间的数量关系,并说明理由;(3)将图1中的三角板绕点O按每秒5°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,请你直接写出t的值为多少.【答案】(1)90°,OM平分∠CON.理由如下:∵∠BOC=135°,∴∠MOC=135°-90°=45°,而∠MON=45°,∴∠MOC=∠MON(2)∠AOM=∠CON.理由如下:如图3,∵∠MON=45°,∴∠AOM=45°-∠AON,∵∠AOC=45°,∴∠NOC=45°-∠AON,∴∠AOM=∠CON(3)解:t= ×45°÷5°=4.5(秒)或t=(180°+22.5°)÷5°=40.5(秒).故答案为90°;4.5秒或40.5秒.【解析】【分析】(1)利用旋转的性质可得∠BOM的度数,然后计算∠MOC的度数判断OM是否平分∠CON;(2)利用∠AOM=45°-∠AON和∠NOC=45°-∠AON可判断∠AOM与∠CON之间的数量关系;(3)ON旋转22.5度和202.5度时,ON平分∠AOC,然后利用速度公式计算t的值.7.点O为直线AB上一点,过点O作射线OC,使∠AOC:∠BOC=2:1,将一直角的顶点放在点O处,∠MON=90°.(1)如图1,当∠MON的一边OM与射线OB重合时,则∠NOC=________;(2)将∠MON绕点O逆时针运动至图2时,若∠MOC=15°,则∠BOM=________;∠AON=________.(3)在上述∠MON从图1运动到图3的位置过程中,当∠MON的边OM所在直线恰好平分∠AOC时,求此时∠NOC是多少度?【答案】(1)150°(2)45°;135°(3)解:由(1)可知:∠AOC=120°,∠BOC=60°,∵OM平分∠AOC,∴∠COM= ∠AOC=60°,∵∠MON=90°,∴∠NOC=∠MON-∠COM=90°-60°=30°.【解析】【解答】(1)∵∠AOC:∠BOC=2:1,∠AOC+∠BOC=180°,∴∠AOC=180°× =120°,∠BOC=180°× =60°,∵∠MON=90°,∴∠NOC=∠BOC+∠MON=90°+60°=150°.故答案为:150°( 2 )由(1)可知:∠BOC=60°,∵∠MOC=15°,∴∠BOM=∠BOC-∠MOC=60°-15°=45°,∵∠MON=90°,∴∠BON=90°-∠BOM=45°,∴∠AON=180°-∠AON=135°,故答案为:45°,135°【分析】(1)由∠AOC:∠BOC=2:1,根据平角的定义可求出∠AOC、∠BOC的度数,根据角的和差关系即可求出∠NOC的度数;(2)根据∠BOC和∠MOC的度数可求出∠BOM 的度数,根据角的和差关系即可求出∠BOM的度数,根据∠MON=90°可求出∠NOB的度数,根据平角的定义即可求出∠AON的度数;(3)利用角平分线的定义可求出∠MOC的度数,进而可求出∠NOC的度数.8.如图1,O为直线AB上一点,过点O作射线OC,∠AOC=30°,将一直角三角板(其中∠P=30°)的直角顶点放在点O处,一边OQ在射线OA上,另一边OP与OC都在直线AB 的上方.将图1中的三角板绕点O以每秒3°的速度沿顺时针方向旋转一周.(1)如图2,经过t秒后,OP恰好平分∠BOC.①求t的值;②此时OQ是否平分∠AOC?请说明理由;(2)若在三角板转动的同时,射线OC也绕O点以每秒6°的速度沿顺时针方向旋转一周,如图3,那么经过多长时间OC平分∠POQ?请说明理由;(3)在(2)问的基础上,经过多少秒OC平分∠POB?(直接写出结果).【答案】(1)解:①∵∠AOC=30°,∴∠BOC=180°﹣30°=150°,∵OP平分∠BOC,∴∠COP=∠BOC=75°,∴∠COQ=90°﹣75°=15°,∴∠AOQ=∠AOC﹣∠COQ=30°﹣15°=15°,t=15÷3=5;②是,理由如下:∵∠COQ=15°,∠AOQ=15°,∴OQ平分∠AOC;(2)解:∵OC平分∠POQ,∴∠COQ=∠POQ=45°.设∠AOQ=3t,∠AOC=30°+6t,由∠AOC﹣∠AOQ=45°,可得30+6t﹣3t=45,解得:t=5,当30+6t﹣3t=225,也符合条件,解得:t=65,∴5秒或65秒时,OC平分∠POQ;(3)解:设经过t秒后OC平分∠POB,∵OC平分∠POB,∴∠BOC=∠BOP,∵∠AOQ+∠BOP=90°,∴∠BOP=90°﹣3t,又∠BOC=180°﹣∠AOC=180°﹣30°﹣6t,∴180﹣30﹣6t=(90﹣3t),解得t= .【解析】【分析】(1)①由∠AOC=30°得到∠BOC=150°,借助角平分线定义求出∠POC 度数,根据角的和差关系求出∠COQ度数,再算出旋转角∠AOQ度数,最后除以旋转速度3即可求出t值;②根据∠AOQ和∠COQ度数比较判断即可;(2)根据旋转的速度和起始位置,可知∠AOQ=3t,∠AOC=30°+6t,根据角平分线定义可知∠COQ=45°,利用∠AOQ、∠AOC、∠COQ角之间的关系构造方程求出时间t;(3)先证明∠AOQ与∠POB 互余,从而用t表示出∠POB=90°﹣3t,根据角平分线定义再用t表示∠BOC度数;同时旋转后∠AOC=30°+6t,则根据互补关系表示出∠BOC度数,同理再把∠BOC度数用新的式子表达出来.先后两个关于∠BOC的式子相等,构造方程求解.9.已知:在和中,,,将如图摆放,使得的两条边分别经过点和点 .(1)当将如图1摆放时,则 ________度.(2)当将如图2摆放时,请求出的度数,并说明理由.(3)能否将摆放到某个位置时,使得、同时平分和?直接写出结论________(填“能”或“不能”)【答案】(1)240(2)∠ABD+∠ACD=40°;理由如下:∵∠E+∠F=100°∴∠D=180°−(∠E+∠F)=80°∴∠ABD+∠ACD=180°−∠A−∠DBC−∠DCB=180°−40°−(180°−80°)=40°;(3)不能【解析】【解答】解:(1)在△ABC中,∠A+∠ABC+∠ACB=180°,∠A=40°∴∠ABC+∠ACB=180°−∠A=180°−40°=140°在△BCD中,∠D+∠BCD+∠CBD=180°∴∠BCD+∠CBD=180°−∠D在△DEF中,∠D+∠E+∠F=180°∴∠E+∠F=180°−∠D∴∠CBD+∠BCD=∠E+∠F=100°∴∠ABD+∠ACD=∠ABC+∠CBD+∠ACB+∠BCD=140°+100°=240°;故答案为:240;( 3 )不能.假设能将△DEF摆放到某个位置时,使得BD、CD同时平分∠ABC和∠ACB.则∠CBD+∠BCD=∠ABD+∠ACD=100°,那么∠ABC+∠ACB=200°,与三角形内角和定理矛盾,所以不能.【分析】(1)要求∠ABD+∠ACD的度数,只要求出∠ABC+∠CBD+∠ACB+∠BCD,利用三角形内角和定理得出∠ABC+∠ACB=180°-∠A=180°-40°=140°;∠CBD+∠BCD=∠E+∠F=100°,从而得出答案;(2)要求∠ABD+∠ACD的度数,只要求出∠ABC+∠ACB-(∠BCD+∠CBD)的度数.根据三角形内角和定理,∠CBD+∠BCD=∠E+∠F=100°;根据三角形内角和定理得,∠ABC+∠ACB=180°-∠A=140°,得出∠ABD+∠ACD=∠ABC+∠ACB-(∠BCD+∠CBD)=140°-100°=40°;(3)不能,假设能将△DEF摆放到某个位置时,使得BD、CD同时平分∠ABC和∠ACB,则∠CBD+∠BCD=∠ABD+∠ACD=100°,那么∠ABC+∠ACB=200°,与三角形内角和定理矛盾,所以不能.10.如图,数轴上线段AB=2(单位长度),CD=4(单位长度),点A在数轴上表示的数是﹣10,点C在数轴上表示的数是16.若线段AB以6个单位长度/秒的速度向右匀速运动,同时线段CD以2个单位长度/秒的速度向左匀速运动.(1)问运动多少时BC=8(单位长度)?(2)当运动到BC=8(单位长度)时,点B在数轴上表示的数是________;(3)P是线段AB上一点,当B点运动到线段CD上时,是否存在关系式 =3,若存在,求线段PD的长;若不存在,请说明理由.【答案】(1)解:设运动t秒时,BC=8单位长度,①当点B在点C的左边时,由题意得:6t+8+2t=24解得:t=2(秒);②当点B在点C的右边时,由题意得:6t﹣8+2t=24解得:t=4(秒)(2)解:4或16(3)解:存在关系式 =3.设运动时间为t秒,1)当t=3时,点B和点C重合,点P在线段AB上,0<PC≤2,且BD=CD=4,AP+3PC=AB+2PC=2+2PC,当PC=1时,BD=AP+3PC,即 =3;2)当3<t<时,点C在点A和点B之间,0<PC<2,①点P在线段AC上时,BD=CD﹣BC=4﹣BC,AP+3PC=AC+2PC=AB﹣BC+2PC=2﹣BC+2PC,当PC=1时,有BD=AP+3PC,即 =3;点P在线段BC上时,BD=CD﹣BC=4﹣BC,AP+3PC=AC+4PC=AB﹣BC+4PC=2﹣BC+4PC,当PC= 时,有BD=AP+3PC,即 =3;3°当t= 时,点A与点C重合,0<PC≤2,BD=CD﹣AB=2,AP+3PC=4PC,当PC= 时,有BD=AP+3PC,即 =3;4°当<t 时,0<PC<4,BD=CD﹣BC=4﹣BC,AP+3PC=AB﹣BC+4PC=2﹣BC+4PC,PC= 时,有BD=AP+3PC,即 =3.∵P在C点左侧或右侧,∴PD的长有3种可能,即5或3.5【解析】【解答】解:(2)当运动2秒时,点B在数轴上表示的数是4;当运动4秒时,点B在数轴上表示的数是16.【分析】(1)设运动t秒时,BC=8(单位长度),然后分点B在点C的左边和右边两种情况,根据题意列出方程求解即可;(2)由(1)中求出的运动时间即可求出点B在数轴上表示的数;(3)随着点B的运动,分别讨论当点B和点C重合、点C在点A和B之间及点A与点C重合时的情况.11.如图1, .如图2,点分别是上的点,且, .(1)求证: F;(2)若的角平分线与的角平分线交于点,请补全图形并直接写出与之间的关系为________.【答案】(1)证明:如图,延长EH,交CD的延长线与M,(2)∠BFE=2∠P.【解析】【解答】解:(2)结论:∠BFE=2∠P,理由如下:如图,设∠B=∠HEF=y.∠BFE=x=,故答案为:∠BFE=2∠P.【分析】(1)延长EH,交CD的延长线与M,根据平行线的性质及等量代换即可证明;(2)设∠B=∠HEF=y,∠BFE=x,根据平行的性质结合三角形的内角和定理得出∠BFE=2∠P.12.已知:如图所示,直线,另一直线交于,交于,且,点为直线上一动点,过点的直线交于点,且 .(1)如图1,当点在点右边且点在点左边时,的平分线与的平分线交于点,求的度数;(2)如图2,当点在点右边且点在点右边时,的平分线与的平分线交于点,求的度数;(3)当点在点左边且点在点左边时,的平分线与的平分线所在直线交于点,请直接写出的度数,不说明理由.【答案】(1)解:过点作 .∵平分 .∴ .∴(两直线平行,内错角相等).同理可证..∴ .(2)解:过点作 .∵ .∴ .∵平分 .∴ .∴(两直线平行,同旁内角互补).∵平分 .∴(两直线平行,内错角相等).∴ .(3)解:过点作 .∵平分 .∴(两直线平行等,内错角相等).∴平分 ..∴ .∴(两直线平行,同旁内角互补)..【解析】【分析】(1)过点作,由角平分线定义可得,利用两直线平行内错角相等,可得,同理可得∠CPE=∠PCA= ∠DCA=25°,从而求出∠BPC的度数.(2)过点作 . 利用邻补角定义可得∠DBA=100°,由角平分线定义可得∠DBP= ∠DBA=50°,根据两直线平行,同旁内角互补可得∠BPE=130°.根据角平分线定义及两直线平行,内错角相等角可得∠PCA=∠CPE= ∠DCA=25°,从而求∠BPC的度数.(3)过点作 . 根据两直线平行,内错角相等角可得∠DBP=∠DPE=40°,根据邻补角可求出∠CPE的度数,由角平分线的定义可得∠PCA= ∠DCA=65°,根据两直线平行,同旁内角互补可求出∠CPE的度数,继而求出∠BPC的度数.13.已知BE平分∠ABD,DE平分∠BDC,且∠BED =∠ABE +∠EDC.(1)如图1,求证:AB//CD;(2)如图2,若∠ABE=3∠ABF,且∠BFD=30°时,试求的值;(3)如图3,若H是直线CD上一动点(不与D重合),BI平分∠HBD,画出图形,并探究出∠EBI与∠BHD的数量关系.【答案】(1)证明:∵∠BED =∠ABE +∠EDC,∠EBD+∠BED+∠BDE=180°,∴∠ABD+∠BDC=180°,∴AB∥CD(2)解:∵BE平分∠ABD,DE平分∠BDC,∴∠ABE=∠EBD,∠EDC=∠EDB.∵∠ABD+∠BDC=180°,∴∠BED=∠ABE+∠EDC=90°.设∠ABF=α,则∠ABE=3α.如图,过F作FG∥AB,则有:∠ABF+∠CDF=∠BFD,∴∠CDF=30°-α.过E作EH∥AB,则有:∠ABE+∠CDE=∠BED,∴∠CDE=90°-3α,∴∠FDE=60°-2α,∴.(3)解:分两种情况讨论:①当H在点D的左边时,如图3.设∠HBI=∠DBI=x,∠EBH=y,则∠EBD=2x+y,∴∠ABE=∠EBD=2x+y.∵AB∥CD,∴∠BHD=∠ABH=2x+y+y=2(x+y)=2∠EBI;②当H在点D右边时,如图4.设∠HBI=∠DBI=x,∠EBD=y,则∠EBI=x+y,∴∠ABH=2x+2y.∵AB∥CD,∴∠ABH+∠BHD=180°,∴2x+2y+∠BHD=180°,∴∠BHD+2∠EBI=180°.综上所述:∠BHD=2∠EBI或∠BHD+2∠EBI=180°【解析】【分析】(1)由∠BED =∠ABE +∠EDC和三角形内角和定理即可得到∠ABD+∠BDC=180°,再由同旁内角互补,两直线平行即可得到结论;(2)由角平分线定义和∠ABD+∠BDC=180°,得到∠BED=∠ABE+∠EDC=90°.设∠ABF=α,则∠ABE=3α,过F作FG∥AB,则有∠ABF+∠CDF=∠BFD,得到∠CDF=30°-α.过E作EH∥AB,同理可得:∠CDE=90°-3α,根据角的和差得到∠FDE=60°-2α,即可得到结论;(3)分两种情况讨论:①当H在点D的左边时,②当H在点D右边时.14.如图1,直线CB∥OA,∠A=∠B=120°,E ,F在BC上,且满足∠FOC =∠AOC,并且OE 平分∠BOF.(1)求∠AOB及∠EOC的度数;(2)如图2,若平行移动AC,那么∠OCB: ∠OFB的值是否随之发生变化?若变化,找出变化规律或求出变化范围;若不变,求出这个比值;【答案】(1)解:∵CB∥OA∴∠BOA+∠B=180°∴∠BOA=60°∵∠FOC=∠AOC,OE平分∠BOF∴∠EOC=∠EOF+∠FOC= ∠BOF+ ∠F0A= (∠BOF+∠FOA)= ×60°=30°(2)解:不变∵CB∥OA∴∠OCB=∠COA,∠OFB=∠FOA∵∠FOC=∠AOC∴∠COA= ∠FOA, 即∠OCB:∠OFB=1:2【解析】【分析】(1)利用两直线平行,同旁内角互补,易证∠BOA+∠B=180°,即可求出∠AOB的度数;再利用角平分线的定义,可证得∠BOE=∠EOF,从而可推出∠EOC=∠AOB,代入计算求出∠EOC的度数。
