决策树ID3算法的实例解析.
id3算法对天气-打球关系的决策树

ID3算法是一种用于构建决策树的经典机器学习算法,它可以根据给定的数据集,自动构建出一个决策树模型,用于对未知数据进行分类。
在实际应用中,ID3算法被广泛应用于各种领域,包括天气预测和决策制定。
本文将以天气和是否适合打球这一主题为例,具体介绍ID3算法对于天气-打球关系的决策树。
1. 背景介绍天气对于人们的日常生活有着重要的影响,尤其是对于室外活动,比如打球。
在实际生活中,人们往往会根据当天的天气情况来决定是否适合进行打球活动。
而要根据天气来进行决策,就需要建立一个天气-打球的决策模型。
而ID3算法正是用来构建这样的决策模型的利器。
2. 数据采集为了构建天气-打球的决策树模型,首先需要收集一定量的天气相关数据和打球相关数据。
可以记录每天的天气情况(如晴天、阴天、下雨)、温度、湿度等天气指标,以及当天是否适合进行打球活动(是/否)。
通过收集大量的这样的数据,就可以构建出一个合适的数据集。
3. 分析数据在收集到足够的数据后,就可以开始分析这些数据,寻找天气与打球之间的关系。
ID3算法的核心思想是选择最佳的属性来进行划分,以便对数据进行分类。
在本例中,可以将天气指标(如晴天、阴天、下雨)作为属性,将打球活动(是/否)作为分类结果,然后根据ID3算法来选择最佳的属性进行数据划分,从而构建出决策树模型。
4. 构建决策树在进行数据分析后,就可以利用ID3算法来构建天气-打球的决策树。
ID3算法通过计算信息增益来确定最佳的属性,然后进行递归地对数据进行划分,直到构建出完整的决策树模型。
在这个过程中,ID3算法会根据不同的属性值来确定最佳的决策点,从而使得对于未知天气情况的打球决策变得更加准确。
5. 评估和优化构建出决策树模型后,还需要对模型进行评估和优化。
可以利用交叉验证等方法来检验模型的准确性,并根据验证结果对模型进行调整和优化。
这一步骤是非常重要的,可以帮助进一步提高决策树模型的预测能力。
6. 应用和推广构建出决策树模型后,可以将其应用到实际的天气预测和打球决策中。
决策树ID3分类算法
决策树ID3分类算法一、ID3算法介绍决策树学习是一种逼近离散值目标函数的方法,在这种方法中学习到的函数被表示为一颗决策树。
ID3算法的思想就是自顶向下构造决策树,它使用统计测试来确定每一个实例属性单独分类训练样例的能力,继而判断哪个属性是最佳的分类属性,直到建立一棵完整的决策树。
利用这棵决策树,我们可以对新的测试数据进行分类。
二、算法的实现算法实现了对于给定的数据信息, 基于信息增益构造决策树,最后给出决策树和对训练数据集的分类准确率。
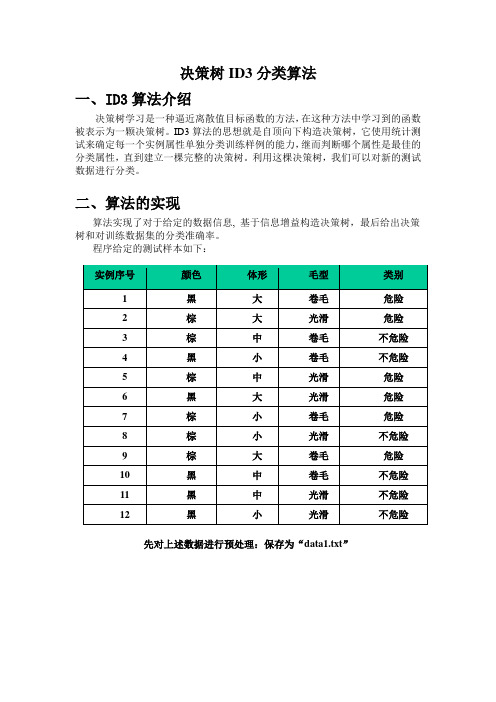
程序给定的测试样本如下:实例序号颜色体形毛型类别1黑大卷毛危险2棕大光滑危险3棕中卷毛不危险4黑小卷毛不危险5棕中光滑危险6黑大光滑危险7棕小卷毛危险8棕小光滑不危险9棕大卷毛危险10黑中卷毛不危险11黑中光滑不危险12黑小光滑不危险先对上述数据进行预处理:保存为“data1.txt”再运行程序,读入数据,输出分析过程和决策规则:中间还有一些过程,为了节约资源,不复制过来了,下面是决策规则:根据该规则,树形图如下:三、程序代码及其部分注释其中最核心的部分:void Generate_decision_tree(Tree_Node * & root,vector<int> Samples, vector<int> attribute_list,int class_id)该函数由给定的训练数据产生一棵判定树。
完整代码:#include <stdio.h>#include <iostream>#include <vector>#include <math.h>#include <string.h>using namespace std;typedef struct tnode{char tdata[100];}tnode;typedef struct Tree_Node{char name[100];bool isLeaf; //标记是否叶子节点vector<tnode> att_list;//属性名称列表vector<Tree_Node * > child_list;}Tree_Node,* pTreeNpde;typedef struct dnode{vector<tnode>row;}dnode;typedef struct D_Node{vector<dnode>DB;vector<tnode> attr_name;tnode class_name;}D_Node;D_Node G_DB;pTreeNpde Root = NULL;typedef struct FreeQNode{char name[100];int count;vector<int> Set_ID;}FreeQNode;typedef struct FreeQNodeDouble{char name[100];int count;vector<int> row_id;vector<FreeQNode> classes;//存放分类属性列表及相应的出现次数}FreeQNodeDouble;typedef struct attr_node{int attr_id;vector<tnode> attr_name;vector<int> count_list;}attr_node;vector<attr_node> G_Attr_List;typedef struct binNode{char name[100];int count;vector<int> Set_ID;struct binNode * lchild;struct binNode * rchild;}binNode;typedef struct binNodeDouble{char name[100];int count;vector<int> row_id;struct binNodeDouble * lchild;struct binNodeDouble * rchild;vector<FreeQNode> classes;}binNodeDouble;void insert_tree(binNode * & r, char str[100]){if (NULL == r){binNode * node = new binNode;strcpy(node->name,str);node->count = 1;//printf("[%s,%d]\n",node->name,node->count);node->lchild = node->rchild = NULL;r = node;}else{if (strcmp(r->name,str) == 0){r->count ++;}else if (strcmp(r->name,str) < 0){insert_tree(r->lchild,str);}else{insert_tree(r->rchild,str);}}}void delete_bin_tree(binNode *& r){if (r != NULL){delete_bin_tree(r->lchild);delete_bin_tree(r->rchild);delete(r);r = NULL;}}void Bin_tree_inorder(binNode * r,vector<FreeQNode> & Fq) {if (r != NULL){Bin_tree_inorder(r->lchild,Fq);FreeQNode ft;//printf("%s,%d\n",r->name,r->count);strcpy(,r->name);ft.count = r->count;for (int i= 0;i < r->Set_ID.size();i++){ft.Set_ID.push_back(r->Set_ID[i]); //保存子集对应的ID号}Fq.push_back(ft); //此处少了这条语句,造成结果无法返回Bin_tree_inorder(r->rchild,Fq);}}void Get_attr(binNode * r,attr_node & attr){if (r != NULL){Get_attr(r->lchild,attr);tnode t;strcpy(t.tdata,r->name);//printf("%s,%d\n",r->name,r->count);attr.attr_name.push_back(t);attr.count_list.push_back(r->count);//保存出现次数Get_attr(r->rchild,attr);}}void insert_tree_double(binNodeDouble *& r, int DB_ID,char attr_name[100],char class_name[100]){if (NULL == r){binNodeDouble * node = new binNodeDouble;strcpy(node->name,attr_name);node->count = 1;node->row_id.push_back(DB_ID);node->lchild = node->rchild = NULL;FreeQNode fq;strcpy(,class_name);fq.count = 1;fq.Set_ID.push_back(DB_ID); //保存子集所对应的ID号node->classes.push_back(fq);r= node;}else{if (strcmp(r->name,attr_name) == 0){r->count ++;r->row_id.push_back(DB_ID);//这里也需要保存相应的ID号bool found = false;for (int i = 0; i< r->classes.size();i++){if (strcmp(r->classes[i].name,class_name) == 0){r->classes[i].count ++;r->classes[i].Set_ID.push_back(DB_ID);//保存子集对应的ID号found = true; //发现相同的变量名,计数器增1,break; //并退出循环}}if (!found){FreeQNode fq;strcpy(,class_name);fq.count = 1;fq.Set_ID.push_back(DB_ID);//保存子集所对应的ID号r->classes.push_back(fq);}}else if (strcmp(r->name,attr_name) < 0){insert_tree_double(r->lchild,DB_ID,attr_name,class_name);}else{insert_tree_double(r->rchild,DB_ID,attr_name,class_name);}}void delete_bin_tree_double(binNodeDouble *& r){if (r != NULL){delete_bin_tree_double(r->lchild);delete_bin_tree_double(r->rchild);delete(r);r = NULL;}}void Bin_tree_inorder_double(binNodeDouble *& r,vector<FreeQNodeDouble> &Fq){if (r != NULL){Bin_tree_inorder_double(r->lchild,Fq);FreeQNodeDouble ft;strcpy(,r->name); //保存候属性的名称ft.count = r->count;for (int k = 0;k< r->row_id.size();k++){ft.row_id.push_back(r->row_id[k]);}//printf("doubleTree. %s,%d\n",r->name,r->count);for (int i = 0;i< r->classes.size();i++){FreeQNode fq;strcpy(,r->classes[i].name);fq.count = r->classes[i].count;for (int j = 0;j < r->classes[i].Set_ID.size();j++){fq.Set_ID.push_back( r->classes[i].Set_ID[j]); //保存子集对应的ID号}ft.classes.push_back(fq);}Fq.push_back(ft);ft.classes.erase(ft.classes.begin(),ft.classes.end());//使用完,必须清空Bin_tree_inorder_double(r->rchild,Fq);}}void getFqI(vector<int> S,int class_id,vector<FreeQNode> & Fq){binNode * root = NULL;for (int i = 0;i< S.size();i++){insert_tree(root,G_DB.DB[S[i]].row[class_id].tdata);}Bin_tree_inorder(root,Fq);delete_bin_tree(root);}void getFqIA(vector<int> S,int attr_id,int class_id,vector<FreeQNodeDouble> & Fq){binNodeDouble * root = NULL;for (int i = 0;i< S.size();i++){insert_tree_double(root,S[i],G_DB.DB[S[i]].row[attr_id].tdata,G_DB.DB[S[i]].row[class_id] .tdata);}Bin_tree_inorder_double(root,Fq);delete_bin_tree_double(root);}void readdata(char *filename){char str[1000];FILE * fp;fp = fopen(filename,"r");fgets(str,1000,fp);int len = strlen(str);int attr_no = 0; //属性个数int row_num = 0;if (str != NULL){row_num = 1;}for (int i = 0;i< len;i++){if (str[i] == '\t'){attr_no ++;}}attr_no ++;//最后一个是回车,整个属性值+1printf("%d\n",attr_no);while(fgets(str,1000,fp) != NULL){row_num ++; //统计行数}fclose(fp);fopen(filename,"r");tnode t;for (i = 0;i<attr_no;i++){fscanf(fp,"%s",t.tdata);G_DB.attr_name.push_back(t);printf("%s\n",t.tdata);}strcpy(G_DB.class_name.tdata,G_DB.attr_name[attr_no-1].tdata); for (int j = 1;j< row_num;j++){dnode dt;tnode temp;for (int i = 0;i<attr_no;i++){fscanf(fp,"%s",temp.tdata);dt.row.push_back(temp);}G_DB.DB.push_back(dt);dt.row.erase(dt.row.begin(),dt.row.end());}printf("%d\n",G_DB.DB.size());for (i = 0;i< G_DB.DB.size();i++){for (int j = 0;j< G_DB.DB[i].row.size();j++){printf("%s\t",G_DB.DB[i].row[j].tdata);}printf("\n");}}double Fnc_I(vector<int> S,int class_id){//给定一个子集,计算其按照class_id所对应的分类属性进行分类时的期望I// printf("called Fnc_I(%d)\n ",class_id);vector<FreeQNode> Fq;getFqI(S,class_id,Fq); //调用getFqI获取按照Class_id为分类标准的分类结果,当Fq中为一条数据时,则子集S都属于一个分类//否则,从中找到出现此时最大的,作为返回结果// printf("begin to compute I \n");double total = 0;for (int i = 0;i< Fq.size();i++){total += Fq[i].count;// printf("%s,%d\n",Fq[i].name,Fq[i].count);}double result = 0;if (0 == total){return 0;}for (i = 0;i< Fq.size();i++){double p = Fq[i].count/total;result += -1*(p * log(p)/log(2));}// printf("FNC_I return\n\n");return result;}double Fnc_IA(vector<int> S,int attr_id,int class_id,vector<FreeQNodeDouble> & Fq) {//给定一个子集,计算其按照class_id所对应的分类属性进行分类时的期望I getFqIA(S,attr_id,class_id,Fq);double total = 0;for (int i = 0;i< Fq.size();i++){total += Fq[i].count;}double result = 0;if (0 == total){return 0;}bool pr= false;for (i = 0;i< Fq.size();i++){double stotal = Fq[i].count;double sresult = 0;if (pr) printf("[%s,%d]\n",Fq[i].name,Fq[i].count);for (int j = 0;j < Fq[i].classes.size();j++){if (pr) printf("%s,%d\n",Fq[i].classes[j].name,Fq[i].classes[j].count);for (int k = 0;k < Fq[i].classes[j].count;k++){// printf("%d\t",Fq[i].classes[j].Set_ID[k]+1);}//printf("\n");double sp = Fq[i].classes[j].count/stotal; //计算子集的频率sresult += -1*(sp*log(sp)/log(2));}result += (stotal/total) * sresult;}if (pr) printf("\n");return result;}int SelectBestAttribute(vector<int> Samples,vector<int> attribute_list,int class_id) {//输入训练数据集Samples,候选属性列表attribute_list//分类属性标记class_id//返回best_attributedouble fi = Fnc_I(Samples,5);// printf("%lf\n",fi);double IA = 999999999;int best_attrib = -1;for (int i = 0;i < attribute_list.size();i++){vector<FreeQNodeDouble> fqd;double tfa = Fnc_IA(Samples,attribute_list[i],class_id,fqd);// printf("%d, FIA = %lf\n",i,tfa);if (IA > tfa){IA = tfa;best_attrib = i;}}//printf("%lf\n",IA);printf("gain(%d) = %lf - %lf = %lf\n",best_attrib,fi,IA,fi - IA);return attribute_list[best_attrib];}void fnc_getattr(vector<int> Samples,int att_id,attr_node &at){binNode * root = NULL;for (int i = 0;i< Samples.size();i++){insert_tree(root,G_DB.DB[Samples[i]].row[att_id].tdata);}Get_attr(root,at);delete_bin_tree(root);}void get_class_num_and_name(vector<int> Samples,int class_id,int & class_num,tnode & class_name){attr_node at;binNode * root = NULL;for (int i = 0;i< Samples.size();i++){insert_tree(root,G_DB.DB[Samples[i]].row[class_id].tdata);}Get_attr(root,at);delete_bin_tree(root);//printf("att_size = %d\n",at.attr_name.size());class_num = at.attr_name.size();int num = 0;int id = 0;if (1 == class_num){strcpy(class_name.tdata,at.attr_name[0].tdata);}else{for (int j = 0;j < at.attr_name.size();j++ ){if (at.count_list[j] > num){num = at.count_list[j];id = j;}}}strcpy(class_name.tdata,at.attr_name[id].tdata);//保存最普通的类名}void getAllTheAttribute(vector<int> Samples,vector<int> attribute_list,int class_id){printf("all the attribute are:\n");for (int i = 0;i < attribute_list.size();i++){attr_node at;at.attr_id = attribute_list[i];fnc_getattr(Samples,attribute_list[i],at);G_Attr_List.push_back(at);}for (i = 0;i <G_Attr_List.size();i++){printf("%d\n",G_Attr_List[i].attr_id);for (int j = 0;j< G_Attr_List[i].attr_name.size();j++){printf("%s\t",G_Attr_List[i].attr_name[j].tdata);}printf("\n");}}void Generate_decision_tree(Tree_Node * & root,vector<int> Samples, vector<int>attribute_list,int class_id){/*算法:Generate_decision_tree(samples, attribute)。
仿照例题,使用id3算法生成决策树

标题:使用ID3算法生成决策树一、概述在机器学习领域,决策树是一种常见的分类和回归算法。
它基于一系列属性对数据进行划分,最终生成一棵树状图来表示数据的分类规则。
在本文中,我们将介绍ID3算法,一种经典的决策树生成算法,并演示如何使用ID3算法生成决策树。
二、ID3算法概述ID3算法是一种基于信息论的决策树生成算法,其全称为Iterative Dichotomiser 3。
它由Ross Quinlan于1986年提出,是C4.5算法的前身。
ID3算法的核心思想是在每个节点选择最佳的属性进行划分,使得各个子节点的纯度提高,从而最终生成一棵有效的决策树。
ID3算法的主要步骤包括计算信息增益、选择最佳属性、递归划分数据集等。
在这一过程中,算法会根据属性的信息增益来确定最佳的划分属性,直到满足停止条件为止。
三、使用ID3算法生成决策树的步骤使用ID3算法生成决策树的步骤如下:1. 收集数据集:需要收集一个包含多个样本的数据集,每个样本包含多个属性和一个类别标签。
2. 计算信息增益:对每个属性计算信息增益,信息增益越大表示该属性对分类的贡献越大。
3. 选择最佳属性:选择信息增益最大的属性作为当前节点的划分属性。
4. 划分数据集:根据选择的属性值将数据集划分成若干子集,每个子集对应属性的一个取值。
5. 递归生成子节点:对每个子集递归调用ID3算法,生成子节点,直到满足停止条件。
6. 生成决策树:将所有节点连接起来,生成一棵完整的决策树。
四、使用ID3算法生成决策树的示例为了更好地理解ID3算法的生成过程,我们以一个简单的示例来说明。
假设有一个包含天气、温度和湿度三个属性的数据集,我们希望使用ID3算法生成一个决策树来预测是否适合外出活动。
我们需要计算每个属性的信息增益。
然后选择信息增益最大的属性进行划分,将数据集划分成若干子集。
接着递归调用ID3算法,直到满足停止条件为止。
经过计算和递归划分,最终我们得到一棵决策树,可以根据天气、温度和湿度来预测是否适合外出活动。
机器学习-ID3决策树算法(附matlaboctave代码)
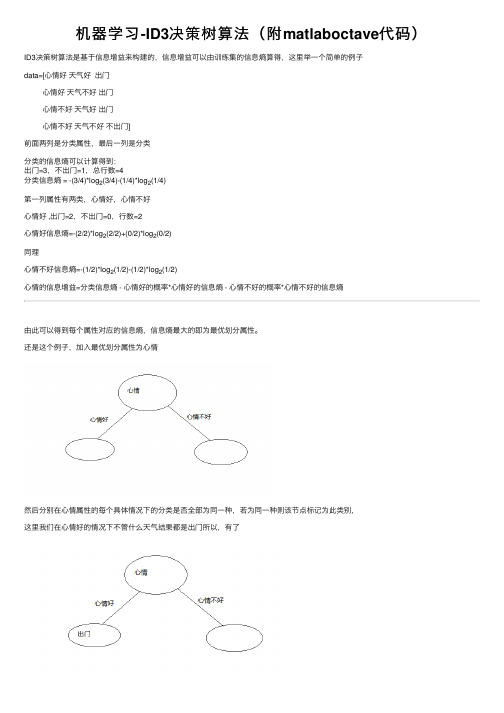
机器学习-ID3决策树算法(附matlaboctave代码)ID3决策树算法是基于信息增益来构建的,信息增益可以由训练集的信息熵算得,这⾥举⼀个简单的例⼦data=[⼼情好天⽓好出门⼼情好天⽓不好出门⼼情不好天⽓好出门⼼情不好天⽓不好不出门]前⾯两列是分类属性,最后⼀列是分类分类的信息熵可以计算得到:出门=3,不出门=1,总⾏数=4分类信息熵 = -(3/4)*log2(3/4)-(1/4)*log2(1/4)第⼀列属性有两类,⼼情好,⼼情不好⼼情好 ,出门=2,不出门=0,⾏数=2⼼情好信息熵=-(2/2)*log2(2/2)+(0/2)*log2(0/2)同理⼼情不好信息熵=-(1/2)*log2(1/2)-(1/2)*log2(1/2)⼼情的信息增益=分类信息熵 - ⼼情好的概率*⼼情好的信息熵 - ⼼情不好的概率*⼼情不好的信息熵由此可以得到每个属性对应的信息熵,信息熵最⼤的即为最优划分属性。
还是这个例⼦,加⼊最优划分属性为⼼情然后分别在⼼情属性的每个具体情况下的分类是否全部为同⼀种,若为同⼀种则该节点标记为此类别,这⾥我们在⼼情好的情况下不管什么天⽓结果都是出门所以,有了⼼情不好的情况下有不同的分类结果,继续计算在⼼情不好的情况下,其它属性的信息增益,把信息增益最⼤的属性作为这个分⽀节点,这个我们只有天⽓这个属性,那么这个节点就是天⽓了,天⽓属性有两种情况,如下图在⼼情不好并且天⽓好的情况下,若分类全为同⼀种,则改节点标记为此类别有训练集可以,⼼情不好并且天⽓好为出门,⼼情不好并且天⽓不好为不出门,结果⼊下图对于分⽀节点下的属性很有可能没有数据,⽐如,我们假设训练集变成data=[⼼情好晴天出门⼼情好阴天出门⼼情好⾬天出门⼼情好雾天出门⼼情不好晴天出门⼼情不好⾬天不出门⼼情不好阴天不出门]如下图:在⼼情不好的情况下,天⽓中并没有雾天,我们如何判断雾天到底是否出门呢?我们可以采⽤该样本最多的分类作为该分类,这⾥天⽓不好的情况下,我们出门=1,不出门=2,那么这⾥将不出门,作为雾天的分类结果在此我们所有属性都划分了,结束递归,我们得到了⼀颗⾮常简单的决策树。
华工人工智能ID3算法问题详解-基于信息熵的ID3算法

华工人工智能ID3算法问题详解基于信息熵的ID3算法 ID3算法是一个典型的决策树学习算法,其核心是在决策树的各级节点上,使用信息增益方法作为属性的选择标准,来帮助确定生成每个节点时所应采用的合适属性。
这样就可以选择具有最高信息增益属性作为当前节点的测试属性,以便使用该属性所划分获得的训练样本子集进行分类所需信息最小。
定义1 设U 是论域,{}n X X ,...,1是U 的一个划分,其上有概率分布)(i i X P p =,则称:∑=-=ni i i p p X H 1log )(为信源X 的信息熵,其中对数取以2为底,而当某个i p 为零时,则可以理解为00log 0=⋅。
定义2 设⎭⎬⎫⎩⎨⎧⋯⋯=n n q q q Y Y Y Y 2121是一个信息源,即{}n Y Y Y ,,,21⋯是U 的另一个划分,j j q Y P =)(,∑==n j j q 11,则已知信息源X 是信息源Y 的条件熵H(Y|X)定义为:∑==ni i i X Y H X P X Y H 1)|()()|(其中∑=-=nj i j i j i X Y P X Y P X Y H 1)|(log )|()|(为事件i X 发生时信息源Y 的条件熵。
在ID3算法分类问题中,每个实体用多个特征来描述,每个特征限于在一个离散集中取互斥的值。
ID3算法的基本原理如下:设n F F F E ⨯⋯⨯⨯=21是n 维有穷向量空间,其中i F 是有穷离散符号集。
E 中的元素>⋯=<n V V V e ,,,21称为样本空间的例子,其中i j F V ∈,),,2,1(n j ⋯=。
为简单起见,假定样本例子在真实世界中仅有两个类别,在这种两个类别的归纳任务中,PE 和NE 的实体分别称为概念的正例和反例。
假设向量空间E 中的正、反例集的大小分别为P 、N ,由决策树的基本思想,ID3算法是基于如下2种假设:(1)在向量空间E 上的一棵正确的决策树对任意样本集的分类概率同E 中的正、反例的概率一致。
决策树ID3算法

决策树ID3算法决策树ID3算法决策树是对数据进行分类,以此达到预测的目的。
该决策树方法先根据训练集数据形成决策树,如果该树不能对所有对象给出正确的分类,那么选择一些例外加入到训练集数据中,重复该过程一直到形成正确的决策集。
决策树代表着决策集的树形结构。
决策树由决策结点、分支和叶子组成。
决策树中最上面的结点为根结点,每个分支是一个新的决策结点,或者是树的叶子。
每个决策结点代表一个问题或决策,通常对应于待分类对象的属性。
每一个叶子结点代表一种可能的分类结果。
沿决策树从上到下遍历的过程中,在每个结点都会遇到一个测试,对每个结点上问题的不同的测试输出导致不同的分支,最后会到达一个叶子结点,这个过程就是利用决策树进行分类的过程,利用若干个变量来判断所属的类别。
2.ID3算法:ID3算法是由Quinlan首先提出的。
该算法是以信息论为基础,以信息熵和信息增益度为衡量标准,从而实现对数据的归纳分类。
以下是一些信息论的基本概念:定义1:若存在n个相同概率的消息,则每个消息的概率p是1/n,一个消息传递的信息量为Log2(n) 定义2:若有n个消息,其给定概率分布为P=(p1,p2…pn),则由该分布传递的信息量称为P的熵,记为I(p)=-(i=1 to n求和)piLog2(pi)。
定义3:若一个记录集合T根据类别属性的值被分成互相独立的类C1C2..Ck,则识别T的一个元素所属哪个类所需要的信息量为Info(T)=I(p),其中P为C1C2…Ck的概率分布,即P=(|C1|/|T|,…..|Ck|/|T|)定义4:若我们先根据非类别属性X的值将T分成集合T1,T2…Tn,则确定T中一个元素类的信息量可通过确定Ti的加权平均值来得到,即Info(Ti)的加权平均值为:Info(X, T)=(i=1 to n 求和)((|Ti|/|T|)Info(Ti))定义5:信息增益度是两个信息量之间的差值,其中一个信息量是需确定T的一个元素的信息量,另一个信息量是在已得到的属性X的值后需确定的T一个元素的信息量,信息增益度公式为:Gain(X, T)=Info(T)-Info(X, T)为方便理解,在此举例说明算法过程,具体算法其实很简单,呵呵:某市高中一年级(共六个班)学生上学期期末考试成绩数据库。
决策树ID3算法的实例解析

根据票数排名筛选出10大算法 (如果票数相同,则按字母顺序进行排名)
数据挖掘10大算法产生过程
1 2 3 4
三步鉴定流程 18种通过审核的候选算法 算法陈述 数据挖掘10大算法:一览
5
开放式讨论
18种通过审核的候选算法
§分类(Classification)
1. C4.5: Quinlan, J. R. 1993. C4.5: Programs for Machine Learning. Morgan Kaufmann Publishers Inc. 2. CART: L. Breiman, J. Friedman, R. Olshen, and C. Stone. Classification and Regression Trees. Wadsworth, Belmont, CA, 1984. 3. K Nearest Neighbours (kNN): Hastie, T. and Tibshirani, R. 1996. Discriminant Adaptive Nearest Neighbor Classification. IEEE Trans. Pattern Anal. Mach. Intell. (TPAMI). 18, 6 (Jun. 1996), 607-616. 4. Naive Bayes Hand, D.J., Yu, K., 2001. Idiot's Bayes: Not So Stupid After All? Internat. Statist. Rev. 69, 385-398.
共有145人参加了ICDM 2006 Panel (会议的专题讨论),并对18种 候选算法进行投票,选出了数据挖掘10大算法
排名 挖掘主题
机器学习-决策树之ID3算法

机器学习-决策树之ID3算法概述决策树(Decision Tree)是⼀种⾮参数的有监督学习⽅法,它是⼀种树形结构,所以叫决策树。
它能够从⼀系列有特征和标签的数据中总结出决策规则,并⽤树状图的结构来呈现这些规则,以解决分类和回归问题。
决策树算法容易理解,适⽤各种数据,在解决各种问题时都有良好表现,尤其是以树模型为核⼼的各种集成算法,在各个⾏业和领域都有⼴泛的应⽤。
决策树的核⼼有三种算法:ID3:ID3 是最早提出的决策树算法,他就是利⽤信息增益来选择特征的。
C4.5:他是 ID3 的改进版,他不是直接使⽤信息增益,⽽是引⼊“信息增益⽐”指标作为特征的选择依据。
CART:这种算法即可以⽤于分类,也可以⽤于回归问题。
CART 算法使⽤了基尼系数取代了信息熵模型。
ID3算法是本教程的重点要讲的内容,其余两种算法将会后续推出。
数据集下⾯举个例⼦,会使⽤ID3算法帮助我们判断今天的天⽓适不适合出去打球。
进⾏判断之前,需要历史天⽓数据和打球活动数据,以下为历史数据集S。
天数天⽓⽓温湿度风⼒是否打球D1晴朗热湿弱否D2晴朗热湿强否D3⼤⾬热湿弱是D4⼩⾬中等湿弱是D5⼩⾬凉爽正常弱是D6⼩⾬凉爽正常强否D7⼤⾬凉爽正常强是D8晴朗中等湿弱否D9晴朗凉爽正常弱是D10⼩⾬中等正常弱是D11晴朗中等正常强是D12⼤⾬中等湿强是D13⼤⾬热正常弱是D14⼩⾬中等湿强否ID3算法ID3算法会选择当前信息增益最⼤的特征作为树中新的节点。
计算过程如下:步骤1假设S为完整的数据集,数据标签(数据类别)共有n个类别,分别为C1,...,Cn。
Si对应Ci类别下数据⼦集,因此,数据集S的信息熵计算如下:\[Entropy(S)=-\sum_{i=1}^{n}p_{i}\log_{2}{p_{i}} \]其中,pi是数据样本为Ci的概率,因此:\[p_i=\frac{|S_i|}{|S|} \]|Si|是类别Ci在数据集S中的数据数量,|S|是数据集S中的数据数量。
