质子交换膜燃料电池温度的神经网络PID控制设计
基于变论域模糊增量理论的质子交换膜燃料电池温度控制

基于变论域模糊增量理论的质子交换膜燃料电池温度控制谢雨岑;邹见效;彭超【摘要】质子交换膜燃料电池(PEMFC)内部的电化学反应过程直接表现为温度的变化,所以有效的温度控制是保证燃料电池可靠性和耐久性的关键.本文将模糊增量控制用于PEMFC热管理系统中,将PEMFC的温度和电堆出入口温度差保持在设定值.首先,建立PEMFC热管理系统的动态模型,包括PEMFC电堆模型和辅助散热设备模型.然后,基于建立的系统模型,设计了一种变论域的模糊增量控制器.该控制器通过伸缩因子来动态调节模糊控制器中的量化因子和比例因子,实现对模糊论域的调节,从而提高控制的灵敏性和精确度.最后,将该温度控制方法用于10 kW燃料电池系统中,实验结果表明变论域模糊增量控制器相比于其他模糊控制方法,不仅具有更快的动态响应速度,还具有更强的鲁棒性和更高的控制精度.【期刊名称】《控制理论与应用》【年(卷),期】2019(036)003【总页数】8页(P428-435)【关键词】燃料电池;动态模型;温度控制;变论域模糊增量控制【作者】谢雨岑;邹见效;彭超【作者单位】电子科技大学自动化工程学院,四川成都611731;电子科技大学自动化工程学院,四川成都611731;电子科技大学自动化工程学院,四川成都611731【正文语种】中文1 引言燃料电池是一种直接将化学能转换为电能的装置,由于其清洁、无污染、能量效率高,被认为是新能源应用的重要方向[1–2].在众多燃料电池中,质子交换膜燃料电池(proton exchange membrane fuel cell,PEMFC)以其工作温度低、结构紧凑、比能量高等突出特点,被认为是具有发展潜力的能源技术[3–4].近年来,PEMFC已被应用于分布式电站、备用电源、电动汽车等领域,成为了新能源领域的研究热点[5].实际应用中PEMFC存在负载动态变化、系统扰动等情况,由此引起的温度变化会影响其输出性能和使用寿命.因此,有效的热管理是保证燃料电池高性能、长寿命运行的关键.将PEMFC工作温度控制在设定值,避免过高温度造成质子交换膜的降解,较低温度导致电池性能的衰减[6].此外,考虑到燃料电池内温度分布的均匀性,避免燃料电池堆出入口温差过大对电堆性能的影响,还需要将PEMFC电堆出入口温差控制在一定的范围内[7].目前,已有学者对燃料电池的温度控制开展了研究,提出了一些控制方法,如比例积分(proportional integral,PI)控制[8]、状态反馈控制[9]、分段预测负反馈控制[10]、非线性前馈与线性二次型调节器(linear quadratic regulator,LQR)反馈控制[11]、广义预测控制[12]等.然而,燃料电池系统固有的非线性以及模型参数的不确定性,使这些控制方法存在局限性.特别是,当负载动态变化和系统参数摄动时,常规的控制策略会造成不可接受的闭环性能.模糊控制是一种基于语言规则的智能控制,它不依赖于精确的被控对象模型,具有结构简单、适应性好、鲁棒性强等优点,近年来被应用于燃料电池热管理系统中[13–14].然而现有的模糊温度控制器还存在一些不足.文献[13]中模糊控制器考虑了外部扰动,却未解决模糊控制器稳态精度较差的问题.文献[14]中增量型模糊控制器可以消除静态误差,但其控制精度却受控制规则数目的限制.所以,本文针对现有模糊控制器存在的不足,设计了变论域模糊增量控制器来实现燃料电池温度的无静差、高精度控制.将模糊增量控制器作为基本控制器,用来消除静差,实现温度的渐进稳定控制[15–16].在控制规则有限的情况下,通过伸缩因子对模糊论域进行收缩或膨胀,间接增加了控制规则数,从而达到提高控制精度的目的.此外,变论域模糊控制还可以加快系统在大误差范围时的动态响应速度,避免系统陷入小偏差范围内的调节死区,进一步提高控制系统的动静态性能和鲁棒性.本文提出了一种变论域模糊增量控制方法用于燃料电池的热管理系统中.首先,介绍PEMFC热管理系统,并在Simulink平台上建立简化的燃料电池热管理系统的动态模型,包括电池堆模型和辅助散热设备模型.然后,基于控制规则设计变论域的模糊增量控制器用于PEMFC温度和电堆出入口温差控制.最后,对设计的模糊控制器进行实验验证,并与其他模糊增量控制器进行性能比较.2 热管理系统描述PEMFC热管理系统结构如图1所示,该系统是由PEM燃料电池堆、水泵、带风扇的散热器、水箱以及相应的管道组成的.考虑到燃料电池堆内冷却水压的限制,将热管理系统中散热器置于电堆入口处,水泵置于电堆和散热器之间,从而避免电堆内水压过高而损坏燃料电池.图1 PEMFC热管理系统结构图Fig.1 The structure diagram of the PEMFC thermal management system在PEMFC电堆运行过程中,水泵驱动管道内的冷却水循环,使燃料电池堆内的温度分布趋于平衡,并将PEMFC电化学反应产生的热量从电堆内部带出到散热器处;散热风扇强制空气对流,从而将系统内多余的热量散出[17].由于电堆内水压的限制,系统中冷却水流速是有限的,冷却水流速的变化对PEMFC温度的影响也是有限的,所以散热器是PEMFC热管理系统的主要散热方式.本文中将冷却水流速和散热器处的空气流量作为控制量,通过调节冷却水流速来控制电堆出入口冷却水的温度差,通过调节散热器处的空气流量实现对PEMFC温度的控制.3 热管理系统模型为了简化热管理系统模型,忽略整个系统的热辐射和管道的散热,并假设每个子系统中冷却水温度是均匀的,则每个子系统的温度均可以采用集总参数法来表示.由于PEMFC电堆的热容很大,将电堆出口处冷却水温度近似为PEMFC电堆温度[14],将电堆出入口冷却水的温度差作为电堆温差[7].3.1 PEMFC电堆模型根据能量守恒定律建立PEMFC电堆的动态热模型,其能量组分包括:电化学反应的总功率tot,负载消耗的电功率Pst,阴阳极气体带入/带出的热功率gas,冷却水带走的热功率cl,以及电堆向外辐射的热功率amb[14].式中:mst是PEMFC电堆的质量,Cpst是电堆的比热容.电化学反应产生的总功率Pst可以表示为电池节数n,电堆电流Ist,法拉第常数F,以及氢的燃烧焓∆H的函数:PEMFC电堆的输出功率Pst是电堆电压Vst和电堆电流Ist的乘积.其中电堆电压可以由文献[18]中的电化学模型得到冷却水带走的热量表示如下:式中:Wcl是冷却水的质量流速,Cpcl是冷却水的比热容,Tst,in是电堆入口冷却水的温度,Tst是电堆出口冷却水温度,即电堆温度.循环冷却水是整个PEMFC系统主要的散热方式,约90%的余热是通过冷水排出的[8].因此,本文忽略系统热辐射amb和由气体带走的热量gas.3.2 水箱模型水箱在PEMFC热管理系统中用作存储冷却水的容器,进入水箱的冷却水温度被认为是PEMFC电堆温度Tst,将水箱出口的冷却水温度视为水箱温度Trv.式中:mrv是水箱的质量,Cprv是水箱的比热容,hrv是水箱自然热传导系数,Tamb 是环境温度.3.3 散热器模型散热器是PEMFC热管理系统中重要的散热部件,它通过风扇将电化学反应产生的大量热量散到周围环境中,其主要的热量交换包括:冷却水与散热器之间的热量交换,以及换热器与环境之间的热量交换.将进入散热器的冷却水温度看作是水箱的温度,将散热器出口的冷却水温度视为散热器温度[11],散热器模型可以表示为式中:Wair是空气的质量流速,Cpair是空气的比热容.散热器出口的空气温度Tra,air等于散热器出入口冷却水温度的平均值[18].4 变论域模糊增量控制器设计PEMFC是一个非线性、时变性、强耦合的复杂动态系统,其运行过程中存在大量随机干扰,例如负载电流、气体流量、气体压强、环境条件等,难以建立精确的热模型[1].模糊控制器不依赖于精确的被控对象模型,具有鲁棒性强、易于实现等优点,适用于PEMFC的热管理.本文基于模糊控制理论提出了一种变论域模糊增量控制器,用于将PEMFC电堆的工作温度稳定在340 K,将电堆出入口温度差稳定在6 K.该控制器可以看成是由伸缩因子模糊调整器和模糊增量控制器组成的,其基本原理如图2所示.增量型模糊控制器相当于PI控制器,可以消除常见模糊控制器存在的静态误差和振荡[16];变论域模糊控制器,通过对伸缩因子的调整来调节模糊控制器的论域,可以克服常见模糊控制规则有限和无积分环节等缺点[19].变论域模糊增量控制器兼具两种控制器的优点,可以实现对电堆温度、电堆出入口温度差的无静差[16]高精度控制.现以PEMFC 温度控制器为例说明变论域模糊增量控制器的设计过程.图2 变论域模糊增量控制器基本原理图Fig.2 The structure diagram of fuzzy incremental controller based on variable universe4.1 模糊增量控制器设计模糊增量控制器的两个输入量分别是:设定温度值与实际温度之间的误差e(k)=Tref(k)−T(k),误差变化率首先,通过数字采样(采样时间为Ts)获得精确的PEMFC电堆温度误差及误差变化率,将其分别通过量化因Ke,Kec转换为模糊语言值;再根据语言控制规则进行模糊推理,将控制量的模糊取值转换为精确的物理控制量,即散热器处的空气流量变化率∆u(k);最后,增量式模糊控制器的输出为散热器处的空气流量u(k)=u(k−1)+∆u(k).当PEMFC电堆温度高于设定值时,增加散热量以便将电池内更多的热量散出;反之,则要减小散热量.传统的PI控制器可以采用如下表示,其中Kp,Ki分别是比例系数和积分系数:对式(7)两边取采样时间的倒数,即有而增量式模糊控制器的输出为因此,增量式模糊控制器可以看作是一个PI控制器,当误差e(k)等于0时,控制量u(k)将不再变化.相比于一般模糊控制器,增量式模糊控制器可以改善控制器稳态精度.对模糊增量控制器的语言变量论域进行有效的划分,并设计合理的模糊控制规则.本文中控制器的输入量温度误差e(k)和温度误差变化率ec(k),输出量空气流量变化率∆u(k)的模糊论域范围均被设定为[−6,6].且模糊论域均被划分为7个模糊子集{NB,NM,NS,ZO,PS,PM,PB},分别表示为{负大,负中,负小,零,正小,正中,正大}[14].其中,考虑计算量和调整的方便性,这7个模糊子集的隶属度函数均采用三角型.为提高模糊控制器的控制性能,在[−6,6]的模糊论域内采用非均匀分布的隶属度函数,具体的隶属度函数曲线如图3所示.图3 e,ec和∆u的隶属度函数Fig.3 The membership degree functionofe,ecand∆u模糊控制规则是模糊控制器设计的重要部分,本文根据控制过程经验,按照AND–OR的逻辑推理,得到49条具有if-then表达形式的模糊规则,具体的模糊规则表[20]如表1所示.其中,当温度误差为负小或为零,且温度上升较快即负大或负中时,需要适当增大散热量;当温度误差为负大或负中,且温度下降很快即正大或正中时,不需调整散热;当温度误差为正大或正中时,且温度变化速率为零或正小时,需要减小散热. 表1 温度控制器的模糊规则表Table 1 Fuzzy control rules of temperature controller∆e e NBNMNSZO PS PM PB NBPBPB PB PB PM ZO ZO NMPBPB PB PB PM ZO ZO NSPMPM PM PM ZO NS NS ZOPMPMPS ZONSNMNM PS PSPS ZONMNMNMNM PMZOZONMNBNBNB NB PB ZOZONMNBNBNB NB由模糊控制规则完成模糊推理后,需要将获得的模糊集合转换成相应的能直接用于控制的精确输出量.本文采用计算方便且具有较高精度的重心法进行解模糊化,得到模糊控制器的精确控制量.4.2 变论域模糊控制设计由于常规模糊控制器的模糊论域是固定的,当被控对象存在不确定因素时,不能很好地适应情况的变化,难以获得预期的控制效果.变论域模糊控制器,根据实际控制误差,采用伸缩因子来调节模糊论域的范围,即误差变小时收缩论域,误差增大时扩大论域[19],实现了控制器的动态调节,具有更高的控制精度.变论域控制的关键在于确定适当的伸缩因子.基于函数模型的伸缩因子虽然构造简单,但控制效果受函数模型及其参数的影响,且单一模型形式难以精确表述论域的伸缩变化.而基于模糊推理的伸缩因子模型满足伸缩因子的对偶性、避零性、单调性、协调性和正规性[21],可以避免对伸缩因子函数模型及其参数的选择[22],且用模糊规则来表述论域伸缩变化规律可以实现对模糊论域的在线自动调整.因此,本文采用模糊推理来设计变论域控制器.本文设计的伸缩因子调整器是一个二维三输出的模糊控制器,输入为PEMFC温度误差e(k)和温度误差变化率ec(k),输出为温度误差论域的伸缩因子α1,误差变化率论域的伸缩因子α2和输出论域的伸缩因子β.将模糊控制器中温度误差e(k)和温度误差变化率e(kc)的量化因子Ke,Kec分别除以对应的伸缩因子α1,α2,将比例因子K∆u乘以相应的伸缩因子β,即可实现模糊控制器论域的收缩与膨胀[23].变论域模糊控制器的设计过程与模糊增量控制器一致,包括模糊化,模糊推理,模糊抉择和去模糊化.由于变论域模糊控制器的输入量与模糊增量控制器的一致,所以其输入量e(k)和ec(k)的模糊化、各变量的语言取值及其隶属函数的设定与模糊增量控制器相同,如图3所示.考虑伸缩因子的避零性和单调性,输出量伸缩因子α1和α2的模糊论域均被划分为4个模糊子集{B,M,S,Z},其峰值点对应的横坐标取值为{1,0.75,0.5,0.25},采用均匀分布的三角形隶属度函数,如图4所示;伸缩因子β的模糊论域被划分为4个模糊子集{B,M,S,Z},其峰值点对应的横坐标取值为{1,0.8333,0.6667,0.5},采用均匀分布的三角形隶属度函数,如图5所示.由图4和图5可以看出,不论伸缩因子如何变化,模糊控制器的论域始终不会超出初始论域范围[−6,6],即满足伸缩因子的协调性.图4 α1和α2的隶属度函数Fig.4 The membership degree functionofα1andα2图5 β的隶属度函数Fig.5 The membership degree function ofβ基于变论域理论,根据参考文献[21],可以得到伸缩因子α1,α2和β各自的模糊控制规则表.本文将3个伸缩因子的模糊控制规则表合并为一张,如表2所示.3个伸缩因子的模糊控制规则表均按照AND–OR的逻辑推理,且都含有49条具有if-then表达形式的模糊规则.具体的,当e(k)和ec(k)为PS,ZO或NS时,缩小伸缩因子α1和α2(即增大量化因子Ke和Kec),可以使模糊论域被映射到更大论域中,相当于间接增加了控制规则的数量,不仅提高了控制灵敏度及稳态精度,还可以提高响应速度.由表2可以看出基于模糊推理的伸缩因子满足对偶性和正规性.表2 伸缩因子α1,α2和β的模糊控制规则表Table 2 Fuzzy control rules of contraction-expansion factors∆e e NB NM NS ZO PS PM PB NB B/B/BB/B/B M/M/B M/M/M M/M/M B/B/M B/B/B NM B/B/M M/B/B M/M/MS/S/M M/M/S M/B/M B/B/M NS M/M/S S/S/M S/S/S Z/Z/S S/S/Z S/S/SM/M/S ZO S/M/Z S/S/S Z/Z/S Z/Z/Z Z/Z/Z S/S/Z S/M/S PS M/M/S S/S/M Z/Z/S Z/Z/Z S/S/Z S/S/S M/M/S PM B/B/M M/B/B M/M/M S/S/M M/M/S M/B/M B/B/M PB B/B/B B/B/B M/M/B M/M/M M/M/M B/B/M B/B/B模糊推理后需要选择适合的模糊判决方法进行解模糊化.重心法是基于模糊输出的标准权值分布进行估计输出的,可以产生平滑的输出曲面,具有较高的控制精度和计算方便性,因此变论域模糊控制器采用重心法进行解模糊化.4.3 控制器参数设计质子交换膜燃料电池是一个非线性、强耦合的复杂系统.电堆出入口温度差由冷却水流量来调节,电堆温度则受冷却水流量和散热空气流量的影响,所以燃料电池温度和电堆出入口温度差的调节容易出现耦合现象,导致调节时间变长.文献[8]提出,反馈回路设置不同的时间常数可以减少控制量之间的耦合性.本文将PEMFC电堆温度和出入口温度差的采样周期分别设为1 s和0.5 s,以此来最小化控制变量Tst和∆Tst之间的耦合关系.通过设计PEMFC温度控制器和温差控制器实现将电堆温度维持在340 K,将电堆出入口温差维持在6 K的控制目标.通常,燃料电池的运行温度一般在320~360 K之间,而本文的目标工作温度为340 K,由此得到温度控制器中温度误差e(k)的物理论域为[−20,20]K,量化因子Ke为0.3.通过电流阶跃实验得到PEMFC电堆温度的最大误差变化率为0.126 K/s,则ec(k)的物理论域为[−0.126,0.126]K/s,量化因子Kec为47.6.在燃料电池出入口温差控制中,目标温度差为6 K,设该控制器中的误差e(k)的范围为[−3,3]K,则量化因子Ke为2.通过电流阶跃实验得到燃料电池温度差的最大误差变化率ec(k)为0.052 K/s,则该控制器中的ec(k)物理论域为[−0.052,0.052]K/s,量化因子Kec为115.4.5 实验仿真与比较为了验证所设计的变论域模糊增量控制器的性能,在Simulink软件搭建了PEMFC 的热管理系统模型,并设计了两组仿真实验:一组用于研究所设计的控制器在负载电流扰动下的控制性能,另一组用于研究所设计控制器在PEMFC模型参数变化下的控制性能.此外,在本仿真算例中将模糊增量控制器,带积分的模糊增量控制器[16]作为对比方法,研究模糊增量控制在PEMFC热管理系统中的应用,并说明变论域模糊增量控制器的有效性.仿真模型中,PEMFC电堆是由126个单电池串联而成的10 kW水冷型电堆,且单电池的活化面积为232 cm2,电堆的热容mstCpst=72 kJ/K,水箱的热容为mrvCprv=9 kJ/K[14].为简化PEMFC的控制,假设膜的水含量λm为14,并保证阴阳极供气系统的稳定,阳极压强为2.9 atm,氢气过量比为1.5,阴极压强为3 atm,氧气过量比为2.5.1 电流扰动下的性能比较在PEMFC运用中,负载电流的变化会影响燃料电池内的电化学反应,从而影响PEMFC电堆温度和温差的变化.为研究所设计的模糊增量控制器的抗扰动能力,将负载电流的阶跃变化曲线作为外部扰动(如图6所示).图6 负载电流测试信号Fig.6 Load current test signal在模糊增量控制器的作用下,通过实时调节散热量来控制PEMFC的温度,调节冷却水流速来控制电堆的温差,相应的散热器处的风速如图7所示,冷却水流量如图8所示.由此可以得到模糊增量控制器作用下PEMFC电堆温度变化曲线(如图9所示)和PEMFC电堆出入口温差曲线(如图10所示).通过图9和图10可以看出,当负载电流阶跃变化时,三类模糊增量控制器均可以将PEMFC温度维持在340 K,且将PEMFC电堆出入口温差维持在6 K,调节时间不超过500 s.带积分的模糊增量控制器[14]通过增加积分器来消除静差,积分系数越大,系统响应得越快,但会存在超调.变论域的模糊增量控制器的控制效果明显优于另两种模糊增量控制器,在其控制作用下PEMFC温度和温差的变化范围均小于1 K,且当系统稳定后无静态误差.除更高的控制精度外,变论域的模糊增量控制器具有更快的动态响应速度,相比于一般模糊增量控制器调节时间缩短100 s,相比于带积分模糊增量控制器调节时间最少缩短50 s.图7 负载电流扰动下散热器风量Fig.7 Air flow rate under disturbance of load current图8 负载电流扰动下冷却水流量Fig.8 Cooling water flow rate under disturbance of load current图9 负载电流扰动下的温度曲线Fig.9 Temperature curve under disturbance of load current图10 负载电流扰动下的温差曲线Fig.10 Temperature difference curve under disturbance of load current5.2 参数变化下的性能比较PEMFC是一个非线性、时变性的复杂动态系统,模型参数存在由于环境因素和系统非线性特性引起的摄动,所以设计的温度控制器应具有良好的鲁棒性.为了研究所设计的模糊增量控制器在PEMFC模型参数变化下的控制性能,将电堆电流稳定在120 A,设定测试信号为:在1000 s时质子交换膜中的水含量由10阶跃到18[24];在2000 s到2080 s时环境温度由298 K变为302 K;在3000 s时PEMFC电堆入口冷却水温度由334 K变为334.5 K;在4000 s时电堆阴极压强由3 atm阶跃到5 atm.当PEMFC模型参数变化时,3类模糊增量控制器均可以将PEMFC温度和电堆温差稳定在设定值,电堆温度的动态变化曲线如图11所示.图11 系统参数变化下的温度曲线Fig.11 Temperature curve under under system parameter changes电堆出入口温差的动态变化过程如图12所示.通过仿真实验对比可以看出,本文所设计的变论域模糊增量控制器的动态调节速度更快,相比于一般模糊增量控制器调节时间至少可以缩短100 s,相比于带积分模糊增量控制器调节时间最少缩短50 s.变论域模糊增量控制器的控制精度更高,超调幅度明显小于另外两种模糊增量控制器,确保了燃料电池运行的可靠性.变论域模糊增量控制器跟随温度误差和误差变化率在线实时修正模糊控制器的参数,增强了模糊控制器的自适应能力,使控制器具有更好的动静态性能和更强的鲁棒性.图12 系统参数变化下的温差曲线Fig.12 Temperature difference curve under system parameter changes通过两组测试信号研究模糊增量控制器的抗干扰性和鲁棒性,变论域模糊增量控制器在系统超调、响应速度、稳态误差等方面都得到了提高,使系统的抗扰性和鲁棒性均优于另两种模糊增量控制器,能满足PEMFC系统的热管理需求.6 结论有效的热管理是保证质子交换膜燃料电池高可靠性、长寿命运行的关键.本文基于建立的PEMFC热管理系统动态模型设计了一种变论域模糊增量控制器,用于将PEMFC电堆温度维持在340 K,将电堆温差控制在6 K.该控制器基于模糊理论采用变论域控制器来获得伸缩因子,实现了对模糊增量控制器论域的实时动态调节.变论域控制器改变了模糊增量控制器单一论域反复调节的方式,通过伸缩因子实现了模糊增量控制器论域的伸缩变化,局部细化了控制规则,从而提高了控制的精度和系统的响应速度.通过两组仿真实验可以看出当负载电流和PEMFC模型参数变化时,基于变论域的模糊增量控制器相比于其他模糊增量控制方法,调整时间最少缩短了50 s,具有更快的动态响应速度;控制精度明显提高,具有更强的鲁棒性和自适应性能. 参考文献:【相关文献】[1]JIAO K,NI M.Challenges and opportunities in modelling of proton exchange membrane fuel cells(PEMFC).International Journal of Energy Research,2017,41(13):1–5.[2]RAHGOSHAY S M,RANJBAR A A,RAMIAR A,et al.Thermal investigation of a PEM Fuel Cell with cooling flow field.Energy,2017,134(1):61–73.[3]ANDREASEN K P,SOVACOOL B K.Hydrogen technological innovation systems in practice:comparing Danish and American approaches to fuel cell development.Journal of Cleaner Production,2017,94(1):359–368.[4]GAO F,BLUNIER B,MIRAOUI A,et al.A multiphysic dynamic 1-D model of a proton-exchange-membrane fuel-cell stack for realtime simulation.IEEE Transactions on Industrial Electronics,2010,57(6):1853–1864.[5]GARRAIN D,LECHON Y,RUA C D L.Polymer electrolyte membrane fuel cells(PEMFC)in automotive applications:environmental relevance of the manufacturing stage.SmartGrid&Renewable Energy,2011,2(2):68–74.[6]NOLAN J,KOLODZIEJ J.Modeling of an automotive fuel cell thermal system.Journal ofPower Sources,2010,195(15):4743–4752.[7]GUO A,CHEN W,LIU Z,et al.Tempreture model and predictive control for fuel cells in switcher locomotive.The 35th Chinese ControlConference(CCC).Chengdu:IEEE,2016,7:1934–1768.[8]AHN J W,CHOE S Y.Coolant controls of a PEM fuel cell system.Journal of Power Sources,2008,179(1):252–264.[9]LISO V,NIELSEN M P,KAR S K,et al.Thermal modeling and temperature control of a PEM fuel cell system for forklift applications.International Journal of HydrogenEnergy,2014,39(16):8410–8420.[10]YOU Z,XU T,LIU Z,et al.Study on air-cooled self-humidifying PEMFC control method based on segmented predict negative feedback control.ElectrochimicaActa,2014,132(19):389–396.[11]CHENG S,FANG C,XU L,et al.Model-based temperature regulation of a PEM fuel cell system on a city bus.International Journal of Hydrogen Energy,2015,40(39):13566–13575.[12]POHJORANTA A,HALINEN M,PENNANEN J,et al.Model predictive control of the solid oxide fuel cell stack temperature with models based on experimental data.Journal of Power Sources,2015,277(3):239–250.[13]WANG Y,QIN F,OU K,et al.Temperature control for a polymer electrolyte membrane fuel cell by using fuzzy rule.IEEE Transactions on Energy Conversion,2016,31(2):1–9. [14]HU P,CAO G,ZHU X,et al.Coolant circuit modeling and temperature fuzzy control of proton exchange membrane fuel cells.International Journal of HydrogenEnergy,2010,35(17):9110–9123.[15]WANG Guangjun,SHEN Shuguang,PENG Xiaoyan.A fuzzy increment control method of delay system and its application.Proceedings of the CSEE,2006,26(19):93–96.(王广军,沈曙光,彭晓艳.延迟系统的一种模糊增量控制方法及应用.中国电机工程学报,2006,26(19):93–96.) [16]LU Zhaomei,YU Yuehai.Polynomial reset incremental fuzzy controller.Journal of Southeast University,1991,29(1):49–53.(路兆梅,于跃海.多项式重置增量型模糊控制器.东南大学学报(自然科学版),1999,29(1):49–53.)[17]GU Jing,LU Languang,OUYANG Minggao.Thermal management subsystem model and temperature control for fuel cells.Journal of Tsinghua University,2007,47(11):2036–2039.(谷靖,卢兰光,欧阳明高.燃料电池系统热管理子系统建模与温度控制.清华大学学报(自然科学版),2007,47(11):2036–2039.)[18]ZHAO X,LI Y,LIU Z,et al.Thermal management system modeling of a water-cooled proton exchange membrane fuel cell.International Journal of HydrogenEnergy,2015,40(7):3048–3056.[19]LI Hongxing.Variable universe adaptive fuzzy controller.Science China(SeriesE),1999,29(1):32–42.(李洪兴.变论域自适应模糊控制器.中国科学(E辑),1999,29(1):32–42.)。
400W质子交换膜燃料电池控制系统设计

机 电技术
6 9
4 0 0 W 质 子交换膜燃 料 电池控 制系统设计
张 玉 林瑞全 翟 少琼
( 福州大学 电气工程 与 自动化 学院 , 福建 福州 3 5 0 1 0 8 ) 摘 要 : 为 了使 质子交换膜燃料 电池系统 能够 高效可靠稳定 地工作 , 设 计 了一种基 于 A T m e g a 1 2 8 单片机作 为核心控 制单元 的4 0 0 W空冷型燃料 电池控制器 , 有效地整合 了燃 料电池发电系统 , 实现了对氢气供给 、 空气供给 、 风扇 、 模拟量监 测和显示等子系统 的控制 。试 验结 果表明 , 该 系统设计可靠 , 运行稳定 。 关键词 : 质子交换膜燃料 电池 ; A T m e g a 1 2 8 单片机 ; 燃 料电池控制器
既能满足 电堆空气需要 , 又能降低风机消耗能量 ,
提 高系统 效率 的 目的 一 。 阴极 的尾 气 中包 含 有 部 分 的水 蒸 汽 , 一 部 分
经 过膜 管 加 湿 器 给 入 口空气 加 湿 , 另一 部 分 的水 直接 排 出 。 1 . 3 氢气 供应 单 元
l 质子 交换膜燃 料 电池发 电系统组成
制 。在 自动模 式 下 , 出 口电磁 阀每 隔 一 段 时 间打
开 一次 。 1 . 4 热 管理 单 元
P E MF C电堆 的 整 体 温 度 和 温 度 分 布 状 况 对 维持 电化 学 反应 的正 常进 行 和质 子交 换 膜长 期稳
定工作具有重要 的影 响, 过高的温度容易造成膜 的降解甚至破裂 , 而温度过低则会 降低 电堆化学
率场合的应用 , 燃料 电池作为便携式 电源 、 移动 电
源 的优 势也 日益 凸显 1 。 目前 , 提高 P E MF C发 电
PEMFC电化学建模及其PID控制

V cell = EN ernst - V EN ernst 为单电池的可逆电动势 , Vact 为阴阳极活化过电
压 , Vohm i 为欧姆极化过电压 。( 1) 式中的第一项表示在没有
负载时电池工作的开路电压 ,其余二项表示第一项电压的减
少量 ,从而得到 Vcell,即供给外电路实际电压值 。 外电路开路时 ,可逆电动势是在热动态平衡条件下获得
要因素 。
PEM FC 是 一 个
时变 、非线性的强耦
合系统 , 在其工作中
易受到负载 、温度和
膜的湿度变化等干扰
因素的影响 , 因此对 我们采用增量式 P ID
图 2 PEM FC 的 P ID 控制结构
控制算法 ,并对其三个参数进行调整 ,调整气体压力使输出
电压达到理想值 ,其控制结构图如 2所示 。
A BSTRACT: The mode l of p ro ton exchange m em brane fue l ce ll ( PEM FC) is hard to be u sed in the design of contro l system at p re sent, so a e lec trochem ical m ethod is pu t fo rwa rd to estab lish PEM FC m athem a tic s mode l, and the P ID a lgo rithm is adop ted to con tro l the outpu t vo ltage. Firstly, ana lyzing the ope ra tion m echanism w ith in PEM FC, and adop ting the elec trochem ica l m e thod to estab lish its m a them a tic model; then a ssum ing under the situa tion that the exte rnal load curren t in te rfe re s, the ope ra ting tempe ra ture of PEM FC stabilizes in 80 ℃. A nd se tting up the mode l of system under the environm en t of M atlab / sim ulink and sim ula ting the dynam ic change course of ou tp ut vo ltage; u sing P ID a lgo rithm to contro l the inle t ga s p re ssure of anode and ca thode of stack to m ake the ou tp ut vo ltage of PEM FC system reach the setting value. Sim ula tion results show that this model can reflec t the dynam ic charac te ristic of powe r gene ration system , and P ID a lgo rithm can be u sed in the contro l system of PEM FC. KEYW O RD S: Pro ton exchange m em b rane fue l cell ( PEM FC) ; Elec trochem ica l modeling; Propo rtion - integral - differen tia l a lgo rithm
质子交换膜燃料电池系统温度稳定性控制研究

质子交换膜燃料电池系统温度稳定性控制研究作者:谢义淳郑丽萍赖联锋郭玮韡林玉祥来源:《时代汽车》2021年第21期摘要:質子交换膜燃料电池温度控制系统设计时以满足高环境温度和高负载等极端工况下的散热需求为目标,常忽略了在低温以及低负载下温度控制的稳定性;为了提高在低环境温度下、低负载下温度控制系统对燃料电池温度控制的稳定性,在传统的PID控制的基础上,改进了控制策略,有效提升了燃料电池在低环境下低负载时温度的稳定性,对提高燃料电池性能与耐久性有积极影响。
关键词:燃料电池控制温度稳定性1 引言以煤和石油为主的化石燃料作为驱动工业社会发展的主要能源被大量使用,导致了严重的环境污染问题和自然资源被过度开采,所以寻求一种高效、洁净的新能源已经成为全世界的共同目标。
燃料电池由于具有高转换效率、低污染、低排放而备受关注。
质子交换膜燃料电池是燃料电池中最常见的类型,质子交换膜燃料电池(PEMFC)的电解质是一种能够传导质子的固体聚合物,其结构简单,通常以氢气作为燃料,工作温度为60~80℃,具有功率密度高、启动时间快、效率高、安全可靠等优点,被认为目前最有希望取代内燃机作为汽车动力的能源1;温度对质子交换膜燃料电池的性能有非常重要的影响,燃料电池电堆工作温度直接影响催化剂的催化活性以及CO耐受能力,同时还影响燃料电池内部的湿度、质子交换膜电导率、膜电极含水量等,这些因素直接关系的燃料电池的可靠性、稳定性和安全性,所以控制质子交换膜燃料电池在合理的温度范围内运行,并且避免温度出现较大幅度的波动尤为重要2。
刘洋等3建立了燃料电池热管理模型,设计了基于模糊-PID 算法的控制策略对PEMFC发电系统进行温度控制试验,结果显示该算法对PEMFC发电系统温度动态响应效果良好,温度超调量小。
文献4在PID控制器调节方式转速基础上,将水泵和散热风扇的控制输入量解耦,前馈与反馈控制相结合,提出了一种流量跟随电流控制冷却水流量的水冷PEMFC 热管理系统控制策略。
pid神经网络控制器的设计方案
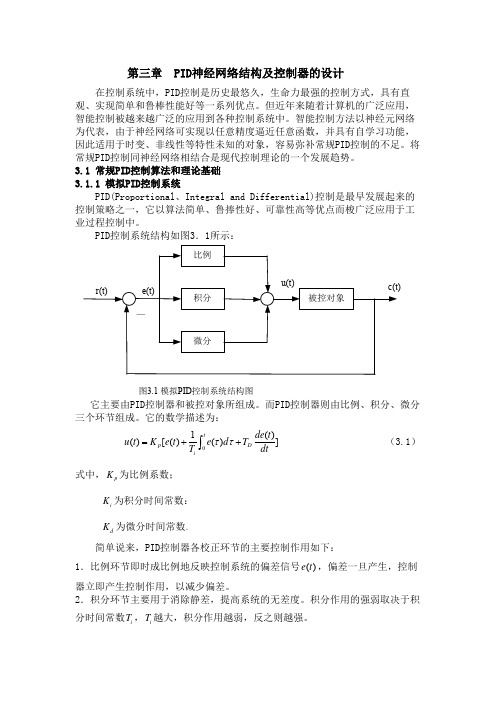
第三章 PID 神经网络结构及控制器的设计在控制系统中,PID 控制是历史最悠久,生命力最强的控制方式,具有直观、实现简单和鲁棒性能好等一系列优点。
但近年来随着计算机的广泛应用,智能控制被越来越广泛的应用到各种控制系统中。
智能控制方法以神经元网络为代表,由于神经网络可实现以任意精度逼近任意函数,并具有自学习功能,因此适用于时变、非线性等特性未知的对象,容易弥补常规PID 控制的不足。
将常规PID 控制同神经网络相结合是现代控制理论的一个发展趋势。
3.1 常规PID 控制算法和理论基础 3.1.1 模拟PID 控制系统PID(Proportional 、Integral and Differential)控制是最早发展起来的控制策略之一,它以算法简单、鲁捧性好、可靠性高等优点而梭广泛应用于工业过程控制中。
PID 控制系统结构如图3.1所示:图3.1 模拟PID 控制系统结构图它主要由PID 控制器和被控对象所组成。
而PID 控制器则由比例、积分、微分三个环节组成。
它的数学描述为:1()()[()()]tp Dide t u t K e t e d T T dtττ=++⎰(3.1) 式中,p K 为比例系数;i K 为积分时间常数:d K 为微分时间常数。
简单说来,PID 控制器各校正环节的主要控制作用如下:1.比例环节即时成比例地反映控制系统的偏差信号()e t ,偏差一旦产生,控制器立即产生控制作用,以减少偏差。
2.积分环节主要用于消除静差,提高系统的无差度。
积分作用的强弱取决于积分时间常数i T ,i T 越大,积分作用越弱,反之则越强。
3.微分环节能反映偏差信号的变化趋势(变化速率),并能在偏差信号值变得太大之前,在系统中引入一个有效的早期修正信号,从而加快系统的动作速度,减少调节时间。
具体说来,PID 控制器有如下特点:(1)原理简单,实现方便,是一种能够满足大多数实际需要的基本控制器; (2)控制器能适用于多种截然不同的对象,算法在结构上具有较强的鲁棒性,在很多情况下,其控制品质对被控对象的结构和参数摄动不敏感。
基于DSP的质子交换膜燃料电池测控系统设计

1 P MF E C测控 系统简 介
P MF 系统 除 了核 , E C t部分 质 子 交换 膜燃 料 电 S 池 堆外 ,还 需要 一 辅助 系统才 能正 常上作 。总的 些 来 说 ,一个 完整 的燃 料 电池 系 统大致 上 由发 电系统
波 失真 较高 、效 率较低 、 可靠性 不好 。为 了提高 电 池 系统 的通用 性 ,针对风 冷 型的 P MF E C,设计 了一 种 基于 D P的测摔 系统 ,实验 效 l令 人满意 。本 文 S 粜
针 对测控 系 统 的基 本 组成与 功 能特 点 ,主要 对整 个 测 控 系统的 软硬件 设计进 行 了详 细 的介绍与讨 论 。
,
t ee p c e e f r a c . h x e td p ro m n e
Ke r s PEM FC; DSP; me s r me ta d c nto yse : ha d r n ofwa e y wo d : a u e n n o r ls t m r wa e a d s t r
质 子交换 膜燃料 电池 ( E C)因其 低噪音 、 P MF
和 控制系 统两大 部分组 成 。通 用 的 P MF 测 控系 E C 统 主要 由以下几部 分构 成 :传 感器 、控制 单元 、数
零 污 染、无 腐蚀 、长 寿命及 窄 相对较 少等 优 点 , 成为 2 1世 纪 最 有 前 途 的 “ 色 能源 ” ] 绿 l。但 由于 】 P MF E C发 电系统性 能输 出的影 响 素有 很多 , 括 包
燃 料 的温 度 、湿度 、浓 度 、压 力、 电气 负载 ,以及
据 采集 单元 、执行 单元 、通信 单元 、报 警及显 示单 元 等 。本 实验 室使 用 的是百 瓦级风冷 型发 电系 统 , 整 个实验 系统 的结构 示意 图如下 图 1 所示 。
神经网络PID控制
动量系数=0.05,加权系数初始值取区间-0.5 0.5
上的随机数。
当输入信号为幅值是1的正弦信号r(t )sin(2t)时,
取采样时间为0.001s, 仿真结果如图所示。
神经网络PID控制
27
神经网络PID控制
g
net
( l
3
)
(
k
)
l 1,2,3
(15)
O1(3) (k ) K P
O2(3) (k ) K I
O3(3) (k ) K D
式
中
(3 li
)为
输
出
层
权
系
数
,
(3) lQ
l为阈值,
g[] 1 [1 tanh( x)] 2
神经网络PID控制
21
取性能指标
J 1 r(k 1) y(k 1) 2 1 e2(k 1)
神经网络PID控制
25
7.
由(20)式
,
计
算
修
正
输
出
层
的权
系
数
(3) li
(
k
);
8.
由(21)式
,
计
算
修
正
隐
含
层
的权
系
数
(2) ij
(k
);
9. 置k k 1, 返回到“3”,直到性能指标J
满足要求。
神经网络PID控制
26
仿真实例: 设被控对象的近似数学模型为
a(k) y(k 1) y(k) 1 y2 (k 1) u(k 1) 系数a(k )是慢时变的,a(k ) 1.2(1 0.8e0.1k ), 神经网络 结构为4-5-3,输入层的4个神经元分别为模型的输
水冷型质子交换膜燃料电池温度控制策略

水冷型质子交换膜燃料电池温度控制策略随着全球环保意识的日益增强,燃料电池作为一种清洁能源得到越来越广泛的关注和应用。
质子交换膜燃料电池是一种常见的燃料电池类型,具有高效、清洁、噪音低等优点,因此在汽车、船舶、电力等领域得到了广泛应用。
然而,质子交换膜燃料电池在运行过程中需要保持一定的温度范围,过高或过低的温度都会影响电池的性能和寿命。
因此,如何控制质子交换膜燃料电池的温度成为了一个关键的问题。
水冷型质子交换膜燃料电池是一种常见的燃料电池类型,它通过水冷却来控制电池温度,使其保持在适宜的范围内。
水冷型质子交换膜燃料电池的温度控制策略包括以下几个方面:1. 优化系统结构水冷型质子交换膜燃料电池的系统结构包括电池模块、水冷却模块、空气供给模块等组成部分。
为了优化系统结构,需要考虑各个组成部分之间的热量传递,合理设计水冷却模块的结构和散热面积,以及空气供给模块的流量和温度等参数,从而实现对电池温度的有效控制。
2. 控制水流量和温度水流量和温度是影响水冷型质子交换膜燃料电池温度的重要因素。
通过控制水流量和温度,可以有效地控制电池的温度。
一般来说,当电池温度过高时,需要增加水流量和降低水温,当电池温度过低时,需要减少水流量和提高水温。
因此,需要根据电池的实际运行情况,合理地调节水流量和温度,以保持电池温度在适宜的范围内。
3. 优化电池控制策略电池控制策略是影响水冷型质子交换膜燃料电池温度的关键因素之一。
通过优化电池控制策略,可以更加精确地控制电池温度。
一般来说,电池控制策略包括电压控制、电流控制、功率控制等方式。
在实际应用中,需要根据电池的实际运行情况,选择合适的控制策略,以保证电池的稳定运行和高效工作。
4. 采用智能控制系统随着人工智能技术的不断发展,智能控制系统已经成为了控制水冷型质子交换膜燃料电池温度的重要手段之一。
智能控制系统可以通过感应器、控制器等设备实时监测电池的温度、水流量、水温等参数,并根据这些参数进行智能控制,从而实现对电池温度的精确控制。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第37卷 第1期2009年1月V o l .37 N o .1J a n . 2009质子交换膜燃料电池温度的神经网络P I D 控制设计陈 岩(任城区供电公司,山东济宁 272100)摘 要:根据实验数据,选用合适的智能方法,建立了质子交换膜燃料电池温度辨识模型,然后设计了基于B P 神经网络的P I D 控制器通过调节循环冷却水的流量将电堆温度控制在设定值。
仿真结果表明该控制器可以将电池系统的温度很好的控制在理想的范围内,对实际应用具有很好的指导作用。
关键词:燃料电池;模糊神经网络;系统辨识;神经网络P I D 控制基金项目:国家863课题基金资助项目(2005A A 517020)作者简介:陈 岩(1979-),男,工程师,主要从事电力系统继电保护工作。
中图分类号:T M 911.4 文献标志码:A 文章编号:1001-9529(2009)01-0184-03D e s i g n o f B P N N -P I Dc o n t r o l f o r t e m p e r a t u r e o f PE MF CC H E NY a n(R e c h e n g P o w e r B u r e a u ,J i n i n g 272100,C h i n a )A b s t r a c t :T h e P E M F C ′s o p e r a t i o n a l t e m p e r a t u r e ,w h i c he x e r t s g r e a t i n f l u e n c e s o nt h e t r a n s m i s s i o nc h a r a c t e r i s t i c s o ft h e r e a c t a n t g a s e s ,t h e m e m b r a n e h y d r a t i o nd e g r e e ,a n dt h ec a t a l y z e r a c t i v i t y ,i s av e r y i m p o r t a n t p a r a m e t e r t ot h e s t a c k ′s o u t p u t p e r f o r m a n c e .B y u s i n g e x p e r i m e n t a l d a t a a n d a p p r o p r i a t e i n t e l l e c t u a l a l g o r i t h m ,a P E M F Ct e m p e r a t u r e i d e n t i f i c a t i o n m o d e l w a s c o n s t r u c t e d ,a n da B P N N -P I Dc o n t r o l l e r w a s d e s i g n e d t o c o n t r o l t h e s t a c k t e m p e r a t u r e a t t h e s e t v a l u e b y a d j u s t i n g t h e c y c l e c o o l i n g w a t e r .S i m u l a t i o nr e s u l t s s h o w e dt h a t t h e m o d e l c a nr e f l e c t P E M F C ′s c h a r a c -t e r i s t i c s c o r r e c t l y a n dt h ep e r f o r m a n c e o f t h e c o n t r o l l e r i s i d e a l .K e yw o r d s :f u e l c e l l ;f u z z y n e u r a l n e t w o r k ;s y s t e m i d e n t i f i c a t i o n ;B P N N -P I Dc o n t r o l 质子交换膜燃料电池系统运行温度是影响电堆输出性能的重要参数,对反应气体的传输特性、质子膜水合程度、催化剂反应活度等因素都会产生重要的影响[1,2]。
据实验分析,质子交换膜燃料电池系统的工作温度一般设定在323K~373K 之间。
质子交换膜作为一种有机膜,其耐热程度有限,如果温度过低,电催化活性降低,电化学反应速度降低,质子交换膜中的水扩散系数减小,使质子交换膜内的水分布不均匀,从而使膜电阻增大。
如果温度过高,会产生过高的热应力,造成膜开裂,使质子交换膜的性能下降,严重时甚至会造成膜的损坏[3,4]。
本文设计了基于B P 神经网络的P I D 控制器通过调节循环冷却水的流量将电堆温度控制在设定值。
1质子交换膜燃料电池系统自适应模糊神经网络系统辨识 本文选择自适应模糊推理系统(A N F I S )为质子交换膜燃料电池系统温度模型的辨识器,带有n 个输入M 条规则的自适应模糊神经推理系统结构如图1所示。
图1 自适应模糊神经网络推理系统的结构图图1中,X=[x 1,x 2,…,x n ]T为输入,y 为输出,μA l i 为输入的隶属度函数(i =1,2,…,n ;l =1,2,…,M )。
则自适应模糊推理系统的输出表达式为y (k )=∑Ml =1y l[∏n i =1μF l i(x i)]∑Ml =1[∏ni =1μF l i(x i)](1)由式T k +1=φ(W a n ,W c a ,W w ,T k ),则第k +1个采样周期自适应模糊推理系统的输入向量可写陈 岩 质子交换膜燃料电池温度的神经网络P I D 控制设计185成X (k )=[W a n (k ),W c a (k ),W w (k ),T (k )]T(2)质子交换膜燃料电池系统温度模型的A N F I S辨识模型结构如图2所示。
X (k )为时间延迟阵列T D L 的A N F I S 输入;y (k +1)为质子交换膜燃料电池系统仿真模型的输出;y (k +1)为A N F I S 辨识器的输出;E (k +1)是y (k +1)和y (k +1)之间的误差。
A N A 为A N F I S 的算法。
图2 P E M F C 的A N F I S 温度辨识模型结构图设定控制量阳极流量W a n 的范围为0.28m /s ~1.7m /s ,阴极流量W c a 的范围为1.5m /s ~8m /s ,循环冷却水流量范围为0~2.5m /s ,被控操作量温度T 的范围为323~373K 。
按照上述范围设置,利用1000组输入/输出实验数据对作为训练数据,对温度辨识模型进行训练。
图3为电堆温度为353K 时的辨识结果,图4为训练后氢气的隶属度函数。
由误差变化图5可知A N F I S 模型辨识的最大误差不超过1K。
图3 A N F I S辨识结果与仿真实验数据的比较图4 训练后氢气的隶属度函数图5 训练过程中的误差变化2 质子交换膜燃料电池系统温度的神经网络P I D 控制 P I D 控制是生产过程中最普遍采用的一种控制方法,P I D 控制要取得较好的控制效果,就必须通过调整好比例、积分和微分3种控制作用,形成控制中相互配合相互制约的关系。
神经网络具有任意非线性逼近能力,因此可以利用神经网络通过对系统性能的学习来实现P I D 参数的调整[5,6]。
本文选用的神经网络为B P 网络。
基于B P 神经网络的P I D 控制系统结构如图6所示。
经典的P I D 控制器直接对P E M F C 系统进行闭环控制,并且3个参数k P ,k I ,k D 为在线整定。
神经网络根据系统的运行状态对应于P I D 控制器的3个可调参数k P ,k I ,k D 。
P I D 的控制算式为u (k )=u (k -1)+k P Δe (k )+k Ie (k )+k D Δ2e(k )(3)式中 k I ,k I ,k D 分别为比例、积分和微分系数。
图6 基于B P 神经网络的P I D 控制系统结构图将k P ,k I ,k D 看成依赖于系统运行状态的可调系数时,P I D 的控制算式可描述为u (k )=u (k -1)+k P [e (k )-e (k -1)]+k I e (k )+k D [e(k )-2e (k -1)+e (k -2)](4)式中 k P ,k I ,k D 分别为比例、积分和微分系数;e (k )为系统实际输出和期望值之间的误差;u (k )为控制器的输出。
B P 神经网络的结构如图7所示。
设该网络有M 个输入节点,Q 个隐层节点、3个输出节点。
输出节点分别对应于控制器的3个可调参数k P ,1862009,37(1)k I ,k D 。
输出层激发函数选为非负的S i g m o i d 函数,隐含层取正负对称的S i g m o i d 函数。
依据P E M F C 系统的复杂程度构建了一个结构为4-8-3的3层B P 神经网络。
图7 B P 神经网络结构图基于B P 神经网络的P I D 控制器的实现步骤如下:(1)确定B P 网络结构,并给出各层加权系数初值(控制量、输出量和误差的初值都取为0);(2)采样得到r (k )和γ(k ),计算该时刻误差e (k )=r (k )-γ(k ),然后根据P I D 的控制算式把误差分量作为输入层的输入;(3)计算神经网络各层神经元的输入、输出,B P N N 输出层的输出即为P I D 控制器的3个可调参数;(4)根据公式(5-17)计算P I D 控制器的输出u (k );(5)进行神经网络学习,按共轭梯度算法修正B P 网络的权值和阈值,在线调整加权系数w1i j(k )和w 2l i(k ),实现P I D 控制参数的自适应调整;(6)置k =k +1,返回(2)。
3 基于B P 神经网络的P I D 控制仿真结果根据上节设计的B P 神经网络P I D 控制系统,在M a t l a b /S i m u l i n k 环境下进行仿真实验。
在该仿真实验中,k P 的初值设定为20,k I 的初值设定为1,k D 的初值设定为25,学习效率η设为0.8,惯性系数α设为0.1。
实验中模拟负载变化造成电流密度的变化,从而导致被控温度参数也发生变化的情况。
控制结果如图8所示,超调量分别为1.3K ,1.4K ,1.4K 。
