《概率论概率分布》PPT课件
合集下载
概率论二维随机变量及其分布 ppt课件
二维随机变量的分布函数
F ( x , y ) P { X x , Y y } 就是随机点 (X,Y)落入区域
{t,s ( )|t x ,s y }
的概率(如图1).
由概率的加法法则，随机点(X,Y)落入矩形域
{ x 1 x x 2 ,y 1 y y 2 }
的概率
P { x 1 x x 2 ,y 1 y y 2 } F ( x 2 ,y 2 ) F ( x 2 ,y 1 )
F (x ,y)1 2 2arc 2 x t 2a anrc 3 y .ta
(2)由 (1)式得
P { 2 X , 0 Y 3 } F ( , 3 ) F ( , 0 ) F ( 2 , 3 ) F ( 2 , 0 ) 1/1.6
完 21
三、二维离散型随机变量及其概率分布
Pi1
i
Pi 2
Pij
i
27
联合概率分布表
对离散型随机变量而言，联合概率分布不仅比联合
分布函数更加直观，而且能够更加方便地确定(X,Y)
取值于任何区域 D上的概率. 设二维离散型随机变
量的概率分布为
P { X x i , Y y j } p i ( i j , j 1 , 2 , )
二维离散型随机变量及其概率分布
分布:
p i ( i 1 , 2 , )p , j( j 1 , 2 ).
p i P {X x i} p i,ji 1 ,2 , j
p j P { Y y j}p i,jj 1 ,2 ,25 i
二维离散型随机变量及其概率分布
分布: p i ( i 1 , 2 , )p , j( j 1 , 2 ).
F X ( x ) P { X x } P { X x , Y } F(x, )
概率论及数理统计概率分布-资料
下X 限 1 .9 S 6 为 7 .8 2 1 .9 ： 3 6 .8 6 .3 ( 5 g / 5 L )
上X 限 1 .9 S 6 为 7 .8 2 1 .9 ： 3 6 .8 8 .2 ( 0 g / 5 L )
2019/11/13
38
例：某地调查120名健康成年男性的第一秒肺通气
2019/11/13
25
解：本例由于是大样本，可用样本均数和样本
标准差作为总体、的估计值，即将该地正常
成年女子的血清总蛋白数近似看作服从 N(72.8,3.82)的正态分布。作如下标准化变换：
Z166.03.872.81.79
75.072.8 Z2 3.8 0.58
2019/11/13
48- 56- 64- 72- 80体重（kg）
图1 体重频率密度图
若将各直条顶端的中点顺次连接起来,得 到一条折线。当样本量n越来越大时，组段越 分越细，此时直方渐进直条，这条折线就越来 越接近于一条光滑的曲线（见图1、2），我们 把这条呈中间高，两边低，左右基本对称的 “钟型”曲线称为正态分布曲线，近似于数学 上的正态分布（高斯分布; Gauss）。
参考值范围（reference range)是指所谓“正 常人”的解剖、生理、生化等指标的波动范围。 制定参考值范围时，首先要确定一批样本含量足 够大的“正常人”。所谓“正常人”不是指“健 康人”，而是指排除了影响所研究指标的疾病和 有关因素的同质人群。其次需根据指标的实际用 途确定单侧或双侧界值，根据研究目的和使用要 求选定适当的百分界值，常用95%。
图3 正态分布的概率密度函数
2019/11/13
12
于是，利用概率密度函数 F (x) 可以计算正态 分布变量取值在任意区间（a,b）的概率为
概率论课件第二章
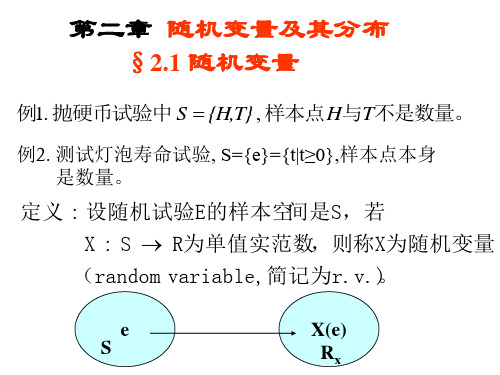
第二章 随机变量及其分布 §2.1 随机变量
例1. 抛硬币试验中S {H,T}, 样本点H与T不是数量。
例2. 测试灯泡寿命试验, S={e}={t|t≥0},样本点本身 是数量。
定义 : 设随机试验E的样本空间是S，若 X : S R为单值实范数，则称X为随机变量 （random variable, 简记为r.v.) 。
2. 特例: (1,) 是参数为的指数分布. （=1） 3. 伽玛函数的性质: (i) (+1)= ();
1 (iii)( ) . 2
(ii) 对于正整数n, (n+1)=n!;
§5. 随机变量的函数的分布
一、 X为离散型r.v. 例1.设X具有以下的分布律,求Y=(X-1)2分布律: X -1 0 1 2 pk 0.2 0.3 0.1 0.4
(二) 贝努利试验
(二项分布)
定 义 : 设 试 验E只 有 两 个 可 能 结 果 A与 A , 且 P( A ) p ( 0 p 1), 将 试 验E独 立 重 复 地 进 行 n次 , 这 样 的 试 验 称 为 贝 努 利 试 验.
设X是n重贝努利试验中事件A发生的次数, 则X 是一个随机变量, 于是
§4. 连续型随机变量及其概率密度
F(x) , 存在非负函 1.定义 : 对于r.v.X的分布函数 数f(x) , 使对于任意的实数 x, 有
则称X为连续型r.v.f(x)称为X概率密度函数, 简称概率密度. 连续型r.v.的分布函数是连续函数.
F(x ) f(t)dt
x
2.概率密度 f(x)的性质:
25
标准正态分布的上分位点:
设X ~ N(0,1), 若z 满足条件
例1. 抛硬币试验中S {H,T}, 样本点H与T不是数量。
例2. 测试灯泡寿命试验, S={e}={t|t≥0},样本点本身 是数量。
定义 : 设随机试验E的样本空间是S，若 X : S R为单值实范数，则称X为随机变量 （random variable, 简记为r.v.) 。
2. 特例: (1,) 是参数为的指数分布. （=1） 3. 伽玛函数的性质: (i) (+1)= ();
1 (iii)( ) . 2
(ii) 对于正整数n, (n+1)=n!;
§5. 随机变量的函数的分布
一、 X为离散型r.v. 例1.设X具有以下的分布律,求Y=(X-1)2分布律: X -1 0 1 2 pk 0.2 0.3 0.1 0.4
(二) 贝努利试验
(二项分布)
定 义 : 设 试 验E只 有 两 个 可 能 结 果 A与 A , 且 P( A ) p ( 0 p 1), 将 试 验E独 立 重 复 地 进 行 n次 , 这 样 的 试 验 称 为 贝 努 利 试 验.
设X是n重贝努利试验中事件A发生的次数, 则X 是一个随机变量, 于是
§4. 连续型随机变量及其概率密度
F(x) , 存在非负函 1.定义 : 对于r.v.X的分布函数 数f(x) , 使对于任意的实数 x, 有
则称X为连续型r.v.f(x)称为X概率密度函数, 简称概率密度. 连续型r.v.的分布函数是连续函数.
F(x ) f(t)dt
x
2.概率密度 f(x)的性质:
25
标准正态分布的上分位点:
设X ~ N(0,1), 若z 满足条件
概率论与数理统计连续型随机变量及其概率分布ppt课件
0 x
则t , dt d
1-(x)
x1
2
3
F(x) 1
(t )2
1 x e
2 2
dt
x
2
e 2 d
( x )
2
2
4. P{a X b} (b ) ( a )
P{X b} (b ) P{X a} 1 (a )
例6
设 X ~ N(1,4) , 求 P (0 X 1.6)
解：X 的密度函数为
f
x
1 10
e
x 10
0
x0 x0
令：B={ 等待时间为10-20分钟 }
则 PB P10 X 20
20
1
x
e 10 dx
10 10
x
e 10
20
e 1
e 2
0.2325
10
例5 假定一大型设备在任何长为 t 的时间内发生
故障的次数 N( t ) 服从参数为t 的Poisson分布,
P(2
X
4)
4
2
2
2
2
(0)
0.3
2
0.8
P( X 0) 0.2
解二 图解法
0.2 0.15
0.1 0.05
0.3 0.2
-2
2
4
6
由图 P( X 0) 0.2
例 3 原理
设 X ~ N ( , 2), 求 P(| X | 3 )
解 P(| X | 3 ) P( 3 X 3 )
应用场合:
若随机变量Ｘ在区间(a,b)内等可能的取值，则
X ~ U a,b
例3 秒表的最小刻度差为0.01秒. 若计时精度 是取最近的刻度值, 求使用该秒表计时产生的 随机误差X 的概率密度, 并计算误差的绝对值 不超过0.004秒的概率.
《概率论》课程PPT：边缘分布及随机变量的相互独立性
F(x, y) FX (x) FY ( y)
例1 设（X，Y）的概率分布（律）为
y x
1/2 1 2
p .j
-1 2/20 2/20 4/20 2/5
0 1/20 1/20 2/20 1/5
2
pi.
2/20 1/4
2/20 1/4
4/20 2/4 2/5
证明：X、Y相互独立。
逐个验证等式 pij pi p j
即
Y
X
y1 y2 y3 …
x1 p11 p12 p13 … x2 p21 p22 p23 … x3 p31 p32 p33 … ……………
二维离散型R.v.的边缘分布
Y
X
y1
y2
y3
…
Pi.
x1
p11
p12
p13
…
P1.
x2
p21
p22
p23
…
P2.
x3
p31
p32
p33
…
P3.
…………… …
p.j p.1 p.2 p.3 …
依次称为二维随机变量 (X ,Y )关于 X 和关于 Y
的边缘分布函数．
FX (x) F(x, ) FY ( y) F(, y)
二维离散型R.v.的边缘分布
如果二维离散型随机变量（X,Y）的联合分布律为
P{X xi ,Y y j} pij i, j 1, 2,3,
关于Y的边缘分布
Y 0 1 1/3 概率 7/12 1/3 1/12
（X，Y）的联合分布列
Y
X
0
1 1/3
-1 0 1/3 1/12 0 1/6 0 0 2 5/12 0 0
例1 设（X，Y）的概率分布（律）为
y x
1/2 1 2
p .j
-1 2/20 2/20 4/20 2/5
0 1/20 1/20 2/20 1/5
2
pi.
2/20 1/4
2/20 1/4
4/20 2/4 2/5
证明：X、Y相互独立。
逐个验证等式 pij pi p j
即
Y
X
y1 y2 y3 …
x1 p11 p12 p13 … x2 p21 p22 p23 … x3 p31 p32 p33 … ……………
二维离散型R.v.的边缘分布
Y
X
y1
y2
y3
…
Pi.
x1
p11
p12
p13
…
P1.
x2
p21
p22
p23
…
P2.
x3
p31
p32
p33
…
P3.
…………… …
p.j p.1 p.2 p.3 …
依次称为二维随机变量 (X ,Y )关于 X 和关于 Y
的边缘分布函数．
FX (x) F(x, ) FY ( y) F(, y)
二维离散型R.v.的边缘分布
如果二维离散型随机变量（X,Y）的联合分布律为
P{X xi ,Y y j} pij i, j 1, 2,3,
关于Y的边缘分布
Y 0 1 1/3 概率 7/12 1/3 1/12
（X，Y）的联合分布列
Y
X
0
1 1/3
-1 0 1/3 1/12 0 1/6 0 0 2 5/12 0 0
概率论课件：第二章随机变量及其概率分布
π 3π ⎞ ⎛ π 0 ⎟ 22.设随机变量 X 的分布律为 ⎜ 2 2 ⎟ ，求 Y 的分布律： ⎜ ⎝ 0.3 0.2 0.4 0.1 ⎠
（1） Y = ( 2 X − π ) ;
2
（2） Y = cos( 2 X − π ). ⎧2 x , 0 < x < 1 f ( x) = ⎨ ⎩0 , 其它
它意味着第 i 次（ i ≥ k ）成功，且 i − 1 次试验中成功 k − 1 次，设这两个事件分别为A1 ，A2，
则A = A 1 A 2 , 且P(A) = P(A 1 A 2 ) = P(A 1 )P(A 2 )(A 1与A 2 独立 ), 而 P(A 1 ) = p,
1 k −1 1 k −1 i − k P( A2 ) = Cik−− ⋅ q i −1−( k −1) = Cik−− q . 1 p 1 ⋅ p
, ( 2,6),
, (6,1),
例如(6,1) , (6,6)} .这里，
8
5 36
9
4 36
10
3 36
11
2 36
12
1 36
PK
1 36
2 36
3 36
4 36
5 36
6 36
概率 P{X = k }, k = 0,1,2,3.
2、分析： 显然 X 服从离散型概率分布，而且 X 的可能取值为 0，1，2，3.问题归结为求
∴ X 的分布律为：
P{X = 0} = P ( A1 ) = 1 / 2; P{X = 1} = P ( A1 A2 ) = 1 / 2 2 ; P{X = 2} = P ( A1 A2 A3 ) = 1 / 2 3 ;
X Pi
《概率论讲义》课件
线性回归
介绍线性回归模型的基本原理和应用案例。
多元非线性回归
探讨多元非线性回归分析的方法和实际应用。
蒙特卡罗方法
1
简介和基本概念
介绍蒙特卡罗方法的基本思想和使用领域。
2
模拟方法
说明蒙特卡罗方法的模拟过程和实际应用。
3
抽样方法
讨论蒙特卡罗方法中的抽样技术和抽样步骤。
应用案例
金融风险管理
探讨概率论在金融风险管理中的应用和重要性。
2
弱大数定律
探讨具体的弱大数定律和其适用性。
3
中心极限定理
详细解释中心极限定理及其在概率论中的重要性。
统计推断
1 点估计
介绍点估计的概念和方法，以及其在概率论中的应用。
2 区间估计
说明区间估计的原理和步骤，并讨论其实际应用。
3 假设检验
讲解假设检验的基本思想和步骤，以及其在统计学中的作用。
回归分析
《概率论讲义》PPT课件
概率论讲义PPT课件大纲
简介
介绍概率论的基本概念和应 用领域，初步了解概率论的 历史和发展。
随机变量
定义随机变量，离散型和连 续型随机变量及其概率分布。
概率分布
二项分布，泊松分布和正态 分布。
大数定律与中心极限定理
1
定义大数定律和中心极限定理
深入了解大数定律和中心极限定理的概念和应用。
人口统计学
展示概率论如何应用于人口统计学数据的分析和预测。
物理学和天文学
介绍概率论在物理学和天文学研究中的关键作用。
结论
总结所学内容，展望概率论的未来发展和应用前景。
参考文献
推荐阅读经典著作和相关文献
提供经典著作和相关文献，供学习和研究参考。
《概率论》课程PPT ： 随机变量的分布函数
4
(1, 5)
0 其它
求 X 的分布函数
y
解 当x1时
x
F (x) f (x)dx
0 1 2345 x x
当1 < x 5 时F (x)
x
f (x)dx
1
f (x)dx
x
f (x)dx
1
0 x 1 dx 1 (x 1)
14
（2)X 的密度函数
(1) P(0.3 X 0.7) F(0.7) F(0.3) 0.72 0.32 0.4
（2）密度函数为
f
(x)
F(x)
2x 0
0 x 1 otherwise
例：已知密度函数求分布函数
已知连续型随机变量X的概率密度为
1
f
(
x)
随机变量的分布函数
Distribution Function 分布函数的定义
设X为一随机变量,则对任意实数x，(X<x) 是一个随机事件，称
F(x) P(X x)
为随机变量X的分布函数
F(x)是一个
普通的函数！
定义域为 （－∞，＋∞）； 值域为 ［０，１］。
分布函数表示事件的概率
引进分布函数F(x)后，事件的概率都可以用 F(x)的函数值来表示。
解
X的概率密度
3 e3x x 0 f (x)
0 x 0
P(x1 X x2)
x2 f (x)dx
x1
P(X 1)
f (x)dx
3e3xdx e3
1
1
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第一章 随机事件及其概率
内容提要
一、随机事件
1、随机试验：观察一定 综合条件的实现。（条 件
实现就完成一次试验） 一般用字母‘ E ’表示试验。
2、样本空间：试验可能 出现的全部结果组成的 集
合。一般用字母‘ ’表示，组成样本空间的 元素称
为样本点，（或称为基 本事件）一般用字母‘ ’表
示。
3、随机事件：样本空间 的子集称为随机事件。 一
这些题目所考的知识点 实际上是相同的， 本质上式一样的。
编辑ppt
பைடு நூலகம்
7
三、随机事件概率的定
义
1 、概率的统计定义：设
随机事件 A 在 n 次重
复试验中出现了
k 次， P ( A ) k 。 n
2 、概率的古典定义：若
随机试验
E 满足
10 { 1, , n } 2 0 P ( 1) P ( n ) 则称 E 是古典概率模型。
A i 表示
A 表示至少有一个盒子无
N
球，则 A A i
i1
B 表示每个盒子至少有一
N
个球，则 B A i
编辑ppt
i1
3
5、事件 A 与 B 互不相容 AB . 6、事件 A 与 B 相互对立 A B 且 AB
注：相互对立的事件一定是互不相容的事件，反
之不一定。
7、两个事件的差A B AB A发生但 B不发生。 8、事件运算的一条性质：
P ( Ai ) 1 P ( Ai )
i 1
i 1
n
n
7 0、 P ( Ai ) P ( Ai )
P ( Ai A j )
P ( Ai A j Ak )
i 1
i 1
1i j n
1i j k n
n
(1) n1 P ( Ai )
i 1
( 概率的加法公式）
编辑ppt
11
概率的加法公式的特殊 情况为
AB AB 或
AB A B
编辑ppt
5
那 A, B 是不是相互对立呢？如 过你对这样的问 题作了思考，那么应付 如下的难题不久容易了 吗？
例、已知 AB A B 且 [ P ( A )] 2 [ P ( B )] 2 0.52 则 P ( A) P ( B ) _____ 。
例、已知 A B A B , 则
般用字母‘ A 、 B 、 C 、 ’表编辑示pp（t 即 A )
1
二、随机事件之间的关系及其运算
1、A B A 发生必然导致B 发生。如：X是
随机变量，Y X 2, A {1 X 1} B {Y 1}. 2
2、A B A B 且 B A。如：X是随机变量
，X ~ N (, 2 ), X1,, X n 是来自X的样本，
n
n
n
0 P ( Ai) P ( Ai) P ( Ai)
i1
i 1 编辑ppt i 1
12
又如关于概率的减法公 式：即
A B P(B A) P(B) P(A) 这实际上是 P ( BA ) P ( B ) P ( A)，如果你不局 限于 A B的情形，思考一下对任 意两个事件 A, B结果又如何呢？即
Ai Ai ,
Ai Ai
i 1
i 1
i 1
i 1
编辑ppt
4
又如关于对立事件的概 念： 定义： A与B至少有一个发生，也最 多只有一个
发生，即 A B 且AB , 称A与B相互对立。记
为A B , B A 。那么，有 A B A B , 同样也 有 AB A B ， 如果你深入思考一下， 若反过来会 有什么结果呢？即若
P ( A B ) P ( A ) P ( A ) P ( AB )
80、 A B P(B A) P(B) P(A) ( 概率的减法公式）
由概率的减法公式可推 出概率的单调性，即
90、 A B P(A) P(B）
0 P ( ABC ) P ( AB ) P ( A ) P ( A B ) 1
X A { X 2} B {
n 2
n}
编辑ppt
2
3 、事件的和 有一个发生。
A i 事件 A1 , A 2 , , A n , 至少
i1
4 、事件的交 发生。
A i 事件 A1 , A 2 , , A n , 同时
i1
例： n 个球随机地放到
N 个盒子中，令
第 i（ i 1,2 , , N ) 个盒子无球。
P ( A B ) _________ .
例、已知 A B A B , 则
P ( A B ) P ( A B ) __________ _ .
编辑ppt
6
例、已知 AB A B ,则
P( A B ) P( A B) ___________ . 例、已知 A B A B
且[P( A)]2 [P(B)]2 0.52 则P( A)P(B) _____。则
若 A 是古典概率模型 E 中的随机事件，则
A 中所含的基本事件数
P(A)
编基辑本pp事t 件总数
8
3、概率的公理化定义： 若 {} 是随机试
验 E 的样本空间，对任意的 A ，赋予一个
实数 P( A)，满足如下三条公理：
10、0 P( A) 1；（非负性）
20、P() 1；（规范性）
30、A1, A2 , An , 互不相容， P( Ai ) P( Ai ).
i 1
i 1
（可列可加性）
则称 P(.)为概率函数， P( A) 称为 A 的概率。
编辑ppt
9
由概率公理化定义中三 条公理可推出概率的
如下性质：
4 0、 P ( ) 0
注：必然事件 的概率为
样，不可能事件 的概率为
P ( A B ) _________
P ( AB ) _________
P ( A B ) _________ 如果掌握了这些结论， 有些考题就很容易了。
编辑ppt
13
四、条件概率
1、条件概率的定义：
P ( A ) 0 , P ( A B ) P ( AB ) P(B)
注：条件概率既然是概 率，则概率的一切性
件不一定是不可能事件 。
1，反之不一定；同 0，但概率为 0 的事
5 0、 A1 , , An互不相容， （有限可加性）
n
n
P ( Ai ) P ( Ai )
i1
i1
由有限可加性可推出如 下对 编辑ppt 立事件公式：
10
60、 P(A ) 1 P(A)
P(AB) 1 P(A B)
n
n
内容提要
一、随机事件
1、随机试验：观察一定 综合条件的实现。（条 件
实现就完成一次试验） 一般用字母‘ E ’表示试验。
2、样本空间：试验可能 出现的全部结果组成的 集
合。一般用字母‘ ’表示，组成样本空间的 元素称
为样本点，（或称为基 本事件）一般用字母‘ ’表
示。
3、随机事件：样本空间 的子集称为随机事件。 一
这些题目所考的知识点 实际上是相同的， 本质上式一样的。
编辑ppt
பைடு நூலகம்
7
三、随机事件概率的定
义
1 、概率的统计定义：设
随机事件 A 在 n 次重
复试验中出现了
k 次， P ( A ) k 。 n
2 、概率的古典定义：若
随机试验
E 满足
10 { 1, , n } 2 0 P ( 1) P ( n ) 则称 E 是古典概率模型。
A i 表示
A 表示至少有一个盒子无
N
球，则 A A i
i1
B 表示每个盒子至少有一
N
个球，则 B A i
编辑ppt
i1
3
5、事件 A 与 B 互不相容 AB . 6、事件 A 与 B 相互对立 A B 且 AB
注：相互对立的事件一定是互不相容的事件，反
之不一定。
7、两个事件的差A B AB A发生但 B不发生。 8、事件运算的一条性质：
P ( Ai ) 1 P ( Ai )
i 1
i 1
n
n
7 0、 P ( Ai ) P ( Ai )
P ( Ai A j )
P ( Ai A j Ak )
i 1
i 1
1i j n
1i j k n
n
(1) n1 P ( Ai )
i 1
( 概率的加法公式）
编辑ppt
11
概率的加法公式的特殊 情况为
AB AB 或
AB A B
编辑ppt
5
那 A, B 是不是相互对立呢？如 过你对这样的问 题作了思考，那么应付 如下的难题不久容易了 吗？
例、已知 AB A B 且 [ P ( A )] 2 [ P ( B )] 2 0.52 则 P ( A) P ( B ) _____ 。
例、已知 A B A B , 则
般用字母‘ A 、 B 、 C 、 ’表编辑示pp（t 即 A )
1
二、随机事件之间的关系及其运算
1、A B A 发生必然导致B 发生。如：X是
随机变量，Y X 2, A {1 X 1} B {Y 1}. 2
2、A B A B 且 B A。如：X是随机变量
，X ~ N (, 2 ), X1,, X n 是来自X的样本，
n
n
n
0 P ( Ai) P ( Ai) P ( Ai)
i1
i 1 编辑ppt i 1
12
又如关于概率的减法公 式：即
A B P(B A) P(B) P(A) 这实际上是 P ( BA ) P ( B ) P ( A)，如果你不局 限于 A B的情形，思考一下对任 意两个事件 A, B结果又如何呢？即
Ai Ai ,
Ai Ai
i 1
i 1
i 1
i 1
编辑ppt
4
又如关于对立事件的概 念： 定义： A与B至少有一个发生，也最 多只有一个
发生，即 A B 且AB , 称A与B相互对立。记
为A B , B A 。那么，有 A B A B , 同样也 有 AB A B ， 如果你深入思考一下， 若反过来会 有什么结果呢？即若
P ( A B ) P ( A ) P ( A ) P ( AB )
80、 A B P(B A) P(B) P(A) ( 概率的减法公式）
由概率的减法公式可推 出概率的单调性，即
90、 A B P(A) P(B）
0 P ( ABC ) P ( AB ) P ( A ) P ( A B ) 1
X A { X 2} B {
n 2
n}
编辑ppt
2
3 、事件的和 有一个发生。
A i 事件 A1 , A 2 , , A n , 至少
i1
4 、事件的交 发生。
A i 事件 A1 , A 2 , , A n , 同时
i1
例： n 个球随机地放到
N 个盒子中，令
第 i（ i 1,2 , , N ) 个盒子无球。
P ( A B ) _________ .
例、已知 A B A B , 则
P ( A B ) P ( A B ) __________ _ .
编辑ppt
6
例、已知 AB A B ,则
P( A B ) P( A B) ___________ . 例、已知 A B A B
且[P( A)]2 [P(B)]2 0.52 则P( A)P(B) _____。则
若 A 是古典概率模型 E 中的随机事件，则
A 中所含的基本事件数
P(A)
编基辑本pp事t 件总数
8
3、概率的公理化定义： 若 {} 是随机试
验 E 的样本空间，对任意的 A ，赋予一个
实数 P( A)，满足如下三条公理：
10、0 P( A) 1；（非负性）
20、P() 1；（规范性）
30、A1, A2 , An , 互不相容， P( Ai ) P( Ai ).
i 1
i 1
（可列可加性）
则称 P(.)为概率函数， P( A) 称为 A 的概率。
编辑ppt
9
由概率公理化定义中三 条公理可推出概率的
如下性质：
4 0、 P ( ) 0
注：必然事件 的概率为
样，不可能事件 的概率为
P ( A B ) _________
P ( AB ) _________
P ( A B ) _________ 如果掌握了这些结论， 有些考题就很容易了。
编辑ppt
13
四、条件概率
1、条件概率的定义：
P ( A ) 0 , P ( A B ) P ( AB ) P(B)
注：条件概率既然是概 率，则概率的一切性
件不一定是不可能事件 。
1，反之不一定；同 0，但概率为 0 的事
5 0、 A1 , , An互不相容， （有限可加性）
n
n
P ( Ai ) P ( Ai )
i1
i1
由有限可加性可推出如 下对 编辑ppt 立事件公式：
10
60、 P(A ) 1 P(A)
P(AB) 1 P(A B)
n
n