最新数字电子技术基础教材第四章答案
《数字电子技术基础》第四章习题答案
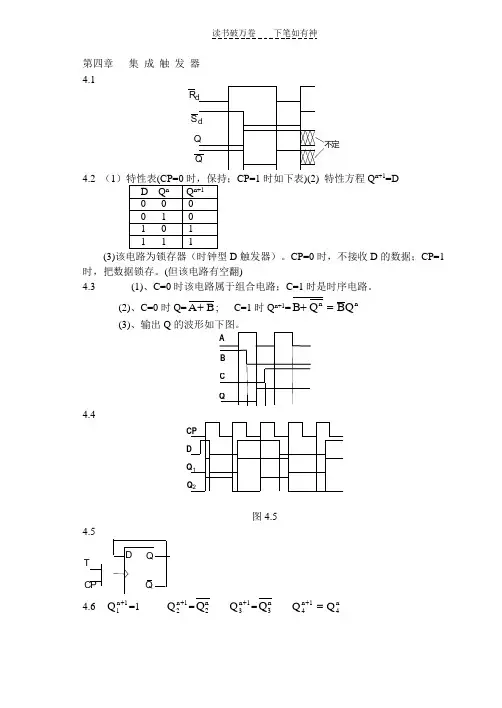
第四章 集 成 触 发 器 4.1R d S d Q Q不定4.2 （1CP=1时如下表)(2) 特性方程Q n+1=D(3)该电路为锁存器（时钟型D 触发器）。
CP=0时，不接收D 的数据；CP=1时，把数据锁存。
(但该电路有空翻)4.3 (1)、C=0时该电路属于组合电路；C=1时是时序电路。
(2)、C=0时Q=A B +; C=1时Q n+1=B Q BQ nn+= (3)、输出Q 的波形如下图。
A B C Q4.4CP D Q 1Q 2图4.54.5 DQ QCPT4.6 Q 1n 1+=1 Q 2n 1+=Q 2n Q n 13+=Q n 3 Q Q 4n 14n+=Q1CP Q2Q3Q44.7 1、CP 作用下的输出Q 1 Q 2和Z 的波形如下图； 2、Z 对CP 三分频。
DQ QCPQ1DQ QQ2ZRd CP Q1Q2Z14.8由Q D J Q KQ J Q KQ n 1n n n n +==+=⋅得D 触发器转换为J-K 触发器的逻辑图如下面的左图；而将J-K 触发器转换为D 触发器的逻辑图如下面的右图CPD Q QJKQ QDQ QJ KCP4.9CP B CA4.10CP X Q1Q2Z4.11 1、555定时器构成多谐振荡器 2、u c, u o 1, u o 2的波形u c u o 1u o 2t t t 1.67V3.33V3、u o 1的频率f 1=1074501316..H z ⨯⨯≈ u o 2的频率f 2=158H z4、如果在555定时器的第5脚接入4V 的电压源，则u o 1的频率变为1113001071501232....H z ⨯⨯+⨯⨯≈4.12 图(a)是由555定时器构成的单稳态触发电路。
1、工作原理（略）；2、暂稳态维持时间t w =1.1RC=10ms(C 改为1μF)；3、u c 和u o 的波形如下图：u ou ct t tu i (ms)(ms)(ms)5 10 25 30 45 503.33V4、若u i 的低电平维持时间为15m s ，要求暂稳态维持时间t w 不变，可加入微分电路4.13由555定时器构成的施密特触发器如图(a)所示 1、电路的电压传输特性曲线如左下图； 2、u o 的波形如右下图；3、为使电路能识别出u i 中的第二个尖峰，应降低555定时器5脚的电压至3V 左右。
数字电子技术基础(第4版)课后习题答案详解
(b)当v i＝0V时， vB为负值 ∴ T截止 vo＝5V
当
v
i＝5V时，
I
＝
B
5－0.7 54。7
−
8.7 18
=
0.42 mA
I BS
≈
5 50 × 2
= 0.05mA <
IB
∴ T饱和
vo ≈ 0.2V (0 ~ 0.3V都行）
悬空时，
I
＝
B
5－0.7 4.7
−
8.7 18
=
0.08 mA
I BS
(5)Y =1
2
Y = ABC + ABC + ABC
(2)Y = CD + ACD (4)Y = BC + B D
(2)Y = B + AD + AC (4)Y = A + B D (6)Y = CD + B D + AC
数字电路 习题答案 （第二章）
第二章
2.1 解:
2
数字电路 习题答案 （第二章）
2.10 (1) vi2 = 1.4V (2) vi2 = 0.2V (3) vi2 = 1.4V (4) vi2 = 0.2V (5) vi2 = 1.4V
2.11 各种情况均为 1.4V 2.12 解：
输出为高电平时：Vo = Vcc − (0.2 × 2 − iL )RL = 4.6 + iL RL
114化简下列逻辑函数bdce120将下列函数化为最简与或式wwwplczonecom数字电路习题答案第二章第二章213010截止负值悬空时都行饱和悬空时都行饱和截止为负值200200ililil1010ihccihccih2002ohol系数输出为高电平时扇出系数输出为低电平时扇出所以n2025为输入端的个数分母中的系数输出为高电平时扇出系数输出为低电平时扇出2imaxohol所以n5wwwplczonecom数字电路习题答案第二章26解
数字电子技术基础教材第四章答案
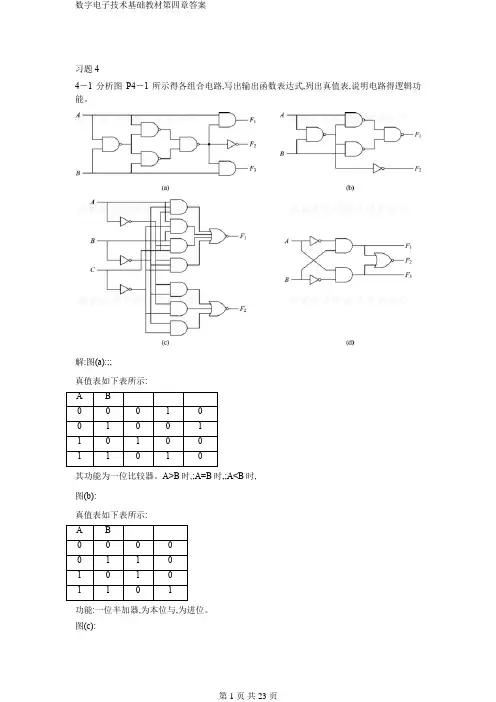
习题44－1 分析图P4－1所示得各组合电路,写出输出函数表达式,列出真值表,说明电路得逻辑功能。
解:图(a):;;真值表如下表所示:其功能为一位比较器。
A>B时,;A=B时,;A<B时,图(b):真值表如下表所示:功能:一位半加器,为本位与,为进位。
图(c):真值表如下表所示:功能:一位全加器,为本位与,为本位向高位得进位。
图(d):;;功能:为一位比较器,A<B时,＝1;A=B时,＝1;A>B时,＝14－2 分析图P4－2所示得组合电路,写出输出函数表达式,列出真值表,指出该电路完成得逻辑功能。
解:该电路得输出逻辑函数表达式为:因此该电路就是一个四选一数据选择器,其真值表如下表所示:,当M＝1时,完成4为二进制码至格雷码得转换;当M＝0时,完成4为格雷码至二进制得转换。
试分别写出,,,得逻辑函数得表达式,并列出真值表,说明该电路得工作原理。
解:该电路得输入为,输出为。
真值表如下:由此可得:完成二进制至格雷码得转换。
完成格雷码至二进制得转换。
4－4 图P4－4就是一个多功能逻辑运算电路,图中,,,为控制输入端。
试列表说明电路在,,,得各种取值组合下F与A,B得逻辑关系。
解:,功能如下表所示,两个变量有四个最小项,最多可构造种不同得组合,因此该电路就是一个能产生十六种函数得多功能逻辑运算器电路。
4－5 已知某组合电路得输出波形如图P4－5所示,试用最少得或非门实现之。
解:电路图如下:4－6 用逻辑门设计一个受光,声与触摸控制得电灯开关逻辑电路,分别用A,B,C表示光,声与触摸信号,用F表示电灯。
灯亮得条件就是:无论有无光,声信号,只要有人触摸开关,灯就亮;当无人触摸开关时,只有当无关,有声音时灯才亮。
试列出真值表,写出输出函数表达式,并画出最简逻辑电路图。
解:根据题意,列出真值表如下:由真值表可以作出卡诺图,如下图:C AB 00 10 11 100 1由卡诺图得到它得逻辑表达式为: 由此得到逻辑电路为:4－7 用逻辑门设计一个多输出逻辑电路,输入为8421BCD 码,输出为3个检测信号。
数字电子技术第四节课后习题答案(江晓安等编)
第四章组合逻辑电路1. 解：(a)(b)是相同的电路，均为同或电路。
2. 解：分析结果表明图(a)、(b)是相同的电路，均为同或电路。
同或电路的功能：输入相同输出为“1”；输入相异输出为“0”。
因此，输出为“0”(低电平)时，输入状态为AB＝01或103. 由真值表可看出，该电路是一名二进制数的全加电路，A为被加数，B为加数，C为低位向本位的进位，F1为本位向高位的进位，F2为本位的和位。
4. 解：函数关系如下：SF++⊕=+ABSABS BABS将具体的S值代入，求得312F值，填入表中。
AA FB A B A B A A F B A B A A F A A F AB AB F B B A AB F AB B A B A B A AB F BA A AB F B A B A B A F B A AB AB B A B A F B B A B A B A B A B A B A F ABBA A A B A A B A F F B A B A F B A B A F A A F S S S S =⊕==+==+⊕===+⊕===⊕===⊕===+⊕===+=+⊕===⊕==+==⊕==Θ=+=+⊕===+++=+⊕===+=⊕===⊕==+=+⊕==+=+⊕===⊕==01111111011010110001011101010011000001110110)(01010100101001110010100011000001235. （1）用异或门实现，电路图如图(a)所示。
(2) 用与或门实现，电路图如图(b)所示。
6. 解因为一天24小时，所以需要5个变量。
P变量表示上午或下午，P＝0为上午，P=1为下午；ABCD表示时刻数值。
真值表如表所示。
利用卡诺图化简如图(a)所示。
化简后的函数表达式为DC A PD B A P C B A P A P D C A P D B A P C B A P A P F =+++=用与非门实现的逻辑图如图(b)所示。
数字电子技术基础(第4版)_课后习题答案
第一章1.1二进制到十六进制、十进制(1)(10010111)2=(97)16=(151)10 (2)(1101101)2=(6D)16=(109)10(3)(0.01011111)2=(0.5F)16=(0.37109375)10 (4)(11.001)2=(3.2)16=(3.125)10 1.2十进制到二进制、十六进制(1)(17)10=(10001)2=(11)16 (2)(127)10=(1111111)2=(7F)161621016210)3.19()1010 1(11001.101(25.7)(4))A D7030.6()0101 0000 0111 1101 0110 (0.0110(0.39)(3) B ====1.8用公式化简逻辑函数(1)Y=A+B (3)Y=1）＝＋（解：1A A 1)2(=+++=+++=+++=C B A C C B A C B Y CB AC B A Y ADC C B AD C B C B AD DC A ABD CD B A Y =++=++=++=)()(Y )4(解：(5)Y=0 (7)Y=A+CDE ABCD E C ABCD CE AD B BC CE AD B BC Y CE AD B BC B A D C AC Y =+=⋅+=+⋅=++++=)()()()()()6(解：CB AC B C B A A C B A C B A C B A C B C B A A C B A C B A C B A Y C B A C B A C B A Y +=++=+++=++++=++++⋅+=++++++=)())(())()(())()((8解：）（D A D A C B Y ++=)9(E BD E D BF E A AD AC Y ++++=)10(1.9 (a) C B C B A Y += (b) C B A ABC Y +=(c) ACD D C A D C A B A Y D AC B A Y +++=+=21,(d) C B A ABC C B A C B A Y BC AC AB Y +++=++=21, 1.10 求下列函数的反函数并化简为最简与或式(1)C B C A Y += (2)DC A Y++=CB C B AC C B AC B A BC AC C A B A BC AC C A B A Y BCAC C A B A Y +=++++=⋅+++=+++=+++=))((]))([())(())(()3(解： (4)C B A Y ++=DC ABD C B D C A D C B D A C A C D C B C A D A Y CD C B C A D A Y =++=+++=++++=+++=)())(())()(()5(解： (6)0=Y1.11 将函数化简为最小项之和的形式CB AC B A ABC BC A C B A C B A C B A ABC BC A CB A AC B B A BC A C B AC BC A Y CB AC BC A Y +++=++++=++++=++=++=)()()1(解：D C B A CD B A D C B A ABCD BCD A D C B A Y +++++=）（2)13()()()(3CD B A BCD A D BC A D C B A D C B A ABCD D ABC D C AB D C AB CD B A D C B A D C B A D C B A CD AB B A B A B A ACD D AC D C A D C A CD A D C A D C A D C A B BCD D BC D C B D C B CD B D C B D C B D C B A Y CDB A Y ++++++++++++=+++++++++++++++++++=++=解：）（(4)CD B A D ABC D BC A D C AB D C AB CD B A ABCD BCD A Y +++++++= (5)MN L N M L N LM N M L N M L N M L Y +++++=1.12 将下列各函数式化为最大项之积的形式(1)))()((C B A C B A C B A Y ++++++= (2)))()((C B A C B A C B A Y ++++++= (3)76430M M M M M Y ⋅⋅⋅⋅= (4)13129640M M M M M M Y ⋅⋅⋅⋅⋅= (5)530M M M Y ⋅⋅=1.13 用卡诺图化简法将下列函数化为最简与或形式：(1)D A Y +=(3)1=Y (2)D C BC C A B A Y +++= (4)B AC B A Y ++=B A DC Y ++=AC B A Y +=(5)D C B Y ++= (6)C B AC B A Y ++=(7)C Y = (9)D C A C B D A D B Y +++=(8))14,11,10,9,8,6,4,3,2,1,0(),,,(m D C B A Y ∑= (10)),,(),,(741m m m C B A Y ∑=D A D C B Y ++=ABC C B A C B A Y ++=1.14化简下列逻辑函数(1)D C B A Y +++= (2)D C A D C Y += (3)C A D AB Y ++= (4)D B C B Y += (5)E D C A D A E BD CE E D B A Y +++++=1.20将下列函数化为最简与或式(1)AD D C B D C A Y ++= (2)AC D A B Y ++= (3)C B A Y ++= (4)D B A Y +=第二章2.1解:Vv v V V v T I mA I mA Vv T V v a o B o B BS B o B 10T 3.0~0(2.017.0230103.0207.101.57.05I V 5v 1021.5201.510V 0v )(i i ≈≈∴<=×≈=−≈∴−=×+−=截止，负值，悬空时，都行）饱和－＝时，＝当截止时，＝当都行）＝饱和，，－＝悬空时，都行）饱和。
数字电子技术基础(第四版)课后习题答案_第四章
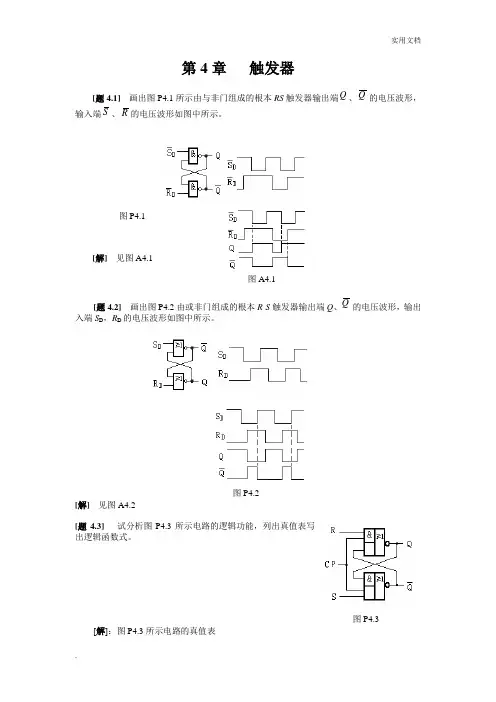
第4章触发器[题4.1]画出图P4.1所示由与非门组成的根本RS触发器输出端Q、Q的电压波形，输入端S、R的电压波形如图中所示。
图P4.1[解]见图A4.1图A4.1[题4.2]画出图P4.2由或非门组成的根本R-S触发器输出端Q、Q的电压波形，输出入端S D，R D的电压波形如图中所示。
图P4.2[解]见图A4.2[题4.3]试分析图P4.3所示电路的逻辑功能，列出真值表写出逻辑函数式。
图P4.3 [解]：图P4.3所示电路的真值表S R Q n Q n+1 0 0 0 0 0 0 1 1 0 1 0 0 0 1 1 0 1 0 0 1 1 0 1 1 1 1 0 0* 1 110*由真值表得逻辑函数式 01=+=+SR Q R S Q nn[题4.4] 图P4.4所示为一个防抖动输出的开关电路。
当拨动开关S 时，由于开关触点接触瞬间发生振颤，D S 和D R 的电压波形如图中所示，试画出Q 、Q 端对应的电压波形。
图P4.4[解] 见图A4.4图A4.4[题4.5] 在图P4.5电路中，假设CP 、S 、R 的电压波形如图中所示，试画出Q 和Q 端与之对应的电压波形。
假定触发器的初始状态为Q =0。
图P4.5[解]见图A4.5图A4.5[题4.6]假设将同步RS触发器的Q与R、Q与S相连如图P4.6所示，试画出在CP 信号作用下Q和Q端的电压波形。
己知CP信号的宽度t w = 4 t Pd 。
t Pd为门电路的平均传输延迟时间，假定t Pd≈t PHL≈t PLH，设触发器的初始状态为Q=0。
图P4.6图A4.6[解]见图A4.6[题4.7]假设主从结构RS触发器各输入端的电压波形如图P4.7中所给出，试画Q、Q端对应的电压波形。
设触发器的初始状态为Q=0。
图P4.7[解] 见图A4.7图A4.7[题4.8]假设主从结构RS触发器的CP、S、R、DR各输入端的电压波形如图P4.8所示，1DS。
数字电路与数字电子技术课后答案第四章
数字电路与数字电子技术-课后答案第四章第四章逻辑函数及其符号简化1．列出下述问题的真值表，并写出逻辑表达式：(1)有A、B、C三个输入信号，如果三个输入信号中出现奇数个1时，输出信号F=1，其余情况下，输出F= 0.(2)有A、B、C三个输入信号，当三个输入信号不一致时，输出信号F=1，其余情况下，输出为0.(3)列出输入三变量表决器的真值表.解: ( 1 )F=A B C+A B C+A B C+ABC ( 2 )F= (A+B+C) ( A+B+C)A BC F0 00 00 0A BC F0 00 00 0F=A BC+A B C+AB C+ABC2. 对下列函数指出变量取哪些组值时,F的值为“1”：(1) F= AB+A B(2) F= AB+A C(3) F= (A+B+C) (A+B+C) (A+B+C) (A+B+C) 解:(1)AB = 00或AB=11时F=1(2)ABC110或111,或001,或011时F=1(3)ABC = 100或101或110或111时F=1 3. 用真值表证明下列等式.(1) A+BC = (A+B) (A+C)(2) A BC+A B C+AB C= BC ABC+AC ABC+AB ABC(3) C A+C B+B A=ABC+A B C(4) AB+BC+AC=(A+B)(B+C)(A+C)(5) ABC+A+B+C=1证:( 1 )A B CA+BC(A+B)(A+C)0 0 00 0( 2 )A B C ABC + ABC + ABCBCABC + ACA B C + ABABC0 0 0 00 0 1 0( 3 )A B C AB +BC + AC ABC + A B C0 0 01 10 0 1( 4 )( 5 )4. 直接写出下列函数的对偶式F ′及反演式F 的函数表达式. A B C AB+BC+AC (A+B)(B+C)(A+C) 0 0 0 0 0 0 0 1 0 A B C ABC + A + B + C 0 0 0 1 0 0 1(1) F= [A B (C+D)][B C D+B (C+D)](2) F= A BC+ (A+B C) (A+C)(3) F= AB+CD+E+D+E C+D+BC(4) F=D+B A•B A+C解:(1)F`= [A+B+CD]+[(B+C+D)(•B+C D]]F= [A+B+C D]+[(B+C+D)(•B+C D]](2)F`= (A+C+B)]AC)C+B(•A[•F= (A+C+B)]C A+)C+B(•A[•(3)F`=)B+A(•C+D•)B+A(F=)B+A(•C+D•)B+A(5. 若已知x+y = x+z，问y = z吗?为什么? 解:y不一定等于z,因为若x=1时,若y=0,z=1,或y=1,z=0,则x+y = x+z = 1,逻辑或的特点,有一个为1则为1。
数字电子技术第四章习题答案
4.8 用4片8线-3线优先编码器组成 线-5线优先编码器。 线优先编码器组成32线 线优先编码器 线优先编码器。 片 线 线优先编码器组成
YS'
1 0 1 0
Y’2(4) 0 1 1 1 1
' YEX
状态 不工作 工作， 工作，但无输入 工作， 工作，且有输入 不可能出现
1 1 0 0
Y’2(3) 1 0 1 1 1
C 0 1 0 1 0 1 0 1
MS 0 1 × 0 × × × 1
ML 0 0 × 1 × × × 1
MS
BC 00 A 0 1 0 x BC 00 0 x
01 1 x
11 0 1
10 x x
ML A 0 1
01 0 x
11 1 1
10 x x
MS=A+B’C ML=B
B ML
《数字电子技术基础》第五版 数字电子技术基础》
《数字电子技术基础》第五版 数字电子技术基础》
4.3
解：输入变量——水位检测结果 输入变量 水位检测结果 来表示， 用A，B，C来表示， ， ， 来表示 高于检测元件时为“ ， 高于检测元件时为“0”， 低于检测元件时为“1”； 低于检测元件时为“ ； 输出变量——水泵工作状态 输出变量 水泵工作状态 用ML，MS分别代表两个水泵 工作为“ ，不工作为“ 。 工作为“1”，不工作为“0”。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
习题44－1 分析图P4－1所示的各组合电路，写出输出函数表达式，列出真值表，说明电路的逻辑功能。
解：图（a ）：1F AB =；2F A B =；3F AB = 真值表如下表所示： A B 1F2F3F0 0 0 1 0 0 1 0 0 1 1 0 1 0 0 111其功能为一位比较器。
A>B 时，11F =；A=B 时，21F =；A<B 时，31F = 图（b ）：12F AB AB F AB =+=； 真值表如下表所示： A B 1F2F功能：一位半加器，1F 为本位和，2F 为进位。
图（c ）：1(0,3,5,6)(1,2,4,7)F M m ==∑∏2(0,1,2,4)(3,5,6,7)F M m ==∑∏真值表如下表所示：功能：一位全加器，1F 为本位和，2F 为本位向高位的进位。
图（d ）：1F AB =；2F A B =；3F AB =功能：为一位比较器，A<B 时，1F ＝1；A=B 时，2F ＝1；A>B 时，3F ＝14－2 分析图P4－2所示的组合电路，写出输出函数表达式，列出真值表，指出该电路完成的逻辑功能。
解：该电路的输出逻辑函数表达式为：100101102103F A A x A A x A A x A A x =+++因此该电路是一个四选一数据选择器，其真值表如下表所示：1A0AF0 0 0x 0 1 1x 1 0 2x 1 13x4－3 图P4－3是一个受M 控制的代码转换电路，当M ＝1时，完成4为二进制码至格雷码的转换；当M ＝0时，完成4为格雷码至二进制的转换。
试分别写出0Y ,1Y ,2Y ,3Y 的逻辑函数的表达式，并列出真值表，说明该电路的工作原理。
解：该电路的输入为3x 2x 1x 0x ，输出为3Y 2Y 1Y 0Y 。
真值表如下：3x2x1x0x3Y2Y1Y0YM=10 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 1 0 0 0 1 1 0 0 1 1 0 0 1 0 0 1 0 0 0 1 1 0 0 1 0 1 0 1 1 1 0 1 1 0 0 1 0 1 01 1 0 0 1 0 0 M=0 1 0 0 0 1 1 1 1 1 0 0 1 1 1 1 0 1 0 1 0 1 1 0 0 1 0 1 1 1 1 0 1 1111 1 0 1 1 0 0 1 1 1 1 0 1 0 1 1 111111由此可得：1M =当时，33232121010Y x Y x x Y x x Y x x =⎧⎪=⊕⎪⎨=⊕⎪⎪=⊕⎩ 完成二进制至格雷码的转换。
0M =当时，332321321210321010Y x Y x x Y x x x Y x Y x x x x Y x =⎧⎪=⊕⎪⎨=⊕⊕=⊕⎪⎪=⊕⊕⊕=⊕⎩ 完成格雷码至二进制的转换。
4－4 图P4－4是一个多功能逻辑运算电路，图中3S ,2S ,1S ,0S 为控制输入端。
试列表说明电路在3S ,2S ,1S ,0S 的各种取值组合下F 与A,B 的逻辑关系。
解：3210()()F S AB S AB S B S B A =+⊕++，功能如下表所示，3S 2S 1S 0SF3S 2S 1S 0SF0 0 0 0 A 1 0 0 0 AB0 0 0 1 A B +1 0 0 1 A B ⊕0 0 1 0 A B +1 0 1 0 B 0 0 1 1 1 1 0 1 1 AB0 1 0 0 AB 1 1 0 0 00 1 0 1 B1 1 0 1 AB 011A B111A B +0 1 1 1A B +1 1 1 1A两个变量有四个最小项，最多可构造42种不同的组合，因此该电路是一个能产生十六种函数的多功能逻辑运算器电路。
4－5 已知某组合电路的输出波形如图P4－5所示，试用最少的或非门实现之。
解：()(1,3,6,7)(0)()F ABC m A C A B φ=+=+++∑∑电路图如下：4－6 用逻辑门设计一个受光，声和触摸控制的电灯开关逻辑电路，分别用A,B,C 表示光，声和触摸信号，用F 表示电灯。
灯亮的条件是：无论有无光，声信号，只要有人触摸开关，灯就亮；当无人触摸开关时，只有当无关，有声音时灯才亮。
试列出真值表，写出输出函数表达式，并画出最简逻辑电路图。
解：根据题意，列出真值表如下：由真值表可以作出卡诺图，如下图：C AB 00 10 11 10 0 1由卡诺图得到它的逻辑表达式为： 由此的到逻辑电路为：F AB C=+C4－7 用逻辑门设计一个多输出逻辑电路，输入为8421BCD 码，输出为3个检测信号。
要求：（1） 当检测到输入数字能被4整除时，1F ＝1。
（2） 当检测到输入数字大于或等于3时，2F ＝1。
（3） 当检测到输入数字小于7时，3F ＝1。
解：1()f ABCD CD =2()f ABCD A B CD =++3()f ABCD AC AB CD =++4－8 用逻辑门设计一个两位二进制数的乘法器。
解：二进制乘法：设两个2位二进制数的乘法运算结果为：10103210()()A A A B B B P P PP ⨯= 电路图如下图所示：4－9 设计一个全加（减）器，其输入为A,B,C 和X(当X ＝0时，实现加法运算；当X ＝1时，实现减法运算)，输出为S(表示和或差)，P （表示进位或借位）。
列出真值表，试用3个异或门和3个与非门实现该电路，画出逻辑电路图。
解：根据全加器和全减器的原理，我们可以作出如下的真值表：1 B 3 B2 B 1 B 0由真值表可以画出卡诺图，由卡诺图得出逻辑表达式，并画出逻辑电路图：A B C XP4－10 设计一个交通灯故障检测电路，要求红，黄，绿三个灯仅有一个灯亮时，输出F ＝0；若无灯亮或有两个以上的灯亮，则均为故障，输出F ＝1。
试用最少的非门和与非门实现该电路。
要求列出真值表，化简逻辑函数，并指出所有74系列器件的型号。
解：根据题意，我们可以列出真值表如下：对上述的真值表可以作出卡诺图，由卡诺图我们可以得出以下的逻辑函数：F AB AC BC ABC ABAC BC ABC =+++=•••逻辑电路图如下所示：A F4－11试用两片8线－3线优先编码器74LS148组成16线－4线优先编码器，画出逻辑电路图，说明其逻辑功能。
解：逻辑电路图如下：逻辑功能：是一个16－4编码器。
4－12 （1）图P4－12为3个单译码逻辑门译码器，指出每个译码器的输出有效电平以及相应的输出二进制码，写出译码器的输出函数表达式。
（2）试画出与下列表达式对应的单译码器逻辑电路图。
①3210Y A A A A=②3210Y A A A A=③43210Y A A A A A=解：对于（a）图来说。
3210Y A A A A=(b)210Y A A A=(c)3210Y A A A A=对于（1）逻辑电路图为：A2A1AAY（2）逻辑电路图如下图：3A2AAA（3）逻辑电路图如下图：1S=3A 2AA 0A 4A4－13 试用一片3－8译码器和少量逻辑门设计下列多地址输入的译码电路。
（1） 有8根地址输入线7A ~1A ,要求当地址码为A8H,A9H ,…,AFH 时，译码器输出为0Y ~7Y 分别被译中，且地电平有效。
（2） 有10根地址输入线9A ～0A ，要求当地址码为2E0H,2E1H, …,2E7H 时，译码器输出0Y ~7Y 分别被译中，且地电平有效。
解：（1）当122100A B E E E =,即75364210111,00,A A A A A A A A ==从000～111变化时07~Y Y 分别被译中，电路如下图所示：Y Y （2）当122100A B E E E =，即97538432101111,000,A A A A A A A A A A ==从000～111变化时，07~Y Y 分别被译中。
电路如下图所示：Y Y 34－14 试用一片3－8译码器74LS138和少量的逻辑门实现下列多输出函数： （1）1F AB ABC =+ (2) 2F A B C =++ (3) 3F AB AB =+ 解：1067(0,6,7)F m Y Y Y==∑211(0,2~7)F m M Y ===∑ 312345(2,3,4,5)F m M Y Y Y Y ===∑电路图如下图所示：1F 2F F4－15 某组合电路的输入X 和输出Y 均为三位二进制数。
当X<2时，Y=1；当25X ≤≤时，Y=X+2；当X>5时，Y=0。
试用一片3－8译码器和少量逻辑门实现该电路。
解：由题意列出真值表如下：电路图如下图所示：输入X ＝ABC ，输出为Y 。
4－16 由3－8译码器74LS138和逻辑门构成的组合 逻辑电路图P4－16所示。
（1） 试分别写出1F ，2F 的最简与或表达式。
（2） 试说明当输入变量A,B,C,D 为何种取值时，1F ＝2F ＝1。
解：（1）当D=1时，21F =⎧⎨=⎩1F当D=0时，0342467(,,)(,,)()()()A B C m m m ABC ABC ABCF A B C m m m A B C A B C A B C ⎧=++=++⎪⎨==++++++⎪⎩1F将1F ，2F 分别填入四变量的卡诺图后可得：(,,)(0,6,8)()()()A B C m D B C B C A B ==+++∑1F 2(,,)(8,12,14)()()F A B C M A B D A C D ==++++∏(2)当ABCD=0000或0110时，1F ＝2F ＝1 4－17 已知逻辑函数(,,,)(1,3,7,9,15)F a b c d m =∑，试用一片3－8译码器74LS138和少量逻辑门实现该电路。
解：由题意的，(,,,)(1,3,7,9,15)()F a b c d m ABC ABC ABC ABC ABC D ==++++∑电路图如下图所示：2A 1A 0A 1E 2A E 2B E 6Y 7Y 5Y 4Y 3Y 2Y 1Y 0Y 38-译码器A B1DF4－18 某2－4译码器的逻辑符号和功能表如图P4－18所示。
试用尽量少的译码器和或门实现下列函数（允许反变量输入）： （1）(,,,)F W X Y Z W X Y X YZ WZ =++ （2）(,,,)G W X Y Z WYZ X Y =+解：根据题意，输入分别为X,Y ,W,Z 。
对于（1）来说，我们可以作出如下的逻辑电路图：（2）由题，我们可以得出如下的逻辑电路图：4－19 由3－8译码器构成的脉冲分配器电路图如图P4－19所示。