材料力学第七章答案+
材料力学第七章课后题答案 弯曲变形
(a) (b)
7
该梁的位移边界条件为：
在x 0处， w0 dw 在x 0处， 0 dx 将条件(c)与(d)分别代入式(b)和(a)，得 D 0，C 0 4．建立挠曲轴方程 将所得 C 与 D 值代入式(b)，得挠曲轴的通用方程为
1 Fa 2 F 3 3Fa [ x x xa EI 4 6 4 由此得 AC 段、 CD 段和 DB 段的挠曲轴方程依次为 w
5．计算 wC 和 θ B 将 x a 代入上述 w1或w2 的表达式中，得截面 C 的挠度为
41qa 4 ( ) 240EI 将以上所得 C 值和 x 2a 代入式(a)，得截面 B 的转角为 wC θB qa 3 7 4 16 1 187 203qa 3 [ ] EI 24 24 24 720 720 EI ()
(4)
D1 0 ， C1
由条件（4） 、式（a）与（c） ，得
qa 3 12 EI
C2
由条件（3） 、式（b）与（d） ，得
qa 3 3EI
D2
7qa 4 24 EI
3. 计算截面 C 的挠度与转角 将所得积分常数值代入式（c）与（d） ，得 CB 段的转角与挠度方程分别为
q 3 qa 3 x2 6 EI 3EI 3 q qa 7 qa 4 4 w2 x2 x2 24 EI 3EI 24 EI 将 x2=0 代入上述二式，即得截面 C 的转角与挠度分别为
5．计算 wC 和 θ B 将 x a 代入上述 w1 或 w2 的表达式中，得截面 C 的挠度为
Fa 3 ( ) 12 EI 将以上所得 C 值和 x 3a 代入式(a)，得截面 B 的转角为 wC
材料力学第五版 第七章 应力状态 答案
第七章应力状态与强度理论一、教学目标和教学内容1．教学目标通过本章学习，掌握应力状态的概念及其研究方法；会从具有受力杆件中截取单元体并标明单元体上的应力情况；会计算平面应力状态下斜截面上的应力；掌握平面应力状态和特殊空间应力状态下的主应力、主方向的计算，并会排列主应力的顺序；掌握广义胡克定律；了解复杂应力状态比能的概念；了解主应力迹线的概念。
掌握强度理论的概念。
了解材料的两种破坏形式（按破坏现象区分）。
了解常用的四个强度理论的观点、破坏条件、强度条件。
掌握常用的四个强度理论的相当应力。
了解莫尔强度理论的基本观点。
会用强度理论对一些简单的杆件结构进行强度计算。
2．教学内容○1应力状态的概念；○2平面应力状态分析；○3三向应力状态下的最大应力；○4广义胡克定律•体应变；○5复杂应力状态的比能；⑥梁的主应力•主应力迹线的概念。
讲解强度理论的概念及材料的两种破坏形式。
讲解常用的四个强度理论的基本观点，并推导其破坏条件从而建立强度计算方法。
介绍几种强度理论的应用范围和各自的优缺点。
简单介绍莫尔强度理论。
二、重点难点重点：1、平面应力状态下斜截面上的应力计算，主应力及主方向的计算，最大剪应力的计算。
2、广义胡克定律及其应用。
难点：1、应力状态的概念，从具体受力杆件中截面单元体并标明单元体上的应力情况。
2、斜截面上的应力计算公式中关于正负符号的约定。
3、应力主平面、主应力的概念，主应力的大小、方向的确定。
4、广义胡克定律及其应用。
5 强度理论的概念、常用的四个强度理论的观点、强度条件及其强度计算。
6 常用四个强度理论的理解。
7 危险点的确定及其强度计算。
三、教学方式采用启发式教学，通过提问，引导学生思考，让学生回答问题。
四、建议学时10学时五、讲课提纲1、应力状态的概念所谓“应力状态”又称为一点处的应力状态（state of stresses at a given point）,是指过一点不同方向面上应力的集合。
材料力学第四版版答案7.docx
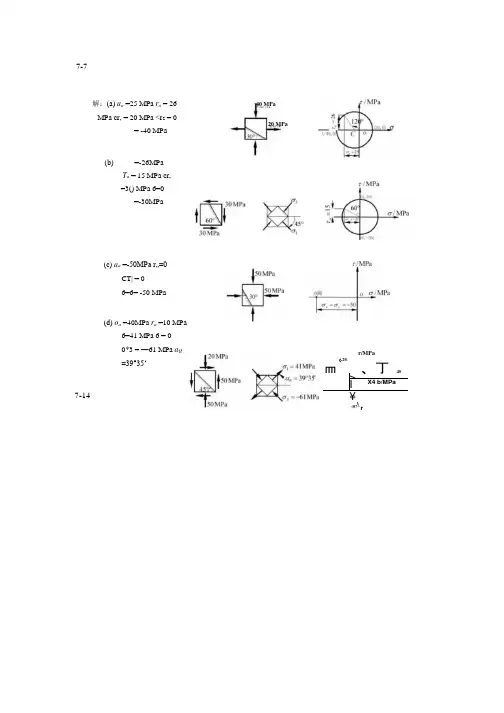
(c) a a =-50MPa r…=0CT| = 0 6=6= -50 MPa(d) o a =40MPa r a =10 MPa6=41 MPa 6 = 0 0*3 = —61 MPa a Q =39°35‘7-7 解：(a) a a =25 MPa r a = 26 MPa cr, = 20 MPa <r 2 = 0= -40 MPa (b) =-26MPa T a = 15 MPa cr, =3() MPa 6=0=-30MPa40 MPa20 MPa7-14(-20.皿、丁40> I X4 b/MPa ¥\ (0?^rr/MPa7-15单元体各面上的应力如图所示。
试用应力圆的儿何关系求主应力及最人切应力。
解：(a)由卩平面内应力值作a, b点,连接"交O•轴得圆心C (5(). 0)应力圆半径心)2+时=44.726 =50+44.7 = 94.7 MPa cr3=50-44.7 = 5.3 MPa (T2 = 50MPa2= 44.7 MPay r/MPa(b)由心平面内应力作g b点,连接血交O•轴丁•(？点，0030.故应力圆半径则: r = >/302 +402 = 506 =30 +50 = 8() MPaa2 =50 MPa a3=-20 MPa= 5() MPa(c)由图7-15 (c)yz平面内应力值作a, b点,圆心为O,半径为50,作应力圆得6 = 5() MPaa2 =-50 MPa6 =-80 MPa50 MPar/MPamax '6 一6 ,二」——=65MPa27-187-19在矩形截面钢拉伸试样的轴向拉力F = 20kN时，测得试样中段B点处与其轴线成30°方向的线应变为a. =3.25x10"。
已知材料的弹性模量£ = 210GPa ,试求泊松比解:F 20X103A " 20x10x10" = 10() MPa CT=a cos2a = —a = 75 MPa4cr|20. = cr cos2a = 25 MPa3.25X10_4 X210X 109 = (75-yx25)x IO6 v = 0.27M c = M n = 690kN- m Fsc 狂=佗 D 右=670 kN7-197-20 D= 120mm,治&hnm 的空心圆轴，两端承受一对扭转力偶矩，如图所示。
材料力学性能-第2版课后习题答案
第一章 单向静拉伸力学性能1、 解释下列名词。
1弹性比功：金属材料吸收弹性变形功的能力，一般用金属开始塑性变形前单位体积吸收的最大弹性变形功表示。
2．滞弹性：金属材料在弹性范围内快速加载或卸载后，随时间延长产生附加弹性应变的现象称为滞弹性，也就是应变落后于应力的现象。
3．循环韧性：金属材料在交变载荷下吸收不可逆变形功的能力称为循环韧性。
4．包申格效应：金属材料经过预先加载产生少量塑性变形,卸载后再同向加载，规定残余伸长应力增加；反向加载，规定残余伸长应力降低的现象。
5．解理刻面：这种大致以晶粒大小为单位的解理面称为解理刻面.6．塑性:金属材料断裂前发生不可逆永久（塑性)变形的能力。
韧性:指金属材料断裂前吸收塑性变形功和断裂功的能力。
7.解理台阶：当解理裂纹与螺型位错相遇时，便形成一个高度为b 的台阶.8。
河流花样：解理台阶沿裂纹前端滑动而相互汇合,同号台阶相互汇合长大,当汇合台阶高度足够大时，便成为河流花样。
是解理台阶的一种标志。
9.解理面：是金属材料在一定条件下，当外加正应力达到一定数值后，以极快速率沿一定晶体学平面产生的穿晶断裂,因与大理石断裂类似，故称此种晶体学平面为解理面。
10.穿晶断裂：穿晶断裂的裂纹穿过晶内,可以是韧性断裂，也可以是脆性断裂.沿晶断裂：裂纹沿晶界扩展，多数是脆性断裂.11。
韧脆转变：具有一定韧性的金属材料当低于某一温度点时，冲击吸收功明显下降，断裂方式由原来的韧性断裂变为脆性断裂，这种现象称为韧脆转变12.弹性不完整性：理想的弹性体是不存在的，多数工程材料弹性变形时,可能出现加载线与卸载线不重合、应变滞后于应力变化等现象,称之为弹性不完整性。
弹性不完整性现象包括包申格效应、弹性后效、弹性滞后和循环韧性等2、 说明下列力学性能指标的意义。
答：E 弹性模量 G 切变模量 r σ规定残余伸长应力 2.0σ屈服强度 gt δ金属材料拉伸时最大应力下的总伸长率 n 应变硬化指数 【P15】3、 金属的弹性模量主要取决于什么因素？为什么说它是一个对组织不敏感的力学性能指标?答：主要决定于原子本性和晶格类型。
材料力学答案第七章
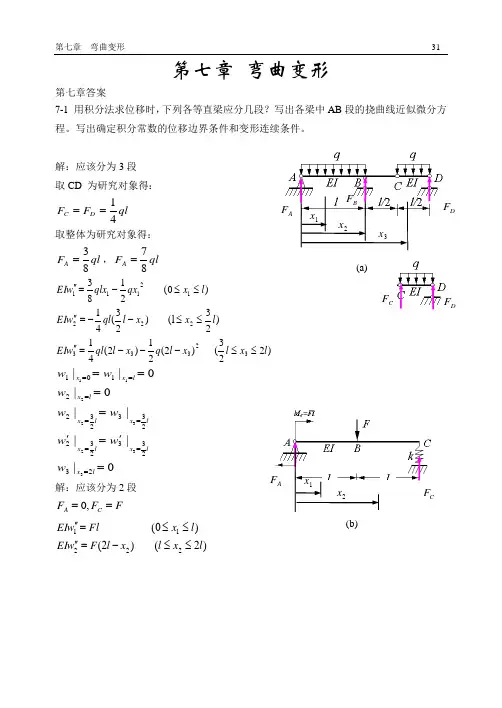
第七章 弯曲变形第七章答案7-1 用积分法求位移时，下列各等直梁应分几段？写出各梁中AB 段的挠曲线近似微分方程。
写出确定积分常数的位移边界条件和变形连续条件。
解：应该分为3段 取CD 为研究对象得：ql F F D C 41==取整体为研究对象得：ql F A 83=，ql F A 87= )223( )2(21)2(41)23(l )23(41)(0 21833233322212111l x l x l q x l ql w EI l x x l ql w EI l x qx qlx w EI ≤≤---=''≤≤--=''≤≤-=''0|||||0|0||23233232233232210133232211='='============l x lx lx lx lx l x l x x w w w w w w w w解：应该分为2段F F F C A ==,0)2( )2()(0 22211l x l x l F w EI l x Fl w EI ≤≤-=''≤≤=''1x x AF DF BF DF(b)AF 1xkFw w w w w w l x l x l x l x l x x -='='========22212101232321|||||0| 7.2 用积分法求图示梁跨度中点的挠度c w 和端截面转角A θ及B θ。
（EI ql w C 76854=，EI ql A 38473=θ，EI ql B 12833-=θ）解：ql F A 81=；ql F B 83=1113111211111 481 161)2(0 81D x C qlx EIw C qlx w EI l x qlx w EI ++=+='≤≤='' 2224232223222222222 )2(241 481 )2(61 161)2( )2(21 81D x C l x q qlx EIw C l x q qlx w EI l x l l x q qlx w EI ++--=+--='≤≤--='' 边界条件：0|011==x w ⇒ 01=D 0|22==l x w ⇒0 162414812244=++⋅-D l C ql ql 222132||l x l x w w ===⇒2211)2( )2(D l C D l C +=+ 222132||l x l x w w =='='⇒021==C C则：021==D D ，4213847ql C C -== 32111133113847 161)2(0 3847 481qlqlx w EI l x x ql qlx EIw -='≤≤-=3847)2(61 161)2( 3847)2(241 48133222222342322ql l x q qlx w EI l x l x ql l x q qlx EIw ---='≤≤---= AF BF1xEI ql w x A 3847|3011-='==θ EI ql w l x B 1283|322='==θ EIql l ql l ql EI w w C 3845)]2(3847 )2(481[13331-=-==7.3 用叠加法求下列各梁的指定位移。
工程力学(静力学和材料力学)范钦珊主编答案全集 (7)
第7章 弯曲强度7－1 直径为d 的圆截面梁，两端在对称面内承受力偶矩为M 的力偶作用，如图所示。
若已知变形后中性层的曲率半径为ρ；材料的弹性模量为E 。
根据d 、ρ、E 可以求得梁所承受的力偶矩M 。
现在有4种答案，请判断哪一种是正确的。
(A) ρ64π4dE M ＝(B) 4π64d E M ρ＝(C) ρ32π3d E M ＝(D) 3π32d E M ρ＝正确答案是 A 。
7－2 关于平面弯曲正应力公式的应用条件，有以下4种答案，请判断哪一种是正确的。
(A) 细长梁、弹性范围内加载；(B) 弹性范围内加载、载荷加在对称面或主轴平面内；(C) 细长梁、弹性范围内加载、载荷加在对称面或主轴平面内；(D) 细长梁、载荷加在对称面或主轴平面内。
正确答案是 C _。
7－3 长度相同、承受同样的均布载荷q 作用的梁，有图中所示的4种支承方式，如果从梁的强度考虑，请判断哪一种支承方式最合理。
正确答案是d 。
7－4 悬臂梁受力及截面尺寸如图所示。
图中的尺寸单位为mm 。
求：梁的1－1截面上A 、习题7－1图习题7－3图5lB 两点的正应力。
解：1. 计算梁的1－1截面上的弯矩：31m 110N 1m+600N/m 1m 1300N m 2M ⎛⎞=−××××=−⋅⎜⎟⎝⎠2. 确定梁的1－1截面上A 、B 两点的正应力： A 点：()3363-3-315010m 1300N m 2010m 210Pa MPa ()10010m 15010m12z A z M y I σ−−⎛⎞×⋅×−×⎜⎟⎝⎠==×=××× 2.54拉应力 B 点：())1.62MPa(Pa 1062.1120.15m 0.1m m 04.020.150m m N 130063压应力=×=×⎟⎠⎞⎜⎝⎛−×⋅==z z B I y M σ7－5 简支梁如图所示。
材料力学第七章答案 景荣春
答
案
网
τ 22.5°
ww
b 解 σ 22.5° =
− 30 + 10 − 30 − 10 cos 45° − 20 sin 45° = −38.3 MPa + 2 2 − 30 − 10 = sin 45° + 20 cos 45° = 0 2
w.
103
kh
da
w.
co
τ 45°
30 + 10 30 − 10 + cos 90° − (− 20 )sin 90° = 40 MPa 2 2 30 − 10 = sin 90° + (− 20 )cos 90° = 10 MPa 2
即
3 ， θ = 36.87° ， α = 90° − θ = 53.13° 4 σ α = 0 ， τ α = 0 ， τ max = 35 MPa σ +σ y σ x −σ y σα = x + cos 2α − τ xy sin 2α = 0 2 2 σ −σ y τα = x sin 2α + τ xy cos 2α = 0 2
代入式（b）得
σ 60° =
后
σ x + 40 σ x − 40
a 解 σ 45° =
课
c 解 σ −60 =
τ −60°
后
10 − 20 10 − (− 20 ) + cos(− 120°) − 15 sin (− 120°) = 0.490 MPa 2 2 10 − (− 20 ) = sin (− 120°) + 15 cos(− 120°) = 20.5 MPa 2
即
w. da
⎛σ x −σ y ⎞ 2 ⎟ τ max = ⎜ ⎜ ⎟ + τ xy = 35 2 ⎝ ⎠ σ x +σ y σ x −σ y + × (− 0.28) − τ xy × 0.96 = 0 2 2 σ x −σ y × 0.96 + τ xy × (− 0.28) = 0 2 2 ⎛σ x −σ y ⎞ 2 ⎜ ⎟ + τ xy = 1 225 ⎜ ⎟ 2 ⎠ ⎝
材料力学答案第7章
∑F
及
n
= 0， σ α dA = 0
∑F
分别得到
t
= 0， τ α dA = 0
σ α = 0，τ α = 0
由于方位角 α 是任取的，这就证明了 A 点处各截面上的正应力与切应力均为零。 顺便指出，本题用图解法来证更为方便，依据 A 点上方两个自由表面上的已知应力（零 应力）画应力图，该应力圆为坐标原点处的一个点圆。至此，原命题得证。
由此可知，主应力各为
σ1 = 60.0MPa, σ 2 = σ 3 = 0
5
σ1 的方位角为
α0 = 0o
对于应力图(b),其正应力和切应力分别为
σB = τB =
| M | | y B | 12 × 20 × 10 3 × 0.050 N = = 3.00 × 10 7 Pa = 30.0MPa 3 2 Iz 0.050 × 0.200 m Fs S z (ω) 12 × 20 × 10 3 × 0.050 × 0.050 × 0.075 N = = 2.25 × 10 6 Pa = 2.25MPa 3 2 I zb 0.050 × 0.200 × 0.050m
σα = (
− 30 + 10 − 30 − 10 + cos45 o − 20sin45 o )MPa = −38.3MPa 2 2 − 30 − 10 τα = ( sin45 o + 20cos45 o )MPa = 0 2
(c)解：由题图所示应力状态可知，
σ x = 10MPa，σ y = −20MPa，τ x = 15MPa，α = −60 o
7-7
已知某点 A 处截面 AB 与 AC 的应力如图所示（应力单位为 MPa） ，试用图解法
材料力学习题及答案
材料力学-学习指导及习题答案第一章绪论1-1 图示圆截面杆，两端承受一对方向相反、力偶矩矢量沿轴线且大小均为M的力偶作用。
试问在杆件的任一横截面m-m上存在何种内力分量，并确定其大小。
解：从横截面m-m将杆切开，横截面上存在沿轴线的内力偶矩分量M x，即扭矩，其大小等于M。
1-2 如图所示，在杆件的斜截面m-m上，任一点A处的应力p=120 MPa，其方位角θ=20°，试求该点处的正应力σ与切应力τ。
解：应力p与斜截面m-m的法线的夹角α=10°，故σ＝p cosα=120×cos10°=118.2MPaτ＝p sinα=120×sin10°=20.8MPa1-3 图示矩形截面杆，横截面上的正应力沿截面高度线性分布，截面顶边各点处的正应力均为σmax=100 MPa，底边各点处的正应力均为零。
试问杆件横截面上存在何种内力分量，并确定其大小。
图中之C点为截面形心。
解：将横截面上的正应力向截面形心C简化，得一合力和一合力偶，其力即为轴力F N=100×106×0.04×0.1/2=200×103 N =200 kN其力偶即为弯矩M z=200×(50-33.33)×10-3 =3.33 kN·m1-4 板件的变形如图中虚线所示。
试求棱边AB与AD的平均正应变及A点处直角BAD的切应变。
解：第二章轴向拉压应力2-1试计算图示各杆的轴力，并指出其最大值。
解：(a) F N AB=F, F N BC=0, F N，max=F(b) F N AB=F, F N BC=－F, F N，max=F(c) F N AB=－2 kN, F N2BC=1 kN, F N CD=3 kN, F N，max=3 kN(d) F N AB=1 kN, F N BC=－1 kN, F N，max=1 kN2-2 图示阶梯形截面杆AC，承受轴向载荷F1=200 kN与F2=100 kN，AB段的直径d1=40 mm。
材料力学第六版答案第07章
习 题7-1 用积分法求图示各悬臂梁自由端的挠度和转角，梁的抗弯刚度EI 为常量。
7－1（a ） 0M()M x = ''0EJ M y ∴='0EJ M y x C =+ 201EJ M 2y x Cx D =++ 边界条件: 0x =时 0y = ；'0y = 代入上面方程可求得：C=D=0201M 2EJ y x ∴='01=M EJ y x θ= 01=M EJ B l θ 201=M 2EJ B y l（b ）222()1M()222q l x qx x ql qlx -==-+- 2''21EJ 22qx y ql qlx ∴=-+-3'2211EJ 226qx y ql x qlx C =-+-+422311EJ 4624qx y ql x qlx Cx D =-+-++边界条件：0x = 时 0y = ；'0y =代入上面方程可求得：C=D=04223111()EJ 4624qx y ql x qlx ∴=-+-'2231111=(-)EJ 226y ql x qlx qx θ=+-3-1=6EJ B ql θ 4-1=8EJB y ql（c ）()()()()()0303''04'050()1()()286EJ 6EJ 24EJ 120l xq x q lq l x M x q x l x l x l q y l x l q y l x Cl q y l x Cx Dl-=-⎛⎫=--=-- ⎪⎝⎭∴=-=--+=-++ 边界条件：0x = 时 0y = ；'0y = 代入上面方程可求得：4024q l C l -= 50120q l D l =()455000232230120EJ 24EJ 120EJ(10105)120EJq q l q l y l x x l l l q x l l lx x l ∴=---+-=-+- 3024EJ B q l θ=- 4030EJB q l y =-(d)'''223()EJ 1EJ 211EJ 26M x Pa Pxy Pa Pxy Pax Px C y Pax Px Cx D=-=-=-+=-++ 边界条件：0x = 时 0y = ；'0y =代入上面方程可求得：C=D=023'232321112611253262B C C B y Pax Px EJy Pax Px EJ Pa Pa Pay y a a EJ EJ EJPa EJθθθ⎛⎫∴=-⎪⎝⎭⎛⎫==-⎪⎝⎭=+=+==(e)()()()21222''1'211231113()02()2223EJ 231EJ ()2231EJ ()46a M x q qax x a q M x a x a x a a y q qaxa y qa x x C a y qa x x C x D =-+≤≤=--≤≤=-+=-++=--+++ 边界条件：0x = 时 0y = ；'0y =代入上面方程可求得：C=D=0()()()22118492024EJ 12EJ qax qax y a x a x x a ∴=--=--≤≤''2223'222242232221EJ ((2)4)21EJ (42)2312EJ (2)2312y q a ax x x y q a x ax C x y q a x ax C x D =--+=--++=---+++边界条件：x a = 时 12y y = ；12θθ=代入上面方程可求得：2296a C = 4224qa D =-()()43223421612838464162384q y x ax a x a a a x a EJ-=-+-+≤≤ 43412476B B qa y EJqa EJθ=-=-(f)()()221222''212'231122341115()20225()2225251EJ 22251EJ 26511EJ 4324qa qx M x qax x a qa qa a M x qax x a x a a y q ax x a y q x ax x C a y q x ax x C x D =-+-≤≤⎛⎫=-+--≤≤ ⎪⎝⎭⎛⎫=--+ ⎪⎝⎭⎛⎫=--++ ⎪⎝⎭⎛⎫=--+++ ⎪⎝⎭边界条件：0x = 时 0y = ；'0y =代入上面方程可求得：C 1=D 1=0''22'2222223222EJ (2)1EJ (2)21EJ ()6y q a ax y q a x ax C y q a x ax C x D =--=--+=---++ 边界条件：x a = 时 12y y = ； ''''12y y =3296a C =- 4224a D =-437124136B B qa y EJqa EJθ=-=-7-2 用积分法求图示各梁的挠曲线方程，端截面转角θA 和θB ，跨度中点的挠度和最大挠度，梁的抗弯刚度EI 为常量。
材料力学习题及答案
材料力学-学习指导及习题答案第一章绪论1-1 图示圆截面杆，两端承受一对方向相反、力偶矩矢量沿轴线且大小均为M的力偶作用。
试问在杆件的任一横截面m-m上存在何种内力分量，并确定其大小。
解：从横截面m-m将杆切开，横截面上存在沿轴线的内力偶矩分量M x，即扭矩，其大小等于M。
1-2 如图所示，在杆件的斜截面m-m上，任一点A处的应力p=120 MPa，其方位角θ=20°，试求该点处的正应力σ与切应力τ。
解：应力p与斜截面m-m的法线的夹角α=10°，故σ＝p cosα=120×cos10°=118.2MPaτ＝p sinα=120×sin10°=20.8MPa1-3 图示矩形截面杆，横截面上的正应力沿截面高度线性分布，截面顶边各点处的正应力均为σmax=100 MPa，底边各点处的正应力均为零。
试问杆件横截面上存在何种内力分量，并确定其大小。
图中之C点为截面形心。
解：将横截面上的正应力向截面形心C简化，得一合力和一合力偶，其力即为轴力F N=100×106×0.04×0.1/2=200×103 N =200 kN其力偶即为弯矩M z=200×(50-33.33)×10-3 =3.33 kN·m1-4 板件的变形如图中虚线所示。
试求棱边AB与AD的平均正应变及A点处直角BAD的切应变。
解：第二章轴向拉压应力2-1试计算图示各杆的轴力，并指出其最大值。
解：(a) F N AB=F, F N BC=0, F N，max=F(b) F N AB=F, F N BC=－F, F N，max=F(c) F N AB=－2 kN, F N2BC=1 kN, F N CD=3 kN, F N，max=3 kN(d) F N AB=1 kN, F N BC=－1 kN, F N，max=1 kN2-2 图示阶梯形截面杆AC，承受轴向载荷F1=200 kN与F2=100 kN，AB段的直径d1=40 mm。
材料力学(上海理工大学)智慧树知到课后章节答案2023年下上海理工大学
材料力学（上海理工大学）智慧树知到课后章节答案2023年下上海理工大学第一章测试1.1、下列结论中是正确的。
A:材料力学主要研究各种材料的力学问题 B:材料力学主要研究杆件受力后变形与破坏的规律 C:材料力学主要研究各类杆件中力与材料的关系 D:材料力学主要研究各种材料的力学性质答案:材料力学主要研究杆件受力后变形与破坏的规律2.2、下列结论中哪些是正确的？答：。
（1）为保证构件能正常工作，应尽量提高构件的强度。
（2）为保证构件能正常工作，应尽量提高构件的刚度。
（3）为保证构件能正常工作，应尽量提高构件的稳定性。
（4）为保证构件能正常工作，应尽量提高构件的强度、刚度和稳定性。
A:全对 B:（1），（2），（3） C:（4） D:全错答案:全错3.3、下列结论中哪些是正确的？答：。
（1）外力是作用在物体外部的力。
（2）杆件的自重不属于外力。
（3）支座约束反力不属于外力。
（4）运动杆件的惯性力不属于外力。
A:（1），（2） B:全错 C:（1），（4） D:全对答案:全错4.4、下列结论中哪些是正确的？答：。
(1)截面法是分析杆件内力的方法。
(2)截面法是分析杆件应力的方法。
(3)截面法是分析杆件截面上内力与应力关系的基本方法。
A:（1） B:全错 C:（3） D:（2）答案:（1）5.5、下列结论中哪些是正确的？答：。
(1)杆件的某个横截面上，若轴力N=0，則各点的正应力σ也为零（既σ=0）。
(2)杆件的某个横截面上，若各点的正应力σ均为零（既σ=0），則轴力必为零（既N=0）。
(3)杆件的某个横截面上，若各点的正应力σ均为零（既σ=0），則弯矩必为零（既M=0）。
A:（2） B:（1） C:（3） D:（2），（3）答案:（2），（3）6.6、构件的强度、刚度、稳定性_______。
A:与二者无关 B:只与材料的力学性质有关 C:与二者都有关 D:只与构件的形状尺寸有关答案:与二者都有关7.7、均匀性假设认为，材料内部各点的_______是相同的。
家电公司研发部资料材料力学习题答案(七)
第七章 应力状态和强度理论7-1 围绕受力构件内某点处取出的微棱柱体的平面图如图所示，已知该点处于平面应力状态，AC 面上的正应力σ＝－14MPa ，切应力为零，试从平衡方程确定σx 和τx 值。
答：σx ＝37.9MPa ,τx ＝74.2MPa 解：利用公式求解x x x x x cos 2sin 222sin 2cos 22yyyαασσσσσατασστατα+-=+--=+代入数据得x x x x x 9292140.3430.94229200.940.3432σστστ+--=+⨯-⨯-=⨯+⨯σx ＝37.9MPa ,τx ＝74.2MPa7-2 试绘出图示水坝内A 、B 、C 三小块各截面上的应力（只考虑平面内受力情况）。
A: B: C:7-3 已知平面应力状态如图所示，已知σx ＝100MPa ，σy =40MPa,以及该点处的最大主应力σ1＝120MPa ，试用应力圆求该点处的τx 及另外两个主应力σ2，σ3和最大剪应力τmax。
答：MPa,60,0MPa,20max 32===τσσx τ＝40 MPa 解：由应力圆分析可得A BC题 7 - 2 图题 7 - 1 图111(100,),(40,),(,0)x x c D D C ττσ'-x 121004070MPa221207050MPa 705020MPayc c c r r σσσσσσσ++====-=-=∴=-=-=是平面应力状态3=0σ∴222x x 13max (100)40MPa120060MPa 22c r σττσστ∴=-+⇒=--===7-4 已知平面应力状态一点处互相垂直平面上作用有拉应力90MPa 和压应力50MPa ，这些面上还有剪应力，如果最大主应力为拉应力100MPa ，试求：(1) 上述面上的切应力； (2) 此平面上另一主应力； (3) 最大切应力平面上的正应力； (4) 最大切应力。
材料力学练习3
材料⼒学练习3第七章强度理论2重点1、材料破坏的两种形式；2、常⽤的四个强度理论及强度条件；3、运⽤强度理论来分析复杂应⼒状态下构件的强度；难点1、强度理论的适⽤条件；2、运⽤强度理论来分析复杂应⼒状态下构件的强度；基本知识点1、强度理论的概念；2、了解材料常见的两种破坏⽅式；3、引起材料破坏的原因及其假说；4、简单应⼒状态下强度条件的建⽴；5、常⽤的四个强度理论及相当应⼒；6、复杂应⼒状态下强度条件的建⽴；判断强度理论1、“塑性材料⽆论处于什麽应⼒状态，都应采⽤第三或第四强度理论，⽽不能采⽤第⼀或第⼆强度理论。
”答案此说法错误答疑塑性材料在塑性流动破坏时采⽤第三或第四强度理论，塑性材料在断裂破坏时应采⽤第⼀或第⼆强度理论。
2、“常⽤的四种强度理论，只适⽤于复杂的应⼒状态，不适⽤于单向应⼒状态。
”答案此说法错误答疑强度理论既适⽤于复杂应⼒状态，也适⽤于简单应⼒状态。
3、“脆性材料不会发⽣塑性屈服破坏。
”答案此说法错误答疑脆性材料在三向⼏乎等值压缩应⼒状态下会体现出塑性流动破坏。
4、“材料的破坏形式由材料的种类⽽定”答案此说法错误答疑材料的破坏形式由危险点所处的应⼒状态和材料的种类综合决定的。
5、“材料的破坏形式与材料所受的应⼒状态⽆关“答案此说法错误答疑材料的破坏形式是由材料的种类、材料所处的应⼒状态综合决定的。
6、“不能直接通过实验来建⽴复杂应⼒状态的强度条件”答案此说法错误答疑⼯程中有可以通过实验得到⼀些复杂应⼒状态的强度条件。
如薄壁筒在内压、轴⼒共同作⽤下的强度条件；薄壁筒在内压、轴⼒、扭矩共同作⽤下的强度条件等可以通过实验得到。
7、“不同强度理论的破坏原因不同”答案此说法正确答疑不同的强度理论的破坏原因分别为：最⼤拉应⼒、最⼤线应变、最⼤剪应⼒、形状⽐能。
8、“第⼆强度理论要求材料直到破坏前都服从虎克定律”答案此说法正确答疑第⼆强度理论是最⼤线应变理论，在推导强度条件时⽤到⼴义虎克定律，固要求材料在破坏前都服从虎克定律。
材料力学七章.pdf
第七章平面弯曲内力1. 试求图示梁指定截面上的剪力和弯矩。
设q，a均为已知。
2. 试求图示梁指定截面上的剪力和弯矩。
设q，a均为已知。
3. 试求图示梁指定截面上的剪力和弯矩。
设q，a均为已知。
4. 试求图示梁指定截面上的剪力和弯矩。
设q，a均为已知。
M max。
设q，l均为已知。
M max。
设l，Me均为已知。
M max。
设l，F均为已知。
8. 试列出图示梁的剪力方程和弯矩方程，画剪力图和弯矩图，并求出F S和，maxM max。
设q，F,l均为已知。
9.试列出图示梁的剪力方程和弯矩方程，画剪力图和弯矩图，并求出F S和，max M max。
设q，l均为已知。
10. 试列出图示梁的剪力方程和弯矩方程，画剪力图和弯矩图，并求出F S，max 和M max。
设q，l，F，M e均为已知。
11. 不列剪力方程和弯矩方程，画出图示各梁的剪力图和弯矩图，并求出F S，max 和M max。
解：（1）由静力平衡方程得：F A=F，M A= Fa，方向如图所示。
（2）利用M，F S，q之间的关系分段作剪力图和弯矩图。
（3）梁最大绝对值剪力在AB段内截面，大小为2F。
梁最大绝对值弯矩在C截面，大小为2Fa。
12. 不列剪力方程和弯矩方程，画出图示各梁的剪力图和弯矩图，并求出F S，max 和M max。
解：（1）由静力平衡方程得：F A=3q l/8（↑），F B=q l/8（↑）。
（2）利用M，F S，q之间的关系分段作剪力图和弯矩图。
（3）梁的最大绝对值剪力在A右截面，大小为3q l/8。
梁的最大弯矩绝对值在距A端3l/8处截面，大小为9q l2/128。
13. 不列剪力方程和弯矩方程，画出图示各梁的剪力图和弯矩图，并求出F S，max 和M max。
解：（1）由静力平衡方程得：F B=2qa，M B=qa2，方向如图所示。
（2）利用M，F S，q之间的关系分段作剪力图和弯矩图。
（3）梁的最大绝对值剪力在B左截面，大小为2qa。
材料力学课后答案07d
F = 10 kN 时杆件的轴向变形量，以及使杆件屈服的荷载。
解：材料屈服的荷载：
Fu
=
1 4
πd 2σ s
=
1 4
× 3.14 ×102
×180
= 14137
N。
故荷载 F = 10 kN 作用时杆件仍处于弹性阶段。由图可知，
E
=
180 0.2 ×10−2
= 90
GPa 。
杆件轴向变形量
σ (MPa) 180
ε y = −νε x 。
q
250
400
题 7-7 图
面积改变量
∆A = A(ε x + ε y ) = Aε x (1 −ν ) 。
故有
ν
=1−
∆A Aε x
=1−
56 400 × 250 × 8 ×10−4
= 0.3 。
7-8 某种材料的试件的应力应变曲线如图。图中上方曲线对应于横坐标中上一排应变标
识，下方曲线对应于下一排应变标识，即低应变区。试确定这种材料的类型，并确定其
弹性模量 E，屈服极限σ s ，强度极限σ b 与伸长率 δ 。
σ (MPa)
500
σ (MPa)
500
400
400
300
300
200
200
100
100
ε (%)
ε (%)
0
5
10 15 20 25 30
0
5
10 15 20 25 30
E．获取许用应力的安全系数必定是大于 1 的；
F． 获取许用应力的安全系数的大小主要取决于构件的尺寸，尺寸越大的构件安全
系数就应越大。
7-4 某杆件横截面为宽 b = 30 mm 、高 h = 50 mm 的矩形。杆件中有一法线方向与杆 轴 线 成 30o 角 的 斜 截 面 。 斜截 面 上 作 用有 均 布 正 应力 σ = 30 MPa 和 均 布切 应 力 τ = 20 MPa 。求该斜截面上所有应力的合力的大小与方位。
材料力学第四版版答案7
塑 _________ ◎刃M 內 47t = CF i = 50解：(a) cr a = 25MPaj =26 MPa<T 1 =20 MPa(7n = 06 = -40 MPa(b> a a = -26MJ'ar… =15 MPaoj =30 MPa6 = 0(y 3 =-30 MPa(c)(r a =-50 MPaJ =() (7, = 06=6= -50 MPa「MPa(d) a t2 = 40MPa z a = 10 MJ J a 6=41 Ml 3a 6 = 06 = -61 MPa % f 3亍 7-147-7 *T ( = 41 MPa[VX/p^ =3 护茫=-61 MPa r/MPa7-15单冗怵各面上的应力如\ 2a, =50 + 44J =94JMPa(?. =50-44.7 = 5.3 MPu6 = 5() MPa仏=^4^= 44.7 MPa(h)由xz平面内应力作nt h点*连接丽交(T轴C点'00=31),故应力圆半径则: r = V3O2 +402 = 50 疗| =30 + 50 = 80 tr2 = 50 MPa6 =-20 MPamax(c)由阁7-15 (c)jz平面内应力值作5 h总圆心为。
半径为M 作应力圆得(T, =50X11^CT2 =-50MPa6 =-80 MPa=65 MPa7-187-19在矩形截而钢拉伸试样的轴向拉力F = 20kN时，测得试样中段B点处与托轴线成卫)"方向的线应变为占奶=3.25x1(T\已知材料的弹性^M^ = 2IOGPa -试求泊松比A' ?() x 10解：<7 = — = ----- --------- =100MPaA 20x1 Ox IO-63rT10, = a cos ~ a = —<y = 75 MPa■4=(7 cos2 ar = 25 M l*a*二評厂呵3.25x]O u x2IOx |()^ =(75-i/x25}xl06 p = 0.27A/ 16 7-25 7-19 HUIX - 2,tM x 10_i zk]_^™xl00% = 5.3% 7-25 一简支钢板梁承愛荷拔如图日所示， 其厳面尺寸见图氐已知钢材的许出应力为 bJiMMP^kJiOOMPx 试栓核梁 内的最人止肿.力和疑人切屁力*井按第四强 戍理论检核危酰柚而上的点：“的强丿£。
材料力学第2版 课后习题答案 第7章 弯曲变形
解：查自重得：
q = 587.02 N / m
J = 15760cm4 Pl 3 5ql 4 f =− − 48EJ 384EJ −176 × 103 × 113 = 48 × 210 × 109 × 15760 × 10−8 × 4 −587.02 × 5 × 114 + 385 × 210 × 109 × 15760 × 10−8 × 4 = 0.0377 m = 3.77cm
(d) 解：
D A P P E
' yC = y E + θ B ia + y C
C B P
− P ( 2a ) − Pa 3 − Pa3 = − − 3EJ 3EJ 3EJ 3 −10 Pa = 3EJ
3
252
7-5 门式起重机横梁由4根36a工字钢组成如图所示， 梁的两端均可视为铰支， 钢的弹 性模量E=210Gpa。试计算当集中载荷P＝176 kN作用在跨中并考虑钢梁自重时，跨中截面 C的挠度yC。
x=l
∴y =−
'
∴D = 0
y=0
∴C =
− M 0l 6
M 0l 2 ⎛ x x 3 ⎞ ⎜ − ⎟ 6 EJ ⎝ l l 3 ⎠
M 0l 2 ⎛ 1 3 x 2 ⎞ ∴θ = y = − ⎜ − ⎟ 6 EJ ⎝ l l 3 ⎠
− M 0l 2 l ；此时挠度最大 f = 3 9 3EJ 2 ⎛ l ⎞ − M 0l 中点挠度 y ⎜ ⎟ = ⎝ 2 ⎠ 16 EJ − M 0l Ml θA = θB = 0 6 EJ 3EJ （b）解： 设中点为C点，则分析CB段
''
C2 = −
D2 = −
a4 24
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
一、选择题
1.B
2.A
3.B
4.A
5.D
6.A
7.D
8.B
9.A 10、C 11D 12A 13C 14D 15B 16B 17C 18C 19D 二、填空题
1、)("x l F EIw -= 2. σr 3= 90 3、边界条件是：（1）当0=x 时 y A =0; (2)当l x =时 y B =0
连续条件是：当 x =a 时，θC 左=θC 右 y C 左=y C 右
4、剪力； （y ′）2
5、στ223+
6、 50 MPa 30MPa -50MPa 三、分析题 1、（1）当
y
x σσ=，且x τ=0时，应力圆一个点圆；
（2）当y x σσ-=时，应力圆圆心在原点； （3）当y x x σστ2=
时，应力圆与τ轴相切
五、计算题
1. 解、由图可知，
斜截面m-m 的方位角为0
30α=
横截面上的正应力
则有斜截面上的正应力 和切应力公式可知：
2、解：（1）该点的主应力大小
220
022300
02303cos cos 3041
sin 2sin 602
2o o
F F h h F h σσατσα=⋅=
⋅==⋅=
⋅=02F F F A h h h
σ=
==⨯()
()
()
(
)12312130502541213050226
x y x y σσσσσσσ=++=+≈=+-=+≈=
该点的主应力方向：
（2）该点的最大切应力 (3)在单元体上画出主应力的方向 3、已知a a a MP 20,MP 30,MP 50-=-==xy y x τσσ
解：（1）ατασσσσσ2sin 2cos 2
2
30xy y
x y
x --+
+=
0060sin 2060cos 230
5023050+++-=
32.172010++=
a MP 32.47=
（2）22max
min )2
(
2
xy
y
x y
x τσσσσσ+-±+=
22
)20()2
3050(23050-++±-=
72.4410±=
⎩⎨⎧-=a
MP 72.34MP 72.54a
a MP 72.541=∴σ 02=σ a MP 72.343-=σ
100
000321120
arctan()arctan()
22305067.522.5x x y στασσσ-==--==的方位角：
的方位角：67.5-9013
max 272
σστ-=
=
画出主应力如图所示
02.730
502022122
10=+⨯=--=arctg arctg
y x xy
σστα
与1σ的夹角为7.02°
（3）a 31max MP 72.44)72.3472.54(21
)(21=+⨯=-=
σστ （4）)]([1
3211σσμσε+-=E
)]72.340(3.072.54[10
20013
-⨯-⨯⨯= 41026.3-⨯=
)]([(1
1322σσμσε+-=
E =)]72.5472.34(3.00[10
2001
3
+--⨯⨯ 5103-⨯-=
)]([1
2133σσμσε+-=
E )]072.54(3.072.34[10
20013
+⨯--⨯⨯= 41056.2-⨯-=
4、解：（1）计算主应力
根据应力状态可知：MPa x 30=σ，MPa y 20-=σ，MPa x 40-=τ，MPa z 50=σ 根据主应力的计算公式：
MPa
x y x y x 2.52)40(4)2030(21
)2030(214)(2
1)(21
222
21=-⨯++⨯+-⨯=
+-+
+=τσσσσσ MPa 502=σ： MPa
x y x y x 2.42)40(4)2030(21
)2030(214)(2
1)(2
1222
23-=-⨯++⨯--⨯=
+--
+=τσσσσσ
（2）相当应力的计算
MPa r 2.5211==σσ MPa r 9.49)2.4250(3.02.52)(3212=--=+-=σσμσσ MPa r 4.94)2.42(2.52313=--=-=σσσ MPa r 3.93)()()[(2132322212
14=-+-+-=
σσσσσσσ
5、解：06-10
540F A F σσ=⨯⨯== ()a 150MP 10
5402F
452sin 2
6
-0
45=⨯⨯⨯=
=
στ KN N F 60106010540210150366=⨯=⨯⨯⨯⨯⨯=-
6、解：（1）判断直杆下端是否能接触刚性支座
N a =P ， N b =0（2分）
e m m A
E Pa
A E b N A E a N l a b b a a >=⨯⨯⨯⨯⨯⨯⨯=
=
+=∆--08.010
1021020010
40010806
393
3
（2）计算直杆下端接触刚性支座以后，各段的轴力 设轴力为 N a 、N b ， 由平衡方程
∑=0y ，N a
-P-N b
=0 （1）
由变形协调方程e l =∆,e A
E b
N A E a N l b b a a =+=
∆ (2) 由（1）、（2）解得 N a ＝70kN ， N b ＝－10kN 。
7 解：单位：
MPa。