2014浙江大学自动控制原理考研真题与解析
2014自动控制原理考试答案(A)
一、(10分)解：传递函数G(s):根据梅逊公式 1()()()ni ii P C s G s R s =∆==∆∑ （2分） 4条回路:123()()()L G s G s H s =-, 24()()L G s H s =-，3123()()(),L G s G s G s =- 414()()L G s G s =- 无互不接触回路。
（2分） 特征式：423412314111()()()()()()()()()()i i L G s G s H s G s H s G s G s G s G s G s =∆=-=++++∑（2分）2条前向通道: 11231()()(), 1P G s G s G s =∆= ；2142()(), 1P G s G s =∆= （2分）12314112223412314()()()()()()()()1()()()()()()()()()()G s G s G s G s G s PP C s G s R s G s G s H s G s H s G s G s G s G s G s +∆+∆∴===∆++++（2分）二、（10分）解：开环传递函数2(1)()K as G s s+=（2分） 闭环传递函数222222()(1)21n n n KK s s K as s Kas K s s s ωφξωω===++++++（2分）已知%0.2eπξσ-==，3p t s ==所以，0.46ξ====（2分）K,a 分别为：21.4n K ω==， （2分）2 1.090.781.4n a K ξω=== （2分） 三、 (14分)解：(1)Ⅰ型系统在跟踪单位斜坡输入信号时，稳态误差为 1ss ve K =（2分） 而静态速度误差系数 0(0.51)lim ()()lim (1)(21)v s s K s K s G s H s s K s s s →→+=⋅=⋅=++ （2分）稳态误差为 11ss v e K K==。
2014自动控制原理年期终试卷(附解答)
2014年期终复习题第一章导论要点：控制的两大模式，反馈控制，控制系统结构。
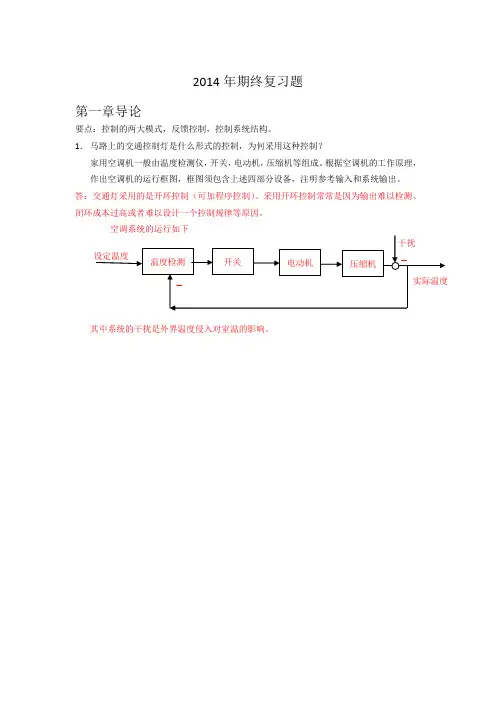
1．马路上的交通控制灯是什么形式的控制，为何采用这种控制？家用空调机一般由温度检测仪，开关，电动机，压缩机等组成。
根据空调机的工作原理，作出空调机的运行框图，框图须包含上述四部分设备，注明参考输入和系统输出。
答：交通灯采用的是开环控制（可加程序控制）。
采用开环控制常常是因为输出难以检测、闭环成本过高或者难以设计一个控制规律等原因。
其中系统的干扰是外界温度侵入对室温的影响。
第二章：控制系统的数学模型要点：三种模型，传递函数。
方框图化简，信号流图和Mason 公式。
2． 有一系统方框图如下，（1）作出系统的信号流图；（2）求出系统的特征式；（3）求C （s ）。
答：（1）（2）这里共有四个圈： e d f g C b e →→→→→→e df h b e →→→→→e d h b e →→→→h bh →→1233124214411G G G H G G G H G G G H ∆=+++-（3）12341312421441(1)(1)()(),()()G G G G H G G G G H G G G H C s C s R s N s -++-==∆∆可得C （s ）。
本题注意点是12∆∆，不是1。
）RCed第三章时域分析要点：性能指标，误差系数，Routh 判据，欠阻尼二阶系统的计算。
3． 有单位反馈控制系统，前向传递函数为 。
（1）如果要求M p <10%,求K 的取值范围；（2）取K 实现M p =10%,时的值，输入为 的稳态误差；（3）取K 同（2），求输入为sin 2t 的稳态误差。
答：10()( 2.5)KG s s s =+。
2 2.5n n ωζω=（1）0.1p M e ==，得0.59ζ=，要求M p <10%，就是0.59ζ>。
得到04490.K <<。
（2）取0.449K =，开环增益为1.796，系统为1型，所以 1.796v K =，位置误差为0，输入为()32tr t =-+时的稳态误差为0.278。
《自动控制原理》试题（卷）与答案解析（A26套）
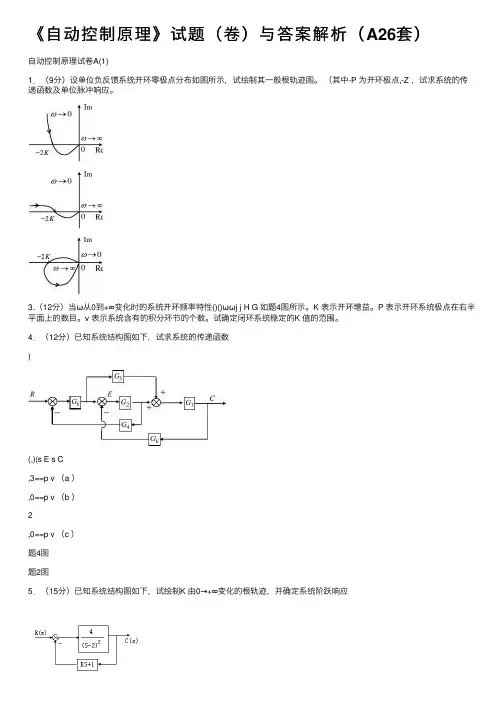
《⾃动控制原理》试题（卷）与答案解析（A26套）⾃动控制原理试卷A(1)1．（9分）设单位负反馈系统开环零极点分布如图所⽰，试绘制其⼀般根轨迹图。
（其中-P 为开环极点,-Z ，试求系统的传递函数及单位脉冲响应。
3.（12分）当ω从0到+∞变化时的系统开环频率特性()()ωωj j H G 如题4图所⽰。
K 表⽰开环增益。
P 表⽰开环系统极点在右半平⾯上的数⽬。
v 表⽰系统含有的积分环节的个数。
试确定闭环系统稳定的K 值的范围。
4．（12分）已知系统结构图如下，试求系统的传递函数)(,)(s E s C,3==p v （a ）,0==p v （b ）2,0==p v （c ）题4图题2图5．（15分）已知系统结构图如下，试绘制K 由0→+∞变化的根轨迹，并确定系统阶跃响应分别为衰减振荡、单调衰减时K 的取值范围。
6．（15分）某最⼩相位系统⽤串联校正，校正前后对数幅频特性渐近线分别如图中曲线(1)、(2)所⽰，试求校正前后和校正装置的传递函数)(),(),(21s G s G s G c ，并指出Gc （S ）是什么类型的校正。
7．（15分）离散系统如下图所⽰，试求当采样周期分别为T=0.1秒和T=0.5秒输⼊)(1)23()(t t t r ?+=时的稳态误差。
8．（12分）⾮线性系统线性部分的开环频率特性曲线与⾮线性元件负倒数描述曲线如下图所⽰，试判断系统稳定性，并指出)(1x N -和G （j ω）的交点是否为⾃振点。
参考答案A(1)1、根轨迹略，2、传递函数)9)(4(36)(++=s s s G ；单位脉冲响应)0(2.72.7)(94≥-=--t e3、 21,21,21><≠K K K 4、6425316324215313211)()(G G G G G G G G G G G G G G G G G G s R s C ++++= 642531632421653111)()(G G G G G G G G G G G G G G G G G s R s E +++-= 5、根轨迹略。
2014浙江大学自动控制原理考研真题与解析
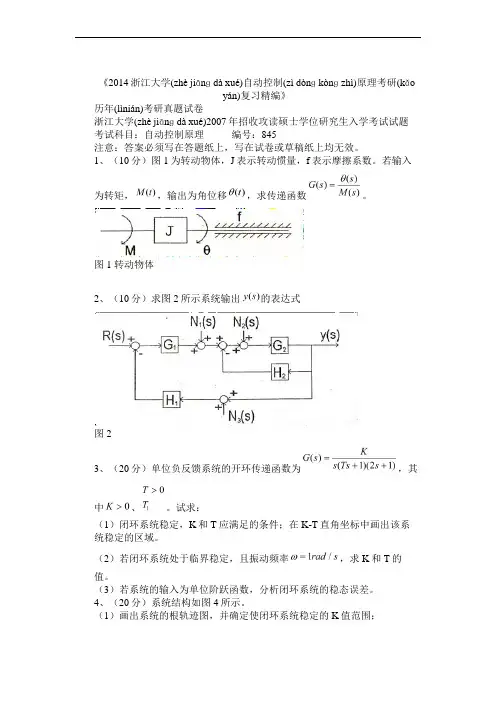
《2014浙江大学(zhè jiānɡ dà xué)自动控制(zì dònɡ kònɡ zhì)原理考研(kǎoyán)复习精编》历年(lìnián)考研真题试卷浙江大学(zhè jiānɡ dà xué)2007年招收攻读硕士学位研究生入学考试试题考试科目：自动控制原理编号：845注意：答案必须写在答题纸上，写在试卷或草稿纸上均无效。
1、（10分）图1为转动物体，J表示转动惯量，f表示摩擦系数。
若输入为转矩，，输出为角位移，求传递函数。
图1 转动物体2、（10分）求图2所示系统输出的表达式图23、（20分）单位负反馈系统的开环传递函数为，其中、。
试求：（1）闭环系统稳定，K和T应满足的条件；在K-T直角坐标中画出该系统稳定的区域。
（2）若闭环系统处于临界稳定，且振动频率，求K和T的值。
（3）若系统的输入为单位阶跃函数，分析闭环系统的稳态误差。
4、（20分）系统结构如图4所示。
（1）画出系统的根轨迹图，并确定使闭环系统稳定的K值范围；（2）若已知闭环系统的一个极点为，试确定闭环传递函数。
图45、（10分）系统(xìtǒng)动态方框图及开环对数频率特性见图5，求、、、的值。
图56、（10分）已知单位(dānwèi)负反馈系统开环频率特性的极坐标如图6所示，图示曲线(qūxiàn)的开环放大倍数K=500，右半s平面(píngmiàn)内的开环极点P=0，试求：（1）图示系统是否(shì fǒu)稳定，为什么？（2）确定使系统稳定的K值范围。
图67、（10分）是非题（若你认为正确，则在题号后打√，否则打×，每题1分）（1）经过状态反馈后的系统，其能控能观性均不发生改变。
（）（2）若一个可观的n维动态系统其输出矩阵的秩为m，则可设计m维的降维观测器。
浙江大学845自动控制原理考研真题试卷
紧急通知本资料由浙江大学控制科学与工程学院16届专业课129分学长，也就是我本人亲自整理编排而成。
大家可以叫我学长，年龄比我大的辞职考的可以叫我小弟。
资料不同于市面上那些看起来非常诱人实则是粗制烂造的资料，而是以一个考过845自控的过来人的经验，完全从学生的体验出发，做到资料最全，资料最好，资料最精致。
全套资料包括葵花宝典一到葵花宝典九共九本资料，每本资料都是我精心编辑整理的，并做了精美的封面，一共650页完美打印发给大家，大家把这650从头到尾肯透了，再做下我推荐的几本资料书（16年有一道15分的大题就是上面的类似题，第三问很多高手都没做出来，注意不是周春晖那本哈），可以说完全没问题了。
这是其它卖家不可能做到的。
同时赠送845自控全套电子资料。
葵花宝典一完全由我本人原创，里面包含了考浙大845自动控制原理的全部问题，比如考多少分比较保险，怎么复习，有哪些好的资料书，最近几年考题变化及应对策略，浙大常考题型，招生名额，复试资料，导师联系，公共课复习用书及方法以及845近年命题风格分析等一系列问题，全是我的心得和经验，方法，技巧等，说句心里话，我自己都觉得这些资料非常宝贵，能帮助学弟学妹们少走很多弯路。
注意：前面是一些关于我的故事，有些地方可能对你有用，如果不感兴趣，可以直接拉到后面去看，资料清单和图片都在后面。
学长自我介绍学长姓邓，名某某，男，本科于14年毕业于四川大学电气信息学院自动化专业，考浙大控制考了3次，14年大三时第一次考浙大控制总分没过线。
当时我们学校有三个同学征战浙大控制科学与工程，结果全军覆没，只有我一人过了300分，由此可见考浙大控制还是很有难度的，其中一个难点就是专业课的信息和专业课的命题走向的获取，当时我们都不是很清楚，蒙着头自己学，去图书馆借了很多自动控制原理的资料书来看，我自我感觉学得还不错，当时我一个同学考电子科大的自动化，经常跑来问我自控的问题，我基本都能给他解答出来，他说我好牛逼，觉对没有问题，然而最后的结果是他考电子科大自动控制原理137，而我只考了96分。
自动控制原理 复习题及答案.概要
自动控制原理1一、 单项选择题（每小题1分，共20分）1. 系统和输入已知，求输出并对动态特性进行研究，称为（ ）A.系统综合B.系统辨识C.系统分析D.系统设计2. 惯性环节和积分环节的频率特性在（ ）上相等。
A.幅频特性的斜率B.最小幅值C.相位变化率D.穿越频率3. 通过测量输出量，产生一个与输出信号存在确定函数比例关系值的元件称为（ ）A.比较元件B.给定元件C.反馈元件D.放大元件4. ω从0变化到+∞时，延迟环节频率特性极坐标图为（ ）A.圆B.半圆C.椭圆D.双曲线5. 当忽略电动机的电枢电感后，以电动机的转速为输出变量，电枢电压为输入变量时，电动机可看作一个（ ）A.比例环节B.微分环节C.积分环节D.惯性环节6. 若系统的开环传 递函数为2)(5 10+s s ，则它的开环增益为（ ） A.1 B.2 C.5 D.107. 二阶系统的传递函数52 5)(2++=s s s G ，则该系统是（ ） A.临界阻尼系统 B.欠阻尼系统 C.过阻尼系统 D.零阻尼系统8. 若保持二阶系统的ζ不变，提高ωn ，则可以（ ）A.提高上升时间和峰值时间B.减少上升时间和峰值时间C.提高上升时间和调整时间D.减少上升时间和超调量9. 一阶微分环节Ts s G +=1)(，当频率T1=ω时，则相频特性)(ωj G ∠为（ ） A.45° B.-45° C.90° D.-90°10.最小相位系统的开环增益越大，其（ ）A.振荡次数越多B.稳定裕量越大C.相位变化越小D.稳态误差越小11.设系统的特征方程为()0516178234=++++=s s s s s D ，则此系统 （ ）A.稳定B.临界稳定C.不稳定D.稳定性不确定。
12.某单位反馈系统的开环传递函数为：())5)(1(++=s s s k s G ，当k =（ ）时，闭环系统临界稳定。
A.10B.20C.30D.4013.设系统的特征方程为()025103234=++++=s s s s s D ，则此系统中包含正实部特征的个数有（ ）A.0B.1C.2D.314.单位反馈系统开环传递函数为()s s s s G ++=652，当输入为单位阶跃时，则其位置误差为（ ）A.2B.0.2C.0.5D.0.0515.若已知某串联校正装置的传递函数为1101)(++=s s s G c ，则它是一种（ ） A.反馈校正 B.相位超前校正C.相位滞后—超前校正D.相位滞后校正16.稳态误差e ss 与误差信号E (s )的函数关系为（ ）A.)(lim 0s E e s ss →=B.)(lim 0s sE e s ss →= C.)(lim s E e s ss ∞→= D.)(lim s sE e s ss ∞→= 17.在对控制系统稳态精度无明确要求时，为提高系统的稳定性，最方便的是（ ）A.减小增益B.超前校正C.滞后校正D.滞后-超前18.相位超前校正装置的奈氏曲线为（）A.圆B.上半圆C.下半圆D.45°弧线K,则实轴上的根轨迹为（）19.开环传递函数为G(s)H(s)=ss)3(3A.(-3，∞)B.(0，∞)C.(-∞，-3)D.(-3，0)20.在直流电动机调速系统中，霍尔传感器是用作（）反馈的传感器。
考研自动控制原理习题集及其解答
自动控制原理习题及其解答第一章（略） 第二章例2-1 弹簧，阻尼器串并联系统如图2-1示，系统为无质量模型，试建立系统的运动方程。
解：(1) 设输入为y r ，输出为y 0。
弹簧与阻尼器并联平行移动。
(2) 列写原始方程式，由于无质量按受力平衡方程，各处任何时刻，均满足∑=0F ，则对于A 点有021=-+K K f F F F其中，F f 为阻尼摩擦力，F K 1，F K 2为弹性恢复力。
(3) 写中间变量关系式220110)()(y K F Y Y K F dty y d f F K r K r f =-=-⋅=(4) 消中间变量得 020110y K y K y K dtdy f dt dy f r r=-+- (5) 化标准形 r r Ky dtdyT y dt dy T +=+00 其中:215K K T +=为时间常数，单位[秒]。
211K K K K +=为传递函数，无量纲。
例2-2 已知单摆系统的运动如图2-2示。
(1) 写出运动方程式 (2) 求取线性化方程 解：（1）设输入外作用力为零，输出为摆角θ ，摆球质量为m 。
（2）由牛顿定律写原始方程。
h mg dtd l m --=θθsin )(22其中，l 为摆长，l θ 为运动弧长，h 为空气阻力。
（3）写中间变量关系式)(dtd lh θα= 式中，α为空气阻力系数dtd l θ为运动线速度。
（4）消中间变量得运动方程式0s i n 22=++θθθmg dt d al dtd ml （2-1)此方程为二阶非线性齐次方程。
（5）线性化由前可知，在θ ＝0的附近，非线性函数sin θ ≈θ ，故代入式（2-1）可得线性化方程为022=++θθθmg dt d al dtd ml 例2-3 已知机械旋转系统如图2-3所示，试列出系统运动方程。
解：（1）设输入量作用力矩M f ，输出为旋转角速度ω 。
（2）列写运动方程式f M f dtd J+-=ωω式中， f ω为阻尼力矩，其大小与转速成正比。
2014年浙江大学845自动控制原理考研试题(回忆版)
2014年浙江大学845自动控制原理考研试题（回忆版）
一、上面一个零点z，下面一个极点p和两对共轭极点，求根轨迹的出射角。
这题就给了一个共轭极点的阻尼比在-1到0，其他什么都没给。
3对关系要讨论起来我估计得8种吧，我就写了两种。
二、一个A阵为5x5的矩阵是个能控标准型，还有B阵和C阵，第一问是问方程有几个极点在右半轴。
第二问是能控能观的判别吧。
三、求一个二型系统的相角裕度最大值时K的值，
四、一个单回路负反馈系统，前向通道是（s+5）(s+10)(s+2)，数字可能错了，但类型没问题，反馈通道是0.5s+1，给了个阻尼比，求下K的值，然后求一个稳态输出吧，是一个正弦波。
五、一个Z变换，第一问求脉冲传函，瞎写的。
第二问求啥输出Z变换。
六、一个双输入的状态空间方程，题出的有问题，如果基础还行，很简单，但题目没给X2，自己随便标了个但还是不能试用，就随便写了个。
七、说一个RC控制系统的作用只有80%，输出和测量总是相等，
八、好像是一个双变量的传函，上面一个a，下面一个k吧，第一问问k和a什么情况下保持系统稳定，随便列了下劳斯判据，没底。
第二问画根轨迹，目测是根轨迹簇，
九、给了三个式子，拉普拉斯变换后求下C(t)对R（t）的稳态误差小于一个值，输入是一个阶跃和斜坡输入，常规题吧算K1的范围，算出来好像是1-
K1K2T1<E
十、考伯德图里有俩二阶衰减振荡环节的，这题20分
十一、第一问求传函，第二问状态反馈，第三问列了下式子求状态观测器极点都配置到-2r，第四问给了超调量和tp的限制，然后列了下求了阻尼比和wn，第五问是问要是观测器反应速度比反馈的快3倍吧。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
《2014浙江大学自动控制原理考研复习精编》
历年考研真题试卷
浙江大学2007年招收攻读硕士学位研究生入学考试试题 考试科目：自动控制原理 编号：845
注意：答案必须写在答题纸上，写在试卷或草稿纸上均无效。
1、（10分）图1为转动物体，J 表示转动惯量，f 表示摩擦系数。
若输入为转矩，()M t ，
输出为角位移()t θ，求传递函数
()
()()s G s M s θ=。
图1 转动物体
2、（10分）求图2所示系统输出()y s 的表达式
图2
3、（20分）单位负反馈系统的开环传递函数为
()(1)(21)K
G s s Ts s =
++，其中0K >、
1
0T T >。
试求：
（1）闭环系统稳定，K 和T 应满足的条件；在K-T 直角坐标中画出该系统稳定的区域。
（2）若闭环系统处于临界稳定，且振动频率1/rad s ω=，求K 和T 的值。
（3）若系统的输入为单位阶跃函数，分析闭环系统的稳态误差。
4、（20分）系统结构如图4所示。
（1）画出系统的根轨迹图，并确定使闭环系统稳定的K 值范围；
（2）若已知闭环系统的一个极点为
11s =-，试确定闭环传递函数。
图4
5、（10分）系统动态方框图及开环对数频率特性见图5，求
1K 、2K 、1T 、2T 的值。
图5
6、（10分）已知单位负反馈系统开环频率特性的极坐标如图6所示，图示曲线的开环放大倍数K=500，右半s 平面内的开环极点P=0，试求： （1）图示系统是否稳定，为什么？ （2）确定使系统稳定的K 值范围。
图6
7、（10分）是非题（若你认为正确，则在题号后打√，否则打×，每题1分）
（1）经过状态反馈后的系统，其能控能观性均不发生改变。
（ ） （2）若一个可观的n 维动态系统其输出矩阵的秩为m ，则可设计m 维的降维观测器。
（ ）
（3）由已知系统的传递函数转化为状态方程，其形式唯一。
（ ）
（4）一个能控能观的连续系统离散化后仍然保持其能控与能观性。
（ ） （5）非线性系统的稳定性概念是全局性的，与系统的初始条件和外部输入无关。
（ ） （6）若系统完全能控能观，则可以设计该系统的状态反馈控制器与状态观测器，但须注
意
的
是
其
设
计
结
果
将
相
互
影
响。
（ ）
（7）描述函数法是线性系统频率法的推广，但它只考虑了主导极点的频率响应。
（ ） （8）对一个n 维的能控能观线性SISO 系统，其状态方程与传递函数描述是等价的。
（ ） （9）系统S1能控的充要条件是其对偶系统S2能观。
（ ） （10）经过非奇异线性变换的线性定常系统不改变其状态的能控性。
（ ） 8、（10分）如图8所示离散系统，T=1，问：系统
s T 取在什么范围，系统是稳定的。
图8
9、（15分）如图9所示电路，当12312,,1/3R R R C C RC ====且。
设在0t t =时，
开关合上，
1020()()x t x t =，状态变量为电容器上的电压。
（1）写出电路的状态空间模型；
（2）求出状态转移矩阵；画出状态变量图； （3）并分析系统的可控性和可观性。
图9
10、（15分）系统的状态空间表达式为：
[]00111
03101
3001
2x u y x
X ∙
-⎡⎤⎡⎤
⎢⎥⎢⎥=-+⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦
=
试判断系统的可控性；若不完全可控，则分解出可控、不可控子空间；讨论能否用状态
反馈*u v K x =+使闭环系统稳定。
11、（20分）如图11所示的被控对象，欲用状态反馈控制满足下列需求： （1）在阶跃作用下没有稳态误差； （2）闭环系统的主导极点为23j -±； （3）对所有的A>0，系统都是稳定的。
图11 要求：
（a ）画出带状态反馈阵K 的方框图；
（b ）将画出的方框图化简为如图A 所示的单回路，分别求出图中的前向通道传递函数与反向通道传递函数G(s)与
()
eq H s ；
（c ）求出所需的反馈系数阵；
（d ）若将图A 转化为如图B 所示的单位负反馈，求出图B 中的()
eq G s 以及系统的静态
误差系数；
（e ）假如输入为单位阶跃，确定该系统的超调量σ和调节时间s t。